| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 2 (Before Exercise 11.1) | Exercise 11.1 | |
Chapter 11 Areas Related To Circles
Welcome to the solutions guide for Chapter 11, "Areas Related to Circles," from the latest Class 10 NCERT mathematics textbook prescribed for the academic session 2024-25. This chapter delves into the fascinating geometry of circles beyond their overall circumference and area, focusing on calculating the measurements of specific portions like sectors and segments, and applying these concepts to find areas of composite figures involving circles or parts of circles. Mastering these calculations requires a solid understanding of basic circle formulas and the ability to apply them in multi-step problems. These solutions provide comprehensive, step-by-step guidance for all exercises within the current syllabus, emphasizing clarity in formulas and accuracy in computation.
The chapter begins by reinforcing the fundamental formulas for a circle with radius $r$:
- Circumference: $C = 2\pi r$
- Area: $A = \pi r^2$
- A Sector is the region enclosed by two radii and the corresponding arc between them. It resembles a slice of pizza.
- A Segment is the region enclosed by a chord and the corresponding arc.
- Length of an Arc of a Sector: $L = \left( \frac{\theta}{360^\circ} \right) \times 2\pi r$
- Area of a Sector: $A_{\text{sector}} = \left( \frac{\theta}{360^\circ} \right) \times \pi r^2$
- Area of a Segment: This is typically calculated by subtracting the area of the triangle formed by the two radii and the chord from the area of the corresponding sector: $A_{\text{segment}} = A_{\text{sector}} - A_{\triangle}$.
A significant focus of this chapter is calculating the areas of combined plane figures. These problems often present complex designs or shapes formed by combining circles, semicircles, quadrants, sectors, segments with other geometric figures like squares, rectangles, and triangles. The solutions meticulously guide students through the process of:
- Carefully analyzing the composite figure.
- Breaking down the shaded or required region into simpler, recognizable geometric shapes whose areas can be calculated using known formulas (including sector and segment formulas).
- Calculating the areas of these individual component parts.
- Adding or subtracting these areas appropriately to find the final area of the desired region.
Regarding the rationalized syllabus for 2024-25, Chapter 11, "Areas Related to Circles" (formerly Chapter 12), has been streamlined. Notably, exercises involving problems based on the central angle of $120^\circ$ and complex combinations of figures requiring intricate calculations or multi-step logic might have been removed or simplified. The core focus remains on calculating the area of sectors and segments (primarily with angles like $60^\circ, 90^\circ$) and finding areas of simpler composite figures involving circles, squares, rectangles, and triangles. By diligently working through these focused solutions, students can master the formulas for sectors and segments, develop effective strategies for tackling problems involving areas of combined shapes, and significantly improve their computational accuracy in mensuration related to circles.
Example 1 to 2 (Before Exercise 11.1)
Example 1. Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14).
Answer:
Given:
Radius of the circle, $r = 4 \text{ cm}$
Angle of the minor sector, $\theta = 30^\circ$
Value of $\pi = 3.14$
To Find:
1. Area of the minor sector.
2. Area of the corresponding major sector.
Solution:
The formula for the area of a sector with angle $\theta$ (in degrees) and radius $r$ is given by:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
Area of the minor sector:
Using the given values, $\theta = 30^\circ$, $r = 4 \text{ cm}$, and $\pi = 3.14$, we get:
Area of minor sector $= \frac{30^\circ}{360^\circ} \times 3.14 \times (4 \text{ cm})^2$
$= \frac{\cancel{30}^{1}}{\cancel{360}_{12}} \times 3.14 \times 16 \text{ cm}^2$
$= \frac{1}{12} \times 3.14 \times 16 \text{ cm}^2$
$= \frac{16 \times 3.14}{12} \text{ cm}^2$
$= \frac{4 \times 3.14}{3} \text{ cm}^2$
$= \frac{12.56}{3} \text{ cm}^2$
Area of minor sector $\approx 4.1867 \text{ cm}^2$
Rounding to two decimal places, Area of minor sector $\approx 4.19 \text{ cm}^2$.
Area of the corresponding major sector:
The angle of the major sector is $360^\circ - \theta = 360^\circ - 30^\circ = 330^\circ$.
The area of the major sector can be calculated by subtracting the area of the minor sector from the total area of the circle.
Area of circle $= \pi r^2 = 3.14 \times (4 \text{ cm})^2 = 3.14 \times 16 \text{ cm}^2$
Area of circle $= 50.24 \text{ cm}^2$
Area of major sector $= \text{Area of circle} - \text{Area of minor sector}$
$= 50.24 \text{ cm}^2 - \frac{12.56}{3} \text{ cm}^2$
$= 50.24 \text{ cm}^2 - 4.1867 \text{ cm}^2$ (using the more precise value)
Area of major sector $\approx 46.0533 \text{ cm}^2$
Rounding to two decimal places, Area of major sector $\approx 46.05 \text{ cm}^2$.
Answer:
The area of the minor sector is approximately $4.19 \text{ cm}^2$.
The area of the corresponding major sector is approximately $46.05 \text{ cm}^2$.
Example 2. Find the area of the segment AYB shown in Fig. 11.6, if radius of the circle is 21 cm and ∠AOB = 120°. (Use π = $\frac{22}{7}$ )
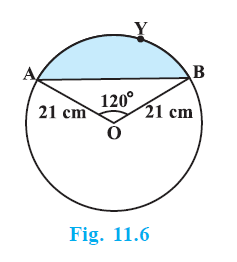
Answer:
Given:
Radius of the circle, $r = 21 \text{ cm}$
Angle of the sector, $\theta = 120^\circ$
Value of $\pi = \frac{22}{7}$
To Find:
Area of the segment AYB.
Solution:
The area of the segment AYB is the difference between the area of the sector OAYB and the area of the triangle OAB.
Area of Sector OAYB:
The formula for the area of a sector with angle $\theta$ and radius $r$ is $\frac{\theta}{360^\circ} \times \pi r^2$.
Area of Sector OAYB $= \frac{120^\circ}{360^\circ} \times \frac{22}{7} \times (21 \text{ cm})^2$
$= \frac{\cancel{120}^{1}}{\cancel{360}_{3}} \times \frac{22}{7} \times 21 \times 21 \text{ cm}^2$
$= \frac{1}{3} \times \frac{22}{\cancel{7}^{1}} \times \cancel{21}^{3} \times 21 \text{ cm}^2$
$= \frac{1}{\cancel{3}^{1}} \times 22 \times \cancel{3}^{1} \times 21 \text{ cm}^2$
$= 22 \times 21 \text{ cm}^2$
Area of Sector OAYB $= 462 \text{ cm}^2$
Area of Triangle OAB:
In $\triangle OAB$, OA = OB = $r = 21 \text{ cm}$ and $\angle AOB = 120^\circ$.
The formula for the area of a triangle with two sides and the included angle is $\frac{1}{2}ab \sin C$. Here, this is $\frac{1}{2} OA \times OB \sin (\angle AOB)$.
Area of $\triangle OAB = \frac{1}{2} \times 21 \text{ cm} \times 21 \text{ cm} \times \sin 120^\circ$
We know that $\sin 120^\circ = \sin (180^\circ - 60^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$.
Area of $\triangle OAB = \frac{1}{2} \times 21 \times 21 \times \frac{\sqrt{3}}{2} \text{ cm}^2$
$= \frac{441}{4}\sqrt{3} \text{ cm}^2$
Using $\sqrt{3} \approx 1.732$ (often used in such problems, though not explicitly given to use in this specific problem, it's standard for $\sin 120^\circ$ calculation unless another value is specified).
Area of $\triangle OAB = \frac{441}{4} \times 1.732 \text{ cm}^2$
$= 110.25 \times 1.732 \text{ cm}^2$
$= 190.953 \text{ cm}^2$
Area of Segment AYB:
Area of Segment AYB = Area of Sector OAYB - Area of $\triangle OAB$
$= 462 \text{ cm}^2 - 190.953 \text{ cm}^2$
$= 271.047 \text{ cm}^2$
Rounding to two decimal places, Area of Segment AYB $\approx 271.05 \text{ cm}^2$.
Answer:
The area of the segment AYB is approximately $271.05 \text{ cm}^2$.
Exercise 11.1
Unless stated otherwise, use π = $\frac{22}{7}$
Question 1. Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Answer:
Given:
Radius of the circle, $r = 6 \text{ cm}$
Angle of the sector, $\theta = 60^\circ$
Value of $\pi = \frac{22}{7}$
To Find:
Area of the sector.
Solution:
The formula for the area of a sector with angle $\theta$ (in degrees) and radius $r$ is given by:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the given values, we have:
Area of sector $= \frac{60^\circ}{360^\circ} \times \frac{22}{7} \times (6 \text{ cm})^2$
$= \frac{\cancel{60}^{1}}{\cancel{360}_{6}} \times \frac{22}{7} \times 36 \text{ cm}^2$
$= \frac{1}{6} \times \frac{22}{7} \times 36 \text{ cm}^2$
$= \frac{1}{\cancel{6}^{1}} \times \frac{22}{7} \times \cancel{36}^{6} \text{ cm}^2$
$= \frac{22 \times 6}{7} \text{ cm}^2$
$= \frac{132}{7} \text{ cm}^2$
Answer:
The area of the sector is $\frac{132}{7} \text{ cm}^2$.
Question 2. Find the area of a quadrant of a circle whose circumference is 22 cm.
Answer:
This problem requires us to find the area of a specific part of a circle called a quadrant, given the circle's circumference.
Given:
Circumference of the circle, $C = 22 \text{ cm}$
Value of $\pi = \frac{22}{7}$
To Find:
Area of a quadrant of the circle.
Solution:
A quadrant of a circle is equivalent to one-fourth of the circle's area. To find the area, we first need to determine the radius ($r$) of the circle using the given circumference.
The formula for the circumference of a circle is $C = 2\pi r$.
Substituting the given value of C and $\pi$ into the formula:
$22 \text{ cm} = 2 \times \frac{22}{7} \times r$
Now, we solve for the radius $r$. We can isolate $r$ by dividing both sides of the equation by $2 \times \frac{22}{7}$:
$r = \frac{22 \text{ cm}}{2 \times \frac{22}{7}}$
$r = \frac{22}{1} \times \frac{7}{2 \times 22} \text{ cm}$
$r = \frac{\cancel{22}^{1} \times 7}{2 \times \cancel{22}^{1}} \text{ cm}$
$r = \frac{7}{2} \text{ cm}$
The radius of the circle is $r = \frac{7}{2} \text{ cm}$ or $3.5 \text{ cm}$.
... (i)
A quadrant of a circle is a sector with a central angle of $90^\circ$. The area of a sector with angle $\theta$ and radius $r$ is given by the formula $\frac{\theta}{360^\circ} \times \pi r^2$.
For a quadrant, the angle $\theta = 90^\circ$.
Area of quadrant $= \frac{90^\circ}{360^\circ} \times \pi r^2$
Area of quadrant $= \frac{\cancel{90}^{1}}{\cancel{360}_{4}} \times \pi r^2$
Area of quadrant $= \frac{1}{4} \times \pi r^2$
Now, substitute the value of $\pi = \frac{22}{7}$ and the radius $r = \frac{7}{2} \text{ cm}$ from (i):
Area of quadrant $= \frac{1}{4} \times \frac{22}{7} \times (\frac{7}{2} \text{ cm})^2$
$= \frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \text{ cm}^2$
$= \frac{1 \times 22 \times 7 \times 7}{4 \times 7 \times 2 \times 2} \text{ cm}^2$
Cancel one 7 from the numerator and denominator:
$= \frac{1 \times 22 \times \cancel{7}^{1} \times 7}{4 \times \cancel{7}^{1} \times 2 \times 2} \text{ cm}^2$
$= \frac{22 \times 7}{4 \times 2 \times 2} \text{ cm}^2$
$= \frac{154}{16} \text{ cm}^2$
Simplify the fraction by dividing the numerator and denominator by 2:
$= \frac{\cancel{154}^{77}}{\cancel{16}^{8}} \text{ cm}^2$
$= \frac{77}{8} \text{ cm}^2$
We can also express the answer as a decimal:
$\frac{77}{8} = 9.625$
So, Area of quadrant $= 9.625 \text{ cm}^2$.
Answer:
The area of a quadrant of the circle is $\frac{77}{8} \text{ cm}^2$ or $9.625 \text{ cm}^2$.
Question 3. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Answer:
This problem asks for the area covered by the minute hand of a clock as it moves for a specific duration. The area swept by the minute hand forms a sector of a circle.
Given:
Length of the minute hand (which is the radius of the circle traced by its tip), $r = 14 \text{ cm}$
Time duration, $t = 5 \text{ minutes}$
Value of $\pi = \frac{22}{7}$ (as is standard unless specified otherwise)
To Find:
The area swept by the minute hand in 5 minutes.
Solution:
The minute hand of a clock completes one full rotation ($360^\circ$) in 60 minutes.
First, we need to find the angle covered by the minute hand in 1 minute.
Angle swept in 60 minutes $= 360^\circ$
Angle swept in 1 minute $= \frac{360^\circ}{60} = 6^\circ$
Now, we find the angle swept in the given time of 5 minutes.
Angle swept in 5 minutes $= 5 \times (\text{Angle swept in 1 minute})$
Angle $\theta = 5 \times 6^\circ = 30^\circ$
The area swept by the minute hand in 5 minutes is the area of a sector of the circle formed by the minute hand's movement. The radius of this sector is the length of the minute hand, $r = 14 \text{ cm}$, and the central angle is $\theta = 30^\circ$.
The formula for the area of a sector with angle $\theta$ (in degrees) and radius $r$ is given by:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the values we have:
Area swept $= \frac{30^\circ}{360^\circ} \times \frac{22}{7} \times (14 \text{ cm})^2$
$= \frac{\cancel{30}^{1}}{\cancel{360}_{12}} \times \frac{22}{7} \times 14 \times 14 \text{ cm}^2$
$= \frac{1}{12} \times \frac{22}{\cancel{7}^{1}} \times \cancel{14}^{2} \times 14 \text{ cm}^2$
$= \frac{1}{12} \times 22 \times 2 \times 14 \text{ cm}^2$
Now, we simplify the expression:
$= \frac{22 \times 2 \times 14}{12} \text{ cm}^2$
Cancel common factors. We can divide 2 and 12 by 2:
$= \frac{22 \times \cancel{2}^{1} \times 14}{\cancel{12}^{6}} \text{ cm}^2$
$= \frac{22 \times 14}{6} \text{ cm}^2$
Now, divide 22 and 6 by 2:
$= \frac{\cancel{22}^{11} \times 14}{\cancel{6}^{3}} \text{ cm}^2$
$= \frac{11 \times 14}{3} \text{ cm}^2$
Multiply the numbers in the numerator:
$11 \times 14 = 154$
So, Area swept $= \frac{154}{3} \text{ cm}^2$
Answer:
The area swept by the minute hand in 5 minutes is $\frac{154}{3} \text{ cm}^2$.
Question 4. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
(i) minor segment
(ii) major sector. (Use π = 3.14)
Answer:
This question asks for the area of a minor segment and a major sector of a circle, given the radius and the angle subtended by a chord at the centre. This problem involves formulas typically taught in Class 10.
Given:
Radius of the circle, $r = 10 \text{ cm}$
Angle subtended by the chord at the centre, $\theta = 90^\circ$
Value of $\pi = 3.14$
To Find:
(i) Area of the corresponding minor segment.
(ii) Area of the corresponding major sector.
Solution:
Let O be the centre of the circle and AB be the chord subtending an angle of $90^\circ$ at the centre. The sector formed by the radii OA and OB and the arc AYB is the minor sector OAYB. The segment AYB is the minor segment.
(i) Area of the corresponding minor segment:
The area of the minor segment is the area of the minor sector OAYB minus the area of the triangle OAB formed by the radii OA, OB and the chord AB.
Area of minor sector OAYB $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the given values:
Area of minor sector OAYB $= \frac{90^\circ}{360^\circ} \times 3.14 \times (10)^2 \text{ cm}^2$
$= \frac{\cancel{90}^{1}}{\cancel{360}_{4}} \times 3.14 \times 100 \text{ cm}^2$
$= \frac{1}{4} \times 314 \text{ cm}^2$
$= \frac{314}{4} \text{ cm}^2$
$= 78.5 \text{ cm}^2$
Since the angle subtended at the centre is $90^\circ$, the triangle OAB is a right-angled triangle with OA and OB as the perpendicular sides (both equal to the radius $r$).
Area of triangle OAB $= \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times OA \times OB$
$= \frac{1}{2} \times r \times r = \frac{1}{2} r^2$
Substituting the radius value:
Area of $\triangle OAB = \frac{1}{2} \times (10 \text{ cm})^2$
$= \frac{1}{2} \times 100 \text{ cm}^2$
$= 50 \text{ cm}^2$
Now, calculate the area of the minor segment:
Area of minor segment = Area of minor sector OAYB - Area of $\triangle OAB$
$= 78.5 \text{ cm}^2 - 50 \text{ cm}^2$
$= 28.5 \text{ cm}^2$
(ii) Area of the corresponding major sector:
The major sector corresponds to the reflex angle subtended at the centre by the major arc. The total angle around the centre is $360^\circ$.
Angle of major sector $= 360^\circ - \text{Angle of minor sector}$
Angle of major sector $= 360^\circ - 90^\circ = 270^\circ$
The area of the major sector can be calculated using the sector area formula with this angle:
Area of major sector $= \frac{\text{Angle of major sector}}{360^\circ} \times \pi r^2$
Substituting the values:
Area of major sector $= \frac{270^\circ}{360^\circ} \times 3.14 \times (10)^2 \text{ cm}^2$
$= \frac{\cancel{270}^{3}}{\cancel{360}_{4}} \times 3.14 \times 100 \text{ cm}^2$
$= \frac{3}{4} \times 314 \text{ cm}^2$
$= \frac{3 \times 314}{4} \text{ cm}^2$
$= \frac{942}{4} \text{ cm}^2$
$= 235.5 \text{ cm}^2$
Alternate method for Area of major sector:
The area of the major sector is also equal to the Area of the whole circle minus the Area of the minor sector.
Area of circle $= \pi r^2 = 3.14 \times (10 \text{ cm})^2 = 3.14 \times 100 \text{ cm}^2 = 314 \text{ cm}^2$
Area of major sector $= \text{Area of circle} - \text{Area of minor sector}$
$= 314 \text{ cm}^2 - 78.5 \text{ cm}^2$ (Using the calculated minor sector area)
$= 235.5 \text{ cm}^2$
Answer:
(i) The area of the corresponding minor segment is $28.5 \text{ cm}^2$.
(ii) The area of the corresponding major sector is $235.5 \text{ cm}^2$.
Question 5. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc
(iii) area of the segment formed by the corresponding chord
Answer:
This question involves calculating the length of an arc, the area of a sector, and the area of a segment, given the radius and the central angle. These are standard formulas in geometry.
Given:
Radius of the circle, $r = 21 \text{ cm}$
Angle subtended by the arc at the centre, $\theta = 60^\circ$
Value of $\pi = \frac{22}{7}$
To Find:
(i) The length of the arc.
(ii) Area of the sector formed by the arc.
(iii) Area of the segment formed by the corresponding chord.
Solution:
(i) The length of the arc:
The formula for the length of an arc with angle $\theta$ (in degrees) and radius $r$ is:
Length of arc $= \frac{\theta}{360^\circ} \times 2\pi r$
Substituting the given values, we get:
Length of arc $= \frac{60^\circ}{360^\circ} \times 2 \times \frac{22}{7} \times 21 \text{ cm}$
$= \frac{\cancel{60}^{1}}{\cancel{360}_{6}} \times 2 \times \frac{22}{\cancel{7}^{1}} \times \cancel{21}^{3} \text{ cm}$
$= \frac{1}{6} \times 2 \times 22 \times 3 \text{ cm}$
$= \frac{1}{\cancel{6}^{1}} \times \cancel{2}^{1} \times 22 \times \cancel{3}^{1} \text{ cm}$ (Cancelling 2 and 3 with 6)
$= 1 \times 1 \times 22 \times 1 \text{ cm}$
$= 22 \text{ cm}$
(ii) Area of the sector formed by the arc:
The formula for the area of a sector with angle $\theta$ and radius $r$ is:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the values, we get:
Area of sector $= \frac{60^\circ}{360^\circ} \times \frac{22}{7} \times (21 \text{ cm})^2$
$= \frac{\cancel{60}^{1}}{\cancel{360}_{6}} \times \frac{22}{7} \times 21 \times 21 \text{ cm}^2$
$= \frac{1}{6} \times \frac{22}{\cancel{7}^{1}} \times \cancel{21}^{3} \times 21 \text{ cm}^2$
$= \frac{1}{\cancel{6}^{2}} \times 22 \times \cancel{3}^{1} \times 21 \text{ cm}^2$
$= \frac{22 \times 21}{2} \text{ cm}^2$
$= \cancel{11}^{11} \times 21 \text{ cm}^2$ (Cancelling 22 with 2)
$= 11 \times 21 \text{ cm}^2$
$= 231 \text{ cm}^2$
(iii) Area of the segment formed by the corresponding chord:
The area of the segment is the area of the sector minus the area of the triangle formed by the radii and the chord.
Let the chord be AB and the centre be O. In $\triangle OAB$, OA = OB = $r = 21 \text{ cm}$ and $\angle AOB = 60^\circ$.
Since OA = OB, $\triangle OAB$ is an isosceles triangle. The base angles are equal: $\angle OAB = \angle OBA = \frac{180^\circ - 60^\circ}{2} = \frac{120^\circ}{2} = 60^\circ$.
Since all three angles are $60^\circ$, $\triangle OAB$ is an equilateral triangle with side length equal to the radius, i.e., side $= r = 21 \text{ cm}$.
Area of equilateral $\triangle OAB = \frac{\sqrt{3}}{4} \times (\text{side})^2 = \frac{\sqrt{3}}{4} \times r^2$
$= \frac{\sqrt{3}}{4} \times (21 \text{ cm})^2$
$= \frac{\sqrt{3}}{4} \times 441 \text{ cm}^2$
$= \frac{441\sqrt{3}}{4} \text{ cm}^2$
Area of segment = Area of sector - Area of $\triangle OAB$
$= 231 \text{ cm}^2 - \frac{441\sqrt{3}}{4} \text{ cm}^2$
$= (231 - \frac{441\sqrt{3}}{4}) \text{ cm}^2$
Answer:
(i) The length of the arc is $22 \text{ cm}$.
(ii) The area of the sector formed by the arc is $231 \text{ cm}^2$.
(iii) The area of the segment formed by the corresponding chord is $(231 - \frac{441\sqrt{3}}{4}) \text{ cm}^2$.
Question 6. A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and $\sqrt{3}$ = 1.73)
Answer:
This problem involves finding the areas of both the minor and major segments of a circle, given the radius, the central angle, and specific values for $\pi$ and $\sqrt{3}$.
Given:
Radius of the circle, $r = 15 \text{ cm}$
Angle subtended by the chord at the centre, $\theta = 60^\circ$
Value of $\pi = 3.14$
Value of $\sqrt{3} = 1.73$
To Find:
1. Area of the corresponding minor segment.
2. Area of the corresponding major segment.
Solution:
Let the chord be AB and the centre be O. The area of the minor segment is the area of the minor sector minus the area of the triangle formed by the radii and the chord.
1. Area of the corresponding minor segment:
Area of minor sector $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the given values:
Area of minor sector $= \frac{60^\circ}{360^\circ} \times 3.14 \times (15 \text{ cm})^2$
$= \frac{\cancel{60}^{1}}{\cancel{360}_{6}} \times 3.14 \times 225 \text{ cm}^2$
$= \frac{1}{6} \times 3.14 \times 225 \text{ cm}^2$
$= \frac{706.5}{6} \text{ cm}^2$
Area of minor sector $= 117.75 \text{ cm}^2$
In $\triangle OAB$, OA = OB = $r = 15 \text{ cm}$ and $\angle AOB = 60^\circ$.
Since OA = OB, $\triangle OAB$ is an isosceles triangle. The base angles are equal: $\angle OAB = \angle OBA = \frac{180^\circ - 60^\circ}{2} = \frac{120^\circ}{2} = 60^\circ$.
Since all three angles are $60^\circ$, $\triangle OAB$ is an equilateral triangle with side length equal to the radius, i.e., side $= r = 15 \text{ cm}$.
Area of equilateral $\triangle OAB = \frac{\sqrt{3}}{4} \times (\text{side})^2 = \frac{\sqrt{3}}{4} \times r^2$
Using the given value $\sqrt{3} = 1.73$:
Area of $\triangle OAB = \frac{1.73}{4} \times (15 \text{ cm})^2$
$= \frac{1.73}{4} \times 225 \text{ cm}^2$
$= \frac{1.73 \times 225}{4} \text{ cm}^2$
$= \frac{389.25}{4} \text{ cm}^2$
Area of $\triangle OAB = 97.3125 \text{ cm}^2$
Area of minor segment = Area of minor sector - Area of $\triangle OAB$
$= 117.75 \text{ cm}^2 - 97.3125 \text{ cm}^2$
$= 20.4375 \text{ cm}^2$
2. Area of the corresponding major segment:
The area of the major segment is the area of the whole circle minus the area of the minor segment.
Area of circle $= \pi r^2 = 3.14 \times (15 \text{ cm})^2 = 3.14 \times 225 \text{ cm}^2$
$= 706.5 \text{ cm}^2$
Area of major segment = Area of circle - Area of minor segment
$= 706.5 \text{ cm}^2 - 20.4375 \text{ cm}^2$
$= 686.0625 \text{ cm}^2$
Answer:
The area of the corresponding minor segment is $20.4375 \text{ cm}^2$.
The area of the corresponding major segment is $686.0625 \text{ cm}^2$.
Question 7. A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and $\sqrt{3}$ = 1.73)
Answer:
This problem requires finding the area of a segment of a circle when the central angle subtended by the chord is $120^\circ$, using specific approximate values for $\pi$ and $\sqrt{3}$.
Given:
Radius of the circle, $r = 12 \text{ cm}$
Angle subtended by the chord at the centre, $\theta = 120^\circ$
Value of $\pi = 3.14$
Value of $\sqrt{3} = 1.73$
To Find:
Area of the corresponding segment of the circle (this refers to the minor segment).
Solution:
The area of the segment is the area of the sector formed by the arc minus the area of the triangle formed by the radii and the chord.
Area of the sector:
The formula for the area of a sector with angle $\theta$ and radius $r$ is $\frac{\theta}{360^\circ} \times \pi r^2$.
Area of sector $= \frac{120^\circ}{360^\circ} \times 3.14 \times (12 \text{ cm})^2$
$= \frac{\cancel{120}^{1}}{\cancel{360}_{3}} \times 3.14 \times 144 \text{ cm}^2$
$= \frac{1}{3} \times 3.14 \times 144 \text{ cm}^2$
$= 3.14 \times \frac{144}{3} \text{ cm}^2$
$= 3.14 \times 48 \text{ cm}^2$
Area of sector $= 150.72 \text{ cm}^2$
Area of the triangle formed by the chord and radii:
Let the chord be AB and the centre be O. In $\triangle OAB$, OA = OB = $r = 12 \text{ cm}$ and $\angle AOB = 120^\circ$.
The formula for the area of a triangle with two sides $a, b$ and the included angle $C$ is $\frac{1}{2}ab \sin C$. Here, $a=OA$, $b=OB$, and $C=\angle AOB$.
Area of $\triangle OAB = \frac{1}{2} \times OA \times OB \times \sin (\angle AOB)$
$= \frac{1}{2} \times 12 \text{ cm} \times 12 \text{ cm} \times \sin 120^\circ$
We know that $\sin 120^\circ = \sin (180^\circ - 60^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$.
Using the given value $\sqrt{3} = 1.73$, we have $\sin 120^\circ = \frac{1.73}{2}$.
Area of $\triangle OAB = \frac{1}{2} \times 144 \text{ cm}^2 \times \frac{1.73}{2}$
$= \frac{144}{4} \times 1.73 \text{ cm}^2$
$= 36 \times 1.73 \text{ cm}^2$
Area of $\triangle OAB = 62.28 \text{ cm}^2$
Area of the segment:
Area of segment = Area of sector - Area of $\triangle OAB$
$= 150.72 \text{ cm}^2 - 62.28 \text{ cm}^2$
$= 88.44 \text{ cm}^2$
Answer:
The area of the corresponding segment of the circle is $88.44 \text{ cm}^2$.
Question 8. A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig. 11.8). Find
(i) the area of that part of the field in which the horse can graze.
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)

Answer:
Given:
Side of the square field = $15 \text{ m}$
Length of the rope (radius of grazing area) = $5 \text{ m}$ in part (i), $10 \text{ m}$ in part (ii).
Value of $\pi = 3.14$
To Find:
(i) The area of the field the horse can graze with a 5 m rope.
(ii) The increase in grazing area if the rope is 10 m.
Solution:
The horse is tied at one corner of a square field. The area the horse can graze is a sector of a circle with the rope as the radius and the angle at the corner of the square as the sector angle.
The angle at the corner of a square is $90^\circ$. So, the angle of the sector is $\theta = 90^\circ$.
The formula for the area of a sector with angle $\theta$ (in degrees) and radius $r$ is given by:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
(i) Area grazed with a 5 m rope:
Here, radius $r_1 = 5 \text{ m}$.
Area grazed $= \frac{90^\circ}{360^\circ} \times \pi r_1^2$
$= \frac{\cancel{90}^{1}}{\cancel{360}_{4}} \times 3.14 \times (5 \text{ m})^2$
$= \frac{1}{4} \times 3.14 \times 25 \text{ m}^2$
$= \frac{3.14 \times 25}{4} \text{ m}^2$
$= \frac{78.5}{4} \text{ m}^2$
$= 19.625 \text{ m}^2$
(ii) Increase in grazing area if the rope were 10 m long:
Here, the new radius is $r_2 = 10 \text{ m}$.
The new grazing area with a 10 m rope is:
New Area grazed $= \frac{90^\circ}{360^\circ} \times \pi r_2^2$
$= \frac{1}{4} \times 3.14 \times (10 \text{ m})^2$
$= \frac{1}{4} \times 3.14 \times 100 \text{ m}^2$
$= \frac{314}{4} \text{ m}^2$
$= 78.5 \text{ m}^2$
The increase in grazing area is the difference between the new area and the old area:
Increase in area $= \text{New Area grazed} - \text{Area grazed with 5 m rope}$
$= 78.5 \text{ m}^2 - 19.625 \text{ m}^2$
$= 58.875 \text{ m}^2$
Answer:
(i) The area of the field in which the horse can graze with a 5 m rope is $19.625 \text{ m}^2$.
(ii) The increase in the grazing area if the rope were 10 m long instead of 5 m is $58.875 \text{ m}^2$.
Question 9. A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 11.9. Find :
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.
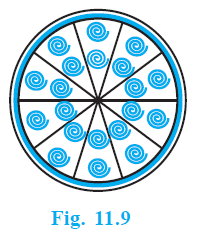
Answer:
Given:
Diameter of the circle, $d = 35 \text{ mm}$
Radius of the circle, $r = \frac{d}{2} = \frac{35}{2} \text{ mm}$
Number of diameters used = 5
These 5 diameters divide the circle into 10 equal sectors.
Value of $\pi = \frac{22}{7}$ (as per the general instruction)
To Find:
(i) The total length of the silver wire required.
(ii) The area of each sector of the brooch.
Solution:
(i) Total length of the silver wire required:
The silver wire is used for the circumference of the circle and for the 5 diameters.
Length of wire = Circumference of circle + Length of 5 diameters
Circumference of circle $= 2\pi r = \pi d = \frac{22}{7} \times 35 \text{ mm}$
$= 22 \times \frac{\cancel{35}^{5}}{\cancel{7}^{1}} \text{ mm}$
$= 22 \times 5 \text{ mm}$
$= 110 \text{ mm}$
Length of 5 diameters $= 5 \times d = 5 \times 35 \text{ mm}$
$= 175 \text{ mm}$
Total length of silver wire $= 110 \text{ mm} + 175 \text{ mm}$
$= 285 \text{ mm}$
(ii) Area of each sector of the brooch:
The circle is divided into 10 equal sectors.
The angle of each sector is $\frac{360^\circ}{10} = 36^\circ$.
The radius of each sector is $r = \frac{35}{2} \text{ mm}$.
The formula for the area of a sector with angle $\theta$ and radius $r$ is $\frac{\theta}{360^\circ} \times \pi r^2$.
Area of each sector $= \frac{36^\circ}{360^\circ} \times \pi r^2$
$= \frac{\cancel{36}^{1}}{\cancel{360}_{10}} \times \frac{22}{7} \times (\frac{35}{2} \text{ mm})^2$
$= \frac{1}{10} \times \frac{22}{7} \times \frac{35}{2} \times \frac{35}{2} \text{ mm}^2$
$= \frac{1}{10} \times \frac{\cancel{22}^{11}}{\cancel{7}^{1}} \times \frac{\cancel{35}^{5}}{2} \times \frac{35}{2} \text{ mm}^2$
$= \frac{1}{10} \times 11 \times \frac{5}{2} \times \frac{35}{2} \text{ mm}^2$
$= \frac{\cancel{1}^{1}}{\cancel{10}^{2}} \times 11 \times \frac{\cancel{5}^{1}}{2} \times \frac{35}{2} \text{ mm}^2$
$= \frac{11 \times 1 \times 35}{2 \times 2 \times 2} \text{ mm}^2$
$= \frac{385}{8} \text{ mm}^2$
Answer:
(i) The total length of the silver wire required is $285 \text{ mm}$.
(ii) The area of each sector of the brooch is $\frac{385}{8} \text{ mm}^2$.
Question 10. An umbrella has 8 ribs which are equally spaced (see Fig. 11.10). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.
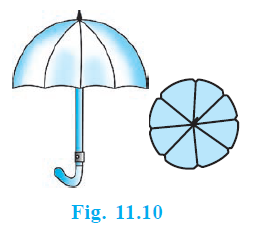
Answer:
Given:
Number of ribs in the umbrella = 8
Umbrella assumed to be a flat circle with radius, $r = 45 \text{ cm}$
Ribs are equally spaced.
Value of $\pi = \frac{22}{7}$
To Find:
The area between two consecutive ribs of the umbrella.
Solution:
Since the 8 ribs are equally spaced, they divide the circle into 8 equal sectors.
The angle of each sector at the centre is the total angle of a circle divided by the number of sectors.
Angle of each sector, $\theta = \frac{360^\circ}{\text{Number of sectors}}$
$\theta = \frac{360^\circ}{8}$
$\theta = 45^\circ$
The area between two consecutive ribs is the area of one such sector with radius $r = 45 \text{ cm}$ and angle $\theta = 45^\circ$.
The formula for the area of a sector is: Area $= \frac{\theta}{360^\circ} \times \pi r^2$
Area of each sector $= \frac{45^\circ}{360^\circ} \times \frac{22}{7} \times (45 \text{ cm})^2$
$= \frac{\cancel{45}^{1}}{\cancel{360}_{8}} \times \frac{22}{7} \times 45 \times 45 \text{ cm}^2$
$= \frac{1}{8} \times \frac{22}{7} \times 2025 \text{ cm}^2$
$= \frac{\cancel{22}^{11} \times 2025}{\cancel{8}^{4} \times 7} \text{ cm}^2$
$= \frac{11 \times 2025}{4 \times 7} \text{ cm}^2$
$= \frac{22275}{28} \text{ cm}^2$
Answer:
The area between two consecutive ribs of the umbrella is $\frac{22275}{28} \text{ cm}^2$.
Question 11. A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Answer:
Given:
Number of wipers = 2
Length of each wiper blade (radius of the sector) = $r = 25 \text{ cm}$
Angle of sweep for each blade = $\theta = 115^\circ$
Wipers do not overlap.
Value of $\pi = \frac{22}{7}$
To Find:
The total area cleaned at each sweep of the blades.
Solution:
The area cleaned by each wiper blade during one sweep is the area of a sector of a circle with radius equal to the length of the blade and angle equal to the sweeping angle.
Area cleaned by one wiper $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the given values for one wiper:
Area cleaned by one wiper $= \frac{115^\circ}{360^\circ} \times \frac{22}{7} \times (25 \text{ cm})^2$
$= \frac{115}{360} \times \frac{22}{7} \times 625 \text{ cm}^2$
Simplifying the fraction $\frac{115}{360}$ by dividing both by 5:
$= \frac{23}{72} \times \frac{22}{7} \times 625 \text{ cm}^2$
Simplifying the fraction $\frac{22}{72}$ by dividing both by 2:
$= \frac{23}{\cancel{72}^{36}} \times \frac{\cancel{22}^{11}}{7} \times 625 \text{ cm}^2$
$= \frac{23 \times 11 \times 625}{36 \times 7} \text{ cm}^2$
$= \frac{253 \times 625}{252} \text{ cm}^2$
$= \frac{158125}{252} \text{ cm}^2$
Since the two wipers do not overlap, the total area cleaned is the sum of the areas cleaned by each wiper.
Total area cleaned $= 2 \times (\text{Area cleaned by one wiper})$
$= 2 \times \frac{158125}{252} \text{ cm}^2$
$= \frac{158125}{\cancel{252}^{126}} \text{ cm}^2$
$= \frac{158125}{126} \text{ cm}^2$
Answer:
The total area cleaned at each sweep of the blades is $\frac{158125}{126} \text{ cm}^2$.
Question 12. To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
Answer:
Given:
Angle of the sector over which the light spreads, $\theta = 80^\circ$
Distance to which the light spreads (radius of the sector), $r = 16.5 \text{ km}$
Value of $\pi = 3.14$
To Find:
The area of the sea over which the ships are warned.
Solution:
The area over which the ships are warned is the area of a sector of a circle with radius $r = 16.5 \text{ km}$ and angle $\theta = 80^\circ$.
The formula for the area of a sector with angle $\theta$ and radius $r$ is:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
Substituting the given values, we get:
Area $= \frac{80^\circ}{360^\circ} \times 3.14 \times (16.5 \text{ km})^2$
$= \frac{\cancel{80}^{2}}{\cancel{360}_{9}} \times 3.14 \times (16.5)^2 \text{ km}^2$
$= \frac{2}{9} \times 3.14 \times 272.25 \text{ km}^2$
$= \frac{2 \times 3.14 \times 272.25}{9} \text{ km}^2$
$= \frac{6.28 \times 272.25}{9} \text{ km}^2$
$= \frac{1709.58}{9} \text{ km}^2$
Performing the division:
$1709.58 \div 9 \approx 189.9533...$
Area $\approx 189.95 \text{ km}^2$ (rounding to two decimal places)
Answer:
The area of the sea over which the ships are warned is approximately $189.95 \text{ km}^2$.
Question 13. A round table cover has six equal designs as shown in Fig. 11.11. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of 0.35 per cm2 . (Use $\sqrt{3}$ = 1.7)

Answer:
This problem involves calculating the area of multiple identical segments of a circle and then finding the total cost based on the area and a given rate. The designs are segments of the circle.
Given:
Radius of the round table cover, $r = 28 \text{ cm}$
Number of equal designs = 6
Rate of making designs = $\textsf{₹} 0.35 \text{ per cm}^2$
Use $\sqrt{3} = 1.7$
Use $\pi = \frac{22}{7}$ (as per the standard value and common practice)
To Find:
The total cost of making the designs.
Solution:
The round table cover has 6 equal designs. These designs are segments of the circle. Since the designs are equal and equally spaced, they divide the circle into 6 equal sectors.
The angle subtended by each sector at the centre is found by dividing the total angle of the circle ($360^\circ$) by the number of designs:
Central angle for each sector, $\theta = \frac{360^\circ}{\text{Number of designs}} = \frac{360^\circ}{6} = 60^\circ$.
Each design is the area of a segment corresponding to a sector with radius $r = 28 \text{ cm}$ and central angle $\theta = 60^\circ$.
The area of a segment is calculated as the area of the corresponding sector minus the area of the triangle formed by the radii and the chord of the segment.
Area of one sector:
The formula for the area of a sector with angle $\theta$ and radius $r$ is $\frac{\theta}{360^\circ} \times \pi r^2$.
Area of one sector $= \frac{60^\circ}{360^\circ} \times \frac{22}{7} \times (28 \text{ cm})^2$
$= \frac{\cancel{60}^{1}}{\cancel{360}_{6}} \times \frac{22}{7} \times 28 \times 28 \text{ cm}^2$
$= \frac{1}{6} \times \frac{22}{\cancel{7}^{1}} \times \cancel{28}^{4} \times 28 \text{ cm}^2$
$= \frac{1}{6} \times 22 \times 4 \times 28 \text{ cm}^2$
$= \frac{2464}{6} \text{ cm}^2$
Simplifying the fraction:
$= \frac{\cancel{2464}^{1232}}{\cancel{6}^{3}} \text{ cm}^2$
Area of one sector $= \frac{1232}{3} \text{ cm}^2$
Area of the triangle formed by the radii and the chord:
Let the radii forming the sector be OA and OB, and the chord be AB. In $\triangle OAB$, OA = OB = $r = 28 \text{ cm}$, and $\angle AOB = 60^\circ$.
Since OA = OB, $\triangle OAB$ is an isosceles triangle. The angles opposite to equal sides are equal: $\angle OAB = \angle OBA$.
Sum of angles in a triangle is $180^\circ$. So, $\angle OAB + \angle OBA + \angle AOB = 180^\circ$.
$2 \times \angle OAB + 60^\circ = 180^\circ$
$2 \times \angle OAB = 180^\circ - 60^\circ = 120^\circ$
$\angle OAB = \frac{120^\circ}{2} = 60^\circ$
Since all angles of $\triangle OAB$ are $60^\circ$, it is an equilateral triangle with side length equal to the radius, i.e., side $= r = 28 \text{ cm}$.
The formula for the area of an equilateral triangle with side 's' is $\frac{\sqrt{3}}{4} s^2$. Here, $s = r = 28 \text{ cm}$.
Area of $\triangle OAB = \frac{\sqrt{3}}{4} \times r^2$
Using the given value $\sqrt{3} = 1.7$:
Area of $\triangle OAB = \frac{1.7}{4} \times (28 \text{ cm})^2$
$= \frac{1.7}{4} \times 784 \text{ cm}^2$
$= 1.7 \times \frac{\cancel{784}^{196}}{\cancel{4}^{1}} \text{ cm}^2$
$= 1.7 \times 196 \text{ cm}^2$
$= 333.2 \text{ cm}^2$
Area of one design (segment):
Area of one segment = Area of sector - Area of $\triangle OAB$
$= (\frac{1232}{3} - 333.2) \text{ cm}^2$
To combine these, we can convert $333.2$ to a fraction or decimal. Using decimal:
$\frac{1232}{3} \approx 410.666...$
Area of one segment $\approx 410.666... - 333.2 = 77.466... \text{ cm}^2$
Using fractions:
$333.2 = \frac{3332}{10} = \frac{1666}{5}$
Area of one segment $= \frac{1232}{3} - \frac{1666}{5} = \frac{1232 \times 5 - 1666 \times 3}{15}$
$= \frac{6160 - 4998}{15} = \frac{1162}{15} \text{ cm}^2$
Total area of 6 designs:
Total area $= 6 \times (\text{Area of one segment})$
Using the fractional value of the segment area:
Total area $= 6 \times \frac{1162}{15} \text{ cm}^2$
$= \cancel{6}^{2} \times \frac{1162}{\cancel{15}^{5}} \text{ cm}^2$
$= \frac{2 \times 1162}{5} \text{ cm}^2$
$= \frac{2324}{5} \text{ cm}^2$
As a decimal: $\frac{2324}{5} = 464.8 \text{ cm}^2$
Let's check using the decimal approximation of the segment area:
Total area $\approx 6 \times 77.466...$
Using the exact subtraction from the sector area: $6 \times (\frac{1232}{3} - 333.2) = 6 \times \frac{1232}{3} - 6 \times 333.2 = 2 \times 1232 - 1999.2 = 2464 - 1999.2 = 464.8 \text{ cm}^2$. This matches the fractional result.
Total area of 6 designs $= 464.8 \text{ cm}^2$.
Cost of making the designs:
Cost = Total area $\times$ Rate per cm$^2$
Cost $= 464.8 \text{ cm}^2 \times \textsf{₹} 0.35/\text{cm}^2$
Cost $= \textsf{₹} (464.8 \times 0.35)$
The product of $464.8$ and $0.35$ is $162.68$.
Cost $= \textsf{₹} 162.68$
Answer:
The cost of making the designs is $\textsf{₹} 162.68$.
Question 14. Tick the correct answer in the following :
Area of a sector of angle p (in degrees) of a circle with radius R is
(A) $\frac{p}{180}$ × 2πR
(B) $\frac{p}{180}$ × πR2
(C) $\frac{p}{360}$ × 2πR
(D) $\frac{p}{720}$ × 2πR2
Answer:
Question:
Area of a sector of angle p (in degrees) of a circle with radius R is
(A) $\frac{p}{180}$ × 2πR
(B) $\frac{p}{180}$ × πR2
(C) $\frac{p}{360}$ × 2πR
(D) $\frac{p}{720}$ × 2πR2
Solution:
The formula for the area of a sector of a circle with radius $r$ and angle $\theta$ (in degrees) at the centre is given by:
Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$
In this question, the angle is given as $p$ degrees and the radius is $R$.
So, the area of the sector is $\frac{p}{360} \times \pi R^2$.
Let's look at the given options and see which one matches this formula.
Option (D) is $\frac{p}{720}$ × 2πR2.
We can rewrite this as $\frac{2 \times p}{720} \times \pi R^2$
Simplifying the fraction $\frac{2}{720}$, we get $\frac{1}{360}$.
So, option (D) simplifies to $\frac{p}{360} \times \pi R^2$.
This matches the correct formula for the area of the sector.
Answer:
The correct answer is (D).

