| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 10 Vector Algebra
Welcome to the detailed solutions resource for Chapter 10: Vector Algebra, a critical chapter in the Class 12 Mathematics syllabus as per the Latest NCERT (2024-25) textbook. Vector algebra provides the mathematical framework for dealing with quantities that possess both magnitude and direction, such as displacement, velocity, acceleration, and force, making it indispensable in physics and engineering. It also offers powerful tools for three-dimensional geometry. These solutions aim to provide comprehensive guidance through the algebraic operations and geometric interpretations of vectors, fully aligned with the current rationalized syllabus.
The initial part revisits fundamental concepts, clearly distinguishing between vectors (magnitude and direction) and scalars (magnitude only). The solutions reinforce understanding the magnitude (or length) of a vector, its direction represented through Direction Ratios (DRs) and the crucial Direction Cosines (DCs). If a vector makes angles $\alpha, \beta, \gamma$ with the positive x, y, and z axes respectively, its DCs are $l = \cos\alpha$, $m = \cos\beta$, $n = \cos\gamma$, satisfying the fundamental identity $\mathbf{l^2 + m^2 + n^2 = 1}$. Various types of vectors are defined: the zero vector, unit vectors (magnitude 1), collinear vectors (parallel vectors), equal vectors, and the negative of a vector. The concept of a Position Vector, which represents the position of a point in space relative to the origin, is foundational. Vector addition, explained via the Triangle Law and the Parallelogram Law, along with the properties of scalar multiplication, are reviewed and applied. A key skill demonstrated is finding a unit vector in the direction of a given vector $\vec{a}$ using the formula $\mathbf{\hat{a} = \frac{\vec{a}}{|\vec{a}|}}$.
Building on these basics, the solutions cover the Section Formula in vector form. This provides the position vector $\vec{r}$ of a point dividing the line segment joining two points with position vectors $\vec{a}$ and $\vec{b}$ internally in the ratio $m:n$ as $\mathbf{\vec{r} = \frac{m\vec{b} + n\vec{a}}{m+n}}$. The formula for external division is also addressed. These formulas are applied to solve geometric problems involving division of line segments.
A significant portion of the chapter focuses on the two primary ways to multiply vectors:
- Scalar (Dot) Product: Defined as $\mathbf{\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta}$, where $\theta$ is the angle between the vectors. This results in a scalar quantity. In terms of components ($\vec{a} = a_1\hat{\mathbf{i}} + a_2\hat{\mathbf{j}} + a_3\hat{\mathbf{k}}$, $\vec{b} = b_1\hat{\mathbf{i}} + b_2\hat{\mathbf{j}} + b_3\hat{\mathbf{k}}$), it's calculated as $\mathbf{\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3}$. Solutions extensively demonstrate its applications:
- Finding the angle between two vectors: $\theta = \cos^{-1}\left( \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} \right)$.
- Checking for perpendicularity (orthogonality): Two non-zero vectors $\vec{a}$ and $\vec{b}$ are perpendicular if and only if $\mathbf{\vec{a} \cdot \vec{b} = 0}$.
- Finding the scalar projection of vector $\vec{a}$ onto vector $\vec{b}$: $\mathbf{\text{proj}_{\vec{b}} \vec{a} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}}$.
- Vector (Cross) Product: Defined as $\mathbf{\vec{a} \times \vec{b} = (|\vec{a}||\vec{b}|\sin\theta) \hat{\mathbf{n}}}$, where $\theta$ is the angle between the vectors and $\hat{\mathbf{n}}$ is a unit vector perpendicular to both $\vec{a}$ and $\vec{b}$, determined by the right-hand rule. This results in a vector quantity. It is most commonly calculated using the determinant form:
$\qquad \mathbf{\vec{a} \times \vec{b} = \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = (a_2b_3 - a_3b_2)\hat{\mathbf{i}} - (a_1b_3 - a_3b_1)\hat{\mathbf{j}} + (a_1b_2 - a_2b_1)\hat{\mathbf{k}}}$.
Solutions meticulously cover its calculation and key applications:
- Finding a vector perpendicular to two given vectors.
- Checking for parallelism (collinearity): Two non-zero vectors $\vec{a}$ and $\vec{b}$ are parallel if and only if $\mathbf{\vec{a} \times \vec{b} = \vec{0}}$.
- Calculating the Area of a Parallelogram with adjacent sides $\vec{a}$ and $\vec{b}$: $\mathbf{\text{Area} = |\vec{a} \times \vec{b}|}$.
- Calculating the Area of a Triangle with adjacent sides $\vec{a}$ and $\vec{b}$: $\mathbf{\text{Area} = \frac{1}{2}|\vec{a} \times \vec{b}|}$.
(Note: The Scalar Triple Product, $[\vec{a} \ \vec{b} \ \vec{c}] = \vec{a} \cdot (\vec{b} \times \vec{c})$, which represents the volume of the parallelepiped formed by the three vectors, might have reduced emphasis or be excluded based on the specifics of the rationalized syllabus; the solutions will reflect the current scope.) By diligently studying these detailed solutions, students can solidify their understanding of vector operations, direction cosines and ratios, confidently compute both dot and cross products, appreciate their profound geometric significance, and skillfully apply these concepts to solve problems involving angles, projections, areas, and conditions of perpendicularity or parallelism.
Example 1 to 3 (Before Exercise 10.1)
Example 1: Represent graphically a displacement of 40 km, 30° west of south.
Answer:
Given:
Displacement: Magnitude = 40 km, Direction = 30° west of south.
To Represent:
Represent the given displacement graphically as a vector.
Representation:
To represent the displacement vector graphically, we draw a directed line segment. The length of the segment represents the magnitude (40 km), and the direction of the segment represents the direction (30° west of south).
1. Draw a point O, which represents the starting point.
2. Draw lines representing the cardinal directions (North, South, East, West) from O.
3. Identify the South direction (vertical downwards) and the West direction (horizontal to the left).
4. The direction "30° west of south" means starting from the South direction line and rotating $30^\circ$ towards the West direction.
5. Draw a line segment starting from O along this direction. The length of this segment is proportional to 40 km. We can choose a suitable scale, for example, 1 cm = 10 km, so the length of the segment would be 4 cm.
6. Place an arrowhead at the end of the line segment to indicate the direction of the displacement.
7. Label the magnitude (40 km) near the vector and indicate the angle $30^\circ$ between the South direction line and the vector.
Here is a graphical representation:
In the diagram, the arrow originating from O represents the displacement vector. The angle between the downward vertical line (South) and the vector is $30^\circ$, measured towards the left (West). The length of the arrow corresponds to 40 km according to a chosen scale (though the scale itself is not explicitly shown in the diagram, the length relative to the value is understood).
Example 2: Classify the following measures as scalars and vectors.
(i) 5 seconds
(ii) 1000 cm3
(iii) 10 Newton
(iv) 30 km/hr
(v) 10 g/cm3
(vi) 20 m/s towards north
Answer:
A scalar quantity is a physical quantity that has only magnitude.
A vector quantity is a physical quantity that has both magnitude and direction.
(i) 5 seconds:
This measures time. Time has only magnitude.
It is a scalar.
(ii) 1000 cm$^3$:
This measures volume. Volume has only magnitude.
It is a scalar.
(iii) 10 Newton:
This measures force. Force has both magnitude and direction.
It is a vector.
(iv) 30 km/hr:
This measures speed. Speed has only magnitude.
It is a scalar.
(v) 10 g/cm$^3$:
This measures density. Density has only magnitude.
It is a scalar.
(vi) 20 m/s towards north:
This measures velocity. It has both magnitude (20 m/s) and direction (towards north).
It is a vector.
Example 3: In Fig 10.5, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Coinitia
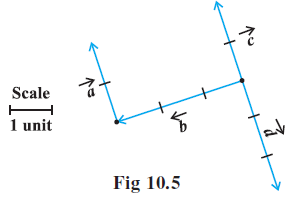
Answer:
Given:
A figure (Fig 10.5) showing four vectors $\vec{a}$, $\vec{b}$, $\vec{c}$, and $\vec{d}$.
To Classify:
Identify which of the given vectors are collinear, equal, and coinitial, based on the figure.
Classification:
(i) Collinear vectors: Vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitude and direction. Looking at the figure, the vectors $\vec{a}$, $\vec{c}$, and $\vec{d}$ appear to be parallel to each other.
Therefore, the vectors $\vec{a}$, $\vec{c}$, and $\vec{d}$ are collinear.
(ii) Equal vectors: Vectors are said to be equal if they have the same magnitude (length) and the same direction. Observing the figure, the vectors $\vec{a}$ and $\vec{c}$ appear to have the same length and point in the same direction.
Therefore, the vectors $\vec{a}$ and $\vec{c}$ are equal.
(iii) Coinitial vectors: Vectors are said to be coinitial if they have the same initial point (starting point). From the figure, the vectors $\vec{b}$, $\vec{c}$, and $\vec{d}$ start from the same point.
Therefore, the vectors $\vec{b}$, $\vec{c}$, and $\vec{d}$ are coinitial.
Exercise 10.1
Question 1. Represent graphically a displacement of 40 km, 30° east of north.
Answer:
Given:
Displacement with magnitude 40 km and direction 30° east of north.
To Represent:
Represent the given displacement graphically as a vector.
Representation:
To represent the displacement vector graphically, we use a directed line segment where the length represents the magnitude and the direction of the segment represents the direction.
1. Draw a point O, which will be the origin or starting point.
2. Draw a vertical line upwards from O to represent the North direction and a horizontal line to the right from O to represent the East direction.
3. The direction "30° east of north" means we start from the North direction line and measure an angle of $30^\circ$ towards the East direction (clockwise from North towards East in the first quadrant).
4. Draw a line segment starting from O along this direction.
5. The length of this segment should represent 40 km. You can choose a suitable scale (e.g., 1 cm represents 10 km) to draw the segment with the correct proportional length.
6. Add an arrowhead at the end of the line segment to indicate the direction of the displacement vector.
7. Label the magnitude of the vector (40 km) and indicate the angle ($30^\circ$) between the North direction and the vector.
Here is a graphical representation:
In the figure, the arrow starting from O represents the displacement vector. The angle between the upward vertical line (North) and the vector is $30^\circ$, measured towards the right (East). The length of the arrow is proportional to 40 km.
Question 2. Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 watt
(v) 10–19 coulomb
(vi) 20 m/s2
Answer:
A scalar quantity is a physical quantity that has only magnitude.
A vector quantity is a physical quantity that has both magnitude and direction.
(i) 10 kg:
This measures mass. Mass is specified by its magnitude only.
It is a scalar.
(ii) 2 meters north-west:
This measures displacement. It has a magnitude (2 meters) and a specific direction (north-west).
It is a vector.
(iii) 40°:
This measures an angle. An angle itself is typically considered a scalar quantity, representing the amount of rotation or separation.
It is a scalar.
(iv) 40 watt:
This measures power. Power is the rate at which work is done or energy is transferred and is specified by its magnitude only.
It is a scalar.
(v) 10$^{–19}$ coulomb:
This measures electric charge. Electric charge is specified by its magnitude (and sign, which is not a direction in space).
It is a scalar.
(vi) 20 m/s$^2$:
This measures acceleration. Acceleration is the rate of change of velocity and has both magnitude and direction.
It is a vector.
Question 3. Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
Answer:
A scalar quantity is a physical quantity that has only magnitude.
A vector quantity is a physical quantity that has both magnitude and direction.
(i) time period:
Time period is the duration of one cycle of a recurring event. It has only magnitude.
It is a scalar.
(ii) distance:
Distance is the total length of the path traveled between two points. It has only magnitude.
It is a scalar.
(iii) force:
Force is a push or a pull that can cause a change in motion. It has both magnitude and direction.
It is a vector.
(iv) velocity:
Velocity is the rate of change of displacement. It has both magnitude (speed) and direction.
It is a vector.
(v) work done:
Work done by a force is the product of the force and the displacement in the direction of the force. Although force and displacement are vectors, work is a scalar quantity representing the energy transferred.
It is a scalar.
Question 4. In Fig 10.6 (a square), identify the following vectors.
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
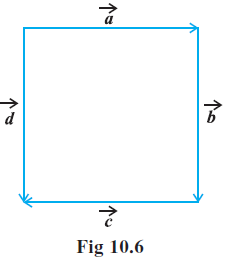
Answer:
Given:
A figure (Fig 10.6) showing a square with four vectors labelled $\vec{a}$, $\vec{b}$, $\vec{c}$, and $\vec{d}$.
To Identify:
Identify the vectors belonging to the following categories based on the provided correct classification:
(i) Coinitial vectors.
(ii) Equal vectors.
(iii) Collinear but not equal vectors.
Identification (Based on the provided classification):
(i) Coinitial vectors: Vectors are coinitial if they have the same initial point (starting point). Observing the figure, vectors $\vec{a}$ and $\vec{b}$ both originate from the top-left vertex of the square.
Therefore, the coinitial vectors are $\mathbf{\vec{a}}$ and $\mathbf{\vec{b}}$.
(ii) Equal vectors: Vectors are equal if they have the same magnitude (length) and the same direction. Based on the provided classification, the vectors $\vec{b}$ and $\vec{d}$ are equal. (This implies they have the same magnitude and direction, although visually their directions appear opposite in the diagram).
Therefore, the equal vectors are $\mathbf{\vec{b}}$ and $\mathbf{\vec{d}}$.
(iii) Collinear but not equal vectors: Collinear vectors are vectors that are parallel to the same line. Vectors that are collinear but not equal are parallel but differ in either magnitude or direction (if magnitudes are equal, they must have opposite directions). Based on the provided classification, the vectors $\vec{a}$ and $\vec{c}$ are collinear but not equal. (These vectors are visually parallel and appear to have the same magnitude and direction, but are classified as not equal).
Therefore, the vectors that are collinear but not equal are $\mathbf{\vec{a}}$ and $\mathbf{\vec{c}}$.
Question 5. Answer the following as true or false
(i) $\vec{a}$ and $–\vec{a}$ are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Answer:
(i) $\vec{a}$ and $–\vec{a}$ are collinear.
Explanation: Two vectors are collinear if they are parallel to the same line. The vector $-\vec{a}$ has the same magnitude as $\vec{a}$ but points in the opposite direction. Both vectors lie on the same line or parallel lines, making them parallel. Therefore, they are collinear.
Answer: True
(ii) Two collinear vectors are always equal in magnitude.
Explanation: Collinear vectors are vectors that are parallel to the same line. Their magnitudes can be different. For example, a vector of length 2 units pointing east and a vector of length 5 units pointing east are collinear, but they do not have equal magnitude.
Answer: False
(iii) Two vectors having same magnitude are collinear.
Explanation: Two vectors having the same magnitude can point in different directions. For example, a vector representing a displacement of 10 km north and a vector representing a displacement of 10 km east have the same magnitude (10 km) but are not collinear (they are perpendicular).
Answer: False
(iv) Two collinear vectors having the same magnitude are equal.
Explanation: Two vectors are equal if they have the same magnitude AND the same direction. Two collinear vectors having the same magnitude can point in opposite directions (e.g., $\vec{a}$ and $-\vec{a}$, where $|\vec{a}| = |-\vec{a}|$ but they are not equal unless $\vec{a} = \vec{0}$).
Answer: False
Example 4 to 12 (Before Exercise 10.2)
Example 4: Find the values of x, y and z so that the vectors $\vec{a} = x\hat{i} + 2\hat{j} + z\hat{k}$ and $\vec{b} = 2\hat{i} + y\hat{j} + \hat{k}$ are equal.
Answer:
Given:
Two vectors $\vec{a} = x\hat{i} + 2\hat{j} + z\hat{k}$ and $\vec{b} = 2\hat{i} + y\hat{j} + \hat{k}$.
The condition that the two vectors are equal, i.e., $\vec{a} = \vec{b}$.
To Find:
The values of $x$, $y$, and $z$ that satisfy the condition.
Solution:
Two vectors are equal if and only if their corresponding components are equal.
Given that $\vec{a} = \vec{b}$, we have:
$x\hat{i} + 2\hat{j} + z\hat{k} = 2\hat{i} + y\hat{j} + \hat{k}$
Equating the coefficients of $\hat{i}$, $\hat{j}$, and $\hat{k}$ on both sides:
Coefficient of $\hat{i}$:
$x = 2$
Coefficient of $\hat{j}$:
$2 = y$
Coefficient of $\hat{k}$:
$z = 1$
Therefore, for the vectors $\vec{a}$ and $\vec{b}$ to be equal, the values of $x$, $y$, and $z$ must be $x=2$, $y=2$, and $z=1$.
The values are:
$x = 2$
$y = 2$
$z = 1$
Example 5: Let $\vec{a} = \hat{i} + 2\hat{j}$ and $\vec{b} = 2\hat{i} + \hat{j}$ . Is $|\vec{a}| = |\vec{b}|$ ? Are the vectors $\vec{a}$ and $\vec{b}$ equal ?
Answer:
Given:
Vector $\vec{a} = \hat{i} + 2\hat{j}$.
Vector $\vec{b} = 2\hat{i} + \hat{j}$.
To Determine:
(i) Is $|\vec{a}| = |\vec{b}|$?
(ii) Are the vectors $\vec{a}$ and $\vec{b}$ equal?
Solution:
The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j}$ is given by $|\vec{v}| = \sqrt{v_1^2 + v_2^2}$.
Calculate the magnitude of vector $\vec{a} = \hat{i} + 2\hat{j}$:
$|\vec{a}| = \sqrt{1^2 + 2^2}$
$|\vec{a}| = \sqrt{1 + 4}$
$|\vec{a}| = \sqrt{5}$
Calculate the magnitude of vector $\vec{b} = 2\hat{i} + \hat{j}$:
$|\vec{b}| = \sqrt{2^2 + 1^2}$
$|\vec{b}| = \sqrt{4 + 1}$
$|\vec{b}| = \sqrt{5}$
Comparing the magnitudes, we have $|\vec{a}| = \sqrt{5}$ and $|\vec{b}| = \sqrt{5}$.
Thus, $|\vec{a}| = |\vec{b}|$.
Two vectors are equal if and only if their corresponding components are equal.
Vector $\vec{a} = 1\hat{i} + 2\hat{j}$.
Vector $\vec{b} = 2\hat{i} + 1\hat{j}$.
Comparing the components of $\hat{i}$:
Coefficient of $\hat{i}$ in $\vec{a}$ is $1$.
Coefficient of $\hat{i}$ in $\vec{b}$ is $2$.
Since $1 \neq 2$, the $\hat{i}$ components are not equal.
Comparing the components of $\hat{j}$:
Coefficient of $\hat{j}$ in $\vec{a}$ is $2$.
Coefficient of $\hat{j}$ in $\vec{b}$ is $1$.
Since $2 \neq 1$, the $\hat{j}$ components are not equal.
Since the corresponding components of $\vec{a}$ and $\vec{b}$ are not equal, the vectors $\vec{a}$ and $\vec{b}$ are not equal.
Answers:
(i) Yes, $|\vec{a}| = |\vec{b}|$.
(ii) No, the vectors $\vec{a}$ and $\vec{b}$ are not equal.
Example 6: Find unit vector in the direction of vector $\vec{a} = 2\hat{i} + 3\hat{j} + \hat{k}$
Answer:
Given:
The vector $\vec{a} = 2\hat{i} + 3\hat{j} + \hat{k}$.
To Find:
The unit vector in the direction of $\vec{a}$.
Solution:
The unit vector in the direction of a non-zero vector $\vec{a}$ is given by the formula:
$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$
First, we need to find the magnitude of the vector $\vec{a}$. The magnitude of a vector $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ is given by $|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$.
For the given vector $\vec{a} = 2\hat{i} + 3\hat{j} + \hat{k}$, we have $a_1 = 2$, $a_2 = 3$, and $a_3 = 1$.
Calculate the magnitude $|\vec{a}| $:
$|\vec{a}| = \sqrt{(2)^2 + (3)^2 + (1)^2}$
$|\vec{a}| = \sqrt{4 + 9 + 1}$
$|\vec{a}| = \sqrt{14}$
Now, substitute the vector $\vec{a}$ and its magnitude $|\vec{a}|$ into the formula for the unit vector:
$\hat{a} = \frac{2\hat{i} + 3\hat{j} + \hat{k}}{\sqrt{14}}$
This can be written as:
$\hat{a} = \frac{2}{\sqrt{14}}\hat{i} + \frac{3}{\sqrt{14}}\hat{j} + \frac{1}{\sqrt{14}}\hat{k}$
The unit vector in the direction of $\vec{a}$ is:
$\frac{2}{\sqrt{14}}\hat{i} + \frac{3}{\sqrt{14}}\hat{j} + \frac{1}{\sqrt{14}}\hat{k}$
Example 7: Find a vector in the direction of vector $\vec{a} = \hat{i} - 2\hat{j}$ that has magnitude 7 units.
Answer:
Given:
The vector $\vec{a} = \hat{i} - 2\hat{j}$.
The desired magnitude of the new vector is 7 units.
To Find:
A vector that is in the same direction as $\vec{a}$ and has a magnitude of 7.
Solution:
A vector in the direction of $\vec{a}$ can be obtained by scaling the unit vector in the direction of $\vec{a}$ by the desired magnitude.
First, find the magnitude of the given vector $\vec{a}$. The magnitude of a vector $\vec{a} = a_1\hat{i} + a_2\hat{j}$ is given by $|\vec{a}| = \sqrt{a_1^2 + a_2^2}$.
For $\vec{a} = \hat{i} - 2\hat{j}$, we have $a_1 = 1$ and $a_2 = -2$.
Calculate the magnitude $|\vec{a}| $:
$|\vec{a}| = \sqrt{(1)^2 + (-2)^2}$
$|\vec{a}| = \sqrt{1 + 4}$
$|\vec{a}| = \sqrt{5}$
Next, find the unit vector in the direction of $\vec{a}$. The unit vector $\hat{a}$ is given by $\hat{a} = \frac{\vec{a}}{|\vec{a}|}$.
$\hat{a} = \frac{\hat{i} - 2\hat{j}}{\sqrt{5}}$
$\hat{a} = \frac{1}{\sqrt{5}}\hat{i} - \frac{2}{\sqrt{5}}\hat{j}$
Now, to find a vector with magnitude 7 in the direction of $\vec{a}$, we multiply the unit vector $\hat{a}$ by the desired magnitude 7.
Let the required vector be $\vec{b}$. Then $\vec{b} = 7 \hat{a}$.
$\vec{b} = 7 \left( \frac{1}{\sqrt{5}}\hat{i} - \frac{2}{\sqrt{5}}\hat{j} \right)$
$\vec{b} = \frac{7}{\sqrt{5}}\hat{i} - \frac{14}{\sqrt{5}}\hat{j}$
The required vector is:
$\frac{7}{\sqrt{5}}\hat{i} - \frac{14}{\sqrt{5}}\hat{j}$
Example 8: Find the unit vector in the direction of the sum of the vectors, $\vec{a} = 2\hat{i} + 2\hat{j} - 5\hat{k}$ and $\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$ .
Answer:
Given:
Vector $\vec{a} = 2\hat{i} + 2\hat{j} - 5\hat{k}$.
Vector $\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$.
To Find:
The unit vector in the direction of the sum of $\vec{a}$ and $\vec{b}$.
Solution:
First, find the sum of the vectors $\vec{a}$ and $\vec{b}$. Let the sum be $\vec{c}$.
$\vec{c} = \vec{a} + \vec{b}$
$\vec{c} = (2\hat{i} + 2\hat{j} - 5\hat{k}) + (2\hat{i} + \hat{j} + 3\hat{k})$
Combine the corresponding components:
$\vec{c} = (2 + 2)\hat{i} + (2 + 1)\hat{j} + (-5 + 3)\hat{k}$
$\vec{c} = 4\hat{i} + 3\hat{j} - 2\hat{k}$
Now, we need to find the unit vector in the direction of $\vec{c}$. The unit vector in the direction of a vector $\vec{c}$ is given by $\hat{c} = \frac{\vec{c}}{|\vec{c}|}$.
Calculate the magnitude of $\vec{c}$. The magnitude of a vector $\vec{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$ is $|\vec{c}| = \sqrt{c_1^2 + c_2^2 + c_3^2}$.
For $\vec{c} = 4\hat{i} + 3\hat{j} - 2\hat{k}$, we have $c_1 = 4$, $c_2 = 3$, and $c_3 = -2$.
$|\vec{c}| = \sqrt{(4)^2 + (3)^2 + (-2)^2}$
$|\vec{c}| = \sqrt{16 + 9 + 4}$
$|\vec{c}| = \sqrt{29}$
Now, divide the vector $\vec{c}$ by its magnitude to find the unit vector:
$\hat{c} = \frac{4\hat{i} + 3\hat{j} - 2\hat{k}}{\sqrt{29}}$
This can be written as:
$\hat{c} = \frac{4}{\sqrt{29}}\hat{i} + \frac{3}{\sqrt{29}}\hat{j} - \frac{2}{\sqrt{29}}\hat{k}$
The unit vector in the direction of the sum of the given vectors is:
$\frac{4}{\sqrt{29}}\hat{i} + \frac{3}{\sqrt{29}}\hat{j} - \frac{2}{\sqrt{29}}\hat{k}$
Example 9: Write the direction ratio’s of the vector $\vec{a} = \hat{i} + \hat{j} - 2\hat{k}$ and hence calculate its direction cosines.
Answer:
Given:
The vector $\vec{a} = \hat{i} + \hat{j} - 2\hat{k}$.
To Find:
The direction ratios and the direction cosines of the vector $\vec{a}$.
Solution:
Let the given vector be $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$.
The direction ratios of the vector $\vec{a}$ are the coefficients of $\hat{i}$, $\hat{j}$, and $\hat{k}$, which are $a_1$, $a_2$, and $a_3$.
For $\vec{a} = \hat{i} + \hat{j} - 2\hat{k}$, we have $a_1 = 1$, $a_2 = 1$, and $a_3 = -2$.
Therefore, the direction ratios of $\vec{a}$ are $1, 1, -2$.
The direction cosines of a vector $\vec{a}$ are given by the ratios of its components to its magnitude. Let the direction cosines be $l$, $m$, and $n$. They are given by:
$l = \frac{a_1}{|\vec{a}|}$, $m = \frac{a_2}{|\vec{a}|}$, $n = \frac{a_3}{|\vec{a}|}$.
First, calculate the magnitude of the vector $\vec{a}$: $|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$.
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (-2)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 4}$
$|\vec{a}| = \sqrt{6}$
Now, calculate the direction cosines using the components and the magnitude:
$l = \frac{1}{\sqrt{6}}$
$m = \frac{1}{\sqrt{6}}$
$n = \frac{-2}{\sqrt{6}}$
The direction cosines are $\frac{1}{\sqrt{6}}$, $\frac{1}{\sqrt{6}}$, and $\frac{-2}{\sqrt{6}}$.
The direction ratios of $\vec{a}$ are:
$1, 1, -2$
The direction cosines of $\vec{a}$ are:
$\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{-2}{\sqrt{6}}$
Example 10: Find the vector joining the points P(2, 3, 0) and Q(– 1, – 2, – 4) directed from P to Q.
Answer:
Given:
Point P with coordinates $(2, 3, 0)$.
Point Q with coordinates $(-1, -2, -4)$.
To Find:
The vector joining points P and Q, directed from P to Q.
Solution:
Let O be the origin. The position vector of point P is $\vec{OP} = 2\hat{i} + 3\hat{j} + 0\hat{k}$.
The position vector of point Q is $\vec{OQ} = -1\hat{i} - 2\hat{j} - 4\hat{k}$.
The vector joining point P to point Q, denoted by $\vec{PQ}$, is given by the position vector of Q minus the position vector of P.
$\vec{PQ} = \vec{OQ} - \vec{OP}$
$\vec{PQ} = (-1\hat{i} - 2\hat{j} - 4\hat{k}) - (2\hat{i} + 3\hat{j} + 0\hat{k})$
Combine the corresponding components:
$\vec{PQ} = (-1 - 2)\hat{i} + (-2 - 3)\hat{j} + (-4 - 0)\hat{k}$
$\vec{PQ} = -3\hat{i} - 5\hat{j} - 4\hat{k}$
The vector joining P to Q is:
$-3\hat{i} - 5\hat{j} - 4\hat{k}$
Example 11: Consider two points P and Q with position vectors $\overline{OP} = 3\vec{a} - 2\vec{b}$ and $\overrightarrow{OQ} = \vec{a} + \vec{b}$ . Find the position vector of a point R which divides the line joining P and Q in the ratio 2:1,
(i) internally, and
(ii) externally
Answer:
Given:
Position vector of point P, $\vec{p} = \vec{OP} = 3\vec{a} - 2\vec{b}$.
Position vector of point Q, $\vec{q} = \vec{OQ} = \vec{a} + \vec{b}$.
Point R divides the line joining P and Q in the ratio $m:n = 2:1$.
To Find:
The position vector of point R when it divides the line segment PQ:
(i) internally, and
(ii) externally.
Solution:
Let the position vector of point R be $\vec{r} = \vec{OR}$.
We use the section formula for vectors.
The point R divides the line joining P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) in the ratio $m:n$.
(i) Internal Division:
If R divides PQ internally in the ratio $m:n$, its position vector is given by:
$\vec{r} = \frac{n\vec{p} + m\vec{q}}{m + n}$
Given $m = 2$, $n = 1$, $\vec{p} = 3\vec{a} - 2\vec{b}$, and $\vec{q} = \vec{a} + \vec{b}$.
Substitute these values into the formula:
$\vec{r} = \frac{1 \cdot (3\vec{a} - 2\vec{b}) + 2 \cdot (\vec{a} + \vec{b})}{2 + 1}$
$\vec{r} = \frac{3\vec{a} - 2\vec{b} + 2\vec{a} + 2\vec{b}}{3}$
Combine like terms in the numerator:
$\vec{r} = \frac{(3\vec{a} + 2\vec{a}) + (-2\vec{b} + 2\vec{b})}{3}$
$\vec{r} = \frac{5\vec{a} + 0\vec{b}}{3}$
$\vec{r} = \frac{5\vec{a}}{3}$
(ii) External Division:
If R divides PQ externally in the ratio $m:n$, its position vector is given by:
$\vec{r} = \frac{n\vec{p} - m\vec{q}}{n - m}$
Given $m = 2$, $n = 1$, $\vec{p} = 3\vec{a} - 2\vec{b}$, and $\vec{q} = \vec{a} + \vec{b}$.
Substitute these values into the formula:
$\vec{r} = \frac{1 \cdot (3\vec{a} - 2\vec{b}) - 2 \cdot (\vec{a} + \vec{b})}{1 - 2}$
$\vec{r} = \frac{3\vec{a} - 2\vec{b} - (2\vec{a} + 2\vec{b})}{-1}$
$\vec{r} = \frac{3\vec{a} - 2\vec{b} - 2\vec{a} - 2\vec{b}}{-1}$
Combine like terms in the numerator:
$\vec{r} = \frac{(3\vec{a} - 2\vec{a}) + (-2\vec{b} - 2\vec{b})}{-1}$
$\vec{r} = \frac{\vec{a} - 4\vec{b}}{-1}$
$\vec{r} = -(\vec{a} - 4\vec{b})$
$\vec{r} = -\vec{a} + 4\vec{b}$
$\vec{r} = 4\vec{b} - \vec{a}$
The position vector of point R when it divides the line segment PQ:
(i) Internally: $\frac{5}{3}\vec{a}$
(ii) Externally: $4\vec{b} - \vec{a}$
Example 12: Show that the points $A(2\hat{i} - \hat{j} + \hat{k})$ , $B(\hat{i} - 3\hat{j} − 5\hat{k})$, $C(3\hat{i} - 4\hat{j} - 4\hat{k})$ are the vertices of a right angled triangle.
Answer:
Given:
The position vectors of points A, B, and C are:
$\vec{a} = \vec{OA} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{b} = \vec{OB} = \hat{i} - 3\hat{j} - 5\hat{k}$
$\vec{c} = \vec{OC} = 3\hat{i} - 4\hat{j} - 4\hat{k}$
To Show:
That the points A, B, and C are the vertices of a right-angled triangle.
Proof:
To show that the points A, B, and C form a right-angled triangle, we can find the vectors representing the sides of the triangle and check if any pair of these vectors is perpendicular. Two vectors are perpendicular if their dot product is zero.
Let's find the vectors representing the sides $\vec{AB}$, $\vec{BC}$, and $\vec{CA}$.
Vector $\vec{AB} = \vec{OB} - \vec{OA}$:
$\vec{AB} = (\hat{i} - 3\hat{j} - 5\hat{k}) - (2\hat{i} - \hat{j} + \hat{k})$
$\vec{AB} = (1 - 2)\hat{i} + (-3 - (-1))\hat{j} + (-5 - 1)\hat{k}$
$\vec{AB} = -1\hat{i} - 2\hat{j} - 6\hat{k}$
Vector $\vec{BC} = \vec{OC} - \vec{OB}$:
$\vec{BC} = (3\hat{i} - 4\hat{j} - 4\hat{k}) - (\hat{i} - 3\hat{j} - 5\hat{k})$
$\vec{BC} = (3 - 1)\hat{i} + (-4 - (-3))\hat{j} + (-4 - (-5))\hat{k}$
$\vec{BC} = 2\hat{i} - \hat{j} + \hat{k}$
Vector $\vec{CA} = \vec{OA} - \vec{OC}$:
$\vec{CA} = (2\hat{i} - \hat{j} + \hat{k}) - (3\hat{i} - 4\hat{j} - 4\hat{k})$
$\vec{CA} = (2 - 3)\hat{i} + (-1 - (-4))\hat{j} + (1 - (-4))\hat{k}$
$\vec{CA} = -1\hat{i} + 3\hat{j} + 5\hat{k}$
Now, let's calculate the dot product of pairs of these side vectors.
Consider the dot product $\vec{AB} \cdot \vec{BC}$:
$\vec{AB} \cdot \vec{BC} = (-1)(2) + (-2)(-1) + (-6)(1)$
$= -2 + 2 - 6$
$= -6$
Since $\vec{AB} \cdot \vec{BC} \neq 0$, the angle at B is not $90^\circ$.
Consider the dot product $\vec{BC} \cdot \vec{CA}$:
$\vec{BC} \cdot \vec{CA} = (2)(-1) + (-1)(3) + (1)(5)$
$= -2 - 3 + 5$
$= 0$
Since $\vec{BC} \cdot \vec{CA} = 0$, the vectors $\vec{BC}$ and $\vec{CA}$ are perpendicular. The angle between $\vec{BC}$ and $\vec{CA}$ is the angle at the vertex C.
Thus, the angle $\angle BCA = 90^\circ$.
Since one of the angles of the triangle ABC is $90^\circ$, the triangle ABC is a right-angled triangle with the right angle at C.
Conclusion:
Since $\vec{BC} \cdot \vec{CA} = 0$, the vectors $\vec{BC}$ and $\vec{CA}$ are orthogonal. This proves that the angle at vertex C is $90^\circ$.
Therefore, the points A, B, and C are the vertices of a right-angled triangle.
Exercise 10.2
Question 1. Compute the magnitude of the following vectors:
$\vec{a} = \hat{i} + \hat{j} + \hat{k}$ ; $\vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k}$ ; $\vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k}$
Answer:
Given:
Three vectors: $\vec{a} = \hat{i} + \hat{j} + \hat{k}$, $\vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k}$, and $\vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k}$.
To Compute:
The magnitude of each given vector.
Solution:
The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is given by the formula $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
For vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$:
Here, $v_1 = 1$, $v_2 = 1$, and $v_3 = 1$.
The magnitude of $\vec{a}$ is:
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (1)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 1}$
$|\vec{a}| = \sqrt{3}$
For vector $\vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k}$:
Here, $v_1 = 2$, $v_2 = -7$, and $v_3 = -3$.
The magnitude of $\vec{b}$ is:
$|\vec{b}| = \sqrt{(2)^2 + (-7)^2 + (-3)^2}$
$|\vec{b}| = \sqrt{4 + 49 + 9}$
$|\vec{b}| = \sqrt{62}$
For vector $\vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k}$:
Here, $v_1 = \frac{1}{\sqrt{3}}$, $v_2 = \frac{1}{\sqrt{3}}$, and $v_3 = -\frac{1}{\sqrt{3}}$.
The magnitude of $\vec{c}$ is:
$|\vec{c}| = \sqrt{\left(\frac{1}{\sqrt{3}}\right)^2 + \left(\frac{1}{\sqrt{3}}\right)^2 + \left(-\frac{1}{\sqrt{3}}\right)^2}$
$|\vec{c}| = \sqrt{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}}$
$|\vec{c}| = \sqrt{\frac{1 + 1 + 1}{3}}$
$|\vec{c}| = \sqrt{\frac{3}{3}}$
$|\vec{c}| = \sqrt{1}$
$|\vec{c}| = 1$
The magnitudes of the vectors are:
$|\vec{a}| = \sqrt{3}$
$|\vec{b}| = \sqrt{62}$
$|\vec{c}| = 1$
Question 2. Write two different vectors having same magnitude.
Answer:
Given:
The requirement is to provide two different vectors that have the same magnitude.
To Provide:
Two examples of vectors $\vec{u}$ and $\vec{v}$ such that $\vec{u} \neq \vec{v}$ but $|\vec{u}| = |\vec{v}|$.
Solution:
Two vectors are different if they differ in magnitude or direction (or both). If they have the same magnitude, they must differ in direction to be different vectors.
Consider vectors in a 2-dimensional plane using $\hat{i}$ and $\hat{j}$. The magnitude of $\vec{v} = a\hat{i} + b\hat{j}$ is $|\vec{v}| = \sqrt{a^2 + b^2}$.
Let's choose simple non-zero components for the vectors.
Consider the vector $\vec{u} = \hat{i} + \hat{j}$.
Its magnitude is $|\vec{u}| = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2}$.
Now, we need another vector $\vec{v}$ such that $|\vec{v}| = \sqrt{2}$ but $\vec{v} \neq \vec{u}$. We can achieve this by changing the signs of the components or swapping them.
Let's try changing the sign of one component:
Consider the vector $\vec{v}_1 = -\hat{i} + \hat{j}$.
Its magnitude is $|\vec{v}_1| = \sqrt{(-1)^2 + (1)^2} = \sqrt{1 + 1} = \sqrt{2}$.
Since the components of $\vec{u} = \hat{i} + \hat{j}$ are $(1, 1)$ and the components of $\vec{v}_1 = -\hat{i} + \hat{j}$ are $(-1, 1)$, and $(1, 1) \neq (-1, 1)$, these two vectors are different. They have the same magnitude, $\sqrt{2}$.
Another example could be by swapping the components:
Consider the vector $\vec{v}_2 = \hat{j} + \hat{i} = \hat{i} + \hat{j}$. This is the same vector. Let's swap and change a sign:
Consider the vector $\vec{v}_3 = 2\hat{i} + 3\hat{j}$. Its magnitude is $\sqrt{2^2+3^2} = \sqrt{4+9} = \sqrt{13}$.
Consider the vector $\vec{v}_4 = 3\hat{i} + 2\hat{j}$. Its magnitude is $\sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13}$.
Here, $\vec{v}_3 = 2\hat{i} + 3\hat{j}$ and $\vec{v}_4 = 3\hat{i} + 2\hat{j}$. Their components are $(2, 3)$ and $(3, 2)$, which are different. Their magnitudes are both $\sqrt{13}$. So, $\vec{v}_3$ and $\vec{v}_4$ are two different vectors with the same magnitude.
Using the first pair identified:
Let $\vec{u} = \hat{i} + \hat{j}$.
Let $\vec{v} = \hat{i} - \hat{j}$.
$|\vec{u}| = \sqrt{1^2 + 1^2} = \sqrt{2}$.
$|\vec{v}| = \sqrt{1^2 + (-1)^2} = \sqrt{1 + 1} = \sqrt{2}$.
The components of $\vec{u}$ are $(1, 1)$ and the components of $\vec{v}$ are $(1, -1)$. Since the components are different, the vectors are different. Their magnitudes are equal.
Two different vectors having the same magnitude are:
$\vec{u} = \hat{i} + \hat{j}$
$\vec{v} = \hat{i} - \hat{j}$
Alternatively, using the second pair identified:
$\vec{u} = 2\hat{i} + 3\hat{j}$
$\vec{v} = 3\hat{i} + 2\hat{j}$
Question 3. Write two different vectors having same direction.
Answer:
Given:
The requirement is to provide two different vectors that have the same direction.
To Provide:
Two examples of vectors $\vec{u}$ and $\vec{v}$ such that $\vec{u} \neq \vec{v}$ and their directions are the same.
Solution:
Two non-zero vectors have the same direction if one is a positive scalar multiple of the other. That is, if $\vec{v} = k \vec{u}$ for some positive scalar $k > 0$.
For the vectors to be different, we must have $\vec{u} \neq \vec{v}$, which implies the scalar multiplier $k$ must not be equal to 1 ($k \neq 1$).
Let's choose a simple non-zero vector, for example:
$\vec{u} = \hat{i} + \hat{j} + \hat{k}$
Now, choose a positive scalar $k$ other than 1. For example, let $k = 2$.
Let the second vector be $\vec{v} = k \vec{u}$.
$\vec{v} = 2 \cdot (\hat{i} + \hat{j} + \hat{k})$
$\vec{v} = 2\hat{i} + 2\hat{j} + 2\hat{k}$
Let's check if these two vectors are different and have the same direction.
The components of $\vec{u}$ are $(1, 1, 1)$. The components of $\vec{v}$ are $(2, 2, 2)$. Since the corresponding components are not equal ($1 \neq 2$), the vectors $\vec{u}$ and $\vec{v}$ are different.
To check the direction, we can find the unit vector in the direction of each vector. The unit vector in the direction of $\vec{w} = w_1\hat{i} + w_2\hat{j} + w_3\hat{k}$ is $\hat{w} = \frac{\vec{w}}{|\vec{w}|} = \frac{w_1\hat{i} + w_2\hat{j} + w_3\hat{k}}{\sqrt{w_1^2 + w_2^2 + w_3^2}}$.
Unit vector in the direction of $\vec{u}$:
$|\vec{u}| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3}$
$\hat{u} = \frac{\hat{i} + \hat{j} + \hat{k}}{\sqrt{3}} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k}$
Unit vector in the direction of $\vec{v}$:
$|\vec{v}| = \sqrt{2^2 + 2^2 + 2^2} = \sqrt{4 + 4 + 4} = \sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}$
$\hat{v} = \frac{2\hat{i} + 2\hat{j} + 2\hat{k}}{2\sqrt{3}} = \frac{2(\hat{i} + \hat{j} + \hat{k})}{2\sqrt{3}} = \frac{\hat{i} + \hat{j} + \hat{k}}{\sqrt{3}} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k}$
Since $\hat{u} = \hat{v}$, the vectors $\vec{u}$ and $\vec{v}$ have the same direction.
We have found two vectors, $\vec{u} = \hat{i} + \hat{j} + \hat{k}$ and $\vec{v} = 2\hat{i} + 2\hat{j} + 2\hat{k}$, which are different but have the same direction.
Two different vectors having the same direction are:
$\vec{u} = \hat{i} + \hat{j} + \hat{k}$
$\vec{v} = 2\hat{i} + 2\hat{j} + 2\hat{k}$
Question 4. Find the values of x and y so that the vectors $2\hat{i} + 3\hat{j}$ and $x\hat{i} + y\hat{j}$ are equal.
Answer:
Given:
Two vectors: $\vec{u} = 2\hat{i} + 3\hat{j}$ and $\vec{v} = x\hat{i} + y\hat{j}$.
The condition that the two vectors are equal, i.e., $\vec{u} = \vec{v}$.
To Find:
The values of $x$ and $y$ that satisfy the condition.
Solution:
Two vectors are equal if and only if their corresponding components are equal.
Given that $\vec{u} = \vec{v}$, we have:
$2\hat{i} + 3\hat{j} = x\hat{i} + y\hat{j}$
Equating the coefficients of $\hat{i}$ on both sides:
$2 = x$
Equating the coefficients of $\hat{j}$ on both sides:
$3 = y$
Therefore, for the vectors to be equal, the value of $x$ must be 2 and the value of $y$ must be 3.
The values are:
$x = 2$
$y = 3$
Question 5. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
Answer:
Given:
Initial point P(2, 1).
Terminal point Q(– 5, 7).
To Find:
The scalar and vector components of the vector with initial point P and terminal point Q.
Solution:
Let the initial point be $P(x_1, y_1) = (2, 1)$ and the terminal point be $Q(x_2, y_2) = (-5, 7)$.
The vector joining the initial point $P(x_1, y_1)$ to the terminal point $Q(x_2, y_2)$ is given by the formula:
$\vec{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j}$
Substitute the coordinates of P and Q:
$\vec{PQ} = (-5 - 2)\hat{i} + (7 - 1)\hat{j}$
$\vec{PQ} = (-7)\hat{i} + (6)\hat{j}$
$\vec{PQ} = -7\hat{i} + 6\hat{j}$
For a vector $\vec{v} = v_1\hat{i} + v_2\hat{j}$, the scalar components are $v_1$ and $v_2$.
The vector components are $v_1\hat{i}$ and $v_2\hat{j}$.
From $\vec{PQ} = -7\hat{i} + 6\hat{j}$, we have:
The scalar components are $-7$ and $6$.
The vector components are $-7\hat{i}$ and $6\hat{j}$.
The scalar components of the vector are:
$-7, 6$
The vector components of the vector are:
$-7\hat{i}, 6\hat{j}$
Question 6. Find the sum of the vectors $\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$ , $\vec{b} = -2\hat{i} + 4\hat{j} + 5\hat{k}$ and $\vec{c} = \hat{i} - 6\hat{j} - 7\hat{k}$.
Answer:
Given:
Vector $\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$.
Vector $\vec{b} = -2\hat{i} + 4\hat{j} + 5\hat{k}$.
Vector $\vec{c} = \hat{i} - 6\hat{j} - 7\hat{k}$.
To Find:
The sum of the vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Solution:
To find the sum of vectors, we add their corresponding components.
Let the sum of the vectors be $\vec{S}$.
$\vec{S} = \vec{a} + \vec{b} + \vec{c}$
$\vec{S} = (\hat{i} - 2\hat{j} + \hat{k}) + (-2\hat{i} + 4\hat{j} + 5\hat{k}) + (\hat{i} - 6\hat{j} - 7\hat{k})$
Group the coefficients of $\hat{i}$, $\hat{j}$, and $\hat{k}$:
$\vec{S} = (1 + (-2) + 1)\hat{i} + (-2 + 4 + (-6))\hat{j} + (1 + 5 + (-7))\hat{k}$
$\vec{S} = (1 - 2 + 1)\hat{i} + (-2 + 4 - 6)\hat{j} + (1 + 5 - 7)\hat{k}$
Calculate the sum of the coefficients for each component:
For $\hat{i}$: $1 - 2 + 1 = 0$
For $\hat{j}$: $-2 + 4 - 6 = 2 - 6 = -4$
For $\hat{k}$: $1 + 5 - 7 = 6 - 7 = -1$
So, the sum vector is:
$\vec{S} = 0\hat{i} - 4\hat{j} - 1\hat{k}$
$\vec{S} = -4\hat{j} - \hat{k}$
The sum of the given vectors is:
$-4\hat{j} - \hat{k}$
Question 7. Find the unit vector in the direction of the vector $\vec{a} = \hat{i} + \hat{j} + 2\hat{k}$.
Answer:
Given:
The vector $\vec{a} = \hat{i} + \hat{j} + 2\hat{k}$.
To Find:
The unit vector in the direction of $\vec{a}$.
Solution:
The unit vector in the direction of a non-zero vector $\vec{a}$ is given by the formula:
$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$
First, we need to find the magnitude of the vector $\vec{a}$. The magnitude of a vector $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ is given by $|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$.
For the given vector $\vec{a} = \hat{i} + \hat{j} + 2\hat{k}$, we have $a_1 = 1$, $a_2 = 1$, and $a_3 = 2$.
Calculate the magnitude $|\vec{a}| $:
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (2)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 4}$
$|\vec{a}| = \sqrt{6}$
Now, substitute the vector $\vec{a}$ and its magnitude $|\vec{a}|$ into the formula for the unit vector:
$\hat{a} = \frac{\hat{i} + \hat{j} + 2\hat{k}}{\sqrt{6}}$
This can be written as:
$\hat{a} = \frac{1}{\sqrt{6}}\hat{i} + \frac{1}{\sqrt{6}}\hat{j} + \frac{2}{\sqrt{6}}\hat{k}$
The unit vector in the direction of $\vec{a}$ is:
$\frac{1}{\sqrt{6}}\hat{i} + \frac{1}{\sqrt{6}}\hat{j} + \frac{2}{\sqrt{6}}\hat{k}$
Question 8. Find the unit vector in the direction of vector $\overrightarrow{PQ}$, where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
Answer:
Given:
Initial point P(1, 2, 3).
Terminal point Q(4, 5, 6).
To Find:
The unit vector in the direction of the vector $\overrightarrow{PQ}$.
Solution:
First, find the vector $\overrightarrow{PQ}$. The vector joining the initial point $P(x_1, y_1, z_1)$ to the terminal point $Q(x_2, y_2, z_2)$ is given by the formula:
$\overrightarrow{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$
Here, $(x_1, y_1, z_1) = (1, 2, 3)$ and $(x_2, y_2, z_2) = (4, 5, 6)$.
Substitute the coordinates of P and Q:
$\overrightarrow{PQ} = (4 - 1)\hat{i} + (5 - 2)\hat{j} + (6 - 3)\hat{k}$
$\overrightarrow{PQ} = 3\hat{i} + 3\hat{j} + 3\hat{k}$
Let $\vec{v} = \overrightarrow{PQ} = 3\hat{i} + 3\hat{j} + 3\hat{k}$.
Now, find the unit vector in the direction of $\vec{v}$. The unit vector $\hat{v}$ is given by $\hat{v} = \frac{\vec{v}}{|\vec{v}|}$.
Calculate the magnitude of $\vec{v}$. The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
For $\vec{v} = 3\hat{i} + 3\hat{j} + 3\hat{k}$, we have $v_1 = 3$, $v_2 = 3$, and $v_3 = 3$.
$|\vec{v}| = \sqrt{(3)^2 + (3)^2 + (3)^2}$
$|\vec{v}| = \sqrt{9 + 9 + 9}$
$|\vec{v}| = \sqrt{27}$
We can simplify $\sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}$.
$|\vec{v}| = 3\sqrt{3}$
Now, divide the vector $\vec{v}$ by its magnitude to find the unit vector:
$\hat{v} = \frac{3\hat{i} + 3\hat{j} + 3\hat{k}}{3\sqrt{3}}$
Factor out 3 from the numerator:
$\hat{v} = \frac{3(\hat{i} + \hat{j} + \hat{k})}{3\sqrt{3}}$
Cancel out the common factor of 3:
$\hat{v} = \frac{\hat{i} + \hat{j} + \hat{k}}{\sqrt{3}}$
This can be written as:
$\hat{v} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k}$
The unit vector in the direction of vector $\overrightarrow{PQ}$ is:
$\frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k}$
Question 9. For given vectors, $\vec{a} = 2\hat{i} - \hat{j} + 2\hat{k}$ and $\vec{b} = -\hat{i} + \hat{j} - \hat{k}$, find the unit vector in the direction of the vector $\vec{a} + \vec{b}$.
Answer:
Given:
Vector $\vec{a} = 2\hat{i} - \hat{j} + 2\hat{k}$.
Vector $\vec{b} = -\hat{i} + \hat{j} - \hat{k}$.
To Find:
The unit vector in the direction of the vector $\vec{a} + \vec{b}$.
Solution:
First, find the sum of the vectors $\vec{a}$ and $\vec{b}$. Let the sum be $\vec{c}$.
$\vec{c} = \vec{a} + \vec{b}$
$\vec{c} = (2\hat{i} - \hat{j} + 2\hat{k}) + (-\hat{i} + \hat{j} - \hat{k})$
Combine the corresponding components:
$\vec{c} = (2 + (-1))\hat{i} + (-1 + 1)\hat{j} + (2 + (-1))\hat{k}$
$\vec{c} = (2 - 1)\hat{i} + (-1 + 1)\hat{j} + (2 - 1)\hat{k}$
$\vec{c} = 1\hat{i} + 0\hat{j} + 1\hat{k}$
$\vec{c} = \hat{i} + \hat{k}$
Now, find the unit vector in the direction of $\vec{c}$. The unit vector $\hat{c}$ is given by $\hat{c} = \frac{\vec{c}}{|\vec{c}|}$.
Calculate the magnitude of $\vec{c}$. The magnitude of a vector $\vec{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$ is $|\vec{c}| = \sqrt{c_1^2 + c_2^2 + c_3^2}$.
For $\vec{c} = \hat{i} + 0\hat{j} + \hat{k}$, we have $c_1 = 1$, $c_2 = 0$, and $c_3 = 1$.
$|\vec{c}| = \sqrt{(1)^2 + (0)^2 + (1)^2}$
$|\vec{c}| = \sqrt{1 + 0 + 1}$
$|\vec{c}| = \sqrt{2}$
Now, divide the vector $\vec{c}$ by its magnitude to find the unit vector:
$\hat{c} = \frac{\hat{i} + \hat{k}}{\sqrt{2}}$
This can be written as:
$\hat{c} = \frac{1}{\sqrt{2}}\hat{i} + \frac{0}{\sqrt{2}}\hat{j} + \frac{1}{\sqrt{2}}\hat{k}$
$\hat{c} = \frac{1}{\sqrt{2}}\hat{i} + \frac{1}{\sqrt{2}}\hat{k}$
The unit vector in the direction of the vector $\vec{a} + \vec{b}$ is:
$\frac{1}{\sqrt{2}}\hat{i} + \frac{1}{\sqrt{2}}\hat{k}$
Question 10. Find a vector in the direction of vector $5\hat{i} - \hat{j} + 2\hat{k}$, which has magnitude 8 units.
Answer:
Given:
The vector $\vec{a} = 5\hat{i} - \hat{j} + 2\hat{k}$.
The desired magnitude of the new vector is 8 units.
To Find:
A vector that is in the same direction as $\vec{a}$ and has a magnitude of 8.
Solution:
A vector in the direction of $\vec{a}$ with a specific magnitude can be found by scaling the unit vector in the direction of $\vec{a}$ by the desired magnitude.
First, find the magnitude of the given vector $\vec{a}$. The magnitude of a vector $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ is given by $|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$.
For $\vec{a} = 5\hat{i} - \hat{j} + 2\hat{k}$, we have $a_1 = 5$, $a_2 = -1$, and $a_3 = 2$.
Calculate the magnitude $|\vec{a}| $:
$|\vec{a}| = \sqrt{(5)^2 + (-1)^2 + (2)^2}$
$|\vec{a}| = \sqrt{25 + 1 + 4}$
$|\vec{a}| = \sqrt{30}$
Next, find the unit vector in the direction of $\vec{a}$. The unit vector $\hat{a}$ is given by $\hat{a} = \frac{\vec{a}}{|\vec{a}|}$.
$\hat{a} = \frac{5\hat{i} - \hat{j} + 2\hat{k}}{\sqrt{30}}$
$\hat{a} = \frac{5}{\sqrt{30}}\hat{i} - \frac{1}{\sqrt{30}}\hat{j} + \frac{2}{\sqrt{30}}\hat{k}$
Now, to find a vector with magnitude 8 in the direction of $\vec{a}$, we multiply the unit vector $\hat{a}$ by the desired magnitude 8.
Let the required vector be $\vec{b}$. Then $\vec{b} = 8 \hat{a}$.
$\vec{b} = 8 \left( \frac{5}{\sqrt{30}}\hat{i} - \frac{1}{\sqrt{30}}\hat{j} + \frac{2}{\sqrt{30}}\hat{k} \right)$
$\vec{b} = \frac{8 \times 5}{\sqrt{30}}\hat{i} - \frac{8 \times 1}{\sqrt{30}}\hat{j} + \frac{8 \times 2}{\sqrt{30}}\hat{k}$
$\vec{b} = \frac{40}{\sqrt{30}}\hat{i} - \frac{8}{\sqrt{30}}\hat{j} + \frac{16}{\sqrt{30}}\hat{k}$
The required vector is:
$\frac{40}{\sqrt{30}}\hat{i} - \frac{8}{\sqrt{30}}\hat{j} + \frac{16}{\sqrt{30}}\hat{k}$
Question 11. Show that the vectors $2\hat{i} - 3\hat{j} + 4\hat{k}$ and $-4\hat{i} + 6\hat{j} - 8\hat{k}$. are collinear.
Answer:
Given:
Vector $\vec{a} = 2\hat{i} - 3\hat{j} + 4\hat{k}$.
Vector $\vec{b} = -4\hat{i} + 6\hat{j} - 8\hat{k}$.
To Show:
That the vectors $\vec{a}$ and $\vec{b}$ are collinear.
Proof:
Two vectors $\vec{a}$ and $\vec{b}$ are said to be collinear if there exists a non-zero scalar $k$ such that $\vec{b} = k\vec{a}$.
Let the components of $\vec{a}$ be $a_1, a_2, a_3$ and the components of $\vec{b}$ be $b_1, b_2, b_3$.
$\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$
$\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$
If $\vec{b} = k\vec{a}$, then $b_1\hat{i} + b_2\hat{j} + b_3\hat{k} = k(a_1\hat{i} + a_2\hat{j} + a_3\hat{k}) = ka_1\hat{i} + ka_2\hat{j} + ka_3\hat{k}$.
This implies that the corresponding components are proportional: $b_1 = ka_1$, $b_2 = ka_2$, and $b_3 = ka_3$. Provided the components of $\vec{a}$ are non-zero, this is equivalent to $\frac{b_1}{a_1} = \frac{b_2}{a_2} = \frac{b_3}{a_3} = k$. If some components are zero, we check the scalar multiplication directly.
Given $\vec{a} = 2\hat{i} - 3\hat{j} + 4\hat{k}$ and $\vec{b} = -4\hat{i} + 6\hat{j} - 8\hat{k}$.
Compare the corresponding components of $\vec{b}$ with $\vec{a}$:
Coefficient of $\hat{i}$: $-4$ compared to $2$. The ratio is $\frac{-4}{2} = -2$.
Coefficient of $\hat{j}$: $6$ compared to $-3$. The ratio is $\frac{6}{-3} = -2$.
Coefficient of $\hat{k}$: $-8$ compared to $4$. The ratio is $\frac{-8}{4} = -2$.
Since the ratios of the corresponding components are equal, i.e., $\frac{-4}{2} = \frac{6}{-3} = \frac{-8}{4} = -2$, we can write $\vec{b}$ as a scalar multiple of $\vec{a}$.
$\vec{b} = -4\hat{i} + 6\hat{j} - 8\hat{k} = -2(2\hat{i}) + (-2)(-3\hat{j}) + (-2)(4\hat{k})$
$\vec{b} = -2(2\hat{i} - 3\hat{j} + 4\hat{k})$
$\vec{b} = -2\vec{a}$
Here, we found a non-zero scalar $k = -2$ such that $\vec{b} = k\vec{a}$.
Conclusion:
Since vector $\vec{b}$ can be expressed as a scalar multiple of vector $\vec{a}$ ($\vec{b} = -2\vec{a}$), the vectors $\vec{a}$ and $\vec{b}$ are collinear.
Question 12. Find the direction cosines of the vector $\hat{i} + 2\hat{j} + 3\hat{k}$.
Answer:
Given:
The vector $\vec{v} = \hat{i} + 2\hat{j} + 3\hat{k}$.
To Find:
The direction cosines of the vector $\vec{v}$.
Solution:
Let the given vector be $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$.
For $\vec{v} = \hat{i} + 2\hat{j} + 3\hat{k}$, the components are $v_1 = 1$, $v_2 = 2$, and $v_3 = 3$.
The direction cosines of a vector are the cosines of the angles that the vector makes with the positive x, y, and z axes. These are given by the ratios of the vector's components to its magnitude.
Let the direction cosines be $l$, $m$, and $n$. The formula for direction cosines is:
$l = \frac{v_1}{|\vec{v}|}$, $m = \frac{v_2}{|\vec{v}|}$, $n = \frac{v_3}{|\vec{v}|}$.
First, we need to calculate the magnitude of the vector $\vec{v}$. The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is given by $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
Calculate the magnitude of $\vec{v}$:
$|\vec{v}| = \sqrt{(1)^2 + (2)^2 + (3)^2}$
$|\vec{v}| = \sqrt{1 + 4 + 9}$
$|\vec{v}| = \sqrt{14}$
Now, calculate the direction cosines using the components and the magnitude:
$l = \frac{1}{\sqrt{14}}$
$m = \frac{2}{\sqrt{14}}$
$n = \frac{3}{\sqrt{14}}$
The direction cosines of the vector $\hat{i} + 2\hat{j} + 3\hat{k}$ are $\frac{1}{\sqrt{14}}$, $\frac{2}{\sqrt{14}}$, and $\frac{3}{\sqrt{14}}$.
The direction cosines are:
$\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}$
Question 13. Find the direction cosines of the vector joining the points A (1, 2, –3) and B(–1, –2, 1), directed from A to B.
Answer:
Given:
Initial point A(1, 2, –3).
Terminal point B(–1, –2, 1).
To Find:
The direction cosines of the vector joining A to B.
Solution:
First, find the vector joining point A to point B, denoted by $\overrightarrow{AB}$. The vector joining the initial point $A(x_1, y_1, z_1)$ to the terminal point $B(x_2, y_2, z_2)$ is given by the formula:
$\overrightarrow{AB} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$
Here, $(x_1, y_1, z_1) = (1, 2, -3)$ and $(x_2, y_2, z_2) = (-1, -2, 1)$.
Substitute the coordinates of A and B:
$\overrightarrow{AB} = (-1 - 1)\hat{i} + (-2 - 2)\hat{j} + (1 - (-3))\hat{k}$
$\overrightarrow{AB} = (-2)\hat{i} + (-4)\hat{j} + (1 + 3)\hat{k}$
$\overrightarrow{AB} = -2\hat{i} - 4\hat{j} + 4\hat{k}$
Let the vector $\vec{v} = \overrightarrow{AB} = -2\hat{i} - 4\hat{j} + 4\hat{k}$. The components are $v_1 = -2$, $v_2 = -4$, and $v_3 = 4$.
The direction cosines of $\vec{v}$ are given by $l = \frac{v_1}{|\vec{v}|}$, $m = \frac{v_2}{|\vec{v}|}$, $n = \frac{v_3}{|\vec{v}|}$.
First, calculate the magnitude of the vector $\vec{v}$:
$|\vec{v}| = \sqrt{(-2)^2 + (-4)^2 + (4)^2}$
$|\vec{v}| = \sqrt{4 + 16 + 16}$
$|\vec{v}| = \sqrt{36}$
$|\vec{v}| = 6$
Now, calculate the direction cosines using the components and the magnitude:
$l = \frac{-2}{6} = -\frac{1}{3}$
$m = \frac{-4}{6} = -\frac{2}{3}$
$n = \frac{4}{6} = \frac{2}{3}$
The direction cosines of the vector $\overrightarrow{AB}$ are $-\frac{1}{3}$, $-\frac{2}{3}$, and $\frac{2}{3}$.
The direction cosines of the vector joining A to B are:
$-\frac{1}{3}, -\frac{2}{3}, \frac{2}{3}$
Question 14. Show that the vector $\hat{i} + \hat{j} + \hat{k}$ is equally inclined to the axes OX, OY and OZ.
Answer:
Given:
The vector $\vec{v} = \hat{i} + \hat{j} + \hat{k}$.
To Show:
That the vector $\vec{v}$ is equally inclined to the axes OX, OY, and OZ.
Proof:
A vector is equally inclined to the axes if the angles it makes with the positive x-axis, y-axis, and z-axis are equal. Let these angles be $\alpha$, $\beta$, and $\gamma$, respectively. The cosines of these angles are the direction cosines of the vector.
The direction cosines of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ are given by:
$l = \cos \alpha = \frac{v_1}{|\vec{v}|}$
$m = \cos \beta = \frac{v_2}{|\vec{v}|}$
$n = \cos \gamma = \frac{v_3}{|\vec{v}|}$
For the given vector $\vec{v} = \hat{i} + \hat{j} + \hat{k}$, we have $v_1 = 1$, $v_2 = 1$, and $v_3 = 1$.
First, calculate the magnitude of the vector $\vec{v}$:
$|\vec{v}| = \sqrt{(1)^2 + (1)^2 + (1)^2}$
$|\vec{v}| = \sqrt{1 + 1 + 1}$
$|\vec{v}| = \sqrt{3}$
Now, calculate the direction cosines:
$\cos \alpha = \frac{1}{\sqrt{3}}$
$\cos \beta = \frac{1}{\sqrt{3}}$
$\cos \gamma = \frac{1}{\sqrt{3}}$
Since $\cos \alpha = \cos \beta = \cos \gamma$, and the angles $\alpha, \beta, \gamma$ are typically considered in the range $[0, \pi]$, having the same cosine value implies the angles are equal.
$\cos \alpha = \cos \beta = \cos \gamma$
$\alpha = \beta = \gamma$
This means the angle the vector makes with the x-axis is equal to the angle it makes with the y-axis, which is also equal to the angle it makes with the z-axis.
Conclusion:
Since the direction cosines of the vector $\hat{i} + \hat{j} + \hat{k}$ are equal, the angles it makes with the coordinate axes OX, OY, and OZ are also equal.
Therefore, the vector $\hat{i} + \hat{j} + \hat{k}$ is equally inclined to the axes OX, OY, and OZ.
Question 15. Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $\hat{i} + 2\hat{j} - \hat{k}$ and $-\hat{i} + \hat{j} + \hat{k}$ respectively, in the ratio 2 : 1.
(i) internally
(ii) externally
Answer:
Given:
Position vector of point P, $\vec{p} = \hat{i} + 2\hat{j} - \hat{k}$.
Position vector of point Q, $\vec{q} = -\hat{i} + \hat{j} + \hat{k}$.
Point R divides the line joining P and Q in the ratio $m:n = 2:1$.
To Find:
The position vector of point R when it divides the line segment PQ:
(i) internally, and
(ii) externally.
Solution:
Let the position vector of point R be $\vec{r}$.
We use the section formula for vectors.
The point R divides the line joining P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) in the ratio $m:n$.
(i) Internal Division:
If R divides PQ internally in the ratio $m:n$, its position vector is given by:
$\vec{r}_{\text{internal}} = \frac{n\vec{p} + m\vec{q}}{m + n}$
Given $m = 2$, $n = 1$, $\vec{p} = \hat{i} + 2\hat{j} - \hat{k}$, and $\vec{q} = -\hat{i} + \hat{j} + \hat{k}$.
Substitute these values into the formula:
$\vec{r}_{\text{internal}} = \frac{1 \cdot (\hat{i} + 2\hat{j} - \hat{k}) + 2 \cdot (-\hat{i} + \hat{j} + \hat{k})}{2 + 1}$
$\vec{r}_{\text{internal}} = \frac{\hat{i} + 2\hat{j} - \hat{k} + (-2\hat{i} + 2\hat{j} + 2\hat{k})}{3}$
$\vec{r}_{\text{internal}} = \frac{(\hat{i} - 2\hat{i}) + (2\hat{j} + 2\hat{j}) + (-\hat{k} + 2\hat{k})}{3}$
$\vec{r}_{\text{internal}} = \frac{-\hat{i} + 4\hat{j} + \hat{k}}{3}$
$\vec{r}_{\text{internal}} = -\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k}$
(ii) External Division:
If R divides PQ externally in the ratio $m:n$, its position vector is given by:
$\vec{r}_{\text{external}} = \frac{n\vec{p} - m\vec{q}}{n - m}$
Given $m = 2$, $n = 1$, $\vec{p} = \hat{i} + 2\hat{j} - \hat{k}$, and $\vec{q} = -\hat{i} + \hat{j} + \hat{k}$.
Substitute these values into the formula:
$\vec{r}_{\text{external}} = \frac{1 \cdot (\hat{i} + 2\hat{j} - \hat{k}) - 2 \cdot (-\hat{i} + \hat{j} + \hat{k})}{1 - 2}$
$\vec{r}_{\text{external}} = \frac{\hat{i} + 2\hat{j} - \hat{k} - (-2\hat{i} + 2\hat{j} + 2\hat{k})}{-1}$
$\vec{r}_{\text{external}} = \frac{\hat{i} + 2\hat{j} - \hat{k} + 2\hat{i} - 2\hat{j} - 2\hat{k}}{-1}$
$\vec{r}_{\text{external}} = \frac{(\hat{i} + 2\hat{i}) + (2\hat{j} - 2\hat{j}) + (-\hat{k} - 2\hat{k})}{-1}$
$\vec{r}_{\text{external}} = \frac{3\hat{i} + 0\hat{j} - 3\hat{k}}{-1}$
$\vec{r}_{\text{external}} = \frac{3\hat{i} - 3\hat{k}}{-1}$
$\vec{r}_{\text{external}} = -3\hat{i} + 3\hat{k}$
The position vector of point R when it divides the line segment PQ:
(i) Internally: $-\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k}$
(ii) Externally: $-3\hat{i} + 3\hat{k}$
Question 16. Find the position vector of the mid point of the vector joining the points P(2, 3, 4) and Q(4, 1, –2).
Answer:
Given:
Point P with coordinates (2, 3, 4).
Point Q with coordinates (4, 1, –2).
To Find:
The position vector of the midpoint of the line segment PQ.
Solution:
Let the position vector of point P be $\vec{p} = 2\hat{i} + 3\hat{j} + 4\hat{k}$.
Let the position vector of point Q be $\vec{q} = 4\hat{i} + 1\hat{j} - 2\hat{k}$.
The midpoint of the line segment joining two points P and Q with position vectors $\vec{p}$ and $\vec{q}$ is the point that divides the segment in the ratio $1:1$.
Using the section formula for internal division with $m=1$ and $n=1$, the position vector of the midpoint M, denoted by $\vec{m}$, is given by:
$\vec{m} = \frac{1\vec{p} + 1\vec{q}}{1 + 1}$
$\vec{m} = \frac{\vec{p} + \vec{q}}{2}$
Substitute the position vectors of P and Q:
$\vec{m} = \frac{(2\hat{i} + 3\hat{j} + 4\hat{k}) + (4\hat{i} + \hat{j} - 2\hat{k})}{2}$
Combine the corresponding components in the numerator:
$\vec{m} = \frac{(2 + 4)\hat{i} + (3 + 1)\hat{j} + (4 - 2)\hat{k}}{2}$
$\vec{m} = \frac{6\hat{i} + 4\hat{j} + 2\hat{k}}{2}$
Divide each component by 2:
$\vec{m} = \frac{6}{2}\hat{i} + \frac{4}{2}\hat{j} + \frac{2}{2}\hat{k}$
$\vec{m} = 3\hat{i} + 2\hat{j} + \hat{k}$
The position vector of the midpoint is:
$3\hat{i} + 2\hat{j} + \hat{k}$
Question 17. Show that the points A, B and C with position vectors, $\vec{a} = 3\hat{i} - 4\hat{j} - 4\hat{k}$, $\vec{b} = 2\hat{i} - \hat{j} + \hat{k}$ and $\vec{c} = \hat{i} - 3\hat{j} - 5\hat{k}$, respectively form the vertices of a right angled triangle.
Answer:
Given:
The position vectors of points A, B, and C are:
$\vec{a} = \vec{OA} = 3\hat{i} - 4\hat{j} - 4\hat{k}$
$\vec{b} = \vec{OB} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{c} = \vec{OC} = \hat{i} - 3\hat{j} - 5\hat{k}$
To Show:
That the points A, B, and C are the vertices of a right-angled triangle.
Proof:
To show that the points A, B, and C form a right-angled triangle, we can find the vectors representing the sides of the triangle and check if the sum of the squares of the magnitudes of two sides is equal to the square of the magnitude of the third side (Pythagorean theorem), or equivalently, check if the dot product of any two side vectors is zero (orthogonality).
Let's find the vectors representing the sides $\overrightarrow{AB}$, $\overrightarrow{BC}$, and $\overrightarrow{CA}$.
Vector $\overrightarrow{AB} = \vec{OB} - \vec{OA}$:
$\overrightarrow{AB} = (2\hat{i} - \hat{j} + \hat{k}) - (3\hat{i} - 4\hat{j} - 4\hat{k})$
$\overrightarrow{AB} = (2 - 3)\hat{i} + (-1 - (-4))\hat{j} + (1 - (-4))\hat{k}$
$\overrightarrow{AB} = -\hat{i} + 3\hat{j} + 5\hat{k}$
Vector $\overrightarrow{BC} = \vec{OC} - \vec{OB}$:
$\overrightarrow{BC} = (\hat{i} - 3\hat{j} - 5\hat{k}) - (2\hat{i} - \hat{j} + \hat{k})$
$\overrightarrow{BC} = (1 - 2)\hat{i} + (-3 - (-1))\hat{j} + (-5 - 1)\hat{k}$
$\overrightarrow{BC} = -\hat{i} - 2\hat{j} - 6\hat{k}$
Vector $\overrightarrow{CA} = \vec{OA} - \vec{OC}$:
$\overrightarrow{CA} = (3\hat{i} - 4\hat{j} - 4\hat{k}) - (\hat{i} - 3\hat{j} - 5\hat{k})$
$\overrightarrow{CA} = (3 - 1)\hat{i} + (-4 - (-3))\hat{j} + (-4 - (-5))\hat{k}$
$\overrightarrow{CA} = 2\hat{i} - \hat{j} + \hat{k}$
Now, calculate the dot product of pairs of these side vectors to check for perpendicularity.
Consider the dot product $\overrightarrow{AB} \cdot \overrightarrow{BC}$:
$\overrightarrow{AB} \cdot \overrightarrow{BC} = (-1)(-1) + (3)(-2) + (5)(-6)$
$= 1 - 6 - 30$
$= -35$
Since $\overrightarrow{AB} \cdot \overrightarrow{BC} \neq 0$, the angle at B is not $90^\circ$.
Consider the dot product $\overrightarrow{BC} \cdot \overrightarrow{CA}$:
$\overrightarrow{BC} \cdot \overrightarrow{CA} = (-1)(2) + (-2)(-1) + (-6)(1)$
$= -2 + 2 - 6$
$= -6$
Since $\overrightarrow{BC} \cdot \overrightarrow{CA} \neq 0$, the angle at C is not $90^\circ$.
Consider the dot product $\overrightarrow{CA} \cdot \overrightarrow{AB}$:
$\overrightarrow{CA} \cdot \overrightarrow{AB} = (2)(-1) + (-1)(3) + (1)(5)$
$= -2 - 3 + 5$
$= 0$
Since $\overrightarrow{CA} \cdot \overrightarrow{AB} = 0$, the vectors $\overrightarrow{CA}$ and $\overrightarrow{AB}$ are perpendicular. The angle between $\overrightarrow{CA}$ and $\overrightarrow{AB}$ is the angle at vertex A.
Thus, the angle $\angle CAB = 90^\circ$.
Since one of the angles of the triangle ABC is $90^\circ$, the triangle ABC is a right-angled triangle with the right angle at A.
Conclusion:
Since $\overrightarrow{CA} \cdot \overrightarrow{AB} = 0$, the vectors $\overrightarrow{CA}$ and $\overrightarrow{AB}$ are orthogonal. This proves that the angle at vertex A is $90^\circ$.
Therefore, the points A, B, and C are the vertices of a right-angled triangle.
Question 18. In triangle ABC (Fig 10.18), which of the following is not true:
(A) $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \vec{0}$
(B) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}$
(C) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \vec{0}$
(D) $\overrightarrow{AB} - \overrightarrow{CB} + \overrightarrow{AC} = \vec{0}$
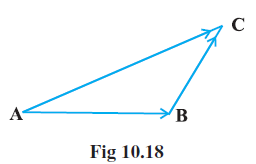
Answer:
In triangle ABC, according to the triangle law of vector addition, the sum of two sides taken in order is equal to the third side taken in the opposite order. That is, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.
Let's analyze each option:
(A) $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \vec{0}$
Using the triangle law, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$. Substituting this into the expression, we get $\overrightarrow{AC} + \overrightarrow{CA}$. Since $\overrightarrow{CA} = -\overrightarrow{AC}$, this becomes $\overrightarrow{AC} + (-\overrightarrow{AC}) = \vec{0}$. This statement is true.
(B) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}$
Using the triangle law, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$. Substituting this into the expression, we get $\overrightarrow{AC} - \overrightarrow{AC} = \vec{0}$. This statement is true.
(C) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \vec{0}$
Using the triangle law, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$. Substituting this into the expression, we get $\overrightarrow{AC} - \overrightarrow{CA} = \vec{0}$.
Since $\overrightarrow{CA} = -\overrightarrow{AC}$, the equation becomes:
$\overrightarrow{AC} - (-\overrightarrow{AC}) = \vec{0}$
$\overrightarrow{AC} + \overrightarrow{AC} = \vec{0}$
$2\overrightarrow{AC} = \vec{0}$
This implies $\overrightarrow{AC} = \vec{0}$. This is only possible if point A and point C coincide, which is not the case in a triangle. Therefore, this statement is not true.
(D) $\overrightarrow{AB} - \overrightarrow{CB} + \overrightarrow{AC} = \vec{0}$
We know that $\overrightarrow{-CB} = \overrightarrow{BC}$. Substituting this into the expression, we get $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{AC} = \vec{0}$.
Using the triangle law, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$. Substituting this, we get $\overrightarrow{AC} + \overrightarrow{AC} = \vec{0}$, which is $2\overrightarrow{AC} = \vec{0}$. Similar to (C), this implies $\overrightarrow{AC} = \vec{0}$, which is not possible in a triangle. Therefore, this statement is also not true.
In a multiple-choice question asking for the statement that is "not true", there is expected to be only one such statement among the options provided for a non-degenerate triangle. While both (C) and (D) simplify to $2\overrightarrow{AC} = \vec{0}$ (which is false for a triangle), option (C) is the commonly accepted answer for this specific question in NCERT.
The statement which is not true is (C) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \vec{0}$.
Question 19. If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then which of the following are incorrect:
(A) $\vec{b} = λ \vec{a}$, for some scalar λ
(B) $\vec{a} = ± \vec{b}$
(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional
(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.
Answer:
Two vectors $\vec{a}$ and $\vec{b}$ are said to be collinear if they are parallel to the same line. This means that one vector can be expressed as a scalar multiple of the other. Formally, $\vec{a}$ and $\vec{b}$ are collinear if and only if there exists a scalar $\lambda$ such that $\vec{b} = \lambda \vec{a}$ (assuming $\vec{a} \neq \vec{0}$) or there exists a scalar $\mu$ such that $\vec{a} = \mu \vec{b}$ (assuming $\vec{b} \neq \vec{0}$). If both are zero vectors, they are also collinear.
Let's analyse each statement:
(A) $\vec{b} = λ \vec{a}$, for some scalar λ
This is a fundamental definition and property of collinear vectors. If $\vec{a}$ and $\vec{b}$ are collinear, then $\vec{b}$ must be a scalar multiple of $\vec{a}$ (unless $\vec{a} = \vec{0}$, in which case $\vec{b}$ must also be $\vec{0}$, and $\vec{0} = \lambda \vec{0}$ holds for any $\lambda$, but more specifically $\vec{b}=0\vec{a}$ is true). Conversely, if $\vec{b} = \lambda \vec{a}$ for some scalar $\lambda$, then $\vec{a}$ and $\vec{b}$ are parallel and hence collinear. This statement is always correct.
(B) $\vec{a} = ± \vec{b}$
This statement means $\vec{a} = \vec{b}$ or $\vec{a} = -\vec{b}$. This implies that the vectors have the same magnitude ($|\vec{a}| = |\vec{b}|$) and are either in the same direction ($\vec{a} = \vec{b}$) or in opposite directions ($\vec{a} = -\vec{b}$). While these are cases of collinearity, not all collinear vectors satisfy this condition. For example, if $\vec{a}$ is a non-zero vector, the vector $2\vec{a}$ is collinear with $\vec{a}$, but $2\vec{a} \neq \pm \vec{a}$ (unless $\vec{a}=\vec{0}$). The statement claims that *if* vectors are collinear, *then* this must be true. This is false. This statement is incorrect.
(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional
If $\vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}$ and $\vec{b} = b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k}$ are two non-zero collinear vectors, then $\vec{b} = \lambda \vec{a}$ for some non-zero scalar $\lambda$. This implies that their corresponding components are related by $b_1 = \lambda a_1$, $b_2 = \lambda a_2$, and $b_3 = \lambda a_3$. If the components $a_1, a_2, a_3$ are non-zero, this means $\frac{b_1}{a_1} = \frac{b_2}{a_2} = \frac{b_3}{a_3} = \lambda$. This shows that their respective components are proportional. If some components of $\vec{a}$ are zero, the corresponding components of $\vec{b}$ must also be zero, and proportionality still holds (e.g., $b_i = \lambda \cdot 0 = 0$). The statement claims that the components are *not* proportional, which contradicts the property of collinear vectors. This statement is incorrect.
(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.
If two collinear vectors $\vec{a}$ and $\vec{b}$ have the same direction, then $\vec{b} = \lambda \vec{a}$ where $\lambda > 0$. If they also have different magnitudes, it means $|\vec{b}| \neq |\vec{a}|$. This corresponds to the case where $\lambda > 0$ and $\lambda \neq 1$. While this describes a specific subset of collinear vectors, it does not describe all collinear vectors. Collinear vectors can have opposite directions (e.g., $\vec{b} = -\vec{a}$), or they can have the same magnitude (e.g., $\vec{b} = \vec{a}$). The statement claims that *if* vectors are collinear, *then* they *must* have the same direction and different magnitudes. This is false. This statement is incorrect.
Based on the analysis, statements (B), (C), and (D) are incorrect assertions that are not true for all pairs of collinear vectors.
The incorrect statements are:
(B) $\vec{a} = ± \vec{b}$
(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional
(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.
Example 13 to 21 (Before Exercise 10.3)
Example 13: Find the angle between two vectors $\vec{a}$ and $\vec{b}$ with magnitudes 1 and 2 respectively and when $\vec{a} \;.\; \vec{b} = 1$.
Answer:
Given:
Magnitude of vector $\vec{a}$, $|\vec{a}| = 1$.
Magnitude of vector $\vec{b}$, $|\vec{b}| = 2$.
Dot product of $\vec{a}$ and $\vec{b}$, $\vec{a} \;.\; \vec{b} = 1$.
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The dot product of two vectors $\vec{a}$ and $\vec{b}$ is given by the formula:
$\vec{a} \;.\; \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
where $\theta$ is the angle between the vectors.
Substitute the given values into the formula:
$1 = (1)(2) \cos \theta$
Simplify the equation:
$1 = 2 \cos \theta$
Solve for $\cos \theta$:
$\cos \theta = \frac{1}{2}$
To find the angle $\theta$, we take the inverse cosine of $\frac{1}{2}$. The principal value of $\theta$ lies in the interval $[0, \pi]$.
$\theta = \cos^{-1} \left(\frac{1}{2}\right)$
The angle whose cosine is $\frac{1}{2}$ is $\frac{\pi}{3}$ (or $60^\circ$).
$\theta = \frac{\pi}{3}$
Thus, the angle between the two vectors $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{3}$.
Example 14: Find angle ‘θ’ between the vectors $\vec{a} = \hat{i} + \hat{j} - \hat{k}$ and $\vec{b} = \hat{i} - \hat{j} + \hat{k}$.
Answer:
Given:
Vector $\vec{a} = \hat{i} + \hat{j} - \hat{k}$.
Vector $\vec{b} = \hat{i} - \hat{j} + \hat{k}$.
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The angle $\theta$ between two vectors $\vec{a}$ and $\vec{b}$ is given by the formula:
$\cos \theta = \frac{\vec{a} \;.\; \vec{b}}{|\vec{a}| |\vec{b}|}$
First, calculate the dot product $\vec{a} \;.\; \vec{b}$:
$\vec{a} \;.\; \vec{b} = (\hat{i} + \hat{j} - \hat{k}) \;.\; (\hat{i} - \hat{j} + \hat{k})$
$\vec{a} \;.\; \vec{b} = (1)(1) + (1)(-1) + (-1)(1)$
$\vec{a} \;.\; \vec{b} = 1 - 1 - 1$
$\vec{a} \;.\; \vec{b} = -1$
Next, calculate the magnitude of vector $\vec{a}$:
$|\vec{a}| = |\hat{i} + \hat{j} - \hat{k}|$
$|\vec{a}| = \sqrt{1^2 + 1^2 + (-1)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 1}$
$|\vec{a}| = \sqrt{3}$
Now, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = |\hat{i} - \hat{j} + \hat{k}|$
$|\vec{b}| = \sqrt{1^2 + (-1)^2 + 1^2}$
$|\vec{b}| = \sqrt{1 + 1 + 1}$
$|\vec{b}| = \sqrt{3}$
Substitute the dot product and magnitudes into the formula for $\cos \theta$:
$\cos \theta = \frac{-1}{(\sqrt{3})(\sqrt{3})}$
$\cos \theta = \frac{-1}{3}$
To find the angle $\theta$, take the inverse cosine of $\left(-\frac{1}{3}\right)$:
$\theta = \cos^{-1} \left(-\frac{1}{3}\right)$
The angle between the vectors $\vec{a}$ and $\vec{b}$ is $\cos^{-1} \left(-\frac{1}{3}\right)$.
Example 15: If $\vec{a} = 5\hat{i} - \hat{j} - 3\hat{k}$, then $\vec{b} = \hat{i} + 3\hat{j} - 5\hat{k}$, then show that the vectors $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$ are prependicular.
Answer:
Given:
Vector $\vec{a} = 5\hat{i} - \hat{j} - 3\hat{k}$.
Vector $\vec{b} = \hat{i} + 3\hat{j} - 5\hat{k}$.
To Show:
Vectors $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$ are perpendicular.
Solution:
Two non-zero vectors are perpendicular if their dot product is zero.
First, let's find the vector $\vec{a} + \vec{b}$:
$\vec{a} + \vec{b} = (5\hat{i} - \hat{j} - 3\hat{k}) + (\hat{i} + 3\hat{j} - 5\hat{k})$
$\vec{a} + \vec{b} = (5+1)\hat{i} + (-1+3)\hat{j} + (-3-5)\hat{k}$
$\vec{a} + \vec{b} = 6\hat{i} + 2\hat{j} - 8\hat{k}$
Next, let's find the vector $\vec{a} - \vec{b}$:
$\vec{a} - \vec{b} = (5\hat{i} - \hat{j} - 3\hat{k}) - (\hat{i} + 3\hat{j} - 5\hat{k})$
$\vec{a} - \vec{b} = (5-1)\hat{i} + (-1-3)\hat{j} + (-3-(-5))\hat{k}$
$\vec{a} - \vec{b} = 4\hat{i} - 4\hat{j} + (-3+5)\hat{k}$
$\vec{a} - \vec{b} = 4\hat{i} - 4\hat{j} + 2\hat{k}$
Now, calculate the dot product of $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = (6\hat{i} + 2\hat{j} - 8\hat{k}) \;.\; (4\hat{i} - 4\hat{j} + 2\hat{k})$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = (6)(4) + (2)(-4) + (-8)(2)$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 24 - 8 - 16$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 24 - 24$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 0$
Since the dot product of $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$ is 0, the two vectors are perpendicular.
Example 16: Find the projection of the vector $\vec{a} = 2\hat{i} + 3\hat{j} + 2\hat{k}$ on the vector $\vec{b} = \hat{i} + 2\hat{j} + \hat{k}$.
Answer:
Given:
Vector $\vec{a} = 2\hat{i} + 3\hat{j} + 2\hat{k}$.
Vector $\vec{b} = \hat{i} + 2\hat{j} + \hat{k}$.
To Find:
The projection of vector $\vec{a}$ on the vector $\vec{b}$.
Solution:
The projection of vector $\vec{a}$ on vector $\vec{b}$ (scalar projection) is given by the formula:
Projection of $\vec{a}$ on $\vec{b} = \frac{\vec{a} \;.\; \vec{b}}{|\vec{b}|}$
First, calculate the dot product $\vec{a} \;.\; \vec{b}$:
$\vec{a} \;.\; \vec{b} = (2\hat{i} + 3\hat{j} + 2\hat{k}) \;.\; (\hat{i} + 2\hat{j} + \hat{k})$
$\vec{a} \;.\; \vec{b} = (2)(1) + (3)(2) + (2)(1)$
$\vec{a} \;.\; \vec{b} = 2 + 6 + 2$
$\vec{a} \;.\; \vec{b} = 10$
Next, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = |\hat{i} + 2\hat{j} + \hat{k}|$
$|\vec{b}| = \sqrt{1^2 + 2^2 + 1^2}$
$|\vec{b}| = \sqrt{1 + 4 + 1}$
$|\vec{b}| = \sqrt{6}$
Now, substitute the dot product and magnitude into the formula for the projection:
Projection of $\vec{a}$ on $\vec{b} = \frac{10}{\sqrt{6}}$
The projection can be rationalized by multiplying the numerator and denominator by $\sqrt{6}$:
Projection of $\vec{a}$ on $\vec{b} = \frac{10}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}$
Projection of $\vec{a}$ on $\vec{b} = \frac{10\sqrt{6}}{6}$
Projection of $\vec{a}$ on $\vec{b} = \frac{5\sqrt{6}}{3}$
The projection of vector $\vec{a}$ on vector $\vec{b}$ is $\frac{10}{\sqrt{6}}$ or $\frac{5\sqrt{6}}{3}$.
Example 17: Find $|\;\vec{a} - \vec{b}\;|$, if two vectors $\vec{a}$ and $\vec{b}$ are such that $|\;\vec{a}\;| = 2$, $|\;\vec{b}\;| = 3$ and $\vec{a} \;.\; \vec{b} = 4$.
Answer:
Given:
Magnitude of vector $\vec{a}$, $|\vec{a}| = 2$.
Magnitude of vector $\vec{b}$, $|\vec{b}| = 3$.
Dot product of $\vec{a}$ and $\vec{b}$, $\vec{a} \;.\; \vec{b} = 4$.
To Find:
The magnitude of the difference between vectors $\vec{a}$ and $\vec{b}$, $|\;\vec{a} - \vec{b}\;|$.
Solution:
We know that the square of the magnitude of a vector is equal to the dot product of the vector with itself. Therefore, $|\;\vec{a} - \vec{b}\;|^2 = (\vec{a} - \vec{b}) \;.\; (\vec{a} - \vec{b})$.
Expand the dot product:
$|\;\vec{a} - \vec{b}\;|^2 = \vec{a} \;.\; \vec{a} - \vec{a} \;.\; \vec{b} - \vec{b} \;.\; \vec{a} + \vec{b} \;.\; \vec{b}$
Using the properties of the dot product, $\vec{a} \;.\; \vec{a} = |\;\vec{a}\;|^2$, $\vec{b} \;.\; \vec{b} = |\;\vec{b}\;|^2$, and $\vec{b} \;.\; \vec{a} = \vec{a} \;.\; \vec{b}$:
$|\;\vec{a} - \vec{b}\;|^2 = |\;\vec{a}\;|^2 - 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2$
Substitute the given values into this equation:
$|\;\vec{a} - \vec{b}\;|^2 = (2)^2 - 2(4) + (3)^2$
$|\;\vec{a} - \vec{b}\;|^2 = 4 - 8 + 9$
$|\;\vec{a} - \vec{b}\;|^2 = 5$
To find $|\;\vec{a} - \vec{b}\;|$, take the square root of both sides:
$|\;\vec{a} - \vec{b}\;| = \sqrt{5}$
The magnitude of the vector $\vec{a} - \vec{b}$ is $\sqrt{5}$.
Example 18: If $\vec{a}$ is a unit vector and $(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 8$, then find $|\;\vec{x}\;|$.
Answer:
Given:
Vector $\vec{a}$ is a unit vector, which means its magnitude is 1. Thus, $|\vec{a}| = 1$.
The dot product equation: $(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 8$.
To Find:
The magnitude of vector $\vec{x}$, i.e., $|\;\vec{x}\;|$.
Solution:
We are given the equation $(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 8$.
Using the distributive property of the dot product, we can expand the left side of the equation:
$(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = \vec{x} \;.\; (\vec{x} + \vec{a}) - \vec{a} \;.\; (\vec{x} + \vec{a})$
$= (\vec{x} \;.\; \vec{x} + \vec{x} \;.\; \vec{a}) - (\vec{a} \;.\; \vec{x} + \vec{a} \;.\; \vec{a})$
$= \vec{x} \;.\; \vec{x} + \vec{x} \;.\; \vec{a} - \vec{a} \;.\; \vec{x} - \vec{a} \;.\; \vec{a}$
We know that $\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$ and that the dot product is commutative, i.e., $\vec{a} \;.\; \vec{x} = \vec{x} \;.\; \vec{a}$.
So, the expansion becomes:
$= |\;\vec{x}\;|^2 + \vec{x} \;.\; \vec{a} - \vec{x} \;.\; \vec{a} - |\;\vec{a}\;|^2$
$= |\;\vec{x}\;|^2 - |\;\vec{a}\;|^2$
Now, substitute this back into the given equation:
$|\;\vec{x}\;|^2 - |\;\vec{a}\;|^2 = 8$
We are given that $\vec{a}$ is a unit vector, so $|\;\vec{a}\;| = 1$. Substitute this value into the equation:
$|\;\vec{x}\;|^2 - (1)^2 = 8$
$|\;\vec{x}\;|^2 - 1 = 8$
Solve for $|\;\vec{x}\;|^2$:
$|\;\vec{x}\;|^2 = 8 + 1$
$|\;\vec{x}\;|^2 = 9$
To find $|\;\vec{x}\;|$, take the square root of both sides. Since magnitude is always non-negative, we take the positive root:
$|\;\vec{x}\;| = \sqrt{9}$
$|\;\vec{x}\;| = 3$
The magnitude of vector $\vec{x}$ is 3.
Example 19: For any two vectors $\vec{a}$ and $\vec{b}$, we always have $|\;\vec{a}\;.\; \vec{b}\;| ≤ |\;\vec{a}\;|\; |\;\vec{b}\;|$ (Cauchy-Schwartz inequality).
Answer:
Given:
Two vectors $\vec{a}$ and $\vec{b}$.
To Prove:
The Cauchy-Schwartz inequality: $|\;\vec{a} \;.\; \vec{b}\;| ≤ |\;\vec{a}\;|\; |\;\vec{b}\;|$.
Proof:
The dot product of two vectors $\vec{a}$ and $\vec{b}$ is defined as:
$\vec{a} \;.\; \vec{b} = |\;\vec{a}\;|\; |\;\vec{b}\;| \cos \theta$
... (i)
where $\theta$ is the angle between the vectors $\vec{a}$ and $\vec{b}$ ($0 \leq \theta \leq \pi$).
Taking the absolute value of both sides of equation (i):
$|\;\vec{a} \;.\; \vec{b}\;| = |\; |\;\vec{a}\;|\; |\;\vec{b}\;| \cos \theta \;|$
$|\;\vec{a} \;.\; \vec{b}\;| = |\;\vec{a}\;|\; |\;\vec{b}\;| |\;\cos \theta\;|$
[Since $|\;\vec{a}\;|$ and $|\;\vec{b}\;|$ are non-negative magnitudes]
We know that the value of $\cos \theta$ is always between -1 and 1, i.e., $-1 \leq \cos \theta \leq 1$.
Taking the absolute value, we get:
$0 \leq |\;\cos \theta\;| \leq 1$
Multiplying the inequality $|\;\cos \theta\;| \leq 1$ by the non-negative quantity $|\;\vec{a}\;|\; |\;\vec{b}\;|$, we get:
$|\;\vec{a}\;|\; |\;\vec{b}\;| |\;\cos \theta\;| \leq |\;\vec{a}\;|\; |\;\vec{b}\;| (1)$
$|\;\vec{a}\;|\; |\;\vec{b}\;| |\;\cos \theta\;| \leq |\;\vec{a}\;|\; |\;\vec{b}\;|$
From the step where we took the absolute value of the dot product, we have $|\;\vec{a} \;.\; \vec{b}\;| = |\;\vec{a}\;|\; |\;\vec{b}\;| |\;\cos \theta\;|$.
Substituting this into the inequality above:
$|\;\vec{a} \;.\; \vec{b}\;| ≤ |\;\vec{a}\;|\; |\;\vec{b}\;|$
This proves the Cauchy-Schwartz inequality for vectors.
Special Case:
If either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a} \;.\; \vec{b} = 0$, $|\;\vec{a}\;| = 0$ (if $\vec{a} = \vec{0}$) or $|\;\vec{b}\;| = 0$ (if $\vec{b} = \vec{0}$). In this case, $|\;\vec{a} \;.\; \vec{b}\;| = 0$ and $|\;\vec{a}\;|\; |\;\vec{b}\;| = 0$, so the inequality becomes $0 \leq 0$, which is true.
Example 20: For any two vectors $\vec{a}$ and $\vec{b}$, we always have $|\;\vec{a} + \vec{b}\;| ≤ |\;\vec{a}\;| + |\;\vec{b}\;|$ (triangle inequality).
Answer:
Given:
Two vectors $\vec{a}$ and $\vec{b}$.
To Prove:
The triangle inequality: $|\;\vec{a} + \vec{b}\;| ≤ |\;\vec{a}\;| + |\;\vec{b}\;|$.
Proof:
Consider the square of the magnitude of the vector $(\vec{a} + \vec{b})$. Using the property $|\vec{v}|^2 = \vec{v} \;.\; \vec{v}$, we have:
$|\;\vec{a} + \vec{b}\;|^2 = (\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b})$
Expand the dot product using the distributive property:
$|\;\vec{a} + \vec{b}\;|^2 = \vec{a} \;.\; (\vec{a} + \vec{b}) + \vec{b} \;.\; (\vec{a} + \vec{b})$
$|\;\vec{a} + \vec{b}\;|^2 = \vec{a} \;.\; \vec{a} + \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{a} + \vec{b} \;.\; \vec{b}$
Using the properties $\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$ and $\vec{b} \;.\; \vec{a} = \vec{a} \;.\; \vec{b}$ (commutativity of dot product):
$|\;\vec{a} + \vec{b}\;|^2 = |\;\vec{a}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2$
From the definition of the dot product, $\vec{a} \;.\; \vec{b} = |\;\vec{a}\;|\; |\;\vec{b}\;| \cos \theta$, where $\theta$ is the angle between $\vec{a}$ and $\vec{b}$.
Since $-1 \leq \cos \theta \leq 1$, it follows that $\vec{a} \;.\; \vec{b} = |\;\vec{a}\;|\; |\;\vec{b}\;| \cos \theta \leq |\;\vec{a}\;|\; |\;\vec{b}\;| (1)$.
Thus, $\vec{a} \;.\; \vec{b} \leq |\;\vec{a}\;|\; |\;\vec{b}\;|$. This is also directly obtainable from the Cauchy-Schwartz inequality, which states $|\;\vec{a} \;.\; \vec{b}\;| \leq |\;\vec{a}\;|\; |\;\vec{b}\;|$, which implies $\vec{a} \;.\; \vec{b} \leq |\;\vec{a} \;.\; \vec{b}\;| \leq |\;\vec{a}\;|\; |\;\vec{b}\;|$.
Substitute the inequality $\vec{a} \;.\; \vec{b} \leq |\;\vec{a}\;|\; |\;\vec{b}\;|$ into the expression for $|\;\vec{a} + \vec{b}\;|^2$:
$|\;\vec{a} + \vec{b}\;|^2 = |\;\vec{a}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2$
$|\;\vec{a} + \vec{b}\;|^2 \leq |\;\vec{a}\;|^2 + 2|\;\vec{a}\;|\; |\;\vec{b}\;| + |\;\vec{b}\;|^2$
The right side of the inequality is a perfect square:
$|\;\vec{a} + \vec{b}\;|^2 \leq (|\;\vec{a}\;| + |\;\vec{b}\;|)^2$
Since both $|\;\vec{a} + \vec{b}\;|$ and $|\;\vec{a}\;| + |\;\vec{b}\;|$ are non-negative quantities (as magnitudes are always non-negative), taking the square root of both sides preserves the inequality sign:
$\sqrt{|\;\vec{a} + \vec{b}\;|^2} \leq \sqrt{(|\;\vec{a}\;| + |\;\vec{b}\;|)^2}$
$|\;\vec{a} + \vec{b}\;| ≤ |\;\vec{a}\;| + |\;\vec{b}\;|$
This proves the triangle inequality for vectors. The equality holds if and only if the vectors $\vec{a}$ and $\vec{b}$ are collinear and point in the same direction (i.e., $\vec{b} = \lambda \vec{a}$ for some $\lambda \geq 0$).
Example 21: Show that the points $A(-2\hat{i} + 3\hat{j} + 5\hat{k})$ , $B(\hat{i} + 2\hat{j} + 3\hat{k})$ and $C(7\hat{i} − \hat{k})$ are collinear.
Answer:
Given:
The position vectors of the points A, B, and C are given as:
Position vector of A, $\vec{a} = -2\hat{i} + 3\hat{j} + 5\hat{k}$.
Position vector of B, $\vec{b} = \hat{i} + 2\hat{j} + 3\hat{k}$.
Position vector of C, $\vec{c} = 7\hat{i} - \hat{k} = 7\hat{i} + 0\hat{j} - \hat{k}$.
To Show:
The points A, B, and C are collinear.
Solution:
To show that points A, B, and C are collinear, we can show that the vectors formed by these points are collinear. For example, we can show that $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are collinear vectors.
First, let's find the vector $\overrightarrow{AB}$:
$\overrightarrow{AB} = \text{Position vector of B} - \text{Position vector of A}$
$\overrightarrow{AB} = \vec{b} - \vec{a}$
$\overrightarrow{AB} = (\hat{i} + 2\hat{j} + 3\hat{k}) - (-2\hat{i} + 3\hat{j} + 5\hat{k})$
$\overrightarrow{AB} = (1 - (-2))\hat{i} + (2 - 3)\hat{j} + (3 - 5)\hat{k}$
$\overrightarrow{AB} = 3\hat{i} - \hat{j} - 2\hat{k}$
Next, let's find the vector $\overrightarrow{BC}$:
$\overrightarrow{BC} = \text{Position vector of C} - \text{Position vector of B}$
$\overrightarrow{BC} = \vec{c} - \vec{b}$
$\overrightarrow{BC} = (7\hat{i} + 0\hat{j} - \hat{k}) - (\hat{i} + 2\hat{j} + 3\hat{k})$
$\overrightarrow{BC} = (7 - 1)\hat{i} + (0 - 2)\hat{j} + (-1 - 3)\hat{k}$
$\overrightarrow{BC} = 6\hat{i} - 2\hat{j} - 4\hat{k}$
Now, we check if $\overrightarrow{BC}$ is a scalar multiple of $\overrightarrow{AB}$. We can write $\overrightarrow{BC}$ as:
$\overrightarrow{BC} = 6\hat{i} - 2\hat{j} - 4\hat{k}$
$\overrightarrow{BC} = 2(3\hat{i} - \hat{j} - 2\hat{k})$
We observe that the expression in the parenthesis is the vector $\overrightarrow{AB}$.
$\overrightarrow{BC} = 2 \overrightarrow{AB}$
Since $\overrightarrow{BC}$ is a scalar multiple of $\overrightarrow{AB}$ (with scalar $\lambda = 2$), the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are collinear. Since these two vectors share a common point B, the points A, B, and C must lie on the same line. Therefore, the points A, B, and C are collinear.
Alternate Solution (using magnitudes):
We can also show collinearity by calculating the magnitudes of the vectors $\overrightarrow{AB}$, $\overrightarrow{BC}$, and $\overrightarrow{AC}$. If the sum of the magnitudes of two vectors equals the magnitude of the third vector, the points are collinear (e.g., $|\overrightarrow{AB}| + |\overrightarrow{BC}| = |\overrightarrow{AC}|$).
$\overrightarrow{AB} = 3\hat{i} - \hat{j} - 2\hat{k}$
$|\overrightarrow{AB}| = \sqrt{3^2 + (-1)^2 + (-2)^2} = \sqrt{9 + 1 + 4} = \sqrt{14}$
$\overrightarrow{BC} = 6\hat{i} - 2\hat{j} - 4\hat{k}$
$|\overrightarrow{BC}| = \sqrt{6^2 + (-2)^2 + (-4)^2} = \sqrt{36 + 4 + 16} = \sqrt{56} = \sqrt{4 \times 14} = 2\sqrt{14}$
Now, let's find the vector $\overrightarrow{AC}$:
$\overrightarrow{AC} = \text{Position vector of C} - \text{Position vector of A}$
$\overrightarrow{AC} = \vec{c} - \vec{a}$
$\overrightarrow{AC} = (7\hat{i} + 0\hat{j} - \hat{k}) - (-2\hat{i} + 3\hat{j} + 5\hat{k})$
$\overrightarrow{AC} = (7 - (-2))\hat{i} + (0 - 3)\hat{j} + (-1 - 5)\hat{k}$
$\overrightarrow{AC} = 9\hat{i} - 3\hat{j} - 6\hat{k}$
Calculate the magnitude of $\overrightarrow{AC}$:
$|\overrightarrow{AC}| = \sqrt{9^2 + (-3)^2 + (-6)^2} = \sqrt{81 + 9 + 36} = \sqrt{126} = \sqrt{9 \times 14} = 3\sqrt{14}$
Check if the sum of the magnitudes of two vectors equals the magnitude of the third:
$|\overrightarrow{AB}| + |\overrightarrow{BC}| = \sqrt{14} + 2\sqrt{14} = 3\sqrt{14}$
We see that $|\overrightarrow{AC}| = 3\sqrt{14}$ and $|\overrightarrow{AB}| + |\overrightarrow{BC}| = 3\sqrt{14}$.
$|\overrightarrow{AB}| + |\overrightarrow{BC}| = |\overrightarrow{AC}|$
Since the sum of the magnitudes of $\overrightarrow{AB}$ and $\overrightarrow{BC}$ is equal to the magnitude of $\overrightarrow{AC}$, the points A, B, and C are collinear, with point B lying between A and C.
Exercise 10.3
Question 1. Find the angle between two vectors $\vec{a}$ and $\vec{b}$ with magnitudes $\sqrt{3}$ and 2. Respectively having $\vec{a}\;.\;\vec{b} = \sqrt{6}$.
Answer:
Given:
Magnitude of vector $\vec{a}$, $|\vec{a}| = \sqrt{3}$.
Magnitude of vector $\vec{b}$, $|\vec{b}| = 2$.
Dot product of $\vec{a}$ and $\vec{b}$, $\vec{a} \;.\; \vec{b} = \sqrt{6}$.
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The dot product of two vectors $\vec{a}$ and $\vec{b}$ is given by the formula:
$\vec{a} \;.\; \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
where $\theta$ is the angle between the vectors ($0 \leq \theta \leq \pi$).
Substitute the given values into the formula:
$\sqrt{6} = (\sqrt{3})(2) \cos \theta$
Simplify the equation:
$\sqrt{6} = 2\sqrt{3} \cos \theta$
Solve for $\cos \theta$:
$\cos \theta = \frac{\sqrt{6}}{2\sqrt{3}}$
Simplify the expression for $\cos \theta$:
$\cos \theta = \frac{\sqrt{2 \times 3}}{2\sqrt{3}}$
$\cos \theta = \frac{\sqrt{2} \times \sqrt{3}}{2\sqrt{3}}$
Cancel out the common factor $\sqrt{3}$ (assuming $\sqrt{3} \neq 0$, which is true):
$\cos \theta = \frac{\sqrt{2}}{2}$
$\cos \theta = \frac{1}{\sqrt{2}}$
To find the angle $\theta$, we take the inverse cosine of $\frac{1}{\sqrt{2}}$. The principal value of $\theta$ lies in the interval $[0, \pi]$.
$\theta = \cos^{-1} \left(\frac{1}{\sqrt{2}}\right)$
The angle whose cosine is $\frac{1}{\sqrt{2}}$ is $\frac{\pi}{4}$ (or $45^\circ$).
$\theta = \frac{\pi}{4}$
Thus, the angle between the two vectors $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$.
Question 2. Find the angle between the vectors $\hat{i} - 2\hat{j} + 3\hat{k}$ and $3\hat{i} - 2\hat{j} + \hat{k}$
Answer:
Given:
Let the two vectors be $\vec{a}$ and $\vec{b}$.
Vector $\vec{a} = \hat{i} - 2\hat{j} + 3\hat{k}$.
Vector $\vec{b} = 3\hat{i} - 2\hat{j} + \hat{k}$.
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The angle $\theta$ between two vectors $\vec{a}$ and $\vec{b}$ is given by the formula:
$\cos \theta = \frac{\vec{a} \;.\; \vec{b}}{|\vec{a}| |\vec{b}|}$
where $\theta$ is the angle between the vectors ($0 \leq \theta \leq \pi$).
First, calculate the dot product $\vec{a} \;.\; \vec{b}$:
$\vec{a} \;.\; \vec{b} = (\hat{i} - 2\hat{j} + 3\hat{k}) \;.\; (3\hat{i} - 2\hat{j} + \hat{k})$
$\vec{a} \;.\; \vec{b} = (1)(3) + (-2)(-2) + (3)(1)$
$\vec{a} \;.\; \vec{b} = 3 + 4 + 3$
$\vec{a} \;.\; \vec{b} = 10$
Next, calculate the magnitude of vector $\vec{a}$:
$|\vec{a}| = |\hat{i} - 2\hat{j} + 3\hat{k}|$
$|\vec{a}| = \sqrt{1^2 + (-2)^2 + 3^2}$
$|\vec{a}| = \sqrt{1 + 4 + 9}$
$|\vec{a}| = \sqrt{14}$
Now, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = |3\hat{i} - 2\hat{j} + \hat{k}|$
$|\vec{b}| = \sqrt{3^2 + (-2)^2 + 1^2}$
$|\vec{b}| = \sqrt{9 + 4 + 1}$
$|\vec{b}| = \sqrt{14}$
Substitute the dot product and magnitudes into the formula for $\cos \theta$:
$\cos \theta = \frac{10}{(\sqrt{14})(\sqrt{14})}$
$\cos \theta = \frac{10}{14}$
Simplify the fraction:
$\cos \theta = \frac{5}{7}$
To find the angle $\theta$, take the inverse cosine of $\left(\frac{5}{7}\right)$:
$\theta = \cos^{-1} \left(\frac{5}{7}\right)$
The angle between the vectors $\hat{i} - 2\hat{j} + 3\hat{k}$ and $3\hat{i} - 2\hat{j} + \hat{k}$ is $\cos^{-1} \left(\frac{5}{7}\right)$.
Question 3. Find the projection of the vector $\hat{i} - \hat{j}$ on the vector $\hat{i} + \hat{j}$.
Answer:
Given:
Let the vectors be $\vec{a} = \hat{i} - \hat{j}$ and $\vec{b} = \hat{i} + \hat{j}$.
To Find:
The projection of vector $\vec{a}$ on the vector $\vec{b}$.
Solution:
The scalar projection of vector $\vec{a}$ on vector $\vec{b}$ is given by the formula:
Projection of $\vec{a}$ on $\vec{b} = \frac{\vec{a} \;.\; \vec{b}}{|\vec{b}|}$
First, calculate the dot product $\vec{a} \;.\; \vec{b}$:
$\vec{a} \;.\; \vec{b} = (\hat{i} - \hat{j}) \;.\; (\hat{i} + \hat{j})$
$\vec{a} \;.\; \vec{b} = (1)(1) + (-1)(1)$
$\vec{a} \;.\; \vec{b} = 1 - 1$
$\vec{a} \;.\; \vec{b} = 0$
Next, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = |\hat{i} + \hat{j}|$
$|\vec{b}| = \sqrt{1^2 + 1^2}$
$|\vec{b}| = \sqrt{1 + 1}$
$|\vec{b}| = \sqrt{2}$
Now, substitute the dot product and magnitude into the formula for the projection:
Projection of $\vec{a}$ on $\vec{b} = \frac{0}{\sqrt{2}}$
Projection of $\vec{a}$ on $\vec{b} = 0$
The projection of vector $\hat{i} - \hat{j}$ on the vector $\hat{i} + \hat{j}$ is 0. This indicates that the two vectors are perpendicular.
Question 4. Find the projection of the vector $\hat{i} + 3\hat{j} + 7\hat{k}$ on the vector $7\hat{i} - \hat{j} + 8\hat{k}$.
Answer:
Given:
Let the vectors be $\vec{a} = \hat{i} + 3\hat{j} + 7\hat{k}$ and $\vec{b} = 7\hat{i} - \hat{j} + 8\hat{k}$.
To Find:
The projection of vector $\vec{a}$ on the vector $\vec{b}$.
Solution:
The scalar projection of vector $\vec{a}$ on vector $\vec{b}$ is given by the formula:
Projection of $\vec{a}$ on $\vec{b} = \frac{\vec{a} \;.\; \vec{b}}{|\vec{b}|}$
First, calculate the dot product $\vec{a} \;.\; \vec{b}$:
$\vec{a} \;.\; \vec{b} = (\hat{i} + 3\hat{j} + 7\hat{k}) \;.\; (7\hat{i} - \hat{j} + 8\hat{k})$
$\vec{a} \;.\; \vec{b} = (1)(7) + (3)(-1) + (7)(8)$
$\vec{a} \;.\; \vec{b} = 7 - 3 + 56$
$\vec{a} \;.\; \vec{b} = 60$
Next, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = |7\hat{i} - \hat{j} + 8\hat{k}|$
$|\vec{b}| = \sqrt{7^2 + (-1)^2 + 8^2}$
$|\vec{b}| = \sqrt{49 + 1 + 64}$
$|\vec{b}| = \sqrt{114}$
Now, substitute the dot product and magnitude into the formula for the projection:
Projection of $\vec{a}$ on $\vec{b} = \frac{60}{\sqrt{114}}$
The projection of vector $\hat{i} + 3\hat{j} + 7\hat{k}$ on the vector $7\hat{i} - \hat{j} + 8\hat{k}$ is $\frac{60}{\sqrt{114}}$.
Question 5. Show that each of the given three vectors is a unit vector:
$\frac{1}{7} (2\hat{i} + 3\hat{j} + 6\hat{k})$, $\frac{1}{7} (3\hat{i} - 6\hat{j} + 2\hat{k})$, $\frac{1}{7} (6\hat{i} + 2\hat{j} - 3\hat{k})$
Also, show that they are mutually perpendicular to each other.
Answer:
Given:
Let the three vectors be $\vec{a}$, $\vec{b}$, and $\vec{c}$:
$\vec{a} = \frac{1}{7} (2\hat{i} + 3\hat{j} + 6\hat{k}) = \frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} + \frac{6}{7}\hat{k}$
$\vec{b} = \frac{1}{7} (3\hat{i} - 6\hat{j} + 2\hat{k}) = \frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}$
$\vec{c} = \frac{1}{7} (6\hat{i} + 2\hat{j} - 3\hat{k}) = \frac{6}{7}\hat{i} + \frac{2}{7}\hat{j} - \frac{3}{7}\hat{k}$
To Show:
1. Each vector is a unit vector (i.e., their magnitudes are 1).
2. They are mutually perpendicular (i.e., the dot product of any two distinct vectors is 0).
Solution:
Part 1: Showing each is a unit vector
The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is given by $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$. A unit vector has a magnitude of 1.
Magnitude of $\vec{a}$:
$|\vec{a}| = \left| \frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} + \frac{6}{7}\hat{k} \right|$
$|\vec{a}| = \sqrt{\left(\frac{2}{7}\right)^2 + \left(\frac{3}{7}\right)^2 + \left(\frac{6}{7}\right)^2}$
$|\vec{a}| = \sqrt{\frac{4}{49} + \frac{9}{49} + \frac{36}{49}}$
$|\vec{a}| = \sqrt{\frac{4 + 9 + 36}{49}}$
$|\vec{a}| = \sqrt{\frac{49}{49}}$
$|\vec{a}| = \sqrt{1} = 1$
Thus, $\vec{a}$ is a unit vector.
Magnitude of $\vec{b}$:
$|\vec{b}| = \left| \frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k} \right|$
$|\vec{b}| = \sqrt{\left(\frac{3}{7}\right)^2 + \left(-\frac{6}{7}\right)^2 + \left(\frac{2}{7}\right)^2}$
$|\vec{b}| = \sqrt{\frac{9}{49} + \frac{36}{49} + \frac{4}{49}}$
$|\vec{b}| = \sqrt{\frac{9 + 36 + 4}{49}}$
$|\vec{b}| = \sqrt{\frac{49}{49}}$
$|\vec{b}| = \sqrt{1} = 1$
Thus, $\vec{b}$ is a unit vector.
Magnitude of $\vec{c}$:
$|\vec{c}| = \left| \frac{6}{7}\hat{i} + \frac{2}{7}\hat{j} - \frac{3}{7}\hat{k} \right|$
$|\vec{c}| = \sqrt{\left(\frac{6}{7}\right)^2 + \left(\frac{2}{7}\right)^2 + \left(-\frac{3}{7}\right)^2}$
$|\vec{c}| = \sqrt{\frac{36}{49} + \frac{4}{49} + \frac{9}{49}}$
$|\vec{c}| = \sqrt{\frac{36 + 4 + 9}{49}}$
$|\vec{c}| = \sqrt{\frac{49}{49}}$
$|\vec{c}| = \sqrt{1} = 1$
Thus, $\vec{c}$ is a unit vector.
All three given vectors have a magnitude of 1, so they are unit vectors.
Part 2: Showing they are mutually perpendicular
Two vectors are perpendicular if their dot product is zero.
Dot product of $\vec{a}$ and $\vec{b}$:
$\vec{a} \;.\; \vec{b} = \left(\frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} + \frac{6}{7}\hat{k}\right) \;.\; \left(\frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}\right)$
$\vec{a} \;.\; \vec{b} = \left(\frac{2}{7}\right)\left(\frac{3}{7}\right) + \left(\frac{3}{7}\right)\left(-\frac{6}{7}\right) + \left(\frac{6}{7}\right)\left(\frac{2}{7}\right)$
$\vec{a} \;.\; \vec{b} = \frac{6}{49} - \frac{18}{49} + \frac{12}{49}$
$\vec{a} \;.\; \vec{b} = \frac{6 - 18 + 12}{49}$
$\vec{a} \;.\; \vec{b} = \frac{0}{49} = 0$
Since $\vec{a} \;.\; \vec{b} = 0$, vectors $\vec{a}$ and $\vec{b}$ are perpendicular.
Dot product of $\vec{b}$ and $\vec{c}$:
$\vec{b} \;.\; \vec{c} = \left(\frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}\right) \;.\; \left(\frac{6}{7}\hat{i} + \frac{2}{7}\hat{j} - \frac{3}{7}\hat{k}\right)$
$\vec{b} \;.\; \vec{c} = \left(\frac{3}{7}\right)\left(\frac{6}{7}\right) + \left(-\frac{6}{7}\right)\left(\frac{2}{7}\right) + \left(\frac{2}{7}\right)\left(-\frac{3}{7}\right)$
$\vec{b} \;.\; \vec{c} = \frac{18}{49} - \frac{12}{49} - \frac{6}{49}$
$\vec{b} \;.\; \vec{c} = \frac{18 - 12 - 6}{49}$
$\vec{b} \;.\; \vec{c} = \frac{0}{49} = 0$
Since $\vec{b} \;.\; \vec{c} = 0$, vectors $\vec{b}$ and $\vec{c}$ are perpendicular.
Dot product of $\vec{a}$ and $\vec{c}$:
$\vec{a} \;.\; \vec{c} = \left(\frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} + \frac{6}{7}\hat{k}\right) \;.\; \left(\frac{6}{7}\hat{i} + \frac{2}{7}\hat{j} - \frac{3}{7}\hat{k}\right)$
$\vec{a} \;.\; \vec{c} = \left(\frac{2}{7}\right)\left(\frac{6}{7}\right) + \left(\frac{3}{7}\right)\left(\frac{2}{7}\right) + \left(\frac{6}{7}\right)\left(-\frac{3}{7}\right)$
$\vec{a} \;.\; \vec{c} = \frac{12}{49} + \frac{6}{49} - \frac{18}{49}$
$\vec{a} \;.\; \vec{c} = \frac{12 + 6 - 18}{49}$
$\vec{a} \;.\; \vec{c} = \frac{0}{49} = 0$
Since $\vec{a} \;.\; \vec{c} = 0$, vectors $\vec{a}$ and $\vec{c}$ are perpendicular.
Since the dot product of every pair of distinct vectors among $\vec{a}$, $\vec{b}$, and $\vec{c}$ is zero, they are mutually perpendicular to each other.
Conclusion: As shown above, each vector has a magnitude of 1, proving they are unit vectors. Also, the dot product of each distinct pair is 0, proving they are mutually perpendicular. Thus, the given vectors form an orthonormal system.
Question 6. Find $|\;\vec{a}\;|$ and $|\;\vec{b}\;|$, if $(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 8$ and $|\;\vec{a}\;| = 8\;|\;\vec{b}\;|$.
Answer:
Given:
Equation 1: $(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 8$.
Equation 2: $|\;\vec{a}\;| = 8\;|\;\vec{b}\;|$.
To Find:
$|\;\vec{a}\;|$ and $|\;\vec{b}\;|$.
Solution:
Consider the first given equation:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 8$
Expand the dot product using the distributive property:
$\vec{a} \;.\; (\vec{a} - \vec{b}) + \vec{b} \;.\; (\vec{a} - \vec{b}) = 8$
$\vec{a} \;.\; \vec{a} - \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{a} - \vec{b} \;.\; \vec{b} = 8$
Using the properties $\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$ and $\vec{a} \;.\; \vec{b} = \vec{b} \;.\; \vec{a}$ (commutativity of dot product):
$|\;\vec{a}\;|^2 - \vec{a} \;.\; \vec{b} + \vec{a} \;.\; \vec{b} - |\;\vec{b}\;|^2 = 8$
The terms $-\vec{a} \;.\; \vec{b}$ and $+\vec{a} \;.\; \vec{b}$ cancel out:
$|\;\vec{a}\;|^2 - |\;\vec{b}\;|^2 = 8$
... (1)
Now, consider the second given equation:
$|\;\vec{a}\;| = 8\;|\;\vec{b}\;|$
... (2)
Square both sides of equation (2):
$(|\;\vec{a}\;|)^2 = (8\;|\;\vec{b}\;|)^2$
$|\;\vec{a}\;|^2 = 64|\;\vec{b}\;|^2$
... (3)
Substitute equation (3) into equation (1):
$64|\;\vec{b}\;|^2 - |\;\vec{b}\;|^2 = 8$
Combine like terms:
$63|\;\vec{b}\;|^2 = 8$
Solve for $|\;\vec{b}\;|^2$:
$|\;\vec{b}\;|^2 = \frac{8}{63}$
Take the square root to find $|\;\vec{b}\;|$ (magnitude is non-negative):
$|\;\vec{b}\;| = \sqrt{\frac{8}{63}}$
We can simplify and rationalize the expression for $|\;\vec{b}\;|$:
$|\;\vec{b}\;| = \frac{\sqrt{8}}{\sqrt{63}} = \frac{\sqrt{4 \times 2}}{\sqrt{9 \times 7}} = \frac{2\sqrt{2}}{3\sqrt{7}}$
$|\;\vec{b}\;| = \frac{2\sqrt{2}}{3\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{2\sqrt{14}}{3 \times 7}$
$|\;\vec{b}\;| = \frac{2\sqrt{14}}{21}$
Now, substitute the value of $|\;\vec{b}\;|$ back into equation (2) to find $|\;\vec{a}\;|$:
$|\;\vec{a}\;| = 8\;|\;\vec{b}\;|$
$|\;\vec{a}\;| = 8 \times \frac{2\sqrt{14}}{21}$
$|\;\vec{a}\;| = \frac{16\sqrt{14}}{21}$
The magnitudes of the vectors are $|\;\vec{a}\;| = \frac{16\sqrt{14}}{21}$ and $|\;\vec{b}\;| = \frac{2\sqrt{14}}{21}$.
Question 7. Evaluate the product $(3\vec{a} − 5\vec{b}) \;.\; (2\vec{a} + 7\vec{b})$.
Answer:
Given:
The expression to evaluate: $(3\vec{a} − 5\vec{b}) \;.\; (2\vec{a} + 7\vec{b})$.
To Evaluate:
The dot product of the two vector expressions.
Solution:
We use the distributive property of the dot product, similar to multiplying binomials:
$(3\vec{a} − 5\vec{b}) \;.\; (2\vec{a} + 7\vec{b}) = (3\vec{a}) \;.\; (2\vec{a}) + (3\vec{a}) \;.\; (7\vec{b}) + (-5\vec{b}) \;.\; (2\vec{a}) + (-5\vec{b}) \;.\; (7\vec{b})$
Using the property $(k\vec{u}) \;.\; (l\vec{v}) = kl (\vec{u} \;.\; \vec{v})$:
$= (3 \times 2) (\vec{a} \;.\; \vec{a}) + (3 \times 7) (\vec{a} \;.\; \vec{b}) + (-5 \times 2) (\vec{b} \;.\; \vec{a}) + (-5 \times 7) (\vec{b} \;.\; \vec{b})$
$= 6 (\vec{a} \;.\; \vec{a}) + 21 (\vec{a} \;.\; \vec{b}) - 10 (\vec{b} \;.\; \vec{a}) - 35 (\vec{b} \;.\; \vec{b})$
Using the properties $\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$ and $\vec{b} \;.\; \vec{a} = \vec{a} \;.\; \vec{b}$ (commutativity of dot product):
$= 6 |\;\vec{a}\;|^2 + 21 (\vec{a} \;.\; \vec{b}) - 10 (\vec{a} \;.\; \vec{b}) - 35 |\;\vec{b}\;|^2$
Combine the terms involving $\vec{a} \;.\; \vec{b}$:
$= 6 |\;\vec{a}\;|^2 + (21 - 10) (\vec{a} \;.\; \vec{b}) - 35 |\;\vec{b}\;|^2$
$= 6 |\;\vec{a}\;|^2 + 11 (\vec{a} \;.\; \vec{b}) - 35 |\;\vec{b}\;|^2$
The evaluated product is $6 |\;\vec{a}\;|^2 + 11 (\vec{a} \;.\; \vec{b}) - 35 |\;\vec{b}\;|^2$.
Question 8. Find the magnitude of two vectors $\vec{a}$ and $\vec{b}$ , having the same magnitude and such that the angle between them is 60o and their scalar product is $\frac{1}{2}$.
Answer:
Given:
Magnitude of vector $\vec{a}$ is equal to the magnitude of vector $\vec{b}$. Let this common magnitude be $x$. So, $|\vec{a}| = |\vec{b}| = x$.
The angle between vectors $\vec{a}$ and $\vec{b}$ is $\theta = 60^\circ$.
The scalar product of $\vec{a}$ and $\vec{b}$ is $\vec{a} \;.\; \vec{b} = \frac{1}{2}$.
To Find:
The magnitudes $|\vec{a}|$ and $|\vec{b}|$.
Solution:
The dot product (scalar product) of two vectors $\vec{a}$ and $\vec{b}$ is defined by the formula:
$\vec{a} \;.\; \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
Substitute the given values into this formula:
$\frac{1}{2} = (x)(x) \cos 60^\circ$
We know that $\cos 60^\circ = \frac{1}{2}$. Substitute this value into the equation:
$\frac{1}{2} = x^2 \left(\frac{1}{2}\right)$
Multiply both sides of the equation by 2:
$1 = x^2$
Take the square root of both sides to find $x$. Since $x$ represents a magnitude, it must be non-negative:
$x = \sqrt{1}$
$x = 1$
Since $|\vec{a}| = x$ and $|\vec{b}| = x$, we have:
$|\vec{a}| = 1$
$|\vec{b}| = 1$
The magnitudes of the two vectors $\vec{a}$ and $\vec{b}$ are both 1.
Question 9. Question 9. Find $|\;\vec{x}\;|$, if for a unit vector $\vec{a} \;,\; (\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 12$.
Answer:
Given:
Vector $\vec{a}$ is a unit vector, which means its magnitude is 1. Thus, $|\vec{a}| = 1$.
The dot product equation: $(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 12$.
To Find:
The magnitude of vector $\vec{x}$, i.e., $|\;\vec{x}\;|$.
Solution:
We are given the equation $(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 12$.
Using the distributive property of the dot product, we can expand the left side of the equation:
$(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = \vec{x} \;.\; (\vec{x} + \vec{a}) - \vec{a} \;.\; (\vec{x} + \vec{a})$
$= (\vec{x} \;.\; \vec{x} + \vec{x} \;.\; \vec{a}) - (\vec{a} \;.\; \vec{x} + \vec{a} \;.\; \vec{a})$
$= \vec{x} \;.\; \vec{x} + \vec{x} \;.\; \vec{a} - \vec{a} \;.\; \vec{x} - \vec{a} \;.\; \vec{a}$
We know that $\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$ and that the dot product is commutative, i.e., $\vec{a} \;.\; \vec{x} = \vec{x} \;.\; \vec{a}$.
So, the expansion becomes:
$= |\;\vec{x}\;|^2 + \vec{x} \;.\; \vec{a} - \vec{x} \;.\; \vec{a} - |\;\vec{a}\;|^2$
$= |\;\vec{x}\;|^2 - |\;\vec{a}\;|^2$
Now, substitute this back into the given equation:
$|\;\vec{x}\;|^2 - |\;\vec{a}\;|^2 = 12$
We are given that $\vec{a}$ is a unit vector, so $|\;\vec{a}\;| = 1$. Substitute this value into the equation:
$|\;\vec{x}\;|^2 - (1)^2 = 12$
$|\;\vec{x}\;|^2 - 1 = 12$
Solve for $|\;\vec{x}\;|^2$:
$|\;\vec{x}\;|^2 = 12 + 1$
$|\;\vec{x}\;|^2 = 13$
To find $|\;\vec{x}\;|$, take the square root of both sides. Since magnitude is always non-negative, we take the positive root:
$|\;\vec{x}\;| = \sqrt{13}$
The magnitude of vector $\vec{x}$ is $\sqrt{13}$.
Question 10. If $\vec{a} = 2\hat{i} + 2\hat{j} + 3\hat{k}$, $\vec{b} = -\hat{i} + 2\hat{j} + \hat{k}$ and $\vec{c} = 3\hat{i} + \hat{j}$ are such that $\vec{a} + λ\vec{b}$ is perpendicular to $\vec{c}$, then find the value of λ.
Answer:
Given:
Vector $\vec{a} = 2\hat{i} + 2\hat{j} + 3\hat{k}$.
Vector $\vec{b} = -\hat{i} + 2\hat{j} + \hat{k}$.
Vector $\vec{c} = 3\hat{i} + \hat{j} = 3\hat{i} + \hat{j} + 0\hat{k}$.
The condition is that $\vec{a} + λ\vec{b}$ is perpendicular to $\vec{c}$.
To Find:
The value of the scalar $\lambda$.
Solution:
If two non-zero vectors are perpendicular, their dot product is zero.
The vector $\vec{a} + λ\vec{b}$ is perpendicular to vector $\vec{c}$. Therefore, their dot product is 0:
$(\vec{a} + λ\vec{b}) \;.\; \vec{c} = 0$
First, let's find the vector $\vec{a} + λ\vec{b}$:
$\vec{a} + λ\vec{b} = (2\hat{i} + 2\hat{j} + 3\hat{k}) + λ(-\hat{i} + 2\hat{j} + \hat{k})$
$\vec{a} + λ\vec{b} = (2\hat{i} + 2\hat{j} + 3\hat{k}) + (-λ\hat{i} + 2λ\hat{j} + λ\hat{k})$
$\vec{a} + λ\vec{b} = (2 - λ)\hat{i} + (2 + 2λ)\hat{j} + (3 + λ)\hat{k}$
Now, calculate the dot product of $(\vec{a} + λ\vec{b})$ and $\vec{c}$:
$(\vec{a} + λ\vec{b}) \;.\; \vec{c} = ((2 - λ)\hat{i} + (2 + 2λ)\hat{j} + (3 + λ)\hat{k}) \;.\; (3\hat{i} + \hat{j} + 0\hat{k})$
$(\vec{a} + λ\vec{b}) \;.\; \vec{c} = (2 - λ)(3) + (2 + 2λ)(1) + (3 + λ)(0)$
$(\vec{a} + λ\vec{b}) \;.\; \vec{c} = 6 - 3λ + 2 + 2λ + 0$
$(\vec{a} + λ\vec{b}) \;.\; \vec{c} = 8 - λ$
Since $(\vec{a} + λ\vec{b})$ is perpendicular to $\vec{c}$, their dot product is 0:
$8 - λ = 0$
Solve for $\lambda$:
$λ = 8$
The value of $\lambda$ is 8.
Question 11. Show that $|\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a}$ is perpendicular to $|\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a}$, for any two nonzero vectors $\vec{a}$ and $\vec{b}$.
Answer:
Given:
Two non-zero vectors $\vec{a}$ and $\vec{b}$.
To Show:
The vector $|\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a}$ is perpendicular to the vector $|\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a}$.
Solution:
Two non-zero vectors are perpendicular if their dot product is zero.
Let $\vec{v}_1 = |\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a}$ and $\vec{v}_2 = |\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a}$.
We need to calculate the dot product $\vec{v}_1 \;.\; \vec{v}_2$ and show it is equal to 0.
Consider the dot product:
$\vec{v}_1 \;.\; \vec{v}_2 = (|\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a}) \;.\; (|\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a})$
Using the distributive property of the dot product:
$= (|\;\vec{a}\;| \;\vec{b}) \;.\; (|\;\vec{a}\;| \;\vec{b}) - (|\;\vec{a}\;| \;\vec{b}) \;.\; (|\;\vec{b}\;|\;\vec{a}) + (|\;\vec{b}\;|\;\vec{a}) \;.\; (|\;\vec{a}\;| \;\vec{b}) - (|\;\vec{b}\;|\;\vec{a}) \;.\; (|\;\vec{b}\;|\;\vec{a})$
Using the property $(k\vec{u}) \;.\; (l\vec{v}) = kl (\vec{u} \;.\; \vec{v})$ for scalars $k$ and $l$, and the property $\vec{w} \;.\; \vec{w} = |\;\vec{w}\;|^2$:
$= (|\;\vec{a}\;|\; |\;\vec{a}\;|) (\vec{b} \;.\; \vec{b}) - (|\;\vec{a}\;|\; |\;\vec{b}\;|) (\vec{b} \;.\; \vec{a}) + (|\;\vec{b}\;|\; |\;\vec{a}\;|) (\vec{a} \;.\; \vec{b}) - (|\;\vec{b}\;|\; |\;\vec{b}\;|) (\vec{a} \;.\; \vec{a})$
$= |\;\vec{a}\;|^2 |\;\vec{b}\;|^2 - |\;\vec{a}\;|\; |\;\vec{b}\;| (\vec{b} \;.\; \vec{a}) + |\;\vec{a}\;|\; |\;\vec{b}\;| (\vec{a} \;.\; \vec{b}) - |\;\vec{b}\;|^2 |\;\vec{a}\;|^2$
Using the commutativity of the dot product, $\vec{b} \;.\; \vec{a} = \vec{a} \;.\; \vec{b}$:
$= |\;\vec{a}\;|^2 |\;\vec{b}\;|^2 - |\;\vec{a}\;|\; |\;\vec{b}\;| (\vec{a} \;.\; \vec{b}) + |\;\vec{a}\;|\; |\;\vec{b}\;| (\vec{a} \;.\; \vec{b}) - |\;\vec{b}\;|^2 |\;\vec{a}\;|^2$
The two middle terms cancel each other out:
$= |\;\vec{a}\;|^2 |\;\vec{b}\;|^2 - |\;\vec{b}\;|^2 |\;\vec{a}\;|^2$
$= |\;\vec{a}\;|^2 |\;\vec{b}\;|^2 - |\;\vec{a}\;|^2 |\;\vec{b}\;|^2$
$= 0$
Since the dot product of the two vectors $(|\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a})$ and $(|\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a})$ is 0, and we are given that $\vec{a}$ and $\vec{b}$ are nonzero (which implies $|\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a}$ and $|\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a}$ are also non-zero unless $\vec{a}$ and $\vec{b}$ are collinear with opposite directions and equal scaled magnitudes, which is covered by the dot product being 0), the vectors are perpendicular to each other.
Question 12. If $\vec{a}\;.\; \vec{a} = 0$ and $\vec{a} \;.\; \vec{b} = 0$, then what can be concluded about the vector $\vec{b}$ ?
Answer:
Given:
$\vec{a} \;.\; \vec{a} = 0$.
$\vec{a} \;.\; \vec{b} = 0$.
To Conclude:
What can be concluded about the vector $\vec{b}$.
Solution:
We are given the first condition $\vec{a} \;.\; \vec{a} = 0$.
Using the property that the dot product of a vector with itself is equal to the square of its magnitude, $\vec{a} \;.\; \vec{a} = |\;\vec{a}\;|^2$, we have:
$|\;\vec{a}\;|^2 = 0$
The square of the magnitude of a vector is zero if and only if the magnitude of the vector is zero:
$ \sqrt{|\;\vec{a}\;|^2} = \sqrt{0}$
$|\;\vec{a}\;| = 0$
The magnitude of a vector is zero if and only if the vector is the zero vector. Therefore, from $|\;\vec{a}\;| = 0$, we conclude:
$\vec{a} = \vec{0}$
Now, consider the second given condition $\vec{a} \;.\; \vec{b} = 0$.
Substitute the conclusion $\vec{a} = \vec{0}$ into this equation:
$\vec{0} \;.\; \vec{b} = 0$
The dot product of the zero vector with any vector $\vec{b}$ is always the scalar zero. This is a fundamental property of the zero vector.
Thus, the equation becomes:
$0 = 0$
This is an identity which is true for any vector $\vec{b}$. The condition $\vec{a} \;.\; \vec{b} = 0$ does not constrain $\vec{b}$ at all when $\vec{a}$ is the zero vector.
Therefore, based on the given conditions, the vector $\vec{a}$ must be the zero vector. The second condition then provides no information about $\vec{b}$.
Thus, the vector $\vec{b}$ can be any vector.
Question 13. If $\vec{a}\;,\; \vec{b}\;,\; \vec{c}$ are unit vectors such that $\vec{a} + \vec{b} + \vec{c} = \vec{0}$, find the value of $\vec{a}\;.\;\vec{b} \;+\; \vec{b}\;.\; \vec{c} \;+\; \vec{c}\;.\; \vec{a}$.
Answer:
Given:
Vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ are unit vectors.
This means $|\vec{a}| = 1$, $|\vec{b}| = 1$, $|\vec{c}| = 1$.
The sum of the vectors is the zero vector: $\vec{a} + \vec{b} + \vec{c} = \vec{0}$.
To Find:
The value of $\vec{a}\;.\;\vec{b} \;+\; \vec{b}\;.\; \vec{c} \;+\; \vec{c}\;.\; \vec{a}$.
Solution:
We are given the vector equation $\vec{a} + \vec{b} + \vec{c} = \vec{0}$.
Take the dot product of this equation with itself:
$(\vec{a} + \vec{b} + \vec{c}) \;.\; (\vec{a} + \vec{b} + \vec{c}) = \vec{0} \;.\; \vec{0}$
Expand the dot product on the left side:
$(\vec{a} + \vec{b} + \vec{c}) \;.\; (\vec{a} + \vec{b} + \vec{c}) = \vec{a} \;.\; \vec{a} + \vec{a} \;.\; \vec{b} + \vec{a} \;.\; \vec{c} + \vec{b} \;.\; \vec{a} + \vec{b} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a} + \vec{c} \;.\; \vec{b} + \vec{c} \;.\; \vec{c}$
The dot product of the zero vector with itself is 0: $\vec{0} \;.\; \vec{0} = 0$.
Using the properties $\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$ and $\vec{u} \;.\; \vec{v} = \vec{v} \;.\; \vec{u}$ (commutativity):
$|\;\vec{a}\;|^2 + \vec{a} \;.\; \vec{b} + \vec{c} \;.\; \vec{a} + \vec{a} \;.\; \vec{b} + |\;\vec{b}\;|^2 + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a} + \vec{b} \;.\; \vec{c} + |\;\vec{c}\;|^2 = 0$
Group the terms:
$|\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + 2(\vec{b} \;.\; \vec{c}) + 2(\vec{c} \;.\; \vec{a}) = 0$
Since $\vec{a}$, $\vec{b}$, and $\vec{c}$ are unit vectors, their magnitudes are 1:
$(1)^2 + (1)^2 + (1)^2 + 2(\vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}) = 0$
$1 + 1 + 1 + 2(\vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}) = 0$
$3 + 2(\vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}) = 0$
Now, solve for the required expression $\vec{a}\;.\;\vec{b} \;+\; \vec{b}\;.\; \vec{c} \;+\; \vec{c}\;.\; \vec{a}$:
$2(\vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}) = -3$
$\vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a} = -\frac{3}{2}$
The value of $\vec{a}\;.\;\vec{b} \;+\; \vec{b}\;.\; \vec{c} \;+\; \vec{c}\;.\; \vec{a}$ is $-\frac{3}{2}$.
Question 14. If either vector $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a}\;.\; \vec{b} = 0$. But the converse need not be true. Justify your answer with an example.
Answer:
Given Statement:
If either vector $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a} \;.\; \vec{b} = 0$.
Statement to Justify:
The converse of the given statement, which is "If $\vec{a} \;.\; \vec{b} = 0$, then either vector $\vec{a} = \vec{0}$ or vector $\vec{b} = \vec{0}$", need not be true.
Justification:
The dot product of two vectors $\vec{a}$ and $\vec{b}$ is defined as $\vec{a} \;.\; \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$, where $\theta$ is the angle between $\vec{a}$ and $\vec{b}$.
If $\vec{a} \;.\; \vec{b} = 0$, it implies that $|\vec{a}| |\vec{b}| \cos \theta = 0$.
This equation holds true if any of the factors are zero:
1. $|\vec{a}| = 0$, which means $\vec{a} = \vec{0}$.
2. $|\vec{b}| = 0$, which means $\vec{b} = \vec{0}$.
3. $\cos \theta = 0$. This occurs when the angle $\theta$ between the vectors is $\frac{\pi}{2}$ (or $90^\circ$). In this case, the vectors are perpendicular to each other.
The converse statement claims that if the dot product is zero, then at least one of the vectors must be the zero vector. However, as seen from the dot product formula, the dot product can also be zero if $\cos \theta = 0$, provided that neither $|\vec{a}|$ nor $|\vec{b}|$ is zero. This happens when $\vec{a}$ and $\vec{b}$ are non-zero vectors that are perpendicular to each other.
Thus, $\vec{a} \;.\; \vec{b} = 0$ does not necessarily imply that $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$. It can also mean that $\vec{a}$ and $\vec{b}$ are non-zero vectors that are perpendicular.
Example:
Let $\vec{a} = \hat{i}$ and $\vec{b} = \hat{j}$.
These are two non-zero vectors:
$|\vec{a}| = |\hat{i}| = \sqrt{1^2 + 0^2 + 0^2} = 1 \neq 0$.
$|\vec{b}| = |\hat{j}| = \sqrt{0^2 + 1^2 + 0^2} = 1 \neq 0$.
Now, let's calculate their dot product:
$\vec{a} \;.\; \vec{b} = \hat{i} \;.\; \hat{j}$
Using the property that the dot product of orthogonal standard unit vectors is 0 ($\hat{i} \;.\; \hat{j} = 0$, $\hat{j} \;.\; \hat{k} = 0$, $\hat{k} \;.\; \hat{i} = 0$):
$\vec{a} \;.\; \vec{b} = 0$
In this example, we have $\vec{a} \;.\; \vec{b} = 0$, but neither $\vec{a}$ nor $\vec{b}$ is the zero vector.
This example demonstrates that the converse statement ("If $\vec{a} \;.\; \vec{b} = 0$, then either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$") is not always true.
Question 15. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$].
Answer:
Given:
The vertices of triangle ABC are A(1, 2, 3), B(-1, 0, 0), and C(0, 1, 2).
To Find:
The angle $\angle$ABC, which is the angle between the vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$.
Solution:
First, we need to find the vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$.
The position vector of a point $(x, y, z)$ is $x\hat{i} + y\hat{j} + z\hat{k}$.
Position vector of A: $\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$
Position vector of B: $\vec{b} = -\hat{i} + 0\hat{j} + 0\hat{k} = -\hat{i}$
Position vector of C: $\vec{c} = 0\hat{i} + \hat{j} + 2\hat{k} = \hat{j} + 2\hat{k}$
Vector $\overrightarrow{BA}$ is given by the position vector of A minus the position vector of B:
$\overrightarrow{BA} = \vec{a} - \vec{b} = (\hat{i} + 2\hat{j} + 3\hat{k}) - (-\hat{i})$
$\overrightarrow{BA} = (1 - (-1))\hat{i} + (2 - 0)\hat{j} + (3 - 0)\hat{k}$
$\overrightarrow{BA} = 2\hat{i} + 2\hat{j} + 3\hat{k}$
Vector $\overrightarrow{BC}$ is given by the position vector of C minus the position vector of B:
$\overrightarrow{BC} = \vec{c} - \vec{b} = (\hat{j} + 2\hat{k}) - (-\hat{i})$
$\overrightarrow{BC} = (0 - (-1))\hat{i} + (1 - 0)\hat{j} + (2 - 0)\hat{k}$
$\overrightarrow{BC} = \hat{i} + \hat{j} + 2\hat{k}$
The angle $\theta = \angle$ABC between two vectors $\vec{u}$ and $\vec{v}$ is given by the formula:
$\cos \theta = \frac{\vec{u} \;.\; \vec{v}}{|\vec{u}| |\vec{v}|}$
Here, $\vec{u} = \overrightarrow{BA}$ and $\vec{v} = \overrightarrow{BC}$.
Calculate the dot product $\overrightarrow{BA} \;.\; \overrightarrow{BC}$:
$\overrightarrow{BA} \;.\; \overrightarrow{BC} = (2\hat{i} + 2\hat{j} + 3\hat{k}) \;.\; (\hat{i} + \hat{j} + 2\hat{k})$
$\overrightarrow{BA} \;.\; \overrightarrow{BC} = (2)(1) + (2)(1) + (3)(2)$
$\overrightarrow{BA} \;.\; \overrightarrow{BC} = 2 + 2 + 6$
$\overrightarrow{BA} \;.\; \overrightarrow{BC} = 10$
Calculate the magnitude of vector $\overrightarrow{BA}$:
$|\overrightarrow{BA}| = |2\hat{i} + 2\hat{j} + 3\hat{k}|$
$|\overrightarrow{BA}| = \sqrt{2^2 + 2^2 + 3^2}$
$|\overrightarrow{BA}| = \sqrt{4 + 4 + 9}$
$|\overrightarrow{BA}| = \sqrt{17}$
Calculate the magnitude of vector $\overrightarrow{BC}$:
$|\overrightarrow{BC}| = |\hat{i} + \hat{j} + 2\hat{k}|$
$|\overrightarrow{BC}| = \sqrt{1^2 + 1^2 + 2^2}$
$|\overrightarrow{BC}| = \sqrt{1 + 1 + 4}$
$|\overrightarrow{BC}| = \sqrt{6}$
Substitute the dot product and magnitudes into the formula for $\cos(\angle\text{ABC})$:
$\cos(\angle\text{ABC}) = \frac{10}{(\sqrt{17})(\sqrt{6})}$
$\cos(\angle\text{ABC}) = \frac{10}{\sqrt{17 \times 6}}$
$\cos(\angle\text{ABC}) = \frac{10}{\sqrt{102}}$
To find $\angle$ABC, take the inverse cosine of $\frac{10}{\sqrt{102}}$:
$\angle\text{ABC} = \cos^{-1} \left(\frac{10}{\sqrt{102}}\right)$
The angle $\angle$ABC is $\cos^{-1} \left(\frac{10}{\sqrt{102}}\right)$.
Question 16. Show that the points A(1, 2, 7), B(2, 6, 3) and C(3, 10, –1) are collinear.
Answer:
Given:
The coordinates of the points are A(1, 2, 7), B(2, 6, 3), and C(3, 10, –1).
To Show:
The points A, B, and C are collinear.
Solution:
Points A, B, and C are collinear if the vector $\overrightarrow{AC}$ is a scalar multiple of the vector $\overrightarrow{AB}$ (or any other pair of vectors formed by these points), and they share a common point (which they do).
First, find the position vectors of the points:
Position vector of A: $\vec{a} = \hat{i} + 2\hat{j} + 7\hat{k}$
Position vector of B: $\vec{b} = 2\hat{i} + 6\hat{j} + 3\hat{k}$
Position vector of C: $\vec{c} = 3\hat{i} + 10\hat{j} - \hat{k}$
Calculate the vector $\overrightarrow{AB}$:
$\overrightarrow{AB} = \text{Position vector of B} - \text{Position vector of A}$
$\overrightarrow{AB} = \vec{b} - \vec{a}$
$\overrightarrow{AB} = (2\hat{i} + 6\hat{j} + 3\hat{k}) - (\hat{i} + 2\hat{j} + 7\hat{k})$
$\overrightarrow{AB} = (2-1)\hat{i} + (6-2)\hat{j} + (3-7)\hat{k}$
$\overrightarrow{AB} = \hat{i} + 4\hat{j} - 4\hat{k}$
Calculate the vector $\overrightarrow{AC}$:
$\overrightarrow{AC} = \text{Position vector of C} - \text{Position vector of A}$
$\overrightarrow{AC} = \vec{c} - \vec{a}$
$\overrightarrow{AC} = (3\hat{i} + 10\hat{j} - \hat{k}) - (\hat{i} + 2\hat{j} + 7\hat{k})$
$\overrightarrow{AC} = (3-1)\hat{i} + (10-2)\hat{j} + (-1-7)\hat{k}$
$\overrightarrow{AC} = 2\hat{i} + 8\hat{j} - 8\hat{k}$
Now, check if $\overrightarrow{AC}$ is a scalar multiple of $\overrightarrow{AB}$:
$\overrightarrow{AC} = 2\hat{i} + 8\hat{j} - 8\hat{k}$
$\overrightarrow{AC} = 2(\hat{i} + 4\hat{j} - 4\hat{k})$
$\overrightarrow{AC} = 2 \overrightarrow{AB}$
... (i)
Since $\overrightarrow{AC}$ is a scalar multiple of $\overrightarrow{AB}$ (with scalar $\lambda = 2$), the vectors $\overrightarrow{AC}$ and $\overrightarrow{AB}$ are collinear.
Since these two vectors share the common starting point A, the points A, B, and C lie on the same line.
Therefore, the points A, B, and C are collinear.
Alternate Solution (using magnitudes):
Points A, B, and C are collinear if the sum of the magnitudes of two vectors equals the magnitude of the third vector formed by these points (e.g., $|\overrightarrow{AB}| + |\overrightarrow{BC}| = |\overrightarrow{AC}|$ or $|\overrightarrow{BA}| + |\overrightarrow{AC}| = |\overrightarrow{BC}|$ etc.).
We already calculated the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$. Let's also calculate $\overrightarrow{BC}$.
$\overrightarrow{AB} = \hat{i} + 4\hat{j} - 4\hat{k}$
$\overrightarrow{AC} = 2\hat{i} + 8\hat{j} - 8\hat{k}$
Calculate the vector $\overrightarrow{BC}$:
$\overrightarrow{BC} = \vec{c} - \vec{b} = (3\hat{i} + 10\hat{j} - \hat{k}) - (2\hat{i} + 6\hat{j} + 3\hat{k})$
$\overrightarrow{BC} = (3-2)\hat{i} + (10-6)\hat{j} + (-1-3)\hat{k}$
$\overrightarrow{BC} = \hat{i} + 4\hat{j} - 4\hat{k}$
Calculate the magnitudes of the vectors:
$|\overrightarrow{AB}| = \sqrt{1^2 + 4^2 + (-4)^2} = \sqrt{1 + 16 + 16} = \sqrt{33}$
$|\overrightarrow{BC}| = \sqrt{1^2 + 4^2 + (-4)^2} = \sqrt{1 + 16 + 16} = \sqrt{33}$
$|\overrightarrow{AC}| = \sqrt{2^2 + 8^2 + (-8)^2} = \sqrt{4 + 64 + 64} = \sqrt{132} = \sqrt{4 \times 33} = 2\sqrt{33}$
Check if the sum of two magnitudes equals the third:
$|\overrightarrow{AB}| + |\overrightarrow{BC}| = \sqrt{33} + \sqrt{33} = 2\sqrt{33}$
We see that $|\overrightarrow{AC}| = 2\sqrt{33}$.
$|\overrightarrow{AB}| + |\overrightarrow{BC}| = |\overrightarrow{AC}|$
... (ii)
Since the sum of the magnitudes of $\overrightarrow{AB}$ and $\overrightarrow{BC}$ is equal to the magnitude of $\overrightarrow{AC}$, the points A, B, and C are collinear, with point B lying between A and C.
Question 17. Show that the vectors $2\hat{i} - \hat{j} + \hat{k} \;,\; \hat{i} - 3\hat{j} - 5\hat{k}$ and $3\hat{i} - 4\hat{j} - 4\hat{k}$ form the vertices of a right angled triangle.
Answer:
Given:
Let the vertices of the triangle be A, B, and C, with the given vectors as their position vectors:
Position vector of A, $\vec{a} = 2\hat{i} - \hat{j} + \hat{k}$.
Position vector of B, $\vec{b} = \hat{i} - 3\hat{j} - 5\hat{k}$.
Position vector of C, $\vec{c} = 3\hat{i} - 4\hat{j} - 4\hat{k}$.
To Show:
The points A, B, and C form the vertices of a right-angled triangle.
Solution:
To show that the points form a right-angled triangle, we can find the vectors representing the sides of the triangle and check if the dot product of any two side vectors is zero. If the dot product of two non-zero vectors is zero, they are perpendicular.
First, calculate the vectors representing the sides of the triangle:
Vector $\overrightarrow{AB}$: $\overrightarrow{AB} = \text{Position vector of B} - \text{Position vector of A}$
$\overrightarrow{AB} = \vec{b} - \vec{a} = (\hat{i} - 3\hat{j} - 5\hat{k}) - (2\hat{i} - \hat{j} + \hat{k})$
$\overrightarrow{AB} = (1-2)\hat{i} + (-3-(-1))\hat{j} + (-5-1)\hat{k}$
$\overrightarrow{AB} = -\hat{i} - 2\hat{j} - 6\hat{k}$
Vector $\overrightarrow{BC}$: $\overrightarrow{BC} = \text{Position vector of C} - \text{Position vector of B}$
$\overrightarrow{BC} = \vec{c} - \vec{b} = (3\hat{i} - 4\hat{j} - 4\hat{k}) - (\hat{i} - 3\hat{j} - 5\hat{k})$
$\overrightarrow{BC} = (3-1)\hat{i} + (-4-(-3))\hat{j} + (-4-(-5))\hat{k}$
$\overrightarrow{BC} = 2\hat{i} + (-4+3)\hat{j} + (-4+5)\hat{k}$
$\overrightarrow{BC} = 2\hat{i} - \hat{j} + \hat{k}$
Vector $\overrightarrow{CA}$: $\overrightarrow{CA} = \text{Position vector of A} - \text{Position vector of C}$
$\overrightarrow{CA} = \vec{a} - \vec{c} = (2\hat{i} - \hat{j} + \hat{k}) - (3\hat{i} - 4\hat{j} - 4\hat{k})$
$\overrightarrow{CA} = (2-3)\hat{i} + (-1-(-4))\hat{j} + (1-(-4))\hat{k}$
$\overrightarrow{CA} = -1\hat{i} + (-1+4)\hat{j} + (1+4)\hat{k}$
$\overrightarrow{CA} = -\hat{i} + 3\hat{j} + 5\hat{k}$
Check the dot product of each pair of side vectors:
$\overrightarrow{AB} \;.\; \overrightarrow{BC} = (-\hat{i} - 2\hat{j} - 6\hat{k}) \;.\; (2\hat{i} - \hat{j} + \hat{k})$
$\overrightarrow{AB} \;.\; \overrightarrow{BC} = (-1)(2) + (-2)(-1) + (-6)(1) = -2 + 2 - 6 = -6$
$\overrightarrow{BC} \;.\; \overrightarrow{CA} = (2\hat{i} - \hat{j} + \hat{k}) \;.\; (-\hat{i} + 3\hat{j} + 5\hat{k})$
$\overrightarrow{BC} \;.\; \overrightarrow{CA} = (2)(-1) + (-1)(3) + (1)(5) = -2 - 3 + 5 = 0$
$\overrightarrow{CA} \;.\; \overrightarrow{AB} = (-\hat{i} + 3\hat{j} + 5\hat{k}) \;.\; (-\hat{i} - 2\hat{j} - 6\hat{k})$
$\overrightarrow{CA} \;.\; \overrightarrow{AB} = (-1)(-1) + (3)(-2) + (5)(-6) = 1 - 6 - 30 = -35$
Since $\overrightarrow{BC} \;.\; \overrightarrow{CA} = 0$, the vectors $\overrightarrow{BC}$ and $\overrightarrow{CA}$ are perpendicular. This means the sides BC and CA of the triangle are perpendicular.
Also, calculate the magnitudes of the vectors to ensure they are non-zero (which is evident from their components):
$|\overrightarrow{BC}| = \sqrt{2^2 + (-1)^2 + 1^2} = \sqrt{4+1+1} = \sqrt{6} \neq 0$
$|\overrightarrow{CA}| = \sqrt{(-1)^2 + 3^2 + 5^2} = \sqrt{1+9+25} = \sqrt{35} \neq 0$
Because two sides of the triangle (BC and CA) are perpendicular, the triangle ABC is a right-angled triangle with the right angle at vertex C.
Question 18. If $\vec{a}$ is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then $λ\vec{a}$ is unit vector if
(A) λ = 1
(B) λ = – 1
(C) a = |λ|
(D) $a = \frac{1}{|λ|}$
Answer:
Given:
Vector $\vec{a}$ is a nonzero vector.
The magnitude of $\vec{a}$ is $|\vec{a}| = a$, where $a > 0$ since $\vec{a}$ is nonzero.
$\lambda$ is a nonzero scalar, so $\lambda \neq 0$.
The vector $λ\vec{a}$ is a unit vector.
To Find:
The condition under which $λ\vec{a}$ is a unit vector.
Solution:
A vector is a unit vector if its magnitude is equal to 1.
We are given that $λ\vec{a}$ is a unit vector, so its magnitude must be 1:
$|λ\vec{a}| = 1$
The magnitude of a scalar multiple of a vector is given by the product of the absolute value of the scalar and the magnitude of the vector:
$|λ\vec{a}| = |λ| |\vec{a}|$
We are given that $|\vec{a}| = a$. Substituting this into the equation:
$|λ| a = 1$
We need to find the condition for this equation to be true. Since $\lambda$ is a nonzero scalar, $|λ|$ is a nonzero positive number. Since $\vec{a}$ is a nonzero vector, $a = |\vec{a}|$ is a nonzero positive number.
We can rearrange the equation to solve for $a$ in terms of $|λ|$:
$a = \frac{1}{|λ|}$
This is the required condition for the vector $λ\vec{a}$ to be a unit vector.
Compare this result with the given options:
(A) $\lambda = 1$: If $\lambda = 1$, then $|λ|=1$, so $a = \frac{1}{1} = 1$. This implies $|\vec{a}|=1$. This is a specific case where $\vec{a}$ is a unit vector and $\lambda=1$.
(B) $\lambda = – 1$: If $\lambda = -1$, then $|λ|=1$, so $a = \frac{1}{1} = 1$. This implies $|\vec{a}|=1$. This is another specific case where $\vec{a}$ is a unit vector and $\lambda=-1$.
(C) a = |λ|: If $a = |λ|$, substitute this into $|λ| a = 1$: $|λ| |λ| = 1 \implies |λ|^2 = 1 \implies |λ| = 1$. This means $\lambda = \pm 1$. This is not true for all nonzero $\lambda$.
(D) $a = \frac{1}{|λ|}$: This matches the condition we derived.
The correct condition is $a = \frac{1}{|λ|}$.
The correct option is (D) $a = \frac{1}{|λ|}$.
Example 22 to 25 (Before Exercise 10.4)
Example 22: Find $|\;\vec{a}\; × \;\vec{b}\;|$, if $\vec{a} = 2\hat{i} + \hat{j} + 3\hat{k}$ and $\vec{b} = 3\hat{i} + 5\hat{j} - 2\hat{k}$
Answer:
Given:
Vector $\vec{a} = 2\hat{i} + \hat{j} + 3\hat{k}$.
Vector $\vec{b} = 3\hat{i} + 5\hat{j} - 2\hat{k}$.
To Find:
The magnitude of the cross product of $\vec{a}$ and $\vec{b}$, i.e., $|\;\vec{a}\; × \;\vec{b}\;|$.
Solution:
The cross product of two vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$ is given by the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
For the given vectors $\vec{a} = 2\hat{i} + \hat{j} + 3\hat{k}$ and $\vec{b} = 3\hat{i} + 5\hat{j} - 2\hat{k}$, the cross product is:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 3 \\ 3 & 5 & -2 \end{vmatrix}$
Expand the determinant along the first row:
$\vec{a} × \vec{b} = \hat{i}((1)(-2) - (3)(5)) - \hat{j}((2)(-2) - (3)(3)) + \hat{k}((2)(5) - (1)(3))$
$\vec{a} × \vec{b} = \hat{i}(-2 - 15) - \hat{j}(-4 - 9) + \hat{k}(10 - 3)$
$\vec{a} × \vec{b} = \hat{i}(-17) - \hat{j}(-13) + \hat{k}(7)$
$\vec{a} × \vec{b} = -17\hat{i} + 13\hat{j} + 7\hat{k}$
Now, calculate the magnitude of the resulting vector $\vec{a} × \vec{b}$. The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
$|\;\vec{a} × \vec{b}\;| = |-17\hat{i} + 13\hat{j} + 7\hat{k}|$
$|\;\vec{a} × \vec{b}\;| = \sqrt{(-17)^2 + (13)^2 + (7)^2}$
$|\;\vec{a} × \vec{b}\;| = \sqrt{289 + 169 + 49}$
$|\;\vec{a} × \vec{b}\;| = \sqrt{507}$
We can simplify the square root $\sqrt{507}$ by looking for perfect square factors of 507.
$507 = 3 \times 169 = 3 \times 13^2$.
$|\;\vec{a} × \vec{b}\;| = \sqrt{13^2 \times 3}$
$|\;\vec{a} × \vec{b}\;| = 13\sqrt{3}$
The magnitude of $\vec{a} × \vec{b}$ is $13\sqrt{3}$.
Example 23: Find a unit vector perpendicular to each of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$, where $\vec{a} = \hat{i} + \hat{j} + \hat{k} \;,\; \vec{b} = \hat{i} + 2\hat{j} + 3\hat{k}$.
Answer:
Given:
Vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$.
Vector $\vec{b} = \hat{i} + 2\hat{j} + 3\hat{k}$.
To Find:
A unit vector perpendicular to each of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$.
Solution:
A vector that is perpendicular to two given vectors is parallel to their cross product. To find a unit vector perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$, we can first find their cross product $(\vec{a} + \vec{b}) × (\vec{a} − \vec{b})$ and then normalize the resulting vector.
First, calculate the vector sum $\vec{a} + \vec{b}$:
$\vec{a} + \vec{b} = (\hat{i} + \hat{j} + \hat{k}) + (\hat{i} + 2\hat{j} + 3\hat{k})$
$\vec{a} + \vec{b} = (1+1)\hat{i} + (1+2)\hat{j} + (1+3)\hat{k} = 2\hat{i} + 3\hat{j} + 4\hat{k}$
Next, calculate the vector difference $\vec{a} - \vec{b}$:
$\vec{a} - \vec{b} = (\hat{i} + \hat{j} + \hat{k}) - (\hat{i} + 2\hat{j} + 3\hat{k})$
$\vec{a} - \vec{b} = (1-1)\hat{i} + (1-2)\hat{j} + (1-3)\hat{k} = 0\hat{i} - \hat{j} - 2\hat{k} = -\hat{j} - 2\hat{k}$
Now, calculate the cross product of $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$. Let $\vec{u} = \vec{a} + \vec{b}$ and $\vec{v} = \vec{a} - \vec{b}$.
$\vec{u} × \vec{v} = (2\hat{i} + 3\hat{j} + 4\hat{k}) × (-\hat{j} - 2\hat{k})$
We can compute this using the determinant form:
$\vec{u} × \vec{v} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 0 & -1 & -2 \end{vmatrix}$
Expand the determinant along the first row:
$\vec{u} × \vec{v} = \hat{i}((3)(-2) - (4)(-1)) - \hat{j}((2)(-2) - (4)(0)) + \hat{k}((2)(-1) - (3)(0))$
$\vec{u} × \vec{v} = \hat{i}(-6 - (-4)) - \hat{j}(-4 - 0) + \hat{k}(-2 - 0)$
$\vec{u} × \vec{v} = \hat{i}(-6 + 4) - \hat{j}(-4) + \hat{k}(-2)$
$\vec{u} × \vec{v} = -2\hat{i} + 4\hat{j} - 2\hat{k}$
This vector $-2\hat{i} + 4\hat{j} - 2\hat{k}$ is perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$. To find a unit vector in this direction, we need to divide this vector by its magnitude.
Calculate the magnitude of the cross product vector:
$|\vec{u} × \vec{v}| = |-2\hat{i} + 4\hat{j} - 2\hat{k}|$
$|\vec{u} × \vec{v}| = \sqrt{(-2)^2 + 4^2 + (-2)^2}$
$|\vec{u} × \vec{v}| = \sqrt{4 + 16 + 4}$
$|\vec{u} × \vec{v}| = \sqrt{24}$
Simplify the square root: $\sqrt{24} = \sqrt{4 \times 6} = 2\sqrt{6}$.
$|\vec{u} × \vec{v}| = 2\sqrt{6}$
The unit vector perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$ is given by:
$\hat{n} = \pm \frac{\vec{u} × \vec{v}}{|\vec{u} × \vec{v}|}$
$\hat{n} = \pm \frac{-2\hat{i} + 4\hat{j} - 2\hat{k}}{2\sqrt{6}}$
Factor out 2 from the numerator:
$\hat{n} = \pm \frac{2(-\hat{i} + 2\hat{j} - \hat{k})}{2\sqrt{6}}$
Cancel out the 2:
$\hat{n} = \pm \frac{-\hat{i} + 2\hat{j} - \hat{k}}{\sqrt{6}}$
This can also be written as:
$\hat{n} = \pm \left(-\frac{1}{\sqrt{6}}\hat{i} + \frac{2}{\sqrt{6}}\hat{j} - \frac{1}{\sqrt{6}}\hat{k}\right)$
There are two unit vectors perpendicular to the plane containing $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$, pointing in opposite directions. Both are valid answers.
The unit vectors are $\frac{-2\hat{i} + 4\hat{j} - 2\hat{k}}{2\sqrt{6}}$ and $\frac{2\hat{i} - 4\hat{j} + 2\hat{k}}{2\sqrt{6}}$.
Example 24: Find the area of a triangle having the points A(1, 1, 1), B(1, 2, 3) and C(2, 3, 1) as its vertices.
Answer:
Given:
The vertices of triangle ABC are A(1, 1, 1), B(1, 2, 3), and C(2, 3, 1).
To Find:
The area of triangle ABC.
Solution:
The area of a triangle with vertices A, B, and C can be calculated using the formula: Area $= \frac{1}{2} |\overrightarrow{AB} × \overrightarrow{AC}|$.
First, we find the vectors representing two sides originating from the same vertex, say A. We will find $\overrightarrow{AB}$ and $\overrightarrow{AC}$.
Vector $\overrightarrow{AB}$: $\overrightarrow{AB} = \text{Position vector of B} - \text{Position vector of A}$
The position vector of a point $(x, y, z)$ is $x\hat{i} + y\hat{j} + z\hat{k}$.
Position vector of A: $\hat{i} + \hat{j} + \hat{k}$
Position vector of B: $\hat{i} + 2\hat{j} + 3\hat{k}$
$\overrightarrow{AB} = (\hat{i} + 2\hat{j} + 3\hat{k}) - (\hat{i} + \hat{j} + \hat{k})$
$\overrightarrow{AB} = (1-1)\hat{i} + (2-1)\hat{j} + (3-1)\hat{k}$
$\overrightarrow{AB} = 0\hat{i} + \hat{j} + 2\hat{k}$
Vector $\overrightarrow{AC}$: $\overrightarrow{AC} = \text{Position vector of C} - \text{Position vector of A}$
Position vector of C: $2\hat{i} + 3\hat{j} + \hat{k}$
$\overrightarrow{AC} = (2\hat{i} + 3\hat{j} + \hat{k}) - (\hat{i} + \hat{j} + \hat{k})$
$\overrightarrow{AC} = (2-1)\hat{i} + (3-1)\hat{j} + (1-1)\hat{k}$
$\overrightarrow{AC} = \hat{i} + 2\hat{j} + 0\hat{k}$
Now, calculate the cross product $\overrightarrow{AB} × \overrightarrow{AC}$:
$\overrightarrow{AB} × \overrightarrow{AC} = (0\hat{i} + \hat{j} + 2\hat{k}) × (\hat{i} + 2\hat{j} + 0\hat{k})$
$\overrightarrow{AB} × \overrightarrow{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{vmatrix}$
Expand the determinant:
$\overrightarrow{AB} × \overrightarrow{AC} = \hat{i}((1)(0) - (2)(2)) - \hat{j}((0)(0) - (2)(1)) + \hat{k}((0)(2) - (1)(1))$
$\overrightarrow{AB} × \overrightarrow{AC} = \hat{i}(0 - 4) - \hat{j}(0 - 2) + \hat{k}(0 - 1)$
$\overrightarrow{AB} × \overrightarrow{AC} = -4\hat{i} + 2\hat{j} - \hat{k}$
Next, calculate the magnitude of the cross product vector:
$|\overrightarrow{AB} × \overrightarrow{AC}| = |-4\hat{i} + 2\hat{j} - \hat{k}|$
$|\overrightarrow{AB} × \overrightarrow{AC}| = \sqrt{(-4)^2 + 2^2 + (-1)^2}$
$|\overrightarrow{AB} × \overrightarrow{AC}| = \sqrt{16 + 4 + 1}$
$|\overrightarrow{AB} × \overrightarrow{AC}| = \sqrt{21}$
Finally, calculate the area of the triangle:
Area of $\triangle$ABC $= \frac{1}{2} |\overrightarrow{AB} × \overrightarrow{AC}|$
Area of $\triangle$ABC $= \frac{1}{2} \sqrt{21}$
The area of the triangle having vertices A(1, 1, 1), B(1, 2, 3) and C(2, 3, 1) is $\frac{\sqrt{21}}{2}$ square units.
Example 25: Find the area of a parallelogram whose adjacent sides are given by the vectors $\vec{a} = 3\hat{i} + \hat{j} + 4\hat{k}$ and $\vec{b} = \hat{i} − \hat{j} + \hat{k}$
Answer:
Given:
The adjacent sides of the parallelogram are given by the vectors:
$\vec{a} = 3\hat{i} + \hat{j} + 4\hat{k}$.
$\vec{b} = \hat{i} - \hat{j} + \hat{k}$.
To Find:
The area of the parallelogram.
Solution:
The area of a parallelogram with adjacent sides given by vectors $\vec{a}$ and $\vec{b}$ is equal to the magnitude of their cross product, i.e., Area $= |\;\vec{a} × \vec{b}\;|$.
First, calculate the cross product $\vec{a} × \vec{b}$. The cross product of two vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$ is given by the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
Substitute the components of $\vec{a}$ and $\vec{b}$ into the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 4 \\ 1 & -1 & 1 \end{vmatrix}$
Expand the determinant along the first row:
$\vec{a} × \vec{b} = \hat{i}((1)(1) - (4)(-1)) - \hat{j}((3)(1) - (4)(1)) + \hat{k}((3)(-1) - (1)(1))$
$\vec{a} × \vec{b} = \hat{i}(1 - (-4)) - \hat{j}(3 - 4) + \hat{k}(-3 - 1)$
$\vec{a} × \vec{b} = \hat{i}(1 + 4) - \hat{j}(-1) + \hat{k}(-4)$
$\vec{a} × \vec{b} = 5\hat{i} + \hat{j} - 4\hat{k}$
Now, calculate the magnitude of the cross product vector $\vec{a} × \vec{b}$. The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
Area $= |\;\vec{a} × \vec{b}\;| = |5\hat{i} + \hat{j} - 4\hat{k}|$
Area $= \sqrt{5^2 + 1^2 + (-4)^2}$
Area $= \sqrt{25 + 1 + 16}$
Area $= \sqrt{42}$
The area of the parallelogram is $\sqrt{42}$ square units.
Exercise 10.4
Question 1. Find $|\;\vec{a} \;×\; \vec{b}\;|$, if $\vec{a} = \hat{i} − 7\hat{j} + 7\hat{k}$ and $\vec{b} = 3\hat{i} − 2\hat{j} + 2\hat{k}$.
Answer:
Given:
Vector $\vec{a} = \hat{i} − 7\hat{j} + 7\hat{k}$.
Vector $\vec{b} = 3\hat{i} − 2\hat{j} + 2\hat{k}$.
To Find:
The magnitude of the cross product of $\vec{a}$ and $\vec{b}$, i.e., $|\;\vec{a}\; × \;\vec{b}\;|$.
Solution:
The cross product of two vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$ is given by the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
For the given vectors $\vec{a} = \hat{i} - 7\hat{j} + 7\hat{k}$ and $\vec{b} = 3\hat{i} - 2\hat{j} + 2\hat{k}$, the cross product is:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -7 & 7 \\ 3 & -2 & 2 \end{vmatrix}$
Expand the determinant along the first row:
$\vec{a} × \vec{b} = \hat{i}((-7)(2) - (7)(-2)) - \hat{j}((1)(2) - (7)(3)) + \hat{k}((1)(-2) - (-7)(3))$
$\vec{a} × \vec{b} = \hat{i}(-14 - (-14)) - \hat{j}(2 - 21) + \hat{k}(-2 - (-21))$
$\vec{a} × \vec{b} = \hat{i}(-14 + 14) - \hat{j}(-19) + \hat{k}(-2 + 21)$
$\vec{a} × \vec{b} = 0\hat{i} + 19\hat{j} + 19\hat{k}$
$\vec{a} × \vec{b} = 19\hat{j} + 19\hat{k}$
Now, calculate the magnitude of the resulting vector $\vec{a} × \vec{b}$. The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
$|\;\vec{a} × \vec{b}\;| = |0\hat{i} + 19\hat{j} + 19\hat{k}|$
$|\;\vec{a} × \vec{b}\;| = \sqrt{0^2 + 19^2 + 19^2}$
$|\;\vec{a} × \vec{b}\;| = \sqrt{0 + 361 + 361}$
$|\;\vec{a} × \vec{b}\;| = \sqrt{2 \times 361}$
$|\;\vec{a} × \vec{b}\;| = \sqrt{19^2 \times 2}$
$|\;\vec{a} × \vec{b}\;| = 19\sqrt{2}$
The magnitude of $\vec{a} × \vec{b}$ is $19\sqrt{2}$.
Question 2. Find a unit vector perpendicular to each of the vector $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$, where $\vec{a} = 3\hat{i} + 2\hat{j} + 2\hat{k}$ and $\vec{b} = \hat{i} + 2\hat{j} − 2\hat{k}$ .
Answer:
Given:
Vector $\vec{a} = 3\hat{i} + 2\hat{j} + 2\hat{k}$.
Vector $\vec{b} = \hat{i} + 2\hat{j} − 2\hat{k}$.
To Find:
A unit vector perpendicular to each of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$.
Solution:
A vector perpendicular to two given vectors is parallel to their cross product. To find a unit vector perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$, we can first find their cross product $(\vec{a} + \vec{b}) × (\vec{a} − \vec{b})$ and then normalize the resulting vector.
First, calculate the vector sum $\vec{a} + \vec{b}$:
$\vec{a} + \vec{b} = (3\hat{i} + 2\hat{j} + 2\hat{k}) + (\hat{i} + 2\hat{j} − 2\hat{k})$
$\vec{a} + \vec{b} = (3+1)\hat{i} + (2+2)\hat{j} + (2-2)\hat{k} = 4\hat{i} + 4\hat{j} + 0\hat{k}$
Next, calculate the vector difference $\vec{a} - \vec{b}$:
$\vec{a} - \vec{b} = (3\hat{i} + 2\hat{j} + 2\hat{k}) - (\hat{i} + 2\hat{j} − 2\hat{k})$
$\vec{a} - \vec{b} = (3-1)\hat{i} + (2-2)\hat{j} + (2-(-2))\hat{k} = 2\hat{i} + 0\hat{j} + 4\hat{k}$
Now, calculate the cross product of $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$. Let $\vec{u} = \vec{a} + \vec{b}$ and $\vec{v} = \vec{a} - \vec{b}$.
$\vec{u} × \vec{v} = (4\hat{i} + 4\hat{j} + 0\hat{k}) × (2\hat{i} + 0\hat{j} + 4\hat{k})$
We compute this using the determinant form:
$\vec{u} × \vec{v} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 4 & 0 \\ 2 & 0 & 4 \end{vmatrix}$
Expand the determinant along the first row:
$\vec{u} × \vec{v} = \hat{i}((4)(4) - (0)(0)) - \hat{j}((4)(4) - (0)(2)) + \hat{k}((4)(0) - (4)(2))$
$\vec{u} × \vec{v} = \hat{i}(16 - 0) - \hat{j}(16 - 0) + \hat{k}(0 - 8)$
$\vec{u} × \vec{v} = 16\hat{i} - 16\hat{j} - 8\hat{k}$
This vector $16\hat{i} - 16\hat{j} - 8\hat{k}$ is perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$. To find a unit vector in this direction, we need to divide this vector by its magnitude.
Calculate the magnitude of the cross product vector:
$|\vec{u} × \vec{v}| = |16\hat{i} - 16\hat{j} - 8\hat{k}|$
$|\vec{u} × \vec{v}| = \sqrt{16^2 + (-16)^2 + (-8)^2}$
$|\vec{u} × \vec{v}| = \sqrt{256 + 256 + 64}$
$|\vec{u} × \vec{v}| = \sqrt{576}$
Recognizing that $576 = 24^2$:
$|\vec{u} × \vec{v}| = 24$
The unit vector perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$ is given by:
$\hat{n} = \pm \frac{\vec{u} × \vec{v}}{|\vec{u} × \vec{v}|}$
$\hat{n} = \pm \frac{16\hat{i} - 16\hat{j} - 8\hat{k}}{24}$
Divide each component by 24:
$\hat{n} = \pm \left(\frac{16}{24}\hat{i} - \frac{16}{24}\hat{j} - \frac{8}{24}\hat{k}\right)$
Simplify the fractions:
$\hat{n} = \pm \left(\frac{2}{3}\hat{i} - \frac{2}{3}\hat{j} - \frac{1}{3}\hat{k}\right)$
There are two unit vectors perpendicular to the plane containing $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$, pointing in opposite directions. Both are valid answers.
The unit vectors are $\frac{2}{3}\hat{i} - \frac{2}{3}\hat{j} - \frac{1}{3}\hat{k}$ and $-\frac{2}{3}\hat{i} + \frac{2}{3}\hat{j} + \frac{1}{3}\hat{k}$.
Question 3. If a unit vector $\vec{a}$ makes angles $\frac{π}{3}$ with $\hat{i}$ , $\frac{π}{4}$ with $\hat{j}$ and an acute angle θ with $\hat{k}$, then find θ and hence, the components of $\vec{a}$.
Answer:
Given:
$\vec{a}$ is a unit vector, so $|\vec{a}| = 1$.
The angle between $\vec{a}$ and $\hat{i}$ is $\alpha = \frac{\pi}{3}$.
The angle between $\vec{a}$ and $\hat{j}$ is $\beta = \frac{\pi}{4}$.
The angle between $\vec{a}$ and $\hat{k}$ is $\theta$, where $\theta$ is an acute angle ($0 \leq \theta < \frac{\pi}{2}$).
To Find:
The value of $\theta$ and the components of $\vec{a}$.
Solution:
Let the unit vector $\vec{a}$ be written in terms of its components as $\vec{a} = l\hat{i} + m\hat{j} + n\hat{k}$, where $l, m, n$ are the direction cosines of $\vec{a}$ along the x, y, and z axes, respectively.
The direction cosines are related to the angles made with the axes ($\alpha, \beta, \gamma$) by:
$l = \cos \alpha$
$m = \cos \beta$
$n = \cos \gamma$
We are given $\alpha = \frac{\pi}{3}$, $\beta = \frac{\pi}{4}$, and $\gamma = \theta$.
$l = \cos \left(\frac{\pi}{3}\right) = \frac{1}{2}$
$m = \cos \left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}$
$n = \cos \theta$
For any vector, the sum of the squares of its direction cosines is equal to 1. For a unit vector, this property is expressed as:
$l^2 + m^2 + n^2 = 1$
Substitute the values of $l$ and $m$ and the expression for $n$ into this equation:
$\left(\frac{1}{2}\right)^2 + \left(\frac{1}{\sqrt{2}}\right)^2 + (\cos \theta)^2 = 1$
$\frac{1}{4} + \frac{1}{2} + \cos^2 \theta = 1$}
To add the fractions, find a common denominator (4):
$\frac{1}{4} + \frac{2}{4} + \cos^2 \theta = 1$
$\frac{3}{4} + \cos^2 \theta = 1$
Solve for $\cos^2 \theta$:
$\cos^2 \theta = 1 - \frac{3}{4}$
$\cos^2 \theta = \frac{4-3}{4} = \frac{1}{4}$
Take the square root of both sides to find $\cos \theta$:
$\cos \theta = \pm \sqrt{\frac{1}{4}}$
$\cos \theta = \pm \frac{1}{2}$
We are given that $\theta$ is an acute angle. An acute angle $\theta$ lies in the interval $[0, \frac{\pi}{2})$. In this interval, $\cos \theta$ must be positive.
Therefore, we take the positive value for $\cos \theta$:
$\cos \theta = \frac{1}{2}$
To find the value of $\theta$, we find the inverse cosine of $\frac{1}{2}$. The angle $\theta$ in the interval $[0, \frac{\pi}{2})$ such that $\cos \theta = \frac{1}{2}$ is $\frac{\pi}{3}$.
$\theta = \frac{\pi}{3}$
Now that we have found $\theta$, we can find the components of $\vec{a}$. The components are the direction cosines $l, m, n$.
$l = \cos \left(\frac{\pi}{3}\right) = \frac{1}{2}$
$m = \cos \left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}$
$n = \cos \theta = \cos \left(\frac{\pi}{3}\right) = \frac{1}{2}$
The components of $\vec{a}$ are the coefficients of $\hat{i}$, $\hat{j}$, and $\hat{k}$ respectively.
So, $\vec{a} = l\hat{i} + m\hat{j} + n\hat{k}$.
$\vec{a} = \frac{1}{2}\hat{i} + \frac{1}{\sqrt{2}}\hat{j} + \frac{1}{2}\hat{k}$
The value of the acute angle $\theta$ is $\frac{\pi}{3}$, and the components of the unit vector $\vec{a}$ are $\left(\frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}\right)$.
Question 4. Show that $(\;\vec{a} - \vec{b}) \;×\; (\vec{a} + \vec{b}) = 2(\vec{a} \;×\; \vec{b})$
Answer:
Given:
Two vectors $\vec{a}$ and $\vec{b}$.
To Show:
The vector identity: $(\;\vec{a} - \vec{b}) \;×\; (\vec{a} + \vec{b}) = 2(\vec{a} \;×\; \vec{b})$.
Solution:
We start by evaluating the left side of the equation, $(\;\vec{a} - \vec{b}) \;×\; (\vec{a} + \vec{b})$.
Using the distributive property of the cross product, $\vec{u} × (\vec{v} + \vec{w}) = \vec{u} × \vec{v} + \vec{u} × \vec{w}$:
$(\;\vec{a} - \vec{b}) \;×\; (\vec{a} + \vec{b}) = (\;\vec{a} - \vec{b}) \;×\; \vec{a} + (\;\vec{a} - \vec{b}) \;×\; \vec{b}$
Now, apply the distributive property again, $(\vec{u} - \vec{v}) × \vec{w} = \vec{u} × \vec{w} - \vec{v} × \vec{w}$:
$= (\vec{a} \;×\; \vec{a} - \vec{b} \;×\; \vec{a}) + (\vec{a} \;×\; \vec{b} - \vec{b} \;×\; \vec{b})$
We know that the cross product of any vector with itself is the zero vector, i.e., $\vec{v} \;×\; \vec{v} = \vec{0}$.
So, $\vec{a} \;×\; \vec{a} = \vec{0}$ and $\vec{b} \;×\; \vec{b} = \vec{0}$.
Substitute these into the expression:
$= (\vec{0} - \vec{b} \;×\; \vec{a}) + (\vec{a} \;×\; \vec{b} - \vec{0})$
$= -\vec{b} \;×\; \vec{a} + \vec{a} \;×\; \vec{b}$
Using the property that the cross product is anticommutative, $\vec{b} \;×\; \vec{a} = -(\vec{a} \;×\; \vec{b})$:
$= -(-(\vec{a} \;×\; \vec{b})) + \vec{a} \;×\; \vec{b}$
$= \vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{b}$
$= 2(\vec{a} \;×\; \vec{b})$
The left side simplifies to $2(\vec{a} \;×\; \vec{b})$, which is equal to the right side of the given equation.
Thus, we have shown that $(\;\vec{a} - \vec{b}) \;×\; (\vec{a} + \vec{b}) = 2(\vec{a} \;×\; \vec{b})$.
Question 5. Find λ and µ if $(2\hat{i} + 6\hat{j} + 27\hat{k}) \;×\; (\hat{i} + λ\hat{j} + µ\hat{k}) = \vec{0}$.
Answer:
Given:
The cross product of two vectors is the zero vector:
$(2\hat{i} + 6\hat{j} + 27\hat{k}) \;×\; (\hat{i} + λ\hat{j} + µ\hat{k}) = \vec{0}$
To Find:
The values of the scalars $\lambda$ and $\mu$.
Solution:
The cross product of two vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$ is given by the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
Let $\vec{u} = 2\hat{i} + 6\hat{j} + 27\hat{k}$ and $\vec{v} = \hat{i} + λ\hat{j} + µ\hat{k}$. We are given $\vec{u} × \vec{v} = \vec{0}$.
Calculate the cross product $\vec{u} × \vec{v}$:
$\vec{u} × \vec{v} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 6 & 27 \\ 1 & λ & µ \end{vmatrix}$
Expand the determinant along the first row:
$\vec{u} × \vec{v} = \hat{i}((6)(µ) - (27)(λ)) - \hat{j}((2)(µ) - (27)(1)) + \hat{k}((2)(λ) - (6)(1))$
$\vec{u} × \vec{v} = \hat{i}(6µ - 27λ) - \hat{j}(2µ - 27) + \hat{k}(2λ - 6)$
We are given that $\vec{u} × \vec{v} = \vec{0}$, which is the zero vector $0\hat{i} + 0\hat{j} + 0\hat{k}$.
Equating the components of $\vec{u} × \vec{v}$ to the components of the zero vector:
$6µ - 27λ = 0$
... (1)
$-(2µ - 27) = 0 \implies 2µ - 27 = 0$
... (2)
$2λ - 6 = 0$
... (3)
Solve the system of equations for $\lambda$ and $\mu$.
From equation (3):
$2λ - 6 = 0$
$2λ = 6$
$λ = 3$
From equation (2):
$2µ - 27 = 0$
$2µ = 27$
$µ = \frac{27}{2}$
We can verify these values using equation (1):
$6µ - 27λ = 6\left(\frac{27}{2}\right) - 27(3)$
$= 3 \times 27 - 81$
$= 81 - 81 = 0$
The values satisfy all three equations.
Alternatively, since the cross product of two non-zero vectors is the zero vector if and only if they are collinear, we must have $(2\hat{i} + 6\hat{j} + 27\hat{k}) = k (\hat{i} + λ\hat{j} + µ\hat{k})$ for some scalar $k$.
$2\hat{i} + 6\hat{j} + 27\hat{k} = k\hat{i} + kλ\hat{j} + kµ\hat{k}$
Comparing components: $2 = k$, $6 = kλ$, $27 = kµ$.
Substitute $k=2$ into the other two equations:
$6 = 2λ \implies λ = 3$
$27 = 2µ \implies µ = \frac{27}{2}$
This gives the same result.
The values of $\lambda$ and $\mu$ are $3$ and $\frac{27}{2}$, respectively.
Question 6. Given that $\vec{a} \;.\; \vec{b} = 0$ and $\vec{a} \;\times\; \vec{b} = \vec{0}$. What can you conclude about the vectors $\vec{a}$ and $\vec{b}$ ?
Answer:
Given:
$\vec{a} \;.\; \vec{b} = 0$.
$\vec{a} \;\times\; \vec{b} = \vec{0}$.
To Conclude:
What can be concluded about the vectors $\vec{a}$ and $\vec{b}$.
Solution:
Let $\theta$ be the angle between the vectors $\vec{a}$ and $\vec{b}$, where $0 \leq \theta \leq \pi$.
Consider the first given condition: $\vec{a} \;.\; \vec{b} = 0$.
The dot product of two vectors is defined as $\vec{a} \;.\; \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$.
So, the condition $\vec{a} \;.\; \vec{b} = 0$ implies:
$|\vec{a}| |\vec{b}| \cos \theta = 0$
... (1)
Consider the second given condition: $\vec{a} \;\times\; \vec{b} = \vec{0}$.
The magnitude of the cross product of two vectors is defined as $|\vec{a} \;\times\; \vec{b}| = |\vec{a}| |\vec{b}| \sin \theta$.
The condition $\vec{a} \;\times\; \vec{b} = \vec{0}$ means its magnitude is 0, so:
$|\vec{a}| |\vec{b}| \sin \theta = 0$
... (2)
From equation (1), at least one of the factors must be zero: $|\vec{a}| = 0$, $|\vec{b}| = 0$, or $\cos \theta = 0$.
From equation (2), at least one of the factors must be zero: $|\vec{a}| = 0$, $|\vec{b}| = 0$, or $\sin \theta = 0$.
If $|\vec{a}| = 0$, then $\vec{a}$ is the zero vector. In this case, $\vec{a} \;.\; \vec{b} = \vec{0} \;.\; \vec{b} = 0$ and $\vec{a} \;\times\; \vec{b} = \vec{0} \;\times\; \vec{b} = \vec{0}$ are both true for any vector $\vec{b}$.
If $|\vec{b}| = 0$, then $\vec{b}$ is the zero vector. In this case, $\vec{a} \;.\; \vec{b} = \vec{a} \;.\; \vec{0} = 0$ and $\vec{a} \;\times\; \vec{b} = \vec{a} \;\times\; \vec{0} = \vec{0}$ are both true for any vector $\vec{a}$.
Now, consider the case where neither $\vec{a}$ nor $\vec{b}$ is the zero vector, i.e., $|\vec{a}| \neq 0$ and $|\vec{b}| \neq 0$.
In this case, from equation (1): $|\vec{a}| |\vec{b}| \cos \theta = 0$ implies $\cos \theta = 0$. This means $\theta = \frac{\pi}{2}$ (or $90^\circ$). The vectors $\vec{a}$ and $\vec{b}$ are perpendicular.
From equation (2): $|\vec{a}| |\vec{b}| \sin \theta = 0$ implies $\sin \theta = 0$. This means $\theta = 0$ or $\theta = \pi$ (or $0^\circ$ or $180^\circ$). The vectors $\vec{a}$ and $\vec{b}$ are parallel or collinear.
For non-zero vectors $\vec{a}$ and $\vec{b}$, they cannot be simultaneously perpendicular ($\theta = \frac{\pi}{2}$) and parallel/collinear ($\theta = 0$ or $\pi$). These are contradictory conditions for a single pair of vectors.
Therefore, the only way for both $\vec{a} \;.\; \vec{b} = 0$ and $\vec{a} \;\times\; \vec{b} = \vec{0}$ to be true is if our assumption that neither vector is zero is incorrect.
This means at least one of the vectors must be the zero vector.
Conclusion:
From the given conditions, we can conclude that at least one of the vectors $\vec{a}$ or $\vec{b}$ must be the zero vector. That is, $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$.
Question 7. Let the vectors $\vec{a} \;,\; \vec{b} \;,\; \vec{c}$ be given as $a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ , $b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$ , $c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$. Then show that $\vec{a} \;×\; (\vec{b} + \vec{c}) = \vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{c}$.
Answer:
Given:
Vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$, $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$, and $\vec{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$.
To Show:
The distributive property of the cross product: $\vec{a} \;×\; (\vec{b} + \vec{c}) = \vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{c}$.
Solution:
We will evaluate both the left-hand side (LHS) and the right-hand side (RHS) of the equation and show that they are equal.
Left-Hand Side (LHS): $\vec{a} \;×\; (\vec{b} + \vec{c})$
First, calculate the sum of vectors $\vec{b} + \vec{c}$:
$\vec{b} + \vec{c} = (b_1\hat{i} + b_2\hat{j} + b_3\hat{k}) + (c_1\hat{i} + c_2\hat{j} + c_3\hat{k})$
$\vec{b} + \vec{c} = (b_1 + c_1)\hat{i} + (b_2 + c_2)\hat{j} + (b_3 + c_3)\hat{k}$
Now, calculate the cross product $\vec{a} \;×\; (\vec{b} + \vec{c})$ using the determinant formula:
$\vec{a} \;×\; (\vec{b} + \vec{c}) = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1+c_1 & b_2+c_2 & b_3+c_3 \end{vmatrix}$
Expand the determinant:
$\vec{a} \;×\; (\vec{b} + \vec{c}) = \hat{i} [a_2(b_3+c_3) - a_3(b_2+c_2)]$
$ - \hat{j} [a_1(b_3+c_3) - a_3(b_1+c_1)]$
$ + \hat{k} [a_1(b_2+c_2) - a_2(b_1+c_1)]$
Distribute the terms inside the brackets:
$\vec{a} \;×\; (\vec{b} + \vec{c}) = \hat{i} [a_2b_3 + a_2c_3 - a_3b_2 - a_3c_2]$
$ - \hat{j} [a_1b_3 + a_1c_3 - a_3b_1 - a_3c_1]$
$ + \hat{k} [a_1b_2 + a_1c_2 - a_2b_1 - a_2c_1]$
Rearrange the terms by grouping those related to $\vec{b}$ and those related to $\vec{c}$:
$\vec{a} \;×\; (\vec{b} + \vec{c}) = \hat{i} [(a_2b_3 - a_3b_2) + (a_2c_3 - a_3c_2)]$
$ - \hat{j} [(a_1b_3 - a_3b_1) + (a_1c_3 - a_3c_1)]$
$ + \hat{k} [(a_1b_2 - a_2b_1) + (a_1c_2 - a_2c_1)]$
Separate the terms into two vector expressions:
$\vec{a} \;×\; (\vec{b} + \vec{c}) = [\hat{i}(a_2b_3 - a_3b_2) - \hat{j}(a_1b_3 - a_3b_1) + \hat{k}(a_1b_2 - a_2b_1)]$
$ + [\hat{i}(a_2c_3 - a_3c_2) - \hat{j}(a_1c_3 - a_3c_1) + \hat{k}(a_1c_2 - a_2c_1)]$
... (1)
Right-Hand Side (RHS): $\vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{c}$
Calculate the cross product $\vec{a} \;×\; \vec{b}$:
$\vec{a} \;×\; \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
$\vec{a} \;×\; \vec{b} = \hat{i}(a_2b_3 - a_3b_2) - \hat{j}(a_1b_3 - a_3b_1) + \hat{k}(a_1b_2 - a_2b_1)$
Calculate the cross product $\vec{a} \;×\; \vec{c}$:
$\vec{a} \;×\; \vec{c} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ c_1 & c_2 & c_3 \end{vmatrix}$
$\vec{a} \;×\; \vec{c} = \hat{i}(a_2c_3 - a_3c_2) - \hat{j}(a_1c_3 - a_3c_1) + \hat{k}(a_1c_2 - a_2c_1)$
Add the resulting vectors $\vec{a} \;×\; \vec{b}$ and $\vec{a} \;×\; \vec{c}$ by adding their corresponding components:
$\vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{c} = [\hat{i}(a_2b_3 - a_3b_2) - \hat{j}(a_1b_3 - a_3b_1) + \hat{k}(a_1b_2 - a_2b_1)]$
$ + [\hat{i}(a_2c_3 - a_3c_2) - \hat{j}(a_1c_3 - a_3c_1) + \hat{k}(a_1c_2 - a_2c_1)]$
... (2)
Comparing the expression for the LHS in (1) and the expression for the RHS in (2), we see that they are identical.
$\vec{a} \;×\; (\vec{b} + \vec{c}) = \vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{c}$
Thus, the distributive property of the cross product over vector addition is shown.
Question 8. If either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$ then $\vec{a} \;×\; \vec{b} = \vec{0}$. Is the converse true? Justify your answer with an example.
Answer:
Given Statement:
If either vector $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a} \;×\; \vec{b} = \vec{0}$.
Statement to Justify:
The converse of the given statement, which is "If $\vec{a} \;×\; \vec{b} = \vec{0}$, then either vector $\vec{a} = \vec{0}$ or vector $\vec{b} = \vec{0}$", is not necessarily true.
Justification:
The cross product of two vectors $\vec{a}$ and $\vec{b}$ is a vector whose magnitude is given by $|\vec{a} \;\times\; \vec{b}| = |\vec{a}| |\vec{b}| \sin \theta$, where $\theta$ is the angle between the vectors $\vec{a}$ and $\vec{b}$ ($0 \leq \theta \leq \pi$).
The condition $\vec{a} \;×\; \vec{b} = \vec{0}$ means that the magnitude of the cross product is zero:
$|\vec{a} \;\times\; \vec{b}| = 0$
Substituting the formula for the magnitude:
$|\vec{a}| |\vec{b}| \sin \theta = 0$
... (i)
From equation (i), the product $|\vec{a}| |\vec{b}| \sin \theta$ is zero if and only if at least one of the factors is zero:
1. $|\vec{a}| = 0$, which implies $\vec{a} = \vec{0}$.
2. $|\vec{b}| = 0$, which implies $\vec{b} = \vec{0}$.
3. $\sin \theta = 0$. For $0 \leq \theta \leq \pi$, this occurs when $\theta = 0$ or $\theta = \pi$. This condition means the vectors $\vec{a}$ and $\vec{b}$ are collinear (parallel or antiparallel).
The converse statement "If $\vec{a} \;×\; \vec{b} = \vec{0}$, then either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$" claims that only the first two possibilities ($|\vec{a}|=0$ or $|\vec{b}|=0$) can lead to $\vec{a} \;×\; \vec{b} = \vec{0}$. However, the third possibility ($\sin \theta = 0$) also results in a zero cross product, and this can happen even if neither $\vec{a}$ nor $\vec{b}$ is the zero vector (i.e., if they are non-zero collinear vectors).
Therefore, $\vec{a} \;×\; \vec{b} = \vec{0}$ only implies that $\vec{a}$ and $\vec{b}$ are collinear, which does not necessarily mean that one of them must be the zero vector.
Example:
Let $\vec{a} = \hat{i}$ and $\vec{b} = 2\hat{i}$.
These are two non-zero vectors:
$|\vec{a}| = |\hat{i}| = 1 \neq 0$.
$|\vec{b}| = |2\hat{i}| = 2|\hat{i}| = 2 \neq 0$.
Now, let's calculate their cross product:
$\vec{a} \;×\; \vec{b} = \hat{i} \;×\; (2\hat{i})$
Using the property $(k\vec{u}) × \vec{v} = k(\vec{u} × \vec{v})$ and $\vec{v} × \vec{v} = \vec{0}$:
$\vec{a} \;×\; \vec{b} = 2 (\hat{i} \;×\; \hat{i})$
$\vec{a} \;×\; \vec{b} = 2 (\vec{0}) = \vec{0}$
In this example, we have $\vec{a} \;×\; \vec{b} = \vec{0}$, but neither $\vec{a}$ nor $\vec{b}$ is the zero vector. This is because $\vec{a}$ and $\vec{b}$ are non-zero and collinear.
This example justifies that the converse statement is not true.
Question 9. Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
Answer:
Given:
The vertices of triangle ABC are A(1, 1, 2), B(2, 3, 5), and C(1, 5, 5).
To Find:
The area of triangle ABC.
Solution:
To find the area of a triangle with vertices A, B, and C, we can use the formula: Area $= \frac{1}{2} |\overrightarrow{AB} \times \overrightarrow{AC}|$.
First, we need to find the vectors representing two sides originating from the same vertex, say A. We will calculate $\overrightarrow{AB}$ and $\overrightarrow{AC}$.
The position vector of a point P$(x, y, z)$ is $\vec{p} = x\hat{i} + y\hat{j} + z\hat{k}$.
Position vector of A: $\vec{a} = \hat{i} + \hat{j} + 2\hat{k}$
Position vector of B: $\vec{b} = 2\hat{i} + 3\hat{j} + 5\hat{k}$
Position vector of C: $\vec{c} = \hat{i} + 5\hat{j} + 5\hat{k}$
Vector $\overrightarrow{AB}$: $\overrightarrow{AB} = \vec{b} - \vec{a}$
$\overrightarrow{AB} = (2\hat{i} + 3\hat{j} + 5\hat{k}) - (\hat{i} + \hat{j} + 2\hat{k})$
$\overrightarrow{AB} = (2-1)\hat{i} + (3-1)\hat{j} + (5-2)\hat{k}$
$\overrightarrow{AB} = \hat{i} + 2\hat{j} + 3\hat{k}$
Vector $\overrightarrow{AC}$: $\overrightarrow{AC} = \vec{c} - \vec{a}$
$\overrightarrow{AC} = (\hat{i} + 5\hat{j} + 5\hat{k}) - (\hat{i} + \hat{j} + 2\hat{k})$
$\overrightarrow{AC} = (1-1)\hat{i} + (5-1)\hat{j} + (5-2)\hat{k}$
$\overrightarrow{AC} = 0\hat{i} + 4\hat{j} + 3\hat{k} = 4\hat{j} + 3\hat{k}$
Now, calculate the cross product $\overrightarrow{AB} × \overrightarrow{AC}$. The cross product of two vectors $\vec{u} = u_1\hat{i} + u_2\hat{j} + u_3\hat{k}$ and $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is:
$\vec{u} × \vec{v} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix}$
$\overrightarrow{AB} × \overrightarrow{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ 0 & 4 & 3 \end{vmatrix}$
Expand the determinant along the first row:
$\overrightarrow{AB} × \overrightarrow{AC} = \hat{i}((2)(3) - (3)(4)) - \hat{j}((1)(3) - (3)(0)) + \hat{k}((1)(4) - (2)(0))$
$\overrightarrow{AB} × \overrightarrow{AC} = \hat{i}(6 - 12) - \hat{j}(3 - 0) + \hat{k}(4 - 0)$
$\overrightarrow{AB} × \overrightarrow{AC} = -6\hat{i} - 3\hat{j} + 4\hat{k}$
Next, calculate the magnitude of the cross product vector:
$|\overrightarrow{AB} × \overrightarrow{AC}| = |-6\hat{i} - 3\hat{j} + 4\hat{k}|$
$|\overrightarrow{AB} × \overrightarrow{AC}| = \sqrt{(-6)^2 + (-3)^2 + 4^2}$
$|\overrightarrow{AB} × \overrightarrow{AC}| = \sqrt{36 + 9 + 16}$
$|\overrightarrow{AB} × \overrightarrow{AC}| = \sqrt{61}$
Finally, calculate the area of the triangle using the formula:
Area of $\triangle$ABC $= \frac{1}{2} |\overrightarrow{AB} × \overrightarrow{AC}|$
Area of $\triangle$ABC $= \frac{1}{2} \sqrt{61}$
The area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5) is $\frac{\sqrt{61}}{2}$ square units.
Question 10. Find the area of the parallelogram whose adjacent sides are determined by the vectors $\vec{a} = \hat{i} - \hat{j} + 3\hat{k}$ and $\vec{b} = 2\hat{i} − 7\hat{j} + \hat{k}$
Answer:
Given:
The adjacent sides of the parallelogram are given by the vectors:
$\vec{a} = \hat{i} - \hat{j} + 3\hat{k}$.
$\vec{b} = 2\hat{i} − 7\hat{j} + \hat{k}$.
To Find:
The area of the parallelogram.
Solution:
The area of a parallelogram with adjacent sides given by vectors $\vec{a}$ and $\vec{b}$ is equal to the magnitude of their cross product, i.e., Area $= |\;\vec{a} × \vec{b}\;|$.
First, calculate the cross product $\vec{a} × \vec{b}$. The cross product of two vectors $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$ is given by the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
Substitute the components of $\vec{a}$ and $\vec{b}$ into the determinant:
$\vec{a} × \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 3 \\ 2 & -7 & 1 \end{vmatrix}$
Expand the determinant along the first row:
$\vec{a} × \vec{b} = \hat{i}((-1)(1) - (3)(-7)) - \hat{j}((1)(1) - (3)(2)) + \hat{k}((1)(-7) - (-1)(2))$
$\vec{a} × \vec{b} = \hat{i}(-1 - (-21)) - \hat{j}(1 - 6) + \hat{k}(-7 - (-2))$
$\vec{a} × \vec{b} = \hat{i}(-1 + 21) - \hat{j}(-5) + \hat{k}(-7 + 2)$
$\vec{a} × \vec{b} = 20\hat{i} + 5\hat{j} - 5\hat{k}$
Now, calculate the magnitude of the cross product vector $\vec{a} × \vec{b}$. The magnitude of a vector $\vec{v} = v_1\hat{i} + v_2\hat{j} + v_3\hat{k}$ is $|\vec{v}| = \sqrt{v_1^2 + v_2^2 + v_3^2}$.
Area $= |\;\vec{a} × \vec{b}\;| = |20\hat{i} + 5\hat{j} - 5\hat{k}|$
Area $= \sqrt{20^2 + 5^2 + (-5)^2}$
Area $= \sqrt{400 + 25 + 25}$
Area $= \sqrt{450}$
Simplify the square root $\sqrt{450}$:
$\sqrt{450} = \sqrt{225 \times 2}$
$\sqrt{450} = \sqrt{15^2 \times 2}$
Area $= 15\sqrt{2}$
The area of the parallelogram whose adjacent sides are determined by the vectors $\vec{a}$ and $\vec{b}$ is $15\sqrt{2}$ square units.
Question 11. Let the vectores $\vec{a}$ and $\vec{b}$ be such that $|\;\vec{a}\;| = 3$ and $|\;\vec{b}\;| = \frac{\sqrt{2}}{3}$ , then $\vec{a} \;×\; \vec{b}$ is a unit vector, if the angle between $\vec{a}$ and $\vec{b}$ is
(A) $\frac{π}{6}$
(B) $\frac{π}{4}$
(C) $\frac{π}{3}$
(D) $\frac{π}{2}$
Answer:
Given:
Magnitude of vector $\vec{a}$, $|\vec{a}| = 3$.
Magnitude of vector $\vec{b}$, $|\vec{b}| = \frac{\sqrt{2}}{3}$.
The cross product $\vec{a} \;×\; \vec{b}$ is a unit vector, so $|\;\vec{a} \;×\; \vec{b}\;| = 1$.
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The magnitude of the cross product of two vectors $\vec{a}$ and $\vec{b}$ is given by the formula:
$|\;\vec{a} \;×\; \vec{b}\;| = |\;\vec{a}\;| |\;\vec{b}\;| \sin \theta$
where $\theta$ is the angle between the vectors, with $0 \leq \theta \leq \pi$.
Substitute the given values into the formula:
$1 = (3) \left(\frac{\sqrt{2}}{3}\right) \sin \theta$
Simplify the equation:
$1 = \sqrt{2} \sin \theta$
Solve for $\sin \theta$:
$\sin \theta = \frac{1}{\sqrt{2}}$
For $0 \leq \theta \leq \pi$, the angles whose sine is $\frac{1}{\sqrt{2}}$ are $\frac{\pi}{4}$ and $\frac{3\pi}{4}$.
The possible values for $\theta$ are $\frac{\pi}{4}$ and $\frac{3\pi}{4}$.
Comparing these possible values with the given options:
(A) $\frac{π}{6}$ ($\sin \frac{\pi}{6} = \frac{1}{2} \neq \frac{1}{\sqrt{2}}$)
(B) $\frac{π}{4}$ ($\sin \frac{\pi}{4} = \frac{1}{\sqrt{2}}$)
(C) $\frac{π}{3}$ ($\sin \frac{\pi}{3} = \frac{\sqrt{3}}{2} \neq \frac{1}{\sqrt{2}}$)
(D) $\frac{π}{2}$ ($\sin \frac{\pi}{2} = 1 \neq \frac{1}{\sqrt{2}}$)
The only option that satisfies the condition $\sin \theta = \frac{1}{\sqrt{2}}$ is $\theta = \frac{\pi}{4}$.
The correct angle between $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$.
The correct option is (B) $\frac{π}{4}$.
Question 12. Area of a rectangle having vertices A, B, C and D with position vectors $-\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k} ̂\;,\; \hat{i} + \frac{1}{2}\hat{j} + 4\hat{k} \;,\; \hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}$ and $−\hat{i} − \frac{1}{2}\hat{j} + 4\hat{k}$ , respectively is
(A) $\frac{1}{2}$
(B) 1
(C) 2
(D) 4
Answer:
Given:
The vertices of the rectangle are A, B, C, and D with position vectors:
Position vector of A, $\vec{a} = -\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k}$.
Position vector of B, $\vec{b} = \hat{i} + \frac{1}{2}\hat{j} + 4\hat{k}$.
Position vector of C, $\vec{c} = \hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}$.
Position vector of D, $\vec{d} = -\hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}$.
To Find:
The area of the rectangle ABCD.
Solution:
To find the area of the rectangle, we can determine the vectors representing two adjacent sides and then find the product of their magnitudes.
Let's find the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$.
Vector $\overrightarrow{AB}$: $\overrightarrow{AB} = \text{Position vector of B} - \text{Position vector of A}$
$\overrightarrow{AB} = (\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k}) - (-\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k})$
$\overrightarrow{AB} = (1 - (-1))\hat{i} + (\frac{1}{2} - \frac{1}{2})\hat{j} + (4 - 4)\hat{k}$
$\overrightarrow{AB} = 2\hat{i} + 0\hat{j} + 0\hat{k} = 2\hat{i}$
Vector $\overrightarrow{BC}$: $\overrightarrow{BC} = \text{Position vector of C} - \text{Position vector of B}$
$\overrightarrow{BC} = (\hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}) - (\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k})$
$\overrightarrow{BC} = (1 - 1)\hat{i} + (-\frac{1}{2} - \frac{1}{2})\hat{j} + (4 - 4)\hat{k}$
$\overrightarrow{BC} = 0\hat{i} - \hat{j} + 0\hat{k} = -\hat{j}$
The lengths of these adjacent sides are their magnitudes:
Length of side AB, $|\overrightarrow{AB}| = |2\hat{i}| = \sqrt{2^2} = 2$.
Length of side BC, $|\overrightarrow{BC}| = |-\hat{j}| = \sqrt{(-1)^2} = 1$.
Since it is a rectangle, the adjacent sides are perpendicular. We can confirm this by checking their dot product:
$\overrightarrow{AB} \;.\; \overrightarrow{BC} = (2\hat{i}) \;.\; (-\hat{j}) = (2)(0) + (0)(-1) + (0)(0) = 0$.
Since the dot product is 0, $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are perpendicular, confirming that A, B, C form a right angle at B, consistent with the figure being a rectangle.
The area of a rectangle is the product of the lengths of its adjacent sides:
Area $= |\overrightarrow{AB}| \times |\overrightarrow{BC}|$
Area $= 2 \times 1$
Area $= 2$
Alternatively, the area of the parallelogram formed by adjacent vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$ (which is the rectangle in this case) is given by the magnitude of their cross product:
Area $= |\overrightarrow{AB} \times \overrightarrow{BC}|$
$\overrightarrow{AB} \times \overrightarrow{BC} = (2\hat{i}) \times (-\hat{j}) = 2 (\hat{i} \times (-\hat{j})) = -2 (\hat{i} \times \hat{j})$
Using the property $\hat{i} \times \hat{j} = \hat{k}$:
$\overrightarrow{AB} \times \overrightarrow{BC} = -2\hat{k}$
Area $= |-2\hat{k}| = \sqrt{(-2)^2} = \sqrt{4} = 2$.
The area of the rectangle is 2 square units.
The correct option is (C) 2.
Example 26 to 30 - Miscellaneous Examples
Example 26: Write all the unit vectors in XY-plane.
Answer:
A unit vector is a vector that has a magnitude (or length) of 1.
A vector in the XY-plane can be represented in terms of its components along the x-axis and y-axis using the standard unit vectors $\hat{i}$ and $\hat{j}$. Let $\vec{v}$ be a vector in the XY-plane. It can be written as:
$\vec{v} = x\hat{i} + y\hat{j}$
where $x$ and $y$ are the scalar components of the vector along the x and y axes, respectively.
The magnitude of the vector $\vec{v}$ is calculated using the formula $|\vec{v}| = \sqrt{x^2 + y^2}$.
For $\vec{v}$ to be a unit vector, its magnitude must be equal to 1.
$|\vec{v}| = 1$
... (i)
Substituting the magnitude formula into equation (i):
$\sqrt{x^2 + y^2} = 1$
Squaring both sides of the equation, we get:
$x^2 + y^2 = 1$
... (ii)
Equation (ii), $x^2 + y^2 = 1$, is the equation of a circle centered at the origin $(0,0)$ with a radius of 1 in the XY-plane. Every point $(x,y)$ on this circle corresponds to the terminal point of a unit vector that starts from the origin.
Any point $(x, y)$ on the unit circle can be described by its polar coordinates $(r, \theta)$, where $r=1$ (the radius) and $\theta$ is the angle measured counterclockwise from the positive x-axis to the vector. The relationship between Cartesian and polar coordinates is:
$x = r\cos\theta = 1\cos\theta = \cos\theta$
$y = r\sin\theta = 1\sin\theta = \sin\theta$
Substituting these expressions for $x$ and $y$ back into the vector form $\vec{v} = x\hat{i} + y\hat{j}$, we get the general representation of a unit vector in the XY-plane:
$\vec{u} = \cos\theta\hat{i} + \sin\theta\hat{j}$
Here, $\theta$ represents the angle the unit vector makes with the positive x-axis. By varying the angle $\theta$ from $0$ to $2\pi$ radians (or $0^\circ$ to $360^\circ$), we can generate all possible unit vectors in the XY-plane.
Graphically, all unit vectors in the XY-plane have their tail at the origin and their head lying on the unit circle $x^2 + y^2 = 1$.
The set of all unit vectors in the XY-plane is the set of vectors whose components $(x, y)$ satisfy $x^2 + y^2 = 1$. This set can be parameterized as $\{ \cos\theta\hat{i} + \sin\theta\hat{j} \mid \theta \in \mathbb{R} \}$.
Example 27: If $\hat{i} + \hat{j} + \hat{k} ̂\;,\; 2\hat{i} + 5\hat{j} \;,\; 3\hat{i} + 2\hat{j} − 3\hat{k}$ and $\hat{i} − 6\hat{j} − \hat{k}$ are the position vectors of points A, B, C and D respectively, then find the angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$. Deduce that $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Answer:
Given:
Position vector of point A, $\overrightarrow{OA} = \hat{i} + \hat{j} + \hat{k}$.
Position vector of point B, $\overrightarrow{OB} = 2\hat{i} + 5\hat{j}$.
Position vector of point C, $\overrightarrow{OC} = 3\hat{i} + 2\hat{j} - 3\hat{k}$.
Position vector of point D, $\overrightarrow{OD} = \hat{i} - 6\hat{j} - \hat{k}$.
To Find:
1. The angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$.
2. Deduce that $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Solution:
First, we find the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$.
$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$
$\overrightarrow{AB} = (2\hat{i} + 5\hat{j}) - (\hat{i} + \hat{j} + \hat{k})$
$\overrightarrow{AB} = (2-1)\hat{i} + (5-1)\hat{j} + (0-1)\hat{k}$
$\overrightarrow{AB} = \hat{i} + 4\hat{j} - \hat{k}$
$\overrightarrow{CD} = \overrightarrow{OD} - \overrightarrow{OC}$
$\overrightarrow{CD} = (\hat{i} - 6\hat{j} - \hat{k}) - (3\hat{i} + 2\hat{j} - 3\hat{k})$
$\overrightarrow{CD} = (1-3)\hat{i} + (-6-2)\hat{j} + (-1-(-3))\hat{k}$
$\overrightarrow{CD} = -2\hat{i} - 8\hat{j} + 2\hat{k}$
To find the angle $\theta$ between $\overrightarrow{AB}$ and $\overrightarrow{CD}$, we use the dot product formula:
$\overrightarrow{AB} \cdot \overrightarrow{CD} = |\overrightarrow{AB}| |\overrightarrow{CD}| \cos\theta$
From this, we have:
$\cos\theta = \frac{\overrightarrow{AB} \cdot \overrightarrow{CD}}{|\overrightarrow{AB}| |\overrightarrow{CD}|}$
First, calculate the dot product $\overrightarrow{AB} \cdot \overrightarrow{CD}$:
$\overrightarrow{AB} \cdot \overrightarrow{CD} = (\hat{i} + 4\hat{j} - \hat{k}) \cdot (-2\hat{i} - 8\hat{j} + 2\hat{k})$
$\overrightarrow{AB} \cdot \overrightarrow{CD} = (1)(-2) + (4)(-8) + (-1)(2)$
$\overrightarrow{AB} \cdot \overrightarrow{CD} = -2 - 32 - 2$
$\overrightarrow{AB} \cdot \overrightarrow{CD} = -36$
Next, calculate the magnitudes of $\overrightarrow{AB}$ and $\overrightarrow{CD}$:
$|\overrightarrow{AB}| = \sqrt{(1)^2 + (4)^2 + (-1)^2}$
$|\overrightarrow{AB}| = \sqrt{1 + 16 + 1}$
$|\overrightarrow{AB}| = \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}$
$|\overrightarrow{CD}| = \sqrt{(-2)^2 + (-8)^2 + (2)^2}$
$|\overrightarrow{CD}| = \sqrt{4 + 64 + 4}$
$|\overrightarrow{CD}| = \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}$
Now, substitute the values into the formula for $\cos\theta$:
$\cos\theta = \frac{-36}{(3\sqrt{2})(6\sqrt{2})}$
$\cos\theta = \frac{-36}{18 \times 2}$
$\cos\theta = \frac{-36}{36}$
$\cos\theta = -1$
Since $\cos\theta = -1$, the angle $\theta$ is $180^\circ$.
Deduction for Collinearity:
Two vectors are collinear if the angle between them is $0^\circ$ or $180^\circ$. Since the angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$ is $180^\circ$, the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Alternatively, two vectors $\vec{a}$ and $\vec{b}$ are collinear if one is a scalar multiple of the other, i.e., $\vec{a} = k\vec{b}$ for some scalar $k$.
We have $\overrightarrow{AB} = \hat{i} + 4\hat{j} - \hat{k}$ and $\overrightarrow{CD} = -2\hat{i} - 8\hat{j} + 2\hat{k}$.
Observe that $\overrightarrow{CD} = -2(\hat{i} + 4\hat{j} - \hat{k})$.
$\overrightarrow{CD} = -2\overrightarrow{AB}$
Since $\overrightarrow{CD}$ can be expressed as a scalar multiple of $\overrightarrow{AB}$ (with scalar $k = -2$), the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear. The negative scalar indicates that they point in opposite directions.
Conclusion:
The angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$ is $180^\circ$. Since the angle is $180^\circ$ (or one vector is a scalar multiple of the other), $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Example 28: Let $\vec{a} \;,\; \vec{b}$ and $\vec{c}$ be three vectors such that $|\;\vec{a}\;| = 3 \;,\; |\;\vec{b}\;| = 4 \;,\; |\;\vec{c}\;| = 5$ and each one of them being perpendicular to the sum of the other two, find $|\;\vec{a} + \vec{b} + \vec{c}\;|$.
Answer:
Given:
$|\vec{a}| = 3$
$|\vec{b}| = 4$
$|\vec{c}| = 5$
Each vector is perpendicular to the sum of the other two. This means:
$\vec{a} \perp (\vec{b} + \vec{c})$
$\vec{b} \perp (\vec{a} + \vec{c})$
$\vec{c} \perp (\vec{a} + \vec{b})$
To Find:
$|\vec{a} + \vec{b} + \vec{c}|$
Solution:
From the condition that each vector is perpendicular to the sum of the other two, we can write the following dot products:
$\vec{a} \cdot (\vec{b} + \vec{c}) = 0$
$\vec{b} \cdot (\vec{a} + \vec{c}) = 0$
$\vec{c} \cdot (\vec{a} + \vec{b}) = 0$
Expanding these dot products, we get:
$\vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} = 0$
$\vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{c} = 0$
$\vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} = 0$
Since the dot product is commutative ($\vec{x} \cdot \vec{y} = \vec{y} \cdot \vec{x}$), we can rewrite the equations as:
$\vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} = 0$
$\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} = 0$
$\vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} = 0$
Adding these three equations:
$(\vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}) + (\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c}) + (\vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}) = 0 + 0 + 0$
$2(\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{a} \cdot \vec{c}) = 0$
$\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{a} \cdot \vec{c} = 0$
Now, consider the magnitude of the sum of the vectors, squared:
$|\vec{a} + \vec{b} + \vec{c}|^2 = (\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c})$
Expanding the dot product:
$|\vec{a} + \vec{b} + \vec{c}|^2 = \vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} + \vec{c} \cdot \vec{c}$
$|\vec{a} + \vec{b} + \vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2 + 2(\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{a} \cdot \vec{c})$
Using the result from the dot products ($\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{a} \cdot \vec{c} = 0$):
$|\vec{a} + \vec{b} + \vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2 + 2(0)$
$|\vec{a} + \vec{b} + \vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2$
Substitute the given magnitudes:
$|\vec{a} + \vec{b} + \vec{c}|^2 = (3)^2 + (4)^2 + (5)^2$
$|\vec{a} + \vec{b} + \vec{c}|^2 = 9 + 16 + 25$
$|\vec{a} + \vec{b} + \vec{c}|^2 = 50$
Taking the square root of both sides:
$|\vec{a} + \vec{b} + \vec{c}| = \sqrt{50}$
$|\vec{a} + \vec{b} + \vec{c}| = \sqrt{25 \times 2}$
$|\vec{a} + \vec{b} + \vec{c}| = 5\sqrt{2}$
Final Answer:
The value of $|\vec{a} + \vec{b} + \vec{c}|$ is $5\sqrt{2}$.
Example 29: Three vectors $\vec{a}$ , $\vec{b}$ and $\vec{c}$ satisfy the condition $\vec{a} + \vec{b} + \vec{c} = \vec{0}$. Evaluate the quantity $µ = \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}$, if $|\;\vec{a}\;| = 3 \;,\; |\;\vec{b}\;| = 4$ and $|\;\vec{c}\;| = 2$.
Answer:
Given:
The vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ satisfy the condition:
$\vec{a} + \vec{b} + \vec{c} = \vec{0}$
The magnitudes of the vectors are:
$|\vec{a}| = 3$
$|\vec{b}| = 4$
$|\vec{c}| = 2$
To Find:
The value of the quantity $µ = \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}$.
Solution:
We are given the condition $\vec{a} + \vec{b} + \vec{c} = \vec{0}$.
Take the dot product of this equation with itself:
$(\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c}) = \vec{0} \cdot \vec{0}$
Expand the left side using the distributive property of the dot product:
$\vec{a} \cdot (\vec{a} + \vec{b} + \vec{c}) + \vec{b} \cdot (\vec{a} + \vec{b} + \vec{c}) + \vec{c} \cdot (\vec{a} + \vec{b} + \vec{c}) = 0$
$\vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} + \vec{c} \cdot \vec{c} = 0$
Using the properties $\vec{x} \cdot \vec{x} = |\vec{x}|^2$ and $\vec{x} \cdot \vec{y} = \vec{y} \cdot \vec{x}$, we can group the terms:
$|\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2 + 2(\vec{a} \cdot \vec{b}) + 2(\vec{b} \cdot \vec{c}) + 2(\vec{c} \cdot \vec{a}) = 0$
$|\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2 + 2(\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}) = 0$
We are given the magnitudes $|\vec{a}| = 3$, $|\vec{b}| = 4$, and $|\vec{c}| = 2$. Substitute these values into the equation:
$(3)^2 + (4)^2 + (2)^2 + 2(\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}) = 0$
$9 + 16 + 4 + 2(\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}) = 0$
$29 + 2(\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}) = 0$
The quantity we need to evaluate is $µ = \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}$. Substitute $µ$ into the equation:
$29 + 2µ = 0$
Now, solve for $µ$:
$2µ = -29$
$µ = -\frac{29}{2}$
$µ = -14.5$
Final Answer:
The value of the quantity $µ$ is -14.5.
Example 30: If with reference to the right handed system of mutually perpendicular unit vectors $\hat{i} \;,\; \hat{j}$ and $\hat{k}$, $\vec{α} = 3\hat{i} − \hat{j}$ , $\vec{β} = 2\hat{i} + \hat{j} − 3\hat{k}$ , then express $\vec{β}$ in the form $\vec{β} = \vec{β}_1 + \vec{β}_2$ , where $\vec{β}_1$ is parallel to $\vec{α}$ and $\vec{β}_2$ is perpendicular to $\vec{α}$ .
Answer:
Given:
Vector $\vec{\alpha} = 3\hat{i} - \hat{j}$
Vector $\vec{\beta} = 2\hat{i} + \hat{j} - 3\hat{k}$
To Express:
Express $\vec{\beta}$ in the form $\vec{\beta} = \vec{\beta}_1 + \vec{\beta}_2$, where $\vec{\beta}_1 \parallel \vec{\alpha}$ and $\vec{\beta}_2 \perp \vec{\alpha}$.
Solution:
The vector $\vec{\beta}_1$ is the component of $\vec{\beta}$ parallel to $\vec{\alpha}$. This is the projection of $\vec{\beta}$ onto $\vec{\alpha}$. The formula for the projection of $\vec{\beta}$ onto $\vec{\alpha}$ is given by:
$\vec{\beta}_1 = \text{proj}_{\vec{\alpha}}\vec{\beta} = \frac{(\vec{\beta} \cdot \vec{\alpha})}{|\vec{\alpha}|^2}\vec{\alpha}$
First, calculate the dot product $\vec{\beta} \cdot \vec{\alpha}$:
$\vec{\beta} \cdot \vec{\alpha} = (2\hat{i} + \hat{j} - 3\hat{k}) \cdot (3\hat{i} - \hat{j})$
$\vec{\beta} \cdot \vec{\alpha} = (2)(3) + (1)(-1) + (-3)(0)$
$\vec{\beta} \cdot \vec{\alpha} = 6 - 1 + 0$
$\vec{\beta} \cdot \vec{\alpha} = 5$
Next, calculate the magnitude squared of $\vec{\alpha}$, $|\vec{\alpha}|^2$:
$|\vec{\alpha}|^2 = |3\hat{i} - \hat{j}|^2$
$|\vec{\alpha}|^2 = (3)^2 + (-1)^2 + (0)^2$
$|\vec{\alpha}|^2 = 9 + 1 + 0$
$|\vec{\alpha}|^2 = 10$
Now, calculate $\vec{\beta}_1$ using the formula:
$\vec{\beta}_1 = \frac{5}{10}(3\hat{i} - \hat{j})$
$\vec{\beta}_1 = \frac{1}{2}(3\hat{i} - \hat{j})$
$\vec{\beta}_1 = \frac{3}{2}\hat{i} - \frac{1}{2}\hat{j}$
The vector $\vec{\beta}_2$ is the component of $\vec{\beta}$ perpendicular to $\vec{\alpha}$. Since $\vec{\beta} = \vec{\beta}_1 + \vec{\beta}_2$, we have $\vec{\beta}_2 = \vec{\beta} - \vec{\beta}_1$.
Calculate $\vec{\beta}_2$:
$\vec{\beta}_2 = (2\hat{i} + \hat{j} - 3\hat{k}) - (\frac{3}{2}\hat{i} - \frac{1}{2}\hat{j})$
$\vec{\beta}_2 = (2 - \frac{3}{2})\hat{i} + (1 - (-\frac{1}{2}))\hat{j} + (-3 - 0)\hat{k}$
$\vec{\beta}_2 = (\frac{4 - 3}{2})\hat{i} + (\frac{2 + 1}{2})\hat{j} - 3\hat{k}$
$\vec{\beta}_2 = \frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k}$
Thus, the vector $\vec{\beta}$ is expressed as the sum of $\vec{\beta}_1$ (parallel to $\vec{\alpha}$) and $\vec{\beta}_2$ (perpendicular to $\vec{\alpha}$) as:
$\vec{\beta} = \vec{\beta}_1 + \vec{\beta}_2$
$\vec{\beta} = (\frac{3}{2}\hat{i} - \frac{1}{2}\hat{j}) + (\frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k})$
We can verify that $\vec{\beta}_1$ is parallel to $\vec{\alpha}$ because $\vec{\beta}_1 = \frac{1}{2}(3\hat{i} - \hat{j}) = \frac{1}{2}\vec{\alpha}$.
We can verify that $\vec{\beta}_2$ is perpendicular to $\vec{\alpha}$ by checking their dot product:
$\vec{\beta}_2 \cdot \vec{\alpha} = (\frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k}) \cdot (3\hat{i} - \hat{j})$
$\vec{\beta}_2 \cdot \vec{\alpha} = (\frac{1}{2})(3) + (\frac{3}{2})(-1) + (-3)(0)$
$\vec{\beta}_2 \cdot \vec{\alpha} = \frac{3}{2} - \frac{3}{2} + 0 = 0$
Since the dot product is 0, $\vec{\beta}_2$ is perpendicular to $\vec{\alpha}$.
Final Answer:
The expression for $\vec{\beta}$ is $\vec{\beta} = \mathbf{(\frac{3}{2}\hat{i} - \frac{1}{2}\hat{j})} + \mathbf{(\frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k})}$, where $\vec{\beta}_1 = \frac{3}{2}\hat{i} - \frac{1}{2}\hat{j}$ and $\vec{\beta}_2 = \frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k}$.
Miscellaneous Exercise on Chapter 10
Question 1. Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
Answer:
Given:
A unit vector in the XY-plane makes an angle of $30^\circ$ with the positive direction of the x-axis.
To Find:
The unit vector.
Solution:
A vector in the XY-plane making an angle $\theta$ with the positive x-axis can be represented in terms of its components along the x and y axes. For a unit vector, the magnitude is 1.
Let $\vec{u}$ be the unit vector. The components of this unit vector are given by $\cos\theta$ along the x-axis and $\sin\theta$ along the y-axis.
So, the unit vector $\vec{u}$ can be written as:
$\vec{u} = \cos\theta \hat{i} + \sin\theta \hat{j}$
We are given that the angle $\theta = 30^\circ$.
Substitute $\theta = 30^\circ$ into the formula:
$\vec{u} = \cos(30^\circ) \hat{i} + \sin(30^\circ) \hat{j}$
We know the values of $\cos(30^\circ)$ and $\sin(30^\circ)$:
$\cos(30^\circ) = \frac{\sqrt{3}}{2}$
$\sin(30^\circ) = \frac{1}{2}$
Substitute these values into the expression for $\vec{u}$:
$\vec{u} = \frac{\sqrt{3}}{2}\hat{i} + \frac{1}{2}\hat{j}$
Final Answer:
The unit vector in the XY-plane making an angle of $30^\circ$ with the positive direction of the x-axis is $\mathbf{\frac{\sqrt{3}}{2}\hat{i} + \frac{1}{2}\hat{j}}$.
Question 2. Find the scalar components and magnitude of the vector joining the points P(x1 , y1 , z1) and Q (x2 , y2 , z2).
Answer:
Given:
Point P with coordinates $(x_1, y_1, z_1)$.
Point Q with coordinates $(x_2, y_2, z_2)$.
To Find:
1. The scalar components of the vector joining P and Q ($\overrightarrow{PQ}$).
2. The magnitude of the vector $\overrightarrow{PQ}$.
Solution:
Let the position vector of point P with respect to the origin be $\overrightarrow{OP}$ and the position vector of point Q be $\overrightarrow{OQ}$.
$\overrightarrow{OP} = x_1\hat{i} + y_1\hat{j} + z_1\hat{k}$
$\overrightarrow{OQ} = x_2\hat{i} + y_2\hat{j} + z_2\hat{k}$
The vector joining point P to point Q is given by $\overrightarrow{PQ}$. This vector can be found by subtracting the position vector of P from the position vector of Q.
$\overrightarrow{PQ} = \overrightarrow{OQ} - \overrightarrow{OP}$
$\overrightarrow{PQ} = (x_2\hat{i} + y_2\hat{j} + z_2\hat{k}) - (x_1\hat{i} + y_1\hat{j} + z_1\hat{k})$
$\overrightarrow{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$
The scalar components of the vector $\overrightarrow{PQ}$ are the coefficients of the unit vectors $\hat{i}$, $\hat{j}$, and $\hat{k}$.
The scalar components are $\mathbf{(x_2 - x_1)}$, $\mathbf{(y_2 - y_1)}$, and $\mathbf{(z_2 - z_1)}$.
The magnitude of the vector $\overrightarrow{PQ} = a\hat{i} + b\hat{j} + c\hat{k}$ is given by the formula $\sqrt{a^2 + b^2 + c^2}$.
In this case, $a = (x_2 - x_1)$, $b = (y_2 - y_1)$, and $c = (z_2 - z_1)$.
$|\overrightarrow{PQ}| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$
Final Answer:
The scalar components of the vector joining P and Q are $\mathbf{(x_2 - x_1)}$, $\mathbf{(y_2 - y_1)}$, and $\mathbf{(z_2 - z_1)}$.
The magnitude of the vector joining P and Q is $\mathbf{\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}}$.
Question 3. A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
Answer:
Given:
First displacement: 4 km towards west.
Second displacement: 3 km in a direction 30° east of north.
To Find:
The girl's total displacement from her initial point of departure.
Solution:
We can represent the displacements as vectors and find the total displacement by adding these vectors. Let's set up a coordinate system with the initial point at the origin (0,0). Let the positive x-axis point East and the positive y-axis point North.
The first displacement is 4 km towards west. This is a vector purely in the negative x-direction.
Let $\vec{d}_1$ be the first displacement vector.
$\vec{d}_1 = -4\hat{i}$ km
... (i)
The second displacement is 3 km in a direction 30° east of north. Starting from the North direction (positive y-axis), we move 30° towards the East (positive x-axis). The angle this vector makes with the positive x-axis is $90^\circ - 30^\circ = 60^\circ$.
Let $\vec{d}_2$ be the second displacement vector. Its magnitude is $|\vec{d}_2| = 3$ km.
The components of $\vec{d}_2$ in the x and y directions are:
x-component = $|\vec{d}_2| \cos(60^\circ) = 3 \times \frac{1}{2} = \frac{3}{2}$ km
y-component = $|\vec{d}_2| \sin(60^\circ) = 3 \times \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{2}$ km
So, the second displacement vector is:
$\vec{d}_2 = \frac{3}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$ km
... (ii)
The total displacement $\vec{D}$ from the initial point is the vector sum of the individual displacements:
$\vec{D} = \vec{d}_1 + \vec{d}_2$
Substitute the component forms from (i) and (ii):
$\vec{D} = (-4\hat{i}) + \left(\frac{3}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}\right)$
Combine the $\hat{i}$ components and the $\hat{j}$ components:
$\vec{D} = \left(-4 + \frac{3}{2}\right)\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$
Calculate the $\hat{i}$ component: $-4 + \frac{3}{2} = \frac{-8}{2} + \frac{3}{2} = \frac{-8 + 3}{2} = -\frac{5}{2}$.
So, the total displacement vector is:
$\vec{D} = -\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$ km
To find the magnitude of the total displacement, we calculate the magnitude of the resultant vector $\vec{D}$:
$|\vec{D}| = \sqrt{(\text{x-component of } \vec{D})^2 + (\text{y-component of } \vec{D})^2}$
$|\vec{D}| = \sqrt{\left(-\frac{5}{2}\right)^2 + \left(\frac{3\sqrt{3}}{2}\right)^2}$
$|\vec{D}| = \sqrt{\frac{(-5)^2}{2^2} + \frac{(3\sqrt{3})^2}{2^2}}$
$|\vec{D}| = \sqrt{\frac{25}{4} + \frac{9 \times 3}{4}}$
$|\vec{D}| = \sqrt{\frac{25}{4} + \frac{27}{4}}$
$|\vec{D}| = \sqrt{\frac{25 + 27}{4}}$
$|\vec{D}| = \sqrt{\frac{52}{4}}$
$|\vec{D}| = \sqrt{13}$
The magnitude of the displacement is $\sqrt{13}$ km.
The direction of the displacement vector $\vec{D} = -\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$ is in the second quadrant (negative x-component, positive y-component). Let $\phi$ be the angle the resultant vector makes with the positive x-axis.
$\tan \phi = \frac{\text{y-component}}{\text{x-component}} = \frac{3\sqrt{3}/2}{-5/2} = -\frac{3\sqrt{3}}{5}$
$\phi = \tan^{-1}\left(-\frac{3\sqrt{3}}{5}\right)$
Since the x-component is negative and the y-component is positive, the angle $\phi$ is in the second quadrant. The angle measured counterclockwise from the positive x-axis is $180^\circ - \tan^{-1}\left(\frac{3\sqrt{3}}{5}\right)$ (using the absolute value for arctan). Alternatively, the direction can be described relative to the cardinal directions based on the components.
Here is a graphical representation of the vector addition:
In the diagram, O is the starting point. $\vec{d}_1$ is drawn 4 km towards the west. From the endpoint of $\vec{d}_1$, $\vec{d}_2$ is drawn 3 km at 30° east of north. The resultant displacement vector $\vec{D}$ is the vector from the initial point O to the final point B.
Final Answer:
The girl's displacement from her initial point of departure is $\mathbf{\sqrt{13}}$ km. The direction is given by the vector $\mathbf{-\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}}$ km.
Question 4. If $\vec{a} = \vec{b} + \vec{c}$ , then is it true that $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ ? justify your answer.
Answer:
Given:
The vector equation $\vec{a} = \vec{b} + \vec{c}$.
To Determine:
Is it true that $|\vec{a}| = |\vec{b}| + |\vec{c}|$? Justify the answer.
Justification:
The given equation is $\vec{a} = \vec{b} + \vec{c}$.
Taking the magnitude of both sides, we get $|\vec{a}| = |\vec{b} + \vec{c}|$.
According to the triangle inequality for vectors, the magnitude of the sum of two vectors is less than or equal to the sum of their magnitudes.
$|\vec{b} + \vec{c}| \leq |\vec{b}| + |\vec{c}|$
Substituting $|\vec{a}| = |\vec{b} + \vec{c}|$, we get:
$|\vec{a}| \leq |\vec{b}| + |\vec{c}|$
The equality $|\vec{b} + \vec{c}| = |\vec{b}| + |\vec{c}|$ holds if and only if the vectors $\vec{b}$ and $\vec{c}$ are collinear and act in the same direction (or if one of the vectors is the zero vector).
If $\vec{b}$ and $\vec{c}$ are not collinear and in the same direction, they form two sides of a triangle, and the vector $\vec{a} = \vec{b} + \vec{c}$ forms the third side. In this case, the length of one side of a triangle is strictly less than the sum of the lengths of the other two sides.
For example, consider $\vec{b} = \hat{i}$ and $\vec{c} = \hat{j}$.
Then $\vec{a} = \vec{b} + \vec{c} = \hat{i} + \hat{j}$.
The magnitudes are:
$|\vec{a}| = |\hat{i} + \hat{j}| = \sqrt{1^2 + 1^2} = \sqrt{2}$
$|\vec{b}| = |\hat{i}| = \sqrt{1^2} = 1$
$|\vec{c}| = |\hat{j}| = \sqrt{1^2} = 1$
The sum of the magnitudes of $\vec{b}$ and $\vec{c}$ is $|\vec{b}| + |\vec{c}| = 1 + 1 = 2$.
In this example, $\sqrt{2} \approx 1.414$, which is not equal to 2.
Thus, $|\vec{a}| \neq |\vec{b}| + |\vec{c}|$ in this case.
Final Answer:
No, it is not true that $|\vec{a}| = |\vec{b}| + |\vec{c}|$ in general when $\vec{a} = \vec{b} + \vec{c}$. The equality holds only in the specific case where the vectors $\vec{b}$ and $\vec{c}$ are collinear and point in the same direction (or one or both are zero vectors). In all other cases, the strict inequality $|\vec{a}| < |\vec{b}| + |\vec{c}|$ holds.
Question 5. Find the value of x for which $x(\hat{i} + \hat{j} + \hat{k})$ is a unit vector.
Answer:
Given:
The vector is $x(\hat{i} + \hat{j} + \hat{k})$.
The vector is a unit vector.
To Find:
The value of $x$.
Solution:
Let $\vec{v} = x(\hat{i} + \hat{j} + \hat{k})$.
We can write this vector as $\vec{v} = x\hat{i} + x\hat{j} + x\hat{k}$.
A vector is a unit vector if its magnitude is equal to 1.
The magnitude of the vector $\vec{v} = a\hat{i} + b\hat{j} + c\hat{k}$ is given by $|\vec{v}| = \sqrt{a^2 + b^2 + c^2}$.
In this case, $a=x$, $b=x$, and $c=x$.
So, the magnitude of $\vec{v}$ is:
$|\vec{v}| = \sqrt{x^2 + x^2 + x^2}$
$|\vec{v}| = \sqrt{3x^2}$
$|\vec{v}| = |x|\sqrt{3}$
Since $\vec{v}$ is a unit vector, its magnitude is 1.
$|x|\sqrt{3} = 1$
$|x| = \frac{1}{\sqrt{3}}$
This means $x$ can be either positive or negative.
$x = \pm \frac{1}{\sqrt{3}}$
Final Answer:
The value of $x$ for which $x(\hat{i} + \hat{j} + \hat{k})$ is a unit vector is $\mathbf{\pm \frac{1}{\sqrt{3}}}$.
Question 6. Find a vector of magnitude 5 units, and parallel to the resultant of the vectors $\vec{a} = 2\hat{i} + 3\hat{j} − \hat{k}$ and $\vec{b} = \hat{i} − 2\hat{j} + \hat{k}$
Answer:
Given:
Vector $\vec{a} = 2\hat{i} + 3\hat{j} - \hat{k}$
Vector $\vec{b} = \hat{i} - 2\hat{j} + \hat{k}$
Required magnitude of the vector = 5 units.
The required vector is parallel to the resultant of $\vec{a}$ and $\vec{b}$.
To Find:
A vector of magnitude 5 units parallel to the resultant of $\vec{a}$ and $\vec{b}$.
Solution:
Let $\vec{r}$ be the resultant vector of $\vec{a}$ and $\vec{b}$.
$\vec{r} = \vec{a} + \vec{b}$
Substitute the given vectors:
$\vec{r} = (2\hat{i} + 3\hat{j} - \hat{k}) + (\hat{i} - 2\hat{j} + \hat{k})$
$\vec{r} = (2+1)\hat{i} + (3-2)\hat{j} + (-1+1)\hat{k}$
$\vec{r} = 3\hat{i} + \hat{j} + 0\hat{k}$
$\vec{r} = 3\hat{i} + \hat{j}$
To find a vector parallel to $\vec{r}$, we first find the unit vector in the direction of $\vec{r}$.
The magnitude of $\vec{r}$ is:
$|\vec{r}| = \sqrt{3^2 + 1^2 + 0^2}$
$|\vec{r}| = \sqrt{9 + 1}$
$|\vec{r}| = \sqrt{10}$
The unit vector in the direction of $\vec{r}$ is $\hat{r}$:
$\hat{r} = \frac{\vec{r}}{|\vec{r}|} = \frac{3\hat{i} + \hat{j}}{\sqrt{10}}$
$\hat{r} = \frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j}$
A vector parallel to $\vec{r}$ with magnitude 5 units can be in the same direction as $\vec{r}$ or in the opposite direction.
So, the required vector is $\pm 5\hat{r}$.
Required Vector = $\pm 5 \left( \frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j} \right)$
Required Vector = $\pm \left( \frac{15}{\sqrt{10}}\hat{i} + \frac{5}{\sqrt{10}}\hat{j} \right)$
We can write this as two separate vectors:
Vector 1 = $\frac{15}{\sqrt{10}}\hat{i} + \frac{5}{\sqrt{10}}\hat{j}$
Vector 2 = $-\frac{15}{\sqrt{10}}\hat{i} - \frac{5}{\sqrt{10}}\hat{j}$
(Optionally, rationalizing the denominator gives $\frac{15\sqrt{10}}{10}\hat{i} + \frac{5\sqrt{10}}{10}\hat{j} = \frac{3\sqrt{10}}{2}\hat{i} + \frac{\sqrt{10}}{2}\hat{j}$ and $-\frac{3\sqrt{10}}{2}\hat{i} - \frac{\sqrt{10}}{2}\hat{j}$)
Final Answer:
The vectors of magnitude 5 units parallel to the resultant of $\vec{a}$ and $\vec{b}$ are $\mathbf{\frac{15}{\sqrt{10}}\hat{i} + \frac{5}{\sqrt{10}}\hat{j}}$ and $\mathbf{-\frac{15}{\sqrt{10}}\hat{i} - \frac{5}{\sqrt{10}}\hat{j}}$.
Question 7. If $\vec{a} = \hat{i} + \hat{j} + \hat{k}$ , $\vec{b} = 2\hat{i} − \hat{j} + 3\hat{k}$ and $\vec{c} = \hat{i} − 2\hat{j} + \hat{k}$, find a unit vector parallel to the vector $2\vec{a} − \vec{b} + 3\vec{c}$.
Answer:
Given:
Vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$
Vector $\vec{b} = 2\hat{i} - \hat{j} + 3\hat{k}$
Vector $\vec{c} = \hat{i} - 2\hat{j} + \hat{k}$
To Find:
A unit vector parallel to the vector $2\vec{a} - \vec{b} + 3\vec{c}$.
Solution:
Let $\vec{v} = 2\vec{a} - \vec{b} + 3\vec{c}$.
Substitute the given vectors into the expression for $\vec{v}$:
$\vec{v} = 2(\hat{i} + \hat{j} + \hat{k}) - (2\hat{i} - \hat{j} + 3\hat{k}) + 3(\hat{i} - 2\hat{j} + \hat{k})$
Distribute the scalar multiples:
$\vec{v} = (2\hat{i} + 2\hat{j} + 2\hat{k}) - (2\hat{i} - \hat{j} + 3\hat{k}) + (3\hat{i} - 6\hat{j} + 3\hat{k})$
Combine the components:
$\vec{v} = (2 - 2 + 3)\hat{i} + (2 - (-1) - 6)\hat{j} + (2 - 3 + 3)\hat{k}$
$\vec{v} = (2 - 2 + 3)\hat{i} + (2 + 1 - 6)\hat{j} + (2 - 3 + 3)\hat{k}$
$\vec{v} = 3\hat{i} - 3\hat{j} + 2\hat{k}$
To find a unit vector parallel to $\vec{v}$, we need to find the magnitude of $\vec{v}$ and divide $\vec{v}$ by its magnitude.
The magnitude of $\vec{v}$ is:
$|\vec{v}| = \sqrt{(3)^2 + (-3)^2 + (2)^2}$
$|\vec{v}| = \sqrt{9 + 9 + 4}$
$|\vec{v}| = \sqrt{22}$
The unit vector parallel to $\vec{v}$, denoted by $\hat{v}$, is given by:
$\hat{v} = \frac{\vec{v}}{|\vec{v}|}$
$\hat{v} = \frac{3\hat{i} - 3\hat{j} + 2\hat{k}}{\sqrt{22}}$
$\hat{v} = \frac{3}{\sqrt{22}}\hat{i} - \frac{3}{\sqrt{22}}\hat{j} + \frac{2}{\sqrt{22}}\hat{k}$
A vector parallel to $\vec{v}$ can be in the same direction or the opposite direction. Therefore, the unit vectors parallel to $\vec{v}$ are $\pm \hat{v}$.
Unit vector = $\pm \left( \frac{3}{\sqrt{22}}\hat{i} - \frac{3}{\sqrt{22}}\hat{j} + \frac{2}{\sqrt{22}}\hat{k} \right)$
Final Answer:
A unit vector parallel to the vector $2\vec{a} - \vec{b} + 3\vec{c}$ is $\mathbf{\pm \left( \frac{3}{\sqrt{22}}\hat{i} - \frac{3}{\sqrt{22}}\hat{j} + \frac{2}{\sqrt{22}}\hat{k} \right)}$.
Question 8. Show that the points A(1, – 2, – 8), B(5, 0, –2) and C(11, 3, 7) are collinear, and find the ratio in which B divides AC.
Answer:
Given:
The points are A(1, -2, -8), B(5, 0, -2), and C(11, 3, 7).
To Show:
The points A, B, and C are collinear.
To Find:
The ratio in which B divides AC.
Solution:
We can show that the points A, B, and C are collinear by showing that the vector $\vec{AB}$ is parallel to the vector $\vec{BC}$, and that B is a common point.
First, let's find the components of the vectors $\vec{AB}$ and $\vec{BC}$.
$\vec{AB} = B - A = (5 - 1, 0 - (-2), -2 - (-8))$
$\vec{AB} = (4, 2, 6)$
$\vec{BC} = C - B = (11 - 5, 3 - 0, 7 - (-2))$
$\vec{BC} = (6, 3, 9)$
For the vectors $\vec{AB}$ and $\vec{BC}$ to be parallel, there must exist a scalar $\lambda$ such that $\vec{BC} = \lambda \vec{AB}$.
$(6, 3, 9) = \lambda (4, 2, 6)$
Comparing the corresponding components:
$6 = 4\lambda \implies \lambda = \frac{6}{4} = \frac{3}{2}$
$3 = 2\lambda \implies \lambda = \frac{3}{2}$
$9 = 6\lambda \implies \lambda = \frac{9}{6} = \frac{3}{2}$
Since the value of $\lambda$ is consistent for all components, we have $\vec{BC} = \frac{3}{2} \vec{AB}$.
This shows that the vectors $\vec{AB}$ and $\vec{BC}$ are parallel. Since point B is common to both vectors, the points A, B, and C must lie on the same line.
Hence, the points A, B, and C are collinear.
Now, let's find the ratio in which B divides AC. Let B divide AC in the ratio $k:1$.
Using the section formula, the coordinates of a point dividing the line segment joining $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ in the ratio $k:1$ are given by:
$(\frac{1 \cdot x_1 + k \cdot x_2}{k+1}, \frac{1 \cdot y_1 + k \cdot y_2}{k+1}, \frac{1 \cdot z_1 + k \cdot z_2}{k+1})$
Here, $(x_1, y_1, z_1) = (1, -2, -8)$, $(x_2, y_2, z_2) = (11, 3, 7)$, and the dividing point is $(x, y, z) = (5, 0, -2)$.
Equating the coordinates of B with the section formula:
$x$-coordinate:
$5 = \frac{1(1) + k(11)}{k+1}$
$5(k+1) = 1 + 11k$
$5k + 5 = 1 + 11k$
$5 - 1 = 11k - 5k$
$4 = 6k$
$k = \frac{4}{6} = \frac{2}{3}$
$y$-coordinate:
$0 = \frac{1(-2) + k(3)}{k+1}$
$0 = -2 + 3k$
$3k = 2$
$k = \frac{2}{3}$
$z$-coordinate:
$-2 = \frac{1(-8) + k(7)}{k+1}$
$-2(k+1) = -8 + 7k$
$-2k - 2 = -8 + 7k$
$-2 + 8 = 7k + 2k$
$6 = 9k$
$k = \frac{6}{9} = \frac{2}{3}$
Since the value of $k$ is consistently $\frac{2}{3}$ for all three coordinates, B divides AC in the ratio $k:1 = \frac{2}{3}:1$.
Multiplying by 3 to get integer ratio:
Ratio $= (\frac{2}{3} \times 3) : (1 \times 3) = 2:3$
So, B divides AC in the ratio 2:3.
The fact that a consistent value of $k$ is found confirms that B lies on the line segment AC (or the line extended through AC), which again proves collinearity.
Therefore, the points A, B, and C are collinear, and B divides AC in the ratio 2:3.
Question 9. Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $(2\vec{a} + \vec{b})$ and $(\vec{a} − 3\vec{b})$ externally in the ratio 1 : 2. Also, show that P is the mid point of the line segment RQ.
Answer:
Given:
Position vector of point P, $\vec{p} = 2\vec{a} + \vec{b}$.
Position vector of point Q, $\vec{q} = \vec{a} - 3\vec{b}$.
Point R divides the line joining P and Q externally in the ratio 1:2.
To Find:
The position vector of point R.
To Show:
Point P is the midpoint of the line segment RQ.
Solution:
Let the position vector of point R be $\vec{r}$.
Since R divides the line joining P and Q externally in the ratio 1:2, we can use the section formula for external division.
If a point R divides the line segment joining points P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) externally in the ratio $m:n$, its position vector $\vec{r}$ is given by:
$\vec{r} = \frac{m\vec{q} - n\vec{p}}{m - n}$
... (i)
In this case, $m = 1$ and $n = 2$. $\vec{p} = 2\vec{a} + \vec{b}$ and $\vec{q} = \vec{a} - 3\vec{b}$.
Substituting these values into the formula (i):
$\vec{r} = \frac{1(\vec{a} - 3\vec{b}) - 2(2\vec{a} + \vec{b})}{1 - 2}$
$\vec{r} = \frac{\vec{a} - 3\vec{b} - 4\vec{a} - 2\vec{b}}{-1}$
$\vec{r} = \frac{(\vec{a} - 4\vec{a}) + (-3\vec{b} - 2\vec{b})}{-1}$
$\vec{r} = \frac{-3\vec{a} - 5\vec{b}}{-1}$
$\vec{r} = 3\vec{a} + 5\vec{b}$
The position vector of point R is $3\vec{a} + 5\vec{b}$.
Now, we need to show that P is the midpoint of the line segment RQ.
The position vector of P is $\vec{p} = 2\vec{a} + \vec{b}$.
The position vector of Q is $\vec{q} = \vec{a} - 3\vec{b}$.
The position vector of R is $\vec{r} = 3\vec{a} + 5\vec{b}$.
Let M be the midpoint of the line segment RQ. The position vector of the midpoint M is given by:
$\vec{m} = \frac{\vec{r} + \vec{q}}{2}$
Substituting the position vectors of R and Q:
$\vec{m} = \frac{(3\vec{a} + 5\vec{b}) + (\vec{a} - 3\vec{b})}{2}$
$\vec{m} = \frac{3\vec{a} + 5\vec{b} + \vec{a} - 3\vec{b}}{2}$
$\vec{m} = \frac{(3\vec{a} + \vec{a}) + (5\vec{b} - 3\vec{b})}{2}$
$\vec{m} = \frac{4\vec{a} + 2\vec{b}}{2}$
$\vec{m} = 2\vec{a} + \vec{b}$
The position vector of the midpoint of RQ is $2\vec{a} + \vec{b}$.
We observe that the position vector of the midpoint M is equal to the position vector of point P ($\vec{p} = 2\vec{a} + \vec{b}$).
$\vec{m} = \vec{p}$
This shows that point P is the midpoint of the line segment RQ.
Conclusion:
The position vector of point R is $3\vec{a} + 5\vec{b}$, and it has been shown that P is the midpoint of the line segment RQ.
Question 10. The two adjacent sides of a parallelogram are $2\hat{i} − 4\hat{j} + 5\hat{k}$ and $\hat{i} − 2\hat{j} − 3\hat{k}$. Find the unit vector parallel to its diagonal. Also, find its area.
Answer:
Given:
The two adjacent sides of a parallelogram are given by vectors $\vec{a} = 2\hat{i} - 4\hat{j} + 5\hat{k}$ and $\vec{b} = \hat{i} - 2\hat{j} - 3\hat{k}$.
To Find:
1. The unit vector parallel to its diagonal.
2. The area of the parallelogram.
Solution:
Let the two adjacent sides of the parallelogram be represented by the vectors $\vec{a}$ and $\vec{b}$.
$\vec{a} = 2\hat{i} - 4\hat{j} + 5\hat{k}$
$\vec{b} = \hat{i} - 2\hat{j} - 3\hat{k}$
Part 1: Unit vector parallel to the diagonal
The diagonal of the parallelogram formed by adjacent sides $\vec{a}$ and $\vec{b}$ is given by the vector sum $\vec{d} = \vec{a} + \vec{b}$.
$\vec{d} = (2\hat{i} - 4\hat{j} + 5\hat{k}) + (\hat{i} - 2\hat{j} - 3\hat{k})$
$\vec{d} = (2+1)\hat{i} + (-4-2)\hat{j} + (5-3)\hat{k}$
$\vec{d} = 3\hat{i} - 6\hat{j} + 2\hat{k}$
To find the unit vector parallel to $\vec{d}$, we need to find the magnitude of $\vec{d}$.
$|\vec{d}| = \sqrt{(3)^2 + (-6)^2 + (2)^2}$
$|\vec{d}| = \sqrt{9 + 36 + 4}$
$|\vec{d}| = \sqrt{49}$
$|\vec{d}| = 7$
The unit vector parallel to $\vec{d}$ is given by $\hat{d} = \frac{\vec{d}}{|\vec{d}|}$.
$\hat{d} = \frac{3\hat{i} - 6\hat{j} + 2\hat{k}}{7}$
$\hat{d} = \frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}$
The unit vector parallel to the diagonal is $\frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}$.
Part 2: Area of the parallelogram
The area of a parallelogram with adjacent sides $\vec{a}$ and $\vec{b}$ is given by the magnitude of their cross product, i.e., Area $= |\vec{a} \times \vec{b}|$.
First, let's calculate the cross product $\vec{a} \times \vec{b}$.
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -4 & 5 \\ 1 & -2 & -3 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}[(-4)(-3) - (5)(-2)] - \hat{j}[(2)(-3) - (5)(1)] + \hat{k}[(2)(-2) - (-4)(1)]$
$\vec{a} \times \vec{b} = \hat{i}[12 - (-10)] - \hat{j}[-6 - 5] + \hat{k}[-4 - (-4)]$
$\vec{a} \times \vec{b} = \hat{i}[12 + 10] - \hat{j}[-11] + \hat{k}[-4 + 4]$
$\vec{a} \times \vec{b} = 22\hat{i} + 11\hat{j} + 0\hat{k}$
Now, we find the magnitude of $\vec{a} \times \vec{b}$.
Area $= |\vec{a} \times \vec{b}| = \sqrt{(22)^2 + (11)^2 + (0)^2}$
Area $= \sqrt{484 + 121 + 0}$
Area $= \sqrt{605}$
We can simplify $\sqrt{605}$. $605 = 5 \times 121 = 5 \times 11^2$.
Area $= \sqrt{121 \times 5} = 11\sqrt{5}$
The area of the parallelogram is $11\sqrt{5}$ square units.
Question 11. Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are $± \left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)$ .
Answer:
Given:
A vector is equally inclined to the axes OX, OY, and OZ.
To Show:
The direction cosines of the vector are $\pm \left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)$.
Solution:
Let the vector be $\vec{v}$. Let the angles made by the vector $\vec{v}$ with the positive directions of the x-axis, y-axis, and z-axis be $\alpha$, $\beta$, and $\gamma$ respectively.
The direction cosines of the vector $\vec{v}$ are $l = \cos\alpha$, $m = \cos\beta$, and $n = \cos\gamma$.
We know that the sum of the squares of the direction cosines of any vector is always equal to 1.
$l^2 + m^2 + n^2 = 1$
... (i)
Since the vector is equally inclined to the axes OX, OY, and OZ, the angles it makes with the axes are equal.
$\alpha = \beta = \gamma$
(Given)
Therefore, the direction cosines are equal:
$\cos\alpha = \cos\beta = \cos\gamma$
So, $l = m = n$.
Substituting $l=m=n$ into equation (i):
$l^2 + l^2 + l^2 = 1$
$3l^2 = 1$
$l^2 = \frac{1}{3}$
Taking the square root of both sides:
$l = \pm\frac{1}{\sqrt{3}}$
Since $l = m = n$, the direction cosines are:
$l = \pm\frac{1}{\sqrt{3}} \;,\; m = \pm\frac{1}{\sqrt{3}} \;,\; n = \pm\frac{1}{\sqrt{3}}$
As the angles $\alpha, \beta, \gamma$ are equal, their cosines must have the same sign simultaneously (either all positive or all negative). Therefore, the direction cosines are either all $+\frac{1}{\sqrt{3}}$ or all $-\frac{1}{\sqrt{3}}$.
Thus, the direction cosines of a vector equally inclined to the axes OX, OY, and OZ are $\left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)$ or $\left( -\frac{1}{\sqrt{3}} \;,\; -\frac{1}{\sqrt{3}} \;,\; -\frac{1}{\sqrt{3}} \right)$.
This can be expressed concisely as $\pm \left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)$.
Hence, the direction cosines of a vector equally inclined to the axes OX, OY and OZ are $\pm \left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)$.
Question 12. Let $\vec{a} = \hat{i} + 4\hat{j} + 2\hat{k}$ , $\vec{b} = 3\hat{i} − 2\hat{j} + 7\hat{k}$ and $\vec{c} = 2\hat{i} − \hat{j} + 4\hat{k}$ . Find a vector $\vec{d}$ which is perpendicular to both $\vec{a}$ and $\vec{b}$ , and $\vec{c} \;.\; \vec{d} = 15$.
Answer:
Given:
The vectors are $\vec{a} = \hat{i} + 4\hat{j} + 2\hat{k}$, $\vec{b} = 3\hat{i} - 2\hat{j} + 7\hat{k}$, and $\vec{c} = 2\hat{i} - \hat{j} + 4\hat{k}$.
A vector $\vec{d}$ is perpendicular to both $\vec{a}$ and $\vec{b}$, and $\vec{c} \;.\; \vec{d} = 15$.
To Find:
The vector $\vec{d}$.
Solution:
Since the vector $\vec{d}$ is perpendicular to both $\vec{a}$ and $\vec{b}$, $\vec{d}$ must be parallel to the cross product of $\vec{a}$ and $\vec{b}$, i.e., $\vec{a} \times \vec{b}$.
So, $\vec{d}$ can be written in the form $\vec{d} = \lambda (\vec{a} \times \vec{b})$ for some scalar $\lambda$.
First, we calculate the cross product $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 4 & 2 \\ 3 & -2 & 7 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}[(4)(7) - (2)(-2)] - \hat{j}[(1)(7) - (2)(3)] + \hat{k}[(1)(-2) - (4)(3)]$
$\vec{a} \times \vec{b} = \hat{i}[28 - (-4)] - \hat{j}[7 - 6] + \hat{k}[-2 - 12]$
$\vec{a} \times \vec{b} = \hat{i}[28 + 4] - \hat{j}[1] + \hat{k}[-14]$
$\vec{a} \times \vec{b} = 32\hat{i} - \hat{j} - 14\hat{k}$
So, the vector $\vec{d}$ is of the form:
$\vec{d} = \lambda (32\hat{i} - \hat{j} - 14\hat{k}) = 32\lambda\hat{i} - \lambda\hat{j} - 14\lambda\hat{k}$
We are also given that $\vec{c} \;.\; \vec{d} = 15$.
Substitute the expressions for $\vec{c}$ and $\vec{d}$ into the dot product equation:
$(2\hat{i} - \hat{j} + 4\hat{k}) \;.\; (32\lambda\hat{i} - \lambda\hat{j} - 14\lambda\hat{k}) = 15$
$(2)(32\lambda) + (-1)(-\lambda) + (4)(-14\lambda) = 15$
$64\lambda + \lambda - 56\lambda = 15$
$(64 + 1 - 56)\lambda = 15$
$9\lambda = 15$
Solving for $\lambda$:
$\lambda = \frac{15}{9} = \frac{5}{3}$
Now, substitute the value of $\lambda$ back into the expression for $\vec{d}$:
$\vec{d} = \frac{5}{3} (32\hat{i} - \hat{j} - 14\hat{k})$
$\vec{d} = \frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k}$
The vector $\vec{d}$ is $\frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k}$.
Question 13. The scalar product of the vector $\hat{i} + \hat{j} + \hat{k}$ with a unit vector along the sum of vectors $2\hat{i} + 4\hat{j} − 5\hat{k}$ and $λ\hat{i} + 2\hat{j} + 3\hat{k}$ is equal to one. Find the value of λ.
Answer:
Given:
Vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$.
Vector $\vec{b} = 2\hat{i} + 4\hat{j} - 5\hat{k}$.
Vector $\vec{c} = \lambda\hat{i} + 2\hat{j} + 3\hat{k}$.
The scalar product of $\vec{a}$ with a unit vector along the sum of vectors $\vec{b}$ and $\vec{c}$ is equal to one.
To Find:
The value of $\lambda$.
Solution:
Let $\vec{v}$ be the sum of vectors $\vec{b}$ and $\vec{c}$.
$\vec{v} = \vec{b} + \vec{c}$
$\vec{v} = (2\hat{i} + 4\hat{j} - 5\hat{k}) + (\lambda\hat{i} + 2\hat{j} + 3\hat{k})$
$\vec{v} = (2+\lambda)\hat{i} + (4+2)\hat{j} + (-5+3)\hat{k}$
$\vec{v} = (2+\lambda)\hat{i} + 6\hat{j} - 2\hat{k}$
The unit vector along $\vec{v}$ is given by $\hat{v} = \frac{\vec{v}}{|\vec{v}|}$.
First, find the magnitude of $\vec{v}$:
$|\vec{v}| = \sqrt{(2+\lambda)^2 + (6)^2 + (-2)^2}$
$|\vec{v}| = \sqrt{(2+\lambda)^2 + 36 + 4}$
$|\vec{v}| = \sqrt{(2+\lambda)^2 + 40}$
The unit vector along the sum of $\vec{b}$ and $\vec{c}$ is:
$\hat{v} = \frac{(2+\lambda)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{(2+\lambda)^2 + 40}}$
According to the problem statement, the scalar product of $\vec{a}$ with $\hat{v}$ is equal to one.
$\vec{a} \;.\; \hat{v} = 1$
... (i)
Substitute the expressions for $\vec{a}$ and $\hat{v}$ into equation (i):
$(\hat{i} + \hat{j} + \hat{k}) \;.\; \frac{(2+\lambda)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{(2+\lambda)^2 + 40}} = 1$
Calculate the dot product in the numerator:
$(1)(2+\lambda) + (1)(6) + (1)(-2) = 2+\lambda + 6 - 2 = 6+\lambda$
So the equation becomes:
$\frac{6+\lambda}{\sqrt{(2+\lambda)^2 + 40}} = 1$
Multiply both sides by the denominator:
$6+\lambda = \sqrt{(2+\lambda)^2 + 40}$
Square both sides to eliminate the square root:
$(6+\lambda)^2 = (2+\lambda)^2 + 40$
Expand both sides:
$36 + 12\lambda + \lambda^2 = (4 + 4\lambda + \lambda^2) + 40$
$36 + 12\lambda + \lambda^2 = 4 + 4\lambda + \lambda^2 + 40$
$36 + 12\lambda + \lambda^2 = 44 + 4\lambda + \lambda^2$
Subtract $\lambda^2$ from both sides:
$36 + 12\lambda = 44 + 4\lambda$
Rearrange the terms to solve for $\lambda$:
$12\lambda - 4\lambda = 44 - 36$
$8\lambda = 8$
$\lambda = \frac{8}{8}$
$\lambda = 1$
We should check if this value of $\lambda$ satisfies the original equation $6+\lambda = \sqrt{(2+\lambda)^2 + 40}$. Since the left side $6+\lambda = 6+1=7$ is positive, and the right side (a square root) is always taken as the positive root, $\lambda=1$ is a valid solution.
The value of $\lambda$ is 1.
Question 14. If $\vec{a}$, $\vec{b}$, $\vec{c}$ are mutually perpendicular vectors of equal magnitudes, show that the vector $\vec{c} \;.\; \vec{d} = 15$ is equally inclined to $\vec{a}$ , $\vec{b}$ and $\vec{c}$.
Answer:
Given:
Vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ are mutually perpendicular vectors of equal magnitudes.
This means:
$\vec{a} \cdot \vec{b} = 0$
$\vec{b} \cdot \vec{c} = 0$
$\vec{c} \cdot \vec{a} = 0$
And $|\vec{a}| = |\vec{b}| = |\vec{c}|$. Let the common magnitude be $k$, where $k > 0$. So, $|\vec{a}| = |\vec{b}| = |\vec{c}| = k$.
To Show:
The vector $\vec{d} = \vec{a} + \vec{b} + \vec{c}$ is equally inclined to $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Solution:
Let $\vec{d} = \vec{a} + \vec{b} + \vec{c}$.
To show that $\vec{d}$ is equally inclined to $\vec{a}$, $\vec{b}$, and $\vec{c}$, we need to show that the angle between $\vec{d}$ and $\vec{a}$, the angle between $\vec{d}$ and $\vec{b}$, and the angle between $\vec{d}$ and $\vec{c}$ are all equal.
The cosine of the angle $\theta$ between two vectors $\vec{u}$ and $\vec{v}$ is given by $\cos\theta = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}| |\vec{v}|}$.
First, let's find the magnitude of $\vec{d}$.
$|\vec{d}|^2 = \vec{d} \cdot \vec{d} = (\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c})$
$|\vec{d}|^2 = \vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} + \vec{c} \cdot \vec{c}$
Using the given conditions ($\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} = 0$, $\vec{a} \cdot \vec{c} = \vec{c} \cdot \vec{a} = 0$, $\vec{b} \cdot \vec{c} = \vec{c} \cdot \vec{b} = 0$) and the property $\vec{v} \cdot \vec{v} = |\vec{v}|^2$:
$|\vec{d}|^2 = |\vec{a}|^2 + 0 + 0 + 0 + |\vec{b}|^2 + 0 + 0 + 0 + |\vec{c}|^2$
Since $|\vec{a}| = |\vec{b}| = |\vec{c}| = k$:
$|\vec{d}|^2 = k^2 + k^2 + k^2 = 3k^2$
$|\vec{d}| = \sqrt{3k^2} = k\sqrt{3}$
(Since $k > 0$)
Now, let's find the cosine of the angle between $\vec{d}$ and $\vec{a}$. Let this angle be $\theta_a$.
$\cos\theta_a = \frac{\vec{d} \cdot \vec{a}}{|\vec{d}| |\vec{a}|}$
Calculate the dot product $\vec{d} \cdot \vec{a}$:
$\vec{d} \cdot \vec{a} = (\vec{a} + \vec{b} + \vec{c}) \cdot \vec{a} = \vec{a} \cdot \vec{a} + \vec{b} \cdot \vec{a} + \vec{c} \cdot \vec{a}$
$\vec{d} \cdot \vec{a} = |\vec{a}|^2 + 0 + 0 = k^2$
So, $\cos\theta_a = \frac{k^2}{(k\sqrt{3})(k)} = \frac{k^2}{k^2\sqrt{3}}$
$\cos\theta_a = \frac{1}{\sqrt{3}}$
Next, let's find the cosine of the angle between $\vec{d}$ and $\vec{b}$. Let this angle be $\theta_b$.
$\cos\theta_b = \frac{\vec{d} \cdot \vec{b}}{|\vec{d}| |\vec{b}|}$
Calculate the dot product $\vec{d} \cdot \vec{b}$:
$\vec{d} \cdot \vec{b} = (\vec{a} + \vec{b} + \vec{c}) \cdot \vec{b} = \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{b} + \vec{c} \cdot \vec{b}$
$\vec{d} \cdot \vec{b} = 0 + |\vec{b}|^2 + 0 = k^2$
So, $\cos\theta_b = \frac{k^2}{(k\sqrt{3})(k)} = \frac{k^2}{k^2\sqrt{3}}$
$\cos\theta_b = \frac{1}{\sqrt{3}}$
Finally, let's find the cosine of the angle between $\vec{d}$ and $\vec{c}$. Let this angle be $\theta_c$.
$\cos\theta_c = \frac{\vec{d} \cdot \vec{c}}{|\vec{d}| |\vec{c}|}$
Calculate the dot product $\vec{d} \cdot \vec{c}$:
$\vec{d} \cdot \vec{c} = (\vec{a} + \vec{b} + \vec{c}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{c}$
$\vec{d} \cdot \vec{c} = 0 + 0 + |\vec{c}|^2 = k^2$
So, $\cos\theta_c = \frac{k^2}{(k\sqrt{3})(k)} = \frac{k^2}{k^2\sqrt{3}}$
$\cos\theta_c = \frac{1}{\sqrt{3}}$
Since $\cos\theta_a = \cos\theta_b = \cos\theta_c = \frac{1}{\sqrt{3}}$, and the angle between two vectors is usually taken in $[0, \pi]$, this implies $\theta_a = \theta_b = \theta_c = \arccos\left(\frac{1}{\sqrt{3}}\right)$.
Thus, the vector $\vec{a} + \vec{b} + \vec{c}$ makes equal angles with vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Hence, the vector $\vec{a} + \vec{b} + \vec{c}$ is equally inclined to $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Question 15. Prove that $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$, if and only if $\vec{a}\;,\; \vec{b}$ are perpendicular, given $\vec{a} ≠ \vec{0} \;,\; \vec{b} ≠ \vec{0}$.
Answer:
Given:
Vectors $\vec{a}$ and $\vec{b}$, such that $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$.
To Prove:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$ if and only if $\vec{a}$ is perpendicular to $\vec{b}$.
Proof:
The statement is an "if and only if" statement, which requires proving two implications:
1. If $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$, then $\vec{a} \perp \vec{b}$.
2. If $\vec{a} \perp \vec{b}$, then $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$.
Let's first expand the left side of the given equation using the properties of the dot product:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = \vec{a} \cdot (\vec{a} + \vec{b}) + \vec{b} \cdot (\vec{a} + \vec{b})$
Using the distributive property:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = \vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b}$
Using the property $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and the commutative property of the dot product ($\vec{b} \cdot \vec{a} = \vec{a} \cdot \vec{b}$):
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\vec{a}|^2 + \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{b} + |\vec{b}|^2$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\vec{a}|^2 + |\vec{b}|^2 + 2(\vec{a} \cdot \vec{b})$
... (i)
Part 1: Proving the first implication
Assume that $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$.
Substitute this into equation (i):
$|\vec{a}|^2 + |\vec{b}|^2 = |\vec{a}|^2 + |\vec{b}|^2 + 2(\vec{a} \cdot \vec{b})$
Subtract $|\vec{a}|^2 + |\vec{b}|^2$ from both sides:
$0 = 2(\vec{a} \cdot \vec{b})$
$\vec{a} \cdot \vec{b} = 0$
Since it is given that $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$, a dot product of zero implies that the vectors are perpendicular.
$\vec{a} \perp \vec{b}$
Thus, if $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$, then $\vec{a}$ and $\vec{b}$ are perpendicular.
Part 2: Proving the second implication
Assume that $\vec{a}$ is perpendicular to $\vec{b}$, given $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$.
The condition that $\vec{a}$ and $\vec{b}$ are perpendicular means their dot product is zero:
$\vec{a} \cdot \vec{b} = 0$
Now, consider the expression for $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b})$ from equation (i):
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\vec{a}|^2 + |\vec{b}|^2 + 2(\vec{a} \cdot \vec{b})$
Substitute $\vec{a} \cdot \vec{b} = 0$ into this equation:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\vec{a}|^2 + |\vec{b}|^2 + 2(0)$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\vec{a}|^2 + |\vec{b}|^2$
Thus, if $\vec{a}$ and $\vec{b}$ are perpendicular, then $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$.
Since both implications have been proved, the statement $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$ if and only if $\vec{a}\;,\; \vec{b}$ are perpendicular is proven, given that $\vec{a} ≠ \vec{0}$ and $\vec{b} ≠ \vec{0}$.
Choose the correct answer in Exercises 16 to 19.
Question 16. If θ is the angle between two vectors $\vec{a}$ and $\vec{b}$, then $\vec{a} \;.\; \vec{b} ≥ 0$ only when
(A) $0 < θ < \frac{π}{2}$
(B) $0 ≤ θ ≤ \frac{π}{2}$
(C) $0 < θ < π$
(D) $0 ≤ θ ≤ π$
Answer:
Solution:
Let $\theta$ be the angle between two vectors $\vec{a}$ and $\vec{b}$. The scalar product (dot product) of $\vec{a}$ and $\vec{b}$ is given by the formula:
$\vec{a} \;.\; \vec{b} = |\vec{a}| |\vec{b}| \cos\theta$
We are given that $\vec{a} \;.\; \vec{b} \ge 0$.
Assuming $\vec{a}$ and $\vec{b}$ are non-zero vectors (as an angle between them is considered), $|\vec{a}| > 0$ and $|\vec{b}| > 0$. Their product $|\vec{a}| |\vec{b}|$ is positive.
So, the inequality $\vec{a} \;.\; \vec{b} \ge 0$ becomes:
$|\vec{a}| |\vec{b}| \cos\theta \ge 0$
Dividing by the positive value $|\vec{a}| |\vec{b}|$, we get:
$\cos\theta \ge 0$
The angle $\theta$ between two vectors is typically considered in the range $0 \le \theta \le \pi$.
We need to find the values of $\theta$ in the interval $[0, \pi]$ for which $\cos\theta \ge 0$.
The cosine function is non-negative in the first quadrant and at the boundary points where $\theta=0$ and $\theta=\frac{\pi}{2}$.
Specifically, $\cos\theta \ge 0$ for $0 \le \theta \le \frac{\pi}{2}$.
Let's examine the given options:
(A) $0 < \theta < \frac{\pi}{2}$: $\cos\theta > 0$. This satisfies $\ge 0$, but excludes $\theta=0$ and $\theta=\frac{\pi}{2}$.
(B) $0 ≤ θ ≤ \frac{π}{2}$: $\cos\theta \ge 0$. This exactly matches the condition.
(C) $0 < θ < π$: Includes angles in the second quadrant where $\cos\theta < 0$.
(D) $0 ≤ θ ≤ π$: Includes angles in the second quadrant where $\cos\theta < 0$.
Therefore, the condition $\vec{a} \;.\; \vec{b} \ge 0$ holds when $0 \le \theta \le \frac{\pi}{2}$.
The correct answer is (B) $0 ≤ θ ≤ \frac{π}{2}$.
Question 17. Let $\vec{a}$ and $\vec{b}$ be two unit vectors and θ is the angle between them. Then $\vec{a} + \vec{b}$ is a unit vector if
(A) $θ = \frac{π}{4}$
(B) $θ = \frac{π}{3}$
(C) $θ = \frac{π}{2}$
(D) $θ = \frac{2π}{3}$
Answer:
Given:
$\vec{a}$ and $\vec{b}$ are unit vectors, so $|\vec{a}| = 1$ and $|\vec{b}| = 1$.
$\theta$ is the angle between $\vec{a}$ and $\vec{b}$.
The vector $\vec{a} + \vec{b}$ is a unit vector, so $|\vec{a} + \vec{b}| = 1$.
To Find:
The value of $\theta$ that satisfies the given conditions.
Solution:
We are given that $|\vec{a} + \vec{b}| = 1$. Squaring both sides, we get:
$|\vec{a} + \vec{b}|^2 = 1^2$
$|\vec{a} + \vec{b}|^2 = 1$
We know that for any vector $\vec{v}$, $|\vec{v}|^2 = \vec{v} \cdot \vec{v}$. So,
$(\vec{a} + \vec{b}) \cdot (\vec{a} + \vec{b}) = 1$
Expand the dot product:
$\vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} = 1$
Using the properties $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and $\vec{b} \cdot \vec{a} = \vec{a} \cdot \vec{b}$:
$|\vec{a}|^2 + 2(\vec{a} \cdot \vec{b}) + |\vec{b}|^2 = 1$
We are given that $\vec{a}$ and $\vec{b}$ are unit vectors, so $|\vec{a}| = 1$ and $|\vec{b}| = 1$. Also, the dot product $\vec{a} \cdot \vec{b}$ is defined as $|\vec{a}| |\vec{b}| \cos\theta$.
Substitute these values into the equation:
$(1)^2 + 2(|\vec{a}| |\vec{b}| \cos\theta) + (1)^2 = 1$
$1 + 2((1)(1) \cos\theta) + 1 = 1$
$1 + 2\cos\theta + 1 = 1$
$2 + 2\cos\theta = 1$
Subtract 2 from both sides:
$2\cos\theta = 1 - 2$
$2\cos\theta = -1$
Divide by 2:
$\cos\theta = -\frac{1}{2}$
We need to find the value of $\theta$ in the range $0 \le \theta \le \pi$ for which $\cos\theta = -\frac{1}{2}$.
The angle whose cosine is $-\frac{1}{2}$ is $\frac{2\pi}{3}$.
$\theta = \frac{2\pi}{3}$
Now, let's check the given options:
(A) $\theta = \frac{\pi}{4}$
(B) $\theta = \frac{\pi}{3}$
(C) $\theta = \frac{\pi}{2}$
(D) $\theta = \frac{2\pi}{3}$
The calculated value of $\theta$ matches option (D).
The correct answer is (D) $\theta = \frac{2π}{3}$.
Question 18. The value of $\hat{i} \;. (\hat{j} × \hat{k}) + \hat{j} \;. (\hat{i} × \hat{k}) + \hat{k} \;. (\hat{i} × \hat{j})$ is
(A) 0
(B) –1
(C) 1
(D) 3
Answer:
Solution:
We need to evaluate the expression $\hat{i} \;. (\hat{j} × \hat{k}) + \hat{j} \;. (\hat{i} × \hat{k}) + \hat{k} \;. (\hat{i} × \hat{j})$.
Let's evaluate each term separately.
The standard unit vectors $\hat{i}$, $\hat{j}$, and $\hat{k}$ form a right-handed orthonormal system.
For the first term, we have $\hat{j} × \hat{k}$. The cross product of $\hat{j}$ and $\hat{k}$ in a right-handed system is $\hat{i}$.
$\hat{j} × \hat{k} = \hat{i}$
So the first term is $\hat{i} \;. (\hat{j} × \hat{k}) = \hat{i} \;. \hat{i}$.
The dot product of a unit vector with itself is 1.
$\hat{i} \;. \hat{i} = |\hat{i}|^2 = 1^2 = 1$
Alternatively, the first term is the scalar triple product $[\hat{i}, \hat{j}, \hat{k}]$, which represents the volume of the unit cube formed by the basis vectors. $[\hat{i}, \hat{j}, \hat{k}] = 1$.
For the second term, we have $\hat{i} × \hat{k}$. The cross product of $\hat{i}$ and $\hat{k}$ in a right-handed system is $-\hat{j}$.
$\hat{i} × \hat{k} = -\hat{j}$
So the second term is $\hat{j} \;. (\hat{i} × \hat{k}) = \hat{j} \;. (-\hat{j})$.
The dot product is:
$\hat{j} \;. (-\hat{j}) = -(\hat{j} \;. \hat{j}) = -|\hat{j}|^2 = -(1^2) = -1$
Alternatively, the second term is the scalar triple product $[\hat{j}, \hat{i}, \hat{k}]$. Swapping the first two vectors in $[\hat{i}, \hat{j}, \hat{k}]$ changes the sign. $[\hat{j}, \hat{i}, \hat{k}] = -[\hat{i}, \hat{j}, \hat{k}] = -1$.
For the third term, we have $\hat{i} × \hat{j}$. The cross product of $\hat{i}$ and $\hat{j}$ in a right-handed system is $\hat{k}$.
$\hat{i} × \hat{j} = \hat{k}$
So the third term is $\hat{k} \;. (\hat{i} × \hat{j}) = \hat{k} \;. \hat{k}$.
The dot product is:
$\hat{k} \;. \hat{k} = |\hat{k}|^2 = 1^2 = 1$
Alternatively, the third term is the scalar triple product $[\hat{k}, \hat{i}, \hat{j}]$. This is a cyclic permutation of $[\hat{i}, \hat{j}, \hat{k}]$, so the value is the same. $[\hat{k}, \hat{i}, \hat{j}] = [\hat{i}, \hat{j}, \hat{k}] = 1$.
Now, we sum the values of the three terms:
Value $= 1 + (-1) + 1$
Value $= 1 - 1 + 1$
Value $= 1$
The value of the expression is 1.
Comparing with the given options:
(A) 0
(B) –1
(C) 1
(D) 3
The correct option is (C).
The correct answer is (C) 1.
Question 19. If θ is the angle between any two vectors $\vec{a}$ and $\vec{b}$, then $|\;\vec{a}\;.\;\vec{b}\;| = |\;\vec{a}\;×\;\vec{b}\;|$ when θ is equal to
(A) 0
(B) $\frac{π}{4}$
(C) $\frac{π}{2}$
(D) π
Answer:
Given:
$\theta$ is the angle between two vectors $\vec{a}$ and $\vec{b}$.
We are given the condition $|\;\vec{a}\;.\;\vec{b}\;| = |\;\vec{a}\;×\;\vec{b}\;|$.
We assume $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$ since an angle between them is considered.
To Find:
The value of $\theta$ for which the given condition holds.
Solution:
The magnitudes of the dot product and the cross product of two vectors $\vec{a}$ and $\vec{b}$ are given by:
$|\vec{a} \cdot \vec{b}| = ||\vec{a}| |\vec{b}| \cos\theta|$
$|\vec{a} \times \vec{b}| = ||\vec{a}| |\vec{b}| \sin\theta|$
We are given the condition $|\;\vec{a}\;.\;\vec{b}\;| = |\;\vec{a}\;×\;\vec{b}\;|$.
$||\vec{a}| |\vec{b}| \cos\theta| = ||\vec{a}| |\vec{b}| \sin\theta|$
... (i)
Since $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$, we have $|\vec{a}| > 0$ and $|\vec{b}| > 0$. Therefore, $|\vec{a}| |\vec{b}| > 0$.
Equation (i) can be written as:
$|\vec{a}| |\vec{b}| |\cos\theta| = |\vec{a}| |\vec{b}| |\sin\theta|$
Divide both sides by $|\vec{a}| |\vec{b}|$ (since it is non-zero):
$|\cos\theta| = |\sin\theta|$
The angle $\theta$ between two vectors is usually taken in the range $0 \le \theta \le \pi$.
We need to find the values of $\theta$ in $[0, \pi]$ that satisfy $|\cos\theta| = |\sin\theta|$.
This equality holds when $\cos\theta = \sin\theta$ or $\cos\theta = -\sin\theta$.
Case 1: $\cos\theta = \sin\theta$.
In the range $[0, \pi]$, $\cos\theta = \sin\theta$ occurs at $\theta = \frac{\pi}{4}$.
Check: $|\cos(\frac{\pi}{4})| = |\frac{1}{\sqrt{2}}| = \frac{1}{\sqrt{2}}$, $|\sin(\frac{\pi}{4})| = |\frac{1}{\sqrt{2}}| = \frac{1}{\sqrt{2}}$. The equality holds.
Case 2: $\cos\theta = -\sin\theta$.
This can be written as $\sin\theta + \cos\theta = 0$. If $\cos\theta \neq 0$, we can divide by $\cos\theta$ to get $\tan\theta = -1$.
In the range $[0, \pi]$, $\tan\theta = -1$ occurs at $\theta = \frac{3\pi}{4}$.
Check: $|\cos(\frac{3\pi}{4})| = |-\frac{1}{\sqrt{2}}| = \frac{1}{\sqrt{2}}$, $|\sin(\frac{3\pi}{4})| = |\frac{1}{\sqrt{2}}| = \frac{1}{\sqrt{2}}$. The equality holds.
So the possible values for $\theta$ in the range $[0, \pi]$ are $\frac{\pi}{4}$ and $\frac{3\pi}{4}$.
Now, let's check the given options:
(A) 0: $|\cos 0| = 1$, $|\sin 0| = 0$. $1 \neq 0$.
(B) $\frac{\pi}{4}$: $|\cos \frac{\pi}{4}| = \frac{1}{\sqrt{2}}$, $|\sin \frac{\pi}{4}| = \frac{1}{\sqrt{2}}$. Equal.
(C) $\frac{\pi}{2}$: $|\cos \frac{\pi}{2}| = 0$, $|\sin \frac{\pi}{2}| = 1$. $0 \neq 1$.
(D) $\pi$: $|\cos \pi| = 1$, $|\sin \pi| = 0$. $1 \neq 0$.
Out of the given options, only $\theta = \frac{\pi}{4}$ satisfies the condition.
The correct answer is (B) $\frac{π}{4}$.

