| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 3.1 | Example 1 & 2 (Before Exercise 3.2) | Exercise 3.2 |
| Example 3 to 6 (Before Exercise 3.3) | Exercise 3.3 | Example 7 & 8 (Before Exercise 3.4) |
| Exercise 3.4 | ||
Chapter 3 Understanding Quadrilaterals
Welcome to the detailed solutions guide for Chapter 3, "Understanding Quadrilaterals," from the latest Class 8 NCERT mathematics textbook designated for the academic session 2024-25. This chapter delves into the fascinating world of polygons, with a special focus on quadrilaterals – four-sided figures that are ubiquitous in geometry and the world around us. Understanding their classification and properties is fundamental to building strong geometric intuition and reasoning skills. These solutions provide comprehensive, step-by-step explanations for all exercises, ensuring students grasp the concepts thoroughly and can apply them effectively.
The exploration begins with polygons in general – closed figures formed entirely by line segments. The solutions clarify how polygons are classified based on the number of sides (triangle - 3 sides, quadrilateral - 4 sides, pentagon - 5 sides, etc.). Key distinctions are drawn between convex polygons (where all interior angles are less than $180^\circ$ and diagonals lie entirely inside) and concave polygons (which have at least one interior angle greater than $180^\circ$ and at least one diagonal lying partially or wholly outside). The difference between regular polygons (all sides equal and all angles equal) and irregular polygons is also highlighted. A fundamental property discussed is the Angle Sum Property of Polygons. The solutions demonstrate the application of the formula for the sum ($S$) of interior angles of a convex polygon with $n$ sides: $S = (n-2) \times 180^\circ$. This formula is crucial for finding unknown angles in various polygons.
The primary focus, however, shifts to the specific family of four-sided polygons: Quadrilaterals. These solutions meticulously explore the hierarchy and unique properties of various special types of quadrilaterals. The journey often starts with the Parallelogram, a foundational shape whose properties apply to several others:
- Opposite sides are equal in length.
- Opposite sides are parallel.
- Opposite angles are equal in measure.
- Adjacent angles are supplementary (sum to $180^\circ$).
- Diagonals bisect each other (intersect at their midpoints).
- Rhombus: Possesses all properties of a parallelogram PLUS all four sides are equal, and its diagonals bisect each other perpendicularly.
- Rectangle: Has all properties of a parallelogram PLUS all four angles are right angles ($90^\circ$), and its diagonals are equal in length.
- Square: Combines the properties of both a rhombus and a rectangle; it's a regular quadrilateral.
- Kite: Characterized by two distinct pairs of equal-length adjacent sides. Its diagonals are perpendicular, and one diagonal bisects the other.
- Trapezium (or Trapezoid): Defined by having exactly one pair of opposite sides parallel.
A significant part of learning involves applying these properties. The solutions expertly guide students on how to use the defining characteristics of each quadrilateral type to solve problems. This often involves finding the measures of unknown angles or side lengths within a given figure by applying the relevant properties, angle sum rules, or relationships between angles (like supplementary adjacent angles or equal opposite angles in parallelograms). Logical deduction is key – starting with known information and applying theorems and properties step-by-step to reach a conclusion. Problems requiring verification or simple proofs of properties using logical arguments are also addressed systematically.
Regarding the rationalized syllabus for 2024-25, Chapter 3, "Understanding Quadrilaterals," in the Class 8 NCERT textbook has maintained its core focus on the classification of polygons, the angle sum property, and the key properties of parallelograms and its special types (rectangle, rhombus, square). The rationalization primarily involved streamlining the number and complexity of exercises, potentially reducing the emphasis on intricate problems involving kites, general trapeziums, or complex deductive proofs, ensuring a solid grasp of the fundamental properties of the most common quadrilaterals. By engaging with these detailed solutions, students can develop a thorough understanding of polygon and quadrilateral classifications, master their distinct properties, significantly enhance their geometric reasoning abilities, and apply these concepts effectively to solve a variety of problems.
Exercise 3.1
Question 1. Given here are some figures.

Classify each of them on the basis of the following.
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Answer:
We classify each figure based on the given properties:
(a) Simple curve: A curve that does not cross itself.
Figures: 1, 2, 5, 6, and 7
(b) Simple closed curve: A simple curve that begins and ends at the same point.
Figures: 1, 2, 5, 6, and 7
(c) Polygon: A simple closed curve made up entirely of line segments.
Figures: 1 and 2
(d) Convex polygon: A polygon where all its interior angles are less than $180^\circ$.
Figure: 2
(e) Concave polygon: A polygon that has at least one interior angle greater than $180^\circ$.
Figure: 1
Question 2. What is a regular polygon?
State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides
Answer:
Definition:
A regular polygon is a polygon that is both equiangular and equilateral. This means that all its interior angles are equal in measure, and all its sides are equal in length.
Names of regular polygons:
(i) A regular polygon of 3 sides is called an Equilateral Triangle.
(ii) A regular polygon of 4 sides is called a Square.
(iii) A regular polygon of 6 sides is called a Regular Hexagon.
Example 1 & 2 (Before Exercise 3.2)
Example 1: Find measure x in Fig 3.3.
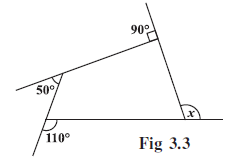
Answer:
Given:
A quadrilateral with interior angles $x^\circ$, $90^\circ$, $50^\circ$, and $110^\circ$. Note that the square symbol indicates a $90^\circ$ angle.
To Find:
The measure of angle $x$.
Solution:
The given figure is a quadrilateral.
We know that the sum of the interior angles of a quadrilateral is $360^\circ$.
Therefore, we can write the equation:
$x + 90^\circ + 50^\circ + 110^\circ = 360^\circ$
(Sum of all the exterior angles of a quadrilateral)
Add the known angles on the left side:
$(90 + 50 + 110)^\circ = 140^\circ + 110^\circ = 250^\circ$
The equation becomes:
$x + 250^\circ = 360^\circ$
To find $x$, subtract $250^\circ$ from both sides of the equation:
$x = 360^\circ - 250^\circ$
Calculate the result:
$x = 110^\circ$
The measure of angle $x$ is $\mathbf{110^\circ}$.
Example 2: Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°.
Answer:
Given:
The polygon is regular.
Measure of each exterior angle $= 45^\circ$.
To Find:
The number of sides of the regular polygon.
Solution:
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
For a regular polygon, all exterior angles are equal in measure.
Let the number of sides of the regular polygon be $n$.
The measure of each exterior angle of a regular polygon with $n$ sides is given by the formula:
Measure of each exterior angle $= \frac{\text{Sum of exterior angles}}{\text{Number of sides}}$
Measure of each exterior angle $= \frac{360^\circ}{n}$
We are given that the measure of each exterior angle is $45^\circ$. So, we have the equation:
$45^\circ = \frac{360^\circ}{n}$
$45^\circ \times n = 360^\circ$
(Multiplying both sides by $n$)
$n = \frac{360^\circ}{45^\circ}$
(Dividing both sides by $45^\circ$)
Perform the division:
$n = 8$
Therefore, the regular polygon has $8$ sides.
A regular polygon with $8$ sides is called a regular octagon.
Exercise 3.2
Question 1. Find x in the following figures.

Answer:
We will use the properties of linear pairs and the sum of angles in a polygon to find the value of $x$ in each figure.
Recall that angles in a linear pair sum up to $180^\circ$. Also, the sum of interior angles of a polygon with $n$ sides is given by $(n-2) \times 180^\circ$.
Figure (a):
The figure shows a triangle with exterior angles $125^\circ$, $125^\circ$, and $x^\circ$. Let the interior angles adjacent to the $125^\circ$ exterior angles be $m$ and $n$ respectively.
Using the linear pair property:
$125^\circ + m = 180^\circ$
(Linear pair)
$m = 180^\circ - 125^\circ$
$m = 55^\circ$
Similarly, for the other angle:
$125^\circ + n = 180^\circ$
(Linear pair)
$n = 180^\circ - 125^\circ$
$n = 55^\circ$
Now, we can use the exterior angle property of a triangle, which states that an exterior angle is equal to the sum of the two opposite interior angles.
In this figure, the exterior angle $x$ is opposite to the interior angles $m$ and $n$.
$x = m + n$
(Exterior angle property of a triangle)
Substitute the values of $m$ and $n$:
$x = 55^\circ + 55^\circ$
$x = 110^\circ$
Therefore, the value of $x$ in Figure (a) is $110^\circ$.
Figure (b):
The figure is a pentagon (5 sides). It has exterior angles $x^\circ$, $70^\circ$, $60^\circ$, and two $90^\circ$ (adjacent to the interior right angles). The angles given are $x^\circ$, $70^\circ$, and $60^\circ$ as exterior angles, and two right angles ($90^\circ$) as interior angles.
Let's find the interior angles adjacent to the exterior angles $70^\circ$ and $60^\circ$. Let them be $m$ and $n$ respectively.
Using the linear pair property for the $70^\circ$ exterior angle:
$70^\circ + m = 180^\circ$
(Linear pair)
$m = 180^\circ - 70^\circ$
$m = 110^\circ$
Using the linear pair property for the $60^\circ$ exterior angle:
$60^\circ + n = 180^\circ$
(Linear pair)
$n = 180^\circ - 60^\circ$
$n = 120^\circ$
The interior angles of the pentagon are $90^\circ$, $90^\circ$, $m (110^\circ)$, $n (120^\circ)$, and let the interior angle adjacent to the exterior angle $x^\circ$ be $y^\circ$.
The sum of interior angles of a pentagon (a polygon with $n=5$ sides) is $(5-2) \times 180^\circ = 3 \times 180^\circ = 540^\circ$.
Sum of interior angles = $90^\circ + 90^\circ + m + n + y = 540^\circ$
$90^\circ + 90^\circ + 110^\circ + 120^\circ + y = 540^\circ$
$(90+90+110+120)^\circ + y = 540^\circ$
$410^\circ + y = 540^\circ$
Subtract $410^\circ$ from both sides:
$y = 540^\circ - 410^\circ$
$y = 130^\circ$
Finally, the exterior angle $x$ and the interior angle $y$ form a linear pair.
$x + y = 180^\circ$
(Linear pair)
Substitute the value of $y$:
$x + 130^\circ = 180^\circ$
Subtract $130^\circ$ from both sides:
$x = 180^\circ - 130^\circ$
$x = 50^\circ$
Therefore, the value of $x$ in Figure (b) is $50^\circ$.
Question 2. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Answer:
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
For a regular polygon, all exterior angles are equal in measure.
The measure of each exterior angle of a regular polygon with $n$ sides is given by the formula:
Measure of each exterior angle $= \frac{360^\circ}{\text{Number of sides}}$
(i) Regular polygon of 9 sides:
Given:
Number of sides, $n = 9$.
The polygon is regular.
To Find:
Measure of each exterior angle.
Solution:
Using the formula:
Measure of each exterior angle $= \frac{360^\circ}{n}$
Substitute $n = 9$:
Measure of each exterior angle $= \frac{360^\circ}{9}$
Performing the division:
$\frac{360}{9} = 40^\circ$
So, the measure of each exterior angle is $40^\circ$.
(ii) Regular polygon of 15 sides:
Given:
Number of sides, $n = 15$.
The polygon is regular.
To Find:
Measure of each exterior angle.
Solution:
Using the formula:
Measure of each exterior angle $= \frac{360^\circ}{n}$
Substitute $n = 15$:
Measure of each exterior angle $= \frac{360^\circ}{15}$
Performing the division:
$\frac{360}{15} = 24^\circ$
So, the measure of each exterior angle is $24^\circ$.
Question 3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Answer:
Given:
The polygon is regular.
Measure of each exterior angle $= 24^\circ$.
To Find:
The number of sides of the regular polygon.
Solution:
We know that the sum of the measures of the exterior angles of any convex polygon is $360^\circ$.
For a regular polygon, all exterior angles are equal in measure.
Let the number of sides of the regular polygon be $n$.
The measure of each exterior angle of a regular polygon with $n$ sides is given by the formula:
Measure of each exterior angle $= \frac{\text{Sum of exterior angles}}{\text{Number of sides}}$
Measure of each exterior angle $= \frac{360^\circ}{n}$
We are given that the measure of each exterior angle is $24^\circ$. So, we have the equation:
$24^\circ = \frac{360^\circ}{n}$
To find $n$, we can rearrange the equation. Multiply both sides by $n$:
$24^\circ \times n = 360^\circ$
(Multiplying both sides by $n$)
Now, divide both sides by $24^\circ$:
$n = \frac{360^\circ}{24^\circ}$
(Dividing both sides by $24^\circ$)
Perform the division:
$n = \frac{360}{24}$
$n = 15$
$n = 15$
Therefore, the regular polygon has $15$ sides.
Question 4. How many sides does a regular polygon have if each of its interior angles is 165°?
Answer:
Solution:
Let the number of sides of the regular polygon be $n$.
The measure of each interior angle is given as $165^\circ$.
For any polygon, the sum of an interior angle and its corresponding exterior angle is $180^\circ$.
So, the measure of each exterior angle of the regular polygon is:
Exterior Angle = $180^\circ$ - Interior Angle
Exterior Angle = $180^\circ$ - $165^\circ$
Exterior Angle = $15^\circ$
For a regular polygon with $n$ sides, the measure of each exterior angle is also given by the formula:
Exterior Angle = $\frac{360^\circ}{n}$
We can now set up an equation using the calculated exterior angle:
$15^\circ = \frac{360^\circ}{n}$
To find the number of sides $n$, we rearrange the equation:
$n = \frac{360^\circ}{15^\circ}$
Now, we calculate the value of $n$:
$n = 24$
Alternatively, we can use the formula for the interior angle of a regular polygon with $n$ sides, which is given by:
Interior Angle = $\frac{(n-2) \times 180^\circ}{n}$
We are given that the interior angle is $165^\circ$. So, we have:
$165^\circ = \frac{(n-2) \times 180^\circ}{n}$
Now, we solve this equation for $n$:
$165n = (n-2) \times 180$
$165n = 180n - 360$
Subtract $180n$ from both sides:
$165n - 180n = -360$
$-15n = -360$
Divide both sides by $-15$:
$n = \frac{-360}{-15}$
$n = 24$
Both methods give the same result.
Thus, the regular polygon has 24 sides.
Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Answer:
Solution:
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
For a regular polygon with $n$ sides, the measure of each exterior angle is given by the formula:
Exterior Angle = $\frac{360^\circ}{n}$
If the measure of each exterior angle is $22^\circ$, then we have:
$22^\circ = \frac{360^\circ}{n}$
Solving for $n$, we get:
$n = \frac{360}{22}$
$n = \frac{180}{11}$
For a polygon to exist, the number of sides $n$ must be a positive integer. Since $\frac{180}{11}$ is not an integer (it's approximately 16.36), it is not possible to have a regular polygon with an exterior angle of $22^\circ$.
Answer for (a): No, it is not possible.
(b) Can it be an interior angle of a regular polygon? Why?
If $22^\circ$ were the measure of each interior angle of a regular polygon, then the measure of each exterior angle would be:
Exterior Angle = $180^\circ$ - Interior Angle
Exterior Angle = $180^\circ$ - $22^\circ$
Exterior Angle = $158^\circ$
Now, using the formula relating the exterior angle and the number of sides $n$:
Exterior Angle = $\frac{360^\circ}{n}$
We would have:
$158^\circ = \frac{360^\circ}{n}$
Solving for $n$, we get:
$n = \frac{360}{158}$
$n = \frac{180}{79}$
Since $\frac{180}{79}$ is not an integer, it is not possible to have a regular polygon with an interior angle of $22^\circ$.
Reason:
The smallest possible interior angle for a regular polygon occurs for the regular triangle (equilateral triangle) where $n=3$. The interior angle is $\frac{(3-2) \times 180^\circ}{3} = \frac{1 \times 180^\circ}{3} = 60^\circ$.
As the number of sides ($n$) of a regular polygon increases, the interior angle increases and approaches $180^\circ$.
Since $22^\circ$ is less than the smallest possible interior angle ($60^\circ$) of any regular polygon, it cannot be an interior angle of a regular polygon.
Answer for (b): No, it cannot be an interior angle of a regular polygon. The minimum interior angle for a regular polygon is $60^\circ$ (for an equilateral triangle), and $22^\circ$ is less than $60^\circ$.
Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Answer:
Solution:
(a) What is the minimum interior angle possible for a regular polygon? Why?
The interior angle of a regular polygon with $n$ sides is given by the formula:
Interior Angle = $\frac{(n-2) \times 180^\circ}{n}$
For a polygon to exist, the number of sides $n$ must be an integer greater than or equal to 3. The smallest possible number of sides for a polygon is $n=3$ (a triangle).
Let's find the interior angle for $n=3$:
Interior Angle (for $n=3$) = $\frac{(3-2) \times 180^\circ}{3}$
Interior Angle = $\frac{1 \times 180^\circ}{3}$
Interior Angle = $60^\circ$
Why: As the number of sides $n$ increases, the value of $\frac{n-2}{n} = 1 - \frac{2}{n}$ increases (since $\frac{2}{n}$ decreases). Therefore, the interior angle, which is proportional to $1 - \frac{2}{n}$, also increases. The minimum interior angle occurs at the minimum possible value of $n$, which is 3.
The minimum interior angle possible for a regular polygon is $60^\circ$.
(b) What is the maximum exterior angle possible for a regular polygon?
The exterior angle of a regular polygon is related to its interior angle by the formula:
Exterior Angle = $180^\circ$ - Interior Angle
To maximize the exterior angle, we need to minimize the interior angle. From part (a), we found that the minimum interior angle is $60^\circ$, which occurs for a regular polygon with $n=3$ sides (an equilateral triangle).
Using the formula for the exterior angle for $n=3$:
Exterior Angle (for $n=3$) = $\frac{360^\circ}{n}$
Exterior Angle = $\frac{360^\circ}{3}$
Exterior Angle = $120^\circ$
Alternatively, using the relationship with the minimum interior angle:
Maximum Exterior Angle = $180^\circ$ - Minimum Interior Angle
Maximum Exterior Angle = $180^\circ$ - $60^\circ$
Maximum Exterior Angle = $120^\circ$
The maximum exterior angle possible for a regular polygon is $120^\circ$.
Example 3 to 6 (Before Exercise 3.3)
Example 3: Find the perimeter of the parallelogram PQRS (Fig 3.16).
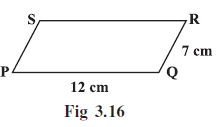
Answer:
Given:
Parallelogram PQRS.
From the figure (Fig 3.16) and the context of the problem, the adjacent side lengths are SR = $12$ cm and PS = $7$ cm.
To Find:
The perimeter of parallelogram PQRS.
Solution:
In a parallelogram, the opposite sides have the same length.
Therefore, in parallelogram PQRS:
PQ = SR = $12$ cm
(Opposite sides of a parallelogram)
QR = PS = $7$ cm
(Opposite sides of a parallelogram)
The perimeter of a parallelogram is the sum of the lengths of its four sides.
Perimeter of parallelogram PQRS = PQ + QR + RS + SP
Substitute the side lengths:
Perimeter = $12$ cm + $7$ cm + $12$ cm + $7$ cm
We can group the equal sides:
Perimeter = $(12 + 12)$ cm + $(7 + 7)$ cm
Perimeter = $24$ cm + $14$ cm
Add the values:
Perimeter = $38$ cm
Alternatively, the perimeter of a parallelogram is also given by $2 \times (\text{sum of adjacent sides})$.
Perimeter = $2 \times (SR + PS)$
Perimeter = $2 \times (12 + 7)$ cm
Perimeter = $2 \times (19)$ cm
Perimeter = $38$ cm
The perimeter of the parallelogram PQRS is $38$ cm.
Example 4: In Fig 3.20, BEST is a parallelogram. Find the values x, y and z.
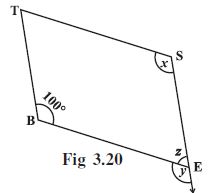
Answer:
Solution:
Given:
BEST is a parallelogram.
$\angle$B = $100^\circ$
$\angle$E = $z$
Exterior Angle adjacent to $\angle$E = $y$
$\angle$S = $x$
To Find:
The values of $x$, $y$, and $z$.
Solution:
In a parallelogram, opposite angles are equal.
S is opposite to B.
$x = 100^\circ$
(Opposite angles property)
Exterior Angle adjacent to $\angle$B = $y$
Since BT || SE, using the property of alternate interior angles:
$y = 100^\circ$
(Alternate interior angles formed by parallel lines BT and SE)
Using the concept of linear pair between $\angle y$ and $\angle z$:
$z + y = 180^\circ$
(Linear pair)
Substitute the value of $y$ found in the previous step:
$z + 100^\circ = 180^\circ$
Subtract $100^\circ$ from both sides:
$z = 180^\circ - 100^\circ$
$z = 80^\circ$
Hence, $x = 100^\circ$, $y = 100^\circ$, and $z = 80^\circ$.
Example 5: In a parallelogram RING, (Fig 3.22) if m∠R = 70°, find all the other angles.
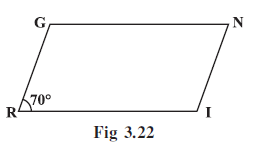
Answer:
Given:
Parallelogram RING.
$m\angle R = 70^\circ$.
To Find:
$m\angle I$, $m\angle N$, and $m\angle G$.
Solution:
In a parallelogram, opposite angles are equal.
Therefore, $\angle$R and $\angle$N are opposite angles.
$\angle$N = $\angle$R
(Opposite angles of a parallelogram)
$\angle$N = $70^\circ$
Adjacent angles in a parallelogram are supplementary (their sum is $180^\circ$).
Consider adjacent angles $\angle$R and $\angle$I:
$\angle$R + $\angle$I = $180^\circ$
(Adjacent angles of a parallelogram)
Substitute the given value of $\angle$R:
$70^\circ + \angle$I = $180^\circ$
Subtract $70^\circ$ from both sides:
$\angle$I = $180^\circ - 70^\circ$
$\angle$I = $110^\circ$
Now, consider opposite angles $\angle$G and $\angle$I:
$\angle$G = $\angle$I
(Opposite angles of a parallelogram)
Substitute the value of $\angle$I we found:
$\angle$G = $110^\circ$
Thus, the other angles are:
$m\angle I = 110^\circ$
$m\angle N = 70^\circ$
$m\angle G = 110^\circ$
The other angles of parallelogram RING are $m\angle I = 110^\circ$, $m\angle N = 70^\circ$, and $m\angle G = 110^\circ$.
Example 6: In Fig 3.25 HELP is a parallelogram. (Lengths are in cms). Given that OE = 4 and HL is 5 more than PE? Find OH.
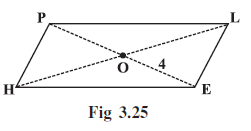
Answer:
Given:
HELP is a parallelogram.
O is the point of intersection of the diagonals HE and PL.
OE = 4 cm.
Length of diagonal HL is 5 more than the length of diagonal PE.
To Find:
The length of OH.
Solution:
In a parallelogram, the diagonals bisect each other. This means the point of intersection O divides each diagonal into two equal parts.
Given OE = $4$. According to the property of diagonals bisecting each other, O is the midpoint of the diagonal PE. Thus, OP = OE.
If OE = $4$, then OP = $4$
(Diagonals of a parallelogram bisect each other)
The length of the diagonal PE is the sum of OP and OE:
So PE = OP + OE
PE = $4 + 4 = 8$
The length of the diagonal PE is $8$ cm.
We are given that HL is 5 more than PE.
Therefore HL = PE + 5
(Given)
Substitute the value of PE:
HL = $8 + 5 = 13$
The length of the diagonal HL is $13$ cm.
The question asks for the length of OH. OH is half of the diagonal HL.
Hence OH = $\frac{1}{2} \times \text{HL}$
OH = $\frac{1}{2} \times 13$
OH = $\frac{13}{2} = 6.5$ cm
The value of OH is $6.5$ cm.
Exercise 3.3
Question 1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = ......
(ii) ∠DCB = ......
(iii) OC =
(iv) m∠DAB + m∠CDA = ...…
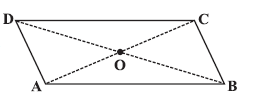
Answer:
(i) AD = BC
Property: Opposite sides of a parallelogram are of equal length.
(ii) $\angle$DCB = $\angle$DAB
Property: Opposite angles of a parallelogram are of equal measure.
(iii) OC = OA
Property: Diagonals of a parallelogram bisect each other.
(iv) m$\angle$DAB + m$\angle$CDA = $180^\circ$
Property: Adjacent angles in a parallelogram are supplementary.
Question 2. Consider the following parallelograms. Find the values of the unknowns x, y, z.
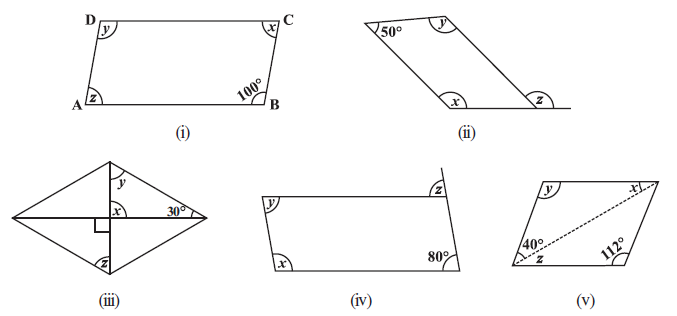
Answer:
Given:
Various parallelograms with unknown angles $x$, $y$, and $z$.
To Find:
The values of $x$, $y$, and $z$ for each parallelogram.
Solution:
We will use the properties of parallelograms: opposite angles are equal, adjacent angles are supplementary, and diagonals bisect each other. We will also use properties of angles formed by parallel lines and angle sum property of a triangle.
Figure (i):
From the figure, the angle marked $y$ is opposite to the angle with measure $100^\circ$.
$y = 100^\circ$
(Opposite angles of a parallelogram)
The angle marked $x$ and the angle with measure $100^\circ$ are adjacent angles.
$x + 100^\circ = 180^\circ$
(Adjacent angles of a parallelogram)
Subtract $100^\circ$ from both sides:
$x = 180^\circ - 100^\circ$
$x = 80^\circ$
The angle marked $z$ is opposite to the angle marked $x$.
$x = z$
(Opposite angles of a parallelogram)
Since $x = 80^\circ$, we have:
$z = 80^\circ$
Thus, for Figure (i), $x = 80^\circ$, $y = 100^\circ$, and $z = 80^\circ$.
Figure (ii):
The angle with measure $50^\circ$ and the angle marked $x$ are adjacent angles.
$50^\circ + x = 180^\circ$
(Adjacent angles of a parallelogram)
Subtract $50^\circ$ from both sides:
$x = 180^\circ - 50^\circ$
$x = 130^\circ$
The angle marked $y$ is opposite to the angle marked $x$.
$x = y$
(Opposite angles of a parallelogram)
Since $x = 130^\circ$, we have:
$y = 130^\circ$
The angle marked $z$ is a corresponding angle to the angle marked $x$ (considering the parallel sides and the transversal).
$x = z$
(Corresponding angle)
Since $x = 130^\circ$, we have:
$z = 130^\circ$
Thus, for Figure (ii), $x = 130^\circ$, $y = 130^\circ$, and $z = 130^\circ$.
Figure (iii):
The angle marked $x$ and the angle marked $90^\circ$ are vertically opposite angles.
$x = 90^\circ$
(Vertically opposite angles)
Consider the triangle formed by the intersection of the diagonals. The angles of this triangle are $x$, $y$, and $30^\circ$.
The sum of angles in a triangle is $180^\circ$.
$x + y + 30^\circ = 180^\circ$
(Angle sum property of a triangle)
Substitute the value of $x = 90^\circ$:
$90^\circ + y + 30^\circ = 180^\circ$
$120^\circ + y = 180^\circ$
Subtract $120^\circ$ from both sides:
$y = 180^\circ - 120^\circ$
$y = 60^\circ$
The angle marked $y$ and the angle marked $z$ are alternate interior angles formed by the transversal and the parallel sides of the parallelogram.
$y = z$
(Alternate interior angles)
Since $y = 60^\circ$, we have:
$z = 60^\circ$
Thus, for Figure (iii), $x = 90^\circ$, $y = 60^\circ$, and $z = 60^\circ$.
Figure (iv):
The angle marked $z$ is a corresponding angle to the angle with measure $80^\circ$ (considering the parallel sides and the transversal).
$z = 80^\circ$
(Corresponding angle)
The angle marked $y$ and the angle marked $z$ are alternate interior angles formed by the transversal and the parallel sides.
$y = z$
(Alternate interior angles)
Since $z = 80^\circ$, we have:
$y = 80^\circ$
The angle marked $x$ and the angle marked $y$ are adjacent angles.
$x + y = 180^\circ$
(Adjacent angles)
Substitute the value of $y = 80^\circ$:
$x + 80^\circ = 180^\circ$
Subtract $80^\circ$ from both sides:
$x = 180^\circ - 80^\circ$
$x = 100^\circ$
Thus, for Figure (iv), $x = 100^\circ$, $y = 80^\circ$, and $z = 80^\circ$.
Figure (v):
In a parallelogram, opposite angles are equal.
The angle marked $y$ is opposite to the angle with measure $112^\circ$.
$y = 112^\circ$
(Opposite angles of a parallelogram)
Consider the triangle formed by one diagonal and two sides. The angles of this triangle are $x$, $40^\circ$, and the angle with measure $112^\circ$.
The sum of angles in a triangle is $180^\circ$.
$x + 40^\circ + 112^\circ = 180^\circ$
(Angle sum property of a triangle)
Combine the known angles:
$x + 152^\circ = 180^\circ$
Subtract $152^\circ$ from both sides:
$x = 180^\circ - 152^\circ$
$x = 28^\circ$
The angle marked $x$ and the angle marked $z$ form a pair of alternate interior angles (considering one of the parallel sides and the diagonal as a transversal).
$z = x$
(Alternate interior angles)
Since $x = 28^\circ$, we have:
$z = 28^\circ$
Thus, for Figure (v), $x = 28^\circ$, $y = 112^\circ$, and $z = 28^\circ$.
Question 3. Can a quadrilateral ABCD be a parallelogram if
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) ∠A = 70° and ∠C = 65°?
Answer:
Let's analyse each condition for a quadrilateral ABCD to be a parallelogram.
(i) $\angle$D + $\angle$B = $180^\circ$
In a parallelogram, opposite angles are equal. So, $\angle$B = $\angle$D.
If $\angle$D + $\angle$B = $180^\circ$ and $\angle$B = $\angle$D, then $2\angle$B = $180^\circ$, which implies $\angle$B = $90^\circ$. Similarly, $\angle$D = $90^\circ$.
If it were a parallelogram, the adjacent angles would be supplementary. So, $\angle$A + $\angle$B = $180^\circ$ and $\angle$B + $\angle$C = $180^\circ$. If $\angle$B = $90^\circ$, then $\angle$A = $180^\circ - 90^\circ = 90^\circ$ and $\angle$C = $180^\circ - 90^\circ = 90^\circ$.
In this case, all angles are $90^\circ$. A quadrilateral with all angles equal to $90^\circ$ is a rectangle, and a rectangle is a parallelogram.
Therefore, a quadrilateral ABCD can be a parallelogram if $\angle$D + $\angle$B = $180^\circ$ (for example, if it is a rectangle).
However, it is important to note that having one pair of opposite angles summing to $180^\circ$ does not guarantee that the quadrilateral is a parallelogram. For instance, in a cyclic quadrilateral, opposite angles sum to $180^\circ$, but a cyclic quadrilateral is not always a parallelogram.
So, the answer is Yes, it can be a parallelogram, but it is not always the case for any quadrilateral satisfying this condition.
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm
In a parallelogram, opposite sides must be equal in length.
We are given that one pair of opposite sides AB and DC are equal in length ($8$ cm).
We are given that the other pair of opposite sides AD and BC have lengths $4$ cm and $4.4$ cm respectively.
For ABCD to be a parallelogram, AD must be equal to BC.
Here, $AD = 4$ cm and $BC = 4.4$ cm.
Since $AD \neq BC$, the second pair of opposite sides are not equal.
Therefore, a quadrilateral with these side lengths cannot be a parallelogram.
The answer is No.
(iii) $\angle$A = $70^\circ$ and $\angle$C = $65^\circ$
In a parallelogram, opposite angles must be equal.
Assuming $\angle$A and $\angle$C are opposite angles in the quadrilateral ABCD, for it to be a parallelogram, $\angle$A must be equal to $\angle$C.
We are given $\angle$A = $70^\circ$ and $\angle$C = $65^\circ$.
Since $\angle$A $\neq$ $\angle$C ($70^\circ \neq 65^\circ$), the opposite angles are not equal.
Therefore, a quadrilateral with these angle measures cannot be a parallelogram.
The answer is No.
Question 4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Answer:
Solution:
We need to draw a quadrilateral that is not a parallelogram, but has exactly two opposite angles of equal measure.
A Kite is a quadrilateral that satisfies this property.
Properties of a Kite:
- Two pairs of adjacent sides are equal in length.
- One pair of opposite angles is equal.
- The diagonals are perpendicular to each other.
- One diagonal bisects the other diagonal.
- One diagonal bisects the pair of opposite angles that are equal.
Consider a kite ABCD where AB = AD and CB = CD. The angles between the unequal sides are equal.
In Kite ABCD, $\angle$ABC and $\angle$ADC are the angles formed between unequal pairs of adjacent sides (AB and BC, AD and DC, assuming AB $\neq$ BC). These opposite angles are equal.
$\angle$ABC = $\angle$ADC
(Property of a kite)
The other pair of opposite angles, $\angle$BAD and $\angle$BCD, are generally not equal in a kite unless it is a rhombus (which is a parallelogram). Since we need a quadrilateral that is NOT a parallelogram, we consider a kite where adjacent sides are not all equal (i.e., AB $\neq$ BC).
In such a kite, exactly one pair of opposite angles is equal ($\angle$ABC = $\angle$ADC), and the other pair is unequal ($\angle$BAD $\neq$ $\angle$BCD).
This fits the conditions: it is a quadrilateral, it is not a parallelogram (because not both pairs of opposite angles are equal), and it has exactly two opposite angles of equal measure.
Rough Figure:
(Imagine a figure of a kite with vertices labelled A, B, C, D in clockwise order. Sides AB and AD are equal, sides BC and CD are equal. The angles at B and D are equal, and the diagonal AC bisects the angle at A and the angle at C, and is perpendicular to the diagonal BD).
Thus, a kite is an example of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Question 5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Answer:
Let the measures of the two adjacent angles of the parallelogram be $3x$ and $2x$, according to the given ratio.
We know that adjacent angles in a parallelogram are supplementary. This means their sum is $180^\circ$.
So, we can write the equation:
$3x + 2x = 180^\circ$
$5x = 180^\circ$
Now, we solve for $x$:
$x = \frac{180^\circ}{5}$
$x = 36^\circ$
Now, we can find the measure of each of the adjacent angles:
First adjacent angle = $3x = 3 \times 36^\circ = 108^\circ$
Second adjacent angle = $2x = 2 \times 36^\circ = 72^\circ$
In a parallelogram, opposite angles are equal.
Therefore, the other two angles of the parallelogram will have measures equal to these adjacent angles.
The four angles of the parallelogram are $108^\circ$, $72^\circ$, $108^\circ$, and $72^\circ$.
Let's verify the sum of adjacent angles: $108^\circ + 72^\circ = 180^\circ$. This is correct.
Let's verify the sum of all angles: $108^\circ + 72^\circ + 108^\circ + 72^\circ = 360^\circ$. This is correct for a quadrilateral.
The measures of the angles of the parallelogram are $108^\circ$, $72^\circ$, $108^\circ$, and $72^\circ$.
Question 6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Answer:
Let the measure of each of the two equal adjacent angles of the parallelogram be $a$.
We know that adjacent angles in a parallelogram are supplementary.
Therefore, the sum of the measures of these two adjacent angles is $180^\circ$.
So, we can write the equation:
$a + a = 180^\circ$
$2a = 180^\circ$
Now, we solve for $a$:
$a = \frac{180^\circ}{2}$
$a = 90^\circ$
So, the measure of each of the two adjacent angles is $90^\circ$.
In a parallelogram, opposite angles are equal.
Since one angle is $90^\circ$, its opposite angle is also $90^\circ$.
Since the adjacent angle is also $90^\circ$, its opposite angle is also $90^\circ$.
Thus, all four angles of the parallelogram measure $90^\circ$.
The measure of each of the angles of the parallelogram is $90^\circ$.
Note that a parallelogram with all angles equal to $90^\circ$ is a rectangle.
Question 7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
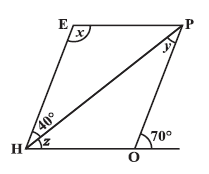
Answer:
Given:
HOPE is a parallelogram.
Angles are marked as $\angle PEH = x$, $\angle HPO = y$, $\angle OHP = z$, and $\angle PHE = 40^\circ$.
Exterior angle at vertex O is $70^\circ$.
To Find:
The values of angle measures $x$, $y$, and $z$.
Solution:
We will use the properties of parallelograms and angles formed by parallel lines and transversals.
The exterior angle at vertex O is $70^\circ$. The interior angle $\angle$HOP at vertex O and this exterior angle form a linear pair. Linear pairs are supplementary.
$\angle\text{HOP} + 70^\circ = 180^\circ$
(Linear Pair)
Subtract $70^\circ$ from both sides:
$\angle\text{HOP} = 180^\circ - 70^\circ$
$\angle\text{HOP} = 110^\circ$
In a parallelogram, opposite angles are equal.
The angle marked $x$ is the interior angle at vertex E ($\angle$PEH). This angle is opposite to the interior angle at vertex O ($\angle$HOP).
$x = \angle\text{HOP}$
(Opposite angles of a parallelogram)
$x = 110^\circ$
In a parallelogram, opposite sides are parallel. So, HE is parallel to OP (HE || OP), and HO is parallel to PE (HO || PE).
Consider the parallel lines HE and OP, and the transversal HP.
The angle $\angle$HPO (marked as $y$) and the angle $\angle$PHE (marked as $40^\circ$) are alternate interior angles.
$y = 40^\circ$
(Alternate interior angles, HE || OP, transversal HP)
Now, consider the triangle POH formed by the intersection of the diagonals.
The angles of triangle POH are $\angle$HPO (marked as $y$), $\angle$OHP (marked as $z$), and $\angle$POH (which is the same as $\angle$HOP = $110^\circ$).
The sum of angles in a triangle is $180^\circ$ (Angle Sum Property of a Triangle).
$\angle\text{HPO} + \angle\text{OHP} + \angle\text{POH} = 180^\circ$
(Angle Sum Property of a Triangle)
Substitute the known values ($y = 40^\circ$, $\angle$POH = $110^\circ$) and $z$:
$40^\circ + z + 110^\circ = 180^\circ$
Combine the known angles:
$150^\circ + z = 180^\circ$
Subtract $150^\circ$ from both sides:
$z = 180^\circ - 150^\circ$
$z = 30^\circ$
Thus, the values of the angle measures are:
$x = 110^\circ$
$y = 40^\circ$
$z = 30^\circ$
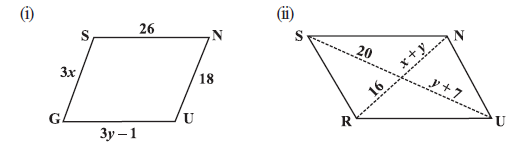
Question 8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
Answer:
We will find the values of $x$ and $y$ for each parallelogram using the properties of parallelograms.
Figure 1: Parallelogram GUNS
Given:
GUNS is a parallelogram with side lengths GU = $(3y - 1)$ cm, SN = $26$ cm, GS = $(3x)$ cm, and UN = $18$ cm.
To Find:
The values of $x$ and $y$.
Solution:
In a parallelogram, opposite sides are equal in length.
Applying this property to parallelogram GUNS:
GU = SN
(Opposite sides of a parallelogram)
Substitute the given expressions for the side lengths:
$3y - 1 = 26$
Add 1 to both sides of the equation:
$3y = 26 + 1$
$3y = 27$
Divide both sides by 3:
$y = \frac{27}{3}$
$y = 9$
Also,
GS = UN
(Opposite sides of a parallelogram)
Substitute the given expressions:
$3x = 18$
Divide both sides by 3:
$x = \frac{18}{3}$
$x = 6$
For parallelogram GUNS, $x = 6$ and $y = 9$.
Figure 2: Parallelogram RUNS
Given:
RUNS is a parallelogram with diagonals intersecting at O. Segments of diagonals are RO = $20$ cm, ON = $(y + 7)$ cm, SO = $16$ cm, and OU = $(x + y)$ cm.
To Find:
The values of $x$ and $y$.
Solution:
In a parallelogram, the diagonals bisect each other. This means the point of intersection O divides each diagonal into two equal parts.
Applying this property to the diagonal RN in parallelogram RUNS:
RO = ON
(Diagonals bisect each other)
Substitute the given expressions for the segments:
$20 = y + 7$
Subtract 7 from both sides:
$y = 20 - 7$
$y = 13$
Applying the property to the diagonal SU:
SO = OU
(Diagonals bisect each other)
Substitute the given expressions:
$16 = x + y$
Substitute the value of $y = 13$ into this equation:
$16 = x + 13$
Subtract 13 from both sides:
$x = 16 - 13$
$x = 3$
For parallelogram RUNS, $x = 3$ and $y = 13$.
Question 9.
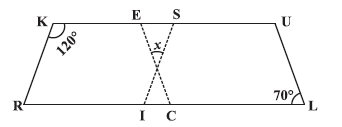
In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Answer:
Given:
RISK is a parallelogram.
CLUE is a parallelogram.
$\angle$K = $120^\circ$ in parallelogram RISK.
$\angle$L = $70^\circ$ in parallelogram CLUE.
x is the angle formed at the intersection of lines SI and CE.
To Find:
The value of x.
Solution:
Consider the parallelogram RISK.
In a parallelogram, adjacent angles are supplementary.
So, $\angle$S + $\angle$K = $180^\circ$.
Given $\angle$K = $120^\circ$.
$\angle$S = $180^\circ - \angle$K
(Adjacent angles of a parallelogram)
$\angle$S = $180^\circ - 120^\circ$
$\angle$S = $60^\circ$.
Consider the parallelogram CLUE.
In a parallelogram, opposite angles are equal.
So, $\angle$E = $\angle$L.
Given $\angle$L = $70^\circ$.
$\angle$E = $70^\circ$
(Opposite angles of a parallelogram)
Let the intersection point of lines SI and CE be O.
The triangle formed by the intersection of these lines is $\triangle$SOE.
The angles of $\triangle$SOE are $\angle$OSE, $\angle$SEO, and $\angle$SOE.
The angle $\angle$OSE is part of $\angle$S from parallelogram RISK.
$\angle$OSE = $\angle$S = $60^\circ$.
The angle $\angle$SEO is part of $\angle$E from parallelogram CLUE.
$\angle$SEO = $\angle$E = $70^\circ$.
The angle $\angle$SOE and the angle marked as x are vertically opposite angles.
$\angle$SOE = x
(Vertically opposite angles)
In $\triangle$SOE, the sum of interior angles is $180^\circ$.
$\angle$OSE + $\angle$SEO + $\angle$SOE = $180^\circ$
(Angle sum property of a triangle)
Substitute the values we found:
$60^\circ + 70^\circ + x = 180^\circ$
$130^\circ + x = 180^\circ$
Subtract $130^\circ$ from both sides:
$x = 180^\circ - 130^\circ$
$x = 50^\circ$
The value of x is $50^\circ$.
Question 10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.26)

Answer:
Given:
A quadrilateral KLMN with $\angle$L = $80^\circ$ and $\angle$M = $100^\circ$.
To Explain and Find:
How the figure KLMN is a trapezium, and which of its two sides are parallel.
Solution:
A trapezium is a quadrilateral that has at least one pair of parallel sides.
We need to check if any pair of opposite sides in quadrilateral KLMN are parallel.
Consider the sides KL and NM. The line segment LM is a transversal intersecting these two sides.
The angles $\angle$L and $\angle$M are interior angles on the same side of the transversal LM.
Let's find the sum of these two angles:
Sum of angles = $\angle$L + $\angle$M
Substitute the given values:
Sum of angles = $80^\circ$ + $100^\circ$
Sum of angles = $180^\circ$
We know that if a transversal intersects two lines such that the sum of the interior angles on the same side of the transversal is $180^\circ$, then the two lines are parallel.
In this case, the transversal LM intersects lines KL and NM, and the sum of consecutive interior angles $\angle$L and $\angle$M is $180^\circ$.
Therefore,
KL || NM
(Sum of consecutive interior angles is $180^\circ$)
Since the quadrilateral KLMN has a pair of parallel sides (KL and NM), it is a trapezium.
Conclusion:
The figure KLMN is a trapezium because the sum of consecutive interior angles $\angle$L and $\angle$M is $180^\circ$, which implies that the sides KL and NM are parallel.
The two parallel sides are KL and NM.
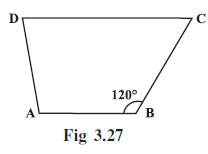
Question 11. Find m∠C in Fig 3.27 if $\overline{AB}$ || $\overline{DC}$ .
Answer:
Given:
A quadrilateral ABCD.
Side $\overline{AB}$ is parallel to side $\overline{DC}$ ($\overline{AB}$ || $\overline{DC}$).
$\text{m}\angle$B = $120^\circ$.
To Find:
The measure of angle C ($\text{m}\angle$C).
Solution:
The given figure is a quadrilateral where $\overline{AB}$ || $\overline{DC}$. This means the quadrilateral is a trapezium.
When two parallel lines are intersected by a transversal, the interior angles on the same side of the transversal are supplementary (their sum is $180^\circ$).
In the figure, AB and DC are parallel lines, and BC is a transversal line intersecting them.
The angles $\angle$B and $\angle$C are interior angles on the same side of the transversal BC.
Therefore, the sum of $\text{m}\angle$B and $\text{m}\angle$C must be $180^\circ$.
$\text{m}\angle\text{B} + \text{m}\angle\text{C} = 180^\circ$
(Interior angles on the same side of transversal are supplementary)
Substitute the given value of $\text{m}\angle$B = $120^\circ$:
$120^\circ + \text{m}\angle\text{C} = 180^\circ$
Subtract $120^\circ$ from both sides to find $\text{m}\angle$C:
$\text{m}\angle\text{C} = 180^\circ - 120^\circ$
$\text{m}\angle\text{C} = 60^\circ$
The measure of angle C is $60^\circ$.
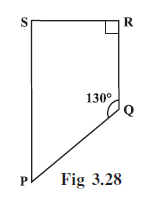
Question 12. Find the measure of ∠P and ∠S if $\overline{SP}$ || $\overline{RQ}$ in Fig 3.28.
(If you find m∠R, is there more than one method to find m∠P?)
Answer:
Given:
Quadrilateral PQRS.
Side $\overline{SP}$ is parallel to side $\overline{RQ}$ ($\overline{SP}$ || $\overline{RQ}$).
$\text{m}\angle$Q = $130^\circ$.
$\text{m}\angle$R = $90^\circ$. (Indicated by the square symbol)
To Find:
The measure of $\angle$P and $\angle$S.
Solution:
Since $\overline{SP}$ || $\overline{RQ}$, PQ and SR are transversals. The quadrilateral PQRS is a trapezium.
When two parallel lines are intersected by a transversal, the interior angles on the same side of the transversal are supplementary (their sum is $180^\circ$).
Consider the parallel lines SP and RQ, and the transversal PQ.
The angles $\angle$P and $\angle$Q are interior angles on the same side of the transversal PQ.
Therefore, the sum of $\text{m}\angle$P and $\text{m}\angle$Q must be $180^\circ$.
$\text{m}\angle\text{P} + \text{m}\angle\text{Q} = 180^\circ$
(Interior angles on the same side of transversal PQ)
Substitute the given value of $\text{m}\angle$Q = $130^\circ$:
$\text{m}\angle\text{P} + 130^\circ = 180^\circ$
Subtract $130^\circ$ from both sides:
$\text{m}\angle\text{P} = 180^\circ - 130^\circ$
$\text{m}\angle\text{P} = 50^\circ$
Consider the parallel lines SP and RQ, and the transversal SR.
The angles $\angle$S and $\angle$R are interior angles on the same side of the transversal SR.
Therefore, the sum of $\text{m}\angle$S and $\text{m}\angle$R must be $180^\circ$.
$\text{m}\angle\text{S} + \text{m}\angle\text{R} = 180^\circ$
(Interior angles on the same side of transversal SR)
Substitute the given value of $\text{m}\angle$R = $90^\circ$:
$\text{m}\angle\text{S} + 90^\circ = 180^\circ$
Subtract $90^\circ$ from both sides:
$\text{m}\angle\text{S} = 180^\circ - 90^\circ$
$\text{m}\angle\text{S} = 90^\circ$
Second Part of the Question:
If you find $\text{m}\angle$R, is there more than one method to find $\text{m}\angle$P?
Yes, there is more than one method to find $\text{m}\angle$P once we know the measures of $\angle$Q, $\angle$R, and $\angle$S.
Method 1 (already used): Using the property of interior angles on the same side of the transversal PQ being supplementary, since SP || RQ:
$\text{m}\angle\text{P} + \text{m}\angle\text{Q} = 180^\circ$
$\text{m}\angle\text{P} + 130^\circ = 180^\circ$
$\text{m}\angle\text{P} = 50^\circ$
Method 2: Using the angle sum property of a quadrilateral.
The sum of interior angles of a quadrilateral is $360^\circ$.
$\text{m}\angle\text{P} + \text{m}\angle\text{Q} + \text{m}\angle\text{R} + \text{m}\angle\text{S} = 360^\circ$
(Angle sum property of a quadrilateral)
Substitute the known values $\text{m}\angle$Q = $130^\circ$, $\text{m}\angle$R = $90^\circ$, and $\text{m}\angle$S = $90^\circ$:
$\text{m}\angle\text{P} + 130^\circ + 90^\circ + 90^\circ = 360^\circ$
$\text{m}\angle\text{P} + 310^\circ = 360^\circ$
Subtract $310^\circ$ from both sides:
$\text{m}\angle\text{P} = 360^\circ - 310^\circ$
$\text{m}\angle\text{P} = 50^\circ$
Both methods give the same result for $\text{m}\angle$P.
The measure of $\angle$P is $50^\circ$ and the measure of $\angle$S is $90^\circ$. Yes, there is more than one method to find $\text{m}\angle$P if $\text{m}\angle$R is known.
Example 7 & 8 (Before Exercise 3.4)
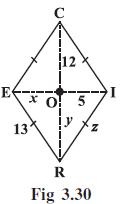
Example 7: RICE is a rhombus (Fig 3.30). Find x, y, z. Justify your findings.
Answer:
Given:
RICE is a rhombus.
The diagonals RC and IE intersect at O.
Lengths of segments are labelled as: RO = y, OC = 12, IO = 5, OE = x.
Side length RE = 13.
Side length RI = z.
To Find:
The values of $x$, $y$, and $z$.
Solution:
We will use the properties of a rhombus to find the unknown values.
Properties of a Rhombus:
- All sides are equal in length.
- Opposite angles are equal.
- Adjacent angles are supplementary.
- The diagonals bisect each other at right angles.
- The diagonals bisect the opposite angles.
In a rhombus, the diagonals bisect each other.
This means that the point of intersection O divides each diagonal into two equal parts.
Consider the diagonal IE. O is the midpoint of IE.
IO = OE
(Diagonals of a rhombus bisect each other)
From the figure, IO = 5 and OE = x.
$x = 5$
Consider the diagonal RC. O is the midpoint of RC.
RO = OC
(Diagonals of a rhombus bisect each other)
From the figure, RO = y and OC = 12.
$y = 12$
In a rhombus, all sides are equal in length.
From the figure, we are given that RE = 13.
Therefore, all sides of the rhombus RICE have a length of 13.
RI = IC = CE = ER
(All sides of a rhombus are equal)
From the figure, RI = z and RE = 13.
$z = 13$
Justification of findings:
- $x=5$ because the diagonals of a rhombus bisect each other, so OE = IO = 5.
- $y=12$ because the diagonals of a rhombus bisect each other, so RO = OC = 12.
- $z=13$ because all sides of a rhombus are equal in length, and one side RE is given as 13.
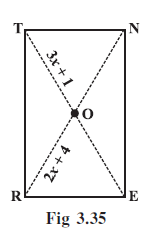
Example 8: RENT is a rectangle (Fig 3.35). Its diagonals meet at O. Find x, if OR = 2x + 4 and OT = 3x + 1.
Answer:
Given:
RENT is a rectangle.
Diagonals RN and TE intersect at O.
OR = 2x + 4.
OT = 3x + 1.
To Find:
The value of x.
Solution:
We know that in a rectangle, the diagonals are equal in length and bisect each other.
Since the diagonals bisect each other at O, O is the midpoint of both diagonals RN and TE. This means RO = ON and TO = OE.
Also, since the diagonals are equal in length (RN = TE), their halves are also equal.
Therefore, OR = ON = OT = OE.
From the given information, we have expressions for OR and OT. Since OR = OT, we can set up an equation:
OR = OT
(Diagonals of a rectangle are equal and bisect each other)
Substitute the given expressions:
$2x + 4 = 3x + 1$
Now, we solve this linear equation for $x$.
Subtract $2x$ from both sides of the equation:
$4 = 3x - 2x + 1$
$4 = x + 1$
Subtract 1 from both sides of the equation:
$4 - 1 = x$
$3 = x$
So, the value of $x$ is 3.
The value of $x$ is $3$.
Exercise 3.4
Question 1. State whether True or False.
(a) All rectangles are squares
(b) All rhombuses are parallelograms
(c) All squares are rhombuses and also rectangles
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Answer:
Solution:
Let's examine each statement:
(a) All rectangles are squares
False. A square is a special type of rectangle where all sides are equal. However, a rectangle only requires opposite sides to be equal and all angles to be $90^\circ$. A rectangle does not necessarily have all sides equal.
(b) All rhombuses are parallelograms
True. A rhombus is defined as a quadrilateral with all four sides of equal length. This property automatically implies that opposite sides are parallel (a property of a parallelogram). Therefore, every rhombus is also a parallelogram.
(c) All squares are rhombuses and also rectangles
True. A square has all sides equal, which is the defining property of a rhombus. A square also has all interior angles equal to $90^\circ$ (right angles), which is the defining property of a rectangle. Thus, a square is both a rhombus and a rectangle.
(d) All squares are not parallelograms.
False. A square has both pairs of opposite sides parallel and equal, which is the definition of a parallelogram. So, every square is indeed a parallelogram.
(e) All kites are rhombuses.
False. A rhombus is a special type of kite where all four sides are equal. A general kite only requires two distinct pairs of equal adjacent sides. A kite does not necessarily have all sides equal.
(f) All rhombuses are kites.
True. A rhombus has all four sides equal. This means it has two pairs of equal adjacent sides (since all sides are equal, any two adjacent sides form a pair of equal adjacent sides), which satisfies the definition of a kite.
(g) All parallelograms are trapeziums.
True. A parallelogram is a quadrilateral with two pairs of parallel sides. A trapezium is defined as a quadrilateral with at least one pair of parallel sides. Since a parallelogram has two pairs of parallel sides, it certainly has at least one pair of parallel sides. Therefore, every parallelogram is a trapezium.
(h) All squares are trapeziums.
True. From part (d), all squares are parallelograms. From part (g), all parallelograms are trapeziums. Therefore, all squares are also trapeziums.
Question 2. Identify all the quadrilaterals that have.
(a) four sides of equal length
(b) four right angles
Answer:
Solution:
Let's identify the quadrilaterals based on the given properties:
(a) quadrilaterals that have four sides of equal length
A quadrilateral with all four sides of equal length is called a Rhombus.
A square is a special type of rhombus where all angles are right angles. So, a Square also has four sides of equal length.
The quadrilaterals with four sides of equal length are: Rhombus and Square.
(b) quadrilaterals that have four right angles
A quadrilateral with all four interior angles equal to $90^\circ$ is called a Rectangle.
A square is a special type of rectangle where all sides are equal. So, a Square also has four right angles.
The quadrilaterals with four right angles are: Rectangle and Square.
Question 3. Explain how a square is.
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
Answer:
Solution:
Let's explain how a square fits the definition of each type of quadrilateral:
(i) a quadrilateral
A quadrilateral is any closed figure formed by four line segments (sides). A square has four sides and four vertices, making it a four-sided polygon.
Thus, a square is a quadrilateral because it is a closed figure with four sides.
(ii) a parallelogram
A parallelogram is a quadrilateral where both pairs of opposite sides are parallel. In a square, all adjacent sides are perpendicular (form $90^\circ$ angles), which means opposite sides are parallel to each other. For example, if side AB is perpendicular to BC and DC is perpendicular to BC, then AB is parallel to DC. Similarly, AD is parallel to BC.
Thus, a square is a parallelogram because its opposite sides are parallel.
(iii) a rhombus
A rhombus is a quadrilateral where all four sides are equal in length. By definition, a square has all four sides equal in length.
Thus, a square is a rhombus because all its sides are equal.
(iv) a rectangle
A rectangle is a quadrilateral where all four interior angles are right angles ($90^\circ$). By definition, a square has all four interior angles equal to $90^\circ$. A rectangle is also a parallelogram, and a square is a parallelogram with right angles.
Thus, a square is a rectangle because all its interior angles are $90^\circ$.
In conclusion, a square possesses the defining properties of a quadrilateral, a parallelogram, a rhombus, and a rectangle, making it a special case of each of these figures.
Question 4. Name the quadrilaterals whose diagonals.
(i) bisect each other
(ii) are perpendicular bisectors of each other
(iii) are equal
Answer:
Solution:
Let's name the quadrilaterals whose diagonals satisfy the given conditions:
(i) diagonals bisect each other
When the diagonals of a quadrilateral cut each other into two equal halves at their point of intersection, we say they bisect each other. This property holds true for all parallelograms.
The quadrilaterals whose diagonals bisect each other are:
Parallelogram
Rhombus (since it's a parallelogram)
Rectangle (since it's a parallelogram)
Square (since it's a parallelogram)
(ii) diagonals are perpendicular bisectors of each other
This means the diagonals not only bisect each other but also intersect at a right angle ($90^\circ$). This property is specific to rhombuses and squares.
The quadrilaterals whose diagonals are perpendicular bisectors of each other are:
Rhombus
Square (since it's a rhombus with right angles)
(iii) diagonals are equal
When the lengths of the two diagonals are the same, the quadrilaterals are rectangles and squares. In some special trapeziums (isosceles trapeziums), the diagonals are also equal.
The quadrilaterals whose diagonals are equal are:
Rectangle
Square (since it's a rectangle)
Isosceles Trapezium
Question 5. Explain why a rectangle is a convex quadrilateral
Answer:
Solution:
A convex quadrilateral is defined as a quadrilateral where all its interior angles are less than $180^\circ$.
In a rectangle, all four interior angles are right angles. The measure of a right angle is $90^\circ$.
Since $90^\circ < 180^\circ$, all interior angles of a rectangle are less than $180^\circ$.
Another way to understand a convex quadrilateral is that if you connect any two points inside the quadrilateral with a straight line segment, the entire segment lies inside the quadrilateral.
In a rectangle, no interior angle "points inwards". All vertices "point outwards". Any line segment joining two points within a rectangle will remain within its boundary.
Therefore, because all its interior angles are $90^\circ$ (which is less than $180^\circ$), a rectangle is a convex quadrilateral.
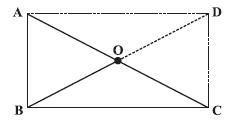
Question 6. ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
Answer:
Solution:
Given:
ABC is a right-angled triangle with the right angle at vertex B ($\angle$B = $90^\circ$).
O is the midpoint of the hypotenuse AC.
To Explain:
Why O is equidistant from vertices A, B, and C.
Solution:
To explain this, we can use the additional dotted lines shown in the figure. These lines are drawn to form a quadrilateral ABCD by extending BO to D such that BO = OD and joining AD and CD.
Since O is the midpoint of AC (given) and O is the midpoint of BD (by construction), the diagonals AC and BD of the quadrilateral ABCD bisect each other at O.
A quadrilateral whose diagonals bisect each other is a parallelogram.
Therefore, ABCD is a parallelogram.
We are given that $\angle$B = $90^\circ$.
A parallelogram with one interior angle equal to $90^\circ$ is a rectangle.
Therefore, ABCD is a rectangle.
In a rectangle, the diagonals are equal in length and they bisect each other.
The diagonals of rectangle ABCD are AC and BD.
AC = BD
(Diagonals of a rectangle are equal)
Since the diagonals bisect each other at O, O is the midpoint of both diagonals.
AO = OC = $\frac{1}{2}$ AC
(O is the midpoint of AC)
BO = OD = $\frac{1}{2}$ BD
(O is the midpoint of BD)
Since AC = BD, it follows that their halves are also equal:
$\frac{1}{2}$ AC = $\frac{1}{2}$ BD
Substituting the segments, we get:
AO = OC = BO = OD
(From the above equalities)
This shows that the distance from O to A, O to B, and O to C are all equal (AO = BO = OC).
Therefore, O is equidistant from A, B, and C.
This is a general property that the midpoint of the hypotenuse of a right-angled triangle is always equidistant from all three vertices of the triangle.

