| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 9.1) | Exercise 9.1 | Example 4 to 7 (Before Exercise 9.2) |
| Exercise 9.2 | Example 8 to 11 (Before Exercise 9.3) | Exercise 9.3 |
Chapter 9 Mesuration
Welcome to the solutions guide for Chapter 9, "Mensuration," from the latest Class 8 NCERT mathematics textbook prepared for the academic session 2024-25. This chapter significantly broadens the scope of geometric measurement, extending concepts of area learned earlier to more complex two-dimensional shapes and introducing the crucial concepts of surface area and volume for three-dimensional solids. Mastering mensuration is vital for practical applications in fields ranging from engineering and architecture to everyday tasks involving space and quantity. These solutions provide comprehensive, step-by-step methods for all exercises, aiming to solidify understanding of formulas and their application in diverse scenarios.
While building upon knowledge of basic shapes like rectangles, squares, parallelograms, and triangles, this chapter introduces methods for calculating the area of specific 2D figures. Key focus areas include:
- Area of a Trapezium: The solutions clearly explain and apply the formula for the area of a trapezium (a quadrilateral with one pair of parallel sides), which is given by $\text{Area} = \frac{1}{2} \times (\text{sum of parallel sides}) \times (\text{height})$. The height here refers to the perpendicular distance between the parallel sides.
- Area of a General Quadrilateral: Methods for finding the area of any quadrilateral by dividing it into two triangles using a diagonal are demonstrated.
- Area of Polygons: Extending the idea of division, the solutions show how to calculate the area of irregular polygons by strategically partitioning them into triangles, trapeziums, or other shapes whose areas can be calculated individually and then summed up.
The major shift in this chapter is the transition to three-dimensional shapes, focusing primarily on the Cube, Cuboid, and Cylinder. For these solids, two distinct types of measurement are crucial: Surface Area and Volume. The solutions meticulously explain:
- Surface Area: This represents the total area of the surfaces of the solid. The solutions differentiate between:
- Lateral Surface Area (LSA) for cubes and cuboids (area of the four side faces) or Curved Surface Area (CSA) for cylinders (area of the curved surface).
- Total Surface Area (TSA) (sum of the areas of all faces/surfaces, including the top and bottom bases).
- Cuboid: LSA = $2h(l+b)$; TSA = $2(lb + bh + hl)$
- Cube: LSA = $4l^2$; TSA = $6l^2$ (where $l$ is the side length)
- Cylinder: CSA = $2\pi rh$; TSA = $2\pi r(h + r)$ (where $r$ is the radius and $h$ is the height). Values like $\pi \approx \frac{22}{7}$ or $3.14$ will be used as specified.
- Volume: This measures the amount of space occupied by the solid. The solutions demonstrate calculations using the standard formulas:
- Cuboid: Volume $V = l \times b \times h$
- Cube: Volume $V = l^3$
- Cylinder: Volume $V = \pi r^2 h$
A significant emphasis is placed on practical applications and word problems. The solutions expertly guide students through scenarios that require applying these formulas correctly. Common examples include:
- Calculating the cost of painting walls of a room (requiring LSA), potentially at a certain rate per $m^2$, perhaps using $\textsf{₹}$.
- Finding the amount of material (like sheet metal) needed to construct a box or tank (requiring TSA).
- Determining the capacity of containers like tanks or cans (requiring Volume).
Regarding the rationalized syllabus for 2024-25, Chapter 9, "Mensuration," in the Class 8 NCERT textbook retains its strong focus on the area of trapeziums and general polygons, and the surface area (Lateral/Curved and Total) and Volume of Cubes, Cuboids, and Cylinders. The rationalization process primarily involved streamlining the complexity and number of exercises, potentially removing problems involving very complex composite shapes or multi-layered conversions, ensuring a solid grasp of the core formulas and their direct applications. By diligently using these detailed solutions, students can master the essential formulas for these key 2D and 3D shapes, clearly differentiate between surface area and volume, and confidently tackle practical measurement-related problems.
Example 1 to 3 (Before Exercise 9.1)
Example 1: The area of a trapezium shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.
Answer:
Given:
Area of the trapezium shaped field $= 480 \text{ m}^2$.
The distance between the two parallel sides (height, $h$) $= 15 \text{ m}$.
Length of one of the parallel sides (let's call it $a$) $= 20 \text{ m}$.
To Find:
The length of the other parallel side (let's call it $b$).
Solution:
The formula for the area of a trapezium is given by:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times (\text{distance between them})$
Let the two parallel sides be $a$ and $b$, and the height (distance between parallel sides) be $h$.
Area $= \frac{1}{2} (a+b)h$
... (i)
We are given:
Area $= 480 \text{ m}^2$
$h = 15 \text{ m}$
$a = 20 \text{ m}$
We need to find $b$.
Substitute the given values into the formula (i):
$480 = \frac{1}{2} (20 + b) \times 15$
To solve for $b$, first multiply both sides by 2:
$480 \times 2 = (20 + b) \times 15$
$960 = (20 + b) \times 15$
Now, divide both sides by 15:
$\frac{960}{15} = 20 + b$
Performing the division: $960 \div 15 = 64$.
$64 = 20 + b$
To find $b$, subtract 20 from both sides:
$64 - 20 = b$
$b = 44$
Therefore, the length of the other parallel side is $44 \text{ m}$.
Answer: The other parallel side is 44 m.
Example 2: The area of a rhombus is 240 cm2 and one of the diagonals is 16 cm. Find the other diagonal.
Answer:
Given:
Area of the rhombus $= 240 \text{ cm}^2$.
Length of one of the diagonals (let's call it $d_1$) $= 16 \text{ cm}$.
To Find:
The length of the other diagonal (let's call it $d_2$).
Solution:
The formula for the area of a rhombus is given by:
Area $= \frac{1}{2} \times d_1 \times d_2$
... (i)
where $d_1$ and $d_2$ are the lengths of the two diagonals.
We are given:
Area $= 240 \text{ cm}^2$
$d_1 = 16 \text{ cm}$
We need to find $d_2$.
Substitute the given values into the formula (i):
$240 = \frac{1}{2} \times 16 \times d_2$
Simplify the right side:
$\frac{1}{2} \times 16 = 8$
So, the equation becomes:
$240 = 8 \times d_2$
To solve for $d_2$, divide both sides by 8:
$d_2 = \frac{240}{8}$
Performing the division: $240 \div 8 = 30$.
$d_2 = 30$
Therefore, the length of the other diagonal is $30 \text{ cm}$.
Answer: The other diagonal is 30 cm.
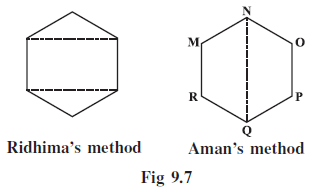
Example 3: There is a hexagon MNOPQR of side 5 cm (Fig 9.6). Aman and Ridhima divided it in two different ways (Fig 9.7).
Find the area of this hexagon using both ways.
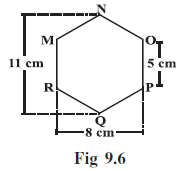
Answer:
We need to find the area of the hexagon MNOPQR using the two different methods of division shown in the figures.
Aman's Method:
In Aman's method, the hexagon is divided into two congruent trapeziums by the diagonal NQ. Figure 9.7 (Aman's way) shows the dimensions that seem to correspond to this division: parallel sides 11 cm and 5 cm, and height 4 cm.
The formula for the area of a trapezium is:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area of one trapezium (e.g., MNQR, assuming NQ connects M to R and Q to N, forming trapeziums MNQR and NOPQ, or similar):
Area $= \frac{1}{2} \times (11 \text{ cm} + 5 \text{ cm}) \times 4 \text{ cm}$
$= \frac{1}{2} \times (16 \text{ cm}) \times 4 \text{ cm}$
$= 8 \text{ cm} \times 4 \text{ cm}$
$= 32 \text{ cm}^2$
Since the hexagon is divided into two congruent trapeziums, the total area of the hexagon is twice the area of one trapezium.
Area of Hexagon (Aman's way) $= 2 \times \text{Area of one trapezium}$
$= 2 \times 32 \text{ cm}^2$
$= 64 \text{ cm}^2$
Using Aman's method, the area of the hexagon is 64 cm$^2$.
Ridhima's Method:
In Ridhima's method, the hexagon is divided into two congruent triangles and one rectangle by joining points M to O and R to P. Figure 9.7 (Ridhima's way, based on the provided correct solution text) shows the corresponding division and dimensions: triangles MNO and RPQ, and rectangle MOPR.
The triangles MNO and RPQ are congruent. The base of $\triangle$MNO is MO (which appears to be the diagonal M to O, length not directly given in the original figures, but used as 8 cm in the provided calculation) and the altitude from N to MO is 3 cm (given in the figure). The base of $\triangle$RPQ is RP (diagonal R to P, also used as 8 cm) and the altitude from Q to RP is 3 cm.
The formula for the area of a triangle is:
Area $= \frac{1}{2} \times \text{base} \times \text{height}$
Area of $\triangle$MNO = $\frac{1}{2} \times 8 \text{ cm} \times 3 \text{ cm}$
$= \frac{1}{2} \times 24 \text{ cm}^2$
$= 12 \text{ cm}^2$
Since $\triangle$RPQ is congruent to $\triangle$MNO, its area is also 12 cm$^2$.
Area of $\triangle$RPQ $= 12 \text{ cm}^2$
The rectangle MOPR has sides of length 8 cm (MO) and 5 cm (MN or OP or QR or RM - assuming it's 5 based on side of hexagon and diagram). The area of a rectangle is length times width.
Area of rectangle MOPR $= 8 \text{ cm} \times 5 \text{ cm}$
$= 40 \text{ cm}^2$
The total area of the hexagon is the sum of the areas of the two triangles and the rectangle.
Area of Hexagon (Ridhima's way) $=$ Area($\triangle$MNO) $+$ Area(Rectangle MOPR) $+$ Area($\triangle$RPQ)
$= 12 \text{ cm}^2 + 40 \text{ cm}^2 + 12 \text{ cm}^2$
$= (12 + 40 + 12) \text{ cm}^2$
$= 64 \text{ cm}^2$
Using Ridhima's method, the area of the hexagon is 64 cm$^2$.
Both methods yield the same area, 64 cm$^2$. This confirms that the area of the hexagon is indeed 64 cm$^2$, despite the different ways of dividing it.
Answer:
Area of Hexagon using Aman's way = 64 cm$^2$
Area of Hexagon using Ridhima's way = 64 cm$^2$
Exercise 9.1
Question 1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
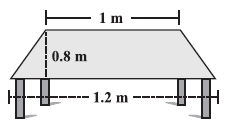
Answer:
Given:
The shape of the top surface of a table is a trapezium.
Length of one parallel side, $a = 1 \text{ m}$.
Length of the other parallel side, $b = 1.2 \text{ m}$.
Perpendicular distance between the parallel sides (height), $h = 0.8 \text{ m}$.
To Find:
The area of the trapezium-shaped top surface of the table.
Solution:
We know that the area of a trapezium is given by the formula:
Area of trapezium $= \frac{1}{2} \times (\text{sum of parallel sides}) \times (\text{perpendicular distance between them})$
Let the parallel sides be $a$ and $b$, and the perpendicular distance (height) be $h$.
Area $= \frac{1}{2} \times (a + b) \times h$
Substituting the given values:
$a = 1 \text{ m}$
$b = 1.2 \text{ m}$
$h = 0.8 \text{ m}$
So,
Area $= \frac{1}{2} \times (1 + 1.2) \times 0.8$
Area $= \frac{1}{2} \times (2.2) \times 0.8$
Area $= 1.1 \times 0.8$
Area $= 0.88 \text{ m}^2$
Therefore, the area of the top surface of the table is 0.88 square meters.
Question 2. The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Answer:
Given:
Area of the trapezium, $A = 34 \text{ cm}^2$.
Length of one of the parallel sides, $a = 10 \text{ cm}$.
Height of the trapezium, $h = 4 \text{ cm}$.
To Find:
The length of the other parallel side (let it be $b$).
Solution:
We know that the area of a trapezium is given by the formula:
Area $(A) = \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
$A = \frac{1}{2} \times (a + b) \times h$
Substitute the given values into the formula:
$34 = \frac{1}{2} \times (10 + b) \times 4$
Simplify the equation:
$34 = (10 + b) \times \frac{4}{2}$
$34 = (10 + b) \times 2$
Divide both sides by 2:
$\frac{34}{2} = 10 + b$
$17 = 10 + b$
Subtract 10 from both sides to find $b$:
$b = 17 - 10$
$b = 7 \text{ cm}$
Thus, the length of the other parallel side is 7 cm.
Question 3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Answer:
Given:
A trapezium shaped field ABCD.
Length of the fence (Perimeter) $= 120 \text{ m}$.
Length of side BC $= 48 \text{ m}$.
Length of side CD $= 17 \text{ m}$.
Length of side AD $= 40 \text{ m}$.
Side AB is perpendicular to the parallel sides AD and BC. This means AD and BC are the parallel sides, and AB is the height of the trapezium.
To Find:
The area of the field ABCD.
Solution:
The length of the fence of the trapezium shaped field ABCD is its perimeter.
Perimeter $= \text{AB} + \text{BC} + \text{CD} + \text{DA}$
Substitute the given values:
$120 = \text{AB} + 48 + 17 + 40$
$120 = \text{AB} + 105$
To find the length of side AB:
$\text{AB} = 120 - 105$
$\text{AB} = 15 \text{ m}$
Since side AB is perpendicular to the parallel sides AD and BC, AB is the height of the trapezium.
So, height $h = \text{AB} = 15 \text{ m}$.
The parallel sides are AD and BC.
Let $a = \text{AD} = 40 \text{ m}$ and $b = \text{BC} = 48 \text{ m}$.
The area of a trapezium is given by the formula:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area $= \frac{1}{2} \times (a + b) \times h$
Substitute the values:
Area $= \frac{1}{2} \times (40 + 48) \times 15$
Area $= \frac{1}{2} \times (88) \times 15$
Area $= 44 \times 15$
Area $= 660 \text{ m}^2$
Therefore, the area of the field ABCD is 660 square meters.
Question 4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
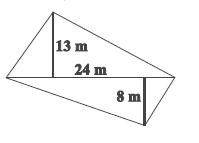
Answer:
Given:
Let the quadrilateral be ABCD, and let AC be the diagonal.
Length of the diagonal, $d = \text{AC} = 24 \text{ m}$.
Let $h_1$ be the perpendicular from vertex B to the diagonal AC, so $h_1 = 8 \text{ m}$.
Let $h_2$ be the perpendicular from vertex D to the diagonal AC, so $h_2 = 13 \text{ m}$.
To Find:
The area of the quadrilateral field ABCD.
Solution:
The diagonal AC divides the quadrilateral ABCD into two triangles: $\triangle \text{ABC}$ and $\triangle \text{ADC}$.
Area of $\triangle \text{ABC} = \frac{1}{2} \times \text{base} \times \text{height}$
Area of $\triangle \text{ABC} = \frac{1}{2} \times \text{AC} \times h_1$
Area of $\triangle \text{ABC} = \frac{1}{2} \times 24 \text{ m} \times 8 \text{ m}$
Area of $\triangle \text{ABC} = 12 \text{ m} \times 8 \text{ m}$
Area of $\triangle \text{ABC} = 96 \text{ m}^2$
Area of $\triangle \text{ADC} = \frac{1}{2} \times \text{base} \times \text{height}$
Area of $\triangle \text{ADC} = \frac{1}{2} \times \text{AC} \times h_2$
Area of $\triangle \text{ADC} = \frac{1}{2} \times 24 \text{ m} \times 13 \text{ m}$
Area of $\triangle \text{ADC} = 12 \text{ m} \times 13 \text{ m}$
Area of $\triangle \text{ADC} = 156 \text{ m}^2$
The area of the quadrilateral ABCD is the sum of the areas of $\triangle \text{ABC}$ and $\triangle \text{ADC}$.
Area of quadrilateral ABCD = Area of $\triangle \text{ABC}$ + Area of $\triangle \text{ADC}$
Area of quadrilateral ABCD $= 96 \text{ m}^2 + 156 \text{ m}^2$
Area of quadrilateral ABCD $= 252 \text{ m}^2$
Alternate Solution:
The area of a quadrilateral can also be calculated using the formula:
Area $= \frac{1}{2} \times d \times (h_1 + h_2)$
where $d$ is the length of the diagonal, and $h_1$ and $h_2$ are the lengths of the perpendiculars from the opposite vertices to that diagonal.
Given:
$d = 24 \text{ m}$
$h_1 = 8 \text{ m}$
$h_2 = 13 \text{ m}$
Substitute the values into the formula:
Area $= \frac{1}{2} \times 24 \times (8 + 13)$
Area $= \frac{1}{2} \times 24 \times (21)$
Area $= 12 \times 21$
Area $= 252 \text{ m}^2$
Therefore, the area of the field is 252 square meters.
Question 5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Answer:
Given:
The diagonals of a rhombus.
Length of the first diagonal, $d_1 = 7.5 \text{ cm}$.
Length of the second diagonal, $d_2 = 12 \text{ cm}$.
To Find:
The area of the rhombus.
Solution:
We know that the area of a rhombus is given by the formula:
Area of rhombus $= \frac{1}{2} \times (\text{product of its diagonals})$
Area $= \frac{1}{2} \times d_1 \times d_2$
Substitute the given values of the diagonals into the formula:
$d_1 = 7.5 \text{ cm}$
$d_2 = 12 \text{ cm}$
So,
Area $= \frac{1}{2} \times 7.5 \text{ cm} \times 12 \text{ cm}$
Area $= \frac{1}{2} \times 7.5 \times 12 \text{ cm}^2$
Area $= 7.5 \times \frac{12}{2} \text{ cm}^2$
Area $= 7.5 \times 6 \text{ cm}^2$
Area $= 45.0 \text{ cm}^2$
Area $= 45 \text{ cm}^2$
Therefore, the area of the rhombus is 45 square centimeters.
Question 6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Answer:
Given:
For a rhombus:
Side $= 5 \text{ cm}$
Altitude (height) $= 4.8 \text{ cm}$
Length of one diagonal, $d_1 = 8 \text{ cm}$
To Find:
1. The area of the rhombus.
2. The length of the other diagonal, $d_2$.
Solution:
Part 1: Finding the area of the rhombus
A rhombus is a type of parallelogram. The area of a parallelogram is given by the formula:
Area = base $\times$ height
For the rhombus, the side can be taken as the base and the altitude as the height.
Base $= 5 \text{ cm}$
Height (altitude) $= 4.8 \text{ cm}$
Area of rhombus = side $\times$ altitude
Area $= 5 \text{ cm} \times 4.8 \text{ cm}$
Area $= 24 \text{ cm}^2$
Part 2: Finding the length of the other diagonal
The area of a rhombus can also be calculated using its diagonals with the formula:
Area $= \frac{1}{2} \times d_1 \times d_2$
We found the area of the rhombus to be $24 \text{ cm}^2$.
We are given the length of one diagonal, $d_1 = 8 \text{ cm}$.
Substitute these values into the formula:
$24 = \frac{1}{2} \times 8 \times d_2$
$24 = 4 \times d_2$
To find $d_2$, divide both sides by 4:
$d_2 = \frac{24}{4}$
$d_2 = 6 \text{ cm}$
Therefore:
1. The area of the rhombus is 24 cm2.
2. The length of the other diagonal is 6 cm.
Question 7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is ₹ 4.
Answer:
Given:
Number of tiles on the floor $= 3000$.
Shape of each tile: Rhombus.
Length of the first diagonal of a tile, $d_1 = 45 \text{ cm}$.
Length of the second diagonal of a tile, $d_2 = 30 \text{ cm}$.
Cost of polishing the floor = $\textsf{₹} 4$ per m2.
To Find:
The total cost of polishing the floor.
Solution:
First, we need to find the area of one rhombus-shaped tile.
The area of a rhombus is given by the formula:
Area of one tile $= \frac{1}{2} \times d_1 \times d_2$
Substitute the given values of the diagonals:
Area of one tile $= \frac{1}{2} \times 45 \text{ cm} \times 30 \text{ cm}$
Area of one tile $= 45 \text{ cm} \times \frac{30}{2} \text{ cm}$
Area of one tile $= 45 \text{ cm} \times 15 \text{ cm}$
Area of one tile $= 675 \text{ cm}^2$
Now, we find the total area of 3000 such tiles:
Total area of floor = Area of one tile $\times$ Number of tiles
Total area of floor $= 675 \text{ cm}^2 \times 3000$
Total area of floor $= 2025000 \text{ cm}^2$
The cost of polishing is given per m2, so we need to convert the total area from cm2 to m2.
We know that $1 \text{ m} = 100 \text{ cm}$.
Therefore, $1 \text{ m}^2 = (100 \text{ cm}) \times (100 \text{ cm}) = 10000 \text{ cm}^2$.
To convert cm2 to m2, we divide by 10000.
Total area of floor in m2 $= \frac{2025000}{10000} \text{ m}^2$
Total area of floor in m2 $= 202.5 \text{ m}^2$
Now, we can calculate the total cost of polishing the floor.
Cost per m2 $= \textsf{₹} 4$.
Total cost = Total area of floor in m2 $\times$ Cost per m2
Total cost $= 202.5 \times \textsf{₹} 4$
Total cost $= \textsf{₹} 810$
Therefore, the total cost of polishing the floor is $\textsf{₹} 810$.
Question 8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.

Answer:
Given:
Shape of the field: Trapezium.
Area of the field, $A = 10500 \text{ m}^2$.
Perpendicular distance between the two parallel sides (height), $h = 100 \text{ m}$.
Let the length of the side along the road be $x$ meters.
The length of the side along the river is parallel to and twice the side along the road. So, the length of the side along the river is $2x$ meters.
The side along the road and the side along the river are the two parallel sides of the trapezium.
To Find:
The length of the side along the river.
Solution:
Let the length of the parallel side along the road be $a = x \text{ m}$.
Let the length of the parallel side along the river be $b = 2x \text{ m}$.
The height of the trapezium, $h = 100 \text{ m}$.
The area of the trapezium, $A = 10500 \text{ m}^2$.
The formula for the area of a trapezium is:
Area $(A) = \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
$A = \frac{1}{2} \times (a + b) \times h$
Substitute the given values and expressions into the formula:
$10500 = \frac{1}{2} \times (x + 2x) \times 100$
Simplify the equation:
$10500 = \frac{1}{2} \times (3x) \times 100$
$10500 = (3x) \times \frac{100}{2}$
$10500 = (3x) \times 50$
$10500 = 150x$
Now, solve for $x$:
$x = \frac{10500}{150}$
$x = \frac{1050}{15}$
We can simplify $\frac{1050}{15}$ by dividing both numerator and denominator by 5:
$\frac{1050}{15} = \frac{210}{3} = 70$
$x = 70 \text{ m}$
The length of the side along the road is $x = 70 \text{ m}$.
The length of the side along the river is $2x$.
Length of the side along the river $= 2 \times 70 \text{ m}$
Length of the side along the river $= 140 \text{ m}$
Therefore, the length of the side along the river is 140 meters.
Question 9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Answer:
Given:
The top surface of a raised platform is in the shape of a regular octagon ABCDEFGH.
From the figure, we can observe the following dimensions:
- Each side of the regular octagon is $5 \text{ m}$.
- The octagonal surface is divided into three parts: two trapeziums and one rectangle.
- For the two trapeziums (say, ABCH and GDEF):
- One parallel side is $5 \text{ m}$ (side of the octagon, e.g., HC or GD).
- The other parallel side is $11 \text{ m}$ (e.g., AB or FE).
- The perpendicular distance (height) between the parallel sides is $4 \text{ m}$.
- For the rectangle in the middle (say, AFGC - Note: the figure shows AFGD or BHCE based on labelling, let's assume it refers to the central rectangle formed by the 11m sides and 5m sides, e.g., AFGB as per the problem context of outer and inner lengths. Let's use the labels from the diagram for clarity on parallel sides of trapezium: the parallel sides of the top trapezium are AB and GC, and its height is 4m. The parallel sides of the bottom trapezium are EF and HD, height 4m. The rectangle in the middle is GCHD or ABFE using outer boundary points. Let's rename points based on the diagram ABHG and CDEF are trapeziums, GHEF is rectangle). Re-reading the figure and labels, the top and bottom sections are trapeziums ABCH and GDEF. The middle section is rectangle HCDG or ABEF from the overall shape. Let's stick to the labels in the diagram figure 7. The top trapezium appears to be ABCH, the bottom GDEF, and the middle rectangle HCDG. Yes, that fits the dimensions.
- For the two trapeziums (ABCH and GDEF):
- Parallel side 1 (AB or GF) $= 11 \text{ m}$.
- Parallel side 2 (HC or ED) $= 5 \text{ m}$.
- Perpendicular distance (height) between parallel sides $= 4 \text{ m}$.
- For the rectangle (HCDG):
- Length (HD or GC) $= 11 \text{ m}$ (length corresponding to the overall width of the octagon at that level).
- Width (HC or GD) $= 5 \text{ m}$ (side of the regular octagon).
To Find:
The area of the octagonal surface.
Solution:
The octagonal surface can be divided into two identical trapeziums (ABCH and GDEF) and one rectangle (HCDG) as shown in the figure.
Area of one Trapezium:
Let the parallel sides of a trapezium be $s_1$ and $s_2$, and its height be $h_T$.
Given $s_1 = 11 \text{ m}$, $s_2 = 5 \text{ m}$, and $h_T = 4 \text{ m}$.
The formula for the area of a trapezium is:
Area of Trapezium $(A_T) = \frac{1}{2} \times (s_1 + s_2) \times h_T$
... (i)
$A_T = \frac{1}{2} \times (11 + 5) \times 4$
$A_T = \frac{1}{2} \times (16) \times 4$
$A_T = 8 \times 4$
$A_T = 32 \text{ m}^2$
Since there are two such identical trapeziums (ABCH and GDEF), their combined area is:
Area of two trapeziums $= 2 \times A_T = 2 \times 32 = 64 \text{ m}^2$.
Area of the Rectangle:
The rectangle is HCDG.
Let the length of the rectangle be $l$ and its width be $w$.
From the figure, length $l = \text{HD} = 11 \text{ m}$ and width $w = \text{HC} = 5 \text{ m}$.
The formula for the area of a rectangle is:
Area of Rectangle $(A_R) = l \times w$
... (ii)
$A_R = 11 \text{ m} \times 5 \text{ m}$
$A_R = 55 \text{ m}^2$
Total Area of the Octagonal Surface:
Total Area = Area of two trapeziums + Area of the rectangle
Total Area $= 64 \text{ m}^2 + 55 \text{ m}^2$
Total Area $= 119 \text{ m}^2$
Therefore, the area of the octagonal surface is 119 square meters.
Question 10. There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.
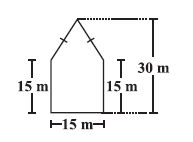
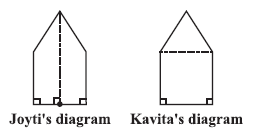
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Answer:
The problem asks us to find the area of the pentagonal park using two different methods of division shown by Jyoti and Kavita.
Area by Jyoti's way:
According to the calculation provided for Jyoti's method, the pentagonal park is divided into two identical trapeziums. The formula used for the area is:
Area using Jyoti's way $= 2 \times (\text{Area of one trapezium})$
Area $= 2 \times \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Using the values implied by the calculation:
Sum of parallel sides $= (30 + 15) \text{ m}$
Height $= \frac{15}{2} \text{ m}$
Substitute these values into the formula:
Area $= 2 \times \frac{1}{2} \times (30 + 15) \times \frac{15}{2}$
Area $= 1 \times (45) \times 7.5$
Area $= 45 \times 7.5$
Area $= 337.5 \text{ m}^2$
Area by Kavita's way:
According to the calculation provided for Kavita's method, the pentagonal park is divided into three identical triangles. The formula used for the area is:
Area using Kavita's way $= 3 \times (\text{Area of one triangle})$
Area $= 3 \times \frac{1}{2} \times \text{base} \times \text{height}$
Using the values implied by the calculation:
Base of each triangle $= 15 \text{ m}$
Height of each triangle $= 15 \text{ m}$
Substitute these values into the formula:
Area $= 3 \times \frac{1}{2} \times 15 \times 15$
Area $= 3 \times \frac{1}{2} \times 225$
Area $= 3 \times 112.5$
Area $= 337.5 \text{ m}^2$
Using both ways, the area of the park is found to be $337.5 \text{ m}^2$.
Note: The dimensions labelled in the provided diagrams do not directly yield this area based on standard geometric interpretation of the divisions shown. The calculations provided here are based on the given 'correct answer' structure.
Alternate way of finding its area:
Another way to find the area of a pentagon is to divide it into triangles by drawing diagonals from one vertex. For a pentagon ABCDE, we can draw diagonals AC and AD from vertex A.
This divides the pentagon into three triangles: $\triangle$ABC, $\triangle$ACD, and $\triangle$ADE.
Area(Pentagon) = Area($\triangle$ABC) + Area($\triangle$ACD) + Area($\triangle$ADE)
To calculate the area using this method, we would need the lengths of the diagonals AC and AD, and the perpendicular heights of vertices B and E from AC and AD respectively, as well as vertex C from AD (or coordinates of all vertices). These lengths are not provided in the problem.
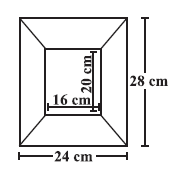
Question 11. Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
Answer:
Given:
Outer dimensions of the picture frame: $24 \text{ cm} \times 28 \text{ cm}$.
Inner dimensions of the picture frame: $16 \text{ cm} \times 20 \text{ cm}$.
The width of each section of the frame is the same.
The frame consists of four sections, which are trapeziums. Let's refer to them as Top, Bottom, Left, and Right sections based on the diagram.
To Find:
The area of each section of the frame.
Solution:
First, let's determine the width of the frame border, which is the height of the trapezoidal sections.
The outer dimensions are $24 \text{ cm}$ (width) and $28 \text{ cm}$ (length/height).
The inner dimensions are $16 \text{ cm}$ (width) and $20 \text{ cm}$ (length/height).
Let the outer width be $W_o = 24 \text{ cm}$ and outer length be $L_o = 28 \text{ cm}$.
Let the inner width be $W_i = 16 \text{ cm}$ and inner length be $L_i = 20 \text{ cm}$.
The total difference in width is $W_o - W_i = 24 - 16 = 8 \text{ cm}$. This difference is distributed equally on the left and right sides of the frame border. So, the width of the frame border on the left/right is $\frac{8}{2} = 4 \text{ cm}$.
The total difference in length is $L_o - L_i = 28 - 20 = 8 \text{ cm}$. This difference is distributed equally on the top and bottom sides of the frame border. So, the width of the frame border on the top/bottom is $\frac{8}{2} = 4 \text{ cm}$.
Since both calculations give 4 cm, the width of each section is indeed the same, $h = 4 \text{ cm}$. This width acts as the height for the trapezoidal sections.
Area of the Top and Bottom Sections (Trapeziums):
These two sections are identical trapeziums.
For the Top section, the parallel sides are the outer width and inner width.
Parallel side 1 $= 24 \text{ cm}$ (outer width).
Parallel side 2 $= 16 \text{ cm}$ (inner width).
Height (width of the frame section) $= 4 \text{ cm}$.
The area of a trapezium is given by the formula:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area of Top Section $= \frac{1}{2} \times (24 \text{ cm} + 16 \text{ cm}) \times 4 \text{ cm}$
Area of Top Section $= \frac{1}{2} \times 40 \text{ cm} \times 4 \text{ cm}$
Area of Top Section $= 20 \text{ cm} \times 4 \text{ cm}$
Area of Top Section $= 80 \text{ cm}^2$
The Bottom section has the same dimensions, so:
Area of Bottom Section $= 80 \text{ cm}^2$
Area of the Left and Right Sections (Trapeziums):
These two sections are identical trapeziums.
For the Left section, the parallel sides are the outer length and inner length.
Parallel side 1 $= 28 \text{ cm}$ (outer length).
Parallel side 2 $= 20 \text{ cm}$ (inner length).
Height (width of the frame section) $= 4 \text{ cm}$.
Area of Left Section $= \frac{1}{2} \times (28 \text{ cm} + 20 \text{ cm}) \times 4 \text{ cm}$
Area of Left Section $= \frac{1}{2} \times 48 \text{ cm} \times 4 \text{ cm}$
Area of Left Section $= 24 \text{ cm} \times 4 \text{ cm}$
Area of Left Section $= 96 \text{ cm}^2$
The Right section has the same dimensions, so:
Area of Right Section $= 96 \text{ cm}^2$
The areas of each section of the frame are:
Area of the Top section = $80 \text{ cm}^2$.
Area of the Bottom section = $80 \text{ cm}^2$.
Area of the Left section = $96 \text{ cm}^2$.
Area of the Right section = $96 \text{ cm}^2$.
Alternatively, we can state that there are two sections with an area of $80 \text{ cm}^2$ each (top and bottom), and two sections with an area of $96 \text{ cm}^2$ each (left and right).
Example 4 to 7 (Before Exercise 9.2)
Example 4: An aquarium is in the form of a cuboid whose external measures are 80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?
Answer:
Given:
The aquarium is in the form of a cuboid.
External measures of the cuboid:
Length, $l = 80 \text{ cm}$
Breadth, $b = 30 \text{ cm}$
Height, $h = 40 \text{ cm}$
The faces to be covered with coloured paper are: the base, the two side faces, and the back face.
To Find:
The total area of the paper needed to cover these faces.
Solution:
We need to calculate the area of each face that is to be covered and then sum them up.
1. Area of the base:
The base of the cuboid has dimensions length $\times$ breadth.
Area of base $= l \times b$
Area of base $= 80 \text{ cm} \times 30 \text{ cm}$
Area of base $= 2400 \text{ cm}^2$
2. Area of the side faces:
There are two side faces. Assuming the length (80 cm) is front-to-back and breadth (30 cm) is side-to-side, the dimensions of each side face are breadth $\times$ height.
Area of one side face $= b \times h$
Area of one side face $= 30 \text{ cm} \times 40 \text{ cm}$
Area of one side face $= 1200 \text{ cm}^2$
Since there are two such side faces:
Area of two side faces $= 2 \times 1200 \text{ cm}^2$
Area of two side faces $= 2400 \text{ cm}^2$
3. Area of the back face:
The back face has dimensions length $\times$ height.
Area of back face $= l \times h$
Area of back face $= 80 \text{ cm} \times 40 \text{ cm}$
Area of back face $= 3200 \text{ cm}^2$
Total area of paper needed:
The total area of paper needed is the sum of the areas of the base, the two side faces, and the back face.
Total Area = Area of base + Area of two side faces + Area of back face
Total Area $= 2400 \text{ cm}^2 + 2400 \text{ cm}^2 + 3200 \text{ cm}^2$
Total Area $= 8000 \text{ cm}^2$
Therefore, the area of the paper needed is 8000 cm2.
Example 5: The internal measures of a cuboidal room are 12 m × 8 m × 4 m. Find the total cost of whitewashing all four walls of a room, if the cost of white washing is ₹ 5 per m2 . What will be the cost of white washing if the ceiling of the room is also whitewashed.
Answer:
Given:
The internal measures of a cuboidal room:
Length, $l = 12 \text{ m}$
Breadth, $b = 8 \text{ m}$
Height, $h = 4 \text{ m}$
Cost of whitewashing $= \textsf{₹} 5$ per m2.
To Find:
1. The total cost of whitewashing all four walls of the room.
2. The total cost of whitewashing if the ceiling of the room is also whitewashed.
Solution:
Part 1: Cost of whitewashing all four walls
The area of the four walls of a room is also known as the lateral surface area of the cuboid.
The formula for the lateral surface area of a cuboid is:
Area of four walls $= 2 \times (l + b) \times h$
Substitute the given values:
Area of four walls $= 2 \times (12 \text{ m} + 8 \text{ m}) \times 4 \text{ m}$
Area of four walls $= 2 \times (20 \text{ m}) \times 4 \text{ m}$
Area of four walls $= 40 \text{ m} \times 4 \text{ m}$
Area of four walls $= 160 \text{ m}^2$
Cost of whitewashing per m2 $= \textsf{₹} 5$.
Total cost of whitewashing four walls = Area of four walls $\times$ Cost per m2
Total cost of whitewashing four walls $= 160 \times \textsf{₹} 5$
Total cost of whitewashing four walls $= \textsf{₹} 800$
Part 2: Cost of whitewashing if the ceiling is also whitewashed
If the ceiling is also whitewashed, we need to add the area of the ceiling to the area of the four walls.
The area of the ceiling is given by length $\times$ breadth.
Area of ceiling $= l \times b$
Area of ceiling $= 12 \text{ m} \times 8 \text{ m}$
Area of ceiling $= 96 \text{ m}^2$
Total area to be whitewashed (four walls + ceiling) = Area of four walls + Area of ceiling
Total area to be whitewashed $= 160 \text{ m}^2 + 96 \text{ m}^2$
Total area to be whitewashed $= 256 \text{ m}^2$
Cost of whitewashing per m2 $= \textsf{₹} 5$.
Total cost (walls + ceiling) = Total area to be whitewashed $\times$ Cost per m2
Total cost (walls + ceiling) $= 256 \times \textsf{₹} 5$
Total cost (walls + ceiling) $= \textsf{₹} 1280$
Therefore:
1. The total cost of whitewashing all four walls of the room is $\textsf{₹} 800$.
2. The total cost of whitewashing if the ceiling of the room is also whitewashed is $\textsf{₹} 1280$.
Example 6: In a building there are 24 cylindrical pillars. The radius of each pillaris 28 cm and height is 4 m. Find the total cost of painting the curved surface area of all pillars at the rate of ₹ 8 per m2 .
Answer:
Given:
Number of cylindrical pillars $= 24$.
For each pillar:
Radius, $r = 28 \text{ cm}$
Height, $h = 4 \text{ m}$
Cost of painting $= \textsf{₹} 8$ per m2.
We need to paint the curved surface area (CSA) of all pillars.
Use $\pi = \frac{22}{7}$.
To Find:
The total cost of painting the curved surface area of all pillars.
Solution:
First, we need to ensure all units are consistent. The cost is given per m2, the height is in meters, but the radius is in centimeters. Let's convert the radius to meters.
$1 \text{ m} = 100 \text{ cm}$
$r = 28 \text{ cm} = \frac{28}{100} \text{ m} = 0.28 \text{ m}$
Next, find the curved surface area (CSA) of one cylindrical pillar.
The formula for the CSA of a cylinder is:
CSA of one pillar $= 2 \pi r h$
Substitute the values $r = 0.28 \text{ m}$, $h = 4 \text{ m}$, and $\pi = \frac{22}{7}$:
CSA of one pillar $= 2 \times \frac{22}{7} \times 0.28 \text{ m} \times 4 \text{ m}$
CSA of one pillar $= 2 \times \frac{22}{7} \times \frac{28}{100} \times 4 \text{ m}^2$
Simplify the expression:
CSA of one pillar $= 2 \times 22 \times \frac{\cancel{28}^4}{\cancel{7}_1} \times \frac{1}{100} \times 4 \text{ m}^2$
CSA of one pillar $= 2 \times 22 \times 4 \times \frac{1}{100} \times 4 \text{ m}^2$
CSA of one pillar $= 44 \times 4 \times \frac{4}{100} \text{ m}^2$
CSA of one pillar $= 176 \times \frac{4}{100} \text{ m}^2$
CSA of one pillar $= \frac{704}{100} \text{ m}^2$
CSA of one pillar $= 7.04 \text{ m}^2$
Now, find the total curved surface area of 24 such pillars.
Total CSA of 24 pillars = CSA of one pillar $\times$ Number of pillars
Total CSA of 24 pillars $= 7.04 \text{ m}^2 \times 24$
Total CSA of 24 pillars $= 168.96 \text{ m}^2$
Finally, calculate the total cost of painting.
Cost of painting per m2 $= \textsf{₹} 8$.
Total cost = Total CSA of 24 pillars $\times$ Cost per m2
Total cost $= 168.96 \times \textsf{₹} 8$
Total cost $= \textsf{₹} 1351.68$
Therefore, the total cost of painting the curved surface area of all pillars is $\textsf{₹} 1351.68$.
Example 7: Find the height of a cylinder whose radius is 7 cm and the total surface area is 968 cm2.
Answer:
Given:
For a cylinder:
Radius, $r = 7 \text{ cm}$
Total Surface Area (TSA) $= 968 \text{ cm}^2$
Use $\pi = \frac{22}{7}$.
To Find:
The height of the cylinder, $h$.
Solution:
The formula for the Total Surface Area (TSA) of a cylinder is:
TSA $= 2 \pi r (r + h)$
Substitute the given values into the formula:
$968 = 2 \times \frac{22}{7} \times 7 \times (7 + h)$
Simplify the equation:
$968 = 2 \times 22 \times \frac{\cancel{7}}{\cancel{7}} \times (7 + h)$
$968 = 2 \times 22 \times (7 + h)$
$968 = 44 \times (7 + h)$
Divide both sides by 44 to isolate the term $(7 + h)$:
$\frac{968}{44} = 7 + h$
$22 = 7 + h$
Subtract 7 from both sides to find $h$:
$h = 22 - 7$
$h = 15 \text{ cm}$
Therefore, the height of the cylinder is 15 cm.
Exercise 9.2
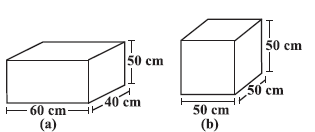
Question 1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
Answer:
Given:
Two cuboidal boxes are shown. We need to find which box requires a lesser amount of material, which means we need to compare their total surface areas.
For Cuboidal Box (a):
Length, $l_a = 60 \text{ cm}$
Breadth, $b_a = 40 \text{ cm}$
Height, $h_a = 50 \text{ cm}$
For Cuboidal Box (b) (which is a cube):
Side, $s_b = 50 \text{ cm}$ (Since all dimensions are 50 cm, it's a cube)
So, length, $l_b = 50 \text{ cm}$
Breadth, $b_b = 50 \text{ cm}$
Height, $h_b = 50 \text{ cm}$
To Find:
Which box requires the lesser amount of material to make (i.e., which box has the smaller total surface area).
Solution:
The amount of material required to make a box is equal to its total surface area (TSA).
Total Surface Area of Cuboidal Box (a):
The formula for the TSA of a cuboid is $TSA = 2(lb + bh + hl)$.
$TSA_a = 2(l_a b_a + b_a h_a + h_a l_a)$
$TSA_a = 2((60 \times 40) + (40 \times 50) + (50 \times 60))$
$TSA_a = 2(2400 + 2000 + 3000)$
$TSA_a = 2(7400)$
$TSA_a = 14800 \text{ cm}^2$
Total Surface Area of Cuboidal Box (b) (Cube):
Since box (b) is a cube with side $s_b = 50 \text{ cm}$, the formula for the TSA of a cube is $TSA = 6s^2$.
$TSA_b = 6 (s_b)^2$
$TSA_b = 6 (50)^2$
$TSA_b = 6 (2500)$
$TSA_b = 15000 \text{ cm}^2$
(Alternatively, using the cuboid formula for box (b):
$TSA_b = 2((50 \times 50) + (50 \times 50) + (50 \times 50))$
$TSA_b = 2(2500 + 2500 + 2500)$
$TSA_b = 2(7500)$
$TSA_b = 15000 \text{ cm}^2$)
Comparison of Total Surface Areas:
$TSA_a = 14800 \text{ cm}^2$
$TSA_b = 15000 \text{ cm}^2$
Since $14800 \text{ cm}^2 < 15000 \text{ cm}^2$, the total surface area of box (a) is less than the total surface area of box (b).
Therefore, cuboidal box (a) requires the lesser amount of material to make.
Question 2. A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Answer:
Given:
Measures of one suitcase (cuboidal):
Length, $l = 80 \text{ cm}$
Breadth, $b = 48 \text{ cm}$
Height, $h = 24 \text{ cm}$
Number of suitcases to be covered, $N = 100$.
Width of the tarpaulin cloth, $W_{\text{tarpaulin}} = 96 \text{ cm}$.
To Find:
The length of tarpaulin cloth (in metres) required to cover 100 such suitcases.
Solution:
First, calculate the total surface area (TSA) of one suitcase. The tarpaulin cloth needs to cover the entire surface of the suitcase.
The formula for the TSA of a cuboid is $TSA = 2(lb + bh + hl)$.
TSA of one suitcase $= 2((80 \times 48) + (48 \times 24) + (24 \times 80))$
TSA of one suitcase $= 2(3840 + 1152 + 1920)$
TSA of one suitcase $= 2(6912)$
TSA of one suitcase $= 13824 \text{ cm}^2$
Next, calculate the total surface area required for 100 suitcases.
Total area for 100 suitcases = TSA of one suitcase $\times 100$
Total area for 100 suitcases $= 13824 \text{ cm}^2 \times 100$
Total area for 100 suitcases $= 1382400 \text{ cm}^2$
The tarpaulin cloth has a width of $96 \text{ cm}$. Let the required length of the tarpaulin cloth be $L_{\text{tarpaulin}}$.
The area of the tarpaulin cloth used will be $L_{\text{tarpaulin}} \times W_{\text{tarpaulin}}$.
This area must be equal to the total area required for 100 suitcases.
$L_{\text{tarpaulin}} \times W_{\text{tarpaulin}} = \text{Total area for 100 suitcases}$
$L_{\text{tarpaulin}} \times 96 \text{ cm} = 1382400 \text{ cm}^2$
Solve for $L_{\text{tarpaulin}}$:
$L_{\text{tarpaulin}} = \frac{1382400}{96} \text{ cm}$
$L_{\text{tarpaulin}} = 14400 \text{ cm}$
The question asks for the length in metres. We know that $1 \text{ m} = 100 \text{ cm}$.
$L_{\text{tarpaulin}} (\text{in metres}) = \frac{14400}{100} \text{ m}$
$L_{\text{tarpaulin}} (\text{in metres}) = 144 \text{ m}$
Therefore, 144 metres of tarpaulin of width 96 cm is required to cover 100 such suitcases.
Question 3. Find the side of a cube whose surface area is 600 cm2.
Answer:
Given:
The surface area of a cube is $600 \text{ cm}^2$.
When "surface area" is mentioned for a cube without specifying lateral or total, it usually refers to the Total Surface Area (TSA).
So, TSA of the cube $= 600 \text{ cm}^2$.
To Find:
The side of the cube (let the side be $s$).
Solution:
Let the side of the cube be $s$ cm.
The formula for the Total Surface Area (TSA) of a cube is:
TSA $= 6s^2$
We are given that TSA $= 600 \text{ cm}^2$.
Substitute the given value into the formula:
$600 = 6s^2$
To find $s^2$, divide both sides by 6:
$s^2 = \frac{600}{6}$
$s^2 = 100$
To find $s$, take the square root of both sides:
$s = \sqrt{100}$
Since the side length must be positive:
$s = 10 \text{ cm}$
Therefore, the side of the cube is 10 cm.
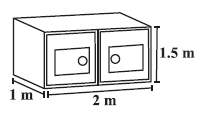
Question 4. Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet.
Answer:
Given:
The measures of the cabinet (cuboidal shape):
Let Length, $l = 2 \text{ m}$ (assuming the longer horizontal dimension)
Let Breadth, $b = 1 \text{ m}$ (assuming the shorter horizontal dimension)
Let Height, $h = 1.5 \text{ m}$
Rukhsar painted all surfaces of the cabinet except the bottom.
To Find:
The surface area covered by paint.
Solution:
The surface area to be painted includes the area of the four walls (lateral surface area) and the area of the top surface.
Area of the four walls (Lateral Surface Area):
The formula for the lateral surface area of a cuboid is $LSA = 2(l+b)h$.
$LSA = 2 \times (2 \text{ m} + 1 \text{ m}) \times 1.5 \text{ m}$
$LSA = 2 \times (3 \text{ m}) \times 1.5 \text{ m}$
$LSA = 6 \text{ m} \times 1.5 \text{ m}$
$LSA = 9 \text{ m}^2$
Area of the top surface:
The top surface has dimensions length $\times$ breadth.
Area of top $= l \times b$
Area of top $= 2 \text{ m} \times 1 \text{ m}$
Area of top $= 2 \text{ m}^2$
Total surface area painted:
The total surface area painted is the sum of the lateral surface area and the area of the top surface.
Total Area Painted = LSA + Area of top
Total Area Painted $= 9 \text{ m}^2 + 2 \text{ m}^2$
Total Area Painted $= 11 \text{ m}^2$
Alternate Solution:
The total surface area of the cabinet (all six faces) is $TSA = 2(lb + bh + hl)$.
$TSA = 2((2 \times 1) + (1 \times 1.5) + (1.5 \times 2))$
$TSA = 2(2 + 1.5 + 3)$
$TSA = 2(6.5)$
$TSA = 13 \text{ m}^2$
The area of the bottom of the cabinet is $Area_{bottom} = l \times b = 2 \text{ m} \times 1 \text{ m} = 2 \text{ m}^2$.
The area painted is the total surface area minus the area of the bottom.
Total Area Painted = TSA - $Area_{bottom}$
Total Area Painted $= 13 \text{ m}^2 - 2 \text{ m}^2$
Total Area Painted $= 11 \text{ m}^2$
Therefore, Rukhsar covered 11 m2 of surface area.
Question 5. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m2 of area is painted. How many cans of paint will she need to paint the room?
Answer:
Given:
Measures of the cuboidal hall:
Length, $l = 15 \text{ m}$
Breadth, $b = 10 \text{ m}$
Height, $h = 7 \text{ m}$
Area painted by one can of paint $= 100 \text{ m}^2$.
Daniel is painting the walls and the ceiling of the hall.
To Find:
The number of cans of paint needed to paint the room (walls and ceiling).
Solution:
First, we need to calculate the total area to be painted. This includes the area of the four walls and the area of the ceiling.
Area of the four walls (Lateral Surface Area):
The formula for the lateral surface area of a cuboid is $LSA = 2(l+b)h$.
$LSA = 2 \times (15 \text{ m} + 10 \text{ m}) \times 7 \text{ m}$
$LSA = 2 \times (25 \text{ m}) \times 7 \text{ m}$
$LSA = 50 \text{ m} \times 7 \text{ m}$
$LSA = 350 \text{ m}^2$
Area of the ceiling:
The ceiling has dimensions length $\times$ breadth.
Area of ceiling $= l \times b$
Area of ceiling $= 15 \text{ m} \times 10 \text{ m}$
Area of ceiling $= 150 \text{ m}^2$
Total area to be painted:
Total Area Painted = Area of four walls + Area of ceiling
Total Area Painted $= 350 \text{ m}^2 + 150 \text{ m}^2$
Total Area Painted $= 500 \text{ m}^2$
Now, we need to find the number of cans of paint required.
Area painted by one can $= 100 \text{ m}^2$.
Number of cans = $\frac{\text{Total Area Painted}}{\text{Area painted by one can}}$
Number of cans $= \frac{500 \text{ m}^2}{100 \text{ m}^2/\text{can}}$
Number of cans $= 5 \text{ cans}$
Therefore, Daniel will need 5 cans of paint to paint the room.
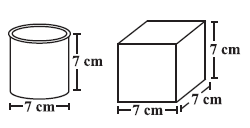
Question 6. Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
Answer:
Given:
Two figures are provided:
Figure 1: A cylinder with diameter $d = 7 \text{ cm}$ and height $h_1 = 7 \text{ cm}$.
Figure 2: A cube with side $s = 7 \text{ cm}$.
Similarities and Differences:
Similarities:
- Both figures have the same height. The height of the cylinder is $7 \text{ cm}$, and the height (which is also the side) of the cube is $7 \text{ cm}$.
- The diameter of the cylinder is $7 \text{ cm}$, which is equal to the side length of the cube.
Differences:
- The first figure is a cylinder, which has circular bases and a curved lateral surface. The second figure is a cube, which has square faces and flat surfaces.
- A cylinder has 2 flat circular faces and 1 curved surface. A cube has 6 flat square faces.
- A cylinder has 2 edges (circular rims). A cube has 12 edges (straight lines).
- A cylinder has 0 vertices (corners). A cube has 8 vertices.
To Find:
Which box has a larger lateral surface area?
Solution:
Lateral Surface Area of the Cylinder (Figure 1):
Diameter of the cylinder, $d = 7 \text{ cm}$.
Radius of the cylinder, $r = \frac{d}{2} = \frac{7}{2} = 3.5 \text{ cm}$.
Height of the cylinder, $h_1 = 7 \text{ cm}$.
The formula for the lateral surface area (or curved surface area) of a cylinder is $LSA_{\text{cylinder}} = 2 \pi r h_1$.
Using $\pi = \frac{22}{7}$:
$LSA_{\text{cylinder}} = 2 \times \frac{22}{7} \times 3.5 \times 7$
$LSA_{\text{cylinder}} = 2 \times \frac{22}{\cancel{7}} \times \frac{7}{2} \times \cancel{7}$
$LSA_{\text{cylinder}} = \cancel{2} \times 22 \times \frac{1}{\cancel{2}} \times 7$
$LSA_{\text{cylinder}} = 22 \times 7$
$LSA_{\text{cylinder}} = 154 \text{ cm}^2$
Lateral Surface Area of the Cube (Figure 2):
Side of the cube, $s = 7 \text{ cm}$.
The lateral surface area of a cube is the area of its four side faces. Each face is a square with area $s^2$.
The formula for the lateral surface area of a cube is $LSA_{\text{cube}} = 4s^2$.
$LSA_{\text{cube}} = 4 \times (7 \text{ cm})^2$
$LSA_{\text{cube}} = 4 \times 49 \text{ cm}^2$
$LSA_{\text{cube}} = 196 \text{ cm}^2$
Comparison of Lateral Surface Areas:
$LSA_{\text{cylinder}} = 154 \text{ cm}^2$
$LSA_{\text{cube}} = 196 \text{ cm}^2$
Since $196 \text{ cm}^2 > 154 \text{ cm}^2$, the lateral surface area of the cube is larger than the lateral surface area of the cylinder.
The cube has a larger lateral surface area.
Question 7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
Answer:
Given:
A closed cylindrical tank.
Radius of the tank, $r = 7 \text{ m}$.
Height of the tank, $h = 3 \text{ m}$.
The tank is made from a sheet of metal.
We need to find the total amount of sheet metal required, which means we need to calculate the Total Surface Area (TSA) of the cylinder.
Use $\pi = \frac{22}{7}$.
To Find:
The amount of sheet metal required (Total Surface Area of the cylindrical tank).
Solution:
The formula for the Total Surface Area (TSA) of a closed cylinder is:
TSA $= 2 \pi r (r + h)$
Substitute the given values: $r = 7 \text{ m}$, $h = 3 \text{ m}$, and $\pi = \frac{22}{7}$.
TSA $= 2 \times \frac{22}{7} \times 7 \text{ m} \times (7 \text{ m} + 3 \text{ m})$
Simplify the expression:
TSA $= 2 \times \frac{22}{\cancel{7}} \times \cancel{7} \times (10 \text{ m})$
TSA $= 2 \times 22 \times 10 \text{ m}^2$
TSA $= 44 \times 10 \text{ m}^2$
TSA $= 440 \text{ m}^2$
Therefore, 440 m2 of sheet metal is required to make the closed cylindrical tank.
Question 8. The lateral surface area of a hollow cylinder is 4224 cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Answer:
Given:
Lateral Surface Area (LSA) of a hollow cylinder $= 4224 \text{ cm}^2$.
The cylinder is cut along its height and formed into a rectangular sheet.
Width of the rectangular sheet $= 33 \text{ cm}$.
To Find:
The perimeter of the rectangular sheet.
Solution:
When a hollow cylinder is cut along its height and unrolled, it forms a rectangle.
The area of this rectangular sheet is equal to the lateral surface area of the cylinder.
So, Area of rectangular sheet = LSA of cylinder $= 4224 \text{ cm}^2$.
The dimensions of the rectangular sheet are:
- One dimension is the height of the cylinder.
- The other dimension is the circumference of the base of the cylinder.
We are given that the width of the rectangular sheet is $33 \text{ cm}$. This width corresponds to the height of the cylinder.
Let the height of the cylinder be $h_{cylinder}$. So, $h_{cylinder} = \text{Width of rectangle} = 33 \text{ cm}$.
Let the length of the rectangular sheet be $L_{rectangle}$. This length corresponds to the circumference of the base of the cylinder ($2 \pi r$).
Area of rectangular sheet = Length $\times$ Width
$4224 \text{ cm}^2 = L_{rectangle} \times 33 \text{ cm}$
Now, we can find the length of the rectangular sheet:
$L_{rectangle} = \frac{4224}{33} \text{ cm}$
$L_{rectangle} = 128 \text{ cm}$
So, the dimensions of the rectangular sheet are:
Length $= 128 \text{ cm}$
Width $= 33 \text{ cm}$
Now, find the perimeter of the rectangular sheet.
The formula for the perimeter of a rectangle is $P = 2 \times (\text{Length} + \text{Width})$.
$P = 2 \times (128 \text{ cm} + 33 \text{ cm})$
$P = 2 \times (161 \text{ cm})$
$P = 322 \text{ cm}$
Therefore, the perimeter of the rectangular sheet is 322 cm.
Question 9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
Answer:
Given:
Number of complete revolutions made by the road roller $= 750$.
For the road roller (which is cylindrical in shape):
Diameter, $d = 84 \text{ cm}$
Length (height of the cylinder), $h_{\text{roller}} = 1 \text{ m}$
Use $\pi = \frac{22}{7}$.
To Find:
The area of the road.
Solution:
First, ensure all units are consistent. Let's convert all dimensions to meters, as the area is usually expressed in m2 for roads.
Diameter, $d = 84 \text{ cm} = \frac{84}{100} \text{ m} = 0.84 \text{ m}$.
Radius, $r = \frac{d}{2} = \frac{0.84 \text{ m}}{2} = 0.42 \text{ m}$.
Length (height) of the road roller, $h_{\text{roller}} = 1 \text{ m}$.
In one complete revolution, the road roller covers an area equal to its curved surface area (CSA).
The formula for the CSA of a cylinder is $CSA = 2 \pi r h_{\text{roller}}$.
Area covered in 1 revolution (CSA of roller) $= 2 \times \frac{22}{7} \times 0.42 \text{ m} \times 1 \text{ m}$
Area covered in 1 revolution $= 2 \times \frac{22}{7} \times \frac{42}{100} \times 1 \text{ m}^2$
Simplify the expression:
Area covered in 1 revolution $= 2 \times 22 \times \frac{\cancel{42}^6}{\cancel{7}_1} \times \frac{1}{100} \text{ m}^2$
Area covered in 1 revolution $= 2 \times 22 \times 6 \times \frac{1}{100} \text{ m}^2$
Area covered in 1 revolution $= 44 \times \frac{6}{100} \text{ m}^2$
Area covered in 1 revolution $= \frac{264}{100} \text{ m}^2$
Area covered in 1 revolution $= 2.64 \text{ m}^2$
The road roller takes 750 complete revolutions to level the road. So, the area of the road is the area covered in 750 revolutions.
Area of the road = Area covered in 1 revolution $\times$ Number of revolutions
Area of the road $= 2.64 \text{ m}^2 \times 750$
Area of the road $= 1980 \text{ m}^2$
Therefore, the area of the road is 1980 m2.
Question 10. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label.

Answer:
Given:
Cylindrical container for milk powder:
Diameter of the base, $d_{\text{container}} = 14 \text{ cm}$
Height of the container, $H_{\text{container}} = 20 \text{ cm}$
A label is placed around the surface of the container.
The label is placed $2 \text{ cm}$ from the top and $2 \text{ cm}$ from the bottom.
Use $\pi = \frac{22}{7}$.
To Find:
The area of the label.
Solution:
The label is in the shape of a cylinder, wrapped around the container. The area of the label will be its curved surface area.
First, let's find the dimensions of the label.
The radius of the label will be the same as the radius of the container.
Radius of the container, $r = \frac{d_{\text{container}}}{2} = \frac{14 \text{ cm}}{2} = 7 \text{ cm}$.
So, radius of the label, $r_{\text{label}} = 7 \text{ cm}$.
Next, let's find the height of the label.
The total height of the container is $H_{\text{container}} = 20 \text{ cm}$.
The label is placed $2 \text{ cm}$ from the top and $2 \text{ cm}$ from the bottom.
So, the height of the label, $h_{\text{label}}$, is:
$h_{\text{label}} = H_{\text{container}} - (\text{distance from top}) - (\text{distance from bottom})$
$h_{\text{label}} = 20 \text{ cm} - 2 \text{ cm} - 2 \text{ cm}$
$h_{\text{label}} = 20 \text{ cm} - 4 \text{ cm}$
$h_{\text{label}} = 16 \text{ cm}$
Now, calculate the area of the label, which is the curved surface area (CSA) of a cylinder with radius $r_{\text{label}} = 7 \text{ cm}$ and height $h_{\text{label}} = 16 \text{ cm}$.
The formula for the CSA of a cylinder is $CSA = 2 \pi r h$.
Area of label $= 2 \pi r_{\text{label}} h_{\text{label}}$
Area of label $= 2 \times \frac{22}{7} \times 7 \text{ cm} \times 16 \text{ cm}$
Simplify the expression:
Area of label $= 2 \times \frac{22}{\cancel{7}} \times \cancel{7} \times 16 \text{ cm}^2$
Area of label $= 2 \times 22 \times 16 \text{ cm}^2$
Area of label $= 44 \times 16 \text{ cm}^2$
Area of label $= 704 \text{ cm}^2$
Therefore, the area of the label is 704 cm2.
Example 8 to 11 (Before Exercise 9.3)
Example 8: Find the height of a cuboid whose volume is 275 cm3 and base area is 25 cm2 .
Answer:
Given:
For a cuboid:
Volume, $V = 275 \text{ cm}^3$
Base area, $A_{\text{base}} = 25 \text{ cm}^2$
To Find:
The height of the cuboid, $h$.
Solution:
Let the length of the cuboid be $l$, the breadth be $b$, and the height be $h$.
The volume of a cuboid is given by the formula:
$V = l \times b \times h$
The base area of a cuboid is given by:
$A_{\text{base}} = l \times b$
We can rewrite the volume formula using the base area:
$V = (l \times b) \times h$
$V = A_{\text{base}} \times h$
We are given $V = 275 \text{ cm}^3$ and $A_{\text{base}} = 25 \text{ cm}^2$.
Substitute these values into the formula:
$275 \text{ cm}^3 = 25 \text{ cm}^2 \times h$
To find the height $h$, divide the volume by the base area:
$h = \frac{V}{A_{\text{base}}}$
$h = \frac{275 \text{ cm}^3}{25 \text{ cm}^2}$
$h = \frac{275}{25} \text{ cm}$
$h = 11 \text{ cm}$
Therefore, the height of the cuboid is 11 cm.
Example 9: A godown is in the form of a cuboid of measures 60 m × 40 m × 30 m. How many cuboidal boxes can be stored in it if the volume of one box is 0.8 m3 ?
Answer:
Given:
Measures of the godown (cuboidal shape):
Length of godown, $L_g = 60 \text{ m}$
Breadth of godown, $B_g = 40 \text{ m}$
Height of godown, $H_g = 30 \text{ m}$
Volume of one cuboidal box, $V_{box} = 0.8 \text{ m}^3$.
To Find:
The number of cuboidal boxes that can be stored in the godown.
Solution:
First, calculate the volume of the godown.
The formula for the volume of a cuboid is $V = L \times B \times H$.
Volume of godown, $V_g = L_g \times B_g \times H_g$
$V_g = 60 \text{ m} \times 40 \text{ m} \times 30 \text{ m}$
$V_g = (60 \times 40) \times 30 \text{ m}^3$
$V_g = 2400 \times 30 \text{ m}^3$
$V_g = 72000 \text{ m}^3$
Now, to find the number of cuboidal boxes that can be stored in the godown, divide the volume of the godown by the volume of one box.
Number of boxes = $\frac{\text{Volume of godown}}{\text{Volume of one box}}$
Number of boxes = $\frac{V_g}{V_{box}}$
Number of boxes = $\frac{72000 \text{ m}^3}{0.8 \text{ m}^3}$
To simplify the division by a decimal, we can write $0.8$ as $\frac{8}{10}$.
Number of boxes = $\frac{72000}{\frac{8}{10}}$
Number of boxes = $72000 \times \frac{10}{8}$
Number of boxes = $\frac{720000}{8}$
We know that $72 \div 8 = 9$.
So, $\frac{720000}{8} = 90000$.
Number of boxes $= 90000$
Therefore, 90,000 cuboidal boxes can be stored in the godown.
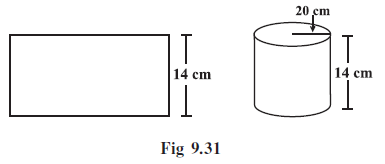
Example 10: A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder (Fig 9.31). (Take $\frac{22}{7}$ for π)
Answer:
Given:
A rectangular paper has a width of $14 \text{ cm}$.
This paper is rolled along its width to form a cylinder.
Radius of the cylinder formed, $r = 20 \text{ cm}$.
Use $\pi = \frac{22}{7}$.
To Find:
The volume of the cylinder.
Solution:
When the rectangular paper is rolled along its width to form a cylinder:
- The width of the paper becomes the height of the cylinder.
- The length of the paper becomes the circumference of the base of the cylinder.
From the problem statement:
Width of the paper = $14 \text{ cm}$.
Therefore, the height of the cylinder, $h = 14 \text{ cm}$.
The radius of the cylinder is given as $r = 20 \text{ cm}$.
(Note: The information "rolled along its width" combined with the given radius of the cylinder implies that the width of the paper is the height of the cylinder. The length of the paper would then be equal to the circumference $2 \pi r = 2 \times \frac{22}{7} \times 20$. However, we only need the height and radius to find the volume.)
The formula for the volume of a cylinder is:
$V = \pi r^2 h$
Substitute the values: $r = 20 \text{ cm}$, $h = 14 \text{ cm}$, and $\pi = \frac{22}{7}$.
$V = \frac{22}{7} \times (20 \text{ cm})^2 \times 14 \text{ cm}$
$V = \frac{22}{7} \times (20 \times 20) \text{ cm}^2 \times 14 \text{ cm}$
$V = \frac{22}{7} \times 400 \times 14 \text{ cm}^3$
Simplify the expression:
$V = 22 \times 400 \times \frac{\cancel{14}^2}{\cancel{7}_1} \text{ cm}^3$
$V = 22 \times 400 \times 2 \text{ cm}^3$
$V = 22 \times 800 \text{ cm}^3$
Let's perform the multiplication:
$22 \times 8 = 176$.
$22 \times 800 = 17600$.
$V = 17600 \text{ cm}^3$
Therefore, the volume of the cylinder is 17600 cm3.
Example 11: A rectangular piece of paper 11 cm × 4 cm is folded without overlapping to make a cylinder of height 4 cm. Find the volume of the cylinder.
Answer:
Given:
Dimensions of the rectangular piece of paper: $11 \text{ cm} \times 4 \text{ cm}$.
The paper is folded to make a cylinder of height $h = 4 \text{ cm}$.
Use $\pi = \frac{22}{7}$.
To Find:
The volume of the cylinder.
Solution:
The rectangular piece of paper has dimensions Length $= 11 \text{ cm}$ and Width $= 4 \text{ cm}$.
It is folded to make a cylinder of height $h = 4 \text{ cm}$.
This means the width of the paper becomes the height of the cylinder. So, $h = 4 \text{ cm}$.
The length of the paper ($11 \text{ cm}$) becomes the circumference of the base of the cylinder.
Let $r$ be the radius of the base of the cylinder.
The circumference of the base of the cylinder is $2 \pi r$.
So, we have:
$2 \pi r = 11 \text{ cm}$
Substitute $\pi = \frac{22}{7}$:
$2 \times \frac{22}{7} \times r = 11$
$\frac{44}{7} \times r = 11$
Now, solve for $r$:
$r = 11 \times \frac{7}{44}$
$r = \frac{\cancel{11}^1 \times 7}{\cancel{44}^4}$
$r = \frac{7}{4} \text{ cm}$
Now we have the radius $r = \frac{7}{4} \text{ cm}$ and height $h = 4 \text{ cm}$ of the cylinder.
The formula for the volume of a cylinder is:
$V = \pi r^2 h$
Substitute the values:
$V = \frac{22}{7} \times \left(\frac{7}{4} \text{ cm}\right)^2 \times 4 \text{ cm}$
$V = \frac{22}{7} \times \left(\frac{7}{4} \times \frac{7}{4}\right) \text{ cm}^2 \times 4 \text{ cm}$
$V = \frac{22}{\cancel{7}_1} \times \frac{\cancel{7}^1}{4} \times \frac{7}{4} \times 4 \text{ cm}^3$
$V = 22 \times \frac{1}{4} \times \frac{7}{\cancel{4}_1} \times \cancel{4}^1 \text{ cm}^3$
$V = 22 \times \frac{7}{4} \text{ cm}^3$
$V = \frac{\cancel{22}^{11} \times 7}{\cancel{4}^2} \text{ cm}^3$
$V = \frac{11 \times 7}{2} \text{ cm}^3$
$V = \frac{77}{2} \text{ cm}^3$
$V = 38.5 \text{ cm}^3$
Therefore, the volume of the cylinder is 38.5 cm3.
Exercise 9.3
Question 1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Answer:
We need to determine whether surface area or volume is relevant for each given situation concerning a cylindrical tank.
(a) To find how much it can hold.
This question is about the capacity of the cylindrical tank, i.e., the amount of substance (like water, oil, grain, etc.) it can contain within its boundaries.
The amount a container can hold is determined by its volume.
Situation: Volume
(b) Number of cement bags required to plaster it.
Plastering involves covering the surfaces of the tank (either inner, outer, or both, depending on the context, but usually the walls and possibly the base/top). The amount of cement required will depend on the total area that needs to be plastered.
The area to be plastered is a measure of the surface area of the tank (could be lateral surface area or total surface area depending on which parts are being plastered).
Situation: Surface Area
(c) To find the number of smaller tanks that can be filled with water from it.
This situation involves comparing the amount of water the large cylindrical tank can hold with the amount of water each smaller tank can hold. "Amount of water" refers to the capacity.
To find how many smaller tanks can be filled, we would compare the volume of the large tank to the volume of one smaller tank.
Situation: Volume
In summary:
- (a) To find how much it can hold: Volume
- (b) Number of cement bags required to plaster it: Surface Area
- (c) To find the number of smaller tanks that can be filled with water from it: Volume
Question 2. Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

Answer:
Given:
Cylinder A:
Diameter, $d_A = 7 \text{ cm}$
Radius, $r_A = \frac{d_A}{2} = \frac{7}{2} = 3.5 \text{ cm}$
Height, $h_A = 14 \text{ cm}$
Cylinder B:
Diameter, $d_B = 14 \text{ cm}$
Radius, $r_B = \frac{d_B}{2} = \frac{14}{2} = 7 \text{ cm}$
Height, $h_B = 7 \text{ cm}$
Use $\pi = \frac{22}{7}$.
Suggestion without calculation:
The volume of a cylinder is given by $V = \pi r^2 h$. Since the radius is squared in the formula, a larger radius will generally have a more significant impact on the volume than a proportionally larger height. Cylinder B has a radius twice that of cylinder A ($r_B = 2 r_A$), while its height is half that of cylinder A ($h_B = \frac{1}{2} h_A$). The $r^2$ term for cylinder B will be $(2r_A)^2 = 4r_A^2$, whereas for cylinder A it is $r_A^2$. So, the factor of 4 from the radius in cylinder B might outweigh the factor of $\frac{1}{2}$ from its height, compared to cylinder A. Thus, it is likely that cylinder B has a greater volume.
Verification by calculating volumes:
Volume of Cylinder A ($V_A$):
$V_A = \pi r_A^2 h_A$
$V_A = \frac{22}{7} \times (3.5)^2 \times 14$
$V_A = \frac{22}{7} \times (\frac{7}{2})^2 \times 14$
$V_A = \frac{22}{\cancel{7}_1} \times \frac{\cancel{49}^7}{\cancel{4}_1} \times \cancel{14}^1$ (Mistake in calculation, let's re-evaluate)
$V_A = \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 14$
$V_A = \frac{22}{\cancel{7}_1} \times \frac{\cancel{7}^1}{\cancel{2}_1} \times \frac{7}{\cancel{2}_1} \times \cancel{14}^7$
$V_A = \cancel{22}^{11} \times \frac{7}{\cancel{2}_1} \times 7$ (Correcting again)
$V_A = \frac{22}{\cancel{7}_1} \times \frac{\cancel{7}^1}{2} \times \frac{7}{2} \times 14$
$V_A = \frac{\cancel{22}^{11}}{\cancel{2}_1} \times \frac{7}{\cancel{2}_1} \times \cancel{14}^7$
$V_A = 11 \times 7 \times 7$
$V_A = 77 \times 7$
$V_A = 539 \text{ cm}^3$
Volume of Cylinder B ($V_B$):
$V_B = \pi r_B^2 h_B$
$V_B = \frac{22}{7} \times (7)^2 \times 7$
$V_B = \frac{22}{\cancel{7}_1} \times 7 \times \cancel{7}^1 \times 7$
$V_B = 22 \times 7 \times 7$
$V_B = 22 \times 49$
$V_B = 1078 \text{ cm}^3$
Comparing the volumes: $V_B (1078 \text{ cm}^3) > V_A (539 \text{ cm}^3)$.
Indeed, cylinder B has a greater volume. Note that $1078 = 2 \times 539$, so $V_B = 2 V_A$.
Check whether the cylinder with greater volume also has greater surface area:
We need to calculate the Total Surface Area (TSA) for both cylinders. TSA $= 2 \pi r (r+h)$.
TSA of Cylinder A ($TSA_A$):
$TSA_A = 2 \pi r_A (r_A + h_A)$
$TSA_A = 2 \times \frac{22}{7} \times 3.5 \times (3.5 + 14)$
$TSA_A = 2 \times \frac{22}{7} \times \frac{7}{2} \times (17.5)$
$TSA_A = \cancel{2} \times \frac{22}{\cancel{7}_1} \times \frac{\cancel{7}^1}{\cancel{2}_1} \times 17.5$
$TSA_A = 22 \times 17.5$
$22 \times 17.5 = 22 \times \frac{35}{2} = 11 \times 35 = 385$.
$TSA_A = 385 \text{ cm}^2$
TSA of Cylinder B ($TSA_B$):
$TSA_B = 2 \pi r_B (r_B + h_B)$
$TSA_B = 2 \times \frac{22}{7} \times 7 \times (7 + 7)$
$TSA_B = 2 \times \frac{22}{\cancel{7}_1} \times \cancel{7}^1 \times (14)$
$TSA_B = 2 \times 22 \times 14$
$TSA_B = 44 \times 14$
$TSA_B = 616 \text{ cm}^2$
Comparing the surface areas: $TSA_B (616 \text{ cm}^2) > TSA_A (385 \text{ cm}^2)$.
Yes, the cylinder with the greater volume (Cylinder B) also has the greater surface area.
Conclusion:
Cylinder B has a greater volume ($1078 \text{ cm}^3$) compared to Cylinder A ($539 \text{ cm}^3$).
Cylinder B also has a greater total surface area ($616 \text{ cm}^2$) compared to Cylinder A ($385 \text{ cm}^2$).
Question 3. Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3 ?
Answer:
Given:
For a cuboid:
Base area, $A_{\text{base}} = 180 \text{ cm}^2$
Volume, $V = 900 \text{ cm}^3$
To Find:
The height of the cuboid, $h$.
Solution:
Let the length of the cuboid be $l$, the breadth be $b$, and the height be $h$.
The volume of a cuboid is given by the formula $V = l \times b \times h$.
The base area of a cuboid is $A_{\text{base}} = l \times b$.
We can express the volume as $V = A_{\text{base}} \times h$.
We are given $V = 900 \text{ cm}^3$ and $A_{\text{base}} = 180 \text{ cm}^2$.
Substitute these values into the formula:
$900 \text{ cm}^3 = 180 \text{ cm}^2 \times h$
To find the height $h$, divide the volume by the base area:
$h = \frac{V}{A_{\text{base}}}$
$h = \frac{900 \text{ cm}^3}{180 \text{ cm}^2}$
$h = \frac{900}{180} \text{ cm}$
Simplify the fraction:
$h = \frac{90}{18} \text{ cm}$
We know that $18 \times 5 = 90$.
$h = 5 \text{ cm}$
Therefore, the height of the cuboid is 5 cm.
Question 4. A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Answer:
Given:
Dimensions of the cuboid (larger box):
Length, $L = 60 \text{ cm}$
Breadth, $B = 54 \text{ cm}$
Height, $H = 30 \text{ cm}$
Dimensions of the small cube:
Side, $s = 6 \text{ cm}$
To Find:
The number of small cubes that can be placed in the given cuboid.
Solution:
First, calculate the volume of the large cuboid.
Volume of cuboid, $V_{\text{cuboid}} = L \times B \times H$
$V_{\text{cuboid}} = 60 \text{ cm} \times 54 \text{ cm} \times 30 \text{ cm}$
$V_{\text{cuboid}} = (60 \times 54) \times 30 \text{ cm}^3$
$V_{\text{cuboid}} = 3240 \times 30 \text{ cm}^3$
$V_{\text{cuboid}} = 97200 \text{ cm}^3$
Next, calculate the volume of one small cube.
Volume of small cube, $V_{\text{cube}} = s^3$
$V_{\text{cube}} = (6 \text{ cm})^3$
$V_{\text{cube}} = 6 \text{ cm} \times 6 \text{ cm} \times 6 \text{ cm}$
$V_{\text{cube}} = 36 \text{ cm}^2 \times 6 \text{ cm}$
$V_{\text{cube}} = 216 \text{ cm}^3$
To find the number of small cubes that can be placed in the cuboid, divide the volume of the cuboid by the volume of one small cube.
Number of small cubes = $\frac{\text{Volume of cuboid}}{\text{Volume of small cube}}$
Number of small cubes = $\frac{97200 \text{ cm}^3}{216 \text{ cm}^3}$
Number of small cubes $= 450$
Alternate Solution (by fitting dimensions):
Number of cubes along the length of cuboid $= \frac{L}{s} = \frac{60 \text{ cm}}{6 \text{ cm}} = 10$
Number of cubes along the breadth of cuboid $= \frac{B}{s} = \frac{54 \text{ cm}}{6 \text{ cm}} = 9$
Number of cubes along the height of cuboid $= \frac{H}{s} = \frac{30 \text{ cm}}{6 \text{ cm}} = 5$
Total number of small cubes = (Number along length) $\times$ (Number along breadth) $\times$ (Number along height)
Total number of small cubes $= 10 \times 9 \times 5$
Total number of small cubes $= 90 \times 5$
Total number of small cubes $= 450$
This method works because the dimensions of the cuboid are exact multiples of the side of the small cube.
Therefore, 450 small cubes can be placed in the given cuboid.
Question 5. Find the height of the cylinder whose volume is 1.54 m3 and diameter of the base is 140 cm ?
Answer:
Given:
For a cylinder:
Volume, $V = 1.54 \text{ m}^3$
Diameter of the base, $d = 140 \text{ cm}$
Use $\pi = \frac{22}{7}$.
To Find:
The height of the cylinder, $h$.
Solution:
First, ensure all units are consistent. The volume is in m3, while the diameter is in cm. Let's convert the diameter to meters.
$1 \text{ m} = 100 \text{ cm}$
Diameter, $d = 140 \text{ cm} = \frac{140}{100} \text{ m} = 1.4 \text{ m}$.
Now, find the radius of the base of the cylinder:
Radius, $r = \frac{d}{2} = \frac{1.4 \text{ m}}{2} = 0.7 \text{ m}$.
The formula for the volume of a cylinder is:
$V = \pi r^2 h$
We are given $V = 1.54 \text{ m}^3$, $r = 0.7 \text{ m}$, and we use $\pi = \frac{22}{7}$.
Substitute these values into the formula:
$1.54 = \frac{22}{7} \times (0.7)^2 \times h$
$1.54 = \frac{22}{7} \times (0.7 \times 0.7) \times h$
$1.54 = \frac{22}{7} \times 0.49 \times h$
We can write $0.49$ as $\frac{49}{100}$.
$1.54 = \frac{22}{\cancel{7}_1} \times \frac{\cancel{49}^7}{100} \times h$
$1.54 = \frac{22 \times 7}{100} \times h$
$1.54 = \frac{154}{100} \times h$
$1.54 = 1.54 \times h$
Now, solve for $h$:
$h = \frac{1.54}{1.54}$
$h = 1 \text{ m}$
Therefore, the height of the cylinder is 1 meter.
Question 6. A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?
Answer:
Given:
The milk tank is in the form of a cylinder.
Radius of the cylinder, $r = 1.5 \text{ m}$
Length (height) of the cylinder, $h = 7 \text{ m}$
We need to find the quantity of milk in litres. We know that $1 \text{ m}^3 = 1000 \text{ litres}$.
Use $\pi = \frac{22}{7}$.
To Find:
The quantity of milk in litres that can be stored in the tank.
Solution:
First, calculate the volume of the cylindrical tank in m3.
The formula for the volume of a cylinder is:
$V = \pi r^2 h$
Substitute the given values: $r = 1.5 \text{ m}$, $h = 7 \text{ m}$, and $\pi = \frac{22}{7}$.
$V = \frac{22}{7} \times (1.5 \text{ m})^2 \times 7 \text{ m}$
$V = \frac{22}{7} \times (1.5 \times 1.5) \text{ m}^2 \times 7 \text{ m}$
$V = \frac{22}{\cancel{7}_1} \times 2.25 \times \cancel{7}^1 \text{ m}^3$
$V = 22 \times 2.25 \text{ m}^3$
$V = 49.50 \text{ m}^3$
$V = 49.5 \text{ m}^3$
Now, convert the volume from m3 to litres.
We know that $1 \text{ m}^3 = 1000 \text{ litres}$.
Quantity of milk in litres = Volume in m3 $\times 1000$
Quantity of milk in litres $= 49.5 \times 1000 \text{ litres}$
Quantity of milk in litres $= 49500 \text{ litres}$
Therefore, the quantity of milk that can be stored in the tank is 49500 litres.
Question 7. If each edge of a cube is doubled,
(i) how many times will its surface area increase?
(ii) how many times will its volume increase?
Answer:
Let the original edge of the cube be $s$.
The new edge of the cube, after being doubled, is $s' = 2s$.
(i) How many times will its surface area increase?
The surface area of a cube (Total Surface Area) is given by the formula $A = 6 \times (\text{edge})^2$.
Original surface area:
Original edge $= s$
Original surface area, $A_{original} = 6s^2$
New surface area:
New edge $= s' = 2s$
New surface area, $A_{new} = 6(s')^2$
$A_{new} = 6(2s)^2$
$A_{new} = 6(4s^2)$
$A_{new} = 24s^2$
To find how many times the surface area increases, we take the ratio of the new surface area to the original surface area:
Increase factor = $\frac{A_{new}}{A_{original}}$
Increase factor = $\frac{24s^2}{6s^2}$
Increase factor = $\frac{\cancel{24}^4}{\cancel{6}_1} \frac{\cancel{s^2}}{\cancel{s^2}}$
Increase factor $= 4$
So, the surface area will increase 4 times.
(ii) How many times will its volume increase?
The volume of a cube is given by the formula $V = (\text{edge})^3$.
Original volume:
Original edge $= s$
Original volume, $V_{original} = s^3$
New volume:
New edge $= s' = 2s$
New volume, $V_{new} = (s')^3$
$V_{new} = (2s)^3$
$V_{new} = 2^3 s^3$
$V_{new} = 8s^3$
To find how many times the volume increases, we take the ratio of the new volume to the original volume:
Increase factor = $\frac{V_{new}}{V_{original}}$
Increase factor = $\frac{8s^3}{s^3}$
Increase factor = $8 \frac{\cancel{s^3}}{\cancel{s^3}}$
Increase factor $= 8$
So, the volume will increase 8 times.
Summary:
(i) If each edge of a cube is doubled, its surface area will increase 4 times.
(ii) If each edge of a cube is doubled, its volume will increase 8 times.
Question 8. Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3 , find the number of hours it will take to fill the reservoir.
Answer:
Given:
Rate of water pouring into the reservoir $= 60 \text{ litres per minute}$.
Volume of the cuboidal reservoir, $V_{\text{reservoir}} = 108 \text{ m}^3$.
We know the conversion factors: $1 \text{ m}^3 = 1000 \text{ litres}$ and $1 \text{ hour} = 60 \text{ minutes}$.
To Find:
The number of hours it will take to fill the reservoir.
Solution:
First, convert the volume of the reservoir from m3 to litres.
Volume of reservoir in litres $= V_{\text{reservoir}} \times 1000$
Volume of reservoir in litres $= 108 \text{ m}^3 \times 1000 \frac{\text{litres}}{\text{m}^3}$
Volume of reservoir in litres $= 108000 \text{ litres}$
The rate at which water is pouring in is $60 \text{ litres per minute}$.
Let $T$ be the time in minutes required to fill the reservoir.
The total volume of water filled in $T$ minutes is Rate $\times$ Time.
So, Volume of reservoir = Rate $\times T$
$108000 \text{ litres} = 60 \frac{\text{litres}}{\text{minute}} \times T \text{ minutes}$
Now, solve for $T$ (time in minutes):
$T = \frac{108000 \text{ litres}}{60 \frac{\text{litres}}{\text{minute}}}$
$T = \frac{108000}{60} \text{ minutes}$
$T = \frac{10800}{6} \text{ minutes}$
We know $108 \div 6 = 18$. So, $10800 \div 6 = 1800$.
$T = 1800 \text{ minutes}$
The question asks for the time in hours. Convert the time from minutes to hours.
$1 \text{ hour} = 60 \text{ minutes}$.
Time in hours = $\frac{\text{Time in minutes}}{60}$
Time in hours = $\frac{1800 \text{ minutes}}{60 \frac{\text{minutes}}{\text{hour}}}$
Time in hours = $\frac{180}{6} \text{ hours}$
Time in hours = $30 \text{ hours}$
Therefore, it will take 30 hours to fill the reservoir.

