| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 1 Number Systems
Welcome to the detailed solutions guide for Chapter 1, "Number Systems," from the latest Class 9 NCERT mathematics textbook prescribed for the academic session 2024-25. This foundational chapter significantly broadens the mathematical landscape studied in previous classes, moving beyond rational numbers to encompass the complete set of Real Numbers. Understanding the structure and properties of real numbers, including the crucial distinction between rational and irrational numbers, is paramount for building the necessary groundwork for algebra, geometry, calculus, and virtually all higher mathematics. These solutions provide comprehensive, step-by-step explanations designed to clarify concepts, demonstrate techniques, and build confidence in handling various types of numbers.
The journey begins by revisiting Rational Numbers (those expressible as $\frac{p}{q}$, where $p, q$ are integers, $q \neq 0$) and formally introducing their counterpart: Irrational Numbers. The solutions meticulously explain how irrational numbers are characterized by their non-terminating and non-recurring decimal expansions. Classic examples like $\sqrt{2}$, $\sqrt{3}$, $\sqrt{5}$, and the mathematical constant $\pi$ are discussed, contrasting them with rational numbers whose decimal representations either terminate (like $\frac{1}{4} = 0.25$) or are non-terminating but recurring (like $\frac{1}{3} = 0.333... = 0.\overline{3}$). A key skill addressed is converting non-terminating recurring decimals back into the $\frac{p}{q}$ form using algebraic methods, clearly illustrated in the solutions.
Visualizing numbers is crucial. The solutions demonstrate how to represent numbers on the number line. While locating rational numbers is relatively straightforward, accurately placing irrational numbers requires geometric construction. The solutions provide step-by-step guidance, often implicitly using the Pythagorean theorem ($a^2 + b^2 = c^2$), to construct lengths corresponding to irrational numbers like $\sqrt{2}$ (hypotenuse of a right triangle with legs of length 1) or $\sqrt{5}$ (hypotenuse with legs 1 and 2) and then transfer these lengths to the number line using a compass.
Operations involving real numbers, particularly those involving irrational numbers (often in the form of surds like $\sqrt{a}$), are a major focus. The solutions demonstrate procedures for adding, subtracting, multiplying, and dividing expressions containing radicals, including simplification techniques (e.g., simplifying $\sqrt{12}$ as $2\sqrt{3}$). A vital technique covered extensively is the rationalization of the denominator. This process eliminates radicals from the denominator, making expressions easier to work with. The solutions detail methods for:
- Monomial denominators: Rationalizing $\frac{1}{\sqrt{a}}$ by multiplying numerator and denominator by $\sqrt{a}$.
- Binomial denominators: Rationalizing expressions like $\frac{1}{\sqrt{a} + \sqrt{b}}$ or $\frac{1}{a + \sqrt{b}}$ by multiplying numerator and denominator by the conjugate of the denominator (e.g., the conjugate of $\sqrt{a} + \sqrt{b}$ is $\sqrt{a} - \sqrt{b}$), utilizing the identity $(x+y)(x-y) = x^2 - y^2$.
Finally, the chapter revisits the Laws of Exponents, extending their applicability from integer exponents to rational exponents. The solutions explain the meaning of fractional powers, such as $a^{\frac{m}{n}} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m$, and demonstrate how the standard laws ($a^p \cdot a^q = a^{p+q}$, $\frac{a^p}{a^q} = a^{p-q}$, $(a^p)^q = a^{pq}$, $(ab)^p = a^p b^p$, $(\frac{a}{b})^p = \frac{a^p}{b^p}$) apply universally when $p$ and $q$ are rational numbers (assuming the base is positive). Numerous examples show how to simplify complex expressions involving fractional exponents using these generalized laws.
Regarding the rationalized syllabus for 2024-25, Chapter 1, "Number Systems," in the Class 9 NCERT textbook has seen some streamlining. Notably, exercises related to visualizing real numbers through successive magnification on the number line have been removed. The core concepts regarding rational/irrational numbers, number line representation of irrationals, operations, rationalization, and laws of exponents with rational powers remain central. By diligently working through these comprehensive solutions, students can build a robust understanding of the real number system, master essential algebraic manipulations involving radicals and exponents, and establish a critical foundation for subsequent mathematical studies.
Example 1 & 2 (Before Exercise 1.1)
Example 1: Are the following statements true or false? Give reasons for your answers.
(i) Every whole number is a natural number.
(ii) Every integer is a rational number.
(iii) Every rational number is an integer.
Answer:
(i) The provided statement is: Every whole number is a natural number.
The given statement is false.
- The set of Whole Numbers is {0, 1, 2, 3, ...}.
- The set of Natural Numbers is {1, 2, 3, ...}.
- The number 0 is included in the set of whole numbers but is not included in the set of natural numbers.
- Since there exists at least one whole number (0) that is not a natural number, the statement is false.
(ii) The provided statement is: Every integer is a rational number.
The given statement is true.
- A rational number is any number that can be expressed in the form $\frac{p}{q}$, where p and q are integers and q ≠ 0.
- Any integer 'm' can be written in the form $\frac{m}{1}$.
- In this form, p = m (an integer) and q = 1 (an integer, and 1 ≠ 0).
- Therefore, every integer satisfies the definition of a rational number.
(iii) The provided statement is: Every rational number is an integer.
The given statement is false.
- A rational number is any number that can be expressed in the form $\frac{p}{q}$, where p and q are integers and q ≠ 0.
- Integers are whole numbers and their negatives {..., -2, -1, 0, 1, 2, ...}.
- Consider the number $\frac{1}{2}$. Here, p=1 and q=2. Both are integers and q ≠ 0, so $\frac{1}{2}$ is a rational number.
- However, $\frac{1}{2}$ (or 0.5) is not an integer.
- Since we found a rational number that is not an integer, the statement that *every* rational number is an integer is false. (Other examples include $\frac{3}{4}$, $-\frac{2}{5}$, etc.)
Example 2: Find five rational numbers between 1 and 2. We can approach this problem in at least two ways.
Answer:

Solution 1:
We need to find five rational numbers between 1 and 2.
One way is to find the average of two numbers to find a rational number between them.
Let $q_i$ be the rational number between 1 and 2, where i = 1 to 5.
So, five rational numbers can be found as follows:
$q_1 = \frac{1\ +\ 2}{2}=\frac{3}{2};$
This means that $\frac{3}{2}$ is between 1 and 2.
$1 < \frac{3}{2} < 2$
Now find a number between 1 and $\frac{3}{2}$.
$q_2 = \frac{1\ +\ \frac{3}{2}}{2}=\frac{\frac{2+3}{2}}{2}=\frac{\frac{5}{2}}{2}=\frac{5}{4};$
So we have found another rational number.
$1 < \frac{5}{4} < \frac{3}{2} < 2$
Now find a number between 2 and $\frac{3}{2}$.
$q_3 = \frac{2\ +\ \frac{3}{2}}{2}=\frac{\frac{4+3}{2}}{2}=\frac{\frac{7}{2}}{2}=\frac{7}{4};$
So we have found a third rational number.
$1 \ < \frac{5}{4} < \frac{3}{2} < \frac{7}{4} < 2$
Now find a number between $\frac{3}{2}$ and $\frac{5}{4}$.
$q_4 = \frac{\frac{3}{2}\ +\ \frac{5}{4}}{2}=\frac{\frac{6\ +\ 5}{4}}{2}=\frac{\frac{11}{4}}{2}=\frac{11}{8};$
So we have found a fourth rational number.
$1 < \frac{5}{4} < \frac{11}{8} < \frac{3}{2} < \frac{7}{4} < 2$
Now find a number between $\frac{3}{2}$ and $\frac{7}{4}$.
$q_5 = \frac{\frac{3}{2}\ +\ \frac{7}{4}}{2}=\frac{\frac{6\ +\ 7}{4}}{2}=\frac{\frac{13}{4}}{2}=\frac{13}{8};$
So we have found a fifth rational number.
$1 < \frac{5}{4} < \frac{11}{8} < \frac{3}{2} < \frac{13}{8} < \frac{7}{4} < 2$
Thus, the five rational numbers between 1 and 2 found using this method are $\frac{3}{2},\ \frac{5}{4},\ \frac{7}{4},\ \frac{11}{8}$ and $\frac{13}{8}$ .
Solution 2:
We need to find five rational numbers between 1 and 2.
We can write 1 and 2 as rational numbers with a common denominator.
Since we need to find five rational numbers, we can multiply the numerator and denominator by $5+1=6$. We can choose any number greater than 5.
Write 1 as a fraction with denominator 6:
$1 = \frac{1\ \times\ 6}{1\ \times\ 6} = \frac{6}{6}$
Write 2 as a fraction with denominator 6:
$2 = \frac{2\ \times\ 6}{1\ \times\ 6} = \frac{12}{6}$
Now we need to find five rational numbers between $\frac{6}{6}$ and $\frac{12}{6}$.
We can simply list the fractions with denominator 6 and numerators between 6 and 12.
These numbers are $\frac{7}{6},\ \frac{8}{6},\ \frac{9}{6},\ \frac{10}{6},\ \frac{11}{6}$.
All these numbers are greater than $\frac{6}{6}$ (which is 1) and less than $\frac{12}{6}$ (which is 2).
$\frac{6}{6} < \frac{7}{6} < \frac{8}{6} < \frac{9}{6} < \frac{10}{6} < \frac{11}{6} < \frac{12}{6}$
So, five rational numbers between 1 and 2 are $\frac{7}{6},\ \frac{8}{6},\ \frac{9}{6},\ \frac{10}{6},\ \frac{11}{6}$.
Note that $\frac{8}{6}$ can be simplified to $\frac{4}{3}$, $\frac{9}{6}$ to $\frac{3}{2}$, and $\frac{10}{6}$ to $\frac{5}{3}$.
Exercise 1.1
Question 1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0?
Answer:
Yes, zero is a rational number.
A rational number is any number that can be written in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q$ is not equal to zero ($q \neq 0$).
We can write zero in the form $\frac{p}{q}$ in many ways.
For example, we can write:
$0 = \frac{0}{1}$
Here, $p = 0$ and $q = 1$. Both 0 and 1 are integers, and $q=1$ is not zero.
We can also write:
$0 = \frac{0}{2}$
Here, $p = 0$ and $q = 2$. Both 0 and 2 are integers, and $q=2$ is not zero.
We can even use negative integers for $q$:
$0 = \frac{0}{-3}$
Here, $p = 0$ and $q = -3$. Both 0 and -3 are integers, and $q=-3$ is not zero.
Since zero can be expressed as a fraction $\frac{p}{q}$ where $p$ and $q$ are integers and the denominator $q$ is not zero, zero is a rational number.
Question 2. Find six rational numbers between 3 and 4.
Answer:

Solution 1: Using the average method
We need to find six rational numbers between 3 and 4.
We can find a rational number between any two distinct rational numbers by taking their average (sum divided by 2).
Let's find the first rational number, $q_1$, between 3 and 4:
$q_1 = \frac{3\ +\ 4}{2} = \frac{7}{2}$
So, $\frac{7}{2}$ is between 3 and 4.
$3 < \frac{7}{2} < 4$
Now let's find a rational number, $q_2$, between 3 and $\frac{7}{2}$:
$q_2 = \frac{3\ +\ \frac{7}{2}}{2} = \frac{\frac{3 \times 2 + 7}{2}}{2} = \frac{\frac{6+7}{2}}{2} = \frac{\frac{13}{2}}{2} = \frac{13}{2} \times \frac{1}{2} = \frac{13}{4}$
So, $\frac{13}{4}$ is between 3 and $\frac{7}{2}$.
$3 < \frac{13}{4} < \frac{7}{2} < 4$
Now let's find a rational number, $q_3$, between $\frac{7}{2}$ and 4:
$q_3 = \frac{\frac{7}{2}\ +\ 4}{2} = \frac{\frac{7 + 4 \times 2}{2}}{2} = \frac{\frac{7+8}{2}}{2} = \frac{\frac{15}{2}}{2} = \frac{15}{2} \times \frac{1}{2} = \frac{15}{4}$
So, $\frac{15}{4}$ is between $\frac{7}{2}$ and 4.
$3 < \frac{13}{4} < \frac{7}{2} < \frac{15}{4} < 4$
Now let's find a rational number, $q_4$, between $\frac{13}{4}$ and $\frac{7}{2}$:
$q_4 = \frac{\frac{13}{4}\ +\ \frac{7}{2}}{2} = \frac{\frac{13\ +\ 7 \times 2}{4}}{2} = \frac{\frac{13\ +\ 14}{4}}{2} = \frac{\frac{27}{4}}{2} = \frac{27}{4} \times \frac{1}{2} = \frac{27}{8}$
So, $\frac{27}{8}$ is between $\frac{13}{4}$ and $\frac{7}{2}$.
$3 < \frac{13}{4} < \frac{27}{8} < \frac{7}{2} < \frac{15}{4} < 4$
Now let's find a rational number, $q_5$, between $\frac{7}{2}$ and $\frac{15}{4}$:
$q_5 = \frac{\frac{7}{2}\ +\ \frac{15}{4}}{2} = \frac{\frac{7 \times 2\ +\ 15}{4}}{2} = \frac{\frac{14\ +\ 15}{4}}{2} = \frac{\frac{29}{4}}{2} = \frac{29}{4} \times \frac{1}{2} = \frac{29}{8}$
So, $\frac{29}{8}$ is between $\frac{7}{2}$ and $\frac{15}{4}$.
$3 < \frac{13}{4} < \frac{27}{8} < \frac{7}{2} < \frac{29}{8} < \frac{15}{4} < 4$
Now let's find a rational number, $q_6$, between $\frac{13}{4}$ and $\frac{27}{8}$:
$q_6 = \frac{\frac{13}{4}\ +\ \frac{27}{8}}{2} = \frac{\frac{13 \times 2\ +\ 27}{8}}{2} = \frac{\frac{26\ +\ 27}{8}}{2} = \frac{\frac{53}{8}}{2} = \frac{53}{8} \times \frac{1}{2} = \frac{53}{16}$
So, $\frac{53}{16}$ is between $\frac{13}{4}$ and $\frac{27}{8}$.
Placing all the six numbers in order:
$3 < \frac{13}{4} < \frac{53}{16} < \frac{27}{8} < \frac{7}{2} < \frac{29}{8} < \frac{15}{4} < 4$
Thus, six rational numbers between 3 and 4 found using this method are $\frac{7}{2},\ \frac{13}{4},\ \frac{15}{4},\ \frac{27}{8},\ \frac{29}{8}$ and $\frac{53}{16}$ .
Solution 2: Using equivalent fractions
We need to find six rational numbers between 3 and 4.
We can write 3 and 4 as rational numbers with a common denominator.
Since we need to find six rational numbers, we can multiply the numerator and denominator of 3 and 4 by a number greater than 6, for example, $6+1=7$.
Write 3 as a fraction with denominator 7:
$3 = \frac{3}{1} = \frac{3\ \times\ 7}{1\ \times\ 7} = \frac{21}{7}$
Write 4 as a fraction with denominator 7:
$4 = \frac{4}{1} = \frac{4\ \times\ 7}{1\ \times\ 7} = \frac{28}{7}$
Now we need to find six rational numbers between $\frac{21}{7}$ and $\frac{28}{7}$.
Since the denominators are the same, we can find rational numbers by choosing numerators between 21 and 28.
These integers between 21 and 28 are 22, 23, 24, 25, 26, and 27.
So, six rational numbers between $\frac{21}{7}$ and $\frac{28}{7}$ are $\frac{22}{7},\ \frac{23}{7},\ \frac{24}{7},\ \frac{25}{7},\ \frac{26}{7},\ and\ \frac{27}{7}$.
Since $\frac{21}{7} = 3$ and $\frac{28}{7} = 4$, these six fractions are between 3 and 4.
$3 = \frac{21}{7} < \frac{22}{7} < \frac{23}{7} < \frac{24}{7} < \frac{25}{7} < \frac{26}{7} < \frac{27}{7} < \frac{28}{7} = 4$
Thus, six rational numbers between 3 and 4 are $\frac{22}{7},\ \frac{23}{7},\ \frac{24}{7},\ \frac{25}{7},\ \frac{26}{7}$ and $\frac{27}{7}$.
Question 3. Find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ .
Answer:

Solution 1: Using the average method
We need to find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$.
We can find a rational number between any two distinct rational numbers by taking their average (sum divided by 2).
Let's find the first rational number, $q_1$, between $\frac{3}{5}$ and $\frac{4}{5}$:
$q_1 = \frac{\frac{3}{5}\ +\ \frac{4}{5}}{2} = \frac{\frac{3\ +\ 4}{5}}{2} = \frac{\frac{7}{5}}{2} = \frac{7}{5} \times \frac{1}{2} = \frac{7}{10};$
$\therefore \frac{3}{5}<\frac{7}{10}<\frac{4}{5}$
Now let's find a rational number, $q_2$, between $\frac{3}{5}$ and $\frac{7}{10}$:
$q_2 = \frac{\frac{3}{5}\ +\ \frac{7}{10}}{2} = \frac{\frac{3 \times 2}{5 \times 2}\ +\ \frac{7}{10}}{2} = \frac{\frac{6}{10}\ +\ \frac{7}{10}}{2} = \frac{\frac{6\ +\ 7}{10}}{2} = \frac{\frac{13}{10}}{2} = \frac{13}{10} \times \frac{1}{2} = \frac{13}{20};$
$\therefore \frac{3}{5}<\frac{13}{20}<\frac{7}{10}<\frac{4}{5}$
Now let's find a rational number, $q_3$, between $\frac{7}{10}$ and $\frac{4}{5}$:
$q_3 = \frac{\frac{7}{10}\ +\ \frac{4}{5}}{2} = \frac{\frac{7}{10}\ +\ \frac{4 \times 2}{5 \times 2}}{2} = \frac{\frac{7}{10}\ +\ \frac{8}{10}}{2} = \frac{\frac{7\ +\ 8}{10}}{2} = \frac{\frac{15}{10}}{2} = \frac{15}{10} \times \frac{1}{2} = \frac{15}{20};$
$\therefore \frac{3}{5}<\frac{13}{20}<\frac{7}{10}<\frac{15}{20}<\frac{4}{5}$
Now let's find a rational number, $q_4$, between $\frac{13}{20}$ and $\frac{7}{10}$:
$q_4 = \frac{\frac{13}{20}\ +\ \frac{7}{10}}{2} = \frac{\frac{13}{20}\ +\ \frac{7 \times 2}{10 \times 2}}{2} = \frac{\frac{13}{20}\ +\ \frac{14}{20}}{2} = \frac{\frac{13\ +\ 14}{20}}{2} = \frac{\frac{27}{20}}{2} = \frac{27}{20} \times \frac{1}{2} = \frac{27}{40};$
$\therefore \frac{3}{5}<\frac{13}{20}<\frac{27}{40}<\frac{7}{10}<\frac{15}{20}<\frac{4}{5}$
Now let's find a rational number, $q_5$, between $\frac{7}{10}$ and $\frac{15}{20}$:
$q_5 = \frac{\frac{7}{10}\ +\ \frac{15}{20}}{2} = \frac{\frac{7 \times 2}{10 \times 2}\ +\ \frac{15}{20}}{2} = \frac{\frac{14}{20}\ +\ \frac{15}{20}}{2} = \frac{\frac{14\ +\ 15}{20}}{2} = \frac{\frac{29}{20}}{2} = \frac{29}{20} \times \frac{1}{2} = \frac{29}{40};$
$\therefore \frac{3}{5}<\frac{13}{20}<\frac{27}{40}<\frac{7}{10}<\frac{29}{40}<\frac{15}{20}<\frac{4}{5}$
Thus, the five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ found using this method are $\frac{7}{10},\ \frac{13}{20},\ \frac{15}{20},\ \frac{27}{40}$ and $\frac{29}{40}$ .
Solution 2: Using equivalent fractions
We need to find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$.
We can write $\frac{3}{5}$ and $\frac{4}{5}$ as rational numbers with a common denominator.
Since we need to find five rational numbers, we can multiply the numerator and denominator by a number greater than 5, for example, $5+1=6$.
Write $\frac{3}{5}$ as an equivalent fraction with denominator $5 \times 6 = 30$:
$\frac{3}{5}=\frac{3\ \times\ 6}{5\ \times\ 6}=\frac{18}{30}$
Write $\frac{4}{5}$ as an equivalent fraction with denominator $5 \times 6 = 30$:
$\frac{4}{5}=\frac{4\ \times\ 6}{5\ \times\ 6}=\frac{24}{30}$
Now we need to find five rational numbers between $\frac{18}{30}$ and $\frac{24}{30}$.
Since the denominators are the same, we can find rational numbers by choosing numerators between 18 and 24.
These integers between 18 and 24 are 19, 20, 21, 22, and 23.
So, five rational numbers between $\frac{18}{30}$ and $\frac{24}{30}$ are $\frac{19}{30},\ \frac{20}{30},\ \frac{21}{30},\ \frac{22}{30},\ and\ \frac{23}{30}$.
Since $\frac{18}{30} = \frac{3}{5}$ and $\frac{24}{30} = \frac{4}{5}$, these five fractions are between $\frac{3}{5}$ and $\frac{4}{5}$.
$\frac{3}{5} = \frac{18}{30} < \frac{19}{30} < \frac{20}{30} < \frac{21}{30} < \frac{22}{30} < \frac{23}{30} < \frac{24}{30} = \frac{4}{5}$
Thus, five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ are $\frac{19}{30},\ \frac{20}{30},\ \frac{21}{30},\ \frac{22}{30}$ and $\frac{23}{30}$.
Note that some of these fractions can be simplified: $\frac{20}{30} = \frac{2}{3}$, $\frac{21}{30} = \frac{7}{10}$, $\frac{22}{30} = \frac{11}{15}$.
So the five rational numbers can also be written as $\frac{19}{30},\ \frac{2}{3},\ \frac{7}{10},\ \frac{11}{15},\ and\ \frac{23}{30}$.
Question 4. State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Answer:
(i) The provided statement is: Every natural number is a whole number.
The given statement is true.
- The set of Natural Numbers is {1, 2, 3, ...}.
- The set of Whole Numbers is {0, 1, 2, 3, ...}.
- Every number in the set of natural numbers is also present in the set of whole numbers.
- Therefore, every natural number is indeed a whole number.
(ii) The provided statement is: Every integer is a whole number.
The given statement is false.
- The set of Integers is {..., -3, -2, -1, 0, 1, 2, 3, ...}.
- The set of Whole Numbers is {0, 1, 2, 3, ...}.
- Integers include negative numbers, such as -1, -2, -3, etc.
- Whole numbers are non-negative and start from 0.
- Since there exist integers (like -1, -2, etc.) that are not whole numbers, the statement is false.
(iii) The provided statement is: Every rational number is a whole number.
The given statement is false.
- A rational number is any number that can be expressed in the form $\frac{p}{q}$, where p and q are integers and q ≠ 0.
- Whole Numbers are non-negative integers starting from 0 (i.e., 0, 1, 2, 3,...).
- Consider the rational number $\frac{1}{2}$. Here, p=1 and q=2, both integers and q ≠ 0.
- Thus, $\frac{1}{2}$ is a rational number. However, $\frac{1}{2}$ (or 0.5) is not a whole number.
- Since we have found a rational number that is not a whole number, the statement that *every* rational number is a whole number is false. (Other examples: $\frac{3}{4}$, $-\frac{2}{5}$, etc.)
Example 3 & 4 (Before Exercise 1.2)
Example 3: Locate $\sqrt{2}$ on the number line.
Answer:
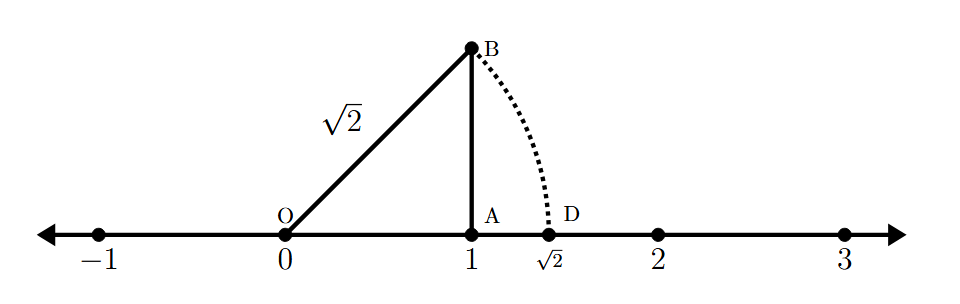
Construction Steps:
1. Draw a number line. Mark a point O on it to represent 0.
2. Mark a point A on the number line at a distance of 1 unit from O to the right. So, OA = 1 unit.
3. At point A, draw a line segment AB perpendicular to OA, such that the length of AB is also 1 unit.
4. Join the points O and B. We now have a right-angled triangle OAB, with the right angle at A.
Explanation:
In the right-angled triangle OAB, we can use the Pythagoras theorem to find the length of the hypotenuse OB.
$OB^2 = OA^2 + AB^2$
(By Pythagoras Theorem)
Substitute the lengths of OA and AB, which are both 1 unit:
$OB^2 = 1^2 + 1^2$
$OB^2 = 1 + 1$
$OB^2 = 2$
To find the length OB, we take the square root of both sides:
$OB = \sqrt{2}$
So, the length of the line segment OB is $\sqrt{2}$ units.
Locating $\sqrt{2}$ on the Number Line:
1. With O as the centre and OB as the radius, draw an arc that cuts the number line.
2. The point where the arc cuts the number line (to the right of O) represents the number $\sqrt{2}$. Let's call this point P.
Thus, the point P on the number line is at a distance of $\sqrt{2}$ units from 0, representing the irrational number $\sqrt{2}$.
Example 4: Locate $\sqrt{3}$ on the number line.
Answer:
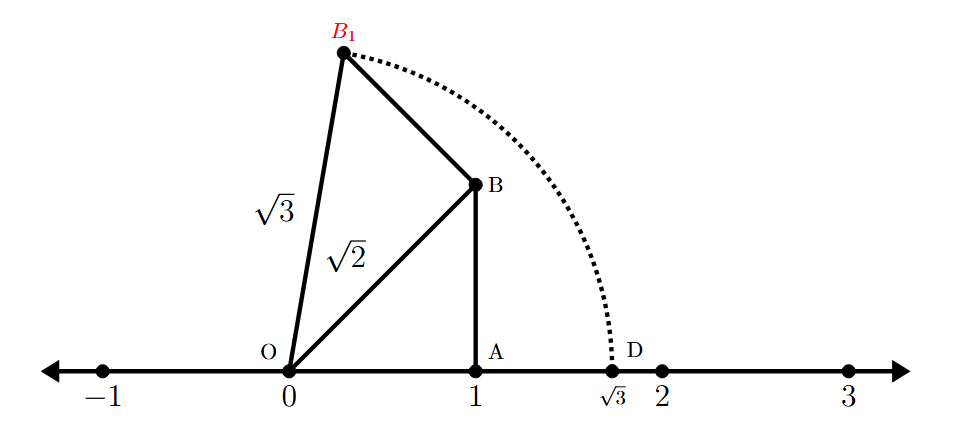
Construction Steps:
To locate $\sqrt{3}$ on the number line, we first need to locate $\sqrt{2}$ on the number line, as $\sqrt{3} = \sqrt{(\sqrt{2})^2 + 1^2}$.
1. Draw a number line. Mark a point O on it to represent 0.
2. Mark a point A on the number line at a distance of 1 unit from O to the right. So, OA = 1 unit.
3. At point A, draw a line segment AB perpendicular to OA, such that the length of AB is also 1 unit.
4. Join the points O and B.
Finding the length of OB:
In the right-angled triangle OAB, using the Pythagoras theorem:
$OB^2 = OA^2 + AB^2$
(By Pythagoras Theorem)
Substitute OA = 1 unit and AB = 1 unit:
$OB^2 = 1^2 + 1^2$
$OB^2 = 1 + 1$
$OB^2 = 2$
Taking the square root on both sides:
$OB = \sqrt{2}$
So, the length of OB is $\sqrt{2}$ units.
Continuing the Construction for $\sqrt{3}$:
5. Now, from point B (which is at a distance of $\sqrt{2}$ from O), draw a line segment BB$_1$ perpendicular to OB, such that the length of BB$_1$ is 1 unit.
6. Join the points O and B$_1$. We now have another right-angled triangle OBB$_1$, with the right angle at B.
Finding the length of OB$_1$:
In the right-angled triangle OBB$_1$, using the Pythagoras theorem:
$OB_1^2 = OB^2 + BB_1^2$
(Pythagoras Theorem)
Substitute OB = $\sqrt{2}$ units and BB$_1$ = 1 unit:
$OB_1^2 = (\sqrt{2})^2 + 1^2$
$OB_1^2 = 2 + 1$
$OB_1^2 = 3$
Taking the square root on both sides:
$OB_1 = \sqrt{3}$
So, the length of OB$_1$ is $\sqrt{3}$ units.
Locating $\sqrt{3}$ on the Number Line:
1. With O as the centre and OB$_1$ as the radius, draw an arc that cuts the number line.
2. The point where the arc cuts the number line (to the right of O) represents the number $\sqrt{3}$. Let's call this point D.
Thus, the point D on the number line is at a distance of $\sqrt{3}$ units from 0, representing the irrational number $\sqrt{3}$.
Exercise 1.2
Question 1. State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form $\sqrt{m}$ , where m is a natural number.
(iii) Every real number is an irrational number.
Answer:
(i) The provided statement is: Every irrational number is a real number.
The given statement is true.
- The set of Real Numbers is defined as the collection (union) of all Rational Numbers and all Irrational Numbers.
- Therefore, by definition, every irrational number falls within the category of real numbers.
(ii) The provided statement is: Every point on the number line is of the form $\sqrt{\mathbf{m}}$, where m is a natural number.
The given statement is false.
- The number line represents all real numbers, including negative numbers and positive numbers that are not perfect squares.
- The expression $\sqrt{m}$, where m is a natural number (m = 1, 2, 3, ...), can only represent non-negative numbers (e.g., $\sqrt{1}=1$, $\sqrt{2}$, $\sqrt{3}$, $\sqrt{4}=2$, etc.).
- Negative numbers, such as -1, -2, etc., are points on the number line but cannot be represented in the form $\sqrt{m}$ because the square root of a natural number is never negative.
- Furthermore, many positive real numbers like 0.5 or $\frac{3}{4}$ are on the number line, but they cannot be written as $\sqrt{m}$ where m is a natural number (e.g., if $\sqrt{m} = 0.5$, then $m = 0.25$, which is not natural).
- Since there are many points on the number line (negative numbers, certain positive fractions/decimals) that do not fit the form $\sqrt{m}$ (with m being natural), the statement is false.
(iii) The provided statement is: Every real number is an irrational number.
The given statement is false.
- The set of Real Numbers includes both Rational Numbers and Irrational Numbers.
- Rational numbers, such as 2 (which can be written as $\frac{2}{1}$) or $\frac{1}{2}$, are real numbers.
- However, these rational numbers are, by definition, *not* irrational numbers.
- Since there exist real numbers (the rationals) that are not irrational, the statement that *every* real number is irrational is false.
Question 2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Answer:
No, the square roots of all positive integers are not irrational.
An irrational number is a number that cannot be expressed as a simple fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. Rational numbers can be expressed in this form.
Consider the positive integers which are perfect squares, such as 4, 9, 16, 25, etc.
Here are some examples of the square roots of such numbers:
The square root of 4 is 2.
$\sqrt{4} = 2$
We can write 2 as a rational number $\frac{2}{1}$. Here $p=2$ and $q=1$, which are integers and $q \neq 0$.
The square root of 9 is 3.
$\sqrt{9} = 3$
We can write 3 as a rational number $\frac{3}{1}$. Here $p=3$ and $q=1$, which are integers and $q \neq 0$.
The square root of 16 is 4.
$\sqrt{16} = 4$
We can write 4 as a rational number $\frac{4}{1}$. Here $p=4$ and $q=1$, which are integers and $q \neq 0$.
Since the square roots of positive integers like 4, 9, and 16 can be written in the form $\frac{p}{q}$, they are rational numbers.
Therefore, the square roots of all positive integers are not irrational.
An example of the square root of a number that is a rational number is $\sqrt{4}=2$.
Question 3. Show how $\sqrt{5}$ can be represented on the number line.
Answer:
Solution 1: Using the spiral construction
We can locate $\sqrt{5}$ on the number line by constructing a spiral of right-angled triangles. We start by locating $\sqrt{2}$, then $\sqrt{3}$, then $\sqrt{4}$, and finally $\sqrt{5}$.
We use the Pythagorean theorem which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Step 1: Locate $\sqrt{2}$
Draw a number line and mark a point O to represent 0.
Mark a point A on the number line such that OA = 1 unit.
At point A, draw a line segment AB perpendicular to OA, such that AB = 1 unit.
Join OB. In the right-angled triangle OAB:
$OB^2 = OA^2 + AB^2$
(Pythagoras Theorem)
$OB^2 = 1^2 + 1^2 = 1 + 1 = 2$
$OB = \sqrt{2}$ units.
Step 2: Locate $\sqrt{3}$
At point B, draw a line segment $BB_1$ perpendicular to OB, such that $BB_1 = 1$ unit.
Join $OB_1$. In the right-angled triangle OBB$_1$:
$OB_1^2 = OB^2 + BB_1^2$
(Pythagoras Theorem)
$OB_1^2 = (\sqrt{2})^2 + 1^2 = 2 + 1 = 3$
$OB_1 = \sqrt{3}$ units.
Step 3: Locate $\sqrt{4}$ ($=2$)
At point $B_1$, draw a line segment $B_1B_2$ perpendicular to $OB_1$, such that $B_1B_2 = 1$ unit.
Join $OB_2$. In the right-angled triangle OB$_1$B$_2$:
$OB_2^2 = OB_1^2 + B_1B_2^2$
(Pythagoras Theorem)
$OB_2^2 = (\sqrt{3})^2 + 1^2 = 3 + 1 = 4$
$OB_2 = \sqrt{4} = 2$ units.
Step 4: Locate $\sqrt{5}$
At point $B_2$ (which is at a distance of 2 units from O on the number line if projected), draw a line segment $B_2B_3$ perpendicular to $OB_2$, such that $B_2B_3 = 1$ unit.
Join $OB_3$. In the right-angled triangle OB$_2$B$_3$:
$OB_3^2 = OB_2^2 + B_2B_3^2$
(Pythagoras Theorem)
$OB_3^2 = (2)^2 + 1^2 = 4 + 1 = 5$
$OB_3 = \sqrt{5}$ units.
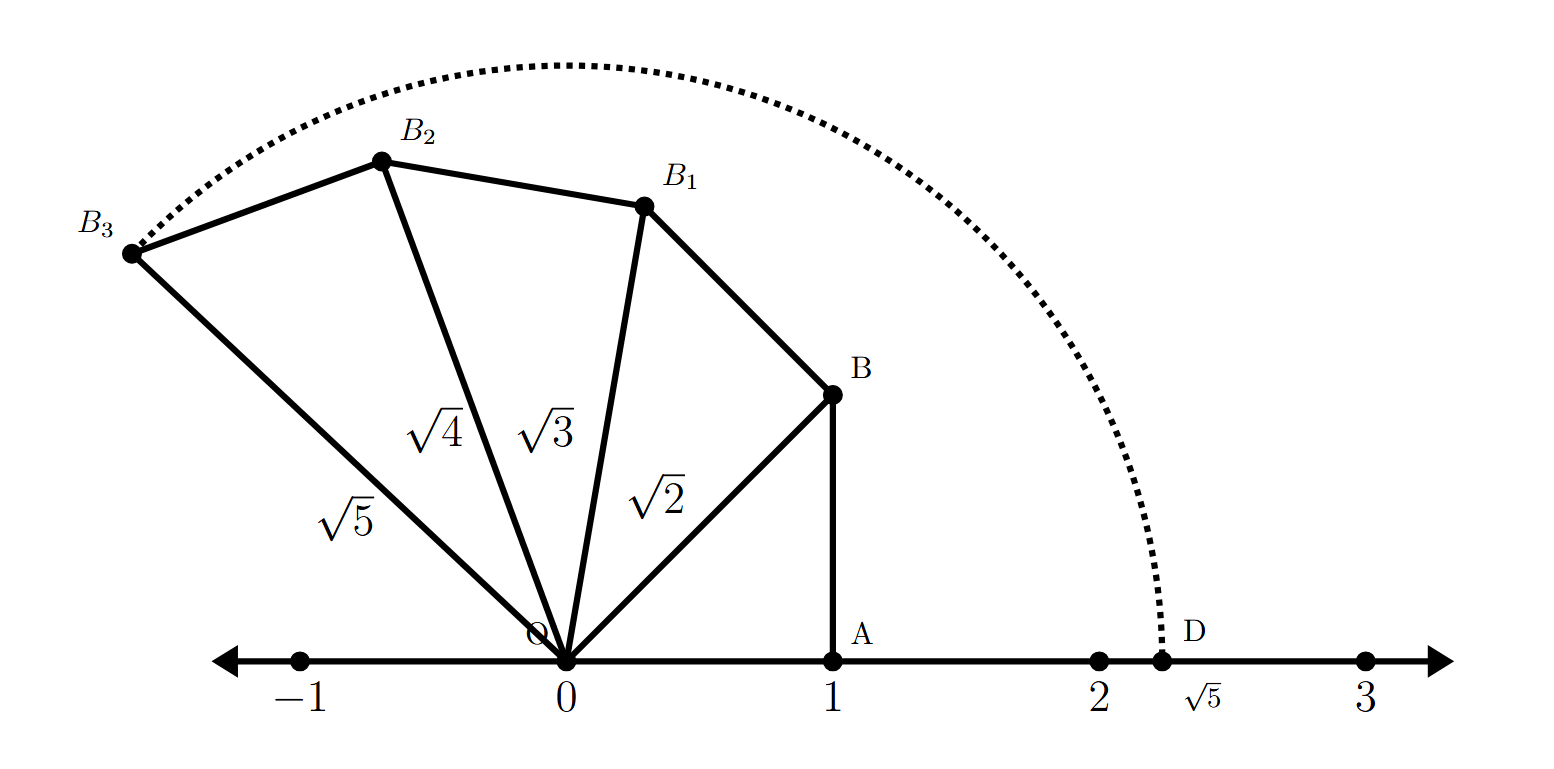
Step 5: Project onto the number line
With O as the centre and $OB_3$ as the radius, draw an arc that cuts the number line at point D.
The distance OD is equal to $OB_3$, which is $\sqrt{5}$ units.
Therefore, the point D on the number line represents $\sqrt{5}$.
Solution 2: Using direct construction
We know that $\sqrt{5}$ can be obtained from a right-angled triangle with legs of lengths $a$ and $b$ such that $a^2 + b^2 = (\sqrt{5})^2 = 5$.
We can write 5 as the sum of squares of two integers: $5 = 2^2 + 1^2$.
This means we can construct a right-angled triangle with legs of length 2 units and 1 unit. The hypotenuse of such a triangle will have length $\sqrt{2^2 + 1^2} = \sqrt{5}$ units.
Method A: Base = 2 units, Perpendicular = 1 unit
Draw a number line and mark a point O to represent 0.
Mark a point A on the number line such that OA = 2 units. Point A is at position 2 on the number line.
At point A, draw a line segment AB perpendicular to OA, such that AB = 1 unit.
Join OB. In the right-angled triangle OAB:
$OB^2 = OA^2 + AB^2$
(Pythagoras Theorem)
$OB^2 = 2^2 + 1^2 = 4 + 1 = 5$
$OB = \sqrt{5}$ units.

With O as the centre and OB as the radius, draw an arc that cuts the number line at point D.
The distance OD is equal to OB, which is $\sqrt{5}$ units.
Therefore, the point D on the number line represents $\sqrt{5}$.
Method B: Base = 1 unit, Perpendicular = 2 units
Draw a number line and mark a point O to represent 0.
Mark a point A on the number line such that OA = 1 unit. Point A is at position 1 on the number line.
At point A, draw a line segment AB perpendicular to OA, such that AB = 2 units.
Join OB. In the right-angled triangle OAB:
$OB^2 = OA^2 + AB^2$
(Pythagoras Theorem)
$OB^2 = 1^2 + 2^2 = 1 + 4 = 5$
$OB = \sqrt{5}$ units.
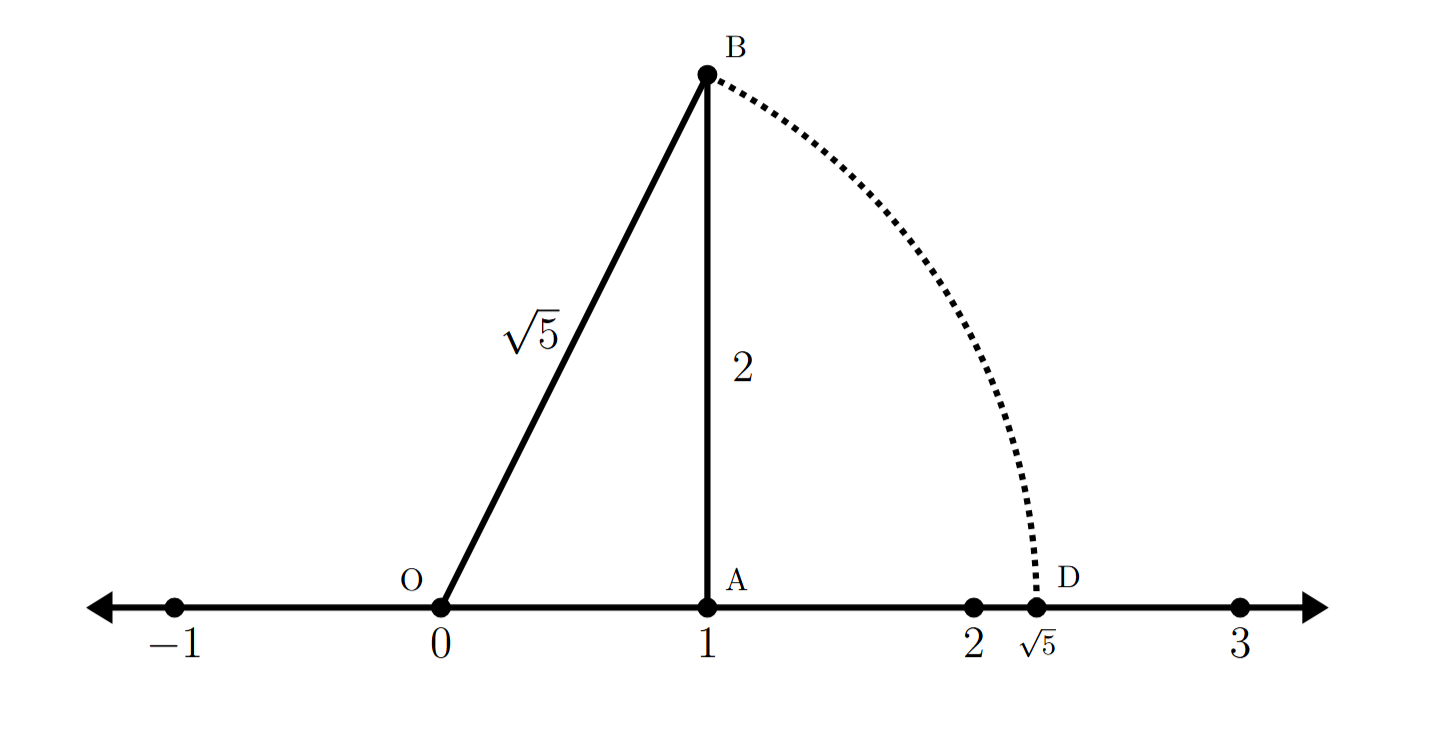
With O as the centre and OB as the radius, draw an arc that cuts the number line at point D.
The distance OD is equal to OB, which is $\sqrt{5}$ units.
Therefore, the point D on the number line represents $\sqrt{5}$.
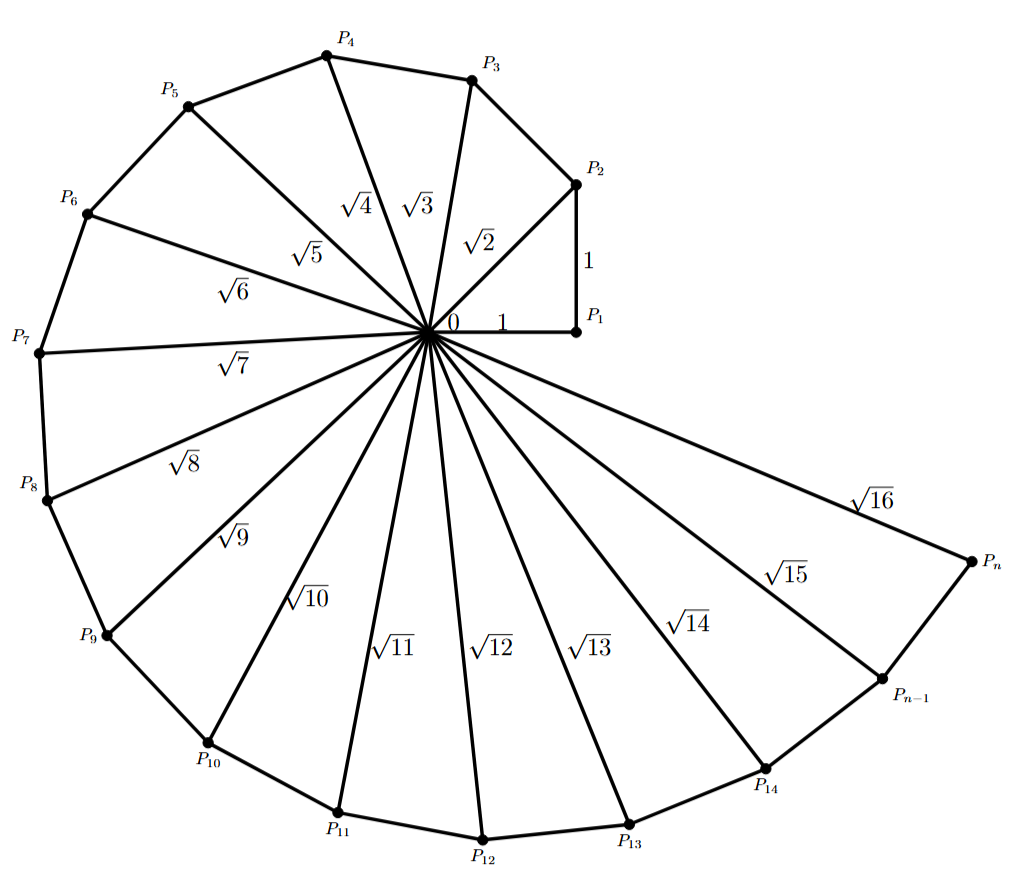
Question 4. Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2, P3,...., Pn,... ., and joined them to create a beautiful spiral depicting $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{4}$ ,…..
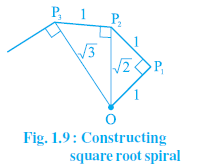
Answer:
Procedure:
- Choose a Unit Length: Decide on a standard length for "1 unit" (e.g., 2 cm, 3 cm, or 1 inch). Using a larger unit makes the initial steps clearer.
- Starting Point ($O$): Mark a point $O$ near the center of your paper. This is your origin.
- Draw $OP_1$: From $O$, draw a horizontal line segment $OP_1$ to the right, with a length equal to 1 unit.
- Draw $P_1P_2$: At point $P_1$, use your protractor or set square to draw a line segment $P_1P_2$ that is perpendicular (at a $90^\circ$ angle) to $OP_1$. Make the length of $P_1P_2$ equal to 1 unit.
- Draw Hypotenuse $OP_2$: Connect point $O$ to point $P_2$. Triangle $OP_1P_2$ is a right-angled triangle.
- Draw $P_2P_3$: At point $P_2$, draw a line segment $P_2P_3$ that is perpendicular to the hypotenuse $OP_2$. Make the length of $P_2P_3$ equal to 1 unit.
- Draw Hypotenuse $OP_3$: Connect point $O$ to point $P_3$. Triangle $OP_2P_3$ is a right-angled triangle.
- Draw $P_3P_4$: At point $P_3$, draw a line segment $P_3P_4$ that is perpendicular to the hypotenuse $OP_3$. Make the length of $P_3P_4$ equal to 1 unit.
- Draw Hypotenuse $OP_4$: Connect point $O$ to point $P_4$. Triangle $OP_3P_4$ is a right-angled triangle.
- Continue the Pattern: Repeat the process. For each step $n$:
- At point $P_{n-1}$, draw a segment $P_{n-1}P_n$ of 1 unit length, perpendicular to the hypotenuse $OP_{n-1}$.
- Connect $O$ to $P_n$. The length of this new hypotenuse $OP_n$ will be $\sqrt{n}$ units.
Calculation (Pythagorean Theorem):
$$(OP_2)^2 = (OP_1)^2 + (P_1P_2)^2 = 1^2 + 1^2 = 1 + 1 = 2$$
Therefore, the length of $\mathbf{OP_2 = \sqrt{2}}$ units.
Calculation (Pythagorean Theorem):
$(OP_3)^2 = (OP_2)^2 + (P_2P_3)^2 = (\sqrt{2})^2 + 1^2 = 2 + 1 = 3$
Therefore, the length of $\mathbf{OP_3 = \sqrt{3}}$ units.
Calculation (Pythagorean Theorem):
$(OP_4)^2 = (OP_3)^2 + (P_3P_4)^2 = (\sqrt{3})^2 + 1^2 = 3 + 1 = 4$
Therefore, the length of $\mathbf{OP_4 = \sqrt{4} = 2}$ units.
Outcome:
As you continue constructing points $P_5, P_6, P_7, \dots$, you will create a spiral shape. The lengths of the hypotenuses $OP_1, OP_2, OP_3, OP_4, OP_5, \dots$ will be $1, \sqrt{2}, \sqrt{3}, \sqrt{4} (=2), \sqrt{5}, \dots$ respectively, visually demonstrating these irrational (and some rational) square root lengths.
Example 5 to 10 (Before Exercise 1.3)
Example 5: Find the decimal expansions of $\frac{10}{3}$ , $\frac{7}{8}$ and $\frac{1}{7}$ .
Answer:
We perform long division to find the decimal expansion of each fraction.
Decimal Expansion of $\frac{10}{3}$:
Performing long division of 10 by 3:
$\begin{array}{r} 3.333... \\ 3{\overline{\smash{\big)}\,10.000\phantom{)}}} \\ \underline{-~\phantom{(}9\phantom{-b)}} \\ 10\phantom{00)} \\ \underline{-~\phantom{()}9\phantom{00)}} \\ 10\phantom{0)} \\ \underline{-~\phantom{()})9\phantom{0)}} \\ 10\phantom{)} \\ \underline{-~\phantom{()})9\phantom{)}} \\ 1\phantom{)} \end{array}$
The remainder 1 repeats at every step.
Therefore, the decimal expansion of $\frac{10}{3}$ is $3.333...$.
We write this as $\mathbf{3.\overline{3}}$.
This is a non-terminating recurring decimal expansion.
Decimal Expansion of $\frac{7}{8}$:
Performing long division of 7 by 8:
$\begin{array}{r} 0.875 \\ 8{\overline{\smash{\big)}\,7.000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{-b)}} \\ 70\phantom{00)} \\ \underline{-~\phantom{()}64\phantom{0)}} \\ 60\phantom{0)} \\ \underline{-~\phantom{()})56\phantom{0)}} \\ 40\phantom{)} \\ \underline{-~\phantom{()})40\phantom{)}} \\ 0\phantom{)} \end{array}$
The remainder becomes 0.
Therefore, the decimal expansion of $\frac{7}{8}$ is $\mathbf{0.875}$.
This is a terminating decimal expansion.
Decimal Expansion of $\frac{1}{7}$:
Performing long division of 1 by 7:
$\begin{array}{r} 0.142857... \\ 7{\overline{\smash{\big)}\,1.000000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{-b)}} \\ 10\phantom{00000)} \\ \underline{-~\phantom{()})7\phantom{00000)}} \\ 30\phantom{0000)} \\ \underline{-~\phantom{()})28\phantom{0000)}} \\ 20\phantom{000)} \\ \underline{-~\phantom{()})14\phantom{000)}} \\ 60\phantom{00)} \\ \underline{-~\phantom{()})56\phantom{00)}} \\ 40\phantom{0)} \\ \underline{-~\phantom{()})35\phantom{0)}} \\ 50\phantom{)} \\ \underline{-~\phantom{()})49\phantom{)}} \\ 1\phantom{)} \end{array}$
The remainder 1 repeats, and the block of digits 142857 in the quotient repeats.
Therefore, the decimal expansion of $\frac{1}{7}$ is $0.142857142857...$.
We write this as $\mathbf{0.\overline{142857}}$.
This is a non-terminating recurring decimal expansion.
Example 6: Show that 3.142678 is a rational number. In other words, express 3.142678 in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0.
Answer:
Given:
The number 3.142678.
To Show:
That 3.142678 is a rational number by expressing it in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Solution:
A number is rational if it can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
The given number is $3.142678$.
This is a terminating decimal expansion.
A terminating decimal can be expressed as a fraction by writing the number without the decimal point as the numerator and a power of 10 corresponding to the number of decimal places as the denominator.
The number of decimal places in 3.142678 is 6.
So, we can write:
$3.142678 = \frac{3142678}{1000000}$
Here, $p = 3142678$ and $q = 1000000$.
$p$ and $q$ are both integers, and $q = 1000000 \neq 0$.
Therefore, 3.142678 can be expressed in the form $\frac{p}{q}$.
We have shown that $3.142678 = \frac{3142678}{1000000}$.
Since the number can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$, it is a rational number.
(Note: This fraction can be simplified by dividing the numerator and denominator by their greatest common divisor, which is 2 in this case, yielding $\frac{1571339}{500000}$. However, the question only requires expressing it in the form $\frac{p}{q}$, which we have done with $\frac{3142678}{1000000}$.)
Conclusion:
The number $3.142678$ is a rational number as it can be written as the fraction $\mathbf{\frac{3142678}{1000000}}$.
Example 7: Show that 0.3333... = 0.$\overline{3}$ can be expressed in the form $\frac{p}{q}$ ,, where p and q are integers and q ≠ 0.
Answer:
Given:
The recurring decimal $0.3333... = 0.\overline{3}$.
To Show:
That $0.\overline{3}$ can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Solution:
Let $x$ be the given decimal number.
$x = 0.3333...$
$x = 0.\overline{3}$
... (i)
Since only one digit is repeating after the decimal point, we multiply equation (i) by 10.
$10x = 3.3333...$
... (ii)
Now, subtract equation (i) from equation (ii):
$10x - x = 3.3333... - 0.3333...$
$9x = 3$
(Subtracting (i) from (ii))
Now, solve for $x$:
$x = \frac{3}{9}$
Simplify the fraction:
$x = \frac{1}{3}$
Here, $p = 1$ and $q = 3$.
Both $p$ and $q$ are integers, and $q = 3 \neq 0$.
Thus, $0.\overline{3}$ can be expressed in the form $\frac{p}{q}$.
Conclusion:
The number $0.\overline{3}$ is a rational number because it can be expressed as the fraction $\mathbf{\frac{1}{3}}$.
Example 8: Show that 1.272727... = 1.$\overline{27}$ can be expressed in the form $\frac{p}{q}$ , , where p and q are integers and q ≠ 0.
Answer:
Given:
The recurring decimal $1.272727... = 1.\overline{27}$.
To Show:
That $1.\overline{27}$ can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Solution:
Let $x$ be the given decimal number.
$x = 1.272727...$
$x = 1.\overline{27}$
... (i)
Since two digits (27) are repeating after the decimal point, we multiply equation (i) by $10^2 = 100$.
$100x = 127.272727...$
... (ii)
Now, subtract equation (i) from equation (ii):
$100x - x = 127.272727... - 1.272727...$
$99x = 126$
(Subtracting (i) from (ii))
Now, solve for $x$:
$x = \frac{126}{99}$
We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 9.
$x = \frac{\cancel{126}^{14}}{\cancel{99}_{11}}$
$x = \frac{14}{11}$
Here, $p = 14$ and $q = 11$.
Both $p$ and $q$ are integers, and $q = 11 \neq 0$.
Thus, $1.\overline{27}$ can be expressed in the form $\frac{p}{q}$.
Conclusion:
The number $1.\overline{27}$ is a rational number because it can be expressed as the fraction $\mathbf{\frac{14}{11}}$.
Example 9: Show that 0.2353535... = 0.2$\overline{35}$ can be expressed in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0.
Answer:
Given:
The recurring decimal $0.2353535... = 0.2\overline{35}$.
To Show:
That $0.2\overline{35}$ can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Solution:
Let $x$ be the given decimal number.
$x = 0.2353535...$
$x = 0.2\overline{35}$
... (i)
Here, one digit (2) is not repeating and two digits (35) are repeating after the decimal point.
First, multiply equation (i) by 10 to move the non-repeating part to the left of the decimal point.
$10x = 2.353535...$
... (ii)
Now, in equation (ii), the repeating block $\overline{35}$ starts immediately after the decimal point.
Since there are two digits in the repeating block, multiply equation (ii) by $10^2 = 100$.
$100 \times (10x) = 100 \times (2.353535...)$
$1000x = 235.353535...$
... (iii)
Now, subtract equation (ii) from equation (iii) to eliminate the repeating part:
$1000x - 10x = 235.353535... - 2.353535...$
$990x = 233$
(Subtracting (ii) from (iii))
Now, solve for $x$:
$x = \frac{233}{990}$
Here, $p = 233$ and $q = 990$.
Both $p$ and $q$ are integers, and $q = 990 \neq 0$.
The fraction $\frac{233}{990}$ cannot be simplified further as 233 is a prime number and 990 is not divisible by 233.
Thus, $0.2\overline{35}$ can be expressed in the form $\frac{p}{q}$.
Conclusion:
The number $0.2\overline{35}$ is a rational number because it can be expressed as the fraction $\mathbf{\frac{233}{990}}$.
Example 10: Find an irrational number between $\frac{1}{7}$ and $\frac{2}{7}$ .
Answer:
Given:
The rational numbers $\frac{1}{7}$ and $\frac{2}{7}$.
To Find:
An irrational number between $\frac{1}{7}$ and $\frac{2}{7}$.
Solution:
First, find the decimal expansions of $\frac{1}{7}$ and $\frac{2}{7}$.
The decimal expansion of $\frac{1}{7}$ is found by long division (as shown in a previous example):
$\frac{1}{7} = 0.142857142857...$
$ = 0.\overline{142857}$
Now, find the decimal expansion of $\frac{2}{7}$:
$\frac{2}{7} = 2 \times \frac{1}{7} = 2 \times 0.\overline{142857}$
$\frac{2}{7} = 2 \times 0.142857142857...$
So, the repeating block is $285714$.
$\frac{2}{7} = 0.285714285714...$
$ = 0.\overline{285714}$
We need to find an irrational number between $0.\overline{142857}$ and $0.\overline{285714}$.
An irrational number has a non-terminating and non-recurring decimal expansion.
We can construct such a number by choosing digits that fall between the two decimal expansions and ensure the digits do not repeat in a pattern.
Consider a number starting with $0.15...$ (which is greater than $0.142857...$) and less than $0.285714...$
Let's pick a number like $0.15015001500015...$ or $0.16116111611116...$ or $0.2020020002...$
All these numbers are greater than $0.\overline{142857}$ and less than $0.\overline{285714}$. They also have non-terminating and non-recurring decimal expansions by construction.
For example, let's take the number $\mathbf{0.15015001500015...}$.
This number is greater than $0.142857...$ because $0.15 > 0.14$.
This number is less than $0.285714...$ because $0.15 < 0.28$.
The pattern of zeros between the 15s increases ($0.15\underline{0}15\underline{00}15\underline{000}15...$), so the decimal expansion is non-recurring.
Since it is non-terminating and non-recurring, it is an irrational number.
Answer:
An irrational number between $\frac{1}{7}$ and $\frac{2}{7}$ is $\mathbf{0.15015001500015...}$ (or any number with a non-terminating, non-recurring decimal expansion between $0.\overline{142857}$ and $0.\overline{285714}$).
Exercise 1.3
Question 1. Write the following in decimal form and say what kind of decimal expansion each has :
(i) $\frac{36}{100}$
(ii) $\frac{1}{11}$
(iii) $4\frac{1}{8}$
(iv) $\frac{3}{13}$
(v) $\frac{2}{11}$
(vi) $\frac{329}{400}$
Answer:
(i) $\frac{36}{100}$
To find the decimal expansion, we divide 36 by 100.
$\frac{36}{100} = 0.36$
Since the decimal expansion ends after a finite number of digits, it is a terminating decimal expansion.
(ii) $\frac{1}{11}$
To find the decimal expansion, we perform long division of 1 by 11.
$\begin{array}{r} 0.0909... \\ 11{\overline{\smash{\big)}\,1.0000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{-b)}} \\ 100\phantom{00)} \\ \underline{-~\phantom{()}99\phantom{00)}} \\ 10\phantom{0)} \\ \underline{-~\phantom{()})0\phantom{0)}} \\ 100\phantom{)} \\ \underline{-~\phantom{()})99\phantom{)}} \\ 1\phantom{)} \end{array}$
The remainder 1 repeats, and the digits 09 in the quotient repeat.
$\frac{1}{11} = 0.090909... = 0.\overline{09}$
Since the decimal expansion does not end and the digits repeat in a pattern, it is a non-terminating recurring decimal expansion.
(iii) $4\frac{1}{8}$
First, convert the mixed fraction to an improper fraction.
$4\frac{1}{8} = \frac{4 \times 8 + 1}{8} = \frac{32 + 1}{8} = \frac{33}{8}$
Now, perform long division of 33 by 8.
$\begin{array}{r} 4.125 \\ 8{\overline{\smash{\big)}\,33.000\phantom{)}}} \\ \underline{-~\phantom{(}32\phantom{-b)}} \\ 10\phantom{00)} \\ \underline{-~\phantom{()}8\phantom{00)}} \\ 20\phantom{0)} \\ \underline{-~\phantom{()})16\phantom{0)}} \\ 40\phantom{)} \\ \underline{-~\phantom{()})40\phantom{)}} \\ 0\phantom{)} \end{array}$
The remainder becomes 0.
$4\frac{1}{8} = \frac{33}{8} = 4.125$
Since the decimal expansion ends, it is a terminating decimal expansion.
(iv) $\frac{3}{13}$
To find the decimal expansion, we perform long division of 3 by 13.
$\begin{array}{r} 0.230769... \\ 13{\overline{\smash{\big)}\,3.000000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{-b)}} \\ 30\phantom{00000)} \\ \underline{-~\phantom{()}26\phantom{00000)}} \\ 40\phantom{0000)} \\ \underline{-~\phantom{()})39\phantom{0000)}} \\ 10\phantom{000)} \\ \underline{-~\phantom{()})0\phantom{000)}} \\ 100\phantom{00)} \\ \underline{-~\phantom{()})91\phantom{00)}} \\ 90\phantom{0)} \\ \underline{-~\phantom{()})78\phantom{0)}} \\ 120\phantom{)} \\ \underline{-~\phantom{()})117\phantom{)}} \\ 3\phantom{)} \end{array}$
The remainder 3 repeats, and the block of digits 230769 repeats in the quotient.
$\frac{3}{13} = 0.230769230769... = 0.\overline{230769}$
Since the decimal expansion does not end and the digits repeat in a pattern, it is a non-terminating recurring decimal expansion.
(v) $\frac{2}{11}$
To find the decimal expansion, we perform long division of 2 by 11.
$\begin{array}{r} 0.1818... \\ 11{\overline{\smash{\big)}\,2.0000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{-b)}} \\ 20\phantom{000)} \\ \underline{-~\phantom{()}11\phantom{000)}} \\ 90\phantom{00)} \\ \underline{-~\phantom{()})88\phantom{00)}} \\ 20\phantom{0)} \\ \underline{-~\phantom{()})11\phantom{0)}} \\ 90\phantom{)} \\ \underline{-~\phantom{()})88\phantom{)}} \\ 2\phantom{)} \end{array}$
The remainder 2 repeats, and the digits 18 in the quotient repeat.
$\frac{2}{11} = 0.181818... = 0.\overline{18}$
Since the decimal expansion does not end and the digits repeat in a pattern, it is a non-terminating recurring decimal expansion.
(vi) $\frac{329}{400}$
To find the decimal expansion, we perform long division of 329 by 400.
$\begin{array}{r} 0.8225 \\ 400{\overline{\smash{\big)}\,329.0000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{-b)}} \\ 3290\phantom{000)} \\ \underline{-~\phantom{()}3200\phantom{000)}} \\ 900\phantom{00)} \\ \underline{-~\phantom{()})800\phantom{00)}} \\ 1000\phantom{0)} \\ \underline{-~\phantom{()})800\phantom{0)}} \\ 2000\phantom{)} \\ \underline{-~\phantom{()})2000\phantom{)}} \\ 0\phantom{)} \end{array}$
The remainder becomes 0.
$\frac{329}{400} = 0.8225$
Since the decimal expansion ends, it is a terminating decimal expansion.
Question 2. You know that $\frac{1}{7}$ = 0.$\overline{142857}$ Can you predict what the decimal expansions of $\frac{2}{7}$ , $\frac{3}{7}$ , $\frac{4}{7}$ , $\frac{5}{7}$ , $\frac{6}{7}$ are, without actually doing the long division? If so, how?
[Hint : Study the remainders while finding the value of $\frac{1}{7}$ carefully.]
Answer:
Given:
The decimal expansion of $\frac{1}{7} = 0.\overline{142857}$.
To Predict:
The decimal expansions of $\frac{2}{7}$, $\frac{3}{7}$, $\frac{4}{7}$, $\frac{5}{7}$, and $\frac{6}{7}$ without long division.
Solution:
Yes, we can predict the decimal expansions without performing long division for each fraction.
We know that $\frac{n}{7} = n \times \frac{1}{7}$.
Since $\frac{1}{7} = 0.\overline{142857}$, we can find the decimal expansions by multiplying the decimal expansion of $\frac{1}{7}$ by the numerator $n$ (for $n = 2, 3, 4, 5, 6$).
The decimal expansion of $\frac{1}{7}$ is $0.142857142857...$. The repeating block is 142857.
Let's calculate the decimal expansions:
For $\frac{2}{7}$:
$\frac{2}{7} = 2 \times \frac{1}{7} = 2 \times 0.\overline{142857}$
Multiplying 0.142857... by 2:
$2 \times 0.142857... = 0.285714...$
So, $\frac{2}{7} = \mathbf{0.\overline{285714}}$.
For $\frac{3}{7}$:
$\frac{3}{7} = 3 \times \frac{1}{7} = 3 \times 0.\overline{142857}$
Multiplying 0.142857... by 3:
$3 \times 0.142857... = 0.428571...$
So, $\frac{3}{7} = \mathbf{0.\overline{428571}}$.
For $\frac{4}{7}$:
$\frac{4}{7} = 4 \times \frac{1}{7} = 4 \times 0.\overline{142857}$
Multiplying 0.142857... by 4:
$4 \times 0.142857... = 0.571428...$
So, $\frac{4}{7} = \mathbf{0.\overline{571428}}$.
For $\frac{5}{7}$:
$\frac{5}{7} = 5 \times \frac{1}{7} = 5 \times 0.\overline{142857}$
Multiplying 0.142857... by 5:
$5 \times 0.142857... = 0.714285...$
So, $\frac{5}{7} = \mathbf{0.\overline{714285}}$.
For $\frac{6}{7}$:
$\frac{6}{7} = 6 \times \frac{1}{7} = 6 \times 0.\overline{142857}$
Multiplying 0.142857... by 6:
$6 \times 0.142857... = 0.857142...$
So, $\frac{6}{7} = \mathbf{0.\overline{857142}}$.
Explanation using remainders:
When finding the decimal expansion of $\frac{1}{7}$ using long division, the sequence of remainders obtained is 3, 2, 6, 4, 5, 1, and then it repeats. The digits in the repeating block $142857$ correspond to the sequence of these remainders.
Specifically, the digit '1' comes after remainder 3, '4' after remainder 2, '2' after remainder 6, '8' after remainder 4, '5' after remainder 5, and '7' after remainder 1.
When we divide $n$ by 7 (for $n<7$), the first remainder (after the decimal point) dictates the starting point in the cyclic sequence of digits $142857$.
For $\frac{2}{7}$, the first step in long division is $20 \div 7$, which gives a quotient 2 and remainder 6. The decimal expansion starts with the digit corresponding to remainder 6 in the $\frac{1}{7}$ sequence, which is '2'. The subsequent digits follow the cycle $285714$.
For $\frac{3}{7}$, the first step $30 \div 7$ gives quotient 4 and remainder 2. The expansion starts with the digit corresponding to remainder 2 ('4'), followed by $428571$.
And so on for the other fractions. The decimal expansions are cyclic shifts of the digits in $0.\overline{142857}$.
Predicted Decimal Expansions:
$\frac{2}{7} = \mathbf{0.\overline{285714}}$
$\frac{3}{7} = \mathbf{0.\overline{428571}}$
$\frac{4}{7} = \mathbf{0.\overline{571428}}$
$\frac{5}{7} = \mathbf{0.\overline{714285}}$
$\frac{6}{7} = \mathbf{0.\overline{857142}}$
Question 3. Express the following in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0.
(i) 0.$\overline{6}$
(ii) 0.4$\overline{7}$
(iii) 0.$\overline{001}$
Answer:
(i) Express 0.$\overline{6}$ in the form $\frac{p}{q}$:
Let $x$ be the given decimal number.
$x = 0.6666...$
... (i)
Since one digit (6) is repeating after the decimal point, multiply equation (i) by 10.
$10x = 6.6666...$
... (ii)
Subtract equation (i) from equation (ii):
$10x - x = 6.6666... - 0.6666...$
$9x = 6$
Solve for $x$:
$x = \frac{6}{9}$
Simplify the fraction:
$x = \frac{\cancel{6}^2}{\cancel{9}_3}$
$x = \frac{2}{3}$
So, $0.\overline{6} = \frac{2}{3}$. Here $p=2$ and $q=3$, which are integers and $q \neq 0$.
(ii) Express 0.4$\overline{7}$ in the form $\frac{p}{q}$:
Let $x$ be the given decimal number.
$x = 0.47777...$
... (i)
Multiply equation (i) by 10 to move the non-repeating part to the left of the decimal point.
$10x = 4.7777...$
... (ii)
Since one digit (7) is repeating after the decimal point in equation (ii), multiply equation (ii) by 10.
$10 \times (10x) = 10 \times (4.7777...)$
$100x = 47.7777...$
... (iii)
Subtract equation (ii) from equation (iii):
$100x - 10x = 47.7777... - 4.7777...$
$90x = 43$
Solve for $x$:
$x = \frac{43}{90}$
The fraction $\frac{43}{90}$ cannot be simplified further.
So, $0.4\overline{7} = \frac{43}{90}$. Here $p=43$ and $q=90$, which are integers and $q \neq 0$.
(iii) Express 0.$\overline{001}$ in the form $\frac{p}{q}$:
Let $x$ be the given decimal number.
$x = 0.001001001...$
... (i)
Since three digits (001) are repeating after the decimal point, multiply equation (i) by $10^3 = 1000$.
$1000x = 1.001001001...$
... (ii)
Subtract equation (i) from equation (ii):
$1000x - x = 1.001001001... - 0.001001001...$
$999x = 1$
Solve for $x$:
$x = \frac{1}{999}$
The fraction $\frac{1}{999}$ cannot be simplified further.
So, $0.\overline{001} = \frac{1}{999}$. Here $p=1$ and $q=999$, which are integers and $q \neq 0$.
Question 4. Express 0.99999 .... in the form $\frac{p}{q}$ . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Answer:
Given:
The repeating decimal number $0.99999....$, which can be written as $0.\overline{9}$.
To Express:
The number $0.\overline{9}$ in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Also, to discuss if the answer is surprising and why it makes sense.
Solution:
Let $x$ be the given decimal number.
$x = 0.99999....$
... (i)
Since only one digit (9) is repeating after the decimal point, we multiply both sides of equation (i) by 10.
$10x = 9.99999....$
... (ii)
Now, subtract equation (i) from equation (ii).
$10x - x = (9.99999....) - (0.99999....)$
The subtraction results in 9.
$9x = 9$
(Subtracting (i) from (ii))
To find $x$, divide both sides by 9.
$x = \frac{9}{9}$
Simplifying the fraction:
$x = 1$
So, we have expressed $0.99999....$ as 1.
We can write 1 in the form $\frac{p}{q}$ as $\frac{1}{1}$. Here, $p=1$ and $q=1$. Both 1 and 1 are integers, and the denominator $q=1$ is not zero. Thus, 1 is a rational number.
Discussion: Is the answer surprising? Why does it make sense?
Yes, the answer $0.99999.... = 1$ can be surprising at first.
Most people initially think that $0.99999....$ must be slightly less than 1.
However, the key is that the '9' repeats infinitely.
Let's think about the difference between 1 and $0.99999....$.
If there were a difference, no matter how small, we would find a number between $0.99999....$ and 1.
For example, if we thought the difference was a tiny number like 0.0000001, then $1 - 0.9999999 = 0.0000001$.
But the decimal $0.99999....$ has an endless sequence of 9s. When we subtract it from 1, we get an endless sequence of 0s:
$\begin{array}{ccccccc} & 1 & . & 0 & 0 & 0 & ... \\ - & 0 & . & 9 & 9 & 9 & ... \\ \hline & 0 & . & 0 & 0 & 0 & ... \\ \hline \end{array}$
The result is exactly $0.00000....$, which is equal to 0. The only number that is equal to zero is 0 itself.
Since $1 - 0.99999.... = 0$, it must be true that $1 = 0.99999....$.
This shows that the infinite repeating decimal $0.99999....$ is precisely equal to 1.
In mathematics, some numbers have more than one decimal representation. For example, $\frac{1}{2}$ can be $0.5$ or $0.4999....$. Similarly, 1 can be $1.0$ or $0.9999....$.
Final Answer:
Yes, $0.99999....$ is a rational number. It can be expressed in the form $\frac{p}{q}$ as $\mathbf{\frac{1}{1}}$. The answer is surprising because it seems counter-intuitive, but mathematically it makes sense because the difference between 1 and $0.\overline{9}$ is exactly zero, meaning they are the same number.
Question 5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.
Answer:
Given:
The fraction $\frac{1}{17}$.
To Find:
The maximum number of digits in the repeating block of the decimal expansion of $\frac{1}{17}$ and verify it by performing the division.
Solution:
For a rational number of the form $\frac{1}{p}$, where $p$ is a prime number other than 2 or 5, the maximum number of digits in the repeating block of its decimal expansion is equal to $p-1$. This is a result from number theory concerning the order of the decimal expansion in modulo $p$.
In this case, the denominator is 17, which is a prime number.
Therefore, the maximum number of digits in the repeating block for the decimal expansion of $\frac{1}{17}$ is $17-1 = 16$.
To verify this, we perform the long division of 1 by 17.
We divide 1 by 17. Since 1 is less than 17, we place a decimal point and add zeros.
The division process proceeds by finding the quotient and remainder at each step. The length of the repeating block is determined by the sequence of non-zero remainders obtained during the division until a remainder repeats for the first time.
Let's perform the division:
$$\begin{array}{r} 0.0588235294117647... \\ 17{\overline{\smash{\big)}\,1.0000000000000000}} \\ \underline{-\ 0 \downarrow} \\ 100 \\ \underline{-\ 85 \downarrow} \\ 150 \\ \underline{-\ 136 \downarrow} \\ 140 \\ \underline{-\ 136 \downarrow} \\ 40 \\ \underline{-\ 34 \downarrow} \\ 60 \\ \underline{-\ 51 \downarrow} \\ 90 \\ \underline{-\ 85 \downarrow} \\ 50 \\ \underline{-\ 34 \downarrow} \\ 160 \\ \underline{-\ 153 \downarrow} \\ 70 \\ \underline{-\ 68 \downarrow} \\ 20 \\ \underline{-\ 17 \downarrow} \\ 30 \\ \underline{-\ 17 \downarrow} \\ 130 \\ \underline{-\ 119 \downarrow} \\ 110 \\ \underline{-\ 102 \downarrow} \\ 80 \\ \underline{-\ 68 \downarrow} \\ 120 \\ \underline{-\ 119} \\ 1 \end{array}$$
The sequence of remainders obtained during the division is 1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12, and then the remainder 1 repeats.
The repeating block of digits in the quotient corresponds to the sequence of digits obtained between the first occurrence of a remainder (1) and its repetition.
The digits in the quotient are obtained as follows:
$1 \div 17$: Quotient 0, Remainder 1
$10 \div 17$: Quotient 0, Remainder 10
$100 \div 17$: Quotient 5, Remainder 15
$150 \div 17$: Quotient 8, Remainder 14
$140 \div 17$: Quotient 8, Remainder 4
$40 \div 17$: Quotient 2, Remainder 6
$60 \div 17$: Quotient 3, Remainder 9
$90 \div 17$: Quotient 5, Remainder 5
$50 \div 17$: Quotient 2, Remainder 16
$160 \div 17$: Quotient 9, Remainder 7
$70 \div 17$: Quotient 4, Remainder 2
$20 \div 17$: Quotient 1, Remainder 3
$30 \div 17$: Quotient 1, Remainder 13
$130 \div 17$: Quotient 7, Remainder 11
$110 \div 17$: Quotient 6, Remainder 8
$80 \div 17$: Quotient 4, Remainder 12
$120 \div 17$: Quotient 7, Remainder 1
The quotient digits are 0, 5, 8, 8, 2, 3, 5, 2, 9, 4, 1, 1, 7, 6, 4, 7 before the remainder 1 repeats. Including the initial 0 after the decimal point (from dividing 10 by 17), the repeating block starts from the first digit after the decimal point.
The decimal expansion of $\frac{1}{17}$ is $0.\overline{0588235294117647}$.
Counting the digits in the repeating block, we find there are 16 digits.
This matches the maximum number of digits predicted by the formula $p-1$ for $p=17$.
Conclusion:
The maximum number of digits in the repeating block of the decimal expansion of $\frac{1}{17}$ is 16.
The division confirms that the repeating block is $0588235294117647$, which contains 16 digits.
Question 6. Look at several examples of rational numbers in the form $\frac{p}{q}$ (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Answer:
Given:
Rational numbers of the form $\frac{p}{q}$, where $q \neq 0$, $p$ and $q$ are integers with $\gcd(p, q) = 1$ (in simplest form), and the decimal expansion is terminating.
To Find:
The property that the denominator $q$ must satisfy.
Solution:
Let's consider several examples of rational numbers in simplest form that have terminating decimal expansions and examine their denominators:
$\frac{1}{2} = 0.5$. Here, $q=2$. The prime factorization of 2 is $2^1$.
$\frac{1}{4} = 0.25$. Here, $q=4$. The prime factorization of 4 is $2^2$.
$\frac{3}{8} = 0.375$. Here, $q=8$. The prime factorization of 8 is $2^3$.
$\frac{1}{5} = 0.2$. Here, $q=5$. The prime factorization of 5 is $5^1$.
$\frac{2}{5} = 0.4$. Here, $q=5$. The prime factorization of 5 is $5^1$.
$\frac{3}{10} = 0.3$. Here, $q=10$. The prime factorization of 10 is $2^1 \times 5^1$.
$\frac{7}{20} = 0.35$. Here, $q=20$. The prime factorization of 20 is $2^2 \times 5^1$.
$\frac{1}{25} = 0.04$. Here, $q=25$. The prime factorization of 25 is $5^2$.
$\frac{3}{50} = 0.06$. Here, $q=50$. The prime factorization of 50 is $2^1 \times 5^2$.
$\frac{13}{125} = 0.104$. Here, $q=125$. The prime factorization of 125 is $5^3$.
Looking at the prime factorizations of the denominators (2, 4, 8, 5, 10, 20, 25, 50, 125), we observe that the only prime factors present are 2 and 5.
A rational number $\frac{p}{q}$, where $p$ and $q$ are integers with no common factors other than 1, has a terminating decimal expansion if and only if the prime factorization of the denominator $q$ contains only powers of 2 and/or powers of 5.
This is because a terminating decimal can always be expressed as a fraction with a denominator that is a power of 10 ($10^n = (2 \times 5)^n = 2^n \times 5^n$). If a rational number $\frac{p}{q}$ is in simplest form, its denominator $q$ must be a factor of some power of 10 for it to be convertible into a terminating decimal form. This implies that the prime factors of $q$ can only be 2 and 5.
Conclusion:
The property that the denominator $q$ must satisfy is that its prime factorization should have only powers of 2 or powers of 5 or both.
In other words, the prime factors of $q$ must be limited to 2 and 5.
Question 7. Write three numbers whose decimal expansions are non-terminating non-recurring.
Answer:
Given:
Request to provide three numbers whose decimal expansions are non-terminating and non-recurring.
Solution:
Numbers whose decimal expansions are non-terminating and non-recurring are called irrational numbers. They cannot be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Here are three examples of such numbers:
1. The value of Pi ($\pi$). Its decimal expansion is approximately $3.1415926535...$ It is known to be non-terminating and non-recurring.
2. The square root of any positive integer that is not a perfect square. For example, $\sqrt{2}$. Its decimal expansion is approximately $1.41421356237...$ It is non-terminating and non-recurring.
3. We can construct numbers with non-terminating and non-recurring decimal expansions by creating a pattern that does not repeat periodically. For example, consider the number $0.01001000100001...$, where the number of zeros between consecutive ones increases by one each time.
So, three numbers whose decimal expansions are non-terminating non-recurring are:
a) $\pi$
b) $\sqrt{2}$
c) $0.01001000100001...$ (and so on, with an increasing number of zeros between the ones)
Question 8. Find three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$ .
Answer:
Given:
The rational numbers $\frac{5}{7}$ and $\frac{9}{11}$.
To Find:
Three different irrational numbers between $\frac{5}{7}$ and $\frac{9}{11}$.
Solution:
First, we convert the given rational numbers into their decimal form by performing long division:
For $\frac{5}{7}$:
$\frac{5}{7} = 0.714285714285... = 0.\overline{714285}$
For $\frac{9}{11}$:
$\frac{9}{11} = 0.818181... = 0.\overline{81}$
We need to find three different irrational numbers between $0.714285...$ and $0.818181...$
Recall that irrational numbers are non-terminating and non-recurring decimals.
We can construct irrational numbers by writing decimals that fall between these two values and do not have a repeating pattern. We can pick decimal numbers that start with digits within the range and follow them with a pattern that clearly shows non-recurrence (e.g., increasing zeros between digits).
Here are three such irrational numbers:
1. $0.73073007300073...$ (The digit '3' is followed by an increasing number of zeros and then '73' again)
2. $0.761761176111761111...$ (The sequence '761' is followed by an increasing number of '1's)
3. $0.80800800080000...$ (The digit '8' is followed by an increasing number of zeros and then '8' again)
These three numbers are greater than $0.714285...$ and less than $0.818181...$, and their decimal expansions are non-terminating and non-recurring, making them irrational numbers.
Question 9. Classify the following numbers as rational or irrational :
(i) $\sqrt{23}$
(ii) $\sqrt{225}$
(iii) 0.3796
(iv) 7.478478…
(v) 1.101001000100001...
Answer:
We classify the given numbers as rational or irrational based on their decimal expansions or whether they can be expressed in the form $\frac{p}{q}$.
(i) $\sqrt{23}$
The number 23 is not a perfect square. The square root of a positive integer that is not a perfect square is an irrational number.
(ii) $\sqrt{225}$
We find the value of $\sqrt{225}$. Since $15 \times 15 = 225$, $\sqrt{225} = 15$. The number 15 is an integer, and any integer can be written in the form $\frac{p}{q}$ (e.g., $\frac{15}{1}$). Therefore, $\sqrt{225}$ is a rational number.
(iii) 0.3796
The decimal expansion 0.3796 is a terminating decimal. Any number with a terminating decimal expansion is a rational number. It can be written as $\frac{3796}{10000}$.
(iv) 7.478478…
The decimal expansion 7.478478… is non-terminating but repeating (the block of digits '478' repeats). Any number with a non-terminating and repeating decimal expansion is a rational number. This can be written as $7.\overline{478}$.
(v) 1.101001000100001...
The decimal expansion 1.101001000100001... is non-terminating and non-recurring (the pattern of zeros between the ones increases, showing no fixed repeating block). Any number with a non-terminating and non-recurring decimal expansion is an irrational number.
Example 11 & 19 (Before Exercise 1.4)
Example 11: Check whether 7$\sqrt{5}$ , $\frac{7}{\sqrt{5}}$ , $\sqrt{2}$ + 21, π − 2 are irrational numbers or not.
Answer:
We need to check whether the given numbers are irrational or not.
Recall that irrational numbers are numbers that cannot be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. Their decimal expansions are non-terminating and non-recurring.
Also, we know that $\sqrt{n}$ is irrational if $n$ is not a perfect square. In this case, 2, 3, 5, etc., are not perfect squares, so $\sqrt{2}$, $\sqrt{3}$, $\sqrt{5}$ are irrational numbers.
We also know that $\pi$ is an irrational number.
We use the properties of operations involving rational and irrational numbers:
1. The sum or difference of a rational number and an irrational number is irrational.
2. The product or quotient of a non-zero rational number and an irrational number is irrational.
Let's examine each number:
(i) $7\sqrt{5}$
Here, 7 is a rational number ($7 = \frac{7}{1}$), and $\sqrt{5}$ is an irrational number (since 5 is not a perfect square).
The product of a non-zero rational number and an irrational number is irrational.
Therefore, $7\sqrt{5}$ is an irrational number.
(ii) $\frac{7}{\sqrt{5}}$
Here, 7 is a rational number, and $\sqrt{5}$ is an irrational number.
The quotient of a non-zero rational number and an irrational number is irrational.
Alternatively, we can rationalize the denominator:
$\frac{7}{\sqrt{5}} = \frac{7}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{7\sqrt{5}}{5} = \frac{7}{5}\sqrt{5}$
Here, $\frac{7}{5}$ is a rational number, and $\sqrt{5}$ is an irrational number.
The product of a non-zero rational number ($\frac{7}{5}$) and an irrational number ($\sqrt{5}$) is irrational.
Therefore, $\frac{7}{\sqrt{5}}$ is an irrational number.
(iii) $\sqrt{2} + 21$
Here, $\sqrt{2}$ is an irrational number (since 2 is not a perfect square), and 21 is a rational number ($21 = \frac{21}{1}$).
The sum of an irrational number and a rational number is irrational.
Therefore, $\sqrt{2} + 21$ is an irrational number.
(iv) $\pi - 2$
Here, $\pi$ is an irrational number, and 2 is a rational number ($2 = \frac{2}{1}$).
The difference of an irrational number and a rational number is irrational.
Therefore, $\pi - 2$ is an irrational number.
All the given numbers ($7\sqrt{5}$, $\frac{7}{\sqrt{5}}$, $\sqrt{2} + 21$, $\pi - 2$) are irrational numbers.
Example 12: Add $2\sqrt{2}$ + 5$\sqrt{3}$ and $\sqrt{2}$ − 3$\sqrt{3}$ .
Answer:
Given:
Two expressions: $2\sqrt{2} + 5\sqrt{3}$ and $\sqrt{2} - 3\sqrt{3}$.
To Find:
The sum of the two given expressions.
Solution:
To add the given expressions, we combine the terms with the same irrational parts.
Let the sum be S.
$S = (2\sqrt{2} + 5\sqrt{3}) + (\sqrt{2} - 3\sqrt{3})$
Remove the parentheses:
$S = 2\sqrt{2} + 5\sqrt{3} + \sqrt{2} - 3\sqrt{3}$
Group the like terms (terms containing $\sqrt{2}$ and terms containing $\sqrt{3}$):
$S = (2\sqrt{2} + \sqrt{2}) + (5\sqrt{3} - 3\sqrt{3})$
Combine the coefficients of the like terms:
$S = (2+1)\sqrt{2} + (5-3)\sqrt{3}$
Perform the addition and subtraction of coefficients:
$S = 3\sqrt{2} + 2\sqrt{3}$
The terms $3\sqrt{2}$ and $2\sqrt{3}$ are unlike terms (because the irrational parts $\sqrt{2}$ and $\sqrt{3}$ are different), so they cannot be combined further.
Result:
The sum of $2\sqrt{2} + 5\sqrt{3}$ and $\sqrt{2} - 3\sqrt{3}$ is $3\sqrt{2} + 2\sqrt{3}$.
Example 13: Multiply 6$\sqrt{5}$ by 2$\sqrt{5}$ .
Answer:
Given:
Two numbers: $6\sqrt{5}$ and $2\sqrt{5}$.
To Find:
The product of the two given numbers.
Solution:
To multiply the two numbers, we multiply the rational parts together and the irrational parts together.
Let the product be P.
$P = (6\sqrt{5}) \times (2\sqrt{5})$
Group the rational and irrational parts:
$P = (6 \times 2) \times (\sqrt{5} \times \sqrt{5})$
Multiply the rational parts:
$6 \times 2 = 12$
Multiply the irrational parts:
$\sqrt{5} \times \sqrt{5} = (\sqrt{5})^2 = 5$
Now, combine the results:
$P = 12 \times 5$
Perform the final multiplication:
$P = 60$
The product is a rational number.
Result:
The product of $6\sqrt{5}$ and $2\sqrt{5}$ is 60.
Example 14: Divide 8$\sqrt{15}$ by 2$\sqrt{3}$ .
Answer:
Given:
Two numbers: $8\sqrt{15}$ and $2\sqrt{3}$.
To Find:
The result of dividing $8\sqrt{15}$ by $2\sqrt{3}$.
Solution:
To divide the first number by the second, we can write the division as a fraction:
$\frac{8\sqrt{15}}{2\sqrt{3}}$
We can separate the rational and irrational parts of the fraction:
$\frac{8}{2} \times \frac{\sqrt{15}}{\sqrt{3}}$
Simplify the rational part:
$\frac{8}{2} = 4$
Simplify the irrational part using the property $\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$ (where $b \neq 0$):
$\frac{\sqrt{15}}{\sqrt{3}} = \sqrt{\frac{15}{3}}$
Perform the division inside the square root:
$\sqrt{\frac{15}{3}} = \sqrt{5}$
Now, combine the simplified rational and irrational parts:
$4 \times \sqrt{5} = 4\sqrt{5}$
The result is an irrational number.
Result:
Dividing $8\sqrt{15}$ by $2\sqrt{3}$ gives $4\sqrt{5}$.
Example 15: Simplify the following expressions:
(i) (5 + $\sqrt{7}$) (2 + $\sqrt{5}$)
(ii) (5 + $\sqrt{5}$)(5 - $\sqrt{5}$)
(iii) ($\sqrt{3}$ + $\sqrt{7}$)2
(iv) ($\sqrt{11}$ - $\sqrt{7}$)($\sqrt{11}$ + $\sqrt{7}$)
Answer:
We will simplify each expression using algebraic identities and the properties of square roots.
(i) $(5 + \sqrt{7})(2 + \sqrt{5})$
This is a product of two binomials. We use the distributive property:
$(a+b)(c+d) = ac + ad + bc + bd$
$(5 + \sqrt{7})(2 + \sqrt{5}) = 5 \times 2 + 5 \times \sqrt{5} + \sqrt{7} \times 2 + \sqrt{7} \times \sqrt{5}$
$= 10 + 5\sqrt{5} + 2\sqrt{7} + \sqrt{7 \times 5}$
$= 10 + 5\sqrt{5} + 2\sqrt{7} + \sqrt{35}$
These terms cannot be combined further as the irrational parts are different.
(ii) $(5 + \sqrt{5})(5 - \sqrt{5})$
This is in the form $(a+b)(a-b)$. We use the identity:
$(a+b)(a-b) = a^2 - b^2$
$(5 + \sqrt{5})(5 - \sqrt{5}) = 5^2 - (\sqrt{5})^2$
$= 25 - 5$
$= 20$
(iii) $(\sqrt{3} + \sqrt{7})^2$
This is in the form $(a+b)^2$. We use the identity:
$(a+b)^2 = a^2 + 2ab + b^2$
$(\sqrt{3} + \sqrt{7})^2 = (\sqrt{3})^2 + 2 \times \sqrt{3} \times \sqrt{7} + (\sqrt{7})^2$
$= 3 + 2\sqrt{3 \times 7} + 7$
$= 3 + 2\sqrt{21} + 7$
Combine the rational terms:
$= (3+7) + 2\sqrt{21}$
$= 10 + 2\sqrt{21}$
(iv) $(\sqrt{11} - \sqrt{7})(\sqrt{11} + \sqrt{7})$
This is in the form $(a-b)(a+b)$, which is equivalent to $(a+b)(a-b)$. We use the identity:
$(a+b)(a-b) = a^2 - b^2$
$(\sqrt{11} - \sqrt{7})(\sqrt{11} + \sqrt{7}) = (\sqrt{11})^2 - (\sqrt{7})^2$
$= 11 - 7$
$= 4$
Results:
(i) $(5 + \sqrt{7})(2 + \sqrt{5}) = 10 + 5\sqrt{5} + 2\sqrt{7} + \sqrt{35}$
(ii) $(5 + \sqrt{5})(5 - \sqrt{5}) = 20$
(iii) $(\sqrt{3} + \sqrt{7})^2 = 10 + 2\sqrt{21}$
(iv) $(\sqrt{11} - \sqrt{7})(\sqrt{11} + \sqrt{7}) = 4$
Example 16: Rationalise the denominator of $\frac{1}{\sqrt{2}}$ .
Answer:
Given:
The fraction $\frac{1}{\sqrt{2}}$.
To Rationalise:
The denominator of the given fraction.
Solution:
To rationalise the denominator of a fraction like $\frac{1}{\sqrt{a}}$, where $a$ is a positive number, we multiply both the numerator and the denominator by $\sqrt{a}$. This is because $(\sqrt{a})^2 = a$, which is a rational number.
In the given fraction $\frac{1}{\sqrt{2}}$, the denominator is $\sqrt{2}$. We multiply the numerator and the denominator by $\sqrt{2}$.
$\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$
Multiply the numerators and the denominators:
Numerator: $1 \times \sqrt{2} = \sqrt{2}$
Denominator: $\sqrt{2} \times \sqrt{2} = (\sqrt{2})^2 = 2$
So, the fraction becomes:
$\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$
The denominator is now 2, which is a rational number. Thus, the denominator has been rationalised.
Result:
The rationalised form of $\frac{1}{\sqrt{2}}$ is $\frac{\sqrt{2}}{2}$.
Example 17: Rationalise the denominator of $\frac{1}{2 \;+\; \sqrt{3}}$ .
Answer:
Given:
The fraction $\frac{1}{2 + \sqrt{3}}$.
To Rationalise:
The denominator of the given fraction.
Solution:
To rationalise the denominator of a fraction of the form $\frac{1}{a + \sqrt{b}}$ or $\frac{1}{\sqrt{a} + \sqrt{b}}$, we multiply both the numerator and the denominator by the conjugate of the denominator.
The conjugate of $a + \sqrt{b}$ is $a - \sqrt{b}$.
The conjugate of $\sqrt{a} + \sqrt{b}$ is $\sqrt{a} - \sqrt{b}$.
The conjugate of $a - \sqrt{b}$ is $a + \sqrt{b}$.
The conjugate of $\sqrt{a} - \sqrt{b}$ is $\sqrt{a} + \sqrt{b}$.
In the given fraction $\frac{1}{2 + \sqrt{3}}$, the denominator is $2 + \sqrt{3}$. The conjugate of $2 + \sqrt{3}$ is $2 - \sqrt{3}$.
We multiply both the numerator and the denominator by the conjugate $2 - \sqrt{3}$.
$\frac{1}{2 + \sqrt{3}} = \frac{1}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}}$
Multiply the numerators and the denominators:
Numerator: $1 \times (2 - \sqrt{3}) = 2 - \sqrt{3}$
Denominator: $(2 + \sqrt{3})(2 - \sqrt{3})$
Use the identity $(a+b)(a-b) = a^2 - b^2$ for the denominator:
$(2 + \sqrt{3})(2 - \sqrt{3}) = 2^2 - (\sqrt{3})^2$
$= 4 - 3$
$= 1$
So, the fraction becomes:
$\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{1}$
$= 2 - \sqrt{3}$
The denominator is now 1, which is a rational number. Thus, the denominator has been rationalised.
Result:
The rationalised form of $\frac{1}{2 + \sqrt{3}}$ is $2 - \sqrt{3}$.
Example 18: Rationalise the denominator of $\frac{5}{\sqrt{3} \;-\; \sqrt{5}}$ .
Answer:
Given:
The fraction is $\frac{5}{\sqrt{3} - \sqrt{5}}$.
To Rationalise:
The denominator of the given fraction.
Solution:
To rationalise the denominator of a fraction which has a sum or difference of two square roots in the denominator, we multiply both the numerator and the denominator by the conjugate of the denominator.
The denominator is $\sqrt{3} - \sqrt{5}$.
The conjugate of $\sqrt{3} - \sqrt{5}$ is $\sqrt{3} + \sqrt{5}$.
We multiply both the numerator and the denominator of the given fraction by the conjugate $\sqrt{3} + \sqrt{5}$.
$\frac{5}{\sqrt{3} - \sqrt{5}} = \frac{5}{\sqrt{3} - \sqrt{5}} \times \frac{\sqrt{3} + \sqrt{5}}{\sqrt{3} + \sqrt{5}}$
Now, we multiply the numerators together and the denominators together.
Numerator: $5 \times (\sqrt{3} + \sqrt{5}) = 5\sqrt{3} + 5\sqrt{5}$
Denominator: $(\sqrt{3} - \sqrt{5})(\sqrt{3} + \sqrt{5})$
We use the algebraic identity $(a-b)(a+b) = a^2 - b^2$ for the denominator.
Here, $a = \sqrt{3}$ and $b = \sqrt{5}$.
So, $(\sqrt{3} - \sqrt{5})(\sqrt{3} + \sqrt{5}) = (\sqrt{3})^2 - (\sqrt{5})^2$
We know that $(\sqrt{3})^2 = 3$ and $(\sqrt{5})^2 = 5$.
$= 3 - 5$
$= -2$
Now, put the numerator and the denominator back together:
$\frac{5}{\sqrt{3} - \sqrt{5}} = \frac{5\sqrt{3} + 5\sqrt{5}}{-2}$
We can write the negative sign in the numerator or in front of the fraction:
$\frac{5\sqrt{3} + 5\sqrt{5}}{-2} = -\frac{5\sqrt{3} + 5\sqrt{5}}{2}$
The denominator is now -2, which is a rational number. So, the denominator has been rationalised.
Result:
The rationalised form of $\frac{5}{\sqrt{3} - \sqrt{5}}$ is $\mathbf{-\frac{5\sqrt{3} + 5\sqrt{5}}{2}}$.
Example 19: Rationalise the denominator of $\frac{1}{7 \;+\; 3\sqrt{2}}$ .
Answer:
Given:
The fraction $\frac{1}{7 + 3\sqrt{2}}$.
To Rationalise:
The denominator of the given fraction.
Solution:
To rationalise the denominator of a fraction of the form $\frac{1}{a + b\sqrt{c}}$, we multiply both the numerator and the denominator by the conjugate of the denominator.
The conjugate of $a + b\sqrt{c}$ is $a - b\sqrt{c}$.
In the given fraction $\frac{1}{7 + 3\sqrt{2}}$, the denominator is $7 + 3\sqrt{2}$. The conjugate of $7 + 3\sqrt{2}$ is $7 - 3\sqrt{2}$.
We multiply both the numerator and the denominator by the conjugate $7 - 3\sqrt{2}$.
$\frac{1}{7 + 3\sqrt{2}} = \frac{1}{7 + 3\sqrt{2}} \times \frac{7 - 3\sqrt{2}}{7 - 3\sqrt{2}}$
Multiply the numerators and the denominators:
Numerator: $1 \times (7 - 3\sqrt{2}) = 7 - 3\sqrt{2}$
Denominator: $(7 + 3\sqrt{2})(7 - 3\sqrt{2})$
Use the identity $(a+b)(a-b) = a^2 - b^2$ for the denominator, where $a=7$ and $b=3\sqrt{2}$:
$(7 + 3\sqrt{2})(7 - 3\sqrt{2}) = 7^2 - (3\sqrt{2})^2$
Calculate the terms:
$7^2 = 49$
$(3\sqrt{2})^2 = 3^2 \times (\sqrt{2})^2 = 9 \times 2 = 18$
So, the denominator is:
$49 - 18 = 31$
Thus, the fraction becomes:
$\frac{1}{7 + 3\sqrt{2}} = \frac{7 - 3\sqrt{2}}{31}$
The denominator is now 31, which is a rational number. Thus, the denominator has been rationalised.
Result:
The rationalised form of $\frac{1}{7 + 3\sqrt{2}}$ is $\frac{7 - 3\sqrt{2}}{31}$.
Exercise 1.4
Question 1. Classify the following numbers as rational or irrational:
(i) 2 − $\sqrt{5}$
(ii) (3 + $\sqrt{23}$) − $\sqrt{23}$
(iii) $\frac{2\sqrt{7}}{7\sqrt{7}}$
(iv) $\frac{1}{\sqrt{2}}$
(v) 2π
Answer:
We classify each number as rational or irrational based on their properties.
(i) $2 - \sqrt{5}$
Here, 2 is a rational number, and $\sqrt{5}$ is an irrational number (since 5 is not a perfect square).
The difference between a rational number and an irrational number is always irrational.
Therefore, $2 - \sqrt{5}$ is an irrational number.
(ii) $(3 + \sqrt{23}) - \sqrt{23}$
Simplify the expression:
$(3 + \sqrt{23}) - \sqrt{23} = 3 + \sqrt{23} - \sqrt{23}$
$= 3 + (\sqrt{23} - \sqrt{23})$
$= 3 + 0$
$= 3$
The number 3 is an integer, which can be written as $\frac{3}{1}$ (in the form $\frac{p}{q}$).
Therefore, $(3 + \sqrt{23}) - \sqrt{23}$ is a rational number.
(iii) $\frac{2\sqrt{7}}{7\sqrt{7}}$
Simplify the expression by cancelling the common term $\sqrt{7}$ (since $\sqrt{7} \neq 0$):
$\frac{2\cancel{\sqrt{7}}}{7\cancel{\sqrt{7}}} = \frac{2}{7}$
The number $\frac{2}{7}$ is in the form $\frac{p}{q}$, where $p=2$ and $q=7$ are integers and $q \neq 0$.
Therefore, $\frac{2\sqrt{7}}{7\sqrt{7}}$ is a rational number.
(iv) $\frac{1}{\sqrt{2}}$
Here, 1 is a rational number, and $\sqrt{2}$ is an irrational number (since 2 is not a perfect square).
The quotient of a non-zero rational number and an irrational number is always irrational.
Alternatively, the decimal expansion of $\frac{1}{\sqrt{2}} \approx \frac{1}{1.414...}$ is non-terminating and non-recurring.
Therefore, $\frac{1}{\sqrt{2}}$ is an irrational number.
(v) $2\pi$
Here, 2 is a rational number, and $\pi$ is an irrational number.
The product of a non-zero rational number and an irrational number is always irrational.
Therefore, $2\pi$ is an irrational number.
Question 2. Simplify each of the following expressions:
(i) (3 + $\sqrt{3}$)(2 + $\sqrt{2}$)
(ii) (3 + $\sqrt{3}$)(3 − $\sqrt{3}$)
(iii) ($\sqrt{5}$ + $\sqrt{2}$)2
(iv) ($\sqrt{5}$- $\sqrt{2}$)($\sqrt{5}$ + $\sqrt{2}$)
Answer:
We simplify each expression using algebraic identities and the properties of square roots.
(i) $(3 + \sqrt{3})(2 + \sqrt{2})$
We use the distributive property (FOIL method):
$(3 + \sqrt{3})(2 + \sqrt{2}) = 3 \times 2 + 3 \times \sqrt{2} + \sqrt{3} \times 2 + \sqrt{3} \times \sqrt{2}$
$= 6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{3 \times 2}$
$= 6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{6}$
These terms cannot be combined further as the irrational parts are different.
(ii) $(3 + \sqrt{3})(3 - \sqrt{3})$
This is in the form $(a+b)(a-b)$. We use the identity:
$(a+b)(a-b) = a^2 - b^2$
Here, $a=3$ and $b=\sqrt{3}$.
$(3 + \sqrt{3})(3 - \sqrt{3}) = 3^2 - (\sqrt{3})^2$
$= 9 - 3$
$= 6$
(iii) $(\sqrt{5} + \sqrt{2})^2$
This is in the form $(a+b)^2$. We use the identity:
$(a+b)^2 = a^2 + 2ab + b^2$
Here, $a=\sqrt{5}$ and $b=\sqrt{2}$.
$(\sqrt{5} + \sqrt{2})^2 = (\sqrt{5})^2 + 2 \times \sqrt{5} \times \sqrt{2} + (\sqrt{2})^2$
$= 5 + 2\sqrt{5 \times 2} + 2$
$= 5 + 2\sqrt{10} + 2$
Combine the rational terms:
$= (5+2) + 2\sqrt{10}$
$= 7 + 2\sqrt{10}$
(iv) $(\sqrt{5} - \sqrt{2})(\sqrt{5} + \sqrt{2})$
This is in the form $(a-b)(a+b)$, which is equivalent to $(a+b)(a-b)$. We use the identity:
$(a+b)(a-b) = a^2 - b^2$
Here, $a=\sqrt{5}$ and $b=\sqrt{2}$.
$(\sqrt{5} - \sqrt{2})(\sqrt{5} + \sqrt{2}) = (\sqrt{5})^2 - (\sqrt{2})^2$
$= 5 - 2$
$= 3$
Results:
(i) $(3 + \sqrt{3})(2 + \sqrt{2}) = 6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{6}$
(ii) $(3 + \sqrt{3})(3 - \sqrt{3}) = 6$
(iii) $(\sqrt{5} + \sqrt{2})^2 = 7 + 2\sqrt{10}$
(iv) $(\sqrt{5} - \sqrt{2})(\sqrt{5} + \sqrt{2}) = 3$
Question 3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = $\frac{c}{d}$ . This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Answer:
Given:
The definition of $\pi$ as the ratio of the circumference ($c$) of a circle to its diameter ($d$), i.e., $\pi = \frac{c}{d}$.
The fact that $\pi$ is an irrational number.
Contradiction:
The definition $\pi = \frac{c}{d}$ represents $\pi$ as a ratio of two quantities ($c$ and $d$). If $c$ and $d$ were both rational numbers, their ratio $\frac{c}{d}$ would also be a rational number. This seems to contradict the known fact that $\pi$ is irrational.
Resolution:
The apparent contradiction arises from the assumption that $c$ and $d$ must be rational when measured. When we measure a length with any physical instrument (like a ruler or measuring tape), we only obtain an approximate value. This measured value is always a finite decimal, which is a rational number.
However, the mathematical definition $\pi = \frac{c}{d}$ holds true for the exact values of the circumference and the diameter. Since $\pi$ is an irrational number, it cannot be expressed as a ratio of two integers.
For the ratio $\frac{c}{d}$ to be equal to the irrational number $\pi$, it is necessary that at least one of the lengths, $c$ or $d$, must be irrational. Since we cannot measure irrational lengths exactly with any physical instrument, any measurement we make of $c$ and $d$ will yield only rational approximations.
For example, if you have a circle with a diameter of exactly 1 unit (which is rational), its circumference must be $\pi \times 1 = \pi$ units, which is irrational. If you try to measure this circumference, you will get a rational approximation of $\pi$. Conversely, if you have a circle with a circumference of exactly 1 unit (rational), its diameter must be $\frac{1}{\pi}$ units, which is also irrational. If the diameter is rational, the circumference is irrational, and vice versa, unless both $c$ and $d$ are irrational in a specific way that their ratio is exactly $\pi$.
Therefore, the definition $\pi = \frac{c}{d}$ does not contradict the irrationality of $\pi$. It simply implies that for any circle, the circumference and the diameter cannot both be rational numbers simultaneously.
Conclusion:
The contradiction is resolved by understanding that when we deal with the exact values of $c$ and $d$, their ratio $\frac{c}{d}$ equals $\pi$. Since $\pi$ is irrational, it implies that $c$ and $d$ cannot both be rational. Any measured values of $c$ and $d$ are rational approximations, which is why $\pi$ appears as a ratio of two 'measured' numbers, but these are not the exact values.
Question 4. Represent $\sqrt{9.3}$ on the number line.
Answer:
Given:
The number $\sqrt{9.3}$.
To Represent:
Represent $\sqrt{9.3}$ on the number line.
Construction:
We can represent $\sqrt{x}$ geometrically on the number line for any positive real number $x$. Here, $x = 9.3$.
Follow these steps:
1. Draw a line and mark a point A on it. Let this be the origin for convenience in steps, although in the final representation B will often be the origin.
2. Mark a point B on the line such that the distance from A to B is 9.3 units. So, AB = 9.3.
3. Extend the line segment AB to the right and mark a point C such that BC = 1 unit. The total length of the segment AC is $AB + BC = 9.3 + 1 = 10.3$ units.
4. Find the midpoint of the segment AC. Let this midpoint be O. The length $AO = OC = \frac{AC}{2} = \frac{10.3}{2} = 5.15$ units.
5. With O as the center and radius OA (or OC), draw a semicircle above the line AC.
6. Draw a line perpendicular to AC passing through the point B. Let this perpendicular line intersect the semicircle at point D.
7. The length of the line segment BD is equal to $\sqrt{9.3}$.
8. Now, taking B as the center and BD as the radius, draw an arc that intersects the number line at a point E.
9. The point E represents the number $\sqrt{9.3}$ on the number line. If we consider B as the origin (0) on the number line, then the coordinate of point E is $\sqrt{9.3}$.
Verification:
We can verify that the length BD is indeed $\sqrt{9.3}$ using the Pythagorean theorem.
In the construction, O is the midpoint of AC, and O is the center of the semicircle.
The radius of the semicircle is $r = OA = OC = OD = \frac{9.3 + 1}{2} = 5.15$.
Consider the right-angled triangle OBD (since BD is perpendicular to AC).
The length OB can be calculated as the distance from O to B. We can express OB in terms of the radius and BC (or AB).
$OB = OC - BC = 5.15 - 1 = 4.15$.
Alternatively, if B is at 0, A is at -9.3, C is at 1. O is at $\frac{-9.3+1}{2} = -4.15$. The distance OB $= |0 - (-4.15)| = 4.15$.
Using the Pythagorean theorem in $\triangle OBD$:
$OB^2 + BD^2 = OD^2$
$BD^2 = OD^2 - OB^2$
Substitute the values of OD (radius) and OB:
$BD^2 = (5.15)^2 - (4.15)^2$
Using the difference of squares identity $a^2 - b^2 = (a-b)(a+b)$:
$BD^2 = (5.15 - 4.15)(5.15 + 4.15)$
$BD^2 = (1)(9.3)$
$BD^2 = 9.3$
Since BD is a length, it must be positive:
$BD = \sqrt{9.3}$
Thus, the length BD represents $\sqrt{9.3}$. When this length is transferred to the number line from point B (assumed to be at 0 or the starting point of measurement), the point E represents $\sqrt{9.3}$.
Question 5. Rationalise the denominators of the following:
(i) $\frac{1}{\sqrt{7}}$
(ii) $\frac{1}{\sqrt{7} \;-\; \sqrt{6}}$
(iii) $\frac{1}{\sqrt{5} \;+\; \sqrt{2}}$
(iv) $\frac{1}{\sqrt{7} \;-\; 2}$
Answer:
We rationalise the denominator for each fraction.
(i) $\frac{1}{\sqrt{7}}$
Given: The fraction $\frac{1}{\sqrt{7}}$.
To Rationalise: The denominator of $\frac{1}{\sqrt{7}}$.
Solution: To rationalise the denominator $\sqrt{7}$, we multiply the numerator and denominator by $\sqrt{7}$.
$\frac{1}{\sqrt{7}} = \frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}$
$= \frac{1 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}}$
$= \frac{\sqrt{7}}{(\sqrt{7})^2}$
$= \frac{\sqrt{7}}{7}$
The denominator is now the rational number 7.
(ii) $\frac{1}{\sqrt{7} - \sqrt{6}}$
Given: The fraction $\frac{1}{\sqrt{7} - \sqrt{6}}$.
To Rationalise: The denominator of $\frac{1}{\sqrt{7} - \sqrt{6}}$.
Solution: To rationalise the denominator $\sqrt{7} - \sqrt{6}$, we multiply the numerator and denominator by its conjugate, which is $\sqrt{7} + \sqrt{6}$.
$\frac{1}{\sqrt{7} - \sqrt{6}} = \frac{1}{\sqrt{7} - \sqrt{6}} \times \frac{\sqrt{7} + \sqrt{6}}{\sqrt{7} + \sqrt{6}}$
$= \frac{1 \times (\sqrt{7} + \sqrt{6})}{(\sqrt{7} - \sqrt{6})(\sqrt{7} + \sqrt{6})}$
Use the identity $(a-b)(a+b) = a^2 - b^2$ in the denominator:
$= \frac{\sqrt{7} + \sqrt{6}}{(\sqrt{7})^2 - (\sqrt{6})^2}$
$= \frac{\sqrt{7} + \sqrt{6}}{7 - 6}$
$= \frac{\sqrt{7} + \sqrt{6}}{1}$
$= \sqrt{7} + \sqrt{6}$
The denominator is now the rational number 1.
(iii) $\frac{1}{\sqrt{5} + \sqrt{2}}$
Given: The fraction $\frac{1}{\sqrt{5} + \sqrt{2}}$.
To Rationalise: The denominator of $\frac{1}{\sqrt{5} + \sqrt{2}}$.
Solution: To rationalise the denominator $\sqrt{5} + \sqrt{2}$, we multiply the numerator and denominator by its conjugate, which is $\sqrt{5} - \sqrt{2}$.
$\frac{1}{\sqrt{5} + \sqrt{2}} = \frac{1}{\sqrt{5} + \sqrt{2}} \times \frac{\sqrt{5} - \sqrt{2}}{\sqrt{5} - \sqrt{2}}$
$= \frac{1 \times (\sqrt{5} - \sqrt{2})}{(\sqrt{5} + \sqrt{2})(\sqrt{5} - \sqrt{2})}$
Use the identity $(a+b)(a-b) = a^2 - b^2$ in the denominator:
$= \frac{\sqrt{5} - \sqrt{2}}{(\sqrt{5})^2 - (\sqrt{2})^2}$
$= \frac{\sqrt{5} - \sqrt{2}}{5 - 2}$
$= \frac{\sqrt{5} - \sqrt{2}}{3}$
The denominator is now the rational number 3.
(iv) $\frac{1}{\sqrt{7} - 2}$
Given: The fraction $\frac{1}{\sqrt{7} - 2}$.
To Rationalise: The denominator of $\frac{1}{\sqrt{7} - 2}$.
Solution: To rationalise the denominator $\sqrt{7} - 2$, we multiply the numerator and denominator by its conjugate, which is $\sqrt{7} + 2$.
$\frac{1}{\sqrt{7} - 2} = \frac{1}{\sqrt{7} - 2} \times \frac{\sqrt{7} + 2}{\sqrt{7} + 2}$
$= \frac{1 \times (\sqrt{7} + 2)}{(\sqrt{7} - 2)(\sqrt{7} + 2)}$
Use the identity $(a-b)(a+b) = a^2 - b^2$ in the denominator:
$= \frac{\sqrt{7} + 2}{(\sqrt{7})^2 - (2)^2}$
$= \frac{\sqrt{7} + 2}{7 - 4}$
$= \frac{\sqrt{7} + 2}{3}$
The denominator is now the rational number 3.
Example 20 (Before Exercise 1.5)
Example 20: Simplify
(i) $2^{\frac{2}{3}}$ . $2^{\frac{1}{3}}$
(ii) $\left( 3^{\frac{1}{5}} \right)^4$
(iii) $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}$
(iv) $13^{\frac{1}{5}}$ . $17^{\frac{1}{5}}$
Answer:
We simplify each expression using the laws of exponents.
Recall the laws of exponents for positive real numbers $a$ and $b$, and rational exponents $p$ and $q$:
1. $a^p \cdot a^q = a^{p+q}$ (Product of powers with the same base)
2. $(a^p)^q = a^{pq}$ (Power of a power)
3. $\frac{a^p}{a^q} = a^{p-q}$ (Quotient of powers with the same base, $a \neq 0$)
4. $a^p b^p = (ab)^p$ (Product of powers with the same exponent)
(i) $2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}}$
This matches the form $a^p \cdot a^q$ with $a=2$, $p=\frac{2}{3}$, and $q=\frac{1}{3}$.
Using the law $a^p \cdot a^q = a^{p+q}$:
$2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}} = 2^{\frac{2}{3} + \frac{1}{3}}$
Add the exponents:
$\frac{2}{3} + \frac{1}{3} = \frac{2+1}{3} = \frac{3}{3} = 1$
So, $2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}} = 2^1 = 2$.
(ii) $(3^{\frac{1}{5}})^4$
This matches the form $(a^p)^q$ with $a=3$, $p=\frac{1}{5}$, and $q=4$.
Using the law $(a^p)^q = a^{pq}$:
$(3^{\frac{1}{5}})^4 = 3^{\frac{1}{5} \times 4}$
Multiply the exponents:
$\frac{1}{5} \times 4 = \frac{4}{5}$
So, $(3^{\frac{1}{5}})^4 = 3^{\frac{4}{5}}$.
(iii) $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}$
This matches the form $\frac{a^p}{a^q}$ with $a=7$, $p=\frac{1}{5}$, and $q=\frac{1}{3}$.
Using the law $\frac{a^p}{a^q} = a^{p-q}$:
$\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}} = 7^{\frac{1}{5} - \frac{1}{3}}$
Subtract the exponents. Find a common denominator for $\frac{1}{5}$ and $\frac{1}{3}$, which is 15.
$\frac{1}{5} - \frac{1}{3} = \frac{1 \times 3}{5 \times 3} - \frac{1 \times 5}{3 \times 5} = \frac{3}{15} - \frac{5}{15} = \frac{3-5}{15} = -\frac{2}{15}$
So, $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}} = 7^{-\frac{2}{15}}$.
(iv) $13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}}$
This matches the form $a^p b^p$ with $a=13$, $b=17$, and $p=\frac{1}{5}$.
Using the law $a^p b^p = (ab)^p$:
$13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}} = (13 \times 17)^{\frac{1}{5}}$
Multiply the bases:
$13 \times 17 = 221$
So, $13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}} = (221)^{\frac{1}{5}}$.
Results:
(i) $2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}} = 2$
(ii) $(3^{\frac{1}{5}})^4 = 3^{\frac{4}{5}}$
(iii) $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}} = 7^{-\frac{2}{15}}$
(iv) $13^{\frac{1}{5}} \cdot 17^{\frac{1}{5}} = (221)^{\frac{1}{5}}$
Exercise 1.5
Question 1. Find:
(i) $64^{\frac{1}{2}}$
(ii) $32^{\frac{1}{5}}$
(iii) $125^{\frac{1}{3}}$
Answer:
Given:
The expressions: (i) $64^{\frac{1}{2}}$, (ii) $32^{\frac{1}{5}}$, (iii) $125^{\frac{1}{3}}$.
To Find:
The value of each expression.
Solution:
We use the definition of fractional exponents, which states that for a positive real number $a$ and a positive integer $n$, $a^{\frac{1}{n}} = \sqrt[n]{a}$. This represents the $n$-th root of $a$.
(i) $64^{\frac{1}{2}}$
This expression means the square root of 64.
$64^{\frac{1}{2}} = \sqrt{64}$
We know that $8 \times 8 = 64$.
So, $\sqrt{64} = 8$.
Thus, $64^{\frac{1}{2}} = 8$.
(ii) $32^{\frac{1}{5}}$
This expression means the 5th root of 32.
$32^{\frac{1}{5}} = \sqrt[5]{32}$
We need to find a number that, when multiplied by itself 5 times, equals 32.
Let's find the prime factorization of 32:
$\begin{array}{c|cc} 2 & 32 \\ \hline 2 & 16 \\ \hline 2 & 8 \\ \hline 2 & 4 \\ \hline 2 & 2 \\ \hline & 1 \end{array}$
So, $32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5$.
Therefore, $\sqrt[5]{32} = \sqrt[5]{2^5} = 2$.
Thus, $32^{\frac{1}{5}} = 2$.
(iii) $125^{\frac{1}{3}}$
This expression means the cube root (3rd root) of 125.
$125^{\frac{1}{3}} = \sqrt[3]{125}$
We need to find a number that, when multiplied by itself 3 times, equals 125.
Let's find the prime factorization of 125:
$\begin{array}{c|cc} 5 & 125 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
So, $125 = 5 \times 5 \times 5 = 5^3$.
Therefore, $\sqrt[3]{125} = \sqrt[3]{5^3} = 5$.
Thus, $125^{\frac{1}{3}} = 5$.
Results:
(i) $64^{\frac{1}{2}} = 8$
(ii) $32^{\frac{1}{5}} = 2$
(iii) $125^{\frac{1}{3}} = 5$
Question 2. Find:
(i) $9^{\frac{3}{2}}$
(ii) $32^{\frac{2}{5}}$
(iii) $16^{\frac{3}{4}}$
(iv) $125^{\frac{-1}{3}}$
Answer:
Given:
The expressions: (i) $9^{\frac{3}{2}}$, (ii) $32^{\frac{2}{5}}$, (iii) $16^{\frac{3}{4}}$, (iv) $125^{\frac{-1}{3}}$.
To Find:
The value of each expression.
Solution:
We use the laws of exponents, specifically $a^{\frac{p}{q}} = (a^{\frac{1}{q}})^p = (\sqrt[q]{a})^p$ and $a^{-p} = \frac{1}{a^p}$.
(i) $9^{\frac{3}{2}}$
We can write this as $(9^{\frac{1}{2}})^3$ or $(9^3)^{\frac{1}{2}}$. Calculating the root first is usually simpler.
$9^{\frac{3}{2}} = (9^{\frac{1}{2}})^3$
Calculate the square root of 9:
$9^{\frac{1}{2}} = \sqrt{9} = 3$
Now raise the result to the power of 3:
$(3)^3 = 3 \times 3 \times 3 = 27$
Thus, $9^{\frac{3}{2}} = 27$.
(ii) $32^{\frac{2}{5}}$
We can write this as $(32^{\frac{1}{5}})^2$.
$32^{\frac{2}{5}} = (32^{\frac{1}{5}})^2$
Calculate the 5th root of 32. We know $32 = 2^5$, so $32^{\frac{1}{5}} = \sqrt[5]{32} = 2$.
Now raise the result to the power of 2:
$(2)^2 = 2 \times 2 = 4$
Thus, $32^{\frac{2}{5}} = 4$.
(iii) $16^{\frac{3}{4}}$
We can write this as $(16^{\frac{1}{4}})^3$.
$16^{\frac{3}{4}} = (16^{\frac{1}{4}})^3$
Calculate the 4th root of 16. We know $16 = 2 \times 2 \times 2 \times 2 = 2^4$, so $16^{\frac{1}{4}} = \sqrt[4]{16} = 2$.
Now raise the result to the power of 3:
$(2)^3 = 2 \times 2 \times 2 = 8$
Thus, $16^{\frac{3}{4}} = 8$.
(iv) $125^{\frac{-1}{3}}$
This has a negative exponent. We use the rule $a^{-p} = \frac{1}{a^p}$.
$125^{\frac{-1}{3}} = \frac{1}{125^{\frac{1}{3}}}$
Calculate the denominator $125^{\frac{1}{3}}$. This is the cube root of 125. We know $125 = 5^3$, so $125^{\frac{1}{3}} = \sqrt[3]{125} = 5$.
Substitute this value into the fraction:
$\frac{1}{125^{\frac{1}{3}}} = \frac{1}{5}$
Thus, $125^{\frac{-1}{3}} = \frac{1}{5}$.
Results:
(i) $9^{\frac{3}{2}} = 27$
(ii) $32^{\frac{2}{5}} = 4$
(iii) $16^{\frac{3}{4}} = 8$
(iv) $125^{\frac{-1}{3}} = \frac{1}{5}$
Question 3. Simplify:
(i) $2^{\frac{2}{3}}$ . $2^{\frac{1}{5}}$
(ii) $\left( \frac{1}{3^3}\right)^{7}$
(iii) $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}$
(iv) $7^{\frac{1}{2}}$ . $8^{\frac{1}{2}}$
Answer:
We simplify each expression using the laws of exponents.
Recall the laws of exponents for positive real numbers $a$ and $b$, and rational exponents $p$ and $q$:
1. $a^p \cdot a^q = a^{p+q}$
2. $(a^p)^q = a^{pq}$
3. $\frac{a^p}{a^q} = a^{p-q}$
4. $a^p b^p = (ab)^p$
Also, $(\frac{a}{b})^p = \frac{a^p}{b^p}$ and $\frac{1}{a^n} = a^{-n}$.
(i) $2^{\frac{2}{3}} \cdot 2^{\frac{1}{5}}$
This matches the form $a^p \cdot a^q$ with $a=2$, $p=\frac{2}{3}$, and $q=\frac{1}{5}$.
Using the law $a^p \cdot a^q = a^{p+q}$:
$2^{\frac{2}{3}} \cdot 2^{\frac{1}{5}} = 2^{\frac{2}{3} + \frac{1}{5}}$
Add the exponents. Find a common denominator for $\frac{2}{3}$ and $\frac{1}{5}$, which is 15.
$\frac{2}{3} + \frac{1}{5} = \frac{2 \times 5}{3 \times 5} + \frac{1 \times 3}{5 \times 3} = \frac{10}{15} + \frac{3}{15} = \frac{10+3}{15} = \frac{13}{15}$
So, $2^{\frac{2}{3}} \cdot 2^{\frac{1}{5}} = 2^{\frac{13}{15}}$.
(ii) $\left( \frac{1}{3^3} \right)^7$
We can use the rule $(\frac{a}{b})^p = \frac{a^p}{b^p}$ and $(a^m)^n = a^{mn}$.
$\left( \frac{1}{3^3} \right)^7 = \frac{1^7}{(3^3)^7}$
$1^7 = 1$
$(3^3)^7 = 3^{3 \times 7} = 3^{21}$
So, $\left( \frac{1}{3^3} \right)^7 = \frac{1}{3^{21}}$.
Alternatively, we can first write $\frac{1}{3^3}$ as $3^{-3}$.
$\left( \frac{1}{3^3} \right)^7 = (3^{-3})^7$
Using the law $(a^p)^q = a^{pq}$:
$(3^{-3})^7 = 3^{-3 \times 7} = 3^{-21}$
Using the rule $a^{-p} = \frac{1}{a^p}$:
$3^{-21} = \frac{1}{3^{21}}$
Both methods give the same result.
(iii) $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}$
This matches the form $\frac{a^p}{a^q}$ with $a=11$, $p=\frac{1}{2}$, and $q=\frac{1}{4}$.
Using the law $\frac{a^p}{a^q} = a^{p-q}$:
$\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}} = 11^{\frac{1}{2} - \frac{1}{4}}$
Subtract the exponents. Find a common denominator for $\frac{1}{2}$ and $\frac{1}{4}$, which is 4.
$\frac{1}{2} - \frac{1}{4} = \frac{1 \times 2}{2 \times 2} - \frac{1}{4} = \frac{2}{4} - \frac{1}{4} = \frac{2-1}{4} = \frac{1}{4}$
So, $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}} = 11^{\frac{1}{4}}$.
(iv) $7^{\frac{1}{2}} \cdot 8^{\frac{1}{2}}$
This matches the form $a^p b^p$ with $a=7$, $b=8$, and $p=\frac{1}{2}$.
Using the law $a^p b^p = (ab)^p$:
$7^{\frac{1}{2}} \cdot 8^{\frac{1}{2}} = (7 \times 8)^{\frac{1}{2}}$
Multiply the bases:
$7 \times 8 = 56$
So, $7^{\frac{1}{2}} \cdot 8^{\frac{1}{2}} = 56^{\frac{1}{2}}$.
This can also be written as $\sqrt{56}$. We can simplify $\sqrt{56}$ if 56 has a perfect square factor other than 1.
$56 = 4 \times 14 = 2^2 \times 14$
So, $\sqrt{56} = \sqrt{4 \times 14} = \sqrt{4} \times \sqrt{14} = 2\sqrt{14}$.
Both $56^{\frac{1}{2}}$ and $2\sqrt{14}$ are acceptable simplified forms.
Results:
(i) $2^{\frac{2}{3}} \cdot 2^{\frac{1}{5}} = 2^{\frac{13}{15}}$
(ii) $\left( \frac{1}{3^3} \right)^7 = \frac{1}{3^{21}}$ or $3^{-21}$
(iii) $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}} = 11^{\frac{1}{4}}$
(iv) $7^{\frac{1}{2}} \cdot 8^{\frac{1}{2}} = 56^{\frac{1}{2}}$ or $\sqrt{56}$ or $2\sqrt{14}$

