| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 11 Surface Areas And Volumes
Welcome to the comprehensive solutions guide for Chapter 11, "Surface Areas And Volumes," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. This crucial chapter significantly expands upon the mensuration concepts studied in Class 8, introducing students to the calculation of surface areas and volumes for a wider range of important three-dimensional geometric solids. Mastering these formulas and their applications is essential for various fields, including engineering, architecture, physics, and for solving numerous practical problems involving space and measurement. These solutions offer meticulous, step-by-step derivations and calculations for all exercises, ensuring a solid grasp of the concepts.
Building upon the knowledge of cubes, cuboids, and cylinders, this chapter introduces calculations for several new shapes. The solutions cover the surface area and volume for all the key solids studied at this level:
- Cube: Reinforcing TSA = $6l^2$ and Volume $V = l^3$.
- Cuboid: Reinforcing TSA = $2(lb + bh + hl)$ and Volume $V = l \times b \times h$.
- Right Circular Cylinder: Reinforcing CSA = $2\pi rh$, TSA = $2\pi r(h+r)$, and Volume $V = \pi r^2 h$.
- Right Circular Cone: Introducing concepts like slant height ($l$), its relation to height ($h$) and radius ($r$) via the Pythagorean theorem ($l = \sqrt{r^2 + h^2}$), Curved Surface Area (CSA) = $\pi r l$, Total Surface Area (TSA) = $\pi r(l+r)$, and Volume $V = \frac{1}{3} \pi r^2 h$.
- Sphere: Introducing Surface Area $SA = 4\pi r^2$ and Volume $V = \frac{4}{3}\pi r^3$.
- Hemisphere: Introducing Curved Surface Area (CSA) = $2\pi r^2$, Total Surface Area (TSA) = $3\pi r^2$, and Volume $V = \frac{2}{3}\pi r^3$.
The solutions provided tackle a diverse array of problems designed to build proficiency and understanding. These range from straightforward calculations where dimensions (like radius, height, side length) are given, to more complex problems where the surface area or volume is provided, and a missing dimension needs to be calculated. A significant focus is placed on practical word problems that require students to apply these formulas in real-world contexts. Examples explored in the solutions include:
- Calculating the amount of canvas needed for a conical tent (CSA of cone).
- Finding the cost of painting a hemispherical dome (CSA or TSA of hemisphere), potentially involving rates in $\textsf{₹}$ per $m^2$.
- Determining the capacity (volume) of cylindrical tanks, conical vessels, or spherical containers.
- Calculating the amount of metal in a solid sphere or the volume of ice cream in a cone topped with a hemisphere.
Accuracy in calculations often hinges on maintaining unit consistency. The solutions emphasize the importance of ensuring all dimensions are in the same unit before applying formulas and guide students through necessary unit conversions, particularly between cubic units and capacity units (e.g., $1 \, m^3 = 1000 \, L$, $1000 \, cm^3 = 1 \, L$).
Regarding the rationalized syllabus for 2024-25, Chapter 11, "Surface Areas And Volumes" (formerly Chapter 13), has been significantly streamlined. The most notable change is the complete removal of the topic 'Frustum of a Cone' and all related exercises. The curriculum now focuses exclusively on the surface areas and volumes of the Cube, Cuboid, Cylinder, Cone, Sphere, and Hemisphere. This ensures students develop a strong mastery of the formulas and applications for these fundamental solids. By diligently working through these comprehensive solutions, students can memorize and confidently apply the necessary formulas, understand the distinction between surface area and volume, and adeptly solve complex, multi-step real-world problems involving geometric measurements.
Example 1 to 3 (Before Exercise 11.1)
Example 1. Find the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm.
Answer:
Given:
Base radius of the right circular cone, $r = 7$ cm.
Slant height of the right circular cone, $l = 10$ cm.
To Find:
The curved surface area of the cone.
Solution:
The formula for the curved surface area (CSA) of a right circular cone is given by:
CSA $= \pi r l$
where $r$ is the base radius and $l$ is the slant height.
Substitute the given values into the formula. We use the value of $\pi$ as $\frac{22}{7}$ since the radius is 7.
CSA $= \frac{22}{7} \times 7 \times 10$
Cancel the 7 in the denominator with the 7 in the numerator:
CSA $= \frac{22}{\cancel{7}} \times \cancel{7} \times 10$
CSA $= 22 \times 10$
CSA $= 220$
The unit for area is square centimeters.
Thus, the curved surface area of the cone is $220$ cm$^2$.
The curved surface area of the right circular cone is $220$ cm$^2$.
Example 2. The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone (Use π = 3.14).
Answer:
Given:
Height of the cone, $h = 16$ cm.
Base radius of the cone, $r = 12$ cm.
Use $\pi = 3.14$.
To Find:
1. The curved surface area (CSA) of the cone.
2. The total surface area (TSA) of the cone.
Solution:
First, we need to find the slant height ($l$) of the cone. The relationship between slant height, height, and radius is given by the Pythagorean theorem:
$l^2 = r^2 + h^2$
So, $l = \sqrt{r^2 + h^2}$
Substitute the given values of $r$ and $h$:
$l = \sqrt{(12)^2 + (16)^2}$
$l = \sqrt{144 + 256}$
$l = \sqrt{400}$
$l = 20$ cm
The slant height of the cone is $20$ cm.
Now, we can calculate the Curved Surface Area (CSA) of the cone using the formula:
CSA $= \pi r l$
Substitute the values of $\pi$, $r$, and $l$:
CSA $= 3.14 \times 12 \times 20$
CSA $= 3.14 \times (12 \times 20)$
CSA $= 3.14 \times 240$
CSA $= 3.14 \times 240 = \frac{314}{100} \times 240 = \frac{314 \times 240}{100} = \frac{314 \times 24}{10}$
CSA $= \frac{7536}{10} = 753.6$
The curved surface area is $753.6$ cm$^2$.
Next, we calculate the Total Surface Area (TSA) of the cone. The TSA is the sum of the curved surface area and the area of the base.
Area of base $= \pi r^2$
Area of base $= 3.14 \times (12)^2$
Area of base $= 3.14 \times 144$
Area of base $= 3.14 \times 144 = \frac{314}{100} \times 144 = \frac{314 \times 144}{100}$
Area of base $= \frac{45216}{100} = 452.16$ cm$^2$
TSA = CSA + Area of base
TSA $= 753.6 + 452.16$
TSA $= 1205.76$ cm$^2$
Alternatively, we can use the formula for TSA directly:
TSA $= \pi r (l+r)$
TSA $= 3.14 \times 12 \times (20 + 12)$
TSA $= 3.14 \times 12 \times 32$
TSA $= 3.14 \times (12 \times 32)$
TSA $= 3.14 \times 384$
TSA $= 3.14 \times 384 = \frac{314}{100} \times 384 = \frac{314 \times 384}{100}$
TSA $= \frac{120576}{100} = 1205.76$
The total surface area is $1205.76$ cm$^2$.
The curved surface area of the cone is $753.6$ cm$^2$.
The total surface area of the cone is $1205.76$ cm$^2$.
Example 3. A corn cob (see Fig. 11.5), shaped somewhat like a cone, has the radius of its broadest end as 2.1 cm and length (height) as 20 cm. If each 1 cm2 of the surface of the cob carries an average of four grains, find how many grains you would find on the entire cob.
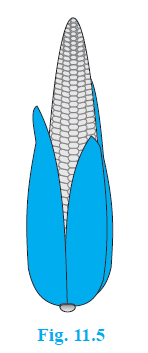
Answer:
Given:
Radius of the broadest end of the corn cob, $r = 2.1$ cm.
Length (height) of the corn cob, $h = 20$ cm.
Average number of grains per $1$ cm$^2$ of surface area = $4$.
To Find:
The total number of grains on the entire cob.
Solution:
The grains are present on the curved surface of the corn cob. To find the total number of grains, we first need to calculate the curved surface area (CSA) of the corn cob, assuming it is shaped like a cone.
The formula for the curved surface area of a cone is CSA $= \pi r l$, where $r$ is the base radius and $l$ is the slant height.
We are given the radius ($r$) and the height ($h$), but we need the slant height ($l$). The slant height, height, and radius of a cone are related by the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substituting the given values:
$l^2 = (2.1)^2 + (20)^2$
$l^2 = 4.41 + 400$
$l^2 = 404.41$
Taking the square root of both sides to find $l$:
$l = \sqrt{404.41}$
$l = 20.1$ cm
The slant height of the corn cob is $20.1$ cm.
Now, we can calculate the Curved Surface Area (CSA) using the formula CSA $= \pi r l$. We use $\pi = \frac{22}{7}$ for calculation as $r=2.1 = \frac{21}{10}$ is a multiple of $\frac{7}{10}$.
CSA $= \frac{22}{7} \times 2.1 \times 20.1$
Convert decimals to fractions for easier cancellation:
CSA $= \frac{22}{7} \times \frac{21}{10} \times \frac{201}{10}$
Cancel the 7 in the denominator with 21 in the numerator:
CSA $= 22 \times \frac{\cancel{21}^{3}}{\cancel{7}_{1}} \times \frac{201}{100}$
CSA $= 22 \times 3 \times \frac{201}{100}$
CSA $= 66 \times \frac{201}{100}$
Multiply $66$ by $201$:
$66 \times 201 = 66 \times (200 + 1) = 66 \times 200 + 66 \times 1 = 13200 + 66 = 13266$
CSA $= \frac{13266}{100}$
CSA $= 132.66$ cm$^2$
The curved surface area of the corn cob is $132.66$ cm$^2$.
We are given that each $1$ cm$^2$ of the surface carries an average of $4$ grains.
Total number of grains $=$ Curved Surface Area $\times$ Grains per cm$^2$
Total number of grains $= 132.66 \times 4$
$132.66 \times 4 = 530.64$
Since the number of grains must be a whole number, we should round this value to the nearest integer.
Total number of grains $\approx 531$
Approximately $531$ grains would be found on the entire cob.
Exercise 11.1
Assume π = $\frac{22}{7}$ , unless stated otherwise.
Question 1. Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Answer:
Given:
Diameter of the base of the cone = $10.5$ cm.
Slant height of the cone, $l = 10$ cm.
To Find:
The curved surface area of the cone.
Solution:
The radius of the base ($r$) is half of the diameter.
$r = \frac{\text{Diameter}}{2}$
$r = \frac{10.5}{2}$ cm
$r = 5.25$ cm
The formula for the curved surface area (CSA) of a cone is given by:
CSA $= \pi r l$
We will use the value of $\pi = \frac{22}{7}$ as the radius $5.25$ is easily divisible by $7$ ($5.25 = 7 \times 0.75$).
CSA $= \frac{22}{7} \times 5.25 \times 10$
Perform the multiplication:
CSA $= \frac{22}{7} \times (5.25 \times 10)$
CSA $= \frac{22}{7} \times 52.5$
Now divide $52.5$ by $7$:
$\frac{52.5}{7} = 7.5$
So,
CSA $= 22 \times 7.5$
Multiply $22$ by $7.5$:
$22 \times 7.5 = 22 \times \frac{15}{2}$
Cancel the common factor 2:
$= \cancel{22}^{11} \times \frac{15}{\cancel{2}_{1}}$
$= 11 \times 15$
$= 165$
The curved surface area is $165$ cm$^2$.
The curved surface area of the cone is $165$ cm$^2$.
Question 2. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Answer:
Given:
Diameter of the base of the cone = $24$ m.
Slant height of the cone, $l = 21$ m.
To Find:
The total surface area (TSA) of the cone.
Solution:
First, find the radius ($r$) of the base from the given diameter.
$r = \frac{\text{Diameter}}{2}$
$r = \frac{24}{2}$ m
$r = 12$ m
The formula for the Total Surface Area (TSA) of a cone is the sum of its curved surface area and the area of its base. The formula is:
TSA $= \pi r (r + l)$
where $r$ is the base radius and $l$ is the slant height.
Substitute the given values of $r = 12$ m and $l = 21$ m into the formula. We use the value of $\pi = \frac{22}{7}$.
TSA $= \frac{22}{7} \times 12 \times (12 + 21)$
TSA $= \frac{22}{7} \times 12 \times 33$
Multiply the numbers in the numerator:
$22 \times 12 = 264$
Now, multiply $264$ by $33$:
TSA $= \frac{264 \times 33}{7}$
$264 \times 33 = 8712$
TSA $= \frac{8712}{7}$
The unit for area is square meters.
Thus, the total surface area of the cone is $\frac{8712}{7}$ m$^2$.
The total surface area of the cone is $\frac{8712}{7}$ m$^2$.
Question 3. Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
(i) radius of the base and
(ii) total surface area of the cone.
Answer:
Given:
Curved surface area (CSA) of the cone = $308$ cm$^2$.
Slant height of the cone, $l = 14$ cm.
To Find:
(i) Radius of the base ($r$).
(ii) Total surface area (TSA) of the cone.
Solution:
(i) Find the radius of the base.
The formula for the curved surface area (CSA) of a cone is:
CSA $= \pi r l$
Substitute the given values: CSA $= 308$ cm$^2$ and $l = 14$ cm. Use $\pi = \frac{22}{7}$.
$308 = \frac{22}{7} \times r \times 14$
... (i)
Simplify the equation:
$308 = 22 \times r \times \frac{14}{7}$
$308 = 22 \times r \times 2$
$308 = 44r$
To find $r$, divide both sides by $44$:
$r = \frac{308}{44}$
We can simplify the fraction by dividing both numerator and denominator by common factors. Both are divisible by 4:
$r = \frac{\cancel{308}^{77}}{\cancel{44}_{11}}$
Now, divide $77$ by $11$:
$r = \frac{77}{11}$
$r = 7$
The radius of the base is $7$ cm.
(ii) Find the total surface area of the cone.
The Total Surface Area (TSA) of a cone is the sum of its curved surface area (CSA) and the area of its base.
TSA = CSA + Area of base
The area of the base is given by the formula $\pi r^2$.
Area of base $= \pi r^2$
Substitute the value of $r = 7$ cm and $\pi = \frac{22}{7}$:
Area of base $= \frac{22}{7} \times (7)^2$
Area of base $= \frac{22}{7} \times 49$
Cancel the 7 in the denominator with one of the 7s in $49$:
Area of base $= 22 \times \frac{\cancel{49}^{7}}{\cancel{7}_{1}}$
Area of base $= 22 \times 7$
Area of base $= 154$ cm$^2$
Now, add the CSA and the area of the base to find the TSA:
TSA = CSA + Area of base
TSA $= 308 + 154$
TSA $= 462$ cm$^2$
Alternatively, we can use the direct formula for TSA:
TSA $= \pi r (r+l)$
Substitute the values $r=7$ cm and $l=14$ cm, and $\pi = \frac{22}{7}$:
TSA $= \frac{22}{7} \times 7 \times (7 + 14)$
TSA $= \frac{22}{7} \times 7 \times 21$
Cancel the 7 in the denominator with the 7 in the numerator:
TSA $= 22 \times \cancel{7}^{1} \times 21 / \cancel{7}_{1}$
TSA $= 22 \times 21$
TSA $= 462$ cm$^2$
Both methods give the same result.
The radius of the base is $7$ cm.
The total surface area of the cone is $462$ cm$^2$.
Question 4. A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
Answer:
Given:
Height of the conical tent, $h = 10$ m.
Radius of the base of the tent, $r = 24$ m.
Cost of 1 m$^2$ canvas = $\textsf{₹} 70$.
To Find:
(i) Slant height of the tent ($l$).
(ii) Cost of the canvas required to make the tent.
Solution:
(i) Find the slant height of the tent.
The relationship between the slant height ($l$), height ($h$), and radius ($r$) of a cone is given by the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substitute the given values $r = 24$ m and $h = 10$ m:
$l^2 = (24)^2 + (10)^2$
$l^2 = 576 + 100$
$l^2 = 676$
Take the square root of both sides to find $l$:
$l = \sqrt{676}$
$l = 26$
The slant height of the tent is $26$ m.
(ii) Find the cost of the canvas required to make the tent.
The canvas is used for the curved surface of the tent. So, we need to find the curved surface area (CSA) of the cone.
The formula for the curved surface area of a cone is:
CSA $= \pi r l$
Substitute the values $r = 24$ m, $l = 26$ m, and use $\pi = \frac{22}{7}$:
CSA $= \frac{22}{7} \times 24 \times 26$
Multiply the numbers:
$24 \times 26 = 624$
CSA $= \frac{22}{7} \times 624$
CSA $= \frac{22 \times 624}{7}$
$22 \times 624 = 13728$
CSA $= \frac{13728}{7}$ m$^2$
The curved surface area of the tent is $\frac{13728}{7}$ m$^2$.
The cost of 1 m$^2$ canvas is $\textsf{₹} 70$.
The total cost of the canvas is the CSA multiplied by the cost per square meter:
Total Cost $= \text{CSA} \times \text{Cost per m}^2$
Total Cost $= \frac{13728}{7} \times 70$
Cancel the common factor 7:
Total Cost $= \frac{13728}{\cancel{7}_{1}} \times \cancel{70}^{10}$
Total Cost $= 13728 \times 10$
Total Cost $= 137280$
The total cost of the canvas is $\textsf{₹} 137280$.
(i) The slant height of the tent is $26$ m.
(ii) The cost of the canvas required is $\textsf{₹} 137280$.
Question 5. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14).
Answer:
Given:
Width of the tarpaulin = $3$ m.
Height of the conical tent, $h = 8$ m.
Base radius of the conical tent, $r = 6$ m.
Extra length of material for stitching and wastage = $20$ cm.
Use $\pi = 3.14$.
To Find:
The required length of the tarpaulin.
Solution:
The tarpaulin is used to make the curved surface of the conical tent. So, we first need to find the curved surface area (CSA) of the tent.
The formula for CSA of a cone is $\pi r l$, where $r$ is the base radius and $l$ is the slant height.
We are given $r = 6$ m and $h = 8$ m. We need to find the slant height $l$ using the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substitute the values:
$l^2 = (6)^2 + (8)^2$
$l^2 = 36 + 64$
$l^2 = 100$
Take the square root:
$l = \sqrt{100}$
$l = 10$ m
The slant height of the tent is $10$ m.
Now, calculate the Curved Surface Area (CSA) of the tent using CSA $= \pi r l$ with $\pi = 3.14$, $r = 6$ m, and $l = 10$ m.
CSA $= 3.14 \times 6 \times 10$
CSA $= 3.14 \times 60$
CSA $= 188.4$ m$^2$
The curved surface area of the tent is $188.4$ m$^2$.
The area of the tarpaulin required is equal to the curved surface area of the tent.
Area of tarpaulin $= 188.4$ m$^2$
The tarpaulin is in the shape of a rectangle with a width of $3$ m. Let the required length be $L$ m.
Area of rectangular tarpaulin $= \text{Length} \times \text{Width}$
Area of tarpaulin $= L \times 3$
Equating the area of the tarpaulin to the CSA of the tent:
$L \times 3 = 188.4$
To find the length $L$, divide the area by the width:
$L = \frac{188.4}{3}$
Perform the division:
$L = 62.8$ m
This is the length of the tarpaulin required for the curved surface, without considering wastage.
We are given that an extra length of $20$ cm is required for stitching margins and wastage.
Convert the extra length to meters: $20$ cm $= \frac{20}{100}$ m $= 0.2$ m.
Total length of tarpaulin required $=$ Length for CSA + Extra length
Total length $= 62.8 \text{ m} + 0.2 \text{ m}$
Total length $= 63.0$ m
The total length of tarpaulin required is $63$ m.
The required length of tarpaulin is $63$ m.
Question 6. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2 .
Answer:
Given:
Slant height of the conical tomb, $l = 25$ m.
Base diameter of the conical tomb = $14$ m.
Cost of white-washing = $\textsf{₹} 210$ per $100$ m$^2$.
To Find:
The cost of white-washing its curved surface.
Solution:
First, we find the radius ($r$) of the base from the given diameter.
$r = \frac{\text{Diameter}}{2}$
$r = \frac{14}{2}$ m
$r = 7$ m
The area to be white-washed is the curved surface area (CSA) of the conical tomb.
The formula for the curved surface area of a cone is:
CSA $= \pi r l$
Substitute the values $r = 7$ m and $l = 25$ m. We use $\pi = \frac{22}{7}$.
CSA $= \frac{22}{7} \times 7 \times 25$
Cancel the 7 in the denominator with the 7 in the numerator:
CSA $= 22 \times \cancel{7}^{1} \times 25 / \cancel{7}_{1}$
CSA $= 22 \times 25$
CSA $= 550$ m$^2$
The curved surface area of the tomb is $550$ m$^2$.
The rate of white-washing is given as $\textsf{₹} 210$ per $100$ m$^2$.
This means the cost for $1$ m$^2$ is $\frac{\textsf{₹} 210}{100} = \textsf{₹} 2.10$.
The total cost of white-washing is the curved surface area multiplied by the cost per square meter.
Total Cost $= \text{CSA} \times \text{Cost per m}^2$
Total Cost $= 550 \text{ m}^2 \times \textsf{₹} 2.10 / \text{m}^2$
Total Cost $= 550 \times 2.10$
$550 \times 2.1 = 550 \times \frac{21}{10} = 55 \times 21$
$55 \times 21 = 1155$
Total Cost $= \textsf{₹} 1155$
The cost of white-washing its curved surface is $\textsf{₹} 1155$.
Question 7. A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Answer:
Given:
Base radius of the conical joker's cap, $r = 7$ cm.
Height of the conical joker's cap, $h = 24$ cm.
Number of caps to be made = $10$.
To Find:
The total area of the sheet required to make 10 such caps.
Solution:
The sheet required to make a conical cap is for its curved surface. So, we need to find the curved surface area (CSA) of one cap first.
The formula for the curved surface area of a cone is CSA $= \pi r l$, where $r$ is the base radius and $l$ is the slant height.
We are given the radius ($r$) and the height ($h$). We need to calculate the slant height ($l$) using the relationship $l^2 = r^2 + h^2$ derived from the Pythagorean theorem.
Substitute the given values $r = 7$ cm and $h = 24$ cm:
$l^2 = (7)^2 + (24)^2$
$l^2 = 49 + 576$
$l^2 = 625$
Taking the square root of both sides:
$l = \sqrt{625}$
$l = 25$ cm
The slant height of the cap is $25$ cm.
Now, calculate the Curved Surface Area (CSA) of one cap using CSA $= \pi r l$. We use the value of $\pi = \frac{22}{7}$ since the radius is 7.
CSA of one cap $= \frac{22}{7} \times 7 \times 25$
Cancel the 7 in the denominator with the 7 in the numerator:
CSA of one cap $= 22 \times \cancel{7}^{1} \times 25 / \cancel{7}_{1}$
CSA of one cap $= 22 \times 25$
$22 \times 25 = 550$
The curved surface area of one cap is $550$ cm$^2$.
We need to find the total area of the sheet required to make 10 such caps.
Total area of sheet $=$ CSA of one cap $\times$ Number of caps
Total area of sheet $= 550$ cm$^2 \times 10$
Total area of sheet $= 5500$ cm$^2$
The total area of the sheet required to make 10 such caps is $5500$ cm$^2$.
Question 8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2 , what will be the cost of painting all these cones? (Use π = 3.14 and take $\sqrt{1.04}$ = 1.02)
Answer:
Given:
Number of hollow cones = $50$.
Base diameter of each cone = $40$ cm.
Height of each cone, $h = 1$ m.
Cost of painting = $\textsf{₹} 12$ per m$^2$.
Use $\pi = 3.14$ and $\sqrt{1.04} = 1.02$.
To Find:
The total cost of painting all 50 cones.
Solution:
First, we need to calculate the surface area of one cone that is to be painted. Since the cones are hollow and are used for barricading, only the curved surface is painted.
Convert the base diameter from centimeters to meters. Diameter $= 40$ cm $= \frac{40}{100}$ m $= 0.4$ m.
The radius ($r$) of the base is half of the diameter.
$r = \frac{\text{Diameter}}{2} = \frac{0.4}{2} = 0.2$ m.
The height is given as $h = 1$ m.
To find the curved surface area (CSA) of a cone, we need the slant height ($l$). The relationship is $l^2 = r^2 + h^2$.
Substitute the values $r = 0.2$ m and $h = 1$ m:
$l^2 = (0.2)^2 + (1)^2$
$l^2 = 0.04 + 1$
$l^2 = 1.04$
Take the square root to find $l$. We are given to use $\sqrt{1.04} = 1.02$.
$l = \sqrt{1.04} = 1.02$ m.
The slant height of each cone is $1.02$ m.
Now, calculate the Curved Surface Area (CSA) of one cone using CSA $= \pi r l$. Use $\pi = 3.14$, $r = 0.2$ m, and $l = 1.02$ m.
CSA of one cone $= 3.14 \times 0.2 \times 1.02$
CSA of one cone $= 0.64056$ m$^2$
There are 50 such cones to be painted. The total area to be painted is the sum of the CSA of all 50 cones.
Total area to be painted $= \text{CSA of one cone} \times \text{Number of cones}$
Total area to be painted $= 0.64056 \text{ m}^2 \times 50$
Multiply $0.64056$ by $50$ (which is $0.64056 \times \frac{100}{2} = 64.056 / 2$):
$0.64056 \times 50 = 32.028$ m$^2$
The total area to be painted is $32.028$ m$^2$.
The cost of painting is $\textsf{₹} 12$ per m$^2$.
Total cost of painting $=$ Total area to be painted $\times$ Cost per m$^2$
Total cost $= 32.028 \text{ m}^2 \times \textsf{₹} 12 / \text{m}^2$
Total cost $= \textsf{₹} 384.336$
Since cost is usually expressed in two decimal places (for paise), we round the result.
Total cost $\approx \textsf{₹} 384.34$
The total cost of painting all these cones will be approximately $\textsf{₹} 384.34$.
Example 4 to 7 (Before Exercise 11.2)
Example 4. Find the surface area of a sphere of radius 7 cm.
Answer:
Given:
Radius of the sphere, $r = 7$ cm.
To Find:
The surface area of the sphere.
Solution:
The formula for the surface area of a sphere is given by:
Surface Area $= 4 \pi r^2$
where $r$ is the radius of the sphere.
Substitute the given value of the radius, $r = 7$ cm. We will use $\pi = \frac{22}{7}$ since the radius is a multiple of 7.
Surface Area $= 4 \times \frac{22}{7} \times (7)^2$
Surface Area $= 4 \times \frac{22}{7} \times (7 \times 7)$
Cancel the 7 in the denominator with one of the 7s in the numerator:
Surface Area $= 4 \times 22 \times \frac{\cancel{7}^{1} \times 7}{\cancel{7}_{1}}$
Surface Area $= 4 \times 22 \times 7$
Multiply the numbers:
$4 \times 22 = 88$
Surface Area $= 88 \times 7$
$88 \times 7 = 616$
The unit for area is square centimeters.
Surface Area $= 616$ cm$^2$
The surface area of the sphere is $616$ cm$^2$.
Example 5. Find
(i) the curved surface area and
(ii) the total surface area of a hemisphere of radius 21 cm.
Answer:
Given:
Radius of the hemisphere, $r = 21$ cm.
To Find:
(i) The curved surface area (CSA) of the hemisphere.
(ii) The total surface area (TSA) of the hemisphere.
Solution:
(i) Find the curved surface area.
The formula for the curved surface area (CSA) of a hemisphere is given by:
CSA $= 2 \pi r^2$
where $r$ is the radius of the hemisphere.
Substitute the given value of the radius, $r = 21$ cm. We use $\pi = \frac{22}{7}$ as the radius is a multiple of 7.
CSA $= 2 \times \frac{22}{7} \times (21)^2$
CSA $= 2 \times \frac{22}{7} \times (21 \times 21)$
Cancel the 7 in the denominator with one of the 21s in the numerator:
CSA $= 2 \times 22 \times \frac{\cancel{21}^{3} \times 21}{\cancel{7}_{1}}$
CSA $= 2 \times 22 \times 3 \times 21$
Multiply the numbers:
$2 \times 22 = 44$
CSA $= 44 \times 3 \times 21$
$44 \times 3 = 132$
CSA $= 132 \times 21$
$132 \times 21 = 132 \times (20 + 1) = 132 \times 20 + 132 \times 1 = 2640 + 132 = 2772$
The unit for area is square centimeters.
CSA $= 2772$ cm$^2$
(ii) Find the total surface area.
The total surface area (TSA) of a solid hemisphere includes the curved surface area and the area of its flat circular base.
TSA = Curved Surface Area + Area of Base
Area of Base $= \pi r^2$
TSA $= 2 \pi r^2 + \pi r^2$
TSA $= 3 \pi r^2$
Substitute the given value of the radius, $r = 21$ cm, and $\pi = \frac{22}{7}$.
TSA $= 3 \times \frac{22}{7} \times (21)^2$
TSA $= 3 \times \frac{22}{7} \times (21 \times 21)$
Cancel the 7 in the denominator with one of the 21s in the numerator:
TSA $= 3 \times 22 \times \frac{\cancel{21}^{3} \times 21}{\cancel{7}_{1}}$
TSA $= 3 \times 22 \times 3 \times 21$
Multiply the numbers:
$3 \times 22 = 66$
TSA $= 66 \times 3 \times 21$
$66 \times 3 = 198$
TSA $= 198 \times 21$
$198 \times 21 = 198 \times (20 + 1) = 198 \times 20 + 198 \times 1 = 3960 + 198 = 4158$
The unit for area is square centimeters.
TSA $= 4158$ cm$^2$
(i) The curved surface area of the hemisphere is $2772$ cm$^2$.
(ii) The total surface area of the hemisphere is $4158$ cm$^2$.
Example 6. The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.
Answer:
Given:
Diameter of the hollow sphere = $7$ m.
To Find:
The area available to the motorcyclist for riding (Inner surface area).
Solution:
The area available to the motorcyclist for riding inside the hollow sphere is its inner surface area. Since it is a hollow sphere, the inner surface area is the same as the surface area of a sphere with the given diameter.
First, find the radius ($r$) of the sphere from the given diameter.
$r = \frac{\text{Diameter}}{2}$
$r = \frac{7}{2}$ m
$r = 3.5$ m
The formula for the surface area of a sphere is given by:
Surface Area $= 4 \pi r^2$
Substitute the value of the radius, $r = \frac{7}{2}$ m, and use $\pi = \frac{22}{7}$ since the radius is a multiple of 7.
Surface Area $= 4 \times \frac{22}{7} \times \left(\frac{7}{2}\right)^2$
Surface Area $= 4 \times \frac{22}{7} \times \frac{7 \times 7}{2 \times 2}$
Surface Area $= 4 \times \frac{22}{7} \times \frac{49}{4}$
Cancel the common factors:
Surface Area $= \cancel{4}^{1} \times \frac{22}{\cancel{7}_{1}} \times \frac{\cancel{49}^{7}}{\cancel{4}_{1}}$
Surface Area $= 1 \times 22 \times 7$
Surface Area $= 154$
The unit for area is square meters.
The area available for riding is $154$ m$^2$.
The area available to the motorcyclist for riding is $154$ m$^2$.
Example 7. A hemispherical dome of a building needs to be painted (see Fig. 11.9). If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is ₹ 5 per 100 cm2.
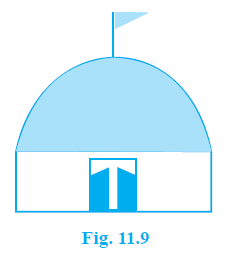
Answer:
Given:
The dome is hemispherical.
Circumference of the base of the dome = $17.6$ m.
Cost of painting = $\textsf{₹} 5$ per $100$ cm$^2$.
To Find:
The cost of painting the curved surface of the dome.
Solution:
The base of the hemispherical dome is a circle. The circumference of the base is given by the formula $C = 2 \pi r$, where $r$ is the radius of the base.
We are given the circumference $C = 17.6$ m.
$17.6 = 2 \pi r$
... (i)
To find the radius $r$, substitute $\pi = \frac{22}{7}$:
$17.6 = 2 \times \frac{22}{7} \times r$
$17.6 = \frac{44}{7} \times r$
$r = 17.6 \times \frac{7}{44}$
$r = \frac{176}{10} \times \frac{7}{44}$
We can simplify the fraction by cancelling common factors. $176$ is divisible by $44$ ($176 = 4 \times 44$).
$r = \frac{\cancel{176}^{4}}{10} \times \frac{7}{\cancel{44}_{1}}$
$r = \frac{4}{10} \times 7$
$r = 0.4 \times 7$
$r = 2.8$ m
The radius of the base of the dome is $2.8$ m.
The area to be painted is the curved surface area (CSA) of the hemisphere.
The formula for the curved surface area of a hemisphere is:
CSA $= 2 \pi r^2$
Substitute the value of $r = 2.8$ m and $\pi = \frac{22}{7}$:
CSA $= 2 \times \frac{22}{7} \times (2.8)^2$
CSA $= 2 \times \frac{22}{7} \times 2.8 \times 2.8$
Cancel 7 with 2.8 ($2.8 / 7 = 0.4$):
CSA $= 2 \times 22 \times \frac{\cancel{2.8}^{0.4}}{\cancel{7}_{1}} \times 2.8$
CSA $= 2 \times 22 \times 0.4 \times 2.8$
CSA $= 44 \times (0.4 \times 2.8)$
CSA $= 44 \times 1.12$
CSA $= 49.28$ m$^2$
The curved surface area of the dome is $49.28$ m$^2$.
The cost of painting is $\textsf{₹} 5$ per $100$ cm$^2$.
First, convert the unit area for the cost from cm$^2$ to m$^2$.
$1$ m $= 100$ cm
$1$ m$^2 = (100 \text{ cm})^2 = 10000$ cm$^2$
The cost is $\textsf{₹} 5$ for $100$ cm$^2$.
The cost for $1$ cm$^2 = \textsf{₹} \frac{5}{100}$.
The cost for $1$ m$^2 = \textsf{₹} \frac{5}{100} \times 10000$
Cost per m$^2 = \textsf{₹} 5 \times \frac{10000}{100} = \textsf{₹} 5 \times 100 = \textsf{₹} 500$ per m$^2$.
Now, calculate the total cost of painting the dome.
Total Cost $=$ CSA in m$^2 \times$ Cost per m$^2$
Total Cost $= 49.28 \times 500$
Total Cost $= 49.28 \times 5 \times 100$
$49.28 \times 5 = 246.40$
Total Cost $= 246.40 \times 100$
Total Cost $= 24640$
The total cost of painting the dome is $\textsf{₹} 24640$.
The cost of painting the hemispherical dome is $\textsf{₹} 24640$.
Exercise 11.2
Assume π = $\frac{22}{7}$ , unless stated otherwise.
Question 1. Find the surface area of a sphere of radius:
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
Answer:
Given:
The formula for the surface area of a sphere is $4 \pi r^2$.
The value of $\pi$ to be used is $\frac{22}{7}$, unless stated otherwise.
To Find:
The surface area of a sphere for the given radii.
Solution:
The surface area of a sphere with radius $r$ is given by the formula:
Surface Area $= 4 \pi r^2$
(i) Radius $r = 10.5$ cm
Substitute the value of $r$ and $\pi = \frac{22}{7}$ into the formula:
Surface Area $= 4 \times \frac{22}{7} \times (10.5)^2$
Surface Area $= 4 \times \frac{22}{7} \times (10.5 \times 10.5)$
We can write $10.5 = \frac{105}{10} = \frac{21}{2}$.
Surface Area $= 4 \times \frac{22}{7} \times \left(\frac{21}{2}\right)^2$
Surface Area $= 4 \times \frac{22}{7} \times \frac{21 \times 21}{2 \times 2}$
Surface Area $= 4 \times \frac{22}{7} \times \frac{441}{4}$
Cancel common factors:
Surface Area $= \cancel{4} \times \frac{22}{\cancel{7}} \times \frac{\cancel{441}^{63}}{\cancel{4}}$
Surface Area $= 22 \times 63$
Surface Area $= 1386$ cm$^2$
(ii) Radius $r = 5.6$ cm
Substitute the value of $r$ and $\pi = \frac{22}{7}$ into the formula:
Surface Area $= 4 \times \frac{22}{7} \times (5.6)^2$
Surface Area $= 4 \times \frac{22}{7} \times (5.6 \times 5.6)$
Cancel 7 with 5.6 ($5.6 \div 7 = 0.8$):
Surface Area $= 4 \times 22 \times \frac{\cancel{5.6}^{0.8}}{\cancel{7}_{1}} \times 5.6$
Surface Area $= 88 \times 0.8 \times 5.6$
Surface Area $= 88 \times (0.8 \times 5.6)$
Surface Area $= 88 \times 4.48$
So, $88 \times 448 = 39424$. Since $4.48$ has two decimal places, $88 \times 4.48$ has two decimal places.
Surface Area $= 394.24$ cm$^2$
(iii) Radius $r = 14$ cm
Substitute the value of $r$ and $\pi = \frac{22}{7}$ into the formula:
Surface Area $= 4 \times \frac{22}{7} \times (14)^2$
Surface Area $= 4 \times \frac{22}{7} \times (14 \times 14)$
Cancel 7 with one of the 14s ($14 \div 7 = 2$):
Surface Area $= 4 \times 22 \times \frac{\cancel{14}^{2}}{\cancel{7}_{1}} \times 14$
Surface Area $= 4 \times 22 \times 2 \times 14$
Surface Area $= 88 \times 28$
Surface Area $= 2464$ cm$^2$
The surface area of the spheres are:
(i) $1386$ cm$^2$ for radius $10.5$ cm.
(ii) $394.24$ cm$^2$ for radius $5.6$ cm.
(iii) $2464$ cm$^2$ for radius $14$ cm.
Question 2. Find the surface area of a sphere of diameter
(i) 14cm
(ii) 21cm
(iii) 3.5cm
Answer:
Given:
The formula for the surface area of a sphere is $4 \pi r^2$.
The value of $\pi$ to be used is $\frac{22}{7}$.
To Find:
The surface area of a sphere for the given diameters.
Solution:
The radius ($r$) of a sphere is half of its diameter ($d$). $r = \frac{d}{2}$.
The surface area of a sphere with radius $r$ is given by the formula:
Surface Area $= 4 \pi r^2$
(i) Diameter $d = 14$ cm
Radius $r = \frac{14}{2} = 7$ cm.
Substitute the value of $r$ and $\pi = \frac{22}{7}$ into the formula:
Surface Area $= 4 \times \frac{22}{7} \times (7)^2$
Surface Area $= 4 \times \frac{22}{7} \times (7 \times 7)$
Cancel the 7 in the denominator with one of the 7s in the numerator:
Surface Area $= 4 \times 22 \times \cancel{7}^{1} \times 7 / \cancel{7}_{1}$
Surface Area $= 4 \times 22 \times 7$
Surface Area $= 88 \times 7$
Surface Area $= 616$ cm$^2$
(ii) Diameter $d = 21$ cm
Radius $r = \frac{21}{2} = 10.5$ cm.
Substitute the value of $r$ and $\pi = \frac{22}{7}$ into the formula:
Surface Area $= 4 \times \frac{22}{7} \times (10.5)^2$
Surface Area $= 4 \times \frac{22}{7} \times (10.5 \times 10.5)$
We can write $10.5 = \frac{21}{2}$.
Surface Area $= 4 \times \frac{22}{7} \times \left(\frac{21}{2}\right)^2$
Surface Area $= 4 \times \frac{22}{7} \times \frac{21 \times 21}{2 \times 2}$
Surface Area $= 4 \times \frac{22}{7} \times \frac{441}{4}$
Cancel common factors:
Surface Area $= \cancel{4}^{1} \times \frac{22}{\cancel{7}_{1}} \times \frac{\cancel{441}^{63}}{\cancel{4}_{1}}$
Surface Area $= 22 \times 63$
Surface Area $= 1386$ cm$^2$
(iii) Diameter $d = 3.5$ cm
Radius $r = \frac{3.5}{2} = 1.75$ cm.
We can write $1.75 = \frac{175}{100} = \frac{7}{4}$.
Substitute the value of $r$ and $\pi = \frac{22}{7}$ into the formula:
Surface Area $= 4 \times \frac{22}{7} \times (1.75)^2$
Surface Area $= 4 \times \frac{22}{7} \times \left(\frac{7}{4}\right)^2$
Surface Area $= 4 \times \frac{22}{7} \times \frac{7 \times 7}{4 \times 4}$
Surface Area $= 4 \times \frac{22}{7} \times \frac{49}{16}$
Cancel common factors:
Surface Area $= \cancel{4}^{1} \times \frac{22}{\cancel{7}_{1}} \times \frac{\cancel{49}^{7}}{\cancel{16}_{4}}$
Surface Area $= \frac{22 \times 7}{4}$
Surface Area $= \frac{154}{4}$
Surface Area $= 38.5$ cm$^2$
The surface area of the spheres are:
(i) $616$ cm$^2$ for diameter $14$ cm.
(ii) $1386$ cm$^2$ for diameter $21$ cm.
(iii) $38.5$ cm$^2$ for diameter $3.5$ cm.
Question 3. Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Answer:
Given:
Radius of the hemisphere, $r = 10$ cm.
Use $\pi = 3.14$.
To Find:
The total surface area (TSA) of the hemisphere.
Solution:
The total surface area (TSA) of a solid hemisphere consists of the curved surface area and the area of its circular base.
The formula for the total surface area of a hemisphere is:
TSA $= 3 \pi r^2$
where $r$ is the radius of the hemisphere.
Substitute the given value of the radius, $r = 10$ cm, and $\pi = 3.14$ into the formula:
TSA $= 3 \times 3.14 \times (10)^2$
First, calculate $(10)^2$:
$(10)^2 = 10 \times 10 = 100$
So, the formula becomes:
TSA $= 3 \times 3.14 \times 100$
Multiply $3.14$ by $100$. Multiplying a decimal by 100 moves the decimal point two places to the right:
$3.14 \times 100 = 314$
Now, multiply the result by 3:
TSA $= 3 \times 314$
TSA $= 942$
The unit for area is square centimeters.
TSA $= 942$ cm$^2$
The total surface area of the hemisphere is $942$ cm$^2$.
Question 4. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Answer:
Given:
Initial radius of the spherical balloon, $r_1 = 7$ cm.
Final radius of the spherical balloon, $r_2 = 14$ cm.
To Find:
The ratio of the surface areas of the balloon in the two cases.
Solution:
The formula for the surface area (SA) of a sphere with radius $r$ is given by:
SA $= 4 \pi r^2$
Case 1: Initial radius $r_1 = 7$ cm.
Surface area in the first case (SA$_1$) is:
SA$_1 = 4 \pi (r_1)^2$
SA$_1 = 4 \pi (7)^2$
SA$_1 = 4 \pi \times 49$
SA$_1 = 196 \pi$ cm$^2$.
Case 2: Final radius $r_2 = 14$ cm.
Surface area in the second case (SA$_2$) is:
SA$_2 = 4 \pi (r_2)^2$
SA$_2 = 4 \pi (14)^2$
SA$_2 = 4 \pi \times 196$
SA$_2 = 784 \pi$ cm$^2$.
We need to find the ratio of the surface areas in the two cases, i.e., SA$_1$ : SA$_2$.
Ratio $= \frac{\text{SA}_1}{\text{SA}_2} = \frac{196 \pi}{784 \pi}$
Cancel $\pi$ from the numerator and the denominator:
Ratio $= \frac{196}{784}$
We can simplify this fraction. Note that $196 \times 4 = 784$.
Ratio $= \frac{196}{196 \times 4} = \frac{1}{4}$
The ratio of the surface areas is $1:4$.
Alternatively, we can find the ratio directly using the formula for surface area:
Ratio $= \frac{\text{SA}_1}{\text{SA}_2} = \frac{4 \pi r_1^2}{4 \pi r_2^2}$
Cancel $4 \pi$ from the numerator and denominator:
Ratio $= \frac{r_1^2}{r_2^2} = \left(\frac{r_1}{r_2}\right)^2$
Substitute the values of $r_1$ and $r_2$:
Ratio $= \left(\frac{7}{14}\right)^2$
Simplify the fraction inside the parenthesis:
Ratio $= \left(\frac{1}{2}\right)^2$
Ratio $= \frac{1^2}{2^2} = \frac{1}{4}$
The ratio is $1:4$.
The ratio of the surface areas of the balloon in the two cases is $1:4$.
Question 5. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2 .
Answer:
Given:
Inner diameter of the hemispherical bowl = $10.5$ cm.
Rate of tin-plating = $\textsf{₹} 16$ per $100$ cm$^2$.
To Find:
The cost of tin-plating the inside of the bowl.
Solution:
The inner surface to be tin-plated is the curved surface area of the hemispherical bowl.
First, find the inner radius ($r$) from the given inner diameter.
Inner radius $r = \frac{\text{Inner diameter}}{2}$
$r = \frac{10.5}{2}$ cm
$r = 5.25$ cm
We can write $5.25$ cm as $\frac{525}{100} = \frac{21}{4}$ cm.
The formula for the curved surface area (CSA) of a hemisphere is:
CSA $= 2 \pi r^2$
Substitute the value of $r = \frac{21}{4}$ cm and $\pi = \frac{22}{7}$ into the formula:
CSA $= 2 \times \frac{22}{7} \times \left(\frac{21}{4}\right)^2$
CSA $= 2 \times \frac{22}{7} \times \frac{21 \times 21}{4 \times 4}$
CSA $= 2 \times \frac{22}{7} \times \frac{441}{16}$
Cancel common factors:
CSA $= \cancel{2}^{1} \times \frac{22}{\cancel{7}_{1}} \times \frac{\cancel{441}^{63}}{\cancel{16}_{8}}$
CSA $= \frac{22 \times 63}{8}$
Simplify further by dividing 22 and 8 by 2:
CSA $= \frac{\cancel{22}^{11} \times 63}{\cancel{8}_{4}}$
CSA $= \frac{11 \times 63}{4}$
Multiply $11 \times 63$:
$11 \times 63 = 693$
CSA $= \frac{693}{4}$ cm$^2$
The cost of tin-plating is $\textsf{₹} 16$ per $100$ cm$^2$.
This means the cost for $1$ cm$^2$ is $\textsf{₹} \frac{16}{100}$.
The total cost of tin-plating is the CSA multiplied by the cost per square centimeter.
Total Cost $=$ CSA $\times$ Cost per cm$^2$
Total Cost $= \frac{693}{4} \times \frac{16}{100}$
Cancel the common factor 4:
Total Cost $= \frac{693}{\cancel{4}_{1}} \times \frac{\cancel{16}^{4}}{100}$
Total Cost $= \frac{693 \times 4}{100}$
Multiply $693 \times 4$:
$693 \times 4 = 2772$
Total Cost $= \frac{2772}{100}$
Total Cost $= 27.72$
The total cost is $\textsf{₹} 27.72$.
The cost of tin-plating the inside of the hemispherical bowl is $\textsf{₹} 27.72$.
Question 6. Find the radius of a sphere whose surface area is 154 cm2 .
Answer:
Given:
Surface area of the sphere = $154$ cm$^2$.
To Find:
The radius of the sphere ($r$).
Solution:
The formula for the surface area (SA) of a sphere with radius $r$ is given by:
SA $= 4 \pi r^2$
We are given the surface area SA $= 154$ cm$^2$. Substitute this value and $\pi = \frac{22}{7}$ into the formula.
$154 = 4 \times \frac{22}{7} \times r^2$
... (i)
Simplify the right side of the equation:
$154 = \frac{4 \times 22}{7} \times r^2$
$154 = \frac{88}{7} \times r^2$
Now, solve for $r^2$ by multiplying both sides by $\frac{7}{88}$:
$r^2 = 154 \times \frac{7}{88}$
Simplify the fraction $\frac{154}{88}$ by dividing both numerator and denominator by common factors. Both are divisible by 2:
$\frac{154}{88} = \frac{77}{44}$
Now, divide both by 11:
$\frac{77}{44} = \frac{7}{4}$
So, the equation becomes:
$r^2 = \frac{7}{4} \times 7$
$r^2 = \frac{49}{4}$
To find the radius $r$, take the square root of both sides:
$r = \sqrt{\frac{49}{4}}$
$r = \frac{\sqrt{49}}{\sqrt{4}}$
$r = \frac{7}{2}$
$r = 3.5$
The unit for radius is centimeters.
The radius of the sphere is $3.5$ cm.
The radius of the sphere is $3.5$ cm.
Question 7. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Answer:
Given:
The diameter of the moon is approximately one fourth of the diameter of the earth.
To Find:
The ratio of the surface areas of the moon and the earth.
Solution:
Let the diameter of the earth be $d_e$.
Let the diameter of the moon be $d_m$.
According to the given information:
$d_m = \frac{1}{4} d_e$
... (i)
The radius ($r$) of a sphere is half of its diameter ($d$), so $r = \frac{d}{2}$.
Let the radius of the earth be $r_e = \frac{d_e}{2}$.
Let the radius of the moon be $r_m = \frac{d_m}{2}$.
Substitute the expression for $d_m$ from (i) into the formula for $r_m$:
$r_m = \frac{\frac{1}{4} d_e}{2}$
$r_m = \frac{1}{4} \times \frac{d_e}{2}$
$r_m = \frac{1}{4} r_e$
... (ii)
The formula for the surface area (SA) of a sphere with radius $r$ is SA $= 4 \pi r^2$.
Surface area of the earth (SA$_e$) $= 4 \pi r_e^2$.
Surface area of the moon (SA$_m$) $= 4 \pi r_m^2$.
We need to find the ratio of the surface areas of the moon and the earth, i.e., SA$_m$ : SA$_e$.
Ratio $= \frac{\text{SA}_m}{\text{SA}_e} = \frac{4 \pi r_m^2}{4 \pi r_e^2}$
Cancel $4 \pi$ from the numerator and the denominator:
Ratio $= \frac{r_m^2}{r_e^2} = \left(\frac{r_m}{r_e}\right)^2$
Substitute the expression for $r_m$ from (ii) into the ratio:
Ratio $= \left(\frac{\frac{1}{4} r_e}{r_e}\right)^2$
Cancel $r_e$ from the numerator and denominator:
Ratio $= \left(\frac{1}{4}\right)^2$
Ratio $= \frac{1^2}{4^2} = \frac{1}{16}$
The ratio of the surface areas of the moon and the earth is $1:16$.
The ratio of their surface areas is $1:16$.
Question 8. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Answer:
Given:
Thickness of the steel bowl, $t = 0.25$ cm.
Inner radius of the bowl, $r_{inner} = 5$ cm.
To Find:
The outer curved surface area of the bowl.
Solution:
The outer radius ($r_{outer}$) of the hemispherical bowl is the sum of the inner radius and the thickness of the steel.
$r_{outer} = r_{inner} + t$
Substitute the given values:
$r_{outer} = 5 \text{ cm} + 0.25 \text{ cm}$
$r_{outer} = 5.25$ cm
The outer curved surface area of the hemispherical bowl is given by the formula for the curved surface area of a hemisphere, using the outer radius.
Outer CSA $= 2 \pi (r_{outer})^2$
Substitute the value of $r_{outer} = 5.25$ cm and $\pi = \frac{22}{7}$ (as $5.25 = \frac{21}{4}$, which is a multiple of $\frac{7}{4}$).
Outer CSA $= 2 \times \frac{22}{7} \times (5.25)^2$
Outer CSA $= 2 \times \frac{22}{7} \times (5.25 \times 5.25)$
Convert $5.25$ to a fraction: $5.25 = \frac{525}{100} = \frac{21}{4}$.
Outer CSA $= 2 \times \frac{22}{7} \times \left(\frac{21}{4}\right)^2$
Outer CSA $= 2 \times \frac{22}{7} \times \frac{21 \times 21}{4 \times 4}$
Outer CSA $= 2 \times \frac{22}{7} \times \frac{441}{16}$
Cancel common factors:
Outer CSA $= \cancel{2}^{1} \times \frac{22}{\cancel{7}_{1}} \times \frac{\cancel{441}^{63}}{\cancel{16}_{8}}$
Outer CSA $= \frac{22 \times 63}{8}$
Cancel 22 and 8 by 2:
Outer CSA $= \frac{\cancel{22}^{11} \times 63}{\cancel{8}_{4}}$
Outer CSA $= \frac{11 \times 63}{4}$
Multiply $11 \times 63$:
$11 \times 63 = 693$
Outer CSA $= \frac{693}{4}$
Perform the division:
Outer CSA $= 173.25$
The unit for area is square centimeters.
The outer curved surface area is $173.25$ cm$^2$.
The outer curved surface area of the bowl is $173.25$ cm$^2$.
Question 9. A right circular cylinder just encloses a sphere of radius r (see Fig. 11.10). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).

Answer:
Given:
A right circular cylinder just encloses a sphere of radius $r$.
From the given information:
Since the cylinder just encloses the sphere, the radius of the base of the cylinder must be equal to the radius of the sphere.
Radius of cylinder base $= r$
The height of the cylinder must be equal to the diameter of the sphere.
Height of sphere diameter $= 2 \times \text{radius} = 2r$
Height of cylinder, $h = 2r$
To Find:
(i) Surface area of the sphere.
(ii) Curved surface area of the cylinder.
(iii) Ratio of the areas obtained in (i) and (ii).
Solution:
(i) Surface area of the sphere.
The formula for the surface area (SA) of a sphere with radius $r$ is:
SA of sphere $= 4 \pi r^2$
(ii) Curved surface area of the cylinder.
The formula for the curved surface area (CSA) of a right circular cylinder with radius $R$ and height $H$ is:
CSA of cylinder $= 2 \pi R H$
In this case, the radius of the cylinder base $R = r$ and the height of the cylinder $H = 2r$. Substitute these values into the formula:
CSA of cylinder $= 2 \pi (r) (2r)$
CSA of cylinder $= 2 \pi \times 2r^2$
CSA of cylinder $= 4 \pi r^2$
(iii) Ratio of the areas obtained in (i) and (ii).
We need to find the ratio of the surface area of the sphere to the curved surface area of the cylinder.
Ratio $= \frac{\text{Surface area of sphere}}{\text{Curved surface area of cylinder}}$
Ratio $= \frac{4 \pi r^2}{4 \pi r^2}$
Cancel the common term $4 \pi r^2$ from the numerator and the denominator:
Ratio $= \frac{1}{1}$
The ratio is $1:1$.
(i) The surface area of the sphere is $4 \pi r^2$.
(ii) The curved surface area of the cylinder is $4 \pi r^2$.
(iii) The ratio of the areas obtained in (i) and (ii) is $1:1$.
Example 8 & 9 (Before Exercise 11.3)
Example 8. The height and the slant height of a cone are 21 cm and 28 cm respectively. Find the volume of the cone.
Answer:
Given:
Height of the cone, $h = 21$ cm.
Slant height of the cone, $l = 28$ cm.
To Find:
The volume of the cone.
Solution:
The formula for the volume ($V$) of a cone is $V = \frac{1}{3} \pi r^2 h$, where $r$ is the base radius and $h$ is the height.
We are given the height ($h$) and slant height ($l$), but we need the radius ($r$) to calculate the volume.
The relationship between slant height, radius, and height of a cone is given by the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substitute the given values $l = 28$ cm and $h = 21$ cm:
$(28)^2 = r^2 + (21)^2$
... (i)
$784 = r^2 + 441$
Now, solve for $r^2$:
$r^2 = 784 - 441$
$r^2 = 343$ cm$^2$
To find $r$, take the square root of $r^2$:
$r = \sqrt{343}$
$r = \sqrt{7^3} = \sqrt{7^2 \times 7} = 7\sqrt{7}$ cm
Now, calculate the volume of the cone using $V = \frac{1}{3} \pi r^2 h$. We use $r^2 = 343$ and $h = 21$. We will use $\pi = \frac{22}{7}$.
Volume $V = \frac{1}{3} \times \frac{22}{7} \times 343 \times 21$
Volume $V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{7} \times 343 \times \cancel{21}^{7}$
Volume $V = \frac{22}{\cancel{7}} \times 343 \times \cancel{7}$
Volume $V = 22 \times 343$
Volume $V = 7546$ cm$^3$
The volume of the cone is $7546$ cm$^3$.
Example 9. Monica has a piece of canvas whose area is 551 m2 . She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately 1 m2 , find the volume of the tent that can be made with it.
Answer:
Given:
Total area of the canvas = $551$ m$^2$.
Base radius of the conical tent, $r = 7$ m.
Wastage of canvas = $1$ m$^2$.
To Find:
The volume of the tent that can be made.
Solution:
The canvas is used to make the conical tent. The area of the canvas used for the tent is the total area of the canvas minus the wastage.
Area of canvas used for tent $=$ Total area of canvas $-$ Wastage
Area of canvas used for tent $= 551 \text{ m}^2 - 1 \text{ m}^2 = 550$ m$^2$
This area is the curved surface area (CSA) of the conical tent.
CSA of tent $= 550$ m$^2$
The formula for the curved surface area of a cone is CSA $= \pi r l$, where $r$ is the base radius and $l$ is the slant height.
We are given the radius $r = 7$ m and the CSA $= 550$ m$^2$. We can use this to find the slant height $l$. We use $\pi = \frac{22}{7}$.
$550 = \frac{22}{7} \times 7 \times l$
... (i)
$550 = 22l$
To find $l$, divide both sides by 22:
$l = \frac{550}{22}$
Simplify the fraction. Both are divisible by 11:
$l = \frac{\cancel{550}^{50}}{\cancel{22}_{2}}$
Now, divide 50 by 2:
$l = \frac{50}{2} = 25$
The slant height of the tent is $25$ m.
To find the volume of the tent, we need the height ($h$). The relationship between the slant height ($l$), radius ($r$), and height ($h$) is $l^2 = r^2 + h^2$ (Pythagorean theorem).
Substitute the values $l = 25$ m and $r = 7$ m:
$(25)^2 = (7)^2 + h^2$
$625 = 49 + h^2$
Solve for $h^2$:
$h^2 = 625 - 49$
$h^2 = 576$
To find $h$, take the square root of 576:
$h = \sqrt{576}$
We know that $24^2 = 576$, so $h = 24$ m.
The height of the tent is $24$ m.
Now, calculate the volume ($V$) of the cone using the formula $V = \frac{1}{3} \pi r^2 h$. Substitute the values $r = 7$ m, $h = 24$ m, and $\pi = \frac{22}{7}$.
Volume $V = \frac{1}{3} \times \frac{22}{7} \times (7)^2 \times 24$
Volume $V = \frac{1}{3} \times \frac{22}{7} \times (7 \times 7) \times 24$
Cancel the 3 in the denominator with 24 in the numerator:
Volume $V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{7} \times (7 \times 7) \times \cancel{24}^{8}$
Volume $V = \frac{22}{7} \times 49 \times 8$
Cancel the 7 in the denominator with 49 in the numerator:
Volume $V = 22 \times \frac{\cancel{49}^{7}}{\cancel{7}_{1}} \times 8$
Volume $V = 22 \times 7 \times 8$
Volume $V = 1232$
The unit for volume is cubic meters.
The volume of the tent is $1232$ m$^3$.
The volume of the tent that can be made with the canvas is $1232$ m$^3$.
Exercise 11.3
Assume π = $\frac{22}{7}$ , unless stated otherwise
Question 1. Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
Answer:
Given:
The formula for the volume of a right circular cone is $V = \frac{1}{3} \pi r^2 h$.
Assume $\pi = \frac{22}{7}$.
To Find:
The volume of the right circular cone for the given radius and height in two cases.
Solution:
The volume of a right circular cone with radius $r$ and height $h$ is given by:
$V = \frac{1}{3} \pi r^2 h$
(i) Radius $r = 6$ cm, height $h = 7$ cm
Substitute the given values into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times (6)^2 \times 7$
... (a)
Simplify the expression:
$V = \frac{1}{3} \times \frac{22}{7} \times 36 \times 7$
Cancel the common factors:
$V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{\cancel{7}_{1}} \times \cancel{36}^{12} \times \cancel{7}^{1}$
$V = 22 \times 12$
Multiply the numbers:
$V = 264$
The unit for volume is cubic centimeters.
The volume of the cone is $264$ cm$^3$.
(ii) Radius $r = 3.5$ cm, height $h = 12$ cm
The radius can be written as $3.5 = \frac{35}{10} = \frac{7}{2}$ cm.
Substitute the given values into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times (3.5)^2 \times 12$
... (b)
Simplify the expression using the fractional form of the radius:
$V = \frac{1}{3} \times \frac{22}{7} \times \left(\frac{7}{2}\right)^2 \times 12$
$V = \frac{1}{3} \times \frac{22}{7} \times \frac{49}{4} \times 12$
Cancel the common factors:
$V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{\cancel{7}_{1}} \times \frac{\cancel{49}^{7}}{\cancel{4}_{1}} \times \cancel{12}^{4}$ (Cancelling 3 with 12, 7 with 49, and 4 with 4)
$V = 22 \times 7 \times \frac{\cancel{4}^{1}}{\cancel{4}_{1}}$
$V = 22 \times 7$
Multiply the numbers:
$V = 154$
The unit for volume is cubic centimeters.
The volume of the cone is $154$ cm$^3$.
The volume of the right circular cone is:
(i) $264$ cm$^3$ when radius is $6$ cm and height is $7$ cm.
(ii) $154$ cm$^3$ when radius is $3.5$ cm and height is $12$ cm.
Question 2. Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
Answer:
Given:
The formula for the volume of a right circular cone is $V = \frac{1}{3} \pi r^2 h$.
The relationship between height, radius, and slant height is $l^2 = r^2 + h^2$.
The conversion factor for volume is $1$ litre $= 1000$ cm$^3$.
Assume $\pi = \frac{22}{7}$.
To Find:
The capacity (volume in litres) of the conical vessel for the given dimensions.
Solution:
The volume of a conical vessel with radius $r$ and height $h$ is given by $V = \frac{1}{3} \pi r^2 h$. We need to find the volume in cm$^3$ and then convert it to litres.
(i) Radius $r = 7$ cm, slant height $l = 25$ cm
First, we need to find the height ($h$) of the cone using the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substitute the given values:
$(25)^2 = (7)^2 + h^2$
... (a)
$625 = 49 + h^2$
Solve for $h^2$:
$h^2 = 625 - 49$
$h^2 = 576$
Taking the square root:
$h = \sqrt{576} = 24$ cm
The height of the cone is $24$ cm.
Now, calculate the volume of the cone using $V = \frac{1}{3} \pi r^2 h$ with $r = 7$ cm and $h = 24$ cm:
$V = \frac{1}{3} \times \frac{22}{7} \times (7)^2 \times 24$
$V = \frac{1}{3} \times \frac{22}{7} \times 49 \times 24$
Cancel common factors:
$V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{\cancel{7}_{1}} \times \cancel{49}^{7} \times \cancel{24}^{8}$
$V = 22 \times 7 \times 8$
$V = 22 \times 56$
$V = 1232$ cm$^3$
Convert the volume from cm$^3$ to litres ($1$ litre $= 1000$ cm$^3$).
Capacity $= \frac{1232}{1000}$ litres
Capacity $= 1.232$ litres
(ii) Height $h = 12$ cm, slant height $l = 13$ cm
First, we need to find the radius ($r$) of the cone using the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substitute the given values:
$(13)^2 = r^2 + (12)^2$
... (b)
$169 = r^2 + 144$
Solve for $r^2$:
$r^2 = 169 - 144$
$r^2 = 25$
Taking the square root:
$r = \sqrt{25} = 5$ cm
The radius of the cone is $5$ cm.
Now, calculate the volume of the cone using $V = \frac{1}{3} \pi r^2 h$ with $r = 5$ cm and $h = 12$ cm:
$V = \frac{1}{3} \times \frac{22}{7} \times (5)^2 \times 12$
$V = \frac{1}{3} \times \frac{22}{7} \times 25 \times 12$
Cancel common factors:
$V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{7} \times 25 \times \cancel{12}^{4}$
$V = \frac{22 \times 25 \times 4}{7}$
$V = \frac{22 \times 100}{7}$
$V = \frac{2200}{7}$ cm$^3$
Convert the volume from cm$^3$ to litres ($1$ litre $= 1000$ cm$^3$).
Capacity $= \frac{\frac{2200}{7}}{1000}$ litres
Capacity $= \frac{2200}{7 \times 1000}$ litres
Capacity $= \frac{2200}{7000}$ litres
Simplify the fraction by cancelling common zeros:
Capacity $= \frac{22}{70}$ litres
Simplify further by dividing by 2:
Capacity $= \frac{11}{35}$ litres
The capacity of the conical vessel is:
(i) $1.232$ litres when radius is $7$ cm and slant height is $25$ cm.
(ii) $\frac{11}{35}$ litres when height is $12$ cm and slant height is $13$ cm.
Question 3. The height of a cone is 15 cm. If its volume is 1570 cm3 , find the radius of the base. (Use π = 3.14)
Answer:
Given:
Height of the cone, $h = 15$ cm.
Volume of the cone, $V = 1570$ cm$^3$.
Use $\pi = 3.14$.
To Find:
The radius of the base ($r$) of the cone.
Solution:
The formula for the volume ($V$) of a cone with radius $r$ and height $h$ is:
$V = \frac{1}{3} \pi r^2 h$
Substitute the given values $V = 1570$ cm$^3$, $h = 15$ cm, and $\pi = 3.14$ into the formula.
$1570 = \frac{1}{3} \times 3.14 \times r^2 \times 15$
... (i)
Simplify the right side of the equation:
Cancel the 3 in the denominator with 15:
$1570 = \frac{1}{\cancel{3}_{1}} \times 3.14 \times r^2 \times \cancel{15}^{5}$
$1570 = 3.14 \times r^2 \times 5$
$1570 = (3.14 \times 5) \times r^2$
Multiply $3.14$ by $5$:
$3.14 \times 5 = 15.70 = 15.7$
So, the equation becomes:
$1570 = 15.7 \times r^2$
To find $r^2$, divide both sides by $15.7$:
$r^2 = \frac{1570}{15.7}$
To simplify the division, multiply the numerator and denominator by 10 to remove the decimal point:
$r^2 = \frac{1570 \times 10}{15.7 \times 10}$
$r^2 = \frac{15700}{157}$
Divide $15700$ by $157$:
$r^2 = 100$
To find the radius $r$, take the square root of $r^2$:
$r = \sqrt{100}$
$r = 10$
The unit for radius is centimeters.
The radius of the base is $10$ cm.
The radius of the base of the cone is $10$ cm.
Question 4. If the volume of a right circular cone of height 9 cm is 48 π cm3 , find the diameter of its base.
Answer:
Given:
Height of the right circular cone, $h = 9$ cm.
Volume of the cone, $V = 48 \pi$ cm$^3$.
To Find:
The diameter of the base ($d$) of the cone.
Solution:
The formula for the volume ($V$) of a cone with radius $r$ and height $h$ is:
$V = \frac{1}{3} \pi r^2 h$
Substitute the given values $V = 48 \pi$ cm$^3$ and $h = 9$ cm into the formula.
$48 \pi = \frac{1}{3} \pi r^2 \times 9$
... (i)
Simplify the right side of the equation:
Cancel the 3 in the denominator with 9:
$48 \pi = \frac{1}{\cancel{3}_{1}} \times \pi r^2 \times \cancel{9}^{3}$
$48 \pi = \pi r^2 \times 3$
$48 \pi = 3 \pi r^2$
To solve for $r^2$, divide both sides by $3 \pi$:
$r^2 = \frac{48 \pi}{3 \pi}$
Cancel $\pi$ from the numerator and denominator:
$r^2 = \frac{48}{3}$
Divide 48 by 3:
$r^2 = 16$
To find the radius $r$, take the square root of $r^2$. Since the radius must be positive:
$r = \sqrt{16}$
$r = 4$ cm
The radius of the base is $4$ cm.
We are asked to find the diameter of the base. The diameter ($d$) is twice the radius ($r$).
$d = 2 \times r$
$d = 2 \times 4$ cm
$d = 8$ cm
The diameter of the base is $8$ cm.
The diameter of the base of the cone is $8$ cm.
Question 5. A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Answer:
Given:
Shape of the pit: Conical
Top diameter ($d$) = $3.5$ m
Depth (height, $h$) = $12$ m
To Find:
Capacity of the pit in kilolitres.
Solution:
The pit is in the shape of a cone. The volume of the cone represents its capacity.
The radius ($r$) of the top of the cone is half of the diameter.
$r = \frac{\text{Diameter}}{2} = \frac{3.5}{2}$ m
We can write $3.5$ as $\frac{35}{10}$, which simplifies to $\frac{7}{2}$.
So, $r = \frac{7/2}{2} = \frac{7}{2} \times \frac{1}{2} = \frac{7}{4}$ m
The depth of the pit is the height ($h$) of the cone.
$h = 12$ m
The volume ($V$) of a cone is given by the formula:
$V = \frac{1}{3} \pi r^2 h$
We will use the value of $\pi \approx \frac{22}{7}$ for calculations.
Substitute the values of $r$ and $h$ into the formula:
$V = \frac{1}{3} \times \frac{22}{7} \times \left(\frac{7}{4}\right)^2 \times 12$
$V = \frac{1}{3} \times \frac{22}{7} \times \frac{7^2}{4^2} \times 12$
$V = \frac{1}{3} \times \frac{22}{7} \times \frac{49}{16} \times 12$
$V = \frac{1}{\cancel{3}} \times \frac{22}{\cancel{7}} \times \frac{\cancel{49}^{7}}{16} \times \cancel{12}^{4}$
$V = 22 \times 7 \times \frac{\cancel{4}}{\cancel{16}_4}$
$V = 22 \times 7 \times \frac{1}{4}$
$V = \frac{22 \times 7}{4}$
$V = \frac{\cancel{22}^{11} \times 7}{\cancel{4}_{2}}$
$V = \frac{11 \times 7}{2} = \frac{77}{2}$
$V = 38.5$ cubic meters ($m^3$)
The volume of the conical pit is $38.5 \text{ m}^3$.
We need to find the capacity in kilolitres.
We know that $1$ cubic meter ($m^3$) is equal to $1000$ litres.
Also, $1$ kilolitre is equal to $1000$ litres.
Therefore, $1 \text{ m}^3 = 1$ kilolitre.
So, the capacity of the pit in kilolitres is the same as its volume in cubic meters.
Capacity $= 38.5$ kilolitres.
Answer:
The capacity of the conical pit is $38.5$ kilolitres.
Question 6. The volume of a right circular cone is 9856 cm3 . If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
Answer:
Given:
Volume of the right circular cone, $V = 9856$ cm$^3$.
Diameter of the base = $28$ cm.
To Find:
(i) Height of the cone ($h$).
(ii) Slant height of the cone ($l$).
(iii) Curved surface area of the cone (CSA).
Solution:
First, find the radius ($r$) of the base from the given diameter.
$r = \frac{\text{Diameter}}{2} = \frac{28}{2} = 14$ cm.
(i) Find the height of the cone.
The formula for the volume ($V$) of a cone is $V = \frac{1}{3} \pi r^2 h$.
Substitute the given values $V = 9856$, $r = 14$, and $\pi = \frac{22}{7}$ into the formula.
$9856 = \frac{1}{3} \times \frac{22}{7} \times (14)^2 \times h$
... (a)
$9856 = \frac{1}{3} \times \frac{22}{7} \times (14 \times 14) \times h$
$9856 = \frac{1}{3} \times \frac{22}{7} \times 196 \times h$
$9856 = \frac{1}{3} \times 22 \times \cancel{196}^{28} \times \frac{h}{\cancel{7}_{1}}$
$9856 = \frac{22 \times 28}{3} \times h$
$9856 = \frac{616}{3} \times h$
To solve for $h$, multiply both sides by $\frac{3}{616}$:
$h = \cancel{9856}^{16} \times \frac{3}{\cancel{616}}$
So, $h = 16 \times 3$
$h = 48$ cm
The height of the cone is $48$ cm.
(ii) Find the slant height of the cone.
The relationship between the slant height ($l$), radius ($r$), and height ($h$) is given by the Pythagorean theorem:
$l^2 = r^2 + h^2$
Substitute the values $r = 14$ cm and $h = 48$ cm:
$l^2 = (14)^2 + (48)^2$
$l^2 = 196 + 2304$
$l^2 = 2500$
To find $l$, take the square root of 2500. Since slant height must be positive:
$l = \sqrt{2500}$
$l = \sqrt{25 \times 100}$
$l = \sqrt{25} \times \sqrt{100}$
$l = 5 \times 10$
$l = 50$ cm
The slant height of the cone is $50$ cm.
(iii) Find the curved surface area of the cone.
The formula for the curved surface area (CSA) of a cone is:
CSA $= \pi r l$
Substitute the values $r = 14$ cm and $l = 50$ cm. Use $\pi = \frac{22}{7}$.
CSA $= \frac{22}{7} \times 14 \times 50$
Cancel the 7 in the denominator with 14 in the numerator:
CSA $= 22 \times \frac{\cancel{14}^{2}}{\cancel{7}_{1}} \times 50$
CSA $= 22 \times 2 \times 50$
CSA $= 44 \times 50$
CSA $= 2200$ cm$^2$
The curved surface area of the cone is $2200$ cm$^2$.
(i) The height of the cone is $48$ cm.
(ii) The slant height of the cone is $50$ cm.
(iii) The curved surface area of the cone is $2200$ cm$^2$.
Question 7. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Answer:
Given:
A right triangle ABC with sides 5 cm, 12 cm, and 13 cm.
The triangle is revolved about the side 12 cm.
To Find:
The volume of the solid so obtained.
Solution:
When a right triangle is revolved about one of its legs, the solid formed is a right circular cone.
In this case, the triangle is revolved about the side measuring 12 cm. This side becomes the height of the cone.
Height of the cone, $h = 12$ cm.
The other leg (the side perpendicular to the axis of revolution) becomes the radius of the base of the cone.
Radius of the cone base, $r = 5$ cm.
The hypotenuse (13 cm) becomes the slant height of the cone, but it is not needed for calculating the volume.
The formula for the volume ($V$) of a right circular cone with radius $r$ and height $h$ is:
$V = \frac{1}{3} \pi r^2 h$
Substitute the values $r = 5$ cm, $h = 12$ cm, and use $\pi = \frac{22}{7}$ into the formula.
$V = \frac{1}{3} \times \frac{22}{7} \times (5)^2 \times 12$
... (i)
Simplify the expression:
$V = \frac{1}{3} \times \frac{22}{7} \times 25 \times 12$
Cancel the 3 in the denominator with 12:
$V = \frac{1}{\cancel{3}_{1}} \times \frac{22}{7} \times 25 \times \cancel{12}^{4}$
$V = \frac{22}{7} \times 25 \times 4$
$V = \frac{22}{7} \times 100$
$V = \frac{2200}{7}$
The unit for volume is cubic centimeters.
The volume of the solid obtained is $\frac{2200}{7}$ cm$^3$.
The volume of the solid so obtained is $\frac{2200}{7}$ cm$^3$.
Question 8. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Answer:
Given:
The same right triangle ABC with sides 5 cm, 12 cm, and 13 cm as in Question 7.
The triangle is revolved about the side 5 cm.
From Question 7, the volume of the solid obtained by revolving about the side 12 cm is $V_1 = \frac{2200}{7}$ cm$^3$.
To Find:
1. The volume of the solid obtained by revolving the triangle about the side 5 cm.
2. The ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
When the right triangle ABC with sides 5 cm, 12 cm, and 13 cm is revolved about the side measuring 5 cm, the solid formed is a right circular cone.
In this case, the side measuring 5 cm becomes the height of the cone.
Height of the cone, $h_2 = 5$ cm.
The other leg (the side perpendicular to the axis of revolution) becomes the radius of the base of the cone.
Radius of the cone base, $r_2 = 12$ cm.
The hypotenuse (13 cm) is the slant height of this new cone.
Find the volume of the solid obtained by revolving about the 5 cm side.
The formula for the volume ($V$) of a right circular cone is $V = \frac{1}{3} \pi r^2 h$.
Substitute the values $r_2 = 12$ cm, $h_2 = 5$ cm, and use $\pi = \frac{22}{7}$ into the formula.
$V_2 = \frac{1}{3} \times \frac{22}{7} \times (12)^2 \times 5$
... (i)
Simplify the expression:
$V_2 = \frac{1}{3} \times \frac{22}{7} \times 144 \times 5$
Cancel the 3 in the denominator with 144 ($144 \div 3 = 48$):
$V_2 = \frac{1}{\cancel{3}_{1}} \times \frac{22}{7} \times \cancel{144}^{48} \times 5$
$V_2 = \frac{22}{7} \times 48 \times 5$
$V_2 = \frac{22}{7} \times 240$
$V_2 = \frac{5280}{7}$
The unit for volume is cubic centimeters.
The volume of the solid obtained is $\frac{5280}{7}$ cm$^3$.
Find the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Volume from Question 7 (revolved about 12 cm side), $V_1 = \frac{2200}{7}$ cm$^3$.
Volume from Question 8 (revolved about 5 cm side), $V_2 = \frac{5280}{7}$ cm$^3$.
The ratio of $V_1$ to $V_2$ is:
Ratio $= \frac{V_1}{V_2} = \frac{\frac{2200}{7}}{\frac{5280}{7}}$
Ratio $= \frac{2200}{7} \times \frac{7}{5280}$
Ratio $= \frac{2200}{5280}$
Cancel common zeros:
Ratio $= \frac{220}{528}$
Simplify the fraction. Both are divisible by 4:
$\frac{220}{4} = 55$
$\frac{528}{4} = 132$
Ratio $= \frac{55}{132}$
Both are divisible by 11:
$\frac{55}{11} = 5$
$\frac{132}{11} = 12$
Ratio $= \frac{5}{12}$
The ratio of the volumes $V_1 : V_2$ is $5:12$.
The volume of the solid obtained by revolving about the side 5 cm is $\frac{5280}{7}$ cm$^3$.
The ratio of the volumes of the two solids obtained in Questions 7 and 8 ($V_1 : V_2$) is $5:12$.
Question 9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Answer:
Given:
Diameter of the conical heap, $d = 10.5$ m
Height of the conical heap, $h = 3$ m
To Find:
1. Volume of the heap (cone).
2. Area of the canvas required to cover the heap (Curved Surface Area of the cone).
Solution:
First, calculate the radius of the base of the cone.
$r = \frac{\text{Diameter}}{2} = \frac{10.5}{2} = 5.25 \text{ m}$
Now, calculate the volume of the cone using the formula $V = \frac{1}{3}\pi r^2 h$. We will use $\pi = \frac{22}{7}$.
$V = \frac{1}{3} \times \frac{22}{7} \times (5.25)^2 \times 3$
$V = \frac{1}{\cancel{3}} \times \frac{22}{7} \times (5.25 \times 5.25) \times \cancel{3}$
$V = \frac{22}{7} \times 27.5625$
$V = \frac{606.375}{7}$
$V = 86.625 \text{ m}^3$
The volume of the heap of wheat is $86.625 \text{ m}^3$.
Next, calculate the area of the canvas required, which is the curved surface area of the cone.
For this, we first need to find the slant height ($l$) of the cone using the Pythagorean theorem: $l = \sqrt{r^2 + h^2}$.
$l = \sqrt{(5.25)^2 + 3^2}$
$l = \sqrt{27.5625 + 9}$
$l = \sqrt{36.5625}$
Using a calculator, $l \approx 6.0467 \text{ m}$ (approximately)
Now, calculate the curved surface area (CSA) using the formula $CSA = \pi r l$. We will use $\pi = \frac{22}{7}$ and the approximate value of $l$.
$CSA = \frac{22}{7} \times 5.25 \times 6.0467$
$CSA = 22 \times \frac{5.25}{7} \times 6.0467$
$CSA = 22 \times 0.75 \times 6.0467$
$CSA = 16.5 \times 6.0467$
$CSA \approx 99.77055 \text{ m}^2$
Rounding to two decimal places, the area of the canvas required is approximately $99.77 \text{ m}^2$.
Final Answer Summary:
The volume of the heap of wheat is $86.625 \text{ m}^3$.
The area of the canvas required to cover the heap is approximately $99.77 \text{ m}^2$.
Example 10 to 12 (Before Exercise 11.4)
Example 10. Find the volume of a sphere of radius 11.2 cm.
Answer:
Given:
Radius of the sphere, $r = 11.2$ cm
To Find:
Volume of the sphere.
Solution:
The formula for the volume of a sphere is $V = \frac{4}{3}\pi r^3$.
We will use the value $\pi = \frac{22}{7}$.
Substitute the given radius $r = 11.2$ cm into the formula:
$V = \frac{4}{3} \times \frac{22}{7} \times (11.2)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 11.2 \times 11.2 \times 11.2$
$V = \frac{4}{3} \times \frac{22}{\cancel{7}^1} \times \cancel{11.2}^{1.6} \times 11.2 \times 11.2$
$V = \frac{4}{3} \times 22 \times 1.6 \times 11.2 \times 11.2$
$V = \frac{88}{3} \times (1.6 \times 11.2 \times 11.2)$
$V = \frac{88}{3} \times (1.6 \times 125.44)$
$V = \frac{88}{3} \times 200.704$
$V = \frac{17661.952}{3}$
$V \approx 5887.317$ cm$^3$
Rounding to two decimal places, the volume is approximately $5887.32$ cm$^3$.
The volume of the sphere is approximately $5887.32 \text{ cm}^3$.
Example 11. A shot-putt is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g per cm3 , find the mass of the shot-putt.
Answer:
Given:
Radius of the metallic sphere (shot-putt), $r = 4.9$ cm
Density of the metal $= 7.8$ g per cm$^3$
To Find:
Mass of the shot-putt.
Solution:
First, we need to find the volume of the metallic sphere. The formula for the volume of a sphere is $V = \frac{4}{3}\pi r^3$.
Using $\pi = \frac{22}{7}$ and $r = 4.9$ cm:
$V = \frac{4}{3} \times \frac{22}{7} \times (4.9)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 4.9 \times 4.9 \times 4.9$
$V = \frac{4}{3} \times 22 \times \frac{\cancel{4.9}^{0.7}}{\cancel{7}_1} \times 4.9 \times 4.9$
$V = \frac{88}{3} \times 0.7 \times 4.9 \times 4.9$
$V = \frac{88}{3} \times (0.7 \times 24.01)$
$V = \frac{88}{3} \times 16.807$
$V = \frac{1479.016}{3}$
$V \approx 493.0053$ cm$^3$
Now, we use the relationship between density, mass, and volume:
Density = $\frac{\text{Mass}}{\text{Volume}}$
So, Mass = Density $\times$ Volume
Mass = $7.8 \text{ g/cm}^3 \times 493.0053 \text{ cm}^3$
Mass $\approx 3845.44134$ g
Rounding to two decimal places, the mass of the shot-putt is approximately $3845.44$ g.
We can convert this mass to kilograms by dividing by 1000.
Mass $\approx \frac{3845.44}{1000}$ kg
Mass $\approx 3.84544$ kg
The mass of the shot-putt is approximately $3845.44$ g or $3.85$ kg (rounded to two decimal places for kilograms).
Example 12. A hemispherical bowl has a radius of 3.5 cm. What would be the volume of water it would contain?
Answer:
Given:
Radius of the hemispherical bowl, $r = 3.5$ cm
To Find:
Volume of water the bowl would contain.
Solution:
The volume of a hemisphere is given by the formula:
Volume $(V) = \frac{2}{3}\pi r^3$
... (i)
Substitute the given radius $r = 3.5$ cm and take $\pi = \frac{22}{7}$ in equation (i):
$V = \frac{2}{3} \times \frac{22}{7} \times (3.5)^3 \text{ cm}^3$
We can write $3.5$ as $\frac{7}{2}$. So $(3.5)^3 = (\frac{7}{2})^3 = \frac{7^3}{2^3} = \frac{343}{8}$.
$V = \frac{2}{3} \times \frac{22}{7} \times \frac{343}{8}$
Simplify the expression by cancelling common factors:
$V = \frac{\cancel{2}}{3} \times \frac{22}{\cancel{7}} \times \frac{\cancel{343}^{49}}{\cancel{8}^4}$
$V = \frac{1}{3} \times 22 \times \frac{49}{4}$
$V = \frac{22 \times 49}{3 \times 4}$
$V = \frac{\cancel{22}^{11} \times 49}{3 \times \cancel{4}_2}$
$V = \frac{11 \times 49}{3 \times 2}$
$V = \frac{539}{6}$
... (ii)
Convert the fraction to a decimal value:
$V \approx 89.83$
[Calculated value] ... (iii)
The volume of water the hemispherical bowl can contain is approximately $89.83 \text{ cm}^3$.
Exercise 11.4
Assume π = $\frac{22}{7}$ , unless stated otherwise
Question 1. Find the volume of a sphere whose radius is
(i) 7 cm
(ii) 0.63 m
Answer:
The formula for the volume of a sphere with radius $r$ is $V = \frac{4}{3}\pi r^3$. We are given that $\pi = \frac{22}{7}$.
Part (i):
Given:
Radius of the sphere, $r = 7$ cm
To Find:
Volume of the sphere.
Solution:
Using the formula for the volume of a sphere:
$V = \frac{4}{3} \times \frac{22}{7} \times (7)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 7 \times 7 \times 7$
$V = \frac{4}{3} \times 22 \times \cancel{7} \times 7 \times 7 / \cancel{7}$
$V = \frac{4}{3} \times 22 \times 49$
$V = \frac{88}{3} \times 49$
$V = \frac{4312}{3}$
$V = 1437\frac{1}{3}$ cm$^3$ or $1437.33...$ cm$^3$
The volume of the sphere is $1437\frac{1}{3} \text{ cm}^3$ or approximately $1437.33 \text{ cm}^3$.
Part (ii):
Given:
Radius of the sphere, $r = 0.63$ m
To Find:
Volume of the sphere.
Solution:
Using the formula for the volume of a sphere:
$V = \frac{4}{3} \times \frac{22}{7} \times (0.63)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 0.63 \times 0.63 \times 0.63$
$V = \frac{4}{3} \times 22 \times \frac{\cancel{0.63}^{0.09}}{\cancel{7}_1} \times 0.63 \times 0.63$
$V = \frac{88}{3} \times 0.09 \times 0.63 \times 0.63$
$V = 88 \times \frac{0.09}{3} \times 0.63 \times 0.63$
$V = 88 \times 0.03 \times 0.3969$
$V = 2.64 \times 0.3969$
$V = 1.047816$ m$^3$
The volume of the sphere is $1.047816 \text{ m}^3$.
Question 2. Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm
(ii) 0.21 m
Answer:
The amount of water displaced by a solid spherical ball is equal to the volume of the sphere.
The formula for the volume of a sphere with radius $r$ is $V = \frac{4}{3}\pi r^3$. We are given that $\pi = \frac{22}{7}$.
Part (i):
Given:
Diameter of the spherical ball, $d = 28$ cm
To Find:
Volume of water displaced.
Solution:
First, calculate the radius of the spherical ball:
$r = \frac{\text{Diameter}}{2} = \frac{28}{2} = 14 \text{ cm}$
Now, calculate the volume of the sphere:
$V = \frac{4}{3}\pi r^3$
$V = \frac{4}{3} \times \frac{22}{7} \times (14)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 14 \times 14 \times 14$
$V = \frac{4}{3} \times 22 \times \frac{\cancel{14}^2}{\cancel{7}_1} \times 14 \times 14$
$V = \frac{88}{3} \times 2 \times 196$
$V = \frac{176}{3} \times 196$
$V = \frac{34496}{3}$
$V = 11498\frac{2}{3}$ cm$^3$ or $11498.67...$ cm$^3$
The amount of water displaced is $11498\frac{2}{3} \text{ cm}^3$ or approximately $11498.67 \text{ cm}^3$.
Part (ii):
Given:
Diameter of the spherical ball, $d = 0.21$ m
To Find:
Volume of water displaced.
Solution:
First, calculate the radius of the spherical ball:
$r = \frac{\text{Diameter}}{2} = \frac{0.21}{2} = 0.105 \text{ m}$
Now, calculate the volume of the sphere:
$V = \frac{4}{3}\pi r^3$
$V = \frac{4}{3} \times \frac{22}{7} \times (0.105)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 0.105 \times 0.105 \times 0.105$
$V = \frac{4}{3} \times 22 \times \frac{\cancel{0.105}^{0.015}}{\cancel{7}_1} \times 0.105 \times 0.105$
$V = \frac{88}{3} \times 0.015 \times 0.105 \times 0.105$
$V = 88 \times \frac{0.015}{3} \times 0.011025$
$V = 88 \times 0.005 \times 0.011025$
$V = 0.44 \times 0.011025$
$V = 0.004851$ m$^3$
The amount of water displaced is $0.004851 \text{ m}^3$.
Question 3. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3 ?
Answer:
Given:
Diameter of the metallic ball, $d = 4.2$ cm
Density of the metal $= 8.9$ g per cm$^3$
To Find:
Mass of the metallic ball.
Solution:
First, we need to find the volume of the metallic ball. The ball is spherical.
Calculate the radius of the sphere:
$r = \frac{\text{Diameter}}{2} = \frac{4.2}{2} = 2.1 \text{ cm}$
The formula for the volume of a sphere is $V = \frac{4}{3}\pi r^3$. We will use $\pi = \frac{22}{7}$.
Substitute the value of $r$ into the formula:
$V = \frac{4}{3} \times \frac{22}{7} \times (2.1)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 2.1$
$V = \frac{4}{3} \times 22 \times \frac{\cancel{2.1}^{0.3}}{\cancel{7}_1} \times 2.1 \times 2.1$
$V = \frac{88}{3} \times 0.3 \times 2.1 \times 2.1$
$V = 88 \times \frac{0.3}{3} \times 2.1 \times 2.1$
$V = 88 \times 0.1 \times 4.41$
$V = 8.8 \times 4.41$
$V = 38.808 \text{ cm}^3$
Now, calculate the mass using the density and volume.
Mass = Density $\times$ Volume
Mass = $8.9 \text{ g/cm}^3 \times 38.808 \text{ cm}^3$
Mass = $345.3912$ g
The mass of the metallic ball is $345.3912$ g.
Question 4. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Answer:
Given:
Diameter of the moon is approximately one-fourth of the diameter of the earth.
To Find:
The fraction of the volume of the earth that is the volume of the moon.
Solution:
Let $d_e$ be the diameter of the earth and $d_m$ be the diameter of the moon.
According to the given information:
$d_m = \frac{1}{4} d_e$
The radius of a sphere is half of its diameter. Let $r_e$ be the radius of the earth and $r_m$ be the radius of the moon.
$r_e = \frac{d_e}{2}$
$r_m = \frac{d_m}{2}$
Substitute the relationship between the diameters into the equation for $r_m$:
$r_m = \frac{\frac{1}{4} d_e}{2} = \frac{1}{4} \times \frac{d_e}{2}$
Since $r_e = \frac{d_e}{2}$, we have:
$r_m = \frac{1}{4} r_e$
The formula for the volume of a sphere with radius $r$ is $V = \frac{4}{3}\pi r^3$.
The volume of the earth ($V_e$) is:
$V_e = \frac{4}{3}\pi r_e^3$
The volume of the moon ($V_m$) is:
$V_m = \frac{4}{3}\pi r_m^3$
Now, we want to find the fraction $\frac{V_m}{V_e}$.
Substitute the expression for $V_m$ and $V_e$:
$\frac{V_m}{V_e} = \frac{\frac{4}{3}\pi r_m^3}{\frac{4}{3}\pi r_e^3}$
Cancel out the common terms $\frac{4}{3}\pi$ from the numerator and the denominator:
$\frac{V_m}{V_e} = \frac{\cancel{\frac{4}{3}\pi} r_m^3}{\cancel{\frac{4}{3}\pi} r_e^3} = \frac{r_m^3}{r_e^3} = \left(\frac{r_m}{r_e}\right)^3$
Substitute the relationship $r_m = \frac{1}{4} r_e$ into the equation:
$\frac{V_m}{V_e} = \left(\frac{\frac{1}{4} r_e}{r_e}\right)^3$
Cancel out $r_e$:
$\frac{V_m}{V_e} = \left(\frac{1}{4}\right)^3$
Calculate the value of $\left(\frac{1}{4}\right)^3$:
$\left(\frac{1}{4}\right)^3 = \frac{1^3}{4^3} = \frac{1}{4 \times 4 \times 4} = \frac{1}{64}$
So, $\frac{V_m}{V_e} = \frac{1}{64}$.
This means the volume of the moon is $\frac{1}{64}$ of the volume of the earth.
The fraction of the volume of the earth that is the volume of the moon is $\frac{1}{64}$.
Question 5. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Answer:
Given:
Diameter of the hemispherical bowl, $d = 10.5$ cm
To Find:
The amount of milk the bowl can hold (Volume of the hemisphere) in litres.
Solution:
First, calculate the radius of the hemispherical bowl.
$r = \frac{\text{Diameter}}{2} = \frac{10.5}{2} = 5.25 \text{ cm}$
The formula for the volume of a hemisphere with radius $r$ is $V = \frac{2}{3}\pi r^3$. We will use $\pi = \frac{22}{7}$.
Substitute the value of $r$ into the formula:
$V = \frac{2}{3} \times \frac{22}{7} \times (5.25)^3$
$V = \frac{2}{3} \times \frac{22}{7} \times 5.25 \times 5.25 \times 5.25$
$V = \frac{44}{21} \times 144.703125$
$V = \frac{6366.9375}{21}$
$V = 303.1875 \text{ cm}^3$
The volume of the bowl is $303.1875$ cm$^3$.
To convert this volume to litres, we use the conversion factor $1$ litre $= 1000$ cm$^3$.
Volume in litres = $\frac{\text{Volume in cm}^3}{1000}$
Volume in litres = $\frac{303.1875}{1000}$
Volume in litres = $0.3031875$ litres
The hemispherical bowl can hold $0.3031875$ litres of milk.
Rounding to a few decimal places, the bowl can hold approximately $0.303$ litres of milk.
Question 6. A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Answer:
Given:
Thickness of the iron sheet, $t = 1$ cm
Inner radius of the hemispherical tank, $r_{inner} = 1$ m
To Find:
Volume of the iron used to make the tank.
Solution:
First, ensure all dimensions are in the same unit. Convert the inner radius from meters to centimeters.
$r_{inner} = 1 \text{ m} = 1 \times 100 \text{ cm} = 100 \text{ cm}$
The outer radius ($r_{outer}$) of the hemispherical tank is the sum of the inner radius and the thickness of the sheet.
$r_{outer} = r_{inner} + t$
$r_{outer} = 100 \text{ cm} + 1 \text{ cm} = 101 \text{ cm}$
The volume of the iron used to make the tank is the difference between the volume of the outer hemisphere and the volume of the inner hemisphere.
Volume of a hemisphere = $\frac{2}{3}\pi r^3$
Volume of inner hemisphere, $V_{inner} = \frac{2}{3}\pi r_{inner}^3 = \frac{2}{3}\pi (100)^3 \text{ cm}^3$
Volume of outer hemisphere, $V_{outer} = \frac{2}{3}\pi r_{outer}^3 = \frac{2}{3}\pi (101)^3 \text{ cm}^3$
Volume of iron, $V_{iron} = V_{outer} - V_{inner}$
$V_{iron} = \frac{2}{3}\pi (101)^3 - \frac{2}{3}\pi (100)^3$
$V_{iron} = \frac{2}{3}\pi [(101)^3 - (100)^3]$
Calculate $(101)^3$ and $(100)^3$:
$(101)^3 = 101 \times 101 \times 101 = 1030301$
$(100)^3 = 100 \times 100 \times 100 = 1000000$
$(101)^3 - (100)^3 = 1030301 - 1000000 = 30301$
So, $V_{iron} = \frac{2}{3}\pi (30301)$ cm$^3$.
Using $\pi = \frac{22}{7}$:
$V_{iron} = \frac{2}{3} \times \frac{22}{7} \times 30301$
$V_{iron} = \frac{44}{21} \times 30301$
$V_{iron} = \frac{44 \times 30301}{21}$
$V_{iron} = \frac{1333244}{21} \text{ cm}^3$
Calculating the decimal value:
$V_{iron} \approx 63487.8095$ cm$^3$
Rounding to two decimal places, the volume of iron used is approximately $63487.81 \text{ cm}^3$.
Question 7. Find the volume of a sphere whose surface area is 154 cm2 .
Answer:
Given:
Surface area of the sphere, $SA = 154 \text{ cm}^2$
To Find:
Volume of the sphere.
Solution:
The formula for the surface area of a sphere with radius $r$ is $SA = 4\pi r^2$. We are given $SA = 154 \text{ cm}^2$ and we will use $\pi = \frac{22}{7}$.
Substitute the given value into the formula:
$154 = 4 \times \frac{22}{7} \times r^2$
$154 = \frac{88}{7} \times r^2$
Now, solve for $r^2$:
$r^2 = 154 \times \frac{7}{88}$
$r^2 = \frac{\cancel{154}^{7} \times 7}{\cancel{88}^{4}}$ (Dividing 154 and 88 by 22)
$r^2 = \frac{49}{4}$
Take the square root to find the radius $r$:
$r = \sqrt{\frac{49}{4}}$
$r = \frac{7}{2} = 3.5$ cm
Now that we have the radius, we can find the volume of the sphere using the formula $V = \frac{4}{3}\pi r^3$.
Substitute the value of $r$ and $\pi$:
$V = \frac{4}{3} \times \frac{22}{7} \times (3.5)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 3.5 \times 3.5 \times 3.5$
$V = \frac{88}{21} \times (3.5)^3$
$V = \frac{88}{21} \times 42.875$
Alternatively, using fractions:
$V = \frac{4}{3} \times \frac{22}{7} \times \left(\frac{7}{2}\right)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times \frac{7^3}{2^3}$
$V = \frac{\cancel{4}}{\cancel{3}} \times \frac{22}{\cancel{7}} \times \frac{\cancel{7} \times 7 \times 7}{\cancel{2} \times \cancel{2} \times 2}$
$V = \frac{1}{3} \times 22 \times \frac{7 \times 7}{2}$
$V = \frac{22}{3} \times \frac{49}{2}$
$V = \frac{\cancel{22}^{11}}{3} \times \frac{49}{\cancel{2}^1}$
$V = \frac{11 \times 49}{3}$
$V = \frac{539}{3}$ cm$^3$
The volume of the sphere is $\frac{539}{3} \text{ cm}^3$ or approximately $179.67 \text{ cm}^3$.
Question 8. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹ 4989.60. If the cost of white-washing is ₹ 20 per square metre, find the
(i) inside surface area of the dome,
(ii) volume of the air inside the dome.
Answer:
Given:
Total cost of white-washing the inside of the dome = $\textsf{₹} 4989.60$
Cost of white-washing per square metre = $\textsf{₹} 20 \text{ per m}^2$
The dome is in the form of a hemisphere.
To Find:
(i) Inside surface area of the dome.
(ii) Volume of the air inside the dome.
Solution:
Part (i): Inside surface area of the dome
The total cost of white-washing is the product of the inside surface area and the cost per square metre.
Total Cost = Inside Surface Area $\times$ Cost per m$^2$
Inside Surface Area = $\frac{\text{Total Cost}}{\text{Cost per m}^2}$
Inside Surface Area = $\frac{\textsf{₹} 4989.60}{\textsf{₹} 20/\text{m}^2}$
Inside Surface Area = $\frac{4989.60}{20} \text{ m}^2$
Inside Surface Area = $249.48 \text{ m}^2$
The inside surface area of the dome is $249.48 \text{ m}^2$.
Part (ii): Volume of the air inside the dome
The inside surface area of a hemispherical dome is its curved surface area, which is given by the formula $2\pi r^2$, where $r$ is the inside radius of the dome.
We have calculated the inside surface area as $249.48 \text{ m}^2$. Using $\pi = \frac{22}{7}$:
$2\pi r^2 = 249.48$
$2 \times \frac{22}{7} \times r^2 = 249.48$
$\frac{44}{7} r^2 = 249.48$
$r^2 = 249.48 \times \frac{7}{44}$
$r^2 = \frac{1746.36}{44}$
$r^2 = 39.69$
To find the radius $r$, take the square root of $r^2$:
$r = \sqrt{39.69}$
$r = 6.3$ m
The volume of the air inside the dome is the volume of a hemisphere with radius $r = 6.3$ m. The formula for the volume of a hemisphere is $V = \frac{2}{3}\pi r^3$.
Using $\pi = \frac{22}{7}$ and $r = 6.3$ m:
$V = \frac{2}{3} \times \frac{22}{7} \times (6.3)^3$
$V = \frac{44}{21} \times (6.3)^3$
$V = \frac{44}{21} \times 6.3 \times 6.3 \times 6.3$
$V = \frac{44}{\cancel{21}_3} \times \cancel{6.3}^{0.9} \times 6.3 \times 6.3$
$V = \frac{44}{3} \times 0.9 \times 6.3 \times 6.3$
$V = 44 \times \frac{0.9}{3} \times 39.69$
$V = 44 \times 0.3 \times 39.69$
$V = 13.2 \times 39.69$
$V = 523.908 \text{ m}^3$
The volume of the air inside the dome is $523.908 \text{ m}^3$.
Question 9. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S′. Find the
(i) radius r′ of the new sphere,
(ii) ratio of S and S′.
Answer:
Given:
Number of small solid iron spheres = 27
Radius of each small sphere = $r$
Surface area of each small sphere = $S$
These 27 spheres are melted to form a new single sphere with radius $r'$ and surface area $S'$.
To Find:
(i) Radius $r'$ of the new sphere.
(ii) Ratio of $S$ and $S'$, i.e., $\frac{S}{S'}$.
Solution:
When spheres are melted and reformed into a new sphere, the total volume of the material remains constant.
The volume of a sphere with radius $R$ is given by $V = \frac{4}{3}\pi R^3$.
Volume of one small sphere = $\frac{4}{3}\pi r^3$
Total volume of 27 small spheres = $27 \times (\text{Volume of one small sphere})$
$V_{total} = 27 \times \frac{4}{3}\pi r^3$
$V_{total} = \cancel{27}^9 \times \frac{4}{\cancel{3}_1}\pi r^3$
$V_{total} = 9 \times 4\pi r^3 = 36\pi r^3$
The volume of the new large sphere with radius $r'$ is:
$V' = \frac{4}{3}\pi (r')^3$
Since the total volume is conserved:
$V' = V_{total}$
(Volume is conserved)
$\frac{4}{3}\pi (r')^3 = 36\pi r^3$
Now, we solve for $r'$:
Divide both sides by $\frac{4}{3}\pi$:
$(r')^3 = \frac{36\pi r^3}{\frac{4}{3}\pi}$
$(r')^3 = \frac{36\cancel{\pi} r^3}{1} \times \frac{3}{4\cancel{\pi}}$
$(r')^3 = \frac{\cancel{36}^9 r^3 \times 3}{\cancel{4}_1}$
$(r')^3 = 9 \times 3 \times r^3 = 27 r^3$
Take the cube root of both sides:
$r' = \sqrt[3]{27 r^3}$
$r' = \sqrt[3]{27} \times \sqrt[3]{r^3}$
$r' = 3r$
(i) The radius $r'$ of the new sphere is $3r$.
Part (ii): Ratio of S and S′
The surface area of a sphere with radius $R$ is given by $SA = 4\pi R^2$.
Surface area of one small sphere = $S = 4\pi r^2$
Surface area of the new large sphere = $S' = 4\pi (r')^2$
We found that $r' = 3r$. Substitute this into the expression for $S'$:
$S' = 4\pi (3r)^2$
$S' = 4\pi (9r^2)$
$S' = 36\pi r^2$
Now, find the ratio of $S$ and $S'$:
$\frac{S}{S'} = \frac{4\pi r^2}{36\pi r^2}$
Cancel out the common terms $4\pi r^2$ from the numerator and the denominator:
$\frac{S}{S'} = \frac{\cancel{4\pi r^2}}{\cancel{36\pi r^2}^{\,9}}$
$\frac{S}{S'} = \frac{1}{9}$
(ii) The ratio of $S$ and $S'$ is $1:9$ or $\frac{1}{9}$.
Question 10. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
Answer:
Given:
Diameter of the spherical capsule, $d = 3.5$ mm
To Find:
Volume of medicine needed to fill the capsule (Volume of the sphere) in mm$^3$.
Solution:
First, calculate the radius of the spherical capsule.
$r = \frac{\text{Diameter}}{2} = \frac{3.5}{2} = 1.75 \text{ mm}$
The volume of medicine needed is equal to the volume of the sphere. The formula for the volume of a sphere with radius $r$ is $V = \frac{4}{3}\pi r^3$. We will use $\pi = \frac{22}{7}$.
Substitute the value of $r$ into the formula:
$V = \frac{4}{3} \times \frac{22}{7} \times (1.75)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times 1.75 \times 1.75 \times 1.75$
We can write $1.75$ as $\frac{175}{100} = \frac{7}{4}$.
$V = \frac{4}{3} \times \frac{22}{7} \times \left(\frac{7}{4}\right)^3$
$V = \frac{4}{3} \times \frac{22}{7} \times \frac{7^3}{4^3}$
$V = \frac{\cancel{4}}{\cancel{3}} \times \frac{22}{\cancel{7}} \times \frac{\cancel{7} \times 7 \times 7}{\cancel{4} \times 4 \times 4}$
$V = \frac{1}{3} \times 22 \times \frac{7 \times 7}{4 \times 4}$
$V = \frac{22}{3} \times \frac{49}{16}$
$V = \frac{\cancel{22}^{11} \times 49}{3 \times \cancel{16}^8}$
$V = \frac{11 \times 49}{3 \times 8}$
$V = \frac{539}{24} \text{ mm}^3$
Alternatively, using decimals:
$V = \frac{4}{3} \times \frac{22}{7} \times (1.75)^3$
$V = \frac{88}{21} \times 5.359375$
$V = \frac{471.625}{21}$
$V \approx 22.47619$ mm$^3$
The amount of medicine needed to fill the capsule is $\frac{539}{24} \text{ mm}^3$ or approximately $22.48 \text{ mm}^3$.

