| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 9.1 | Example 1 (Before Exercise 9.2) | Exercise 9.2 |
| Example 2 to 5 (Before Exercise 9.3) | Exercise 9.3 | |
Chapter 9 Circles
Welcome to the solutions guide for Chapter 9, "Circles," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. Circles, with their perfect symmetry and unique properties, are fundamental geometric figures with vast applications. This chapter delves into the essential theorems that govern the relationships between different elements associated with a circle, such as chords, arcs, and the angles they subtend. Understanding these theorems and learning to apply them logically is crucial for advancing in geometry and developing deductive proof skills. These comprehensive solutions provide detailed explanations, rigorous proofs, and step-by-step application methods for all exercises.
The exploration begins by reinforcing the basic terminology associated with circles, ensuring clarity on concepts like the centre, radius ($r$), diameter ($d=2r$), chord (a line segment joining any two points on the circle), arc (a part of the circle's circumference), sector (region between two radii and an arc), and segment (region between a chord and an arc). Building on this foundation, the solutions focus on proving and applying several key theorems related to chords:
- "Equal chords of a circle subtend equal angles at the centre," along with its converse.
- "The perpendicular from the centre of a circle to a chord bisects the chord," and its crucial converse ("The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord").
- "Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres)," and its converse.
A significant portion of the chapter deals with the relationship between arcs and the angles they subtend. The solutions provide rigorous proofs and extensive applications for the central theorem:
- "The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle."
- "Angles in the same segment of a circle are equal."
- "Angle in a semicircle is a right angle ($90^\circ$)."
Finally, the concept of Cyclic Quadrilaterals (quadrilaterals whose vertices all lie on a circle) is introduced. The solutions focus on proving and applying the defining property:
- "The sum of either pair of opposite angles of a cyclic quadrilateral is $180^\circ$."
Regarding the rationalized syllabus for 2024-25, Chapter 9, "Circles" (formerly Chapter 10 in older editions), remains a significant part of the Class 9 curriculum. However, the rationalization process involved removing the section and exercises related to constructing a circle passing through three non-collinear points and potentially streamlining some complex proofs or applications. The core theorems concerning chords, angles subtended by arcs, and properties of cyclic quadrilaterals remain central. By engaging with these detailed solutions, students can thoroughly understand the proofs of fundamental circle theorems, master their application in diverse geometric problems, and significantly enhance their deductive reasoning skills.
Exercise 9.1
Question 1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer:
Given:
Two congruent circles with centres O and O'.
Let the radius of circle O be $r$ and the radius of circle O' be $r'$. Since the circles are congruent, their radii are equal.
r = r'
(Radii of congruent circles)
AB is a chord of circle O and CD is a chord of circle O'.
The chords are equal in length.
AB = CD
(Given)
To Prove:
The angles subtended by the chords at the centres are equal.
i.e., $\angle$AOB = $\angle$CO'D.
Figure:
Draw two congruent circles with centres O and O'. Draw equal chords AB in the first circle and CD in the second circle. Join the endpoints of the chords to their respective centres to form triangles AOB and CO'D.
Proof:
Consider the triangles $\Delta$AOB and $\Delta$CO'D.
1. Side OA and side O'C are equal.
OA = O'C
(Radii of congruent circles are equal)
2. Side OB and side O'D are equal.
OB = O'D
(Radii of congruent circles are equal)
3. Side AB and side CD are equal.
AB = CD
(Given equal chords)
So, in $\Delta$AOB and $\Delta$CO'D, we have three pairs of corresponding sides that are equal.
Therefore, by the SSS (Side-Side-Side) congruence criterion, $\Delta$AOB is congruent to $\Delta$CO'D.
$\Delta$AOB $\cong$ $\Delta$CO'D
(SSS Congruence Rule)
Since the triangles are congruent, their corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
The angle $\angle$AOB in $\Delta$AOB corresponds to the angle $\angle$CO'D in $\Delta$CO'D.
Therefore,
$\angle$AOB = $\angle$CO'D
(CPCT)
Hence, equal chords of congruent circles subtend equal angles at their centres.
Hence Proved.
Question 2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:
Given:
Two congruent circles with centres O and O'.
Let the radius of circle O be $r$ and the radius of circle O' be $r'$. Since the circles are congruent, their radii are equal.
r = r'
(Radii of congruent circles)
AB is a chord of circle O and CD is a chord of circle O'.
The angles subtended by the chords at the centres are equal.
$\angle$AOB = $\angle$CO'D
(Given)
To Prove:
The chords are equal in length.
i.e., AB = CD.
Figure:
Draw two congruent circles with centres O and O'. Draw chords AB and CD such that the angles $\angle$AOB and $\angle$CO'D at the centres are equal. Join the endpoints of the chords to their respective centres to form triangles AOB and CO'D.
Proof:
Consider the triangles $\Delta$AOB and $\Delta$CO'D.
1. Side OA and side O'C are equal.
OA = O'C
(Radii of congruent circles are equal)
2. The angle $\angle$AOB and angle $\angle$CO'D are equal.
$\angle$AOB = $\angle$CO'D
(Given)
3. Side OB and side O'D are equal.
OB = O'D
(Radii of congruent circles are equal)
So, in $\Delta$AOB and $\Delta$CO'D, we have two pairs of corresponding sides equal and the included angle equal.
Therefore, by the SAS (Side-Angle-Side) congruence criterion, $\Delta$AOB is congruent to $\Delta$CO'D.
$\Delta$AOB $\cong$ $\Delta$CO'D
(SAS Congruence Rule)
Since the triangles are congruent, their corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
The chord AB in $\Delta$AOB corresponds to the chord CD in $\Delta$CO'D.
Therefore,
AB = CD
(CPCT)
Hence, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Hence Proved.
Example 1 (Before Exercise 9.2)
Example 1. If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
Answer:
Given:
A circle with centre O.
Two chords AB and CD intersecting at point P inside the circle.
A diameter XY of the circle passes through the point of intersection P.
The chords make equal angles with the diameter at P, i.e., $\angle$APX = $\angle$CPX (where X is a point on the diameter).
To Prove:
The chords are equal, i.e., AB = CD.
Construction Required:
Draw a perpendicular line segment from the centre O to chord AB, meeting AB at M. So, OM $\perp$ AB.
Draw a perpendicular line segment from the centre O to chord CD, meeting CD at N. So, ON $\perp$ CD.
Proof:
Consider the two right-angled triangles $\triangle$OMP and $\triangle$ONP.
1. The angles at M and N are right angles.
$\angle$OMP = $90^\circ$
(By construction OM $\perp$ AB)
$\angle$ONP = $90^\circ$
(By construction ON $\perp$ CD)
So, both $\Delta$OMP and $\Delta$ONP are right triangles.
2. The hypotenuse OP is common to both triangles.
OP = OP
(Common side)
3. The angles $\angle$ OPM and $\angle$ OPN are equal.
We are given that the chords make equal angles with the diameter XY at the point of intersection P. So, $\angle$ APX = $\angle$ CPX.
Note that $\angle$ APX is the same angle as $\angle$ OPM because P, M are on the chord AB and O, P, X are on the diameter XY.
Similarly, $\angle$ CPX is the same angle as $\angle$ OPN because P, N are on the chord CD and O, P, X are on the diameter XY.
$\angle$ OPM = $\angle$ OPN
(Since $\angle$ APX = $\angle$ CPX (Given))
Now, by AAS (Angle-Angle-Side) congruence criterion, if two angles and a non-included side of one triangle are equal to the corresponding angles and non-included side of another triangle, then the triangles are congruent.
In $\Delta$OMP and $\Delta$ONP, we have $\angle$OMP = $\angle$ONP = $90^\circ$, $\angle$OPM = $\angle$OPN, and the common side OP.
Therefore, by AAS congruence criterion,
$\Delta$OMP $\cong$ $\Delta$ONP
(AAS Congruence Rule)
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding sides are equal.
The side OM in $\Delta$OMP corresponds to the side ON in $\Delta$ONP.
OM = ON
(CPCT)
The distance of a chord from the centre is the length of the perpendicular drawn from the centre to the chord.
The distance of chord AB from the centre O is OM.
The distance of chord CD from the centre O is ON.
Since OM = ON, the chords AB and CD are equidistant from the centre O.
We know a theorem that states: Chords which are equidistant from the centre of a circle are equal in length.
Therefore, AB = CD.
Hence Proved.
Exercise 9.2
Question 1. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer:
Given:
Radius of the first circle ($r_1$) = 5 cm.
Radius of the second circle ($r_2$) = 3 cm.
Distance between their centres (d) = 4 cm.
To Find:
Length of the common chord.
Figure:
Let the two circles have centres O and O'. Let the radius of the circle with centre O be $r_1 = 5$ cm, and the radius of the circle with centre O' be $r_2 = 3$ cm. The distance between the centres is OO' = 4 cm. Let the circles intersect at points A and B. AB is the common chord. The line joining the centres OO' intersects AB at M.
Solution:
Let the two circles have centres O and O'. The distance between the centres is OO' = 4 cm.
The line joining the centres of two intersecting circles is the perpendicular bisector of the common chord.
Let the common chord be AB, and let the line segment OO' intersect AB at M. Then OO' $\perp$ AB and AM = MB.
In the circle with centre O, OA is the radius ($r_1$), and in the circle with centre O', O'A is the radius ($r_2$).
OA = $r_1 = 5$ cm
O'A = $r_2 = 3$ cm
OO' = 4 cm
Consider the right-angled triangle $\Delta$OMA (since OO' $\perp$ AB, $\angle$OMA = $90^\circ$). By the Pythagoras theorem:
OA$^2$ = OM$^2$ + AM$^2$
$5^2 = OM^2 + AM^2$
$25 = OM^2 + AM^2$
... (i)
Now consider the right-angled triangle $\Delta$O'MA (since OO' $\perp$ AB, $\angle$O'MA = $90^\circ$). By the Pythagoras theorem:
O'A$^2$ = O'M$^2$ + AM$^2$
$3^2 = O'M^2 + AM^2$
$9 = O'M^2 + AM^2$
... (ii)
From equation (i), we can express $AM^2$ as:
$AM^2 = 25 - OM^2$
... (iii)
From equation (ii), we can express $AM^2$ as:
$AM^2 = 9 - O'M^2$
... (iv)
Equating the expressions for $AM^2$ from equation (iii) and equation (iv):
$25 - OM^2 = 9 - O'M^2$
Rearrange the terms:
$25 - 9 = OM^2 - O'M^2$
$16 = OM^2 - O'M^2$
... (v)
We know that OO' = OM + O'M = 4 cm. So, O'M = 4 - OM.
Substitute O'M = (4 - OM) into equation (v):
$16 = OM^2 - (4 - OM)^2$
$16 = OM^2 - (16 - 8 \cdot OM + OM^2)$
$16 = OM^2 - 16 + 8 \cdot OM - OM^2$
The $OM^2$ terms cancel out:
$16 = -16 + 8 \cdot OM$
Add 16 to both sides:
$16 + 16 = 8 \cdot OM$
$32 = 8 \cdot OM$
Divide by 8 to find OM:
$OM = \frac{32}{8}$
$OM = 4$ cm
... (vi)
Now substitute the value of OM = 4 cm into equation (iii) to find $AM^2$:
$AM^2 = 25 - OM^2$
$AM^2 = 25 - 4^2$
$AM^2 = 25 - 16$
$AM^2 = 9$
Taking the square root of both sides (length must be positive):
$AM = \sqrt{9}$
$AM = 3$ cm
... (vii)
Since the line joining the centres bisects the common chord, AB = 2 * AM.
$AB = 2 \times AM$
$AB = 2 \times 3$ cm
$AB = 6$ cm
Notice that the distance between centers (4 cm) plus the radius of the smaller circle (3 cm) equals the radius of the larger circle (5 cm + 3 cm = 8 cm != 4 cm). Also, $4^2 + 3^2 = 16 + 9 = 25 = 5^2$. This means the distance between the centers (4 cm) and the radius of the smaller circle (3 cm) form the sides of a right-angled triangle with the radius of the larger circle (5 cm) as the hypotenuse. Specifically, if we consider $\Delta$ O'MA, we have O'M = OO' - OM = 4 - 4 = 0 cm from equation (vi). This implies that the point M coincides with O', the center of the smaller circle. This is consistent, as in $\Delta$ OAO', if O'=M, then OO'$^2$ + O'A$^2$ = OA$^2$, i.e., $4^2 + 3^2 = 5^2$, which is true ($16+9=25$). This means the common chord passes through the center of the smaller circle and is perpendicular to the line of centers at that point.
Answer:
The length of the common chord is 6 cm.
Question 2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer:
Given:
A circle with centre O.
Two equal chords AB and CD intersect within the circle at point E.
AB = CD
(Given)
To Prove:
The segments of one chord are equal to the corresponding segments of the other chord.
We need to prove that AE = DE and BE = CE.
Construction Required:
Draw a perpendicular line segment from the centre O to chord AB, meeting AB at M. So, OM $\perp$ AB.
Draw a perpendicular line segment from the centre O to chord CD, meeting CD at N. So, ON $\perp$ CD.
Join OE.
Proof:
We know that equal chords of a circle are equidistant from the centre.
Since AB and CD are equal chords (AB = CD), their distances from the centre O are equal.
OM = ON
(Equal chords are equidistant from the centre) ... (i)
Consider the right-angled triangles $\Delta$OME and $\Delta$ONE.
1. The angles at M and N are right angles.
$\angle$OME = $90^\circ$
(By construction OM $\perp$ AB)
$\angle$ONE = $90^\circ$
(By construction ON $\perp$ CD)
So, both $\Delta$OME and $\Delta$ONE are right triangles.
2. The hypotenuse OE is common to both triangles.
OE = OE
(Common side)
3. The sides OM and ON are equal.
OM = ON
(Proved in equation (i))
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence criterion, $\Delta$OME is congruent to $\Delta$ONE.
$\Delta$OME $\cong$ $\Delta$ONE
(RHS Congruence Rule) ... (ii)
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding sides are equal.
ME = NE
(CPCT) ... (iii)
We know that the perpendicular from the centre to a chord bisects the chord.
So, OM bisects AB, and ON bisects CD.
AM = MB = $\frac{1}{2}$AB
CN = ND = $\frac{1}{2}$CD
Since AB = CD (Given), it follows that $\frac{1}{2}$AB = $\frac{1}{2}$CD.
AM = CN
... (iv)
Now, consider the segments of the chords formed by the intersection point E.
From the figure, segment AE = AM + ME and segment DE = DN + NE.
From equation (iii), we have ME = NE.
From equation (iv), we have AM = CN. Also, ON bisects CD, so CN = DN.
Thus, AM = DN.
Substitute AM = DN and ME = NE into the expressions for AE and DE:
AE = AM + ME
DE = DN + NE
Since AM = DN and ME = NE, by adding equals to equals, we get:
AE = DE
... (v)
Now, consider the other segments: BE and CE.
BE = AB - AE
CE = CD - DE
Since AB = CD (Given) and AE = DE (Proved in equation (v)), by subtracting equals from equals, we get:
AB - AE = CD - DE
Therefore,
BE = CE
... (vi)
From equation (v) and equation (vi), we have proved that AE = DE and BE = CE.
This means the segments of one chord are equal to the corresponding segments of the other chord.
Hence Proved.
Question 3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
Given:
A circle with centre O.
Two equal chords AB and CD intersect within the circle at point E.
AB = CD
(Given)
To Prove:
The line joining the point of intersection E to the centre O makes equal angles with the chords AB and CD.
That is, $\angle$OEA = $\angle$OEC (or equivalently, $\angle$OEB = $\angle$OED).
Construction Required:
Draw a perpendicular line segment from the centre O to chord AB, meeting AB at M. So, OM $\perp$ AB.
Draw a perpendicular line segment from the centre O to chord CD, meeting CD at N. So, ON $\perp$ CD.
Join OE.
Proof:
We know that equal chords of a circle are equidistant from the centre.
Since AB and CD are equal chords (AB = CD), their distances from the centre O are equal.
OM = ON
(Equal chords are equidistant from the centre) ... (i)
Consider the two right-angled triangles $\Delta$OME and $\Delta$ONE.
1. The angles at M and N are right angles.
$\angle$OME = $90^\circ$
(By construction OM $\perp$ AB)
$\angle$ONE = $90^\circ$
(By construction ON $\perp$ CD)
So, both $\Delta$OME and $\Delta$ONE are right triangles.
2. The hypotenuse OE is common to both triangles.
OE = OE
(Common side)
3. The sides OM and ON are equal.
OM = ON
(Proved in equation (i))
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence criterion, $\Delta$OME is congruent to $\Delta$ONE.
$\Delta$OME $\cong$ $\Delta$ONE
(RHS Congruence Rule) ... (ii)
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding angles are equal.
The angle $\angle$OEM in $\Delta$OME corresponds to the angle $\angle$OEN in $\Delta$ONE.
$\angle$OEM = $\angle$OEN
(CPCT)
Since M lies on chord AB and N lies on chord CD, $\angle$OEM is the angle made by the line segment OE with chord AB, and $\angle$OEN is the angle made by the line segment OE with chord CD.
Therefore, the line joining the point of intersection E to the centre O makes equal angles with the chords AB and CD.
$\angle$OEA = $\angle$OEC
Hence Proved.
Question 4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig. 9.12).
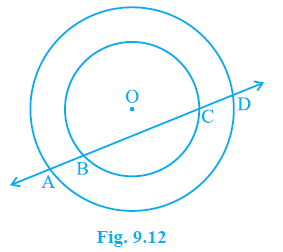
Answer:
Given:
Two concentric circles with the same centre O.
A line intersects the outer circle at points A and D and the inner circle at points B and C.
To Prove:
AB = CD.
Construction Required:
Draw a line segment OM from the centre O perpendicular to the line AD. So, OM $\perp$ AD.
Proof:
We know that the perpendicular from the centre of a circle to a chord bisects the chord.
For the outer circle, AD is a chord, and OM is the perpendicular drawn from the centre O to the chord AD.
Therefore, OM bisects the chord AD at point M.
AM = MD
(Perpendicular from centre bisects the chord) ... (i)
For the inner circle, BC is a chord, and OM is the perpendicular drawn from the centre O to the chord BC (since BC lies on the same line AD, and OM is perpendicular to AD, OM is also perpendicular to BC).
Therefore, OM bisects the chord BC at point M.
BM = MC
(Perpendicular from centre bisects the chord) ... (ii)
From the figure, we can see that the segment AM is the sum of segments AB and BM.
AM = AB + BM
Similarly, the segment MD is the sum of segments MC and CD.
MD = MC + CD
From equation (i), we know that AM = MD. So, we can set the expressions for AM and MD equal to each other:
AB + BM = MC + CD
... (iii)
From equation (ii), we know that BM = MC.
Substitute BM for MC in equation (iii):
AB + BM = BM + CD
Subtract BM from both sides of the equation:
AB = CD
Thus, the segments of the line between the two concentric circles (AB and CD) are equal.
Hence Proved.
Question 5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Answer:
Given:
Radius of the circle (OR = OS = OM) = $5$ m.
Distance between Reshma and Salma (RS) = $6$ m.
Distance between Salma and Mandip (SM) = $6$ m.
To Find:
The distance between Reshma and Mandip (RM).
Solution:
Let the positions of Reshma, Salma, and Mandip on the circle be R, S, and M respectively. Let O be the center of the circle.
We have OR = OS = OM = $5$ m (radius).
RS = $6$ m and SM = $6$ m.
Since RS = SM, $\triangle$RSM is an isosceles triangle inscribed in the circle. In such a case, the line segment joining the vertex S to the center O is the perpendicular bisector of the base RM.
Thus, the line segment SO is the perpendicular bisector of RM. Let K be the point where SO intersects RM. Then K is the midpoint of RM, and RM $\perp$ SO.
Consider the right-angled triangle $\triangle$ORK. By Pythagoras theorem:
OR$^2$ = OK$^2$ + RK$^2$
(Pythagoras theorem)
$5^2 = \text{OK}^2 + \left(\frac{\text{RM}}{2}\right)^2$
... (i)
Consider the right-angled triangle $\triangle$RSK. By Pythagoras theorem:
RS$^2$ = SK$^2$ + RK$^2$
(Pythagoras theorem)
$6^2 = \text{SK}^2 + \left(\frac{\text{RM}}{2}\right)^2$
... (ii)
Points S, O, and K are collinear. SO is the radius of the circle, so SO = $5$ m.
The distance OK is the distance from the center O to the chord RM. The distance SO is the radius 5. Since K is the midpoint of chord RM and lies on the line SO, and chord RM is generally closer to the center than points on the circle, K lies between S and O.
Therefore, SK = SO - OK.
SK = $5 - \text{OK}$
Substitute SK = $5$ - OK into equation (ii):
$36 = (5 - \text{OK})^2 + \left(\frac{\text{RM}}{2}\right)^2$
$36 = (25 - 10 \cdot \text{OK} + \text{OK}^2) + \left(\frac{\text{RM}}{2}\right)^2$
From equation (i), we know that $\text{OK}^2 + \left(\frac{\text{RM}}{2}\right)^2 = 5^2 = 25$. Substitute this into the equation above:
$36 = 25 - 10 \cdot \text{OK} + 25$
$36 = 50 - 10 \cdot \text{OK}$
Now, we solve for OK:
$10 \cdot \text{OK} = 50 - 36$
$10 \cdot \text{OK} = 14$
$OK = \frac{14}{10} = 1.4$ m
... (iii)
Now substitute the value of OK back into equation (i):
$5^2 = (1.4)^2 + \left(\frac{\text{RM}}{2}\right)^2$
$25 = 1.96 + \left(\frac{\text{RM}}{2}\right)^2$
Solve for $\left(\frac{\text{RM}}{2}\right)^2$:
$\left(\frac{\text{RM}}{2}\right)^2 = 25 - 1.96$
$\left(\frac{\text{RM}}{2}\right)^2 = 23.04$
Take the square root of both sides to find RM/2:
$\frac{\text{RM}}{2} = \sqrt{23.04}$
We find $\sqrt{23.04}$ by calculating $\sqrt{2304}$ and dividing by $\sqrt{100} = 10$. Let's find $\sqrt{2304}$ using the long division method for square roots:
$\begin{array}{c|cc} & 4 \ . \ 8 & \\ \hline \phantom{()} 4 & \overline{23} \; . \overline{04} \\ + \; 4 & 16 \phantom{....} \\ \hline \phantom{()} 8 \; 8 & 7 \; 04 \\ + \; 8 & 7 \; 04 \\ \hline \phantom{()} 96 & 0 \end{array}$
So, $\sqrt{2304} = 48$. Therefore, $\sqrt{23.04} = 4.8$.
$\frac{\text{RM}}{2} = 4.8$ m
Finally, find RM:
$RM = 2 \cdot 4.8$ m
$RM = 9.6$ m
Answer:
The distance between Reshma and Mandip is $9.6$ m.
Question 6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Answer:
Given:
A circular park with centre O and radius $R = 20$ m.
Three boys, Ankur (A), Syed (S), and David (D), are sitting at equal distances on the boundary of the circle.
To Find:
The length of the string of each phone, which is the distance between each pair of boys (AS, SD, and DA).
Figure:
Draw a circle with centre O and radius 20 m. Mark three points A, S, and D on the boundary such that the arc lengths between them are equal, which implies the chord lengths are equal. Join A, S, and D to form a triangle ASD inscribed in the circle.
Solution:
Since the three boys Ankur, Syed, and David are sitting at equal distances on the boundary of the circle, the chords connecting them are of equal length. Thus, the triangle $\Delta$ASD formed by their positions is an equilateral triangle inscribed in the circle.
AS = SD = DA
The length of the string of each phone is the side length of this equilateral triangle. Let the side length be 'a'.
The circular park is the circumcircle of the equilateral triangle $\Delta$ASD.
The radius of the park (20 m) is the circumradius ($R$) of the equilateral triangle $\Delta$ASD.
R = 20 m
(Given)
There is a direct relationship between the side length 'a' of an equilateral triangle and its circumradius R:
R = $\frac{a}{\sqrt{3}}$
We want to find 'a', so we can rearrange the formula:
a = $R\sqrt{3}$
Substitute the given value of R = 20 m into the formula:
a = $20\sqrt{3}$ m
The length of the string of each phone is equal to the side length 'a' of the equilateral triangle.
Therefore, the length of the string of each phone is $20\sqrt{3}$ m.
Answer:
The length of the string of each phone is $20\sqrt{3}$ m.
Example 2 to 5 (Before Exercise 9.3)
Example 2. In Fig. 9.19, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠ AEB = 60°.
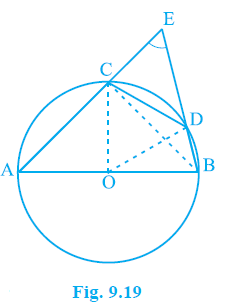
Answer:
Given:
AB is the diameter of the circle with center O.
CD is a chord such that its length is equal to the radius of the circle (CD = OC = OD).
Lines AC and BD are extended to intersect at point E.
To Prove:
$\angle$AEB = $60^\circ$.
Proof:
Let O be the center of the circle. Since AB is the diameter, O is the midpoint of AB.
We are given that the chord CD is equal to the radius of the circle.
CD = Radius
(Given)
Also, the radius is OC and OD.
CD = OC = OD
In $\triangle$OCD, since all three sides are equal to the radius, $\triangle$OCD is an equilateral triangle.
In an equilateral triangle, each angle is $60^\circ$. Therefore, the angle subtended by the chord CD at the center O is $60^\circ$.
$\angle$COD = $60^\circ$
... (i)
The angle subtended by an arc at the center is double the angle subtended by the same arc at any point on the remaining part of the circle.
Arc CD subtends $\angle$COD at the center and $\angle$CAD and $\angle$CBD at the circumference.
$\angle$CAD = $\frac{1}{2} \angle$COD
(Angle at circumference is half the angle at center)
Substituting the value from (i):
$\angle$CAD = $\frac{1}{2} \cdot 60^\circ = 30^\circ$
... (ii)
$\angle$CBD = $\frac{1}{2} \angle$COD
(Angles subtended by the same arc CD)
$\angle$CBD = $\frac{1}{2} \cdot 60^\circ = 30^\circ$
... (iii)
Now, consider the angles in a semicircle. The angle subtended by a diameter at any point on the circumference is a right angle ($90^\circ$).
Since AB is the diameter, $\angle$ACB and $\angle$BDA are angles in a semicircle.
$\angle$ACB = $90^\circ$
(Angle in a semicircle)
$\angle$BDA = $90^\circ$
... (iv)
We are given that AC is extended to E, so the line passing through A, C, E is a straight line. Similarly, BD is extended to E, so the line passing through B, D, E is a straight line. E is the intersection of these two lines.
Consider $\triangle$EAD. The angles of this triangle are $\angle$AEB (or $\angle$E), $\angle$EAD (angle at vertex A), and $\angle$EDA (angle at vertex D).
The angle $\angle$EAD is the same as $\angle$CAD, because E lies on the line passing through A and C extended. So, $\angle$EAD = $\angle$CAD.
From (ii), $\angle$CAD = $30^\circ$.
$\angle$EAD = $30^\circ$
[Since E lies on AC extended]
The angle $\angle$EDA is the same as $\angle$BDA, because E lies on the line passing through B and D extended. So, $\angle$EDA = $\angle$BDA.
From (iv), $\angle$BDA = $90^\circ$.
$\angle$EDA = $90^\circ$
[Since E lies on BD extended]
Now, apply the angle sum property to $\triangle$EAD. The sum of angles in a triangle is $180^\circ$.
$\angle$E + $\angle$EAD + $\angle$EDA = $180^\circ$
(Angle sum property of a triangle)
Substituting the values we found for $\angle$EAD and $\angle$EDA:
$\angle$AEB + $30^\circ + 90^\circ = 180^\circ$
$\angle$AEB + $120^\circ = 180^\circ$
Subtract $120^\circ$ from both sides:
$\angle$AEB = $180^\circ - 120^\circ$
$\angle$AEB = $60^\circ$
Thus, we have proved that $\angle$AEB = $60^\circ$.
Alternative Proof using $\triangle$EBC:
Consider $\triangle$EBC. The angles are $\angle$AEB (or $\angle$E), $\angle$EBC (angle at vertex B), and $\angle$ECB (angle at vertex C).
The angle $\angle$EBC is the same as $\angle$CBD, because E lies on the line passing through B and D extended. So, $\angle$EBC = $\angle$CBD.
From (iii), $\angle$CBD = $30^\circ$.
$\angle$EBC = $30^\circ$
[Since E lies on BD extended]
The angle $\angle$ECB is the same as $\angle$ACB, because E lies on the line passing through A and C extended. So, $\angle$ECB = $\angle$ACB.
From (iv), $\angle$ACB = $90^\circ$.
$\angle$ECB = $90^\circ$
[Since E lies on AC extended]
Apply the angle sum property to $\triangle$EBC:
$\angle$E + $\angle$EBC + $\angle$ECB = $180^\circ$
(Angle sum property of a triangle)
Substituting the values we found for $\angle$EBC and $\angle$ECB:
$\angle$AEB + $30^\circ + 90^\circ = 180^\circ$
$\angle$AEB + $120^\circ = 180^\circ$
Subtract $120^\circ$ from both sides:
$\angle$AEB = $180^\circ - 120^\circ$
$\angle$AEB = $60^\circ$
Both methods yield the same result.
Example 3. In Fig 9.20, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.

Answer:
Given:
ABCD is a cyclic quadrilateral.
AC and BD are its diagonals.
$\angle$DBC = $55^\circ$
(Given)
$\angle$BAC = $45^\circ$
(Given)
To Find:
$\angle$BCD.
Solution:
In the given circle, angles subtended by the same arc are equal.
Consider the arc CD. The angle subtended by arc CD at the circumference in segment ADC is $\angle$CAD.
The angle subtended by arc CD at the circumference in segment CBD is $\angle$CBD.
$\angle$CAD = $\angle$CBD
(Angles in the same segment)
$\angle$CAD = $55^\circ$
(Since $\angle$DBC = $55^\circ$)
Consider the arc BC. The angle subtended by arc BC at the circumference in segment BAC is $\angle$BAC.
The angle subtended by arc BC at the circumference in segment BDC is $\angle$BDC.
$\angle$BDC = $\angle$BAC
(Angles in the same segment)
$\angle$BDC = $45^\circ$
(Since $\angle$BAC = $45^\circ$)
Now, consider the triangle $\triangle$BCD.
The sum of the angles in a triangle is $180^\circ$.
In $\triangle$BCD, the angles are $\angle$BCD, $\angle$CBD, and $\angle$BDC.
$\angle$BCD + $\angle$CBD + $\angle$BDC = $180^\circ$
(Sum of angles in $\triangle$BCD)
Substitute the known values of $\angle$CBD and $\angle$BDC:
$\angle$BCD + $55^\circ$ + $45^\circ$ = $180^\circ$
$\angle$BCD + $100^\circ$ = $180^\circ$
Subtract $100^\circ$ from both sides:
$\angle$BCD = $180^\circ - 100^\circ$
$\angle$BCD = $80^\circ$
The measure of $\angle$BCD is $80^\circ$.
The final answer is $80^\circ$.
Example 4. Two circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.9.21). Prove that B lies on the line segment DC.
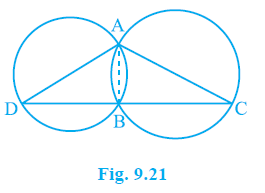
Answer:
Given:
Two circles intersecting at points A and B.
AD is the diameter of one circle.
AC is the diameter of the other circle.
To Prove:
Point B lies on the line segment DC.
Proof:
Consider the circle with diameter AD.
The angle subtended by the diameter AD at any point on the circumference is $90^\circ$.
Since B is a point on this circle, the angle subtended by the diameter AD at B is $\angle$ABD.
$\angle$ABD = $90^\circ$
(Angle in a semicircle)
Consider the circle with diameter AC.
The angle subtended by the diameter AC at any point on the circumference is $90^\circ$.
Since B is a point on this circle, the angle subtended by the diameter AC at B is $\angle$ABC.
$\angle$ABC = $90^\circ$
(Angle in a semicircle)
Now, consider the sum of the angles $\angle$ABD and $\angle$ABC.
$\angle$ABD + $\angle$ABC = $90^\circ$ + $90^\circ$
$\angle$ABD + $\angle$ABC = $180^\circ$
The angles $\angle$ABD and $\angle$ABC are adjacent angles.
If the sum of two adjacent angles is $180^\circ$, then their non-common arms form a straight line.
The non-common arms of $\angle$ABD and $\angle$ABC are BD and BC.
Since $\angle$ABD + $\angle$ABC = $180^\circ$, the points D, B, and C are collinear.
This means that point B lies on the straight line passing through D and C.
Therefore, B lies on the line segment DC.
Hence Proved.
Example 5. Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.
Answer:
Given:
A quadrilateral ABCD.
Let the internal angle bisectors of $\angle$A, $\angle$B, $\angle$C, and $\angle$D be $l_A, l_B, l_C, l_D$ respectively.
Let $l_A$ and $l_B$ intersect at P.
Let $l_B$ and $l_C$ intersect at Q.
Let $l_C$ and $l_D$ intersect at R.
Let $l_D$ and $l_A$ intersect at S.
These intersections form the quadrilateral PQRS.
To Prove:
The quadrilateral PQRS is cyclic.
Proof:
Consider the triangle $\triangle$APB formed by the intersection of the angle bisectors of $\angle$A and $\angle$B at point P.
The angles in $\triangle$APB are $\angle$PAB, $\angle$PBA, and $\angle$APB.
Since AP is the angle bisector of $\angle$A, we have:
$\angle$PAB = $\frac{1}{2}\angle$A
Since BP is the angle bisector of $\angle$B, we have:
$\angle$PBA = $\frac{1}{2}\angle$B
The sum of angles in any triangle is $180^\circ$. In $\triangle$APB, we have:
$\angle$APB + $\angle$PAB + $\angle$PBA = $180^\circ$
(Angle sum property of a triangle)
Rearranging the terms:
$\angle$APB = $180^\circ - (\angle$PAB + $\angle$PBA)
Substitute the values of $\angle$PAB and $\angle$PBA:
$\angle$APB = $180^\circ - (\frac{1}{2}\angle$A + $\frac{1}{2}\angle$B)
$\angle$APB = $180^\circ - \frac{1}{2}(\angle$A + $\angle$B)
... (i)
The angle at vertex P of the quadrilateral PQRS is $\angle$SPQ. This is the same as the angle $\angle$APB because they are vertically opposite angles.
$\angle$SPQ = $\angle$APB
(Vertically opposite angles)
So, from equation (i):
$\angle$SPQ = $180^\circ - \frac{1}{2}(\angle$A + $\angle$B)
... (ii)
Now consider the triangle $\triangle$CRD formed by the intersection of the angle bisectors of $\angle$C and $\angle$D at point R.
The angles in $\triangle$CRD are $\angle$RCD, $\angle$RDC, and $\angle$CRD.
Since CR is the angle bisector of $\angle$C, we have:
$\angle$RCD = $\frac{1}{2}\angle$C
Since DR is the angle bisector of $\angle$D, we have:
$\angle$RDC = $\frac{1}{2}\angle$D
In $\triangle$CRD, we have:
$\angle$CRD + $\angle$RCD + $\angle$RDC = $180^\circ$
(Angle sum property of a triangle)
Rearranging the terms:
$\angle$CRD = $180^\circ - (\angle$RCD + $\angle$RDC)
Substitute the values of $\angle$RCD and $\angle$RDC:
$\angle$CRD = $180^\circ - (\frac{1}{2}\angle$C + $\frac{1}{2}\angle$D)
$\angle$CRD = $180^\circ - \frac{1}{2}(\angle$C + $\angle$D)
... (iii)
The angle at vertex R of the quadrilateral PQRS is $\angle$QRS. This is the same as the angle $\angle$CRD because they are vertically opposite angles.
$\angle$QRS = $\angle$CRD
(Vertically opposite angles)
So, from equation (iii):
$\angle$QRS = $180^\circ - \frac{1}{2}(\angle$C + $\angle$D)
... (iv)
Now, let's find the sum of the opposite angles $\angle$SPQ and $\angle$QRS of the quadrilateral PQRS by adding equation (ii) and equation (iv).
$\angle$SPQ + $\angle$QRS = $(180^\circ - \frac{1}{2}(\angle$A + $\angle$B)) + $(180^\circ - \frac{1}{2}(\angle$C + $\angle$D))
$\angle$SPQ + $\angle$QRS = $180^\circ + 180^\circ - \frac{1}{2}(\angle$A + $\angle$B) - $\frac{1}{2}(\angle$C + $\angle$D)
$\angle$SPQ + $\angle$QRS = $360^\circ - \frac{1}{2}(\angle$A + $\angle$B + $\angle$C + $\angle$D)
We know that the sum of the interior angles of any quadrilateral ABCD is $360^\circ$.
$\angle$A + $\angle$B + $\angle$C + $\angle$D = $360^\circ$
(Sum of angles in quadrilateral ABCD)
Substitute this into the equation for the sum of opposite angles of PQRS:
$\angle$SPQ + $\angle$QRS = $360^\circ - \frac{1}{2}(360^\circ)$
$\angle$SPQ + $\angle$QRS = $360^\circ - 180^\circ$
$\angle$SPQ + $\angle$QRS = $180^\circ$
... (v)
Since the sum of one pair of opposite angles of quadrilateral PQRS ($\angle$SPQ and $\angle$QRS) is $180^\circ$, the quadrilateral PQRS is a cyclic quadrilateral.
Hence Proved.
Exercise 9.3
Question 1. In Fig. 9.23, A,B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.

Answer:
Given:
A circle with centre O.
Points A, B, and C are on the circle.
$\angle$BOC = $30^\circ$
$\angle$AOB = $60^\circ$
D is a point on the circle other than the arc ABC.
To Find:
$\angle$ADC.
Solution:
The angle subtended by the arc AC at the centre is the sum of $\angle$AOB and $\angle$BOC.
$\angle$AOC = $\angle$AOB + $\angle$BOC
$\angle$AOC = $60^\circ + 30^\circ$
$\angle$AOC = $90^\circ$
The arc AC subtends $\angle$AOC at the centre and $\angle$ADC at point D on the remaining part of the circle.
According to the theorem, the angle subtended by an arc at the centre is double the angle subtended by the same arc at any point on the remaining part of the circle.
$\angle$AOC = $2 \times \angle$ADC
(Angle at the centre is double the angle at the circumference)
Substitute the value of $\angle$AOC:
$90^\circ = 2 \times \angle$ADC
Divide both sides by 2:
$\angle$ADC = $\frac{90^\circ}{2}$
$\angle$ADC = $45^\circ$
The measure of $\angle$ADC is $45^\circ$.
The final answer is $45^\circ$.
Question 2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Answer:
Given:
A circle with centre O.
A chord AB such that the length of the chord is equal to the radius of the circle.
AB = radius
To Find:
The angle subtended by the chord at a point on the minor arc.
The angle subtended by the chord at a point on the major arc.
Solution:
Let the radius of the circle be $r$. The centre of the circle is O.
We are given that the chord AB is equal to the radius.
AB = $r$
Consider the triangle $\triangle$OAB formed by joining the endpoints of the chord to the centre.
In $\triangle$OAB:
OA = $r$
(Radius)
OB = $r$
(Radius)
AB = $r$
(Given)
Since OA = OB = AB = $r$, $\triangle$OAB is an equilateral triangle.
In an equilateral triangle, all angles are $60^\circ$.
The angle subtended by the chord AB at the centre O is $\angle$AOB.
$\angle$AOB = $60^\circ$
... (i)
Let D be a point on the major arc AB. The angle subtended by the arc AB at point D on the major arc is $\angle$ADB.
The angle subtended by an arc at the centre is double the angle subtended by the same arc at any point on the remaining part of the circle (i.e., the major arc in this case).
$\angle$AOB = $2 \times \angle$ADB
(Theorem)
Substitute the value of $\angle$AOB from (i):
$60^\circ = 2 \times \angle$ADB
Divide both sides by 2:
$\angle$ADB = $\frac{60^\circ}{2}$
$\angle$ADB = $30^\circ$
... (ii)
The angle subtended by the chord at a point on the major arc is $30^\circ$.
Now, let C be a point on the minor arc AB. The angle subtended by the chord AB at point C on the minor arc is $\angle$ACB.
The points A, C, B, and D lie on the circle. Thus, ACBD forms a cyclic quadrilateral.
In a cyclic quadrilateral, the sum of opposite angles is $180^\circ$.
$\angle$ACB + $\angle$ADB = $180^\circ$
(Opposite angles of a cyclic quadrilateral)
Substitute the value of $\angle$ADB from (ii):
$\angle$ACB + $30^\circ = 180^\circ$
Subtract $30^\circ$ from both sides:
$\angle$ACB = $180^\circ - 30^\circ$
$\angle$ACB = $150^\circ$
... (iii)
The angle subtended by the chord at a point on the minor arc is $150^\circ$.
Final Answer:
The angle subtended by the chord at a point on the minor arc is $150^\circ$.
The angle subtended by the chord at a point on the major arc is $30^\circ$.
Question 3. In Fig. 9.24, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

Answer:
Given:
A circle with centre O.
Points P, Q, and R are on the circle.
$\angle$PQR = $100^\circ$
To Find:
$\angle$OPR.
Solution:
The angle $\angle$PQR is the angle subtended by the major arc PR at the point Q on the circumference.
The angle subtended by the major arc PR at the centre O is the reflex angle $\angle$POR.
According to the theorem, the angle subtended by an arc at the centre is double the angle subtended by the same arc at any point on the remaining part of the circle.
Reflex $\angle$POR = $2 \times \angle$PQR
Substitute the value of $\angle$PQR:
Reflex $\angle$POR = $2 \times 100^\circ$
Reflex $\angle$POR = $200^\circ$
Now, we can find the angle $\angle$POR (the angle subtended by the minor arc PR at the centre O).
The sum of angles around the centre is $360^\circ$.
$\angle$POR + Reflex $\angle$POR = $360^\circ$
(Angles around a point)
$\angle$POR + $200^\circ$ = $360^\circ$
Subtract $200^\circ$ from both sides:
$\angle$POR = $360^\circ - 200^\circ$
$\angle$POR = $160^\circ$
Now, consider $\triangle$OPR.
OP and OR are radii of the same circle.
OP = OR
(Radii of the same circle)
Therefore, $\triangle$OPR is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$OPR = $\angle$ORP
(Base angles of isosceles triangle)
The sum of angles in a triangle is $180^\circ$. In $\triangle$OPR, we have:
$\angle$OPR + $\angle$ORP + $\angle$POR = $180^\circ$
(Angle sum property of a triangle)
Substitute $\angle$OPR for $\angle$ORP and the value of $\angle$POR:
$\angle$OPR + $\angle$OPR + $160^\circ$ = $180^\circ$
$2 \times \angle$OPR + $160^\circ$ = $180^\circ$
Subtract $160^\circ$ from both sides:
$2 \times \angle$OPR = $180^\circ - 160^\circ$
$2 \times \angle$OPR = $20^\circ$
Divide both sides by 2:
$\angle$OPR = $\frac{20^\circ}{2}$
$\angle$OPR = $10^\circ$
The measure of $\angle$OPR is $10^\circ$.
The final answer is $10^\circ$.
Question 4. In Fig. 9.25, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

Answer:
Given:
Points A, B, C, and D are on the circle.
$\angle$ABC = $69^\circ$
$\angle$ACB = $31^\circ$
To Find:
$\angle$BDC.
Solution:
Consider $\triangle$ABC.
The sum of the angles in a triangle is $180^\circ$.
$\angle$BAC + $\angle$ABC + $\angle$ACB = $180^\circ$
(Angle sum property of a triangle)
Substitute the given values of $\angle$ABC and $\angle$ACB:
$\angle$BAC + $69^\circ + 31^\circ = 180^\circ$
$\angle$BAC + $100^\circ = 180^\circ$
Subtract $100^\circ$ from both sides:
$\angle$BAC = $180^\circ - 100^\circ$
$\angle$BAC = $80^\circ$
... (i)
Now, consider the angles subtended by the arc BC at points A and D on the circumference.
Angles subtended by the same arc in the same segment of a circle are equal.
$\angle$BDC = $\angle$BAC
(Angles in the same segment)
Substitute the value of $\angle$BAC from (i):
$\angle$BDC = $80^\circ$
The measure of $\angle$BDC is $80^\circ$.
The final answer is $80^\circ$.
Question 5. In Fig. 9.26, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
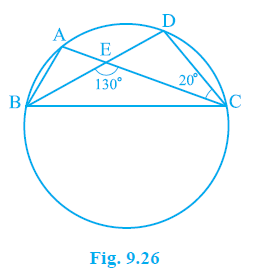
Answer:
Given:
Points A, B, C, and D are on a circle.
Diagonals AC and BD intersect at point E.
$\angle$BEC = $130^\circ$
$\angle$ECD = $20^\circ$
To Find:
$\angle$BAC.
Solution:
The angles $\angle$BEC and $\angle$CED form a linear pair.
$\angle$BEC + $\angle$CED = $180^\circ$
(Linear Pair)
Substitute the given value of $\angle$BEC:
$130^\circ + \angle$CED = $180^\circ$
Subtract $130^\circ$ from both sides:
$\angle$CED = $180^\circ - 130^\circ$
$\angle$CED = $50^\circ$
Now, consider $\triangle$CED.
The sum of the angles in a triangle is $180^\circ$.
$\angle$EDC + $\angle$CED + $\angle$ECD = $180^\circ$
(Angle sum property of a triangle)
Substitute the values of $\angle$CED and $\angle$ECD:
$\angle$EDC + $50^\circ + 20^\circ = 180^\circ$
$\angle$EDC + $70^\circ = 180^\circ$
Subtract $70^\circ$ from both sides:
$\angle$EDC = $180^\circ - 70^\circ$
$\angle$EDC = $110^\circ$
... (i)
The angle $\angle$EDC is the same as $\angle$BDC.
$\angle$BDC = $110^\circ$
Now, consider the angles subtended by the arc BC at points A and D on the circumference.
Angles subtended by the same arc in the same segment of a circle are equal.
$\angle$BAC = $\angle$BDC
(Angles in the same segment)
Substitute the value of $\angle$BDC from (i):
$\angle$BAC = $110^\circ$
The measure of $\angle$BAC is $110^\circ$.
The final answer is $110^\circ$.
Question 6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Answer:
Given:
ABCD is a cyclic quadrilateral.
Diagonals AC and BD intersect at E.
$\angle$DBC = $70^\circ$
$\angle$BAC = $30^\circ$
To Find:
$\angle$BCD.
If AB = BC, find $\angle$ECD.
Solution:
In a circle, angles subtended by the same arc in the same segment are equal.
Consider the arc BC. The angle subtended by arc BC at the circumference at point D is $\angle$BDC.
The angle subtended by arc BC at the circumference at point A is $\angle$BAC.
$\angle$BDC = $\angle$BAC
(Angles in the same segment)
Substitute the given value of $\angle$BAC:
$\angle$BDC = $30^\circ$
... (i)
Now, consider the triangle $\triangle$BCD.
The sum of the angles in any triangle is $180^\circ$. Apply this property to $\triangle$BCD.
$\angle$BCD + $\angle$CBD + $\angle$BDC = $180^\circ$
(Angle sum property of $\triangle$BCD)
Substitute the given value of $\angle$CBD ($70^\circ$) and the value of $\angle$BDC ($30^\circ$) from (i):
$\angle$BCD + $70^\circ + 30^\circ = 180^\circ$
$\angle$BCD + $100^\circ = 180^\circ$
Subtract $100^\circ$ from both sides to find $\angle$BCD:
$\angle$BCD = $180^\circ - 100^\circ$
$\angle$BCD = $80^\circ$
... (ii)
To find $\angle$ECD when AB = BC:
We are given the additional condition that the side AB is equal to the side BC.
AB = BC
(Given)
Consider $\triangle$ABC. Since AB = BC, $\triangle$ABC is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
The angle opposite to side BC is $\angle$BAC.
The angle opposite to side AB is $\angle$BCA.
$\angle$BCA = $\angle$BAC
(Angles opposite equal sides in $\triangle$ABC)
Substitute the given value of $\angle$BAC:
$\angle$BCA = $30^\circ$
... (iii)
The angle $\angle$ECD is the same angle as $\angle$BCA because the points E, C, A are collinear (since AC is a diagonal), and E lies on the extension of AC (or simply on AC). Thus, the line segment CE is part of the line segment CA.
$\angle$ECD = $\angle$BCA
[C lies on AE]
From (iii), we have:
$\angle$ECD = $30^\circ$
Final Answer:
The measure of $\angle$BCD is $80^\circ$.
If AB = BC, the measure of $\angle$ECD is $30^\circ$.
Question 7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer:
Given:
ABCD is a cyclic quadrilateral inscribed in a circle with centre O.
Diagonals AC and BD are diameters of the circle.
To Prove:
ABCD is a rectangle.
Proof:
In the given cyclic quadrilateral ABCD, the diagonal AC is also a diameter of the circle.
We know that the angle subtended by a diameter at any point on the circumference of the circle is always a right angle ($90^\circ$). This is a property of circles.
Consider the angle subtended by the diameter AC at vertex B on the circumference:
$\angle$ABC = $90^\circ$
(Angle in a semicircle)
Consider the angle subtended by the diameter AC at vertex D on the circumference:
$\angle$ADC = $90^\circ$
(Angle in a semicircle)
Similarly, the diagonal BD is also a diameter of the circle.
Consider the angle subtended by the diameter BD at vertex A on the circumference:
$\angle$BAD = $90^\circ$
(Angle in a semicircle)
Consider the angle subtended by the diameter BD at vertex C on the circumference:
$\angle$BCD = $90^\circ$
(Angle in a semicircle)
From the above steps, we have found that all four interior angles of the quadrilateral ABCD are $90^\circ$:
$\angle$BAD = $90^\circ$
$\angle$ABC = $90^\circ$
$\angle$BCD = $90^\circ$
$\angle$ADC = $90^\circ$
A quadrilateral is defined as a rectangle if all its interior angles are right angles ($90^\circ$).
Since all angles of quadrilateral ABCD are $90^\circ$, it satisfies the condition of being a rectangle.
Therefore, ABCD is a rectangle.
Hence Proved.
Question 8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
Given:
A trapezium ABCD in which AB is parallel to CD (AB || CD).
The non-parallel sides are equal, i.e., AD = BC.
To Prove:
Trapezium ABCD is a cyclic quadrilateral.
(A quadrilateral is cyclic if the sum of opposite angles is $180^\circ$).
Construction Required:
Draw AM $\perp$ CD and BN $\perp$ CD from A and B respectively, where M and N are points on CD.
Proof:
Since AB is parallel to CD (AB || CD), and AM is perpendicular to CD, and BN is perpendicular to CD, the perpendicular distance between the parallel lines AB and CD is constant everywhere.
AM = BN
(Perpendicular distance between parallel lines)
Now, consider the two right-angled triangles $\triangle$ADM and $\triangle$BCN.
In $\triangle$ADM and $\triangle$BCN:
$\angle$AMD = $\angle$BNC = $90^\circ$
(By construction)
AD = BC
(Given non-parallel sides are equal)
AM = BN
(Proved above)
Therefore, by the Right-angle-Hypotenuse-Side (RHS) congruence criterion, $\triangle$ADM is congruent to $\triangle$BCN.
$\triangle$ADM $\cong$ $\triangle$BCN
(RHS Congruence Rule)
By Corresponding Parts of Congruent Triangles (CPCT), the corresponding angles of congruent triangles are equal.
$\angle$D = $\angle$C
(CPCT) ... (i)
Since AB is parallel to CD, the line segments AD and BC are transversals intersecting these parallel lines.
The sum of consecutive interior angles on the same side of a transversal intersecting parallel lines is $180^\circ$.
Consider the transversal AD intersecting parallel lines AB and CD:
$\angle$A + $\angle$D = $180^\circ$
(Consecutive interior angles)
Consider the transversal BC intersecting parallel lines AB and CD:
$\angle$B + $\angle$C = $180^\circ$
(Consecutive interior angles)
We know from (i) that $\angle$D = $\angle$C. Let's use this in the angle sum equations.
We have $\angle$A + $\angle$D = $180^\circ$. Substituting $\angle$D = $\angle$C, we get:
$\angle$A + $\angle$C = $180^\circ$
... (ii)
This shows that one pair of opposite angles of quadrilateral ABCD ($\angle$A and $\angle$C) sums to $180^\circ$.
Now consider the other pair of opposite angles, $\angle$B and $\angle$D.
We have $\angle$B + $\angle$C = $180^\circ$. Substituting $\angle$C = $\angle$D from (i), we get:
$\angle$B + $\angle$D = $180^\circ$
... (iii)
This shows that the other pair of opposite angles of quadrilateral ABCD ($\angle$B and $\angle$D) also sums to $180^\circ$.
A quadrilateral is cyclic if and only if the sum of each pair of opposite angles is $180^\circ$.
Since both pairs of opposite angles of the quadrilateral ABCD sum to $180^\circ$ (from (ii) and (iii)), the quadrilateral ABCD is cyclic.
Hence Proved.
Question 9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 9.27). Prove that ∠ACP = ∠ QCD.
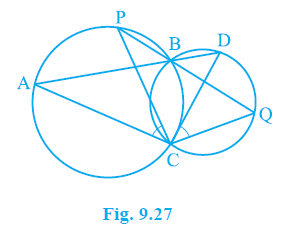
Answer:
Given:
Two circles intersect at points B and C.
Line segment ABD intersects the first circle at A and B, and the second circle at B and D.
Line segment PBQ intersects the first circle at P and B, and the second circle at B and Q.
To Prove:
$\angle$ACP = $\angle$QCD.
Proof:
Consider the first circle passing through points A, P, C, and B.
The points A, P, C, and B form a cyclic quadrilateral APBC.
In a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.
Consider the line segment ABD. The angle $\angle$DBC is an exterior angle to the cyclic quadrilateral APBC at vertex B.
The interior opposite angle to $\angle$DBC is $\angle$ACP.
$\angle$DBC = $\angle$ACP
(Exterior angle of cyclic quadrilateral APBC is equal to the interior opposite angle) ... (i)
Now, consider the second circle passing through points D, Q, C, and B.
The points D, Q, C, and B form a cyclic quadrilateral DQCB.
Consider the line segment PBQ. The angle $\angle$PBC is an exterior angle to the cyclic quadrilateral DQCB at vertex B.
The interior opposite angle to $\angle$PBC is $\angle$QCD.
$\angle$PBC = $\angle$QCD
(Exterior angle of cyclic quadrilateral DQCB is equal to the interior opposite angle) ... (ii)
The line segments AD and PQ intersect at B.
The angles $\angle$DBC and $\angle$PBC are vertically opposite angles formed by the intersection of lines AD and PQ at B.
$\angle$DBC = $\angle$PBC
(Vertically opposite angles) ... (iii)
From equation (i), we have $\angle$ACP = $\angle$DBC.
From equation (ii), we have $\angle$QCD = $\angle$PBC.
From equation (iii), we have $\angle$DBC = $\angle$PBC.
Therefore, by combining these equalities:
$\angle$ACP = $\angle$DBC = $\angle$PBC = $\angle$QCD
Thus, we can conclude that $\angle$ACP = $\angle$QCD.
$\angle$ACP = $\angle$QCD
Hence Proved.
Question 10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Answer:
Given:
Let $\triangle$ABC be any triangle.
A circle is drawn with side AB as diameter.
Another circle is drawn with side AC as diameter.
To Prove:
The point of intersection of these two circles (other than A) lies on the third side BC.
Proof:
Let the circle with AB as diameter and the circle with AC as diameter intersect at points A and P. We need to prove that P lies on the line segment BC.
Consider the circle with AB as diameter. Any angle subtended by the diameter at a point on the circumference is a right angle ($90^\circ$). Since P lies on this circle, the angle $\angle$APB is subtended by the diameter AB.
$\angle$APB = $90^\circ$
(Angle in a semicircle)
Now, consider the circle with AC as diameter. Since P also lies on this circle, the angle $\angle$APC is subtended by the diameter AC.
$\angle$APC = $90^\circ$
(Angle in a semicircle)
Consider the sum of these two adjacent angles $\angle$APB and $\angle$APC, which share the common vertex P and the common arm AP.
$\angle$APB + $\angle$APC = $90^\circ + 90^\circ$
$\angle$APB + $\angle$APC = $180^\circ$
If the sum of two adjacent angles is $180^\circ$, then their non-common arms (PB and PC) form a straight line.
Therefore, the points B, P, and C are collinear. This means that the point P lies on the line containing the side BC.
For a non-degenerate triangle, P will lie on the line segment BC.
Thus, the point of intersection of the two circles (other than A) lies on the third side BC of the triangle.
Hence Proved.
Question 11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Answer:
Given:
$\triangle$ABC is a right triangle with hypotenuse AC. So, $\angle$ABC = $90^\circ$.
$\triangle$ADC is a right triangle with hypotenuse AC. So, $\angle$ADC = $90^\circ$.
AC is the common hypotenuse for both triangles.
To Prove:
$\angle$CAD = $\angle$CBD.
Proof:
Consider the points A, B, and C.
In $\triangle$ABC, $\angle$ABC = $90^\circ$. We know that the locus of points subtending a right angle at the endpoints of a line segment is a circle having that line segment as its diameter.
Since $\angle$ABC is a right angle and AC is the hypotenuse, point B must lie on the circle with AC as its diameter.
Similarly, consider the points A, D, and C.
In $\triangle$ADC, $\angle$ADC = $90^\circ$. Since $\angle$ADC is a right angle and AC is the hypotenuse, point D must lie on the circle with AC as its diameter.
Since both points B and D lie on the same circle which has AC as its diameter, the four points A, B, C, and D are concyclic. This means that the quadrilateral ABCD is a cyclic quadrilateral.
In a circle, angles subtended by the same arc in the same segment are equal.
Consider the arc CD.
The angle subtended by arc CD at point A on the circumference is $\angle$CAD.
The angle subtended by the same arc CD at point B on the circumference is $\angle$CBD.
These two angles, $\angle$CAD and $\angle$CBD, lie in the same segment of the circle formed by the chord CD (the major segment).
Therefore, according to the theorem for angles in the same segment:
$\angle$CAD = $\angle$CBD
(Angles in the same segment)
Hence Proved.
Question 12. Prove that a cyclic parallelogram is a rectangle.
Answer:
Given:
ABCD is a parallelogram.
ABCD is a cyclic quadrilateral (all vertices lie on a circle).
To Prove:
ABCD is a rectangle.
Proof:
Since ABCD is a parallelogram, its opposite angles are equal in measure.
$\angle$A = $\angle$C
(Opposite angles of a parallelogram) ... (i)
$\angle$B = $\angle$D
(Opposite angles of a parallelogram) ... (ii)
Since ABCD is a cyclic quadrilateral, the sum of each pair of opposite angles is $180^\circ$.
$\angle$A + $\angle$C = $180^\circ$
(Opposite angles of a cyclic quadrilateral) ... (iii)
$\angle$B + $\angle$D = $180^\circ$
(Opposite angles of a cyclic quadrilateral) ... (iv)
Now, substitute the value of $\angle$C from equation (i) into equation (iii):
$\angle$A + $\angle$A = $180^\circ$
$2\angle$A = $180^\circ$
Divide both sides by 2:
$\angle$A = $\frac{180^\circ}{2}$
$\angle$A = $90^\circ$
... (v)
From equation (i) and equation (v), we get:
$\angle$C = $90^\circ$
... (vi)
Next, substitute the value of $\angle$D from equation (ii) into equation (iv):
$\angle$B + $\angle$B = $180^\circ$
$2\angle$B = $180^\circ$
Divide both sides by 2:
$\angle$B = $\frac{180^\circ}{2}$
$\angle$B = $90^\circ$
... (vii)
From equation (ii) and equation (vii), we get:
$\angle$D = $90^\circ$
... (viii)
From equations (v), (vi), (vii), and (viii), we have shown that all four interior angles of the parallelogram ABCD are equal to $90^\circ$ ($\angle$A = $\angle$B = $\angle$C = $\angle$D = $90^\circ$).
A parallelogram is a rectangle if and only if all its interior angles are right angles ($90^\circ$).
Since ABCD is a parallelogram with all angles equal to $90^\circ$, it is a rectangle.
Hence Proved.

