| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 10 Vector Algebra
Welcome to the solutions guide for Chapter 10: Vector Algebra. This chapter introduces vectors, mathematical entities possessing both magnitude (size or length) and direction. Unlike scalars, which are fully described by a single numerical value (like temperature, mass, or speed), vectors are essential for representing quantities where direction is inherent (like displacement, velocity, force, or acceleration). Vector algebra provides a powerful framework for manipulating these directed quantities geometrically and algebraically, with profound applications in physics (mechanics, electromagnetism), engineering, computer graphics, and geometry itself. This chapter lays the foundation by defining vectors, exploring their properties, establishing rules for vector operations (addition, scalar multiplication, and vector products), and applying these concepts to solve geometric problems.
The solutions begin by establishing the fundamental concepts:
- Distinguishing between scalars and vectors.
- Defining a vector geometrically (directed line segment) and its magnitude (length) and direction.
- The concept of a position vector, which represents the position of a point in space relative to a fixed origin.
- Defining direction cosines ($l, m, n$, where $l=\cos\alpha, m=\cos\beta, n=\cos\gamma$ are cosines of angles the vector makes with positive x, y, z axes, satisfying $l^2+m^2+n^2=1$) and direction ratios ($a, b, c$, which are proportional to direction cosines).
- Classifying different types of vectors: zero vector (magnitude 0), unit vector (magnitude 1), collinear vectors (parallel), equal vectors (same magnitude and direction), negative vector (same magnitude, opposite direction).
Vector operations are then introduced:
- Vector Addition: Defined geometrically using the Triangle Law or the Parallelogram Law. Its properties, including commutativity and associativity, are explained.
- Scalar Multiplication: Multiplying a vector by a scalar changes its magnitude (and possibly reverses direction if the scalar is negative) but keeps it parallel to the original vector.
Representing vectors in component form using the standard unit vectors $\mathbf{\hat{i}}, \mathbf{\hat{j}}, \mathbf{\hat{k}}$ along the x, y, and z axes respectively (e.g., $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$) is fundamental for algebraic manipulation. Solutions demonstrate performing operations like addition, subtraction, scalar multiplication, and checking equality using these components. Calculating the magnitude of a vector $\vec{a}$ is then $|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$. Finding the unit vector in the direction of $\vec{a}$ is crucial: $\mathbf{\hat{a}} = \frac{\vec{a}}{|\vec{a}|}$. The section formula is extended to vectors, allowing calculation of the position vector of a point dividing the line segment joining two points (with given position vectors) internally or externally in a given ratio.
The core of vector algebra involves defining products of vectors:
- Scalar (Dot) Product: This product of two vectors $\vec{a}$ and $\vec{b}$ results in a scalar quantity. It's defined geometrically as $\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$, where $\theta$ is the angle between the vectors, or algebraically using components as $\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3$. The solutions demonstrate calculating the dot product and its key applications: finding the angle between two vectors ($\cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$), checking for orthogonality (perpendicularity: $\vec{a} \cdot \vec{b} = 0$), and finding the scalar projection of vector $\vec{a}$ onto vector $\vec{b}$ ($\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$) or the vector projection ($(\vec{a} \cdot \hat{b})\hat{b}$). Properties like commutativity ($\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$) and distributivity over addition are utilized.
- Vector (Cross) Product: This product of two vectors $\vec{a}$ and $\vec{b}$ results in a vector quantity, denoted $\vec{a} \times \vec{b}$. Its magnitude is $|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin \theta$, and its direction is perpendicular to the plane containing $\vec{a}$ and $\vec{b}$, determined by the right-hand rule. Algebraically, it's most conveniently calculated using a determinant: $\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$. Solutions show how to compute the cross product and use it to find a vector perpendicular to two given vectors. Important geometric interpretations include the magnitude $|\vec{a} \times \vec{b}|$ representing the area of the parallelogram with adjacent sides $\vec{a}$ and $\vec{b}$, and $\frac{1}{2} |\vec{a} \times \vec{b}|$ representing the area of the triangle with sides $\vec{a}$ and $\vec{b}$. Key properties include non-commutativity ($\vec{a} \times \vec{b} = - \vec{b} \times \vec{a}$) and distributivity over addition.
- Scalar Triple Product (often non-rationalised): Defined for three vectors $\vec{a}, \vec{b}, \vec{c}$ as $[\vec{a} \ \vec{b} \ \vec{c}] = \vec{a} \cdot (\vec{b} \times \vec{c})$. It results in a scalar value and can be calculated using a determinant: $[\vec{a} \ \vec{b} \ \vec{c}] = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix}$. The solutions explain its calculation and its geometric interpretation: the absolute value $|[\vec{a} \ \vec{b} \ \vec{c}]|$ represents the volume of the parallelepiped formed by the three vectors as coterminous edges. A crucial application is checking for coplanarity of three vectors: they are coplanar if and only if their scalar triple product is zero ($[\vec{a} \ \vec{b} \ \vec{c}] = 0$).
These tools provide a robust framework for analyzing geometric and physical problems involving direction and magnitude.
Example 1 to 3 (Before Exercise 10.1)
Example 1: Represent graphically a displacement of 40 km, 30° west of south.
Answer:
To represent the displacement graphically, we first establish a coordinate system representing the cardinal directions.
Let the origin O represent the starting point.
- The positive y-axis represents the North direction.
- The negative y-axis represents the South direction.
- The positive x-axis represents the East direction.
- The negative x-axis represents the West direction.
The given displacement is 40 km, 30° west of south.
This means:
1. The magnitude of the displacement is 40 km.
2. The direction is measured starting from the South direction and rotating $30^\circ$ towards the West direction.
Graphical Representation Steps:
1. Draw the coordinate axes (North-South and East-West) intersecting at the origin O.
2. Identify the South direction (negative y-axis).
3. From the South direction line (OS), measure an angle of $30^\circ$ towards the West direction (negative x-axis). This angle will be in the third quadrant (South-West quadrant).
4. Draw a vector $\vec{OP}$ starting from the origin O along this direction.
5. The length of the vector $\vec{OP}$ should represent 40 km. Choose a suitable scale (e.g., 1 cm = 10 km, then the vector length would be 4 cm).
6. Label the angle between the vector $\vec{OP}$ and the South direction (OS) as $30^\circ$.
The vector $\vec{OP}$ represents the displacement of 40 km, 30° west of south.
Summary:
The vector $\vec{OP}$ has:
- Magnitude: $|\vec{OP}| = 40$ km.
- Direction: Makes an angle of $30^\circ$ with the negative y-axis (South) towards the negative x-axis (West).
Example 2: Classify the following measures as scalars and vectors.
(i) 5 seconds
(ii) 1000 cm3
(iii) 10 Newton
(iv) 30 km/hr
(v) 10 g/cm3
(vi) 20 m/s towards north
Answer:
A scalar quantity is one that has only magnitude, while a vector quantity has both magnitude and direction.
(i) 5 seconds
This represents time. Time has only magnitude (5 seconds) and no direction. Therefore, it is a scalar.
(ii) 1000 cm3
This represents volume. Volume has only magnitude (1000 cm3) and no direction. Therefore, it is a scalar.
(iii) 10 Newton
Newton is the unit of force. Force has both magnitude (10 N) and a direction in which it acts. Therefore, it is a vector.
(iv) 30 km/hr
This represents speed, which is the magnitude of velocity. It has magnitude (30 km/hr) but no specified direction. Therefore, it is a scalar.
(v) 10 g/cm3
This represents density. Density has only magnitude (10 g/cm3) and no direction. Therefore, it is a scalar.
(vi) 20 m/s towards north
This represents velocity. It has magnitude (20 m/s) and a specific direction (towards north). Therefore, it is a vector.
Example 3: In Fig 10.5, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Coinitial
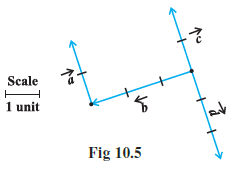
Answer:
We need to analyze the vectors $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ shown in Figure 10.5 based on the definitions of collinear, equal, and coinitial vectors.
Observing the standard representation of Fig 10.5 in NCERT textbooks:
- Vector $\vec{a}$ and vector $\vec{c}$ point in the same direction (horizontally to the right) and appear to have the same length.
- Vector $\vec{b}$ and vector $\vec{d}$ point in the same direction (diagonally down and to the left) and appear to have the same length.
- Vectors $\vec{a}$ and $\vec{c}$ are parallel.
- Vectors $\vec{b}$ and $\vec{d}$ are parallel.
- All four vectors appear to start from different initial points.
(i) Collinear Vectors:
Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.
In the figure:
- $\vec{a}$ is parallel to $\vec{c}$.
- $\vec{b}$ is parallel to $\vec{d}$.
Therefore, the sets of collinear vectors are $\{\vec{a}, \vec{c}\}$ and $\{\vec{b}, \vec{d}\}$.
(ii) Equal Vectors:
Two vectors are said to be equal if they have the same magnitude and the same direction.
In the figure:
- $\vec{a}$ and $\vec{c}$ have the same direction (right) and the same magnitude (length). Thus, $\vec{a} = \vec{c}$.
- $\vec{b}$ and $\vec{d}$ have the same direction (down-left) and the same magnitude (length). Thus, $\vec{b} = \vec{d}$.
Therefore, the pairs of equal vectors are $(\vec{a}, \vec{c})$ and $(\vec{b}, \vec{d})$.
(iii) Coinitial Vectors:
Two or more vectors are said to be coinitial if they have the same initial point.
In the figure, all four vectors $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ start from different points.
Therefore, there are no coinitial vectors among the given set.
Exercise 10.1
Question 1. Represent graphically a displacement of 40 km, 30° east of north.
Answer:
To represent the displacement graphically, we first establish a coordinate system representing the cardinal directions.
Let the origin O represent the starting point.
- The positive y-axis represents the North direction.
- The negative y-axis represents the South direction.
- The positive x-axis represents the East direction.
- The negative x-axis represents the West direction.
The given displacement is 40 km, 30° east of north.
This means:
1. The magnitude of the displacement is 40 km.
2. The direction is measured starting from the North direction and rotating $30^\circ$ towards the East direction.
Graphical Representation Steps:
1. Draw the coordinate axes (North-South and East-West) intersecting at the origin O.
2. Identify the North direction (positive y-axis).
3. From the North direction line (ON), measure an angle of $30^\circ$ towards the East direction (positive x-axis). This angle will be in the first quadrant (North-East quadrant).
4. Draw a vector $\vec{OP}$ starting from the origin O along this direction.
5. The length of the vector $\vec{OP}$ should represent 40 km. Choose a suitable scale (e.g., 1 cm = 10 km, then the vector length would be 4 cm).
6. Label the angle between the vector $\vec{OP}$ and the North direction (ON) as $30^\circ$.
Summary:
The vector $\vec{OP}$ represents the displacement and has:
- Magnitude: $|\vec{OP}| = 40$ km.
- Direction: Makes an angle of $30^\circ$ with the positive y-axis (North) towards the positive x-axis (East).
Question 2. Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 watt
(v) 10–19 coulomb
(vi) 20 m/s2
Answer:
Definition:
A scalar quantity is one that has only magnitude and no direction.
A vector quantity is one that has both magnitude and direction.
(i) 10 kg
This quantity represents mass. Mass has only magnitude (10 kg) and no specific direction.
Therefore, it is a Scalar.
(ii) 2 meters north-west
This quantity represents displacement. It clearly specifies both magnitude (2 meters) and direction (north-west).
Therefore, it is a Vector.
(iii) 40°
This quantity represents an angle or temperature. Both have magnitude (40°) but no associated direction in the vector sense.
Therefore, it is a Scalar.
(iv) 40 watt
This quantity represents power. Power is the rate of energy transfer or work done per unit time. It has magnitude (40 watt) but no direction.
Therefore, it is a Scalar.
(v) $10^{-19}$ coulomb
This quantity represents electric charge. Electric charge has magnitude ($10^{-19}$ coulomb) but is not associated with a direction.
Therefore, it is a Scalar.
(vi) 20 $m/s^2$
This quantity represents acceleration. Acceleration is the rate of change of velocity (a vector quantity). Hence, acceleration has both magnitude (20 $m/s^2$) and direction.
Therefore, it is a Vector.
Question 3. Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
Answer:
Definition:
A scalar quantity is a physical quantity that has only magnitude and no direction. It is described by a single number.
A vector quantity is a physical quantity that has both magnitude and direction.
(i) time period
Time period is the duration of one cycle in a repeating event. It has only magnitude (e.g., 5 seconds) and no associated direction.
Therefore, it is a Scalar.
(ii) distance
Distance is the total path length covered by an object. It only specifies how much ground an object has covered, which is a magnitude, without specifying the direction of motion.
Therefore, it is a Scalar.
(iii) force
Force is a push or pull upon an object resulting from the object's interaction with another object. Applying a force requires specifying not only how strong the push or pull is (magnitude) but also in which direction it is applied.
Therefore, it is a Vector.
(iv) velocity
Velocity is the rate of change of an object's position with respect to a frame of reference and is a function of time. It specifies both the speed (magnitude) and the direction of motion.
Therefore, it is a Vector.
(v) work done
Work done by a constant force is defined as the dot product of the force vector and the displacement vector ($W = \vec{F} \cdot \vec{d}$). The dot product of two vectors results in a scalar quantity. Work represents energy transfer and has magnitude but no direction.
Therefore, it is a Scalar.
Question 4. In Fig 10.6 (a square), identify the following vectors.
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
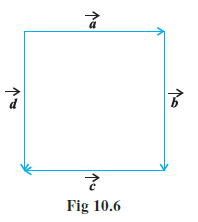
Answer:
Definitions:
Coinitial vectors: Two or more vectors having the same initial point.
Equal vectors: Two or more vectors having the same magnitude and the same direction.
Collinear vectors: Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.
Collinear but not equal vectors: Collinear vectors that are not equal (i.e., they may have different magnitudes, or opposite directions, or both).
Analysis of Figure 10.6 (Square):
From the figure (assuming the standard representation often used for this problem, as described in the image alt text):
- Vectors $\vec{a}$ and $\vec{d}$ start from the same initial point.
- Vectors $\vec{b}$ and $\vec{d}$ are parallel, have the same magnitude (side length of the square), and point in the same direction (upwards).
- Vectors $\vec{a}$ and $\vec{c}$ are parallel, have the same magnitude (side length of the square), but point in opposite directions ($\vec{a}$ points right, $\vec{c}$ points left).
(i) Coinitial vectors:
Vectors that start from the same point are coinitial.
In the given figure, vectors $\vec{a}$ and $\vec{d}$ share the same initial point.
Therefore, the coinitial vectors are $\vec{a}$ and $\vec{d}$.
(ii) Equal vectors:
Vectors that have the same magnitude and the same direction are equal.
In the figure, vectors $\vec{b}$ and $\vec{d}$ have the same magnitude (equal to the side length of the square) and the same direction (upwards).
Therefore, the equal vectors are $\vec{b}$ and $\vec{d}$.
(iii) Collinear but not equal vectors:
Vectors that are parallel but not equal (either different magnitudes or opposite directions).
In the figure, vectors $\vec{a}$ and $\vec{c}$ are parallel (collinear) and have the same magnitude. However, their directions are opposite ($\vec{a}$ points right, $\vec{c}$ points left). Hence, they are not equal.
Therefore, the collinear but not equal vectors are $\vec{a}$ and $\vec{c}$.
Question 5. Answer the following as true or false
(i) $\vec{a}$ and $–\vec{a}$ are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Answer:
Definitions:
Collinear vectors: Two or more vectors are collinear if they are parallel to the same line, irrespective of their magnitudes and directions. This means one vector can be expressed as a scalar multiple of the other ($\vec{b} = \lambda \vec{a}$ for some scalar $\lambda$).
Equal vectors: Two vectors $\vec{a}$ and $\vec{b}$ are equal if they have the same magnitude ($|\vec{a}| = |\vec{b}|$) and the same direction.
Negative of a vector: The vector $-\vec{a}$ has the same magnitude as $\vec{a}$ but the opposite direction.
(i) $\vec{a}$ and $–\vec{a}$ are collinear.
The vector $-\vec{a}$ is defined as the vector having the same magnitude as $\vec{a}$ but pointing in the exactly opposite direction. Since they lie along the same line (or parallel lines) but in opposite directions, they fit the definition of collinear vectors.
Mathematically, $-\vec{a} = (-1)\vec{a}$. Since $-\vec{a}$ is a scalar multiple of $\vec{a}$, they are collinear.
Therefore, the statement is True.
(ii) Two collinear vectors are always equal in magnitude.
Collinear vectors are parallel. Consider a vector $\vec{a}$ and another vector $2\vec{a}$. These two vectors are collinear because $2\vec{a}$ is a scalar multiple of $\vec{a}$. However, their magnitudes are $|\vec{a}|$ and $|2\vec{a}| = 2|\vec{a}|$. Unless $|\vec{a}| = 0$, these magnitudes are different.
Therefore, the statement is False.
(iii) Two vectors having same magnitude are collinear.
Consider two vectors $\vec{a}$ and $\vec{b}$ such that $|\vec{a}| = |\vec{b}| = 5$. Let $\vec{a}$ point along the positive x-axis and $\vec{b}$ point along the positive y-axis. They have the same magnitude, but they are not parallel (they are perpendicular), so they are not collinear.
Therefore, the statement is False.
(iv) Two collinear vectors having the same magnitude are equal.
Collinear vectors are parallel, meaning they can have the same direction or opposite directions. If two collinear vectors $\vec{a}$ and $\vec{b}$ have the same magnitude ($|\vec{a}| = |\vec{b}|$), they could either have the same direction (making them equal, $\vec{a} = \vec{b}$) or opposite directions (making one the negative of the other, $\vec{a} = -\vec{b}$).
For example, $\vec{a}$ and $-\vec{a}$ are collinear and have the same magnitude ($|\vec{a}| = |-\vec{a}|$), but they are not equal because their directions are opposite (unless $\vec{a} = \vec{0}$).
Therefore, the statement is False.
Example 4 to 12 (Before Exercise 10.2)
Example 4: Find the values of x, y and z so that the vectors $\vec{a} = x\hat{i} + 2\hat{j} + z\hat{k}$ and $\vec{b} = 2\hat{i} + y\hat{j} + \hat{k}$ are equal.
Answer:
Given:
Two vectors are given as:
$\vec{a} = x\hat{i} + 2\hat{j} + z\hat{k}$
$\vec{b} = 2\hat{i} + y\hat{j} + \hat{k}$
The condition is that the vectors are equal, i.e., $\vec{a} = \vec{b}$.
To Find:
The values of $x$, $y$, and $z$.
Solution:
Two vectors are equal if and only if their corresponding components are equal.
Given $\vec{a} = \vec{b}$, we can write:
$x\hat{i} + 2\hat{j} + z\hat{k} = 2\hat{i} + y\hat{j} + \hat{k}$
For these two vectors to be equal, their respective components along $\hat{i}$, $\hat{j}$, and $\hat{k}$ must be equal.
Comparing the coefficients of $\hat{i}$:
$x = 2$
Comparing the coefficients of $\hat{j}$:
$2 = y$
Comparing the coefficients of $\hat{k}$:
$z = 1$
Therefore, the values are:
$x = 2$
$y = 2$
$z = 1$
Example 5: Let $\vec{a} = \hat{i} + 2\hat{j}$ and $\vec{b} = 2\hat{i} + \hat{j}$ . Is $|\vec{a}| = |\vec{b}|$ ? Are the vectors $\vec{a}$ and $\vec{b}$ equal ?
Answer:
Given:
Two vectors are given as:
$\vec{a} = \hat{i} + 2\hat{j}$
$\vec{b} = 2\hat{i} + \hat{j}$
To Find:
1. Whether the magnitudes of the vectors are equal, i.e., if $|\vec{a}| = |\vec{b}|$.
2. Whether the vectors themselves are equal, i.e., if $\vec{a} = \vec{b}$.
Solution:
Calculating Magnitudes:
The magnitude of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ is given by $|\vec{v}| = \sqrt{x^2 + y^2 + z^2}$.
For vector $\vec{a} = \hat{i} + 2\hat{j} = 1\hat{i} + 2\hat{j} + 0\hat{k}$, the magnitude is:
$|\vec{a}| = \sqrt{(1)^2 + (2)^2 + (0)^2} = \sqrt{1 + 4 + 0} = \sqrt{5}$
For vector $\vec{b} = 2\hat{i} + \hat{j} = 2\hat{i} + 1\hat{j} + 0\hat{k}$, the magnitude is:
$|\vec{b}| = \sqrt{(2)^2 + (1)^2 + (0)^2} = \sqrt{4 + 1 + 0} = \sqrt{5}$
Comparing the magnitudes:
$|\vec{a}| = \sqrt{5}$ and $|\vec{b}| = \sqrt{5}$.
So, yes, $|\vec{a}| = |\vec{b}|$.
Checking Equality of Vectors:
Two vectors are equal if and only if their corresponding components are equal.
Vector $\vec{a} = 1\hat{i} + 2\hat{j}$
Vector $\vec{b} = 2\hat{i} + 1\hat{j}$
Comparing the coefficients of $\hat{i}$: The component of $\vec{a}$ is $1$ and the component of $\vec{b}$ is $2$. Since $1 \neq 2$, the $\hat{i}$ components are not equal.
Comparing the coefficients of $\hat{j}$: The component of $\vec{a}$ is $2$ and the component of $\vec{b}$ is $1$. Since $2 \neq 1$, the $\hat{j}$ components are not equal.
Since the corresponding components are not equal, the vectors are not equal.
So, no, the vectors $\vec{a}$ and $\vec{b}$ are not equal.
Conclusion:
The magnitudes of the vectors $\vec{a}$ and $\vec{b}$ are equal ($|\vec{a}| = |\vec{b}| = \sqrt{5}$), but the vectors themselves are not equal ($\vec{a} \neq \vec{b}$) because their corresponding components are different.
Example 6: Find init vector in the direction of vector $\vec{a} = 2\hat{i} + 3\hat{j} + \hat{k}$
Answer:
Given:
The vector $\vec{a} = 2\hat{i} + 3\hat{j} + \hat{k}$.
To Find:
The unit vector in the direction of $\vec{a}$.
Solution:
A unit vector in the direction of a given vector $\vec{a}$ is denoted by $\hat{a}$ and is calculated using the formula:
$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$
First, we need to find the magnitude of the vector $\vec{a}$. The magnitude of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ is given by $|\vec{v}| = \sqrt{x^2 + y^2 + z^2}$.
For $\vec{a} = 2\hat{i} + 3\hat{j} + 1\hat{k}$, the magnitude is:
$|\vec{a}| = \sqrt{(2)^2 + (3)^2 + (1)^2}$
$|\vec{a}| = \sqrt{4 + 9 + 1}$
$|\vec{a}| = \sqrt{14}$
Now, we can find the unit vector $\hat{a}$ by dividing the vector $\vec{a}$ by its magnitude $|\vec{a}| = \sqrt{14}$:
$\hat{a} = \frac{2\hat{i} + 3\hat{j} + \hat{k}}{\sqrt{14}}$
$\hat{a} = \frac{2}{\sqrt{14}}\hat{i} + \frac{3}{\sqrt{14}}\hat{j} + \frac{1}{\sqrt{14}}\hat{k}$
Therefore, the unit vector in the direction of $\vec{a}$ is:
$\hat{a} = \frac{2}{\sqrt{14}}\hat{i} + \frac{3}{\sqrt{14}}\hat{j} + \frac{1}{\sqrt{14}}\hat{k}$
Example 7: Find a vector in the direction of vector $\vec{a} = \hat{i} - 2\hat{j}$ that has magnitude 7 units.
Answer:
Given:
The vector $\vec{a} = \hat{i} - 2\hat{j}$.
The desired magnitude is 7 units.
To Find:
A vector $\vec{v}$ such that:
1. $\vec{v}$ is in the direction of $\vec{a}$.
2. The magnitude of $\vec{v}$ is $|\vec{v}| = 7$.
Solution:
To find a vector in the direction of $\vec{a}$ with a specific magnitude, we first find the unit vector in the direction of $\vec{a}$, and then multiply this unit vector by the desired magnitude.
The unit vector in the direction of $\vec{a}$ is given by $\hat{a} = \frac{\vec{a}}{|\vec{a}|}$.
First, calculate the magnitude of $\vec{a}$:
$\vec{a} = 1\hat{i} - 2\hat{j}$
$|\vec{a}| = \sqrt{(1)^2 + (-2)^2}$
$|\vec{a}| = \sqrt{1 + 4}$
$|\vec{a}| = \sqrt{5}$
Now, find the unit vector $\hat{a}$:
$\hat{a} = \frac{\vec{a}}{|\vec{a}|} = \frac{\hat{i} - 2\hat{j}}{\sqrt{5}}$
$\hat{a} = \frac{1}{\sqrt{5}}\hat{i} - \frac{2}{\sqrt{5}}\hat{j}$
This unit vector $\hat{a}$ has magnitude 1 and is in the direction of $\vec{a}$.
To get a vector $\vec{v}$ in the same direction but with magnitude 7, we multiply the unit vector $\hat{a}$ by 7:
$\vec{v} = 7 \times \hat{a}$
$\vec{v} = 7 \left( \frac{1}{\sqrt{5}}\hat{i} - \frac{2}{\sqrt{5}}\hat{j} \right)$
$\vec{v} = \frac{7}{\sqrt{5}}\hat{i} - \frac{14}{\sqrt{5}}\hat{j}$
Therefore, the required vector is:
$\vec{v} = \frac{7}{\sqrt{5}}\hat{i} - \frac{14}{\sqrt{5}}\hat{j}$
Example 8: Find the unit vector in the direction of the sum of the vectors, $\vec{a} = 2\hat{i} + 2\hat{j} - 5\hat{k}$ and $\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$ .
Answer:
Given:
The vectors are:
$\vec{a} = 2\hat{i} + 2\hat{j} - 5\hat{k}$
$\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$
To Find:
The unit vector in the direction of the sum of the vectors $\vec{a}$ and $\vec{b}$.
Solution:
First, find the sum of the two vectors. Let the sum be $\vec{c}$.
$\vec{c} = \vec{a} + \vec{b}$
$\vec{c} = (2\hat{i} + 2\hat{j} - 5\hat{k}) + (2\hat{i} + \hat{j} + 3\hat{k})$
Combine the corresponding components:
$\vec{c} = (2+2)\hat{i} + (2+1)\hat{j} + (-5+3)\hat{k}$
$\vec{c} = 4\hat{i} + 3\hat{j} - 2\hat{k}$
Now, we need to find the unit vector in the direction of $\vec{c}$. The unit vector $\hat{c}$ is given by the formula:
$\hat{c} = \frac{\vec{c}}{|\vec{c}|}$
Calculate the magnitude of $\vec{c}$:
$|\vec{c}| = \sqrt{(4)^2 + (3)^2 + (-2)^2}$
$|\vec{c}| = \sqrt{16 + 9 + 4}$
$|\vec{c}| = \sqrt{29}$
Now, find the unit vector $\hat{c}$ by dividing $\vec{c}$ by its magnitude $|\vec{c}| = \sqrt{29}$:
$\hat{c} = \frac{4\hat{i} + 3\hat{j} - 2\hat{k}}{\sqrt{29}}$
$\hat{c} = \frac{4}{\sqrt{29}}\hat{i} + \frac{3}{\sqrt{29}}\hat{j} - \frac{2}{\sqrt{29}}\hat{k}$
Therefore, the unit vector in the direction of the sum of $\vec{a}$ and $\vec{b}$ is:
$\hat{c} = \frac{4}{\sqrt{29}}\hat{i} + \frac{3}{\sqrt{29}}\hat{j} - \frac{2}{\sqrt{29}}\hat{k}$
Example 9: Write the direction ratio’s of the vector $\vec{a} = \hat{i} + \hat{j} - 2\hat{k}$ and hence calculate its direction cosines.
Answer:
Given:
The vector $\vec{a} = \hat{i} + \hat{j} - 2\hat{k}$.
To Find:
1. The direction ratios of the vector $\vec{a}$.
2. The direction cosines of the vector $\vec{a}$.
Solution:
Direction Ratios:
For a vector given in component form $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$, the scalar components $x, y, z$ are its direction ratios.
Given vector $\vec{a} = 1\hat{i} + 1\hat{j} - 2\hat{k}$.
Comparing this with $x\hat{i} + y\hat{j} + z\hat{k}$, we get:
$x = 1$
$y = 1$
$z = -2$
Therefore, the direction ratios of $\vec{a}$ are (1, 1, -2).
Direction Cosines:
The direction cosines ($l, m, n$) of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ are given by:
$l = \frac{x}{|\vec{v}|}$, $m = \frac{y}{|\vec{v}|}$, $n = \frac{z}{|\vec{v}|}$
where $|\vec{v}| = \sqrt{x^2 + y^2 + z^2}$ is the magnitude of the vector.
First, calculate the magnitude of $\vec{a}$:
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (-2)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 4}$
$|\vec{a}| = \sqrt{6}$
Now, calculate the direction cosines:
$l = \frac{x}{|\vec{a}|} = \frac{1}{\sqrt{6}}$
$m = \frac{y}{|\vec{a}|} = \frac{1}{\sqrt{6}}$
$n = \frac{z}{|\vec{a}|} = \frac{-2}{\sqrt{6}}$
Therefore, the direction cosines of $\vec{a}$ are $\left( \frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{-2}{\sqrt{6}} \right)$.
Summary:
The direction ratios are (1, 1, -2).
The direction cosines are $\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, \frac{-2}{\sqrt{6}}$.
Example 10: Find the vector joining the points P(2, 3, 0) and Q(– 1, – 2, – 4) directed from P to Q.
Answer:
Given:
The initial point P has coordinates (2, 3, 0).
The terminal point Q has coordinates (– 1, – 2, – 4).
To Find:
The vector $\vec{PQ}$ directed from P to Q.
Solution:
The position vector of point P is $\vec{OP} = 2\hat{i} + 3\hat{j} + 0\hat{k}$.
The position vector of point Q is $\vec{OQ} = -1\hat{i} - 2\hat{j} - 4\hat{k}$.
The vector joining points P and Q, directed from P to Q, is given by $\vec{PQ}$.
Using the triangle law of vector addition or the definition of the vector joining two points:
$\vec{PQ} = \vec{OQ} - \vec{OP}$
Alternatively, if P = $(x_1, y_1, z_1)$ and Q = $(x_2, y_2, z_2)$, then the vector $\vec{PQ}$ is given by:
$\vec{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$
Substituting the coordinates of P and Q:
$x_1 = 2, y_1 = 3, z_1 = 0$
$x_2 = -1, y_2 = -2, z_2 = -4$
$\vec{PQ} = (-1 - 2)\hat{i} + (-2 - 3)\hat{j} + (-4 - 0)\hat{k}$
$\vec{PQ} = -3\hat{i} - 5\hat{j} - 4\hat{k}$
Therefore, the vector joining the points P and Q directed from P to Q is:
$\vec{PQ} = -3\hat{i} - 5\hat{j} - 4\hat{k}$
Example 11: Consider two points P and Q with position vectors $\overline{OP} = 3\vec{a} - 2\vec{b}$ and $\overrightarrow{OQ} = \vec{a} + \vec{b}$ . Find the position vector of a point R which divides the line joining P and Q in the ratio 2:1,
(i) internally, and
(ii) externally
Answer:
Given:
Position vector of point P: $\vec{p} = \vec{OP} = 3\vec{a} - 2\vec{b}$
Position vector of point Q: $\vec{q} = \vec{OQ} = \vec{a} + \vec{b}$
Point R divides the line segment PQ in the ratio $m:n = 2:1$.
To Find:
The position vector $\vec{r}$ of point R when the division is:
(i) Internal
(ii) External
Solution:
(i) Internal Division:
The formula for the position vector $\vec{r}$ of a point R dividing the line segment joining P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) internally in the ratio $m:n$ is:
$\vec{r} = \frac{n\vec{p} + m\vec{q}}{m+n}$
Here, $m=2$, $n=1$, $\vec{p} = 3\vec{a} - 2\vec{b}$, and $\vec{q} = \vec{a} + \vec{b}$.
Substituting the values:
$\vec{r} = \frac{1(3\vec{a} - 2\vec{b}) + 2(\vec{a} + \vec{b})}{2+1}$
$\vec{r} = \frac{3\vec{a} - 2\vec{b} + 2\vec{a} + 2\vec{b}}{3}$
Combine like terms:
$\vec{r} = \frac{(3+2)\vec{a} + (-2+2)\vec{b}}{3}$
$\vec{r} = \frac{5\vec{a} + 0\vec{b}}{3}$
$\vec{r} = \frac{5}{3}\vec{a}$
So, the position vector of R for internal division is $\frac{5}{3}\vec{a}$.
(ii) External Division:
The formula for the position vector $\vec{r}$ of a point R dividing the line segment joining P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) externally in the ratio $m:n$ is:
$\vec{r} = \frac{m\vec{q} - n\vec{p}}{m-n}$
Here, $m=2$, $n=1$, $\vec{p} = 3\vec{a} - 2\vec{b}$, and $\vec{q} = \vec{a} + \vec{b}$.
Substituting the values:
$\vec{r} = \frac{2(\vec{a} + \vec{b}) - 1(3\vec{a} - 2\vec{b})}{2-1}$
$\vec{r} = \frac{2\vec{a} + 2\vec{b} - 3\vec{a} + 2\vec{b}}{1}$
Combine like terms:
$\vec{r} = (2-3)\vec{a} + (2+2)\vec{b}$
$\vec{r} = -\vec{a} + 4\vec{b}$
So, the position vector of R for external division is $-\vec{a} + 4\vec{b}$.
Example 12: Show that the points $A(2\hat{i} - \hat{j} + \hat{k})$ , $B(\hat{i} - 3\hat{j} − 5\hat{k})$, $C(3\hat{i} - 4\hat{j} - 4\hat{k})$ are the vertices of a right angled triangle.
Answer:
Given:
The position vectors of the vertices of a triangle are:
$\vec{OA} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{OB} = \hat{i} - 3\hat{j} - 5\hat{k}$
$\vec{OC} = 3\hat{i} - 4\hat{j} - 4\hat{k}$
To Prove:
The points A, B, and C form the vertices of a right-angled triangle.
Proof:
We first find the vectors representing the sides of the triangle ABC.
$\vec{AB} = \vec{OB} - \vec{OA}$
$\vec{AB} = (\hat{i} - 3\hat{j} - 5\hat{k}) - (2\hat{i} - \hat{j} + \hat{k})$
$\vec{AB} = (1-2)\hat{i} + (-3 - (-1))\hat{j} + (-5 - 1)\hat{k}$
$\vec{AB} = -\hat{i} - 2\hat{j} - 6\hat{k}$
$\vec{BC} = \vec{OC} - \vec{OB}$
$\vec{BC} = (3\hat{i} - 4\hat{j} - 4\hat{k}) - (\hat{i} - 3\hat{j} - 5\hat{k})$
$\vec{BC} = (3-1)\hat{i} + (-4 - (-3))\hat{j} + (-4 - (-5))\hat{k}$
$\vec{BC} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{CA} = \vec{OA} - \vec{OC}$
$\vec{CA} = (2\hat{i} - \hat{j} + \hat{k}) - (3\hat{i} - 4\hat{j} - 4\hat{k})$
$\vec{CA} = (2-3)\hat{i} + (-1 - (-4))\hat{j} + (1 - (-4))\hat{k}$
$\vec{CA} = -\hat{i} + 3\hat{j} + 5\hat{k}$
Method 1: Using Magnitudes and Pythagoras Theorem
We calculate the square of the magnitudes (lengths) of the sides:
$|\vec{AB}|^2 = (-1)^2 + (-2)^2 + (-6)^2 = 1 + 4 + 36 = 41$
$|\vec{BC}|^2 = (2)^2 + (-1)^2 + (1)^2 = 4 + 1 + 1 = 6$
$|\vec{CA}|^2 = (-1)^2 + (3)^2 + (5)^2 = 1 + 9 + 25 = 35$
Now, we check if the Pythagorean theorem holds. We see that:
$|\vec{BC}|^2 + |\vec{CA}|^2 = 6 + 35 = 41$
And we also found that $|\vec{AB}|^2 = 41$.
Since $|\vec{BC}|^2 + |\vec{CA}|^2 = |\vec{AB}|^2$, the triangle satisfies the Pythagorean theorem.
The side AB is the hypotenuse, and the right angle is at vertex C.
Method 2: Using Dot Product
A triangle is right-angled if two of its sides are perpendicular. Two vectors are perpendicular if their dot product is zero.
Let's check the dot product of the vectors representing the sides meeting at vertex C, which are $\vec{CA}$ and $\vec{CB}$.
Note that $\vec{CB} = -\vec{BC} = -(2\hat{i} - \hat{j} + \hat{k}) = -2\hat{i} + \hat{j} - \hat{k}$.
$\vec{CA} \cdot \vec{CB} = (-\hat{i} + 3\hat{j} + 5\hat{k}) \cdot (-2\hat{i} + \hat{j} - \hat{k})$
$\vec{CA} \cdot \vec{CB} = (-1)(-2) + (3)(1) + (5)(-1)$
$\vec{CA} \cdot \vec{CB} = 2 + 3 - 5 = 0$
Since the dot product $\vec{CA} \cdot \vec{CB} = 0$, the vectors $\vec{CA}$ and $\vec{CB}$ are perpendicular. This means the angle at vertex C is $90^\circ$.
Conclusion:
Both methods show that the triangle formed by points A, B, and C has a right angle at C (or that the square of the length of one side equals the sum of the squares of the lengths of the other two sides).
Therefore, the points A, B, C are the vertices of a right-angled triangle.
Exercise 10.2
Question 1. Compute the magnitude of the following vectors:
$\vec{a} = \hat{i} + \hat{j} + \hat{k}$ ; $\vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k}$ ; $\vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k}$
Answer:
The magnitude of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ is given by the formula:
$|\vec{v}| = \sqrt{x^2 + y^2 + z^2}$
For vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$:
Here, $x=1$, $y=1$, $z=1$.
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (1)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 1}$
$|\vec{a}| = \sqrt{3}$
The magnitude of $\vec{a}$ is $\sqrt{3}$.
For vector $\vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k}$:
Here, $x=2$, $y=-7$, $z=-3$.
$|\vec{b}| = \sqrt{(2)^2 + (-7)^2 + (-3)^2}$
$|\vec{b}| = \sqrt{4 + 49 + 9}$
$|\vec{b}| = \sqrt{62}$
The magnitude of $\vec{b}$ is $\sqrt{62}$.
For vector $\vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k}$:
Here, $x=\frac{1}{\sqrt{3}}$, $y=\frac{1}{\sqrt{3}}$, $z=-\frac{1}{\sqrt{3}}$.
$|\vec{c}| = \sqrt{\left(\frac{1}{\sqrt{3}}\right)^2 + \left(\frac{1}{\sqrt{3}}\right)^2 + \left(-\frac{1}{\sqrt{3}}\right)^2}$
$|\vec{c}| = \sqrt{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}}$
$|\vec{c}| = \sqrt{\frac{1+1+1}{3}}$
$|\vec{c}| = \sqrt{\frac{3}{3}}$
$|\vec{c}| = \sqrt{1}$
$|\vec{c}| = 1$
The magnitude of $\vec{c}$ is 1. (Note: $\vec{c}$ is a unit vector).
Question 2. Write two different vectors having same magnitude.
Answer:
We need to find two vectors, say $\vec{p}$ and $\vec{q}$, such that $\vec{p} \neq \vec{q}$ but $|\vec{p}| = |\vec{q}|$.
Let's choose a vector $\vec{a}$. We can easily find its magnitude. Then we can construct another vector $\vec{b}$ by rearranging the components or changing their signs, which will often result in a different vector with the same magnitude.
Consider the vector:
$\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$
Its magnitude is:
$|\vec{a}| = \sqrt{(1)^2 + (2)^2 + (3)^2}$
$|\vec{a}| = \sqrt{1 + 4 + 9}$
$|\vec{a}| = \sqrt{14}$
Now consider a different vector $\vec{b}$ by rearranging the components of $\vec{a}$:
$\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$
This vector $\vec{b}$ is different from $\vec{a}$ because their corresponding components are not all equal (the $\hat{i}$ and $\hat{j}$ components are swapped).
Let's calculate the magnitude of $\vec{b}$:
$|\vec{b}| = \sqrt{(2)^2 + (1)^2 + (3)^2}$
$|\vec{b}| = \sqrt{4 + 1 + 9}$
$|\vec{b}| = \sqrt{14}$
We have found two vectors, $\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$ and $\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$.
Clearly, $\vec{a} \neq \vec{b}$.
However, $|\vec{a}| = \sqrt{14}$ and $|\vec{b}| = \sqrt{14}$.
Thus, they have the same magnitude.
Therefore, two different vectors having the same magnitude are:
$\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$ and $\vec{b} = 2\hat{i} + \hat{j} + 3\hat{k}$.
(Note: Many other pairs exist, e.g., $\hat{i}$ and $\hat{j}$, or $3\hat{i} + 4\hat{j}$ and $4\hat{i} + 3\hat{j}$)
Question 3. Write two different vectors having same direction.
Answer:
Two vectors $\vec{a}$ and $\vec{b}$ are said to have the same direction if they are positive scalar multiples of each other. This means $\vec{b} = \lambda \vec{a}$ for some scalar $\lambda > 0$.
To find two different vectors with the same direction, we need to choose a vector $\vec{a}$ and a positive scalar $\lambda$ such that $\lambda \neq 1$. Then the vector $\vec{b} = \lambda \vec{a}$ will be different from $\vec{a}$ but will have the same direction.
Let's choose a simple vector:
$\vec{a} = \hat{i} + \hat{j} + \hat{k}$
Now, let's choose a positive scalar $\lambda = 3$ ($\lambda > 0$ and $\lambda \neq 1$).
Calculate the second vector $\vec{b}$:
$\vec{b} = \lambda \vec{a} = 3 (\hat{i} + \hat{j} + \hat{k})$
$\vec{b} = 3\hat{i} + 3\hat{j} + 3\hat{k}$
The two vectors are:
$\vec{a} = \hat{i} + \hat{j} + \hat{k}$
$\vec{b} = 3\hat{i} + 3\hat{j} + 3\hat{k}$
These vectors are different ($\vec{a} \neq \vec{b}$).
They have the same direction because $\vec{b}$ is a positive scalar multiple of $\vec{a}$ ($\vec{b} = 3\vec{a}$ and $3 > 0$).
Therefore, two different vectors having the same direction are $\hat{i} + \hat{j} + \hat{k}$ and $3\hat{i} + 3\hat{j} + 3\hat{k}$.
(Note: Any vector and any positive scalar multiple (other than 1) of it would work. For example, $\vec{p} = 2\hat{i} - \hat{j}$ and $\vec{q} = 4\hat{i} - 2\hat{j}$ is another valid pair as $\vec{q} = 2\vec{p}$.)
Question 4. Find the values of x and y so that the vectors $2\hat{i} + 3\hat{j}$ and $x\hat{i} + y\hat{j}$ are equal.
Answer:
Given:
Two vectors are given:
Vector 1: $2\hat{i} + 3\hat{j}$
Vector 2: $x\hat{i} + y\hat{j}$
The condition is that the two vectors are equal.
To Find:
The values of $x$ and $y$.
Solution:
Two vectors are considered equal if and only if their corresponding components are identical.
We are given the condition:
$2\hat{i} + 3\hat{j} = x\hat{i} + y\hat{j}$
For this equality to hold, the coefficient of the $\hat{i}$ component on the left side must be equal to the coefficient of the $\hat{i}$ component on the right side. Similarly, the coefficients of the $\hat{j}$ components must be equal.
Equating the coefficients of the $\hat{i}$ components:
$2 = x$
Equating the coefficients of the $\hat{j}$ components:
$3 = y$
Therefore, the values of $x$ and $y$ that make the vectors equal are:
$x = 2$
$y = 3$
Question 5. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
Answer:
Given:
Initial Point P = (2, 1)
Terminal Point Q = (– 5, 7)
To Find:
1. The scalar components of the vector joining P to Q.
2. The vector components of the vector joining P to Q.
Solution:
Let the vector joining the initial point P$(x_1, y_1)$ to the terminal point Q$(x_2, y_2)$ be $\vec{PQ}$.
The formula for the vector $\vec{PQ}$ is:
$\vec{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j}$
Substituting the given coordinates:
$x_1 = 2$, $y_1 = 1$
$x_2 = -5$, $y_2 = 7$
$\vec{PQ} = (-5 - 2)\hat{i} + (7 - 1)\hat{j}$
$\vec{PQ} = -7\hat{i} + 6\hat{j}$
The scalar components are the coefficients of $\hat{i}$ and $\hat{j}$.
Scalar component along the x-axis = -7
Scalar component along the y-axis = 6
The vector components are the terms $-7\hat{i}$ and $6\hat{j}$.
Vector component along the x-axis = $-7\hat{i}$
Vector component along the y-axis = $6\hat{j}$
Results:
The scalar components are -7 and 6.
The vector components are $-7\hat{i}$ and $6\hat{j}$.
Question 6. Find the sum of the vectors $\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$ , $\vec{b} = -2\hat{i} + 4\hat{j} + 5\hat{k}$ and $\vec{c} = \hat{i} - 6\hat{j} - 7\hat{k}$.
Answer:
Given:
The vectors are:
$\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$
$\vec{b} = -2\hat{i} + 4\hat{j} + 5\hat{k}$
$\vec{c} = \hat{i} - 6\hat{j} - 7\hat{k}$
To Find:
The sum of the vectors $\vec{a} + \vec{b} + \vec{c}$.
Solution:
To find the sum of the vectors, we add their corresponding components (the coefficients of $\hat{i}$, $\hat{j}$, and $\hat{k}$).
Let the sum vector be $\vec{s}$.
$\vec{s} = \vec{a} + \vec{b} + \vec{c}$
$\vec{s} = (\hat{i} - 2\hat{j} + \hat{k}) + (-2\hat{i} + 4\hat{j} + 5\hat{k}) + (\hat{i} - 6\hat{j} - 7\hat{k})$
Group the components together:
$\vec{s} = (1 - 2 + 1)\hat{i} + (-2 + 4 - 6)\hat{j} + (1 + 5 - 7)\hat{k}$
Calculate the sum for each component:
For $\hat{i}$: $1 - 2 + 1 = 0$
For $\hat{j}$: $-2 + 4 - 6 = 2 - 6 = -4$
For $\hat{k}$: $1 + 5 - 7 = 6 - 7 = -1$
Combine the results to get the sum vector:
$\vec{s} = 0\hat{i} - 4\hat{j} - 1\hat{k}$
$\vec{s} = -4\hat{j} - \hat{k}$
Therefore, the sum of the given vectors is:
$\vec{s} = -4\hat{j} - \hat{k}$
Question 7. Find the unit vector in the direction of the vector $\vec{a} = \hat{i} + \hat{j} + 2\hat{k}$.
Answer:
Given:
The vector $\vec{a} = \hat{i} + \hat{j} + 2\hat{k}$.
To Find:
The unit vector in the direction of $\vec{a}$.
Solution:
A unit vector in the direction of a given vector $\vec{a}$ is denoted by $\hat{a}$ and is calculated using the formula:
$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$
First, we need to find the magnitude of the vector $\vec{a}$. The magnitude of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ is given by $|\vec{v}| = \sqrt{x^2 + y^2 + z^2}$.
For $\vec{a} = 1\hat{i} + 1\hat{j} + 2\hat{k}$, the magnitude is:
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (2)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 4}$
$|\vec{a}| = \sqrt{6}$
Now, we can find the unit vector $\hat{a}$ by dividing the vector $\vec{a}$ by its magnitude $|\vec{a}| = \sqrt{6}$:
$\hat{a} = \frac{\hat{i} + \hat{j} + 2\hat{k}}{\sqrt{6}}$
$\hat{a} = \frac{1}{\sqrt{6}}\hat{i} + \frac{1}{\sqrt{6}}\hat{j} + \frac{2}{\sqrt{6}}\hat{k}$
Therefore, the unit vector in the direction of $\vec{a}$ is:
$\hat{a} = \frac{1}{\sqrt{6}}\hat{i} + \frac{1}{\sqrt{6}}\hat{j} + \frac{2}{\sqrt{6}}\hat{k}$
Question 8. Find the unit vector in the direction of vector $\overrightarrow{PQ}$, where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
Answer:
Given:
The initial point P = (1, 2, 3).
The terminal point Q = (4, 5, 6).
To Find:
The unit vector in the direction of the vector $\overrightarrow{PQ}$.
Solution:
First, we need to find the vector $\overrightarrow{PQ}$. The vector joining point P$(x_1, y_1, z_1)$ to point Q$(x_2, y_2, z_2)$ is given by:
$\overrightarrow{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$
Substituting the coordinates of P and Q:
$\overrightarrow{PQ} = (4 - 1)\hat{i} + (5 - 2)\hat{j} + (6 - 3)\hat{k}$
$\overrightarrow{PQ} = 3\hat{i} + 3\hat{j} + 3\hat{k}$
Next, we find the magnitude of the vector $\overrightarrow{PQ}$. The magnitude $|\overrightarrow{PQ}|$ is calculated as:
$|\overrightarrow{PQ}| = \sqrt{(3)^2 + (3)^2 + (3)^2}$
$|\overrightarrow{PQ}| = \sqrt{9 + 9 + 9}$
$|\overrightarrow{PQ}| = \sqrt{27}$
$|\overrightarrow{PQ}| = \sqrt{9 \times 3} = 3\sqrt{3}$
The unit vector in the direction of $\overrightarrow{PQ}$ is given by the formula:
$\hat{u} = \frac{\overrightarrow{PQ}}{|\overrightarrow{PQ}|}$
Substituting the vector $\overrightarrow{PQ}$ and its magnitude:
$\hat{u} = \frac{3\hat{i} + 3\hat{j} + 3\hat{k}}{3\sqrt{3}}$
Divide each component by the magnitude:
$\hat{u} = \frac{3}{3\sqrt{3}}\hat{i} + \frac{3}{3\sqrt{3}}\hat{j} + \frac{3}{3\sqrt{3}}\hat{k}$
Simplify the coefficients:
$\hat{u} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k}$
Therefore, the unit vector in the direction of $\overrightarrow{PQ}$ is:
$\hat{u} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k}$
Question 9. For given vectors, $\vec{a} = 2\hat{i} - \hat{j} + 2\hat{k}$ and $\vec{b} = -\hat{i} + \hat{j} - \hat{k}$, find the unit vector in the direction of the vector $\vec{a} + \vec{b}$.
Answer:
Given:
The vectors are:
$\vec{a} = 2\hat{i} - \hat{j} + 2\hat{k}$
$\vec{b} = -\hat{i} + \hat{j} - \hat{k}$
To Find:
The unit vector in the direction of the sum vector $\vec{a} + \vec{b}$.
Solution:
First, find the sum of the two vectors. Let the sum be $\vec{s}$.
$\vec{s} = \vec{a} + \vec{b}$
$\vec{s} = (2\hat{i} - \hat{j} + 2\hat{k}) + (-\hat{i} + \hat{j} - \hat{k})$
Combine the corresponding components:
$\vec{s} = (2 - 1)\hat{i} + (-1 + 1)\hat{j} + (2 - 1)\hat{k}$
$\vec{s} = 1\hat{i} + 0\hat{j} + 1\hat{k}$
$\vec{s} = \hat{i} + \hat{k}$
Now, we need to find the unit vector in the direction of $\vec{s}$. The unit vector $\hat{s}$ is given by the formula:
$\hat{s} = \frac{\vec{s}}{|\vec{s}|}$
Calculate the magnitude of $\vec{s}$:
$|\vec{s}| = \sqrt{(1)^2 + (0)^2 + (1)^2}$
$|\vec{s}| = \sqrt{1 + 0 + 1}$
$|\vec{s}| = \sqrt{2}$
Now, find the unit vector $\hat{s}$ by dividing $\vec{s}$ by its magnitude $|\vec{s}| = \sqrt{2}$:
$\hat{s} = \frac{\hat{i} + \hat{k}}{\sqrt{2}}$
$\hat{s} = \frac{1}{\sqrt{2}}\hat{i} + \frac{0}{\sqrt{2}}\hat{j} + \frac{1}{\sqrt{2}}\hat{k}$
$\hat{s} = \frac{1}{\sqrt{2}}\hat{i} + \frac{1}{\sqrt{2}}\hat{k}$
Therefore, the unit vector in the direction of $\vec{a} + \vec{b}$ is:
$\hat{s} = \frac{1}{\sqrt{2}}\hat{i} + \frac{1}{\sqrt{2}}\hat{k}$
Question 10. Find a vector in the direction of vector $5\hat{i} - \hat{j} + 2\hat{k}$, which has magnitude 8 units.
Answer:
Given:
The vector $\vec{a} = 5\hat{i} - \hat{j} + 2\hat{k}$.
The desired magnitude is 8 units.
To Find:
A vector $\vec{v}$ such that:
1. $\vec{v}$ is in the direction of $\vec{a}$.
2. The magnitude of $\vec{v}$ is $|\vec{v}| = 8$.
Solution:
To find a vector in the direction of $\vec{a}$ with a specific magnitude, we first find the unit vector in the direction of $\vec{a}$, and then multiply this unit vector by the desired magnitude.
The unit vector in the direction of $\vec{a}$ is given by $\hat{a} = \frac{\vec{a}}{|\vec{a}|}$.
First, calculate the magnitude of $\vec{a}$:
$|\vec{a}| = \sqrt{(5)^2 + (-1)^2 + (2)^2}$
$|\vec{a}| = \sqrt{25 + 1 + 4}$
$|\vec{a}| = \sqrt{30}$
Now, find the unit vector $\hat{a}$:
$\hat{a} = \frac{\vec{a}}{|\vec{a}|} = \frac{5\hat{i} - \hat{j} + 2\hat{k}}{\sqrt{30}}$
$\hat{a} = \frac{5}{\sqrt{30}}\hat{i} - \frac{1}{\sqrt{30}}\hat{j} + \frac{2}{\sqrt{30}}\hat{k}$
This unit vector $\hat{a}$ has magnitude 1 and is in the direction of $\vec{a}$.
To get a vector $\vec{v}$ in the same direction but with magnitude 8, we multiply the unit vector $\hat{a}$ by 8:
$\vec{v} = 8 \times \hat{a}$
$\vec{v} = 8 \left( \frac{5}{\sqrt{30}}\hat{i} - \frac{1}{\sqrt{30}}\hat{j} + \frac{2}{\sqrt{30}}\hat{k} \right)$
$\vec{v} = \frac{8 \times 5}{\sqrt{30}}\hat{i} - \frac{8 \times 1}{\sqrt{30}}\hat{j} + \frac{8 \times 2}{\sqrt{30}}\hat{k}$
$\vec{v} = \frac{40}{\sqrt{30}}\hat{i} - \frac{8}{\sqrt{30}}\hat{j} + \frac{16}{\sqrt{30}}\hat{k}$
Therefore, the required vector is:
$\vec{v} = \frac{40}{\sqrt{30}}\hat{i} - \frac{8}{\sqrt{30}}\hat{j} + \frac{16}{\sqrt{30}}\hat{k}$
Alternatively, we can rationalize the denominator:
$\vec{v} = \frac{40\sqrt{30}}{30}\hat{i} - \frac{8\sqrt{30}}{30}\hat{j} + \frac{16\sqrt{30}}{30}\hat{k}$
$\vec{v} = \frac{4\sqrt{30}}{3}\hat{i} - \frac{4\sqrt{30}}{15}\hat{j} + \frac{8\sqrt{30}}{15}\hat{k}$
Question 11. Show that the vectors $2\hat{i} - 3\hat{j} + 4\hat{k}$ and $-4\hat{i} + 6\hat{j} - 8\hat{k}$ are collinear.
Answer:
Given:
Let the two vectors be:
$\vec{a} = 2\hat{i} - 3\hat{j} + 4\hat{k}$
$\vec{b} = -4\hat{i} + 6\hat{j} - 8\hat{k}$
To Show:
The vectors $\vec{a}$ and $\vec{b}$ are collinear.
Proof:
Two vectors are said to be collinear if one vector can be expressed as a scalar multiple of the other. That is, $\vec{a}$ and $\vec{b}$ are collinear if there exists a scalar $\lambda$ such that $\vec{b} = \lambda \vec{a}$ or $\vec{a} = \lambda \vec{b}$.
Let's examine the relationship between $\vec{a}$ and $\vec{b}$. We can try to factor out a common scalar from the components of $\vec{b}$.
$\vec{b} = -4\hat{i} + 6\hat{j} - 8\hat{k}$
Notice that each component of $\vec{b}$ is -2 times the corresponding component of $\vec{a}$:
$-4 = (-2) \times 2$
$6 = (-2) \times (-3)$
$-8 = (-2) \times 4$
Therefore, we can factor out -2 from $\vec{b}$:
$\vec{b} = -2(2\hat{i}) -2(-3\hat{j}) -2(4\hat{k})$
$\vec{b} = -2(2\hat{i} - 3\hat{j} + 4\hat{k})$
Substituting $\vec{a} = 2\hat{i} - 3\hat{j} + 4\hat{k}$, we get:
$\vec{b} = -2\vec{a}$
Since $\vec{b}$ is a scalar multiple of $\vec{a}$ (with the scalar $\lambda = -2$), the vectors $\vec{a}$ and $\vec{b}$ are parallel to the same line, but in opposite directions.
Conclusion:
Because $\vec{b} = -2\vec{a}$, the vector $\vec{b}$ is a scalar multiple of $\vec{a}$.
Therefore, the vectors $2\hat{i} - 3\hat{j} + 4\hat{k}$ and $-4\hat{i} + 6\hat{j} - 8\hat{k}$ are collinear.
Question 12. Find the direction cosines of the vector $\hat{i} + 2\hat{j} + 3\hat{k}$.
Answer:
Given:
The vector $\vec{v} = \hat{i} + 2\hat{j} + 3\hat{k}$.
To Find:
The direction cosines of the vector $\vec{v}$.
Solution:
Let the given vector be $\vec{v} = 1\hat{i} + 2\hat{j} + 3\hat{k}$.
The direction cosines ($l, m, n$) of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ are given by the formulae:
$l = \frac{x}{|\vec{v}|}$
$m = \frac{y}{|\vec{v}|}$
$n = \frac{z}{|\vec{v}|}$
where $|\vec{v}| = \sqrt{x^2 + y^2 + z^2}$ is the magnitude of the vector.
First, we need to calculate the magnitude of $\vec{v}$:
$|\vec{v}| = \sqrt{(1)^2 + (2)^2 + (3)^2}$
$|\vec{v}| = \sqrt{1 + 4 + 9}$
$|\vec{v}| = \sqrt{14}$
Now, we can find the direction cosines using the components $x=1$, $y=2$, $z=3$ and the magnitude $|\vec{v}| = \sqrt{14}$:
$l = \frac{x}{|\vec{v}|} = \frac{1}{\sqrt{14}}$
$m = \frac{y}{|\vec{v}|} = \frac{2}{\sqrt{14}}$
$n = \frac{z}{|\vec{v}|} = \frac{3}{\sqrt{14}}$
Therefore, the direction cosines of the vector $\hat{i} + 2\hat{j} + 3\hat{k}$ are:
$\left( \frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}} \right)$
Question 13. Find the direction cosines of the vector joining the points A (1, 2, –3) and B(–1, –2, 1), directed from A to B.
Answer:
Given:
The initial point A = (1, 2, –3).
The terminal point B = (–1, –2, 1).
To Find:
The direction cosines of the vector $\overrightarrow{AB}$.
Solution:
First, we find the vector $\overrightarrow{AB}$ joining point A to point B.
Let the position vector of A be $\vec{OA} = 1\hat{i} + 2\hat{j} - 3\hat{k}$.
Let the position vector of B be $\vec{OB} = -1\hat{i} - 2\hat{j} + 1\hat{k}$.
The vector $\overrightarrow{AB}$ is given by:
$\overrightarrow{AB} = \vec{OB} - \vec{OA}$
$\overrightarrow{AB} = (-1\hat{i} - 2\hat{j} + 1\hat{k}) - (1\hat{i} + 2\hat{j} - 3\hat{k})$
$\overrightarrow{AB} = (-1 - 1)\hat{i} + (-2 - 2)\hat{j} + (1 - (-3))\hat{k}$
$\overrightarrow{AB} = -2\hat{i} - 4\hat{j} + (1 + 3)\hat{k}$
$\overrightarrow{AB} = -2\hat{i} - 4\hat{j} + 4\hat{k}$
Next, we find the magnitude of the vector $\overrightarrow{AB}$.
$|\overrightarrow{AB}| = \sqrt{(-2)^2 + (-4)^2 + (4)^2}$
$|\overrightarrow{AB}| = \sqrt{4 + 16 + 16}$
$|\overrightarrow{AB}| = \sqrt{36}$
$|\overrightarrow{AB}| = 6$
The direction cosines ($l, m, n$) of a vector $\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}$ are given by $l = \frac{x}{|\vec{v}|}$, $m = \frac{y}{|\vec{v}|}$, $n = \frac{z}{|\vec{v}|}$.
For $\overrightarrow{AB} = -2\hat{i} - 4\hat{j} + 4\hat{k}$, the components are $x = -2$, $y = -4$, $z = 4$, and the magnitude is $|\overrightarrow{AB}| = 6$.
The direction cosines are:
$l = \frac{-2}{6} = -\frac{1}{3}$
$m = \frac{-4}{6} = -\frac{2}{3}$
$n = \frac{4}{6} = \frac{2}{3}$
Therefore, the direction cosines of the vector $\overrightarrow{AB}$ are:
$\left( -\frac{1}{3}, -\frac{2}{3}, \frac{2}{3} \right)$
Question 14. Show that the vector $\hat{i} + \hat{j} + \hat{k}$ is equally inclined to the axes OX, OY and OZ.
Answer:
Given:
The vector $\vec{v} = \hat{i} + \hat{j} + \hat{k}$.
To Show:
The vector $\vec{v}$ is equally inclined to the axes OX, OY, and OZ.
Proof:
A vector is equally inclined to the coordinate axes OX, OY, and OZ if the angles it makes with the positive directions of these axes are equal.
Let $\alpha$, $\beta$, and $\gamma$ be the angles that the vector $\vec{v}$ makes with the positive OX, OY, and OZ axes, respectively.
The direction cosines of the vector $\vec{v}$ are given by $l = \cos \alpha$, $m = \cos \beta$, and $n = \cos \gamma$.
To show that the vector is equally inclined, we need to show that $\alpha = \beta = \gamma$, which is equivalent to showing that the direction cosines $l$, $m$, and $n$ are equal.
The vector is $\vec{v} = 1\hat{i} + 1\hat{j} + 1\hat{k}$.
First, calculate the magnitude of the vector $\vec{v}$:
$|\vec{v}| = \sqrt{(1)^2 + (1)^2 + (1)^2}$
$|\vec{v}| = \sqrt{1 + 1 + 1}$
$|\vec{v}| = \sqrt{3}$
Now, calculate the direction cosines:
$l = \frac{x}{|\vec{v}|} = \frac{1}{\sqrt{3}}$
$m = \frac{y}{|\vec{v}|} = \frac{1}{\sqrt{3}}$
$n = \frac{z}{|\vec{v}|} = \frac{1}{\sqrt{3}}$
Since $l = m = n = \frac{1}{\sqrt{3}}$, we have:
$\cos \alpha = \frac{1}{\sqrt{3}}$
$\cos \beta = \frac{1}{\sqrt{3}}$
$\cos \gamma = \frac{1}{\sqrt{3}}$
As the direction cosines are equal, the angles $\alpha$, $\beta$, and $\gamma$ must also be equal (since these angles are between $0^\circ$ and $180^\circ$).
$\alpha = \beta = \gamma = \cos^{-1}\left(\frac{1}{\sqrt{3}}\right)$
Conclusion:
Since the direction cosines of the vector $\hat{i} + \hat{j} + \hat{k}$ are equal, the vector is equally inclined to the axes OX, OY, and OZ.
Question 15. Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $\hat{i} + 2\hat{j} - \hat{k}$ and $-\hat{i} + \hat{j} + \hat{k}$ respectively, in the ratio 2 : 1.
(i) internally
(ii) externally
Answer:
Given:
Position vector of point P: $\vec{p} = \hat{i} + 2\hat{j} - \hat{k}$
Position vector of point Q: $\vec{q} = -\hat{i} + \hat{j} + \hat{k}$
Point R divides the line segment PQ in the ratio $m:n = 2:1$.
To Find:
The position vector $\vec{r}$ of point R when the division is:
(i) Internal
(ii) External
Solution:
(i) Internal Division:
The formula for the position vector $\vec{r}$ of a point R dividing the line segment joining P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) internally in the ratio $m:n$ is:
$\vec{r} = \frac{n\vec{p} + m\vec{q}}{m+n}$
Here, $m=2$, $n=1$, $\vec{p} = \hat{i} + 2\hat{j} - \hat{k}$, and $\vec{q} = -\hat{i} + \hat{j} + \hat{k}$.
Substituting the values:
$\vec{r} = \frac{1(\hat{i} + 2\hat{j} - \hat{k}) + 2(-\hat{i} + \hat{j} + \hat{k})}{2+1}$
$\vec{r} = \frac{(\hat{i} + 2\hat{j} - \hat{k}) + (-2\hat{i} + 2\hat{j} + 2\hat{k})}{3}$
Combine the corresponding components:
$\vec{r} = \frac{(1-2)\hat{i} + (2+2)\hat{j} + (-1+2)\hat{k}}{3}$
$\vec{r} = \frac{-1\hat{i} + 4\hat{j} + 1\hat{k}}{3}$
$\vec{r} = -\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k}$
So, the position vector of R for internal division is $-\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k}$.
(ii) External Division:
The formula for the position vector $\vec{r}$ of a point R dividing the line segment joining P (with position vector $\vec{p}$) and Q (with position vector $\vec{q}$) externally in the ratio $m:n$ is:
$\vec{r} = \frac{m\vec{q} - n\vec{p}}{m-n}$
Here, $m=2$, $n=1$, $\vec{p} = \hat{i} + 2\hat{j} - \hat{k}$, and $\vec{q} = -\hat{i} + \hat{j} + \hat{k}$.
Substituting the values:
$\vec{r} = \frac{2(-\hat{i} + \hat{j} + \hat{k}) - 1(\hat{i} + 2\hat{j} - \hat{k})}{2-1}$
$\vec{r} = \frac{(-2\hat{i} + 2\hat{j} + 2\hat{k}) - (\hat{i} + 2\hat{j} - \hat{k})}{1}$
$\vec{r} = (-2\hat{i} + 2\hat{j} + 2\hat{k}) - \hat{i} - 2\hat{j} + \hat{k}$
Combine the corresponding components:
$\vec{r} = (-2-1)\hat{i} + (2-2)\hat{j} + (2+1)\hat{k}$
$\vec{r} = -3\hat{i} + 0\hat{j} + 3\hat{k}$
$\vec{r} = -3\hat{i} + 3\hat{k}$
So, the position vector of R for external division is $-3\hat{i} + 3\hat{k}$.
Question 16. Find the position vector of the mid point of the vector joining the points P(2, 3, 4) and Q(4, 1, –2).
Answer:
Given:
The coordinates of the initial point P are (2, 3, 4).
The coordinates of the terminal point Q are (4, 1, –2).
To Find:
The position vector of the midpoint R of the line segment PQ.
Solution:
Let the position vector of point P be $\vec{p}$ and the position vector of point Q be $\vec{q}$.
From the coordinates, we have:
$\vec{p} = \vec{OP} = 2\hat{i} + 3\hat{j} + 4\hat{k}$
$\vec{q} = \vec{OQ} = 4\hat{i} + 1\hat{j} - 2\hat{k}$
Let R be the midpoint of the line segment PQ. The position vector of the midpoint R, denoted by $\vec{r}$, is given by the midpoint formula:
$\vec{r} = \frac{\vec{p} + \vec{q}}{2}$
Substitute the position vectors $\vec{p}$ and $\vec{q}$ into the formula:
$\vec{r} = \frac{(2\hat{i} + 3\hat{j} + 4\hat{k}) + (4\hat{i} + 1\hat{j} - 2\hat{k})}{2}$
Add the corresponding components of the vectors in the numerator:
$\vec{r} = \frac{(2+4)\hat{i} + (3+1)\hat{j} + (4-2)\hat{k}}{2}$
$\vec{r} = \frac{6\hat{i} + 4\hat{j} + 2\hat{k}}{2}$
Divide each component by 2:
$\vec{r} = \frac{6}{2}\hat{i} + \frac{4}{2}\hat{j} + \frac{2}{2}\hat{k}$
$\vec{r} = 3\hat{i} + 2\hat{j} + 1\hat{k}$
$\vec{r} = 3\hat{i} + 2\hat{j} + \hat{k}$
Therefore, the position vector of the midpoint R is:
$\vec{r} = 3\hat{i} + 2\hat{j} + \hat{k}$
Question 17. Show that the points A, B and C with position vectors, $\vec{a} = 3\hat{i} - 4\hat{j} - 4\hat{k}$, $\vec{b} = 2\hat{i} - \hat{j} + \hat{k}$ and $\vec{c} = \hat{i} - 3\hat{j} - 5\hat{k}$, respectively form the vertices of a right angled triangle.
Answer:
Given:
The position vectors of the vertices of a triangle A, B, and C are:
$\vec{OA} = \vec{a} = 3\hat{i} - 4\hat{j} - 4\hat{k}$
$\vec{OB} = \vec{b} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{OC} = \vec{c} = \hat{i} - 3\hat{j} - 5\hat{k}$
To Prove:
The points A, B, and C form the vertices of a right-angled triangle.
Proof:
We first find the vectors representing the sides of the triangle ABC.
$\vec{AB} = \vec{OB} - \vec{OA} = \vec{b} - \vec{a}$
$\vec{AB} = (2\hat{i} - \hat{j} + \hat{k}) - (3\hat{i} - 4\hat{j} - 4\hat{k})$
$\vec{AB} = (2-3)\hat{i} + (-1 - (-4))\hat{j} + (1 - (-4))\hat{k}$
$\vec{AB} = -\hat{i} + 3\hat{j} + 5\hat{k}$
$\vec{BC} = \vec{OC} - \vec{OB} = \vec{c} - \vec{b}$
$\vec{BC} = (\hat{i} - 3\hat{j} - 5\hat{k}) - (2\hat{i} - \hat{j} + \hat{k})$
$\vec{BC} = (1-2)\hat{i} + (-3 - (-1))\hat{j} + (-5 - 1)\hat{k}$
$\vec{BC} = -\hat{i} - 2\hat{j} - 6\hat{k}$
$\vec{CA} = \vec{OA} - \vec{OC} = \vec{a} - \vec{c}$
$\vec{CA} = (3\hat{i} - 4\hat{j} - 4\hat{k}) - (\hat{i} - 3\hat{j} - 5\hat{k})$
$\vec{CA} = (3-1)\hat{i} + (-4 - (-3))\hat{j} + (-4 - (-5))\hat{k}$
$\vec{CA} = 2\hat{i} - \hat{j} + \hat{k}$
Method 1: Using Magnitudes and Pythagoras Theorem
We calculate the square of the magnitudes (lengths) of the sides:
$|\vec{AB}|^2 = (-1)^2 + (3)^2 + (5)^2 = 1 + 9 + 25 = 35$
$|\vec{BC}|^2 = (-1)^2 + (-2)^2 + (-6)^2 = 1 + 4 + 36 = 41$
$|\vec{CA}|^2 = (2)^2 + (-1)^2 + (1)^2 = 4 + 1 + 1 = 6$
Now, we check if the Pythagorean theorem holds. We see that:
$|\vec{AB}|^2 + |\vec{CA}|^2 = 35 + 6 = 41$
And we also found that $|\vec{BC}|^2 = 41$.
Since $|\vec{AB}|^2 + |\vec{CA}|^2 = |\vec{BC}|^2$, the triangle satisfies the Pythagorean theorem.
The side BC is the hypotenuse, and the right angle is at vertex A.
Method 2: Using Dot Product
A triangle is right-angled if two of its sides meeting at a vertex are perpendicular. Two vectors are perpendicular if their dot product is zero.
Let's check the dot product of the vectors representing the sides meeting at vertex A, which are $\vec{AB}$ and $\vec{AC}$. Note that $\vec{AC} = -\vec{CA} = -(2\hat{i} - \hat{j} + \hat{k}) = -2\hat{i} + \hat{j} - \hat{k}$. Alternatively, we can use the vectors $\vec{AB}$ and $\vec{CA}$ as calculated.
Let's calculate $\vec{AB} \cdot \vec{CA}$:
$\vec{AB} \cdot \vec{CA} = (-\hat{i} + 3\hat{j} + 5\hat{k}) \cdot (2\hat{i} - \hat{j} + \hat{k})$
$\vec{AB} \cdot \vec{CA} = (-1)(2) + (3)(-1) + (5)(1)$
$\vec{AB} \cdot \vec{CA} = -2 - 3 + 5 = 0$
Since the dot product $\vec{AB} \cdot \vec{CA} = 0$, the vectors $\vec{AB}$ and $\vec{CA}$ are perpendicular. This means the angle at vertex A ($\angle BAC$) is $90^\circ$.
Conclusion:
Both methods show that the triangle formed by points A, B, and C has a right angle at A (or that the square of the length of side BC equals the sum of the squares of the lengths of sides AB and CA).
Therefore, the points A, B, C are the vertices of a right-angled triangle.
Question 18. In triangle ABC (Fig 10.18), which of the following is not true:
(A) $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \vec{0}$
(B) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}$
(C) $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}$
(D) $\overrightarrow{AB} - \overrightarrow{CB} + \overrightarrow{CA} = \vec{0}$
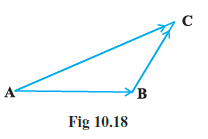
Answer:
We need to analyze each option based on the triangle law of vector addition.
The triangle law states that if two vectors are represented by two sides of a triangle taken in order, then their sum is represented by the third side taken in the opposite order. For triangle ABC, this means:
$\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$
Analysis of Option (A): $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \vec{0}$
Using the triangle law, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.
Substitute this into the equation: $\overrightarrow{AC} + \overrightarrow{CA} = \vec{0}$.
We know that $\overrightarrow{CA}$ is the negative vector of $\overrightarrow{AC}$, i.e., $\overrightarrow{CA} = -\overrightarrow{AC}$.
So, the equation becomes $\overrightarrow{AC} - \overrightarrow{AC} = \vec{0}$, which simplifies to $\vec{0} = \vec{0}$.
This statement represents the sum of vectors forming a closed loop, which is always the zero vector. Thus, option (A) is True.
Analysis of Option (B): $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}$
From the triangle law, we have $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.
Rearranging this equation by subtracting $\overrightarrow{AC}$ from both sides gives:
$\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}$.
Thus, option (B) is True.
Analysis of Option (C): $\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \vec{0}$
From the triangle law, $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$.
Substitute this into the equation: $\overrightarrow{AC} - \overrightarrow{CA} = \vec{0}$.
Since $\overrightarrow{CA} = -\overrightarrow{AC}$, the equation becomes $\overrightarrow{AC} - (-\overrightarrow{AC}) = \vec{0}$.
$\overrightarrow{AC} + \overrightarrow{AC} = \vec{0}$
$2\overrightarrow{AC} = \vec{0}$
This implies $\overrightarrow{AC} = \vec{0}$, which means point A and point C coincide. This is not generally true for a triangle.
Thus, option (C) is Not True.
Analysis of Option (D): $\overrightarrow{AB} - \overrightarrow{CB} + \overrightarrow{CA} = \vec{0}$
We know that $-\overrightarrow{CB} = \overrightarrow{BC}$.
Substitute this into the equation: $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \vec{0}$.
This is the same statement as option (A), which we already found to be true.
Thus, option (D) is True.
The only statement that is not true is (C).
Final Answer: The final answer is $\boxed{(C)}$
Question 19. If $\vec{a}$ and $\vec{b}$ are two collinear vectors, then which of the following are incorrect:
(A) $\vec{b} = λ \vec{a}$, for some scalar λ
(B) $\vec{a} = ± \vec{b}$
(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional
(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.
Answer:
Definition of Collinear Vectors:
Two vectors $\vec{a}$ and $\vec{b}$ are collinear if they are parallel to the same line. Mathematically, this means that one vector is a scalar multiple of the other. Assuming $\vec{a} \neq \vec{0}$, then $\vec{b}$ is collinear with $\vec{a}$ if there exists a scalar $\lambda$ such that $\vec{b} = \lambda \vec{a}$.
Let $\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$ and $\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$. If $\vec{b} = \lambda \vec{a}$, then $b_1 = \lambda a_1$, $b_2 = \lambda a_2$, and $b_3 = \lambda a_3$. This implies that the respective components are proportional: $\frac{b_1}{a_1} = \frac{b_2}{a_2} = \frac{b_3}{a_3} = \lambda$ (assuming non-zero components for $\vec{a}$).
The scalar $\lambda$ determines the relationship between the directions and magnitudes:
- If $\lambda > 0$, $\vec{a}$ and $\vec{b}$ have the same direction.
- If $\lambda < 0$, $\vec{a}$ and $\vec{b}$ have opposite directions.
- If $|\lambda| = 1$ (i.e., $\lambda = 1$ or $\lambda = -1$), then $|\vec{a}| = |\vec{b}|$.
- If $|\lambda| \neq 1$, then $|\vec{a}| \neq |\vec{b}|$.
Analysis of the Options:
(A) $\vec{b} = \lambda \vec{a}$, for some scalar λ
This is the definition of collinear vectors (assuming $\vec{a} \neq \vec{0}$). This statement is Correct.
(B) $\vec{a} = \pm \vec{b}$
This statement implies $\vec{b} = \pm \vec{a}$, which means $\lambda = 1$ or $\lambda = -1$. This is only true if the collinear vectors also have the same magnitude ($|\vec{a}| = |\vec{b}|$). However, collinear vectors do not necessarily have the same magnitude (e.g., $\vec{a}=\hat{i}$ and $\vec{b}=2\hat{i}$). Therefore, this statement is not always true for any pair of collinear vectors. Hence, it is an Incorrect general statement about collinear vectors.
(C) the respective components of $\vec{a}$ and $\vec{b}$ are not proportional
As shown from the definition ($\vec{b} = \lambda \vec{a}$ implies $b_i = \lambda a_i$), the components of collinear vectors *must* be proportional. This statement claims they are not proportional, which directly contradicts the property of collinear vectors. Therefore, this statement is Incorrect.
(D) both the vectors $\vec{a}$ and $\vec{b}$ have same direction, but different magnitudes.
This statement implies that for collinear vectors, it must be true that $\lambda > 0$ (same direction) and $|\lambda| \neq 1$ (different magnitudes). This is not always true. Collinear vectors can have opposite directions (if $\lambda < 0$) or the same magnitude (if $|\lambda| = 1$). For example, $\vec{a} = \hat{i}$ and $\vec{b} = -\hat{i}$ are collinear but have opposite directions and the same magnitude. $\vec{a} = \hat{i}$ and $\vec{b} = 2\hat{i}$ have the same direction and different magnitudes. $\vec{a} = \hat{i}$ and $\vec{b} = -2\hat{i}$ have opposite directions and different magnitudes. Since this statement does not cover all possibilities for collinear vectors, it is an Incorrect general statement about collinear vectors.
Conclusion:
Statements (B), (C), and (D) are all incorrect statements when applied generally to any pair of collinear vectors.
Statement (C) is incorrect because components of collinear vectors are always proportional.
Statement (B) is incorrect because collinear vectors are not always equal or negatives of each other (magnitudes might differ).
Statement (D) is incorrect because collinear vectors might have opposite directions or the same magnitude.
Typically, multiple-choice questions ask for *the* incorrect statement. Statement (C) is a direct contradiction to a fundamental property derived from the definition. Statements (B) and (D) describe specific sub-cases of collinearity as if they were general properties.
Considering the options, the statement that the components are not proportional (C) is fundamentally false for collinear vectors. The components must be proportional.
Final Answer: The final answer is $\boxed{(C)}$ (Assuming the question asks for the single most fundamentally incorrect statement, although B and D are also incorrect generalisations).
Note: In some contexts, a question might ask to identify all incorrect statements. In that case, B, C, and D would be selected. However, standard MCQs usually have one best answer.
Example 13 to 21 (Before Exercise 10.3)
Example 13: Find the angle between two vectors $\vec{a}$ and $\vec{b}$ with magnitudes 1 and 2 respectively and when $\vec{a} \;.\; \vec{b} = 1$.
Answer:
Given:
Magnitude of vector $\vec{a}$: $|\vec{a}| = 1$
Magnitude of vector $\vec{b}$: $|\vec{b}| = 2$
Dot product of $\vec{a}$ and $\vec{b}$: $\vec{a} \cdot \vec{b} = 1$
To Find:
The angle $\theta$ between the vectors $\vec{a}$ and $\vec{b}$.
Solution:
The definition of the scalar (dot) product of two vectors $\vec{a}$ and $\vec{b}$ is given by:
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
where $\theta$ is the angle between the vectors $\vec{a}$ and $\vec{b}$ ($0 \le \theta \le \pi$).
We can rearrange this formula to find $\cos \theta$:
$\cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$
Substitute the given values into the formula:
$\cos \theta = \frac{1}{(1)(2)}$
$\cos \theta = \frac{1}{2}$
We need to find the angle $\theta$ in the range $[0, \pi]$ such that its cosine is $\frac{1}{2}$.
We know that $\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}$.
Therefore, the angle $\theta$ between the vectors $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{3}$ radians or $60^\circ$.
The angle between the vectors $\vec{a}$ and $\vec{b}$ is $\theta = \frac{\pi}{3}$ or $60^\circ$.
Example 14: Find angle ‘θ’ between the vectors $\vec{a} = \hat{i} + \hat{j} - \hat{k}$ and $\vec{b} = \hat{i} - \hat{j} + \hat{k}$.
Answer:
Given:
The vectors are:
$\vec{a} = \hat{i} + \hat{j} - \hat{k}$
$\vec{b} = \hat{i} - \hat{j} + \hat{k}$
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The angle $\theta$ between two vectors $\vec{a}$ and $\vec{b}$ is given by the formula involving the dot product:
$\cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$
First, calculate the dot product $\vec{a} \cdot \vec{b}$:
$\vec{a} \cdot \vec{b} = (1)(\hat{i} + \hat{j} - \hat{k}) \cdot (\hat{i} - \hat{j} + \hat{k})$
$\vec{a} \cdot \vec{b} = (1)(1) + (1)(-1) + (-1)(1)$
$\vec{a} \cdot \vec{b} = 1 - 1 - 1$
$\vec{a} \cdot \vec{b} = -1$
Next, calculate the magnitudes of $\vec{a}$ and $\vec{b}$:
$|\vec{a}| = \sqrt{(1)^2 + (1)^2 + (-1)^2}$
$|\vec{a}| = \sqrt{1 + 1 + 1} = \sqrt{3}$
$|\vec{b}| = \sqrt{(1)^2 + (-1)^2 + (1)^2}$
$|\vec{b}| = \sqrt{1 + 1 + 1} = \sqrt{3}$
Now, substitute these values into the formula for $\cos \theta$:
$\cos \theta = \frac{-1}{(\sqrt{3})(\sqrt{3})}$
$\cos \theta = \frac{-1}{3}$
Finally, the angle $\theta$ is:
$\theta = \cos^{-1}\left(-\frac{1}{3}\right)$
Therefore, the angle between the vectors $\vec{a}$ and $\vec{b}$ is $\theta = \cos^{-1}\left(-\frac{1}{3}\right)$.
Example 15: If $\vec{a} = 5\hat{i} - \hat{j} - 3\hat{k}$, then $\vec{b} = \hat{i} + 3\hat{j} - 5\hat{k}$, then show that the vectors $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$ are prependicular.
Answer:
Given:
The vectors are:
$\vec{a} = 5\hat{i} - \hat{j} - 3\hat{k}$
$\vec{b} = \hat{i} + 3\hat{j} - 5\hat{k}$
To Show:
The vectors $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$ are perpendicular.
Proof:
Two vectors are perpendicular if their scalar (dot) product is equal to zero.
First, let's find the vector sum $\vec{a} + \vec{b}$:
$\vec{a} + \vec{b} = (5\hat{i} - \hat{j} - 3\hat{k}) + (\hat{i} + 3\hat{j} - 5\hat{k})$
$\vec{a} + \vec{b} = (5+1)\hat{i} + (-1+3)\hat{j} + (-3-5)\hat{k}$
$\vec{a} + \vec{b} = 6\hat{i} + 2\hat{j} - 8\hat{k}$
Next, let's find the vector difference $\vec{a} - \vec{b}$:
$\vec{a} - \vec{b} = (5\hat{i} - \hat{j} - 3\hat{k}) - (\hat{i} + 3\hat{j} - 5\hat{k})$
$\vec{a} - \vec{b} = (5-1)\hat{i} + (-1-3)\hat{j} + (-3 - (-5))\hat{k}$
$\vec{a} - \vec{b} = 4\hat{i} - 4\hat{j} + (-3 + 5)\hat{k}$
$\vec{a} - \vec{b} = 4\hat{i} - 4\hat{j} + 2\hat{k}$
Now, calculate the dot product of $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$:
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = (6\hat{i} + 2\hat{j} - 8\hat{k}) \cdot (4\hat{i} - 4\hat{j} + 2\hat{k})$
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = (6)(4) + (2)(-4) + (-8)(2)$
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = 24 - 8 - 16$
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = 24 - 24$
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = 0$
Conclusion:
Since the dot product of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$ is zero, the two vectors are perpendicular.
Example 16: Find the projection of the vector $\vec{a} = 2\hat{i} + 3\hat{j} + 2\hat{k}$ on the vector $\vec{b} = \hat{i} + 2\hat{j} + \hat{k}$.
Answer:
Given:
Vector $\vec{a} = 2\hat{i} + 3\hat{j} + 2\hat{k}$
Vector $\vec{b} = \hat{i} + 2\hat{j} + \hat{k}$
To Find:
The scalar projection of vector $\vec{a}$ onto vector $\vec{b}$.
Solution:
The scalar projection of vector $\vec{a}$ onto vector $\vec{b}$ is given by the formula:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$
First, calculate the dot product $\vec{a} \cdot \vec{b}$:
$\vec{a} \cdot \vec{b} = (2\hat{i} + 3\hat{j} + 2\hat{k}) \cdot (\hat{i} + 2\hat{j} + \hat{k})$
$\vec{a} \cdot \vec{b} = (2)(1) + (3)(2) + (2)(1)$
$\vec{a} \cdot \vec{b} = 2 + 6 + 2$
$\vec{a} \cdot \vec{b} = 10$
Next, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = \sqrt{(1)^2 + (2)^2 + (1)^2}$
$|\vec{b}| = \sqrt{1 + 4 + 1}$
$|\vec{b}| = \sqrt{6}$
Now, substitute the dot product and the magnitude into the projection formula:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{10}{\sqrt{6}}$
To rationalize the denominator, multiply the numerator and denominator by $\sqrt{6}$:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{10}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}} = \frac{10\sqrt{6}}{6}$
Simplify the fraction:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{\cancel{10}^5 \sqrt{6}}{\cancel{6}_3} = \frac{5\sqrt{6}}{3}$
Therefore, the projection of vector $\vec{a}$ on vector $\vec{b}$ is:
$\frac{10}{\sqrt{6}}$ or $\frac{5\sqrt{6}}{3}$
Example 17: Find $|\;\vec{a} - \vec{b}\;|$, if two vectors $\vec{a}$ and $\vec{b}$ are such that $|\;\vec{a}\;| = 2$, $|\;\vec{b}\;| = 3$ and $\vec{a} \;.\; \vec{b} = 4$.
Answer:
Given:
Magnitude of vector $\vec{a}$: $|\vec{a}| = 2$
Magnitude of vector $\vec{b}$: $|\vec{b}| = 3$
Dot product of $\vec{a}$ and $\vec{b}$: $\vec{a} \cdot \vec{b} = 4$
To Find:
The magnitude of the difference between the vectors, $|\vec{a} - \vec{b}|$.
Solution:
We know that for any vector $\vec{v}$, its magnitude squared is given by the dot product of the vector with itself, i.e., $|\vec{v}|^2 = \vec{v} \cdot \vec{v}$.
Applying this to the vector $\vec{a} - \vec{b}$:
$|\vec{a} - \vec{b}|^2 = (\vec{a} - \vec{b}) \cdot (\vec{a} - \vec{b})$
Expand the dot product using the distributive property:
$|\vec{a} - \vec{b}|^2 = \vec{a} \cdot (\vec{a} - \vec{b}) - \vec{b} \cdot (\vec{a} - \vec{b})$
$|\vec{a} - \vec{b}|^2 = \vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} - \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b}$
Since the dot product is commutative ($\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$), and using $\vec{v} \cdot \vec{v} = |\vec{v}|^2$, we can write:
$|\vec{a} - \vec{b}|^2 = |\vec{a}|^2 - 2(\vec{a} \cdot \vec{b}) + |\vec{b}|^2$
Now, substitute the given values $|\vec{a}| = 2$, $|\vec{b}| = 3$, and $\vec{a} \cdot \vec{b} = 4$ into the equation:
$|\vec{a} - \vec{b}|^2 = (2)^2 - 2(4) + (3)^2$
$|\vec{a} - \vec{b}|^2 = 4 - 8 + 9$
$|\vec{a} - \vec{b}|^2 = -4 + 9$
$|\vec{a} - \vec{b}|^2 = 5$
To find the magnitude $|\vec{a} - \vec{b}|$, we take the square root of both sides. Since magnitude must be non-negative:
$|\vec{a} - \vec{b}| = \sqrt{5}$
Therefore, the magnitude of the vector difference is:
$|\vec{a} - \vec{b}| = \sqrt{5}$
Example 18: If $\vec{a}$ is a unit vector and $(\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 8$, then find $|\;\vec{x}\;|$.
Answer:
Given:
$\vec{a}$ is a unit vector. This implies $|\vec{a}| = 1$.
The equation $(\vec{x} - \vec{a}) \cdot (\vec{x} + \vec{a}) = 8$.
To Find:
The magnitude of vector $\vec{x}$, denoted as $|\vec{x}|$.
Solution:
We are given the equation:
$(\vec{x} - \vec{a}) \cdot (\vec{x} + \vec{a}) = 8$
We can expand the dot product using the distributive property:
$(\vec{x} - \vec{a}) \cdot (\vec{x} + \vec{a}) = \vec{x} \cdot (\vec{x} + \vec{a}) - \vec{a} \cdot (\vec{x} + \vec{a})$
$= \vec{x} \cdot \vec{x} + \vec{x} \cdot \vec{a} - \vec{a} \cdot \vec{x} - \vec{a} \cdot \vec{a}$
Using the property $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and the commutative property of the dot product ($\vec{x} \cdot \vec{a} = \vec{a} \cdot \vec{x}$):
$= |\vec{x}|^2 + \vec{x} \cdot \vec{a} - \vec{x} \cdot \vec{a} - |\vec{a}|^2$
$= |\vec{x}|^2 - |\vec{a}|^2$
So, the given equation becomes:
$|\vec{x}|^2 - |\vec{a}|^2 = 8$
We are given that $\vec{a}$ is a unit vector, so $|\vec{a}| = 1$. Substituting this value:
$|\vec{x}|^2 - (1)^2 = 8$
$|\vec{x}|^2 - 1 = 8$
Add 1 to both sides:
$|\vec{x}|^2 = 8 + 1$
$|\vec{x}|^2 = 9$
Taking the square root of both sides, and noting that magnitude must be non-negative:
$|\vec{x}| = \sqrt{9}$
$|\vec{x}| = 3$
Therefore, the magnitude of vector $\vec{x}$ is:
$|\vec{x}| = 3$
Example 19: For any two vectors $\vec{a}$ and $\vec{b}$, we always have $|\;\vec{a}\;.\; \vec{b}\;| ≤ |\;\vec{a}\;|\; |\;\vec{b}\;|$ (Cauchy-Schwartz inequality).
Answer:
To Prove:
For any two vectors $\vec{a}$ and $\vec{b}$, the inequality $|\vec{a} \cdot \vec{b}| \le |\vec{a}| |\vec{b}|$ holds.
Proof:
Case 1: If either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$ (or both).
If $\vec{a} = \vec{0}$, then $|\vec{a}| = 0$ and $\vec{a} \cdot \vec{b} = \vec{0} \cdot \vec{b} = 0$.
The inequality becomes $|\,0\,| \le 0 \times |\vec{b}|$, which simplifies to $0 \le 0$. This is true.
Similarly, if $\vec{b} = \vec{0}$, then $|\vec{b}| = 0$ and $\vec{a} \cdot \vec{b} = \vec{a} \cdot \vec{0} = 0$.
The inequality becomes $|\,0\,| \le |\vec{a}| \times 0$, which simplifies to $0 \le 0$. This is also true.
So, the inequality holds if either vector is the zero vector.
Case 2: If both $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$.
In this case, $|\vec{a}| > 0$ and $|\vec{b}| > 0$.
Let $\theta$ be the angle between the vectors $\vec{a}$ and $\vec{b}$. By the definition of the scalar (dot) product:
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
Taking the absolute value of both sides:
$|\vec{a} \cdot \vec{b}| = |\,|\vec{a}| |\vec{b}| \cos \theta \,|$
Since $|\vec{a}|$ and $|\vec{b}|$ are non-negative magnitudes, we can write:
$|\vec{a} \cdot \vec{b}| = |\vec{a}| |\vec{b}| |\cos \theta|$
We know that for any angle $\theta$, the value of $\cos \theta$ lies between -1 and 1, i.e., $-1 \le \cos \theta \le 1$.
This implies that the absolute value of $\cos \theta$ is always less than or equal to 1:
$|\cos \theta| \le 1$
Now, multiply both sides of this inequality by the non-negative quantity $|\vec{a}| |\vec{b}|$:
$|\vec{a}| |\vec{b}| |\cos \theta| \le |\vec{a}| |\vec{b}| \times 1$
Substitute $|\vec{a} \cdot \vec{b}|$ for $|\vec{a}| |\vec{b}| |\cos \theta|$:
$|\vec{a} \cdot \vec{b}| \le |\vec{a}| |\vec{b}|$
This proves the Cauchy-Schwarz inequality for the non-trivial case.
Conclusion:
Combining both cases, we have shown that for any two vectors $\vec{a}$ and $\vec{b}$, the inequality $|\vec{a} \cdot \vec{b}| \le |\vec{a}| |\vec{b}|$ always holds.
The equality $|\vec{a} \cdot \vec{b}| = |\vec{a}| |\vec{b}|$ holds if and only if $|\cos \theta| = 1$, which means $\theta = 0$ or $\theta = \pi$. This occurs if and only if the vectors $\vec{a}$ and $\vec{b}$ are collinear, or if one (or both) of the vectors is the zero vector.
Example 20: For any two vectors $\vec{a}$ and $\vec{b}$, we always have $|\;\vec{a} + \vec{b}\;| ≤ |\;\vec{a}\;| + |\;\vec{b}\;|$ (triangle inequality).
Answer:
To Prove:
For any two vectors $\vec{a}$ and $\vec{b}$, the inequality $|\vec{a} + \vec{b}| \le |\vec{a}| + |\vec{b}|$ holds.
Proof:
We start by considering the square of the magnitude of the sum $\vec{a} + \vec{b}$:
$|\vec{a} + \vec{b}|^2 = (\vec{a} + \vec{b}) \cdot (\vec{a} + \vec{b})$
Using the distributive property of the dot product:
$|\vec{a} + \vec{b}|^2 = \vec{a} \cdot (\vec{a} + \vec{b}) + \vec{b} \cdot (\vec{a} + \vec{b})$
$|\vec{a} + \vec{b}|^2 = \vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b}$
Using the properties $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and the commutative property $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$:
$|\vec{a} + \vec{b}|^2 = |\vec{a}|^2 + 2(\vec{a} \cdot \vec{b}) + |\vec{b}|^2$
From the definition of the dot product, $\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$, where $\theta$ is the angle between $\vec{a}$ and $\vec{b}$.
Since $\cos \theta \le 1$, we have $\vec{a} \cdot \vec{b} \le |\vec{a}| |\vec{b}|$.
Alternatively, we know that for any real number $x$, $x \le |x|$. So, $\vec{a} \cdot \vec{b} \le |\vec{a} \cdot \vec{b}|$.
By the Cauchy-Schwarz inequality (proven in Example 19), we have $|\vec{a} \cdot \vec{b}| \le |\vec{a}| |\vec{b}|$.
Combining these, we get $\vec{a} \cdot \vec{b} \le |\vec{a} \cdot \vec{b}| \le |\vec{a}| |\vec{b}|$.
Therefore, $\vec{a} \cdot \vec{b} \le |\vec{a}| |\vec{b}|$.
Substituting this inequality back into the expression for $|\vec{a} + \vec{b}|^2$:
$|\vec{a} + \vec{b}|^2 = |\vec{a}|^2 + 2(\vec{a} \cdot \vec{b}) + |\vec{b}|^2 \le |\vec{a}|^2 + 2|\vec{a}| |\vec{b}| + |\vec{b}|^2$
The right side of the inequality is the expansion of $(|\vec{a}| + |\vec{b}|)^2$.
$|\vec{a} + \vec{b}|^2 \le (|\vec{a}| + |\vec{b}|)^2$
Since magnitudes are always non-negative ($|\vec{a} + \vec{b}| \ge 0$ and $|\vec{a}| + |\vec{b}| \ge 0$), we can take the non-negative square root of both sides without changing the direction of the inequality:
$\sqrt{|\vec{a} + \vec{b}|^2} \le \sqrt{(|\vec{a}| + |\vec{b}|)^2}$
$|\vec{a} + \vec{b}| \le |\vec{a}| + |\vec{b}|$
Conclusion:
We have shown that for any two vectors $\vec{a}$ and $\vec{b}$, the triangle inequality $|\vec{a} + \vec{b}| \le |\vec{a}| + |\vec{b}|$ always holds.
The equality $|\vec{a} + \vec{b}| = |\vec{a}| + |\vec{b}|$ holds if and only if $\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}|$, which means $\cos \theta = 1$, so $\theta = 0$. This occurs if and only if the vectors $\vec{a}$ and $\vec{b}$ are collinear and have the same direction, or if one (or both) of the vectors is the zero vector.
Example 21: Show that the points $A(-2\hat{i} + 3\hat{j} + 5\hat{k})$ , $B(\hat{i} + 2\hat{j} + 3\hat{k})$ and $C(7\hat{i} − \hat{k})$ are collinear.
Answer:
Given:
The position vectors of the points A, B, and C are:
$\vec{OA} = -2\hat{i} + 3\hat{j} + 5\hat{k}$
$\vec{OB} = \hat{i} + 2\hat{j} + 3\hat{k}$
$\vec{OC} = 7\hat{i} + 0\hat{j} - \hat{k}$
To Show:
The points A, B, and C are collinear.
Proof:
Points A, B, and C are collinear if the vectors formed by joining these points in pairs are collinear (parallel).
Let's find the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$.
Calculating $\overrightarrow{AB}$:
$\overrightarrow{AB} = \vec{OB} - \vec{OA}$
$\overrightarrow{AB} = (\hat{i} + 2\hat{j} + 3\hat{k}) - (-2\hat{i} + 3\hat{j} + 5\hat{k})$
$\overrightarrow{AB} = (1 - (-2))\hat{i} + (2 - 3)\hat{j} + (3 - 5)\hat{k}$
$\overrightarrow{AB} = (1 + 2)\hat{i} - 1\hat{j} - 2\hat{k}$
$\overrightarrow{AB} = 3\hat{i} - \hat{j} - 2\hat{k}$
Calculating $\overrightarrow{BC}$:
$\overrightarrow{BC} = \vec{OC} - \vec{OB}$
$\overrightarrow{BC} = (7\hat{i} + 0\hat{j} - \hat{k}) - (\hat{i} + 2\hat{j} + 3\hat{k})$
$\overrightarrow{BC} = (7 - 1)\hat{i} + (0 - 2)\hat{j} + (-1 - 3)\hat{k}$
$\overrightarrow{BC} = 6\hat{i} - 2\hat{j} - 4\hat{k}$
Now, we check if $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are collinear. Two vectors are collinear if one is a scalar multiple of the other.
Let's see if $\overrightarrow{BC} = \lambda \overrightarrow{AB}$ for some scalar $\lambda$.
$6\hat{i} - 2\hat{j} - 4\hat{k} = \lambda (3\hat{i} - \hat{j} - 2\hat{k})$
Comparing the coefficients of $\hat{i}$, $\hat{j}$, and $\hat{k}$:
For $\hat{i}$: $6 = \lambda \times 3 \implies \lambda = 2$
For $\hat{j}$: $-2 = \lambda \times (-1) \implies \lambda = 2$
For $\hat{k}$: $-4 = \lambda \times (-2) \implies \lambda = 2$
Since the value of $\lambda$ is the same (λ = 2) for all components, we have:
$\overrightarrow{BC} = 2 \overrightarrow{AB}$
This shows that the vector $\overrightarrow{BC}$ is a scalar multiple of the vector $\overrightarrow{AB}$, meaning $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are parallel (collinear).
Since $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are collinear and share the common point B, the points A, B, and C must lie on the same straight line.
Conclusion:
The points A, B, and C are collinear.
Exercise 10.3
Question 1. Find the angle between two vectors $\vec{a}$ and $\vec{b}$ with magnitudes $\sqrt{3}$ and 2. Respectively having $\vec{a}\;.\;\vec{b} = \sqrt{6}$.
Answer:
Given:
Magnitude of vector $\vec{a}$: $|\vec{a}| = \sqrt{3}$
Magnitude of vector $\vec{b}$: $|\vec{b}| = 2$
Dot product of $\vec{a}$ and $\vec{b}$: $\vec{a} \cdot \vec{b} = \sqrt{6}$
To Find:
The angle $\theta$ between the vectors $\vec{a}$ and $\vec{b}$.
Solution:
The definition of the scalar (dot) product of two vectors $\vec{a}$ and $\vec{b}$ is given by:
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
where $\theta$ is the angle between the vectors $\vec{a}$ and $\vec{b}$ ($0 \le \theta \le \pi$).
We can rearrange this formula to solve for $\cos \theta$:
$\cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$
Substitute the given values into the formula:
$\cos \theta = \frac{\sqrt{6}}{(\sqrt{3})(2)}$
Simplify the expression. Note that $\sqrt{6} = \sqrt{3 \times 2} = \sqrt{3} \sqrt{2}$.
$\cos \theta = \frac{\sqrt{3} \sqrt{2}}{2\sqrt{3}}$
Cancel the $\sqrt{3}$ term from the numerator and denominator:
$\cos \theta = \frac{\cancel{\sqrt{3}} \sqrt{2}}{2\cancel{\sqrt{3}}} = \frac{\sqrt{2}}{2}$
We need to find the angle $\theta$ in the range $[0, \pi]$ such that its cosine is $\frac{\sqrt{2}}{2}$.
We know that $\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}$.
Therefore, the angle $\theta$ between the vectors $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$ radians or $45^\circ$.
The angle between the vectors $\vec{a}$ and $\vec{b}$ is $\theta = \frac{\pi}{4}$ or $45^\circ$.
Question 2. Find the angle between the vectors $\hat{i} - 2\hat{j} + 3\hat{k}$ and $3\hat{i} - 2\hat{j} + \hat{k}$
Answer:
Given:
Let the two vectors be:
$\vec{a} = \hat{i} - 2\hat{j} + 3\hat{k}$
$\vec{b} = 3\hat{i} - 2\hat{j} + \hat{k}$
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
The angle $\theta$ between two vectors $\vec{a}$ and $\vec{b}$ is given by the formula involving the dot product:
$\cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$
First, calculate the dot product $\vec{a} \cdot \vec{b}$:
$\vec{a} \cdot \vec{b} = (\hat{i} - 2\hat{j} + 3\hat{k}) \cdot (3\hat{i} - 2\hat{j} + \hat{k})$
$\vec{a} \cdot \vec{b} = (1)(3) + (-2)(-2) + (3)(1)$
$\vec{a} \cdot \vec{b} = 3 + 4 + 3$
$\vec{a} \cdot \vec{b} = 10$
Next, calculate the magnitudes of $\vec{a}$ and $\vec{b}$:
$|\vec{a}| = \sqrt{(1)^2 + (-2)^2 + (3)^2}$
$|\vec{a}| = \sqrt{1 + 4 + 9} = \sqrt{14}$
$|\vec{b}| = \sqrt{(3)^2 + (-2)^2 + (1)^2}$
$|\vec{b}| = \sqrt{9 + 4 + 1} = \sqrt{14}$
Now, substitute these values into the formula for $\cos \theta$:
$\cos \theta = \frac{10}{(\sqrt{14})(\sqrt{14})}$
$\cos \theta = \frac{10}{14}$
$\cos \theta = \frac{5}{7}$
Finally, the angle $\theta$ is the inverse cosine of $\frac{5}{7}$:
$\theta = \cos^{-1}\left(\frac{5}{7}\right)$
Therefore, the angle between the given vectors is $\theta = \cos^{-1}\left(\frac{5}{7}\right)$.
Question 3. Find the projection of the vector $\hat{i} - \hat{j}$ on the vector $\hat{i} + \hat{j}$.
Answer:
Given:
Let the vector to be projected be $\vec{a} = \hat{i} - \hat{j}$.
Let the vector onto which the projection is made be $\vec{b} = \hat{i} + \hat{j}$.
To Find:
The scalar projection of vector $\vec{a}$ onto vector $\vec{b}$.
Solution:
The scalar projection of vector $\vec{a}$ onto vector $\vec{b}$ is given by the formula:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$
First, calculate the dot product $\vec{a} \cdot \vec{b}$:
$\vec{a} = 1\hat{i} - 1\hat{j} + 0\hat{k}$
$\vec{b} = 1\hat{i} + 1\hat{j} + 0\hat{k}$
$\vec{a} \cdot \vec{b} = (1)(1) + (-1)(1) + (0)(0)$
$\vec{a} \cdot \vec{b} = 1 - 1 + 0$
$\vec{a} \cdot \vec{b} = 0$
Next, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = \sqrt{(1)^2 + (1)^2 + (0)^2}$
$|\vec{b}| = \sqrt{1 + 1 + 0}$
$|\vec{b}| = \sqrt{2}$
Now, substitute the dot product and the magnitude into the projection formula:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{0}{\sqrt{2}}$
$\text{Projection}_{\vec{b}} \vec{a} = 0$
Therefore, the projection of vector $\hat{i} - \hat{j}$ on the vector $\hat{i} + \hat{j}$ is 0.
(This indicates that the two vectors are perpendicular).
Question 4. Find the projection of the vector $\hat{i} + 3\hat{j} + 7\hat{k}$ on the vector $7\hat{i} - \hat{j} + 8\hat{k}$.
Answer:
Given:
Let the vector to be projected be $\vec{a} = \hat{i} + 3\hat{j} + 7\hat{k}$.
Let the vector onto which the projection is made be $\vec{b} = 7\hat{i} - \hat{j} + 8\hat{k}$.
To Find:
The scalar projection of vector $\vec{a}$ onto vector $\vec{b}$.
Solution:
The scalar projection of vector $\vec{a}$ onto vector $\vec{b}$ is given by the formula:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$
First, calculate the dot product $\vec{a} \cdot \vec{b}$:
$\vec{a} \cdot \vec{b} = (1\hat{i} + 3\hat{j} + 7\hat{k}) \cdot (7\hat{i} - 1\hat{j} + 8\hat{k})$
$\vec{a} \cdot \vec{b} = (1)(7) + (3)(-1) + (7)(8)$
$\vec{a} \cdot \vec{b} = 7 - 3 + 56$
$\vec{a} \cdot \vec{b} = 4 + 56 = 60$
Next, calculate the magnitude of vector $\vec{b}$:
$|\vec{b}| = \sqrt{(7)^2 + (-1)^2 + (8)^2}$
$|\vec{b}| = \sqrt{49 + 1 + 64}$
$|\vec{b}| = \sqrt{50 + 64}$
$|\vec{b}| = \sqrt{114}$
Now, substitute the dot product and the magnitude into the projection formula:
$\text{Projection}_{\vec{b}} \vec{a} = \frac{60}{\sqrt{114}}$
Therefore, the projection of vector $\hat{i} + 3\hat{j} + 7\hat{k}$ on the vector $7\hat{i} - \hat{j} + 8\hat{k}$ is $\frac{60}{\sqrt{114}}$.
(This can also be written in rationalized form as $\frac{60\sqrt{114}}{114} = \frac{10\sqrt{114}}{19}$)
Question 5. Show that each of the given three vectors is a unit vector:
$\frac{1}{7} (2\hat{i} + 3\hat{j} + 6\hat{k})$, $\frac{1}{7} (3\hat{i} - 6\hat{j} + 2\hat{k})$, $\frac{1}{7} (6\hat{i} + 2\hat{j} - 3\hat{k})$
Also, show that they are mutually perpendicular to each other.
Answer:
Given:
Let the three vectors be:
$\vec{a} = \frac{1}{7} (2\hat{i} + 3\hat{j} + 6\hat{k}) = \frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} + \frac{6}{7}\hat{k}$
$\vec{b} = \frac{1}{7} (3\hat{i} - 6\hat{j} + 2\hat{k}) = \frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}$
$\vec{c} = \frac{1}{7} (6\hat{i} + 2\hat{j} - 3\hat{k}) = \frac{6}{7}\hat{i} + \frac{2}{7}\hat{j} - \frac{3}{7}\hat{k}$
To Show:
1. That $\vec{a}$, $\vec{b}$, and $\vec{c}$ are unit vectors (i.e., $|\vec{a}|=1$, $|\vec{b}|=1$, $|\vec{c}|=1$).
2. That $\vec{a}$, $\vec{b}$, and $\vec{c}$ are mutually perpendicular (i.e., $\vec{a} \cdot \vec{b} = 0$, $\vec{a} \cdot \vec{c} = 0$, $\vec{b} \cdot \vec{c} = 0$).
Proof:
Part 1: Showing the vectors are unit vectors
Calculate the magnitude of $\vec{a}$:
$|\vec{a}| = \sqrt{\left(\frac{2}{7}\right)^2 + \left(\frac{3}{7}\right)^2 + \left(\frac{6}{7}\right)^2}$
$|\vec{a}| = \sqrt{\frac{4}{49} + \frac{9}{49} + \frac{36}{49}}$
$|\vec{a}| = \sqrt{\frac{4+9+36}{49}} = \sqrt{\frac{49}{49}} = \sqrt{1} = 1$
Calculate the magnitude of $\vec{b}$:
$|\vec{b}| = \sqrt{\left(\frac{3}{7}\right)^2 + \left(-\frac{6}{7}\right)^2 + \left(\frac{2}{7}\right)^2}$
$|\vec{b}| = \sqrt{\frac{9}{49} + \frac{36}{49} + \frac{4}{49}}$
$|\vec{b}| = \sqrt{\frac{9+36+4}{49}} = \sqrt{\frac{49}{49}} = \sqrt{1} = 1$
Calculate the magnitude of $\vec{c}$:
$|\vec{c}| = \sqrt{\left(\frac{6}{7}\right)^2 + \left(\frac{2}{7}\right)^2 + \left(-\frac{3}{7}\right)^2}$
$|\vec{c}| = \sqrt{\frac{36}{49} + \frac{4}{49} + \frac{9}{49}}$
$|\vec{c}| = \sqrt{\frac{36+4+9}{49}} = \sqrt{\frac{49}{49}} = \sqrt{1} = 1$
Since $|\vec{a}|=1$, $|\vec{b}|=1$, and $|\vec{c}|=1$, all three vectors are unit vectors.
Part 2: Showing the vectors are mutually perpendicular
Calculate the dot product $\vec{a} \cdot \vec{b}$:
$\vec{a} \cdot \vec{b} = \left(\frac{2}{7}\right)\left(\frac{3}{7}\right) + \left(\frac{3}{7}\right)\left(-\frac{6}{7}\right) + \left(\frac{6}{7}\right)\left(\frac{2}{7}\right)$
$\vec{a} \cdot \vec{b} = \frac{6}{49} - \frac{18}{49} + \frac{12}{49} = \frac{6 - 18 + 12}{49} = \frac{0}{49} = 0$
Calculate the dot product $\vec{a} \cdot \vec{c}$:
$\vec{a} \cdot \vec{c} = \left(\frac{2}{7}\right)\left(\frac{6}{7}\right) + \left(\frac{3}{7}\right)\left(\frac{2}{7}\right) + \left(\frac{6}{7}\right)\left(-\frac{3}{7}\right)$
$\vec{a} \cdot \vec{c} = \frac{12}{49} + \frac{6}{49} - \frac{18}{49} = \frac{12 + 6 - 18}{49} = \frac{0}{49} = 0$
Calculate the dot product $\vec{b} \cdot \vec{c}$:
$\vec{b} \cdot \vec{c} = \left(\frac{3}{7}\right)\left(\frac{6}{7}\right) + \left(-\frac{6}{7}\right)\left(\frac{2}{7}\right) + \left(\frac{2}{7}\right)\left(-\frac{3}{7}\right)$
$\vec{b} \cdot \vec{c} = \frac{18}{49} - \frac{12}{49} - \frac{6}{49} = \frac{18 - 12 - 6}{49} = \frac{0}{49} = 0$
Since $\vec{a} \cdot \vec{b} = 0$, $\vec{a} \cdot \vec{c} = 0$, and $\vec{b} \cdot \vec{c} = 0$, the vectors are mutually perpendicular to each other.
Conclusion:
We have shown that each of the three given vectors is a unit vector and that they are mutually perpendicular.
Question 6. Find $|\;\vec{a}\;|$ and $|\;\vec{b}\;|$, if $(\vec{a} + \vec{b}) \;.\; (\vec{a} - \vec{b}) = 8$ and $|\;\vec{a}\;| = 8\;|\;\vec{b}\;|$.
Answer:
Given:
Two conditions involving vectors $\vec{a}$ and $\vec{b}$:
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = 8$
... (i)
$|\vec{a}| = 8 |\vec{b}|$
... (ii)
To Find:
The magnitudes $|\vec{a}|$ and $|\vec{b}|$.
Solution:
Start with the first given condition (i):
$(\vec{a} + \vec{b}) \cdot (\vec{a} - \vec{b}) = 8$
Expand the dot product using the distributive property and properties of dot products:
$\vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{a} - \vec{b} \cdot \vec{b} = 8$
Using $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and the commutative property $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$, the equation simplifies to:
$|\vec{a}|^2 - |\vec{b}|^2 = 8$
Now use the second given condition (ii), $|\vec{a}| = 8 |\vec{b}|$.
Substitute this into the equation $|\vec{a}|^2 - |\vec{b}|^2 = 8$:
$(8 |\vec{b}|)^2 - |\vec{b}|^2 = 8$
$64 |\vec{b}|^2 - |\vec{b}|^2 = 8$
$63 |\vec{b}|^2 = 8$
$|\vec{b}|^2 = \frac{8}{63}$
Taking the square root (magnitude must be non-negative):
$|\vec{b}| = \sqrt{\frac{8}{63}}$
$|\vec{b}| = \frac{\sqrt{8}}{\sqrt{63}} = \frac{\sqrt{4 \times 2}}{\sqrt{9 \times 7}} = \frac{2\sqrt{2}}{3\sqrt{7}}$
Rationalize the denominator:
$|\vec{b}| = \frac{2\sqrt{2}}{3\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{2\sqrt{14}}{3 \times 7} = \frac{2\sqrt{14}}{21}$
Now find $|\vec{a}|$ using the relation $|\vec{a}| = 8 |\vec{b}|$:
$|\vec{a}| = 8 \times \left( \frac{2\sqrt{14}}{21} \right)$
$|\vec{a}| = \frac{16\sqrt{14}}{21}$
Therefore, the magnitudes are:
$|\vec{a}| = \frac{16\sqrt{14}}{21}$
$|\vec{b}| = \frac{2\sqrt{14}}{21}$
Question 7. Evaluate the product $(3\vec{a} − 5\vec{b}) \;.\; (2\vec{a} + 7\vec{b})$.
Answer:
To Evaluate:
The scalar product $(3\vec{a} - 5\vec{b}) \cdot (2\vec{a} + 7\vec{b})$.
Solution:
We use the distributive property of the scalar (dot) product:
$(3\vec{a} - 5\vec{b}) \cdot (2\vec{a} + 7\vec{b})$
$= (3\vec{a}) \cdot (2\vec{a} + 7\vec{b}) - (5\vec{b}) \cdot (2\vec{a} + 7\vec{b})$
$= (3\vec{a}) \cdot (2\vec{a}) + (3\vec{a}) \cdot (7\vec{b}) - (5\vec{b}) \cdot (2\vec{a}) - (5\vec{b}) \cdot (7\vec{b})$
Using the property $(k\vec{u}) \cdot (l\vec{v}) = kl(\vec{u} \cdot \vec{v})$:
$= (3)(2)(\vec{a} \cdot \vec{a}) + (3)(7)(\vec{a} \cdot \vec{b}) - (5)(2)(\vec{b} \cdot \vec{a}) - (5)(7)(\vec{b} \cdot \vec{b})$
$= 6(\vec{a} \cdot \vec{a}) + 21(\vec{a} \cdot \vec{b}) - 10(\vec{b} \cdot \vec{a}) - 35(\vec{b} \cdot \vec{b})$
Using the properties $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and the commutative property $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$:
$= 6|\vec{a}|^2 + 21(\vec{a} \cdot \vec{b}) - 10(\vec{a} \cdot \vec{b}) - 35|\vec{b}|^2$
Combine the terms involving $\vec{a} \cdot \vec{b}$:
$= 6|\vec{a}|^2 + (21 - 10)(\vec{a} \cdot \vec{b}) - 35|\vec{b}|^2$
$= 6|\vec{a}|^2 + 11(\vec{a} \cdot \vec{b}) - 35|\vec{b}|^2$
Therefore, the evaluated product is:
$6|\vec{a}|^2 + 11(\vec{a} \cdot \vec{b}) - 35|\vec{b}|^2$
Question 8. Find the magnitude of two vectors $\vec{a}$ and $\vec{b}$ , having the same magnitude and such that the angle between them is 60o and their scalar product is $\frac{1}{2}$.
Answer:
Given:
Two vectors $\vec{a}$ and $\vec{b}$ such that:
1. They have the same magnitude: $|\vec{a}| = |\vec{b}|$.
2. The angle between them is $\theta = 60^\circ$.
3. Their scalar product is $\vec{a} \cdot \vec{b} = \frac{1}{2}$.
To Find:
The magnitudes $|\vec{a}|$ and $|\vec{b}|$.
Solution:
Let the common magnitude of the vectors be $m$. So, $|\vec{a}| = m$ and $|\vec{b}| = m$.
The formula for the scalar (dot) product of two vectors is:
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
We are given $\vec{a} \cdot \vec{b} = \frac{1}{2}$ and $\theta = 60^\circ$.
We know that $\cos 60^\circ = \frac{1}{2}$.
Substitute the given values and the common magnitude $m$ into the formula:
$\frac{1}{2} = (m)(m) \cos 60^\circ$
$\frac{1}{2} = m^2 \left(\frac{1}{2}\right)$
Multiply both sides by 2:
$2 \times \frac{1}{2} = 2 \times m^2 \left(\frac{1}{2}\right)$
$1 = m^2$
Since magnitude $m$ must be non-negative, we take the positive square root:
$m = \sqrt{1} = 1$
Therefore, the magnitude of each vector is 1.
$|\vec{a}| = m = 1$
$|\vec{b}| = m = 1$
The magnitudes of the vectors are:
$|\vec{a}| = 1$ and $|\vec{b}| = 1$.
Question 9. Question 9. Find $|\;\vec{x}\;|$, if for a unit vector $\vec{a} \;,\; (\vec{x} - \vec{a}) \;.\; (\vec{x} + \vec{a}) = 12$.
Answer:
Given:
$\vec{a}$ is a unit vector. This implies $|\vec{a}| = 1$.
The equation $(\vec{x} - \vec{a}) \cdot (\vec{x} + \vec{a}) = 12$.
To Find:
The magnitude of vector $\vec{x}$, denoted as $|\vec{x}|$.
Solution:
We are given the equation:
$(\vec{x} - \vec{a}) \cdot (\vec{x} + \vec{a}) = 12$
We expand the dot product using the distributive property, similar to the algebraic difference of squares $(p-q)(p+q) = p^2 - q^2$:
$(\vec{x} - \vec{a}) \cdot (\vec{x} + \vec{a}) = \vec{x} \cdot \vec{x} + \vec{x} \cdot \vec{a} - \vec{a} \cdot \vec{x} - \vec{a} \cdot \vec{a}$
Using the property $\vec{v} \cdot \vec{v} = |\vec{v}|^2$ and the commutative property of the dot product ($\vec{x} \cdot \vec{a} = \vec{a} \cdot \vec{x}$):
$= |\vec{x}|^2 + \vec{x} \cdot \vec{a} - \vec{x} \cdot \vec{a} - |\vec{a}|^2$
$= |\vec{x}|^2 - |\vec{a}|^2$
So, the given equation becomes:
$|\vec{x}|^2 - |\vec{a}|^2 = 12$
We are given that $\vec{a}$ is a unit vector, so $|\vec{a}| = 1$. Substitute this value into the equation:
$|\vec{x}|^2 - (1)^2 = 12$
$|\vec{x}|^2 - 1 = 12$
Add 1 to both sides:
$|\vec{x}|^2 = 12 + 1$
$|\vec{x}|^2 = 13$
Taking the square root of both sides, and noting that magnitude must be non-negative:
$|\vec{x}| = \sqrt{13}$
Therefore, the magnitude of vector $\vec{x}$ is:
$|\vec{x}| = \sqrt{13}$
Question 10. If $\vec{a} = 2\hat{i} + 2\hat{j} + 3\hat{k}$, $\vec{b} = -\hat{i} + 2\hat{j} + \hat{k}$ and $\vec{c} = 3\hat{i} + \hat{j}$ are such that $\vec{a} + λ\vec{b}$ is perpendicular to $\vec{c}$, then find the value of λ.
Answer:
Given:
The vectors are:
$\vec{a} = 2\hat{i} + 2\hat{j} + 3\hat{k}$
$\vec{b} = -\hat{i} + 2\hat{j} + \hat{k}$
$\vec{c} = 3\hat{i} + \hat{j} = 3\hat{i} + 1\hat{j} + 0\hat{k}$
The condition that the vector $(\vec{a} + \lambda\vec{b})$ is perpendicular to $\vec{c}$.
To Find:
The value of the scalar $\lambda$.
Solution:
Two vectors are perpendicular if their scalar (dot) product is zero.
The condition given is that $(\vec{a} + \lambda\vec{b})$ is perpendicular to $\vec{c}$. This means:
$(\vec{a} + \lambda\vec{b}) \cdot \vec{c} = 0$
First, let's find the vector $\vec{a} + \lambda\vec{b}$:
$\lambda\vec{b} = \lambda(-\hat{i} + 2\hat{j} + \hat{k}) = -\lambda\hat{i} + 2\lambda\hat{j} + \lambda\hat{k}$
$\vec{a} + \lambda\vec{b} = (2\hat{i} + 2\hat{j} + 3\hat{k}) + (-\lambda\hat{i} + 2\lambda\hat{j} + \lambda\hat{k})$
Combine the corresponding components:
$\vec{a} + \lambda\vec{b} = (2 - \lambda)\hat{i} + (2 + 2\lambda)\hat{j} + (3 + \lambda)\hat{k}$
Now, substitute this into the dot product condition $(\vec{a} + \lambda\vec{b}) \cdot \vec{c} = 0$:
$((2 - \lambda)\hat{i} + (2 + 2\lambda)\hat{j} + (3 + \lambda)\hat{k}) \cdot (3\hat{i} + 1\hat{j} + 0\hat{k}) = 0$
Calculate the dot product:
$(2 - \lambda)(3) + (2 + 2\lambda)(1) + (3 + \lambda)(0) = 0$
$3(2 - \lambda) + 1(2 + 2\lambda) + 0 = 0$
$6 - 3\lambda + 2 + 2\lambda = 0$
Combine the constant terms and the $\lambda$ terms:
$(6 + 2) + (-3\lambda + 2\lambda) = 0$
$8 - \lambda = 0$
Solve for $\lambda$:
$\lambda = 8$
Therefore, the value of $\lambda$ is 8.
Question 11. Show that $|\;\vec{a}\;| \;\vec{b} + |\;\vec{b}\;|\;\vec{a}$ is perpendicular to $|\;\vec{a}\;| \;\vec{b} - |\;\vec{b}\;|\;\vec{a}$, for any two nonzero vectors $\vec{a}$ and $\vec{b}$.
Answer:
Given:
Two nonzero vectors $\vec{a}$ and $\vec{b}$.
Vector 1: $\vec{u} = |\vec{a}| \vec{b} + |\vec{b}| \vec{a}$
Vector 2: $\vec{v} = |\vec{a}| \vec{b} - |\vec{b}| \vec{a}$
To Show:
That vector $\vec{u}$ is perpendicular to vector $\vec{v}$.
Proof:
Two vectors are perpendicular if their scalar (dot) product is zero. We need to calculate the dot product $\vec{u} \cdot \vec{v}$.
$\vec{u} \cdot \vec{v} = (|\vec{a}| \vec{b} + |\vec{b}| \vec{a}) \cdot (|\vec{a}| \vec{b} - |\vec{b}| \vec{a})$
This is in the form $(X + Y) \cdot (X - Y)$, where $X = |\vec{a}| \vec{b}$ and $Y = |\vec{b}| \vec{a}$.
Using the distributive property of the dot product, this expands to $X \cdot X - Y \cdot Y$.
$\vec{u} \cdot \vec{v} = (|\vec{a}| \vec{b}) \cdot (|\vec{a}| \vec{b}) - (|\vec{b}| \vec{a}) \cdot (|\vec{b}| \vec{a})$
Using the property $(k\vec{p}) \cdot (l\vec{q}) = kl(\vec{p} \cdot \vec{q})$:
$\vec{u} \cdot \vec{v} = (|\vec{a}|)(|\vec{a}|)(\vec{b} \cdot \vec{b}) - (|\vec{b}|)(|\vec{b}|)(\vec{a} \cdot \vec{a})$
Using the property $\vec{p} \cdot \vec{p} = |\vec{p}|^2$:
$\vec{u} \cdot \vec{v} = |\vec{a}|^2 |\vec{b}|^2 - |\vec{b}|^2 |\vec{a}|^2$
Since scalar multiplication is commutative, $|\vec{a}|^2 |\vec{b}|^2 = |\vec{b}|^2 |\vec{a}|^2$.
Therefore,
$\vec{u} \cdot \vec{v} = |\vec{a}|^2 |\vec{b}|^2 - |\vec{a}|^2 |\vec{b}|^2$
$\vec{u} \cdot \vec{v} = 0$
Conclusion:
Since the dot product of the two vectors $(|\vec{a}| \vec{b} + |\vec{b}| \vec{a})$ and $(|\vec{a}| \vec{b} - |\vec{b}| \vec{a})$ is zero, the two vectors are perpendicular to each other for any two nonzero vectors $\vec{a}$ and $\vec{b}$.
Question 12. If $\vec{a}\;.\; \vec{a} = 0$ and $\vec{a} \;.\; \vec{b} = 0$, then what can be concluded about the vector $\vec{b}$?
Answer:
Given:
1. $\vec{a} \cdot \vec{a} = 0$
2. $\vec{a} \cdot \vec{b} = 0$
To Find:
What can be concluded about the vector $\vec{b}$.
Solution:
Consider the first condition: $\vec{a} \cdot \vec{a} = 0$.
We know that the dot product of a vector with itself is equal to the square of its magnitude:
$\vec{a} \cdot \vec{a} = |\vec{a}|^2$
Therefore, the first condition implies:
$|\vec{a}|^2 = 0$
The magnitude of a vector is zero if and only if the vector is the zero vector.
So, $|\vec{a}| = 0 \implies \vec{a} = \vec{0}$.
Now consider the second condition: $\vec{a} \cdot \vec{b} = 0$.
Substitute $\vec{a} = \vec{0}$ into this condition:
$\vec{0} \cdot \vec{b} = 0$
The dot product of the zero vector with any vector $\vec{b}$ is always zero.
$0 = 0$
This equation holds true for any vector $\vec{b}$. The conditions given force $\vec{a}$ to be the zero vector, but they do not impose any restriction on $\vec{b}$.
Conclusion:
From the given conditions, we can only conclude that $\vec{a}$ must be the zero vector ($\vec{a} = \vec{0}$). No conclusion can be drawn about the vector $\vec{b}$. The vector $\vec{b}$ can be any vector.
Question 13. If $\vec{a}\;,\; \vec{b}\;,\; \vec{c}$ are unit vectors such that $\vec{a} + \vec{b} + \vec{c} = \vec{0}$, find the value of $\vec{a}\;.\;\vec{b} \;+\; \vec{b}\;.\; \vec{c} \;+\; \vec{c}\;.\; \vec{a}$.
Answer:
Given:
Vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ are unit vectors. This means:
$|\vec{a}| = 1$
$|\vec{b}| = 1$
$|\vec{c}| = 1$
Also given the condition:
$\vec{a} + \vec{b} + \vec{c} = \vec{0}$
To Find:
The value of the expression $\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}$.
Solution:
We start with the given vector equation:
$\vec{a} + \vec{b} + \vec{c} = \vec{0}$
Take the dot product of this equation with itself:
$(\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c}) = \vec{0} \cdot \vec{0}$
Expand the left side using the distributive property of the dot product:
$\vec{a}\cdot(\vec{a} + \vec{b} + \vec{c}) + \vec{b}\cdot(\vec{a} + \vec{b} + \vec{c}) + \vec{c}\cdot(\vec{a} + \vec{b} + \vec{c}) = 0$
$\vec{a}\cdot\vec{a} + \vec{a}\cdot\vec{b} + \vec{a}\cdot\vec{c} + \vec{b}\cdot\vec{a} + \vec{b}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a} + \vec{c}\cdot\vec{b} + \vec{c}\cdot\vec{c} = 0$
Using the properties $\vec{v}\cdot\vec{v} = |\vec{v}|^2$ and the commutative property $\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{u}$:
$|\vec{a}|^2 + \vec{a}\cdot\vec{b} + \vec{c}\cdot\vec{a} + \vec{a}\cdot\vec{b} + |\vec{b}|^2 + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a} + \vec{b}\cdot\vec{c} + |\vec{c}|^2 = 0$
Group the terms:
$(|\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2) + (2\vec{a}\cdot\vec{b} + 2\vec{b}\cdot\vec{c} + 2\vec{c}\cdot\vec{a}) = 0$
$(|\vec{a}|^2 + |\vec{b}|^2 + |\vec{c}|^2) + 2(\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}) = 0$
Substitute the magnitudes of the unit vectors: $|\vec{a}| = 1$, $|\vec{b}| = 1$, $|\vec{c}| = 1$.
$(1^2 + 1^2 + 1^2) + 2(\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}) = 0$
$(1 + 1 + 1) + 2(\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}) = 0$
$3 + 2(\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}) = 0$
Rearrange the equation to solve for the required expression:
$2(\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}) = -3$
$\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a} = -\frac{3}{2}$
Therefore, the value of $\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{a}$ is $-\frac{3}{2}$.
Question 14. If either vector $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a}\;.\; \vec{b} = 0$. But the converse need not be true. Justify your answer with an example.
Answer:
Statement: If either vector $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a} \cdot \vec{b} = 0$.
This statement is true. If $\vec{a} = \vec{0}$, then $\vec{a} \cdot \vec{b} = \vec{0} \cdot \vec{b} = 0$. If $\vec{b} = \vec{0}$, then $\vec{a} \cdot \vec{b} = \vec{a} \cdot \vec{0} = 0$.
Converse Statement: If $\vec{a} \cdot \vec{b} = 0$, then either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$.
We need to show that this converse statement is not always true.
Justification:
The definition of the scalar (dot) product is:
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
where $\theta$ is the angle between the vectors $\vec{a}$ and $\vec{b}$.
The dot product $\vec{a} \cdot \vec{b}$ can be zero under three conditions:
1. $|\vec{a}| = 0$, which means $\vec{a} = \vec{0}$.
2. $|\vec{b}| = 0$, which means $\vec{b} = \vec{0}$.
3. $\cos \theta = 0$, which means $\theta = 90^\circ$ (or $\frac{\pi}{2}$ radians), implying that $\vec{a}$ and $\vec{b}$ are perpendicular.
The converse statement assumes that if $\vec{a} \cdot \vec{b} = 0$, only conditions 1 or 2 can be true. However, condition 3 can also be true even if neither $\vec{a}$ nor $\vec{b}$ is the zero vector.
Example:
Let $\vec{a}$ and $\vec{b}$ be two non-zero vectors that are perpendicular to each other.
Consider $\vec{a} = \hat{i} = 1\hat{i} + 0\hat{j} + 0\hat{k}$.
Consider $\vec{b} = \hat{j} = 0\hat{i} + 1\hat{j} + 0\hat{k}$.
Clearly, neither $\vec{a}$ nor $\vec{b}$ is the zero vector:
$|\vec{a}| = \sqrt{1^2+0^2+0^2} = 1 \neq 0 \implies \vec{a} \neq \vec{0}$.
$|\vec{b}| = \sqrt{0^2+1^2+0^2} = 1 \neq 0 \implies \vec{b} \neq \vec{0}$.
Now, calculate their dot product:
$\vec{a} \cdot \vec{b} = (1)(0) + (0)(1) + (0)(0) = 0 + 0 + 0 = 0$.
In this example, $\vec{a} \cdot \vec{b} = 0$, but neither $\vec{a} = \vec{0}$ nor $\vec{b} = \vec{0}$. This happens because $\vec{a}$ and $\vec{b}$ are perpendicular.
Conclusion:
The converse statement is not necessarily true. If the dot product of two vectors is zero ($\vec{a} \cdot \vec{b} = 0$), it means either at least one of the vectors is the zero vector, or the two vectors are perpendicular to each other (or both).
Question 15. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$].
Answer:
Given:
The coordinates of the vertices of triangle ABC:
A = (1, 2, 3)
B = (–1, 0, 0)
C = (0, 1, 2)
To Find:
The angle ∠ABC, which is the angle between the vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$.
Solution:
First, we find the vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$.
The vector $\overrightarrow{BA}$ is given by the difference between the position vectors of A and B:
$\overrightarrow{BA} = \text{Position vector of A} - \text{Position vector of B}$
$\overrightarrow{BA} = (1\hat{i} + 2\hat{j} + 3\hat{k}) - (-1\hat{i} + 0\hat{j} + 0\hat{k})$
$\overrightarrow{BA} = (1 - (-1))\hat{i} + (2 - 0)\hat{j} + (3 - 0)\hat{k}$
$\overrightarrow{BA} = (1 + 1)\hat{i} + 2\hat{j} + 3\hat{k}$
$\overrightarrow{BA} = 2\hat{i} + 2\hat{j} + 3\hat{k}$
The vector $\overrightarrow{BC}$ is given by the difference between the position vectors of C and B:
$\overrightarrow{BC} = \text{Position vector of C} - \text{Position vector of B}$
$\overrightarrow{BC} = (0\hat{i} + 1\hat{j} + 2\hat{k}) - (-1\hat{i} + 0\hat{j} + 0\hat{k})$
$\overrightarrow{BC} = (0 - (-1))\hat{i} + (1 - 0)\hat{j} + (2 - 0)\hat{k}$
$\overrightarrow{BC} = (0 + 1)\hat{i} + 1\hat{j} + 2\hat{k}$
$\overrightarrow{BC} = \hat{i} + \hat{j} + 2\hat{k}$
Let $\theta$ be the angle ∠ABC between vectors $\overrightarrow{BA}$ and $\overrightarrow{BC}$. We use the dot product formula:
$\cos \theta = \frac{\overrightarrow{BA} \cdot \overrightarrow{BC}}{|\overrightarrow{BA}| |\overrightarrow{BC}|}$
Calculate the dot product $\overrightarrow{BA} \cdot \overrightarrow{BC}$:
$\overrightarrow{BA} \cdot \overrightarrow{BC} = (2\hat{i} + 2\hat{j} + 3\hat{k}) \cdot (\hat{i} + \hat{j} + 2\hat{k})$
$\overrightarrow{BA} \cdot \overrightarrow{BC} = (2)(1) + (2)(1) + (3)(2)$
$\overrightarrow{BA} \cdot \overrightarrow{BC} = 2 + 2 + 6 = 10$
Calculate the magnitudes $|\overrightarrow{BA}|$ and $|\overrightarrow{BC}|$:
$|\overrightarrow{BA}| = \sqrt{(2)^2 + (2)^2 + (3)^2} = \sqrt{4 + 4 + 9} = \sqrt{17}$
$|\overrightarrow{BC}| = \sqrt{(1)^2 + (1)^2 + (2)^2} = \sqrt{1 + 1 + 4} = \sqrt{6}$
Substitute these values into the cosine formula:
$\cos \theta = \frac{10}{(\sqrt{17})(\sqrt{6})}$
$\cos \theta = \frac{10}{\sqrt{17 \times 6}}$
$\cos \theta = \frac{10}{\sqrt{102}}$
The angle ∠ABC is given by:
$\theta = \cos^{-1}\left(\frac{10}{\sqrt{102}}\right)$
Therefore, the angle ∠ABC is $\cos^{-1}\left(\frac{10}{\sqrt{102}}\right)$.
Question 16. Show that the points A(1, 2, 7), B(2, 6, 3) and C(3, 10, –1) are collinear.
Answer:
Given:
The coordinates of the points A, B, and C are:
A = (1, 2, 7)
B = (2, 6, 3)
C = (3, 10, –1)
The corresponding position vectors are:
$\vec{OA} = 1\hat{i} + 2\hat{j} + 7\hat{k}$
$\vec{OB} = 2\hat{i} + 6\hat{j} + 3\hat{k}$
$\vec{OC} = 3\hat{i} + 10\hat{j} - 1\hat{k}$
To Show:
The points A, B, and C are collinear.
Proof:
Three points A, B, and C are collinear if the vectors formed by joining them in pairs are parallel (collinear). We can check if the vector $\overrightarrow{AB}$ is parallel to the vector $\overrightarrow{BC}$.
First, find the vector $\overrightarrow{AB}$:
$\overrightarrow{AB} = \vec{OB} - \vec{OA}$
$\overrightarrow{AB} = (2\hat{i} + 6\hat{j} + 3\hat{k}) - (1\hat{i} + 2\hat{j} + 7\hat{k})$
$\overrightarrow{AB} = (2-1)\hat{i} + (6-2)\hat{j} + (3-7)\hat{k}$
$\overrightarrow{AB} = 1\hat{i} + 4\hat{j} - 4\hat{k}$
Next, find the vector $\overrightarrow{BC}$:
$\overrightarrow{BC} = \vec{OC} - \vec{OB}$
$\overrightarrow{BC} = (3\hat{i} + 10\hat{j} - 1\hat{k}) - (2\hat{i} + 6\hat{j} + 3\hat{k})$
$\overrightarrow{BC} = (3-2)\hat{i} + (10-6)\hat{j} + (-1-3)\hat{k}$
$\overrightarrow{BC} = 1\hat{i} + 4\hat{j} - 4\hat{k}$
Now, we compare $\overrightarrow{AB}$ and $\overrightarrow{BC}$. We observe that:
$\overrightarrow{BC} = \hat{i} + 4\hat{j} - 4\hat{k}$
$\overrightarrow{AB} = \hat{i} + 4\hat{j} - 4\hat{k}$
Thus, $\overrightarrow{BC} = 1 \times \overrightarrow{AB}$.
Since $\overrightarrow{BC}$ is a scalar multiple of $\overrightarrow{AB}$ (with the scalar $\lambda = 1$), the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are parallel.
Furthermore, since the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$ are parallel and share the common point B, the points A, B, and C must lie on the same straight line.
Conclusion:
The points A, B, and C are collinear.
Question 17. Show that the vectors $2\hat{i} - \hat{j} + \hat{k} \;,\; \hat{i} - 3\hat{j} - 5\hat{k}$ and $3\hat{i} - 4\hat{j} - 4\hat{k}$ form the vertices of a right angled triangle.
Answer:
Given:
Let the position vectors of the vertices A, B, and C of a triangle be:
$\vec{OA} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{OB} = \hat{i} - 3\hat{j} - 5\hat{k}$
$\vec{OC} = 3\hat{i} - 4\hat{j} - 4\hat{k}$
To Prove:
The points A, B, and C form the vertices of a right-angled triangle.
Proof:
To show that A, B, and C form a right-angled triangle, we can find the vectors representing the sides of the triangle and check if they satisfy the Pythagorean theorem (sum of squares of two sides equals the square of the third side) or if the dot product of two adjacent side vectors is zero.
Let's find the vectors representing the sides:
$\vec{AB} = \vec{OB} - \vec{OA}$
$\vec{AB} = (\hat{i} - 3\hat{j} - 5\hat{k}) - (2\hat{i} - \hat{j} + \hat{k})$
$\vec{AB} = (1-2)\hat{i} + (-3 - (-1))\hat{j} + (-5 - 1)\hat{k}$
$\vec{AB} = -\hat{i} - 2\hat{j} - 6\hat{k}$
$\vec{BC} = \vec{OC} - \vec{OB}$
$\vec{BC} = (3\hat{i} - 4\hat{j} - 4\hat{k}) - (\hat{i} - 3\hat{j} - 5\hat{k})$
$\vec{BC} = (3-1)\hat{i} + (-4 - (-3))\hat{j} + (-4 - (-5))\hat{k}$
$\vec{BC} = 2\hat{i} - \hat{j} + \hat{k}$
$\vec{CA} = \vec{OA} - \vec{OC}$
$\vec{CA} = (2\hat{i} - \hat{j} + \hat{k}) - (3\hat{i} - 4\hat{j} - 4\hat{k})$
$\vec{CA} = (2-3)\hat{i} + (-1 - (-4))\hat{j} + (1 - (-4))\hat{k}$
$\vec{CA} = -\hat{i} + 3\hat{j} + 5\hat{k}$
Using Magnitudes and Pythagoras Theorem:
We calculate the square of the magnitudes (lengths) of the sides:
$|\vec{AB}|^2 = (-1)^2 + (-2)^2 + (-6)^2 = 1 + 4 + 36 = 41$
$|\vec{BC}|^2 = (2)^2 + (-1)^2 + (1)^2 = 4 + 1 + 1 = 6$
$|\vec{CA}|^2 = (-1)^2 + (3)^2 + (5)^2 = 1 + 9 + 25 = 35$
Now, we check if the Pythagorean theorem holds:
$|\vec{BC}|^2 + |\vec{CA}|^2 = 6 + 35 = 41$
We see that $|\vec{BC}|^2 + |\vec{CA}|^2 = |\vec{AB}|^2$.
Since the sum of the squares of the lengths of two sides equals the square of the length of the third side, the triangle satisfies the Pythagorean theorem.
Conclusion:
The points represented by the given position vectors form the vertices of a right-angled triangle.
Alternate Method (Using Dot Product):
We can check if any two adjacent side vectors are perpendicular by checking if their dot product is zero.
$\vec{BC} \cdot \vec{CA} = (2\hat{i} - \hat{j} + \hat{k}) \cdot (-\hat{i} + 3\hat{j} + 5\hat{k})$
$\vec{BC} \cdot \vec{CA} = (2)(-1) + (-1)(3) + (1)(5)$
$\vec{BC} \cdot \vec{CA} = -2 - 3 + 5 = 0$
Since $\vec{BC} \cdot \vec{CA} = 0$, the sides BC and CA are perpendicular. Therefore, the angle at vertex C is $90^\circ$, and the triangle is right-angled.
Question 18. If $\vec{a}$ is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then $λ\vec{a}$ is unit vector if
(A) λ = 1
(B) λ = – 1
(C) a = |λ|
(D) $a = \frac{1}{|λ|}$
Answer:
Given:
Vector $\vec{a}$ is nonzero, so $\vec{a} \neq \vec{0}$.
The magnitude of $\vec{a}$ is $a$, so $|\vec{a}| = a$. Since $\vec{a}$ is nonzero, $a > 0$.
$\lambda$ is a nonzero scalar, so $\lambda \neq 0$.
The vector $\lambda \vec{a}$ is a unit vector.
To Find:
The condition relating $a$ and $\lambda$ for $\lambda \vec{a}$ to be a unit vector.
Solution:
A vector is a unit vector if its magnitude is equal to 1.
We are given that $\lambda \vec{a}$ is a unit vector. Therefore, its magnitude must be 1:
$|\lambda \vec{a}| = 1$
Using the property of magnitudes $|k \vec{v}| = |k| |\vec{v}|$ for any scalar $k$ and vector $\vec{v}$:
$|\lambda| |\vec{a}| = 1$
We are given that $|\vec{a}| = a$. Substitute this into the equation:
$|\lambda| a = 1$
Since $\lambda$ is a nonzero scalar, $|\lambda| \neq 0$. Since $\vec{a}$ is a nonzero vector, $a \neq 0$. We can divide by $|\lambda|$ to solve for $a$:
$a = \frac{1}{|\lambda|}$
This condition must be satisfied for $\lambda \vec{a}$ to be a unit vector.
Comparing this result with the given options:
(A) λ = 1 implies $a = 1/|1| = 1$. This is only true if $\vec{a}$ itself is a unit vector.
(B) λ = – 1 implies $a = 1/|-1| = 1$. This is only true if $\vec{a}$ itself is a unit vector.
(C) a = |λ| is incorrect.
(D) $a = \frac{1}{|λ|}$ matches our derived condition.
Final Answer: The final answer is $\boxed{(D)}$
Example 22 to 25 (Before Exercise 10.4)
Example 22: Find $|\;\vec{a}\; × \;\vec{b}\;|$, if $\vec{a} = 2\hat{i} + \hat{j} + 3\hat{k}$ and $\vec{b} = 3\hat{i} + 5\hat{j} - 2\hat{k}$
Answer:
Given:
The vectors are:
$\vec{a} = 2\hat{i} + \hat{j} + 3\hat{k}$
$\vec{b} = 3\hat{i} + 5\hat{j} - 2\hat{k}$
To Find:
The magnitude of the cross product of $\vec{a}$ and $\vec{b}$, denoted as $|\vec{a} \times \vec{b}|$.
Solution:
We first compute the cross product $\vec{a} \times \vec{b}$ using the determinant formula:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 3 \\ 3 & 5 & -2 \end{vmatrix}$
Expanding the determinant along the first row:
$\vec{a} \times \vec{b} = \hat{i} \begin{vmatrix} 1 & 3 \\ 5 & -2 \end{vmatrix} - \hat{j} \begin{vmatrix} 2 & 3 \\ 3 & -2 \end{vmatrix} + \hat{k} \begin{vmatrix} 2 & 1 \\ 3 & 5 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}((1)(-2) - (3)(5)) - \hat{j}((2)(-2) - (3)(3)) + \hat{k}((2)(5) - (1)(3))$
$\vec{a} \times \vec{b} = \hat{i}(-2 - 15) - \hat{j}(-4 - 9) + \hat{k}(10 - 3)$
$\vec{a} \times \vec{b} = \hat{i}(-17) - \hat{j}(-13) + \hat{k}(7)$
$\vec{a} \times \vec{b} = -17\hat{i} + 13\hat{j} + 7\hat{k}$
Now, we find the magnitude of the resulting vector $\vec{a} \times \vec{b}$:
$|\vec{a} \times \vec{b}| = | -17\hat{i} + 13\hat{j} + 7\hat{k} |$
The magnitude of a vector $x\hat{i} + y\hat{j} + z\hat{k}$ is given by $\sqrt{x^2 + y^2 + z^2}$.
$|\vec{a} \times \vec{b}| = \sqrt{(-17)^2 + (13)^2 + (7)^2}$
$|\vec{a} \times \vec{b}| = \sqrt{289 + 169 + 49}$
$|\vec{a} \times \vec{b}| = \sqrt{507}$
Thus, the magnitude of the cross product is $\sqrt{507}$.
Example 23: Find a unit vector perpendicular to each of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$, where $\vec{a} = \hat{i} + \hat{j} + \hat{k} \;,\; \vec{b} = \hat{i} + 2\hat{j} + 3\hat{k}$.
Answer:
Given:
Two vectors:
$\vec{a} = \hat{i} + \hat{j} + \hat{k}$
$\vec{b} = \hat{i} + 2\hat{j} + 3\hat{k}$
To Find:
A unit vector perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$.
Solution:
Let $\vec{c} = \vec{a} + \vec{b}$ and $\vec{d} = \vec{a} - \vec{b}$.
First, we calculate $\vec{c}$:
$\vec{c} = (\hat{i} + \hat{j} + \hat{k}) + (\hat{i} + 2\hat{j} + 3\hat{k})$
$\vec{c} = (1+1)\hat{i} + (1+2)\hat{j} + (1+3)\hat{k}$
$\vec{c} = 2\hat{i} + 3\hat{j} + 4\hat{k}$
Next, we calculate $\vec{d}$:
$\vec{d} = (\hat{i} + \hat{j} + \hat{k}) - (\hat{i} + 2\hat{j} + 3\hat{k})$
$\vec{d} = (1-1)\hat{i} + (1-2)\hat{j} + (1-3)\hat{k}$
$\vec{d} = 0\hat{i} - 1\hat{j} - 2\hat{k}$
$\vec{d} = -\hat{j} - 2\hat{k}$
A vector perpendicular to both $\vec{c}$ and $\vec{d}$ is given by their cross product, $\vec{c} \times \vec{d}$.
$\vec{c} \times \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 3 & 4 \\ 0 & -1 & -2 \end{vmatrix}$
Expanding the determinant:
$\vec{c} \times \vec{d} = \hat{i}((3)(-2) - (4)(-1)) - \hat{j}((2)(-2) - (4)(0)) + \hat{k}((2)(-1) - (3)(0))$
$\vec{c} \times \vec{d} = \hat{i}(-6 + 4) - \hat{j}(-4 - 0) + \hat{k}(-2 - 0)$
$\vec{c} \times \vec{d} = -2\hat{i} + 4\hat{j} - 2\hat{k}$
Let $\vec{v} = \vec{c} \times \vec{d} = -2\hat{i} + 4\hat{j} - 2\hat{k}$. This vector is perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$.
To find a unit vector perpendicular to both, we need to divide $\vec{v}$ by its magnitude, $|\vec{v}|$.
$|\vec{v}| = |\vec{c} \times \vec{d}| = |-2\hat{i} + 4\hat{j} - 2\hat{k}|$
$|\vec{v}| = \sqrt{(-2)^2 + (4)^2 + (-2)^2}$
$|\vec{v}| = \sqrt{4 + 16 + 4}$
$|\vec{v}| = \sqrt{24} = \sqrt{4 \times 6} = 2\sqrt{6}$
The unit vector $\hat{n}$ is given by:
$\hat{n} = \frac{\vec{v}}{|\vec{v}|} = \frac{-2\hat{i} + 4\hat{j} - 2\hat{k}}{2\sqrt{6}}$
$\hat{n} = \frac{-2}{2\sqrt{6}}\hat{i} + \frac{4}{2\sqrt{6}}\hat{j} - \frac{2}{2\sqrt{6}}\hat{k}$
$\hat{n} = -\frac{1}{\sqrt{6}}\hat{i} + \frac{2}{\sqrt{6}}\hat{j} - \frac{1}{\sqrt{6}}\hat{k}$
$\hat{n} = \frac{1}{\sqrt{6}}(-\hat{i} + 2\hat{j} - \hat{k})$
Thus, a unit vector perpendicular to each of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} − \vec{b})$ is $\frac{1}{\sqrt{6}}(-\hat{i} + 2\hat{j} - \hat{k})$.
(Note: The negative of this vector, $\frac{1}{\sqrt{6}}(\hat{i} - 2\hat{j} + \hat{k})$, is also a valid answer.)
Example 24: Find the area of a triangle having the points A(1, 1, 1), B(1, 2, 3) and C(2, 3, 1) as its vertices.
Answer:
Given:
The vertices of the triangle are A(1, 1, 1), B(1, 2, 3), and C(2, 3, 1).
To Find:
The area of the triangle ABC.
Solution:
Let the position vectors of the vertices be $\vec{OA}$, $\vec{OB}$, and $\vec{OC}$.
$\vec{OA} = \hat{i} + \hat{j} + \hat{k}$
$\vec{OB} = \hat{i} + 2\hat{j} + 3\hat{k}$
$\vec{OC} = 2\hat{i} + 3\hat{j} + \hat{k}$
The area of the triangle ABC is given by half the magnitude of the cross product of two adjacent side vectors, for example, $\vec{AB}$ and $\vec{AC}$.
First, find the vectors representing the sides $\vec{AB}$ and $\vec{AC}$:
$\vec{AB} = \vec{OB} - \vec{OA}$
$\vec{AB} = (\hat{i} + 2\hat{j} + 3\hat{k}) - (\hat{i} + \hat{j} + \hat{k})$
$\vec{AB} = (1-1)\hat{i} + (2-1)\hat{j} + (3-1)\hat{k}$
$\vec{AB} = 0\hat{i} + 1\hat{j} + 2\hat{k} = \hat{j} + 2\hat{k}$
$\vec{AC} = \vec{OC} - \vec{OA}$
$\vec{AC} = (2\hat{i} + 3\hat{j} + \hat{k}) - (\hat{i} + \hat{j} + \hat{k})$
$\vec{AC} = (2-1)\hat{i} + (3-1)\hat{j} + (1-1)\hat{k}$
$\vec{AC} = 1\hat{i} + 2\hat{j} + 0\hat{k} = \hat{i} + 2\hat{j}$
Now, compute the cross product $\vec{AB} \times \vec{AC}$:
$\vec{AB} \times \vec{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 1 & 2 \\ 1 & 2 & 0 \end{vmatrix}$
$\vec{AB} \times \vec{AC} = \hat{i}((1)(0) - (2)(2)) - \hat{j}((0)(0) - (2)(1)) + \hat{k}((0)(2) - (1)(1))$
$\vec{AB} \times \vec{AC} = \hat{i}(0 - 4) - \hat{j}(0 - 2) + \hat{k}(0 - 1)$
$\vec{AB} \times \vec{AC} = -4\hat{i} + 2\hat{j} - \hat{k}$
The magnitude of this cross product is:
$|\vec{AB} \times \vec{AC}| = |-4\hat{i} + 2\hat{j} - \hat{k}|$
$|\vec{AB} \times \vec{AC}| = \sqrt{(-4)^2 + (2)^2 + (-1)^2}$
$|\vec{AB} \times \vec{AC}| = \sqrt{16 + 4 + 1}$
$|\vec{AB} \times \vec{AC}| = \sqrt{21}$
The area of the triangle ABC is half the magnitude of the cross product:
Area $(\triangle ABC) = \frac{1}{2} |\vec{AB} \times \vec{AC}|$
Area $(\triangle ABC) = \frac{1}{2} \sqrt{21}$
Thus, the area of the triangle is $\frac{\sqrt{21}}{2}$ square units.
Example 25: Find the area of a parallelogram whose adjacent sides are given by the vectors $\vec{a} = 3\hat{i} + \hat{j} + 4\hat{k}$ and $\vec{b} = \hat{i} − \hat{j} + \hat{k}$
Answer:
Given:
The adjacent sides of the parallelogram are represented by the vectors:
$\vec{a} = 3\hat{i} + \hat{j} + 4\hat{k}$
$\vec{b} = \hat{i} - \hat{j} + \hat{k}$
To Find:
The area of the parallelogram.
Solution:
The area of a parallelogram whose adjacent sides are represented by vectors $\vec{a}$ and $\vec{b}$ is given by the magnitude of their cross product, i.e., Area $= |\vec{a} \times \vec{b}|$.
First, we compute the cross product $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 4 \\ 1 & -1 & 1 \end{vmatrix}$
Expanding the determinant along the first row:
$\vec{a} \times \vec{b} = \hat{i}((1)(1) - (4)(-1)) - \hat{j}((3)(1) - (4)(1)) + \hat{k}((3)(-1) - (1)(1))$
$\vec{a} \times \vec{b} = \hat{i}(1 - (-4)) - \hat{j}(3 - 4) + \hat{k}(-3 - 1)$
$\vec{a} \times \vec{b} = \hat{i}(1 + 4) - \hat{j}(-1) + \hat{k}(-4)$
$\vec{a} \times \vec{b} = 5\hat{i} + \hat{j} - 4\hat{k}$
Now, we find the magnitude of the resulting vector $\vec{a} \times \vec{b}$:
$|\vec{a} \times \vec{b}| = |5\hat{i} + \hat{j} - 4\hat{k}|$
$|\vec{a} \times \vec{b}| = \sqrt{(5)^2 + (1)^2 + (-4)^2}$
$|\vec{a} \times \vec{b}| = \sqrt{25 + 1 + 16}$
$|\vec{a} \times \vec{b}| = \sqrt{42}$
The area of the parallelogram is the magnitude of the cross product.
Area $= |\vec{a} \times \vec{b}| = \sqrt{42}$
Thus, the area of the parallelogram is $\sqrt{42}$ square units.
Exercise 10.4
Question 1. Find $|\;\vec{a} \;×\; \vec{b}\;|$, if $\vec{a} = \hat{i} − 7\hat{j} + 7\hat{k}$ and $\vec{b} = 3\hat{i} − 2\hat{j} + 2\hat{k}$.
Answer:
Given:
The vectors are:
$\vec{a} = \hat{i} - 7\hat{j} + 7\hat{k}$
$\vec{b} = 3\hat{i} - 2\hat{j} + 2\hat{k}$
To Find:
The magnitude of the cross product of $\vec{a}$ and $\vec{b}$, denoted as $|\vec{a} \times \vec{b}|$.
Solution:
We first compute the cross product $\vec{a} \times \vec{b}$ using the determinant formula:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -7 & 7 \\ 3 & -2 & 2 \end{vmatrix}$
Expanding the determinant along the first row:
$\vec{a} \times \vec{b} = \hat{i} \begin{vmatrix} -7 & 7 \\ -2 & 2 \end{vmatrix} - \hat{j} \begin{vmatrix} 1 & 7 \\ 3 & 2 \end{vmatrix} + \hat{k} \begin{vmatrix} 1 & -7 \\ 3 & -2 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}((-7)(2) - (7)(-2)) - \hat{j}((1)(2) - (7)(3)) + \hat{k}((1)(-2) - (-7)(3))$
$\vec{a} \times \vec{b} = \hat{i}(-14 - (-14)) - \hat{j}(2 - 21) + \hat{k}(-2 - (-21))$
$\vec{a} \times \vec{b} = \hat{i}(-14 + 14) - \hat{j}(-19) + \hat{k}(-2 + 21)$
$\vec{a} \times \vec{b} = 0\hat{i} + 19\hat{j} + 19\hat{k}$
$\vec{a} \times \vec{b} = 19\hat{j} + 19\hat{k}$
Now, we find the magnitude of the resulting vector $\vec{a} \times \vec{b}$:
$|\vec{a} \times \vec{b}| = |0\hat{i} + 19\hat{j} + 19\hat{k}|$
The magnitude of a vector $x\hat{i} + y\hat{j} + z\hat{k}$ is given by $\sqrt{x^2 + y^2 + z^2}$.
$|\vec{a} \times \vec{b}| = \sqrt{(0)^2 + (19)^2 + (19)^2}$
$|\vec{a} \times \vec{b}| = \sqrt{0 + 361 + 361}$
$|\vec{a} \times \vec{b}| = \sqrt{722}$
$|\vec{a} \times \vec{b}| = \sqrt{361 \times 2}$
$|\vec{a} \times \vec{b}| = 19\sqrt{2}$
Thus, the magnitude of the cross product is $19\sqrt{2}$.
Question 2. Find a unit vector perpendicular to each of the vector $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$, where $\vec{a} = 3\hat{i} + 2\hat{j} + 2\hat{k}$ and $\vec{b} = \hat{i} + 2\hat{j} − 2\hat{k}$ .
Answer:
Given:
Two vectors:
$\vec{a} = 3\hat{i} + 2\hat{j} + 2\hat{k}$
$\vec{b} = \hat{i} + 2\hat{j} - 2\hat{k}$
To Find:
A unit vector perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$.
Solution:
Let $\vec{c} = \vec{a} + \vec{b}$ and $\vec{d} = \vec{a} - \vec{b}$.
First, we calculate $\vec{c}$:
$\vec{c} = (3\hat{i} + 2\hat{j} + 2\hat{k}) + (\hat{i} + 2\hat{j} - 2\hat{k})$
$\vec{c} = (3+1)\hat{i} + (2+2)\hat{j} + (2-2)\hat{k}$
$\vec{c} = 4\hat{i} + 4\hat{j} + 0\hat{k} = 4\hat{i} + 4\hat{j}$
Next, we calculate $\vec{d}$:
$\vec{d} = (3\hat{i} + 2\hat{j} + 2\hat{k}) - (\hat{i} + 2\hat{j} - 2\hat{k})$
$\vec{d} = (3-1)\hat{i} + (2-2)\hat{j} + (2-(-2))\hat{k}$
$\vec{d} = 2\hat{i} + 0\hat{j} + 4\hat{k} = 2\hat{i} + 4\hat{k}$
A vector perpendicular to both $\vec{c}$ and $\vec{d}$ is given by their cross product, $\vec{c} \times \vec{d}$.
$\vec{c} \times \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 4 & 0 \\ 2 & 0 & 4 \end{vmatrix}$
Expanding the determinant:
$\vec{c} \times \vec{d} = \hat{i}((4)(4) - (0)(0)) - \hat{j}((4)(4) - (0)(2)) + \hat{k}((4)(0) - (4)(2))$
$\vec{c} \times \vec{d} = \hat{i}(16 - 0) - \hat{j}(16 - 0) + \hat{k}(0 - 8)$
$\vec{c} \times \vec{d} = 16\hat{i} - 16\hat{j} - 8\hat{k}$
Let $\vec{v} = \vec{c} \times \vec{d} = 16\hat{i} - 16\hat{j} - 8\hat{k}$. This vector is perpendicular to both $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$.
To find a unit vector perpendicular to both, we need to divide $\vec{v}$ by its magnitude, $|\vec{v}|$.
$|\vec{v}| = |\vec{c} \times \vec{d}| = |16\hat{i} - 16\hat{j} - 8\hat{k}|$
$|\vec{v}| = \sqrt{(16)^2 + (-16)^2 + (-8)^2}$
$|\vec{v}| = \sqrt{256 + 256 + 64}$
$|\vec{v}| = \sqrt{576}$
$|\vec{v}| = 24$
The unit vector $\hat{n}$ is given by:
$\hat{n} = \frac{\vec{v}}{|\vec{v}|} = \frac{16\hat{i} - 16\hat{j} - 8\hat{k}}{24}$
$\hat{n} = \frac{16}{24}\hat{i} - \frac{16}{24}\hat{j} - \frac{8}{24}\hat{k}$
$\hat{n} = \frac{2}{3}\hat{i} - \frac{2}{3}\hat{j} - \frac{1}{3}\hat{k}$
$\hat{n} = \frac{1}{3}(2\hat{i} - 2\hat{j} - \hat{k})$
Thus, a unit vector perpendicular to each of the vectors $(\vec{a} + \vec{b})$ and $(\vec{a} - \vec{b})$ is $\frac{1}{3}(2\hat{i} - 2\hat{j} - \hat{k})$.
(Note: The negative of this vector, $-\frac{1}{3}(2\hat{i} - 2\hat{j} - \hat{k}) = \frac{1}{3}(-2\hat{i} + 2\hat{j} + \hat{k})$, is also a valid answer.)
Question 3. If a unit vector $\vec{a}$ makes angles $\frac{π}{3}$ with $\hat{i}$ , $\frac{π}{4}$ with $\hat{j}$ and an acute angle θ with $\hat{k}$, then find θ and hence, the components of $\vec{a}$.
Answer:
Given:
$\vec{a}$ is a unit vector, so $|\vec{a}| = 1$.
The angle between $\vec{a}$ and $\hat{i}$ is $\alpha = \frac{\pi}{3}$.
The angle between $\vec{a}$ and $\hat{j}$ is $\beta = \frac{\pi}{4}$.
The angle between $\vec{a}$ and $\hat{k}$ is $\gamma = \theta$, where $\theta$ is an acute angle ($0 < \theta < \frac{\pi}{2}$).
To Find:
1. The value of the angle $\theta$.
2. The components of the vector $\vec{a}$.
Solution:
Let the direction cosines of the unit vector $\vec{a}$ be $l, m, n$.
The direction cosines are given by:
$l = \cos \alpha = \cos\left(\frac{\pi}{3}\right)$
$m = \cos \beta = \cos\left(\frac{\pi}{4}\right)$
$n = \cos \gamma = \cos \theta$
We know that for any vector, the sum of the squares of its direction cosines is equal to 1:
$l^2 + m^2 + n^2 = 1$
Substituting the values of $\alpha$ and $\beta$:
$\cos^2\left(\frac{\pi}{3}\right) + \cos^2\left(\frac{\pi}{4}\right) + \cos^2 \theta = 1$
We know $\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}$ and $\cos\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}$.
Substituting these values into the equation:
$\left(\frac{1}{2}\right)^2 + \left(\frac{1}{\sqrt{2}}\right)^2 + \cos^2 \theta = 1$
$\frac{1}{4} + \frac{1}{2} + \cos^2 \theta = 1$
To add the fractions, find a common denominator (4):
$\frac{1}{4} + \frac{2}{4} + \cos^2 \theta = 1$
$\frac{3}{4} + \cos^2 \theta = 1$
$\cos^2 \theta = 1 - \frac{3}{4}$
$\cos^2 \theta = \frac{4}{4} - \frac{3}{4}$
$\cos^2 \theta = \frac{1}{4}$
Taking the square root of both sides:
$\cos \theta = \pm\sqrt{\frac{1}{4}}$
$\cos \theta = \pm\frac{1}{2}$
Since it is given that $\theta$ is an acute angle ($0 < \theta < \frac{\pi}{2}$), its cosine must be positive.
Therefore, $\cos \theta = \frac{1}{2}$.
The acute angle $\theta$ for which $\cos \theta = \frac{1}{2}$ is $\theta = \frac{\pi}{3}$.
Now, we find the components of the unit vector $\vec{a}$.
For a unit vector, the components are equal to its direction cosines.
Let $\vec{a} = a_x\hat{i} + a_y\hat{j} + a_z\hat{k}$.
Then $a_x = l = \cos\left(\frac{\pi}{3}\right) = \frac{1}{2}$.
$a_y = m = \cos\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}$.
$a_z = n = \cos \theta = \cos\left(\frac{\pi}{3}\right) = \frac{1}{2}$.
So, the components of $\vec{a}$ are $\left(\frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}\right)$.
The vector $\vec{a}$ can be written as $\vec{a} = \frac{1}{2}\hat{i} + \frac{1}{\sqrt{2}}\hat{j} + \frac{1}{2}\hat{k}$.
The value of the angle is $\theta = \frac{\pi}{3}$.
The components of the vector $\vec{a}$ are $\left(\frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}\right)$.
Question 4. Show that $(\;\vec{a} - \vec{b}) \;×\; (\vec{a} + \vec{b}) = 2(\vec{a} \;×\; \vec{b})$
Answer:
To Prove:
$(\vec{a} - \vec{b}) \times (\vec{a} + \vec{b}) = 2(\vec{a} \times \vec{b})$
Proof:
We start with the Left Hand Side (LHS) of the equation:
LHS $= (\vec{a} - \vec{b}) \times (\vec{a} + \vec{b})$
Using the distributive property of the vector cross product:
LHS $= (\vec{a} - \vec{b}) \times \vec{a} + (\vec{a} - \vec{b}) \times \vec{b}$
Applying the distributive property again:
LHS $= (\vec{a} \times \vec{a}) - (\vec{b} \times \vec{a}) + (\vec{a} \times \vec{b}) - (\vec{b} \times \vec{b})$
We know that the cross product of any vector with itself is the zero vector ($\vec{0}$):
$\vec{a} \times \vec{a} = \vec{0}$
[Property of cross product]
$\vec{b} \times \vec{b} = \vec{0}$
[Property of cross product]
Substituting these into the expression:
LHS $= \vec{0} - (\vec{b} \times \vec{a}) + (\vec{a} \times \vec{b}) - \vec{0}$
LHS $= -(\vec{b} \times \vec{a}) + (\vec{a} \times \vec{b})$
We also know that the cross product is anti-commutative:
$\vec{b} \times \vec{a} = -(\vec{a} \times \vec{b})$
[Property of cross product]
Substituting this into the expression for LHS:
LHS $= -(-(\vec{a} \times \vec{b})) + (\vec{a} \times \vec{b})$
LHS $= (\vec{a} \times \vec{b}) + (\vec{a} \times \vec{b})$
LHS $= 2(\vec{a} \times \vec{b})$
This is equal to the Right Hand Side (RHS).
Hence, we have shown that $(\vec{a} - \vec{b}) \times (\vec{a} + \vec{b}) = 2(\vec{a} \times \vec{b})$.
Question 5. Find λ and µ if $(2\hat{i} + 6\hat{j} + 27\hat{k}) \;×\; (\hat{i} + λ\hat{j} + µ\hat{k}) = \vec{0}$.
Answer:
Given:
Let $\vec{a} = 2\hat{i} + 6\hat{j} + 27\hat{k}$
Let $\vec{b} = \hat{i} + \lambda\hat{j} + \mu\hat{k}$
The condition is $\vec{a} \times \vec{b} = \vec{0}$.
To Find:
The values of $\lambda$ and $\mu$.
Solution:
We compute the cross product $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 6 & 27 \\ 1 & \lambda & \mu \end{vmatrix}$
Expanding the determinant:
$\vec{a} \times \vec{b} = \hat{i}(6\mu - 27\lambda) - \hat{j}(2\mu - 27(1)) + \hat{k}(2\lambda - 6(1))$
$\vec{a} \times \vec{b} = (6\mu - 27\lambda)\hat{i} - (2\mu - 27)\hat{j} + (2\lambda - 6)\hat{k}$
We are given that $\vec{a} \times \vec{b} = \vec{0}$, which means $\vec{a} \times \vec{b} = 0\hat{i} + 0\hat{j} + 0\hat{k}$.
Equating the components of $\vec{a} \times \vec{b}$ to the components of the zero vector:
$6\mu - 27\lambda = 0$
... (i)
$-(2\mu - 27) = 0$
... (ii)
$2\lambda - 6 = 0$
... (iii)
From equation (iii):
$2\lambda = 6$
$\lambda = \frac{6}{2}$
$\lambda = 3$
From equation (ii):
$2\mu - 27 = 0$
$2\mu = 27$
$\mu = \frac{27}{2}$
We can check these values using equation (i):
$6\mu - 27\lambda = 6\left(\frac{27}{2}\right) - 27(3) = 3(27) - 81 = 81 - 81 = 0$.
The values satisfy all conditions.
Thus, the values are $\lambda = 3$ and $\mu = \frac{27}{2}$.
Alternate Solution:
If the cross product of two non-zero vectors is the zero vector, then the vectors must be parallel (collinear).
$\vec{a} \times \vec{b} = \vec{0} \implies \vec{a}$ is parallel to $\vec{b}$.
This means that the ratio of their corresponding components must be equal:
$\frac{2}{1} = \frac{6}{\lambda} = \frac{27}{\mu}$
Considering the first equality:
$\frac{2}{1} = \frac{6}{\lambda}$
$2\lambda = 6$
$\lambda = 3$
Considering the second equality:
$\frac{2}{1} = \frac{27}{\mu}$
$2\mu = 27$
$\mu = \frac{27}{2}$
Thus, the values are $\lambda = 3$ and $\mu = \frac{27}{2}$.
Question 6. Given that $\vec{a} \;.\; \vec{b} = 0$ and $\vec{a} \;\times\; \vec{b} = \vec{0}$. What can you conclude about the vectors $\vec{a}$ and $\vec{b}$ ?
Answer:
Given:
We are given two conditions for vectors $\vec{a}$ and $\vec{b}$:
$\vec{a} \cdot \vec{b} = 0$
...(i)
$\vec{a} \times \vec{b} = \vec{0}$
...(ii)
To Find:
The conclusion about vectors $\vec{a}$ and $\vec{b}$.
Solution:
Let $\theta$ be the angle between vectors $\vec{a}$ and $\vec{b}$.
From condition (i): $\vec{a} \cdot \vec{b} = 0$.
By the definition of the scalar (dot) product:
$|\vec{a}| |\vec{b}| \cos \theta = 0$
This equation holds true if at least one of the following is true:
(a) $|\vec{a}| = 0$, which means $\vec{a} = \vec{0}$.
(b) $|\vec{b}| = 0$, which means $\vec{b} = \vec{0}$.
(c) $\cos \theta = 0$, which means $\theta = \frac{\pi}{2}$ (i.e., $\vec{a}$ is perpendicular to $\vec{b}$), provided $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$.
From condition (ii): $\vec{a} \times \vec{b} = \vec{0}$.
By the definition of the vector (cross) product, the magnitude is:
$|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin \theta$
Since $\vec{a} \times \vec{b} = \vec{0}$, its magnitude must be zero:
$|\vec{a}| |\vec{b}| \sin \theta = 0$
This equation holds true if at least one of the following is true:
(d) $|\vec{a}| = 0$, which means $\vec{a} = \vec{0}$.
(e) $|\vec{b}| = 0$, which means $\vec{b} = \vec{0}$.
(f) $\sin \theta = 0$, which means $\theta = 0$ or $\theta = \pi$ (i.e., $\vec{a}$ is parallel or anti-parallel to $\vec{b}$), provided $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$.
Now, we need both conditions (i) and (ii) to be satisfied simultaneously.
Case 1: If $\vec{a} = \vec{0}$.
Then $\vec{a} \cdot \vec{b} = 0 \cdot |\vec{b}| \cos \theta = 0$. Condition (i) is satisfied.
And $\vec{a} \times \vec{b} = \vec{0}$ (since $|\vec{a} \times \vec{b}| = 0 \cdot |\vec{b}| \sin \theta = 0$). Condition (ii) is satisfied.
So, $\vec{a} = \vec{0}$ is a possible conclusion.
Case 2: If $\vec{b} = \vec{0}$.
Then $\vec{a} \cdot \vec{b} = |\vec{a}| \cdot 0 \cdot \cos \theta = 0$. Condition (i) is satisfied.
And $\vec{a} \times \vec{b} = \vec{0}$ (since $|\vec{a} \times \vec{b}| = |\vec{a}| \cdot 0 \cdot \sin \theta = 0$). Condition (ii) is satisfied.
So, $\vec{b} = \vec{0}$ is a possible conclusion.
Case 3: If $\vec{a} \neq \vec{0}$ and $\vec{b} \neq \vec{0}$.
For condition (i) to be true, we must have $\cos \theta = 0$, which implies $\theta = \frac{\pi}{2}$.
For condition (ii) to be true, we must have $\sin \theta = 0$, which implies $\theta = 0$ or $\theta = \pi$.
It is impossible for the angle $\theta$ to be $\frac{\pi}{2}$ and $(0$ or $\pi)$ at the same time.
Therefore, the assumption that both $\vec{a}$ and $\vec{b}$ are non-zero vectors must be false.
This means that at least one of the vectors must be the zero vector.
Conclusion:
If $\vec{a} \cdot \vec{b} = 0$ and $\vec{a} \times \vec{b} = \vec{0}$, then it must be the case that either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$ (or both vectors are zero).
Question 7. Let the vectors $\vec{a} \;,\; \vec{b} \;,\; \vec{c}$ be given as $a_1\hat{i} + a_2\hat{j} + a_3\hat{k} \;,\; b_1\hat{i} + b_2\hat{j} + b_3\hat{k} \;,\; c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$. Then show that $\vec{a} \;×\; (\vec{b} + \vec{c}) = \vec{a} \;×\; \vec{b} + \vec{a} \;×\; \vec{c}$.
Answer:
Given:
Three vectors:
$\vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k}$
$\vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k}$
$\vec{c} = c_1\hat{i} + c_2\hat{j} + c_3\hat{k}$
To Prove:
The distributive property of the vector cross product over vector addition:
$\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$
Proof:
First, calculate the sum $\vec{b} + \vec{c}$:
$\vec{b} + \vec{c} = (b_1\hat{i} + b_2\hat{j} + b_3\hat{k}) + (c_1\hat{i} + c_2\hat{j} + c_3\hat{k})$
$\vec{b} + \vec{c} = (b_1 + c_1)\hat{i} + (b_2 + c_2)\hat{j} + (b_3 + c_3)\hat{k}$
Now, calculate the Left Hand Side (LHS): $\vec{a} \times (\vec{b} + \vec{c})$
$\vec{a} \times (\vec{b} + \vec{c}) = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ (b_1 + c_1) & (b_2 + c_2) & (b_3 + c_3) \end{vmatrix}$
Expanding the determinant:
LHS $= \hat{i} [a_2(b_3 + c_3) - a_3(b_2 + c_2)] - \hat{j} [a_1(b_3 + c_3) - a_3(b_1 + c_1)] + \hat{k} [a_1(b_2 + c_2) - a_2(b_1 + c_1)]$
LHS $= \hat{i} [a_2b_3 + a_2c_3 - a_3b_2 - a_3c_2] - \hat{j} [a_1b_3 + a_1c_3 - a_3b_1 - a_3c_1] + \hat{k} [a_1b_2 + a_1c_2 - a_2b_1 - a_2c_1]$
Rearranging the terms within the brackets:
LHS $= \hat{i} [(a_2b_3 - a_3b_2) + (a_2c_3 - a_3c_2)] - \hat{j} [(a_1b_3 - a_3b_1) + (a_1c_3 - a_3c_1)] + \hat{k} [(a_1b_2 - a_2b_1) + (a_1c_2 - a_2c_1)]$
LHS $= \hat{i}(a_2b_3 - a_3b_2) - \hat{j}(a_1b_3 - a_3b_1) + \hat{k}(a_1b_2 - a_2b_1) + \hat{i}(a_2c_3 - a_3c_2) - \hat{j}(a_1c_3 - a_3c_1) + \hat{k}(a_1c_2 - a_2c_1)$
Now, calculate the terms on the Right Hand Side (RHS): $\vec{a} \times \vec{b} + \vec{a} \times \vec{c}$.
First, $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}(a_2b_3 - a_3b_2) - \hat{j}(a_1b_3 - a_3b_1) + \hat{k}(a_1b_2 - a_2b_1)$
Next, $\vec{a} \times \vec{c}$:
$\vec{a} \times \vec{c} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ c_1 & c_2 & c_3 \end{vmatrix}$
$\vec{a} \times \vec{c} = \hat{i}(a_2c_3 - a_3c_2) - \hat{j}(a_1c_3 - a_3c_1) + \hat{k}(a_1c_2 - a_2c_1)$
Now add the two results to get the RHS:
RHS $= (\vec{a} \times \vec{b}) + (\vec{a} \times \vec{c})$
RHS $= [\hat{i}(a_2b_3 - a_3b_2) - \hat{j}(a_1b_3 - a_3b_1) + \hat{k}(a_1b_2 - a_2b_1)] + [\hat{i}(a_2c_3 - a_3c_2) - \hat{j}(a_1c_3 - a_3c_1) + \hat{k}(a_1c_2 - a_2c_1)]$
Combining the components:
RHS $= \hat{i}[(a_2b_3 - a_3b_2) + (a_2c_3 - a_3c_2)] - \hat{j}[(a_1b_3 - a_3b_1) + (a_1c_3 - a_3c_1)] + \hat{k}[(a_1b_2 - a_2b_1) + (a_1c_2 - a_2c_1)]$
Comparing the expression for LHS and RHS, we see that they are identical.
LHS $= \hat{i} [(a_2b_3 - a_3b_2) + (a_2c_3 - a_3c_2)] - \hat{j} [(a_1b_3 - a_3b_1) + (a_1c_3 - a_3c_1)] + \hat{k} [(a_1b_2 - a_2b_1) + (a_1c_2 - a_2c_1)]$
RHS $= \hat{i} [(a_2b_3 - a_3b_2) + (a_2c_3 - a_3c_2)] - \hat{j} [(a_1b_3 - a_3b_1) + (a_1c_3 - a_3c_1)] + \hat{k} [(a_1b_2 - a_2b_1) + (a_1c_2 - a_2c_1)]$
Therefore, LHS = RHS, and we have shown that $\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$.
Question 8. If either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$ then $\vec{a} \;×\; \vec{b} = \vec{0}$. Is the converse true? Justify your answer with an example.
Answer:
Given Statement:
If either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$, then $\vec{a} \times \vec{b} = \vec{0}$.
This statement is true.
Justification:
By definition, $\vec{a} \times \vec{b} = |\vec{a}||\vec{b}|\sin\theta\; \hat{n}$, where $\theta$ is the angle between $\vec{a}$ and $\vec{b}$, and $\hat{n}$ is a unit vector perpendicular to both $\vec{a}$ and $\vec{b}$.
If $\vec{a} = \vec{0}$, then $|\vec{a}| = 0$. So, $\vec{a} \times \vec{b} = (0)|\vec{b}|\sin\theta\; \hat{n} = 0 \cdot \hat{n} = \vec{0}$.
If $\vec{b} = \vec{0}$, then $|\vec{b}| = 0$. So, $\vec{a} \times \vec{b} = |\vec{a}|(0)\sin\theta\; \hat{n} = 0 \cdot \hat{n} = \vec{0}$.
Converse Statement:
If $\vec{a} \times \vec{b} = \vec{0}$, then either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$.
This converse statement is not true.
Justification:
We know that $\vec{a} \times \vec{b} = \vec{0}$ implies $|\vec{a} \times \vec{b}| = 0$.
$|\vec{a}||\vec{b}|\sin\theta = 0$
This equation holds true if:
1. $|\vec{a}| = 0$, i.e., $\vec{a} = \vec{0}$.
2. $|\vec{b}| = 0$, i.e., $\vec{b} = \vec{0}$.
3. $\sin\theta = 0$, provided $|\vec{a}| \neq 0$ and $|\vec{b}| \neq 0$.
If $\sin\theta = 0$, then $\theta = 0$ or $\theta = \pi$. This means the vectors $\vec{a}$ and $\vec{b}$ are parallel (or collinear).
So, it is possible for the cross product $\vec{a} \times \vec{b}$ to be $\vec{0}$ even when both $\vec{a}$ and $\vec{b}$ are non-zero vectors, provided they are parallel (collinear).
Example:
Let $\vec{a} = \hat{i} + 2\hat{j} + 3\hat{k}$. Clearly, $\vec{a} \neq \vec{0}$.
Let $\vec{b} = 2\vec{a} = 2(\hat{i} + 2\hat{j} + 3\hat{k}) = 2\hat{i} + 4\hat{j} + 6\hat{k}$. Clearly, $\vec{b} \neq \vec{0}$.
Vectors $\vec{a}$ and $\vec{b}$ are parallel (collinear).
Now, calculate their cross product:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ 2 & 4 & 6 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}((2)(6) - (3)(4)) - \hat{j}((1)(6) - (3)(2)) + \hat{k}((1)(4) - (2)(2))$
$\vec{a} \times \vec{b} = \hat{i}(12 - 12) - \hat{j}(6 - 6) + \hat{k}(4 - 4)$
$\vec{a} \times \vec{b} = \hat{i}(0) - \hat{j}(0) + \hat{k}(0)$
$\vec{a} \times \vec{b} = 0\hat{i} + 0\hat{j} + 0\hat{k} = \vec{0}$
In this example, $\vec{a} \times \vec{b} = \vec{0}$, but neither $\vec{a} = \vec{0}$ nor $\vec{b} = \vec{0}$.
Therefore, the converse is not true. The condition $\vec{a} \times \vec{b} = \vec{0}$ implies that either $\vec{a} = \vec{0}$ or $\vec{b} = \vec{0}$ or $\vec{a}$ and $\vec{b}$ are parallel (collinear).
Question 9. Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
Answer:
Given:
The vertices of the triangle are A(1, 1, 2), B(2, 3, 5), and C(1, 5, 5).
To Find:
The area of the triangle ABC.
Solution:
Let the position vectors of the vertices be $\vec{OA}$, $\vec{OB}$, and $\vec{OC}$.
$\vec{OA} = 1\hat{i} + 1\hat{j} + 2\hat{k}$
$\vec{OB} = 2\hat{i} + 3\hat{j} + 5\hat{k}$
$\vec{OC} = 1\hat{i} + 5\hat{j} + 5\hat{k}$
The area of the triangle ABC is given by half the magnitude of the cross product of two adjacent side vectors, for example, $\vec{AB}$ and $\vec{AC}$.
First, find the vectors representing the sides $\vec{AB}$ and $\vec{AC}$:
$\vec{AB} = \vec{OB} - \vec{OA}$
$\vec{AB} = (2\hat{i} + 3\hat{j} + 5\hat{k}) - (1\hat{i} + 1\hat{j} + 2\hat{k})$
$\vec{AB} = (2-1)\hat{i} + (3-1)\hat{j} + (5-2)\hat{k}$
$\vec{AB} = 1\hat{i} + 2\hat{j} + 3\hat{k}$
$\vec{AC} = \vec{OC} - \vec{OA}$
$\vec{AC} = (1\hat{i} + 5\hat{j} + 5\hat{k}) - (1\hat{i} + 1\hat{j} + 2\hat{k})$
$\vec{AC} = (1-1)\hat{i} + (5-1)\hat{j} + (5-2)\hat{k}$
$\vec{AC} = 0\hat{i} + 4\hat{j} + 3\hat{k}$
Now, compute the cross product $\vec{AB} \times \vec{AC}$:
$\vec{AB} \times \vec{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ 0 & 4 & 3 \end{vmatrix}$
$\vec{AB} \times \vec{AC} = \hat{i}((2)(3) - (3)(4)) - \hat{j}((1)(3) - (3)(0)) + \hat{k}((1)(4) - (2)(0))$
$\vec{AB} \times \vec{AC} = \hat{i}(6 - 12) - \hat{j}(3 - 0) + \hat{k}(4 - 0)$
$\vec{AB} \times \vec{AC} = -6\hat{i} - 3\hat{j} + 4\hat{k}$
The magnitude of this cross product is:
$|\vec{AB} \times \vec{AC}| = |-6\hat{i} - 3\hat{j} + 4\hat{k}|$
$|\vec{AB} \times \vec{AC}| = \sqrt{(-6)^2 + (-3)^2 + (4)^2}$
$|\vec{AB} \times \vec{AC}| = \sqrt{36 + 9 + 16}$
$|\vec{AB} \times \vec{AC}| = \sqrt{61}$
The area of the triangle ABC is half the magnitude of the cross product:
Area $(\triangle ABC) = \frac{1}{2} |\vec{AB} \times \vec{AC}|$
Area $(\triangle ABC) = \frac{1}{2} \sqrt{61}$
Thus, the area of the triangle is $\frac{\sqrt{61}}{2}$ square units.
Question 10. Find the area of the parallelogram whose adjacent sides are determined by the vectors $\vec{a} = \hat{i} - \hat{j} + 3\hat{k}$ and $\vec{b} = 2\hat{i} − 7\hat{j} + \hat{k}$
Answer:
Given:
The adjacent sides of the parallelogram are represented by the vectors:
$\vec{a} = \hat{i} - \hat{j} + 3\hat{k}$
$\vec{b} = 2\hat{i} - 7\hat{j} + \hat{k}$
To Find:
The area of the parallelogram.
Solution:
The area of a parallelogram whose adjacent sides are represented by vectors $\vec{a}$ and $\vec{b}$ is given by the magnitude of their cross product, i.e., Area $= |\vec{a} \times \vec{b}|$.
First, we compute the cross product $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 3 \\ 2 & -7 & 1 \end{vmatrix}$
Expanding the determinant along the first row:
$\vec{a} \times \vec{b} = \hat{i}((-1)(1) - (3)(-7)) - \hat{j}((1)(1) - (3)(2)) + \hat{k}((1)(-7) - (-1)(2))$
$\vec{a} \times \vec{b} = \hat{i}(-1 - (-21)) - \hat{j}(1 - 6) + \hat{k}(-7 - (-2))$
$\vec{a} \times \vec{b} = \hat{i}(-1 + 21) - \hat{j}(-5) + \hat{k}(-7 + 2)$
$\vec{a} \times \vec{b} = 20\hat{i} + 5\hat{j} - 5\hat{k}$
Now, we find the magnitude of the resulting vector $\vec{a} \times \vec{b}$:
$|\vec{a} \times \vec{b}| = |20\hat{i} + 5\hat{j} - 5\hat{k}|$
$|\vec{a} \times \vec{b}| = \sqrt{(20)^2 + (5)^2 + (-5)^2}$
$|\vec{a} \times \vec{b}| = \sqrt{400 + 25 + 25}$
$|\vec{a} \times \vec{b}| = \sqrt{450}$
To simplify $\sqrt{450}$: $\sqrt{450} = \sqrt{225 \times 2} = 15\sqrt{2}$
$|\vec{a} \times \vec{b}| = 15\sqrt{2}$
The area of the parallelogram is the magnitude of the cross product.
Area $= |\vec{a} \times \vec{b}| = 15\sqrt{2}$
Thus, the area of the parallelogram is $15\sqrt{2}$ square units.
Question 11. Let the vectores $\vec{a}$ and $\vec{b}$ be such that $|\;\vec{a}\;| = 3$ and $|\;\vec{b}\;| = \frac{\sqrt{2}}{3}$ , then $\vec{a} \;×\; \vec{b}$ is a unit vector, if the angle between $\vec{a}$ and $\vec{b}$ is
(A) $\frac{π}{6}$
(B) $\frac{π}{4}$
(C) $\frac{π}{3}$
(D) $\frac{π}{2}$
Answer:
Given:
Magnitude of vector $\vec{a}$ is $|\vec{a}| = 3$.
Magnitude of vector $\vec{b}$ is $|\vec{b}| = \frac{\sqrt{2}}{3}$.
The cross product $\vec{a} \times \vec{b}$ is a unit vector, which means $|\vec{a} \times \vec{b}| = 1$.
To Find:
The angle $\theta$ between vectors $\vec{a}$ and $\vec{b}$.
Solution:
We know the formula for the magnitude of the cross product of two vectors $\vec{a}$ and $\vec{b}$:
$|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin\theta$
where $\theta$ is the angle between $\vec{a}$ and $\vec{b}$.
Substituting the given values into the formula:
$1 = (3) \times \left(\frac{\sqrt{2}}{3}\right) \times \sin\theta$
Simplifying the equation:
$1 = \sqrt{2} \sin\theta$
Solving for $\sin\theta$:
$\sin\theta = \frac{1}{\sqrt{2}}$
Since the angle $\theta$ between two vectors is usually considered in the range $[0, \pi]$, the angle $\theta$ for which $\sin\theta = \frac{1}{\sqrt{2}}$ is:
$\theta = \frac{\pi}{4}$
Comparing this result with the given options:
(A) $\frac{\pi}{6}$
(B) $\frac{\pi}{4}$
(C) $\frac{\pi}{3}$
(D) $\frac{\pi}{2}$
The calculated angle $\theta = \frac{\pi}{4}$ matches option (B).
Thus, the angle between $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$.
The correct option is (B).
Question 12. Area of a rectangle having vertices A, B, C and D with position vectors $-\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k} ̂\;,\; \hat{i} + \frac{1}{2}\hat{j} + 4\hat{k} \;,\; \hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}$ and $−\hat{i} − \frac{1}{2}\hat{j} + 4\hat{k}$ , respectively is
(A) $\frac{1}{2}$
(B) 1
(C) 2
(D) 4
Answer:
Given:
The position vectors of the vertices of the rectangle ABCD are:
$\vec{OA} = -\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k}$
$\vec{OB} = \hat{i} + \frac{1}{2}\hat{j} + 4\hat{k}$
$\vec{OC} = \hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}$
$\vec{OD} = -\hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}$
To Find:
The area of the rectangle ABCD.
Solution:
The area of a rectangle is the magnitude of the cross product of two adjacent side vectors. Let's find the vectors representing the adjacent sides $\vec{AB}$ and $\vec{AD}$.
Calculate the vector $\vec{AB}$:
$\vec{AB} = \vec{OB} - \vec{OA}$
$\vec{AB} = (\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k}) - (-\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k})$
$\vec{AB} = (1 - (-1))\hat{i} + (\frac{1}{2} - \frac{1}{2})\hat{j} + (4 - 4)\hat{k}$
$\vec{AB} = 2\hat{i} + 0\hat{j} + 0\hat{k} = 2\hat{i}$
Calculate the vector $\vec{AD}$:
$\vec{AD} = \vec{OD} - \vec{OA}$
$\vec{AD} = (-\hat{i} - \frac{1}{2}\hat{j} + 4\hat{k}) - (-\hat{i} + \frac{1}{2}\hat{j} + 4\hat{k})$
$\vec{AD} = (-1 - (-1))\hat{i} + (-\frac{1}{2} - \frac{1}{2})\hat{j} + (4 - 4)\hat{k}$
$\vec{AD} = 0\hat{i} - 1\hat{j} + 0\hat{k} = -\hat{j}$
The area of the rectangle ABCD is given by the magnitude of the cross product of the adjacent sides $\vec{AB}$ and $\vec{AD}$:
Area $= |\vec{AB} \times \vec{AD}|$
Compute the cross product $\vec{AB} \times \vec{AD}$:
$\vec{AB} \times \vec{AD} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 0 & 0 \\ 0 & -1 & 0 \end{vmatrix}$
$\vec{AB} \times \vec{AD} = \hat{i}((0)(0) - (0)(-1)) - \hat{j}((2)(0) - (0)(0)) + \hat{k}((2)(-1) - (0)(0))$
$\vec{AB} \times \vec{AD} = \hat{i}(0) - \hat{j}(0) + \hat{k}(-2 - 0)$
$\vec{AB} \times \vec{AD} = -2\hat{k}$
Now, find the magnitude of this cross product:
Area $= |\vec{AB} \times \vec{AD}| = |-2\hat{k}|$
Area $= \sqrt{(0)^2 + (0)^2 + (-2)^2} = \sqrt{0 + 0 + 4} = \sqrt{4} = 2$
Alternate Solution:
Since it is a rectangle, the area can also be calculated as the product of the lengths of the adjacent sides.
Length of side AB $= |\vec{AB}| = |2\hat{i}| = \sqrt{2^2 + 0^2 + 0^2} = \sqrt{4} = 2$
Length of side AD $= |\vec{AD}| = |-\hat{j}| = \sqrt{0^2 + (-1)^2 + 0^2} = \sqrt{1} = 1$
Area = Length $\times$ Width $= |\vec{AB}| \times |\vec{AD}| = 2 \times 1 = 2$
Thus, the area of the rectangle is 2 square units.
The correct option is (C).
Example 26 to 30 - Miscellaneous Examples
Example 26: Write all the unit vectors in XY-plane.
Answer:
To write all the unit vectors in the XY-plane, we first need to understand what a unit vector is and how vectors are represented in the XY-plane.
A unit vector is a vector with a magnitude (or length) of 1.
The XY-plane is a two-dimensional coordinate system where vectors can be represented by their components along the x and y axes.
Given:
Vectors are in the XY-plane.
To Find:
All possible unit vectors in the XY-plane.
Solution:
Let $\vec{v}$ be any vector in the XY-plane. We can represent this vector in component form using the standard basis vectors $\hat{i}$ and $\hat{j}$, which point along the positive x and y axes, respectively.
So, a general vector in the XY-plane can be written as:
$\vec{v} = x\hat{i} + y\hat{j}$
where $x$ and $y$ are scalar components along the x and y axes.
For $\vec{v}$ to be a unit vector, its magnitude must be equal to $1$. The magnitude of a vector $\vec{v} = x\hat{i} + y\hat{j}$ is given by the formula:
$|\vec{v}| = \sqrt{x^2 + y^2}$
So, the condition for $\vec{v}$ to be a unit vector is:
$|\vec{v}| = 1$
Substituting the magnitude formula, we get:
$\sqrt{x^2 + y^2} = 1$
Squaring both sides of the equation gives:
$x^2 + y^2 = 1$
This equation, $x^2 + y^2 = 1$, describes the locus of all points $(x, y)$ in the XY-plane that lie on a circle of radius $1$ centered at the origin $(0, 0)$.
Every point $(x, y)$ on this unit circle corresponds to the terminal point of a unit vector $\vec{u} = x\hat{i} + y\hat{j}$ originating from the origin.
Any point on the unit circle can be parameterized by an angle $\theta$ measured counterclockwise from the positive x-axis. The coordinates of such a point are given by:
$x = \cos\theta$
$y = \sin\theta$
Substituting these components back into the vector form, we get the general form of a unit vector $\vec{u}$ in the XY-plane:
$\vec{u} = (\cos\theta)\hat{i} + (\sin\theta)\hat{j}$
Here, $\theta$ can be any real number ($0 \leq \theta < 2\pi$ covers all unique unit vectors, but any real $\theta$ represents a direction in the plane). This form includes all possible unit vectors in the XY-plane by varying the angle $\theta$.
Conclusion:
All the unit vectors in the XY-plane can be represented in the form $\mathbf{\vec{u} = (\cos\theta)\hat{i} + (\sin\theta)\hat{j}}$, where $\theta$ is the angle the vector makes with the positive x-axis.
Example 27: If $\hat{i} + \hat{j} + \hat{k} ̂\;,\; 2\hat{i} + 5\hat{j} \;,\; 3\hat{i} + 2\hat{j} − 3\hat{k}$ ̂ and $\hat{i} − 6\hat{j} − \hat{k}$ are the position vectors of points A, B, C and D respectively, then find the angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$. Deduce that $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Answer:
We are given the position vectors of four points A, B, C, and D in 3D space. We need to find the vector representing the directed line segment from A to B ($\overrightarrow{AB}$) and from C to D ($\overrightarrow{CD}$), calculate the angle between these two vectors, and then use this information to deduce if they are collinear.
Given:
Position vector of point A, $\vec{OA} = \hat{i} + \hat{j} + \hat{k}$
Position vector of point B, $\vec{OB} = 2\hat{i} + 5\hat{j}$
Position vector of point C, $\vec{OC} = 3\hat{i} + 2\hat{j} - 3\hat{k}$
Position vector of point D, $\vec{OD} = \hat{i} - 6\hat{j} - \hat{k}$
To Find:
The angle between vector $\overrightarrow{AB}$ and vector $\overrightarrow{CD}$.
Deduce if $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Solution:
First, we find the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$ using the position vectors of the points. The vector from point A to point B is given by the difference between the position vector of B and the position vector of A.
$\overrightarrow{AB} = \vec{OB} - \vec{OA}$
$\overrightarrow{AB} = (2\hat{i} + 5\hat{j}) - (\hat{i} + \hat{j} + \hat{k})$
$\overrightarrow{AB} = (2 - 1)\hat{i} + (5 - 1)\hat{j} + (0 - 1)\hat{k}$
$\overrightarrow{AB} = \hat{i} + 4\hat{j} - \hat{k}$
Similarly, the vector from point C to point D is given by the difference between the position vector of D and the position vector of C.
$\overrightarrow{CD} = \vec{OD} - \vec{OC}$
$\overrightarrow{CD} = (\hat{i} - 6\hat{j} - \hat{k}) - (3\hat{i} + 2\hat{j} - 3\hat{k})$
$\overrightarrow{CD} = (1 - 3)\hat{i} + (-6 - 2)\hat{j} + (-1 - (-3))\hat{k}$
$\overrightarrow{CD} = -2\hat{i} - 8\hat{j} + 2\hat{k}$
Now, to find the angle $\theta$ between $\overrightarrow{AB}$ and $\overrightarrow{CD}$, we can use the dot product formula:
$\overrightarrow{AB} \cdot \overrightarrow{CD} = |\overrightarrow{AB}| |\overrightarrow{CD}| \cos\theta$
So, $\cos\theta = \frac{\overrightarrow{AB} \cdot \overrightarrow{CD}}{|\overrightarrow{AB}| |\overrightarrow{CD}|}$
First, calculate the dot product $\overrightarrow{AB} \cdot \overrightarrow{CD}$.
$\overrightarrow{AB} \cdot \overrightarrow{CD} = (\hat{i} + 4\hat{j} - \hat{k}) \cdot (-2\hat{i} - 8\hat{j} + 2\hat{k})$
$\overrightarrow{AB} \cdot \overrightarrow{CD} = (1)(-2) + (4)(-8) + (-1)(2)$
$\overrightarrow{AB} \cdot \overrightarrow{CD} = -2 - 32 - 2$
$\overrightarrow{AB} \cdot \overrightarrow{CD} = -36$
Next, calculate the magnitudes of the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$.
$|\overrightarrow{AB}| = \sqrt{(1)^2 + (4)^2 + (-1)^2} = \sqrt{1 + 16 + 1} = \sqrt{18}$
$|\overrightarrow{AB}| = \sqrt{9 \times 2} = 3\sqrt{2}$
$|\overrightarrow{CD}| = \sqrt{(-2)^2 + (-8)^2 + (2)^2} = \sqrt{4 + 64 + 4} = \sqrt{72}$
$|\overrightarrow{CD}| = \sqrt{36 \times 2} = 6\sqrt{2}$
Now, substitute the dot product and magnitudes into the formula for $\cos\theta$.
$\cos\theta = \frac{-36}{(3\sqrt{2})(6\sqrt{2})}$
$\cos\theta = \frac{-36}{18 \times 2}$
$\cos\theta = \frac{-36}{36}$
$\cos\theta = -1$
The angle $\theta$ whose cosine is $-1$ is $180^\circ$ or $\pi$ radians.
$\theta = \cos^{-1}(-1) = 180^\circ$
Deduction of Collinearity:
Two non-zero vectors are collinear if and only if the angle between them is $0^\circ$ or $180^\circ$. In this case, the angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$ is $180^\circ$. This means the vectors are parallel and point in opposite directions.
Alternatively, two vectors $\vec{a}$ and $\vec{b}$ are collinear if one is a scalar multiple of the other, i.e., $\vec{a} = k\vec{b}$ for some scalar $k$. Let's check if this holds for $\overrightarrow{AB}$ and $\overrightarrow{CD}$.
We have $\overrightarrow{AB} = \hat{i} + 4\hat{j} - \hat{k}$ and $\overrightarrow{CD} = -2\hat{i} - 8\hat{j} + 2\hat{k}$.
Observe the components of $\overrightarrow{CD}$: $-2\hat{i}$, $-8\hat{j}$, $+2\hat{k}$. If we factor out $-2$, we get:
$\overrightarrow{CD} = -2(\hat{i}) -2(4\hat{j}) -2(-1\hat{k})$
$\overrightarrow{CD} = -2(\hat{i} + 4\hat{j} - \hat{k})$
We recognize the expression in the parenthesis as $\overrightarrow{AB}$.
$\overrightarrow{CD} = -2 \overrightarrow{AB}$
Since $\overrightarrow{CD}$ is a scalar multiple of $\overrightarrow{AB}$ (with the scalar $k = -2$), the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are collinear.
Result:
The angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$ is $180^\circ$.
Since the angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$ is $180^\circ$, the vectors are collinear.
Example 28: Let $\vec{a} \;,\; \vec{b}$ and $\vec{c}$ be three vectors such that $|\;\vec{a}\;| = 3 \;,\; |\;\vec{b}\;| = 4 \;,\; |\;\vec{c}\;| = 5$ and each one of them being perpendicular to the sum of the other two, find $|\;\vec{a} + \vec{b} + \vec{c}\;|$.
Answer:
We are given three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ with their magnitudes and a condition about their perpendicularity. We need to find the magnitude of their sum.
Given:
Three vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ such that:
$|\;\vec{a}\;| = 3$
$|\;\vec{b}\;| = 4$
$|\;\vec{c}\;| = 5$
Each vector is perpendicular to the sum of the other two.
To Find:
The magnitude of the sum of the three vectors, i.e., $|\;\vec{a} + \vec{b} + \vec{c}\;|$.
Solution:
The condition that each vector is perpendicular to the sum of the other two can be written using the dot product. If two vectors are perpendicular, their dot product is zero.
$\vec{a} \cdot (\vec{b} + \vec{c}) = 0$
... (1)
$\vec{b} \cdot (\vec{a} + \vec{c}) = 0$
... (2)
$\vec{c} \cdot (\vec{a} + \vec{b}) = 0$
... (3)
Using the distributive property of the dot product, we expand these equations:
$\vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} = 0$
... (4)
$\vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{c} = 0$
... (5)
$\vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} = 0$
... (6)
Using the commutative property of the dot product ($\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$), equations (5) and (6) can be written as:
$\vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} = 0$
... (5')
$\vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} = 0$
... (6')
From equation (4), we have $\vec{a} \cdot \vec{c} = -\vec{a} \cdot \vec{b}$.
Substitute this into equation (6'):
$ (-\vec{a} \cdot \vec{b}) + \vec{b} \cdot \vec{c} = 0 $
$ \vec{b} \cdot \vec{c} = \vec{a} \cdot \vec{b} $
Now substitute $\vec{b} \cdot \vec{c} = \vec{a} \cdot \vec{b}$ into equation (5'):
$ \vec{a} \cdot \vec{b} + (\vec{a} \cdot \vec{b}) = 0 $
$ 2 (\vec{a} \cdot \vec{b}) = 0 $
This implies:
$\vec{a} \cdot \vec{b} = 0$
Since $\vec{a} \cdot \vec{b} = 0$, from $\vec{a} \cdot \vec{c} = -\vec{a} \cdot \vec{b}$, we get $\vec{a} \cdot \vec{c} = 0$.
Since $\vec{a} \cdot \vec{b} = 0$, from $\vec{b} \cdot \vec{c} = \vec{a} \cdot \vec{b}$, we get $\vec{b} \cdot \vec{c} = 0$.
So, the conditions imply that $\vec{a} \cdot \vec{b} = 0$, $\vec{a} \cdot \vec{c} = 0$, and $\vec{b} \cdot \vec{c} = 0$. This means the vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ are mutually orthogonal.
Next, we want to find the magnitude of the sum, $|\;\vec{a} + \vec{b} + \vec{c}\;|$. We can calculate the square of the magnitude:
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = (\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c})$
Expanding the dot product:
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = \vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} + \vec{c} \cdot \vec{c}$
Using $\vec{v} \cdot \vec{v} = |\;\vec{v}\;|^2$ and the commutative property of the dot product:
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2(\vec{a} \cdot \vec{b}) + 2(\vec{a} \cdot \vec{c}) + 2(\vec{b} \cdot \vec{c})$
Substitute the results from the perpendicularity condition ($\vec{a} \cdot \vec{b} = 0$, $\vec{a} \cdot \vec{c} = 0$, $\vec{b} \cdot \vec{c} = 0$):
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2(0) + 2(0) + 2(0)$
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2$
Substitute the given magnitudes:
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = (3)^2 + (4)^2 + (5)^2$
... (7)
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = 9 + 16 + 25$
$|\;\vec{a} + \vec{b} + \vec{c}\;|^2 = 50$
To find the magnitude, we take the square root of both sides:
$|\;\vec{a} + \vec{b} + \vec{c}\;| = \sqrt{50}$
$|\;\vec{a} + \vec{b} + \vec{c}\;| = \sqrt{25 \times 2}$
$|\;\vec{a} + \vec{b} + \vec{c}\;| = 5\sqrt{2}$
Result:
The magnitude of the sum of the vectors $\vec{a} + \vec{b} + \vec{c}$ is $5\sqrt{2}$.
Example 29: Three vectors $\vec{a}$ , $\vec{b}$ and $\vec{c}$ satisfy the condition $\vec{a} + \vec{b} + \vec{c} = \vec{0}$. Evaluate the quantity $µ = \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}$, if $|\;\vec{a}\;| = 3 \;,\; |\;\vec{b}\;| = 4$ and $|\;\vec{c}\;| = 2$.
Answer:
We are given a condition relating three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$, along with their magnitudes. We need to evaluate a specific scalar quantity involving dot products of these vectors.
Given:
Three vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ satisfying the condition:
$\vec{a} + \vec{b} + \vec{c} = \vec{0}$
The magnitudes of the vectors are:
$|\;\vec{a}\;| = 3$
$|\;\vec{b}\;| = 4$
$|\;\vec{c}\;| = 2$
To Find:
The quantity $\mu = \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}$.
Solution:
We are given the fundamental relation between the vectors:
$\vec{a} + \vec{b} + \vec{c} = \vec{0}$
... (i)
To involve the dot products and magnitudes, we can take the dot product of the equation (i) with itself. The dot product of a vector with itself is equal to the square of its magnitude, and the dot product of the zero vector with itself is zero.
$(\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c}) = \vec{0} \cdot \vec{0}$
$(\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c}) = 0$
Expand the left side of the equation using the distributive property of the dot product:
$\vec{a} \cdot (\vec{a} + \vec{b} + \vec{c}) + \vec{b} \cdot (\vec{a} + \vec{b} + \vec{c}) + \vec{c} \cdot (\vec{a} + \vec{b} + \vec{c}) = 0$
$\vec{a} \cdot \vec{a} + \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a} + \vec{c} \cdot \vec{b} + \vec{c} \cdot \vec{c} = 0$
Using the properties $\vec{v} \cdot \vec{v} = |\;\vec{v}\;|^2$ and $\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$ (commutative property of dot product), we can rearrange and simplify the equation:
$|\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2(\vec{a} \cdot \vec{b}) + 2(\vec{a} \cdot \vec{c}) + 2(\vec{b} \cdot \vec{c}) = 0$
We can factor out a $2$ from the dot product terms:
$|\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2(\vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}) = 0$
Note that the quantity we need to evaluate is $\mu = \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{a}$. Since $\vec{a} \cdot \vec{c} = \vec{c} \cdot \vec{a}$, the expression in the parenthesis is exactly $\mu$.
$|\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2\mu = 0$
... (ii)
Now, substitute the given magnitudes of the vectors into equation (ii):
$(3)^2 + (4)^2 + (2)^2 + 2\mu = 0$
$9 + 16 + 4 + 2\mu = 0$
$29 + 2\mu = 0$
Now, solve for $\mu$:
$2\mu = -29$
$\mu = -\frac{29}{2}$
Result:
The value of the quantity $\mu = \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{c} + \vec{c} \;.\; \vec{a}$ is $\mathbf{-\frac{29}{2}}$.
Example 30: If with reference to the right handed system of mutually perpendicular unit vectors $\hat{i} \;,\; \hat{j}$ and $\hat{k}$, $\vec{α} = 3\hat{i} − \hat{j}$ , $\vec{β} = 2\hat{i} + \hat{j} − 3\hat{k}$ , then express $\vec{β}$ in the form $\vec{β} = \vec{β}_1 + \vec{β}_2$ , where $\vec{β}_1$ is parallel to $\vec{α}$ and $\vec{β}_2$ is perpendicular to $\vec{α}$ .
Answer:
We are given two vectors $\vec{\alpha}$ and $\vec{\beta}$ and asked to express $\vec{\beta}$ as the sum of two vectors, one parallel to $\vec{\alpha}$ and the other perpendicular to $\vec{\alpha}$. This is a classic vector projection problem.
Given:
Vectors $\vec{\alpha} = 3\hat{i} - \hat{j}$
$\vec{\beta} = 2\hat{i} + \hat{j} - 3\hat{k}$
We need to express $\vec{\beta}$ as $\vec{\beta} = \vec{\beta}_1 + \vec{\beta}_2$, where $\vec{\beta}_1 \parallel \vec{\alpha}$ and $\vec{\beta}_2 \perp \vec{\alpha}$.
To Find:
The vectors $\vec{\beta}_1$ and $\vec{\beta}_2$.
Solution:
Let $\vec{\beta}_1$ be the component of $\vec{\beta}$ parallel to $\vec{\alpha}$, and $\vec{\beta}_2$ be the component of $\vec{\beta}$ perpendicular to $\vec{\alpha}$.
Since $\vec{\beta}_1$ is parallel to $\vec{\alpha}$, it must be a scalar multiple of $\vec{\alpha}$. Let $\vec{\beta}_1 = c\vec{\alpha}$ for some scalar $c$.
The component of $\vec{\beta}$ parallel to $\vec{\alpha}$ is given by the vector projection of $\vec{\beta}$ onto $\vec{\alpha}$. The formula for the vector projection of $\vec{\beta}$ onto $\vec{\alpha}$ is:
$\vec{\beta}_1 = \text{proj}_{\vec{\alpha}} \vec{\beta} = \frac{\vec{\beta} \cdot \vec{\alpha}}{|\;\vec{\alpha}\;|^2} \vec{\alpha}$
First, let's calculate the dot product $\vec{\beta} \cdot \vec{\alpha}$.
$\vec{\beta} \cdot \vec{\alpha} = (2\hat{i} + \hat{j} - 3\hat{k}) \cdot (3\hat{i} - \hat{j})$
$\vec{\beta} \cdot \vec{\alpha} = (2)(3) + (1)(-1) + (-3)(0)$
$\vec{\beta} \cdot \vec{\alpha} = 6 - 1 + 0$
$\vec{\beta} \cdot \vec{\alpha} = 5$
Next, let's calculate the magnitude squared of $\vec{\alpha}$, $|\;\vec{\alpha}\;|^2$.
$|\;\vec{\alpha}\;|^2 = (3)^2 + (-1)^2 + (0)^2$
$|\;\vec{\alpha}\;|^2 = 9 + 1 + 0$
$|\;\vec{\alpha}\;|^2 = 10$
Now, substitute these values into the formula for $\vec{\beta}_1$:
$\vec{\beta}_1 = \frac{5}{10} (3\hat{i} - \hat{j})$
$\vec{\beta}_1 = \frac{1}{2} (3\hat{i} - \hat{j})$
$\vec{\beta}_1 = \frac{3}{2}\hat{i} - \frac{1}{2}\hat{j}$
This is the component of $\vec{\beta}$ parallel to $\vec{\alpha}$.
Now, we find $\vec{\beta}_2$. We know that $\vec{\beta} = \vec{\beta}_1 + \vec{\beta}_2$. Therefore, $\vec{\beta}_2 = \vec{\beta} - \vec{\beta}_1$.
$\vec{\beta}_2 = (2\hat{i} + \hat{j} - 3\hat{k}) - (\frac{3}{2}\hat{i} - \frac{1}{2}\hat{j})$
$\vec{\beta}_2 = (2 - \frac{3}{2})\hat{i} + (1 - (-\frac{1}{2}))\hat{j} + (-3 - 0)\hat{k}$
$\vec{\beta}_2 = (\frac{4}{2} - \frac{3}{2})\hat{i} + (1 + \frac{1}{2})\hat{j} - 3\hat{k}$
$\vec{\beta}_2 = \frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k}$
This is the component of $\vec{\beta}$ perpendicular to $\vec{\alpha}$.
Verification:
To verify that $\vec{\beta}_2$ is perpendicular to $\vec{\alpha}$, we can check their dot product. If $\vec{\alpha} \cdot \vec{\beta}_2 = 0$, they are perpendicular.
$\vec{\alpha} \cdot \vec{\beta}_2 = (3\hat{i} - \hat{j}) \cdot (\frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k})$
$\vec{\alpha} \cdot \vec{\beta}_2 = (3)(\frac{1}{2}) + (-1)(\frac{3}{2}) + (0)(-3)$
$\vec{\alpha} \cdot \vec{\beta}_2 = \frac{3}{2} - \frac{3}{2} + 0$
$\vec{\alpha} \cdot \vec{\beta}_2 = 0$
Since the dot product is zero, $\vec{\beta}_2$ is indeed perpendicular to $\vec{\alpha}$.
We also need to check if $\vec{\beta}_1 + \vec{\beta}_2 = \vec{\beta}$.
$\vec{\beta}_1 + \vec{\beta}_2 = (\frac{3}{2}\hat{i} - \frac{1}{2}\hat{j}) + (\frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k})$
$\vec{\beta}_1 + \vec{\beta}_2 = (\frac{3}{2} + \frac{1}{2})\hat{i} + (-\frac{1}{2} + \frac{3}{2})\hat{j} + (0 - 3)\hat{k}$
$\vec{\beta}_1 + \vec{\beta}_2 = (\frac{4}{2})\hat{i} + (\frac{2}{2})\hat{j} - 3\hat{k}$
$\vec{\beta}_1 + \vec{\beta}_2 = 2\hat{i} + \hat{j} - 3\hat{k}$
This is equal to the given vector $\vec{\beta}$. The decomposition is correct.
Result:
The vector $\vec{\beta}$ can be expressed as the sum of $\vec{\beta}_1$ (parallel to $\vec{\alpha}$) and $\vec{\beta}_2$ (perpendicular to $\vec{\alpha}$) where:
$\vec{\beta}_1 = \frac{3}{2}\hat{i} - \frac{1}{2}\hat{j}$
$\vec{\beta}_2 = \frac{1}{2}\hat{i} + \frac{3}{2}\hat{j} - 3\hat{k}$
Miscellaneous Exercise on Chapter 10
Question 1. Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
Answer:
We need to find a unit vector in the XY-plane that makes a specific angle with the positive x-axis. A unit vector has a magnitude of 1. In the XY-plane, a vector can be represented by its components along the x and y axes.
Given:
The vector is a unit vector in the XY-plane.
The angle made with the positive direction of the x-axis is $30^\circ$.
To Find:
The unit vector satisfying the given conditions.
Solution:
A vector $\vec{v}$ in the XY-plane making an angle $\theta$ with the positive x-axis can be generally expressed in terms of its components as:
$\vec{v} = |\;\vec{v}\;| (\cos\theta \hat{i} + \sin\theta \hat{j})$
where $|\;\vec{v}\;|$ is the magnitude of the vector, $\hat{i}$ is the unit vector along the positive x-axis, and $\hat{j}$ is the unit vector along the positive y-axis.
For a unit vector, the magnitude is $1$. So, $|\;\vec{v}\;| = 1$.
The angle given is $\theta = 30^\circ$.
Substitute these values into the general form of the vector:
$\vec{u} = 1 \cdot (\cos(30^\circ) \hat{i} + \sin(30^\circ) \hat{j})$
$\vec{u} = \cos(30^\circ) \hat{i} + \sin(30^\circ) \hat{j}$
Now, we need to find the values of $\cos(30^\circ)$ and $\sin(30^\circ)$.
$\cos(30^\circ) = \frac{\sqrt{3}}{2}$
$\sin(30^\circ) = \frac{1}{2}$
Substitute these trigonometric values into the expression for the unit vector $\vec{u}$:
$\vec{u} = \frac{\sqrt{3}}{2}\hat{i} + \frac{1}{2}\hat{j}$
Verification:
Let's check the magnitude of the resulting vector $\vec{u}$.
$|\;\vec{u}\;| = \sqrt{(\frac{\sqrt{3}}{2})^2 + (\frac{1}{2})^2}$
$|\;\vec{u}\;| = \sqrt{\frac{3}{4} + \frac{1}{4}}$
$|\;\vec{u}\;| = \sqrt{\frac{3+1}{4}}$
$|\;\vec{u}\;| = \sqrt{\frac{4}{4}}$
$|\;\vec{u}\;| = \sqrt{1}$
$|\;\vec{u}\;| = 1$
The magnitude is 1, so it is a unit vector.
The angle $\theta$ it makes with the positive x-axis is given by $\tan\theta = \frac{\text{y-component}}{\text{x-component}}$.
$\tan\theta = \frac{1/2}{\sqrt{3}/2} = \frac{1}{2} \times \frac{2}{\sqrt{3}} = \frac{1}{\sqrt{3}}$
Since $\tan\theta = \frac{1}{\sqrt{3}}$ and the components are positive (meaning the vector is in the first quadrant), $\theta = 30^\circ$.
The conditions are satisfied.
Result:
The unit vector in the XY-plane making an angle of $30^\circ$ with the positive direction of the x-axis is $\mathbf{\frac{\sqrt{3}}{2}\hat{i} + \frac{1}{2}\hat{j}}$.
Question 2. Find the scalar components and magnitude of the vector joining the points P (x1 , y1 , z1) and Q (x2 , y2 , z2).
Answer:
We are given two points P and Q in three-dimensional space with their coordinates. We need to find the vector that starts at P and ends at Q, determine its scalar components, and calculate its magnitude.
Given:
Point P with coordinates $(x_1, y_1, z_1)$.
Point Q with coordinates $(x_2, y_2, z_2)$.
To Find:
The vector $\overrightarrow{PQ}$.
The scalar components of $\overrightarrow{PQ}$.
The magnitude of $\overrightarrow{PQ}$.
Solution:
The position vector of point P with respect to the origin O is $\vec{OP} = x_1\hat{i} + y_1\hat{j} + z_1\hat{k}$.
The position vector of point Q with respect to the origin O is $\vec{OQ} = x_2\hat{i} + y_2\hat{j} + z_2\hat{k}$.
The vector joining point P to point Q, denoted by $\overrightarrow{PQ}$, is given by the difference between the position vector of the terminal point Q and the position vector of the initial point P.
$\overrightarrow{PQ} = \vec{OQ} - \vec{OP}$
$\overrightarrow{PQ} = (x_2\hat{i} + y_2\hat{j} + z_2\hat{k}) - (x_1\hat{i} + y_1\hat{j} + z_1\hat{k})$
$\overrightarrow{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$
The scalar components of the vector $\overrightarrow{PQ}$ are the coefficients of the unit vectors $\hat{i}$, $\hat{j}$, and $\hat{k}$.
Scalar component along the x-axis: $(x_2 - x_1)$
Scalar component along the y-axis: $(y_2 - y_1)$
Scalar component along the z-axis: $(z_2 - z_1)$
The magnitude of the vector $\overrightarrow{PQ}$ is the length of the line segment PQ. If $\overrightarrow{PQ} = a\hat{i} + b\hat{j} + c\hat{k}$, its magnitude is given by $\sqrt{a^2 + b^2 + c^2}$.
In this case, $a = (x_2 - x_1)$, $b = (y_2 - y_1)$, and $c = (z_2 - z_1)$.
$|\overrightarrow{PQ}| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$
Result:
The vector joining points P$(x_1, y_1, z_1)$ and Q$(x_2, y_2, z_2)$ is $\overrightarrow{PQ} = (x_2 - x_1)\hat{i} + (y_2 - y_1)\hat{j} + (z_2 - z_1)\hat{k}$.
The scalar components of $\overrightarrow{PQ}$ are $\mathbf{(x_2 - x_1)}$, $\mathbf{(y_2 - y_1)}$, and $\mathbf{(z_2 - z_1)}$.
The magnitude of $\overrightarrow{PQ}$ is $\mathbf{\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}}$.
Question 3. A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
Answer:
This problem involves finding the resultant displacement from two successive movements, which can be solved using vector addition.
Given:
First displacement: 4 km towards West.
Second displacement: 3 km in a direction $30^\circ$ East of North.
To Find:
The girl's total displacement from her initial point.
Solution:
Let's set up a coordinate system where the positive x-axis points East and the positive y-axis points North. The initial point of departure is the origin O$(0,0)$.
The first displacement is 4 km towards West. In our coordinate system, West is along the negative x-axis. So, the first displacement vector $\vec{d}_1$ is:
$\vec{d}_1 = -4\hat{i}$
The second displacement is 3 km in a direction $30^\circ$ East of North. This means the angle is measured $30^\circ$ from the North direction (positive y-axis) towards the East direction (positive x-axis). The angle made with the positive x-axis (measured counterclockwise) is $90^\circ - 30^\circ = 60^\circ$.
The magnitude of the second displacement vector $\vec{d}_2$ is $|\vec{d}_2| = 3$ km.
The components of $\vec{d}_2$ are:
x-component: $|\vec{d}_2| \cos(60^\circ) = 3 \times \frac{1}{2} = \frac{3}{2}$
y-component: $|\vec{d}_2| \sin(60^\circ) = 3 \times \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{2}$
So, the second displacement vector $\vec{d}_2$ is:
$\vec{d}_2 = \frac{3}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$
The total displacement $\vec{D}$ is the vector sum of the individual displacements:
$\vec{D} = \vec{d}_1 + \vec{d}_2$
$\vec{D} = (-4\hat{i}) + (\frac{3}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j})$
$\vec{D} = (-4 + \frac{3}{2})\hat{i} + (\frac{3\sqrt{3}}{2})\hat{j}$
To add the x-components:
$-4 + \frac{3}{2} = -\frac{8}{2} + \frac{3}{2} = -\frac{5}{2}$
So, the total displacement vector is:
$\vec{D} = -\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}$
The magnitude of the total displacement is the length of the vector $\vec{D}$. If $\vec{D} = D_x\hat{i} + D_y\hat{j}$, the magnitude is $|\vec{D}| = \sqrt{D_x^2 + D_y^2}$.
$|\vec{D}| = \sqrt{(-\frac{5}{2})^2 + (\frac{3\sqrt{3}}{2})^2}$
$|\vec{D}| = \sqrt{\frac{25}{4} + \frac{9 \times 3}{4}}$
$|\vec{D}| = \sqrt{\frac{25}{4} + \frac{27}{4}}$
$|\vec{D}| = \sqrt{\frac{25 + 27}{4}}$
$|\vec{D}| = \sqrt{\frac{52}{4}}$
$|\vec{D}| = \sqrt{13}$
The magnitude of the displacement is $\sqrt{13}$ km.
The direction of the displacement can be found using the components. The x-component is negative ($-\frac{5}{2}$) and the y-component is positive ($\frac{3\sqrt{3}}{2}$), so the displacement vector lies in the second quadrant (West of North or North of West).
Let $\phi$ be the angle the vector $\vec{D}$ makes with the positive x-axis (East). Then $\tan\phi = \frac{D_y}{D_x}$.
$\tan\phi = \frac{3\sqrt{3}/2}{-5/2} = -\frac{3\sqrt{3}}{5}$
The angle with the negative x-axis (West) is given by $\alpha = \tan^{-1}\left(\left|\frac{3\sqrt{3}}{-5}\right|\right) = \tan^{-1}\left(\frac{3\sqrt{3}}{5}\right)$. This angle is measured upwards from the negative x-axis, which is equivalent to being North of West.
Result:
The girl's total displacement from her initial point is a vector with magnitude $\mathbf{\sqrt{13}}$ km.
The displacement vector is $\mathbf{-\frac{5}{2}\hat{i} + \frac{3\sqrt{3}}{2}\hat{j}}$ km.
The direction of the displacement is $\mathbf{\tan^{-1}(\frac{3\sqrt{3}}{5})}$ North of West.
Question 4. If $\vec{a} = \vec{b} + \vec{c}$ , then is it true that $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ ? justify your answer.
Answer:
We are asked if the equation $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ is true, given the vector equation $\vec{a} = \vec{b} + \vec{c}$.
Given:
Vector equation: $\vec{a} = \vec{b} + \vec{c}$
To Check:
Is $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ always true?
Justification:
The magnitude of the sum of two vectors is related to the sum of their magnitudes by the triangle inequality.
The triangle inequality for vectors states that for any two vectors $\vec{b}$ and $\vec{c}$, the following inequality holds:
$|\;\vec{b} + \vec{c}\;| \leq |\;\vec{b}\;| + |\;\vec{c}\;|$
Given that $\vec{a} = \vec{b} + \vec{c}$, we have $|\;\vec{a}\;| = |\;\vec{b} + \vec{c}\;|$.
Substituting this into the triangle inequality, we get:
$|\;\vec{a}\;| \leq |\;\vec{b}\;| + |\;\vec{c}\;|$
This inequality shows that the magnitude of $\vec{a}$ is generally less than or equal to the sum of the magnitudes of $\vec{b}$ and $\vec{c}$.
The equality $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ holds if and only if the vectors $\vec{b}$ and $\vec{c}$ are collinear and point in the same direction (or if one or both of the vectors are zero vectors). This means that one vector is a non-negative scalar multiple of the other, i.e., $\vec{c} = k\vec{b}$ for some scalar $k \geq 0$, or $\vec{b} = m\vec{c}$ for some scalar $m \geq 0$.
If the vectors $\vec{b}$ and $\vec{c}$ are not collinear or are collinear but point in opposite directions, the strict inequality $|\;\vec{a}\;| < |\;\vec{b}\;| + |\;\vec{c}\;|$ holds.
Counterexample:
Consider two vectors in the XY-plane:
Let $\vec{b} = \hat{i}$
Let $\vec{c} = \hat{j}$
The magnitudes are $|\;\vec{b}\;| = \sqrt{1^2} = 1$ and $|\;\vec{c}\;| = \sqrt{1^2} = 1$.
The sum of the magnitudes is $|\;\vec{b}\;| + |\;\vec{c}\;| = 1 + 1 = 2$.
Now, let's find $\vec{a} = \vec{b} + \vec{c}$:
$\vec{a} = \hat{i} + \hat{j}$
The magnitude of $\vec{a}$ is:
$|\;\vec{a}\;| = \sqrt{(1)^2 + (1)^2} = \sqrt{1 + 1} = \sqrt{2}$
In this case, $|\;\vec{a}\;| = \sqrt{2}$ and $|\;\vec{b}\;| + |\;\vec{c}\;| = 2$.
Since $\sqrt{2} \approx 1.414$, we see that $\sqrt{2} \neq 2$. Specifically, $\sqrt{2} < 2$.
$|\;\vec{a}\;| < |\;\vec{b}\;| + |\;\vec{c}\;|$
This counterexample demonstrates that $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ is not always true when $\vec{a} = \vec{b} + \vec{c}$.
Conclusion:
No, it is not always true that $|\;\vec{a}\;| = |\;\vec{b}\;| + |\;\vec{c}\;|$ if $\vec{a} = \vec{b} + \vec{c}$. The equality holds only when the vectors $\vec{b}$ and $\vec{c}$ are collinear and point in the same direction. Otherwise, the magnitude of the sum is strictly less than the sum of the magnitudes.
Question 5. Find the value of x for which $x(\hat{i} + \hat{j} + \hat{k})$ is a unit vector.
Answer:
We are given a vector expressed as a scalar multiple of a sum of unit vectors and asked to find the value of the scalar such that the resulting vector is a unit vector.
Given:
The vector is $\vec{v} = x(\hat{i} + \hat{j} + \hat{k})$.
The vector $\vec{v}$ is a unit vector.
To Find:
The value of $x$.
Solution:
A unit vector is a vector with a magnitude of 1. The magnitude of the given vector $\vec{v}$ must be equal to 1.
The vector can be written as $\vec{v} = x\hat{i} + x\hat{j} + x\hat{k}$.
The magnitude of $\vec{v}$ is given by:
$|\;\vec{v}\;| = \sqrt{(\text{component along }\hat{i})^2 + (\text{component along }\hat{j})^2 + (\text{component along }\hat{k})^2}$
$|\;\vec{v}\;| = \sqrt{x^2 + x^2 + x^2}$
$|\;\vec{v}\;| = \sqrt{3x^2}$
Since $\vec{v}$ is a unit vector, its magnitude is 1:
$|\;\vec{v}\;| = 1$
$\sqrt{3x^2} = 1$
... (i)
To solve for $x$, square both sides of the equation (i):
$(\sqrt{3x^2})^2 = 1^2$
$3x^2 = 1$
Now, isolate $x^2$:
$x^2 = \frac{1}{3}$
Take the square root of both sides to find the value of $x$:
$x = \pm\sqrt{\frac{1}{3}}$
$x = \pm\frac{\sqrt{1}}{\sqrt{3}}$
$x = \pm\frac{1}{\sqrt{3}}$
We can rationalize the denominator:
$x = \pm\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$x = \pm\frac{\sqrt{3}}{3}$
Thus, there are two possible values for $x$ for which the given vector is a unit vector.
Result:
The values of $x$ for which $x(\hat{i} + \hat{j} + \hat{k})$ is a unit vector are $\mathbf{x = \frac{1}{\sqrt{3}}}$ and $\mathbf{x = -\frac{1}{\sqrt{3}}}$, or $\mathbf{x = \pm\frac{\sqrt{3}}{3}}$.
Question 6. Find a vector of magnitude 5 units, and parallel to the resultant of the vectors $\vec{a} = 2\hat{i} + 3\hat{j} − \hat{k}$ and $\vec{b} = \hat{i} − 2\hat{j} + \hat{k}$ .
Answer:
We need to find a vector that has a specific magnitude (5 units) and is parallel to the sum of two given vectors. A vector parallel to another vector can be obtained by multiplying the latter by a scalar. To control the magnitude, we can use the unit vector in the desired direction.
Given:
Vector $\vec{a} = 2\hat{i} + 3\hat{j} - \hat{k}$
Vector $\vec{b} = \hat{i} - 2\hat{j} + \hat{k}$
The required vector has a magnitude of 5 units.
The required vector is parallel to the resultant of $\vec{a}$ and $\vec{b}$.
To Find:
The vector with magnitude 5 units and parallel to $\vec{a} + \vec{b}$.
Solution:
First, find the resultant vector of $\vec{a}$ and $\vec{b}$, let's call it $\vec{r}$.
$\vec{r} = \vec{a} + \vec{b}$
$\vec{r} = (2\hat{i} + 3\hat{j} - \hat{k}) + (\hat{i} - 2\hat{j} + \hat{k})$
$\vec{r} = (2 + 1)\hat{i} + (3 - 2)\hat{j} + (-1 + 1)\hat{k}$
$\vec{r} = 3\hat{i} + \hat{j} + 0\hat{k}$
$\vec{r} = 3\hat{i} + \hat{j}$
Next, find the unit vector in the direction of $\vec{r}$. A unit vector in the direction of $\vec{r}$ is given by $\hat{r} = \frac{\vec{r}}{|\;\vec{r}\;|}$.
First, calculate the magnitude of $\vec{r}$, $|\;\vec{r}\;|$.
$|\;\vec{r}\;| = \sqrt{(3)^2 + (1)^2 + (0)^2}$
$|\;\vec{r}\;| = \sqrt{9 + 1 + 0}$
$|\;\vec{r}\;| = \sqrt{10}$
Now, find the unit vector $\hat{r}$:
$\hat{r} = \frac{3\hat{i} + \hat{j}}{\sqrt{10}}$
$\hat{r} = \frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j}$
We need a vector with a magnitude of 5 units that is parallel to $\vec{r}$. A vector parallel to $\vec{r}$ can point in the same direction as $\vec{r}$ or in the opposite direction. Both are considered parallel.
Case 1: The vector points in the same direction as $\vec{r}$.
The required vector, let's call it $\vec{v}_1$, will have the direction of $\hat{r}$ and a magnitude of 5. So, $\vec{v}_1 = 5\hat{r}$.
$\vec{v}_1 = 5 \left( \frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j} \right)$
$\vec{v}_1 = \frac{15}{\sqrt{10}}\hat{i} + \frac{5}{\sqrt{10}}\hat{j}$
We can rationalize the denominators:
$\vec{v}_1 = \frac{15\sqrt{10}}{10}\hat{i} + \frac{5\sqrt{10}}{10}\hat{j}$
$\vec{v}_1 = \frac{3\sqrt{10}}{2}\hat{i} + \frac{\sqrt{10}}{2}\hat{j}$
Case 2: The vector points in the opposite direction as $\vec{r}$.
The required vector, let's call it $\vec{v}_2$, will have the direction of $-\hat{r}$ and a magnitude of 5. So, $\vec{v}_2 = 5(-\hat{r}) = -5\hat{r}$.
$\vec{v}_2 = -5 \left( \frac{3}{\sqrt{10}}\hat{i} + \frac{1}{\sqrt{10}}\hat{j} \right)$
$\vec{v}_2 = -\frac{15}{\sqrt{10}}\hat{i} - \frac{5}{\sqrt{10}}\hat{j}$
Rationalizing the denominators:
$\vec{v}_2 = -\frac{15\sqrt{10}}{10}\hat{i} - \frac{5\sqrt{10}}{10}\hat{j}$
$\vec{v}_2 = -\frac{3\sqrt{10}}{2}\hat{i} - \frac{\sqrt{10}}{2}\hat{j}$
Both $\vec{v}_1$ and $\vec{v}_2$ have a magnitude of 5 units and are parallel to $\vec{r}$. The question asks for "a" vector, implying either one is a valid answer. Usually, if not specified, the vector in the same direction is preferred, but both are mathematically correct answers for a vector parallel to the resultant.
Result:
A vector of magnitude 5 units and parallel to the resultant of $\vec{a}$ and $\vec{b}$ can be:
$\mathbf{\frac{3\sqrt{10}}{2}\hat{i} + \frac{\sqrt{10}}{2}\hat{j}}$
or
$\mathbf{-\frac{3\sqrt{10}}{2}\hat{i} - \frac{\sqrt{10}}{2}\hat{j}}$
Question 7. If $\vec{a} = \hat{i} + \hat{j} + \hat{k}$ , $\vec{b} = 2\hat{i} − \hat{j} + 3\hat{k}$ and $\vec{c} = \hat{i} − 2\hat{j} + \hat{k}$, find a unit vector parallel to the vector $2\vec{a} − \vec{b} + 3\vec{c}$.
Answer:
We are given three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$. We need to find a unit vector parallel to a linear combination of these vectors ($2\vec{a} - \vec{b} + 3\vec{c}$). To find a unit vector parallel to any given non-zero vector, we calculate the given vector and then divide it by its magnitude.
Given:
Vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$
Vector $\vec{b} = 2\hat{i} - \hat{j} + 3\hat{k}$
Vector $\vec{c} = \hat{i} - 2\hat{j} + \hat{k}$
To Find:
A unit vector parallel to the vector $2\vec{a} - \vec{b} + 3\vec{c}$.
Solution:
First, let's calculate the vector $2\vec{a} - \vec{b} + 3\vec{c}$. Let's call this vector $\vec{v}$.
$\vec{v} = 2\vec{a} - \vec{b} + 3\vec{c}$
$\vec{v} = 2(\hat{i} + \hat{j} + \hat{k}) - (2\hat{i} - \hat{j} + 3\hat{k}) + 3(\hat{i} - 2\hat{j} + \hat{k})$
Perform the scalar multiplications:
$2\vec{a} = 2\hat{i} + 2\hat{j} + 2\hat{k}$
$3\vec{c} = 3\hat{i} - 6\hat{j} + 3\hat{k}$
Now substitute these back into the expression for $\vec{v}$ and combine the terms:
$\vec{v} = (2\hat{i} + 2\hat{j} + 2\hat{k}) - (2\hat{i} - \hat{j} + 3\hat{k}) + (3\hat{i} - 6\hat{j} + 3\hat{k})$
Group the components along $\hat{i}$, $\hat{j}$, and $\hat{k}$:
$\vec{v} = (2 - 2 + 3)\hat{i} + (2 - (-1) - 6)\hat{j} + (2 - 3 + 3)\hat{k}$
$\vec{v} = (2 - 2 + 3)\hat{i} + (2 + 1 - 6)\hat{j} + (2 - 3 + 3)\hat{k}$
$\vec{v} = (3)\hat{i} + (-3)\hat{j} + (2)\hat{k}$
$\vec{v} = 3\hat{i} - 3\hat{j} + 2\hat{k}$
Now, we need to find a unit vector parallel to $\vec{v}$. A unit vector parallel to $\vec{v}$ is given by $\frac{\vec{v}}{|\;\vec{v}\;|}$.
First, calculate the magnitude of $\vec{v}$, $|\;\vec{v}\;|$.
$|\;\vec{v}\;| = \sqrt{(3)^2 + (-3)^2 + (2)^2}$
$|\;\vec{v}\;| = \sqrt{9 + 9 + 4}$
$|\;\vec{v}\;| = \sqrt{22}$
Now, divide $\vec{v}$ by its magnitude to get the unit vector:
Unit vector parallel to $\vec{v} = \frac{\vec{v}}{|\;\vec{v}\;|}$
Unit vector parallel to $\vec{v} = \frac{3\hat{i} - 3\hat{j} + 2\hat{k}}{\sqrt{22}}$
Unit vector parallel to $\vec{v} = \frac{3}{\sqrt{22}}\hat{i} - \frac{3}{\sqrt{22}}\hat{j} + \frac{2}{\sqrt{22}}\hat{k}$
This is one unit vector parallel to $\vec{v}$. The other unit vector parallel to $\vec{v}$ is in the opposite direction, which is $-\frac{\vec{v}}{|\;\vec{v}\;|}$. However, the question asks for "a" unit vector, so the one in the same direction is usually sufficient.
Result:
A unit vector parallel to the vector $2\vec{a} - \vec{b} + 3\vec{c}$ is $\mathbf{\frac{3}{\sqrt{22}}\hat{i} - \frac{3}{\sqrt{22}}\hat{j} + \frac{2}{\sqrt{22}}\hat{k}}$.
Question 8. Show that the points A (1, – 2, – 8), B(5, 0, –2) and C(11, 3, 7) are collinear, and find the ratio in which B divides AC.
Answer:
We need to show that three given points A, B, and C in 3D space are collinear. Points are collinear if they lie on the same straight line. One way to show this using vectors is to demonstrate that the vector connecting two of the points is parallel to the vector connecting another pair of points (e.g., $\overrightarrow{AB}$ is parallel to $\overrightarrow{BC}$). Parallel vectors are scalar multiples of each other. If they share a common point (like B in this case), they must be collinear.
We also need to find the ratio in which point B divides the line segment AC.
Given:
Point A (1, -2, -8)
Point B (5, 0, -2)
Point C (11, 3, 7)
To Show:
Points A, B, and C are collinear.
To Find:
The ratio in which B divides AC.
Solution:
Let's find the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$.
The position vectors of the points are:
$\vec{OA} = \hat{i} - 2\hat{j} - 8\hat{k}$
$\vec{OB} = 5\hat{i} + 0\hat{j} - 2\hat{k} = 5\hat{i} - 2\hat{k}$
$\vec{OC} = 11\hat{i} + 3\hat{j} + 7\hat{k}$
Vector $\overrightarrow{AB}$:
$\overrightarrow{AB} = \vec{OB} - \vec{OA}$
$\overrightarrow{AB} = (5\hat{i} - 2\hat{k}) - (\hat{i} - 2\hat{j} - 8\hat{k})$
$\overrightarrow{AB} = (5 - 1)\hat{i} + (0 - (-2))\hat{j} + (-2 - (-8))\hat{k}$
$\overrightarrow{AB} = 4\hat{i} + 2\hat{j} + (-2 + 8)\hat{k}$
$\overrightarrow{AB} = 4\hat{i} + 2\hat{j} + 6\hat{k}$
Vector $\overrightarrow{BC}$:
$\overrightarrow{BC} = \vec{OC} - \vec{OB}$
$\overrightarrow{BC} = (11\hat{i} + 3\hat{j} + 7\hat{k}) - (5\hat{i} - 2\hat{k})$
$\overrightarrow{BC} = (11 - 5)\hat{i} + (3 - 0)\hat{j} + (7 - (-2))\hat{k}$
$\overrightarrow{BC} = 6\hat{i} + 3\hat{j} + (7 + 2)\hat{k}$
$\overrightarrow{BC} = 6\hat{i} + 3\hat{j} + 9\hat{k}$
To check for collinearity, we see if $\overrightarrow{BC}$ is a scalar multiple of $\overrightarrow{AB}$. That is, is $\overrightarrow{BC} = k\overrightarrow{AB}$ for some scalar $k$? Compare the components:
$6\hat{i} + 3\hat{j} + 9\hat{k} = k(4\hat{i} + 2\hat{j} + 6\hat{k})$
$6\hat{i} + 3\hat{j} + 9\hat{k} = 4k\hat{i} + 2k\hat{j} + 6k\hat{k}$
Equating the corresponding components:
$6 = 4k \implies k = \frac{6}{4} = \frac{3}{2}$
$3 = 2k \implies k = \frac{3}{2}$
$9 = 6k \implies k = \frac{9}{6} = \frac{3}{2}$
Since the scalar $k$ is the same for all components ($k = \frac{3}{2}$), we have $\overrightarrow{BC} = \frac{3}{2}\overrightarrow{AB}$.
This shows that $\overrightarrow{BC}$ is parallel to $\overrightarrow{AB}$. Since the vectors $\overrightarrow{AB}$ and $\overrightarrow{BC}$ share the common point B, the points A, B, and C must lie on the same line. Therefore, the points A, B, and C are collinear.
Finding the Ratio:
Since $\overrightarrow{BC} = \frac{3}{2}\overrightarrow{AB}$, this means that the length of the vector from B to C is $\frac{3}{2}$ times the length of the vector from A to B, and they point in the same direction.
This implies that point B lies between A and C, and the distance from B to C is $\frac{3}{2}$ times the distance from A to B.
So, the ratio of the length of AB to the length of BC is:
$|\overrightarrow{AB}| : |\overrightarrow{BC}|$
$|\overrightarrow{AB}| : |\frac{3}{2}\overrightarrow{AB}|$
$|\overrightarrow{AB}| : \frac{3}{2}|\overrightarrow{AB}|$
Dividing by $|\overrightarrow{AB}|$ (since A and B are distinct points, $|\overrightarrow{AB}| \neq 0$):
$1 : \frac{3}{2}$
Multiply by 2 to get integer ratio:
$2 : 3$
This means that the ratio in which B divides AC is $2:3$. This is internal division because B lies between A and C.
Alternatively, using the section formula, if B divides AC in the ratio $m:n$, the position vector of B is given by:
$\vec{OB} = \frac{n\vec{OA} + m\vec{OC}}{m+n}$
$m\vec{OC} + n\vec{OA} = (m+n)\vec{OB}$
$m\vec{OC} - m\vec{OB} + n\vec{OA} - n\vec{OB} = \vec{0}$
$m(\vec{OC} - \vec{OB}) + n(\vec{OA} - \vec{OB}) = \vec{0}$
$m\overrightarrow{BC} + n\overrightarrow{BA} = \vec{0}$
$m\overrightarrow{BC} = -n\overrightarrow{BA}$
$m\overrightarrow{BC} = n\overrightarrow{AB}$
We found that $\overrightarrow{BC} = \frac{3}{2}\overrightarrow{AB}$. Substitute this into the equation:
$m\left(\frac{3}{2}\overrightarrow{AB}\right) = n\overrightarrow{AB}$
$\frac{3m}{2} = n$
$\frac{m}{n} = \frac{2}{3}$
So, the ratio $m:n = 2:3$. Point B divides AC internally in the ratio $2:3$.
Result:
Since $\overrightarrow{BC} = \frac{3}{2}\overrightarrow{AB}$, the vectors are parallel and share a common point B, hence the points A, B, and C are collinear.
Point B divides the line segment AC internally in the ratio $\mathbf{2:3}$.
Question 9. Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $(2\vec{a} + \vec{b})$ and $(\vec{a} − 3\vec{b})$ externally in the ratio 1 : 2. Also, show that P is the mid point of the line segment RQ.
Answer:
We are given the position vectors of two points P and Q, and we need to find the position vector of a point R that divides the line joining P and Q externally in a given ratio. We then need to show that P is the midpoint of the line segment RQ.
Given:
Position vector of point P, $\vec{p} = 2\vec{a} + \vec{b}$
Position vector of point Q, $\vec{q} = \vec{a} - 3\vec{b}$
Point R divides the line joining P and Q externally in the ratio $1:2$.
To Find:
The position vector of point R, $\vec{r}$.
To Show that P is the midpoint of the line segment RQ.
Solution:
Let R be the point that divides the line segment PQ externally in the ratio $m:n = 1:2$. The formula for the position vector of a point R that divides the line joining points P and Q with position vectors $\vec{p}$ and $\vec{q}$ externally in the ratio $m:n$ is given by:
$\vec{r} = \frac{m\vec{q} - n\vec{p}}{m - n}$
Substitute the given values $m=1$, $n=2$, $\vec{p} = 2\vec{a} + \vec{b}$, and $\vec{q} = \vec{a} - 3\vec{b}$ into the formula:
$\vec{r} = \frac{1 \cdot (\vec{a} - 3\vec{b}) - 2 \cdot (2\vec{a} + \vec{b})}{1 - 2}$
$\vec{r} = \frac{\vec{a} - 3\vec{b} - (4\vec{a} + 2\vec{b})}{-1}$
$\vec{r} = \frac{\vec{a} - 3\vec{b} - 4\vec{a} - 2\vec{b}}{-1}$
$\vec{r} = \frac{(\vec{a} - 4\vec{a}) + (-3\vec{b} - 2\vec{b})}{-1}$
$\vec{r} = \frac{-3\vec{a} - 5\vec{b}}{-1}$
$\vec{r} = 3\vec{a} + 5\vec{b}$
So, the position vector of point R is $3\vec{a} + 5\vec{b}$.
Showing P is the Midpoint of RQ:
To show that P is the midpoint of the line segment RQ, we can use the midpoint formula. The position vector of the midpoint of a line segment joining points with position vectors $\vec{r}$ and $\vec{q}$ is given by:
Midpoint position vector $= \frac{\vec{r} + \vec{q}}{2}$
Substitute the position vector of R, $\vec{r} = 3\vec{a} + 5\vec{b}$, and the position vector of Q, $\vec{q} = \vec{a} - 3\vec{b}$, into the midpoint formula:
Midpoint position vector of RQ $= \frac{(3\vec{a} + 5\vec{b}) + (\vec{a} - 3\vec{b})}{2}$
Midpoint position vector of RQ $= \frac{(3\vec{a} + \vec{a}) + (5\vec{b} - 3\vec{b})}{2}$
Midpoint position vector of RQ $= \frac{4\vec{a} + 2\vec{b}}{2}$
Midpoint position vector of RQ $= \frac{2(2\vec{a} + \vec{b})}{2}$
Midpoint position vector of RQ $= 2\vec{a} + \vec{b}$
We see that the position vector of the midpoint of RQ is $2\vec{a} + \vec{b}$, which is exactly the position vector of point P ($\vec{p}$).
Midpoint position vector of RQ = $\vec{p}$
This shows that point P is indeed the midpoint of the line segment RQ.
Result:
The position vector of point R is $\mathbf{3\vec{a} + 5\vec{b}}$.
Since the position vector of the midpoint of RQ is equal to the position vector of P, P is the midpoint of the line segment RQ.
Question 10. The two adjacent sides of a parallelogram are $2\hat{i} − 4\hat{j} + 5\hat{k}$ and $\hat{i} − 2\hat{j} − 3\hat{k}$. Find the unit vector parallel to its diagonal. Also, find its area.
Answer:
We are given two adjacent sides of a parallelogram represented by vectors. We need to find a unit vector parallel to one of its diagonals and calculate the area of the parallelogram.
Given:
Adjacent sides of a parallelogram are represented by vectors:
$\vec{a} = 2\hat{i} - 4\hat{j} + 5\hat{k}$
$\vec{b} = \hat{i} - 2\hat{j} - 3\hat{k}$
To Find:
A unit vector parallel to its diagonal.
The area of the parallelogram.
Solution:
In a parallelogram formed by adjacent vectors $\vec{a}$ and $\vec{b}$, the two diagonals are represented by the vectors $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$. Let's consider the diagonal represented by $\vec{d}_1 = \vec{a} + \vec{b}$.
Calculate the diagonal vector $\vec{d}_1$:
$\vec{d}_1 = \vec{a} + \vec{b}$
$\vec{d}_1 = (2\hat{i} - 4\hat{j} + 5\hat{k}) + (\hat{i} - 2\hat{j} - 3\hat{k})$
$\vec{d}_1 = (2 + 1)\hat{i} + (-4 - 2)\hat{j} + (5 - 3)\hat{k}$
$\vec{d}_1 = 3\hat{i} - 6\hat{j} + 2\hat{k}$
To find a unit vector parallel to $\vec{d}_1$, we divide $\vec{d}_1$ by its magnitude $|\;\vec{d}_1\;|$.
Calculate the magnitude $|\;\vec{d}_1\;|$:
$|\;\vec{d}_1\;| = \sqrt{(3)^2 + (-6)^2 + (2)^2}$
$|\;\vec{d}_1\;| = \sqrt{9 + 36 + 4}$
$|\;\vec{d}_1\;| = \sqrt{49}$
$|\;\vec{d}_1\;| = 7$
The unit vector parallel to $\vec{d}_1$ is:
$\hat{d}_1 = \frac{\vec{d}_1}{|\;\vec{d}_1\;|} = \frac{3\hat{i} - 6\hat{j} + 2\hat{k}}{7}$
$\hat{d}_1 = \frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}$
Note that the other diagonal is $\vec{d}_2 = \vec{a} - \vec{b} = (2\hat{i} - 4\hat{j} + 5\hat{k}) - (\hat{i} - 2\hat{j} - 3\hat{k}) = \hat{i} - 2\hat{j} + 8\hat{k}$. The question asks for a unit vector parallel to "its" diagonal, implying either one is acceptable. We used $\vec{a} + \vec{b}$.
The area of a parallelogram with adjacent sides represented by vectors $\vec{a}$ and $\vec{b}$ is given by the magnitude of their cross product, $|\;\vec{a} \times \vec{b}\;|$.
Calculate the cross product $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = (2\hat{i} - 4\hat{j} + 5\hat{k}) \times (\hat{i} - 2\hat{j} - 3\hat{k})$
Using the determinant form:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -4 & 5 \\ 1 & -2 & -3 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}((-4)(-3) - (5)(-2)) - \hat{j}((2)(-3) - (5)(1)) + \hat{k}((2)(-2) - (-4)(1))$
$\vec{a} \times \vec{b} = \hat{i}(12 - (-10)) - \hat{j}(-6 - 5) + \hat{k}(-4 - (-4))$
$\vec{a} \times \vec{b} = \hat{i}(12 + 10) - \hat{j}(-11) + \hat{k}(-4 + 4)$
$\vec{a} \times \vec{b} = 22\hat{i} + 11\hat{j} + 0\hat{k}$
$\vec{a} \times \vec{b} = 22\hat{i} + 11\hat{j}$
Now, calculate the magnitude of the cross product, $|\;\vec{a} \times \vec{b}\;|$.
Area $= |\;\vec{a} \times \vec{b}\;| = \sqrt{(22)^2 + (11)^2 + (0)^2}$
Area $= \sqrt{484 + 121 + 0}$
Area $= \sqrt{605}$
We can simplify $\sqrt{605}$ by finding its prime factorization. $605$ is divisible by $5$.
$\begin{array}{c|cc} 5 & 605 \\ \hline 11 & 121 \\ \hline 11 & 11 \\ \hline & 1 \end{array}$
$605 = 5 \times 11^2$
Area $= \sqrt{5 \times 11^2} = 11\sqrt{5}$
Result:
A unit vector parallel to one of the diagonals is $\mathbf{\frac{3}{7}\hat{i} - \frac{6}{7}\hat{j} + \frac{2}{7}\hat{k}}$. (Note that $-\frac{3}{7}\hat{i} + \frac{6}{7}\hat{j} - \frac{2}{7}\hat{k}$ is also a valid answer).
The area of the parallelogram is $\mathbf{11\sqrt{5}}$ square units.
Question 11. Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are $± \left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)$ .
Answer:
We need to show that if a vector is equally inclined to the coordinate axes OX, OY, and OZ, its direction cosines must be $± \left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right)$.
Given:
A vector is equally inclined to the axes OX, OY, and OZ.
To Show:
The direction cosines of the vector are $± \left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right)$.
Solution:
Let $\vec{r}$ be a vector that is equally inclined to the coordinate axes OX, OY, and OZ. Let the angles that $\vec{r}$ makes with the positive x-axis, positive y-axis, and positive z-axis be $\alpha$, $\beta$, and $\gamma$ respectively.
The direction cosines of the vector $\vec{r}$ are $\cos\alpha$, $\cos\beta$, and $\cos\gamma$. Let these be $l$, $m$, and $n$ respectively. So, $l = \cos\alpha$, $m = \cos\beta$, $n = \cos\gamma$.
Given that the vector is equally inclined to the axes, the angles it makes with each axis are equal. So, $\alpha = \beta = \gamma$.
Let this common angle be $\theta$. Thus, $\alpha = \beta = \gamma = \theta$.
The direction cosines are therefore:
$l = \cos\theta$
$m = \cos\theta$
$n = \cos\theta$
A fundamental property of direction cosines $(l, m, n)$ of any vector is that the sum of the squares of the direction cosines is equal to 1.
$l^2 + m^2 + n^2 = 1$
... (i)
Substitute $l = \cos\theta$, $m = \cos\theta$, and $n = \cos\theta$ into equation (i):
$(\cos\theta)^2 + (\cos\theta)^2 + (\cos\theta)^2 = 1$
$\cos^2\theta + \cos^2\theta + \cos^2\theta = 1$
$3\cos^2\theta = 1$
Now, solve for $\cos^2\theta$:
$\cos^2\theta = \frac{1}{3}$
Take the square root of both sides to find the value of $\cos\theta$:
$\cos\theta = \pm\sqrt{\frac{1}{3}}$
$\cos\theta = \pm\frac{1}{\sqrt{3}}$
Since the direction cosines are $l = \cos\theta$, $m = \cos\theta$, and $n = \cos\theta$, their values must be equal to $\pm\frac{1}{\sqrt{3}}$.
Therefore, the direction cosines $(l, m, n)$ are $\left(\pm\frac{1}{\sqrt{3}}, \pm\frac{1}{\sqrt{3}}, \pm\frac{1}{\sqrt{3}}\right)$.
There are two possibilities for the direction cosines of a vector equally inclined to the axes:
1. If the angle $\theta$ is such that $\cos\theta = \frac{1}{\sqrt{3}}$ (an acute angle), the direction cosines are $\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)$. This corresponds to a vector in the octant where x, y, and z are all positive.
2. If the angle $\theta$ is such that $\cos\theta = -\frac{1}{\sqrt{3}}$ (an obtuse angle), the direction cosines are $\left(-\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}\right)$. This corresponds to a vector pointing towards the origin from that positive octant, or pointing into the octant where x, y, and z are all negative.
However, the phrase "equally inclined to the axes OX, OY and OZ" implies that the angle with the positive direction of each axis is the same value, say $\theta$. In this case, $\alpha = \theta, \beta = \theta, \gamma = \theta$. This leads to the single value $\cos\theta = \pm\frac{1}{\sqrt{3}}$. The direction cosines $(l, m, n)$ must all be equal to this value.
Thus, the set of direction cosines is $(\cos\theta, \cos\theta, \cos\theta)$, where $\cos\theta = \pm\frac{1}{\sqrt{3}}$.
This gives the direction cosines as $\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)$ or $\left(-\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}\right)$.
This can be concisely written as $\pm \left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right)$.
Result:
We have shown that if a vector is equally inclined to the axes OX, OY, and OZ, the cosine of the angle it makes with each axis is $\pm \frac{1}{\sqrt{3}}$. Since the direction cosines are the cosines of these angles, the direction cosines of the vector are $\mathbf{± \left( \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \;,\; \frac{1}{\sqrt{3}} \right)}$.
Question 12. Let $\vec{a} = \hat{i} + 4\hat{j} + 2\hat{k}$ , $\vec{b} = 3\hat{i} − 2\hat{j} + 7\hat{k}$ and $\vec{c} = 2\hat{i} − \hat{j} + 4\hat{k}$ . Find a vector $\vec{d}$ which is perpendicular to both $\vec{a}$ and $\vec{b}$ , and $\vec{c} \;.\; \vec{d} = 15$.
Answer:
We are given three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$. We need to find a vector $\vec{d}$ that satisfies two conditions: it is perpendicular to both $\vec{a}$ and $\vec{b}$, and its dot product with $\vec{c}$ is 15.
Given:
Vector $\vec{a} = \hat{i} + 4\hat{j} + 2\hat{k}$
Vector $\vec{b} = 3\hat{i} - 2\hat{j} + 7\hat{k}$
Vector $\vec{c} = 2\hat{i} - \hat{j} + 4\hat{k}$
Vector $\vec{d}$ is perpendicular to both $\vec{a}$ and $\vec{b}$.
$\vec{c} \;.\; \vec{d} = 15$
To Find:
The vector $\vec{d}$.
Solution:
A vector that is perpendicular to two given vectors is parallel to their cross product. Thus, the vector $\vec{d}$ must be parallel to $\vec{a} \times \vec{b}$.
So, $\vec{d} = \lambda (\vec{a} \times \vec{b})$ for some scalar $\lambda$.
First, calculate the cross product $\vec{a} \times \vec{b}$:
$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 4 & 2 \\ 3 & -2 & 7 \end{vmatrix}$
$\vec{a} \times \vec{b} = \hat{i}((4)(7) - (2)(-2)) - \hat{j}((1)(7) - (2)(3)) + \hat{k}((1)(-2) - (4)(3))$
$\vec{a} \times \vec{b} = \hat{i}(28 - (-4)) - \hat{j}(7 - 6) + \hat{k}(-2 - 12)$
$\vec{a} \times \vec{b} = \hat{i}(28 + 4) - \hat{j}(1) + \hat{k}(-14)$
$\vec{a} \times \vec{b} = 32\hat{i} - \hat{j} - 14\hat{k}$
So, the vector $\vec{d}$ is of the form:
$\vec{d} = \lambda (32\hat{i} - \hat{j} - 14\hat{k})$
$\vec{d} = 32\lambda\hat{i} - \lambda\hat{j} - 14\lambda\hat{k}$
Now, use the second condition, $\vec{c} \cdot \vec{d} = 15$, to find the value of the scalar $\lambda$.
We have $\vec{c} = 2\hat{i} - \hat{j} + 4\hat{k}$ and $\vec{d} = 32\lambda\hat{i} - \lambda\hat{j} - 14\lambda\hat{k}$.
Calculate the dot product $\vec{c} \cdot \vec{d}$:
$\vec{c} \cdot \vec{d} = (2\hat{i} - \hat{j} + 4\hat{k}) \cdot (32\lambda\hat{i} - \lambda\hat{j} - 14\lambda\hat{k})$
$\vec{c} \cdot \vec{d} = (2)(32\lambda) + (-1)(-\lambda) + (4)(-14\lambda)$
$\vec{c} \cdot \vec{d} = 64\lambda + \lambda - 56\lambda$
$\vec{c} \cdot \vec{d} = (64 + 1 - 56)\lambda$
$\vec{c} \cdot \vec{d} = (65 - 56)\lambda$
$\vec{c} \cdot \vec{d} = 9\lambda$
We are given that $\vec{c} \cdot \vec{d} = 15$.
$9\lambda = 15$
... (i)
Solve for $\lambda$ from equation (i):
$\lambda = \frac{15}{9}$
Simplify the fraction:
$\lambda = \frac{5}{3}$
Now, substitute the value of $\lambda$ back into the expression for $\vec{d}$:
$\vec{d} = 32(\frac{5}{3})\hat{i} - (\frac{5}{3})\hat{j} - 14(\frac{5}{3})\hat{k}$
$\vec{d} = \frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k}$
Verification:
Check if $\vec{d}$ is perpendicular to $\vec{a}$ (i.e., $\vec{a} \cdot \vec{d} = 0$).
$\vec{a} \cdot \vec{d} = (\hat{i} + 4\hat{j} + 2\hat{k}) \cdot (\frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k})$
$\vec{a} \cdot \vec{d} = (1)(\frac{160}{3}) + (4)(-\frac{5}{3}) + (2)(-\frac{70}{3})$
$\vec{a} \cdot \vec{d} = \frac{160}{3} - \frac{20}{3} - \frac{140}{3}$
$\vec{a} \cdot \vec{d} = \frac{160 - 20 - 140}{3} = \frac{160 - 160}{3} = \frac{0}{3} = 0$
This is correct.
Check if $\vec{d}$ is perpendicular to $\vec{b}$ (i.e., $\vec{b} \cdot \vec{d} = 0$).
$\vec{b} \cdot \vec{d} = (3\hat{i} - 2\hat{j} + 7\hat{k}) \cdot (\frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k})$
$\vec{b} \cdot \vec{d} = (3)(\frac{160}{3}) + (-2)(-\frac{5}{3}) + (7)(-\frac{70}{3})$
$\vec{b} \cdot \vec{d} = 160 + \frac{10}{3} - \frac{490}{3}$
$\vec{b} \cdot \vec{d} = \frac{480}{3} + \frac{10}{3} - \frac{490}{3}$
$\vec{b} \cdot \vec{d} = \frac{480 + 10 - 490}{3} = \frac{490 - 490}{3} = \frac{0}{3} = 0$
This is correct.
Check if $\vec{c} \cdot \vec{d} = 15$.
$\vec{c} \cdot \vec{d} = (2\hat{i} - \hat{j} + 4\hat{k}) \cdot (\frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k})$
$\vec{c} \cdot \vec{d} = (2)(\frac{160}{3}) + (-1)(-\frac{5}{3}) + (4)(-\frac{70}{3})$
$\vec{c} \cdot \vec{d} = \frac{320}{3} + \frac{5}{3} - \frac{280}{3}$
$\vec{c} \cdot \vec{d} = \frac{320 + 5 - 280}{3} = \frac{325 - 280}{3} = \frac{45}{3} = 15$
This is correct.
Result:
The vector $\vec{d}$ is $\mathbf{\frac{160}{3}\hat{i} - \frac{5}{3}\hat{j} - \frac{70}{3}\hat{k}}$.
Question 13. The scalar product of the vector $\hat{i} + \hat{j} + \hat{k}$ with a unit vector along the sum of vectors $2\hat{i} + 4\hat{j} − 5\hat{k}$ and $λ\hat{i} + 2\hat{j} + 3\hat{k}$ is equal to one. Find the value of λ.
Answer:
We are given three vectors. We need to find the sum of two of the vectors, determine the unit vector along their sum, and then use the information about the scalar product of the first vector with this unit vector to find the value of $\lambda$.
Given:
Vector $\vec{a} = \hat{i} + \hat{j} + \hat{k}$
Vector $\vec{b} = 2\hat{i} + 4\hat{j} - 5\hat{k}$
Vector $\vec{c} = \lambda\hat{i} + 2\hat{j} + 3\hat{k}$
The scalar product of $\vec{a}$ with the unit vector along the sum of $\vec{b}$ and $\vec{c}$ is equal to 1.
To Find:
The value of $\lambda$.
Solution:
First, find the sum of vectors $\vec{b}$ and $\vec{c}$. Let the sum be $\vec{s}$.
$\vec{s} = \vec{b} + \vec{c}$
$\vec{s} = (2\hat{i} + 4\hat{j} - 5\hat{k}) + (\lambda\hat{i} + 2\hat{j} + 3\hat{k})$
$\vec{s} = (2 + \lambda)\hat{i} + (4 + 2)\hat{j} + (-5 + 3)\hat{k}$
$\vec{s} = (2 + \lambda)\hat{i} + 6\hat{j} - 2\hat{k}$
Next, find the unit vector along the sum $\vec{s}$. Let this unit vector be $\hat{s}$.
$\hat{s} = \frac{\vec{s}}{|\;\vec{s}\;|}$
First, calculate the magnitude of $\vec{s}$, $|\;\vec{s}\;|$.
$|\;\vec{s}\;| = \sqrt{(2 + \lambda)^2 + (6)^2 + (-2)^2}$
$|\;\vec{s}\;| = \sqrt{(4 + 4\lambda + \lambda^2) + 36 + 4}$
$|\;\vec{s}\;| = \sqrt{\lambda^2 + 4\lambda + 44}$
The unit vector $\hat{s}$ is:
$\hat{s} = \frac{(2 + \lambda)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{\lambda^2 + 4\lambda + 44}}$
Now, use the given condition that the scalar product of $\vec{a} = \hat{i} + \hat{j} + \hat{k}$ with $\hat{s}$ is equal to 1.
$\vec{a} \cdot \hat{s} = 1$
Substitute the expressions for $\vec{a}$ and $\hat{s}$:
$(\hat{i} + \hat{j} + \hat{k}) \cdot \left( \frac{(2 + \lambda)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{\lambda^2 + 4\lambda + 44}} \right) = 1$
Calculate the dot product in the numerator:
$(1)(2 + \lambda) + (1)(6) + (1)(-2) = 2 + \lambda + 6 - 2 = \lambda + 6$
So, the equation becomes:
$\frac{\lambda + 6}{\sqrt{\lambda^2 + 4\lambda + 44}} = 1$
To solve for $\lambda$, multiply both sides by the denominator:
$\lambda + 6 = \sqrt{\lambda^2 + 4\lambda + 44}$
Square both sides of the equation to eliminate the square root. Note that squaring may introduce extraneous solutions, so we need to check the solution(s) in the original equation.
$(\lambda + 6)^2 = (\sqrt{\lambda^2 + 4\lambda + 44})^2$
$\lambda^2 + 12\lambda + 36 = \lambda^2 + 4\lambda + 44$
Subtract $\lambda^2$ from both sides:
$12\lambda + 36 = 4\lambda + 44$
Subtract $4\lambda$ from both sides:
$12\lambda - 4\lambda + 36 = 44$
$8\lambda + 36 = 44$
Subtract 36 from both sides:
$8\lambda = 44 - 36$
$8\lambda = 8$
Divide by 8:
$\lambda = 1$
Verification:
Check if $\lambda = 1$ satisfies the equation $\lambda + 6 = \sqrt{\lambda^2 + 4\lambda + 44}$ (the step before squaring).
Left side: $\lambda + 6 = 1 + 6 = 7$
Right side: $\sqrt{\lambda^2 + 4\lambda + 44} = \sqrt{(1)^2 + 4(1) + 44} = \sqrt{1 + 4 + 44} = \sqrt{49} = 7$
Since $7 = 7$, the solution $\lambda = 1$ is valid.
Result:
The value of $\lambda$ is $\mathbf{1}$.
Question 14. If $\vec{a}$, $\vec{b}$, $\vec{c}$ are mutually perpendicular vectors of equal magnitudes, show that the vector $\vec{c} \;.\; \vec{d} = 15$ is equally inclined to $\vec{a}$ , $\vec{b}$ and $\vec{c}$.
Answer:
We are given three mutually perpendicular vectors of equal magnitudes and asked to show that their sum is equally inclined to each of the individual vectors. Note that the phrasing in the question "show that the vector $\vec{c} \;.\; \vec{d} = 15$ is equally inclined..." appears to contain a typo, likely intending to refer to the vector sum $\vec{a} + \vec{b} + \vec{c}$ instead of a scalar quantity $\vec{c} \cdot \vec{d} = 15$. We will proceed by showing that the vector $\vec{a} + \vec{b} + \vec{c}$ is equally inclined to $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Given:
Vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ are mutually perpendicular.
Vectors $\vec{a}$, $\vec{b}$, $\vec{c}$ have equal magnitudes.
To Show:
The vector $\vec{a} + \vec{b} + \vec{c}$ is equally inclined to $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Solution:
Let the equal magnitude of the vectors be $k$. Since they are mutually perpendicular, they must be non-zero vectors, so $k > 0$.
$|\;\vec{a}\;| = |\;\vec{b}\;| = |\;\vec{c}\;| = k$
Since $\vec{a}$, $\vec{b}$, and $\vec{c}$ are mutually perpendicular, their dot products are zero:
$\vec{a} \cdot \vec{b} = 0$
... (1)
$\vec{b} \cdot \vec{c} = 0$
... (2)
$\vec{c} \cdot \vec{a} = 0$
... (3)
Also, the dot product of a vector with itself is the square of its magnitude:
$\vec{a} \cdot \vec{a} = |\;\vec{a}\;|^2 = k^2$
$\vec{b} \cdot \vec{b} = |\;\vec{b}\;|^2 = k^2$
$\vec{c} \cdot \vec{c} = |\;\vec{c}\;|^2 = k^2$
Let $\vec{d} = \vec{a} + \vec{b} + \vec{c}$. We want to find the angles between $\vec{d}$ and $\vec{a}$, $\vec{d}$ and $\vec{b}$, and $\vec{d}$ and $\vec{c}$. Let these angles be $\theta_a$, $\theta_b$, and $\theta_c$ respectively.
The cosine of the angle between two vectors $\vec{u}$ and $\vec{v}$ is given by $\cos\theta = \frac{\vec{u} \cdot \vec{v}}{|\;\vec{u}\;|\;|\;\vec{v}\;|}$.
First, calculate the dot products of $\vec{d}$ with $\vec{a}$, $\vec{b}$, and $\vec{c}$.
$\vec{d} \cdot \vec{a} = (\vec{a} + \vec{b} + \vec{c}) \cdot \vec{a} = \vec{a} \cdot \vec{a} + \vec{b} \cdot \vec{a} + \vec{c} \cdot \vec{a}$
Using the given conditions:
$\vec{d} \cdot \vec{a} = |\;\vec{a}\;|^2 + 0 + 0 = k^2$
$\vec{d} \cdot \vec{b} = (\vec{a} + \vec{b} + \vec{c}) \cdot \vec{b} = \vec{a} \cdot \vec{b} + \vec{b} \cdot \vec{b} + \vec{c} \cdot \vec{b}$
Using the given conditions:
$\vec{d} \cdot \vec{b} = 0 + |\;\vec{b}\;|^2 + 0 = k^2$
$\vec{d} \cdot \vec{c} = (\vec{a} + \vec{b} + \vec{c}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} + \vec{c} \cdot \vec{c}$
Using the given conditions:
$\vec{d} \cdot \vec{c} = 0 + 0 + |\;\vec{c}\;|^2 = k^2$
So, we have $\vec{d} \cdot \vec{a} = \vec{d} \cdot \vec{b} = \vec{d} \cdot \vec{c} = k^2$.
Next, calculate the magnitude of $\vec{d} = \vec{a} + \vec{b} + \vec{c}$.
$|\;\vec{d}\;|^2 = \vec{d} \cdot \vec{d} = (\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c})$
$|\;\vec{d}\;|^2 = \vec{a} \cdot \vec{a} + \vec{b} \cdot \vec{b} + \vec{c} \cdot \vec{c} + 2(\vec{a} \cdot \vec{b}) + 2(\vec{b} \cdot \vec{c}) + 2(\vec{c} \cdot \vec{a})$
$|\;\vec{d}\;|^2 = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + |\;\vec{c}\;|^2 + 2(0) + 2(0) + 2(0)$
$|\;\vec{d}\;|^2 = k^2 + k^2 + k^2 = 3k^2$
$|\;\vec{d}\;| = \sqrt{3k^2} = \sqrt{3}k$ (since $k > 0$)
Now, find the cosines of the angles $\theta_a$, $\theta_b$, and $\theta_c$:
$\cos\theta_a = \frac{\vec{d} \cdot \vec{a}}{|\;\vec{d}\;|\;|\;\vec{a}\;|} = \frac{k^2}{(\sqrt{3}k)(k)} = \frac{k^2}{\sqrt{3}k^2} = \frac{1}{\sqrt{3}}$
$\cos\theta_b = \frac{\vec{d} \cdot \vec{b}}{|\;\vec{d}\;|\;|\;\vec{b}\;|} = \frac{k^2}{(\sqrt{3}k)(k)} = \frac{k^2}{\sqrt{3}k^2} = \frac{1}{\sqrt{3}}$
$\cos\theta_c = \frac{\vec{d} \cdot \vec{c}}{|\;\vec{d}\;|\;|\;\vec{c}\;|} = \frac{k^2}{(\sqrt{3}k)(k)} = \frac{k^2}{\sqrt{3}k^2} = \frac{1}{\sqrt{3}}$
Since $\cos\theta_a = \cos\theta_b = \cos\theta_c = \frac{1}{\sqrt{3}}$, and the angles $\theta_a, \theta_b, \theta_c$ are between $0$ and $\pi$, we can conclude that $\theta_a = \theta_b = \theta_c = \cos^{-1}\left(\frac{1}{\sqrt{3}}\right)$.
Thus, the angle between $\vec{a} + \vec{b} + \vec{c}$ and each of the vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ is the same.
Conclusion:
We have shown that the cosine of the angle between the vector $\vec{a} + \vec{b} + \vec{c}$ and each of the vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$ is equal to $\frac{1}{\sqrt{3}}$. Therefore, the vector $\vec{a} + \vec{b} + \vec{c}$ is equally inclined to $\vec{a}$, $\vec{b}$, and $\vec{c}$.
Question 15. Prove that $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$, if and only if $\vec{a}\;,\; \vec{b}$ are perpendicular, given $\vec{a} ≠ \vec{0} \;,\; \vec{b} ≠ \vec{0}$.
Answer:
We need to prove the given statement which is in the form of an "if and only if" condition. This requires proving two parts:
Part 1: If $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$, then $\vec{a}$ and $\vec{b}$ are perpendicular.
Part 2: If $\vec{a}$ and $\vec{b}$ are perpendicular, then $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$.
We are given that $\vec{a} ≠ \vec{0}$ and $\vec{b} ≠ \vec{0}$.
Given:
Vectors $\vec{a} ≠ \vec{0}$ and $\vec{b} ≠ \vec{0}$.
To Prove:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 \iff \vec{a} \perp \vec{b}$.
Proof:
Consider the left side of the given equation and expand the dot product:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = \vec{a} \;.\; (\vec{a} + \vec{b}) + \vec{b} \;.\; (\vec{a} + \vec{b})$
$= \vec{a} \;.\; \vec{a} + \vec{a} \;.\; \vec{b} + \vec{b} \;.\; \vec{a} + \vec{b} \;.\; \vec{b}$
Using the property that the dot product of a vector with itself is the square of its magnitude ($\vec{v} \;.\; \vec{v} = |\;\vec{v}\;|^2$) and the commutative property of the dot product ($\vec{a} \;.\; \vec{b} = \vec{b} \;.\; \vec{a}$), the expression becomes:
$|\;\vec{a}\;|^2 + \vec{a} \;.\; \vec{b} + \vec{a} \;.\; \vec{b} + |\;\vec{b}\;|^2$
...(1)
$= |\;\vec{a}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2$
Now, let's prove the two implications.
Part 1: ($\implies$)
Assume that $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$.
From our expansion, we know that $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2$.
Equating the given condition with the expansion:
$|\;\vec{a}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2 = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$
Subtracting $|\;\vec{a}\;|^2$ and $|\;\vec{b}\;|^2$ from both sides of the equation:
$2(\vec{a} \;.\; \vec{b}) = 0$
Dividing by 2:
$\vec{a} \;.\; \vec{b} = 0$
Since we are given that $\vec{a} ≠ \vec{0}$ and $\vec{b} ≠ \vec{0}$, their dot product being zero implies that the vectors $\vec{a}$ and $\vec{b}$ are perpendicular.
$\vec{a} \perp \vec{b}$
This proves the first part.
Part 2: ($\impliedby$)
Assume that $\vec{a}$ and $\vec{b}$ are perpendicular.
Since $\vec{a} ≠ \vec{0}$ and $\vec{b} ≠ \vec{0}$ are perpendicular, their dot product is zero:
$\vec{a} \;.\; \vec{b} = 0$
... (2)
Now, consider the expansion of $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b})$ from equation (1):
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + 2(\vec{a} \;.\; \vec{b}) + |\;\vec{b}\;|^2$
Substitute the condition $\vec{a} \;.\; \vec{b} = 0$ into this equation:
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + 2(0) + |\;\vec{b}\;|^2$
$(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$
This proves the second part.
Conclusion:
Since both implications have been proven, the statement $(\vec{a} + \vec{b}) \;.\; (\vec{a} + \vec{b}) = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2$ is true if and only if $\vec{a}$ and $\vec{b}$ are perpendicular, given $\vec{a} ≠ \vec{0}$ and $\vec{b} ≠ \vec{0}$.
Choose the correct answer in Exercises 16 to 19.
Question 16. If θ is the angle between two vectors $\vec{a}$ and $\vec{b}$, then $\vec{a} \;.\; \vec{b} ≥ 0$ only when
(A) $0 < θ < \frac{π}{2}$
(B) $0 ≤ θ ≤ \frac{π}{2}$
(C) $0 < θ < π$
(D) $0 ≤ θ ≤ π$
Answer:
We are given the formula for the scalar product (dot product) of two vectors and asked to determine the condition on the angle between them for the dot product to be non-negative.
Given:
$\theta$ is the angle between two vectors $\vec{a}$ and $\vec{b}$.
The condition is $\vec{a} \;.\; \vec{b} ≥ 0$.
To Find:
The range of $\theta$ for which $\vec{a} \;.\; \vec{b} ≥ 0$.
Solution:
The scalar product of two vectors $\vec{a}$ and $\vec{b}$ is defined as:
$\vec{a} \;.\; \vec{b} = |\;\vec{a}\;|\;|\;\vec{b}\;| \cos\theta$
where $|\;\vec{a}\;|$ is the magnitude of $\vec{a}$, $|\;\vec{b}\;|$ is the magnitude of $\vec{b}$, and $\theta$ is the angle between $\vec{a}$ and $\vec{b}$. The angle $\theta$ is typically considered to be in the range $0 \leq \theta \leq \pi$ radians ($0^\circ \leq \theta \leq 180^\circ$).
We are given the condition $\vec{a} \;.\; \vec{b} ≥ 0$.
So, $|\;\vec{a}\;|\;|\;\vec{b}\;| \cos\theta ≥ 0$
Assume that $\vec{a}$ and $\vec{b}$ are non-zero vectors, otherwise the dot product is always zero, and the inequality $\vec{a} \;.\; \vec{b} ≥ 0$ is always satisfied regardless of the angle (the angle is undefined for a zero vector). If they are non-zero, then $|\;\vec{a}\;| > 0$ and $|\;\vec{b}\;| > 0$. Their product $|\;\vec{a}\;|\;|\;\vec{b}\;|$ is also positive.
Therefore, the inequality $|\;\vec{a}\;|\;|\;\vec{b}\;| \cos\theta ≥ 0$ implies:
$\cos\theta ≥ 0$
We need to find the values of $\theta$ in the range $0 \leq \theta \leq \pi$ for which $\cos\theta$ is greater than or equal to zero.
The cosine function is non-negative in the first quadrant and at the boundaries of the first quadrant within the range $0 \leq \theta \leq \pi$.
$\cos\theta \geq 0$ for $0 \leq \theta \leq \frac{\pi}{2}$.
At $\theta = 0$, $\cos(0) = 1$, which is $\geq 0$. This corresponds to vectors pointing in the same direction.
At $\theta = \frac{\pi}{2}$, $\cos(\frac{\pi}{2}) = 0$, which is $\geq 0$. This corresponds to perpendicular vectors.
For $0 < \theta < \frac{\pi}{2}$, $\cos\theta > 0$.
For $\frac{\pi}{2} < \theta \leq \pi$, $\cos\theta < 0$.
So, the condition $\cos\theta ≥ 0$ holds when $0 \leq \theta \leq \frac{\pi}{2}$.
Let's examine the given options:
(A) $0 < θ < \frac{π}{2}$: This range excludes $\theta = 0$ and $\theta = \frac{\pi}{2}$, where $\cos\theta$ is positive or zero. This is not the full range.
(B) $0 ≤ θ ≤ \frac{π}{2}$: This range includes $\theta = 0$ (where $\cos\theta = 1 \geq 0$) and $\theta = \frac{\pi}{2}$ (where $\cos\theta = 0 \geq 0$), and all angles in between where $\cos\theta > 0$. This matches our finding.
(C) $0 < θ < π$: This range includes angles in the second quadrant ($\frac{\pi}{2} < \theta < \pi$) where $\cos\theta < 0$. This is incorrect.
(D) $0 ≤ θ ≤ π$: This is the standard range for the angle between two vectors. It includes angles where $\cos\theta < 0$. This is incorrect.
Therefore, $\vec{a} \;.\; \vec{b} ≥ 0$ when $0 \leq \theta \leq \frac{\pi}{2}$.
Answer:
The correct option is (B).
Question 17. Let $\vec{a}$ and $\vec{b}$ be two unit vectors and θ is the angle between them. Then $\vec{a} + \vec{b}$ is a unit vector if
(A) $θ = \frac{π}{4}$
(B) $θ = \frac{π}{3}$
(C) $θ = \frac{π}{2}$
(D) $θ = \frac{2π}{3}$
Answer:
We are given two unit vectors and the angle between them. We need to find the condition on the angle such that their sum is also a unit vector.
Given:
$\vec{a}$ and $\vec{b}$ are unit vectors, so $|\;\vec{a}\;| = 1$ and $|\;\vec{b}\;| = 1$.
$\theta$ is the angle between $\vec{a}$ and $\vec{b}$.
The vector $\vec{a} + \vec{b}$ is a unit vector, so $|\;\vec{a} + \vec{b}\;| = 1$.
To Find:
The value of $\theta$ that satisfies the condition.
Solution:
We are given that $|\;\vec{a} + \vec{b}\;| = 1$. Let's consider the square of the magnitude:
$|\;\vec{a} + \vec{b}\;|^2 = 1^2 = 1$
We know that $|\;\vec{u} + \vec{v}\;|^2 = (\vec{u} + \vec{v}) \cdot (\vec{u} + \vec{v}) = |\;\vec{u}\;|^2 + |\;\vec{v}\;|^2 + 2(\vec{u} \cdot \vec{v})$.
Using this property for $\vec{a} + \vec{b}$:
$|\;\vec{a} + \vec{b}\;|^2 = |\;\vec{a}\;|^2 + |\;\vec{b}\;|^2 + 2(\vec{a} \cdot \vec{b})$
... (i)
Substitute the given magnitudes and the condition $|\;\vec{a} + \vec{b}\;|^2 = 1$ into equation (i):
$1 = (1)^2 + (1)^2 + 2(\vec{a} \cdot \vec{b})$
$1 = 1 + 1 + 2(\vec{a} \cdot \vec{b})$
$1 = 2 + 2(\vec{a} \cdot \vec{b})$
Now, solve for the dot product $\vec{a} \cdot \vec{b}$:
$1 - 2 = 2(\vec{a} \cdot \vec{b})$
$-1 = 2(\vec{a} \cdot \vec{b})$
$\vec{a} \cdot \vec{b} = -\frac{1}{2}$
We also know that the dot product of two vectors is given by $\vec{a} \cdot \vec{b} = |\;\vec{a}\;|\;|\;\vec{b}\;| \cos\theta$.
Substitute the magnitudes $|\;\vec{a}\;| = 1$, $|\;\vec{b}\;| = 1$, and the calculated value of $\vec{a} \cdot \vec{b} = -\frac{1}{2}$:
$-\frac{1}{2} = (1)(1) \cos\theta$
$\cos\theta = -\frac{1}{2}$
We need to find the value of $\theta$ in the standard range $0 \leq \theta \leq \pi$ for which $\cos\theta = -\frac{1}{2}$.
The angle whose cosine is $\frac{1}{2}$ is $\frac{\pi}{3}$ radians ($60^\circ$). Since the cosine is negative, the angle is in the second quadrant.
The angle is $\pi - \frac{\pi}{3} = \frac{3\pi - \pi}{3} = \frac{2\pi}{3}$.
So, $\theta = \frac{2\pi}{3}$.
Let's check the given options:
(A) $\theta = \frac{\pi}{4}$: $\cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2} \neq -\frac{1}{2}$
(B) $\theta = \frac{\pi}{3}$: $\cos(\frac{\pi}{3}) = \frac{1}{2} \neq -\frac{1}{2}$
(C) $\theta = \frac{\pi}{2}$: $\cos(\frac{\pi}{2}) = 0 \neq -\frac{1}{2}$
(D) $\theta = \frac{2\pi}{3}$: $\cos(\frac{2\pi}{3}) = -\frac{1}{2}$. This matches our finding.
Answer:
The correct option is (D).
Question 18. The value of $\hat{i} \;. (\hat{j} × \hat{k}) + \hat{j} \;. (\hat{i} × \hat{k}) + \hat{k} \;. (\hat{i} × \hat{j})$ is
(A) 0
(B) –1
(C) 1
(D) 3
Answer:
We need to evaluate the given expression which involves dot products and cross products of the standard orthonormal basis vectors $\hat{i}$, $\hat{j}$, and $\hat{k}$.
Given:
The expression $\hat{i} \;. (\hat{j} × \hat{k}) + \hat{j} \;. (\hat{i} × \hat{k}) + \hat{k} \;. (\hat{i} × \hat{j})$.
To Find:
The value of the expression.
Solution:
We need to evaluate each term in the sum separately.
Term 1: $\hat{i} \;. (\hat{j} × \hat{k})$
First, calculate the cross product $\hat{j} × \hat{k}$. The cross product of $\hat{j}$ and $\hat{k}$ (in a right-handed system) is $\hat{i}$.
$\hat{j} × \hat{k} = \hat{i}$
Now, calculate the dot product:
$\hat{i} \;. (\hat{j} × \hat{k}) = \hat{i} \;. \hat{i}$
The dot product of a unit vector with itself is 1.
$\hat{i} \;. \hat{i} = |\;\hat{i}\;|\;|\;\hat{i}\;| \cos(0^\circ) = (1)(1)(1) = 1$
So, the first term is 1.
Term 2: $\hat{j} \;. (\hat{i} × \hat{k})$
First, calculate the cross product $\hat{i} × \hat{k}$. The cross product of $\hat{i}$ and $\hat{k}$ (in a right-handed system) is $-\hat{j}$.
$\hat{i} × \hat{k} = -\hat{j}$
Now, calculate the dot product:
$\hat{j} \;. (\hat{i} × \hat{k}) = \hat{j} \;. (-\hat{j})$
The dot product of a vector with its negative is the negative of the square of its magnitude.
$\hat{j} \;. (-\hat{j}) = -(\hat{j} \;. \hat{j}) = -|\;\hat{j}\;|^2 = -(1)^2 = -1$
So, the second term is -1.
Term 3: $\hat{k} \;. (\hat{i} × \hat{j})$
First, calculate the cross product $\hat{i} × \hat{j}$. The cross product of $\hat{i}$ and $\hat{j}$ (in a right-handed system) is $\hat{k}$.
$\hat{i} × \hat{j} = \hat{k}$
Now, calculate the dot product:
$\hat{k} \;. (\hat{i} × \hat{j}) = \hat{k} \;. \hat{k}$
The dot product of a unit vector with itself is 1.
$\hat{k} \;. \hat{k} = |\;\hat{k}\;|\;|\;\hat{k}\;| \cos(0^\circ) = (1)(1)(1) = 1$
So, the third term is 1.
Now, sum the values of the three terms:
Expression value $= 1 + (-1) + 1$
Expression value $= 1 - 1 + 1$
Expression value $= 1$
Alternative Method using Scalar Triple Product:
The term $\hat{i} \;. (\hat{j} × \hat{k})$ is the scalar triple product $[\hat{i}, \hat{j}, \hat{k}]$. For an orthonormal right-handed system, $[\hat{i}, \hat{j}, \hat{k}] = 1$.
The term $\hat{j} \;. (\hat{i} × \hat{k})$ is the scalar triple product $[\hat{j}, \hat{i}, \hat{k}]$. The scalar triple product is zero if any two vectors are the same. It changes sign if two vectors are swapped.
$[\hat{j}, \hat{i}, \hat{k}] = -[\hat{i}, \hat{j}, \hat{k}] = -1$
The term $\hat{k} \;. (\hat{i} × \hat{j})$ is the scalar triple product $[\hat{k}, \hat{i}, \hat{j}]$. The scalar triple product is unchanged by cyclic permutation of the vectors.
$[\hat{k}, \hat{i}, \hat{j}] = [\hat{i}, \hat{j}, \hat{k}] = 1$
The expression is the sum of these scalar triple products:
Expression value $= [\hat{i}, \hat{j}, \hat{k}] + [\hat{j}, \hat{i}, \hat{k}] + [\hat{k}, \hat{i}, \hat{j}]$
Expression value $= 1 + (-1) + 1$
Expression value $= 1$
The value of the expression is 1.
Let's check the given options:
(A) 0
(B) –1
(C) 1
(D) 3
The calculated value matches option (C).
Answer:
The correct option is (C).
Question 19. If θ is the angle between any two vectors $\vec{a}$ and $\vec{b}$, then $|\;\vec{a}\;.\;\vec{b}\;| = |\;\vec{a}\;×\;\vec{b}\;|$ when θ is equal to
(A) 0
(B) $\frac{π}{4}$
(C) $\frac{π}{2}$
(D) π
Answer:
We are given a condition involving the magnitudes of the dot product and the cross product of two vectors, and we need to find the angle between the vectors that satisfies this condition.
Given:
$\theta$ is the angle between vectors $\vec{a}$ and $\vec{b}$.
The condition is $|\;\vec{a}\;.\;\vec{b}\;| = |\;\vec{a}\;×\;\vec{b}\;|$.
To Find:
The value of $\theta$ that satisfies the given condition.
Solution:
The formulas for the magnitudes of the dot product and the cross product of two vectors $\vec{a}$ and $\vec{b}$ are:
$|\;\vec{a}\;.\;\vec{b}\;| = ||\;\vec{a}\;|\;|\;\vec{b}\;| \cos\theta|$
$|\;\vec{a}\;×\;\vec{b}\;| = |\;\vec{a}\;|\;|\;\vec{b}\;| \sin\theta$
Note that since $|\;\vec{a}\;|\;|\;\vec{b}\;|$ and $\sin\theta$ (for $0 \leq \theta \leq \pi$) are non-negative, $|\;\vec{a}\;|\;|\;\vec{b}\;| \sin\theta = |\;\vec{a}\;|\;|\;\vec{b}\;| |\sin\theta|$. However, in the range $0 \leq \theta \leq \pi$, $\sin\theta \geq 0$, so $|\sin\theta| = \sin\theta$.
The given condition is $|\;\vec{a}\;.\;\vec{b}\;| = |\;\vec{a}\;×\;\vec{b}\;|$.
Substitute the formulas for the magnitudes:
||$\;\vec{a}\;|\;|\;\vec{b}\;| \cos\theta|$ = $|\;\vec{a}\;|\;|\;\vec{b}\;| \sin\theta$
Assume that $\vec{a}$ and $\vec{b}$ are non-zero vectors, otherwise $|\;\vec{a}\;|\;|\;\vec{b}\;| = 0$, and the equation becomes $0=0$, which is true for any angle $\theta$. If they are non-zero, then $|\;\vec{a}\;| \neq 0$ and $|\;\vec{b}\;| \neq 0$, so $|\;\vec{a}\;|\;|\;\vec{b}\;| \neq 0$. We can divide both sides by $|\;\vec{a}\;|\;|\;\vec{b}\;|$.
$|\cos\theta| = \sin\theta$
We are considering the angle $\theta$ in the range $0 \leq \theta \leq \pi$. In this range, $\sin\theta \geq 0$.
We need to find $\theta$ such that $|\cos\theta| = \sin\theta$.
Case 1: $\cos\theta \geq 0$. This occurs when $0 \leq \theta \leq \frac{\pi}{2}$.
In this case, $|\cos\theta| = \cos\theta$. The equation becomes $\cos\theta = \sin\theta$.
If $\cos\theta \neq 0$ (i.e., $\theta \neq \frac{\pi}{2}$), we can divide by $\cos\theta$:
$\frac{\sin\theta}{\cos\theta} = 1$
$\tan\theta = 1$
For $0 \leq \theta \leq \frac{\pi}{2}$, the angle whose tangent is 1 is $\frac{\pi}{4}$.
So, $\theta = \frac{\pi}{4}$.
Let's check if $\theta = \frac{\pi}{2}$ satisfies $\cos\theta = \sin\theta$. $\cos(\frac{\pi}{2}) = 0$ and $\sin(\frac{\pi}{2}) = 1$. $0 \neq 1$. So $\theta = \frac{\pi}{2}$ is not a solution in this case.
Case 2: $\cos\theta < 0$. This occurs when $\frac{\pi}{2} < \theta \leq \pi$.
In this case, $|\cos\theta| = -\cos\theta$. The equation becomes $-\cos\theta = \sin\theta$.
$\sin\theta + \cos\theta = 0$
If $\cos\theta \neq 0$, divide by $\cos\theta$:
$\frac{\sin\theta}{\cos\theta} + \frac{\cos\theta}{\cos\theta} = 0$
$\tan\theta + 1 = 0$
$\tan\theta = -1$
For $\frac{\pi}{2} < \theta \leq \pi$, the angle whose tangent is -1 is $\pi - \frac{\pi}{4} = \frac{3\pi}{4}$.
So, $\theta = \frac{3\pi}{4}$.
Let's check if $\theta = \frac{3\pi}{4}$ satisfies $-\cos\theta = \sin\theta$.
$\cos(\frac{3\pi}{4}) = -\frac{\sqrt{2}}{2}$, $\sin(\frac{3\pi}{4}) = \frac{\sqrt{2}}{2}$.
$- (-\frac{\sqrt{2}}{2}) = \frac{\sqrt{2}}{2}$. $\frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}$. This is true.
However, we also have the condition that $\sin\theta \geq 0$ from $|\cos\theta| = \sin\theta$. For $\theta = \frac{3\pi}{4}$, $\sin(\frac{3\pi}{4}) = \frac{\sqrt{2}}{2}$, which is greater than 0. And $|\cos(\frac{3\pi}{4})| = |-\frac{\sqrt{2}}{2}| = \frac{\sqrt{2}}{2}$, which is equal to $\sin(\frac{3\pi}{4})$.
Wait, let's reconsider $|\cos\theta| = \sin\theta$. Since the right side is $\sin\theta$, and $\sin\theta \geq 0$ for $0 \leq \theta \leq \pi$, the left side $|\cos\theta|$ is always non-negative. This doesn't rule out any angles yet, but it implies that any solution must have $\sin\theta \geq 0$, which is already true for $0 \leq \theta \leq \pi$.
So we need to solve $\cos\theta = \sin\theta$ for $0 \leq \theta \leq \frac{\pi}{2}$ and $-\cos\theta = \sin\theta$ for $\frac{\pi}{2} < \theta \leq \pi$.
From Case 1, the solution is $\theta = \frac{\pi}{4}$.
From Case 2, the solution is $\theta = \frac{3\pi}{4}$.
The possible values of $\theta$ in the range $0 \leq \theta \leq \pi$ satisfying $|\cos\theta| = \sin\theta$ are $\theta = \frac{\pi}{4}$ and $\theta = \frac{3\pi}{4}$.
Let's check the given options:
(A) 0: $|\cos(0)| = |1| = 1$, $\sin(0) = 0$. $1 \neq 0$.
(B) $\frac{\pi}{4}$: $|\cos(\frac{\pi}{4})| = |\frac{\sqrt{2}}{2}| = \frac{\sqrt{2}}{2}$, $\sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$. $\frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}$. This is a solution.
(C) $\frac{\pi}{2}$: $|\cos(\frac{\pi}{2})| = |0| = 0$, $\sin(\frac{\pi}{2}) = 1$. $0 \neq 1$.
(D) $\pi$: $|\cos(\pi)| = |-1| = 1$, $\sin(\pi) = 0$. $1 \neq 0$.
Among the given options, only $\theta = \frac{\pi}{4}$ satisfies the condition.
Answer:
The correct option is (B).

