| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 9 (Before Exercise 10.1) | Exercise 10.1 | Example 10 to 12 (Before Exercise 10.2) |
| Exercise 10.2 | Example 13 to 17 (Before Exercise 10.3) | Exercise 10.3 |
Chapter 10 Mensuration
This section delves into the solutions for Chapter 10: Mensuration, a fundamental area of geometry focusing on the measurement of geometric shapes. The solutions provided offer comprehensive guidance on calculating two key properties: perimeter and area.
The exploration begins with Perimeter, which is formally defined as the total distance around the boundary of a closed two-dimensional figure.
- For irregular polygons, the solutions demonstrate the straightforward method: simply summing the lengths of all constituent sides. If a polygon has sides of lengths $l_1, l_2, l_3, \dots, l_n$, its perimeter $P$ is given by $P = \sum_{i=1}^{n} l_i = l_1 + l_2 + l_3 + \dots + l_n$.
- For regular polygons, where all sides are equal, simplified formulas are derived and applied. Examples include:
- Perimeter of a Square: $P = 4 \times s$, where $s$ is the length of one side.
- Perimeter of an Equilateral Triangle: $P = 3 \times s$, where $s$ is the length of one side.
- Similar formulas apply for regular pentagons ($5 \times s$), hexagons ($6 \times s$), etc.
- Problem types addressed in the solutions often involve practical scenarios like calculating the length of fencing required for a field, the amount of lace needed for a border, or finding missing side lengths given the total perimeter.
Next, the concept of Area is thoroughly examined. Area represents the measure of the surface enclosed within the boundary of a closed figure.
- The solutions initially build intuition by using the technique of counting unit squares on graph paper. This visual method helps estimate or determine the area of both irregular and regular shapes, reinforcing the concept of area as surface coverage.
- Subsequently, standard formulas for common shapes are introduced and utilized extensively:
- Area of a Rectangle: $A = l \times b$, where $l$ is the length and $b$ is the breadth.
- Area of a Square: $A = s \times s = s^2$, where $s$ is the length of a side.
- The solutions expertly guide students through various calculation types: finding the area when dimensions are known, determining a missing dimension (e.g., finding length $l$ if Area $A$ and breadth $b$ are known, using $l = \frac{A}{b}$), and comparing the areas of different figures.
- A significant portion focuses on word problems reflecting real-world applications. Examples include:
- Calculating the cost of tiling a rectangular floor, often involving finding the total area and multiplying by the cost per square unit (e.g., cost per $m^2$ given in $\textsf{₹}$).
- Determining the area of a wall to be painted.
- Calculating the area of pathways built around or inside rectangular parks.
- Figuring out how many smaller items (like tiles or stamps) can fit within a larger area.
Throughout the solutions for Chapter 10, strong emphasis is placed on the critical importance of using correct units. It's highlighted that perimeter is a length measured in linear units (like cm, m, km), whereas area is measured in square units (like $cm^2$, $m^2$, $km^2$). The necessity of performing accurate unit conversions when measurements are given in different units is also clearly demonstrated.
Mastering the concepts and techniques presented in these Mensuration solutions provides students with practical geometric skills that are indispensable not only for further academic pursuits in geometry, physics, and engineering but also for numerous everyday tasks and problem-solving situations.
Example 1 to 9 (Before Exercise 10.1)
Example 1: Shabana wants to put a lace border all around a rectangular table cover (Fig 10.3), 3 m long and 2 m wide. Find the length of the lace required by Shabana.

Answer:
Given:
Shape of the table cover = Rectangular
Length of the rectangular table cover = $3$ m
Width (Breadth) of the rectangular table cover = $2$ m
To Find:
The length of the lace required to put a border all around the table cover.
Solution:
The lace border needs to go all around the rectangular table cover. This means we need to find the perimeter of the rectangle.
The perimeter of a rectangle is the total length of its boundary.
Let the length of the rectangle be $l$ and the width (breadth) be $b$.
Given, $l = 3$ m and $b = 2$ m.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Substituting the given values:
Perimeter = $2 \times (3 \text{ m} + 2 \text{ m})$
Perimeter = $2 \times (5 \text{ m})$
Perimeter = $10$ m
Therefore, the length of the lace required by Shabana is $10$ meters.
Alternate Solution:
The perimeter of a shape is the sum of the lengths of all its sides.
A rectangle has four sides, with opposite sides being equal in length.
So, the lengths of the sides are $3$ m, $2$ m, $3$ m, and $2$ m.
Length of lace required = Sum of all sides
Length of lace required = $length + breadth + length + breadth$
Length of lace required = $3 \text{ m} + 2 \text{ m} + 3 \text{ m} + 2 \text{ m}$
Length of lace required = $(3+2+3+2)$ m
Length of lace required = $10$ m
Hence, the length of the lace required by Shabana is 10 m.
Example 2: An athlete takes 10 rounds of a rectangular park, 50 m long and 25 m wide. Find the total distance covered by him.
Answer:
Given:
Shape of the park: Rectangular
Length of the rectangular park, $l = 50$ m
Width of the rectangular park, $b = 25$ m
Number of rounds taken by the athlete = 10
To Find:
The total distance covered by the athlete.
Solution:
The distance covered by the athlete in one round is equal to the perimeter of the rectangular park.
First, we need to calculate the perimeter of the rectangular park.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (\text{length} + \text{width})$
Perimeter = $2 \times (l + b)$
Substituting the given values of length and width:
Perimeter = $2 \times (50 \text{ m} + 25 \text{ m})$
Perimeter = $2 \times (75 \text{ m})$
Perimeter = $150 \text{ m}$
So, the distance covered in one round is 150 m.
The athlete takes 10 rounds of the park. To find the total distance, we multiply the distance covered in one round by the number of rounds.
Total distance covered = Distance in one round $\times$ Number of rounds
Total distance covered = $150 \text{ m} \times 10$
Total distance covered = $1500 \text{ m}$
We can also express this distance in kilometers. We know that:
$1000 \text{ m} = 1 \text{ km}$
So, $1500 \text{ m} = \frac{1500}{1000} \text{ km} = 1.5 \text{ km}$.
Final Answer:
The total distance covered by the athlete is 1500 m or 1.5 km.
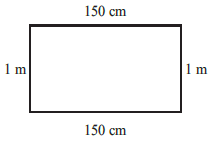
Answer:
Given:
Shape = Rectangle
Length of the rectangle ($l$) = $150$ cm
Breadth of the rectangle ($b$) = $1$ m
To Find:
The perimeter of the rectangle.
Solution:
To calculate the perimeter, both length and breadth must be in the same unit.
Let's convert the breadth from meters (m) to centimeters (cm).
We know the conversion factor:
$1 \text{ m} = 100 \text{ cm}$
So, the breadth $b = 1 \text{ m} = 1 \times 100 \text{ cm} = 100 \text{ cm}$.
Now we have:
Length ($l$) = $150$ cm
Breadth ($b$) = $100$ cm
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the values in centimeters:
Perimeter = $2 \times (150 \text{ cm} + 100 \text{ cm})$
Perimeter = $2 \times (250 \text{ cm})$
Perimeter = $500$ cm
We can also express this in meters.
Since $100 \text{ cm} = 1 \text{ m}$,
$500 \text{ cm} = \frac{500}{100} \text{ m} = 5 \text{ m}$
Therefore, the perimeter of the rectangle is $500$ cm or $5$ m.
Alternate Solution:
We can also convert the length from centimeters (cm) to meters (m).
We know the conversion factor:
$100 \text{ cm} = 1 \text{ m}$
So, $1 \text{ cm} = \frac{1}{100} \text{ m}$
Length ($l$) = $150 \text{ cm} = 150 \times \frac{1}{100} \text{ m} = \frac{150}{100} \text{ m} = 1.5 \text{ m}$.
Now we have:
Length ($l$) = $1.5$ m
Breadth ($b$) = $1$ m
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the values in meters:
Perimeter = $2 \times (1.5 \text{ m} + 1 \text{ m})$
Perimeter = $2 \times (2.5 \text{ m})$
Perimeter = $5$ m
We can also express this in centimeters.
Since $1 \text{ m} = 100 \text{ cm}$,
$5 \text{ m} = 5 \times 100 \text{ cm} = 500 \text{ cm}$
Therefore, the perimeter of the rectangle is $5$ m or $500$ cm.
Example 4: A farmer has a rectangular field of length and breadth 240 m and 180 m respectively. He wants to fence it with 3 rounds of rope as shown in figure 10.4. What is the total length of rope he must use?
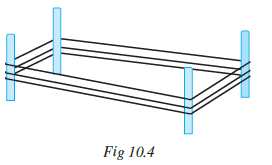
Answer:
Given:
Shape of the field = Rectangular
Length of the rectangular field ($l$) = $240$ m
Breadth of the rectangular field ($b$) = $180$ m
Number of rounds of rope required for fencing = $3$
To Find:
The total length of rope the farmer must use.
Solution:
First, we need to find the length of the rope required for one round of fencing. This is equal to the perimeter of the rectangular field.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the given values:
Perimeter = $2 \times (240 \text{ m} + 180 \text{ m})$
Perimeter = $2 \times (420 \text{ m})$
Perimeter = $840$ m
So, the length of rope required for one round of fencing is $840$ m.
The farmer wants to fence the field with $3$ rounds of rope.
Therefore, the total length of rope required is $3$ times the perimeter.
Total length of rope = $3 \times$ Perimeter
Total length of rope = $3 \times 840 \text{ m}$
Total length of rope = $2520$ m
Hence, the total length of rope the farmer must use is $2520$ m.
Example 5: Find the cost of fencing a rectangular park of length 250 m and breadth 175 m at the rate of ₹ 12 per metre.
Answer:
Given:
Shape of the park = Rectangular
Length of the rectangular park ($l$) = $250$ m
Breadth of the rectangular park ($b$) = $175$ m
Rate of fencing = $\textsf{₹ } 12$ per metre
To Find:
The total cost of fencing the rectangular park.
Solution:
First, we need to find the total length of the fence required. This is equal to the perimeter of the rectangular park.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the given values:
Perimeter = $2 \times (250 \text{ m} + 175 \text{ m})$
Perimeter = $2 \times (425 \text{ m})$
Perimeter = $850$ m
So, the total length of the fence required is $850$ m.
Now, we need to find the total cost of fencing.
The cost is given at the rate of $\textsf{₹ } 12$ per metre.
Total Cost = Perimeter $\times$ Rate per metre
Total Cost = $850 \text{ m} \times \textsf{₹ } 12 \text{ /m}$
Total Cost = $\textsf{₹ } (850 \times 12)$
$\begin{array}{cc} & & 8 & 5 & 0 \\ \times & & & 1 & 2 \\ \hline & 1 & 7 & 0 & 0 \\ & 8 & 5 & 0 & \times \\ \hline 1 & 0 & 2 & 0 & 0 \\ \hline \end{array}$
Total Cost = $\textsf{₹ } 10200$
Therefore, the total cost of fencing the rectangular park is $\textsf{₹ } 10,200$.
Example 6: Find the distance travelled by Shaina if she takes three rounds of a square park of side 70 m.
Answer:
Given:
Shape of the park = Square
Side length of the square park ($s$) = $70$ m
Number of rounds taken by Shaina = $3$
To Find:
The total distance travelled by Shaina.
Solution:
First, we need to find the distance travelled by Shaina in one round. This distance is equal to the perimeter of the square park.
The formula for the perimeter of a square is:
Perimeter = $4 \times side$
Perimeter = $4 \times s$
Substituting the given side length:
Perimeter = $4 \times 70 \text{ m}$
Perimeter = $280$ m
So, the distance covered in one round is $280$ m.
Shaina takes three rounds of the park.
Therefore, the total distance travelled is $3$ times the perimeter.
Total Distance = $3 \times$ Perimeter
Total Distance = $3 \times 280 \text{ m}$
$\begin{array}{cc} & & 2 & 8 & 0 \\ \times & & & & 3 \\ \hline & & 8 & 4 & 0 \\ \hline \end{array}$
Total Distance = $840$ m
Hence, the total distance travelled by Shaina is $840$ m.
Example 7: Pinky runs around a square field of side 75 m, Bob runs around a rectangular field with length 160 m and breadth 105 m. Who covers more distance and by how much?
Answer:
Given:
For Pinky:
Shape of the field = Square
Side of the square field ($s$) = $75$ m
For Bob:
Shape of the field = Rectangle
Length of the rectangular field ($l$) = $160$ m
Breadth of the rectangular field ($b$) = $105$ m
To Find:
1. Who covers more distance?
2. By how much distance?
Solution:
To find out who covers more distance, we need to calculate the distance each person runs. The distance run by each person is equal to the perimeter of the field they run around.
Distance covered by Pinky:
Pinky runs around a square field. The distance covered is the perimeter of the square.
Perimeter of a square = $4 \times side$
Perimeter = $4 \times s$
Perimeter = $4 \times 75 \text{ m}$
Perimeter = $300$ m
So, the distance covered by Pinky = $300$ m.
Distance covered by Bob:
Bob runs around a rectangular field. The distance covered is the perimeter of the rectangle.
Perimeter of a rectangle = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Perimeter = $2 \times (160 \text{ m} + 105 \text{ m})$
Perimeter = $2 \times (265 \text{ m})$
Perimeter = $530$ m
So, the distance covered by Bob = $530$ m.
Comparison:
Distance covered by Bob ($530$ m) is greater than the distance covered by Pinky ($300$ m).
$530 \text{ m} > 300 \text{ m}$
Therefore, Bob covers more distance.
Difference in distance:
Difference = Distance covered by Bob - Distance covered by Pinky
Difference = $530 \text{ m} - 300 \text{ m}$
Difference = $230$ m
Hence, Bob covers more distance than Pinky by $230$ m.
Example 8: Find the perimeter of a regular pentagon with each side measuring 3 cm.
Answer:
Given:
Shape = Regular pentagon
Length of each side ($s$) = $3$ cm
To Find:
The perimeter of the regular pentagon.
Solution:
A regular pentagon is a polygon with 5 sides, and all sides have equal length.
The perimeter of a polygon is the total length of its boundary, which is the sum of the lengths of all its sides.
For a regular polygon with $n$ sides, each of length $s$, the perimeter is given by:
Perimeter = Number of sides $\times$ Length of one side
In this case, the polygon is a regular pentagon, so the number of sides ($n$) is $5$.
The length of each side ($s$) is given as $3$ cm.
Substituting the values into the formula:
Perimeter = $5 \times s$
Perimeter = $5 \times 3 \text{ cm}$
Perimeter = $15$ cm
Therefore, the perimeter of the regular pentagon is $15$ cm.
Example 9: The perimeter of a regular hexagon is 18 cm. How long is its one side?
Answer:
Given:
Shape = Regular hexagon
Perimeter of the regular hexagon = $18$ cm
To Find:
The length of one side of the regular hexagon.
Solution:
A regular hexagon is a polygon with 6 sides, and all sides have equal length.
The perimeter of a regular polygon is given by the formula:
Perimeter = Number of sides $\times$ Length of one side
Let the length of one side of the regular hexagon be $s$.
For a hexagon, the number of sides is $6$.
So, the formula for the perimeter of a regular hexagon is:
Perimeter = $6 \times s$
We are given that the perimeter is $18$ cm.
Substituting the given value:
$18 \text{ cm} = 6 \times s$
To find the length of one side ($s$), we need to divide the perimeter by the number of sides:
$s = \frac{\text{Perimeter}}{\text{Number of sides}}$
$s = \frac{18 \text{ cm}}{6}$
$s = 3 \text{ cm}$
Therefore, the length of one side of the regular hexagon is $3$ cm.
Exercise 10.1
Question 1. Find the perimeter of each of the following figures :
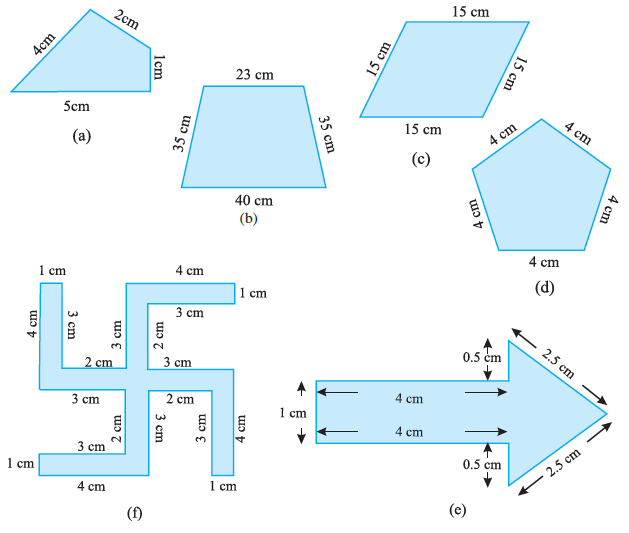
Answer:
The perimeter of a figure is the total length of its boundary, which is found by adding the lengths of all its sides.
(a)
The figure has sides with lengths 4 cm, 2 cm, 1 cm, and 5 cm.
Perimeter = Sum of all sides
Perimeter = $4 \text{ cm} + 2 \text{ cm} + 1 \text{ cm} + 5 \text{ cm}$
Perimeter = $12 \text{ cm}$
The perimeter of figure (a) is $12$ cm.
(b)
The figure has sides with lengths 23 cm, 35 cm, 40 cm, and 35 cm.
Perimeter = Sum of all sides
Perimeter = $23 \text{ cm} + 35 \text{ cm} + 40 \text{ cm} + 35 \text{ cm}$
Perimeter = $133 \text{ cm}$
The perimeter of figure (b) is $133$ cm.
(c)
The figure has four sides, each with length 15 cm.
Perimeter = Sum of all sides
Perimeter = $15 \text{ cm} + 15 \text{ cm} + 15 \text{ cm} + 15 \text{ cm}$
Alternatively, Perimeter = $4 \times \text{side length}$
Perimeter = $4 \times 15 \text{ cm}$
Perimeter = $60 \text{ cm}$
The perimeter of figure (c) is $60$ cm.
(d)
The figure is a pentagon with five sides, each with length 4 cm.
Perimeter = Sum of all sides
Perimeter = $4 \text{ cm} + 4 \text{ cm} + 4 \text{ cm} + 4 \text{ cm} + 4 \text{ cm}$
Alternatively, Perimeter = $5 \times \text{side length}$
Perimeter = $5 \times 4 \text{ cm}$
Perimeter = $20 \text{ cm}$
The perimeter of figure (d) is $20$ cm.
(e)
The figure has sides with lengths 1 cm, 4 cm, 0.5 cm, 2.5 cm, 2.5 cm, 0.5 cm, and 4 cm.
Perimeter = Sum of all sides
Perimeter = $1 \text{ cm} + 4 \text{ cm} + 0.5 \text{ cm} + 2.5 \text{ cm} + 2.5 \text{ cm} + 0.5 \text{ cm} + 4 \text{ cm}$
Perimeter = $(1 + 4 + 0.5 + 2.5 + 2.5 + 0.5 + 4) \text{ cm}$
Perimeter = $15 \text{ cm}$
The perimeter of figure (e) is $15$ cm.
(f)
The figure has many sides. Let's sum their lengths:
Starting from the top horizontal side and moving clockwise:
$4 \text{ cm} + 1 \text{ cm} + 3 \text{ cm} + 2 \text{ cm} + 3 \text{ cm} + 1 \text{ cm} + 4 \text{ cm} \ $$ + 1 \text{ cm} + 3 \text{ cm} \ $$ + 2 \text{ cm} + 3 \text{ cm} + 1 \text{ cm} + 4 \text{ cm} + 1 \text{ cm} + \ $$ 3 \text{ cm} + 2 \text{ cm} + 3 \text{ cm} + 1 \text{ cm} \ $$ + 4 \text{ cm} + 1 \text{ cm} + \ $$ 3 \text{ cm} + 2 \text{ cm} + 3 \text{ cm} + 1 \text{ cm}$
Alternatively, we can count the number of sides of each length:
Number of sides of length 1 cm = $8$
Number of sides of length 2 cm = $4$
Number of sides of length 3 cm = $8$
Number of sides of length 4 cm = $4$
Perimeter = $(8 \times 1 \text{ cm}) + (4 \times 2 \text{ cm}) + (8 \times 3 \text{ cm}) + (4 \times 4 \text{ cm})$
Perimeter = $8 \text{ cm} + 8 \text{ cm} + 24 \text{ cm} + 16 \text{ cm}$
Perimeter = $52 \text{ cm}$
The perimeter of figure (f) is $52$ cm.
Question 2. The lid of a rectangular box of sides 40 cm by 10 cm is sealed all round with tape. What is the length of the tape required?
Answer:
Given:
Shape of the lid = Rectangular
Length of the rectangular lid ($l$) = $40$ cm
Breadth of the rectangular lid ($b$) = $10$ cm
To Find:
The length of the tape required to seal the lid all round.
Solution:
The tape is used to seal the lid all round its boundary. Therefore, the length of the tape required is equal to the perimeter of the rectangular lid.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the given values:
Perimeter = $2 \times (40 \text{ cm} + 10 \text{ cm})$
Perimeter = $2 \times (50 \text{ cm})$
Perimeter = $100$ cm
The length of the tape required is $100$ cm.
Since $100 \text{ cm} = 1 \text{ m}$, the length of the tape required is also $1$ m.
Therefore, the length of the tape required is $100$ cm or $1$ m.
Alternate Solution:
The perimeter is the sum of all sides.
For the rectangular lid, the sides are $40$ cm, $10$ cm, $40$ cm, and $10$ cm.
Length of tape required = Sum of all sides
Length of tape required = $l + b + l + b$
Length of tape required = $40 \text{ cm} + 10 \text{ cm} + 40 \text{ cm} + 10 \text{ cm}$
Length of tape required = $(40+10+40+10) \text{ cm}$
Length of tape required = $100$ cm
Length of tape required = $1$ m
Hence, the length of the tape required is $100$ cm or $1$ m.
Question 3. A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?
Answer:
Given:
Shape of the table-top = Rectangular
Length of the table-top ($l$) = $2$ m $25$ cm
Breadth of the table-top ($b$) = $1$ m $50$ cm
To Find:
The perimeter of the table-top.
Solution:
To find the perimeter, we need to have both length and breadth in the same unit. Let's convert both measurements to meters (m).
We know that $100 \text{ cm} = 1 \text{ m}$, so $1 \text{ cm} = \frac{1}{100} \text{ m} = 0.01 \text{ m}$.
Length $l = 2 \text{ m } 25 \text{ cm} = 2 \text{ m} + 25 \times 0.01 \text{ m} = 2 \text{ m} + 0.25 \text{ m} = 2.25 \text{ m}$.
Breadth $b = 1 \text{ m } 50 \text{ cm} = 1 \text{ m} + 50 \times 0.01 \text{ m} = 1 \text{ m} + 0.50 \text{ m} = 1.50 \text{ m}$.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the values in meters:
Perimeter = $2 \times (2.25 \text{ m} + 1.50 \text{ m})$
Perimeter = $2 \times (3.75 \text{ m})$
$\begin{array}{cc} & & 3 & . & 7 & 5 \\ \times & & & & & 2 \\ \hline & & 7 & . & 5 & 0 \\ \hline \end{array}$
Perimeter = $7.50$ m
We can also express this as 7 meters and 50 centimeters ($7.50 \text{ m} = 7 \text{ m} + 0.50 \text{ m} = 7 \text{ m} + 50 \text{ cm}$).
Therefore, the perimeter of the table-top is $7.50$ m or $7$ m $50$ cm.
Alternate Solution:
Convert both measurements to centimeters (cm).
We know $1 \text{ m} = 100 \text{ cm}$.
Length $l = 2 \text{ m } 25 \text{ cm} = (2 \times 100) \text{ cm} + 25 \text{ cm} = 200 \text{ cm} + 25 \text{ cm} = 225 \text{ cm}$.
Breadth $b = 1 \text{ m } 50 \text{ cm} = (1 \times 100) \text{ cm} + 50 \text{ cm} = 100 \text{ cm} + 50 \text{ cm} = 150 \text{ cm}$.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (l + b)$
Substituting the values in centimeters:
Perimeter = $2 \times (225 \text{ cm} + 150 \text{ cm})$
Perimeter = $2 \times (375 \text{ cm})$
$\begin{array}{cc} & & 3 & 7 & 5 \\ \times & & & & 2 \\ \hline & & 7 & 5 & 0 \\ \hline \end{array}$
Perimeter = $750$ cm
To convert back to meters and centimeters:
$750 \text{ cm} = 700 \text{ cm} + 50 \text{ cm} = \frac{700}{100} \text{ m} + 50 \text{ cm} = 7 \text{ m } 50 \text{ cm}$.
Alternatively, $750 \text{ cm} = \frac{750}{100} \text{ m} = 7.50 \text{ m}$.
Hence, the perimeter of the table-top is $750$ cm or $7$ m $50$ cm or $7.50$ m.
Question 4. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm respectively?
Answer:
Given:
Shape of the photograph = Rectangular
Length of the photograph ($l$) = $32$ cm
Breadth of the photograph ($b$) = $21$ cm
To Find:
The length of the wooden strip required to frame the photograph.
Solution:
The wooden strip is required to frame the photograph, which means it will go around the boundary of the photograph.
Therefore, the length of the wooden strip required is equal to the perimeter of the rectangular photograph.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the given values:
Perimeter = $2 \times (32 \text{ cm} + 21 \text{ cm})$
Perimeter = $2 \times (53 \text{ cm})$
$\begin{array}{cc} & & 5 & 3 \\ \times & & & 2 \\ \hline & 1 & 0 & 6 \\ \hline \end{array}$
Perimeter = $106$ cm
Hence, the length of the wooden strip required is $106$ cm.
Alternate Solution:
The perimeter is the sum of all sides of the rectangle.
The sides of the photograph are $32$ cm, $21$ cm, $32$ cm, and $21$ cm.
Length of wooden strip = Sum of all sides
Length of wooden strip = $l + b + l + b$
Length of wooden strip = $32 \text{ cm} + 21 \text{ cm} + 32 \text{ cm} + 21 \text{ cm}$
Length of wooden strip = $(32 + 21 + 32 + 21) \text{ cm}$
Length of wooden strip = $106 \text{ cm}$
Thus, the required length of the wooden strip is $106$ cm.
Question 5. A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
Answer:
Given:
Shape of the piece of land = Rectangular
Length of the land ($l$) = $0.7$ km
Breadth of the land ($b$) = $0.5$ km
Number of rows of wires for fencing = $4$
To Find:
The total length of the wire needed.
Solution:
First, we need to find the length of the wire required for one row of fencing. This length is equal to the perimeter of the rectangular piece of land.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the given values:
Perimeter = $2 \times (0.7 \text{ km} + 0.5 \text{ km})$
Perimeter = $2 \times (1.2 \text{ km})$
$\begin{array}{cc} & 1 & . & 2 \\ \times & & & 2 \\ \hline & 2 & . & 4 \\ \hline \end{array}$
Perimeter = $2.4$ km
So, the length of wire needed for one row of fencing is $2.4$ km.
Since the fencing is done with $4$ rows of wires, the total length of wire needed is $4$ times the perimeter.
Total length of wire = Number of rows $\times$ Perimeter
Total length of wire = $4 \times 2.4 \text{ km}$
$\begin{array}{cc} & 2 & . & 4 \\ \times & & & 4 \\ \hline & 9 & . & 6 \\ \hline \end{array}$
Total length of wire = $9.6$ km
Therefore, the total length of the wire needed is $9.6$ km.
Question 6. Find the perimeter of each of the following shapes :
(a) A triangle of sides 3 cm, 4 cm and 5 cm.
(b) An equilateral triangle of side 9 cm.
(c) An isosceles triangle with equal sides 8 cm each and third side 6 cm.
Answer:
The perimeter of a shape is the sum of the lengths of all its sides.
(a) A triangle of sides 3 cm, 4 cm and 5 cm.
Given:
Shape = Triangle
Length of side 1 = $3$ cm
Length of side 2 = $4$ cm
Length of side 3 = $5$ cm
To Find:
The perimeter of the triangle.
Solution:
Perimeter = Sum of all sides
Perimeter = $3 \text{ cm} + 4 \text{ cm} + 5 \text{ cm}$
Perimeter = $12 \text{ cm}$
Therefore, the perimeter of the triangle is $12$ cm.
(b) An equilateral triangle of side 9 cm.
Given:
Shape = Equilateral Triangle
Length of each side ($s$) = $9$ cm
To Find:
The perimeter of the equilateral triangle.
Solution:
An equilateral triangle has 3 equal sides.
Perimeter = Sum of all sides = $s + s + s = 3 \times s$
Perimeter = $3 \times 9 \text{ cm}$
Perimeter = $27 \text{ cm}$
Therefore, the perimeter of the equilateral triangle is $27$ cm.
(c) An isosceles triangle with equal sides 8 cm each and third side 6 cm.
Given:
Shape = Isosceles Triangle
Length of equal side 1 = $8$ cm
Length of equal side 2 = $8$ cm
Length of third side = $6$ cm
To Find:
The perimeter of the isosceles triangle.
Solution:
An isosceles triangle has two equal sides.
Perimeter = Sum of all sides
Perimeter = $8 \text{ cm} + 8 \text{ cm} + 6 \text{ cm}$
Perimeter = $22 \text{ cm}$
Therefore, the perimeter of the isosceles triangle is $22$ cm.
Question 7. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Answer:
Given:
Shape = Triangle
Length of side 1 = $10$ cm
Length of side 2 = $14$ cm
Length of side 3 = $15$ cm
To Find:
The perimeter of the triangle.
Solution:
The perimeter of a triangle is the sum of the lengths of its three sides.
Perimeter = Length of side 1 + Length of side 2 + Length of side 3
Substituting the given values:
Perimeter = $10 \text{ cm} + 14 \text{ cm} + 15 \text{ cm}$
Perimeter = $(10 + 14 + 15) \text{ cm}$
Perimeter = $39 \text{ cm}$
Therefore, the perimeter of the triangle is $39$ cm.
Question 8. Find the perimeter of a regular hexagon with each side measuring 8 m.
Answer:
Given:
Shape = Regular hexagon
Length of each side ($s$) = $8$ m
To Find:
The perimeter of the regular hexagon.
Solution:
A regular hexagon is a polygon with 6 sides, and all sides have equal length.
The perimeter of a regular polygon is given by the formula:
Perimeter = Number of sides $\times$ Length of one side
For a hexagon, the number of sides is $6$.
Let the length of one side be $s = 8$ m.
So, the formula for the perimeter of a regular hexagon is:
Perimeter = $6 \times s$
Substituting the given side length:
Perimeter = $6 \times 8 \text{ m}$
$\begin{array}{cc} & & & 8 \\ \times & & & 6 \\ \hline & & 4 & 8 \\ \hline \end{array}$
Perimeter = $48$ m
Therefore, the perimeter of the regular hexagon is $48$ m.
Question 9. Find the side of the square whose perimeter is 20 m.
Answer:
Given:
Shape = Square
Perimeter of the square = $20$ m
To Find:
The length of the side of the square.
Solution:
A square has 4 equal sides.
The formula for the perimeter of a square is:
Perimeter = $4 \times$ Length of one side
Let the length of one side be $s$.
Perimeter = $4 \times s$
We are given that the Perimeter = $20$ m.
So, we have the equation:
$20 \text{ m} = 4 \times s$
To find the length of the side ($s$), we need to divide the perimeter by 4:
$s = \frac{\text{Perimeter}}{4}$
$s = \frac{20 \text{ m}}{4}$
$s = 5 \text{ m}$
Therefore, the side of the square is $5$ m.
Question 10. The perimeter of a regular pentagon is 100 cm. How long is its each side?
Answer:
Given:
Shape = Regular pentagon
Perimeter of the regular pentagon = $100$ cm
To Find:
The length of each side of the regular pentagon.
Solution:
A regular pentagon is a polygon with 5 sides, and all sides have equal length.
The formula for the perimeter of a regular polygon is:
Perimeter = Number of sides $\times$ Length of one side
Let the length of one side of the regular pentagon be $s$.
For a pentagon, the number of sides is $5$.
So, the formula for the perimeter of a regular pentagon is:
Perimeter = $5 \times s$
We are given that the Perimeter = $100$ cm.
Substituting the given value:
$100 \text{ cm} = 5 \times s$
To find the length of each side ($s$), we need to divide the perimeter by the number of sides:
$s = \frac{\text{Perimeter}}{\text{Number of sides}}$
$s = \frac{100 \text{ cm}}{5}$
$s = 20 \text{ cm}$
Therefore, the length of each side of the regular pentagon is $20$ cm.
Question 11. A piece of string is 30 cm long. What will be the length of each side if the string is used to form :
(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?
Answer:
Given:
Total length of the string = $30$ cm.
This length of the string is used to form the boundary of the shapes. Therefore, the perimeter of each shape formed will be $30$ cm.
(a) a square
To Find:
The length of each side of the square.
Solution:
A square has 4 equal sides.
Perimeter of the square = Length of the string = $30$ cm.
The formula for the perimeter of a square is:
Perimeter = $4 \times$ Length of one side
Let the length of one side be $s$.
$30 \text{ cm} = 4 \times s$
To find the side length $s$, we divide the perimeter by 4:
$s = \frac{30 \text{ cm}}{4}$
$s = 7.5 \text{ cm}$
Therefore, the length of each side of the square will be $7.5$ cm.
(b) an equilateral triangle
To Find:
The length of each side of the equilateral triangle.
Solution:
An equilateral triangle has 3 equal sides.
Perimeter of the equilateral triangle = Length of the string = $30$ cm.
The formula for the perimeter of an equilateral triangle is:
Perimeter = $3 \times$ Length of one side
Let the length of one side be $s$.
$30 \text{ cm} = 3 \times s$
To find the side length $s$, we divide the perimeter by 3:
$s = \frac{30 \text{ cm}}{3}$
$s = 10 \text{ cm}$
Therefore, the length of each side of the equilateral triangle will be $10$ cm.
(c) a regular hexagon
To Find:
The length of each side of the regular hexagon.
Solution:
A regular hexagon has 6 equal sides.
Perimeter of the regular hexagon = Length of the string = $30$ cm.
The formula for the perimeter of a regular hexagon is:
Perimeter = $6 \times$ Length of one side
Let the length of one side be $s$.
$30 \text{ cm} = 6 \times s$
To find the side length $s$, we divide the perimeter by 6:
$s = \frac{30 \text{ cm}}{6}$
$s = 5 \text{ cm}$
Therefore, the length of each side of the regular hexagon will be $5$ cm.
Question 12. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
Answer:
Given:
Shape = Triangle
Length of the first side = $12$ cm
Length of the second side = $14$ cm
Perimeter of the triangle = $36$ cm
To Find:
The length of the third side of the triangle.
Solution:
The perimeter of a triangle is the sum of the lengths of its three sides.
Perimeter = Length of side 1 + Length of side 2 + Length of side 3
Let the length of the third side be $x$ cm.
We are given:
Length of side 1 = $12$ cm
Length of side 2 = $14$ cm
Perimeter = $36$ cm
Substituting these values into the perimeter formula:
$36 \text{ cm} = 12 \text{ cm} + 14 \text{ cm} + x$
First, calculate the sum of the two known sides:
$12 \text{ cm} + 14 \text{ cm} = 26 \text{ cm}$
Now, substitute this sum back into the equation:
$36 \text{ cm} = 26 \text{ cm} + x$
To find the length of the third side ($x$), subtract the sum of the known sides from the perimeter:
$x = 36 \text{ cm} - 26 \text{ cm}$
$\begin{array}{cc} & 3 & 6 \\ - & 2 & 6 \\ \hline & 1 & 0 \\ \hline \end{array}$
$x = 10 \text{ cm}$
Therefore, the length of the third side of the triangle is $10$ cm.
Question 13. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.
Answer:
Given:
Shape of the park = Square
Side length of the square park ($s$) = $250$ m
Rate of fencing = $\textsf{₹ } 20$ per metre
To Find:
The total cost of fencing the square park.
Solution:
First, we need to find the total length of the fence required. This is equal to the perimeter of the square park.
The formula for the perimeter of a square is:
Perimeter = $4 \times side$
Perimeter = $4 \times s$
Substituting the given side length:
Perimeter = $4 \times 250 \text{ m}$
$\begin{array}{cc} & & 2 & 5 & 0 \\ \times & & & & 4 \\ \hline & 1 & 0 & 0 & 0 \\ \hline \end{array}$
Perimeter = $1000$ m
So, the total length of the fence required is $1000$ m.
Now, we need to find the total cost of fencing.
The cost is given at the rate of $\textsf{₹ } 20$ per metre.
Total Cost = Perimeter $\times$ Rate per metre
Total Cost = $1000 \text{ m} \times \textsf{₹ } 20 \text{ /m}$
Total Cost = $\textsf{₹ } (1000 \times 20)$
Total Cost = $\textsf{₹ } 20000$
Therefore, the total cost of fencing the square park is $\textsf{₹ } 20,000$.
Question 14. Find the cost of fencing a rectangular park of length 175 m and breadth 125 m at the rate of ₹ 12 per metre.
Answer:
Given:
Shape of the park = Rectangular
Length of the rectangular park ($l$) = $175$ m
Breadth of the rectangular park ($b$) = $125$ m
Rate of fencing = $\textsf{₹ } 12$ per metre
To Find:
The total cost of fencing the rectangular park.
Solution:
First, we need to find the total length of the fence required. This is equal to the perimeter of the rectangular park.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Substituting the given values:
Perimeter = $2 \times (175 \text{ m} + 125 \text{ m})$
Perimeter = $2 \times (300 \text{ m})$
Perimeter = $600$ m
So, the total length of the fence required is $600$ m.
Now, we need to find the total cost of fencing.
The cost is given at the rate of $\textsf{₹ } 12$ per metre.
Total Cost = Perimeter $\times$ Rate per metre
Total Cost = $600 \text{ m} \times \textsf{₹ } 12 \text{ /m}$
Total Cost = $\textsf{₹ } (600 \times 12)$
$\begin{array}{cc} & & & 6 & 0 & 0 \\ \times & & & & 1 & 2 \\ \hline & & 1 & 2 & 0 & 0 \\ & & 6 & 0 & 0 & \times \\ \hline & & 7 & 2 & 0 & 0 \\ \hline \end{array}$
Total Cost = $\textsf{₹ } 7200$
Therefore, the total cost of fencing the rectangular park is $\textsf{₹ } 7,200$.
Question 15. Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with length 60 m and breadth 45 m. Who covers less distance?
Answer:
Given:
For Sweety:
Shape of the park = Square
Side of the square park ($s$) = $75$ m
For Bulbul:
Shape of the park = Rectangle
Length of the rectangular park ($l$) = $60$ m
Breadth of the rectangular park ($b$) = $45$ m
To Find:
Who covers less distance?
Solution:
To find out who covers less distance, we need to calculate the distance each person runs. The distance run by each person is equal to the perimeter of the park they run around.
Distance covered by Sweety:
Sweety runs around a square park. The distance covered is the perimeter of the square.
Perimeter of a square = $4 \times side$
Perimeter = $4 \times s$
Perimeter = $4 \times 75 \text{ m}$
Perimeter = $300$ m
So, the distance covered by Sweety = $300$ m.
Distance covered by Bulbul:
Bulbul runs around a rectangular park. The distance covered is the perimeter of the rectangle.
Perimeter of a rectangle = $2 \times (length + breadth)$
Perimeter = $2 \times (l + b)$
Perimeter = $2 \times (60 \text{ m} + 45 \text{ m})$
Perimeter = $2 \times (105 \text{ m})$
Perimeter = $210$ m
So, the distance covered by Bulbul = $210$ m.
Comparison:
Distance covered by Sweety = $300$ m
Distance covered by Bulbul = $210$ m
Comparing the distances: $210 \text{ m} < 300 \text{ m}$
The distance covered by Bulbul is less than the distance covered by Sweety.
Therefore, Bulbul covers less distance.
Question 16. What is the perimeter of each of the following figures? What do you infer from the answers?

Answer:
To Find:
1. The perimeter of each of the four given figures.
2. An inference based on the calculated perimeters.
Solution:
(a) Figure (a) - Square
Given: Side length ($s$) = $25$ cm
The perimeter of a square is calculated using the formula:
Perimeter = $4 \times side$
Perimeter = $4 \times 25 \text{ cm}$
Perimeter = $100 \text{ cm}$
The perimeter of the square is $100$ cm.
(b) Figure (b) - Rectangle
Given: Length ($l$) = $40$ cm, Breadth ($b$) = $10$ cm
The perimeter of a rectangle is calculated using the formula:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (40 \text{ cm} + 10 \text{ cm})$
Perimeter = $2 \times (50 \text{ cm})$
Perimeter = $100 \text{ cm}$
The perimeter of the rectangle is $100$ cm.
(c) Figure (c) - Rectangle
Given: Length ($l$) = $30$ cm, Breadth ($b$) = $20$ cm
The perimeter of a rectangle is calculated using the formula:
Perimeter = $2 \times (length + breadth)$
Perimeter = $2 \times (30 \text{ cm} + 20 \text{ cm})$
Perimeter = $2 \times (50 \text{ cm})$
Perimeter = $100 \text{ cm}$
The perimeter of the rectangle is $100$ cm.
(d) Figure (d) - Triangle
Given: Sides are $30$ cm, $30$ cm, and $40$ cm.
The perimeter of a triangle is the sum of the lengths of its three sides.
Perimeter = Side 1 + Side 2 + Side 3
Perimeter = $30 \text{ cm} + 30 \text{ cm} + 40 \text{ cm}$
Perimeter = $100 \text{ cm}$
The perimeter of the triangle is $100$ cm.
Inference:
The perimeters of all four figures are:
(a) Square: $100$ cm
(b) Rectangle: $100$ cm
(c) Rectangle: $100$ cm
(d) Triangle: $100$ cm
From the answers, we infer that all the given figures have the same perimeter, which is $100$ cm, even though they are different shapes with different dimensions.
Question 17. Avneet buys 9 square paving slabs, each with a side of $\frac{1}{2}$ m. He lays them in the form of a square.
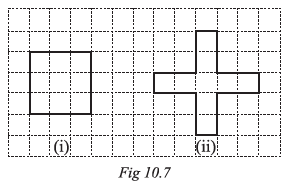
(a) What is the perimeter of his arrangement [Fig 10.7(i)]?
(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What isthe perimeter of her arrangement [(Fig 10.7 (ii)]?
(c) Which has greater perimeter?
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)
Answer:
Given:
Number of square paving slabs = 9
Side length of each square slab ($s_{slab}$) = $\frac{1}{2}$ m = $0.5$ m
(a) What is the perimeter of his arrangement [Fig 10.7(i)]?
Solution (a):
Avneet arranges the 9 slabs in the form of a larger square.
Since there are 9 slabs ($3 \times 3 = 9$), the larger square will have 3 slabs along each side.
The side length of the larger square ($S_{large}$) = $3 \times$ side length of one slab
$S_{large} = 3 \times \frac{1}{2} \text{ m} = \frac{3}{2} \text{ m} = 1.5 \text{ m}$
The perimeter of a square is given by the formula: Perimeter = $4 \times$ side length.
Perimeter of Avneet's arrangement = $4 \times S_{large}$
Perimeter = $4 \times \frac{3}{2} \text{ m}$
Perimeter = $\frac{12}{2} \text{ m} = 6 \text{ m}$
Therefore, the perimeter of Avneet's arrangement (the square) is $6$ m.
(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [(Fig 10.7 (ii)]?
Solution (b):
Shari's arrangement is in the form of a cross using the 9 slabs, as shown in Fig 10.7(ii).
To find the perimeter, we need to sum the lengths of all the outer edges of the cross shape.
Let's count the number of outer edges (each of length $\frac{1}{2}$ m):
Looking at the figure, we can trace the boundary. Each "step" or straight segment of the boundary corresponds to the side of a small slab.
Counting the exposed sides along the boundary:
Top projection: 3 sides (top, left, right)
Left projection: 3 sides (top, left, bottom)
Bottom projection: 3 sides (left, bottom, right)
Right projection: 3 sides (top, bottom, right)
Inner corners (4 corners, each contributing 2 sides to the perimeter): $4 \times 2 = 8$ sides
Total number of exposed sides = $3 + 3 + 3 + 3 + 8 = 20$ sides (Or simply count the edges along the boundary: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20).
Each side has a length of $\frac{1}{2}$ m.
Perimeter of Shari's arrangement = Number of exposed sides $\times$ Length of one side
Perimeter = $20 \times \frac{1}{2} \text{ m}$
Perimeter = $10 \text{ m}$
Therefore, the perimeter of Shari's arrangement (the cross) is $10$ m.
(c) Which has greater perimeter?
Solution (c):
Perimeter of Avneet's arrangement (square) = $6$ m
Perimeter of Shari's arrangement (cross) = $10$ m
Comparing the two perimeters: $10 \text{ m} > 6 \text{ m}$.
Therefore, Shari's arrangement (the cross) has a greater perimeter.
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)
Solution (d):
The perimeter of an arrangement is determined by the number of exposed edges of the slabs.
Each slab has 4 edges. Total edges available = $9 \text{ slabs} \times 4 \text{ edges/slab} = 36$ edges.
When two slabs meet along a complete edge, 2 edges become internal and are not part of the perimeter.
To maximize the perimeter, we need to minimize the number of shared (internal) edges.
For 9 slabs to form a single connected shape, there must be at least $9-1 = 8$ shared edges (connections).
Minimum number of internal edges = $2 \times (\text{minimum number of connections}) = 2 \times 8 = 16$.
Maximum number of exposed edges (Maximum Perimeter) = Total edges - Minimum internal edges
Maximum number of exposed edges = $36 - 16 = 20$ edges.
Maximum possible perimeter = $20 \times \text{length of one edge}$
Maximum possible perimeter = $20 \times \frac{1}{2} \text{ m} = 10 \text{ m}$.
Shari's cross arrangement already has a perimeter of $10$ m, which is the maximum possible perimeter for a connected arrangement of 9 square slabs.
Another arrangement that gives this maximum perimeter is laying all 9 slabs in a single row ($1 \times 9$). This also has 20 exposed edges: $(9 \text{ top} + 9 \text{ bottom} + 1 \text{ left end} + 1 \text{ right end}) = 20$. Perimeter = $20 \times \frac{1}{2} = 10$ m.
Since the maximum possible perimeter is $10$ m, Avneet cannot make an arrangement with an even greater perimeter than Shari's arrangement.
Example 10 to 12 (Before Exercise 10.2)
Example 10: Find the area of the shape shown in the figure 10.10.

Answer:
To Find:
The area of the shape shown in the figure by counting the enclosed squares.
Solution:
The shape is made up of line segments, and it covers a combination of full squares and half squares. We can find the total area by adding the areas of the fully-filled squares and the half-filled squares.
1. Count the number of fully-filled squares:
By observing the figure, we can count the number of squares that are completely inside the boundary of the shape.
Number of fully-filled squares = 3.
2. Count the number of half-filled squares:
Next, we count the number of squares that are exactly half-covered by the shape.
Number of half-filled squares = 3.
3. Calculate the total area:
The total area is the sum of the area covered by the full squares and the area covered by the half squares.
Area covered by full squares = (Number of full squares) $\times$ (Area of one square)
Area covered by full squares = $3 \times 1$ sq unit = 3 sq units.
Area covered by half squares = (Number of half squares) $\times$ (Area of half a square)
Area covered by half squares = $3 \times \frac{1}{2}$ sq units = $1.5$ sq units or $1\frac{1}{2}$ sq units.
Total Area = Area of full squares + Area of half squares
Total Area = $3 + 1\frac{1}{2}$ sq units
Total Area = $4\frac{1}{2}$ sq units.
Final Answer:
The area of the shape is $4\frac{1}{2}$ sq units.
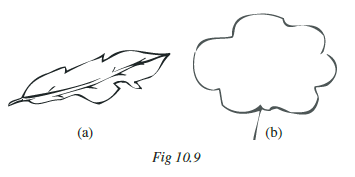
Example 11: By counting squares, estimate the area of the figure 10.9 b.
Answer:
To Find:
Estimate the area of the figure 10.9 (b) by counting squares on the grid.
Solution:
To estimate the area of the irregular shape of the leaf, we place it on a grid paper and count the number of squares it covers using the following rules:
- A square that is fully filled is counted as 1 square unit.
- A square that is more than half-filled is also counted as 1 square unit.
- A square that is exactly half-filled is counted as $\frac{1}{2}$ square unit.
- A square that is less than half-filled is ignored (counted as 0).
By applying these rules to figure 10.9 (b), we can categorize the squares as follows:
| Covered Squares Category | Number of Squares | Estimated Area (sq units) |
| Fully filled squares | 11 | $11 \times 1 = 11$ |
| Half-filled squares | 3 | $3 \times \frac{1}{2} = 1\frac{1}{2}$ |
| More than half-filled squares | 7 | $7 \times 1 = 7$ |
| Less than half-filled squares | 5 | $5 \times 0 = 0$ |
The total estimated area is the sum of the areas from the counted categories (fully filled, half-filled, and more than half-filled).
Total Estimated Area = $11 + (3 \times \frac{1}{2}) + 7$ sq units
Total Estimated Area = $11 + 1\frac{1}{2} + 7$ sq units
Total Estimated Area = $(11 + 7) + 1\frac{1}{2}$ sq units
Total Estimated Area = $18 + 1\frac{1}{2}$ sq units
Total Estimated Area = $19\frac{1}{2}$ sq units
Final Answer:
The estimated area of the figure 10.9 (b) is $19\frac{1}{2}$ sq units.
Example 12: By counting squares, estimate the area of the figure 10.9 a.
Answer:
To Find:
Estimate the area of the figure 10.9 (a) by counting the squares it covers on the grid.
Solution:
To estimate the area of the irregular shape of the leaf in figure (a), we will count the number of squares it covers on the grid paper. The following rules are applied:
- A square that is fully filled is counted as 1 sq unit.
- A square that is more than half-filled is also counted as 1 sq unit.
- A square that is less than half-filled is ignored (counted as 0).
- A square that is exactly half-filled is counted as $\frac{1}{2}$ sq unit.
By applying these rules to figure 10.9 (a), we can categorize the squares as follows:
| Covered Area | Number of Squares | Area Estimate (sq units) |
| (i) Fully-filled squares | 1 | 1 |
| (ii) Half-filled squares | 0 | 0 |
| (iii) More than half-filled squares | 7 | 7 |
| (iv) Less than half-filled squares | 9 | 0 |
The total estimated area is the sum of the areas from the categories that are counted (fully filled and more than half-filled).
Total Area = (Area of fully-filled squares) + (Area of more than half-filled squares)
Total Area = $1 + 7$ sq units
Total Area = $8$ sq units
Final Answer:
The estimated area of the figure 10.9 (a) is 8 sq units.
Exercise 10.2
Question 1. Find the areas of the following figures by counting square:

Answer:
To find the area of each figure, we count the squares enclosed by the figure. We use the following conventions:
- The area of one fully filled square is 1 sq unit.
- The area of a square that is exactly half-filled is $\frac{1}{2}$ sq unit.
- The area of a square that is more than half-filled is counted as 1 sq unit.
- Squares that are less than half-filled are ignored (counted as 0 sq units).
(a)
Number of fully filled squares = 9
Number of half-filled squares = 0
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) = $9 \times 1 = 9$ sq units.
Area = 9 sq units.
(b)
Number of fully filled squares = 5
Number of half-filled squares = 0
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) = $5 \times 1 = 5$ sq units.
Area = 5 sq units.
(c)
Number of fully filled squares = 2
Number of half-filled squares = 4
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) + (Number of half-filled squares $\times$ $\frac{1}{2}$)
Total Area = $(2 \times 1) + (4 \times \frac{1}{2}) = 2 + 2 = 4$ sq units.
Area = 4 sq units.
(d)
Number of fully filled squares = 8
Number of half-filled squares = 0
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) = $8 \times 1 = 8$ sq units.
Area = 8 sq units.
(e)
Number of fully filled squares = 10
Number of half-filled squares = 0
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) = $10 \times 1 = 10$ sq units.
Area = 10 sq units.
(f)
Number of fully filled squares = 2
Number of half-filled squares = 4
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) + (Number of half-filled squares $\times$ $\frac{1}{2}$)
Total Area = $(2 \times 1) + (4 \times \frac{1}{2}) = 2 + 2 = 4$ sq units.
Area = 4 sq units.
(g)
Number of fully filled squares = 4
Number of half-filled squares = 4
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) + (Number of half-filled squares $\times$ $\frac{1}{2}$)
Total Area = $(4 \times 1) + (4 \times \frac{1}{2}) = 4 + 2 = 6$ sq units.
Area = 6 sq units.
(h)
Number of fully filled squares = 5
Number of half-filled squares = 0
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) = $5 \times 1 = 5$ sq units.
Area = 5 sq units.
(i)
Number of fully filled squares = 9
Number of half-filled squares = 0
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) = $9 \times 1 = 9$ sq units.
Area = 9 sq units.
(j)
Number of fully filled squares = 2
Number of half-filled squares = 4
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) + (Number of half-filled squares $\times$ $\frac{1}{2}$)
Total Area = $(2 \times 1) + (4 \times \frac{1}{2}) = 2 + 2 = 4$ sq units.
Area = 4 sq units.
(k)
Number of fully filled squares = 4
Number of half-filled squares = 2
Number of more than half-filled squares = 0
Number of less than half-filled squares = 0
Total Area = (Number of fully filled squares $\times$ 1) + (Number of half-filled squares $\times$ $\frac{1}{2}$)
Total Area = $(4 \times 1) + (2 \times \frac{1}{2}) = 4 + 1 = 5$ sq units.
Area = 5 sq units.
(l) We categorize the squares covered by the figure:
| Covered Squares Category | Number of Squares | Area (sq units) |
| Fully filled squares | 2 | $2 \times 1 = 2$ |
| More than half-filled squares | 4 | $4 \times 1 = 4$ |
| Half-filled squares | 4 | $4 \times \frac{1}{2} = 2$ |
Total Area = $2 + 4 + 2 = 8$ sq units.
Area = 8 sq units.
(m) We categorize the squares covered by the figure:
| Covered Squares Category | Number of Squares | Area (sq units) |
| Fully filled squares | 6 | $6 \times 1 = 6$ |
| More than half-filled squares | 6 | $6 \times 1 = 6$ |
| Half-filled squares | 4 | $4 \times \frac{1}{2} = 2$ |
Total Area = $6 + 6 + 2 = 14$ sq units.
Area = 14 sq units.
(n) We categorize the squares covered by the figure:
| Covered Squares Category | Number of Squares | Area (sq units) |
| Fully filled squares | 9 | $9 \times 1 = 9$ |
| More than half-filled squares | 9 | $9 \times 1 = 9$ |
Total Area = $9 + 9 = 18$ sq units.
Area = 18 sq units.
Example 13 to 17 (Before Exercise 10.3)
Example 13: Find the area of a rectangle whose length and breadth are 12 cm and 4 cm respectively.
Answer:
Given:
Shape = Rectangle
Length of the rectangle ($l$) = $12$ cm
Breadth of the rectangle ($b$) = $4$ cm
To Find:
The area of the rectangle.
Solution:
The formula for the area of a rectangle is given by:
Area = Length $\times$ Breadth
$A = l \times b$
Substituting the given values for length and breadth:
$A = 12 \text{ cm} \times 4 \text{ cm}$
$\begin{array}{cc} & & 1 & 2 \\ \times & & & 4 \\ \hline & & 4 & 8 \\ \hline \end{array}$
$A = 48$ sq cm
Alternatively written using LaTeX:
$A = 48 \text{ cm}^2$
Therefore, the area of the rectangle is $48$ square centimeters.
Example 14: Find the area of a square plot of side 8 m.
Answer:
Given:
Shape = Square plot
Side length of the square plot ($s$) = $8$ m
To Find:
The area of the square plot.
Solution:
The formula for the area of a square is given by:
Area = Side $\times$ Side
$A = s \times s = s^2$
Substituting the given side length:
$A = 8 \text{ m} \times 8 \text{ m}$
$A = 64$ sq m
Alternatively written using LaTeX:
$A = 64 \text{ m}^2$
Therefore, the area of the square plot is $64$ square meters.
Example 15: The area of a rectangular piece of cardboard is 36 sq cm and its length is 9 cm. What is the width of the cardboard?
Answer:
Given:
Shape = Rectangular piece of cardboard
Area of the rectangle ($A$) = $36$ sq cm (or $36 \text{ cm}^2$)
Length of the rectangle ($l$) = $9$ cm
To Find:
The width of the cardboard.
Solution:
The formula for the area of a rectangle is given by:
Area = Length $\times$ Width
$A = l \times w$ (using $w$ for width)
We are given the Area ($A$) and the Length ($l$). We need to find the Width ($w$).
Substitute the given values into the formula:
$36 \text{ cm}^2 = 9 \text{ cm} \times w$
To find the width ($w$), we need to rearrange the formula:
$w = \frac{\text{Area}}{\text{Length}}$
$w = \frac{A}{l}$
Now, substitute the values:
$w = \frac{36 \text{ cm}^2}{9 \text{ cm}}$
$w = 4 \text{ cm}$
Therefore, the width of the cardboard is $4$ cm.
Example 16: Bob wants to cover the floor of a room 3 m wide and 4 m long by squared tiles. If each square tile is of side 0.5 m, then find the number of tiles required to cover the floor of the room.
Answer:
Given:
Shape of the floor = Rectangular
Width of the room ($b$) = $3$ m
Length of the room ($l$) = $4$ m
Shape of the tiles = Square
Side length of each square tile ($s_{tile}$) = $0.5$ m
To Find:
The number of square tiles required to cover the floor of the room.
Solution:
First, calculate the area of the rectangular floor.
Area of floor = Length $\times$ Width
Area of floor = $l \times b$
Area of floor = $4 \text{ m} \times 3 \text{ m}$
Area of floor = $12 \text{ m}^2$ (square meters)
Next, calculate the area of one square tile.
Area of one tile = Side $\times$ Side
Area of one tile = $s_{tile} \times s_{tile}$
Area of one tile = $0.5 \text{ m} \times 0.5 \text{ m}$
Area of one tile = $0.25 \text{ m}^2$ (square meters)
To find the number of tiles required, divide the total area of the floor by the area of one tile.
Number of tiles = $\frac{\text{Area of floor}}{\text{Area of one tile}}$
Number of tiles = $\frac{12 \text{ m}^2}{0.25 \text{ m}^2}$
Number of tiles = $\frac{12}{0.25} = \frac{12}{\frac{1}{4}} = 12 \times 4$
Number of tiles = $48$
Therefore, $48$ tiles are required to cover the floor of the room.
Alternate Solution:
We can find how many tiles fit along the length and how many fit along the width.
Number of tiles along the length = $\frac{\text{Length of the room}}{\text{Side of one tile}}$
Number of tiles along the length = $\frac{4 \text{ m}}{0.5 \text{ m}} = \frac{4}{0.5} = \frac{4}{\frac{1}{2}} = 4 \times 2 = 8$
Number of tiles along the width = $\frac{\text{Width of the room}}{\text{Side of one tile}}$
Number of tiles along the width = $\frac{3 \text{ m}}{0.5 \text{ m}} = \frac{3}{0.5} = \frac{3}{\frac{1}{2}} = 3 \times 2 = 6$
Total number of tiles = (Number of tiles along length) $\times$ (Number of tiles along width)
Total number of tiles = $8 \times 6$
Total number of tiles = $48$
Hence, $48$ tiles are required.
Example 17: Find the area in square metre of a piece of cloth 1m 25 cm wide and 2 m long.
Answer:
Given:
Shape of the piece of cloth = Rectangular
Width of the cloth ($w$) = $1$ m $25$ cm
Length of the cloth ($l$) = $2$ m
To Find:
The area of the piece of cloth in square metres (m²).
Solution:
To find the area in square metres, we need both the length and width to be in meters.
The length is already given in meters: $l = 2$ m.
We need to convert the width from meters and centimeters to meters.
Width ($w$) = $1$ m $25$ cm
We know that $100 \text{ cm} = 1 \text{ m}$, so $1 \text{ cm} = \frac{1}{100} \text{ m} = 0.01 \text{ m}$.
$25 \text{ cm} = 25 \times 0.01 \text{ m} = 0.25 \text{ m}$.
So, the width $w = 1 \text{ m} + 0.25 \text{ m} = 1.25 \text{ m}$.
Now we have:
Length ($l$) = $2$ m
Width ($w$) = $1.25$ m
The formula for the area of a rectangle is:
Area = Length $\times$ Width
$A = l \times w$
Substituting the values in meters:
$A = 2 \text{ m} \times 1.25 \text{ m}$
$\begin{array}{cc} & & 1 & . & 2 & 5 \\ \times & & & & & 2 \\ \hline & & 2 & . & 5 & 0 \\ \hline \end{array}$
$A = 2.50$ sq m
Alternatively written using LaTeX:
$A = 2.5 \text{ m}^2$
Therefore, the area of the piece of cloth is $2.5$ square metres.
Exercise 10.3
Question 1. Find the areas of the rectangles whose sides are :
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Answer:
The area of a rectangle is calculated using the formula:
Area = Length $\times$ Width (or Breadth)
$A = l \times w$
(a) Sides are 3 cm and 4 cm
Let Length ($l$) = $4$ cm
Let Width ($w$) = $3$ cm
Area = $l \times w$
Area = $4 \text{ cm} \times 3 \text{ cm}$
Area = $12 \text{ cm}^2$
The area of the rectangle is $12$ sq cm.
(b) Sides are 12 m and 21 m
Let Length ($l$) = $21$ m
Let Width ($w$) = $12$ m
Area = $l \times w$
Area = $21 \text{ m} \times 12 \text{ m}$
$\begin{array}{cc} & & 2 & 1 \\ \times & & 1 & 2 \\ \hline & & 4 & 2 \\ & 2 & 1 & \times \\ \hline & 2 & 5 & 2 \\ \hline \end{array}$
Area = $252 \text{ m}^2$
The area of the rectangle is $252$ sq m.
(c) Sides are 2 km and 3 km
Let Length ($l$) = $3$ km
Let Width ($w$) = $2$ km
Area = $l \times w$
Area = $3 \text{ km} \times 2 \text{ km}$
Area = $6 \text{ km}^2$
The area of the rectangle is $6$ sq km.
(d) Sides are 2 m and 70 cm
Let Length ($l$) = $2$ m
Let Width ($w$) = $70$ cm
To calculate the area, both dimensions must be in the same unit. Let's convert the width to meters.
We know $100 \text{ cm} = 1 \text{ m}$, so $1 \text{ cm} = \frac{1}{100} \text{ m}$.
Width $w = 70 \text{ cm} = 70 \times \frac{1}{100} \text{ m} = \frac{70}{100} \text{ m} = 0.7 \text{ m}$.
Now, calculate the area:
Area = $l \times w$
Area = $2 \text{ m} \times 0.7 \text{ m}$
Area = $1.4 \text{ m}^2$
The area of the rectangle is $1.4$ sq m.
Question 2. Find the areas of the squares whose sides are :
(a) 10 cm
(b) 14 cm
(c) 5 m
Answer:
The area of a square is calculated using the formula:
Area = Side $\times$ Side
$A = s^2$
(a) Side is 10 cm
Given:
Side of the square ($s$) = $10$ cm
Solution:
Area = $s \times s$
Area = $10 \text{ cm} \times 10 \text{ cm}$
Area = $100 \text{ cm}^2$
The area of the square is $100$ sq cm.
(b) Side is 14 cm
Given:
Side of the square ($s$) = $14$ cm
Solution:
Area = $s \times s$
Area = $14 \text{ cm} \times 14 \text{ cm}$
$\begin{array}{cc} & & 1 & 4 \\ \times & & 1 & 4 \\ \hline & & 5 & 6 \\ & 1 & 4 & \times \\ \hline & 1 & 9 & 6 \\ \hline \end{array}$
Area = $196 \text{ cm}^2$
The area of the square is $196$ sq cm.
(c) Side is 5 m
Given:
Side of the square ($s$) = $5$ m
Solution:
Area = $s \times s$
Area = $5 \text{ m} \times 5 \text{ m}$
Area = $25 \text{ m}^2$
The area of the square is $25$ sq m.
Question 3. The length and breadth of three rectangles are as given below :
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Answer:
To Find:
1. The area of each of the three rectangles.
2. The rectangle with the largest area.
3. The rectangle with the smallest area.
Solution:
We calculate the area of each rectangle using the formula: Area = Length $\times$ Breadth.
(a) Rectangle with sides 9 m and 6 m
Length ($l$) = $9$ m
Breadth ($b$) = $6$ m
Area = $l \times b$
Area = $9 \text{ m} \times 6 \text{ m}$
Area = $54 \text{ m}^2$
Area of rectangle (a) = $54$ sq m.
(b) Rectangle with sides 17 m and 3 m
Length ($l$) = $17$ m
Breadth ($b$) = $3$ m
Area = $l \times b$
Area = $17 \text{ m} \times 3 \text{ m}$
Area = $51 \text{ m}^2$
Area of rectangle (b) = $51$ sq m.
(c) Rectangle with sides 4 m and 14 m
Let Length ($l$) = $14$ m
Let Breadth ($b$) = $4$ m
Area = $l \times b$
Area = $14 \text{ m} \times 4 \text{ m}$
Area = $56 \text{ m}^2$
Area of rectangle (c) = $56$ sq m.
Comparison:
Area (a) = $54 \text{ m}^2$
Area (b) = $51 \text{ m}^2$
Area (c) = $56 \text{ m}^2$
Comparing the areas: $51 < 54 < 56$.
The largest area is $56 \text{ m}^2$, which belongs to rectangle (c).
The smallest area is $51 \text{ m}^2$, which belongs to rectangle (b).
Therefore, rectangle (c) has the largest area and rectangle (b) has the smallest area.
Question 4. The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
Answer:
Given:
Shape of the garden = Rectangular
Length of the garden ($l$) = $50$ m
Area of the garden ($A$) = $300$ sq m (or $300 \text{ m}^2$)
To Find:
The width of the garden.
Solution:
The formula for the area of a rectangle is given by:
Area = Length $\times$ Width
$A = l \times w$ (using $w$ for width)
We are given the Area ($A$) and the Length ($l$). We need to find the Width ($w$).
Substitute the given values into the formula:
$300 \text{ m}^2 = 50 \text{ m} \times w$
To find the width ($w$), we rearrange the formula:
$w = \frac{\text{Area}}{\text{Length}}$
$w = \frac{A}{l}$
Now, substitute the values:
$w = \frac{300 \text{ m}^2}{50 \text{ m}}$
$w = \frac{\cancel{300}^{6}}{\cancel{50}_{1}} \text{ m}$
$w = 6 \text{ m}$
Therefore, the width of the garden is $6$ m.
Question 5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.?
Answer:
Given:
Shape of the plot = Rectangular
Length of the plot ($l$) = $500$ m
Width of the plot ($w$) = $200$ m
Rate of tiling = $\textsf{₹ } 8$ per hundred sq m (i.e., per $100 \text{ m}^2$)
To Find:
The total cost of tiling the rectangular plot.
Solution:
First, calculate the area of the rectangular plot of land.
The formula for the area of a rectangle is:
Area = Length $\times$ Width
$A = l \times w$
Substituting the given values:
$A = 500 \text{ m} \times 200 \text{ m}$
$A = 100000 \text{ m}^2$ (sq m)
So, the area of the plot is $100,000$ square meters.
Next, we need to find the cost of tiling this area.
The rate is given as $\textsf{₹ } 8$ per hundred sq m ($\textsf{₹ } 8 / 100 \text{ m}^2$).
We can find the cost per square meter first:
Cost per sq m = $\frac{\textsf{₹ } 8}{100 \text{ m}^2} = \textsf{₹ } 0.08$ per sq m.
Total Cost = Total Area $\times$ Cost per sq m
Total Cost = $100000 \text{ m}^2 \times \textsf{₹ } 0.08 / \text{m}^2$
Total Cost = $\textsf{₹ } (100000 \times 0.08)$
Total Cost = $\textsf{₹ } 8000$
Alternate Solution:
Calculate the area of the plot: $A = 100,000 \text{ m}^2$.
The rate is $\textsf{₹ } 8$ per $100 \text{ m}^2$.
Find how many units of 'hundred sq m' are in the total area.
Number of ($100 \text{ m}^2$) units = $\frac{\text{Total Area}}{100 \text{ m}^2}$
Number of units = $\frac{100000 \text{ m}^2}{100 \text{ m}^2}$
Number of units = $1000$
Now, calculate the total cost:
Total Cost = Number of units $\times$ Rate per unit
Total Cost = $1000 \times \textsf{₹ } 8$
Total Cost = $\textsf{₹ } 8000$
Therefore, the cost of tiling the rectangular plot is $\textsf{₹ } 8,000$.
Question 6. A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Answer:
Given:
Measurement of the table-top.
Length (L) = 2 m
Width (B) = 1 m 50 cm
To Find:
Area of the table-top in square metres ($m^2$).
Solution:
First, we need to ensure both dimensions are in the same unit (metres).
Length (L) = 2 m
Width (B) = 1 m 50 cm
We know that $100 \text{ cm} = 1 \text{ m}$, so $50 \text{ cm} = \frac{50}{100} \text{ m} = 0.50 \text{ m}$.
Therefore, Width (B) = $1 \text{ m} + 0.50 \text{ m} = 1.50 \text{ m}$.
The area of a rectangle is given by the formula:
Area = Length $\times$ Width
Area = $L \times B$
Area = $2 \text{ m} \times 1.50 \text{ m}$
Area = $3.00 \text{ m}^2$
Thus, the area of the table-top is 3 square metres.
Question 7. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Answer:
Given:
Dimensions of the room floor.
Length (L) = 4 m
Width (B) = 3 m 50 cm
To Find:
Area of carpet needed to cover the floor in square metres ($m^2$).
Solution:
The area of carpet needed is equal to the area of the floor.
First, we convert the width to metres.
Length (L) = 4 m
Width (B) = 3 m 50 cm
Since $100 \text{ cm} = 1 \text{ m}$, we have $50 \text{ cm} = \frac{50}{100} \text{ m} = 0.50 \text{ m}$.
So, Width (B) = $3 \text{ m} + 0.50 \text{ m} = 3.50 \text{ m}$.
The area of the floor (which is rectangular) is calculated as:
Area = Length $\times$ Width
Area = $L \times B$
Area = $4 \text{ m} \times 3.50 \text{ m}$
Area = $14.00 \text{ m}^2$
Therefore, 14 square metres of carpet is needed to cover the floor of the room.
Question 8. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Answer:
Given:
Dimensions of the floor:
Length (L) = 5 m
Width (B) = 4 m
Dimensions of the square carpet:
Side (s) = 3 m
To Find:
The area of the floor that is not carpeted.
Solution:
First, calculate the area of the floor.
The floor is rectangular.
Area of floor = Length $\times$ Width
Area of floor = $L \times B$
Area of floor = $5 \text{ m} \times 4 \text{ m}$
Area of floor = $20 \text{ m}^2$
Next, calculate the area of the square carpet.
Area of square carpet = Side $\times$ Side
Area of square carpet = $s \times s$
Area of square carpet = $3 \text{ m} \times 3 \text{ m}$
Area of square carpet = $9 \text{ m}^2$
To find the area of the floor that is not carpeted, subtract the area of the carpet from the area of the floor.
Area not carpeted = Area of floor - Area of square carpet
Area not carpeted = $20 \text{ m}^2 - 9 \text{ m}^2$
Area not carpeted = $11 \text{ m}^2$
Therefore, the area of the floor that is not carpeted is 11 square metres.
Question 9. Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Answer:
Given:
Dimensions of the piece of land:
Length (L) = 5 m
Width (B) = 4 m
Details of the square flower beds:
Number of flower beds = 5
Side of each square flower bed (s) = 1 m
To Find:
The area of the remaining part of the land.
Solution:
First, calculate the total area of the piece of land.
The land is rectangular.
Area of land = Length $\times$ Width
Area of land = $L \times B$
Area of land = $5 \text{ m} \times 4 \text{ m}$
Area of land = $20 \text{ m}^2$
Next, calculate the area of one square flower bed.
Area of one square flower bed = Side $\times$ Side
Area of one square flower bed = $s \times s$
Area of one square flower bed = $1 \text{ m} \times 1 \text{ m}$
Area of one square flower bed = $1 \text{ m}^2$
Now, calculate the total area occupied by the 5 square flower beds.
Total area of 5 flower beds = Number of beds $\times$ Area of one bed
Total area of 5 flower beds = $5 \times 1 \text{ m}^2$
Total area of 5 flower beds = $5 \text{ m}^2$
Finally, find the area of the remaining part of the land by subtracting the total area of the flower beds from the total area of the land.
Remaining area = Area of land - Total area of 5 flower beds
Remaining area = $20 \text{ m}^2 - 5 \text{ m}^2$
Remaining area = $15 \text{ m}^2$
Therefore, the area of the remaining part of the land is 15 square metres.
Questoion 10. By splitting the following figures into rectangles, find their areas
(The measures are given in centimetres).

Answer:
To Find:
The areas of the given figures by splitting them into rectangles.
Solution:
We can find the area of the given figures by splitting them into smaller rectangles and then adding their individual areas.
(a) Finding the area of the first figure:
As per the provided solution, the figure is split into four rectangular regions: yellow, orange, grey, and brown.
The area of each rectangular region is calculated as follows:
Area of yellow region = $3 \text{ cm} \times 3 \text{ cm} = 9 \text{ cm}^2$
Area of orange region = $1 \text{ cm} \times 2 \text{ cm} = 2 \text{ cm}^2$
Area of grey region = $3 \text{ cm} \times 3 \text{ cm} = 9 \text{ cm}^2$
Area of brown region = $2 \text{ cm} \times 4 \text{ cm} = 8 \text{ cm}^2$
The total area of the figure is the sum of the areas of these four regions.
Total Area = Area(yellow) + Area(orange) + Area(grey) + Area(brown)
Total Area = $9 \text{ cm}^2 + 2 \text{ cm}^2 + 9 \text{ cm}^2 + 8 \text{ cm}^2 = 28 \text{ cm}^2$
Therefore, the total area of figure (a) is 28 cm2.
(b) Finding the area of the second figure:
The cross-shaped figure can be split into three vertical rectangular regions: brown, orange, and grey.
The area of each rectangular region is calculated as follows:
Area of brown region = $3 \text{ cm} \times 1 \text{ cm} = 3 \text{ cm}^2$
Area of orange region = $3 \text{ cm} \times 1 \text{ cm} = 3 \text{ cm}^2$
Area of grey region = $3 \text{ cm} \times 1 \text{ cm} = 3 \text{ cm}^2$
The total area of the figure is the sum of the areas of these three regions.
Total Area = Area(brown) + Area(orange) + Area(grey)
Total Area = $3 \text{ cm}^2 + 3 \text{ cm}^2 + 3 \text{ cm}^2 = 9 \text{ cm}^2$
Therefore, the total area of figure (b) is 9 cm2.
Question 11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)
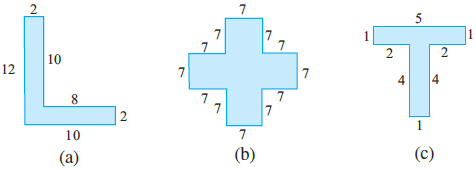
Answer:
To Find:
The area of the given figures by splitting them into rectangles.
Solution:
(a) Splitting Figure (a) into rectangles:
We can find the area by splitting the figure into two rectangular parts.
Area of the first rectangle = $12 \text{ cm} \times 2 \text{ cm} = 24 \text{ cm}^2$
Area of the second rectangle = $8 \text{ cm} \times 2 \text{ cm} = 16 \text{ cm}^2$
Total area of the figure is the sum of the areas of these two rectangles.
Total Area = $24 \text{ cm}^2 + 16 \text{ cm}^2 = 40 \text{ cm}^2$
Therefore, the total area of figure (a) is 40 cm2.
(b) Splitting Figure (b) into rectangles:
The given figure is a plus sign (+) shape. We can observe that it is composed of 5 identical squares, with each side measuring 7 cm.
Area of one square = Side $\times$ Side = $7 \text{ cm} \times 7 \text{ cm} = 49 \text{ cm}^2$
Since the figure is made of 5 such squares, the total area is:
Total Area = $5 \times$ Area of one square
Total Area = $5 \times 49 \text{ cm}^2 = 245 \text{ cm}^2$
Therefore, the total area of figure (b) is 245 cm2.
(c) Splitting Figure (c) into rectangles:
The T-shaped figure can be split into three rectangles. We can split it into a central vertical rectangle and two smaller horizontal rectangles on each side of the top part.
Area of grey rectangle (left part) = $2 \text{ cm} \times 1 \text{ cm} = 2 \text{ cm}^2$
Area of brown rectangle (right part) = $2 \text{ cm} \times 1 \text{ cm} = 2 \text{ cm}^2$
Area of orange rectangle (central vertical part) = $5 \text{ cm} \times 1 \text{ cm} = 5 \text{ cm}^2$
The total area of the figure is the sum of the areas of these three parts.
Total Area = Area(grey) + Area(brown) + Area(orange)
Total Area = $2 \text{ cm}^2 + 2 \text{ cm}^2 + 5 \text{ cm}^2 = 9 \text{ cm}^2$
Therefore, the total area of figure (c) is 9 cm2.
Question 12. How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm.
Answer:
Given:
Dimensions of one tile:
Length ($l_t$) = 12 cm
Breadth ($b_t$) = 5 cm
To Find:
The number of tiles needed for each rectangular region.
Solution:
First, calculate the area of one tile.
Area of one tile = $l_t \times b_t$
Area of one tile = $12 \text{ cm} \times 5 \text{ cm}$
Area of one tile = $60 \text{ cm}^2$
(a) Region dimensions: Length ($L_a$) = 100 cm, Breadth ($B_a$) = 144 cm
Calculate the area of the rectangular region (a).
Area of region (a) = $L_a \times B_a$
Area of region (a) = $100 \text{ cm} \times 144 \text{ cm}$
Area of region (a) = $14400 \text{ cm}^2$
To find the number of tiles needed, divide the area of the region by the area of one tile.
Number of tiles = $\frac{\text{Area of region (a)}}{\text{Area of one tile}}$
Number of tiles = $\frac{14400 \text{ cm}^2}{60 \text{ cm}^2}$
Number of tiles = $\frac{1440}{6}$
Number of tiles = $240$
Therefore, 240 tiles will be needed for region (a).
(b) Region dimensions: Length ($L_b$) = 70 cm, Breadth ($B_b$) = 36 cm
Calculate the area of the rectangular region (b).
Area of region (b) = $L_b \times B_b$
Area of region (b) = $70 \text{ cm} \times 36 \text{ cm}$
Area of region (b) = $2520 \text{ cm}^2$
To find the number of tiles needed, divide the area of the region by the area of one tile.
Number of tiles = $\frac{\text{Area of region (b)}}{\text{Area of one tile}}$
Number of tiles = $\frac{2520 \text{ cm}^2}{60 \text{ cm}^2}$
Number of tiles = $\frac{252}{6}$
Number of tiles = $42$
Therefore, 42 tiles will be needed for region (b).

