Non-Rationalised NCERT Books Solution
6th	7th	8th	9th	10th	11th	12th

Class 6th Chapters
1. Knowing Our Numbers	2. Whole Numbers	3. Playing With Numbers
4. Basic Geometrical Ideas	5. Understanding Elementary Shapes	6. Integers
7. Fractions	8. Decimals	9. Data Handling
10. Mensuration	11. Algebra	12. Ratio And Proportion
13. Symmetry	14. Practical Geometry

Content On This Page
Exercise 13.1	Exercise 13.2	Exercise 13.3

Chapter 13 Symmetry

Welcome to the exploration of Chapter 13: Symmetry, a captivating chapter that delves into a fundamental geometric property shaping our visual world. Symmetry is more than just a mathematical concept; it's a principle of balance, harmony, and beauty observed extensively in nature (from butterflies to snowflakes), art, architecture, design, and countless everyday objects. Understanding symmetry enhances our spatial awareness and appreciation for the inherent order and structure present in various forms. The solutions provided for this chapter meticulously guide students through the identification and application of reflection symmetry, more commonly known as line symmetry, laying a crucial foundation for further geometric studies.

At its core, symmetry deals with transformations that leave an object unchanged. This chapter primarily focuses on line symmetry. The solutions clearly define a line of symmetry as an imaginary line that divides a figure into two congruent (identical in shape and size) halves, where each half is a perfect mirror image of the other. Imagine placing a mirror along this line; the reflection seen in the mirror would perfectly match the other half of the figure. This conceptual understanding is reinforced through various exercises and explanations.

A significant part of the solutions involves developing the skill of identifying and drawing lines of symmetry for a diverse range of figures. Students are guided through:

Geometric Shapes: Investigating common shapes and determining their lines of symmetry. For instance:
- A square exhibits four lines of symmetry (two diagonals, one vertical line through the midpoint of opposite sides, one horizontal line through the midpoint of opposite sides).
- A rectangle (non-square) has two lines of symmetry (one vertical, one horizontal, passing through the midpoints of opposite sides). Note that diagonals are *not* lines of symmetry for a rectangle unless it's also a square.
- An isosceles triangle possesses one line of symmetry (the line from the vertex angle perpendicular to the base).
- An equilateral triangle boasts three lines of symmetry (lines from each vertex to the midpoint of the opposite side).
- Regular polygons consistently have a number of symmetry lines equal to their number of sides (e.g., a regular pentagon has 5, a regular hexagon has 6).
- A circle is unique, possessing an infinite number ($n \to \infty$) of lines of symmetry; any line passing through its center acts as a line of symmetry.
- Some shapes, like a scalene triangle or a parallelogram (non-rectangle/rhombus), have no lines of symmetry.
Letters of the Alphabet: Analyzing uppercase letters to find vertical (like A, M, T, U, V, W, Y), horizontal (like B, C, D, E, H, I, K, O, X), both (H, I, O, X), or no lines of symmetry (like F, G, J, L, N, P, Q, R, S, Z).
Everyday Objects and Patterns: Extending the concept to real-world examples, encouraging observation skills.

The practical technique of folding is often highlighted in the solutions. If a figure can be folded precisely along a line such that the two halves overlap perfectly (coincide), then that fold line represents a line of symmetry. This hands-on approach aids visual and tactile learners in grasping the concept.

Furthermore, the solutions tackle problems that require students to complete a figure given only one half and the line of symmetry. This exercise directly tests the understanding of the mirror image principle. It necessitates visualizing or drawing the corresponding points and lines on the opposite side of the symmetry line, ensuring that each point on the completed half is the same perpendicular distance from the line of symmetry as its corresponding point on the given half, but on the opposite side. This skill is crucial for developing precise spatial reasoning.

The chapter solutions also gently formalize the connection between line symmetry and reflection. The line of symmetry acts as the 'mirror line'. Exercises might involve predicting or drawing the reflection of a shape or pattern across a given line, typically positioned vertically or horizontally. This lays the groundwork for understanding geometric transformations more broadly.

By engaging with the detailed steps and explanations in the Chapter 13 solutions, students cultivate not only their ability to recognize and draw symmetric figures but also enhance their overall spatial visualization skills. They learn to appreciate geometric properties related to reflection and develop a keener eye for the symmetry that permeates the natural and man-made world, fostering a deeper understanding of geometric principles and aesthetic balance.

Exercise 13.1

Question 1. List any four symmetrical objects from your home or school.

Answer:

Solution:

Symmetrical objects are those that can be divided by a line or plane into two identical halves that are mirror images of each other.

Here are four examples of symmetrical objects that can be found in a home or school:

1. A chair: Many chairs have a line of symmetry running vertically down the middle, dividing the chair into two mirror-image halves.

2. A window: Rectangular windows often have at least two lines of symmetry, one horizontal and one vertical, passing through the center.

3. A blackboard/whiteboard: Rectangular blackboards or whiteboards are symmetrical about a vertical and a horizontal line passing through their center.

4. A book: When closed, a book has a line of symmetry running vertically down the spine (if viewed from the front cover).

Other possible examples include a table, a door, a ruler, a clock face, certain types of leaves, a pair of scissors, etc.

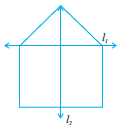
Question 2. For the given figure, which one is the mirror line, l₁ or l₂?

Page 263 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

Answer:

Given:

A figure which is a combination of a square and a triangle on top of it.

There are two lines, a horizontal line l₁ and a vertical line l₂.

To Find:

Which of the two lines, l₁ or l₂, is the mirror line for the given figure.

Solution:

A mirror line, also known as a line of symmetry, is an imaginary line that divides a figure into two identical halves, where one half is the mirror image of the other.

Let's analyze the given figure with respect to both lines:

1. Line l₁ (Horizontal line):

If we fold the figure along the horizontal line l₁, the top part of the figure (the triangle and the upper portion of the square) will not exactly overlap or coincide with the bottom part of the figure (the lower portion of the square). The two parts are not identical. Therefore, l₁ is not a line of symmetry.

2. Line l₂ (Vertical line):

If we fold the figure along the vertical line l₂, the left half of the figure will perfectly superimpose on the right half. The two halves are identical and are mirror images of each other. Therefore, l₂ is a line of symmetry.

Since a mirror line is a line of symmetry, the line l₂ is the mirror line for the given figure.

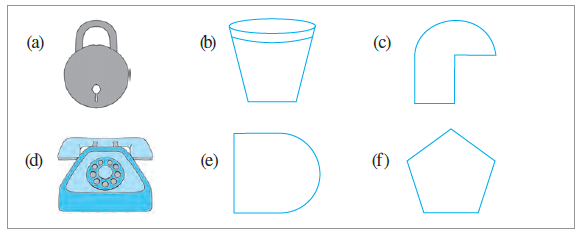
Question 3. Identify the shapes given below. Check whether they are symmetric or not. Draw the line of symmetry as well.

Answer:

To Find:

For each given shape, we need to:

1. Identify the shape.

2. Determine if the shape is symmetric.

3. If it is symmetric, draw the line of symmetry.

(a) The Lock

A lock with a vertical line of symmetry drawn through its center, dividing it into two identical halves.

The shape is a lock.

Yes, this shape is symmetric.

It has one vertical line of symmetry. If you fold the figure along this line, the left half will perfectly coincide with the right half.

(b) The Tumbler

A tumbler or glass with a vertical line of symmetry drawn down its center.

The shape is a tumbler or a glass.

Yes, this shape is symmetric.

It has one vertical line of symmetry that divides the tumbler into two identical mirror-image halves.

(c) The Jug

A jug that is shown to be not symmetric because of its handle on one side.

The shape is a jug or a pitcher.

No, this shape is not symmetric.

The handle is present only on one side of the jug. Because of this, there is no line along which the figure can be folded so that its two halves coincide perfectly. The handle breaks the symmetry.

(d) The Telephone

A telephone (front view) with a vertical line of symmetry drawn through its center.

The shape is a telephone.

Yes, this shape is symmetric.

It has a vertical line of symmetry that runs down the middle of the device. The left side is a perfect mirror image of the right side.

(e) The Square with an attached Semicircle

A composite shape made of a square on the left and a semicircle attached to its right side. A horizontal line of symmetry is drawn through the center of the shape.

The shape is a combination of a square and a semicircle attached to one of its sides.

Yes, this shape is symmetric.

It has a horizontal line of symmetry that passes through the midpoints of the vertical sides of the square and through the center of the semicircle's diameter.

(f) The Pentagon

A regular pentagon. A vertical line of symmetry is drawn from the top vertex to the midpoint of the bottom horizontal edge.

The shape is a regular pentagon.

Yes, this shape is symmetric.

A regular pentagon has 5 lines of symmetry. The image shows one of them, a vertical line that passes through the top vertex and the midpoint of the opposite (bottom) side.

Conclusion:

After examining all the figures, we can conclude that the shapes in (a), (b), (d), (e), and (f) are symmetric. The shape in (c) is not symmetric. Therefore, except for (c), all other shapes are symmetric.

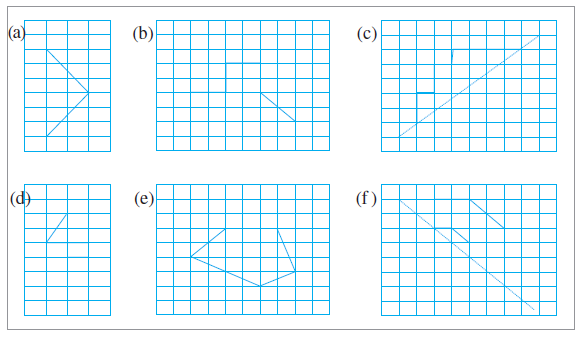
Question 4. Copy the following on a squared paper. A square paper is what you would have used in your arithmetic notebook in earlier classes. Then complete them such that the dotted line is the line of symmetry.

Answer:

To Do:

To complete the given figures on the squared paper by drawing the other half, such that the dotted line becomes the line of symmetry for each completed shape.

Solution:

To make the dotted line a line of symmetry, we must draw the reflection of the given part on the other side of the line. Each point in the reflection is the same distance from the dotted line as the original point, but on the opposite side. The completed figures are shown below.

(a)

The given figure is a triangle. By reflecting it across the vertical dotted line, we complete the figure to form a larger isosceles triangle.

The completed figure for part (a) is a symmetric isosceles triangle. The original left half is reflected across the vertical dotted line to form the right half.

(b)

The given figure consists of two connected line segments. Reflecting this shape across the vertical dotted line completes the figure into a symmetric quadrilateral, which is a kite.

The completed figure for part (b) is a symmetric kite. The original left half is reflected across the vertical dotted line to form the right half.

(c)

The given figure is the top half of a shape. Reflecting it downwards across the horizontal dotted line completes the figure to form a rhombus.

The completed figure for part (c) is a rhombus. The original top half is reflected across the horizontal dotted line to form the bottom half.

(d)

The given figure is a right-angled triangle. By reflecting it across the vertical dotted line, we complete the figure to form an isosceles triangle.

The completed figure for part (d) is an isosceles triangle. The original left triangle is reflected across the vertical dotted line to form the right triangle.

(e)

The given figure is the bottom half of a polygon. By reflecting it upwards across the horizontal dotted line, we complete the figure to form a symmetric hexagon.

The completed figure for part (e) is a symmetric hexagon. The original bottom half is reflected across the horizontal dotted line to form the top half.

(f)

The given figure is a line segment above a diagonal line of symmetry. By reflecting the segment across the dotted line, we get another segment below the line, creating a shape with two parallel segments.

The completed figure for part (f) shows two parallel line segments that are reflections of each other across the diagonal dotted line.

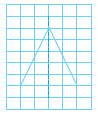
Question 5. In the figure, l is the line of symmetry. Complete the diagram to make it symmetric.

Answer:

Given:

A figure is drawn above a horizontal line 'l'.

The line 'l' is the line of symmetry.

To Do:

Complete the diagram to make it symmetric with respect to the line 'l'.

Solution:

A line of symmetry divides a figure into two parts that are mirror images of each other. To complete the given figure, we need to draw the reflection of the existing part across the line 'l'.

This means we have to draw an identical, inverted shape below the line 'l' such that if the figure is folded along line 'l', the two parts perfectly coincide.

Each point on the reflected part will be at the same perpendicular distance from the line 'l' as the corresponding point on the original part, but on the opposite side.

The completed symmetric diagram is shown below:

The completed symmetric figure. The original right-angled triangle above the line 'l' is reflected downwards, creating an identical inverted triangle below the line. The two triangles together form a kite-like shape with 'l' as the horizontal line of symmetry.

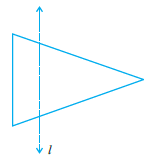
Question 6. In the figure, l is the line of symmetry. Draw the image of the triangle and complete the diagram so that it becomes symmetric.

Page 264 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

Answer:

Given:

A triangle and a vertical line 'l' which is the line of symmetry.

A triangle is intersected by a vertical dotted line labeled 'l'.

To Do:

To draw the image (reflection) of the given triangle and complete the diagram so that it becomes symmetric with respect to the line 'l'.

Solution:

To make the diagram symmetric, we need to draw the reflection of the triangle across the line 'l'. The line of symmetry 'l' acts as a mirror.

The process involves reflecting the part of the triangle on one side of the line to the other side. Specifically:

1. The portion of the triangle on the right side of the line 'l' is reflected to the left side.

2. The portion of the triangle on the left side of the line 'l' is reflected to the right side.

Each vertex of the reflected part will be at the same perpendicular distance from the line 'l' as the original vertex, but on the opposite side. The resulting figure is a composite shape where both sides of the line 'l' are perfect mirror images of each other. The completed diagram will be a six-pointed star-like polygon.

The completed symmetric figure is shown below:

The completed symmetric figure. The original triangle is reflected across the vertical line 'l'. The result is a six-pointed star shape that is perfectly symmetric about the line 'l'.

Exercise 13.2

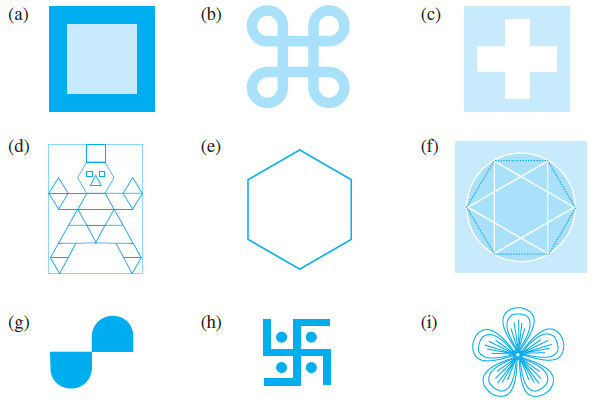
Question 1. Find the number of lines of symmety for each of the following shapes :

Page 267 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

Answer:

To Find:

The number of lines of symmetry for each of the given shapes.

Solution:

A line of symmetry is a line that divides a shape into two identical halves that are mirror images of each other. We will examine each shape to find all such lines.

(a)

A square frame with four lines of symmetry drawn: one vertical, one horizontal, and two diagonal.

This shape is a square frame. A square has four lines of symmetry: two that pass through the midpoints of opposite sides, and two that are the diagonals connecting opposite vertices.

The number of lines of symmetry is 4.

(b)

A looped square symbol with two lines of symmetry drawn: one vertical and one horizontal, both passing through the center.

This shape has two lines of symmetry: one vertical line passing through the center and one horizontal line passing through the center.

The number of lines of symmetry is 2.

(c)

A plus sign with four lines of symmetry drawn: one vertical, one horizontal, and two diagonal.

This shape is a plus sign (or a cross) with arms of equal length. It has four lines of symmetry: a vertical line, a horizontal line, and two diagonal lines.

The number of lines of symmetry is 4.

(d)

A human-like figure made of geometric shapes with one vertical line of symmetry drawn through its center.

This figure is symmetric about the vertical axis. There is only one line of symmetry which divides the figure into two identical left and right halves.

The number of lines of symmetry is 1.

(e)

A regular hexagon with six lines of symmetry drawn: three connecting opposite vertices and three connecting midpoints of opposite sides.

This shape is a regular hexagon. It has six lines of symmetry: three passing through opposite vertices and three passing through the midpoints of opposite sides.

The number of lines of symmetry is 6.

(f)

A hexagram (six-pointed star) in a circle with six lines of symmetry drawn.

This shape is a regular hexagram. It has six lines of symmetry, similar to a regular hexagon.

The number of lines of symmetry is 6.

(g)

An S-shaped figure made of two semicircles, shown to have no lines of symmetry.

This figure does not have any line of symmetry. Although it has rotational symmetry (it looks the same after a 180-degree turn), there is no line that can divide it into two mirror-image halves.

The number of lines of symmetry is 0.

(h)

A Swastika symbol, shown to have no lines of symmetry.

This shape is a swastika. It has rotational symmetry, but it has no line of symmetry. Any line drawn through it will not produce two mirror-image halves.

The number of lines of symmetry is 0.

(i)

A flower with five identical petals, showing five lines of symmetry, each passing through the center and the tip of a petal.

This shape is a flower with five identical petals. It has five lines of symmetry. Each line of symmetry passes through the center of the flower and the tip of one petal, bisecting it.

The number of lines of symmetry is 5.

Question 2. Copy the triangle in each of the following figures on squared paper. In each case, draw the line(s) of symmetry, if any and identify the type of triangle. (Some of you may like to trace the figures and try paper-folding first!)

Answer:

To Do:

For each triangle on the squared paper, we need to draw the line(s) of symmetry (if any) and identify the type of triangle.

Solution:

(a)

An isosceles triangle on a grid with a vertical line of symmetry drawn from the top vertex to the midpoint of the base.

By observing the figure, we can see that the two slanted sides are of equal length. A triangle with two equal sides is an Isosceles triangle.

It has one line of symmetry, which is the vertical line that passes through the top vertex and bisects the base.

(b)

Similar to the first figure, this triangle also has two sides of equal length. Therefore, it is an Isosceles triangle.

It has one line of symmetry, which is the vertical altitude from the top vertex to the base.

(c)

A right-angled scalene triangle on a grid. No lines of symmetry are drawn.

This triangle has one angle that is a right angle ($90^\circ$). The lengths of its three sides are all different (4 units, 5 units, and the hypotenuse). Thus, it is a Right-angled scalene triangle.

A scalene triangle has no lines of symmetry.

(d)

A scalene triangle on a grid. No lines of symmetry are drawn.

By observing the figure on the squared paper, we can determine that all three sides of this triangle are of different lengths. Therefore, it is a Scalene triangle.

It has no lines of symmetry.

Question 3. Complete the following table.

Shape	Rough figure	Number of lines of symmetry
Equilateral triangle		3
Square
Rectangle
Isosceles triangle
Rhombus
Circle

Answer:

To Do:

Complete the table by providing a rough figure and the number of lines of symmetry for each shape.

Solution:

The completed table is as follows:

Shape	Rough figure	Number of lines of symmetry
Equilateral triangle		3
Square		4
Rectangle		2
Isosceles triangle		1
Rhombus		2
Circle		Infinitely many

Question 4. Can you draw a triangle which has

(a) exactly one line of symmetry?

(b) exactly two lines of symmetry?

(d) no lines of symmetry?

Sketch a rough figure in each case.

Answer:

(a) Can you draw a triangle which has exactly one line of symmetry?

Yes, a triangle with exactly one line of symmetry is an Isosceles triangle.

An isosceles triangle has two equal sides, and the line of symmetry is the altitude from the vertex that is between the two equal sides to the base.

A rough sketch of an isosceles triangle with a single vertical line of symmetry drawn from the top vertex to the base.

(b) Can you draw a triangle which has exactly two lines of symmetry?

No, it is not possible to draw a triangle that has exactly two lines of symmetry. A triangle can only have 0, 1, or 3 lines of symmetry. If a triangle were to have two lines of symmetry, it would imply that all three sides are equal, making it an equilateral triangle, which has three lines of symmetry.

(c) Can you draw a triangle which has exactly three lines of symmetry?

Yes, a triangle with exactly three lines of symmetry is an Equilateral triangle.

In an equilateral triangle, all three sides are equal, and all three angles are equal. The three lines of symmetry are the lines that connect each vertex to the midpoint of the opposite side.

A rough sketch of an equilateral triangle with its three lines of symmetry shown. Each line connects a vertex to the midpoint of the opposite side.

(d) Can you draw a triangle which has no lines of symmetry?

Yes, a triangle with no lines of symmetry is a Scalene triangle.

In a scalene triangle, all three sides have different lengths, and all three angles have different measures. Therefore, there is no line that can divide it into two identical mirror-image halves.

A rough sketch of a scalene triangle, indicating that it has no lines of symmetry.

Question 5. On a squared paper, sketch the following:

(a) A triangle with a horizontal line of symmetry but no vertical line of symmetry.

(b) A quadrilateral with both horizontal and vertical lines of symmetry.

(d) A hexagon with exactly two lines of symmetry.

(e) A hexagon with six lines of symmetry.

(Hint: It will be helpful if you first draw the lines of symmetry and then complete the figures.)

Answer:

(a) A triangle with a horizontal line of symmetry but no vertical line of symmetry.

An isosceles triangle has one line of symmetry. To make this line of symmetry horizontal, the triangle's base must be vertical.

An isosceles triangle drawn on a grid. Its base is vertical, and a horizontal dotted line passes through its vertex and the midpoint of the base, showing the line of symmetry.

(b) A quadrilateral with both horizontal and vertical lines of symmetry.

A rectangle is a quadrilateral that has both a horizontal and a vertical line of symmetry. These lines pass through the midpoints of the opposite sides. A square also fits this description.

A rectangle drawn on a grid. A horizontal dotted line passes through the midpoints of the vertical sides, and a vertical dotted line passes through the midpoints of the horizontal sides, showing both lines of symmetry.

(c) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.

A kite with its axis of symmetry oriented horizontally, or an isosceles trapezium with its parallel sides oriented vertically, will have a horizontal line of symmetry but no vertical one.

A kite drawn on a grid, oriented horizontally. A horizontal dotted line is drawn along its main diagonal, representing its single line of symmetry.

(d) A hexagon with exactly two lines of symmetry.

An irregular hexagon can be drawn to have exactly two lines of symmetry. For instance, a hexagon that is stretched or compressed along one axis, but is still symmetric about both the horizontal and vertical axes.

An irregular hexagon drawn on a grid. It is symmetric about a horizontal dotted line and a vertical dotted line that pass through its center.

(e) A hexagon with six lines of symmetry.

A regular hexagon has six lines of symmetry. Three lines connect opposite vertices, and the other three connect the midpoints of opposite sides.

A regular hexagon drawn on a grid with all six of its lines of symmetry shown as dotted lines passing through its center.

Question 6. Trace each figure and draw the lines of symmetry, if any:

Page 268 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

Page 269 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

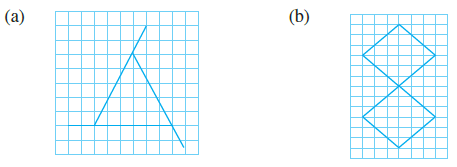
Answer:

To Do:

To trace each figure and draw the lines of symmetry, if any.

Solution:

A line of symmetry is an imaginary line that divides a shape into two identical halves, where one half is the mirror image of the other. The lines of symmetry for each figure are drawn below.

(a)

An isosceles triangle on a grid with a single vertical line of symmetry drawn from the top vertex to the midpoint of the base.

The given figure is an isosceles triangle. It has one line of symmetry, which is the vertical line passing through its top vertex and the midpoint of its base.

(b)

A figure made of two connected rhombuses. It has two lines of symmetry drawn: one horizontal and one vertical, both passing through the center point.

This figure is a composite shape. It has two lines of symmetry: a horizontal line and a vertical line, both passing through the center of the figure.

(c)

A rectangle on a grid with two lines of symmetry drawn: one vertical and one horizontal, passing through the midpoints of the sides.

The given figure is a rectangle. It has two lines of symmetry. One is the vertical line passing through the midpoints of the horizontal sides, and the other is the horizontal line passing through the midpoints of the vertical sides.

(d)

An irregular octagon on a grid with two lines of symmetry drawn: one vertical and one horizontal, both passing through the center.

This figure is an octagon. It has two lines of symmetry: one vertical line and one horizontal line, both passing through the center of the shape.

(e)

An irregular pentagon on a grid with a single horizontal line of symmetry drawn through its side vertices.

This figure is an irregular pentagon. It has one line of symmetry, which is the horizontal line that passes through the figure.

(f)

A four-pointed star on a grid with four lines of symmetry drawn: one vertical, one horizontal, and two diagonal lines.

This figure is a four-pointed star. It has four lines of symmetry: a horizontal line, a vertical line, and two diagonal lines.

Question 7. Consider the letters of English alphabets, A to Z. List among them the letters which have

(a) vertical lines of symmetry (like A)

(b) horizontal lines of symmetry (like B)

Answer:

(a) Letters with vertical lines of symmetry (like A)

These are the letters that can be divided into two identical mirror-image halves by a vertical line passing through their center.

The letters are: A, H, I, M, O, T, U, V, W, X, Y.

(b) Letters with horizontal lines of symmetry (like B)

These are the letters that can be divided into two identical mirror-image halves by a horizontal line passing through their center.

The letters are: B, C, D, E, H, I, K, O, X.

(c) Letters with no lines of symmetry (like Q)

These are the letters that cannot be divided into two identical mirror-image halves by any straight line. Some of these letters may have rotational symmetry, but they do not have line symmetry.

The letters are: F, G, J, L, N, P, Q, R, S, Z.

Question 8. Given here are figures of a few folded sheets and designs drawn about the fold. In each case, draw a rough diagram of the complete figure that would be seen when the design is cut off.

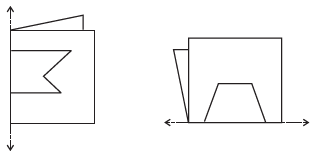
Answer:

To Do:

For each figure, draw a rough diagram of the complete shape that would be seen when the design is cut out from the folded sheet and then the sheet is unfolded.

Solution:

When the folded sheet is cut and then unfolded, the fold line acts as a line of symmetry. The cut-out design on one side of the fold will be mirrored on the other side. We need to visualize the reflection of the cut design to get the complete figure.

Figure 1 (Left):

The sheet is folded along a vertical line. The design cut into the folded paper will be reflected horizontally to the other side when unfolded. The completed figure will be symmetric about the vertical fold line.

The complete figure for the first design. It is a large rectangle with a symmetric, M-shaped cutout in the middle and a triangular shape at the top center. The figure is symmetric about a central vertical line.

Figure 2 (Right):

The sheet is folded along a horizontal line. The design cut into the folded paper will be reflected vertically to the other side when unfolded. The completed figure will be symmetric about the horizontal fold line.

The complete figure for the second design. It is a large shape with a hexagonal cutout in the center and a V-shaped notch on the left side. The figure is symmetric about a central horizontal line.

Exercise 13.3

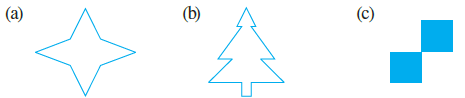
Question 1. Find the number of lines of symmetry in each of the following shapes.

How will you check your answers?

Page 271 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

Page 272 Chapter 13 Class 6th Non-Rationalised NCERT 2019-20

Answer:

To Find:

The number of lines of symmetry for each given shape and the method to check the answers.

Solution:

The number of lines of symmetry for each shape is determined by finding all possible lines that divide the shape into two identical, mirror-image halves.

(a)

A four-pointed star with its four lines of symmetry drawn: one vertical, one horizontal, and two diagonals.

This shape has 4 lines of symmetry.

(b)

A Christmas tree shape with its single vertical line of symmetry drawn down the center.

This shape has 1 line of symmetry.

(c)

A shape made of two diagonally adjacent squares. It is shown to have no lines of symmetry.

This shape has 0 lines of symmetry.

(d)

A shape made of six semicircles with its two lines of symmetry drawn: one vertical and one horizontal.

This shape has 2 lines of symmetry.

(e)

A dragonfly with its single vertical line of symmetry drawn through the center of its body.

This shape has 1 line of symmetry.

(f)

A double-headed arrow with its two lines of symmetry drawn: one vertical and one horizontal.

This shape has 2 lines of symmetry.

How to Check the Answers:

The answers can be verified by either the paper-folding method or by using a mirror.

1. Paper-Folding Method: Trace each figure onto a separate piece of paper and cut it out. Try to fold the shape along the line you believe is a line of symmetry. If the two halves of the shape match up perfectly and overlap completely, then your line of symmetry is correct.

2. Mirror Method: Place a mirror along the line you believe is a line of symmetry. Look at the reflection of one half of the figure in the mirror. If this reflection, combined with the half you are looking at, recreates the original complete figure, then the line is a line of symmetry.

Question 2. Copy the following drawing on squared paper. Complete each one of them such that the resulting figure has two dotted lines as two lines of symmetry

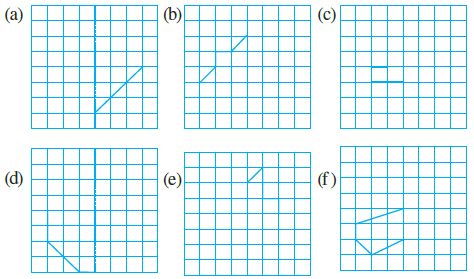
How did you go about completing the picture?

Answer:

To Do:

Complete each of the given drawings on squared paper such that the resulting figure has the two dotted lines as its two lines of symmetry.

Solution:

To complete each figure, we must reflect the given drawing across both dotted lines. The process involves a series of reflections to ensure the final shape is symmetric about both the horizontal and vertical axes.

(a)

The completed figure is a rhombus. The original line segment in the bottom-right quadrant is reflected to the other three quadrants to form the rhombus.

(b)

The completed figure is a pinwheel-like shape. The original two segments in the top-left quadrant are reflected to the other three quadrants.

(c)

The completed figure is a cross or plus shape with indented corners. The original 'L' shape in the top-left quadrant is reflected to the other three quadrants.

(d)

The completed figure is a rhombus. The original small triangle in the bottom-left quadrant is reflected to the other three quadrants.

(e)

The completed figure is a rhombus. The original line segment in the top-right quadrant is reflected to the other three quadrants.

(f)

The completed figure is a complex symmetric polygon with eight sides. The original shape in the bottom-left quadrant is reflected to the other three quadrants.

How did you go about completing the picture?

The process to complete each picture involves two main steps of reflection to ensure symmetry across both dotted lines:

Step 1: Reflect across the first line of symmetry.

I first took the original drawing in one quadrant and reflected it across one of the dotted lines (for example, the vertical line) into the adjacent quadrant. This created a larger shape that was symmetric about that first line.

Step 2: Reflect the new shape across the second line of symmetry.

Next, I took the entire new shape (which now occupied two quadrants) and reflected it across the second dotted line (the horizontal line). This completed the figure in all four quadrants, making the final image symmetric with respect to both dotted lines.

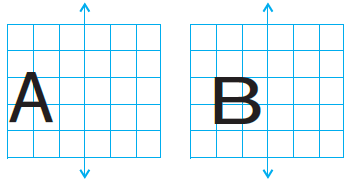
Question 3. In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e. which letters look the same in the image) and which do not. Can you guess why?

Try for

Answer:

To Find:

1. The mirror image of the given letters (A, B, O, E, M, N, P, H, L, T, S, V, X) in the vertical line.

2. Which letters look the same after reflection and which do not.

3. The reason for this observation.

Solution:

When we take the mirror image of a letter across a vertical line, we are essentially looking at its horizontal reflection. The letters that are symmetric about a vertical axis will look the same, while those that are not will appear reversed.

Letter	Mirror Image	Looks the Same?
A		Yes
B		No
O		Yes
E		No
M		Yes
N		No
P		No
H		Yes
L		No
T		Yes
S		No
V		Yes
X		Yes

Letters that look the same after reflection:

The letters that look the same in their mirror image are: A, O, M, H, T, V, X.

Letters that do not look the same after reflection:

The letters that look different (reversed) in their mirror image are: B, E, N, P, L, S.

Reason:

The reason why some letters appear unchanged after reflection in a vertical mirror is because they possess vertical line symmetry.

A vertical line of symmetry is a line that divides the letter into two identical halves—a left half and a right half—that are mirror images of each other. For these letters, reflecting them across a vertical line results in an image that is identical to the original letter.

Letters that do not have a vertical line of symmetry will not look the same when reflected in a vertical mirror.