| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 3 Playing With Numbers
The solutions for Chapter 3, "Playing With Numbers," delve into the fascinating world of factors, multiples, and divisibility, laying the groundwork for number theory. This chapter introduces concepts like factors, multiples, prime and composite numbers, tests for divisibility, common factors and multiples, Highest Common Factor (HCF), and Lowest Common Multiple (LCM), along with prime factorisation.
The solutions meticulously guide students through exercises requiring them to find all factors of a given number, list multiples, and identify numbers as prime or composite. The Sieve of Eratosthenes method for finding prime numbers might be explained or referenced. A major focus is on the tests for divisibility by 2, 3, 4, 5, 6, 8, 9, 10, and 11. The solutions provide clear applications of these rules, showing students how to quickly determine if a number is divisible by another without performing long division. This section often includes problems where students need to find missing digits to make a number divisible by a specific divisor.
Prime factorisation is thoroughly covered, with solutions demonstrating both the factor tree method and the division method to break down composite numbers into their prime factors.
Building on factors and multiples, the concepts of HCF and LCM are introduced. Solutions demonstrate various methods to find the HCF (listing common factors, prime factorisation) and LCM (listing common multiples, prime factorisation, common division method). Crucially, the solutions tackle numerous word problems that require the application of HCF (e.g., finding the largest size of tile to cover a floor, finding the maximum capacity of a container to measure liquids exactly) and LCM (e.g., finding when bells toll together, finding the smallest number divisible by several numbers). These solutions carefully analyse the problem statement to determine whether HCF or LCM is needed and then apply the appropriate method systematically.
This chapter is vital for understanding fractions and algebraic operations later, and the solutions aim to build strong conceptual understanding and procedural fluency in these number theory basics.
Example 1 to 3 (Before Exercise 3.1)
Example 1: Write all the factors of 68.
Answer:
To Find:
All the factors of the number 68.
Solution:
To find the factors of 68, we need to find all the integers that divide 68 exactly, leaving no remainder.
We can check divisibility by integers starting from 1.
If a number $a$ divides 68, then both $a$ and $68/a$ are factors.
$68 \div 1 = 68$. So, 1 and 68 are factors.
$68 \div 2 = 34$. So, 2 and 34 are factors.
68 is not divisible by 3, as the sum of its digits ($6+8=14$) is not divisible by 3.
$68 \div 4 = 17$. So, 4 and 17 are factors.
68 is not divisible by 5, as it does not end in 0 or 5.
68 is not divisible by 6, as it is not divisible by 3.
68 is not divisible by 7 ($68 = 7 \times 9 + 5$).
68 is not divisible by 8 ($68 = 8 \times 8 + 4$).
We only need to check divisibility up to the square root of 68. $\sqrt{68}$ is between $\sqrt{64}=8$ and $\sqrt{81}=9$. Since we have checked up to 8, and found the pairs (1, 68), (2, 34), (4, 17), we have found all the factors.
Listing them in ascending order:
The factors of 68 are 1, 2, 4, 17, 34, 68.
Alternate Solution (Using Prime Factorization):
First, find the prime factorization of 68.
$\begin{array}{c|cc} 2 & 68 \\ \hline 2 & 34 \\ \hline 17 & 17 \\ \hline & 1 \end{array}$
The prime factorization of 68 is $2 \times 2 \times 17 = 2^2 \times 17^1$.
To find all factors, we take combinations of the prime factors with powers ranging from 0 up to their power in the prime factorization.
The factors are of the form $2^a \times 17^b$, where $a \in \{0, 1, 2\}$ and $b \in \{0, 1\}$.
Possible combinations:
$2^0 \times 17^0 = 1 \times 1 = 1$
$2^1 \times 17^0 = 2 \times 1 = 2$
$2^2 \times 17^0 = 4 \times 1 = 4$
$2^0 \times 17^1 = 1 \times 17 = 17$
$2^1 \times 17^1 = 2 \times 17 = 34$
$2^2 \times 17^1 = 4 \times 17 = 68$
Thus, the factors of 68 are 1, 2, 4, 17, 34, 68.
Example 2: Find the factors of 36.
Answer:
To Find:
All the factors of the number 36.
Solution:
To find the factors of 36, we look for all integers that divide 36 without leaving a remainder.
We check integers starting from 1:
$36 \div 1 = 36$. So, 1 and 36 are factors.
$36 \div 2 = 18$. So, 2 and 18 are factors.
$36 \div 3 = 12$. So, 3 and 12 are factors.
$36 \div 4 = 9$. So, 4 and 9 are factors.
36 is not divisible by 5.
$36 \div 6 = 6$. So, 6 is a factor.
Since we reached the square root of 36 ($\sqrt{36} = 6$), we have found all the factor pairs.
The pairs are (1, 36), (2, 18), (3, 12), (4, 9), and (6, 6).
Listing them in ascending order:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
Alternate Solution (Using Prime Factorization):
First, find the prime factorization of 36.
$\begin{array}{c|cc} 2 & 36 \\ \hline 2 & 18 \\ \hline 3 & 9 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
The prime factorization of 36 is $2 \times 2 \times 3 \times 3 = 2^2 \times 3^2$.
To find all factors, we take combinations of the prime factors with powers ranging from 0 up to their power in the prime factorization.
The factors are of the form $2^a \times 3^b$, where $a \in \{0, 1, 2\}$ and $b \in \{0, 1, 2\}$.
Possible combinations:
$2^0 \times 3^0 = 1 \times 1 = 1$
$2^1 \times 3^0 = 2 \times 1 = 2$
$2^2 \times 3^0 = 4 \times 1 = 4$
$2^0 \times 3^1 = 1 \times 3 = 3$
$2^1 \times 3^1 = 2 \times 3 = 6$
$2^2 \times 3^1 = 4 \times 3 = 12$
$2^0 \times 3^2 = 1 \times 9 = 9$
$2^1 \times 3^2 = 2 \times 9 = 18$
$2^2 \times 3^2 = 4 \times 9 = 36$
Thus, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
Example 3: Write first five multiples of 6.
Answer:
To Find:
The first five multiples of the number 6.
Solution:
A multiple of a number is the result of multiplying that number by an integer.
To find the first five multiples of 6, we multiply 6 by the first five positive integers: 1, 2, 3, 4, and 5.
First multiple: $6 \times 1 = 6$
Second multiple: $6 \times 2 = 12$
Third multiple: $6 \times 3 = 18$
Fourth multiple: $6 \times 4 = 24$
Fifth multiple: $6 \times 5 = 30$
Therefore, the first five multiples of 6 are 6, 12, 18, 24, 30.
Exercise 3.1
Question 1. Write all the factors of the following numbers :
(a) 24
(b) 15
(c) 21
(d) 27
(e) 12
(f) 20
(g) 18
(h) 23
(i) 36
Answer:
(a) Factors of 24:
We find pairs of numbers that multiply to give 24:
$1 \times 24 = 24$
$2 \times 12 = 24$
$3 \times 8 = 24$
$4 \times 6 = 24$
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24.
(b) Factors of 15:
We find pairs of numbers that multiply to give 15:
$1 \times 15 = 15$
$3 \times 5 = 15$
The factors of 15 are: 1, 3, 5, 15.
(c) Factors of 21:
We find pairs of numbers that multiply to give 21:
$1 \times 21 = 21$
$3 \times 7 = 21$
The factors of 21 are: 1, 3, 7, 21.
(d) Factors of 27:
We find pairs of numbers that multiply to give 27:
$1 \times 27 = 27$
$3 \times 9 = 27$
The factors of 27 are: 1, 3, 9, 27.
(e) Factors of 12:
We find pairs of numbers that multiply to give 12:
$1 \times 12 = 12$
$2 \times 6 = 12$
$3 \times 4 = 12$
The factors of 12 are: 1, 2, 3, 4, 6, 12.
(f) Factors of 20:
We find pairs of numbers that multiply to give 20:
$1 \times 20 = 20$
$2 \times 10 = 20$
$4 \times 5 = 20$
The factors of 20 are: 1, 2, 4, 5, 10, 20.
(g) Factors of 18:
We find pairs of numbers that multiply to give 18:
$1 \times 18 = 18$
$2 \times 9 = 18$
$3 \times 6 = 18$
The factors of 18 are: 1, 2, 3, 6, 9, 18.
(h) Factors of 23:
We find pairs of numbers that multiply to give 23:
$1 \times 23 = 23$
(23 is a prime number, so it only has two factors: 1 and itself.)
The factors of 23 are: 1, 23.
(i) Factors of 36:
We find pairs of numbers that multiply to give 36:
$1 \times 36 = 36$
$2 \times 18 = 36$
$3 \times 12 = 36$
$4 \times 9 = 36$
$6 \times 6 = 36$
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Question 2. Write first five multiples of :
(a) 5
(b) 8
(c) 9
Answer:
(a) First five multiples of 5:
To find the first five multiples of 5, we multiply 5 by the first five positive integers (1, 2, 3, 4, 5).
$5 \times 1 = 5$
$5 \times 2 = 10$
$5 \times 3 = 15$
$5 \times 4 = 20$
$5 \times 5 = 25$
The first five multiples of 5 are: 5, 10, 15, 20, 25.
(b) First five multiples of 8:
To find the first five multiples of 8, we multiply 8 by the first five positive integers (1, 2, 3, 4, 5).
$8 \times 1 = 8$
$8 \times 2 = 16$
$8 \times 3 = 24$
$8 \times 4 = 32$
$8 \times 5 = 40$
The first five multiples of 8 are: 8, 16, 24, 32, 40.
(c) First five multiples of 9:
To find the first five multiples of 9, we multiply 9 by the first five positive integers (1, 2, 3, 4, 5).
$9 \times 1 = 9$
$9 \times 2 = 18$
$9 \times 3 = 27$
$9 \times 4 = 36$
$9 \times 5 = 45$
The first five multiples of 9 are: 9, 18, 27, 36, 45.
Question 3. Match the items in column 1 with the items in column 2.
Column 1
(i) 35
(ii) 15
(iii) 16
(iv) 20
(v) 25
Column 2
(a) Multiple of 8
(b) Multiple of 7
(c) Multiple of 70
(d) Factor of 30
(e) Factor of 50
(f) Factor of 20
Answer:
We need to match each number in Column 1 with its correct description in Column 2.
(i) 35:
We check the options in Column 2:
(a) 35 is not a multiple of 8 ($8 \times 4 = 32, 8 \times 5 = 40$).
(b) 35 is a multiple of 7, since $7 \times 5 = 35$.
So, (i) matches with (b).
(ii) 15:
We check the options in Column 2:
(d) 15 is a factor of 30, since $30 \div 15 = 2$.
Let's check other factor options: 15 is not a factor of 50 ($50 \div 15$ has a remainder). 15 is not a factor of 20 ($20 \div 15$ has a remainder).
Let's check multiple options: 15 is not a multiple of 8, 7, or 70.
So, (ii) matches with (d).
(iii) 16:
We check the options in Column 2:
(a) 16 is a multiple of 8, since $8 \times 2 = 16$.
So, (iii) matches with (a).
(iv) 20:
We check the options in Column 2:
(f) 20 is a factor of 20, since $20 \div 20 = 1$.
Let's check other factor options: 20 is not a factor of 30. 20 is not a factor of 50.
Let's check multiple options: 20 is not a multiple of 8, 7, or 70.
So, (iv) matches with (f).
(v) 25:
We check the remaining options in Column 2:
(e) 25 is a factor of 50, since $50 \div 25 = 2$.
Let's check other factor options: 25 is not a factor of 30. 25 is not a factor of 20.
Let's check multiple options: 25 is not a multiple of 8, 7 or 70.
So, (v) matches with (e).
Final Matches:
(i) 35 $\longrightarrow$ (b) Multiple of 7
(ii) 15 $\longrightarrow$ (d) Factor of 30
(iii) 16 $\longrightarrow$ (a) Multiple of 8
(iv) 20 $\longrightarrow$ (f) Factor of 20
(v) 25 $\longrightarrow$ (e) Factor of 50
Question 4. Find all the multiples of 9 upto 100.
Answer:
To Find:
All the multiples of 9 that are less than or equal to 100.
Solution:
Multiples of 9 are the numbers obtained by multiplying 9 by consecutive positive integers (1, 2, 3, ...).
We need to find these multiples until they exceed 100.
$9 \times 1 = 9$
$9 \times 2 = 18$
$9 \times 3 = 27$
$9 \times 4 = 36$
$9 \times 5 = 45$
$9 \times 6 = 54$
$9 \times 7 = 63$
$9 \times 8 = 72$
$9 \times 9 = 81$
$9 \times 10 = 90$
$9 \times 11 = 99$
$9 \times 12 = 108$. This is greater than 100, so we stop here.
Therefore, the multiples of 9 up to 100 are:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99.
Example 4 (Before Exercise 3.2)
Example 4: Write all the prime numbers less than 15.
Answer:
To Find:
All the prime numbers that are less than 15.
Solution:
A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself.
We need to list all the natural numbers less than 15 and check if they are prime.
The natural numbers less than 15 are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.
Let's check each number:
- 1: Is not a prime number (by definition, a prime number must be greater than 1).
- 2: Has factors 1 and 2. It is a prime number.
- 3: Has factors 1 and 3. It is a prime number.
- 4: Has factors 1, 2, 4. It is not a prime number (it is composite).
- 5: Has factors 1 and 5. It is a prime number.
- 6: Has factors 1, 2, 3, 6. It is not a prime number (it is composite).
- 7: Has factors 1 and 7. It is a prime number.
- 8: Has factors 1, 2, 4, 8. It is not a prime number (it is composite).
- 9: Has factors 1, 3, 9. It is not a prime number (it is composite).
- 10: Has factors 1, 2, 5, 10. It is not a prime number (it is composite).
- 11: Has factors 1 and 11. It is a prime number.
- 12: Has factors 1, 2, 3, 4, 6, 12. It is not a prime number (it is composite).
- 13: Has factors 1 and 13. It is a prime number.
- 14: Has factors 1, 2, 7, 14. It is not a prime number (it is composite).
The prime numbers less than 15 are those we identified as prime:
2, 3, 5, 7, 11, 13.
Exercise 3.2
Question 1. What is the sum of any two
(a) Odd numbers?
(b) Even numbers?
Answer:
(a) Sum of any two Odd numbers:
Let's find out by taking some examples.
An odd number is a whole number that cannot be divided exactly by 2 (like 1, 3, 5, 7, etc.).
Examples:
$3 + 5 = 8$
$7 + 11 = 18$
$1 + 99 = 100$
In every case, when we add two odd numbers, the result is an even number.
Reason: Every odd number is just one more than an even number. So, when you add two odd numbers, you are adding two even numbers plus two 1s. Since adding two even numbers gives an even number, and adding the two 1s gives 2 (which is also even), the total sum will always be an even number.
(b) Sum of any two Even numbers:
Let's find out by taking some examples.
An even number is a whole number that can be divided exactly by 2 (like 2, 4, 6, 8, etc.).
Examples:
$2 + 6 = 8$
$10 + 14 = 24$
$8 + 20 = 28$
In every case, when we add two even numbers, the result is an even number.
Reason: Even numbers are all multiples of 2. When you add two multiples of 2 together, the result will always be another multiple of 2, which means it will always be an even number.
Question 2. State whether the following statements are True or False:
(a) The sum of three odd numbers is even.
(b) The sum of two odd numbers and one even number is even.
(c) The product of three odd numbers is odd.
(d) If an even number is divided by 2, the quotient is always odd.
(e) All prime numbers are odd.
(f) Prime numbers do not have any factors.
(g) Sum of two prime numbers is always even.
(h) 2 is the only even prime number.
(i) All even numbers are composite numbers.
(j) The product of two even numbers is always even.
Answer:
(a) The sum of three odd numbers is even.
Let's check with an example: $3 + 5 + 7$.
First, $3 + 5 = 8$ (which is even).
Then, $8 + 7 = 15$ (which is odd).
So, the statement is False.
(b) The sum of two odd numbers and one even number is even.
Let's check with an example: $3 + 5 + 6$.
The sum of two odd numbers ($3 + 5$) is $8$ (even).
Then, we add the even number: $8 + 6 = 14$ (even).
So, the statement is True.
(c) The product of three odd numbers is odd.
Let's check with an example: $3 \times 5 \times 7$.
First, $3 \times 5 = 15$ (which is odd).
Then, $15 \times 7 = 105$ (which is odd).
So, the statement is True.
(d) If an even number is divided by 2, the quotient is always odd.
Let's test this. Take the even number 6. $6 \div 2 = 3$ (odd). This works.
Now take the even number 12. $12 \div 2 = 6$ (even). This doesn't work.
Since we found an example where it's not true, the statement is False.
(e) All prime numbers are odd.
A prime number is a number greater than 1 that can only be divided by 1 and itself. The number 2 is prime. Since 2 is an even number, this statement is not true.
So, the statement is False.
(f) Prime numbers do not have any factors.
By definition, prime numbers have exactly two factors: 1 and the number itself. For example, the factors of 5 are 1 and 5.
So, the statement is False.
(g) Sum of two prime numbers is always even.
Let's take two prime numbers, 2 and 3. Their sum is $2 + 3 = 5$. Since 5 is an odd number, this statement is not always true.
So, the statement is False.
(h) 2 is the only even prime number.
Any other even number (like 4, 6, 8, 10, etc.) can be divided by 2. This means they all have at least three factors: 1, 2, and themselves. Therefore, no other even number can be prime. The number 2 is prime and it is even.
So, the statement is True.
(i) All even numbers are composite numbers.
A composite number is a number with more than two factors. The number 2 is an even number, but it is a prime number (it has only two factors, 1 and 2), not a composite number.
So, the statement is False.
(j) The product of two even numbers is always even.
Let's check with an example: $4 \times 6 = 24$. Both 4 and 6 are even, and their product 24 is also even. Since any even number has 2 as a factor, when you multiply two even numbers, the result must also have 2 as a factor, making it even.
So, the statement is True.
Question 3. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers upto 100.
Answer:
To Find:
Pairs of prime numbers less than 100 such that the digits of one number are the reverse of the digits of the other number in the pair.
Solution:
First, we list the prime numbers up to 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
We are looking for pairs of prime numbers $(p, q)$ where $p \neq q$, $p < 100$, $q < 100$, and the digits of $q$ are the reverse of the digits of $p$.
Single-digit primes (2, 3, 5, 7) do not form such pairs.
The prime number 11 has reversed digits 11, which is the same number, so it doesn't form a pair.
We check the two-digit prime numbers:
- 13: The reverse is 31. Both 13 and 31 are prime numbers. So, (13, 31) is a pair.
- 17: The reverse is 71. Both 17 and 71 are prime numbers. So, (17, 71) is a pair.
- 19: The reverse is 91. $91 = 7 \times 13$, so 91 is not prime.
- 23: The reverse is 32. 32 is even and greater than 2, so it is not prime.
- 29: The reverse is 92. 92 is even and greater than 2, so it is not prime.
- 31: The reverse is 13. (Already found the pair 13, 31).
- 37: The reverse is 73. Both 37 and 73 are prime numbers. So, (37, 73) is a pair.
- 41: The reverse is 14. 14 is not prime.
- 43: The reverse is 34. 34 is not prime.
- 47: The reverse is 74. 74 is not prime.
- 53: The reverse is 35. 35 is not prime ($35 = 5 \times 7$).
- 59: The reverse is 95. 95 is not prime ($95 = 5 \times 19$).
- 61: The reverse is 16. 16 is not prime.
- 67: The reverse is 76. 76 is not prime.
- 71: The reverse is 17. (Already found the pair 17, 71).
- 73: The reverse is 37. (Already found the pair 37, 73).
- 79: The reverse is 97. Both 79 and 97 are prime numbers. So, (79, 97) is a pair.
- 83: The reverse is 38. 38 is not prime.
- 89: The reverse is 98. 98 is not prime.
- 97: The reverse is 79. (Already found the pair 79, 97).
The pairs of prime numbers up to 100 with the same digits reversed are:
(13, 31), (17, 71), (37, 73), and (79, 97).
Question 4. Write down separately the prime and composite numbers less than 20.
Answer:
To Find:
The prime numbers and composite numbers that are less than 20.
Definitions:
A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself.
A composite number is a natural number greater than 1 that has more than two distinct positive divisors.
The number 1 is neither prime nor composite.
Solution:
We need to examine the natural numbers from 2 up to 19.
Prime Numbers less than 20:
We look for numbers greater than 1 whose only factors are 1 and themselves.
- 2 (Factors: 1, 2) - Prime
- 3 (Factors: 1, 3) - Prime
- 4 (Factors: 1, 2, 4) - Not Prime
- 5 (Factors: 1, 5) - Prime
- 6 (Factors: 1, 2, 3, 6) - Not Prime
- 7 (Factors: 1, 7) - Prime
- 8 (Factors: 1, 2, 4, 8) - Not Prime
- 9 (Factors: 1, 3, 9) - Not Prime
- 10 (Factors: 1, 2, 5, 10) - Not Prime
- 11 (Factors: 1, 11) - Prime
- 12 (Factors: 1, 2, 3, 4, 6, 12) - Not Prime
- 13 (Factors: 1, 13) - Prime
- 14 (Factors: 1, 2, 7, 14) - Not Prime
- 15 (Factors: 1, 3, 5, 15) - Not Prime
- 16 (Factors: 1, 2, 4, 8, 16) - Not Prime
- 17 (Factors: 1, 17) - Prime
- 18 (Factors: 1, 2, 3, 6, 9, 18) - Not Prime
- 19 (Factors: 1, 19) - Prime
The prime numbers less than 20 are: 2, 3, 5, 7, 11, 13, 17, 19.
Composite Numbers less than 20:
These are the numbers greater than 1 and less than 20 that are not prime.
From the list above, the numbers that are not prime are:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18.
The composite numbers less than 20 are: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18.
Question 5. What is the greatest prime number between 1 and 10?
Answer:
To Find:
The greatest prime number that lies between 1 and 10.
Solution:
First, we list the natural numbers that are strictly between 1 and 10. These are:
2, 3, 4, 5, 6, 7, 8, 9.
Next, we identify which of these numbers are prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- 2 is prime (divisors: 1, 2).
- 3 is prime (divisors: 1, 3).
- 4 is composite (divisors: 1, 2, 4).
- 5 is prime (divisors: 1, 5).
- 6 is composite (divisors: 1, 2, 3, 6).
- 7 is prime (divisors: 1, 7).
- 8 is composite (divisors: 1, 2, 4, 8).
- 9 is composite (divisors: 1, 3, 9).
The prime numbers between 1 and 10 are 2, 3, 5, and 7.
We need to find the greatest among these prime numbers.
Comparing 2, 3, 5, and 7, the greatest number is 7.
Therefore, the greatest prime number between 1 and 10 is 7.
Question 6. Express the following as the sum of two odd primes.
(a) 44
(b) 36
(c) 24
(d) 18
Answer:
We need to express each given even number as the sum of two prime numbers, both of which must be odd.
(a) 44:
We look for two odd prime numbers that add up to 44.
We can try subtracting small odd primes from 44:
$44 - 3 = 41$. Both 3 and 41 are odd prime numbers.
So, $44 = 3 + 41$.
Another possible pair: $44 - 13 = 31$. Both 13 and 31 are odd prime numbers.
So, $44 = 13 + 31$.
One such representation is: $44 = 3 + 41$.
(b) 36:
We look for two odd prime numbers that add up to 36.
We can try subtracting small odd primes from 36:
$36 - 5 = 31$. Both 5 and 31 are odd prime numbers.
So, $36 = 5 + 31$.
Another possible pair: $36 - 7 = 29$. Both 7 and 29 are odd prime numbers.
So, $36 = 7 + 29$.
Another possible pair: $36 - 13 = 23$. Both 13 and 23 are odd prime numbers.
So, $36 = 13 + 23$.
Another possible pair: $36 - 17 = 19$. Both 17 and 19 are odd prime numbers.
So, $36 = 17 + 19$.
One such representation is: $36 = 5 + 31$.
(c) 24:
We look for two odd prime numbers that add up to 24.
We can try subtracting small odd primes from 24:
$24 - 5 = 19$. Both 5 and 19 are odd prime numbers.
So, $24 = 5 + 19$.
Another possible pair: $24 - 7 = 17$. Both 7 and 17 are odd prime numbers.
So, $24 = 7 + 17$.
Another possible pair: $24 - 11 = 13$. Both 11 and 13 are odd prime numbers.
So, $24 = 11 + 13$.
One such representation is: $24 = 5 + 19$.
(d) 18:
We look for two odd prime numbers that add up to 18.
We can try subtracting small odd primes from 18:
$18 - 5 = 13$. Both 5 and 13 are odd prime numbers.
So, $18 = 5 + 13$.
Another possible pair: $18 - 7 = 11$. Both 7 and 11 are odd prime numbers.
So, $18 = 7 + 11$.
One such representation is: $18 = 5 + 13$.
Question 7. Give three pairs of prime numbers whose difference is 2.
[Remark: Two prime numbers whose difference is 2 are called twin primes].
Answer:
To Find:
Three pairs of prime numbers $(p, q)$ such that $p$ and $q$ are prime and $|p - q| = 2$.
Solution:
We are looking for pairs of prime numbers that differ by 2. These are known as twin primes.
We can list the prime numbers and check for pairs with a difference of 2:
Prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 29, 31, 41, 43, 59, 61, 71, 73, ...
Let's find pairs:
- (3, 5): Both are prime, and $5 - 3 = 2$. This is one pair.
- (5, 7): Both are prime, and $7 - 5 = 2$. This is another pair.
- (11, 13): Both are prime, and $13 - 11 = 2$. This is a third pair.
Other examples include (17, 19), (29, 31), (41, 43), (59, 61), (71, 73).
Three required pairs of prime numbers whose difference is 2 are:
(3, 5)
(5, 7)
(11, 13)
Question 8. Which of the following numbers are prime?
(a) 23
(b) 51
(c) 37
(d) 26
Answer:
A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself.
(a) 23:
To check if 23 is prime, we test for divisibility by prime numbers less than or equal to its square root ($\sqrt{23} \approx 4.8$). We only need to check primes 2 and 3.
23 is not divisible by 2 (it is odd).
23 is not divisible by 3 (since $2+3=5$, which is not divisible by 3).
Since 23 is not divisible by any prime number less than or equal to its square root, 23 is a prime number.
Factors of 23 are 1 and 23.
Therefore, 23 is a prime number.
(b) 51:
We test for divisibility by prime numbers.
51 is not divisible by 2 (it is odd).
Is 51 divisible by 3? The sum of digits is $5+1=6$. Since 6 is divisible by 3, 51 is divisible by 3.
$51 \div 3 = 17$.
Since 51 has factors other than 1 and 51 (namely 3 and 17), it is not a prime number.
Factors of 51 are 1, 3, 17, 51.
Therefore, 51 is not a prime number (it is composite).
(c) 37:
To check if 37 is prime, we test for divisibility by prime numbers less than or equal to its square root ($\sqrt{37} \approx 6.1$). We need to check primes 2, 3, and 5.
37 is not divisible by 2 (it is odd).
37 is not divisible by 3 (since $3+7=10$, which is not divisible by 3).
37 is not divisible by 5 (it does not end in 0 or 5).
Since 37 is not divisible by any prime number less than or equal to its square root, 37 is a prime number.
Factors of 37 are 1 and 37.
Therefore, 37 is a prime number.
(d) 26:
We test for divisibility by prime numbers.
26 is an even number, so it is divisible by 2.
$26 \div 2 = 13$.
Since 26 has factors other than 1 and 26 (namely 2 and 13), it is not a prime number.
Factors of 26 are 1, 2, 13, 26.
Therefore, 26 is not a prime number (it is composite).
Conclusion: The prime numbers among the given options are 23 and 37.
Question 9. Write seven consecutive composite numbers less than 100 so that there is no prime number between them.
Answer:
To Find:
A sequence of seven consecutive natural numbers, all of which are less than 100, such that every number in the sequence is composite (i.e., not prime).
Solution:
We need to find a block of 7 consecutive numbers below 100 where none of them are prime. This means we should look for a gap of at least 7 between two consecutive prime numbers.
Let's list the prime numbers up to 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Now, we look for the difference between consecutive primes:
- $3 - 2 = 1$
- $5 - 3 = 2$
- $7 - 5 = 2$
- $11 - 7 = 4$ (Numbers: 8, 9, 10 - 3 composites)
- $13 - 11 = 2$
- $17 - 13 = 4$ (Numbers: 14, 15, 16 - 3 composites)
- $19 - 17 = 2$
- $23 - 19 = 4$ (Numbers: 20, 21, 22 - 3 composites)
- $29 - 23 = 6$ (Numbers: 24, 25, 26, 27, 28 - 5 composites)
- $31 - 29 = 2$
- $37 - 31 = 6$ (Numbers: 32, 33, 34, 35, 36 - 5 composites)
- $41 - 37 = 4$
- $43 - 41 = 2$
- $47 - 43 = 4$
- $53 - 47 = 6$ (Numbers: 48, 49, 50, 51, 52 - 5 composites)
- $59 - 53 = 6$ (Numbers: 54, 55, 56, 57, 58 - 5 composites)
- $61 - 59 = 2$
- $67 - 61 = 6$ (Numbers: 62, 63, 64, 65, 66 - 5 composites)
- $71 - 67 = 4$
- $73 - 71 = 2$
- $79 - 73 = 6$ (Numbers: 74, 75, 76, 77, 78 - 5 composites)
- $83 - 79 = 4$
- $89 - 83 = 6$ (Numbers: 84, 85, 86, 87, 88 - 5 composites)
- $97 - 89 = 8$ (Numbers: 90, 91, 92, 93, 94, 95, 96 - 7 composites)
We found a gap of 8 between the prime numbers 89 and 97. The numbers between them are 90, 91, 92, 93, 94, 95, 96.
Let's verify that these are all composite:
- $90 = 9 \times 10$ (Composite)
- $91 = 7 \times 13$ (Composite)
- $92 = 4 \times 23$ (Composite)
- $93 = 3 \times 31$ (Composite)
- $94 = 2 \times 47$ (Composite)
- $95 = 5 \times 19$ (Composite)
- $96 = 12 \times 8$ (Composite)
These seven numbers are consecutive, all less than 100, and all are composite. There is no prime number between them.
Therefore, the required seven consecutive composite numbers are:
90, 91, 92, 93, 94, 95, 96.
Question 10. Express each of the following numbers as the sum of three odd primes:
(a) 21
(b) 31
(c) 53
(d) 61
Answer:
We need to express each given number as the sum of three prime numbers, all of which must be odd. Odd prime numbers are prime numbers other than 2 (e.g., 3, 5, 7, 11, 13, 17, 19, ...).
(a) 21:
We need to find three odd primes $p_1, p_2, p_3$ such that $p_1 + p_2 + p_3 = 21$.
Let's try starting with the smallest odd prime, 3.
If $p_1 = 3$, then $p_2 + p_3 = 21 - 3 = 18$.
We need to find two odd primes that sum to 18. Possible pairs are (5, 13) or (7, 11).
Using the pair (5, 13): Both 5 and 13 are odd primes.
So, $21 = 3 + 5 + 13$.
Therefore, $21 = 3 + 5 + 13$.
(b) 31:
We need to find three odd primes $p_1, p_2, p_3$ such that $p_1 + p_2 + p_3 = 31$.
Let's try starting with $p_1 = 3$. Then $p_2 + p_3 = 31 - 3 = 28$.
We need to find two odd primes that sum to 28. Possible pairs are (5, 23) or (11, 17).
Using the pair (5, 23): Both 5 and 23 are odd primes.
So, $31 = 3 + 5 + 23$.
Alternatively, starting with $p_1=5$. Then $p_2 + p_3 = 31-5=26$. Possible pairs are (3, 23) or (7, 19) or (13, 13).
Using (3, 23): $31=5+3+23$.
Using (7, 19): $31=5+7+19$.
One possible representation is: $31 = 3 + 5 + 23$.
(c) 53:
We need to find three odd primes $p_1, p_2, p_3$ such that $p_1 + p_2 + p_3 = 53$.
Let's try starting with $p_1 = 3$. Then $p_2 + p_3 = 53 - 3 = 50$.
We need to find two odd primes that sum to 50. Possible pairs are (3, 47), (7, 43), (13, 37), (19, 31).
Using the pair (3, 47): Both 3 and 47 are odd primes.
So, $53 = 3 + 3 + 47$.
Alternatively, let's try $p_1=13$. Then $p_2+p_3 = 53 - 13 = 40$. Possible pairs are (3, 37), (11, 29), (17, 23).
Using the pair (17, 23): Both 17 and 23 are odd primes.
So, $53 = 13 + 17 + 23$.
One possible representation is: $53 = 13 + 17 + 23$.
(d) 61:
We need to find three odd primes $p_1, p_2, p_3$ such that $p_1 + p_2 + p_3 = 61$.
Let's try starting with $p_1 = 3$. Then $p_2 + p_3 = 61 - 3 = 58$.
We need to find two odd primes that sum to 58. Possible pairs are (5, 53), (11, 47), (17, 41), (29, 29).
Using the pair (5, 53): Both 5 and 53 are odd primes.
So, $61 = 3 + 5 + 53$.
Alternatively, let's try $p_1=7$. Then $p_2+p_3 = 61-7 = 54$. Possible pairs are (5, 49 - not prime), (7, 47), (11, 43), (13, 41), (17, 37), (23, 31).
Using the pair (7, 47): Both 7 and 47 are odd primes.
So, $61 = 7 + 7 + 47$.
Using the pair (11, 43): Both 11 and 43 are odd primes.
So, $61 = 7 + 11 + 43$.
One possible representation is: $61 = 7 + 11 + 43$.
Question 11. Write five pairs of prime numbers less than 20 whose sum is divisible by 5.
(Hint: 3 + 7 = 10)
Answer:
To Find:
Five pairs of prime numbers, where each prime number in the pair is less than 20, and the sum of the numbers in each pair is divisible by 5.
Solution:
First, let's list all the prime numbers less than 20:
2, 3, 5, 7, 11, 13, 17, 19.
Now, we need to find pairs $(p_1, p_2)$ from this list such that $p_1 + p_2$ is a multiple of 5 (i.e., the sum ends in 0 or 5).
Let's check possible sums:
- $2 + 3 = 5$. Since 5 is divisible by 5, (2, 3) is one such pair.
- $3 + 7 = 10$. Since 10 is divisible by 5, (3, 7) is another pair (as given in the hint).
- $2 + 13 = 15$. Since 15 is divisible by 5, (2, 13) is another pair.
- $3 + 17 = 20$. Since 20 is divisible by 5, (3, 17) is another pair.
- $7 + 13 = 20$. Since 20 is divisible by 5, (7, 13) is another pair.
- $11 + 19 = 30$. Since 30 is divisible by 5, (11, 19) is another pair.
- $13 + 17 = 30$. Since 30 is divisible by 5, (13, 17) is another pair.
- $5 + 5 = 10$. Since 10 is divisible by 5, (5, 5) could be considered a pair if non-distinct primes are allowed.
We need to provide five pairs. We have found several options. Here are five pairs:
1. (2, 3) $\rightarrow$ Sum = $2+3=5$, which is divisible by 5.
2. (3, 7) $\rightarrow$ Sum = $3+7=10$, which is divisible by 5.
3. (2, 13) $\rightarrow$ Sum = $2+13=15$, which is divisible by 5.
4. (3, 17) $\rightarrow$ Sum = $3+17=20$, which is divisible by 5.
5. (7, 13) $\rightarrow$ Sum = $7+13=20$, which is divisible by 5.
Question 12. Fill in the blanks :
(a) A number which has only two factors is called a ______.
(b) A number which has more than two factors is called a ______.
(c) 1 is neither ______ nor ______.
(d) The smallest prime number is ______.
(e) The smallest composite number is _____.
(f) The smallest even number is ______.
Answer:
(a) A number which has only two factors is called a prime number.
A factor of a number divides the number exactly. A prime number has only two factors: the number 1 and the number itself. For example, the factors of 7 are 1 and 7.
(b) A number which has more than two factors is called a composite number.
A composite number has more than two factors. These are numbers that can be divided evenly by numbers other than just 1 and themselves. For example, the factors of 6 are 1, 2, 3, and 6 (which is more than two factors).
(c) 1 is neither prime nor composite.
Based on the definitions above, a prime number must have exactly two factors, and a composite number must have more than two factors. The number 1 has only one factor, which is 1 itself. Since it doesn't fit either definition, it is considered neither prime nor composite.
(d) The smallest prime number is 2.
Let's look at the first few counting numbers:
- 1 has only 1 factor (1), so it's not prime.
- 2 has factors 1 and 2 (exactly two factors), so it is prime.
- 3 has factors 1 and 3 (exactly two factors), so it is prime.
- 4 has factors 1, 2, and 4 (more than two factors), so it is composite.
The smallest number that fits the definition of a prime number is 2.
(e) The smallest composite number is 4.
Looking at the first few numbers:
- 1 is neither prime nor composite.
- 2 is prime.
- 3 is prime.
- 4 has factors 1, 2, and 4. It has more than two factors, so it is composite. It is the first number in the list (after 1) that is composite.
(f) The smallest even number is 2.
An even number is a whole number that is divisible by 2 without a remainder. Even numbers end in 0, 2, 4, 6, or 8. The positive even numbers are 2, 4, 6, 8, ... The smallest among these is 2.
Exercise 3.3
Question 1. Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10 ; by 11 (say, yes or no):
| Number | Divisibility by | ||||||||
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|
| 128 | Yes | No | Yes | No | No | Yes | No | No | No |
| 990 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 1586 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 275 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 6686 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 639210 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 429714 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 2856 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 3060 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
| 406839 | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... | ..... |
Answer:
The divisibility rules are as follows:
- Divisibility by 2: The last digit must be even (0, 2, 4, 6, 8).
- Divisibility by 3: The sum of the digits must be divisible by 3.
- Divisibility by 4: The number formed by the last two digits must be divisible by 4.
- Divisibility by 5: The last digit must be 0 or 5.
- Divisibility by 6: The number must be divisible by both 2 and 3.
- Divisibility by 8: The number formed by the last three digits must be divisible by 8.
- Divisibility by 9: The sum of the digits must be divisible by 9.
- Divisibility by 10: The last digit must be 0.
- Divisibility by 11: The difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) must be 0 or a multiple of 11.
Applying these rules to the given numbers:
| Number | Divisibility by | ||||||||
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|
| 128 | Yes | No | Yes | No | No | Yes | No | No | No |
| 990 | Yes | Yes | No | Yes | Yes | No | Yes | Yes | Yes |
| 1586 | Yes | No | No | No | No | No | No | No | No |
| 275 | No | No | No | Yes | No | No | No | No | Yes |
| 6686 | Yes | No | No | No | No | No | No | No | No |
| 639210 | Yes | Yes | No | Yes | Yes | No | No | Yes | Yes |
| 429714 | Yes | Yes | No | No | Yes | No | Yes | No | No |
| 2856 | Yes | Yes | Yes | No | Yes | Yes | No | No | No |
| 3060 | Yes | Yes | Yes | Yes | Yes | No | Yes | Yes | No |
| 406839 | No | Yes | No | No | No | No | No | No | No |
Question 2. Using divisibility tests, determine which of the following numbers are divisible by 4; by 8:
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
Answer:
Divisibility Rules:
A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
A number is divisible by 8 if the number formed by its last three digits is divisible by 8.
(a) 572:
Divisibility by 4: The number formed by the last two digits is 72. Since $72 \div 4 = 18$, 72 is divisible by 4. Therefore, 572 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 572. Since $572 \div 8 = 71$ with a remainder of 4 ($572 = 8 \times 71 + 4$), 572 is not divisible by 8. Therefore, 572 is not divisible by 8.
(b) 726352:
Divisibility by 4: The number formed by the last two digits is 52. Since $52 \div 4 = 13$, 52 is divisible by 4. Therefore, 726352 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 352. Since $352 \div 8 = 44$, 352 is divisible by 8. Therefore, 726352 is divisible by 8.
(c) 5500:
Divisibility by 4: The number formed by the last two digits is 00. Since 00 is divisible by 4 ($0 \div 4 = 0$), 5500 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 500. Since $500 \div 8 = 62$ with a remainder of 4 ($500 = 8 \times 62 + 4$), 500 is not divisible by 8. Therefore, 5500 is not divisible by 8.
(d) 6000:
Divisibility by 4: The number formed by the last two digits is 00. Since 00 is divisible by 4, 6000 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 000. Since 000 is divisible by 8 ($0 \div 8 = 0$), 6000 is divisible by 8.
(e) 12159:
Divisibility by 4: The number formed by the last two digits is 59. Since $59 \div 4 = 14$ with a remainder of 3, 59 is not divisible by 4. Therefore, 12159 is not divisible by 4.
Divisibility by 8: Since the number is not divisible by 4, it cannot be divisible by 8. (Alternatively, check the last three digits: 159. $159 \div 8 = 19$ with a remainder of 7). Therefore, 12159 is not divisible by 8.
(f) 14560:
Divisibility by 4: The number formed by the last two digits is 60. Since $60 \div 4 = 15$, 60 is divisible by 4. Therefore, 14560 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 560. Since $560 \div 8 = 70$, 560 is divisible by 8. Therefore, 14560 is divisible by 8.
(g) 21084:
Divisibility by 4: The number formed by the last two digits is 84. Since $84 \div 4 = 21$, 84 is divisible by 4. Therefore, 21084 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 084 (or 84). Since $84 \div 8 = 10$ with a remainder of 4 ($84 = 8 \times 10 + 4$), 84 is not divisible by 8. Therefore, 21084 is not divisible by 8.
(h) 31795072:
Divisibility by 4: The number formed by the last two digits is 72. Since $72 \div 4 = 18$, 72 is divisible by 4. Therefore, 31795072 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 072 (or 72). Since $72 \div 8 = 9$, 72 is divisible by 8. Therefore, 31795072 is divisible by 8.
(i) 1700:
Divisibility by 4: The number formed by the last two digits is 00. Since 00 is divisible by 4, 1700 is divisible by 4.
Divisibility by 8: The number formed by the last three digits is 700. Since $700 \div 8 = 87$ with a remainder of 4 ($700 = 8 \times 87 + 4$), 700 is not divisible by 8. Therefore, 1700 is not divisible by 8.
(j) 2150:
Divisibility by 4: The number formed by the last two digits is 50. Since $50 \div 4 = 12$ with a remainder of 2, 50 is not divisible by 4. Therefore, 2150 is not divisible by 4.
Divisibility by 8: Since the number is not divisible by 4, it cannot be divisible by 8. (Alternatively, check the last three digits: 150. $150 \div 8 = 18$ with a remainder of 6). Therefore, 2150 is not divisible by 8.
Question 3. Using divisibility tests, determine which of following numbers are divisible by 6:
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
Answer:
Divisibility Rule for 6:
A number is divisible by 6 if it is divisible by both 2 and 3.
Rule for 2: The last digit must be even (0, 2, 4, 6, 8).
Rule for 3: The sum of the digits must be divisible by 3.
(a) 297144:
Divisibility by 2: The last digit is 4 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $2+9+7+1+4+4 = 27$. Since $27 \div 3 = 9$, 27 is divisible by 3. So, the number is divisible by 3.
Since 297144 is divisible by both 2 and 3, it is divisible by 6.
(b) 1258:
Divisibility by 2: The last digit is 8 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $1+2+5+8 = 16$. Since 16 is not divisible by 3, the number is not divisible by 3.
Since 1258 is not divisible by 3, it is not divisible by 6.
(c) 4335:
Divisibility by 2: The last digit is 5 (odd). So, it is not divisible by 2.
Since 4335 is not divisible by 2, it is not divisible by 6.
(d) 61233:
Divisibility by 2: The last digit is 3 (odd). So, it is not divisible by 2.
Since 61233 is not divisible by 2, it is not divisible by 6.
(e) 901352:
Divisibility by 2: The last digit is 2 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $9+0+1+3+5+2 = 20$. Since 20 is not divisible by 3, the number is not divisible by 3.
Since 901352 is not divisible by 3, it is not divisible by 6.
(f) 438750:
Divisibility by 2: The last digit is 0 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $4+3+8+7+5+0 = 27$. Since $27 \div 3 = 9$, 27 is divisible by 3. So, the number is divisible by 3.
Since 438750 is divisible by both 2 and 3, it is divisible by 6.
(g) 1790184:
Divisibility by 2: The last digit is 4 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $1+7+9+0+1+8+4 = 30$. Since $30 \div 3 = 10$, 30 is divisible by 3. So, the number is divisible by 3.
Since 1790184 is divisible by both 2 and 3, it is divisible by 6.
(h) 12583:
Divisibility by 2: The last digit is 3 (odd). So, it is not divisible by 2.
Since 12583 is not divisible by 2, it is not divisible by 6.
(i) 639210:
Divisibility by 2: The last digit is 0 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $6+3+9+2+1+0 = 21$. Since $21 \div 3 = 7$, 21 is divisible by 3. So, the number is divisible by 3.
Since 639210 is divisible by both 2 and 3, it is divisible by 6.
(j) 17852:
Divisibility by 2: The last digit is 2 (even). So, it is divisible by 2.
Divisibility by 3: Sum of digits = $1+7+8+5+2 = 23$. Since 23 is not divisible by 3, the number is not divisible by 3.
Since 17852 is not divisible by 3, it is not divisible by 6.
Question 4. Using divisibility tests, determine which of the following numbers are divisible by 11:
(a) 5445
(b) 10824
(c) 7138965
(d) 70169308
(e) 10000001
(f) 901153
Answer:
Divisibility Rule for 11:
A number is divisible by 11 if the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) is either 0 or a multiple of 11.
(a) 5445:
Digits from right: 5, 4, 4, 5
Sum of digits at odd places (1st, 3rd): $5 + 4 = 9$.
Sum of digits at even places (2nd, 4th): $4 + 5 = 9$.
Difference = $|9 - 9| = 0$.
Since the difference is 0, 5445 is divisible by 11.
(b) 10824:
Digits from right: 4, 2, 8, 0, 1
Sum of digits at odd places (1st, 3rd, 5th): $4 + 8 + 1 = 13$.
Sum of digits at even places (2nd, 4th): $2 + 0 = 2$.
Difference = $|13 - 2| = 11$.
Since the difference is 11 (a multiple of 11), 10824 is divisible by 11.
(c) 7138965:
Digits from right: 5, 6, 9, 8, 3, 1, 7
Sum of digits at odd places (1st, 3rd, 5th, 7th): $5 + 9 + 3 + 7 = 24$.
Sum of digits at even places (2nd, 4th, 6th): $6 + 8 + 1 = 15$.
Difference = $|24 - 15| = 9$.
Since the difference is 9 (which is not 0 or a multiple of 11), 7138965 is not divisible by 11.
(d) 70169308:
Digits from right: 8, 0, 3, 9, 6, 1, 0, 7
Sum of digits at odd places (1st, 3rd, 5th, 7th): $8 + 3 + 6 + 0 = 17$.
Sum of digits at even places (2nd, 4th, 6th, 8th): $0 + 9 + 1 + 7 = 17$.
Difference = $|17 - 17| = 0$.
Since the difference is 0, 70169308 is divisible by 11.
(e) 10000001:
Digits from right: 1, 0, 0, 0, 0, 0, 0, 1
Sum of digits at odd places (1st, 3rd, 5th, 7th): $1 + 0 + 0 + 0 = 1$.
Sum of digits at even places (2nd, 4th, 6th, 8th): $0 + 0 + 0 + 1 = 1$.
Difference = $|1 - 1| = 0$.
Since the difference is 0, 10000001 is divisible by 11.
(f) 901153:
Digits from right: 3, 5, 1, 1, 0, 9
Sum of digits at odd places (1st, 3rd, 5th): $3 + 1 + 0 = 4$.
Sum of digits at even places (2nd, 4th, 6th): $5 + 1 + 9 = 15$.
Difference = $|4 - 15| = |-11| = 11$.
Since the difference is 11 (a multiple of 11), 901153 is divisible by 11.
Question 5. Write the smallest digit and the greatest digit in the blank space of each of the following numbers so that the number formed is divisible by 3 :
(a) __ 6724
(b) 4765 __ 2
Answer:
Divisibility Rule for 3:
A number is divisible by 3 if the sum of its digits is divisible by 3.
(a) __ 6724:
Let the digit in the blank space be $x$.
The number is $x6724$.
Sum of the known digits = $6 + 7 + 2 + 4 = 19$.
The total sum of the digits = $x + 19$.
For the number to be divisible by 3, the sum $x + 19$ must be a multiple of 3.
Since $x$ is a single digit, $0 \le x \le 9$.
Therefore, $0 + 19 \le x + 19 \le 9 + 19$, which means $19 \le x + 19 \le 28$.
The multiples of 3 between 19 and 28 are 21, 24, and 27.
Case 1: $x + 19 = 21 \implies x = 21 - 19 = 2$.
Case 2: $x + 19 = 24 \implies x = 24 - 19 = 5$.
Case 3: $x + 19 = 27 \implies x = 27 - 19 = 8$.
The possible digits are 2, 5, and 8.
The smallest digit is 2.
The greatest digit is 8.
(b) 4765 __ 2:
Let the digit in the blank space be $y$.
The number is $4765y2$.
Sum of the known digits = $4 + 7 + 6 + 5 + 2 = 24$.
The total sum of the digits = $24 + y$.
For the number to be divisible by 3, the sum $24 + y$ must be a multiple of 3.
Since 24 is already divisible by 3 ($24 = 3 \times 8$), for $24 + y$ to be divisible by 3, $y$ must also be divisible by 3.
Since $y$ is a single digit ($0 \le y \le 9$), the possible values for $y$ that are divisible by 3 are 0, 3, 6, and 9.
The possible digits are 0, 3, 6, and 9.
The smallest digit is 0.
The greatest digit is 9.
Question 6. Write a digit inthe blank space of each ofthefollowingnumbers so that the number formed is divisible by 11 :
(a) 92 __ 389
(b) 8 __ 9484
Answer:
Divisibility Rule for 11:
A number is divisible by 11 if the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) is either 0 or a multiple of 11.
(a) 92 __ 389:
Let the digit in the blank space be $x$. The number is $92x389$.
Digits from the right: 9, 8, 3, x, 2, 9
Sum of digits at odd places (1st, 3rd, 5th) = $9 + 3 + 2 = 14$.
Sum of digits at even places (2nd, 4th, 6th) = $8 + x + 9 = 17 + x$.
Difference = | (Sum of odd places) - (Sum of even places) |
Difference = $ |14 - (17 + x)| = |-3 - x| $. Since $x \ge 0$, this is $|-(3+x)| = 3+x$.
Alternatively, Difference = | (Sum of even places) - (Sum of odd places) |
Difference = $ |(17 + x) - 14| = |3 + x| $.
For the number to be divisible by 11, the difference $|3 + x|$ must be 0 or a multiple of 11.
Since $x$ is a digit, $0 \le x \le 9$. Therefore, $3 \le 3 + x \le 12$.
The only multiple of 11 in the range [3, 12] is 11.
So, we set the difference equal to 11:
$3 + x = 11$
$x = 11 - 3 = 8$.
The required digit is 8. (The number becomes 928389).
(b) 8 __ 9484:
Let the digit in the blank space be $y$. The number is $8y9484$.
Digits from the right: 4, 8, 4, 9, y, 8
Sum of digits at odd places (1st, 3rd, 5th) = $4 + 4 + y = 8 + y$.
Sum of digits at even places (2nd, 4th, 6th) = $8 + 9 + 8 = 25$.
Difference = | (Sum of odd places) - (Sum of even places) |
Difference = $ |(8 + y) - 25| = |y - 17| $.
Alternatively, Difference = | (Sum of even places) - (Sum of odd places) |
Difference = $ |25 - (8 + y)| = |17 - y| $.
For the number to be divisible by 11, the difference $|17 - y|$ must be 0 or a multiple of 11.
Since $y$ is a digit, $0 \le y \le 9$. Therefore, $17-9 \le 17 - y \le 17-0$, which means $8 \le 17 - y \le 17$.
The only multiple of 11 in the range [8, 17] is 11.
So, we set the difference equal to 11:
$17 - y = 11$
$y = 17 - 11 = 6$.
The required digit is 6. (The number becomes 869484).
Example 5 & 6 (Before Exercise 3.4)
Example 5: Find the common factors of 75, 60 and 210.
Answer:
To Find:
The common factors of the numbers 75, 60, and 210.
Solution:
First, we list the factors of each number.
Factors of 75:
We look for pairs of numbers that multiply to 75:
$1 \times 75 = 75$
$3 \times 25 = 75$
$5 \times 15 = 75$
The factors of 75 are: 1, 3, 5, 15, 25, 75.
Factors of 60:
We look for pairs of numbers that multiply to 60:
$1 \times 60 = 60$
$2 \times 30 = 60$
$3 \times 20 = 60$
$4 \times 15 = 60$
$5 \times 12 = 60$
$6 \times 10 = 60$
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Factors of 210:
We look for pairs of numbers that multiply to 210:
$1 \times 210 = 210$
$2 \times 105 = 210$
$3 \times 70 = 210$
$5 \times 42 = 210$
$6 \times 35 = 210$
$7 \times 30 = 210$
$10 \times 21 = 210$
$14 \times 15 = 210$
The factors of 210 are: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210.
Common Factors:
Now, we identify the numbers that appear in all three lists of factors:
Factors of 75: 1, 3, 5, 15, 25, 75
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Factors of 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
The factors common to 75, 60, and 210 are 1, 3, 5, 15.
Alternate Solution (Using Prime Factorization):
First, find the prime factorization of each number.
Prime factorization of 75:
$\begin{array}{c|cc} 3 & 75 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$75 = 3 \times 5 \times 5 = 3^1 \times 5^2$
Prime factorization of 60:
$\begin{array}{c|cc} 2 & 60 \\ \hline 2 & 30 \\ \hline 3 & 15 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$60 = 2 \times 2 \times 3 \times 5 = 2^2 \times 3^1 \times 5^1$
Prime factorization of 210:
$\begin{array}{c|cc} 2 & 210 \\ \hline 3 & 105 \\ \hline 5 & 35 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
$210 = 2^1 \times 3^1 \times 5^1 \times 7^1$
To find the common factors, we identify the common prime factors and take their lowest powers present in the factorizations.
Common prime factors are 3 and 5.
The lowest power of 3 is $3^1$.
The lowest power of 5 is $5^1$.
The common factors are the factors of the product of these lowest powers, which is $3^1 \times 5^1 = 15$.
The factors of 15 are 1, 3, 5, 15.
Thus, the common factors of 75, 60, and 210 are 1, 3, 5, 15.
Example 6: Find the common multiples of 3, 4 and 9.
Answer:
To Find:
The common multiples of the numbers 3, 4, and 9.
Solution (Listing Multiples):
First, we list the multiples of each number.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, ...
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, ...
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, ...
Now, we identify the numbers that appear in all three lists.
The common multiples are 36, 72, 108, ...
The common multiples of 3, 4, and 9 are 36, 72, 108, ... (which are the multiples of 36).
Alternate Solution (Using LCM):
The common multiples of a set of numbers are the multiples of their Least Common Multiple (LCM).
First, find the LCM of 3, 4, and 9.
We can use the division method:
$\begin{array}{c|cc} 2 & 3 \; , & 4 \; , & 9 \\ \hline 2 & 3 \; , & 2 \; , & 9 \\ \hline 3 & 3 \; , & 1 \; , & 9 \\ \hline 3 & 1 \; , & 1 \; , & 3 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors: $2 \times 2 \times 3 \times 3 = 36$.
Alternatively, using prime factorization:
$3 = 3^1$
$4 = 2^2$
$9 = 3^2$
LCM = (Highest power of 2) $\times$ (Highest power of 3) $= 2^2 \times 3^2 = 4 \times 9 = 36$.
The common multiples of 3, 4, and 9 are the multiples of their LCM, which is 36.
The common multiples are $36 \times 1 = 36$, $36 \times 2 = 72$, $36 \times 3 = 108$, and so on.
Therefore, the common multiples are 36, 72, 108, ...
Exercise 3.4
Question 1. Find the common factors of :
(a) 20 and 28
(b) 15 and 25
(c) 35 and 50
(d) 56 and 120
Answer:
(a) Common factors of 20 and 28:
Factors of 20:
$1 \times 20 = 20$
$2 \times 10 = 20$
$4 \times 5 = 20$
The factors of 20 are 1, 2, 4, 5, 10, 20.
Factors of 28:
$1 \times 28 = 28$
$2 \times 14 = 28$
$4 \times 7 = 28$
The factors of 28 are 1, 2, 4, 7, 14, 28.
Comparing the lists of factors:
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 28: 1, 2, 4, 7, 14, 28
The common factors of 20 and 28 are 1, 2, 4.
(b) Common factors of 15 and 25:
Factors of 15:
$1 \times 15 = 15$
$3 \times 5 = 15$
The factors of 15 are 1, 3, 5, 15.
Factors of 25:
$1 \times 25 = 25$
$5 \times 5 = 25$
The factors of 25 are 1, 5, 25.
Comparing the lists of factors:
Factors of 15: 1, 3, 5, 15
Factors of 25: 1, 5, 25
The common factors of 15 and 25 are 1, 5.
(c) Common factors of 35 and 50:
Factors of 35:
$1 \times 35 = 35$
$5 \times 7 = 35$
The factors of 35 are 1, 5, 7, 35.
Factors of 50:
$1 \times 50 = 50$
$2 \times 25 = 50$
$5 \times 10 = 50$
The factors of 50 are 1, 2, 5, 10, 25, 50.
Comparing the lists of factors:
Factors of 35: 1, 5, 7, 35
Factors of 50: 1, 2, 5, 10, 25, 50
The common factors of 35 and 50 are 1, 5.
(d) Common factors of 56 and 120:
Factors of 56:
$1 \times 56 = 56$
$2 \times 28 = 56$
$4 \times 14 = 56$
$7 \times 8 = 56$
The factors of 56 are 1, 2, 4, 7, 8, 14, 28, 56.
Factors of 120:
$1 \times 120 = 120$
$2 \times 60 = 120$
$3 \times 40 = 120$
$4 \times 30 = 120$
$5 \times 24 = 120$
$6 \times 20 = 120$
$8 \times 15 = 120$
$10 \times 12 = 120$
The factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
Comparing the lists of factors:
Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
Factors of 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
The common factors of 56 and 120 are 1, 2, 4, 8.
Question 2. Find the common factors of :
(a) 4, 8 and 12
(b) 5, 15 and 25
Answer:
(a) Common factors of 4, 8 and 12:
Factors of 4:
$1 \times 4 = 4$
$2 \times 2 = 4$
The factors of 4 are 1, 2, 4.
Factors of 8:
$1 \times 8 = 8$
$2 \times 4 = 8$
The factors of 8 are 1, 2, 4, 8.
Factors of 12:
$1 \times 12 = 12$
$2 \times 6 = 12$
$3 \times 4 = 12$
The factors of 12 are 1, 2, 3, 4, 6, 12.
Comparing the lists of factors:
Factors of 4: 1, 2, 4
Factors of 8: 1, 2, 4, 8
Factors of 12: 1, 2, 3, 4, 6, 12
The common factors of 4, 8 and 12 are 1, 2, 4.
(b) Common factors of 5, 15 and 25:
Factors of 5:
$1 \times 5 = 5$
The factors of 5 are 1, 5. (5 is a prime number)
Factors of 15:
$1 \times 15 = 15$
$3 \times 5 = 15$
The factors of 15 are 1, 3, 5, 15.
Factors of 25:
$1 \times 25 = 25$
$5 \times 5 = 25$
The factors of 25 are 1, 5, 25.
Comparing the lists of factors:
Factors of 5: 1, 5
Factors of 15: 1, 3, 5, 15
Factors of 25: 1, 5, 25
The common factors of 5, 15 and 25 are 1, 5.
Question 3. Find first three common multiples of :
(a) 6 and 8
(b) 12 and 18
Answer:
(a) First three common multiples of 6 and 8:
Method 1: Listing Multiples
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
The first three common multiples appearing in both lists are 24, 48, and 72.
Method 2: Using LCM
First, find the Least Common Multiple (LCM) of 6 and 8.
$\begin{array}{c|cc} 2 & 6 \; , & 8 \\ \hline 2 & 3 \; , & 4 \\ \hline 2 & 3 \; , & 2 \\ \hline 3 & 3 \; , & 1 \\ \hline & 1 \; , & 1 \end{array}$
LCM$(6, 8) = 2 \times 2 \times 2 \times 3 = 24$.
The common multiples are the multiples of the LCM (24).
First common multiple = $1 \times 24 = 24$.
Second common multiple = $2 \times 24 = 48$.
Third common multiple = $3 \times 24 = 72$.
The first three common multiples of 6 and 8 are 24, 48, 72.
(b) First three common multiples of 12 and 18:
Method 1: Listing Multiples
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, ...
Multiples of 18: 18, 36, 54, 72, 90, 108, ...
The first three common multiples appearing in both lists are 36, 72, and 108.
Method 2: Using LCM
First, find the Least Common Multiple (LCM) of 12 and 18.
$\begin{array}{c|cc} 2 & 12 \; , & 18 \\ \hline 2 & 6 \; , & 9 \\ \hline 3 & 3 \; , & 9 \\ \hline 3 & 1 \; , & 3 \\ \hline & 1 \; , & 1 \end{array}$
LCM$(12, 18) = 2 \times 2 \times 3 \times 3 = 36$.
The common multiples are the multiples of the LCM (36).
First common multiple = $1 \times 36 = 36$.
Second common multiple = $2 \times 36 = 72$.
Third common multiple = $3 \times 36 = 108$.
The first three common multiples of 12 and 18 are 36, 72, 108.
Question 4. Write all the numbers less than 100 which are common multiples of 3 and 4.
Answer:
To Find:
All common multiples of 3 and 4 that are less than 100.
Solution:
A common multiple of 3 and 4 is a number that is divisible by both 3 and 4.
The common multiples of two numbers are the multiples of their Least Common Multiple (LCM).
First, we find the LCM of 3 and 4.
Multiples of 3: 3, 6, 9, 12, 15, ...
Multiples of 4: 4, 8, 12, 16, ...
The smallest common multiple (LCM) is 12.
Alternatively, using prime factorization:
$3 = 3^1$
$4 = 2^2$
$LCM(3, 4) = 2^2 \times 3^1 = 4 \times 3 = 12$.
Now, we need to find the multiples of the LCM (12) that are less than 100.
$12 \times 1 = 12$
$12 \times 2 = 24$
$12 \times 3 = 36$
$12 \times 4 = 48$
$12 \times 5 = 60$
$12 \times 6 = 72$
$12 \times 7 = 84$
$12 \times 8 = 96$
$12 \times 9 = 108$ (This is greater than 100, so we stop).
The common multiples of 3 and 4 which are less than 100 are:
12, 24, 36, 48, 60, 72, 84, 96.
Question 5. Which of the following numbers are co-prime?
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
(d) 17 and 68
(e) 216 and 215
(f) 81 and 16
Answer:
Two numbers are co-prime if their only common factor is 1 (i.e., their Highest Common Factor (HCF) or Greatest Common Divisor (GCD) is 1).
(a) 18 and 35:
Factors of 18: 1, 2, 3, 6, 9, 18.
Factors of 35: 1, 5, 7, 35.
The only common factor is 1.
Therefore, 18 and 35 are co-prime.
(b) 15 and 37:
Factors of 15: 1, 3, 5, 15.
Factors of 37: 1, 37 (since 37 is a prime number).
The only common factor is 1.
Therefore, 15 and 37 are co-prime.
(c) 30 and 415:
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
Factors of 415: We can see that 415 ends in 5, so it is divisible by 5. $415 = 5 \times 83$.
The factors of 415 are 1, 5, 83, 415.
The common factors are 1 and 5.
Since the common factors include 5 (in addition to 1), their HCF is 5 (not 1).
Therefore, 30 and 415 are not co-prime.
(d) 17 and 68:
Factors of 17: 1, 17 (since 17 is a prime number).
Factors of 68: 1, 2, 4, 17, 34, 68 ($68 = 4 \times 17$).
The common factors are 1 and 17.
Since the common factors include 17 (in addition to 1), their HCF is 17 (not 1).
Therefore, 17 and 68 are not co-prime.
(e) 216 and 215:
Consecutive natural numbers are always co-prime.
If $d$ is a common factor of $n$ and $n+1$, then $d$ must divide their difference, $(n+1) - n = 1$. The only positive integer that divides 1 is 1.
So, the only common factor of 215 and 216 is 1.
Therefore, 216 and 215 are co-prime.
(f) 81 and 16:
Factors of 81: 1, 3, 9, 27, 81 ($81 = 3^4$).
Factors of 16: 1, 2, 4, 8, 16 ($16 = 2^4$).
The only common factor is 1.
Therefore, 81 and 16 are co-prime.
Question 6. A number is divisible by both 5 and 12. By which other number will that number be always divisible?
Answer:
Given:
A number is divisible by both 5 and 12.
To Find:
Another number by which the given number will always be divisible.
Solution:
If a number is divisible by two different numbers, it must also be divisible by their Least Common Multiple (LCM).
In this case, the number is divisible by both 5 and 12.
We need to find the LCM of 5 and 12.
First, find the prime factorization of each number:
$5 = 5^1$ (5 is a prime number)
$12 = 2 \times 6 = 2 \times 2 \times 3 = 2^2 \times 3^1$
The LCM is found by taking the highest power of all prime factors that appear in either factorization.
LCM$(5, 12) = 2^2 \times 3^1 \times 5^1 = 4 \times 3 \times 5 = 60$.
Since the number is divisible by both 5 and 12, it must be a multiple of their LCM, which is 60.
If a number is a multiple of 60, it means the number is always divisible by 60.
Therefore, the number will always be divisible by 60.
Question 7. A number is divisible by 12. By what other numbers will that number be divisible?
Answer:
Given:
A number is divisible by 12.
To Find:
Other numbers by which the given number will also be divisible.
Solution:
If a number is divisible by another number, it is also divisible by all the factors of that number.
In this case, the given number is divisible by 12.
So, we need to find the factors of 12.
The factors of 12 are the numbers that divide 12 exactly:
$1 \times 12 = 12$
$2 \times 6 = 12$
$3 \times 4 = 12$
The factors of 12 are 1, 2, 3, 4, 6, and 12.
Since the number is divisible by 12, it must also be divisible by all the factors of 12.
Therefore, the other numbers by which the number will be divisible are the factors of 12 (excluding 12 itself, based on the phrasing "other numbers").
The other numbers are 1, 2, 3, 4, 6.
Example 7 (Before Exercise 3.5)
Example 7: Find the prime factorisation of 980.
Answer:
To Find:
The prime factorisation of the number 980.
Solution:
Prime factorisation is the process of finding which prime numbers multiply together to make the original number.
We can use the method of repeated division by prime numbers, starting with the smallest prime number, 2.
$\begin{array}{c|cc} 2 & 980 \\ \hline 2 & 490 \\ \hline 5 & 245 \\ \hline 7 & 49 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
Explanation of steps:
1. $980 \div 2 = 490$
2. $490 \div 2 = 245$
3. $245$ is not divisible by 2 or 3. It is divisible by 5: $245 \div 5 = 49$.
4. $49$ is not divisible by 5. It is divisible by 7: $49 \div 7 = 7$.
5. $7$ is a prime number, divisible by 7: $7 \div 7 = 1$.
The prime factors obtained are 2, 2, 5, 7, 7.
Therefore, the prime factorisation of 980 is:
$980 = 2 \times 2 \times 5 \times 7 \times 7$
This can also be written in exponential form as:
$980 = 2^2 \times 5 \times 7^2$
Exercise 3.5
Question 1. Which of the following statements are true?
(a) If a number is divisible by 3, it must be divisible by 9.
(b) If a number is divisible by 9, it must be divisible by 3.
(c) A number is divisible by 18, if it is divisible by both 3 and 6.
(d) If a number is divisible by 9 and 10 both, then it must be divisible by 90.
(e) If two numbers are co-primes, at least one of them must be prime.
(f) All numbers which are divisible by 4 must also be divisible by 8.
(g) All numbers which are divisible by 8 must also be divisible by 4.
(h) If a number exactly divides two numbers separately, it must exactly divide their sum.
(i) If a number exactly divides the sum of two numbers, it must exactly divide the two numbers separately.
Answer:
(a) If a number is divisible by 3, it must be divisible by 9.
Consider the number 6. It is divisible by 3 ($6 = 3 \times 2$), but it is not divisible by 9.
Therefore, the statement is False.
(b) If a number is divisible by 9, it must be divisible by 3.
If a number is divisible by 9, it means the number can be written as $9k$ for some integer $k$.
Since $9 = 3 \times 3$, we have $9k = (3 \times 3)k = 3 \times (3k)$.
As $3k$ is an integer, $9k$ is a multiple of 3. Thus, any number divisible by 9 is also divisible by 3.
Therefore, the statement is True.
(c) A number is divisible by 18, if it is divisible by both 3 and 6.
A number is divisible by 18 if it is divisible by its co-prime factors, 2 and 9.
If a number is divisible by 6, it is divisible by 2 and 3.
So, if a number is divisible by 3 and 6, it means it's divisible by 3 and (by 2 and 3). This only guarantees divisibility by 2 and 3, which means divisibility by 6.
It does not guarantee divisibility by 9. For example, 12 is divisible by both 3 and 6, but 12 is not divisible by 18.
Therefore, the statement is False.
(d) If a number is divisible by 9 and 10 both, then it must be divisible by 90.
The numbers 9 and 10 are co-prime (their only common factor is 1).
If a number is divisible by two co-prime numbers, it is also divisible by their product.
The product of 9 and 10 is $9 \times 10 = 90$.
Therefore, the statement is True.
(e) If two numbers are co-primes, at least one of them must be prime.
Co-prime numbers are numbers whose only common factor is 1.
Consider the numbers 8 and 9. Factors of 8 are 1, 2, 4, 8 (composite). Factors of 9 are 1, 3, 9 (composite).
The only common factor of 8 and 9 is 1, so they are co-prime. However, neither 8 nor 9 is a prime number.
Therefore, the statement is False.
(f) All numbers which are divisible by 4 must also be divisible by 8.
Consider the number 12. It is divisible by 4 ($12 = 4 \times 3$), but it is not divisible by 8.
Therefore, the statement is False.
(g) All numbers which are divisible by 8 must also be divisible by 4.
If a number is divisible by 8, it can be written as $8k$ for some integer $k$.
Since $8 = 4 \times 2$, we have $8k = (4 \times 2)k = 4 \times (2k)$.
As $2k$ is an integer, $8k$ is a multiple of 4. Thus, any number divisible by 8 is also divisible by 4.
Therefore, the statement is True.
(h) If a number exactly divides two numbers separately, it must exactly divide their sum.
Let the number be $d$, and the two numbers be $a$ and $b$.
If $d$ divides $a$, then $a = d \times k_1$ for some integer $k_1$.
If $d$ divides $b$, then $b = d \times k_2$ for some integer $k_2$.
The sum is $a + b = dk_1 + dk_2 = d(k_1 + k_2)$.
Since $k_1 + k_2$ is an integer, $d$ divides the sum $a+b$.
Therefore, the statement is True.
(i) If a number exactly divides the sum of two numbers, it must exactly divide the two numbers separately.
Let the number be $d$, and the two numbers be $a$ and $b$.
Consider $d=5$, $a=7$, $b=3$.
The sum is $a+b = 7+3 = 10$.
The number 5 divides the sum 10 ($10 = 5 \times 2$).
However, 5 does not divide $a=7$, and 5 does not divide $b=3$.
Therefore, the statement is False.
Question 2. Here are two different factor trees for 60. Write the missing numbers.
(a)
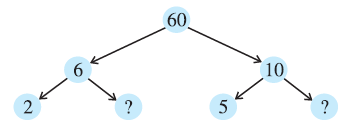
(b)
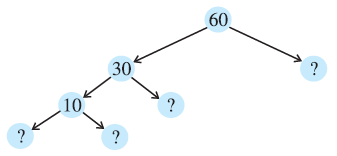
Answer:
(a) Factor Tree Completion:
In this factor tree, 60 is first broken down into 6 and 10.
We need to find the numbers that multiply to give the number directly above them.
For the branch from 6:
$6 = 2 \times ?$
To find the missing number, we divide 6 by 2: $6 \div 2 = 3$. So, the first missing number is 3.
For the branch from 10:
$10 = 5 \times ?$
To find the missing number, we divide 10 by 5: $10 \div 5 = 2$. So, the second missing number is 2.
Here is the completed factor tree:
(b) Factor Tree Completion:
In this factor tree, 60 is first broken down into 30 and a missing number.
We follow the same process, finding the missing factors step-by-step from the top.
For the first branch from 60:
$60 = 30 \times ?$
The missing number is $60 \div 30 = 2$. So, the first missing number is 2.
For the branch from 30:
$30 = 10 \times ?$
The missing number is $30 \div 10 = 3$. So, the second missing number is 3.
For the branch from 10:
$10 = ? \times ?$
We need to find two numbers that multiply to 10. The prime factors of 10 are 2 and 5. So, the last two missing numbers are 2 and 5.
Here is the completed factor tree:
Question 3. Which factors are not included in the prime factorisation of a composite number?
Answer:
The prime factorisation of a composite number expresses that number as a product of only its prime factors.
A composite number, by definition, has factors other than just prime numbers.
The factors that are not included in the prime factorisation of a composite number are:
1. The number 1: Although 1 is a factor of every number, it is not a prime number, and therefore it is not included in the prime factorisation.
2. The composite number itself: The prime factorization breaks the number down into its prime building blocks.
3. Any other composite factors of the number: Only the prime factors are listed. For example, the prime factorisation of 12 is $2 \times 2 \times 3$. The composite factors of 12, which are 4, 6, and 12, are not included in the prime factorisation.
In summary, the factors 1 and all composite factors (including the number itself) are not included in the prime factorisation of a composite number.
Question 4. Write the greatest 4-digit number and express it in terms of its prime factors.
Answer:
Finding the Greatest 4-Digit Number:
The digits used in our number system are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The greatest digit is 9.
To form the greatest 4-digit number, we should use the greatest digit (9) in all four places (thousands, hundreds, tens, and units).
Therefore, the greatest 4-digit number is 9999.
Prime Factorisation of 9999:
Now, we need to express 9999 as a product of its prime factors. We use the method of division by prime numbers.
$\begin{array}{c|cc} 3 & 9999 \\ \hline 3 & 3333 \\ \hline 11 & 1111 \\ \hline 101 & 101 \\ \hline & 1 \end{array}$
Explanation of steps:
1. Check divisibility by 2: 9999 is odd, so not divisible by 2.
2. Check divisibility by 3: Sum of digits = $9+9+9+9=36$. Since 36 is divisible by 3, 9999 is divisible by 3. $9999 \div 3 = 3333$.
3. Check divisibility by 3 again for 3333: Sum of digits = $3+3+3+3=12$. Since 12 is divisible by 3, 3333 is divisible by 3. $3333 \div 3 = 1111$.
4. Check divisibility of 1111 by primes: Not by 3, 5, 7. Check 11: Difference of alternating sums = $(1+1) - (1+1) = 0$. So, it is divisible by 11. $1111 \div 11 = 101$.
5. Check if 101 is prime: We check primes up to $\sqrt{101} \approx 10$. Primes are 2, 3, 5, 7. 101 is not divisible by 2, 3, 5, or 7. So, 101 is a prime number. $101 \div 101 = 1$.
The prime factors are 3, 3, 11, 101.
Therefore, the prime factorisation of 9999 is:
$9999 = 3 \times 3 \times 11 \times 101$
Or in exponential form:
$9999 = 3^2 \times 11 \times 101$
Question 5. Write the smallest 5-digit number and express it in the form of its prime factors.
Answer:
Finding the Smallest 5-Digit Number:
A 5-digit number must have a non-zero digit in the ten thousands place. To make the number as small as possible, this digit should be the smallest non-zero digit, which is 1.
To keep the number smallest, the remaining four digits (thousands, hundreds, tens, units) should be the smallest possible digit, which is 0.
Therefore, the smallest 5-digit number is 10000.
Prime Factorisation of 10000:
Now, we need to express 10000 as a product of its prime factors. We use the method of division by prime numbers.
$\begin{array}{c|cc} 2 & 10000 \\ \hline 2 & 5000 \\ \hline 2 & 2500 \\ \hline 2 & 1250 \\ \hline 5 & 625 \\ \hline 5 & 125 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
Explanation of steps:
1. $10000 \div 2 = 5000$
2. $5000 \div 2 = 2500$
3. $2500 \div 2 = 1250$
4. $1250 \div 2 = 625$
5. $625$ is not divisible by 2 or 3. It ends in 5, so it is divisible by 5: $625 \div 5 = 125$.
6. $125 \div 5 = 25$.
7. $25 \div 5 = 5$.
8. $5$ is prime: $5 \div 5 = 1$.
The prime factors are 2, 2, 2, 2, 5, 5, 5, 5.
Therefore, the prime factorisation of 10000 is:
$10000 = 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 5 \times 5$
Or in exponential form:
$10000 = 2^4 \times 5^4$
Question 6. Find all the prime factors of 1729 and arrange them in ascending order. Now state the relation, if any; between two consecutive prime factors.
Answer:
Finding Prime Factors of 1729:
We will find the prime factors of 1729 by dividing it by prime numbers.
1. Is 1729 divisible by 2? No (it's odd).
2. Is 1729 divisible by 3? Sum of digits $1+7+2+9 = 19$. 19 is not divisible by 3, so 1729 is not divisible by 3.
3. Is 1729 divisible by 5? No (it doesn't end in 0 or 5).
4. Is 1729 divisible by 7? $1729 \div 7 = 247$. Yes.
5. Now we need to factorize 247. Is it divisible by 7? $247 \div 7$ leaves a remainder. No.
6. Is 247 divisible by 11? Alternating sum difference: $(7+2)-4 = 9-4 = 5$. Not divisible by 11.
7. Is 247 divisible by 13? $247 \div 13 = 19$. Yes.
8. 19 is a prime number.
Using the division method visually:
$\begin{array}{c|cc} 7 & 1729 \\ \hline 13 & 247 \\ \hline 19 & 19 \\ \hline & 1 \end{array}$
The prime factors of 1729 are 7, 13, and 19.
Arranging Prime Factors in Ascending Order:
The prime factors, arranged in ascending order, are: 7, 13, 19.
Relation Between Consecutive Prime Factors:
Let's find the difference between consecutive prime factors:
Difference between the second and first prime factor: $13 - 7 = 6$.
Difference between the third and second prime factor: $19 - 13 = 6$.
The relation between two consecutive prime factors is that their difference is 6.
Question 7. The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Answer:
The statement to verify is: The product of any three consecutive numbers is always divisible by 6.
For a number to be divisible by 6, it must be divisible by both 2 and 3.
In any set of three consecutive numbers:
- At least one number must be even (a multiple of 2).
- Exactly one number must be a multiple of 3.
Since the product will contain at least one multiple of 2 and exactly one multiple of 3, the product must be divisible by $2 \times 3 = 6$.
Let's verify this with some examples:
Example 1:
Consider the three consecutive numbers: 2, 3, 4.
Their product is $2 \times 3 \times 4 = 24$.
To check if 24 is divisible by 6: $24 \div 6 = 4$.
So, 24 is divisible by 6. The statement holds true for this example.
Example 2:
Consider the three consecutive numbers: 5, 6, 7.
Their product is $5 \times 6 \times 7 = 210$.
To check if 210 is divisible by 6: $210 \div 6 = 35$.
So, 210 is divisible by 6. The statement holds true for this example.
Example 3:
Consider the three consecutive numbers: 9, 10, 11.
Their product is $9 \times 10 \times 11 = 990$.
To check if 990 is divisible by 6: $990 \div 6 = 165$.
So, 990 is divisible by 6. The statement holds true for this example.
Example 4:
Consider the three consecutive numbers: 14, 15, 16.
Their product is $14 \times 15 \times 16 = 3360$.
To check if 3360 is divisible by 6: $3360 \div 6 = 560$.
So, 3360 is divisible by 6. The statement holds true for this example.
These examples verify the statement that the product of three consecutive numbers is always divisible by 6.
Question 8. The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.
Answer:
The statement to verify is: The sum of any two consecutive odd numbers is always divisible by 4.
Consecutive odd numbers are odd numbers that follow each other, with a difference of 2 between them (e.g., 1 and 3, 7 and 9, 15 and 17).
Let's verify this statement with some examples:
Example 1:
Consider the two consecutive odd numbers: 1 and 3.
Their sum is $1 + 3 = 4$.
To check if 4 is divisible by 4: $4 \div 4 = 1$.
So, 4 is divisible by 4. The statement holds true for this example.
Example 2:
Consider the two consecutive odd numbers: 7 and 9.
Their sum is $7 + 9 = 16$.
To check if 16 is divisible by 4: $16 \div 4 = 4$.
So, 16 is divisible by 4. The statement holds true for this example.
Example 3:
Consider the two consecutive odd numbers: 15 and 17.
Their sum is $15 + 17 = 32$.
To check if 32 is divisible by 4: $32 \div 4 = 8$.
So, 32 is divisible by 4. The statement holds true for this example.
Example 4:
Consider the two consecutive odd numbers: 29 and 31.
Their sum is $29 + 31 = 60$.
To check if 60 is divisible by 4: $60 \div 4 = 15$.
So, 60 is divisible by 4. The statement holds true for this example.
Algebraic Verification (Optional):
Let the first odd number be represented as $2n+1$, where $n$ is any integer.
The next consecutive odd number will be $(2n+1) + 2 = 2n+3$.
Their sum is $(2n+1) + (2n+3) = 4n + 4$.
Factoring out 4, we get $4(n+1)$.
Since $n$ is an integer, $n+1$ is also an integer. Thus, the sum $4(n+1)$ is always a multiple of 4, meaning it is always divisible by 4.
The examples verify the statement.
Question 9. In which of the following expressions, prime factorisation has been done?
(a) 24 = 2 × 3 × 4
(b) 56 = 7 × 2 × 2 × 2
(c) 70 = 2 × 5 × 7
(d) 54 = 2 × 3 × 9
Answer:
Prime factorisation is the process of expressing a number as a product of its prime factors only. A prime factor is a factor that is also a prime number.
(a) 24 = 2 × 3 × 4:
The factors listed are 2, 3, and 4.
2 is a prime number.
3 is a prime number.
4 is a composite number ($4 = 2 \times 2$).
Since the expression includes a composite factor (4), this is not a prime factorisation.
(b) 56 = 7 × 2 × 2 × 2:
The factors listed are 7, 2, 2, and 2.
7 is a prime number.
2 is a prime number.
Since all the factors in the expression are prime numbers, this is a prime factorisation.
(c) 70 = 2 × 5 × 7:
The factors listed are 2, 5, and 7.
2 is a prime number.
5 is a prime number.
7 is a prime number.
Since all the factors in the expression are prime numbers, this is a prime factorisation.
(d) 54 = 2 × 3 × 9:
The factors listed are 2, 3, and 9.
2 is a prime number.
3 is a prime number.
9 is a composite number ($9 = 3 \times 3$).
Since the expression includes a composite factor (9), this is not a prime factorisation.
Therefore, the expressions where prime factorisation has been done are (b) and (c).
Question 10. Determine if 25110 is divisible by 45.
[Hint: 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9].
Answer:
To Determine:
Whether the number 25110 is divisible by 45.
Solution:
To check if a number is divisible by 45, we can use the fact that $45 = 5 \times 9$.
Since 5 and 9 are co-prime numbers (their only common factor is 1), a number is divisible by 45 if and only if it is divisible by both 5 and 9.
We will test the divisibility of 25110 by 5 and 9 separately.
1. Divisibility by 5:
A number is divisible by 5 if its last digit is 0 or 5.
The last digit of 25110 is 0.
Therefore, 25110 is divisible by 5.
2. Divisibility by 9:
A number is divisible by 9 if the sum of its digits is divisible by 9.
The digits of 25110 are 2, 5, 1, 1, and 0.
Sum of digits = $2 + 5 + 1 + 1 + 0 = 9$.
Since the sum of the digits (9) is divisible by 9 ($9 \div 9 = 1$), the number 25110 is divisible by 9.
Therefore, 25110 is divisible by 9.
Conclusion:
Since 25110 is divisible by both 5 and 9, and 5 and 9 are co-prime, the number 25110 must be divisible by their product, $5 \times 9 = 45$.
Thus, 25110 is divisible by 45.
Question 11. 18 is divisible by both 2 and 3. It is also divisible by 2 × 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.
Answer:
The statement that if a number is divisible by $a$ and $b$, then it must be divisible by $a \times b$ is only true if $a$ and $b$ are co-prime (meaning their highest common factor, HCF, is 1).
In the first case:
The number is divisible by 2 and 3. The HCF of 2 and 3 is 1. They are co-prime. Therefore, the number must be divisible by their product, $2 \times 3 = 6$. This is consistent with the given information.
In the second case:
We are asked if a number divisible by both 4 and 6 must be divisible by $4 \times 6 = 24$.
Let's find the HCF of 4 and 6.
Factors of 4: 1, 2, 4.
Factors of 6: 1, 2, 3, 6.
The highest common factor (HCF) of 4 and 6 is 2.
Since the HCF of 4 and 6 is 2 (which is not 1), 4 and 6 are not co-prime.
Therefore, we cannot say that a number divisible by both 4 and 6 must also be divisible by their product, 24.
Justification with an Example:
Consider the number 12.
Is 12 divisible by 4? Yes, $12 \div 4 = 3$.
Is 12 divisible by 6? Yes, $12 \div 6 = 2$.
So, 12 is divisible by both 4 and 6.
Now, is 12 divisible by $4 \times 6 = 24$? No, 12 is smaller than 24, so it cannot be divisible by 24.
Another example is 36.
Is 36 divisible by 4? Yes, $36 \div 4 = 9$.
Is 36 divisible by 6? Yes, $36 \div 6 = 6$.
Is 36 divisible by 24? No, $36 = 24 \times 1 + 12$.
These examples show that a number divisible by both 4 and 6 is not necessarily divisible by 24.
Conclusion: No, we cannot say that the number must also be divisible by 24. The number must only be divisible by the Least Common Multiple (LCM) of 4 and 6, which is 12.
Question 12. I am the smallest number, having four different prime factors. Can you find me?
Answer:
Understanding the Problem:
We need to find the smallest positive integer that is the product of exactly four distinct (different) prime numbers.
Finding the Number:
To make the number as small as possible, we should use the smallest prime numbers available.
The first few prime numbers are 2, 3, 5, 7, 11, 13, ...
We need four different prime factors. The smallest four different prime numbers are 2, 3, 5, and 7.
The smallest number having four different prime factors will be the product of these four smallest prime numbers.
Product = $2 \times 3 \times 5 \times 7$
$2 \times 3 = 6$
$6 \times 5 = 30$
$30 \times 7 = 210$
Therefore, the smallest number having four different prime factors is 210.
The prime factors of 210 are indeed 2, 3, 5, and 7, which are four different prime numbers.
Exercise 3.6
Question 1. Find the HCF of the following numbers :
(a) 18, 48
(b) 30, 42
(c) 18, 60
(d) 27, 63
(e) 36, 84
(f) 34, 102
(g) 70, 105, 175
(h) 91, 112, 49
(i) 18, 54, 81
(j) 12, 45, 75
Answer:
The Highest Common Factor (HCF) is the largest positive integer that divides each of the given integers without leaving a remainder. We will use the prime factorisation method.
(a) HCF of 18 and 48:
Prime factorisation of 18:
$\begin{array}{c|cc} 2 & 18 \\ \hline 3 & 9 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$18 = 2 \times 3 \times 3 = 2 \times 3^2$
Prime factorisation of 48:
$\begin{array}{c|cc} 2 & 48 \\ \hline 2 & 24 \\ \hline 2 & 12 \\ \hline 2 & 6 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3^1$
Common prime factors are 2 and 3.
The lowest power of 2 is $2^1$.
The lowest power of 3 is $3^1$.
HCF(18, 48) = $2^1 \times 3^1 = 2 \times 3 = \mathbf{6}$.
(b) HCF of 30 and 42:
Prime factorisation of 30: $30 = 2 \times 15 = 2 \times 3 \times 5$.
Prime factorisation of 42: $42 = 2 \times 21 = 2 \times 3 \times 7$.
Common prime factors are 2 and 3.
The lowest power of 2 is $2^1$.
The lowest power of 3 is $3^1$.
HCF(30, 42) = $2^1 \times 3^1 = 2 \times 3 = \mathbf{6}$.
(c) HCF of 18 and 60:
Prime factorisation of 18: $18 = 2 \times 3^2$.
Prime factorisation of 60:
$\begin{array}{c|cc} 2 & 60 \\ \hline 2 & 30 \\ \hline 3 & 15 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$60 = 2^2 \times 3 \times 5$.
Common prime factors are 2 and 3.
The lowest power of 2 is $2^1$.
The lowest power of 3 is $3^1$.
HCF(18, 60) = $2^1 \times 3^1 = 2 \times 3 = \mathbf{6}$.
(d) HCF of 27 and 63:
Prime factorisation of 27: $27 = 3 \times 9 = 3 \times 3 \times 3 = 3^3$.
Prime factorisation of 63: $63 = 3 \times 21 = 3 \times 3 \times 7 = 3^2 \times 7$.
The common prime factor is 3.
The lowest power of 3 is $3^2$.
HCF(27, 63) = $3^2 = \mathbf{9}$.
(e) HCF of 36 and 84:
Prime factorisation of 36: $36 = 2 \times 18 = 2 \times 2 \times 9 = 2^2 \times 3^2$.
Prime factorisation of 84: $84 = 2 \times 42 = 2 \times 2 \times 21 = 2^2 \times 3 \times 7$.
Common prime factors are 2 and 3.
The lowest power of 2 is $2^2$.
The lowest power of 3 is $3^1$.
HCF(36, 84) = $2^2 \times 3^1 = 4 \times 3 = \mathbf{12}$.
(f) HCF of 34 and 102:
Prime factorisation of 34: $34 = 2 \times 17$.
Prime factorisation of 102: $102 = 2 \times 51 = 2 \times 3 \times 17$.
Common prime factors are 2 and 17.
The lowest power of 2 is $2^1$.
The lowest power of 17 is $17^1$.
HCF(34, 102) = $2^1 \times 17^1 = 2 \times 17 = \mathbf{34}$.
(g) HCF of 70, 105, 175:
Prime factorisation of 70: $70 = 2 \times 35 = 2 \times 5 \times 7$.
Prime factorisation of 105: $105 = 3 \times 35 = 3 \times 5 \times 7$.
Prime factorisation of 175: $175 = 5 \times 35 = 5 \times 5 \times 7 = 5^2 \times 7$.
Common prime factors are 5 and 7.
The lowest power of 5 is $5^1$.
The lowest power of 7 is $7^1$.
HCF(70, 105, 175) = $5^1 \times 7^1 = 5 \times 7 = \mathbf{35}$.
(h) HCF of 91, 112, 49:
Prime factorisation of 91: $91 = 7 \times 13$.
Prime factorisation of 112:
$\begin{array}{c|cc} 2 & 112 \\ \hline 2 & 56 \\ \hline 2 & 28 \\ \hline 2 & 14 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
$112 = 2^4 \times 7$.
Prime factorisation of 49: $49 = 7 \times 7 = 7^2$.
The common prime factor is 7.
The lowest power of 7 is $7^1$.
HCF(91, 112, 49) = $7^1 = \mathbf{7}$.
(i) HCF of 18, 54, 81:
Prime factorisation of 18: $18 = 2 \times 9 = 2 \times 3^2$.
Prime factorisation of 54: $54 = 2 \times 27 = 2 \times 3^3$.
Prime factorisation of 81: $81 = 3 \times 27 = 3^4$.
The common prime factor is 3.
The lowest power of 3 is $3^2$.
HCF(18, 54, 81) = $3^2 = \mathbf{9}$.
(j) HCF of 12, 45, 75:
Prime factorisation of 12: $12 = 2 \times 6 = 2^2 \times 3$.
Prime factorisation of 45: $45 = 3 \times 15 = 3^2 \times 5$.
Prime factorisation of 75: $75 = 3 \times 25 = 3 \times 5^2$.
The common prime factor is 3.
The lowest power of 3 is $3^1$.
HCF(12, 45, 75) = $3^1 = \mathbf{3}$.
Question 2. What is the HCF of two consecutive
(a) numbers?
(b) even numbers?
(c) odd numbers?
Answer:
The HCF (Highest Common Factor) is the largest number that divides two or more numbers without leaving a remainder.
(a) HCF of two consecutive numbers:
Consecutive numbers are numbers that follow each other in order, like 4 and 5, or 15 and 16.
Let's find the HCF for a few pairs:
Example 1: The numbers 8 and 9.
Factors of 8 are: 1, 2, 4, 8.
Factors of 9 are: 1, 3, 9.
The only common factor is 1. So, the HCF is 1.
Example 2: The numbers 20 and 21.
Factors of 20 are: 1, 2, 4, 5, 10, 20.
Factors of 21 are: 1, 3, 7, 21.
The only common factor is 1. So, the HCF is 1.
Two consecutive numbers do not share any factors other than 1. Therefore, the HCF of two consecutive numbers is always 1.
(b) HCF of two consecutive even numbers:
Consecutive even numbers are even numbers that follow each other, like 6 and 8, or 22 and 24.
Let's find the HCF for a few pairs:
Example 1: The numbers 10 and 12.
Factors of 10 are: 1, 2, 5, 10.
Factors of 12 are: 1, 2, 3, 4, 6, 12.
The common factors are 1 and 2. The highest common factor is 2. So, the HCF is 2.
Example 2: The numbers 30 and 32.
Factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30.
Factors of 32 are: 1, 2, 4, 8, 16, 32.
The common factors are 1 and 2. The highest common factor is 2. So, the HCF is 2.
Since both numbers are even, they are both divisible by 2. After dividing them by 2, you are left with two consecutive numbers (like 5 and 6, or 15 and 16), which we know have no other common factors. Therefore, the HCF of two consecutive even numbers is always 2.
(c) HCF of two consecutive odd numbers:
Consecutive odd numbers are odd numbers that follow each other, like 7 and 9, or 25 and 27.
Let's find the HCF for a few pairs:
Example 1: The numbers 9 and 11.
Factors of 9 are: 1, 3, 9.
Factors of 11 are: 1, 11.
The only common factor is 1. So, the HCF is 1.
Example 2: The numbers 21 and 23.
Factors of 21 are: 1, 3, 7, 21.
Factors of 23 are: 1, 23.
The only common factor is 1. So, the HCF is 1.
Two consecutive odd numbers do not share any factors other than 1. The difference between them is 2, but since they are odd, neither can be divided by 2. Therefore, the HCF of two consecutive odd numbers is always 1.
Question 3. HCF of co-prime numbers 4 and 15 was found as follows by factorisation :
4 = 2 × 2 and 15 = 3 × 5 since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?
Answer:
The reasoning provided states:
Prime factorisation of 4 = $2 \times 2$.
Prime factorisation of 15 = $3 \times 5$.
Conclusion: Since there is no common prime factor, HCF of 4 and 15 is 0.
Is the answer correct?
No, the answer that the HCF is 0 is incorrect.
Reasoning:
The Highest Common Factor (HCF) of two numbers is the largest positive integer that divides both numbers.
1. The HCF cannot be 0. The smallest possible HCF for any pair of positive integers is 1.
2. While it is true that 4 and 15 have no common prime factors, they do have a common factor.
Factors of 4 are: 1, 2, 4.
Factors of 15 are: 1, 3, 5, 15.
The only common factor is 1.
3. The definition of co-prime numbers is that their HCF is 1. The problem states that 4 and 15 are co-prime, which implies their HCF must be 1.
What is the correct HCF?
The correct HCF of 4 and 15 is 1.
Example 8 to 14 (Before Exercise 3.7)
Example 8: Find the LCM of 12 and 18.
Answer:
To Find:
The Least Common Multiple (LCM) of 12 and 18.
Solution (Using Prime Factorisation):
First, find the prime factorisation of each number.
Prime factorisation of 12:
$\begin{array}{c|cc} 2 & 12 \\ \hline 2 & 6 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$12 = 2 \times 2 \times 3 = 2^2 \times 3^1$.
Prime factorisation of 18:
$\begin{array}{c|cc} 2 & 18 \\ \hline 3 & 9 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$18 = 2 \times 3 \times 3 = 2^1 \times 3^2$.
To find the LCM, we take the highest power of each prime factor that appears in either factorisation.
The prime factors involved are 2 and 3.
The highest power of 2 is $2^2$.
The highest power of 3 is $3^2$.
LCM(12, 18) = $2^2 \times 3^2 = 4 \times 9 = 36$.
Therefore, the LCM of 12 and 18 is 36.
Alternate Solution (Using Division Method):
We divide the numbers by common prime factors.
$\begin{array}{c|cc} 2 & 12 \; , & 18 \\ \hline 2 & 6 \; , & 9 \\ \hline 3 & 3 \; , & 9 \\ \hline 3 & 1 \; , & 3 \\ \hline & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(12, 18) = $2 \times 2 \times 3 \times 3 = 36$.
Therefore, the LCM of 12 and 18 is 36.
Example 9: Find the LCM of 24 and 90.
Answer:
To Find:
The Least Common Multiple (LCM) of 24 and 90.
Solution (Using Prime Factorisation):
First, find the prime factorisation of each number.
Prime factorisation of 24:
$\begin{array}{c|cc} 2 & 24 \\ \hline 2 & 12 \\ \hline 2 & 6 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$24 = 2 \times 2 \times 2 \times 3 = 2^3 \times 3^1$.
Prime factorisation of 90:
$\begin{array}{c|cc} 2 & 90 \\ \hline 3 & 45 \\ \hline 3 & 15 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$90 = 2 \times 3 \times 3 \times 5 = 2^1 \times 3^2 \times 5^1$.
To find the LCM, we take the highest power of each prime factor that appears in either factorisation.
The prime factors involved are 2, 3, and 5.
The highest power of 2 is $2^3$.
The highest power of 3 is $3^2$.
The highest power of 5 is $5^1$.
LCM(24, 90) = $2^3 \times 3^2 \times 5^1 = 8 \times 9 \times 5 = 72 \times 5 = 360$.
Therefore, the LCM of 24 and 90 is 360.
Alternate Solution (Using Division Method):
We divide the numbers by common prime factors, and then by any remaining prime factors.
$\begin{array}{c|cc} 2 & 24 \; , & 90 \\ \hline 2 & 12 \; , & 45 \\ \hline 2 & 6 \; , & 45 \\ \hline 3 & 3 \; , & 45 \\ \hline 3 & 1 \; , & 15 \\ \hline 5 & 1 \; , & 5 \\ \hline & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(24, 90) = $2 \times 2 \times 2 \times 3 \times 3 \times 5 = 8 \times 9 \times 5 = 360$.
Therefore, the LCM of 24 and 90 is 360.
Example 10: Find the LCM of 40, 48 and 45.
Answer:
To Find:
The Least Common Multiple (LCM) of 40, 48 and 45.
Solution (Using Prime Factorisation):
First, find the prime factorisation of each number.
Prime factorisation of 40:
$\begin{array}{c|cc} 2 & 40 \\ \hline 2 & 20 \\ \hline 2 & 10 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$40 = 2 \times 2 \times 2 \times 5 = 2^3 \times 5^1$.
Prime factorisation of 48:
$\begin{array}{c|cc} 2 & 48 \\ \hline 2 & 24 \\ \hline 2 & 12 \\ \hline 2 & 6 \\ \hline 3 & 3 \\ \hline & 1 \end{array}$
$48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3^1$.
Prime factorisation of 45:
$\begin{array}{c|cc} 3 & 45 \\ \hline 3 & 15 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$45 = 3 \times 3 \times 5 = 3^2 \times 5^1$.
To find the LCM, we take the highest power of each prime factor that appears in any of the factorisations.
The prime factors involved are 2, 3, and 5.
The highest power of 2 is $2^4$.
The highest power of 3 is $3^2$.
The highest power of 5 is $5^1$.
LCM(40, 48, 45) = $2^4 \times 3^2 \times 5^1 = 16 \times 9 \times 5 = 144 \times 5 = 720$.
Therefore, the LCM of 40, 48 and 45 is 720.
Alternate Solution (Using Division Method):
We divide the numbers by common prime factors, and then by any remaining prime factors.
$\begin{array}{c|ccc} 2 & 40 \; , & 48 \; , & 45 \\ \hline 2 & 20 \; , & 24 \; , & 45 \\ \hline 2 & 10 \; , & 12 \; , & 45 \\ \hline 2 & 5 \; , & 6 \; , & 45 \\ \hline 3 & 5 \; , & 3 \; , & 45 \\ \hline 3 & 5 \; , & 1 \; , & 15 \\ \hline 5 & 5 \; , & 1 \; , & 5 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(40, 48, 45) = $2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 5 = 16 \times 9 \times 5 = 720$.
Therefore, the LCM of 40, 48 and 45 is 720.
Example 11: Find the LCM of 20, 25 and 30.
Answer:
To Find:
The Least Common Multiple (LCM) of 20, 25 and 30.
Solution (Using Prime Factorisation):
First, find the prime factorisation of each number.
Prime factorisation of 20:
$\begin{array}{c|cc} 2 & 20 \\ \hline 2 & 10 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$20 = 2 \times 2 \times 5 = 2^2 \times 5^1$.
Prime factorisation of 25:
$\begin{array}{c|cc} 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$25 = 5 \times 5 = 5^2$.
Prime factorisation of 30:
$\begin{array}{c|cc} 2 & 30 \\ \hline 3 & 15 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$30 = 2 \times 3 \times 5 = 2^1 \times 3^1 \times 5^1$.
To find the LCM, we take the highest power of each prime factor that appears in any of the factorisations.
The prime factors involved are 2, 3, and 5.
The highest power of 2 is $2^2$.
The highest power of 3 is $3^1$.
The highest power of 5 is $5^2$.
LCM(20, 25, 30) = $2^2 \times 3^1 \times 5^2 = 4 \times 3 \times 25 = 12 \times 25 = 300$.
Therefore, the LCM of 20, 25 and 30 is 300.
Alternate Solution (Using Division Method):
We divide the numbers by common prime factors, and then by any remaining prime factors.
$\begin{array}{c|ccc} 2 & 20 \; , & 25 \; , & 30 \\ \hline 2 & 10 \; , & 25 \; , & 15 \\ \hline 3 & 5 \; , & 25 \; , & 15 \\ \hline 5 & 5 \; , & 25 \; , & 5 \\ \hline 5 & 1 \; , & 5 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(20, 25, 30) = $2 \times 2 \times 3 \times 5 \times 5 = 4 \times 3 \times 25 = 12 \times 25 = 300$.
Therefore, the LCM of 20, 25 and 30 is 300.
Example 12: Two tankers contain 850 litres and 680 litres of kerosene oil respectively. Find the maximum capacity of a container which can measure the kerosene oil of both the tankers when used an exact number of times.
Answer:
Given:
Capacity of the first tanker = 850 litres.
Capacity of the second tanker = 680 litres.
To Find:
The maximum capacity of a container that can measure the oil of both tankers exactly.
Solution:
The container must be able to measure both 850 litres and 680 litres using an exact number of full containers. This means the capacity of the container must be a factor of both 850 and 680.
Since we want the maximum capacity of such a container, we need to find the Highest Common Factor (HCF) of 850 and 680.
We will use the prime factorisation method.
Prime factorisation of 850:
$\begin{array}{c|cc} 2 & 850 \\ \hline 5 & 425 \\ \hline 5 & 85 \\ \hline 17 & 17 \\ \hline & 1 \end{array}$
$850 = 2 \times 5 \times 5 \times 17 = 2^1 \times 5^2 \times 17^1$.
Prime factorisation of 680:
$\begin{array}{c|cc} 2 & 680 \\ \hline 2 & 340 \\ \hline 2 & 170 \\ \hline 5 & 85 \\ \hline 17 & 17 \\ \hline & 1 \end{array}$
$680 = 2 \times 2 \times 2 \times 5 \times 17 = 2^3 \times 5^1 \times 17^1$.
To find the HCF, we take the lowest power of each common prime factor.
The common prime factors are 2, 5, and 17.
Lowest power of 2 is $2^1$.
Lowest power of 5 is $5^1$.
Lowest power of 17 is $17^1$.
HCF(850, 680) = $2^1 \times 5^1 \times 17^1 = 2 \times 5 \times 17 = 10 \times 17 = 170$.
The HCF is 170.
Therefore, the maximum capacity of the container is 170 litres.
Alternate Solution (Using Euclidean Algorithm):
We use the division method to find the HCF of 850 and 680.
Divide 850 by 680:
$850 = 1 \times 680 + 170$
Divide 680 by the remainder 170:
$680 = 4 \times 170 + 0$
The last non-zero remainder is 170.
Therefore, HCF(850, 680) = 170.
The maximum capacity of the container is 170 litres.
Example 13: In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that all can cover the same distance in complete steps?
Answer:
Given:
Step length of the first person = 80 cm.
Step length of the second person = 85 cm.
Step length of the third person = 90 cm.
To Find:
The minimum distance each person should walk so that they cover the same distance in complete steps.
Solution:
We need to find a distance that is a multiple of each person's step length (80 cm, 85 cm, and 90 cm), so that each person covers the distance in a whole number of steps.
Since we are looking for the minimum such distance, we need to find the Least Common Multiple (LCM) of 80, 85, and 90.
We can use the division method to find the LCM:
$\begin{array}{c|ccc} 2 & 80 \; , & 85 \; , & 90 \\ \hline 5 & 40 \; , & 85 \; , & 45 \\ \hline 2 & 8 \; , & 17 \; , & 9 \\ \hline 2 & 4 \; , & 17 \; , & 9 \\ \hline 2 & 2 \; , & 17 \; , & 9 \\ \hline 3 & 1 \; , & 17 \; , & 9 \\ \hline 3 & 1 \; , & 17 \; , & 3 \\ \hline 17 & 1 \; , & 17 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM = $2 \times 5 \times 2 \times 2 \times 2 \times 3 \times 3 \times 17$
LCM = $(2 \times 2 \times 2 \times 2) \times (3 \times 3) \times 5 \times 17$
LCM = $2^4 \times 3^2 \times 5^1 \times 17^1$
LCM = $16 \times 9 \times 5 \times 17$
LCM = $144 \times 5 \times 17$
LCM = $720 \times 17$
$\begin{array}{cc}& & 7 & 2 & 0 \\ \times & & & 1 & 7 \\ \hline & 5 & 0 & 4 & 0 \\ & 7 & 2 & 0 & \times \\ \hline 1 & 2 & 2 & 4 & 0 \\ \hline \end{array}$
LCM = 12240.
The minimum distance each person should walk is 12240 cm.
Therefore, the minimum distance required is 12240 cm.
Example 14: Find the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case.
Answer:
Given:
Divisors: 12, 16, 24, 36
Remainder in each case: 7
To Find:
The least number satisfying the given conditions.
Solution:
Let the required number be $N$.
According to the problem, when $N$ is divided by 12, 16, 24, or 36, the remainder is 7.
This means that if we subtract 7 from the number $N$, the result $(N-7)$ will be exactly divisible by each of the divisors 12, 16, 24, and 36.
So, $(N-7)$ must be a common multiple of 12, 16, 24, and 36.
Since we are looking for the least such number $N$, the value of $(N-7)$ must be the Least Common Multiple (LCM) of 12, 16, 24, and 36.
We find the LCM of 12, 16, 24, and 36 using the division method:
$\begin{array}{c|cccc} 2 & 12 \; , & 16 \; , & 24 \; , & 36 \\ \hline 2 & 6 \; , & 8 \; , & 12 \; , & 18 \\ \hline 2 & 3 \; , & 4 \; , & 6 \; , & 9 \\ \hline 2 & 3 \; , & 2 \; , & 3 \; , & 9 \\ \hline 3 & 3 \; , & 1 \; , & 3 \; , & 9 \\ \hline 3 & 1 \; , & 1 \; , & 1 \; , & 3 \\ \hline & 1 \; , & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM = $2 \times 2 \times 2 \times 2 \times 3 \times 3 = 2^4 \times 3^2 = 16 \times 9 = 144$.
So, the least value of $(N-7)$ is 144.
$N - 7 = 144$
To find $N$, we add 7 to both sides:
$N = 144 + 7$
$N = 151$
Therefore, the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case is 151.
Exercise 3.7
Question 1. Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertiliser exact number of times.
Answer:
Given:
Weight of the first bag of fertiliser = 75 kg.
Weight of the second bag of fertiliser = 69 kg.
To Find:
The maximum value of weight that can measure the weight of both bags an exact number of times.
Solution:
The weight that can measure both 75 kg and 69 kg an exact number of times must be a common factor of 75 and 69.
To find the maximum such weight, we need to find the Highest Common Factor (HCF) of 75 and 69.
We will use the prime factorisation method.
Prime factorisation of 75:
$\begin{array}{c|cc} 3 & 75 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$75 = 3 \times 5 \times 5 = 3^1 \times 5^2$.
Prime factorisation of 69:
$\begin{array}{c|cc} 3 & 69 \\ \hline 23 & 23 \\ \hline & 1 \end{array}$
$69 = 3 \times 23 = 3^1 \times 23^1$.
To find the HCF, we take the lowest power of each common prime factor.
The only common prime factor is 3.
The lowest power of 3 is $3^1$.
HCF(75, 69) = $3^1 = 3$.
Therefore, the maximum value of weight which can measure the weight of the fertiliser in both bags an exact number of times is 3 kg.
Question 2. Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the distance in complete steps?
Answer:
Given:
Step length of the first boy = 63 cm.
Step length of the second boy = 70 cm.
Step length of the third boy = 77 cm.
To Find:
The minimum distance each boy should cover so that all can cover the distance in complete steps.
Solution:
We need to find a distance that is a multiple of each boy's step length (63 cm, 70 cm, and 77 cm) so that each boy covers the distance in a whole number of steps.
Since we are looking for the minimum such distance, we need to find the Least Common Multiple (LCM) of 63, 70, and 77.
We can use the division method to find the LCM:
$\begin{array}{c|ccc} 2 & 63 \; , & 70 \; , & 77 \\ \hline 3 & 63 \; , & 35 \; , & 77 \\ \hline 3 & 21 \; , & 35 \; , & 77 \\ \hline 5 & 7 \; , & 35 \; , & 77 \\ \hline 7 & 7 \; , & 7 \; , & 77 \\ \hline 11 & 1 \; , & 1 \; , & 11 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM = $2 \times 3 \times 3 \times 5 \times 7 \times 11$
LCM = $2 \times 9 \times 5 \times 7 \times 11$
LCM = $18 \times 5 \times 7 \times 11$
LCM = $90 \times 7 \times 11$
LCM = $630 \times 11$
$\begin{array}{cc}& & 6 & 3 & 0 \\ \times & & & 1 & 1 \\ \hline & & 6 & 3 & 0 \\ & 6 & 3 & 0 & \times \\ \hline & 6 & 9 & 3 & 0 \\ \hline \end{array}$
LCM = 6930.
The minimum distance each boy should cover is 6930 cm.
Therefore, the minimum distance required is 6930 cm.
Question 3. The length, breadth and height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.
Answer:
Given:
Length of the room = 825 cm.
Breadth of the room = 675 cm.
Height of the room = 450 cm.
To Find:
The length of the longest tape that can measure all three dimensions exactly.
Solution:
The tape must be able to measure 825 cm, 675 cm, and 450 cm using an exact number of full tape lengths. This means the length of the tape must be a common factor of 825, 675, and 450.
Since we want the longest such tape, we need to find the Highest Common Factor (HCF) of 825, 675, and 450.
We will use the prime factorisation method.
Prime factorisation of 825:
$\begin{array}{c|cc} 3 & 825 \\ \hline 5 & 275 \\ \hline 5 & 55 \\ \hline 11 & 11 \\ \hline & 1 \end{array}$
$825 = 3 \times 5 \times 5 \times 11 = 3^1 \times 5^2 \times 11^1$.
Prime factorisation of 675:
$\begin{array}{c|cc} 3 & 675 \\ \hline 3 & 225 \\ \hline 3 & 75 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$675 = 3 \times 3 \times 3 \times 5 \times 5 = 3^3 \times 5^2$.
Prime factorisation of 450:
$\begin{array}{c|cc} 2 & 450 \\ \hline 3 & 225 \\ \hline 3 & 75 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$450 = 2 \times 3 \times 3 \times 5 \times 5 = 2^1 \times 3^2 \times 5^2$.
To find the HCF, we take the lowest power of each common prime factor.
The prime factors present in all three factorisations are 3 and 5.
Lowest power of 3: $3^1$ (from 825).
Lowest power of 5: $5^2$ (common to all).
HCF(825, 675, 450) = $3^1 \times 5^2 = 3 \times 25 = 75$.
The HCF is 75.
Therefore, the length of the longest tape which can measure the three dimensions of the room exactly is 75 cm.
Question 4. Determine the smallest 3-digit number which is exactly divisible by 6, 8 and 12.
Answer:
Given:
The divisors are 6, 8, and 12.
To Find:
The smallest 3-digit number that is exactly divisible by 6, 8, and 12.
Solution:
A number that is exactly divisible by 6, 8, and 12 must be a common multiple of these three numbers.
To find the smallest such number within a certain range (3-digit numbers), we first need to find the Least Common Multiple (LCM) of 6, 8, and 12.
We calculate the LCM using the division method:
$\begin{array}{c|ccc} 2 & 6 \; , & 8 \; , & 12 \\ \hline 2 & 3 \; , & 4 \; , & 6 \\ \hline 2 & 3 \; , & 2 \; , & 3 \\ \hline 3 & 3 \; , & 1 \; , & 3 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(6, 8, 12) = $2 \times 2 \times 2 \times 3 = 8 \times 3 = 24$.
The numbers divisible by 6, 8, and 12 are the multiples of their LCM, which is 24.
Multiples of 24 are: 24, 48, 72, 96, 120, 144, ...
We need the smallest 3-digit multiple of 24.
Listing the multiples, we see:
- 24 (2-digit)
- 48 (2-digit)
- 72 (2-digit)
- 96 (2-digit)
- 120 (3-digit)
The smallest 3-digit number in this list is 120.
Therefore, the smallest 3-digit number which is exactly divisible by 6, 8 and 12 is 120.
Question 5. Determine the greatest 3-digit number exactly divisible by 8, 10 and 12.
Answer:
Given:
The divisors are 8, 10, and 12.
To Find:
The greatest 3-digit number that is exactly divisible by 8, 10, and 12.
Solution:
A number that is exactly divisible by 8, 10, and 12 must be a common multiple of these three numbers.
To find the common multiples, we first need to find the Least Common Multiple (LCM) of 8, 10, and 12.
We calculate the LCM using the division method:
$\begin{array}{c|ccc} 2 & 8 \; , & 10 \; , & 12 \\ \hline 2 & 4 \; , & 5 \; , & 6 \\ \hline 2 & 2 \; , & 5 \; , & 3 \\ \hline 3 & 1 \; , & 5 \; , & 3 \\ \hline 5 & 1 \; , & 5 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(8, 10, 12) = $2 \times 2 \times 2 \times 3 \times 5 = 8 \times 3 \times 5 = 24 \times 5 = 120$.
The numbers divisible by 8, 10, and 12 are the multiples of their LCM, which is 120.
Multiples of 120 are: 120, 240, 360, 480, 600, 720, 840, 960, 1080, ...
We need the greatest 3-digit multiple of 120.
Looking at the list of multiples:
- 120 (3-digit)
- 240 (3-digit)
- 360 (3-digit)
- 480 (3-digit)
- 600 (3-digit)
- 720 (3-digit)
- 840 (3-digit)
- 960 (3-digit)
- 1080 (4-digit - too large)
The greatest 3-digit number in this list is 960.
Therefore, the greatest 3-digit number exactly divisible by 8, 10 and 12 is 960.
Question 6. The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m., at what time will they change simultaneously again?
Answer:
Given:
Time intervals for traffic lights changing: 48 seconds, 72 seconds, 108 seconds.
Time they last changed simultaneously: 7 a.m.
To Find:
The next time the traffic lights will change simultaneously.
Solution:
The time interval after which the lights will change simultaneously again is the Least Common Multiple (LCM) of their individual time intervals (48, 72, and 108 seconds).
We calculate the LCM of 48, 72, and 108 using the division method:
$\begin{array}{c|ccc} 2 & 48 \; , & 72 \; , & 108 \\ \hline 2 & 24 \; , & 36 \; , & 54 \\ \hline 2 & 12 \; , & 18 \; , & 27 \\ \hline 2 & 6 \; , & 9 \; , & 27 \\ \hline 3 & 3 \; , & 9 \; , & 27 \\ \hline 3 & 1 \; , & 3 \; , & 9 \\ \hline 3 & 1 \; , & 1 \; , & 3 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(48, 72, 108) = $2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^4 \times 3^3 = 16 \times 27$.
Calculating the product:
$\begin{array}{cc}& & 1 & 6 \\ \times & & 2 & 7 \\ \hline & 1 & 1 & 2 \\ & 3 & 2 & \times \\ \hline & 4 & 3 & 2 \\ \hline \end{array}$
LCM = 432 seconds.
This means the lights will change simultaneously again after 432 seconds.
Now, we need to convert 432 seconds into minutes and seconds:
Number of minutes = $432 \div 60$.
$432 = 60 \times 7 + 12$.
So, 432 seconds = 7 minutes and 12 seconds.
The lights changed simultaneously at 7 a.m.
They will change simultaneously again after 7 minutes and 12 seconds.
Next simultaneous change time = 7 a.m. + 7 minutes 12 seconds = 7:07:12 a.m.
Therefore, the traffic lights will change simultaneously again at 7 minutes 12 seconds past 7 a.m. (or 7:07:12 a.m.).
Question 7. Three tankers contain 403 litres, 434 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of the three containers exact number of times.
Answer:
Given:
Capacity of the first tanker = 403 litres.
Capacity of the second tanker = 434 litres.
Capacity of the third tanker = 465 litres.
To Find:
The maximum capacity of a container that can measure the diesel of all three tankers an exact number of times.
Solution:
The container must be able to measure 403 litres, 434 litres, and 465 litres using an exact number of full containers. This means the capacity of the container must be a common factor of 403, 434, and 465.
Since we want the maximum capacity of such a container, we need to find the Highest Common Factor (HCF) of 403, 434, and 465.
We will use the prime factorisation method.
Prime factorisation of 403:
Try dividing by primes: Not divisible by 2, 3, 5, 7, 11. $403 \div 13 = 31$. Both 13 and 31 are prime.
$403 = 13 \times 31$.
Prime factorisation of 434:
$434 = 2 \times 217$. Check 217: $217 \div 7 = 31$. Both 7 and 31 are prime.
$434 = 2 \times 7 \times 31$.
Prime factorisation of 465:
$465 = 5 \times 93$. $93 = 3 \times 31$.
$465 = 3 \times 5 \times 31$.
To find the HCF, we identify the common prime factors and take their lowest powers.
The only common prime factor among 403, 434, and 465 is 31.
The lowest power of 31 is $31^1$.
HCF(403, 434, 465) = 31.
Therefore, the maximum capacity of the container is 31 litres.
Alternate Solution (Using Euclidean Algorithm):
First, find the HCF of 403 and 434.
Divide 434 by 403:
$434 = 1 \times 403 + 31$
Divide 403 by the remainder 31:
$403 = 13 \times 31 + 0$
The HCF of 403 and 434 is 31.
Now, find the HCF of this result (31) and the third number (465).
Divide 465 by 31:
$465 = 15 \times 31 + 0$
The HCF of 31 and 465 is 31.
Thus, the HCF of 403, 434, and 465 is 31.
The maximum capacity of the container is 31 litres.
Question 8. Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case.
Answer:
Given:
Divisors: 6, 15, 18
Remainder in each case: 5
To Find:
The least number satisfying the given conditions.
Solution:
Let the required number be $N$.
According to the problem, when $N$ is divided by 6, 15, or 18, the remainder is 5.
This means that if we subtract 5 from the number $N$, the result $(N-5)$ will be exactly divisible by each of the divisors 6, 15, and 18.
So, $(N-5)$ must be a common multiple of 6, 15, and 18.
Since we are looking for the least such number $N$, the value of $(N-5)$ must be the Least Common Multiple (LCM) of 6, 15, and 18.
We find the LCM of 6, 15, and 18 using the division method:
$\begin{array}{c|ccc} 2 & 6 \; , & 15 \; , & 18 \\ \hline 3 & 3 \; , & 15 \; , & 9 \\ \hline 3 & 1 \; , & 5 \; , & 3 \\ \hline 5 & 1 \; , & 5 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(6, 15, 18) = $2 \times 3 \times 3 \times 5 = 2 \times 9 \times 5 = 90$.
So, the least value of $(N-5)$ is 90.
$N - 5 = 90$
To find $N$, we add 5 to both sides:
$N = 90 + 5$
$N = 95$
Therefore, the least number which when divided by 6, 15 and 18 leaves a remainder 5 in each case is 95.
Question 9. Find the smallest 4-digit number which is divisible by 18, 24 and 32.
Answer:
Given:
The divisors are 18, 24, and 32.
To Find:
The smallest 4-digit number that is exactly divisible by 18, 24, and 32.
Solution:
A number that is exactly divisible by 18, 24, and 32 must be a common multiple of these three numbers.
To find the smallest such number within a certain range (4-digit numbers), we first need to find the Least Common Multiple (LCM) of 18, 24, and 32.
We calculate the LCM using the division method:
$\begin{array}{c|ccc} 2 & 18 \; , & 24 \; , & 32 \\ \hline 2 & 9 \; , & 12 \; , & 16 \\ \hline 2 & 9 \; , & 6 \; , & 8 \\ \hline 2 & 9 \; , & 3 \; , & 4 \\ \hline 2 & 9 \; , & 3 \; , & 2 \\ \hline 3 & 9 \; , & 3 \; , & 1 \\ \hline 3 & 3 \; , & 1 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
The LCM is the product of the divisors:
LCM(18, 24, 32) = $2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 = 2^5 \times 3^2 = 32 \times 9 = 288$.
The numbers divisible by 18, 24, and 32 are the multiples of their LCM, which is 288.
Multiples of 288 are: 288, 576, 864, 1152, 1440, ...
We need the smallest 4-digit multiple of 288.
Listing the multiples, we see:
- $288 \times 1 = 288$ (3-digit)
- $288 \times 2 = 576$ (3-digit)
- $288 \times 3 = 864$ (3-digit)
- $288 \times 4 = 1152$ (4-digit)
The smallest 4-digit number in this list is 1152.
Therefore, the smallest 4-digit number which is divisible by 18, 24 and 32 is 1152.
Question 10. Find the LCM of the following numbers :
(a) 9 and 4
(b) 12 and 5
(c) 6 and 5
(d) 15 and 4
Observe a common property in the obtained LCMs. Is LCM the product of two numbers in each case?
Answer:
(a) LCM of 9 and 4:
Prime factorisation: $9 = 3^2$, $4 = 2^2$.
LCM = $2^2 \times 3^2 = 4 \times 9 = \mathbf{36}$.
Product of numbers: $9 \times 4 = 36$.
(b) LCM of 12 and 5:
Prime factorisation: $12 = 2^2 \times 3$, $5 = 5^1$.
LCM = $2^2 \times 3 \times 5 = 4 \times 3 \times 5 = 60$.
Product of numbers: $12 \times 5 = \mathbf{60}$.
(c) LCM of 6 and 5:
Prime factorisation: $6 = 2 \times 3$, $5 = 5^1$.
LCM = $2 \times 3 \times 5 = 30$.
Product of numbers: $6 \times 5 = \mathbf{30}$.
(d) LCM of 15 and 4:
Prime factorisation: $15 = 3 \times 5$, $4 = 2^2$.
LCM = $2^2 \times 3 \times 5 = 4 \times 3 \times 5 = 60$.
Product of numbers: $15 \times 4 = \mathbf{60}$.
Observation:
In all four cases (a), (b), (c), and (d), the Least Common Multiple (LCM) of the two given numbers is equal to the product of the two numbers.
Is LCM the product of two numbers in each case?
Yes, in each of these specific cases, the LCM is equal to the product of the two numbers.
Common Property:
Let's examine the pairs of numbers:
(a) 9 and 4: Factors of 9 are 1, 3, 9. Factors of 4 are 1, 2, 4. HCF(9, 4) = 1. They are co-prime.
(b) 12 and 5: Factors of 12 are 1, 2, 3, 4, 6, 12. Factors of 5 are 1, 5. HCF(12, 5) = 1. They are co-prime.
(c) 6 and 5: Factors of 6 are 1, 2, 3, 6. Factors of 5 are 1, 5. HCF(6, 5) = 1. They are co-prime.
(d) 15 and 4: Factors of 15 are 1, 3, 5, 15. Factors of 4 are 1, 2, 4. HCF(15, 4) = 1. They are co-prime.
A common property observed in all these pairs is that the two numbers in each pair are co-prime (their HCF is 1).
The general property relating HCF and LCM is: For any two positive integers $a$ and $b$,
$\text{HCF}(a, b) \times \text{LCM}(a, b) = a \times b$.
If the numbers $a$ and $b$ are co-prime, their HCF is 1. In this case, the formula becomes:
$1 \times \text{LCM}(a, b) = a \times b$, which means $\text{LCM}(a, b) = a \times b$.
So, the LCM is the product of the two numbers precisely because the numbers in each pair are co-prime.
Question 11. Find the LCM of the following numbers in which one number is the factor of the other.
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
What do you observe in the results obtained?
Answer:
We need to find the LCM for each pair, noting that in each pair, one number is a factor of the other.
(a) LCM of 5 and 20:
Note that 5 is a factor of 20 ($20 = 5 \times 4$).
Prime factorisation: $5 = 5^1$, $20 = 2^2 \times 5^1$.
LCM(5, 20) = $2^2 \times 5^1 = 4 \times 5 = \mathbf{20}$.
(b) LCM of 6 and 18:
Note that 6 is a factor of 18 ($18 = 6 \times 3$).
Prime factorisation: $6 = 2^1 \times 3^1$, $18 = 2^1 \times 3^2$.
LCM(6, 18) = $2^1 \times 3^2 = 2 \times 9 = \mathbf{18}$.
(c) LCM of 12 and 48:
Note that 12 is a factor of 48 ($48 = 12 \times 4$).
Prime factorisation: $12 = 2^2 \times 3^1$, $48 = 2^4 \times 3^1$.
LCM(12, 48) = $2^4 \times 3^1 = 16 \times 3 = \mathbf{48}$.
(d) LCM of 9 and 45:
Note that 9 is a factor of 45 ($45 = 9 \times 5$).
Prime factorisation: $9 = 3^2$, $45 = 3^2 \times 5^1$.
LCM(9, 45) = $3^2 \times 5^1 = 9 \times 5 = \mathbf{45}$.
Observation:
In each case where one number is a factor of the other number, the LCM of the two numbers is equal to the larger of the two numbers.
- LCM(5, 20) = 20
- LCM(6, 18) = 18
- LCM(12, 48) = 48
- LCM(9, 45) = 45
The observation is: If one number is a factor of another number, then their LCM is the larger number itself.

