| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 8 Decimals
Chapter 8 introduces the concept of Decimals, representing a significant expansion of our number system.
Essentially, decimals serve as an alternative notation for fractions. They are particularly useful for representing fractions that have denominators which are powers of 10, such as 10, 100, 1000, and so forth. A solid understanding of decimals is vital as they are encountered frequently in daily life and form a foundation for more advanced mathematical topics.
This chapter, along with its accompanying solutions page, provides comprehensive coverage of key decimal concepts. You will learn about:
- Place Value: Grasping the value of digits to the right of the decimal point – understanding tenths, hundredths, thousandths, etc.
- Number Line Representation: Developing a visual understanding of decimal magnitude by plotting them on a number line.
- Comparing Decimals: Learning systematic methods to determine if one decimal is greater than, less than, or equal to another, similar to comparing whole numbers.
- Conversions: Mastering the techniques to switch between fractions and decimals. For example, understanding how $\frac{3}{5}$ is equivalent to $\frac{6}{10}$, which is written as the decimal $0.6$. Similarly, converting a decimal like $0.85$ back to its fractional form $\frac{85}{100}$ (which simplifies to $\frac{17}{20}$).
- Addition and Subtraction: Performing arithmetic, paying close attention to the critical step of aligning decimal points vertically before calculating.
- Real-World Applications: Seeing how decimals are used in practical scenarios involving:
- Money: Expressing amounts like 50 paise as $\textsf{₹}~0.50$.
- Length: Representing measurements like 75 cm as $0.75$ m.
- Weight: Converting units like 200 g to $0.200$ kg.
The detailed solutions offer clear, step-by-step explanations for various exercises, from interpreting place value tables to solving word problems. These examples reinforce both the theoretical concepts and the practical utility of decimals.
Becoming proficient with decimals is an essential skill, indispensable for navigating everyday financial transactions, measurements, and forming a crucial link to further mathematical learning.
Example 1 to 3 (Before Exercise 8.1)
Example 1: Write the following numbers in the place value table:
(a) 20.5
(b) 4.2
Answer:
The place value table represents the value of each digit in a number based on its position.
For decimal numbers, the places to the left of the decimal point are Ones, Tens, Hundreds, etc., and the places to the right are Tenths, Hundredths, Thousandths, etc.
Let's write the given numbers in the place value table:
| Number | Tens (10) | Ones (1) | Tenths ($\frac{1}{10}$) |
| (a) 20.5 | 2 | 0 | 5 |
| (b) 4.2 | 0 | 4 | 2 |
Explanation:
(a) In 20.5:
- The digit 2 is in the Tens place, so its value is $2 \times 10 = 20$.
- The digit 0 is in the Ones place, so its value is $0 \times 1 = 0$.
- The digit 5 is in the Tenths place, so its value is $5 \times \frac{1}{10} = 0.5$.
(b) In 4.2:
- The digit 4 is in the Ones place, so its value is $4 \times 1 = 4$.
- The digit 2 is in the Tenths place, so its value is $2 \times \frac{1}{10} = 0.2$.
Example 2: Write each of the following as decimals:
(a) Two ones and five-tenths
(b) Thirty and one-tenth
Answer:
To write the given phrases as decimals, we need to understand the place values.
- "Ones" refers to the digit just before the decimal point.
- "Tens" refers to the digit to the left of the ones place.
- "Tenths" refers to the first digit after the decimal point.
(a) Two ones and five-tenths
This means we have:
2 in the ones place.
5 in the tenths place.
Mathematically, this is $2 \times 1 + 5 \times \frac{1}{10}$.
$= 2 + 0.5$
$= 2.5$
So, "Two ones and five-tenths" as a decimal is 2.5.
(b) Thirty and one-tenth
"Thirty" means 3 in the tens place and 0 in the ones place.
This means we have:
3 in the tens place.
0 in the ones place.
1 in the tenths place.
Mathematically, this is $3 \times 10 + 0 \times 1 + 1 \times \frac{1}{10}$.
$= 30 + 0 + 0.1$
$= 30.1$
So, "Thirty and one-tenth" as a decimal is 30.1.
Example 3: Write each of the following as decimals:
(a) $30 + 6 + \frac{2}{10}$
(b) $600 + 2 + \frac{8}{10}$
Answer:
To write these expanded forms as decimals, we combine the whole number parts and place the fractional part (tenths) after the decimal point.
(a) $30 + 6 + \frac{2}{10}$
First, combine the whole number parts:
$30 + 6 = 36$
Next, consider the fractional part:
$\frac{2}{10}$ represents 2 tenths, which is written as 0.2 in decimal form.
Combine the whole number part and the decimal part:
$36 + 0.2 = 36.2$
So, $30 + 6 + \frac{2}{10}$ as a decimal is 36.2.
(b) $600 + 2 + \frac{8}{10}$
First, combine the whole number parts:
$600 + 2 = 602$
Next, consider the fractional part:
$\frac{8}{10}$ represents 8 tenths, which is written as 0.8 in decimal form.
Combine the whole number part and the decimal part:
$602 + 0.8 = 602.8$
So, $600 + 2 + \frac{8}{10}$ as a decimal is 602.8.
Exercise 8.1
Question 1. Write the following as numbers in the given table.
(a)

(b)
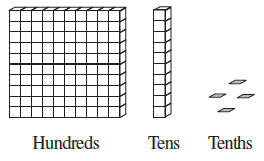
| Hundreds (100) |
Tens (10) |
Ones (1) |
Tenths $\left( \frac{1}{10} \right)$ |
| $ $ | |||
| $ $ |
Answer:
We need to count the blocks representing Hundreds (large squares), Tens (columns of 10), Ones (single squares), and Tenths (small individual pieces) in each image and fill the table accordingly.
(a) Analysis of Image (a):
- There are 0 blocks for Hundreds.
- There are 3 blocks for Tens.
- There is 1 block for Ones.
- There are 2 blocks for Tenths.
So the number represented is $0 \times 100 + 3 \times 10 + 1 \times 1 + 2 \times \frac{1}{10} \ $$ = 0 + 30 + 1 + 0.2 \ $$ = 31.2$.
(b) Analysis of Image (b):
- There is 1 block for Hundreds.
- There is 1 block for Tens.
- There are 0 blocks for Ones.
- There are 4 blocks for Tenths.
So the number represented is $1 \times 100 + 1 \times 10 + 0 \times 1 + 4 \times \frac{1}{10} \ $$ = 100 + 10 + 0 + 0.4 = 110.4$.
Now, let's fill the table with these values:
| Hundreds (100) | Tens (10) | Ones (1) | Tenths ($\frac{1}{10}$) |
| 0 | 3 | 1 | 2 |
| 1 | 1 | 0 | 4 |
Question 2. Write the following decimals in the place value table.
(a) 19.4
(b) 0.3
(c) 10.6
(d) 205.9
Answer:
To write the decimals in the place value table, we identify the digit corresponding to each place value (Hundreds, Tens, Ones, Tenths).
(a) 19.4
In 19.4, the digit 1 is in the Tens place, 9 is in the Ones place, and 4 is in the Tenths place.
(b) 0.3
In 0.3, the digit 0 is in the Ones place, and 3 is in the Tenths place.
(c) 10.6
In 10.6, the digit 1 is in the Tens place, 0 is in the Ones place, and 6 is in the Tenths place.
(d) 205.9
In 205.9, the digit 2 is in the Hundreds place, 0 is in the Tens place, 5 is in the Ones place, and 9 is in the Tenths place.
The place value table is filled as follows:
| Number | Hundreds (100) | Tens (10) | Ones (1) | Tenths ($\frac{1}{10}$) |
| (a) 19.4 | 0 | 1 | 9 | 4 |
| (b) 0.3 | 0 | 0 | 0 | 3 |
| (c) 10.6 | 0 | 1 | 0 | 6 |
| (d) 205.9 | 2 | 0 | 5 | 9 |
Question 3. Write each of the following as decimals :
(a) Seven-tenths
(b) Two tens and nine-tenths
(c) Fourteen point six
(d) One hundred and two ones
(e) Six hundred point eight
Answer:
We need to convert the word representation of numbers into their decimal form based on place values.
(a) Seven-tenths
This represents 7 in the tenths place. There is no whole number part mentioned, so the ones place is 0.
Mathematically: $7 \times \frac{1}{10} = 0.7$
The decimal is 0.7.
(b) Two tens and nine-tenths
"Two tens" means $2 \times 10 = 20$.
"Nine-tenths" means $9 \times \frac{1}{10} = 0.9$.
Combining these: $20 + 0.9 = 20.9$
The decimal is 20.9.
(c) Fourteen point six
"Fourteen" is the whole number 14.
"Point" indicates the decimal point.
"Six" after the decimal point means 6 in the tenths place.
The decimal is 14.6.
(d) One hundred and two ones
"One hundred" means $1 \times 100 = 100$.
"Two ones" means $2 \times 1 = 2$.
Combining the whole number parts: $100 + 2 = 102$.
There is no fractional part mentioned (no tenths). We can write this as a decimal by adding a decimal point and a zero in the tenths place.
The decimal is 102.0 (or simply 102).
(e) Six hundred point eight
"Six hundred" is the whole number 600.
"Point" indicates the decimal point.
"Eight" after the decimal point means 8 in the tenths place.
The decimal is 600.8.
Question 4. Write each of the following as decimals:
(a) $\frac{5}{10}$
(b) 3 + $\frac{7}{10}$
(c) 200 + 60 + 5 + $\frac{1}{10}$
(d) 70 + $\frac{8}{10}$
(e) $\frac{88}{10}$
(f) $4\frac{2}{10}$
(g) $\frac{3}{2}$
(h) $\frac{2}{5}$
(i) $\frac{12}{5}$
(j) $3\frac{3}{5}$
(k) $4\frac{1}{2}$
Answer:
To write the given expressions as decimals, we convert fractions with a denominator of 10 directly to decimals. For other fractions, we first convert them to equivalent fractions with a denominator of 10, or perform division.
(a) $\frac{5}{10}$
This fraction represents 5 tenths.
$\frac{5}{10} = 0.5$
The decimal is 0.5.
(b) 3 + $\frac{7}{10}$
This is a whole number plus 7 tenths.
$\frac{7}{10} = 0.7$
$3 + 0.7 = 3.7$
The decimal is 3.7.
(c) 200 + 60 + 5 + $\frac{1}{10}$
First, sum the whole number parts:
$200 + 60 + 5 = 265$
The fractional part is 1 tenth:
$\frac{1}{10} = 0.1$
Combine them:
$265 + 0.1 = 265.1$
The decimal is 265.1.
(d) 70 + $\frac{8}{10}$
This is a whole number plus 8 tenths.
$\frac{8}{10} = 0.8$
$70 + 0.8 = 70.8$
The decimal is 70.8.
(e) $\frac{88}{10}$
To convert this improper fraction to a decimal, we divide the numerator by the denominator:
$88 \div 10 = 8.8$
Alternatively, we can write it as a mixed number: $\frac{88}{10} = 8 \frac{8}{10} = 8 + \frac{8}{10} \ $$ = 8 + 0.8 = 8.8$.
The decimal is 8.8.
(f) $4\frac{2}{10}$
This is a mixed number. It means $4 + \frac{2}{10}$.
$\frac{2}{10} = 0.2$
$4 + 0.2 = 4.2$
The decimal is 4.2.
(g) $\frac{3}{2}$
To write this as a decimal, we can convert it to an equivalent fraction with a denominator of 10.
Multiply the numerator and denominator by 5:
$\frac{3}{2} = \frac{3 \times 5}{2 \times 5} = \frac{15}{10}$
Now, convert $\frac{15}{10}$ to a decimal:
$\frac{15}{10} = 1.5$
Alternatively, perform division: $3 \div 2 = 1.5$.
The decimal is 1.5.
(h) $\frac{2}{5}$
Convert to an equivalent fraction with a denominator of 10.
Multiply the numerator and denominator by 2:
$\frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10}$
Convert $\frac{4}{10}$ to a decimal:
$\frac{4}{10} = 0.4$
Alternatively, perform division: $2 \div 5 = 0.4$.
The decimal is 0.4.
(i) $\frac{12}{5}$
Convert to an equivalent fraction with a denominator of 10.
Multiply the numerator and denominator by 2:
$\frac{12}{5} = \frac{12 \times 2}{5 \times 2} = \frac{24}{10}$
Convert $\frac{24}{10}$ to a decimal:
$\frac{24}{10} = 2.4$
Alternatively, perform division: $12 \div 5 = 2.4$.
The decimal is 2.4.
(j) $3\frac{3}{5}$
This is a mixed number: $3 + \frac{3}{5}$.
First, convert the fractional part $\frac{3}{5}$ to tenths:
$\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}$
Now substitute back into the mixed number expression:
$3 + \frac{6}{10} = 3 + 0.6 = 3.6$
The decimal is 3.6.
(k) $4\frac{1}{2}$
This is a mixed number: $4 + \frac{1}{2}$.
First, convert the fractional part $\frac{1}{2}$ to tenths:
$\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}$
Now substitute back into the mixed number expression:
$4 + \frac{5}{10} = 4 + 0.5 = 4.5$
The decimal is 4.5.
Question 5. Write the following decimals as fractions. Reduce the fractions to lowest form.
(a) 0.6
(b) 2.5
(c) 1.0
(d) 3.8
(e) 13.7
(f) 21.2
(g) 6.4
Answer:
To convert a decimal to a fraction, we write the decimal as a number over its place value (e.g., tenths, hundredths). Then, we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
(a) 0.6
The digit 6 is in the tenths place.
$0.6 = \frac{6}{10}$
The GCD of 6 and 10 is 2. Divide both numerator and denominator by 2:
$\frac{\cancel{6}^3}{\cancel{10}_5} = \frac{3}{5}$
The fraction in lowest form is $\frac{3}{5}$.
(b) 2.5
This is 2 and 5 tenths.
$2.5 = 2 \frac{5}{10} = \frac{2 \times 10 + 5}{10} = \frac{25}{10}$
The GCD of 25 and 10 is 5. Divide both numerator and denominator by 5:
$\frac{\cancel{25}^5}{\cancel{10}_2} = \frac{5}{2}$
The fraction in lowest form is $\frac{5}{2}$.
(c) 1.0
This is simply the whole number 1.
$1.0 = 1 = \frac{1}{1}$
Alternatively, write as 10 tenths:
$1.0 = \frac{10}{10}$
The GCD of 10 and 10 is 10. Divide both numerator and denominator by 10:
$\frac{\cancel{10}^1}{\cancel{10}_1} = \frac{1}{1}$
The fraction in lowest form is $\frac{1}{1}$ (or simply 1).
(d) 3.8
This is 3 and 8 tenths.
$3.8 = 3 \frac{8}{10} = \frac{3 \times 10 + 8}{10} = \frac{38}{10}$
The GCD of 38 and 10 is 2. Divide both numerator and denominator by 2:
$\frac{\cancel{38}^{19}}{\cancel{10}_5} = \frac{19}{5}$
The fraction in lowest form is $\frac{19}{5}$.
(e) 13.7
This is 13 and 7 tenths.
$13.7 = 13 \frac{7}{10} = \frac{13 \times 10 + 7}{10} = \frac{137}{10}$
The GCD of 137 and 10 is 1 (137 is a prime number not divisible by 2 or 5).
The fraction is already in its lowest form: $\frac{137}{10}$.
(f) 21.2
This is 21 and 2 tenths.
$21.2 = 21 \frac{2}{10} = \frac{21 \times 10 + 2}{10} = \frac{212}{10}$
The GCD of 212 and 10 is 2. Divide both numerator and denominator by 2:
$\frac{\cancel{212}^{106}}{\cancel{10}_5} = \frac{106}{5}$
The fraction in lowest form is $\frac{106}{5}$.
(g) 6.4
This is 6 and 4 tenths.
$6.4 = 6 \frac{4}{10} = \frac{6 \times 10 + 4}{10} = \frac{64}{10}$
The GCD of 64 and 10 is 2. Divide both numerator and denominator by 2:
$\frac{\cancel{64}^{32}}{\cancel{10}_5} = \frac{32}{5}$
The fraction in lowest form is $\frac{32}{5}$.
Question 6. Express the following as cm using decimals.
(a) 2 mm
(b) 30 mm
(c) 116 mm
(d) 4 cm 2 mm
(e) 162 mm
(f) 83 mm
Answer:
We know the relationship between centimeters (cm) and millimeters (mm):
10 mm = 1 cm
Therefore, 1 mm = $\frac{1}{10}$ cm = 0.1 cm.
To convert millimeters to centimeters, we divide the number of millimeters by 10.
(a) 2 mm
$2 \, \text{mm} = \frac{2}{10} \, \text{cm}$
$= 0.2 \, \text{cm}$
So, 2 mm = 0.2 cm.
(b) 30 mm
$30 \, \text{mm} = \frac{30}{10} \, \text{cm}$
$= 3.0 \, \text{cm}$
So, 30 mm = 3.0 cm.
(c) 116 mm
$116 \, \text{mm} = \frac{116}{10} \, \text{cm}$
$= 11.6 \, \text{cm}$
So, 116 mm = 11.6 cm.
(d) 4 cm 2 mm
This means 4 cm plus 2 mm.
First, convert 2 mm to cm:
$2 \, \text{mm} = \frac{2}{10} \, \text{cm} = 0.2 \, \text{cm}$
Now, add this to the 4 cm:
$4 \, \text{cm} + 2 \, \text{mm} = 4 \, \text{cm} + 0.2 \, \text{cm}$
$= 4.2 \, \text{cm}$
So, 4 cm 2 mm = 4.2 cm.
(e) 162 mm
$162 \, \text{mm} = \frac{162}{10} \, \text{cm}$
$= 16.2 \, \text{cm}$
So, 162 mm = 16.2 cm.
(f) 83 mm
$83 \, \text{mm} = \frac{83}{10} \, \text{cm}$
$= 8.3 \, \text{cm}$
So, 83 mm = 8.3 cm.
Question 7. Between which two whole numbers on the number line are the given numbers lie? Which of these whole numbers is nearer the number?

(a) 0.8
(b) 5.1
(c) 2.6
(d) 6.4
(e) 9.1
(f) 4.9
Answer:
To find the whole numbers between which a decimal lies, we look at the whole number part of the decimal. The decimal lies between this whole number and the next consecutive whole number.
To determine which whole number is nearer, we look at the tenths digit (the first digit after the decimal point). If the tenths digit is 5 or greater (0.5, 0.6, 0.7, 0.8, 0.9), the decimal is nearer to the next higher whole number. If the tenths digit is less than 5 (0.1, 0.2, 0.3, 0.4), the decimal is nearer to the preceding whole number (the whole number part of the decimal).
(a) 0.8
The number 0.8 lies between the whole numbers 0 and 1.
The tenths digit is 8, which is greater than 5.
Therefore, 0.8 is nearer to the whole number 1.
(b) 5.1
The number 5.1 lies between the whole numbers 5 and 6.
The tenths digit is 1, which is less than 5.
Therefore, 5.1 is nearer to the whole number 5.
(c) 2.6
The number 2.6 lies between the whole numbers 2 and 3.
The tenths digit is 6, which is greater than 5.
Therefore, 2.6 is nearer to the whole number 3.
(d) 6.4
The number 6.4 lies between the whole numbers 6 and 7.
The tenths digit is 4, which is less than 5.
Therefore, 6.4 is nearer to the whole number 6.
(e) 9.1
The number 9.1 lies between the whole numbers 9 and 10.
The tenths digit is 1, which is less than 5.
Therefore, 9.1 is nearer to the whole number 9.
(f) 4.9
The number 4.9 lies between the whole numbers 4 and 5.
The tenths digit is 9, which is greater than 5.
Therefore, 4.9 is nearer to the whole number 5.
Question 8. Show the following numbers on the number line.
(a) 0.2
(b) 1.9
(c) 1.1
(d) 2.5
Answer:
To show decimal numbers on a number line, we first draw a line and mark the whole numbers (integers). Then, we divide the segment between any two consecutive whole numbers into 10 equal parts. Each of these smaller parts represents one-tenth (0.1).
The following number line from 0 to 3 shows the location of all the given numbers.
(a) 0.2
The number 0.2 lies between the whole numbers 0 and 1. It is located at the second mark to the right of 0.
(b) 1.9
The number 1.9 lies between the whole numbers 1 and 2. It is located at the ninth mark to the right of 1.
(c) 1.1
The number 1.1 lies between the whole numbers 1 and 2. It is located at the first mark to the right of 1.
(d) 2.5
The number 2.5 lies between the whole numbers 2 and 3. It is located at the fifth mark to the right of 2, exactly halfway between 2 and 3.
Question 9. Write the decimal number represented by the points A, B, C, D on the given number line.

Answer:
To find the decimal number represented by each point, we observe its position on the number line.
The number line is divided into segments between whole numbers (0, 1, 2, 3). Each segment (e.g., between 0 and 1) is further divided into 10 equal parts. Each small part represents one-tenth (0.1).
Point A:
Point A is located between 0 and 1.
Counting the marks from 0, point A is at the 8th mark.
Therefore, the decimal number represented by A is $0 + 8 \times 0.1 = 0.8$.
A = 0.8
Point B:
Point B is located between 1 and 2.
Counting the marks from 1, point B is at the 3rd mark.
Therefore, the decimal number represented by B is $1 + 3 \times 0.1 = 1.3$.
B = 1.3
Point C:
Point C is located between 2 and 3.
Counting the marks from 2, point C is at the 2nd mark.
Therefore, the decimal number represented by C is $2 + 2 \times 0.1 = 2.2$.
C = 2.2
Point D:
Point D is located between 2 and 3.
Counting the marks from 2, point D is at the 9th mark.
Therefore, the decimal number represented by D is $2 + 9 \times 0.1 = 2.9$.
D = 2.9
Question 10.
(a) The length of Ramesh’s notebook is 9 cm 5 mm. What will be its length in cm?
(b) The length of a young gram plant is 65 mm. Express its length in cm.
Answer:
We need to use the conversion factor between centimeters (cm) and millimeters (mm).
We know that:
10 mm = 1 cm
Therefore, 1 mm = $\frac{1}{10}$ cm = 0.1 cm.
(a) The length of Ramesh’s notebook is 9 cm 5 mm.
The length is given as a combination of cm and mm.
Length = 9 cm + 5 mm
First, convert the millimeter part to centimeters:
$5 \, \text{mm} = \frac{5}{10} \, \text{cm} = 0.5 \, \text{cm}$
Now, add this to the centimeter part:
Length = $9 \, \text{cm} + 0.5 \, \text{cm}$
Length = $9.5 \, \text{cm}$
So, the length of Ramesh's notebook in cm is 9.5 cm.
(b) The length of a young gram plant is 65 mm.
The length is given entirely in millimeters.
To convert mm to cm, we divide by 10.
Length = $65 \, \text{mm}$
Length = $\frac{65}{10} \, \text{cm}$
Length = $6.5 \, \text{cm}$
So, the length of the young gram plant in cm is 6.5 cm.
Example 4 to 10 (Before Exercise 8.2)
Example 4: Fill the blanks in the table using ‘block’ information given below and write the corresponding number in decimal form.

Answer:
Solution:
We need to analyze the given image which shows blocks representing different place values: Hundreds, Tens, Ones, Tenths, and Hundredths.
Counting the blocks:
By observing the blocks in the figure, we can count the number of blocks for each place value:
- There is 1 block representing Hundreds (100).
- There are 3 blocks representing Tens (10).
- There are 2 blocks representing Ones (1).
- There is 1 block representing Tenths ($\frac{1}{10}$).
- There are 5 blocks representing Hundredths ($\frac{1}{100}$).
Filling the table:
We can now fill the place value table based on the counts above.
| Hundreds (100) | Tens (10) | Ones (1) | Tenths ($\frac{1}{10}$) | Hundredths ($\frac{1}{100}$) |
| 1 | 3 | 2 | 1 | 5 |
Writing the corresponding number in decimal form:
The number is formed by placing the digits from the table into their correct place value positions.
The whole number part is formed by the hundreds, tens, and ones digits: 132.
The decimal part is formed by the tenths and hundredths digits: .15
Combining these gives the number 132.15.
Alternatively, we can write it as a sum:
Number = $(1 \times 100) + (3 \times 10) + (2 \times 1) + (1 \times \frac{1}{10}) + (5 \times \frac{1}{100})$
Number = $100 + 30 + 2 + 0.1 + 0.05$
Number = $132.15$
The corresponding decimal number is 132.15.
Example 5: Fill the blanks in the table and write the corresponding number in decimal form using ‘block’ information given below.
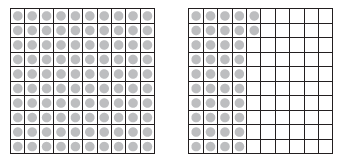
| Ones (1) |
Tenths $\left( \frac{1}{10} \right)$ |
Hundredths $\left( \frac{1}{100} \right)$ |
| $ $ | ||
| $ $ |
Answer:
Solution:
First, let's count the blocks for each place value from the given image:
- Number of Ones blocks = 1
- Number of Tenths blocks = 4
- Number of Hundredths blocks = 2
Now, we fill the place value table with these counts:
| Ones (1) | Tenths ($\frac{1}{10}$) | Hundredths ($\frac{1}{100}$) |
| 1 | 4 | 2 |
To write the corresponding number in decimal form, we combine the values from each place:
Number = (Number of Ones $\times$ 1) + (Number of Tenths $\times \frac{1}{10}$) + (Number of Hundredths $\times \frac{1}{100}$)
Number = $(1 \times 1) + (4 \times 0.1) + (2 \times 0.01)$
Number = $1 + 0.4 + 0.02$
Number = $1.42$
The corresponding decimal number is 1.42.
Example 6: Given the place value table, write the number in decimal form.
|
Hundreds (100) |
Tens (10) |
Ones (1) |
Tenths ($\frac{1}{10}$) |
Hundredths ($\frac{1}{100}$) |
| 2 | 4 | 3 | 2 | 5 |
Answer:
Solution:
The place value table gives the digit for each position:
- Hundreds place: 2
- Tens place: 4
- Ones place: 3
- Tenths place: 2
- Hundredths place: 5
To find the number, we multiply each digit by its corresponding place value and sum the results:
Number = (Hundreds digit $\times$ 100) + (Tens digit $\times$ 10) + (Ones digit $\times$ 1) + (Tenths digit $\times \frac{1}{10}$) + (Hundredths digit $\times \frac{1}{100}$)
Number = $(2 \times 100) + (4 \times 10) + (3 \times 1) + (2 \times \frac{1}{10}) + (5 \times \frac{1}{100})$
Number = $200 + 40 + 3 + \frac{2}{10} + \frac{5}{100}$
Number = $243 + 0.2 + 0.05$
Number = $243.25$
Alternatively, we can directly assemble the number from the table. The digits to the left of the tenths place form the whole number part, and the digits from the tenths place onwards form the decimal part.
Whole number part: 2 (Hundreds) 4 (Tens) 3 (Ones) = 243
Decimal part: 2 (Tenths) 5 (Hundredths) = .25
Combining them gives 243.25.
Example 7: Write as decimals.
(a) $\frac{4}{5}$
(b) $\frac{3}{4}$
(c) $\frac{7}{1000}$
Answer:
Solution:
To convert these fractions to decimals, we can either convert the denominator to a power of 10 (like 10, 100, 1000, etc.) by finding an equivalent fraction, or we can perform division of the numerator by the denominator.
(a) $\frac{4}{5}$
Method 1: Equivalent Fraction
We want a denominator of 10. To get 10 from 5, we multiply by 2.
Multiply both the numerator and the denominator by 2:
$\frac{4}{5} = \frac{4 \times 2}{5 \times 2} = \frac{8}{10}$
A fraction with a denominator of 10 means the numerator represents the tenths place.
$\frac{8}{10} = 0.8$
Method 2: Division
Divide the numerator 4 by the denominator 5:
$4 \div 5 = 0.8$
The decimal is 0.8.
(b) $\frac{3}{4}$
Method 1: Equivalent Fraction
We can convert the denominator to 100. To get 100 from 4, we multiply by 25.
Multiply both the numerator and the denominator by 25:
$\frac{3}{4} = \frac{3 \times 25}{4 \times 25} = \frac{75}{100}$
A fraction with a denominator of 100 means the numerator represents the number of hundredths.
$\frac{75}{100} = 0.75$
Method 2: Division
Divide the numerator 3 by the denominator 4:
$3 \div 4 = 0.75$
The decimal is 0.75.
(c) $\frac{7}{1000}$
Method 1: Direct Conversion
The denominator is already a power of 10 (1000).
This fraction represents 7 thousandths.
To write this as a decimal, we need three digits after the decimal point (for thousandths). The digit 7 goes in the thousandths place.
$\frac{7}{1000} = 0.007$
Method 2: Division
Divide the numerator 7 by the denominator 1000:
$7 \div 1000 = 0.007$
The decimal is 0.007.
Example 8: Write as fractions in lowest terms.
(a) 0.04
(b) 2.34
(c) 0.342
Answer:
(a) 0.04
First, we write the decimal as a fraction. The number 0.04 means "four hundredths", which can be written as a fraction with a denominator of 100.
$0.04 = \frac{4}{100}$
Now, we simplify the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor, which is 4.
$\frac{\cancel{4}^1}{\cancel{100}_{25}} = \frac{1}{25}$
Therefore, the fraction in lowest terms is $\frac{1}{25}$.
(b) 2.34
First, we write the decimal as an improper fraction. The number 2.34 can be written as 234 divided by 100, since the last digit is in the hundredths place.
$2.34 = \frac{234}{100}$
Now, we simplify the fraction. Both the numerator and the denominator are even, so we can divide them by their common factor, 2.
$\frac{\cancel{234}^{117}}{\cancel{100}_{50}} = \frac{117}{50}$
This fraction cannot be simplified further. It can also be expressed as a mixed fraction.
$\frac{117}{50} = 2\frac{17}{50}$
Therefore, the fraction in lowest terms is $\frac{117}{50}$ or $2\frac{17}{50}$.
(c) 0.342
First, we write the decimal as a fraction. The number 0.342 means "three hundred forty-two thousandths", which can be written as a fraction with a denominator of 1000.
$0.342 = \frac{342}{1000}$
Now, we simplify the fraction. Both the numerator and the denominator are even, so we can divide them by 2.
$\frac{\cancel{342}^{171}}{\cancel{1000}_{500}} = \frac{171}{500}$
This fraction cannot be simplified further.
Therefore, the fraction in lowest terms is $\frac{171}{500}$.
Example 9: Write each of the following as a decimal.
(a) 200 + 30 + 5 + $\frac{2}{10}$ + $\frac{9}{100}$
(b) 50 + $\frac{1}{10}$ + $\frac{6}{100}$
(c) 16 + $\frac{3}{10}$ + $\frac{5}{1000}$
Answer:
Solution:
To write these expanded forms as decimals, we first sum the whole number parts. Then, we convert the fractional parts to their decimal equivalents (tenths, hundredths, thousandths) and add them to the whole number part.
(a) 200 + 30 + 5 + $\frac{2}{10}$ + $\frac{9}{100}$
Sum the whole number parts:
$200 + 30 + 5 = 235$
Convert the fractional parts to decimals:
$\frac{2}{10} = 0.2$ (2 tenths)
$\frac{9}{100} = 0.09$ (9 hundredths)
Combine all parts:
$235 + 0.2 + 0.09 = 235.29$
The decimal is 235.29.
(b) 50 + $\frac{1}{10}$ + $\frac{6}{100}$
The whole number part is 50.
Convert the fractional parts to decimals:
$\frac{1}{10} = 0.1$ (1 tenth)
$\frac{6}{100} = 0.06$ (6 hundredths)
Combine all parts:
$50 + 0.1 + 0.06 = 50.16$
The decimal is 50.16.
(c) 16 + $\frac{3}{10}$ + $\frac{5}{1000}$
The whole number part is 16.
Convert the fractional parts to decimals:
$\frac{3}{10} = 0.3$ (3 tenths)
$\frac{5}{1000} = 0.005$ (5 thousandths)
Combine all parts. Note that there are no hundredths, so we place a 0 in the hundredths place:
$16 + 0.3 + 0.005 = 16.305$
The decimal is 16.305.
Example 10: Write each of the following as a decimal.
(a) Three hundred six and seven-hundredths
(b) Eleven point two three five
(c) Nine and twenty five thousandths
Answer:
Solution:
We need to translate the number names into their numerical decimal form, paying attention to place values like tenths, hundredths, and thousandths.
(a) Three hundred six and seven-hundredths
"Three hundred six" represents the whole number part: 306.
"and" indicates the position of the decimal point.
"seven-hundredths" means 7 in the hundredths place. The hundredths place is the second digit after the decimal point. Since no tenths are mentioned, the tenths place is 0.
So, the fractional part is $\frac{7}{100}$, which is written as 0.07.
Combining the whole number part and the decimal part: $306 + 0.07 = 306.07$.
The decimal is 306.07.
(b) Eleven point two three five
"Eleven" represents the whole number part: 11.
"point" indicates the decimal point.
"two three five" represents the digits after the decimal point in order: 2 in the tenths place, 3 in the hundredths place, and 5 in the thousandths place.
So, the decimal part is .235.
Combining the parts gives: 11.235.
The decimal is 11.235.
(c) Nine and twenty five thousandths
"Nine" represents the whole number part: 9.
"and" indicates the position of the decimal point.
"twenty five thousandths" means the fraction $\frac{25}{1000}$. To write this as a decimal, the last digit (5) must be in the thousandths place (the third place after the decimal point). We need three digits after the decimal point. Since 25 only has two digits, we place a 0 in the tenths place.
So, the fractional part is $\frac{25}{1000}$, which is written as 0.025.
Combining the whole number part and the decimal part: $9 + 0.025 = 9.025$.
The decimal is 9.025.
Exercise 8.2
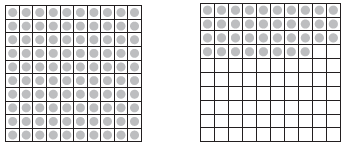
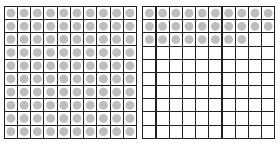
Question 1. Complete the table with the help of these boxes and use decimals to write the number.
(a)

(b)
(c)
|
Ones |
Tenths |
Hundredths |
Number |
|
| (a) | ||||
| (b) | ||||
| (c) |
Answer:
Solution:
We count the number of blocks for Ones, Tenths, and Hundredths in each image and then write the corresponding decimal number.
- Ones are represented by large squares (100 small squares).
- Tenths are represented by columns (10 small squares).
- Hundredths are represented by small individual squares.
Analysis:
(a)
- Ones: 0
- Tenths: 2
- Hundredths: 6
- Number = $0 \times 1 + 2 \times \frac{1}{10} + 6 \times \frac{1}{100} = 0 + 0.2 + 0.06 = 0.26$
(b)
- Ones: 1
- Tenths: 3
- Hundredths: 8
- Number = $1 \times 1 + 3 \times \frac{1}{10} + 8 \times \frac{1}{100} = 1 + 0.3 + 0.08 = 1.38$
(c)
- Ones: 1
- Tenths: 2
- Hundredths: 8
- Number = $1 \times 1 + 2 \times \frac{1}{10} + 8 \times \frac{1}{100} = 1 + 0.2 + 0.08 = 1.28$
Completed Table:
| Ones | Tenths | Hundredths | Number | |
| (a) | 0 | 2 | 6 | 0.26 |
| (b) | 1 | 3 | 8 | 1.38 |
| (c) | 1 | 2 | 8 | 1.28 |
Question 2. Write the numbers given in the following place value table in decimal form.
|
Hundreds (100) |
Tens (10) |
Ones (1) |
Tenths ($\frac{1}{10}$) |
Hundredths ($\frac{1}{100}$) |
Thousandths ($\frac{1}{1000}$) |
|
| (a) | 0 | 0 | 3 | 2 | 5 | 0 |
| (b) | 1 | 0 | 2 | 6 | 3 | 0 |
| (c) | 0 | 3 | 0 | 0 | 2 | 5 |
| (d) | 2 | 1 | 1 | 9 | 0 | 2 |
| (e) | 0 | 1 | 2 | 2 | 4 | 1 |
Answer:
Solution:
We can write the decimal form of each number by combining the digits from the place value table. The digits in the Hundreds, Tens, and Ones places form the whole number part, and the digits in the Tenths, Hundredths, and Thousandths places form the decimal part.
(a)
Number = $0 \times 100 + 0 \times 10 + 3 \times 1 + 2 \times \frac{1}{10} + 5 \times \frac{1}{100} + 0 \times \frac{1}{1000}$
Number = $0 + 0 + 3 + 0.2 + 0.05 + 0$
Number = $3.25$
The decimal form is 3.25.
(b)
Number = $1 \times 100 + 0 \times 10 + 2 \times 1 + 6 \times \frac{1}{10} + 3 \times \frac{1}{100} + 0 \times \frac{1}{1000}$
Number = $100 + 0 + 2 + 0.6 + 0.03 + 0$
Number = $102.63$
The decimal form is 102.63.
(c)
Number = $0 \times 100 + 3 \times 10 + 0 \times 1 + 0 \times \frac{1}{10} + 2 \times \frac{1}{100} + 5 \times \frac{1}{1000}$
Number = $0 + 30 + 0 + 0 + 0.02 + 0.005$
Number = $30.025$
The decimal form is 30.025.
(d)
Number = $2 \times 100 + 1 \times 10 + 1 \times 1 + 9 \times \frac{1}{10} + 0 \times \frac{1}{100} + 2 \times \frac{1}{1000}$
Number = $200 + 10 + 1 + 0.9 + 0 + 0.002$
Number = $211.902$
The decimal form is 211.902.
(e)
Number = $0 \times 100 + 1 \times 10 + 2 \times 1 + 2 \times \frac{1}{10} + 4 \times \frac{1}{100} + 1 \times \frac{1}{1000}$
Number = $0 + 10 + 2 + 0.2 + 0.04 + 0.001$
Number = $12.241$
The decimal form is 12.241.
Question 3. Write the following decimals in the place value table.
(a) 0.29
(b) 2.08
(c) 19.60
(d) 148.32
(e) 200.812
Answer:
Solution:
To write the given decimal numbers in the place value table, we need to identify the digit occupying each place (Hundreds, Tens, Ones, Tenths, Hundredths, Thousandths) for each number.
- For 0.29: 0 is in the Ones place, 2 is in the Tenths place, 9 is in the Hundredths place.
- For 2.08: 2 is in the Ones place, 0 is in the Tenths place, 8 is in the Hundredths place.
- For 19.60: 1 is in the Tens place, 9 is in the Ones place, 6 is in the Tenths place, 0 is in the Hundredths place.
- For 148.32: 1 is in the Hundreds place, 4 is in the Tens place, 8 is in the Ones place, 3 is in the Tenths place, 2 is in the Hundredths place.
- For 200.812: 2 is in the Hundreds place, 0 is in the Tens place, 0 is in the Ones place, 8 is in the Tenths place, 1 is in the Hundredths place, 2 is in the Thousandths place.
The place value table is as follows:
| Number | Hundreds (100) | Tens (10) | Ones (1) | Tenths ($\frac{1}{10}$) | Hundredths ($\frac{1}{100}$) | Thousandths ($\frac{1}{1000}$) |
| (a) 0.29 | 0 | 0 | 0 | 2 | 9 | 0 |
| (b) 2.08 | 0 | 0 | 2 | 0 | 8 | 0 |
| (c) 19.60 | 0 | 1 | 9 | 6 | 0 | 0 |
| (d) 148.32 | 1 | 4 | 8 | 3 | 2 | 0 |
| (e) 200.812 | 2 | 0 | 0 | 8 | 1 | 2 |
Question 4. Write each of the following as decimals.
(a) 20 + 9 + $\frac{4}{10}$ + $\frac{1}{100}$
(b) 137 + $\frac{5}{100}$
(c) $\frac{7}{10}$ + $\frac{6}{100}$ + $\frac{4}{1000}$
(d) 23 + $\frac{2}{10}$ + $\frac{6}{1000}$
(e) 700 + 20 + 5 + $\frac{9}{100}$
Answer:
Solution:
We combine the whole number parts and the fractional parts (tenths, hundredths, thousandths) to form the decimal number.
(a) 20 + 9 + $\frac{4}{10}$ + $\frac{1}{100}$
Whole number part = $20 + 9 = 29$.
Fractional part = $\frac{4}{10} + \frac{1}{100} = 0.4 + 0.01 = 0.41$.
Combining these: $29 + 0.41 = 29.41$.
The decimal is 29.41.
(b) 137 + $\frac{5}{100}$
Whole number part = $137$.
Fractional part = $\frac{5}{100} = 0.05$. (Note: There are 0 tenths).
Combining these: $137 + 0.05 = 137.05$.
The decimal is 137.05.
(c) $\frac{7}{10}$ + $\frac{6}{100}$ + $\frac{4}{1000}$
There is no whole number part, so it is 0.
Fractional part = $\frac{7}{10} + \frac{6}{100} + \frac{4}{1000} = 0.7 + 0.06 + 0.004 = 0.764$.
The decimal is 0.764.
(d) 23 + $\frac{2}{10}$ + $\frac{6}{1000}$
Whole number part = $23$.
Fractional part = $\frac{2}{10} + \frac{6}{1000} = 0.2 + 0.006 = 0.206$. (Note: There are 0 hundredths).
Combining these: $23 + 0.206 = 23.206$.
The decimal is 23.206.
(e) 700 + 20 + 5 + $\frac{9}{100}$
Whole number part = $700 + 20 + 5 = 725$.
Fractional part = $\frac{9}{100} = 0.09$. (Note: There are 0 tenths).
Combining these: $725 + 0.09 = 725.09$.
The decimal is 725.09.
Question 5. Write each of the following decimals in words.
(a) 0.03
(b) 1.20
(c) 108.56
(d) 10.07
(e) 0.032
(f) 5.008
Answer:
Solution:
To write decimals in words, we read the whole number part, say "point" or "and" for the decimal point, and then read the digits after the decimal point, followed by the place value of the last digit (tenths, hundredths, thousandths).
(a) 0.03
The whole number part is zero. The digits after the decimal point are 0 and 3. The last digit, 3, is in the hundredths place.
In words: Zero point zero three or Three hundredths.
(b) 1.20
The whole number part is one. The digits after the decimal point are 2 and 0. The last digit, 0, is in the hundredths place.
In words: One point two zero or One and twenty hundredths.
(c) 108.56
The whole number part is one hundred eight. The digits after the decimal point are 5 and 6. The last digit, 6, is in the hundredths place.
In words: One hundred eight point five six or One hundred eight and fifty-six hundredths.
(d) 10.07
The whole number part is ten. The digits after the decimal point are 0 and 7. The last digit, 7, is in the hundredths place.
In words: Ten point zero seven or Ten and seven hundredths.
(e) 0.032
The whole number part is zero. The digits after the decimal point are 0, 3, and 2. The last digit, 2, is in the thousandths place.
In words: Zero point zero three two or Thirty-two thousandths.
(f) 5.008
The whole number part is five. The digits after the decimal point are 0, 0, and 8. The last digit, 8, is in the thousandths place.
In words: Five point zero zero eight or Five and eight thousandths.
Question 6. Between which two numbers in tenths place on the number line does each of the given number lie?
(a) 0.06
(b) 0.45
(c) 0.19
(d) 0.66
(e) 0.92
(f) 0.57
Answer:
Solution:
To find the two numbers in the tenths place between which a given number lies, we look at the digit in the tenths place of the given number. The number lies between the value formed by the digits up to the tenths place and the next consecutive tenth.
(a) 0.06
The tenths digit is 0. The number 0.06 is greater than 0.0 and less than 0.1.
Therefore, 0.06 lies between 0.0 and 0.1.
(b) 0.45
The tenths digit is 4. The number 0.45 is greater than 0.4 and less than 0.5.
Therefore, 0.45 lies between 0.4 and 0.5.
(c) 0.19
The tenths digit is 1. The number 0.19 is greater than 0.1 and less than 0.2.
Therefore, 0.19 lies between 0.1 and 0.2.
(d) 0.66
The tenths digit is 6. The number 0.66 is greater than 0.6 and less than 0.7.
Therefore, 0.66 lies between 0.6 and 0.7.
(e) 0.92
The tenths digit is 9. The number 0.92 is greater than 0.9 and less than the next tenth, which is 1.0.
Therefore, 0.92 lies between 0.9 and 1.0.
(f) 0.57
The tenths digit is 5. The number 0.57 is greater than 0.5 and less than 0.6.
Therefore, 0.57 lies between 0.5 and 0.6.
Question 7. Write as fractions in lowest terms.
(a) 0.60
(b) 0.05
(c) 0.75
(d) 0.18
(e) 0.25
(f) 0.125
(g) 0.066
Answer:
Solution:
To write decimals as fractions in the lowest terms, we first convert the decimal to a fraction with a denominator of 10, 100, 1000, etc., based on the number of decimal places. Then, we simplify the fraction by dividing the numerator and the denominator by their greatest common divisor (GCD).
(a) 0.60
The decimal 0.60 has two digits after the decimal point, so the denominator is 100.
$0.60 = \frac{60}{100}$
The GCD of 60 and 100 is 20.
Simplify the fraction:
$\frac{\cancel{60}^3}{\cancel{100}_5} = \frac{3}{5}$
The fraction in lowest terms is $\frac{3}{5}$.
(b) 0.05
The decimal 0.05 has two digits after the decimal point, so the denominator is 100.
$0.05 = \frac{5}{100}$
The GCD of 5 and 100 is 5.
Simplify the fraction:
$\frac{\cancel{5}^1}{\cancel{100}_{20}} = \frac{1}{20}$
The fraction in lowest terms is $\frac{1}{20}$.
(c) 0.75
The decimal 0.75 has two digits after the decimal point, so the denominator is 100.
$0.75 = \frac{75}{100}$
The GCD of 75 and 100 is 25.
Simplify the fraction:
$\frac{\cancel{75}^3}{\cancel{100}_4} = \frac{3}{4}$
The fraction in lowest terms is $\frac{3}{4}$.
(d) 0.18
The decimal 0.18 has two digits after the decimal point, so the denominator is 100.
$0.18 = \frac{18}{100}$
The GCD of 18 and 100 is 2.
Simplify the fraction:
$\frac{\cancel{18}^9}{\cancel{100}_{50}} = \frac{9}{50}$
The fraction in lowest terms is $\frac{9}{50}$.
(e) 0.25
The decimal 0.25 has two digits after the decimal point, so the denominator is 100.
$0.25 = \frac{25}{100}$
The GCD of 25 and 100 is 25.
Simplify the fraction:
$\frac{\cancel{25}^1}{\cancel{100}_4} = \frac{1}{4}$
The fraction in lowest terms is $\frac{1}{4}$.
(f) 0.125
The decimal 0.125 has three digits after the decimal point, so the denominator is 1000.
$0.125 = \frac{125}{1000}$
The GCD of 125 and 1000 is 125. ($1000 = 8 \times 125$)
Simplify the fraction:
$\frac{\cancel{125}^1}{\cancel{1000}_8} = \frac{1}{8}$
The fraction in lowest terms is $\frac{1}{8}$.
(g) 0.066
The decimal 0.066 has three digits after the decimal point, so the denominator is 1000.
$0.066 = \frac{66}{1000}$
The GCD of 66 and 1000 is 2.
Simplify the fraction:
$\frac{\cancel{66}^{33}}{\cancel{1000}_{500}} = \frac{33}{500}$
The fraction in lowest terms is $\frac{33}{500}$.
Example 11 (Before Exercise 8.3)
Example 11: Which is greater?
(a) 1 or 0.99
(b) 1.09 or 1.093
Answer:
Solution:
To compare two decimal numbers, we follow these steps:
- Compare the whole number parts (the digits to the left of the decimal point). The number with the larger whole part is greater.
- If the whole number parts are equal, compare the digits in the tenths place (the first digit after the decimal point). The number with the larger tenths digit is greater.
- If the tenths digits are also equal, compare the digits in the hundredths place (the second digit after the decimal point). The number with the larger hundredths digit is greater.
- Continue comparing digits from left to right in the decimal part until you find a difference.
- It can be helpful to make the numbers have the same number of decimal places (like decimals) by adding trailing zeros.
(a) 1 or 0.99
First, compare the whole number parts.
The whole part of 1 is 1.
The whole part of 0.99 is 0.
Since $1 > 0$, the number 1 is greater than 0.99.
Alternatively, we can write 1 as a decimal with two decimal places: $1 = 1.00$.
Compare 1.00 and 0.99.
Comparing whole parts: $1 > 0$.
Thus, 1 is greater than 0.99.
(b) 1.09 or 1.093
First, compare the whole number parts.
The whole part of 1.09 is 1.
The whole part of 1.093 is 1.
The whole parts are equal ($1 = 1$).
Next, compare the tenths digits.
The tenths digit of 1.09 is 0.
The tenths digit of 1.093 is 0.
The tenths digits are equal ($0 = 0$).
Next, compare the hundredths digits.
The hundredths digit of 1.09 is 9.
The hundredths digit of 1.093 is 9.
The hundredths digits are equal ($9 = 9$).
Next, compare the thousandths digits. To do this, we can write 1.09 as 1.090 (adding a trailing zero does not change the value).
Compare 1.090 and 1.093.
The thousandths digit of 1.090 is 0.
The thousandths digit of 1.093 is 3.
Since $3 > 0$, the number 1.093 is greater than 1.090.
Thus, 1.093 is greater than 1.09.
Using a table for comparison:
| Number | Ones | . | Tenths | Hundredths | Thousandths |
| 1.09 | 1 | . | 0 | 9 | 0 |
| 1.093 | 1 | . | 0 | 9 | 3 |
Comparing digit by digit from left to right, the first difference occurs in the thousandths place, where $3 > 0$.
Exercise 8.3
Question 1. Which is greater?
(a) 0.3 or 0.4
(b) 0.07 or 0.02
(c) 3 or 0.8
(d) 0.5 or 0.05
(e) 1.23 or 1.2
(f) 0.099 or 0.19
(g) 1.5 or 1.50
(h) 1.431 or 1.490
(i) 3.3 or 3.300
(j) 5.64 or 5.603
Answer:
Solution:
We compare the decimal numbers by comparing their digits from left to right, starting with the whole number part.
(a) 0.3 or 0.4
Compare the whole number parts: Both are 0.
Compare the tenths digits: $3 < 4$.
Therefore, 0.4 is greater than 0.3.
(b) 0.07 or 0.02
Compare the whole number parts: Both are 0.
Compare the tenths digits: Both are 0.
Compare the hundredths digits: $7 > 2$.
Therefore, 0.07 is greater than 0.02.
(c) 3 or 0.8
Compare the whole number parts: The whole part of 3 is 3. The whole part of 0.8 is 0.
Since $3 > 0$.
Therefore, 3 is greater than 0.8.
(d) 0.5 or 0.05
Compare the whole number parts: Both are 0.
Compare the tenths digits: $5 > 0$.
Therefore, 0.5 is greater than 0.05.
(e) 1.23 or 1.2
Write 1.2 as 1.20 to compare like decimals.
Compare the whole number parts: Both are 1.
Compare the tenths digits: Both are 2.
Compare the hundredths digits: $3 > 0$.
Therefore, 1.23 is greater than 1.20 (or 1.2).
(f) 0.099 or 0.19
Write 0.19 as 0.190 to compare like decimals.
Compare the whole number parts: Both are 0.
Compare the tenths digits: $0 < 1$.
Therefore, 0.19 (or 0.190) is greater than 0.099.
(g) 1.5 or 1.50
Write 1.5 as 1.50.
Compare 1.50 and 1.50.
Compare the whole number parts: Both are 1.
Compare the tenths digits: Both are 5.
Compare the hundredths digits: Both are 0.
All digits are the same. Therefore, 1.5 and 1.50 are equal. (Neither is greater).
(h) 1.431 or 1.490
Compare the whole number parts: Both are 1.
Compare the tenths digits: Both are 4.
Compare the hundredths digits: $3 < 9$.
Therefore, 1.490 is greater than 1.431.
(i) 3.3 or 3.300
Write 3.3 as 3.300.
Compare 3.300 and 3.300.
Compare the whole number parts: Both are 3.
Compare the tenths digits: Both are 3.
Compare the hundredths digits: Both are 0.
Compare the thousandths digits: Both are 0.
All digits are the same. Therefore, 3.3 and 3.300 are equal. (Neither is greater).
(j) 5.64 or 5.603
Write 5.64 as 5.640 to compare like decimals.
Compare 5.640 and 5.603.
Compare the whole number parts: Both are 5.
Compare the tenths digits: Both are 6.
Compare the hundredths digits: $4 > 0$.
Therefore, 5.64 (or 5.640) is greater than 5.603.
Question 2. Make five more examples and find the greater number from them.
Answer:
Solution:
Here are five examples comparing two numbers, identifying the greater one in each case:
Example 1: 2.05 vs 2.50
Compare the whole number parts: Both are 2.
Compare the tenths digits: $0 < 5$.
Therefore, 2.50 is greater than 2.05.
Example 2: 10.01 vs 10.1
Write 10.1 as 10.10 to compare like decimals.
Compare the whole number parts: Both are 10.
Compare the tenths digits: $0 < 1$.
Therefore, 10.1 (or 10.10) is greater than 10.01.
Example 3: 0.009 vs 0.01
Write 0.01 as 0.010 to compare like decimals.
Compare the whole number parts: Both are 0.
Compare the tenths digits: Both are 0.
Compare the hundredths digits: $0 < 1$.
Therefore, 0.01 (or 0.010) is greater than 0.009.
Example 4: 7.0 vs 6.999
Compare the whole number parts: $7 > 6$.
Therefore, 7.0 is greater than 6.999.
Example 5: 4.567 vs 4.56
Write 4.56 as 4.560 to compare like decimals.
Compare the whole number parts: Both are 4.
Compare the tenths digits: Both are 5.
Compare the hundredths digits: Both are 6.
Compare the thousandths digits: $7 > 0$.
Therefore, 4.567 is greater than 4.56 (or 4.560).
Exercise 8.4
Question 1. Express as rupees using decimals.
(a) 5 paise
(b) 75 paise
(c) 20 paise
(d) 50 rupees 90 paise
(e) 725 paise
Answer:
Solution:
We know the relationship between rupees and paise:
100 paise = 1 rupee ($\textsf{₹}$)
Therefore, 1 paisa = $\frac{1}{100}$ rupee = $\textsf{₹}$ 0.01.
To convert paise to rupees, we divide the number of paise by 100.
(a) 5 paise
5 paise = $\frac{5}{100}$ rupees
5 paise = $\textsf{₹}$ 0.05
So, 5 paise is equal to $\textsf{₹}$ 0.05.
(b) 75 paise
75 paise = $\frac{75}{100}$ rupees
75 paise = $\textsf{₹}$ 0.75
So, 75 paise is equal to $\textsf{₹}$ 0.75.
(c) 20 paise
20 paise = $\frac{20}{100}$ rupees
20 paise = $\textsf{₹}$ 0.20
So, 20 paise is equal to $\textsf{₹}$ 0.20.
(d) 50 rupees 90 paise
This is 50 rupees plus 90 paise.
First, convert 90 paise to rupees:
90 paise = $\frac{90}{100}$ rupees = $\textsf{₹}$ 0.90
Now, add this to the 50 rupees:
50 rupees + 90 paise = $\textsf{₹}$ 50 + $\textsf{₹}$ 0.90
= $\textsf{₹}$ 50.90
So, 50 rupees 90 paise is equal to $\textsf{₹}$ 50.90.
(e) 725 paise
725 paise = $\frac{725}{100}$ rupees
To divide by 100, move the decimal point two places to the left.
725 paise = $\textsf{₹}$ 7.25
So, 725 paise is equal to $\textsf{₹}$ 7.25.
Question 2. Express as metres using decimals.
(a) 15 cm
(b) 6 cm
(c) 2 m 45 cm
(d) 9 m 7 cm
(e) 419 cm
Answer:
Solution:
We know the relationship between metres (m) and centimetres (cm):
100 cm = 1 m
Therefore, 1 cm = $\frac{1}{100}$ m = 0.01 m.
To convert centimetres to metres, we divide the number of centimetres by 100.
(a) 15 cm
$15 \, \text{cm} = \frac{15}{100} \, \text{m}$
$15 \, \text{cm} = 0.15 \, \text{m}$
So, 15 cm is equal to 0.15 m.
(b) 6 cm
$6 \, \text{cm} = \frac{6}{100} \, \text{m}$
$6 \, \text{cm} = 0.06 \, \text{m}$
So, 6 cm is equal to 0.06 m.
(c) 2 m 45 cm
This is 2 metres plus 45 centimetres.
First, convert 45 cm to metres:
$45 \, \text{cm} = \frac{45}{100} \, \text{m} = 0.45 \, \text{m}$
Now, add this to the 2 metres:
$2 \, \text{m} + 45 \, \text{cm} = 2 \, \text{m} + 0.45 \, \text{m}$
$= 2.45 \, \text{m}$
So, 2 m 45 cm is equal to 2.45 m.
(d) 9 m 7 cm
This is 9 metres plus 7 centimetres.
First, convert 7 cm to metres:
$7 \, \text{cm} = \frac{7}{100} \, \text{m} = 0.07 \, \text{m}$
Now, add this to the 9 metres:
$9 \, \text{m} + 7 \, \text{cm} = 9 \, \text{m} + 0.07 \, \text{m}$
$= 9.07 \, \text{m}$
So, 9 m 7 cm is equal to 9.07 m.
(e) 419 cm
$419 \, \text{cm} = \frac{419}{100} \, \text{m}$
To divide by 100, move the decimal point two places to the left.
$419 \, \text{cm} = 4.19 \, \text{m}$
So, 419 cm is equal to 4.19 m.
Question 3. Express as cm using decimals.
(a) 5 mm
(b) 60 mm
(c) 164 mm
(d) 9 cm 8 mm
(e) 93 mm
Answer:
Solution:
We know the relationship between centimetres (cm) and millimetres (mm):
10 mm = 1 cm
Therefore, 1 mm = $\frac{1}{10}$ cm = 0.1 cm.
To convert millimetres to centimetres, we divide the number of millimetres by 10.
(a) 5 mm
$5 \, \text{mm} = \frac{5}{10} \, \text{cm}$
$5 \, \text{mm} = 0.5 \, \text{cm}$
So, 5 mm is equal to 0.5 cm.
(b) 60 mm
$60 \, \text{mm} = \frac{60}{10} \, \text{cm}$
$60 \, \text{mm} = 6.0 \, \text{cm}$
So, 60 mm is equal to 6.0 cm (or 6 cm).
(c) 164 mm
$164 \, \text{mm} = \frac{164}{10} \, \text{cm}$
$164 \, \text{mm} = 16.4 \, \text{cm}$
So, 164 mm is equal to 16.4 cm.
(d) 9 cm 8 mm
This is 9 centimetres plus 8 millimetres.
First, convert 8 mm to centimetres:
$8 \, \text{mm} = \frac{8}{10} \, \text{cm} = 0.8 \, \text{cm}$
Now, add this to the 9 centimetres:
$9 \, \text{cm} + 8 \, \text{mm} = 9 \, \text{cm} + 0.8 \, \text{cm}$
$= 9.8 \, \text{cm}$
So, 9 cm 8 mm is equal to 9.8 cm.
(e) 93 mm
$93 \, \text{mm} = \frac{93}{10} \, \text{cm}$
$93 \, \text{mm} = 9.3 \, \text{cm}$
So, 93 mm is equal to 9.3 cm.
Question 4. Express as km using decimals.
(a) 8 m
(b) 88 m
(c) 8888 m
(d) 70 km 5 m
Answer:
Solution:
We know the relationship between kilometres (km) and metres (m):
1000 m = 1 km
Therefore, 1 m = $\frac{1}{1000}$ km = 0.001 km.
To convert metres to kilometres, we divide the number of metres by 1000.
(a) 8 m
$8 \, \text{m} = \frac{8}{1000} \, \text{km}$
$8 \, \text{m} = 0.008 \, \text{km}$
So, 8 m is equal to 0.008 km.
(b) 88 m
$88 \, \text{m} = \frac{88}{1000} \, \text{km}$
$88 \, \text{m} = 0.088 \, \text{km}$
So, 88 m is equal to 0.088 km.
(c) 8888 m
$8888 \, \text{m} = \frac{8888}{1000} \, \text{km}$
To divide by 1000, move the decimal point three places to the left.
$8888 \, \text{m} = 8.888 \, \text{km}$
So, 8888 m is equal to 8.888 km.
(d) 70 km 5 m
This is 70 kilometres plus 5 metres.
First, convert 5 m to kilometres:
$5 \, \text{m} = \frac{5}{1000} \, \text{km} = 0.005 \, \text{km}$
Now, add this to the 70 kilometres:
$70 \, \text{km} + 5 \, \text{m} = 70 \, \text{km} + 0.005 \, \text{km}$
$= 70.005 \, \text{km}$
So, 70 km 5 m is equal to 70.005 km.
Question 5. Express as kg using decimals.
(a) 2 g
(b) 100 g
(c) 3750 g
(d) 5 kg 8 g
(e) 26 kg 50 g
Answer:
Solution:
We know the relationship between kilograms (kg) and grams (g):
1000 g = 1 kg
Therefore, 1 g = $\frac{1}{1000}$ kg = 0.001 kg.
To convert grams to kilograms, we divide the number of grams by 1000.
(a) 2 g
$2 \, \text{g} = \frac{2}{1000} \, \text{kg}$
$2 \, \text{g} = 0.002 \, \text{kg}$
So, 2 g is equal to 0.002 kg.
(b) 100 g
$100 \, \text{g} = \frac{100}{1000} \, \text{kg}$
$100 \, \text{g} = 0.100 \, \text{kg}$ or $0.1 \, \text{kg}$
So, 100 g is equal to 0.1 kg.
(c) 3750 g
$3750 \, \text{g} = \frac{3750}{1000} \, \text{kg}$
To divide by 1000, move the decimal point three places to the left.
$3750 \, \text{g} = 3.750 \, \text{kg}$ or $3.75 \, \text{kg}$
So, 3750 g is equal to 3.75 kg.
(d) 5 kg 8 g
This is 5 kilograms plus 8 grams.
First, convert 8 g to kilograms:
$8 \, \text{g} = \frac{8}{1000} \, \text{kg} = 0.008 \, \text{kg}$
Now, add this to the 5 kilograms:
$5 \, \text{kg} + 8 \, \text{g} = 5 \, \text{kg} + 0.008 \, \text{kg}$
$= 5.008 \, \text{kg}$
So, 5 kg 8 g is equal to 5.008 kg.
(e) 26 kg 50 g
This is 26 kilograms plus 50 grams.
First, convert 50 g to kilograms:
$50 \, \text{g} = \frac{50}{1000} \, \text{kg} = 0.050 \, \text{kg}$ or $0.05 \, \text{kg}$
Now, add this to the 26 kilograms:
$26 \, \text{kg} + 50 \, \text{g} = 26 \, \text{kg} + 0.050 \, \text{kg}$
$= 26.050 \, \text{kg}$ or $26.05 \, \text{kg}$
So, 26 kg 50 g is equal to 26.05 kg.
Example 12 to 14 (Before Exercise 8.5)
Example 12: Lata spent ₹ 9.50 for buying a pen and ₹ 2.50 for one pencil. How much money did she spend?
Answer:
Solution:
Given:
Cost of the pen = $\textsf{₹}$ 9.50
Cost of the pencil = $\textsf{₹}$ 2.50
To Find:
Total money spent by Lata.
Calculation:
To find the total money spent, we need to add the cost of the pen and the cost of the pencil.
Total money spent = Cost of pen + Cost of pencil
Total money spent = $\textsf{₹}$ 9.50 + $\textsf{₹}$ 2.50
We perform the addition by aligning the decimal points:
$\begin{array}{ccc} & \textsf{₹} & 9.50 \\ + & \textsf{₹} & 2.50 \\ \hline & \textsf{₹} & 12.00 \\ \hline \end{array}$Total money spent = $\textsf{₹}$ 12.00
Conclusion:
Lata spent a total of $\textsf{₹}$ 12.00.
Example 13: Samson travelled 5 km 52 m by bus, 2 km 265 m by car and the rest 1km 30 m he walked. How much distance did he travel in all?
Answer:
Solution:
Given:
Distance travelled by bus = 5 km 52 m
Distance travelled by car = 2 km 265 m
Distance walked = 1 km 30 m
To Find:
Total distance travelled by Samson.
Calculation:
To find the total distance, we first need to convert all distances to a single unit, kilometers (km), using decimals.
We know that 1000 m = 1 km, so 1 m = $\frac{1}{1000}$ km = 0.001 km.
Distance by bus:
5 km 52 m = 5 km + 52 m
= 5 km + $\frac{52}{1000}$ km
= 5 km + 0.052 km
= 5.052 km
Distance by car:
2 km 265 m = 2 km + 265 m
= 2 km + $\frac{265}{1000}$ km
= 2 km + 0.265 km
= 2.265 km
Distance walked:
1 km 30 m = 1 km + 30 m
= 1 km + $\frac{30}{1000}$ km
= 1 km + 0.030 km
= 1.030 km
Now, add all the distances in km:
Total distance = Distance by bus + Distance by car + Distance walked
Total distance = 5.052 km + 2.265 km + 1.030 km
Performing the addition:
$\begin{array}{ccc} & 5.052 & \text{km} \\ & 2.265 & \text{km} \\ + & 1.030 & \text{km} \\ \hline & 8.347 & \text{km} \\ \hline \end{array}$Total distance = 8.347 km
Conclusion:
Samson travelled a total distance of 8.347 km.
Example 14: Rahul bought 4 kg 90 g of apples, 2 kg 60 g of grapes and 5 kg 300 g of mangoes. Find the total weight of all the fruits he bought.
Answer:
Solution:
Given:
Weight of apples = 4 kg 90 g
Weight of grapes = 2 kg 60 g
Weight of mangoes = 5 kg 300 g
To Find:
The total weight of all the fruits Rahul bought.
Calculation:
To find the total weight, we first convert all weights to kilograms (kg) using decimals.
We know that 1000 g = 1 kg, so 1 g = $\frac{1}{1000}$ kg = 0.001 kg.
Weight of apples in kg:
4 kg 90 g = 4 kg + 90 g
= 4 kg + $\frac{90}{1000}$ kg
= 4 kg + 0.090 kg
= 4.090 kg
Weight of grapes in kg:
2 kg 60 g = 2 kg + 60 g
= 2 kg + $\frac{60}{1000}$ kg
= 2 kg + 0.060 kg
= 2.060 kg
Weight of mangoes in kg:
5 kg 300 g = 5 kg + 300 g
= 5 kg + $\frac{300}{1000}$ kg
= 5 kg + 0.300 kg
= 5.300 kg
Now, add all the weights in kg:
Total weight = Weight of apples + Weight of grapes + Weight of mangoes
Total weight = 4.090 kg + 2.060 kg + 5.300 kg
Performing the addition:
$\begin{array}{ccc} & 4.090 & \text{kg} \\ & 2.060 & \text{kg} \\ + & 5.300 & \text{kg} \\ \hline & 11.450 & \text{kg} \\ \hline \end{array}$Total weight = 11.450 kg
Conclusion:
The total weight of all the fruits Rahul bought is 11.450 kg.
Exercise 8.5
Question 1. Find the sum in each of the following :
(a) 0.007 + 8.5 + 30.08
(b) 15 + 0.632 + 13.8
(c) 27.076 + 0.55 + 0.004
(d) 25.65 + 9.005 + 3.7
(e) 0.75 + 10.425 + 2
(f) 280.69 + 25.2 + 38
Answer:
Solution:
To find the sum of decimal numbers, we write the numbers one below the other, aligning the decimal points. We can add trailing zeros to make them like decimals (same number of decimal places) if needed. Then, we add the numbers column by column from right to left, just like adding whole numbers, placing the decimal point in the sum directly below the decimal points in the numbers being added.
(a) 0.007 + 8.5 + 30.08
Write as like decimals (3 decimal places): 0.007, 8.500, 30.080
$\begin{array}{ccc} & 0.007 \\ & 8.500 \\ + & 30.080 \\ \hline & 38.587 \\ \hline \end{array}$The sum is 38.587.
(b) 15 + 0.632 + 13.8
Write as like decimals (3 decimal places): 15.000, 0.632, 13.800
$\begin{array}{ccc} & 15.000 \\ & 0.632 \\ + & 13.800 \\ \hline & 29.432 \\ \hline \end{array}$The sum is 29.432.
(c) 27.076 + 0.55 + 0.004
Write as like decimals (3 decimal places): 27.076, 0.550, 0.004
$\begin{array}{ccc} & 27.076 \\ & 0.550 \\ + & 0.004 \\ \hline & 27.630 \\ \hline \end{array}$The sum is 27.630 or 27.63.
(d) 25.65 + 9.005 + 3.7
Write as like decimals (3 decimal places): 25.650, 9.005, 3.700
$\begin{array}{ccc} & 25.650 \\ & 9.005 \\ + & 3.700 \\ \hline & 38.355 \\ \hline \end{array}$The sum is 38.355.
(e) 0.75 + 10.425 + 2
Write as like decimals (3 decimal places): 0.750, 10.425, 2.000
$\begin{array}{ccc} & 0.750 \\ & 10.425 \\ + & 2.000 \\ \hline & 13.175 \\ \hline \end{array}$The sum is 13.175.
(f) 280.69 + 25.2 + 38
Write as like decimals (2 decimal places): 280.69, 25.20, 38.00
$\begin{array}{ccc} & 280.69 \\ & 25.20 \\ + & 38.00 \\ \hline & 343.89 \\ \hline \end{array}$The sum is 343.89.
Question 2. Rashid spent ₹ 35.75 for Maths book and ₹ 32.60 for Science book. Find the total amount spent by Rashid.
Answer:
Solution:
Given:
Amount spent on Maths book = $\textsf{₹}$ 35.75
Amount spent on Science book = $\textsf{₹}$ 32.60
To Find:
The total amount spent by Rashid.
Calculation:
To find the total amount spent, we need to add the amounts spent on both books.
Total amount = Amount for Maths book + Amount for Science book
Total amount = $\textsf{₹}$ 35.75 + $\textsf{₹}$ 32.60
We align the decimal points and add:
$\begin{array}{ccc} & \textsf{₹} & 35.75 \\ + & \textsf{₹} & 32.60 \\ \hline & \textsf{₹} & 68.35 \\ \hline \end{array}$Total amount spent = $\textsf{₹}$ 68.35
Conclusion:
The total amount spent by Rashid is $\textsf{₹}$ 68.35.
Question 3. Radhika’s mother gave her ₹ 10.50 and her father gave her ₹ 15.80, find the total amount given to Radhika by the parents.
Answer:
Solution:
Given:
Amount given by Radhika's mother = $\textsf{₹}$ 10.50
Amount given by Radhika's father = $\textsf{₹}$ 15.80
To Find:
The total amount given to Radhika by her parents.
Calculation:
To find the total amount, we need to add the amount given by her mother and the amount given by her father.
Total amount = Amount from mother + Amount from father
Total amount = $\textsf{₹}$ 10.50 + $\textsf{₹}$ 15.80
We align the decimal points and add:
$\begin{array}{ccc} & \textsf{₹} & 10.50 \\ + & \textsf{₹} & 15.80 \\ \hline & \textsf{₹} & 26.30 \\ \hline \end{array}$Total amount given = $\textsf{₹}$ 26.30
Conclusion:
The total amount given to Radhika by her parents is $\textsf{₹}$ 26.30.
Question 4. Nasreen bought 3 m 20 cm cloth for her shirt and 2 m 5 cm cloth for her trouser. Find the total length of cloth bought by her.
Answer:
Solution:
Given:
Length of cloth for shirt = 3 m 20 cm
Length of cloth for trouser = 2 m 5 cm
To Find:
The total length of cloth bought by Nasreen.
Calculation:
To find the total length, we need to add the lengths of cloth for the shirt and the trouser. First, we convert both lengths to meters (m) using decimals.
We know that 100 cm = 1 m, so 1 cm = $\frac{1}{100}$ m = 0.01 m.
Length for shirt in meters:
3 m 20 cm = 3 m + 20 cm
= 3 m + $\frac{20}{100}$ m
= 3 m + 0.20 m
= 3.20 m
Length for trouser in meters:
2 m 5 cm = 2 m + 5 cm
= 2 m + $\frac{5}{100}$ m
= 2 m + 0.05 m
= 2.05 m
Now, add the lengths in meters:
Total length = Length for shirt + Length for trouser
Total length = 3.20 m + 2.05 m
Performing the addition:
$\begin{array}{ccc} & 3.20 & \text{m} \\ + & 2.05 & \text{m} \\ \hline & 5.25 & \text{m} \\ \hline \end{array}$Total length = 5.25 m
Conclusion:
The total length of cloth bought by Nasreen is 5.25 m.
Question 5. Naresh walked 2 km 35 m in the morning and 1 km 7 m in the evening. How much distance did he walk in all?
Answer:
Solution:
Given:
Distance walked in the morning = 2 km 35 m
Distance walked in the evening = 1 km 7 m
To Find:
The total distance Naresh walked.
Calculation:
To find the total distance, we need to add the distances walked in the morning and evening. First, we convert both distances to kilometers (km) using decimals.
We know that 1000 m = 1 km, so 1 m = $\frac{1}{1000}$ km = 0.001 km.
Morning distance in km:
2 km 35 m = 2 km + 35 m
= 2 km + $\frac{35}{1000}$ km
= 2 km + 0.035 km
= 2.035 km
Evening distance in km:
1 km 7 m = 1 km + 7 m
= 1 km + $\frac{7}{1000}$ km
= 1 km + 0.007 km
= 1.007 km
Now, add the distances in kilometers:
Total distance = Morning distance + Evening distance
Total distance = 2.035 km + 1.007 km
Performing the addition:
$\begin{array}{ccc} & 2.035 & \text{km} \\ + & 1.007 & \text{km} \\ \hline & 3.042 & \text{km} \\ \hline \end{array}$Total distance = 3.042 km
Conclusion:
The total distance Naresh walked is 3.042 km.
Question 6. Sunita travelled 15 km 268 m by bus, 7 km 7 m by car and 500 m on foot in order to reach her school. How far is her school from her residence?
Answer:
Solution:
Given:
Distance travelled by bus = 15 km 268 m
Distance travelled by car = 7 km 7 m
Distance travelled on foot = 500 m
To Find:
The total distance from Sunita's residence to her school.
Calculation:
To find the total distance, we need to add all the distances travelled. First, we convert all distances to kilometers (km) using decimals.
We know that 1000 m = 1 km, so 1 m = $\frac{1}{1000}$ km = 0.001 km.
Distance by bus in km:
15 km 268 m = 15 km + 268 m
= 15 km + $\frac{268}{1000}$ km
= 15 km + 0.268 km
= 15.268 km
Distance by car in km:
7 km 7 m = 7 km + 7 m
= 7 km + $\frac{7}{1000}$ km
= 7 km + 0.007 km
= 7.007 km
Distance on foot in km:
500 m = $\frac{500}{1000}$ km
= 0.500 km
Now, add all the distances in kilometers:
Total distance = Distance by bus + Distance by car + Distance on foot
Total distance = 15.268 km + 7.007 km + 0.500 km
Performing the addition:
$\begin{array}{ccc} & 15.268 & \text{km} \\ & 7.007 & \text{km} \\ + & 0.500 & \text{km} \\ \hline & 22.775 & \text{km} \\ \hline \end{array}$Total distance = 22.775 km
Conclusion:
The distance of the school from her residence is 22.775 km.
Question 7. Ravi purchased 5 kg 400 g rice, 2 kg 20 g sugar and 10 kg 850g flour. Find the total weight of his purchases.
Answer:
Solution:
Given:
Weight of rice = 5 kg 400 g
Weight of sugar = 2 kg 20 g
Weight of flour = 10 kg 850 g
To Find:
The total weight of Ravi's purchases.
Calculation:
To find the total weight, we need to add the weights of all items. First, we convert all weights to kilograms (kg) using decimals.
We know that 1000 g = 1 kg, so 1 g = $\frac{1}{1000}$ kg = 0.001 kg.
Weight of rice in kg:
5 kg 400 g = 5 kg + 400 g
= 5 kg + $\frac{400}{1000}$ kg
= 5 kg + 0.400 kg
= 5.400 kg
Weight of sugar in kg:
2 kg 20 g = 2 kg + 20 g
= 2 kg + $\frac{20}{1000}$ kg
= 2 kg + 0.020 kg
= 2.020 kg
Weight of flour in kg:
10 kg 850 g = 10 kg + 850 g
= 10 kg + $\frac{850}{1000}$ kg
= 10 kg + 0.850 kg
= 10.850 kg
Now, add all the weights in kilograms:
Total weight = Weight of rice + Weight of sugar + Weight of flour
Total weight = 5.400 kg + 2.020 kg + 10.850 kg
Performing the addition:
$\begin{array}{ccc} & 5.400 & \text{kg} \\ & 2.020 & \text{kg} \\ + & 10.850 & \text{kg} \\ \hline & 18.270 & \text{kg} \\ \hline \end{array}$Total weight = 18.270 kg
Conclusion:
The total weight of Ravi's purchases is 18.270 kg.
Example 15 to 17 (Before Exercise 8.6)
Example 15: Abhishek had ₹ 7.45. He bought toffees for ₹ 5.30. Find the balance amount left with Abhishek.
Answer:
Solution:
Given:
Initial amount with Abhishek = $\textsf{₹}$ 7.45
Amount spent on toffees = $\textsf{₹}$ 5.30
To Find:
The balance amount left with Abhishek.
Calculation:
To find the balance amount, we need to subtract the amount spent from the initial amount.
Balance amount = Initial amount - Amount spent
Balance amount = $\textsf{₹}$ 7.45 - $\textsf{₹}$ 5.30
We perform the subtraction by aligning the decimal points:
$\begin{array}{ccc} & \textsf{₹} & 7.45 \\ - & \textsf{₹} & 5.30 \\ \hline & \textsf{₹} & 2.15 \\ \hline \end{array}$Balance amount = $\textsf{₹}$ 2.15
Conclusion:
The balance amount left with Abhishek is $\textsf{₹}$ 2.15.
Example 16: Urmila’s school is at a distance of 5 km 350 m from her house. She travels 1 km 70 m on foot and the rest by bus. How much distance does she travel by bus?
Answer:
Solution:
Given:
Total distance from house to school = 5 km 350 m
Distance travelled on foot = 1 km 70 m
To Find:
The distance Urmila travels by bus.
Calculation:
To find the distance travelled by bus, we need to subtract the distance travelled on foot from the total distance. First, we convert both distances to kilometers (km) using decimals.
We know that 1000 m = 1 km, so 1 m = $\frac{1}{1000}$ km = 0.001 km.
Total distance in km:
5 km 350 m = 5 km + 350 m
= 5 km + $\frac{350}{1000}$ km
= 5 km + 0.350 km
= 5.350 km
Distance on foot in km:
1 km 70 m = 1 km + 70 m
= 1 km + $\frac{70}{1000}$ km
= 1 km + 0.070 km
= 1.070 km
Now, subtract the distance on foot from the total distance:
Distance by bus = Total distance - Distance on foot
Distance by bus = 5.350 km - 1.070 km
Performing the subtraction:
$\begin{array}{ccc} & 5.350 & \text{km} \\ - & 1.070 & \text{km} \\ \hline & 4.280 & \text{km} \\ \hline \end{array}$Distance travelled by bus = 4.280 km
Conclusion:
The distance Urmila travels by bus is 4.280 km.
Example 17: Kanchan bought a watermelon weighing 5 kg 200 g. Out of this she gave 2 kg 750 g to her neighbour. What is the weight of the watermelon left with Kanchan?
Answer:
Solution:
Given:
Total weight of the watermelon = 5 kg 200 g
Weight of watermelon given to the neighbour = 2 kg 750 g
To Find:
The weight of the watermelon left with Kanchan.
Calculation:
To find the weight of the watermelon left, we need to subtract the weight given to the neighbour from the total weight. First, we convert both weights to kilograms (kg) using decimals.
We know that 1000 g = 1 kg, so 1 g = $\frac{1}{1000}$ kg = 0.001 kg.
Total weight in kg:
5 kg 200 g = 5 kg + 200 g
= 5 kg + $\frac{200}{1000}$ kg
= 5 kg + 0.200 kg
= 5.200 kg
Weight given away in kg:
2 kg 750 g = 2 kg + 750 g
= 2 kg + $\frac{750}{1000}$ kg
= 2 kg + 0.750 kg
= 2.750 kg
Now, subtract the weight given away from the total weight:
Weight left = Total weight - Weight given away
Weight left = 5.200 kg - 2.750 kg
Performing the subtraction:
$\begin{array}{ccc} & 5.200 & \text{kg} \\ - & 2.750 & \text{kg} \\ \hline & 2.450 & \text{kg} \\ \hline \end{array}$Weight left = 2.450 kg
Conclusion:
The weight of the watermelon left with Kanchan is 2.450 kg.
Exercise 8.6
Question 1. Subtract :
(a) ₹ 18.25 from ₹ 20.75
(b) 202.54 m from 250 m
(c) ₹ 5.36 from ₹ 8.40
(d) 2.051 km from 5.206 km
(e) 0.314 kg from 2.107 kg
Answer:
Solution:
To subtract decimal numbers, we align the decimal points and subtract as we do with whole numbers, placing the decimal point in the result directly below the aligned points. We may need to add trailing zeros to the minuend if it has fewer decimal places than the subtrahend.
(a) ₹ 18.25 from ₹ 20.75
We need to calculate $\textsf{₹} 20.75 - \textsf{₹} 18.25$.
$\begin{array}{ccc} & \textsf{₹} & 20.75 \\ - & \textsf{₹} & 18.25 \\ \hline & \textsf{₹} & 2.50 \\ \hline \end{array}$The result is $\textsf{₹}$ 2.50.
(b) 202.54 m from 250 m
We need to calculate $250 \, \text{m} - 202.54 \, \text{m}$.
Write 250 m as 250.00 m.
$\begin{array}{ccc} & & 250.00 & \text{m} \\ - & & 202.54 & \text{m} \\ \hline & & 47.46 & \text{m} \\ \hline \end{array}$The result is 47.46 m.
(c) ₹ 5.36 from ₹ 8.40
We need to calculate $\textsf{₹} 8.40 - \textsf{₹} 5.36$.
$\begin{array}{ccc} & \textsf{₹} & 8.40 \\ - & \textsf{₹} & 5.36 \\ \hline & \textsf{₹} & 3.04 \\ \hline \end{array}$The result is $\textsf{₹}$ 3.04.
(d) 2.051 km from 5.206 km
We need to calculate $5.206 \, \text{km} - 2.051 \, \text{km}$.
$\begin{array}{ccc} & & 5.206 & \text{km} \\ - & & 2.051 & \text{km} \\ \hline & & 3.155 & \text{km} \\ \hline \end{array}$The result is 3.155 km.
(e) 0.314 kg from 2.107 kg
We need to calculate $2.107 \, \text{kg} - 0.314 \, \text{kg}$.
$\begin{array}{ccc} & & 2.107 & \text{kg} \\ - & & 0.314 & \text{kg} \\ \hline & & 1.793 & \text{kg} \\ \hline \end{array}$The result is 1.793 kg.
Question 2. Find the value of :
(a) 9.756 – 6.28
(b) 21.05 – 15.27
(c) 18.5 – 6.79
(d) 11.6 – 9.847
Answer:
Solution:
We perform subtraction by aligning the decimal points and adding trailing zeros where necessary to make the numbers have the same number of decimal places.
(a) 9.756 – 6.28
Write 6.28 as 6.280.
$\begin{array}{ccc} & & 9.756 \\ - & & 6.280 \\ \hline & & 3.476 \\ \hline \end{array}$The value is 3.476.
(b) 21.05 – 15.27
Align the decimal points and subtract.
$\begin{array}{ccc} & & 21.05 \\ - & & 15.27 \\ \hline & & 5.78 \\ \hline \end{array}$The value is 5.78.
(c) 18.5 – 6.79
Write 18.5 as 18.50.
$\begin{array}{ccc} & & 18.50 \\ - & & 6.79 \\ \hline & & 11.71 \\ \hline \end{array}$The value is 11.71.
(d) 11.6 – 9.847
Write 11.6 as 11.600.
$\begin{array}{ccc} & & 11.600 \\ - & & 9.847 \\ \hline & & 1.753 \\ \hline \end{array}$The value is 1.753.
Question 3. Raju bought a book for ₹ 35.65. He gave ₹ 50 to the shopkeeper. How much money did he get back from the shopkeeper?
Answer:
Solution:
Given:
Amount given to the shopkeeper = $\textsf{₹}$ 50
Cost of the book = $\textsf{₹}$ 35.65
To Find:
The amount of money Raju got back.
Calculation:
To find the money Raju got back, we need to subtract the cost of the book from the amount he gave to the shopkeeper.
Money got back = Amount given - Cost of book
Money got back = $\textsf{₹}$ 50 - $\textsf{₹}$ 35.65
We write $\textsf{₹}$ 50 as $\textsf{₹}$ 50.00 to perform the subtraction:
$\begin{array}{ccc} & \textsf{₹} & 50.00 \\ - & \textsf{₹} & 35.65 \\ \hline & \textsf{₹} & 14.35 \\ \hline \end{array}$Money got back = $\textsf{₹}$ 14.35
Conclusion:
Raju got back $\textsf{₹}$ 14.35 from the shopkeeper.
Question 4. Rani had ₹ 18.50. She bought one ice-cream for ₹ 11.75. How much money does she have now?
Answer:
Solution:
Given:
Initial amount Rani had = $\textsf{₹}$ 18.50
Cost of the ice-cream = $\textsf{₹}$ 11.75
To Find:
The amount of money Rani has now.
Calculation:
To find the remaining money, we need to subtract the cost of the ice-cream from the initial amount Rani had.
Money left = Initial amount - Cost of ice-cream
Money left = $\textsf{₹}$ 18.50 - $\textsf{₹}$ 11.75
We perform the subtraction by aligning the decimal points:
$\begin{array}{ccc} & \textsf{₹} & 18.50 \\ - & \textsf{₹} & 11.75 \\ \hline & \textsf{₹} & 6.75 \\ \hline \end{array}$Money left = $\textsf{₹}$ 6.75
Conclusion:
Rani now has $\textsf{₹}$ 6.75.
Question 5. Tina had 20 m 5 cm long cloth. She cuts 4 m 50 cm length of cloth from this for making a curtain. How much cloth is left with her?
Answer:
Solution:
Given:
Total length of cloth Tina had = 20 m 5 cm
Length of cloth cut for the curtain = 4 m 50 cm
To Find:
The length of cloth left with Tina.
Calculation:
To find the length of cloth left, we need to subtract the length cut from the total length. First, we convert both lengths to meters (m) using decimals.
We know that 100 cm = 1 m, so 1 cm = $\frac{1}{100}$ m = 0.01 m.
Total length in meters:
20 m 5 cm = 20 m + 5 cm
= 20 m + $\frac{5}{100}$ m
= 20 m + 0.05 m
= 20.05 m
Length cut in meters:
4 m 50 cm = 4 m + 50 cm
= 4 m + $\frac{50}{100}$ m
= 4 m + 0.50 m
= 4.50 m
Now, subtract the length cut from the total length:
Cloth left = Total length - Length cut
Cloth left = 20.05 m - 4.50 m
Performing the subtraction:
$\begin{array}{ccc} & 20.05 & \text{m} \\ - & 4.50 & \text{m} \\ \hline & 15.55 & \text{m} \\ \hline \end{array}$Cloth left = 15.55 m
Conclusion:
The length of cloth left with Tina is 15.55 m.
Question 6. Namita travels 20 km 50 m every day. Out of this she travels 10 km 200 m by bus and the rest by auto. How much distance does she travel by auto?
Answer:
Solution:
Given:
Total distance Namita travels every day = 20 km 50 m
Distance she travels by bus = 10 km 200 m
To Find:
The distance Namita travels by auto.
Calculation:
The distance travelled by auto is the total distance minus the distance travelled by bus. First, convert both distances to kilometers (km) using decimals.
We know that 1000 m = 1 km, so 1 m = $\frac{1}{1000}$ km = 0.001 km.
Total distance in km:
20 km 50 m = 20 km + 50 m
= 20 km + $\frac{50}{1000}$ km
= 20 km + 0.050 km
= 20.050 km
Distance by bus in km:
10 km 200 m = 10 km + 200 m
= 10 km + $\frac{200}{1000}$ km
= 10 km + 0.200 km
= 10.200 km
Now, subtract the distance travelled by bus from the total distance:
Distance by auto = Total distance - Distance by bus
Distance by auto = 20.050 km - 10.200 km
Performing the subtraction:
$\begin{array}{ccc} & 20.050 & \text{km} \\ - & 10.200 & \text{km} \\ \hline & 9.850 & \text{km} \\ \hline \end{array}$Distance travelled by auto = 9.850 km
Conclusion:
The distance Namita travels by auto is 9.850 km.
Question 7. Aakash bought vegetables weighing 10 kg. Out of this, 3 kg 500 g is onions, 2 kg 75 g is tomatoes and the rest is potatoes. What is the weight of the potatoes?
Answer:
Solution:
Given:
Total weight of vegetables = 10 kg
Weight of onions = 3 kg 500 g
Weight of tomatoes = 2 kg 75 g
To Find:
The weight of the potatoes.
Calculation:
First, we convert all weights to kilograms (kg) using decimals.
We know that 1000 g = 1 kg, so 1 g = $\frac{1}{1000}$ kg = 0.001 kg.
Total weight in kg:
10 kg = 10.000 kg
Weight of onions in kg:
3 kg 500 g = 3 kg + 500 g
= 3 kg + $\frac{500}{1000}$ kg
= 3 kg + 0.500 kg
= 3.500 kg
Weight of tomatoes in kg:
2 kg 75 g = 2 kg + 75 g
= 2 kg + $\frac{75}{1000}$ kg
= 2 kg + 0.075 kg
= 2.075 kg
Next, find the combined weight of onions and tomatoes:
Combined weight = Weight of onions + Weight of tomatoes
Combined weight = 3.500 kg + 2.075 kg
Performing the addition:
$\begin{array}{ccc} & 3.500 & \text{kg} \\ + & 2.075 & \text{kg} \\ \hline & 5.575 & \text{kg} \\ \hline \end{array}$Combined weight of onions and tomatoes = 5.575 kg
Finally, subtract the combined weight of onions and tomatoes from the total weight to find the weight of potatoes:
Weight of potatoes = Total weight - Combined weight of onions and tomatoes
Weight of potatoes = 10.000 kg - 5.575 kg
Performing the subtraction:
$\begin{array}{ccc} & 10.000 & \text{kg} \\ - & 5.575 & \text{kg} \\ \hline & 4.425 & \text{kg} \\ \hline \end{array}$Weight of potatoes = 4.425 kg
Conclusion:
The weight of the potatoes is 4.425 kg.

