| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 14.1 | Exercise 14.2 | Exercise 14.3 |
Chapter 14 Symmetry
Welcome to the solutions guide for Chapter 14: Symmetry. This chapter revisits and significantly expands upon the fascinating geometric concept of symmetry, building on the foundations laid in Class 6. Symmetry is a fundamental principle observed throughout nature, art, design, and science, often associated with balance, harmony, and repetition. Understanding symmetry enhances our spatial awareness and provides tools for analyzing and classifying shapes. While earlier introductions focused mainly on line symmetry, this chapter delves deeper into that concept and introduces a new, equally important type: rotational symmetry. The solutions provided offer clear explanations, illustrative diagrams, and systematic approaches to help students master both types of symmetry and recognize them in various geometric figures.
The exploration begins by reinforcing the understanding of Line Symmetry, also known as reflectional symmetry. A figure possesses line symmetry if it can be divided by a line (the line of symmetry or axis of symmetry) into two parts that are mirror images of each other. Imagine folding the figure along this line; if the two halves coincide perfectly, the line is a line of symmetry.
- Solutions guide the identification and drawing of lines of symmetry for a broader range of shapes than previously studied:
- Parallelogram: Generally possesses no lines of symmetry (unless it's a special case like a rhombus or rectangle).
- Rhombus: Has two lines of symmetry (its diagonals).
- Isosceles Trapezium: Has one line of symmetry (the line joining the midpoints of the parallel sides).
- Regular Polygons: A regular polygon with $n$ sides always has exactly $n$ lines of symmetry. For example, an equilateral triangle ($n=3$) has 3 lines, and a square ($n=4$) has 4 lines.
- Other shapes like kites (one line of symmetry) or circles (infinite lines of symmetry) are also explored.
The significant new concept introduced is Rotational Symmetry. A figure exhibits rotational symmetry if it looks identical to its original position after being rotated around a central point by an angle less than a full turn ($360^\circ$).
- Key elements defined and explored in the solutions include:
- Center of Rotation: The fixed point around which the rotation occurs.
- Angle of Rotation: The smallest angle through which the figure must be rotated about its center to map onto itself. For a figure with rotational symmetry of order $n$, the angle of rotation is $\frac{360^\circ}{n}$.
- Order of Rotational Symmetry: The number of times the figure maps onto itself during a complete rotation of $360^\circ$. The order must be at least 1 (as any shape maps onto itself after $360^\circ$), but we usually consider rotational symmetry for orders greater than 1.
- Examples are used extensively:
- A square has rotational symmetry of order 4. Its center of rotation is the intersection of its diagonals, and its angle of rotation is $\frac{360^\circ}{4} = 90^\circ$. It looks the same after rotations of $90^\circ, 180^\circ, 270^\circ,$ and $360^\circ$.
- An equilateral triangle has rotational symmetry of order 3. Its center is the centroid, and its angle of rotation is $\frac{360^\circ}{3} = 120^\circ$. It looks the same after rotations of $120^\circ, 240^\circ,$ and $360^\circ$.
- A rectangle has rotational symmetry of order 2 (angle $180^\circ$).
- A parallelogram also has rotational symmetry of order 2 (angle $180^\circ$).
- A circle has rotational symmetry of infinite order about its center.
The solutions guide students in systematically identifying figures possessing rotational symmetry and determining their center, angle, and order. Exercises often involve completing tables that summarize both line symmetry and rotational symmetry properties for various shapes, encouraging comparative analysis. The relationship between the two types of symmetry, especially in regular polygons where the order of rotational symmetry equals the number of lines of symmetry, is implicitly or explicitly highlighted. Through extensive use of diagrams illustrating reflections and rotations, these solutions foster crucial spatial reasoning skills and a deeper appreciation for geometric transformations.
Exercise 14.1
Question 1. Copy the figures with punched holes and find the axes of symmetry for the following:
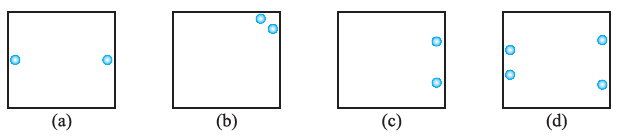
Answer:
An axis of symmetry is a line that divides a figure into two identical halves which are mirror images of each other. The axes of symmetry for the given figures are shown below with dotted lines.
(a)
This figure has two axes of symmetry: one vertical and one horizontal.
(b)
This figure has one axis of symmetry.
(c)
This figure has one horizontal axis of symmetry.
(d)
This figure has one axes of symmetry.
(e)
This figure has four axes of symmetry: one horizontal, one vertical, and two diagonals.
(f)
This figure has one vertical axis of symmetry.
(g)
This figure has one vertical axis of symmetry (the altitude to the base).
(h)
This figure has one horizontal axis of symmetry.
(i)
This figure has one vertical axis of symmetry.
(j)
This figure has two axes of symmetry: the horizontal and vertical diameters.
(k)
This figure has four axes of symmetry.
(l)
This figure has one axes of symmetry.
Question 2. Given the line(s) of symmetry, find the other hole(s):
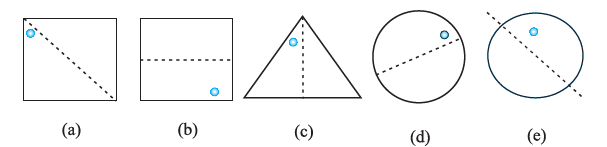
Answer:
To find the location of the other hole(s), we need to imagine folding the figure along the dotted line of symmetry. The new hole will appear at the location where the original hole would land after the fold. This process is called reflection, and the new hole is the reflection of the original hole across the line of symmetry.
(a)
The line of symmetry is the diagonal of the square. The given hole is in the top-left portion. Its reflection will be in the top-right portion, at an equal distance from the diagonal line.
(b)
The line of symmetry is the horizontal line through the middle of the square. The given hole is in the bottom half. Its reflection will be in the top half, directly above the original hole and at the same distance from the symmetry line.
(c)
The line of symmetry is the vertical altitude of the isosceles triangle. The given hole is on the left side. Its reflection will be on the right side, at the same height and the same horizontal distance from the line of symmetry.
(d)
The line of symmetry is a diameter of the circle. The hole is on one side of this diameter. The other hole will be on the opposite side, such that the line connecting the two holes is perpendicular to the diameter and is bisected by it.
(e)
The line of symmetry is a chord of the circle. The given hole is on one side of the chord. Its reflection will be on the other side of the chord, at an equal perpendicular distance from it.
Question 3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
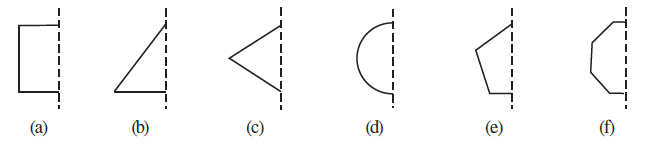
Answer:
The completed figures are obtained by reflecting the given part across the dotted mirror line. The other half of the figure will be a mirror image of the given half. The completed figures and their names are as follows:
(a)
By reflecting the given half-figure across the dotted line, we complete the shape. The resulting figure is a Square.
(b)
Reflecting the given right-angled triangle across the mirror line completes the figure. The resulting figure is a Triangle.
(c)
After reflecting the given shape across the dotted line, the completed figure is a Rhombus.
(d)
Reflecting the given semicircle across its diameter completes the figure. The resulting figure is a Circle.
(e)
When the given figure is reflected, it forms a five-sided polygon. The completed figure is a Pentagon.
(f)
Reflecting the given half across the mirror line results in an eight-sided figure. The completed figure is an Octagon.
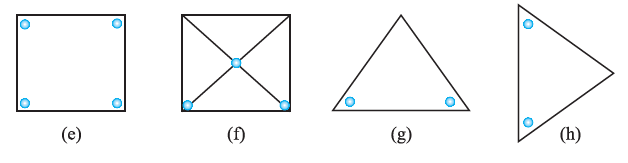
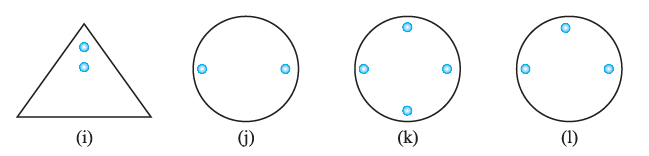
Question 4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry
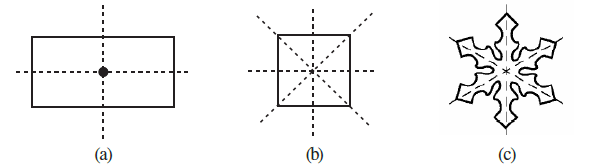
Identify multiple lines of symmetry, if any, in each of the following figures:
Answer:
A line of symmetry is a line that divides a figure into two identical halves that are mirror images of each other. The lines of symmetry for each figure are shown below with dotted lines.
(a)
This figure has 3 lines of symmetry.
(b)
This figure has 2 lines of symmetry.
(c)
This figure has 3 lines of symmetry.
(d)
This figure has only 2 line of symmetry.
(e)
This figure has 4 lines of symmetry.
(f)
This figure has only 1 line of symmetry.
(g)
This figure has 4 lines of symmetry.
(h)
This figure has 6 lines of symmetry.
Question 5. Copy the figure given here.
Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?

Answer:
The task is to take the given figure, choose one diagonal as a line of symmetry, and shade additional squares to make the entire figure symmetric about that chosen diagonal. We then need to determine if there is more than one way to do this and if the resulting figure is symmetric about both diagonals.
The original figure is a 4x4 grid with four squares shaded.
Is there more than one way to do that?
Yes, there are two ways to approach this, because there are two diagonals we can choose as the line of symmetry.
Way 1: Using the diagonal from top-left to bottom-right as the line of symmetry.
We reflect the currently shaded squares across this diagonal. For every shaded square, we must shade the square in its mirror-image position.
Way 2: Using the diagonal from top-right to bottom-left as the line of symmetry.
Similarly, we reflect the originally shaded squares across this second diagonal.
Interestingly, we can see that completing the figure using either diagonal as the line of symmetry results in the exact same final pattern. So, while there are two ways to start the process, they both lead to one unique symmetric figure.
Will the figure be symmetric about both the diagonals?
Yes, the completed figure will be symmetric about both diagonals. As shown above, when we make the figure symmetric with respect to one diagonal, the resulting pattern automatically becomes symmetric with respect to the other diagonal as well.
The final completed figure is shown below with both diagonals drawn to illustrate its dual symmetry.
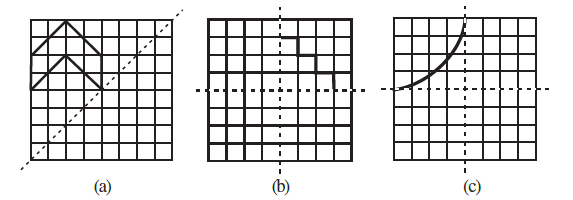
Question 6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):
Answer:
To complete each shape, we must reflect the existing lines across the given mirror line(s). Each point on the completed shape will be a mirror image of a point on the original shape. The completed diagrams are shown below.
(a)
The figure is made symmetric by reflecting the given triangular pattern across the diagonal mirror line. The reflected pattern appears in the bottom-right half of the grid.
(b)
The figure has two lines of symmetry. First, the L-shape in the top-right quadrant is reflected across the vertical line to the top-right quadrant. Then, the entire top half is reflected across the horizontal line to the bottom half, completing the symmetric pattern in all four quadrants.
(c)
This figure also has two lines of symmetry. The arc in the top-left quadrant is reflected across the vertical and horizontal lines to create three more arcs in the other quadrants, forming a complete, symmetric shape in the center of the grid.
Question 7. State the number of lines of symmetry for the following figures:
(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectanglecle
(f) A rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle
Answer:
(a) An equilateral triangle
An equilateral triangle has 3 lines of symmetry. Each line passes through a vertex and the midpoint of the opposite side.
(b) An isosceles triangle
An isosceles triangle has 1 line of symmetry. The line passes through the vertex between the two equal sides and the midpoint of the base (the unequal side).
(c) A scalene triangle
A scalene triangle (where all sides and angles are different) has 0 lines of symmetry.
(d) A square
A square has 4 lines of symmetry. Two lines pass through the midpoints of opposite sides, and two lines are the diagonals passing through opposite vertices.
(e) A rectangle
A rectangle has 2 lines of symmetry. These lines pass through the midpoints of opposite sides (one vertical, one horizontal). The diagonals are generally not lines of symmetry unless it is a square.
(f) A rhombus
A rhombus has 2 lines of symmetry. These are its two diagonals.
(g) A parallelogram
A general parallelogram has 0 lines of symmetry. (Special cases like rectangles, squares, and rhombuses have lines of symmetry).
(h) A quadrilateral
A general quadrilateral has 0 lines of symmetry. (Specific types like squares, rectangles, rhombuses, kites, and isosceles trapezoids can have lines of symmetry).
(i) A regular hexagon
A regular hexagon has 6 lines of symmetry. Three lines pass through opposite vertices, and three lines pass through the midpoints of opposite sides.
(j) A circle
A circle has infinite lines of symmetry. Any line passing through the center of the circle (i.e., any diameter) is a line of symmetry.
Question 8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
(a) a vertical mirror
(b) a horizontal mirror
(c) both horizontal and vertical mirrors
Answer:
(a) A vertical mirror
The letters of the English alphabet that have reflectional symmetry about a vertical mirror are those where the left half is a mirror image of the right half. The vertical line of symmetry passes through the middle of the letter.
These letters are:
A, H, I, M, O, T, U, V, W, X, Y
(b) A horizontal mirror
The letters of the English alphabet that have reflectional symmetry about a horizontal mirror are those where the top half is a mirror image of the bottom half. The horizontal line of symmetry passes through the middle of the letter.
These letters are:
B, C, D, E, H, I, K, O, X
(c) Both horizontal and vertical mirrors
The letters of the English alphabet that have reflectional symmetry about both horizontal and vertical mirrors are those that appear in both of the lists above.
These letters are:
H, I, O, X
Question 9. Give three examples of shapes with no line of symmetry.
Answer:
Here are three examples of shapes that have no line of symmetry:
1. Scalene Triangle
A scalene triangle has all three sides of different lengths and all three angles of different measures. Due to this lack of equality, there is no line along which the triangle can be folded so that the two halves coincide exactly.
2. Parallelogram
A parallelogram has opposite sides parallel and equal, and opposite angles equal. However, it generally does not have any line of symmetry. While it has rotational symmetry of order 2 about its center, there is no line that divides it into two mirror-image halves. (Note: Special parallelograms like rectangles, squares, and rhombuses do have lines of symmetry).
3. General Quadrilateral
A quadrilateral that has no specific properties like equal sides, equal angles, or parallel sides (i.e., it is not a square, rectangle, rhombus, parallelogram, kite, or isosceles trapezoid) will typically have no line of symmetry.
Question 10. What other name can you give to the line of symmetry of
(a) an isosceles triangle?
(b) a circle?
Answer:
(a) An isosceles triangle
The line of symmetry in an isosceles triangle connects the vertex formed by the two equal sides to the midpoint of the opposite side (the base). This line has several properties:
- It is the altitude from the vertex to the base (perpendicular to the base).
- It is the median to the base (connects the vertex to the midpoint of the base).
- It is the angle bisector of the angle at the vertex.
Therefore, other names for the line of symmetry of an isosceles triangle are the median or the altitude corresponding to its base.
(b) A circle
A line of symmetry for a circle is any line that passes through its center. A line segment that passes through the center and has its endpoints on the circle is called a diameter.
Therefore, the line of symmetry of a circle is its diameter (or more precisely, the line containing the diameter).
Exercise 14.2
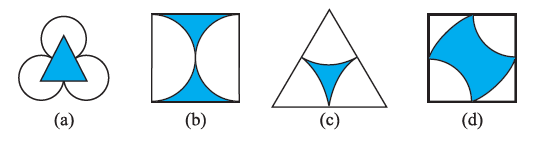
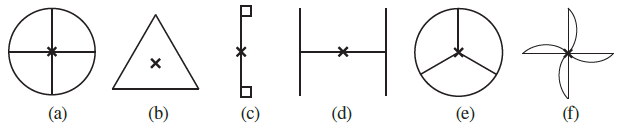
Question 1. Which of the following figures have rotational symmetry of order more than 1:
Answer:
Rotational Symmetry
A figure has rotational symmetry if it looks exactly the same after a rotation about a central point by an angle less than $360^\circ$. The order of rotational symmetry is the number of times the figure looks identical to its original position during a full $360^\circ$ rotation.
We need to identify which of the given figures have an order of rotational symmetry greater than 1.
Figure (a):
This figure is a circle divided into four equal quadrants. It looks the same when rotated by $90^\circ$, $180^\circ$, and $270^\circ$ around its center. In a complete rotation of $360^\circ$, it matches its original position 4 times. Thus, the order of rotational symmetry is 4.
Since $4 > 1$, this figure has rotational symmetry of order more than 1.
Figure (b):
This figure is an equilateral triangle. It looks the same when rotated by $120^\circ$ and $240^\circ$ around its center. In a complete rotation of $360^\circ$, it matches its original position 3 times. Thus, the order of rotational symmetry is 3.
Since $3 > 1$, this figure has rotational symmetry of order more than 1.
Figure (c):
This figure only looks the same after a full rotation of $360^\circ$. If it is rotated by any smaller angle (e.g., $180^\circ$), its appearance will change. Therefore, its order of rotational symmetry is 1.
This figure does not have a rotational symmetry of order more than 1.
Figure (d):
This figure looks the same when rotated by $180^\circ$ around its center point. In a complete rotation of $360^\circ$, it matches its original position 2 times. Thus, the order of rotational symmetry is 2.
Since $2 > 1$, this figure has rotational symmetry of order more than 1.
Figure (e):
This figure is a circle divided into three equal sectors. It looks the same when rotated by $120^\circ$ and $240^\circ$ around its center. In a complete rotation of $360^\circ$, it matches its original position 3 times. Thus, the order of rotational symmetry is 3.
Since $3 > 1$, this figure has rotational symmetry of order more than 1.
Figure (f):
This figure is a four-bladed pinwheel. It looks the same when rotated by $90^\circ$, $180^\circ$, and $270^\circ$ around its center. In a complete rotation of $360^\circ$, it matches its original position 4 times. Thus, the order of rotational symmetry is 4.
Since $4 > 1$, this figure has rotational symmetry of order more than 1.
Conclusion:
The following table summarizes the findings:
| Figure | Order of Rotational Symmetry |
| (a) | 4 |
| (b) | 3 |
| (c) | 1 |
| (d) | 2 |
| (e) | 3 |
| (f) | 4 |
Therefore, the figures with rotational symmetry of order more than 1 are (a), (b), (d), (e), and (f).
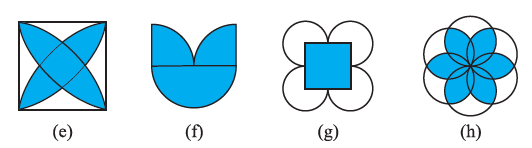
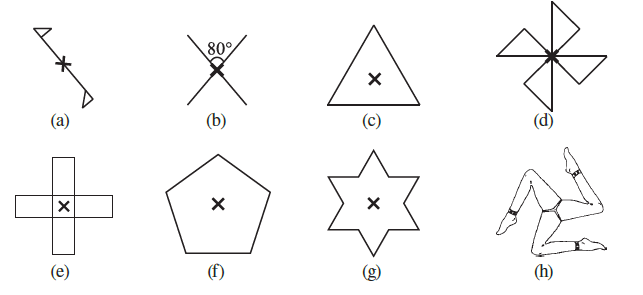
Question 2. Give the order of rotational symmetry for each figure:
Answer:
The order of rotational symmetry of a figure is the number of times it fits onto itself during a full rotation of $360^\circ$ about its center of rotation.
Let's determine the order of rotational symmetry for each of the given figures.
(a) The figure has two identical parts arranged opposite to each other around the center. It will look the same after a rotation of $180^\circ$. In a full $360^\circ$ turn, it aligns with its original position 2 times (at $180^\circ$ and $360^\circ$).
Therefore, the order of rotational symmetry is 2.
(b) The figure consists of two intersecting lines. It will look the same after a rotation of $180^\circ$. In a full $360^\circ$ turn, it aligns with its original position 2 times.
Therefore, the order of rotational symmetry is 2.
(c) This figure is an equilateral triangle. An equilateral triangle has 3 equal sides and can be rotated by $120^\circ$ to look the same. In a full $360^\circ$ turn, it aligns with its original position 3 times (at $120^\circ$, $240^\circ$, and $360^\circ$).
Therefore, the order of rotational symmetry is 3.
(d) This figure has four identical blades. It can be rotated by $90^\circ$ to look the same. In a full $360^\circ$ turn, it aligns with its original position 4 times (at $90^\circ$, $180^\circ$, $270^\circ$, and $360^\circ$).
Therefore, the order of rotational symmetry is 4.
(e) This figure is a cross with four identical arms. It can be rotated by $90^\circ$ to look the same. In a full $360^\circ$ turn, it aligns with its original position 4 times.
Therefore, the order of rotational symmetry is 4.
(f) This figure is a regular pentagon. It has 5 equal sides and can be rotated by $\frac{360^\circ}{5} = 72^\circ$ to look the same. In a full $360^\circ$ turn, it aligns with its original position 5 times.
Therefore, the order of rotational symmetry is 5.
(g) This figure is a six-pointed star (a regular hexagram). It has 6 identical points. It can be rotated by $\frac{360^\circ}{6} = 60^\circ$ to look the same. In a full $360^\circ$ turn, it aligns with its original position 6 times.
Therefore, the order of rotational symmetry is 6.
(h) This figure has three identical legs arranged symmetrically around the center. It can be rotated by $\frac{360^\circ}{3} = 120^\circ$ to look the same. In a full $360^\circ$ turn, it aligns with its original position 3 times.
Therefore, the order of rotational symmetry is 3.
Summary:
| Figure | Order of Rotational Symmetry |
| (a) | 2 |
| (b) | 2 |
| (c) | 3 |
| (d) | 4 |
| (e) | 4 |
| (f) | 5 |
| (g) | 6 |
| (h) | 3 |
Exercise 14.3
Question 1. Name any two figures that have both line symmetry and rotational symmetry.
Answer:
Many figures possess both line symmetry and rotational symmetry (of order greater than 1). Here are two examples:
1. Square
A square has 4 lines of symmetry (a vertical line, a horizontal line, and two diagonal lines passing through the center).
It also has rotational symmetry of order 4, as it looks identical to its original position after rotations of 90°, 180°, and 270° about its center.
2. Equilateral Triangle
An equilateral triangle has 3 lines of symmetry (each line passing through a vertex and the midpoint of the opposite side).
It also has rotational symmetry of order 3, as it looks identical to its original position after rotations of 120° and 240° about its center.
(Other common examples include: Circle, Rectangle, Rhombus, Regular Polygon).
Question 2. Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Answer:
Here are the rough sketches for the required figures based on their symmetry properties.
(i) A triangle with both line and rotational symmetries of order more than 1.
An equilateral triangle is the only triangle that satisfies these conditions.
- It has 3 lines of symmetry, which are its angle bisectors (and also medians and altitudes). Since 3 is more than 1, it satisfies the line symmetry condition.
- It has a rotational symmetry of order 3. It looks identical after rotations of $120^\circ$, $240^\circ$, and $360^\circ$. Since 3 is more than 1, it satisfies the rotational symmetry condition.
Rough Sketch:
(ii) A triangle with only line symmetry and no rotational symmetry of order more than 1.
An isosceles triangle fits this description.
- It has only 1 line of symmetry, which is the altitude from the vertex angle to the non-equal side.
- It has a rotational symmetry of order 1, as it only looks the same after a full $360^\circ$ rotation. The order is not more than 1.
Rough Sketch:
(iii) A quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
A parallelogram is a quadrilateral that meets these criteria.
- It has no lines of symmetry (unless it is a rhombus or a rectangle).
- It has a rotational symmetry of order 2 because it looks the same after a rotation of $180^\circ$ about the intersection point of its diagonals. Since 2 is more than 1, it satisfies the condition.
Rough Sketch:
(iv) A quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
A kite is a good example of such a quadrilateral. An isosceles trapezium also fits this description.
- A kite has exactly 1 line of symmetry, which is its main diagonal connecting the vertices between equal sides.
- It has a rotational symmetry of order 1, as it only matches its original position after a complete $360^\circ$ rotation. The order is not more than 1.
Rough Sketch:
Question 3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Answer:
Yes, if a figure has two or more lines of symmetry, it must have a rotational symmetry of order more than 1.
Explanation:
The lines of symmetry of a figure always intersect at a single point. This point of intersection becomes the center of rotation for that figure.
When there are at least two lines of symmetry, it means the figure's parts are arranged symmetrically around this center in multiple directions. This structural property ensures that there exists an angle of rotation (less than $360^\circ$) that will map the figure onto itself. Since there is at least one such rotation, the order of rotational symmetry must be greater than 1.
Examples:
Let's examine some common shapes that have two or more lines of symmetry:
| Figure | Number of Lines of Symmetry | Order of Rotational Symmetry |
| Square | 4 | 4 |
| Rectangle | 2 | 2 |
| Equilateral Triangle | 3 | 3 |
| Rhombus | 2 | 2 |
| Regular Pentagon | 5 | 5 |
| Circle | Infinite | Infinite |
As you can see from the examples, every figure with 2 or more lines of symmetry also has a rotational symmetry of order 2 or more. The point where the lines of symmetry cross is the center of rotation.
Question 4. Fill in the blanks:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
|---|---|---|---|
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral Triangle | |||
| Regular Hexagon | |||
| Circle | |||
| Semi-circle |
Answer:
The completed table is as follows:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
|---|---|---|---|
| Square | Intersection point of diagonals | 4 | $90^\circ$ |
| Rectangle | Intersection point of diagonals | 2 | $180^\circ$ |
| Rhombus | Intersection point of diagonals | 2 | $180^\circ$ |
| Equilateral Triangle | Intersection point of medians (Centroid) | 3 | $120^\circ$ |
| Regular Hexagon | Intersection point of diagonals | 6 | $60^\circ$ |
| Circle | Center | Infinite | Any angle |
| Semi-circle | Mid-point of the diameter | 1 | $360^\circ$ |
Question 5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Answer:
We need to identify quadrilaterals that satisfy two conditions:
1. They must have line symmetry of order more than 1 (i.e., at least two lines of symmetry).
2. They must have rotational symmetry of order more than 1.
Let's analyze different types of quadrilaterals:
1. Square
- Line Symmetry: A square has 4 lines of symmetry (two diagonals and two lines joining the midpoints of opposite sides). This is more than 1.
- Rotational Symmetry: A square has a rotational symmetry of order 4 about its center. This is more than 1.
Thus, a square satisfies both conditions.
2. Rectangle
- Line Symmetry: A rectangle has 2 lines of symmetry (the lines joining the midpoints of its opposite sides). This is more than 1.
- Rotational Symmetry: A rectangle has a rotational symmetry of order 2 about the intersection point of its diagonals. This is more than 1.
Thus, a rectangle satisfies both conditions.
3. Rhombus
- Line Symmetry: A rhombus has 2 lines of symmetry (its diagonals). This is more than 1.
- Rotational Symmetry: A rhombus has a rotational symmetry of order 2 about the intersection point of its diagonals. This is more than 1.
Thus, a rhombus satisfies both conditions.
Other quadrilaterals like a parallelogram, kite, or isosceles trapezium do not satisfy both conditions. For example, a parallelogram has rotational symmetry of order 2 but no lines of symmetry, while a kite has one line of symmetry but rotational symmetry of order 1.
Therefore, the quadrilaterals which have both line and rotational symmetry of order more than 1 are the square, rectangle, and rhombus.
Question 6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Answer:
The problem is based on the concept of rotational symmetry. If a figure looks the same after being rotated by a certain angle, it will also look the same after being rotated by any multiple of that angle.
Given:
A figure looks exactly the same as its original position after rotating by $60^\circ$ about its center.
This smallest angle for which the figure looks the same is called the angle of rotation.
Angle of rotation = $60^\circ$.
To Find:
The other angles at which the figure will look the same.
Solution:
Since the figure is symmetrical at a $60^\circ$ rotation, it will also be symmetrical for all integer multiples of $60^\circ$, until a full $360^\circ$ rotation is completed.
We can find these angles by multiplying $60^\circ$ by 2, 3, 4, and so on.
- After the 1st rotation (given): $1 \times 60^\circ = 60^\circ$
- After the 2nd rotation: $2 \times 60^\circ = 120^\circ$
- After the 3rd rotation: $3 \times 60^\circ = 180^\circ$
- After the 4th rotation: $4 \times 60^\circ = 240^\circ$
- After the 5th rotation: $5 \times 60^\circ = 300^\circ$
- After the 6th rotation: $6 \times 60^\circ = 360^\circ$ (This is a full rotation, where any figure returns to its original position).
The order of rotational symmetry for this figure is $\frac{360^\circ}{60^\circ} = 6$. An example of such a figure would be a regular hexagon.
Therefore, the other angles at which the figure will look exactly the same as its original position are $120^\circ$, $180^\circ$, $240^\circ$, and $300^\circ$.
Question 7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°?
(ii) 17°?
Answer:
For a figure to have rotational symmetry of order more than 1, its angle of rotation must be a factor of $360^\circ$. In other words, when we divide $360^\circ$ by the angle of rotation, the result must be an integer greater than 1. This resulting integer is the order of rotational symmetry.
The relationship is given by:
Order of Rotational Symmetry = $\frac{360^\circ}{\text{Angle of Rotation}}$
(i) Can the angle of rotation be $45^\circ$?
Let's check if $45^\circ$ is a factor of $360^\circ$.
Order of Rotational Symmetry = $\frac{360^\circ}{45^\circ} = 8$
Since the result is 8, which is an integer greater than 1, it is possible. A figure with this property would have a rotational symmetry of order 8. For example, a regular octagon.
So, yes, we can have a rotational symmetry of order more than 1 with an angle of rotation of $45^\circ$.
(ii) Can the angle of rotation be $17^\circ$?
Let's check if $17^\circ$ is a factor of $360^\circ$.
Potential Order = $\frac{360^\circ}{17^\circ} \approx 21.176$
Since 360 is not perfectly divisible by 17, the result is not an integer. The order of rotational symmetry must be a whole number, as a figure can only fit onto itself a whole number of times during a full rotation.
Therefore, no, we cannot have a rotational symmetry of order more than 1 with an angle of rotation of $17^\circ$.

