| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 (Before Exercise 5.1) | Exercise 5.1 | Exercise 5.2 |
Chapter 5 Lines and Angles
Welcome to the solutions guide for Chapter 5: Lines and Angles. This chapter significantly deepens the exploration of fundamental geometric concepts introduced in earlier classes. Moving beyond basic shapes, it focuses intently on the intricate relationships that exist between different types of angles and the specific properties that emerge when lines interact, particularly when they intersect or when parallel lines are traversed by another line. A thorough understanding of these concepts is crucial for developing spatial reasoning and forms the bedrock for proving geometric theorems later. The solutions provided here offer clear definitions, illustrative diagrams, and step-by-step reasoning to master these essential ideas.
The initial focus is on understanding pairs of Related Angles:
- Complementary Angles: Two angles whose measures add up to exactly $90^\circ$. Solutions guide finding the complement of a given angle (e.g., the complement of $30^\circ$ is $90^\circ - 30^\circ = 60^\circ$).
- Supplementary Angles: Two angles whose measures add up to exactly $180^\circ$. Similarly, solutions demonstrate finding the supplement (e.g., the supplement of $110^\circ$ is $180^\circ - 110^\circ = 70^\circ$).
- Adjacent Angles: Two angles that share a common vertex and a common arm (side), but whose non-common arms lie on opposite sides of the common arm. They sit 'next to' each other without overlapping interiors.
- Linear Pair: A special pair of adjacent angles whose non-common arms form a straight line. Angles in a linear pair are always supplementary (their sum is $180^\circ$). Solutions frequently use this property to find unknown angles on a straight line.
- Vertically Opposite Angles: When two lines intersect, they form two pairs of angles opposite to each other at the vertex. Vertically opposite angles are always equal in measure. Solutions demonstrate identifying these pairs and using their equality to solve for unknowns.
The solutions meticulously guide students in identifying these angle pairs within diagrams and applying their defining properties (sum = $90^\circ$, sum = $180^\circ$, or angles are equal) to calculate unknown angle measures.
A major and critical section of this chapter deals with Parallel Lines and Transversals:
- A transversal is defined as a line that intersects two or more other lines at distinct points.
- When a transversal intersects two lines, several types of angle pairs are formed. Solutions clearly define and illustrate:
- Corresponding Angles: Angles in the same relative position at each intersection (like the 'F' shape).
- Alternate Interior Angles: Angles on opposite sides of the transversal and between the two lines (like the 'Z' shape).
- Alternate Exterior Angles: Angles on opposite sides of the transversal and outside the two lines.
- Consecutive Interior Angles (or Co-interior Angles): Angles on the same side of the transversal and between the two lines (like the 'C' shape).
- The crucial aspect, thoroughly explained in the solutions, is the set of properties that arise specifically when the two lines intersected by the transversal are parallel:
- Corresponding Angles are equal.
- Alternate Interior Angles are equal.
- Alternate Exterior Angles are equal.
- Consecutive Interior Angles are supplementary (their sum is $180^\circ$).
- Solutions provide numerous examples showing how to apply these properties rigorously to find unknown angles in diagrams involving parallel lines, often requiring multiple steps of reasoning.
- Conversely, the solutions also address the conditions for parallelism: if a transversal intersects two lines such that any pair of corresponding angles are equal, or alternate interior angles are equal, or consecutive interior angles are supplementary, then the two lines must be parallel. Exercises involving checking for parallelism based on given angle measures are included.
By working through the exercises detailed in these solutions, complete with clear diagrams and logical reasoning for each step, students will significantly enhance their geometric intuition, their ability to identify complex angle relationships, and their skills in deductive reasoning within spatial contexts. This forms a vital part of their mathematical development.
Example 1 (Before Exercise 5.1)
Example 1 In Fig (5.18) identify:
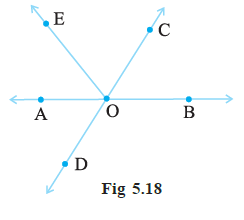
(i) Five pairs of adjacent angles.
(ii) Three linear pairs.
(iii) Two pairs of vertically opposite angles.
Answer:
Based on the definitions of different types of angles and observing the given figure, we can identify the following:
(i) Five pairs of adjacent angles.
Adjacent angles are pairs of angles that have a common vertex, a common arm, and their non-common arms are on different sides of the common arm. Five such pairs are:
1. ($\angle AOE$, $\angle EOC$)
2. ($\angle EOC$, $\angle COB$)
3. ($\angle COB$, $\angle BOD$)
4. ($\angle BOD$, $\angle DOA$)
5. ($\angle AOC$, $\angle COB$)
(ii) Three linear pairs.
A linear pair is a pair of adjacent angles whose non-common sides form a straight line. The sum of angles in a linear pair is $180^\circ$. Three linear pairs are:
1. ($\angle AOE$, $\angle BOE$) --- (Since AOB is a straight line)
2. ($\angle AOD$, $\angle BOD$) --- (Since AOB is a straight line)
3. ($\angle AOD$, $\angle AOC$) --- (Since DOC is a straight line)
(iii) Two pairs of vertically opposite angles.
Vertically opposite angles are formed when two lines intersect each other. They are opposite to each other. Here, lines AB and DE intersect at point O. The two pairs of vertically opposite angles are:
1. ($\angle AOD$, $\angle BOE$)
2. ($\angle AOE$, $\angle BOD$)
Exercise 5.1
Question 1. Find the complement of each of the following angles:
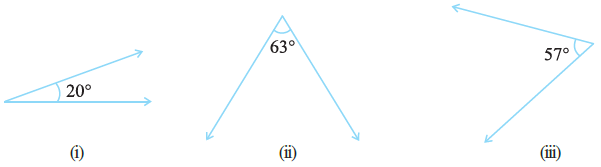
Answer:
Given:
Three angles with measures $20^\circ$, $63^\circ$, and $57^\circ$.
To Find:
The complement of each of the given angles.
Solution:
Two angles are said to be complementary if the sum of their measures is $90^\circ$. If an angle is $\theta$, its complement is $90^\circ - \theta$.
(i) Complement of $20^\circ$:
Complement $= 90^\circ - 20^\circ$
Complement $= 70^\circ$
(ii) Complement of $63^\circ$:
Complement $= 90^\circ - 63^\circ$
Complement $= 27^\circ$
(iii) Complement of $57^\circ$:
Complement $= 90^\circ - 57^\circ$
Complement $= 33^\circ$
Final Answer:
The complement of $20^\circ$ is $\mathbf{70^\circ}$.
The complement of $63^\circ$ is $\mathbf{27^\circ}$.
The complement of $57^\circ$ is $\mathbf{33^\circ}$.
Question 2. Find the supplement of each of the following angles:
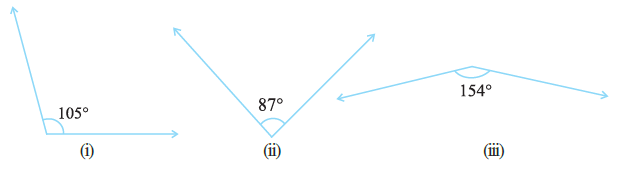
Answer:
Given:
Three angles with measures $105^\circ$, $87^\circ$, and $154^\circ$.
To Find:
The supplement of each of the given angles.
Solution:
Two angles are said to be supplementary if the sum of their measures is $180^\circ$. If an angle is $\theta$, its supplement is $180^\circ - \theta$.
(i) Supplement of $105^\circ$:
Supplement $= 180^\circ - 105^\circ$
Supplement $= 75^\circ$
(ii) Supplement of $87^\circ$:
Supplement $= 180^\circ - 87^\circ$
Supplement $= 93^\circ$
(iii) Supplement of $154^\circ$:
Supplement $= 180^\circ - 154^\circ$
Supplement $= 26^\circ$
Final Answer:
The supplement of $105^\circ$ is $\mathbf{75^\circ}$.
The supplement of $87^\circ$ is $\mathbf{93^\circ}$.
The supplement of $154^\circ$ is $\mathbf{26^\circ}$.
Question 3. Identify which of the following pairs of angles are complementary and which are supplementary.
(i) 65º, 115º
(ii) 63º, 27º
(iii) 112º, 68º
(iv) 130º, 50º
(v) 45º, 45º
(vi) 80º, 10º
Answer:
Given:
Six pairs of angles.
To Identify:
Whether each pair is complementary or supplementary.
Solution:
Two angles are complementary if their sum is $90^\circ$.
Two angles are supplementary if their sum is $180^\circ$.
(i) $65^\circ, 115^\circ$:
Sum $= 65^\circ + 115^\circ = 180^\circ$.
Since the sum is $180^\circ$, the pair is supplementary.
(ii) $63^\circ, 27^\circ$:
Sum $= 63^\circ + 27^\circ = 90^\circ$.
Since the sum is $90^\circ$, the pair is complementary.
(iii) $112^\circ, 68^\circ$:
Sum $= 112^\circ + 68^\circ = 180^\circ$.
Since the sum is $180^\circ$, the pair is supplementary.
(iv) $130^\circ, 50^\circ$:
Sum $= 130^\circ + 50^\circ = 180^\circ$.
Since the sum is $180^\circ$, the pair is supplementary.
(v) $45^\circ, 45^\circ$:
Sum $= 45^\circ + 45^\circ = 90^\circ$.
Since the sum is $90^\circ$, the pair is complementary.
(vi) $80^\circ, 10^\circ$:
Sum $= 80^\circ + 10^\circ = 90^\circ$.
Since the sum is $90^\circ$, the pair is complementary.
Question 4. Find the angle which is equal to its complement.
Answer:
Given:
An angle is equal to its complement.
To Find:
The measure of the angle.
Solution:
Let the measure of the angle be $x$ degrees.
The complement of this angle is $90^\circ - x$ degrees.
According to the problem statement, the angle is equal to its complement.
So, we can write the equation:
$x = 90^\circ - x$
... (i)
Now, we solve for $x$. Add $x$ to both sides of equation (i).
$x + x = 90^\circ - x + x$
(Adding $x$ to both sides)
This simplifies to:
$2x = 90^\circ$
Now, divide both sides by $2$ to find the value of $x$.
$\frac{2x}{2} = \frac{90^\circ}{2}$
(Dividing both sides by 2)
Thus, we get:
$x = 45^\circ$
The angle is $45^\circ$. Its complement is $90^\circ - 45^\circ = 45^\circ$. The angle is indeed equal to its complement.
Final Answer:
The angle which is equal to its complement is $\mathbf{45^\circ}$.
Question 5. Find the angle which is equal to its supplement.
Answer:
Given:
An angle is equal to its supplement.
To Find:
The measure of the angle.
Solution:
Let the measure of the angle be $x$ degrees.
The supplement of this angle is $180^\circ - x$ degrees.
According to the problem statement, the angle is equal to its supplement.
So, we can write the equation:
$x = 180^\circ - x$
... (i)
Now, we solve for $x$. Add $x$ to both sides of equation (i).
$x + x = 180^\circ - x + x$
(Adding $x$ to both sides)
This simplifies to:
$2x = 180^\circ$
Now, divide both sides by $2$ to find the value of $x$.
$\frac{2x}{2} = \frac{180^\circ}{2}$
(Dividing both sides by 2)
Thus, we get:
$x = 90^\circ$
The angle is $90^\circ$. Its supplement is $180^\circ - 90^\circ = 90^\circ$. The angle is indeed equal to its supplement.
Final Answer:
The angle which is equal to its supplement is $\mathbf{90^\circ}$.
Question 6. In the given figure, ∠1 and ∠2 are supplementary angles.

If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.
Answer:
Given that ∠1 and ∠2 are supplementary angles.
This means the sum of their measures must always be equal to $180^\circ$. We can write this as an equation:
$∠1 + ∠2 = 180^\circ$
This equation represents a balance. For the sum to remain constant at $180^\circ$, if one value (∠1) is decreased, the other value (∠2) must be increased to compensate for the change.
Let's consider an example:
Suppose initially, $∠1 = 120^\circ$. Then, for the angles to be supplementary, $∠2 = 180^\circ - 120^\circ = 60^\circ$.
Now, let's decrease ∠1 by $20^\circ$. The new value for ∠1 is $120^\circ - 20^\circ = 100^\circ$.
For the angles to still remain supplementary, the new ∠2 must be:
New ∠2 = $180^\circ - (\text{new } ∠1) = 180^\circ - 100^\circ = 80^\circ$.
The original ∠2 was $60^\circ$, and the new ∠2 is $80^\circ$. This shows that when ∠1 decreased by $20^\circ$, ∠2 increased by $20^\circ$.
Therefore, if ∠1 is decreased, ∠2 must be increased by the same amount so that their sum remains $180^\circ$, and they continue to be supplementary angles.
Question 7. Can two angles be supplementary if both of them are:
(i) acute?
(ii) obtuse?
(iii) right?
Answer:
Given:
Three scenarios regarding pairs of angles: (i) both acute, (ii) both obtuse, (iii) both right.
To Determine:
If two angles can be supplementary in each of the given scenarios.
Solution:
Recall that two angles are supplementary if the sum of their measures is $180^\circ$.
(i) Both acute?
An acute angle is an angle whose measure is less than $90^\circ$. Let the two acute angles be $\angle A$ and $\angle B$.
$\angle A < 90^\circ$
$\angle B < 90^\circ$
If we add these two angles, the sum will be:
$\angle A + \angle B < 90^\circ + 90^\circ$
$\angle A + \angle B < 180^\circ$
Since the sum of two acute angles is always less than $180^\circ$, they cannot be supplementary.
Answer for (i): No
(ii) Both obtuse?
An obtuse angle is an angle whose measure is greater than $90^\circ$ but less than $180^\circ$. Let the two obtuse angles be $\angle C$ and $\angle D$.
$\angle C > 90^\circ$
$\angle D > 90^\circ$
If we add these two angles, the sum will be:
$\angle C + \angle D > 90^\circ + 90^\circ$
$\angle C + \angle D > 180^\circ$
Since the sum of two obtuse angles is always greater than $180^\circ$, they cannot be supplementary.
Answer for (ii): No
(iii) Both right?
A right angle is an angle whose measure is exactly $90^\circ$. Let the two right angles be $\angle E$ and $\angle F$.
$\angle E = 90^\circ$
$\angle F = 90^\circ$
If we add these two angles, the sum will be:
$\angle E + \angle F = 90^\circ + 90^\circ$
$\angle E + \angle F = 180^\circ$
Since the sum of two right angles is exactly $180^\circ$, they are supplementary.
Answer for (iii): Yes
Final Answer:
(i) Two acute angles cannot be supplementary.
(ii) Two obtuse angles cannot be supplementary.
(iii) Two right angles can be supplementary.
Question 8. An angle is greater than 45º. Is its complementary angle greater than 45º or equal to 45º or less than 45º?
Answer:
Given:
An angle is greater than $45^\circ$.
To Determine:
If its complementary angle is greater than $45^\circ$, equal to $45^\circ$, or less than $45^\circ$.
Solution:
Let the angle be $\theta$ degrees.
We are given that $\theta > 45^\circ$.
The complementary angle of $\theta$ is $90^\circ - \theta$.
We need to determine if $90^\circ - \theta$ is greater than, equal to, or less than $45^\circ$.
We start with the given inequality:
$\theta > 45^\circ$
... (i)
To find the range of the complementary angle $90^\circ - \theta$, we can multiply the inequality (i) by $-1$ and then add $90^\circ$ to both sides.
Multiplying inequality (i) by $-1$ reverses the inequality sign:
$-\theta < -45^\circ$
Now, add $90^\circ$ to both sides of this new inequality:
$90^\circ - \theta < 90^\circ - 45^\circ$
Simplifying the right side:
$90^\circ - \theta < 45^\circ$
This shows that if an angle $\theta$ is greater than $45^\circ$, its complementary angle ($90^\circ - \theta$) is less than $45^\circ$.
For example, if the angle is $50^\circ$ (which is $> 45^\circ$), its complement is $90^\circ - 50^\circ = 40^\circ$, which is less than $45^\circ$.
Final Answer:
If an angle is greater than $45^\circ$, its complementary angle is less than $45^\circ$.
Question 9. In the adjoining figure:
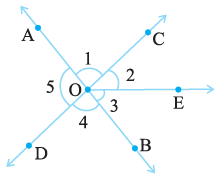
(i) Is ∠1 adjacent to ∠2?
(ii) Is ∠AOC adjacent to ∠AOE?
(iii) Do ∠COE and ∠EOD form a linear pair?
(iv) Are ∠BOD and ∠DOA supplementary?
(v) Is ∠1 vertically opposite to ∠4?
(vi) What is the vertically opposite angle of ∠5?
Answer:
Given:
A figure showing lines AB and CD intersecting at O, with a ray OE emanating from O.
To Determine:
Answers to the questions (i) to (vi) based on the figure and properties of angles.
Solution:
We analyze each question based on the definitions of adjacent angles, linear pairs, supplementary angles, and vertically opposite angles, with reference to the given figure.
(i) Is ∠1 adjacent to ∠2?
$\angle 1$ is $\angle \text{AOC}$. $\angle 2$ is $\angle \text{COE}$.
They share a common vertex O and a common arm OC.
Their non-common arms (OA and OE) are on opposite sides of the common arm OC.
Thus, $\angle 1$ and $\angle 2$ are adjacent angles.
Answer for (i): Yes.
(ii) Is ∠AOC adjacent to ∠AOE?
$\angle \text{AOC}$ is $\angle 1$. $\angle \text{AOE}$ is formed by $\angle 1$ and $\angle 2$ (i.e., $\angle \text{AOC} + \angle \text{COE}$).
They share a common vertex O and a common arm OA.
However, the non-common arm OC of $\angle \text{AOC}$ lies within $\angle \text{AOE}$. They do not have non-common arms on opposite sides of the common arm.
Thus, $\angle \text{AOC}$ and $\angle \text{AOE}$ are not adjacent angles in the strict sense (they are overlapping angles).
Answer for (ii): No.
(iii) Do ∠COE and ∠EOD form a linear pair?
$\angle \text{COE}$ is $\angle 2$. $\angle \text{EOD}$ is $\angle 3$.
They share a common vertex O and a common arm OE.
Their non-common arms OC and OD form a straight line CD.
Thus, $\angle \text{COE}$ and $\angle \text{EOD}$ form a linear pair.
Answer for (iii): Yes.
(iv) Are ∠BOD and ∠DOA supplementary?
$\angle \text{BOD}$ is $\angle 4$. $\angle \text{DOA}$ is $\angle 5$.
These two angles are adjacent angles sharing common vertex O and common arm OD.
Their non-common arms OB and OA form a straight line AB.
Angles that form a straight line are supplementary (their sum is $180^\circ$).
Thus, $\angle \text{BOD}$ and $\angle \text{DOA}$ are supplementary.
Answer for (iv): Yes.
(v) Is ∠1 vertically opposite to ∠4?
$\angle 1$ is $\angle \text{AOC}$. $\angle 4$ is $\angle \text{BOD}$.
Vertically opposite angles are formed by the intersection of two lines and are opposite to each other at the intersection point.
$\angle \text{AOC}$ and $\angle \text{BOD}$ are formed by the intersection of lines AB and CD, and they are directly opposite to each other at O.
Thus, $\angle 1$ is vertically opposite to $\angle 4$.
Answer for (v): Yes.
(vi) What is the vertically opposite angle of ∠5?
$\angle 5$ is $\angle \text{DOA}$.
The vertically opposite angle to $\angle \text{DOA}$ is the angle formed by the intersection of lines AB and CD that is opposite $\angle \text{DOA}$ at O.
This angle is $\angle \text{COB}$, which is represented as $\angle 2$ and $\angle 3$ combined, i.e., $\angle \text{COE} + \angle \text{EOB}$. Looking at the labels, it is $\angle \text{COB}$. The angle opposite to $\angle \text{DOA}$ ($\angle 5$) is $\angle \text{COB}$.
Answer for (vi): The vertically opposite angle of $\angle 5$ is $\mathbf{\angle COB}$ (or $\mathbf{\angle 2 + \angle 3}$).
Summary of Answers:
(i) Yes
(ii) No
(iii) Yes
(iv) Yes
(v) Yes
(vi) $\angle \text{COB}$ (or $\angle \text{EOB} + \angle \text{COE}$)
Question 10. Indicate which pairs of angles are:
(i) Vertically opposite angles.
(ii) Linear pairs.
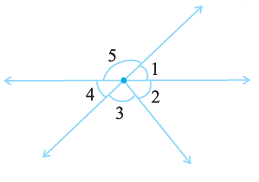
Answer:
(i) Vertically opposite angles:
When two lines intersect, the angles opposite to each other at the point of intersection are called vertically opposite angles. In the given figure, the intersecting lines form the following pairs of vertically opposite angles:
$\angle 1$ and $\angle 4$ form a pair of vertically opposite angles.
$\angle 5$ and the combined angle $(\angle 2 + \angle 3)$ form another pair of vertically opposite angles.
(ii) Linear pairs:
A linear pair is a pair of adjacent angles whose non-common sides are opposite rays (i.e., they form a straight line). In the given figure, the angles that form straight lines are:
$\angle 1$ and $\angle 5$ form a linear pair because they are adjacent and lie on a straight line.
$\angle 5$ and $\angle 4$ form a linear pair because they are adjacent and lie on a straight line.
$\angle 1$ and $(\angle 2 + \angle 3)$ form a linear pair because they are adjacent and lie on a straight line.
$\angle 4$ and $(\angle 2 + \angle 3)$ form a linear pair because they are adjacent and lie on a straight line.
Question 11. In the following figure, is ∠1 adjacent to ∠2? Give reasons.
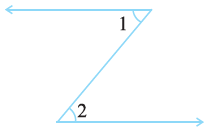
Answer:
No, ∠1 is not adjacent to ∠2.
Reason:
For two angles to be considered adjacent, they must satisfy three conditions:
1. They must have a common vertex.
2. They must have a common arm.
3. The non-common arms must lie on opposite sides of the common arm.
In the given figure, ∠1 and ∠2 do not have a common vertex. The vertex of ∠1 is at the top corner, while the vertex of ∠2 is at the bottom corner. Since they do not share a common vertex, they are not adjacent angles.
Question 12. Find the values of the angles x, y, and z in each of the following:
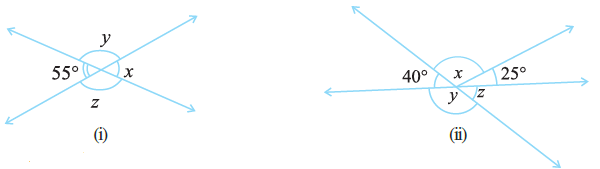
Answer:
(i) Solution for Figure (i):
In this figure, two straight lines intersect, forming four angles.
Finding the value of x:
Angle x and the $55^\circ$ angle are vertically opposite angles. Vertically opposite angles are equal.
Therefore, $x = 55^\circ$.
Finding the value of y:
Angle y and the $55^\circ$ angle are adjacent angles on a straight line, forming a linear pair. The sum of angles in a linear pair is $180^\circ$.
$y + 55^\circ = 180^\circ$
$y = 180^\circ - 55^\circ$
$y = 125^\circ$
Therefore, $y = 125^\circ$.
Finding the value of z:
Angle z and angle y are vertically opposite angles. Vertically opposite angles are equal.
$z = y$
Therefore, $z = 125^\circ$.
(Alternatively, angle z and angle x form a linear pair, so $z + 55^\circ = 180^\circ$, which also gives $z = 125^\circ$.)
(ii) Solution for Figure (ii):
In this figure, three straight lines intersect at a single point.
Finding the value of y:
$y + 40^\circ = 180^\circ$
$y = 180^\circ - 40^\circ$
$y = 140^\circ$
Finding the value of z:
Angle z and the $40^\circ$ angle are vertically opposite angles.
Therefore, $z = 40^\circ$.
Finding the value of x:
The angles $40^\circ$, $x$, and $25^\circ$ are adjacent angles that lie on a straight line. The sum of angles on a straight line is $180^\circ$.
$40^\circ + x + 25^\circ = 180^\circ$
$x + 65^\circ = 180^\circ$
$x = 180^\circ - 65^\circ$
$x = 115^\circ$
Therefore, $x = 115^\circ$.
Question 13. Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is _______.
(ii) If two angles are supplementary, then the sum of their measures is ______.
(iii) Two angles forming a linear pair are _______________.
(iv) If two adjacent angles are supplementary, they form a ___________.
(v) If two lines intersect at a point, then the vertically opposite angles are always _____________.
(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are __________.
Answer:
(i) If two angles are complementary, then the sum of their measures is $90^\circ$.
(ii) If two angles are supplementary, then the sum of their measures is $180^\circ$.
(iii) Two angles forming a linear pair are supplementary.
(iv) If two adjacent angles are supplementary, they form a linear pair.
(v) If two lines intersect at a point, then the vertically opposite angles are always equal.
(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are obtuse angles.
Question 14. In the adjoining figure, name the following pairs of angles.
(i) Obtuse vertically opposite angles
(ii) Adjacent complementary angles
(iii) Equal supplementary angles
(iv) Unequal supplementary angles
(v) Adjacent angles that do not form a linear pair
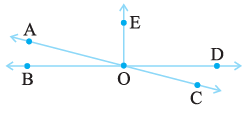
Answer:
By observing the given figure, we can identify the following pairs of angles:
(i) Obtuse vertically opposite angles
Obtuse angles are angles greater than $90^\circ$. Vertically opposite angles are equal angles formed by the intersection of two lines.
In the figure, the lines AC and BD intersect at point O. The angle pair ($\angle AOD$, $\angle BOC$) consists of two obtuse angles that are vertically opposite to each other.
So, the required pair is ($\angle AOD$, $\angle BOC$).
(ii) Adjacent complementary angles
Adjacent angles share a common vertex and a common arm. Complementary angles are angles whose sum is $90^\circ$.
In the figure, $\angle BOE$ is a right angle ($90^\circ$). The angles $\angle AOB$ and $\angle AOE$ are adjacent to each other and their sum is equal to $\angle BOE$.
$\angle AOB + \angle AOE = \angle BOE = 90^\circ$
So, the required pair is ($\angle AOB$, $\angle AOE$).
(iii) Equal supplementary angles
Supplementary angles are angles whose sum is $180^\circ$. If they are equal, each angle must be $90^\circ$.
In the figure, BD is a straight line. The ray OE stands on it, forming a linear pair ($\angle BOE$, $\angle DOE$).
$\angle BOE + \angle DOE = 180^\circ$
From the figure, $\angle BOE = 90^\circ$, which means $\angle DOE = 180^\circ - 90^\circ = 90^\circ$.
So, the required pair is ($\angle BOE$, $\angle DOE$).
(iv) Unequal supplementary angles
These are pairs of supplementary angles (sum is $180^\circ$) that have different measures.
The angles on the straight line BD, ($\angle AOB$, $\angle AOD$), form a linear pair. Since $\angle AOB$ is acute and $\angle AOD$ is obtuse, they are unequal.
Another example is the pair ($\angle BOC$, $\angle COD$) on the same straight line BD.
So, one such pair is ($\angle AOB$, $\angle AOD$).
(v) Adjacent angles that do not form a linear pair
These are pairs of adjacent angles whose non-common arms do not form a straight line.
There are several such pairs:
1. ($\angle AOB$, $\angle AOE$)
2. ($\angle AOE$, $\angle EOD$)
3. ($\angle EOD$, $\angle DOC$)
Any of these pairs is a correct answer. For example, ($\angle AOE$, $\angle EOD$).
Exercise 5.2
Question 1. State the property that is used in each of the following statements?
(i) If a || b, then ∠1 = ∠5.
(ii) If ∠4 = ∠6, then a || b.
(iii) If ∠4 + ∠5 = 180°, then a || b
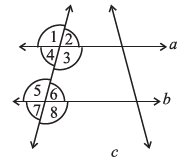
Answer:
(i) If a || b, then $\angle 1 = \angle 5$.
The property used here is the Corresponding Angles Property. According to this property, if two parallel lines are intersected by a transversal, then each pair of corresponding angles is equal.
(ii) If $\angle 4 = \angle 6$, then a || b.
The property used here is the Converse of the Alternate Interior Angles Property. According to this property, if a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
(iii) If $\angle 4 + \angle 5 = 180^\circ$, then a || b
The property used here is the Converse of the Interior Angles on the Same Side of the Transversal Property (or Consecutive Interior Angles Property). According to this property, if a transversal intersects two lines such that the sum of a pair of interior angles on the same side of the transversal is $180^\circ$, then the two lines are parallel.
Question 2. In the adjoining figure, identify
(i) the pairs of corresponding angles.
(ii) the pairs of alternate interior angles.
(iii) the pairs of interior angles on the same side of the transversal.
(iv) the vertically opposite angles.
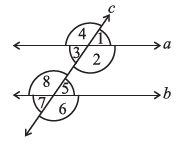
Answer:
By observing the given figure and using the definitions of different angle pairs formed by a transversal intersecting two lines, we can identify the following:
(i) The pairs of corresponding angles.
Corresponding angles are located in the same relative position at each intersection. The pairs are:
1. ($\angle 1$, $\angle 5$)
2. ($\angle 2$, $\angle 6$)
3. ($\angle 4$, $\angle 8$)
4. ($\angle 3$, $\angle 7$)
(ii) The pairs of alternate interior angles.
Alternate interior angles are on opposite sides of the transversal and are between the two lines. The pairs are:
1. ($\angle 3$, $\angle 5$)
2. ($\angle 2$, $\angle 8$)
(iii) The pairs of interior angles on the same side of the transversal.
These are also known as consecutive interior angles. They are on the same side of the transversal and between the two lines. The pairs are:
1. ($\angle 3$, $\angle 8$)
2. ($\angle 2$, $\angle 5$)
(iv) The vertically opposite angles.
Vertically opposite angles are formed at each intersection and are opposite to each other. The pairs are:
1. ($\angle 1$, $\angle 3$)
2. ($\angle 4$, $\angle 2$)
3. ($\angle 5$, $\angle 7$)
4. ($\angle 8$, $\angle 6$)
Question 3. In the adjoining figure, p || q. Find the unknown angles.
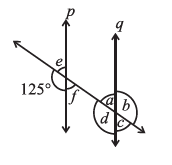
Answer:
Given: Line p is parallel to line q (p || q).
We can find the unknown angles by using the properties of angles formed when a transversal intersects two parallel lines.
Finding angle e:
The angle $125^\circ$ and angle $e$ are adjacent angles on a straight line (the transversal), so they form a linear pair.
$e + 125^\circ = 180^\circ$
(Linear Pair)
$e = 180^\circ - 125^\circ$
$e = 55^\circ$
Finding angle f:
Angle $f$ and angle $e$ are vertically opposite angles. Therefore, they are equal.
$f = e$
(Vertically opposite angles)
$f = 55^\circ$
Finding angle d:
Angle $d$ and the $125^\circ$ angle are corresponding angles. Since p || q, corresponding angles are equal.
$d = 125^\circ$
(Corresponding angles)
Finding angle b:
Angle $b$ and angle $d$ are vertically opposite angles. Therefore, they are equal.
$b = d$
(Vertically opposite angles)
$b = 125^\circ$
Finding angle a:
Angle $a$ and angle $d$ are adjacent angles on a straight line (line q), so they form a linear pair.
$a + d = 180^\circ$
(Linear Pair)
$a + 125^\circ = 180^\circ$
$a = 180^\circ - 125^\circ$
$a = 55^\circ$
(Alternatively, since p || q, angles a and e are corresponding angles, so a = e = 55°.)
Finding angle c:
Angle $c$ and angle $a$ are vertically opposite angles. Therefore, they are equal.
$c = a$
(Vertically opposite angles)
$c = 55^\circ$
(Alternatively, since p || q, angles c and f are corresponding angles, so c = f = 55°.)
Question 4. Find the value of x in each of the following figures if l || m.
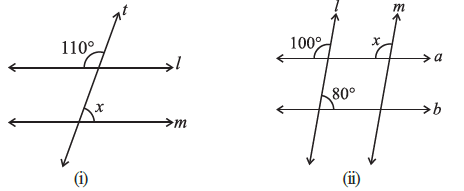
Answer:
(i) Solution for Figure (i):
Given: Line l is parallel to line m (l || m), and t is the transversal.
The angle $110^\circ$ and angle $x$ are interior angles on the same side of the transversal.
When two parallel lines are intersected by a transversal, the interior angles on the same side are supplementary (their sum is $180^\circ$).
$x + 110^\circ = 180^\circ$
(Consecutive interior angles)
$x = 180^\circ - 110^\circ$
$x = 70^\circ$
Therefore, the value of x is $70^\circ$.
Alternate Solution for Figure (i):
Let the angle adjacent to $110^\circ$ on the straight line l be y. They form a linear pair.
$y + 110^\circ = 180^\circ$
$y = 70^\circ$
Now, angle y and angle x are alternate interior angles. Since l || m, alternate interior angles are equal.
$x = y$
Therefore, $x = 70^\circ$.
(ii) Solution for Figure (ii):
Given: Line l is parallel to line m (l || m), and a is the transversal.
In this figure, the angle $100^\circ$ and angle $x$ are corresponding angles.
When two parallel lines are intersected by a transversal, the corresponding angles are equal.
$x = 100^\circ$
(Corresponding angles)
Therefore, the value of x is $100^\circ$.
(Note: In this case, the information about line b and the $80^\circ$ angle is extra information not needed to solve for x.)
Question 5. In the given figure, the arms of two angles are parallel.
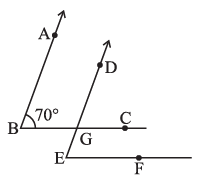
If ∠ABC = 70º, then find
(i) ∠DGC
(ii) ∠DEF
Answer:
Given:
In the given figure, the arms of two angles, $\angle$ABC and $\angle$DEF, are parallel.
AB || DE
BC || EF
$\angle$ABC = $70^\circ$
To Find:
(i) $\angle$DGC
(ii) $\angle$DEF
Solution:
(i) To find $\angle$DGC:
Consider the parallel lines AB and DE intersected by the transversal BC.
$\angle$ABC and $\angle$DGC are corresponding angles.
$\angle$DGC = $\angle$ABC
(Corresponding angles)
$\angle$DGC = $70^\circ$
(Given $\angle$ABC = $70^\circ$)
(ii) To find $\angle$DEF:
Consider the parallel lines BC and EF intersected by the transversal DE.
$\angle$DGC and $\angle$DEF are corresponding angles.
$\angle$DEF = $\angle$DGC
(Corresponding angles)
$\angle$DEF = $70^\circ$
(From (i), $\angle$DGC = $70^\circ$)
Question 6. In the given figures below, decide whether l is parallel to m.
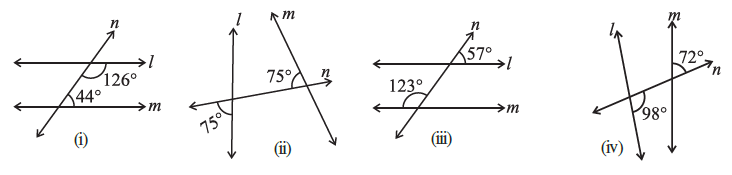
Answer:
To determine if line l is parallel to line m in each case, we must check if the conditions for parallel lines are met (e.g., if corresponding angles are equal, if alternate interior angles are equal, or if interior angles on the same side of the transversal are supplementary).
(i) Figure (i)
In this figure, the given angles are $126^\circ$ and $44^\circ$. These are interior angles on the same side of the transversal n.
For lines l and m to be parallel, the sum of these angles must be $180^\circ$.
Let's check their sum:
$126^\circ + 44^\circ = 170^\circ$
Since the sum is $170^\circ$ and not $180^\circ$, the condition for parallel lines is not satisfied.
Therefore, l is not parallel to m.
(ii) Figure (ii)
In this figure, we are given two angles, both measuring $75^\circ$. Let's find the angle that is vertically opposite to the $75^\circ$ angle on line l. Let's call this angle x.
$x = 75^\circ$
(Vertically opposite angles)
Now, angle x and the other given $75^\circ$ angle (on line m) are interior angles on the same side of the transversal n.
For lines l and m to be parallel, their sum must be $180^\circ$.
Let's check their sum:
$x + 75^\circ = 75^\circ + 75^\circ = 150^\circ$
Since the sum is $150^\circ$ and not $180^\circ$, the condition for parallel lines is not satisfied.
Therefore, l is not parallel to m.
(iii) Figure (iii)
In this figure, we are given a $57^\circ$ angle and a $123^\circ$ angle. Let's find the angle adjacent to the $57^\circ$ angle on the straight line l. Let's call this angle y.
$y + 57^\circ = 180^\circ$
(Linear pair)
$y = 180^\circ - 57^\circ = 123^\circ$
Now, angle y and the given $123^\circ$ angle on line m are corresponding angles. Since both angles are equal to $123^\circ$, the condition for parallel lines is satisfied.
Therefore, l is parallel to m.
(iv) Figure (iv)
In this figure, we are given a $98^\circ$ angle and a $72^\circ$ angle. Let's find the angle adjacent to the $98^\circ$ angle on the straight line l. Let's call this angle z.
$z + 98^\circ = 180^\circ$
(Linear pair)
$z = 180^\circ - 98^\circ = 82^\circ$
Now, angle z and the given $72^\circ$ angle on line m are corresponding angles. For the lines to be parallel, these angles must be equal.
However, $z = 82^\circ$ and the other angle is $72^\circ$. Since $82^\circ \neq 72^\circ$, the corresponding angles are not equal.
Therefore, l is not parallel to m.

