| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 The Triangle and its Properties
Welcome to the detailed solutions for Chapter 6: The Triangle and its Properties. Triangles, as the simplest polygons, are fundamental building blocks in geometry and appear extensively in architecture, engineering, art, and nature. Understanding their unique characteristics is essential for building a strong foundation in geometry. This chapter delves specifically into the core properties related to the angles and side lengths of triangles, moving beyond simple identification towards analytical understanding. The solutions provided here offer comprehensive explanations and step-by-step guidance to help master these crucial concepts and apply them effectively in problem-solving.
Building upon prior knowledge, the chapter briefly revisits the classification of triangles based on:
- Sides: Equilateral (all sides equal), Isosceles (two sides equal), Scalene (no sides equal).
- Angles: Acute-angled (all angles < $90^\circ$), Obtuse-angled (one angle > $90^\circ$), Right-angled (one angle = $90^\circ$).
Furthermore, two important line segments within a triangle are formally introduced:
- Median: A line segment connecting a vertex to the midpoint of the opposite side. Every triangle has three medians.
- Altitude: A perpendicular line segment ($\perp$) from a vertex to the line containing the opposite side. The altitude represents the height of the triangle from that vertex. Every triangle also has three altitudes, which might sometimes fall outside the triangle (in obtuse triangles). Solutions help distinguish between these two key segments.
Two fundamental properties governing the angles of a triangle are explored in depth:
- Exterior Angle Property: This property states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles. If an exterior angle is formed at vertex C, and the interior angles are $\angle A$, $\angle B$, and $\angle C$, then $\text{Exterior } \angle C = \angle A + \angle B$. Solutions demonstrate its application in finding unknown angles without needing all three interior angles.
- Angle Sum Property: A cornerstone property stating that the sum of the measures of the three interior angles of any triangle is always $180^\circ$. Symbolically, $\angle A + \angle B + \angle C = 180^\circ$. Solutions provide extensive practice using this property to find missing angles when two are known, or when relationships between angles are given.
Regarding the sides of a triangle, a crucial constraint is introduced:
- Triangle Inequality Property: This property dictates that the sum of the lengths of any two sides of a triangle must always be greater than the length of the third side. If the side lengths are $a, b, c$, then all three conditions must hold: $a + b > c$, $a + c > b$, and $b + c > a$. Solutions guide students in using this property to determine if a valid triangle can be constructed given three potential side lengths.
Finally, a special and highly significant property related to right-angled triangles is presented:
- Pythagorean Theorem: Named after the ancient Greek mathematician Pythagoras, this theorem applies only to right-angled triangles. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides (called legs). If $c$ is the hypotenuse and $a$ and $b$ are the legs, the theorem is expressed as: $a^2 + b^2 = c^2$. Solutions demonstrate its use in finding the length of an unknown side when two sides are known, and also in checking if three given side lengths could form a right-angled triangle (by seeing if the square of the longest side equals the sum of the squares of the other two).
The chapter solutions consistently apply these properties to solve a variety of numerical and word problems, reinforcing understanding and building geometric reasoning skills necessary for more advanced mathematical concepts.
Exercise 6.1
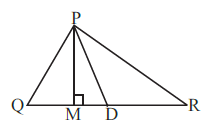
Question 1. In ∆ PQR, D is the mid-point of $\overline{QR}$ .
$\overline{PM}$ is _________________.
PD is _________________.
Is QM = MR?
Answer:
In the given triangle PQR, D is the midpoint of the side QR.
PM is the line segment from vertex P to the side QR, forming a $90^\circ$ angle with QR at point M. A line segment from a vertex perpendicular to the opposite side is called an altitude.
PD is the line segment from vertex P to the midpoint D of the opposite side QR. A line segment from a vertex to the midpoint of the opposite side is called a median.
Based on these definitions:
$\overline{PM}$ is the altitude.
PD is the median.
The question is "Is QM = MR?".
We are given that D is the midpoint of QR, which means QD = DR.
M is the foot of the altitude from P to QR. For QM to be equal to MR, M would have to be the midpoint of QR.
The foot of the altitude (M) coincides with the midpoint of the base (D) only in specific types of triangles, such as an isosceles triangle where the altitude is drawn from the vertex angle to the base, or in an equilateral triangle.
In the given figure, M and D are distinct points, and there is no indication that triangle PQR is isosceles with PQ = PR.
Therefore, QM is not necessarily equal to MR.
Is QM = MR? No.
Question 2. Draw rough sketches for the following:
(a) In ∆ABC, BE is a median.
(b) In ∆PQR, PQ and PR are altitudes of the triangle.
(c) In ∆XYZ, YL is an altitude in the exterior of the triangle.
Answer:
Here are the rough sketches for the given descriptions:
(a) In ∆ABC, BE is a median.
A median connects a vertex to the midpoint of the opposite side. Here, BE connects vertex B to the midpoint E of side AC.

(b) In ∆PQR, PQ and PR are altitudes of the triangle.
An altitude is a perpendicular segment from a vertex to the opposite side (or extension of the opposite side). If two sides of a triangle are altitudes, the triangle must be a right-angled triangle, and the altitudes are the legs that meet at the right angle vertex. Here, PQ is the altitude from P to QR, and PR is the altitude from P to PQ (extended). This implies that the angle at P is $90^\circ$, and PQ is perpendicular to PR.

Note: For PQ to be an altitude to QR, it must be perpendicular to QR. For PR to be an altitude to PQ, it must be perpendicular to PQ. This configuration occurs when the right angle is at vertex P.
(c) In ∆XYZ, YL is an altitude in the exterior of the triangle.
An altitude can lie in the exterior of a triangle if the triangle is obtuse-angled. For the altitude YL from vertex Y to side XZ (or its extension) to be in the exterior, the angle at either X or Z (or both) must be obtuse or right-angled, causing the foot of the perpendicular from Y to fall outside the segment XZ.

In this sketch, $\angle$XZY is obtuse, causing the foot of the altitude from Y to fall on the extension of XZ at point L, outside the triangle.
Question 3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
Answer:
To Verify:
To verify by drawing a diagram if the median and altitude of an isosceles triangle can be the same.
Construction Steps:
1. Draw a line segment BC, which will serve as the base of the triangle.
2. Construct the perpendicular bisector of BC. Let the midpoint of BC be D.
3. Choose any point A on the perpendicular bisector and join A to B and A to C.
4. This forms the triangle ΔABC.
Verification from the Diagram:
Let us analyze the triangle ΔABC that we have constructed.
1. Is the line segment AD an altitude?
By our construction, the line segment AD is perpendicular to the side BC. A line segment from a vertex that is perpendicular to the opposite side is called an altitude. Thus, AD is the altitude of the triangle corresponding to the side BC.
2. Is the line segment AD a median?
By our construction, D is the midpoint of the side BC. A line segment that joins a vertex to the midpoint of the opposite side is called a median. Thus, AD is the median of the triangle corresponding to the side BC.
3. Is the triangle ΔABC an isosceles triangle?
To check this, we can compare the triangles ΔADB and ΔADC.
AD = AD
(Common side)
∠ADB = ∠ADC
(Both are 90° by construction)
BD = CD
(D is the midpoint of BC)
By the SAS (Side-Angle-Side) congruence rule, ΔADB ≅ ΔADC.
Since the triangles are congruent, their corresponding sides must be equal. Therefore, AB = AC.
A triangle with two equal sides is an isosceles triangle. Thus, ΔABC is an isosceles triangle.
Conclusion:
Yes, the diagram verifies that for the isosceles triangle ABC, the line segment AD is both the median and the altitude from the vertex A to the base BC.
Example 1 (Before Exercise 6.2)
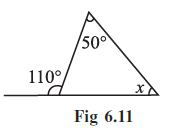
Example 1 Find angle x in Fig 6.11.
Answer:
In the given figure, $x$ is the exterior angle of the triangle.
The angles with measures $50^\circ$ and $70^\circ$ are the two interior opposite angles to the exterior angle $x$.
According to the Exterior Angle Property of a Triangle, the measure of an exterior angle of a triangle is equal to the sum of the measures of its two opposite interior angles.
Applying this property, we have:
$x = 50^\circ + 70^\circ$
$x = 120^\circ$
Thus, the value of angle $x$ is $120^\circ$.
Exercise 6.2
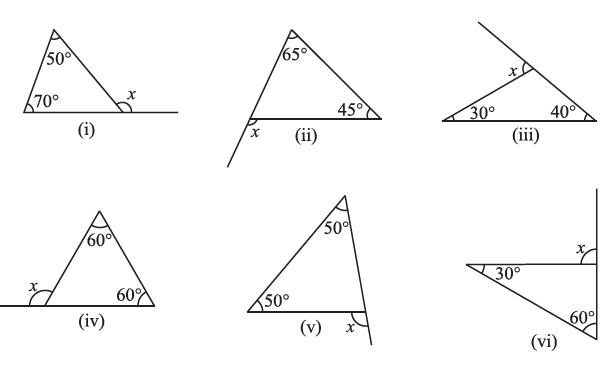
Question 1. Find the value of the unknown exterior angle x in the following diagrams:
Answer:
To find the value of the unknown exterior angle $x$, we will use the Exterior Angle Property of a Triangle, which states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its two opposite interior angles.
Figure (i):
The interior opposite angles are $70^\circ$ and $50^\circ$.
$x = 70^\circ + 50^\circ$
$x = 120^\circ$
Figure (ii):
The interior opposite angles are $65^\circ$ and $45^\circ$.
$x = 65^\circ + 45^\circ$
$x = 110^\circ$
Figure (iii):
The interior opposite angles are $30^\circ$ and $40^\circ$.
$x = 30^\circ + 40^\circ$
$x = 70^\circ$
Figure (iv):
The interior opposite angles are $60^\circ$ and $60^\circ$.
$x = 60^\circ + 60^\circ$
$x = 120^\circ$
Figure (v):
The interior opposite angles are $50^\circ$ and $50^\circ$.
$x = 50^\circ + 50^\circ$
$x = 100^\circ$
Figure (vi):
The interior opposite angles are $30^\circ$ and $60^\circ$.
$x = 30^\circ + 60^\circ$
$x = 90^\circ$
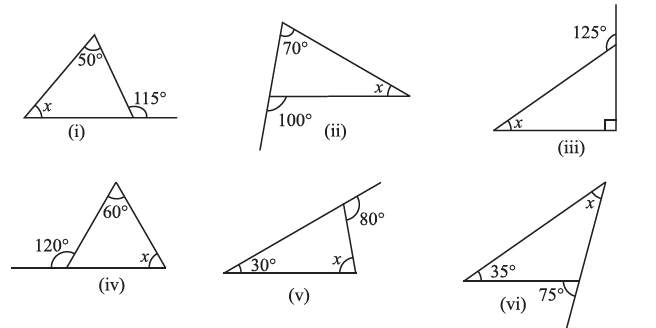
Question 2. Find the value of the unknown interior angle x in the following figures:
Answer:
To find the value of the unknown interior angle $x$, we will again use the Exterior Angle Property of a Triangle, which states that the measure of an exterior angle is equal to the sum of the measures of its two opposite interior angles.
Figure (i):
The exterior angle is $115^\circ$. The interior opposite angles are $x$ and $50^\circ$.
$115^\circ = x + 50^\circ$
To find $x$, subtract $50^\circ$ from $115^\circ$:
$x = 115^\circ - 50^\circ$
$x = 65^\circ$
Figure (ii):
The exterior angle is $100^\circ$. The interior opposite angles are $x$ and $70^\circ$.
$100^\circ = x + 70^\circ$
$x = 100^\circ - 70^\circ$
$x = 30^\circ$
Figure (iii):
The exterior angle is $125^\circ$. The interior opposite angles are $x$ and $90^\circ$ (indicated by the right angle symbol).
$125^\circ = x + 90^\circ$
$x = 125^\circ - 90^\circ$
$x = 35^\circ$
Figure (iv):
The exterior angle is $120^\circ$. The interior opposite angles are $x$ and $60^\circ$.
$120^\circ = x + 60^\circ$
$x = 120^\circ - 60^\circ$
$x = 60^\circ$
Figure (v):
The exterior angle is $80^\circ$. The interior opposite angles are $x$ and $30^\circ$.
$80^\circ = x + 30^\circ$
$x = 80^\circ - 30^\circ$
$x = 50^\circ$
Figure (vi):
The exterior angle is $75^\circ$. The interior opposite angles are $x$ and $35^\circ$.
$75^\circ = x + 35^\circ$
$x = 75^\circ - 35^\circ$
$x = 40^\circ$
Example 2 (Before Exercise 6.3)
Example 2 In the given figure (Fig 6.18) find m∠P.
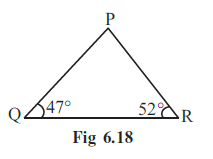
Answer:
Given:
In the given triangle PQR:
$m\angle Q = 47^\circ$
$m\angle R = 52^\circ$
To Find:
The measure of angle P, i.e., $m\angle P$.
Solution:
We know that the sum of the measures of the three interior angles of any triangle is always $180^\circ$. This is called the Angle Sum Property of a Triangle.
Applying this property to ΔPQR, we get:
$m\angle P + m\angle Q + m\angle R = 180^\circ$
(Angle Sum Property)
Now, substitute the given values of $m\angle Q$ and $m\angle R$ into the equation:
$m\angle P + 47^\circ + 52^\circ = 180^\circ$
Add the known angles:
$m\angle P + 99^\circ = 180^\circ$
To find $m\angle P$, subtract $99^\circ$ from $180^\circ$:
$m\angle P = 180^\circ - 99^\circ$
$m\angle P = 81^\circ$
Therefore, the measure of angle P is $81^\circ$.
Exercise 6.3
Question 1. Find the value of the unknown x in the following diagrams:
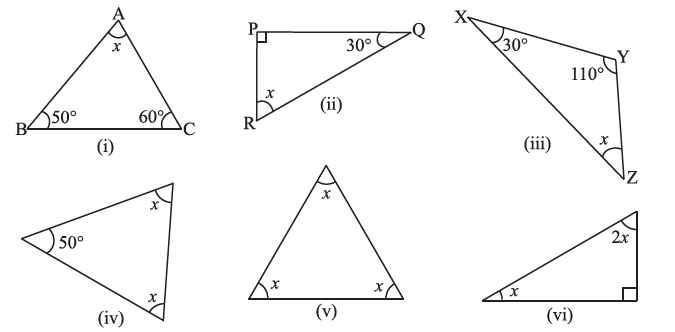
Answer:
We will use the Angle Sum Property of a Triangle, which states that the sum of the interior angles of any triangle is $180^\circ$.
(i) Solution for Figure (i):
The angles in the triangle are $x$, $50^\circ$, and $60^\circ$.
$x + 50^\circ + 60^\circ = 180^\circ$
(Angle Sum Property)
$x + 110^\circ = 180^\circ$
$x = 180^\circ - 110^\circ$
$x = 70^\circ$
(ii) Solution for Figure (ii):
This is a right-angled triangle, so one angle is $90^\circ$. The other angles are $x$ and $30^\circ$.
$x + 90^\circ + 30^\circ = 180^\circ$
(Angle Sum Property)
$x + 120^\circ = 180^\circ$
$x = 180^\circ - 120^\circ$
$x = 60^\circ$
(iii) Solution for Figure (iii):
The angles in the triangle are $x$, $30^\circ$, and $110^\circ$.
$x + 30^\circ + 110^\circ = 180^\circ$
(Angle Sum Property)
$x + 140^\circ = 180^\circ$
$x = 180^\circ - 140^\circ$
$x = 40^\circ$
(iv) Solution for Figure (iv):
The angles in the triangle are $x$, $x$, and $50^\circ$.
$x + x + 50^\circ = 180^\circ$
(Angle Sum Property)
$2x + 50^\circ = 180^\circ$
$2x = 180^\circ - 50^\circ$
$2x = 130^\circ$
$x = \frac{130^\circ}{2}$
$x = 65^\circ$
(v) Solution for Figure (v):
This is an equilateral triangle, so all three angles are equal to $x$.
$x + x + x = 180^\circ$
(Angle Sum Property)
$3x = 180^\circ$
$x = \frac{180^\circ}{3}$
$x = 60^\circ$
(vi) Solution for Figure (vi):
This is a right-angled triangle, so one angle is $90^\circ$. The other angles are $x$ and $2x$.
$x + 2x + 90^\circ = 180^\circ$
(Angle Sum Property)
$3x + 90^\circ = 180^\circ$
$3x = 180^\circ - 90^\circ$
$3x = 90^\circ$
$x = \frac{90^\circ}{3}$
$x = 30^\circ$
Question 2. Find the values of the unknowns x and y in the following diagrams:
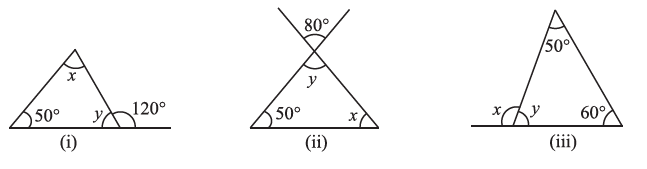
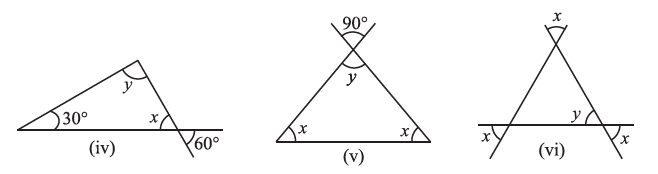
Answer:
We will use the properties of triangles and lines, including the Angle Sum Property (sum of angles in a triangle is $180^\circ$), the Exterior Angle Property, the Linear Pair Property, and the Vertically Opposite Angles Property.
(i) Solution for Figure (i)
First, we find the value of y. The angle y and the angle $120^\circ$ form a linear pair on a straight line.
$y + 120^\circ = 180^\circ$
(Linear Pair)
$y = 180^\circ - 120^\circ = 60^\circ$
Now, we use the Angle Sum Property for the triangle with angles x, y, and $50^\circ$.
$x + y + 50^\circ = 180^\circ$
(Angle Sum Property)
$x + 60^\circ + 50^\circ = 180^\circ$
$x + 110^\circ = 180^\circ$
$x = 180^\circ - 110^\circ = 70^\circ$
So, $x = 70^\circ$ and $y = 60^\circ$.
(ii) Solution for Figure (ii)
First, we find the value of y. The angle y and the angle $80^\circ$ are vertically opposite angles.
$y = 80^\circ$
(Vertically opposite angles)
Now, we use the Angle Sum Property for the triangle with angles x, y, and $50^\circ$.
$x + y + 50^\circ = 180^\circ$
(Angle Sum Property)
$x + 80^\circ + 50^\circ = 180^\circ$
$x + 130^\circ = 180^\circ$
$x = 180^\circ - 130^\circ = 50^\circ$
So, $x = 50^\circ$ and $y = 80^\circ$.
(iii) Solution for Figure (iii)
First, we find the value of y using the Angle Sum Property for the triangle. The angles are $50^\circ$, $60^\circ$, and y.
$y + 50^\circ + 60^\circ = 180^\circ$
(Angle Sum Property)
$y + 110^\circ = 180^\circ$
$y = 180^\circ - 110^\circ = 70^\circ$
The angles x and y are on a straight line, but x is an exterior angle whose opposite interior angles are $50^\circ$ and $60^\circ$. By the Exterior Angle Property:
$x = 50^\circ + 60^\circ$
(Exterior Angle Property)
$x = 110^\circ$
So, $x = 110^\circ$ and $y = 70^\circ$.
(iv) Solution for Figure (iv)
First, we find the value of x. The angle x and the angle $60^\circ$ are vertically opposite angles.
$x = 60^\circ$
(Vertically opposite angles)
Now, we use the Angle Sum Property for the triangle with angles x, y, and $30^\circ$.
$y + x + 30^\circ = 180^\circ$
(Angle Sum Property)
$y + 60^\circ + 30^\circ = 180^\circ$
$y + 90^\circ = 180^\circ$
$y = 180^\circ - 90^\circ = 90^\circ$
So, $x = 60^\circ$ and $y = 90^\circ$.
(v) Solution for Figure (v)
First, we find the value of y. The angle y and the angle $90^\circ$ are vertically opposite angles.
$y = 90^\circ$
(Vertically opposite angles)
Now, we use the Angle Sum Property for the triangle. The angles are x, x, and y. This is an isosceles triangle.
$x + x + y = 180^\circ$
(Angle Sum Property)
$2x + 90^\circ = 180^\circ$
$2x = 180^\circ - 90^\circ$
$2x = 90^\circ$
$x = \frac{90^\circ}{2} = 45^\circ$
So, $x = 45^\circ$ and $y = 90^\circ$.
(vi) Solution for Figure (vi)
By observing the figure, we can see that the angles inside the triangle are vertically opposite to the angles labeled 'x' outside the triangle. Therefore, all three interior angles of the triangle are equal to x.
Using the Angle Sum Property for the triangle:
$x + x + x = 180^\circ$
(Angle Sum Property)
$3x = 180^\circ$
$x = \frac{180^\circ}{3} = 60^\circ$
The angle y is vertically opposite to one of the interior angles of the triangle (which is x).
$y = x$
(Vertically opposite angles)
So, $x = 60^\circ$ and $y = 60^\circ$.
Example 3 & 4 (Before Exercise 6.4)
Example 3 Is there a triangle whose sides have lengths 10.2 cm, 5.8 cm and 4.5 cm?
Answer:
To determine if a triangle can be formed with the given side lengths, we use the Triangle Inequality Property.
The Triangle Inequality Property states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Given side lengths are $a = 10.2$ cm, $b = 5.8$ cm, and $c = 4.5$ cm.
We need to check if the following three conditions are met:
(i) $a + b > c$
(ii) $a + c > b$
(iii) $b + c > a$
Let's check the conditions:
(i) $a + b = 10.2 \text{ cm} + 5.8 \text{ cm} = 16.0 \text{ cm}$
Is $16.0 \text{ cm} > 4.5 \text{ cm}$?
Yes, $16.0 > 4.5$. This condition is satisfied.
(ii) $a + c = 10.2 \text{ cm} + 4.5 \text{ cm} = 14.7 \text{ cm}$
Is $14.7 \text{ cm} > 5.8 \text{ cm}$?
Yes, $14.7 > 5.8$. This condition is satisfied.
(iii) $b + c = 5.8 \text{ cm} + 4.5 \text{ cm} = 10.3 \text{ cm}$
Is $10.3 \text{ cm} > 10.2 \text{ cm}$?
Yes, $10.3 > 10.2$. This condition is satisfied.
Since the sum of the lengths of any two sides is greater than the length of the third side in all three cases, the Triangle Inequality Property is satisfied.
Therefore, a triangle can be formed with side lengths 10.2 cm, 5.8 cm, and 4.5 cm.
Example 4 The lengths of two sides of a triangle are 6 cm and 8 cm. Between which two numbers can length of the third side fall?
Answer:
Let the lengths of the two sides of the triangle be $a = 6$ cm and $b = 8$ cm.
Let the length of the third side be $x$ cm.
According to the Triangle Inequality Property, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
We need to satisfy the following three conditions:
1. Sum of the two given sides > Third side
$a + b > x$
$6 + 8 > x$
$14 > x$ or $x < 14$
2. Sum of the first given side and the third side > Second given side
$a + x > b$
$6 + x > 8$
$x > 8 - 6$
$x > 2$
3. Sum of the second given side and the third side > First given side
$b + x > a$
$8 + x > 6$
$x > 6 - 8$
$x > -2$
Combining the inequalities $x < 14$ and $x > 2$ (the condition $x > -2$ is automatically satisfied since length must be positive), we find the range for the length of the third side $x$.
The length of the third side must be greater than 2 cm and less than 14 cm.
Thus, the length of the third side can fall between 2 cm and 14 cm.
Exercise 6.4
Question 1. Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Answer:
To determine if a triangle can be formed with the given side lengths, we use the Triangle Inequality Property. This property states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
(i) Side lengths: 2 cm, 3 cm, 5 cm
Let's check the sum of each pair of sides against the third side:
$2 + 3 = 5$
Is $5 > 5$? No, $5$ is equal to $5$.
Since the sum of the two smaller sides (2 cm and 3 cm) is equal to the largest side (5 cm), the triangle inequality $2 + 3 > 5$ is not satisfied (it should be strictly greater than). Therefore, it is not possible to form a triangle with these side lengths.
(ii) Side lengths: 3 cm, 6 cm, 7 cm
Let's check the sums:
$3 + 6 = 9$. Is $9 > 7$? Yes.
$3 + 7 = 10$. Is $10 > 6$? Yes.
$6 + 7 = 13$. Is $13 > 3$? Yes.
Since the sum of any two sides is greater than the third side, the triangle inequality is satisfied. Therefore, it is possible to form a triangle with these side lengths.
(iii) Side lengths: 6 cm, 3 cm, 2 cm
Let's check the sums:
$6 + 3 = 9$. Is $9 > 2$? Yes.
$6 + 2 = 8$. Is $8 > 3$? Yes.
$3 + 2 = 5$. Is $5 > 6$? No, $5$ is less than $6$.
Since the sum of the two smaller sides (3 cm and 2 cm) is not greater than the largest side (6 cm), the triangle inequality $3 + 2 > 6$ is not satisfied. Therefore, it is not possible to form a triangle with these side lengths.
Question 2. Take any point O in the interior of a triangle PQR. Is
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Answer:
Let O be any point in the interior of triangle PQR.
We can consider the smaller triangles formed by connecting point O to the vertices of triangle PQR, namely $\triangle$OPQ, $\triangle$OQR, and $\triangle$ORP.
(i) Is OP + OQ > PQ?
Consider $\triangle$OPQ. The sides of this triangle are OP, OQ, and PQ.
According to the Triangle Inequality Property, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Applying the Triangle Inequality to $\triangle$OPQ, we have:
OP + OQ > PQ
OQ + PQ > OP
OP + PQ > OQ
The question asks if OP + OQ > PQ is true.
Since O, P, and Q form a triangle (as O is a point and P and Q are vertices), the sum of two sides OP and OQ must be greater than the third side PQ.
So, the statement OP + OQ > PQ is True.
(ii) Is OQ + OR > QR?
Consider $\triangle$OQR. The sides of this triangle are OQ, OR, and QR.
Applying the Triangle Inequality Property to $\triangle$OQR, we have:
OQ + OR > QR
OQ + QR > OR
OR + QR > OQ
The question asks if OQ + OR > QR is true.
Since O, Q, and R form a triangle, the sum of two sides OQ and OR must be greater than the third side QR.
So, the statement OQ + OR > QR is True.
(iii) Is OR + OP > RP?
Consider $\triangle$ORP. The sides of this triangle are OR, OP, and RP (which is the same as PR).
Applying the Triangle Inequality Property to $\triangle$ORP, we have:
OR + OP > RP
OR + RP > OP
OP + RP > OR
The question asks if OR + OP > RP is true.
Since O, R, and P form a triangle, the sum of two sides OR and OP must be greater than the third side RP.
So, the statement OR + OP > RP is True.
Question 3. AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ∆ABM and ∆AMC.)
Answer:
Given:
AM is a median of $\triangle$ABC.
To Check:
Is AB + BC + CA > 2 AM?
Since AM is a median of $\triangle$ABC, M is the midpoint of the side BC. This means BM = MC.
Also, BC = BM + MC = BM + BM = 2BM.
Consider the triangle $\triangle$ABM.
Applying the Triangle Inequality Property (the sum of the lengths of any two sides of a triangle is greater than the length of the third side) to $\triangle$ABM, we get:
AB + BM > AM
... (i)
Consider the triangle $\triangle$AMC.
Applying the Triangle Inequality Property to $\triangle$AMC, we get:
AC + MC > AM
... (ii)
Now, adding the inequalities (i) and (ii):
$(AB + BM) + (AC + MC) > AM + AM$
$AB + BM + AC + MC > 2 AM$
Rearrange the terms:
$AB + AC + (BM + MC) > 2 AM$
Since M is the midpoint of BC, BM + MC = BC.
Substitute BM + MC with BC:
$AB + AC + BC > 2 AM$
This can be written as:
$AB + BC + CA > 2 AM$
This inequality shows that the sum of the lengths of the three sides of triangle ABC (which is its perimeter) is greater than twice the length of the median AM.
So, the statement AB + BC + CA > 2 AM is True.
Question 4. ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
Answer:
Given:
ABCD is a quadrilateral.
The diagonals are AC and BD.
To Check:
Is AB + BC + CD + DA > AC + BD?
We will use the Triangle Inequality Property, which states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
Consider the triangles formed by the sides and the diagonals of the quadrilateral:
In $\triangle$ABC, applying the Triangle Inequality:
AB + BC > AC
... (i)
In $\triangle$ADC, applying the Triangle Inequality:
AD + CD > AC
... (ii)
In $\triangle$ABD, applying the Triangle Inequality:
AB + AD > BD
... (iii)
In $\triangle$BCD, applying the Triangle Inequality:
BC + CD > BD
... (iv)
Add the inequalities (i), (ii), (iii), and (iv):
$(AB + BC) + (AD + CD) + (AB + AD) + (BC + CD) > AC + AC + BD + BD$
Combine like terms on the left side:
$(AB + AB) + (BC + BC) + (CD + CD) + (AD + AD) > 2AC + 2BD$
$2AB + 2BC + 2CD + 2AD > 2AC + 2BD$
Factor out 2 from both sides:
$2(AB + BC + CD + AD) > 2(AC + BD)$
Divide both sides by 2:
$AB + BC + CD + AD > AC + BD$
This shows that the sum of the lengths of the sides of the quadrilateral is greater than the sum of the lengths of its diagonals.
So, the statement AB + BC + CD + DA > AC + BD is True.
Question 5. ABCD is quadrilateral. Is
AB + BC + CD + DA < 2 (AC + BD)?
Answer:
Given:
ABCD is a quadrilateral.
The diagonals are AC and BD.
To Check:
Is AB + BC + CD + DA < 2 (AC + BD)?
Let O be the point of intersection of the diagonals AC and BD.
Consider the four triangles formed by the diagonals and the point of intersection: $\triangle$OAB, $\triangle$OBC, $\triangle$OCD, and $\triangle$ODA.
We will apply the Triangle Inequality Property to each of these triangles. The property states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
In $\triangle$OAB:
OA + OB > AB
... (i)
In $\triangle$OBC:
OB + OC > BC
... (ii)
In $\triangle$OCD:
OC + OD > CD
... (iii)
In $\triangle$ODA:
OD + OA > DA
... (iv)
Add the inequalities (i), (ii), (iii), and (iv):
$(OA + OB) + (OB + OC) + (OC + OD) + (OD + OA) > AB + BC + CD + DA$
Combine like terms on the left side:
$2OA + 2OB + 2OC + 2OD > AB + BC + CD + DA$
Group the terms involving the diagonal segments:
$2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA$
Since O is the point of intersection of the diagonals AC and BD:
OA + OC = AC
(Length of diagonal AC)
OB + OD = BD
(Length of diagonal BD)
Substitute these into the inequality:
$2(AC) + 2(BD) > AB + BC + CD + DA$
Factor out 2:
$2(AC + BD) > AB + BC + CD + DA$
This inequality can be rewritten as:
$AB + BC + CD + DA < 2(AC + BD)$
This shows that the sum of the lengths of the sides of the quadrilateral is less than twice the sum of the lengths of its diagonals.
So, the statement AB + BC + CD + DA < 2 (AC + BD) is True.
Question 6. The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Answer:
Let the lengths of the two given sides of the triangle be $a = 12$ cm and $b = 15$ cm.
Let the length of the third side be $x$ cm.
According to the Triangle Inequality Property, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Also, the difference between the lengths of any two sides must be less than the length of the third side.
Using the sum property:
The sum of the two given sides must be greater than the third side:
$a + b > x$
$12 + 15 > x$
$27 > x$ or $x < 27$
Using the difference property:
The difference between the two given sides must be less than the third side. Since we are dealing with lengths, the difference should be the absolute difference, $|a - b|$.
$|a - b| < x$
$|12 - 15| < x$
$|-3| < x$
$3 < x$ or $x > 3$
Combining the two inequalities, $x < 27$ and $x > 3$, we find the range for the length of the third side $x$.
The length of the third side must be greater than 3 cm and less than 27 cm.
Thus, the length of the third side should fall between 3 cm and 27 cm.
This means $3 \text{ cm} < x < 27 \text{ cm}$.
Example 5 & 6 (Before Exercise 6.5)
Example 5 Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Answer:
To determine if a triangle is a right-angled triangle given its side lengths, we can use the Pythagorean Property (also known as the converse of the Pythagorean theorem).
The Pythagorean Property states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (legs).
Converse: If, in any triangle, the square of the longest side is equal to the sum of the squares of the other two sides, then the triangle is a right-angled triangle, and the angle opposite the longest side is the right angle.
Given side lengths are 3 cm, 4 cm, and 5 cm.
Identify the longest side, which is the potential hypotenuse. The longest side is 5 cm.
Let $a = 3$ cm, $b = 4$ cm, and $c = 5$ cm.
We need to check if $c^2 = a^2 + b^2$.
Calculate the square of the longest side:
$c^2 = (5 \text{ cm})^2 = 25 \text{ cm}^2$
Calculate the sum of the squares of the other two sides:
$a^2 + b^2 = (3 \text{ cm})^2 + (4 \text{ cm})^2$
$a^2 + b^2 = 9 \text{ cm}^2 + 16 \text{ cm}^2$
$a^2 + b^2 = 25 \text{ cm}^2$
Compare the results:
$c^2 = 25 \text{ cm}^2$
$a^2 + b^2 = 25 \text{ cm}^2$
Since $c^2 = a^2 + b^2$ ($25 = 25$), the Pythagorean property is satisfied.
Therefore, the triangle with side lengths 3 cm, 4 cm, and 5 cm is a right-angled triangle. The angle opposite the side of length 5 cm is the right angle.
Example 6 ∆ ABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.
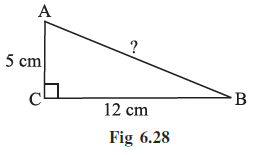
Answer:
Given:
$\triangle$ ABC is right-angled at C.
Length of side AC = 5 cm.
Length of side BC = 12 cm.
To Find:
The length of side AB.
Since $\triangle$ ABC is a right-angled triangle, we can use the Pythagorean Property.
The Pythagorean Property states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs).
In $\triangle$ ABC, the right angle is at C, so the side opposite to angle C is AB. Therefore, AB is the hypotenuse.
The other two sides (legs) are AC and BC.
According to the Pythagorean Property:
$(\text{Hypotenuse})^2 = (\text{Leg 1})^2 + (\text{Leg 2})^2$
In this case:
$(AB)^2 = (AC)^2 + (BC)^2$
Substitute the given lengths:
$(AB)^2 = (5 \text{ cm})^2 + (12 \text{ cm})^2$
Calculate the squares:
$(AB)^2 = 25 \text{ cm}^2 + 144 \text{ cm}^2$
Sum the squares:
$(AB)^2 = 169 \text{ cm}^2$
To find the length of AB, take the square root of both sides:
$AB = \sqrt{169 \text{ cm}^2}$
$AB = 13 \text{ cm}$
Thus, the length of AB is 13 cm.
Exercise 6.5
Question 1. PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Answer:
Given:
$\triangle$ PQR is right-angled at P.
Length of side PQ = 10 cm.
Length of side PR = 24 cm.
To Find:
The length of side QR.
Since $\triangle$ PQR is a right-angled triangle, we can use the Pythagorean Property.
The Pythagorean Property states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs).
In $\triangle$ PQR, the right angle is at P, so the side opposite to angle P is QR. Therefore, QR is the hypotenuse.
The other two sides (legs) are PQ and PR.
According to the Pythagorean Property:
$(\text{Hypotenuse})^2 = (\text{Leg 1})^2 + (\text{Leg 2})^2$
In this case:
$(QR)^2 = (PQ)^2 + (PR)^2$
Substitute the given lengths:
$(QR)^2 = (10 \text{ cm})^2 + (24 \text{ cm})^2$
Calculate the squares:
$(QR)^2 = 100 \text{ cm}^2 + 576 \text{ cm}^2$
Sum the squares:
$(QR)^2 = 676 \text{ cm}^2$
To find the length of QR, take the square root of both sides:
$QR = \sqrt{676 \text{ cm}^2}$
We need to find the square root of 676.
$\sqrt{676} = 26$ (since $26 \times 26 = 676$)
$QR = 26 \text{ cm}$
Thus, the length of QR is 26 cm.
Question 2. ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Answer:
Given:
$\triangle$ ABC is right-angled at C.
Length of side AB = 25 cm.
Length of side AC = 7 cm.
To Find:
The length of side BC.
Since $\triangle$ ABC is a right-angled triangle, we can use the Pythagorean Property.
The Pythagorean Property states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs).
In $\triangle$ ABC, the right angle is at C, so the side opposite to angle C is AB. Therefore, AB is the hypotenuse.
The other two sides (legs) are AC and BC.
According to the Pythagorean Property:
$(AB)^2 = (AC)^2 + (BC)^2$
Substitute the given lengths:
$(25 \text{ cm})^2 = (7 \text{ cm})^2 + (BC)^2$
Calculate the squares:
$625 \text{ cm}^2 = 49 \text{ cm}^2 + (BC)^2$
To find $(BC)^2$, subtract $49 \text{ cm}^2$ from $625 \text{ cm}^2$:
$(BC)^2 = 625 \text{ cm}^2 - 49 \text{ cm}^2$
$(BC)^2 = 576 \text{ cm}^2$
To find the length of BC, take the square root of both sides:
$BC = \sqrt{576 \text{ cm}^2}$
We need to find the square root of 576.
$\sqrt{576} = 24$ (since $24 \times 24 = 576$)
$BC = 24 \text{ cm}$
Thus, the length of BC is 24 cm.
Question 3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
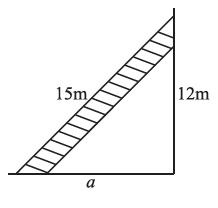
Answer:
Given:
Length of the ladder = 15 m.
Height of the window from the ground = 12 m.
Distance of the foot of the ladder from the wall = $a$ m.
To Find:
The distance $a$ of the foot of the ladder from the wall.
The wall is perpendicular to the ground. The ladder leaning against the wall forms a right-angled triangle with the wall and the ground. The ladder is the hypotenuse, the height of the window on the wall is one leg, and the distance of the foot of the ladder from the wall is the other leg.
Using the Pythagorean Property in the right-angled triangle:
$(\text{Hypotenuse})^2 = (\text{Height on wall})^2 + (\text{Distance from wall})^2$
In this case:
$(\text{Ladder Length})^2 = (\text{Window Height})^2 + (\text{Distance } a)^2$
Substitute the given values:
$(15 \text{ m})^2 = (12 \text{ m})^2 + a^2$
Calculate the squares:
$225 \text{ m}^2 = 144 \text{ m}^2 + a^2$
To find $a^2$, subtract $144 \text{ m}^2$ from $225 \text{ m}^2$:
$a^2 = 225 \text{ m}^2 - 144 \text{ m}^2$
$a^2 = 81 \text{ m}^2$
To find $a$, take the square root of both sides:
$a = \sqrt{81 \text{ m}^2}$
$a = 9 \text{ m}$ (Since distance must be positive)
Thus, the distance of the foot of the ladder from the wall is 9 m.
Question 4. Which of the following can be the sides of a right triangle?
(i) 2.5 cm,6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles
Answer:
To determine if a triangle with given side lengths is a right triangle, we use the Pythagorean Property (Converse). This property states that if the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle, and the angle opposite the longest side is the right angle.
(i) Side lengths: 2.5 cm, 6.5 cm, 6 cm.
The longest side is 6.5 cm. Let's check if the square of the longest side is equal to the sum of the squares of the other two sides.
Square of the longest side: $(6.5)^2$
$(6.5)^2 = 6.5 \times 6.5 = 42.25$
Sum of the squares of the other two sides: $(2.5)^2 + (6)^2$
$(2.5)^2 = 2.5 \times 2.5 = 6.25$
$(6)^2 = 6 \times 6 = 36$
Sum = $6.25 + 36 = 42.25$
Compare: $42.25 = 42.25$.
Since the square of the longest side is equal to the sum of the squares of the other two sides, these side lengths can form a right triangle.
The right angle is opposite the longest side (6.5 cm).
(ii) Side lengths: 2 cm, 2 cm, 5 cm.
The longest side is 5 cm. Let's check the Pythagorean property.
Square of the longest side: $(5)^2$
$(5)^2 = 5 \times 5 = 25$
Sum of the squares of the other two sides: $(2)^2 + (2)^2$
$(2)^2 = 2 \times 2 = 4$
$(2)^2 = 2 \times 2 = 4$
Sum = $4 + 4 = 8$
Compare: $25 \neq 8$.
Since the square of the longest side is not equal to the sum of the squares of the other two sides, these side lengths cannot form a right triangle.
We can also quickly check the Triangle Inequality Property here: $2 + 2 = 4$. Is $4 > 5$? No. So, a triangle cannot even be formed with these side lengths.
(iii) Side lengths: 1.5 cm, 2 cm, 2.5 cm.
The longest side is 2.5 cm. Let's check the Pythagorean property.
Square of the longest side: $(2.5)^2$
$(2.5)^2 = 2.5 \times 2.5 = 6.25$
Sum of the squares of the other two sides: $(1.5)^2 + (2)^2$
$(1.5)^2 = 1.5 \times 1.5 = 2.25$
$(2)^2 = 2 \times 2 = 4$
Sum = $2.25 + 4 = 6.25$
Compare: $6.25 = 6.25$.
Since the square of the longest side is equal to the sum of the squares of the other two sides, these side lengths can form a right triangle.
The right angle is opposite the longest side (2.5 cm).
Question 5. A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Answer:
Solution:
Let's visualize the situation. The tree, after breaking, forms a right-angled triangle with the ground.
- The part of the tree that is still standing forms the perpendicular of the triangle.
- The distance from the base of the tree to the point where the top touches the ground forms the base of the triangle.
- The broken part of the tree forms the hypotenuse of the triangle.
Given:
Let the tree break at point B. Let C be the base of the tree and A be the point where the top touches the ground.
This forms a right-angled triangle ΔBCA, with the right angle at C.
Height of the standing part (Perpendicular), BC = 5 m.
Distance from the base of the tree to the top on the ground (Base), AC = 12 m.
The length of the broken part of the tree is the hypotenuse, AB.
To Find:
The original height of the tree.
Original height = Length of the standing part + Length of the broken part
Original height = BC + AB
Proof:
First, we need to find the length of the broken part (the hypotenuse AB) using the Pythagoras theorem.
According to the Pythagoras theorem, in a right-angled triangle:
$(\text{Hypotenuse})^2 = (\text{Perpendicular})^2 + (\text{Base})^2$
$AB^2 = BC^2 + AC^2$
Substitute the given values:
$AB^2 = (5)^2 + (12)^2$
$AB^2 = 25 + 144$
$AB^2 = 169$
$AB = \sqrt{169}$
$AB = 13$ m
So, the length of the broken part of the tree is 13 m.
Now, we can find the original height of the tree.
Original height = Standing part (BC) + Broken part (AB)
Original height = 5 m + 13 m
Original height = 18 m
Therefore, the original height of the tree was 18 m.
Question 6. Angles Q and R of a ∆PQR are 25º and 65º.
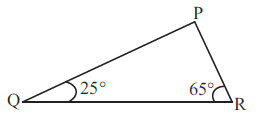
Write which of the following is true:
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2
Answer:
Given:
In $\triangle$PQR,
$\angle$Q = $25^\circ$
$\angle$R = $65^\circ$
To determine which of the given statements is true, we first need to determine if the triangle PQR is a right-angled triangle. If it is, we can apply the Pythagorean property.
We can find the measure of the third angle, $\angle$P, using the Angle Sum Property of a Triangle, which states that the sum of the measures of the interior angles of a triangle is $180^\circ$.
$\angle$P + $\angle$Q + $\angle$R = $180^\circ$
Substitute the given angle measures:
$\angle$P + $25^\circ + 65^\circ = 180^\circ$
$\angle$P + $90^\circ = 180^\circ$
$\angle$P = $180^\circ - 90^\circ$
$\angle$P = $90^\circ$
Since $\angle$P = $90^\circ$, $\triangle$PQR is a right-angled triangle, with the right angle at vertex P.
In a right-angled triangle, the side opposite the right angle is the hypotenuse. The side opposite $\angle$P is QR. Therefore, QR is the hypotenuse.
The other two sides (legs) are PQ and PR (or RP).
According to the Pythagorean Property:
$(\text{Hypotenuse})^2 = (\text{Leg 1})^2 + (\text{Leg 2})^2$
In $\triangle$PQR, where the right angle is at P:
$(QR)^2 = (PQ)^2 + (PR)^2$
This can also be written as:
$(PQ)^2 + (PR)^2 = (QR)^2$
Or, since RP is the same length as PR:
$(PQ)^2 + (RP)^2 = (QR)^2$
Now let's compare this with the given options:
(i) PQ2 + QR2 = RP2 (Incorrect, as QR is the hypotenuse)
(ii) PQ2 + RP2 = QR2 (Correct)
(iii) RP2 + QR2 = PQ2 (Incorrect, as QR is the hypotenuse)
Therefore, the true statement is:
(ii) PQ2 + RP2 = QR2
Question 7. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Answer:
Given:
Length of the rectangle = 40 cm.
Length of a diagonal = 41 cm.
To Find:
The perimeter of the rectangle.
Let the length of the rectangle be $l$ and the width be $w$. The diagonal of a rectangle divides it into two right-angled triangles. The length and width are the legs of the right triangle, and the diagonal is the hypotenuse.
In this case, $l = 40$ cm and the hypotenuse is 41 cm. We need to find the width $w$.
Using the Pythagorean Property in one of the right-angled triangles formed by the diagonal:
$(\text{Diagonal})^2 = (\text{Length})^2 + (\text{Width})^2$
$41^2 = 40^2 + w^2$
Calculate the squares:
$41 \times 41 = 1681$
$40 \times 40 = 1600$
So, $1681 = 1600 + w^2$
To find $w^2$, subtract 1600 from 1681:
$w^2 = 1681 - 1600$
$w^2 = 81$
To find the width $w$, take the square root of both sides:
$w = \sqrt{81}$
$w = 9$ cm (Since width must be positive)
Now that we have the length ($l = 40$ cm) and the width ($w = 9$ cm), we can find the perimeter of the rectangle.
The formula for the perimeter of a rectangle is: Perimeter = $2 \times (\text{Length} + \text{Width})$
Perimeter = $2 \times (l + w)$
Perimeter = $2 \times (40 \text{ cm} + 9 \text{ cm})$
Perimeter = $2 \times (49 \text{ cm})$
Perimeter = $98 \text{ cm}$
Thus, the perimeter of the rectangle is 98 cm.
Question 8. The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter
Answer:
Given:
A rhombus with diagonals of length 16 cm and 30 cm.
Let $d_1 = 30$ cm and $d_2 = 16$ cm.
To Find:
The perimeter of the rhombus.
Solution:
Let the rhombus be ABCD, with diagonals AC and BD intersecting at point O.
We know two important properties of a rhombus:
1. All four sides are equal in length (AB = BC = CD = DA).
2. The diagonals bisect each other at right angles ($90^\circ$).
Since the diagonals bisect each other, they are divided into two equal halves at the point of intersection O.
Length of half of the first diagonal, $AO = OC = \frac{d_1}{2} = \frac{30}{2} = 15$ cm.
Length of half of the second diagonal, $BO = OD = \frac{d_2}{2} = \frac{16}{2} = 8$ cm.
Now, consider the triangle ΔAOB. Since the diagonals intersect at right angles, ΔAOB is a right-angled triangle with the right angle at O.
The sides AO and BO are the legs of the right-angled triangle, and the side of the rhombus AB is the hypotenuse.
We can find the length of the side AB by using the Pythagoras theorem:
$AB^2 = AO^2 + BO^2$
(Pythagoras Theorem)
Substitute the values of AO and BO:
$AB^2 = (15)^2 + (8)^2$
$AB^2 = 225 + 64$
$AB^2 = 289$
$AB = \sqrt{289}$
$AB = 17$ cm
So, the length of one side of the rhombus is 17 cm.
The perimeter of a rhombus is given by the formula:
Perimeter = 4 $\times$ (length of a side)
Perimeter = 4 $\times$ 17 cm
Perimeter = 68 cm
Therefore, the perimeter of the rhombus is 68 cm.

