| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 6 (Before Exercise 8.1) | Exercise 8.1 | Example 7 to 13 (Before Exercise 8.2) |
| Exercise 8.2 | Example 14 to 21 (Before Exercise 8.3) | Exercise 8.3 |
Chapter 8 Comparing Quantities
Welcome to the solutions guide for Chapter 8: Comparing Quantities. This chapter significantly extends the foundational concepts of ratio and proportion learned previously, introducing powerful and widely applicable tools for comparison: percentages and their diverse applications, including the essential real-world concepts of profit and loss, and the fundamentals of simple interest. This chapter stands out for its high degree of practical relevance, bridging mathematical theory with everyday financial literacy, shopping decisions, and basic economic understanding. Mastering these methods allows for more effective comparison and analysis of numerical information encountered daily.
The journey begins by revisiting ratios and equivalent ratios, ensuring a solid base. Then, the powerful concept of Percentages is introduced. Derived from the Latin 'per centum' meaning 'per hundred', a percentage represents a fraction with a denominator of 100, denoted by the symbol $\%$. It provides a standardized way to compare parts of different wholes.
- Solutions provide detailed methods for inter-conversion:
- Converting fractions and decimals to percentages (e.g., $\frac{3}{4} = 0.75$, which is $0.75 \times 100\% = 75\%$).
- Converting percentages back to fractions or decimals (e.g., $40\% = \frac{40}{100} = \frac{2}{5}$ or $0.4$).
- Calculating the percentage of a given quantity is clearly demonstrated (e.g., finding $25\%$ of $\textsf{₹}160$ means calculating $\frac{25}{100} \times 160 = \textsf{₹}40$).
- A major focus is using percentages to compute percentage increase or decrease. This is vital for understanding discounts, price markups, population changes, inflation rates, etc. Solutions show how to calculate the change and express it relative to the original value using the formula: $\text{Percentage Change} = \left( \frac{\text{Actual Increase or Decrease}}{\text{Original Value}} \right) \times 100\%$.
Building on percentages, the chapter delves into the fundamental concepts of Profit and Loss, crucial for understanding basic business transactions:
- Key terms are defined: Cost Price (CP) - the price at which an item is purchased; Selling Price (SP) - the price at which an item is sold.
- Profit arises when the selling price is greater than the cost price ($SP > CP$), calculated as $Profit = SP - CP$.
- Loss occurs when the cost price is greater than the selling price ($CP > SP$), calculated as $Loss = CP - SP$.
- Critically, profit or loss is often expressed as a percentage, always calculated based on the Cost Price:
- $\text{Profit %} = \left( \frac{\text{Profit}}{CP} \right) \times 100$
- $\text{Loss %} = \left( \frac{\text{Loss}}{CP} \right) \times 100$
- Solutions meticulously guide through problems involving finding the SP when CP and profit/loss percent are known (e.g., $SP = CP \times (1 + \frac{\text{Profit %}}{100})$ or $SP = CP \times (1 - \frac{\text{Loss %}}{100})$), and conversely, finding the CP when SP and profit/loss percent are given, often involving algebraic manipulation.
Finally, the fundamentals of Simple Interest (SI) are introduced, providing a basic understanding of interest calculations for loans or investments:
- Core terms are explained: Principal (P) - the initial sum of money borrowed or invested (usually in $\textsf{₹}$); Rate of Interest (R) - the percentage at which interest is charged, typically specified as per annum (% p.a.); Time (T) - the duration for which the money is borrowed or invested, usually measured in years.
- The fundamental formula for calculating Simple Interest is presented: $SI = \frac{P \times R \times T}{100}$.
- The total Amount (A) due at the end of the period is the sum of the Principal and the Simple Interest: $A = P + SI$.
- Solutions apply these formulas to various problems, guiding students in calculating SI, P, R, or T when the other three quantities are provided, demonstrating the practical use of the formulas.
The solutions throughout this chapter are rich with word problems mirroring real-world financial and comparison scenarios. Working through them systematically enhances not only computational skills but also vital quantitative literacy, empowering students to better understand and navigate the economic aspects of everyday life.
Example 1 to 6 (Before Exercise 8.1)
Example 1. Find the ratio of 3 km to 300 m.
Answer:
To find the ratio of two quantities, they must be in the same units.
We are asked to find the ratio of 3 km to 300 m.
We need to convert one of the quantities so that both are in the same unit. Let's convert kilometers to meters.
We know that 1 kilometer (km) = 1000 meters (m).
So, 3 km = $3 \times 1000$ m = 3000 m.
Now, we find the ratio of 3000 m to 300 m.
Ratio = $\frac{\text{Quantity 1}}{\text{Quantity 2}}$
Ratio = $\frac{3000 \text{ m}}{300 \text{ m}}$
We can simplify the fraction by dividing both the numerator and the denominator by a common factor. Both numbers are divisible by 100 and by 3.
Divide by 100:
Ratio = $\frac{30}{3}$
Divide by 3:
Ratio = $\frac{10}{1}$
The ratio can be written as 10 : 1.
Thus, the ratio of 3 km to 300 m is 10 : 1.
Example 2. Are the ratios 1:2 and 2:3 equivalent?
Answer:
To check if two ratios are equivalent, we can write them as fractions and compare the fractions. Two ratios are equivalent if the fractions representing them are equal.
The first ratio is 1:2, which can be written as the fraction $\frac{1}{2}$.
The second ratio is 2:3, which can be written as the fraction $\frac{2}{3}$.
Now, we compare the fractions $\frac{1}{2}$ and $\frac{2}{3}$.
To compare fractions with different denominators, we can find a common denominator or cross-multiply.
Using cross-multiplication:
$1 \times 3 = 3$
$2 \times 2 = 4$
Since the cross-products are not equal ($3 \neq 4$), the fractions are not equal.
Alternatively, using a common denominator (LCM of 2 and 3 is 6):
$\frac{1}{2} = \frac{1 \times 3}{2 \times 3} = \frac{3}{6}$
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
Comparing $\frac{3}{6}$ and $\frac{4}{6}$, we see that $3 \neq 4$, so the fractions are not equal.
Since the fractions representing the ratios are not equal, the ratios 1:2 and 2:3 are not equivalent.
Example 3. Following is the performance of a cricket team in the matches it played:
| Year | Wins | Losses |
|---|---|---|
| Last year | 8 | 2 |
| This year | 4 | 2 |
In which year was the record better?
How can you say so?
Answer:
To compare the performance of the cricket team in the two years, we can look at the ratio of wins to the total number of matches played, or the fraction of matches won.
Last year:
Number of wins = 8
Number of losses = 2
Total number of matches played = Wins + Losses = $8 + 2 = 10$.
Fraction of matches won last year = $\frac{\text{Wins}}{\text{Total Matches}} = \frac{8}{10}$.
This fraction can be simplified by dividing the numerator and denominator by their greatest common divisor, which is 2:
$\frac{8}{10} = \frac{8 \div 2}{10 \div 2} = \frac{4}{5}$.
This year:
Number of wins = 4
Number of losses = 2
Total number of matches played = Wins + Losses = $4 + 2 = 6$.
Fraction of matches won this year = $\frac{\text{Wins}}{\text{Total Matches}} = \frac{4}{6}$.
This fraction can be simplified by dividing the numerator and denominator by their greatest common divisor, which is 2:
$\frac{4}{6} = \frac{4 \div 2}{6 \div 2} = \frac{2}{3}$.
Now we compare the fractions of matches won in the two years: $\frac{4}{5}$ (last year) and $\frac{2}{3}$ (this year).
To compare these fractions, we can find a common denominator (LCM of 5 and 3 is 15):
Last year: $\frac{4}{5} = \frac{4 \times 3}{5 \times 3} = \frac{12}{15}$.
This year: $\frac{2}{3} = \frac{2 \times 5}{3 \times 5} = \frac{10}{15}$.
Comparing the fractions with the same denominator, $\frac{12}{15}$ and $\frac{10}{15}$, we see that $12 > 10$.
So, $\frac{12}{15} > \frac{10}{15}$, which means $\frac{4}{5} > \frac{2}{3}$.
The fraction of matches won last year ($\frac{4}{5}$) is greater than the fraction of matches won this year ($\frac{2}{3}$).
A higher fraction of wins indicates a better performance.
Therefore, the record was better last year.
We can say so because the fraction of matches won last year ($\frac{4}{5}$) is higher than the fraction of matches won this year ($\frac{2}{3}$).
Example 4. A map is given with a scale of 2 cm = 1000 km. What is the actual distance between the two places in kms, if the distance in the map is 2.5 cm?
Answer:
Given:
Scale of the map: 2 cm on the map represents 1000 km in actual distance.
Distance between two places on the map = 2.5 cm.
To Find:
The actual distance between the two places in kilometers.
The scale of the map gives us a ratio relating distance on the map to actual distance:
$\frac{\text{Map Distance}}{\text{Actual Distance}} = \frac{2 \text{ cm}}{1000 \text{ km}}$
We are given a map distance of 2.5 cm and want to find the corresponding actual distance. Let the actual distance be $x$ km.
We can set up a proportion because the ratio of map distance to actual distance is constant according to the scale:
$\frac{2 \text{ cm}}{1000 \text{ km}} = \frac{2.5 \text{ cm}}{x \text{ km}}$
To solve for $x$, we can cross-multiply:
$2 \times x = 1000 \times 2.5$
$2x = 2500$
Divide both sides by 2:
$x = \frac{2500}{2}$
$x = 1250$
So, the actual distance between the two places is 1250 kilometers.
Alternatively, we can find the actual distance represented by 1 cm on the map:
2 cm on map = 1000 km actual distance
1 cm on map = $\frac{1000}{2}$ km actual distance
1 cm on map = 500 km actual distance
Now, for a map distance of 2.5 cm:
Actual distance = $2.5 \times (\text{Actual distance per 1 cm on map})$
Actual distance = $2.5 \times 500$ km
$2.5 \times 500 = (2 + 0.5) \times 500 = 2 \times 500 + 0.5 \times 500 = 1000 + 250 \ $$ = 1250$
Actual distance = 1250 km.
Thus, the actual distance between the two places is 1250 km.
Example 5. 6 bowls cost ₹ 90. What would be the cost of 10 such bowls?
Answer:
Given:
Cost of 6 bowls = $\textsf{₹}$ 90.
To Find:
The cost of 10 such bowls.
We can solve this problem using the unitary method or by setting up a proportion.
Method 1: Unitary Method
Find the cost of one bowl first.
Cost of 6 bowls = $\textsf{₹}$ 90
Cost of 1 bowl = $\frac{\text{Total Cost}}{\text{Number of Bowls}} = \frac{\textsf{₹} 90}{6}$
Cost of 1 bowl = $\textsf{₹}$ 15.
Now, find the cost of 10 bowls.
Cost of 10 bowls = Cost of 1 bowl $\times$ Number of bowls
Cost of 10 bowls = $\textsf{₹} 15 \times 10$
Cost of 10 bowls = $\textsf{₹}$ 150.
Method 2: Using Proportion
Assume the cost of the bowls is directly proportional to the number of bowls (i.e., each bowl costs the same amount).
Let the cost of 10 bowls be $\textsf{₹} x$.
We can set up the proportion:
$\frac{\text{Cost}}{\text{Number of Bowls}} = \text{Constant}$
So, $\frac{\text{Cost of 6 bowls}}{6 \text{ bowls}} = \frac{\text{Cost of 10 bowls}}{10 \text{ bowls}}$
$\frac{90}{6} = \frac{x}{10}$
To solve for $x$, cross-multiply:
$90 \times 10 = 6 \times x$
$900 = 6x$
Divide both sides by 6:
$x = \frac{900}{6}$
$x = 150$
So, the cost of 10 bowls is $\textsf{₹}$ 150.
Thus, the cost of 10 such bowls would be ₹ 150.
Example 6. The car that I own can go 150 km with 25 litres of petrol. How far can it go with 30 litres of petrol?
Answer:
Given:
Distance covered with 25 litres of petrol = 150 km.
To Find:
Distance that can be covered with 30 litres of petrol.
Assume that the distance covered is directly proportional to the amount of petrol (i.e., the mileage of the car is constant).
We can solve this problem using the unitary method or by setting up a proportion.
Method 1: Unitary Method
Find the distance covered per litre of petrol (mileage).
Distance covered with 25 litres = 150 km
Distance covered with 1 litre = $\frac{\text{Total Distance}}{\text{Total Petrol}} = \frac{150 \text{ km}}{25 \text{ litres}}$
Distance covered with 1 litre = 6 km/litre.
Now, find the distance covered with 30 litres of petrol.
Distance covered with 30 litres = Mileage $\times$ Amount of Petrol
Distance covered with 30 litres = $6 \text{ km/litre} \times 30 \text{ litres}$
Distance covered with 30 litres = 180 km.
Method 2: Using Proportion
Let the distance covered with 30 litres of petrol be $x$ km.
We can set up the proportion:
$\frac{\text{Distance}}{\text{Petrol}} = \text{Constant}$
So, $\frac{\text{Distance with 25 litres}}{25 \text{ litres}} = \frac{\text{Distance with 30 litres}}{30 \text{ litres}}$
$\frac{150}{25} = \frac{x}{30}$
To solve for $x$, cross-multiply:
$150 \times 30 = 25 \times x$
$4500 = 25x$
Divide both sides by 25:
$x = \frac{4500}{25}$
$x = \frac{4500 \times 4}{25 \times 4} = \frac{18000}{100} = 180$
$x = 180$
So, the distance covered with 30 litres of petrol is 180 km.
Thus, the car can go 180 km with 30 litres of petrol.
Exercise 8.1
Question 1. Find the ratio of:
(a) ₹ 5 to 50 paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hours
Answer:
To find the ratio of two quantities, their units must be the same. We will convert one quantity's unit to match the other quantity's unit in each case.
(a) Find the ratio of $\textsf{₹}$ 5 to 50 paise.
Convert $\textsf{₹}$ 5 to paise. We know that $\textsf{₹}$ 1 = 100 paise.
$\textsf{₹}$ 5 = $5 \times 100$ paise = 500 paise.
Now find the ratio of 500 paise to 50 paise:
Ratio = $\frac{500 \text{ paise}}{50 \text{ paise}} = \frac{500}{50}$
Simplify the fraction:
$\frac{\cancel{500}^{10}}{\cancel{50}_{1}} = 10$
The ratio is 10 : 1.
(b) Find the ratio of 15 kg to 210 g.
Convert 15 kg to grams. We know that 1 kg = 1000 g.
15 kg = $15 \times 1000$ g = 15000 g.
Now find the ratio of 15000 g to 210 g:
Ratio = $\frac{15000 \text{ g}}{210 \text{ g}} = \frac{15000}{210}$
Simplify the fraction. Divide both numerator and denominator by 10:
$\frac{1500}{21}$
Now divide both by their greatest common divisor, which is 3:
$\frac{\cancel{1500}^{500}}{\cancel{21}_{7}} = \frac{500}{7}$
The ratio is 500 : 7.
(c) Find the ratio of 9 m to 27 cm.
Convert 9 m to centimeters. We know that 1 m = 100 cm.
9 m = $9 \times 100$ cm = 900 cm.
Now find the ratio of 900 cm to 27 cm:
Ratio = $\frac{900 \text{ cm}}{27 \text{ cm}} = \frac{900}{27}$
Simplify the fraction. Divide both numerator and denominator by their greatest common divisor, which is 9:
$\frac{\cancel{900}^{100}}{\cancel{27}_{3}} = \frac{100}{3}$
The ratio is 100 : 3.
(d) Find the ratio of 30 days to 36 hours.
Convert 30 days to hours. We know that 1 day = 24 hours.
30 days = $30 \times 24$ hours = 720 hours.
Now find the ratio of 720 hours to 36 hours:
Ratio = $\frac{720 \text{ hours}}{36 \text{ hours}} = \frac{720}{36}$
Simplify the fraction. We know that $36 \times 2 = 72$, so $36 \times 20 = 720$.
$\frac{\cancel{720}^{20}}{\cancel{36}_{1}} = 20$
The ratio is 20 : 1.
Question 2. In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
Answer:
Given:
Number of computers for 6 students = 3.
To Find:
Number of computers needed for 24 students.
We can solve this problem using the unitary method or by setting up a proportion.
Method 1: Unitary Method
Find the number of students per computer or the number of computers per student.
3 computers are for 6 students.
1 computer is for $\frac{6}{3}$ students = 2 students.
This means the ratio of students to computers is 2:1.
Alternatively, find the number of computers per student:
For 6 students, there are 3 computers.
For 1 student, there are $\frac{3}{6}$ computers = $\frac{1}{2}$ computer.
Now, find the number of computers needed for 24 students.
Number of computers for 24 students = (Number of computers per student) $\times$ Number of students
Number of computers for 24 students = $\frac{1}{2} \times 24$
Number of computers for 24 students = 12.
Method 2: Using Proportion
Assume the ratio of computers to students is constant.
Let the number of computers needed for 24 students be $x$.
We can set up the proportion:
$\frac{\text{Number of Computers}}{\text{Number of Students}} = \text{Constant}$
So, $\frac{3 \text{ computers}}{6 \text{ students}} = \frac{x \text{ computers}}{24 \text{ students}}$
$\frac{3}{6} = \frac{x}{24}$
Simplify the fraction on the left side: $\frac{3}{6} = \frac{1}{2}$.
$\frac{1}{2} = \frac{x}{24}$
To solve for $x$, cross-multiply:
$1 \times 24 = 2 \times x$
$24 = 2x$
Divide both sides by 2:
$x = \frac{24}{2}$
$x = 12$
So, the number of computers needed for 24 students is 12.
Thus, 12 computers will be needed for 24 students.
Question 3. Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.
Area of Rajasthan = 3 lakh km2 and area of UP = 2 lakh km2.
(i) How many people are there per km2 in both these States?
(ii) Which State is less populated?
Answer:
Given:
Rajasthan: Population = 570 lakhs, Area = 3 lakh km$^2$.
Uttar Pradesh (UP): Population = 1660 lakhs, Area = 2 lakh km$^2$.
(i) How many people are there per km$^2$ in both these States?
The number of people per km$^2$ is the population density, which is calculated as $\frac{\text{Population}}{\text{Area}}$.
For Rajasthan:
Population density = $\frac{570 \text{ lakhs}}{3 \text{ lakh km}^2}$
Population density = $\frac{570}{3}$ people per km$^2$
$\frac{570}{3} = 190$
So, there are 190 people per km$^2$ in Rajasthan.
For Uttar Pradesh (UP):
Population density = $\frac{1660 \text{ lakhs}}{2 \text{ lakh km}^2}$
Population density = $\frac{1660}{2}$ people per km$^2$
$\frac{1660}{2} = 830$
So, there are 830 people per km$^2$ in Uttar Pradesh.
Thus, the number of people per km$^2$ is 190 in Rajasthan and 830 in Uttar Pradesh.
(ii) Which State is less populated?
The term "less populated" can refer to either the total population or the population density. Given the context of the previous question (people per km$^2$), it is likely asking about the state with the lower population density.
Compare the population densities:
Rajasthan: 190 people/km$^2$
Uttar Pradesh: 830 people/km$^2$ (which is also the total population density of India)
Since $190 < 830$, Rajasthan has a lower population density than Uttar Pradesh.
Comparing total population directly:
Rajasthan: 570 lakhs
Uttar Pradesh: 1660 lakhs
Since $570 < 1660$, Rajasthan also has a lower total population than Uttar Pradesh.
Both interpretations point to Rajasthan being less populated, though population density is a more precise measure when considering how spread out the population is relative to the area.
Thus, Rajasthan is less populated (both in terms of total population and population density).
Example 7 to 13 (Before Exercise 8.2)
Example 7. Write $\frac{1}{3}$ as per cent.
Answer:
To write a fraction as a per cent, we multiply the fraction by 100 and add the per cent symbol (%).
Solution:
We need to convert the fraction $\frac{1}{3}$ to a per cent.
So, we multiply it by 100%:
$\frac{1}{3} = \left(\frac{1}{3} \times 100\right) \%$
$= \frac{100}{3} \%$
Now, we convert the improper fraction $\frac{100}{3}$ into a mixed fraction.
Dividing 100 by 3 gives a quotient of 33 and a remainder of 1.
So, $\frac{100}{3} = 33 \frac{1}{3}$.
Therefore, $\frac{1}{3}$ as a per cent is $33 \frac{1}{3} \%$.
Example 8. Out of 25 children in a class, 15 are girls. What is the percentage of girls?
Answer:
Given:
Total number of children in the class = 25.
Number of girls = 15.
To Find:
The percentage of girls in the class.
The fraction of girls in the class is the number of girls divided by the total number of children.
Fraction of girls = $\frac{\text{Number of Girls}}{\text{Total Number of Children}} = \frac{15}{25}$.
To convert this fraction to a percentage, we multiply the fraction by 100%.
Percentage of girls = $\frac{15}{25} \times 100\%$
We can simplify the fraction $\frac{15}{25}$ first by dividing the numerator and denominator by their greatest common divisor, which is 5:
$\frac{15}{25} = \frac{15 \div 5}{25 \div 5} = \frac{3}{5}$.
Now, multiply the simplified fraction by 100%:
Percentage of girls = $\frac{3}{5} \times 100\%$
Percentage of girls = $3 \times \frac{100}{5}\%$
Percentage of girls = $3 \times 20\%$
Percentage of girls = $60\%$
Alternatively, multiply the fraction $\frac{15}{25}$ directly by 100%:
Percentage of girls = $\frac{15}{25} \times 100\% = \frac{15 \times 100}{25}\%$
Divide 100 by 25:
Percentage of girls = $\frac{15 \times \cancel{100}^4}{\cancel{25}_1}\%$
Percentage of girls = $15 \times 4\%$
Percentage of girls = $60\%$
Thus, the percentage of girls in the class is 60%.
Example 9. Convert $\frac{5}{4}$ to per cent.
Answer:
To convert a fraction to a per cent, we multiply the fraction by 100%.
We are given the fraction $\frac{5}{4}$.
$\frac{5}{4}$ as per cent = $\frac{5}{4} \times 100\%$
Multiply the numerator by 100 and divide by the denominator:
$\frac{5}{4} \times 100\% = \frac{5 \times 100}{4}\%$
We can simplify the calculation by dividing 100 by 4:
$\frac{5 \times \cancel{100}^{25}}{\cancel{4}_1}\%$
$5 \times 25\% = 125\%$
Thus, $\frac{5}{4}$ as a per cent is 125%.
(A fraction greater than 1 corresponds to a percentage greater than 100%).
Example 10. Convert the given decimals to per cents:
(a) 0.75
(b) 0.09
(c) 0.2
Answer:
To convert a decimal to a per cent, we multiply the decimal by 100%.
(a) Convert 0.75 to per cent.
$0.75 \times 100\% = 75\%$
Thus, 0.75 is equal to 75%.
(b) Convert 0.09 to per cent.
$0.09 \times 100\% = 9\%$
Thus, 0.09 is equal to 9%.
(c) Convert 0.2 to per cent.
$0.2 \times 100\% = 20\%$
Thus, 0.2 is equal to 20%.
Example 11. What per cent of the adjoining figure is shaded?

Answer:
To find what per cent of the figure is shaded, we first need to determine the fraction of the figure that is shaded.
Step 1: Find the fraction of the figure that is shaded.
The figure is divided into three equal rectangular parts.
Let's analyze each part:
- The top part is a rectangle that is divided into two equal triangles by a diagonal. One of these triangles is shaded. So, the shaded fraction of the top part is $\frac{1}{2}$.
- The middle part is a rectangle that is completely shaded. So, the shaded fraction of the middle part is 1 (or the whole part).
- The bottom part is a rectangle that is not shaded at all. So, the shaded fraction of the bottom part is 0.
Since the three main parts are equal in size, we can find the total shaded fraction by averaging the shaded fractions of each part.
Total shaded fraction = $\frac{\text{Shaded part from top} + \text{Shaded part from middle} + \text{Shaded part from bottom}}{\text{Total number of parts}}$
Total shaded fraction = $\frac{\frac{1}{2} + 1 + 0}{3} = \frac{\frac{3}{2}}{3} = \frac{3}{2} \times \frac{1}{3} = \frac{1}{2}$
So, exactly half of the figure is shaded.
Step 2: Convert the fraction to a per cent.
To convert a fraction to a per cent, we multiply it by 100%.
Percentage shaded = $\left(\frac{1}{2} \times 100\right) \%$
$= 50 \%$
Therefore, 50% of the adjoining figure is shaded.
Example 12. A survey of 40 children showed that 25% liked playing football. How many children liked playing football?
Answer:
Given:
Total number of children surveyed = 40.
Percentage of children who liked playing football = 25%.
To Find:
The number of children who liked playing football.
To find the number of children who liked playing football, we need to calculate 25% of the total number of children.
"25% of 40" can be calculated by converting the percentage to a fraction or a decimal and then multiplying by the total number.
Convert 25% to a fraction: $25\% = \frac{25}{100} = \frac{1}{4}$.
Convert 25% to a decimal: $25\% = \frac{25}{100} = 0.25$.
Method 1: Using Fraction
Number of children who liked football = Fraction $\times$ Total Number of Children
Number of children who liked football = $\frac{1}{4} \times 40$
Number of children who liked football = $\frac{40}{4}$
Number of children who liked football = 10.
Method 2: Using Decimal
Number of children who liked football = Decimal $\times$ Total Number of Children
Number of children who liked football = $0.25 \times 40$
$0.25 \times 40 = \frac{25}{100} \times 40 = \frac{25 \times 40}{100} = \frac{1000}{100} = 10$.
Number of children who liked football = 10.
Thus, 10 children liked playing football.
Example 13. Rahul bought a sweater and saved ₹ 200 when a discount of 25% was given. What was the price of the sweater before the discount?
Answer:
Given:
Amount saved (discount amount) = $\textsf{₹}$ 200.
Discount percentage = 25%.
To Find:
The original price of the sweater before the discount (also called the marked price).
The discount amount is a percentage of the original price. We know the discount amount and the discount percentage, and we want to find the original price.
Let the original price of the sweater be $\textsf{₹} P$.
The discount amount is 25% of the original price P.
Discount Amount = 25% of P
We are given that the Discount Amount is $\textsf{₹}$ 200.
So, 25% of P = $\textsf{₹}$ 200.
Convert the percentage to a fraction or decimal:
$25\% = \frac{25}{100} = \frac{1}{4}$.
Now, we can write the equation:
$\frac{1}{4} \times P = 200$
To find P, multiply both sides of the equation by 4:
$P = 200 \times 4$
$P = 800$
Alternatively, using the decimal form:
$0.25 \times P = 200$
$P = \frac{200}{0.25}$
To divide by a decimal, multiply the numerator and denominator by a power of 10 to make the denominator a whole number. Multiply by 100:
$P = \frac{200 \times 100}{0.25 \times 100} = \frac{20000}{25}$
Divide 20000 by 25:
$\frac{20000}{25} = \frac{200 \times 100}{25} = 200 \times 4 = 800$
$P = 800$
The original price of the sweater before the discount was $\textsf{₹}$ 800.
Let's check the answer: 25% of $\textsf{₹}$ 800 = $\frac{1}{4} \times 800 = 200$. The discount amount is indeed $\textsf{₹}$ 200.
The price after discount would be $\textsf{₹}$ 800 - $\textsf{₹}$ 200 = $\textsf{₹}$ 600.
Thus, the price of the sweater before the discount was ₹ 800.
Exercise 8.2
Question 1. Convert the given fractional numbers to per cents.
(a) $\frac{1}{8}$
(b) $\frac{5}{4}$
(c) $\frac{3}{40}$
(d) $\frac{2}{7}$
Answer:
To convert a fractional number to a per cent, we multiply the fraction by 100 and affix the per cent symbol (%).
(a) $\frac{1}{8}$
To convert $\frac{1}{8}$ to a per cent:
$\left(\frac{1}{8} \times 100\right) \% = \frac{100}{8} \%$
Simplifying the fraction:
$\frac{100}{8} = \frac{25}{2} = 12.5$
So, $\frac{1}{8} = \mathbf{12.5\%}$ or $\mathbf{12 \frac{1}{2}\%}$.
(b) $\frac{5}{4}$
To convert $\frac{5}{4}$ to a per cent:
$\left(\frac{5}{4} \times 100\right) \% = \left(5 \times \frac{100}{4}\right) \%$
$= (5 \times 25) \%$
$= 125 \%$
So, $\frac{5}{4} = \mathbf{125\%}$.
(c) $\frac{3}{40}$
To convert $\frac{3}{40}$ to a per cent:
$\left(\frac{3}{40} \times 100\right) \% = \frac{300}{40} \%$
Simplifying the fraction:
$\frac{300}{40} = \frac{30}{4} = \frac{15}{2} = 7.5$
So, $\frac{3}{40} = \mathbf{7.5\%}$ or $\mathbf{7 \frac{1}{2}\%}$.
(d) $\frac{2}{7}$
To convert $\frac{2}{7}$ to a per cent:
$\left(\frac{2}{7} \times 100\right) \% = \frac{200}{7} \%$
To convert the improper fraction to a mixed fraction, we divide 200 by 7.
200 ÷ 7 gives a quotient of 28 and a remainder of 4.
So, $\frac{200}{7} = 28 \frac{4}{7}$.
Therefore, $\frac{2}{7} = \mathbf{28 \frac{4}{7}\%}$.
Question 2. Convert the given decimal fractions to per cents.
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Answer:
To convert a decimal fraction to a per cent, we multiply the decimal by 100%.
(a) Convert 0.65 to per cent.
$0.65 \times 100\% = 65\%$
Thus, 0.65 is equal to 65%.
(b) Convert 2.1 to per cent.
$2.1 \times 100\% = 210\%$
Thus, 2.1 is equal to 210%.
(c) Convert 0.02 to per cent.
$0.02 \times 100\% = 2\%$
Thus, 0.02 is equal to 2%.
(d) Convert 12.35 to per cent.
$12.35 \times 100\% = 1235\%$
Thus, 12.35 is equal to 1235%.
Question 3. Estimate what part of the figures is coloured and hence find the per cent which is coloured.
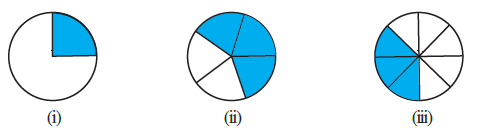
Answer:
To estimate the coloured part as a percentage, we first determine the fraction of the figure that is coloured by dividing the coloured parts by the total number of equal parts. Then we convert this fraction to a percentage.
Figure (i):
The figure is a circle divided into 4 equal parts.
Number of coloured parts = 1.
Total number of equal parts = 4.
Fraction coloured = $\frac{\text{Number of coloured parts}}{\text{Total number of parts}} = \frac{1}{4}$.
Convert the fraction to a percentage:
Percentage coloured = $\frac{1}{4} \times 100\%$
= $\frac{100}{4}\%$
= $25\%$
Thus, 25% of the figure is coloured.
Figure (ii):
The figure appears to be a rectangle divided into 5 equal parts.
Number of coloured parts = 3.
Total number of equal parts = 5.
Fraction coloured = $\frac{3}{5}$.
Convert the fraction to a percentage:
Percentage coloured = $\frac{3}{5} \times 100\%$
= $\frac{3 \times 100}{5}\%$
= $3 \times \frac{100}{5}\%$
= $3 \times 20\%$
= $60\%$
Thus, 60% of the figure is coloured.
Figure (iii):
The figure appears to be a square divided into 8 equal parts (4 large triangles formed by diagonals, and each split into two smaller triangles). Let's count the smaller triangular parts.
Total number of equal triangular parts = 8.
Number of coloured parts = 3.
Fraction coloured = $\frac{3}{8}$.
Convert the fraction to a percentage:
Percentage coloured = $\frac{3}{8} \times 100\%$
= $\frac{3 \times 100}{8}\%$
Simplify the fraction by dividing 100 and 8 by their greatest common divisor, which is 4:
= $\frac{3 \times \cancel{100}^{25}}{\cancel{8}_{2}}\%$
= $\frac{3 \times 25}{2}\% = \frac{75}{2}\%$
= $37.5\%$
Thus, 37.5% of the figure is coloured.
Question 4. Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of ₹ 2500
(d) 75% of 1 kg
Answer:
To find a percentage of a quantity, we convert the percentage to a fraction or a decimal and multiply it by the quantity.
(a) Find 15% of 250.
$15\% \text{ of } 250 = \frac{15}{100} \times 250$
= $\frac{15 \times 250}{100}$
Simplify the fraction by dividing 250 and 100 by their common factor 50:
= $\frac{15 \times \cancel{250}^{5}}{\cancel{100}_{2}}$
= $\frac{15 \times 5}{2} = \frac{75}{2} = 37.5$
Thus, 15% of 250 is 37.5.
(b) Find 1% of 1 hour.
Convert 1 hour to a smaller unit to get a meaningful value. 1 hour = 60 minutes.
$1\% \text{ of } 1 \text{ hour} = 1\% \text{ of } 60 \text{ minutes}$
= $\frac{1}{100} \times 60 \text{ minutes}$
= $\frac{60}{100} \text{ minutes}$
Simplify the fraction by dividing by 20:
= $\frac{\cancel{60}^{3}}{\cancel{100}_{5}} \text{ minutes} = \frac{3}{5} \text{ minutes}$
As a decimal, $\frac{3}{5} \text{ minutes} = 0.6 \text{ minutes}$.
Alternatively, convert to seconds. 1 hour = 60 minutes = $60 \times 60 = 3600$ seconds.
$1\% \text{ of } 1 \text{ hour} = 1\% \text{ of } 3600 \text{ seconds}$
= $\frac{1}{100} \times 3600 \text{ seconds}$
= $\frac{3600}{100} \text{ seconds}$
= $36 \text{ seconds}$.
Thus, 1% of 1 hour is $\frac{3}{5}$ minutes or 36 seconds.
(c) Find 20% of $\textsf{₹}$ 2500.
$20\% \text{ of } \textsf{₹} 2500 = \frac{20}{100} \times \textsf{₹} 2500$
= $\frac{20 \times 2500}{100} \textsf{₹}$
Simplify the fraction by dividing 20 and 100 by 20:
= $\frac{\cancel{20}^{1}}{\cancel{100}_{5}} \times 2500 \textsf{₹}$
= $\frac{1}{5} \times 2500 \textsf{₹}$
= $\frac{2500}{5} \textsf{₹}$
= $500 \textsf{₹}$
Thus, 20% of $\textsf{₹}$ 2500 is ₹ 500.
(d) Find 75% of 1 kg.
Convert 1 kg to grams. 1 kg = 1000 g.
$75\% \text{ of } 1 \text{ kg} = 75\% \text{ of } 1000 \text{ g}$
= $\frac{75}{100} \times 1000 \text{ g}$
= $\frac{75 \times 1000}{100} \text{ g}$
Simplify by dividing 1000 and 100 by 100:
= $75 \times \frac{\cancel{1000}^{10}}{\cancel{100}_{1}} \text{ g}$
= $75 \times 10 \text{ g}$
= $750 \text{ g}$
Alternatively, express 75% as a fraction: $75\% = \frac{75}{100} = \frac{3}{4}$.
$75\% \text{ of } 1 \text{ kg} = \frac{3}{4} \times 1 \text{ kg} = \frac{3}{4} \text{ kg}$.
Thus, 75% of 1 kg is 750 g or $\frac{3}{4}$ kg.
Question 5. Find the whole quantity if
(a) 5% of it is 600.
(b) 12% of it is ₹ 1080.
(c) 40% of it is 500 km.
(d) 70% of it is 14 minutes.
(e) 8% of it is 40 litres.
Answer:
Let the whole quantity be $X$. We are given a percentage of $X$ and the value of that percentage. We can set up an equation and solve for $X$.
(a) 5% of it is 600.
$5\%$ of $X = 600$
Convert the percentage to a fraction:
$\frac{5}{100} \times X = 600$
Multiply both sides by 100 and divide by 5:
$X = 600 \times \frac{100}{5}$
$X = 600 \times 20$
$X = 12000$
The whole quantity is 12000.
(b) 12% of it is $\textsf{₹}$ 1080.
$12\%$ of $X = \textsf{₹} 1080$
$\frac{12}{100} \times X = 1080$
$X = 1080 \times \frac{100}{12}$
Simplify the fraction $\frac{100}{12}$ or divide 1080 by 12.
$1080 \div 12 = 90$ (since $12 \times 9 = 108$)
$X = 90 \times 100$
$X = 9000$
The whole quantity is ₹ 9000.
(c) 40% of it is 500 km.
$40\%$ of $X = 500 \text{ km}$
$\frac{40}{100} \times X = 500$
Simplify the fraction $\frac{40}{100} = \frac{4}{10} = \frac{2}{5}$.
$\frac{2}{5} \times X = 500$
Multiply both sides by $\frac{5}{2}$:
$X = 500 \times \frac{5}{2}$
$X = \frac{500 \times 5}{2} = \frac{2500}{2}$
$X = 1250$
The whole quantity is 1250 km.
(d) 70% of it is 14 minutes.
$70\%$ of $X = 14 \text{ minutes}$
$\frac{70}{100} \times X = 14$
Simplify the fraction $\frac{70}{100} = \frac{7}{10}$.
$\frac{7}{10} \times X = 14$
Multiply both sides by $\frac{10}{7}$:
$X = 14 \times \frac{10}{7}$
$X = \frac{\cancel{14}^{2} \times 10}{\cancel{7}_{1}}$
$X = 2 \times 10 = 20$
The whole quantity is 20 minutes.
(e) 8% of it is 40 litres.
$8\%$ of $X = 40 \text{ litres}$
$\frac{8}{100} \times X = 40$
Multiply both sides by $\frac{100}{8}$:
$X = 40 \times \frac{100}{8}$
Simplify by dividing 40 by 8:
$X = \cancel{40}^{5} \times \frac{100}{\cancel{8}_{1}}$
$X = 5 \times 100 = 500$
The whole quantity is 500 litres.
Question 6. Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Answer:
To convert a percentage to a fraction, we divide the number by 100. To convert a percentage to a decimal, we move the decimal point two places to the left.
(a) 25%
As a fraction in simplest form:
$25\% = \frac{25}{100}$
To simplify, we divide the numerator and the denominator by their greatest common divisor, which is 25.
$\frac{25 \div 25}{100 \div 25} = \frac{1}{4}$
So, 25% = $\frac{1}{4}$.
As a decimal fraction:
$25\% = \frac{25}{100} = 0.25$
So, 25% = 0.25.
(b) 150%
As a fraction in simplest form:
$150\% = \frac{150}{100}$
To simplify, we can first cancel out the zeros and then divide by their greatest common divisor, which is 5.
$\frac{150}{100} = \frac{15}{10} = \frac{15 \div 5}{10 \div 5} = \frac{3}{2}$
So, 150% = $\frac{3}{2}$ (or $1 \frac{1}{2}$).
As a decimal fraction:
$150\% = \frac{150}{100} = 1.5$
So, 150% = 1.5.
(c) 20%
As a fraction in simplest form:
$20\% = \frac{20}{100}$
To simplify, we divide the numerator and the denominator by their greatest common divisor, which is 20.
$\frac{20 \div 20}{100 \div 20} = \frac{1}{5}$
So, 20% = $\frac{1}{5}$.
As a decimal fraction:
$20\% = \frac{20}{100} = 0.20$ or $0.2$
So, 20% = 0.2.
(d) 5%
As a fraction in simplest form:
$5\% = \frac{5}{100}$
To simplify, we divide the numerator and the denominator by their greatest common divisor, which is 5.
$\frac{5 \div 5}{100 \div 5} = \frac{1}{20}$
So, 5% = $\frac{1}{20}$.
As a decimal fraction:
$5\% = \frac{5}{100} = 0.05$
So, 5% = 0.05.
Question 7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?
Answer:
Given:
Percentage of females in the city = 30%.
Percentage of males in the city = 40%.
The remaining are children.
To Find:
The percentage of children in the city.
The total population of the city can be represented as 100%.
The population consists of females, males, and children.
Total Percentage = Percentage of Females + Percentage of Males + Percentage of Children
$100\% = 30\% + 40\% + \text{Percentage of Children}$
$100\% = 70\% + \text{Percentage of Children}$
To find the percentage of children, subtract the sum of the percentages of females and males from 100%:
Percentage of Children = $100\% - 70\%$
Percentage of Children = $30\%$
Thus, 30% of the population are children.
Question 8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Answer:
Given:
Total number of voters in the constituency = 15,000.
Percentage of voters who voted = 60%.
To Find:
The percentage of voters who did not vote.
The actual number of voters who did not vote.
Percentage of voters who did not vote:
The total percentage of voters is 100%.
Percentage of voters who voted + Percentage of voters who did not vote = 100%
$60\% + \text{Percentage of voters who did not vote} = 100\%$
Percentage of voters who did not vote = $100\% - 60\%$
Percentage of voters who did not vote = $40\%$
So, 40% of the voters did not vote.
Number of voters who did not vote:
Yes, we can now find the number of voters who did not vote.
Number of voters who did not vote = Percentage of voters who did not vote $\times$ Total number of voters
Number of voters who did not vote = 40% of 15,000
Convert the percentage to a fraction:
$40\% = \frac{40}{100} = \frac{2}{5}$.
Number of voters who did not vote = $\frac{2}{5} \times 15000$
= $\frac{2 \times 15000}{5}$
Simplify by dividing 15000 by 5:
= $2 \times \frac{\cancel{15000}^{3000}}{\cancel{5}_{1}}$
= $2 \times 3000 = 6000$
Thus, 6000 voters did not vote.
Alternatively, we could find the number of voters who voted and subtract from the total:
Number of voters who voted = 60% of 15000 = $\frac{60}{100} \times 15000 = 0.6 \times 15000 = 9000$.
Number of voters who did not vote = Total voters - Voters who voted = $15000 - 9000 = 6000$.
This confirms the result.
Question 9. Meeta saves ₹4000 from her salary. If this is 10% of her salary. What is her salary?
Answer:
Given:
Amount saved by Meeta = $\textsf{₹}$ 4000.
The amount saved is 10% of her salary.
To Find:
Meeta's total salary.
Let Meeta's total salary be $\textsf{₹} S$.
We are given that 10% of her salary is equal to $\textsf{₹}$ 4000.
So, 10% of $S = \textsf{₹} 4000$.
Convert the percentage to a fraction:
$10\% = \frac{10}{100} = \frac{1}{10}$.
Now, we can set up the equation:
$\frac{1}{10} \times S = 4000$
To find $S$, multiply both sides of the equation by 10:
$S = 4000 \times 10$
$S = 40000$
Alternatively, using the decimal form:
$10\% = 0.10 = 0.1$.
$0.1 \times S = 4000$
$S = \frac{4000}{0.1}$
$S = \frac{4000}{\frac{1}{10}} = 4000 \times 10 = 40000$.
$S = 40000$
Meeta's total salary is $\textsf{₹}$ 40000.
Let's check the answer: 10% of $\textsf{₹}$ 40000 = $\frac{10}{100} \times 40000 = \frac{1}{10} \times 40000 = 4000$. This matches the amount saved.
Thus, Meeta's salary is ₹ 40,000.
Question 10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Answer:
Given:
Total number of matches played by the team = 20.
Percentage of matches won = 25%.
To Find:
The number of matches the team won.
To find the number of matches won, we need to calculate 25% of the total number of matches played.
Number of matches won = 25% of 20.
Convert the percentage to a fraction or decimal:
$25\% = \frac{25}{100} = \frac{1}{4}$.
$25\% = 0.25$.
Method 1: Using Fraction
Number of matches won = $\frac{1}{4} \times 20$
= $\frac{20}{4}$
= 5
Method 2: Using Decimal
Number of matches won = $0.25 \times 20$
$0.25 \times 20 = 5.00 = 5$.
Thus, the team won 5 matches.
Example 14 to 21 (Before Exercise 8.3)
Example 14. Reena’s mother said, to make idlis, you must take two parts rice and one part urad dal. What percentage of such a mixture would be rice and what percentage would be urad dal?
Answer:
Given:
The ratio of rice to urad dal for making idlis is 2 parts rice to 1 part urad dal.
To Find:
The percentage of rice in the mixture.
The percentage of urad dal in the mixture.
Let the number of parts of rice be 2 and the number of parts of urad dal be 1.
The total number of parts in the mixture = Number of parts of rice + Number of parts of urad dal
Total parts = $2 + 1 = 3$.
Percentage of Rice:
The fraction of rice in the mixture is the number of parts of rice divided by the total number of parts.
Fraction of rice = $\frac{\text{Parts of Rice}}{\text{Total Parts}} = \frac{2}{3}$.
To convert this fraction to a percentage, multiply by 100%:
Percentage of rice = $\frac{2}{3} \times 100\%$
= $\frac{200}{3}\%$
Convert the improper fraction to a mixed number or decimal:
$\frac{200}{3}\% = 66 \frac{2}{3}\%$ or approximately $66.67\%$.
Percentage of Urad Dal:
The fraction of urad dal in the mixture is the number of parts of urad dal divided by the total number of parts.
Fraction of urad dal = $\frac{\text{Parts of Urad Dal}}{\text{Total Parts}} = \frac{1}{3}$.
To convert this fraction to a percentage, multiply by 100%:
Percentage of urad dal = $\frac{1}{3} \times 100\%$
= $\frac{100}{3}\%$
Convert the improper fraction to a mixed number or decimal:
$\frac{100}{3}\% = 33 \frac{1}{3}\%$ or approximately $33.33\%$.
Check: Percentage of rice + Percentage of urad dal = $66 \frac{2}{3}\% + 33 \frac{1}{3}\% = (66+33) + (\frac{2}{3} + \frac{1}{3})\% = 99 + \frac{3}{3}\% = 99 + 1\% = 100\%$. This is correct.
Thus, $66 \frac{2}{3}\%$ of the mixture would be rice and $33 \frac{1}{3}\%$ would be urad dal.
Example 15. If ₹ 250 is to be divided amongst Ravi, Raju and Roy, so that Ravi gets two parts, Raju three parts and Roy five parts. How much money will each get? What will it be in percentages?
Answer:
Given:
Total amount of money to be divided = $\textsf{₹}$ 250.
The money is divided among Ravi, Raju, and Roy in the ratio of parts: Ravi gets 2 parts, Raju gets 3 parts, and Roy gets 5 parts.
To Find:
The amount of money each person will get.
The percentage of the total money each person will get.
Solution:
First, find the total number of parts the money is divided into.
Total parts = Ravi's parts + Raju's parts + Roy's parts
Total parts = $2 + 3 + 5 = 10$ parts.
Now, find the value of one part by dividing the total amount by the total number of parts.
Value of one part = $\frac{\text{Total Amount}}{\text{Total Parts}} = \frac{\textsf{₹} 250}{10}$
Value of one part = $\textsf{₹}$ 25.
Amount each person gets:
Ravi gets 2 parts = $2 \times \textsf{₹} 25 = \textsf{₹} 50$.
Raju gets 3 parts = $3 \times \textsf{₹} 25 = \textsf{₹} 75$.
Roy gets 5 parts = $5 \times \textsf{₹} 25 = \textsf{₹} 125$.
Check: $\textsf{₹} 50 + \textsf{₹} 75 + \textsf{₹} 125 = \textsf{₹} 250$. This is correct.
Percentage each person gets:
The percentage each person gets is their share divided by the total amount, multiplied by 100%.
Percentage for Ravi = $\frac{\text{Ravi's Amount}}{\text{Total Amount}} \times 100\% = \frac{\textsf{₹} 50}{\textsf{₹} 250} \times 100\%$
= $\frac{50}{250} \times 100\% = \frac{\cancel{50}^{1}}{\cancel{250}_{5}} \times 100\% = \frac{1}{5} \times 100\% = 20\%$.
Percentage for Raju = $\frac{\text{Raju's Amount}}{\text{Total Amount}} \times 100\% = \frac{\textsf{₹} 75}{\textsf{₹} 250} \times 100\%$
= $\frac{75}{250} \times 100\% = \frac{\cancel{75}^{3}}{\cancel{250}_{10}} \times 100\% = \frac{3}{10} \times 100\% = 30\%$.
Percentage for Roy = $\frac{\text{Roy's Amount}}{\text{Total Amount}} \times 100\% = \frac{\textsf{₹} 125}{\textsf{₹} 250} \times 100\%$
= $\frac{125}{250} \times 100\% = \frac{\cancel{125}^{1}}{\cancel{250}_{2}} \times 100\% = \frac{1}{2} \times 100\% = 50\%$.
Check: $20\% + 30\% + 50\% = 100\%$. This is correct.
Amount each gets:
Ravi: ₹ 50
Raju: ₹ 75
Roy: ₹ 125
Percentage each gets:
Ravi: 20%
Raju: 30%
Roy: 50%
Example 16. A school team won 6 games this year against 4 games won last year. What is the per cent increase?
Answer:
Given:
Number of games won last year = 4.
Number of games won this year = 6.
To Find:
The per cent increase in the number of games won.
First, find the amount of increase in the number of games won.
Increase in games won = Games won this year - Games won last year
Increase = $6 - 4 = 2$ games.
To find the per cent increase, we compare the amount of increase to the original amount (the number of games won last year) and express this as a percentage.
Per cent Increase = $\frac{\text{Increase}}{\text{Original Amount}} \times 100\%$
Original Amount = Number of games won last year = 4.
Per cent Increase = $\frac{2}{4} \times 100\%$
= $\frac{1}{2} \times 100\%$
= $50\%$
Thus, the per cent increase in the number of games won is 50%.
Example 17. The number of illiterate persons in a country decreased from 150 lakhs to 100 lakhs in 10 years. What is the percentage of decrease?
Answer:
Given:
Original number of illiterate persons = 150 lakhs.
Decreased number of illiterate persons = 100 lakhs.
To Find:
The percentage of decrease in the number of illiterate persons.
First, find the amount of decrease in the number of illiterate persons.
Decrease in number = Original number - Decreased number
Decrease = $150 \text{ lakhs} - 100 \text{ lakhs} = 50 \text{ lakhs}$.
To find the percentage of decrease, we compare the amount of decrease to the original amount and express this as a percentage.
Per cent Decrease = $\frac{\text{Decrease}}{\text{Original Amount}} \times 100\%$
Original Amount = Original number of illiterate persons = 150 lakhs.
Per cent Decrease = $\frac{50 \text{ lakhs}}{150 \text{ lakhs}} \times 100\%$
= $\frac{50}{150} \times 100\%$
Simplify the fraction $\frac{50}{150}$ by dividing the numerator and denominator by 50:
= $\frac{\cancel{50}^{1}}{\cancel{150}_{3}} \times 100\%$
= $\frac{1}{3} \times 100\%$
= $\frac{100}{3}\%$
Convert the improper fraction to a mixed number or decimal:
= $33 \frac{1}{3}\%$ or approximately $33.33\%$.
Thus, the percentage of decrease in the number of illiterate persons is $33 \frac{1}{3}\%$ or approximately 33.33%.
Example 18. The cost of a flower vase is ₹ 120. If the shopkeeper sells it at a loss of 10%, find the price at which it is sold.
Answer:
Given:
Cost price (CP) of the flower vase = $\textsf{₹}$ 120.
Loss percentage = 10%.
To Find:
The selling price (SP) of the flower vase.
When there is a loss, the selling price is less than the cost price. The loss amount is a percentage of the cost price.
Loss Amount = Loss Percentage of CP
Loss Amount = 10% of $\textsf{₹}$ 120.
Convert the percentage to a fraction or decimal:
$10\% = \frac{10}{100} = \frac{1}{10}$.
$10\% = 0.10 = 0.1$.
Calculate the Loss Amount:
Loss Amount = $\frac{1}{10} \times \textsf{₹} 120$
Loss Amount = $\frac{120}{10} \textsf{₹}$
Loss Amount = $\textsf{₹}$ 12.
The selling price is the cost price minus the loss amount.
Selling Price (SP) = Cost Price (CP) - Loss Amount
SP = $\textsf{₹}$ 120 - $\textsf{₹}$ 12
SP = $\textsf{₹}$ 108.
Alternatively, if there is a 10% loss, it means the selling price is $100\% - 10\% = 90\%$ of the cost price.
SP = 90% of CP
SP = 90% of $\textsf{₹}$ 120
SP = $\frac{90}{100} \times \textsf{₹} 120$
SP = $\frac{9}{10} \times \textsf{₹} 120$
SP = $9 \times \frac{120}{10} \textsf{₹}$
SP = $9 \times 12 \textsf{₹}$
SP = $\textsf{₹}$ 108.
Thus, the price at which the flower vase is sold is ₹ 108.
Example 19. Selling price of a toy car is ₹ 540. If the profit made by shopkeeper is 20%, what is the cost price of this toy?
Answer:
Given:
Selling price (SP) of the toy car = $\textsf{₹}$ 540.
Profit percentage = 20%.
To Find:
The cost price (CP) of the toy.
When there is a profit, the selling price is greater than the cost price. The profit amount is a percentage of the cost price.
Let the cost price (CP) of the toy car be $\textsf{₹} P$.
Profit Amount = Profit Percentage of CP
Profit Amount = 20% of $P = \frac{20}{100} \times P = \frac{1}{5} P$.
The selling price is the cost price plus the profit amount.
Selling Price (SP) = Cost Price (CP) + Profit Amount
$\textsf{₹} 540 = P + \frac{1}{5} P$
Combine the terms involving P:
$540 = (1 + \frac{1}{5}) P$
$540 = (\frac{5}{5} + \frac{1}{5}) P$
$540 = \frac{6}{5} P$
To find P, multiply both sides of the equation by $\frac{5}{6}$:
$P = 540 \times \frac{5}{6}$
Simplify by dividing 540 by 6:
$540 \div 6 = 90$
$P = 90 \times 5$
$P = 450$
Alternatively, if there is a 20% profit, it means the selling price is $100\% + 20\% = 120\%$ of the cost price.
SP = 120% of CP
$\textsf{₹} 540 = 120\%$ of CP
$\textsf{₹} 540 = \frac{120}{100} \times \text{CP}$
$\textsf{₹} 540 = \frac{12}{10} \times \text{CP}$
$\textsf{₹} 540 = \frac{6}{5} \times \text{CP}$
To find CP, multiply both sides by $\frac{5}{6}$:
CP = $540 \times \frac{5}{6} \textsf{₹}$
CP = $\frac{\cancel{540}^{90} \times 5}{\cancel{6}_{1}} \textsf{₹}$
CP = $90 \times 5 \textsf{₹}$
CP = $\textsf{₹}$ 450.
The cost price of the toy car is $\textsf{₹}$ 450.
Let's check the answer: Profit = 20% of $\textsf{₹}$ 450 = $\frac{1}{5} \times 450 = \textsf{₹}$ 90.
Selling price = CP + Profit = $\textsf{₹}$ 450 + $\textsf{₹}$ 90 = $\textsf{₹}$ 540. This matches the given selling price.
Thus, the cost price of the toy is ₹ 450.
Example 20. Anita takes a loan of ₹ 5,000 at 15% per year as rate of interest. Find the interest she has to pay at the end of one year.
Answer:
Given:
Principal amount (P) = $\textsf{₹}$ 5000.
Rate of interest (R) = 15% per year.
Time period (T) = 1 year.
To Find:
The interest she has to pay at the end of one year.
We are asked to find the simple interest for one year.
The formula for calculating Simple Interest (SI) is:
$SI = \frac{P \times R \times T}{100}$
Where:
P is the principal amount.
R is the rate of interest per year.
T is the time period in years.
Substitute the given values into the formula:
$SI = \frac{\textsf{₹} 5000 \times 15 \times 1}{100}$
$SI = \frac{5000 \times 15}{100} \textsf{₹}$
Simplify by dividing 5000 and 100 by 100:
$SI = \frac{\cancel{5000}^{50} \times 15}{\cancel{100}_{1}} \textsf{₹}$
$SI = 50 \times 15 \textsf{₹}$
$50 \times 15 = 50 \times (10 + 5) = 50 \times 10 + 50 \times 5 = 500 + 250 = 750$.
$SI = \textsf{₹}$ 750.
Thus, the interest Anita has to pay at the end of one year is ₹ 750.
Example 21. If Manohar pays an interest of ₹ 750 for 2 years on a sum of ₹ 4,500, find the rate of interest.
Answer:
Given:
Principal amount (P) = $\textsf{₹}$ 4500.
Simple Interest (SI) paid = $\textsf{₹}$ 750.
Time period (T) = 2 years.
To Find:
The rate of interest (R) per year.
The formula for Simple Interest (SI) is:
$SI = \frac{P \times R \times T}{100}$
We need to find the value of R. We can rearrange the formula to solve for R:
$SI \times 100 = P \times R \times T$
$R = \frac{SI \times 100}{P \times T}$
Substitute the given values into the formula:
$R = \frac{\textsf{₹} 750 \times 100}{\textsf{₹} 4500 \times 2}$
$R = \frac{750 \times 100}{4500 \times 2}$
Simplify the expression:
$R = \frac{750 \times 100}{9000}$
Divide the numerator and denominator by 100:
$R = \frac{750 \times \cancel{100}^{1}}{9000 \div 100}$
$R = \frac{750}{90}$
Divide the numerator and denominator by 10:
$R = \frac{75}{9}$
Divide the numerator and denominator by their greatest common divisor, which is 3:
$R = \frac{\cancel{75}^{25}}{\cancel{9}_{3}}$
$R = \frac{25}{3}$
Convert the fraction to a mixed number or decimal:
$\frac{25}{3} = 8 \frac{1}{3}$ or approximately 8.33.
The rate of interest is usually expressed as a percentage per year.
$R = \frac{25}{3}\% \text{ per year}$
$R = 8 \frac{1}{3}\% \text{ per year}$ or $8.\overline{3}\% \text{ per year}$.
Thus, the rate of interest is $8 \frac{1}{3}\% $ per year or $8.\overline{3}\% $ per year.
Exercise 8.3
Question 1. Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.
(b) A refrigerater bought for ₹ 12,000 and sold at ₹ 13,500.
(c) A cupboard bought for ₹ 2,500 and sold at ₹ 3,000.
(d) A skirt bought for ₹ 250 and sold at ₹ 150.
Answer:
To determine if there is a profit or loss, we compare the selling price (SP) and the cost price (CP).
If SP > CP, there is a profit: Profit = SP - CP.
If SP < CP, there is a loss: Loss = CP - SP.
Profit percentage = $\frac{\text{Profit}}{\text{CP}} \times 100\%$
Loss percentage = $\frac{\text{Loss}}{\text{CP}} \times 100\%$
(a) Gardening shears bought for $\textsf{₹}$ 250 and sold for $\textsf{₹}$ 325.
CP = $\textsf{₹}$ 250, SP = $\textsf{₹}$ 325.
Since SP > CP, there is a profit.
Profit = SP - CP = $\textsf{₹}$ 325 - $\textsf{₹}$ 250 = $\textsf{₹}$ 75.
Profit per cent = $\frac{\text{Profit}}{\text{CP}} \times 100\% = \frac{\textsf{₹} 75}{\textsf{₹} 250} \times 100\%$
= $\frac{75}{250} \times 100\%$
= $\frac{\cancel{75}^{3}}{\cancel{250}_{10}} \times 100\% = \frac{3}{10} \times 100\% = 3 \times 10\% = 30\%$.
Profit = ₹ 75, Profit per cent = 30%.
(b) A refrigerator bought for $\textsf{₹}$ 12,000 and sold at $\textsf{₹}$ 13,500.
CP = $\textsf{₹}$ 12,000, SP = $\textsf{₹}$ 13,500.
Since SP > CP, there is a profit.
Profit = SP - CP = $\textsf{₹}$ 13,500 - $\textsf{₹}$ 12,000 = $\textsf{₹}$ 1,500.
Profit per cent = $\frac{\text{Profit}}{\text{CP}} \times 100\% = \frac{\textsf{₹} 1500}{\textsf{₹} 12000} \times 100\%$
= $\frac{1500}{12000} \times 100\%$
= $\frac{\cancel{1500}^{1}}{\cancel{12000}_{8}} \times 100\% = \frac{1}{8} \times 100\% = \frac{100}{8}\% = 12.5\%$.
Profit = ₹ 1,500, Profit per cent = 12.5%.
(c) A cupboard bought for $\textsf{₹}$ 2,500 and sold at $\textsf{₹}$ 3,000.
CP = $\textsf{₹}$ 2,500, SP = $\textsf{₹}$ 3,000.
Since SP > CP, there is a profit.
Profit = SP - CP = $\textsf{₹}$ 3,000 - $\textsf{₹}$ 2,500 = $\textsf{₹}$ 500.
Profit per cent = $\frac{\text{Profit}}{\text{CP}} \times 100\% = \frac{\textsf{₹} 500}{\textsf{₹} 2500} \times 100\%$
= $\frac{500}{2500} \times 100\%$
= $\frac{\cancel{500}^{1}}{\cancel{2500}_{5}} \times 100\% = \frac{1}{5} \times 100\% = 20\%$.
Profit = ₹ 500, Profit per cent = 20%.
(d) A skirt bought for $\textsf{₹}$ 250 and sold at $\textsf{₹}$ 150.
CP = $\textsf{₹}$ 250, SP = $\textsf{₹}$ 150.
Since SP < CP, there is a loss.
Loss = CP - SP = $\textsf{₹}$ 250 - $\textsf{₹}$ 150 = $\textsf{₹}$ 100.
Loss per cent = $\frac{\text{Loss}}{\text{CP}} \times 100\% = \frac{\textsf{₹} 100}{\textsf{₹} 250} \times 100\%$
= $\frac{100}{250} \times 100\%$
= $\frac{\cancel{100}^{2}}{\cancel{250}_{5}} \times 100\% = \frac{2}{5} \times 100\% = 2 \times 20\% = 40\%$.
Loss = ₹ 100, Loss per cent = 40%.
Question 2. Convert each part of the ratio to percentage:
(a) 3 : 1
(b) 2 : 3 : 5
(c) 1 : 4
(d) 1 : 2 : 5
Answer:
To convert each part of a ratio to a percentage, first find the total number of parts by summing all the parts of the ratio. Then, for each part, calculate the fraction it represents out of the total parts and multiply that fraction by 100%.
(a) Ratio 3 : 1
Total parts = $3 + 1 = 4$.
First part (3) as a fraction of the total = $\frac{3}{4}$.
Percentage of the first part = $\frac{3}{4} \times 100\% = 3 \times 25\% = 75\%$.
Second part (1) as a fraction of the total = $\frac{1}{4}$.
Percentage of the second part = $\frac{1}{4} \times 100\% = 25\%$.
The percentages are 75% and 25%.
(b) Ratio 2 : 3 : 5
Total parts = $2 + 3 + 5 = 10$.
First part (2) as a fraction of the total = $\frac{2}{10} = \frac{1}{5}$.
Percentage of the first part = $\frac{1}{5} \times 100\% = 20\%$.
Second part (3) as a fraction of the total = $\frac{3}{10}$.
Percentage of the second part = $\frac{3}{10} \times 100\% = 3 \times 10\% = 30\%$.
Third part (5) as a fraction of the total = $\frac{5}{10} = \frac{1}{2}$.
Percentage of the third part = $\frac{1}{2} \times 100\% = 50\%$.
The percentages are 20%, 30%, and 50%.
(c) Ratio 1 : 4
Total parts = $1 + 4 = 5$.
First part (1) as a fraction of the total = $\frac{1}{5}$.
Percentage of the first part = $\frac{1}{5} \times 100\% = 20\%$.
Second part (4) as a fraction of the total = $\frac{4}{5}$.
Percentage of the second part = $\frac{4}{5} \times 100\% = 4 \times 20\% = 80\%$.
The percentages are 20% and 80%.
(d) Ratio 1 : 2 : 5
Total parts = $1 + 2 + 5 = 8$.
First part (1) as a fraction of the total = $\frac{1}{8}$.
Percentage of the first part = $\frac{1}{8} \times 100\% = \frac{100}{8}\% = 12.5\%$.
Second part (2) as a fraction of the total = $\frac{2}{8} = \frac{1}{4}$.
Percentage of the second part = $\frac{1}{4} \times 100\% = 25\%$.
Third part (5) as a fraction of the total = $\frac{5}{8}$.
Percentage of the third part = $\frac{5}{8} \times 100\% = 5 \times 12.5\% = 62.5\%$.
The percentages are 12.5%, 25%, and 62.5%.
Question 3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.
Answer:
Given:
Original population of the city = 25,000.
New population of the city = 24,500.
To Find:
The percentage decrease in the population.
First, find the amount of decrease in the population.
Decrease in population = Original population - New population
Decrease = $25000 - 24500 = 500$.
To find the percentage decrease, we compare the amount of decrease to the original population and express this as a percentage.
Percentage Decrease = $\frac{\text{Decrease}}{\text{Original Population}} \times 100\%$
Percentage Decrease = $\frac{500}{25000} \times 100\%$
Simplify the fraction $\frac{500}{25000}$ by dividing the numerator and denominator by 500:
= $\frac{\cancel{500}^{1}}{\cancel{25000}_{50}} \times 100\%$
= $\frac{1}{50} \times 100\%$
= $\frac{100}{50}\%$
= $2\%$
Thus, the percentage decrease in the population is 2%.
Question 4. Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the Percentage of price increase?
Answer:
Given:
Original price of the car = $\textsf{₹}$ 3,50,000.
New price of the car = $\textsf{₹}$ 3,70,000.
To Find:
The percentage of price increase.
First, find the amount of increase in the price.
Increase in price = New price - Original price
Increase = $\textsf{₹} 370000 - \textsf{₹} 350000 = \textsf{₹} 20000$.
To find the percentage of price increase, we compare the amount of increase to the original price and express this as a percentage.
Percentage Increase = $\frac{\text{Increase}}{\text{Original Price}} \times 100\%$
Percentage Increase = $\frac{\textsf{₹} 20000}{\textsf{₹} 350000} \times 100\%$
= $\frac{20000}{350000} \times 100\%$
Simplify the fraction $\frac{20000}{350000}$ by dividing the numerator and denominator by 10000:
= $\frac{\cancel{20000}^{2}}{\cancel{350000}_{35}} \times 100\%$
= $\frac{2}{35} \times 100\%$
= $\frac{2 \times 100}{35}\%$
= $\frac{200}{35}\%$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 5:
= $\frac{\cancel{200}^{40}}{\cancel{35}_{7}}\%$
= $\frac{40}{7}\%$
Convert the improper fraction to a mixed number or decimal:
$\frac{40}{7} = 5 \frac{5}{7}$ or approximately $5.71$.
Percentage Increase = $5 \frac{5}{7}\%$ or approximately $5.71\%$.
Thus, the percentage of price increase was $5 \frac{5}{7}\%$ or approximately 5.71%.
Question 5. I buy a T.V. for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?
Answer:
Given:
Cost price (CP) of the T.V. = $\textsf{₹}$ 10,000.
Profit percentage = 20%.
To Find:
The selling price (SP) of the T.V.
When there is a profit, the selling price is greater than the cost price. The profit amount is a percentage of the cost price.
Profit Amount = Profit Percentage of CP
Profit Amount = 20% of $\textsf{₹}$ 10,000.
Convert the percentage to a fraction or decimal:
$20\% = \frac{20}{100} = \frac{1}{5}$.
$20\% = 0.20 = 0.2$.
Calculate the Profit Amount:
Profit Amount = $\frac{1}{5} \times \textsf{₹} 10000$
Profit Amount = $\frac{10000}{5} \textsf{₹}$
Profit Amount = $\textsf{₹}$ 2000.
The selling price is the cost price plus the profit amount.
Selling Price (SP) = Cost Price (CP) + Profit Amount
SP = $\textsf{₹}$ 10000 + $\textsf{₹}$ 2000
SP = $\textsf{₹}$ 12000.
Alternatively, if there is a 20% profit, it means the selling price is $100\% + 20\% = 120\%$ of the cost price.
SP = 120% of CP
SP = 120% of $\textsf{₹}$ 10000
SP = $\frac{120}{100} \times \textsf{₹} 10000$
SP = $\frac{12}{10} \times \textsf{₹} 10000$
SP = $12 \times \frac{10000}{10} \textsf{₹}$
SP = $12 \times 1000 \textsf{₹}$
SP = $\textsf{₹}$ 12000.
Thus, I get ₹ 12,000 for the T.V.
Question 6. Juhi sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Answer:
Given:
Selling price (SP) of the washing machine = $\textsf{₹}$ 13,500.
Loss percentage = 20%.
To Find:
The cost price (CP) of the washing machine.
When there is a loss, the selling price is less than the cost price. The loss amount is a percentage of the cost price.
Let the cost price (CP) of the washing machine be $\textsf{₹} P$.
Loss Amount = Loss Percentage of CP
Loss Amount = 20% of $P = \frac{20}{100} \times P = \frac{1}{5} P$.
The selling price is the cost price minus the loss amount.
Selling Price (SP) = Cost Price (CP) - Loss Amount
$\textsf{₹} 13500 = P - \frac{1}{5} P$
Combine the terms involving P:
$13500 = (1 - \frac{1}{5}) P$
$13500 = (\frac{5}{5} - \frac{1}{5}) P$
$13500 = \frac{4}{5} P$
To find P, multiply both sides of the equation by $\frac{5}{4}$:
$P = 13500 \times \frac{5}{4}$
$P = \frac{13500 \times 5}{4}$
Divide 13500 by 4:
$13500 \div 4 = 3375$
$P = 3375 \times 5$
$P = 16875$
Alternatively, if there is a 20% loss, it means the selling price is $100\% - 20\% = 80\%$ of the cost price.
SP = 80% of CP
$\textsf{₹} 13500 = 80\%$ of CP
$\textsf{₹} 13500 = \frac{80}{100} \times \text{CP}$
$\textsf{₹} 13500 = \frac{8}{10} \times \text{CP}$
$\textsf{₹} 13500 = \frac{4}{5} \times \text{CP}$
To find CP, multiply both sides by $\frac{5}{4}$:
CP = $13500 \times \frac{5}{4} \textsf{₹}$
CP = $\frac{\cancel{13500}^{3375} \times 5}{\cancel{4}_{1}} \textsf{₹}$
CP = $3375 \times 5 \textsf{₹}$
CP = $\textsf{₹}$ 16875.
The price at which Juhi bought the washing machine (cost price) is $\textsf{₹}$ 16,875.
Let's check the answer: Loss = 20% of $\textsf{₹}$ 16875 = $\frac{1}{5} \times 16875 = \textsf{₹}$ 3375.
Selling price = CP - Loss = $\textsf{₹}$ 16875 - $\textsf{₹}$ 3375 = $\textsf{₹}$ 13500. This matches the given selling price.
Thus, the price at which she bought it was ₹ 16,875.
Question 7.
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find the percentage of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
Answer:
Given:
The ratio of calcium, carbon, and oxygen in chalk is 10 : 3 : 12.
(i) Find the percentage of carbon in chalk.
The ratio is 10 (calcium) : 3 (carbon) : 12 (oxygen).
First, find the total number of parts in the ratio.
Total parts = $10 + 3 + 12 = 25$ parts.
The part representing carbon is 3.
The fraction of carbon in the chalk is $\frac{\text{Parts of Carbon}}{\text{Total Parts}} = \frac{3}{25}$.
Convert this fraction to a percentage by multiplying by 100%:
Percentage of Carbon = $\frac{3}{25} \times 100\%$
= $3 \times \frac{100}{25}\%$
= $3 \times 4\% = 12\%$.
The percentage of carbon in chalk is 12%.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
Given: Amount of carbon in a chalk stick = 3 g.
From part (i), we know that carbon constitutes 12% of the chalk stick's weight.
Let the total weight of the chalk stick be $W$ grams.
We are given that 12% of the total weight is equal to 3 g.
So, 12% of $W = 3$ g.
Convert the percentage to a fraction:
$12\% = \frac{12}{100}$.
Set up the equation:
$\frac{12}{100} \times W = 3$
Multiply both sides by $\frac{100}{12}$ to solve for W:
$W = 3 \times \frac{100}{12}$
Simplify:
$W = \frac{300}{12}$
Divide 300 by 12:
$\frac{300}{12} = \frac{300 \div 6}{12 \div 6} = \frac{50}{2} = 25$.
$W = 25$ grams.
The weight of the chalk stick is 25 g.
Let's check: 12% of 25 g = $\frac{12}{100} \times 25 = 12 \times \frac{25}{100} = 12 \times \frac{1}{4} = 3$ g. This matches the given amount of carbon.
Thus, the weight of the chalk stick is 25 g.
Question 8. Amina buys a book for ₹ 275 and sells it at a loss of 15%. How much does she sell it for?
Answer:
Given:
Cost price (CP) of the book = $\textsf{₹}$ 275.
Loss percentage = 15%.
To Find:
The selling price (SP) of the book.
When there is a loss, the selling price is less than the cost price. The loss amount is a percentage of the cost price.
Loss Amount = Loss Percentage of CP
Loss Amount = 15% of $\textsf{₹}$ 275.
Convert the percentage to a fraction or decimal:
$15\% = \frac{15}{100} = \frac{3}{20}$.
$15\% = 0.15$.
Calculate the Loss Amount:
Loss Amount = $\frac{15}{100} \times \textsf{₹} 275$
= $\frac{15 \times 275}{100} \textsf{₹}$
Simplify by dividing 15 and 100 by 5:
= $\frac{\cancel{15}^{3} \times 275}{\cancel{100}_{20}} \textsf{₹}$
Simplify further by dividing 275 and 20 by 5:
= $\frac{3 \times \cancel{275}^{55}}{\cancel{20}_{4}} \textsf{₹}$
= $\frac{3 \times 55}{4} \textsf{₹} = \frac{165}{4} \textsf{₹}$
Convert the fraction to a decimal:
$\frac{165}{4} = 41.25$
Loss Amount = $\textsf{₹}$ 41.25.
The selling price is the cost price minus the loss amount.
Selling Price (SP) = Cost Price (CP) - Loss Amount
SP = $\textsf{₹}$ 275 - $\textsf{₹}$ 41.25
SP = $\textsf{₹}$ 233.75.
Alternatively, if there is a 15% loss, it means the selling price is $100\% - 15\% = 85\%$ of the cost price.
SP = 85% of CP
SP = 85% of $\textsf{₹}$ 275
SP = $\frac{85}{100} \times \textsf{₹} 275$
SP = $\frac{85 \times 275}{100} $
SP = $\frac{23375}{100} $
SP = $\textsf{₹}$ 233.75.
Thus, Amina sells the book for ₹ 233.75.
Question 9. Find the amount to be paid at the end of 3 years in each case:
(a) Principal = ₹ 1,200 at 12% p.a.
(b) Principal = ₹ 7,500 at 5% p.a.
Answer:
The amount to be paid at the end of a certain period is the sum of the principal amount and the simple interest earned during that period.
Amount (A) = Principal (P) + Simple Interest (SI).
The formula for Simple Interest is $SI = \frac{P \times R \times T}{100}$, where P is the principal, R is the rate per annum, and T is the time in years.
(a) Principal (P) = $\textsf{₹}$ 1,200, Rate (R) = 12% p.a., Time (T) = 3 years.
Calculate the Simple Interest (SI):
$SI = \frac{1200 \times 12 \times 3}{100}$
$SI = \frac{1200 \times 36}{100}$
Simplify by dividing 1200 and 100 by 100:
$SI = 12 \times 36$
$12 \times 36 = 12 \times (30 + 6) = 12 \times 30 + 12 \times 6 = 360 + 72 = 432$.
$SI = \textsf{₹}$ 432.
Calculate the Amount (A):
Amount = Principal + Simple Interest
A = $\textsf{₹}$ 1200 + $\textsf{₹}$ 432
A = $\textsf{₹}$ 1632.
The amount to be paid at the end of 3 years is ₹ 1,632.
(b) Principal (P) = $\textsf{₹}$ 7,500, Rate (R) = 5% p.a., Time (T) = 3 years.
Calculate the Simple Interest (SI):
$SI = \frac{7500 \times 5 \times 3}{100}$
$SI = \frac{7500 \times 15}{100}$
Simplify by dividing 7500 and 100 by 100:
$SI = 75 \times 15$
$75 \times 15 = 75 \times (10 + 5) = 75 \times 10 + 75 \times 5 = 750 + 375 = 1125$.
$SI = \textsf{₹}$ 1125.
Calculate the Amount (A):
Amount = Principal + Simple Interest
A = $\textsf{₹}$ 7500 + $\textsf{₹}$ 1125
A = $\textsf{₹}$ 8625.
The amount to be paid at the end of 3 years is ₹ 8,625.
Question 10. What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?
Answer:
Given:
Principal (P) =
Simple Interest (I) =
Time (T) = 2 years
To Find:
The rate of interest (R) per annum.
Solution:
The formula for Simple Interest (I) is:
$I = \frac{P \times R \times T}{100}$
Where P is the Principal, R is the Rate of interest per annum, and T is the Time in years.
To find the rate (R), we can rearrange the formula:
$R = \frac{I \times 100}{P \times T}$
Now, we substitute the given values into the formula:
$R = \frac{280 \times 100}{56000 \times 2}$
$R = \frac{28000}{112000}$
We can simplify the fraction by cancelling the common factors:
$R = \frac{\cancel{28000}^{1}}{\cancel{112000}_{4}}$
$R = \frac{1}{4}$
To express the rate as a percentage, we can convert the fraction to a decimal:
$R = 0.25$
Thus, the rate of interest is 0.25% per annum.
Therefore, the rate that gives
Question 11. If Meena gives an interest of ₹ 45 for one year at 9% rate p.a.. What is the sum she has borrowed?
Answer:
Given:
Simple Interest (SI) = $\textsf{₹}$ 45.
Time period (T) = 1 year.
Rate of interest (R) = 9% p.a.
To Find:
The principal amount (P) she has borrowed (the sum).
The formula for Simple Interest (SI) is:
$SI = \frac{P \times R \times T}{100}$
We need to find the value of P. We can rearrange the formula to solve for P:
$SI \times 100 = P \times R \times T$
$P = \frac{SI \times 100}{R \times T}$
Substitute the given values into the formula:
$P = \frac{\textsf{₹} 45 \times 100}{9 \times 1}$
$P = \frac{45 \times 100}{9}$
Simplify the expression by dividing 45 by 9:
$P = \frac{\cancel{45}^{5} \times 100}{\cancel{9}_{1}}$
$P = 5 \times 100$
$P = 500$
The principal amount is in Rupees.
P = $\textsf{₹}$ 500.
Thus, the sum Meena has borrowed is ₹ 500.

