| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 5 (Before Exercise 13.1) | Exercise 13.1 | Example 7 to 9 (Before Exercise 13.2) |
| Exercise 13.2 | ||
Chapter 13 Direct and Inverse Proportions
Welcome to the solutions guide for Chapter 13: Direct and Inverse Proportions. This chapter delves into the fundamental ways two quantities can relate to each other as they change. Building upon the unitary method and ratio concepts encountered earlier, we now formalize these relationships into two distinct types: Direct Proportion and Inverse Proportion. Understanding how quantities vary in relation to one another is a critical skill for logical reasoning and problem-solving, allowing us to predict outcomes and make calculations in numerous real-world scenarios, from everyday shopping and travel to scientific experiments and resource management.
The solutions provided offer clear definitions and systematic methods for identifying and solving problems involving these two types of variation:
- Direct Proportion (or Direct Variation):
This describes a relationship where two quantities, let's say $x$ and $y$, increase or decrease together in such a manner that their ratio remains constant. If one quantity doubles, the other also doubles; if one halves, the other halves. Mathematically, this constant relationship is expressed as $\frac{x}{y} = k$, where $k$ is the constant of proportionality. When comparing two situations ($x_1, y_1$) and ($x_2, y_2$) involving direct proportion, the equality of ratios gives us the working formula: $\mathbf{\frac{x_1}{y_1} = \frac{x_2}{y_2}}$.
Solutions guide students in identifying direct proportion scenarios, such as:
- The total cost increases as the number of articles purchased increases (e.g., if 5 pens cost $\textsf{₹}50$, then 10 pens will cost $\textsf{₹}100$).
- The distance covered increases as the time traveled increases (assuming constant speed).
- More wages are earned for working more hours (at a constant hourly rate).
Problems are solved by setting up the proportion $\frac{x_1}{y_1} = \frac{x_2}{y_2}$ and solving for the unknown quantity.
- Inverse Proportion (or Inverse Variation):
This describes a relationship where an increase in one quantity, $x$, causes a proportional decrease in the other quantity, $y$, (and vice versa) such that their product remains constant. If one quantity doubles, the other quantity halves. Mathematically, this constant product is expressed as $x \times y = k$, where $k$ is the constant of proportionality. When comparing two situations ($x_1, y_1$) and ($x_2, y_2$) involving inverse proportion, the equality of products gives the working formula: $\mathbf{x_1 y_1 = x_2 y_2}$.
Solutions help identify inverse proportion situations, such as:
- Increasing the number of workers to complete a specific job decreases the time taken.
- Increasing the speed of a vehicle decreases the time taken to cover a fixed distance.
- Decreasing the number of people sharing food makes the provisions last longer.
Problems are solved by setting up the equation $x_1 y_1 = x_2 y_2$ and solving for the unknown.
A crucial first step emphasized throughout the solutions is the ability to correctly identify the type of proportion involved by carefully analyzing the context of the word problem. Does increasing one quantity naturally lead to an increase (direct) or a decrease (inverse) in the other? Once the type is identified, the appropriate mathematical condition (constant ratio or constant product) is applied systematically to find the missing value.
The solutions cover a wide range of applications through numerous word problems, including scenarios related to time and work, speed, distance, and time, cost and quantity, and resource allocation (like food provisions). By working through these step-by-step solutions, students develop stronger logical reasoning skills, learn to model real-world relationships mathematically, and become proficient in solving practical problems efficiently using the principles of direct and inverse proportion.
Example 1 to 5 (Before Exercise 13.1)
Example 1: The cost of 5 metres of a particular quality of cloth is ₹ 210. Tabulate the cost of 2, 4, 10 and 13 metres of cloth of the same type.
Answer:
Let the length of the cloth be $x$ metres and its cost be $y$ rupees.
Since the cost of cloth is directly proportional to its length (assuming uniform quality), this is a case of direct variation.
The relationship between $x$ and $y$ can be written as:
$y \propto x$
Or, $y = kx$, where $k$ is the constant of proportionality (cost per metre).
We are given that the cost of 5 metres of cloth is $\textsf{₹}$ 210.
So, when $x = 5$, $y = 210$.
Substitute these values into the equation $y = kx$:
$210 = k \times 5$
... (i)
To find $k$, divide both sides of equation (i) by 5:
$k = \frac{210}{5}$
$k = 42$.
The cost per metre of cloth is $\textsf{₹}$ 42.
The relationship is therefore $y = 42x$.
Now we can use this relationship to find the cost for different lengths of cloth.
For $x = 2$ metres:
$y = 42 \times 2 = 84$
Cost = $\textsf{₹}$ 84.
For $x = 4$ metres:
$y = 42 \times 4 = 168$
Cost = $\textsf{₹}$ 168.
For $x = 10$ metres:
$y = 42 \times 10 = 420$
Cost = $\textsf{₹}$ 420.
For $x = 13$ metres:
$y = 42 \times 13$.
$y = 546$.
Cost = $\textsf{₹}$ 546.
We can tabulate the results as follows:
| Length of cloth (metres) ($x$) | Cost (₹) ($y = 42x$) |
| 2 | 84 |
| 4 | 168 |
| 10 | 420 |
| 13 | 546 |
Example 2: An electric pole, 14 metres high, casts a shadow of 10 metres. Find the height of a tree that casts a shadow of 15 metres under similar conditions.
Answer:
This problem involves a relationship between the height of an object and the length of its shadow under similar conditions. Under similar conditions (same time of day, location), the ratio of the height of an object to the length of its shadow is constant.
This is an example of direct proportion.
Let the height of an object be $H$ and the length of its shadow be $S$.
The relationship is $\frac{H}{S} = k$, where $k$ is a constant.
Given the height of the electric pole, $H_{\text{pole}} = 14$ m.
Given the shadow length of the electric pole, $S_{\text{pole}} = 10$ m.
Using the relationship $\frac{H}{S} = k$ for the electric pole:
$k = \frac{H_{\text{pole}}}{S_{\text{pole}}}$
$k = \frac{14}{10}$
$k = 1.4$
The constant ratio of height to shadow length is $1.4$.
We need to find the height of a tree, $H_{\text{tree}}$.
Given the shadow length of the tree, $S_{\text{tree}} = 15$ m.
Using the same relationship $\frac{H}{S} = k$ for the tree:
$\frac{H_{\text{tree}}}{S_{\text{tree}}} = k$
Substitute the known values:
$\frac{H_{\text{tree}}}{15} = 1.4$
To find $H_{\text{tree}}$, multiply both sides by 15:
$H_{\text{tree}} = 1.4 \times 15$
$H_{\text{tree}} = 21$
The height of the tree is 21 metres.
The height of the tree that casts a shadow of 15 metres is 21 metres.
Example 3: If the weight of 12 sheets of thick paper is 40 grams, how many sheets of the same paper would weigh $2\frac{1}{2}$ kilograms?
Answer:
This problem relates the number of sheets of paper to their weight. Assuming the paper is of the same quality and thickness, the weight is directly proportional to the number of sheets.
Let $N$ be the number of sheets and $W$ be the weight. Since it is a direct proportion, the ratio $\frac{N}{W}$ is constant.
We are given that 12 sheets weigh 40 grams.
So, $N_1 = 12$ sheets and $W_1 = 40$ grams.
We need to find the number of sheets ($N_2$) that would weigh $2\frac{1}{2}$ kilograms.
First, convert the weight to the same units as the given weight (grams).
$2\frac{1}{2}$ kilograms $= 2.5$ kilograms.
Since $1$ kilogram $= 1000$ grams:
$2.5$ kilograms $= 2.5 \times 1000$ grams $= 2500$ grams.
So, $W_2 = 2500$ grams.
Using the property of direct proportion, we have:
$\frac{N_1}{W_1} = \frac{N_2}{W_2}$
Substitute the known values:
$\frac{12 \text{ sheets}}{40 \text{ grams}} = \frac{N_2 \text{ sheets}}{2500 \text{ grams}}$
To find $N_2$, multiply both sides by 2500:
$N_2 = \frac{12}{40} \times 2500$
Simplify the fraction:
$N_2 = \frac{\cancel{12}^{3}}{\cancel{40}_{10}} \times 2500$
$N_2 = \frac{3}{10} \times 2500$
$N_2 = 3 \times \frac{2500}{10}$
$N_2 = 3 \times 250$
$N_2 = 750$
Thus, 750 sheets of the same paper would weigh $2\frac{1}{2}$ kilograms.
The number of sheets is 750.
Example 4: A train is moving at a uniform speed of 75 km/hour.
(i) How far will it travel in 20 minutes?
(ii) Find the time required to cover a distance of 250 km.
Answer:
Given that the train is moving at a uniform speed of 75 km/hour.
In uniform speed, the distance covered is directly proportional to the time taken.
The relationship between distance ($D$), speed ($S$), and time ($T$) is given by:
$D = S \times T$
Given speed $S = 75$ km/hour.
(i) We need to find the distance traveled in 20 minutes.
Given time $T = 20$ minutes.
Since the speed is in km/hour, we need to convert the time from minutes to hours.
$1 \text{ hour} = 60 \text{ minutes}$
$20 \text{ minutes} = \frac{20}{60} \text{ hours} = \frac{1}{3} \text{ hours}$.
Now, use the formula $D = S \times T$:
$D = 75 \text{ km/hour} \times \frac{1}{3} \text{ hour}$
$D = \frac{75}{3} \text{ km}$
$D = 25 \text{ km}$
The train will travel 25 km in 20 minutes.
(ii) We need to find the time required to cover a distance of 250 km.
Given distance $D = 250$ km.
Given speed $S = 75$ km/hour.
From the formula $D = S \times T$, we can find the time $T$ as:
$T = \frac{D}{S}$
Substitute the given values:
$T = \frac{250 \text{ km}}{75 \text{ km/hour}}$
$T = \frac{250}{75}$ hours
Simplify the fraction:
$T = \frac{\cancel{250}^{10}}{\cancel{75}_{3}}$ hours
$T = \frac{10}{3}$ hours
We can express this as a mixed number or in hours and minutes:
$\frac{10}{3} \text{ hours} = 3 \frac{1}{3} \text{ hours}$
$3 \frac{1}{3} \text{ hours} = 3 \text{ hours} + \frac{1}{3} \text{ hour}$
$3 \text{ hours} + \frac{1}{3} \times 60 \text{ minutes} = 3 \text{ hours} + 20 \text{ minutes}$.
The time required to cover a distance of 250 km is $\frac{10}{3}$ hours or 3 hours and 20 minutes.
Example 5: The scale of a map is given as 1:30000000. Two cities are 4 cm apart on the map. Find the actual distance between them.
Answer:
The scale of a map represents the ratio of the distance on the map to the corresponding actual distance on the ground.
Given scale = $1:30000000$.
This means that 1 unit of distance on the map represents 30000000 units of the same distance on the ground.
Map distance = 4 cm.
Let the map distance be $d_{\text{map}}$ and the actual distance be $d_{\text{actual}}$.
The scale ratio is $\frac{d_{\text{map}}}{d_{\text{actual}}} = \frac{1}{30000000}$.
We are given $d_{\text{map}} = 4 \text{ cm}$. We need to find $d_{\text{actual}}$.
Using the scale relationship:
$\frac{4 \text{ cm}}{d_{\text{actual}}} = \frac{1}{30000000}$
To find $d_{\text{actual}}$, we can cross-multiply:
$1 \times d_{\text{actual}} = 4 \text{ cm} \times 30000000$
$d_{\text{actual}} = 120000000 \text{ cm}$.
The actual distance is $120000000$ cm. It is more practical to express this distance in kilometers.
We know that $1 \text{ metre} = 100 \text{ cm}$ and $1 \text{ kilometre} = 1000 \text{ metres}$.
So, $1 \text{ kilometre} = 1000 \times 100 \text{ cm} = 100000 \text{ cm}$.
To convert centimeters to kilometers, we divide by 100000.
$d_{\text{actual}} = \frac{120000000}{100000} \text{ km}$
$d_{\text{actual}} = \frac{1200 \cancel{00000}}{\cancel{100000}} \text{ km}$
$d_{\text{actual}} = 1200 \text{ km}$.
The actual distance between the two cities is 1200 km.
Exercise 13.1
Question 1. Following are the car parking charges near a railway station upto
(i) 4 hours
(ii) 8 hours
(iii) 12 hours
(iv) 24 hours
(a)
(b)
(c)
(d)
Check if the parking charges are in direct proportion to the parking time
Answer:
Let the parking time be $t$ and the parking charge be $c$.
For the parking charges to be in direct proportion to the parking time, the ratio $\frac{c}{t}$ must be constant for all given pairs of time and charge.
Given pairs of (time, charge):
(4 hours, $\textsf{₹}$ 60)
(8 hours, $\textsf{₹}$ 100)
(12 hours, $\textsf{₹}$ 140)
(24 hours, $\textsf{₹}$ 180)
Calculate the ratio $\frac{c}{t}$ for each pair:
(i) For 4 hours, charge is $\textsf{₹}$ 60.
Ratio = $\frac{60}{4} = 15$.
(ii) For 8 hours, charge is $\textsf{₹}$ 100.
Ratio = $\frac{100}{8} = \frac{\cancel{100}^{25}}{\cancel{8}_{2}} = \frac{25}{2} = 12.5$.
(iii) For 12 hours, charge is $\textsf{₹}$ 140.
Ratio = $\frac{140}{12} = \frac{\cancel{140}^{35}}{\cancel{12}_{3}} = \frac{35}{3} \approx 11.67$.
(iv) For 24 hours, charge is $\textsf{₹}$ 180.
Ratio = $\frac{180}{24} = \frac{\cancel{180}^{30}}{\cancel{24}_{4}} = \frac{30}{4} = \frac{\cancel{30}^{15}}{\cancel{4}_{2}} = \frac{15}{2} = 7.5$.
Comparing the ratios calculated:
$15 \neq 12.5 \neq \frac{35}{3} \neq 7.5$.
Since the ratio of parking charges to parking time is not constant, the parking charges are not in direct proportion to the parking time.
Question 2. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.
| Parts of red pigment | 1 | 4 | 7 | 12 | 20 |
| Parts of base | 8 | ... | ... | ... | ... |
Answer:
The problem states that the paint mixture is prepared by mixing a certain amount of red pigment with a certain amount of base in a fixed ratio. This indicates a relationship of direct proportion between the parts of red pigment and the parts of base.
Let the parts of red pigment be $R$ and the parts of base be $B$.
The given ratio is 1 part of red pigment to 8 parts of base.
So, $\frac{R}{B} = \frac{1}{8}$.
This relationship can also be written as $B = 8R$.
We need to find the parts of base ($B$) for the given parts of red pigment ($R = 4, 7, 12, 20$).
Case 1: $R = 4$
Using the relationship $B = 8R$:
$B = 8 \times 4$
$B = 32$
When there are 4 parts of red pigment, 32 parts of base are needed.
Case 2: $R = 7$
Using the relationship $B = 8R$:
$B = 8 \times 7$
$B = 56$
When there are 7 parts of red pigment, 56 parts of base are needed.
Case 3: $R = 12$
Using the relationship $B = 8R$:
$B = 8 \times 12$
$B = 96$
When there are 12 parts of red pigment, 96 parts of base are needed.
Case 4: $R = 20$
Using the relationship $B = 8R$:
$B = 8 \times 20$
$B = 160$
When there are 20 parts of red pigment, 160 parts of base are needed.
We can fill the table with the calculated values:
| Parts of red pigment ($R$) | 1 | 4 | 7 | 12 | 20 |
| Parts of base ($B = 8R$) | 8 | 32 | 56 | 96 | 160 |
Question 3. In Question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
Answer:
Based on Question 2, the parts of red pigment and the quantity of base are in direct proportion.
This means that the ratio of the parts of red pigment to the quantity of base is constant.
Let $R$ be the parts of red pigment and $B$ be the quantity of base in mL.
The relationship is $\frac{R}{B} = k$, where $k$ is the constant of proportionality.
We are given that 1 part of red pigment requires 75 mL of base.
So, when $R_1 = 1$, $B_1 = 75$ mL.
Using the ratio $\frac{R}{B} = k$:
$k = \frac{1}{75}$
The relationship is $\frac{R}{B} = \frac{1}{75}$, or $75R = B$.
We need to find the parts of red pigment ($R_2$) required for 1800 mL of base ($B_2 = 1800$ mL).
Using the direct proportion relationship:
$\frac{R_1}{B_1} = \frac{R_2}{B_2}$
Substitute the given values:
$\frac{1 \text{ part}}{75 \text{ mL}} = \frac{R_2 \text{ parts}}{1800 \text{ mL}}$
To find $R_2$, multiply both sides by 1800:
$R_2 = \frac{1}{75} \times 1800$
$R_2 = \frac{1800}{75}$
Simplify the fraction:
$R_2 = \frac{\cancel{1800}^{24}}{\cancel{75}_{1}}$
$R_2 = 24$
Thus, 24 parts of red pigment should be mixed with 1800 mL of base.
The required amount of red pigment is 24 parts.
Question 4. A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Answer:
Assuming the machine works at a uniform rate, the number of bottles filled is directly proportional to the time taken.
Let $N$ be the number of bottles filled and $T$ be the time in hours.
The relationship between $N$ and $T$ is $\frac{N}{T} = k$, where $k$ is a constant (the filling rate per hour).
We are given that the machine fills 840 bottles in 6 hours.
So, $N_1 = 840$ bottles and $T_1 = 6$ hours.
The constant ratio is $k = \frac{N_1}{T_1} = \frac{840}{6}$.
$k = 140$.
The machine fills 140 bottles per hour.
We need to find the number of bottles ($N_2$) the machine will fill in 5 hours ($T_2 = 5$).
Using the direct proportion relationship $\frac{N_2}{T_2} = k$:
$\frac{N_2}{5} = 140$
To find $N_2$, multiply both sides by 5:
$N_2 = 140 \times 5$
$N_2 = 700$
Alternatively, using the property $\frac{N_1}{T_1} = \frac{N_2}{T_2}$:
$\frac{840}{6} = \frac{N_2}{5}$
Cross-multiply:
$6 \times N_2 = 840 \times 5$
$6 N_2 = 4200$
Divide both sides by 6:
$N_2 = \frac{4200}{6}$
$N_2 = 700$
The machine will fill 700 bottles in five hours.
The number of bottles is 700.
Question 5. A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?
Answer:
This problem involves the relationship between the actual size of an object and its size when enlarged by a certain factor. The enlarged size is directly proportional to the actual size and the enlargement factor.
Let the actual length of the bacteria be $L_a$, the enlarged length be $L_e$, and the enlargement factor be $E$.
The relationship is given by:
$L_e = L_a \times E$
This can also be written as $\frac{L_e}{L_a} = E$.
Part 1: Find the actual length of the bacteria.
We are given that when the bacteria is enlarged 50,000 times ($E_1 = 50000$), the enlarged length is 5 cm ($L_{e1} = 5 \text{ cm}$).
Using the relationship $L_{e1} = L_a \times E_1$:
$5 \text{ cm} = L_a \times 50000$
To find the actual length $L_a$, rearrange the formula:
$L_a = \frac{L_{e1}}{E_1}$
Substitute the given values:
$L_a = \frac{5 \text{ cm}}{50000}$
$L_a = \frac{5}{50000} \text{ cm}$
Simplify the fraction:
$L_a = \frac{1}{10000} \text{ cm}$
Expressing this in decimal form:
$L_a = 0.0001 \text{ cm}$
Expressing this in standard form:
$L_a = 1 \times 10^{-4} \text{ cm}$
We can also convert this to meters, as bacterial sizes are often given in micrometers ($1 \text{ μm} = 10^{-6} \text{ m}$).
$1 \text{ cm} = 0.01 \text{ m} = 10^{-2} \text{ m}$.
$L_a = 0.0001 \text{ cm} = 0.0001 \times 10^{-2} \text{ m}$
$L_a = 10^{-4} \times 10^{-2} \text{ m}$
$L_a = 10^{-6} \text{ m}$
So, the actual length of the bacteria is $10^{-6} \text{ m}$, which is 1 micrometer.
The actual length of the bacteria is $0.0001 \text{ cm}$ (or $1 \times 10^{-4} \text{ cm}$ in standard form, or $10^{-6} \text{ m}$).
Part 2: Find the enlarged length at 20,000 times enlargement.
We now know the actual length of the bacteria $L_a = 1 \times 10^{-4} \text{ cm}$ (or $0.0001 \text{ cm}$).
The new enlargement factor is $E_2 = 20000$.
We need to find the new enlarged length $L_{e2}$ using the relationship $L_{e2} = L_a \times E_2$.
$L_{e2} = (1 \times 10^{-4} \text{ cm}) \times 20000$
$L_{e2} = 0.0001 \times 20000 \text{ cm}$
Calculate the product:
$L_{e2} = 2 \text{ cm}$
Alternatively, using standard form:
$L_{e2} = (1 \times 10^{-4}) \times (2 \times 10^4) \text{ cm}$
$L_{e2} = (1 \times 2) \times (10^{-4} \times 10^4) \text{ cm}$
$L_{e2} = 2 \times 10^{-4+4} \text{ cm}$
$L_{e2} = 2 \times 10^0 \text{ cm}$
$L_{e2} = 2 \times 1 \text{ cm}$
$L_{e2} = 2 \text{ cm}$
If the photograph is enlarged 20,000 times, the enlarged length would be $2 \text{ cm}$.
Question 6. In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
Answer:
The dimensions of a model are in direct proportion to the corresponding dimensions of the actual object. This means that the ratio of a dimension on the model to the corresponding dimension on the actual object is constant. This constant ratio is called the scale factor.
Given the height of the mast on the model ship = 9 cm.
Given the height of the mast on the actual ship = 12 m.
First, ensure units are consistent. Convert the height of the actual mast from meters to centimeters.
Since $1 \text{ m} = 100 \text{ cm}$:
Actual mast height = $12 \text{ m} = 12 \times 100 \text{ cm} = 1200 \text{ cm}$.
Now, determine the scale factor using the mast heights:
Scale factor $= \frac{\text{Height of mast on model}}{\text{Height of mast on actual ship}}$
Scale factor $= \frac{9 \text{ cm}}{1200 \text{ cm}} = \frac{9}{1200}$
Simplify the fraction:
Scale factor $= \frac{\cancel{9}^{3}}{\cancel{1200}^{400}} = \frac{3}{400}$
The scale of the model is 3:400. This means 3 units on the model represent 400 units on the actual ship.
Given the length of the actual ship = 28 m.
We need to find the length of the model ship. Let this be $L_{\text{model}}$.
Convert the length of the actual ship from meters to centimeters:
Actual ship length = $28 \text{ m} = 28 \times 100 \text{ cm} = 2800 \text{ cm}$.
Using the scale factor, the ratio of the model ship's length to the actual ship's length must be equal to the scale factor:
$\frac{\text{Length of model ship}}{\text{Length of actual ship}} = \text{Scale factor}$
$\frac{L_{\text{model}}}{2800 \text{ cm}} = \frac{3}{400}$
Solve for $L_{\text{model}}$ by multiplying both sides by 2800 cm:
$L_{\text{model}} = \frac{3}{400} \times 2800 \text{ cm}$
$L_{\text{model}} = 3 \times \frac{2800}{400} \text{ cm}$
Simplify the fraction $\frac{2800}{400}$:
$L_{\text{model}} = 3 \times \frac{\cancel{2800}^{7}}{\cancel{400}_{1}} \text{ cm}$
$L_{\text{model}} = 3 \times 7 \text{ cm}$
$L_{\text{model}} = 21 \text{ cm}$
The length of the model ship is 21 cm.
Question 7. Suppose 2 kg of sugar contains 9 × 106 crystals. How many sugar crystals are there in
(i) 5 kg of sugar?
(ii) 1.2 kg of sugar?
Answer:
This problem involves the relationship between the weight of sugar and the number of sugar crystals. Assuming a consistent number of crystals per unit weight, the number of crystals is directly proportional to the weight of the sugar.
Let $W$ be the weight of the sugar in kg and $N$ be the number of crystals.
In a direct proportion, the ratio $\frac{N}{W}$ is constant.
We are given that 2 kg of sugar contains $9 \times 10^6$ crystals.
So, $W_1 = 2 \text{ kg}$ and $N_1 = 9 \times 10^6$ crystals.
The constant ratio is $\frac{N}{W} = \frac{9 \times 10^6}{2}$.
$\frac{N}{W} = 4.5 \times 10^6$ crystals/kg.
(i) We need to find the number of crystals ($N_2$) in 5 kg of sugar ($W_2 = 5 \text{ kg}$).
Using the direct proportion relationship:
$\frac{N_2}{W_2} = \frac{N_1}{W_1}$
$\frac{N_2}{5} = \frac{9 \times 10^6}{2}$
To find $N_2$, multiply both sides by 5:
$N_2 = \frac{9 \times 10^6}{2} \times 5$
$N_2 = \frac{45 \times 10^6}{2}$
$N_2 = 22.5 \times 10^6$
Expressing in standard form ($a \times 10^n$ where $1 \leq a < 10$):
$N_2 = 2.25 \times 10^1 \times 10^6$
$N_2 = 2.25 \times 10^{1+6}$
$N_2 = 2.25 \times 10^7$
There are $2.25 \times 10^7$ crystals in 5 kg of sugar.
(ii) We need to find the number of crystals ($N_3$) in 1.2 kg of sugar ($W_3 = 1.2 \text{ kg}$).
Using the direct proportion relationship:
$\frac{N_3}{W_3} = \frac{N_1}{W_1}$
$\frac{N_3}{1.2} = \frac{9 \times 10^6}{2}$
To find $N_3$, multiply both sides by 1.2:
$N_3 = \frac{9 \times 10^6}{2} \times 1.2$
$N_3 = 4.5 \times 10^6 \times 1.2$
Calculate $4.5 \times 1.2$:
$4.5 \times 1.2 = 5.4$
So, $N_3 = 5.4 \times 10^6$.
There are $5.4 \times 10^6$ crystals in 1.2 kg of sugar.
Question 8. Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?
Answer:
Given:
Scale of the map: 1 cm represents 18 km.
Actual distance driven by Rashmi = 72 km.
This problem relates the distance on a map to the corresponding actual distance on the ground. The relationship is defined by the map scale and is a case of direct proportion.
The scale means that the ratio of the distance on the map to the actual distance is constant.
$\frac{\text{Distance on map}}{\text{Actual distance}} = \text{Scale} = \frac{1 \text{ cm}}{18 \text{ km}}$.
Let the distance covered by Rashmi on the map be $x$ cm.
The actual distance driven is 72 km.
Using the direct proportion relationship:
$\frac{x \text{ cm}}{72 \text{ km}} = \frac{1 \text{ cm}}{18 \text{ km}}$
To find $x$, multiply both sides of the equation by 72 km:
$x \text{ cm} = \left(\frac{1 \text{ cm}}{18 \text{ km}}\right) \times (72 \text{ km})$
The 'km' units cancel out:
$x = \frac{1}{18} \times 72 \text{ cm}$
$x = \frac{72}{18} \text{ cm}$
Calculate the value of $x$:
$x = 4 \text{ cm}$
The distance covered by Rashmi on the map is 4 cm.
Her distance covered in the map would be 4 cm.
Question 9. A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time
(i) the length of the shadow cast by another pole 10 m 50 cm high
(ii) the height of a pole which casts a shadow 5m long.
Answer:
Under the same conditions (same time of day and location), the ratio of the height of a vertical object to the length of its shadow is constant. This represents a direct proportion.
Let the height of the pole be $H$ and the length of its shadow be $S$.
The relationship is $\frac{H}{S} = k$, where $k$ is the constant of proportionality.
First, convert all given measurements to a consistent unit, such as centimeters.
Given pole's height: 5 m 60 cm
$5 \text{ m } 60 \text{ cm} = 5 \times 100 \text{ cm} + 60 \text{ cm} = 500 \text{ cm} + 60 \text{ cm} = 560 \text{ cm}$.
Given pole's shadow length: 3 m 20 cm
$3 \text{ m } 20 \text{ cm} = 3 \times 100 \text{ cm} + 20 \text{ cm} = 300 \text{ cm} + 20 \text{ cm} = 320 \text{ cm}$.
Using the initial pole's information ($H_1 = 560$ cm, $S_1 = 320$ cm), we can find the constant ratio $k$:
$k = \frac{H_1}{S_1} = \frac{560}{320}$
Simplify the fraction:
$k = \frac{56}{32} = \frac{\cancel{56}^{7}}{\cancel{32}_{4}} = \frac{7}{4}$.
The ratio of Height to Shadow is $\frac{7}{4}$.
(i) Find the length of the shadow cast by another pole 10 m 50 cm high.
New pole height $H_2 = 10 \text{ m } 50 \text{ cm} = 10 \times 100 \text{ cm} + 50 \text{ cm} \ $$ = 1000 \text{ cm} + 50 \text{ cm} = 1050 \text{ cm}$.
Let the length of the shadow be $S_2$.
Using the constant ratio $\frac{H_2}{S_2} = k$:
$\frac{1050}{S_2} = \frac{7}{4}$
Cross-multiply:
$7 \times S_2 = 1050 \times 4$
$7 S_2 = 4200$
Divide by 7:
$S_2 = \frac{4200}{7}$
$S_2 = 600$ cm.
Convert the shadow length back to meters and centimeters:
$600 \text{ cm} = \frac{600}{100} \text{ m} = 6 \text{ m}$.
The length of the shadow cast by the 10 m 50 cm pole is 6 m.
(ii) Find the height of a pole which casts a shadow 5m long.
New shadow length $S_3 = 5 \text{ m} = 5 \times 100 \text{ cm} = 500 \text{ cm}$.
Let the height of the pole be $H_3$.
Using the constant ratio $\frac{H_3}{S_3} = k$:
$\frac{H_3}{500} = \frac{7}{4}$
Multiply both sides by 500:
$H_3 = \frac{7}{4} \times 500$
$H_3 = 7 \times \frac{500}{4}$
$H_3 = 7 \times 125$
$H_3 = 875$ cm.
Convert the height back to meters and centimeters:
$875 \text{ cm} = 800 \text{ cm} + 75 \text{ cm} = 8 \text{ m } + 75 \text{ cm} = 8 \text{ m } 75 \text{ cm}$.
The height of the pole which casts a 5 m long shadow is 8 m 75 cm.
Question 10. A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Answer:
Given that the truck is moving at a uniform speed, the distance covered is directly proportional to the time taken.
Let the distance traveled be $D$ and the time taken be $T$.
Since $D \propto T$ at constant speed, we can write $\frac{D}{T} = k$, where $k$ is a constant (the speed).
Given:
In Time $T_1 = 25$ minutes, Distance $D_1 = 14$ km.
We need to find the distance $D_2$ covered in Time $T_2 = 5$ hours.
First, ensure that the units of time are consistent. Convert 5 hours to minutes.
$1 \text{ hour} = 60 \text{ minutes}$.
$T_2 = 5 \text{ hours} = 5 \times 60 \text{ minutes} = 300 \text{ minutes}$.
Using the property of direct proportion, the ratio $\frac{D}{T}$ must be the same for both cases:
$\frac{D_1}{T_1} = \frac{D_2}{T_2}$
Substitute the given values:
$\frac{14 \text{ km}}{25 \text{ minutes}} = \frac{D_2 \text{ km}}{300 \text{ minutes}}$
To find $D_2$, multiply both sides of the equation by 300 minutes:
$D_2 = \frac{14}{25} \times 300$
$D_2 = 14 \times \frac{300}{25}$
Simplify the fraction:
$D_2 = 14 \times \cancel{\frac{300}{25}}^{12}$
$D_2 = 14 \times 12$
Calculate the product:
$D_2 = 168$.
The distance $D_2$ is in kilometers, consistent with $D_1$.
The truck can travel 168 km in 5 hours.
The distance it can travel is 168 km.
Example 7 to 9 (Before Exercise 13.2)
Example 7: 6 pipes are required to fill a tank in 1 hour 20 minutes. How long will it take if only 5 pipes of the same type are used?
Answer:
This problem involves the relationship between the number of pipes and the time taken to fill a tank. Assuming all pipes are of the same type and work at the same rate, reducing the number of pipes will increase the time taken to fill the tank. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $N$ be the number of pipes and $T$ be the time taken to fill the tank.
The relationship is $N \times T = k$, where $k$ is a constant (representing the total work required to fill the tank).
Given initial conditions:
Number of pipes $N_1 = 6$.
Time taken $T_1 = 1$ hour 20 minutes.
First, convert the time to a single unit, such as minutes.
$1 \text{ hour} = 60 \text{ minutes}$.
$T_1 = 60 \text{ minutes} + 20 \text{ minutes} = 80 \text{ minutes}$.
Using the relationship $N \times T = k$ for the initial conditions:
$k = N_1 \times T_1 = 6 \times 80$.
$k = 480$.
The constant $k$ represents the total 'pipe-minutes' needed to fill the tank.
We need to find the time taken ($T_2$) if only 5 pipes are used ($N_2 = 5$).
Using the same relationship $N \times T = k$ for the new conditions:
$N_2 \times T_2 = k$
Substitute the values of $N_2$ and $k$:
$5 \times T_2 = 480$.
To find $T_2$, divide both sides by 5:
$T_2 = \frac{480}{5}$.
$T_2 = 96$ minutes.
Convert the time back to hours and minutes:
$96 \text{ minutes} = 60 \text{ minutes} + 36 \text{ minutes}$.
$96 \text{ minutes} = 1 \text{ hour } 36 \text{ minutes}$.
It will take 1 hour 36 minutes if only 5 pipes are used.
The time taken is 1 hour 36 minutes.
Example 8: There are 100 students in a hostel. Food provision for them is for 20 days. How long will these provisions last, if 25 more students join the group?
Answer:
This problem involves the relationship between the number of students and the number of days food provisions last. Assuming the total amount of food is fixed, if the number of students increases, the number of days the food will last decreases. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $N$ be the number of students and $D$ be the number of days the provisions last.
The relationship is $N \times D = k$, where $k$ is a constant (representing the total food in 'student-days').
Given initial conditions:
Initial number of students $N_1 = 100$.
Initial number of days provisions last $D_1 = 20$ days.
Using the relationship $N \times D = k$ for the initial conditions:
$k = N_1 \times D_1$
$k = 100 \times 20$
$k = 2000$.
The total food provision is 2000 student-days.
New conditions: 25 more students join the group.
New number of students $N_2 = 100 + 25 = 125$.
We need to find the new number of days the provisions will last ($D_2$).
Using the same relationship $N \times D = k$ for the new conditions:
$N_2 \times D_2 = k$
Substitute the values of $N_2$ and $k$:
$125 \times D_2 = 2000$.
To find $D_2$, divide both sides by 125:
$D_2 = \frac{2000}{125}$.
Calculate the value of $D_2$:
$D_2 = 16$.
The provisions will last for 16 days.
The food provisions will last for 16 days if 25 more students join the group.
Example 9: If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
Answer:
This problem involves the relationship between the number of workers and the time taken to complete a fixed amount of work (building a wall). Assuming all workers work at the same rate, if you increase the number of workers, the time required to build the same wall decreases. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $W$ be the number of workers and $T$ be the time taken in hours.
The relationship is $W \times T = k$, where $k$ is a constant (representing the total work in 'worker-hours').
Given initial conditions:
Initial number of workers $W_1 = 15$.
Initial time taken $T_1 = 48$ hours.
Using the relationship $W \times T = k$ for the initial conditions:
$k = W_1 \times T_1$
$k = 15 \times 48$
$k = 720$.
The total work required to build the wall is 720 worker-hours.
New conditions: The work needs to be done in 30 hours.
New time required $T_2 = 30$ hours.
We need to find the number of workers ($W_2$) required.
Using the same relationship $W \times T = k$ for the new conditions:
$W_2 \times T_2 = k$
Substitute the values of $T_2$ and $k$:
$W_2 \times 30 = 720$.
To find $W_2$, divide both sides by 30:
$W_2 = \frac{720}{30}$.
$W_2 = \frac{72}{3}$.
$W_2 = 24$.
Alternatively, using the property of inverse proportion, $W_1 T_1 = W_2 T_2$:
$15 \times 48 = W_2 \times 30$
$720 = 30 W_2$
$W_2 = \frac{720}{30}$
$W_2 = 24$.
Thus, 24 workers will be required to build the wall in 30 hours.
The number of workers required is 24.
Exercise 13.2
Question 1. Which of the following are in inverse proportion?
(i) The number of workers on a job and the time to complete the job.
(ii) The time taken for a journey and the distance travelled in a uniform speed.
(iii) Area of cultivated land and the crop harvested.
(iv) The time taken for a fixed journey and the speed of the vehicle.
(v) The population of a country and the area of land per person.
Answer:
Two quantities are in inverse proportion if an increase in one quantity causes a decrease in the other quantity, such that their product remains constant. Conversely, a decrease in one quantity causes an increase in the other, with their product remaining constant.
(i) The number of workers on a job and the time to complete the job.
Assuming all workers work at the same rate and the total work is fixed, if the number of workers increases, the time taken to complete the job decreases. The product of the number of workers and the time taken represents the total work done, which is constant.
Therefore, this is in inverse proportion.
(ii) The time taken for a journey and the distance travelled in a uniform speed.
At a uniform speed, if the time taken for a journey increases, the distance travelled also increases. The ratio of distance to time is constant (the speed).
Therefore, this is in direct proportion.
(iii) Area of cultivated land and the crop harvested.
Assuming a constant yield per unit area, if the area of cultivated land increases, the total crop harvested also increases. The ratio of the crop harvested to the area of land is constant.
Therefore, this is in direct proportion.
(iv) The time taken for a fixed journey and the speed of the vehicle.
If the distance of the journey is fixed, increasing the speed of the vehicle will decrease the time taken to cover that distance. The product of speed and time is the fixed distance, which is constant ($Distance = Speed \times Time$).
Therefore, this is in inverse proportion.
(v) The population of a country and the area of land per person.
Assuming the total area of the country's land is constant, if the population increases, the area of land available per person decreases. The product of the population and the area per person is the total land area, which is constant ($Total\ Area = Population \times Area\ per\ person$).
Therefore, this is in inverse proportion.
Question 2. In a Television game show, the prize money of ₹ 1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners?
| Number of winners | 1 | 2 | 4 | 5 | 8 | 10 | 20 |
| Prize for each winner (in ₹) | 1,00,000 | 50,000 | ... | ... | ... | ... | ... |
Answer:
The total prize money is fixed at $\textsf{₹}$ 1,00,000, which is to be divided equally among the winners.
Let the number of winners be $N$ and the prize money given to each winner be $P$.
The total prize money is given by the product of the number of winners and the prize for each winner:
Total Prize Money $= N \times P$
Given Total Prize Money $= \textsf{₹}$ 1,00,000.
So, $N \times P = 100000$.
From this relationship, we can see that as the number of winners ($N$) increases, the prize money for each winner ($P$) must decrease, such that their product remains constant (100000). This is the definition of inverse proportion.
Now, let's complete the table by finding the prize money for each winner ($P = \frac{100000}{N}$) for the given number of winners ($N$).
For $N = 1$: $P = \frac{100000}{1} = 100000$. (Given)
For $N = 2$: $P = \frac{100000}{2} = 50000$. (Given)
For $N = 4$: $P = \frac{100000}{4} = 25000$.
For $N = 5$: $P = \frac{100000}{5} = 20000$.
For $N = 8$: $P = \frac{100000}{8} = 12500$.
For $N = 10$: $P = \frac{100000}{10} = 10000$.
For $N = 20$: $P = \frac{100000}{20} = 5000$.
Completing the table:
| Number of winners ($N$) | 1 | 2 | 4 | 5 | 8 | 10 | 20 |
| Prize for each winner (in ₹) ($P = \frac{100000}{N}$) | 1,00,000 | 50,000 | 25,000 | 20,000 | 12,500 | 10,000 | 5,000 |
Since the product of the number of winners and the prize money for each winner ($N \times P$) is constant (100000), the prize money given to an individual winner is inversely proportional to the number of winners.
Question 3. Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.
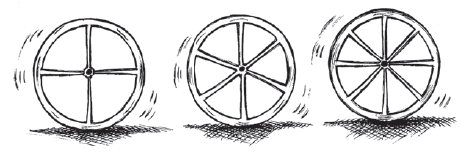
| Number of spokes | 4 | 6 | 8 | 10 | 12 |
| Angle between a pair of consecutive spokes | 90° | 60° | ... | ... | ... |
(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?
(ii) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.
(iii) How many spokes would be needed, if the angle between a pair of consecutive spokes is 40°?
Answer:
The total angle around the center of a wheel is $360^\circ$. When spokes are placed such that the angles between consecutive spokes are equal, this total angle is divided by the number of spokes.
Let $N$ be the number of spokes and $A$ be the angle between a pair of consecutive spokes.
The relationship is $A = \frac{360^\circ}{N}$.
Multiplying both sides by $N$, we get $N \times A = 360^\circ$.
Since the product of the number of spokes and the angle between consecutive spokes is a constant ($360^\circ$), the number of spokes and the angle between them are in inverse proportion.
Completing the table using the relationship $A = \frac{360^\circ}{N}$:
For $N = 4$: $A = \frac{360^\circ}{4} = 90^\circ$. (Given)
For $N = 6$: $A = \frac{360^\circ}{6} = 60^\circ$. (Given)
For $N = 8$: $A = \frac{360^\circ}{8} = 45^\circ$.
For $N = 10$: $A = \frac{360^\circ}{10} = 36^\circ$.
For $N = 12$: $A = \frac{360^\circ}{12} = 30^\circ$.
Completed table:
| Number of spokes ($N$) | 4 | 6 | 8 | 10 | 12 |
| Angle between consecutive spokes ($A$) | 90° | 60° | 45° | 36° | 30° |
(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?
Yes, as shown by the relationship $N \times A = 360^\circ$, the product of the number of spokes and the angle between them is constant. Therefore, they are in inverse proportion.
(ii) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.
Given the number of spokes $N = 15$.
Using the formula $A = \frac{360^\circ}{N}$:
$A = \frac{360^\circ}{15}$
$A = 24^\circ$.
The angle between a pair of consecutive spokes on a wheel with 15 spokes is $24^\circ$.
(iii) How many spokes would be needed, if the angle between a pair of consecutive spokes is 40°?
Given the angle between consecutive spokes $A = 40^\circ$.
Using the relationship $N \times A = 360^\circ$:
$N \times 40^\circ = 360^\circ$.
To find $N$, divide both sides by 40°:
$N = \frac{360}{40}$
$N = \frac{36}{4}$
$N = 9$.
9 spokes would be needed if the angle between a pair of consecutive spokes is $40^\circ$.
The number of spokes needed is 9.
Question 4. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get, if the number of the children is reduced by 4?
Answer:
This problem describes a scenario where a fixed number of sweets are distributed among a group of children. As the number of children changes, the number of sweets each child receives also changes. Since the total number of sweets is constant, if the number of children decreases, the number of sweets per child will increase. This is a case of inverse proportion.
Let $N$ be the number of children and $S$ be the number of sweets each child gets.
In inverse proportion, the product of the two quantities is constant. The total number of sweets is $N \times S$.
So, $N \times S = k$, where $k$ is the total number of sweets in the box.
Given initial conditions:
Initial number of children $N_1 = 24$.
Number of sweets each child gets $S_1 = 5$.
Using the relationship $N \times S = k$ for the initial conditions:
$k = N_1 \times S_1$
$k = 24 \times 5$
$k = 120$.
The total number of sweets in the box is 120.
New conditions: The number of children is reduced by 4.
New number of children $N_2 = N_1 - 4$
$N_2 = 24 - 4 = 20$.
We need to find the number of sweets each child will get ($S_2$) when there are 20 children.
Using the same relationship $N \times S = k$ for the new conditions:
$N_2 \times S_2 = k$
Substitute the values of $N_2$ and $k$:
$20 \times S_2 = 120$.
To find $S_2$, divide both sides by 20:
$S_2 = \frac{120}{20}$.
$S_2 = \frac{12}{2}$.
$S_2 = 6$.
Thus, if the number of children is reduced by 4 (making it 20 children), each child would get 6 sweets.
Each child would get 6 sweets.
Question 5. A farmer has enough food to feed 20 animals in his cattle for 6 days. How long would the food last if there were 10 more animals in his cattle?
Answer:
This problem involves the relationship between the number of animals and the number of days a fixed amount of food will last. Assuming each animal consumes the same amount of food per day, if the number of animals increases, the number of days the food lasts will decrease. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $A$ be the number of animals and $D$ be the number of days the food lasts.
The relationship is $A \times D = k$, where $k$ is a constant representing the total amount of food in 'animal-days'.
Given initial conditions:
Initial number of animals $A_1 = 20$.
Initial number of days food lasts $D_1 = 6$ days.
Using the relationship $A \times D = k$ for the initial conditions:
$k = A_1 \times D_1$
$k = 20 \times 6$
$k = 120$.
The total amount of food is equivalent to 120 animal-days.
New conditions: 10 more animals join the cattle.
New number of animals $A_2 = 20 + 10 = 30$.
We need to find the new number of days the food will last ($D_2$).
Using the same relationship $A \times D = k$ for the new conditions:
$A_2 \times D_2 = k$
Substitute the values of $A_2$ and $k$:
$30 \times D_2 = 120$.
To find $D_2$, divide both sides by 30:
$D_2 = \frac{120}{30}$.
$D_2 = 4$.
Thus, if there were 10 more animals (total 30 animals), the food would last for 4 days.
The food would last for 4 days.
Question 6. A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If, he uses 4 persons instead of three, how long should they take to complete the job?
Answer:
This problem involves the relationship between the number of persons working on a job and the time taken to complete it. Assuming all persons work at the same rate and the total amount of work is fixed, if the number of persons increases, the time taken to complete the job decreases. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $P$ be the number of persons and $D$ be the number of days taken.
The relationship is $P \times D = k$, where $k$ is a constant representing the total work in 'person-days'.
Given initial conditions:
Initial number of persons $P_1 = 3$.
Initial time taken $D_1 = 4$ days.
Using the relationship $P \times D = k$ for the initial conditions:
$k = P_1 \times D_1$
$k = 3 \times 4$
$k = 12$.
The total work required to rewire the house is 12 person-days.
New conditions: The contractor uses 4 persons instead of three.
New number of persons $P_2 = 4$.
We need to find the new time taken ($D_2$).
Using the same relationship $P \times D = k$ for the new conditions:
$P_2 \times D_2 = k$
Substitute the values of $P_2$ and $k$:
$4 \times D_2 = 12$.
To find $D_2$, divide both sides by 4:
$D_2 = \frac{12}{4}$.
$D_2 = 3$.
Thus, if the contractor uses 4 persons, they should take 3 days to complete the job.
The time taken is 3 days.
Question 7. A batch of bottles were packed in 25 boxes with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?
Answer:
This problem involves packing a fixed batch of bottles. The total number of bottles in the batch remains constant. If the number of bottles packed in each box increases, the number of boxes required to hold the entire batch will decrease. This is a case of inverse proportion.
Let $N_b$ be the number of boxes and $B_p$ be the number of bottles per box.
In inverse proportion, the product of the two quantities is constant.
$N_b \times B_p = k$, where $k$ is the total number of bottles in the batch.
Given initial conditions:
Number of boxes $N_{b1} = 25$.
Number of bottles per box $B_{p1} = 12$.
Calculate the total number of bottles in the batch ($k$) using the initial conditions:
$k = N_{b1} \times B_{p1}$
$k = 25 \times 12$
$k = 300$.
The total number of bottles in the batch is 300.
New conditions: The bottles are packed using 20 bottles in each box.
New number of bottles per box $B_{p2} = 20$.
We need to find the new number of boxes ($N_{b2}$) required.
Using the same relationship $N_b \times B_p = k$ for the new conditions:
$N_{b2} \times B_{p2} = k$
Substitute the values of $B_{p2}$ and $k$:
$N_{b2} \times 20 = 300$.
To find $N_{b2}$, divide both sides by 20:
$N_{b2} = \frac{300}{20}$
$N_{b2} = \frac{30}{2}$
$N_{b2} = 15$.
Thus, if the same batch is packed using 20 bottles in each box, 15 boxes would be filled.
The number of boxes filled would be 15.
Question 8. A factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
Answer:
This problem involves the relationship between the number of machines working on a task and the time taken to complete a fixed amount of work (producing a given number of articles). Assuming all machines work at the same rate, if the time available to complete the work decreases, the number of machines required must increase. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $M$ be the number of machines and $D$ be the number of days taken.
The relationship is $M \times D = k$, where $k$ is a constant representing the total work in 'machine-days'.
Given initial conditions:
Initial number of machines $M_1 = 42$.
Initial time taken $D_1 = 63$ days.
Using the relationship $M \times D = k$ for the initial conditions, calculate the constant $k$:
$k = M_1 \times D_1$
$k = 42 \times 63$
$k = 2646$.
The total work required to produce the articles is 2646 machine-days.
New conditions: The same number of articles needs to be produced in 54 days.
New time required $D_2 = 54$ days.
We need to find the number of machines ($M_2$) required.
Using the same relationship $M \times D = k$ for the new conditions:
$M_2 \times D_2 = k$
Substitute the values of $D_2$ and $k$:
$M_2 \times 54 = 2646$.
To find $M_2$, divide both sides by 54:
$M_2 = \frac{2646}{54}$.
Simplify the fraction:
$M_2 = \frac{\cancel{2646}^{1323}}{\cancel{54}_{27}}$
$M_2 = \frac{1323}{27}$
$M_2 = \frac{\cancel{1323}^{441}}{\cancel{27}_{9}}$
$M_2 = \frac{441}{9}$
$M_2 = 49$.
Thus, 49 machines would be required to produce the same number of articles in 54 days.
The number of machines required is 49.
Question 9. A car takes 2 hours to reach a destination by travelling at the speed of 60 km/h. How long will it take when the car travels at the speed of 80 km/h?
Answer:
This problem involves a car traveling a fixed distance to a destination. The relationship between the speed of the car and the time taken to cover a fixed distance is an inverse proportion.
If the speed increases, the time taken decreases, such that the distance (which is Speed $\times$ Time) remains constant.
Let $S$ be the speed of the car and $T$ be the time taken.
The relationship is $S \times T = \text{Constant (Distance)}$.
Given initial conditions:
Initial speed $S_1 = 60$ km/h.
Initial time taken $T_1 = 2$ hours.
Calculate the distance to the destination ($k$) using the initial conditions:
$k = S_1 \times T_1$
$k = 60 \text{ km/h} \times 2 \text{ hours}$
$k = 120$ km.
The distance to the destination is 120 km.
New conditions: The car travels at a speed of 80 km/h.
New speed $S_2 = 80$ km/h.
We need to find the new time taken ($T_2$).
Using the same relationship $S \times T = k$ for the new conditions:
$S_2 \times T_2 = k$
Substitute the values of $S_2$ and $k$:
$80 \times T_2 = 120$.
To find $T_2$, divide both sides by 80:
$T_2 = \frac{120}{80}$
$T_2 = \frac{12}{8}$
Simplify the fraction:
$T_2 = \frac{\cancel{12}^3}{\cancel{8}_2}$
$T_2 = \frac{3}{2}$ hours.
Convert the time to hours and minutes:
$\frac{3}{2} \text{ hours} = 1.5 \text{ hours} = 1 \text{ hour } + 0.5 \text{ hours}$.
$0.5 \text{ hours} = 0.5 \times 60 \text{ minutes} = 30 \text{ minutes}$.
So, $T_2 = 1$ hour 30 minutes.
Alternatively, using the property of inverse proportion $S_1 T_1 = S_2 T_2$:
$60 \times 2 = 80 \times T_2$
$120 = 80 T_2$
$T_2 = \frac{120}{80}$
$T_2 = \frac{3}{2}$ hours.
$T_2 = 1.5$ hours or 1 hour 30 minutes.
When the car travels at the speed of 80 km/h, it will take 1 hour 30 minutes to reach the destination.
The time taken is 1 hour 30 minutes (or $\frac{3}{2}$ hours).
Question 10. Two persons could fit new windows in a house in 3 days.
(i) One of the persons fell ill before the work started. How long would the job take now?
(ii) How many persons would be needed to fit the windows in one day?
Answer:
This problem involves the relationship between the number of persons working on a job and the time taken to complete it. Assuming all persons work at the same rate and the total amount of work is fixed, the number of persons and the time taken are in inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $P$ be the number of persons and $D$ be the number of days taken.
The relationship is $P \times D = k$, where $k$ is a constant representing the total work in 'person-days'.
Given initial conditions:
Initial number of persons $P_1 = 2$.
Initial time taken $D_1 = 3$ days.
Calculate the total work ($k$) using the initial conditions:
$k = P_1 \times D_1$
$k = 2 \times 3$
$k = 6$.
The total work required to fit the windows is 6 person-days.
(i) Find how long the job would take if one person fell ill.
If one person fell ill, the number of persons available is reduced by 1.
New number of persons $P_2 = 2 - 1 = 1$.
Let the new time taken be $D_2$.
Using the inverse proportion relationship $P \times D = k$:
$P_2 \times D_2 = k$
Substitute the values of $P_2$ and $k$:
$1 \times D_2 = 6$.
$D_2 = 6$.
If one person fell ill, the job would take 6 days.
The job would take 6 days.
(ii) Find how many persons would be needed to fit the windows in one day.
New time required $D_3 = 1$ day.
Let the number of persons needed be $P_3$.
Using the inverse proportion relationship $P \times D = k$:
$P_3 \times D_3 = k$
Substitute the values of $D_3$ and $k$:
$P_3 \times 1 = 6$.
$P_3 = 6$.
6 persons would be needed to fit the windows in one day.
The number of persons needed is 6.
Question 11. A school has 8 periods a day each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same?
Answer:
This problem involves the relationship between the number of periods in a school day and the duration of each period, given that the total duration of the school day remains constant. If the number of periods increases, the duration of each period must decrease. This is a case of inverse proportion.
In inverse proportion, the product of the two quantities is constant.
Let $N$ be the number of periods per day and $D$ be the duration of each period in minutes.
The relationship is $N \times D = k$, where $k$ is a constant representing the total duration of the school day in minutes.
Given initial conditions:
Initial number of periods $N_1 = 8$.
Initial duration of each period $D_1 = 45$ minutes.
Calculate the total duration of the school day ($k$) using the initial conditions:
$k = N_1 \times D_1$
$k = 8 \times 45$ minutes
$k = 360$ minutes.
The total duration of the school day is 360 minutes.
New conditions: The school has 9 periods a day.
New number of periods $N_2 = 9$.
We need to find the new duration of each period ($D_2$).
Using the same relationship $N \times D = k$ for the new conditions:
$N_2 \times D_2 = k$
Substitute the values of $N_2$ and $k$:
$9 \times D_2 = 360$.
To find $D_2$, divide both sides by 9:
$D_2 = \frac{360}{9}$.
$D_2 = 40$.
The new duration of each period is 40 minutes.
Alternatively, using the property of inverse proportion $N_1 D_1 = N_2 D_2$:
$8 \times 45 = 9 \times D_2$
$360 = 9 D_2$
$D_2 = \frac{360}{9}$
$D_2 = 40$ minutes.
If the school has 9 periods a day with the same total number of school hours, each period would be 40 minutes long.
Each period would be 40 minutes long.

