| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 1 Number Systems
Welcome to the detailed solutions for Chapter 1: Number Systems. This resource serves as an essential companion, meticulously designed to deepen your understanding of the fascinating world of numbers. Building upon your prior knowledge of rational numbers, this chapter significantly expands the horizon to encompass the complete set of real numbers. We embark on a journey that clearly differentiates between the two fundamental categories within the real number system: the familiar rational numbers and the intriguing irrational numbers.
Our solutions provide comprehensive explanations and step-by-step guidance. A primary focus is the precise identification and classification of numbers. You will learn to recognize rational numbers, which can always be expressed in the form $\frac{p}{q}$ where $p$ and $q$ are integers and $q \neq 0$. Their decimal representations are either terminating (like $\frac{1}{2} = 0.5$) or non-terminating but recurring (like $\frac{1}{3} = 0.333...$). In contrast, irrational numbers cannot be expressed in this fractional form. Their decimal expansions are both non-terminating and non-recurring. Classic examples explored in detail include $\sqrt{2}$, $\sqrt{5}$, and the transcendental number $\pi$ ($3.14159...$). The solutions clearly demonstrate methods to prove the irrationality of certain numbers and understand their unique properties.
Visualizing numbers is key, and therefore, representing real numbers on the number line is a significant component. The provided solutions thoroughly explain the geometrical construction methods required to accurately plot irrational numbers. Techniques often rely implicitly on the Pythagoras theorem, $a^2 + b^2 = c^2$, such as constructing lengths corresponding to $\sqrt{2}$, $\sqrt{3}$, and other square roots, often visualized using the elegant spiral method or basic right-angled triangles. Furthermore, the concept of successive magnification is elucidated, offering a powerful visual technique to zoom in on the number line and pinpoint the location of any real number, whether its decimal expansion terminates, recurs, or does neither, with ever-increasing accuracy.
Beyond identification and representation, manipulating these numbers is crucial. The solutions address:
- Converting non-terminating recurring decimals back into their rational $\frac{p}{q}$ form using algebraic methods.
- Performing arithmetic operations (addition, subtraction, multiplication, division) on real numbers, with a special focus on expressions involving irrational numbers, often termed surds.
- The vital technique of rationalizing the denominator. Solutions cover scenarios with monomial denominators (e.g., $\frac{1}{\sqrt{7}}$) and binomial denominators (e.g., $\frac{1}{2 + \sqrt{3}}$ or $\frac{1}{\sqrt{5} - \sqrt{2}}$), explaining the use of appropriate rationalizing factors, including the conjugate. For example, to rationalize $\frac{1}{\sqrt{a} + \sqrt{b}}$, we multiply by $\frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} - \sqrt{b}}$.
Finally, the fundamental laws of exponents are revisited and extended. Having previously applied them to integer exponents, you'll now see how these rules ($a^m \cdot a^n = a^{m+n}$, $(a^m)^n = a^{mn}$, $\frac{a^m}{a^n} = a^{m-n}$, $a^0 = 1$, $a^{-n} = \frac{1}{a^n}$) are generalized to handle rational exponents. The solutions demonstrate simplifying complex expressions involving fractional powers, understanding that $a^{\frac{m}{n}}$ is equivalent to $(\sqrt[n]{a})^m$ or $\sqrt[n]{a^m}$. Mastering these key areas forms a robust foundation for future algebraic studies.
Example 1 & 2 (Before Exercise 1.1)
Example 1: Are the following statements true or false? Give reasons for your answers.
(i) Every whole number is a natural number.
(ii) Every integer is a rational number.
(iii) Every rational number is an integer.
Answer:
(i) The provided statement is: Every whole number is a natural number.
The given statement is false.
- The set of Whole Numbers is {0, 1, 2, 3, ...}.
- The set of Natural Numbers is {1, 2, 3, ...}.
- The number 0 is included in the set of whole numbers but is not included in the set of natural numbers.
- Since there exists at least one whole number (0) that is not a natural number, the statement is false.
(ii) The provided statement is: Every integer is a rational number.
The given statement is true.
- A rational number is any number that can be expressed in the form $\frac{p}{q}$, where p and q are integers and q ≠ 0.
- Any integer 'm' can be written in the form $\frac{m}{1}$.
- In this form, p = m (an integer) and q = 1 (an integer, and 1 ≠ 0).
- Therefore, every integer satisfies the definition of a rational number.
(iii) The provided statement is: Every rational number is an integer.
The given statement is false.
- A rational number is any number that can be expressed in the form $\frac{p}{q}$, where p and q are integers and q ≠ 0.
- Integers are whole numbers and their negatives {..., -2, -1, 0, 1, 2, ...}.
- Consider the number $\frac{1}{2}$. Here, p=1 and q=2. Both are integers and q ≠ 0, so $\frac{1}{2}$ is a rational number.
- However, $\frac{1}{2}$ (or 0.5) is not an integer.
- Since we found a rational number that is not an integer, the statement that "every rational number is an integer" is false. (Other examples include $\frac{3}{4}$, $-\frac{2}{5}$, etc.)
Example 2: Find five rational numbers between 1 and 2. We can approach this problem in at least two ways.
Answer:
There are infinitely many rational numbers between 1 and 2. We can find any number of them using different methods. Here are two common ways to find five rational numbers between 1 and 2.
Method 1: The Mean Method
A rational number between any two rational numbers 'a' and 'b' can be found by calculating their mean, which is $\frac{a+b}{2}$. We can repeat this process to find more rational numbers.
Step 1: Find a rational number between 1 and 2.
$\frac{1+2}{2} = \frac{3}{2}$
So, we have $1 < \frac{3}{2} < 2$.
Step 2: Find a rational number between 1 and $\frac{3}{2}$.
$\frac{1 + \frac{3}{2}}{2} = \frac{\frac{2+3}{2}}{2} = \frac{5/2}{2} = \frac{5}{4}$
So, we have $1 < \frac{5}{4} < \frac{3}{2} < 2$.
Step 3: Find a rational number between $\frac{3}{2}$ and 2.
$\frac{\frac{3}{2} + 2}{2} = \frac{\frac{3+4}{2}}{2} = \frac{7/2}{2} = \frac{7}{4}$
So, we have $1 < \frac{5}{4} < \frac{3}{2} < \frac{7}{4} < 2$.
Step 4: Find a rational number between 1 and $\frac{5}{4}$.
$\frac{1 + \frac{5}{4}}{2} = \frac{\frac{4+5}{4}}{2} = \frac{9/4}{2} = \frac{9}{8}$
So, we have $1 < \frac{9}{8} < \frac{5}{4} < \frac{3}{2} < \frac{7}{4} < 2$.
Step 5: Find a rational number between $\frac{7}{4}$ and 2.
$\frac{\frac{7}{4} + 2}{2} = \frac{\frac{7+8}{4}}{2} = \frac{15/4}{2} = \frac{15}{8}$
Thus, five rational numbers between 1 and 2 are $\frac{9}{8}, \frac{5}{4}, \frac{3}{2}, \frac{7}{4}, \frac{15}{8}$.
Method 2: Using a Common Denominator
We can convert the given numbers into equivalent rational numbers with a common denominator and then list the numbers in between.
Step 1: Express the numbers 1 and 2 as rational numbers.
$1 = \frac{1}{1}$ and $2 = \frac{2}{1}$.
Step 2: To find 5 rational numbers, we need to multiply the numerator and denominator by a number greater than 5. Let's choose 6 (since $5+1=6$).
$1 = \frac{1 \times 6}{1 \times 6} = \frac{6}{6}$
$2 = \frac{2 \times 6}{1 \times 6} = \frac{12}{6}$
Step 3: Now we can easily find five rational numbers between $\frac{6}{6}$ and $\frac{12}{6}$. We just need to choose numerators between 6 and 12.
The numbers are: $\frac{7}{6}, \frac{8}{6}, \frac{9}{6}, \frac{10}{6}, \frac{11}{6}$.
On simplifying, we get $\frac{7}{6}, \frac{4}{3}, \frac{3}{2}, \frac{5}{3}, \frac{11}{6}$.
Alternatively, we could choose a larger number like 10 to make the calculation even simpler.
$1 = \frac{1 \times 10}{1 \times 10} = \frac{10}{10}$
$2 = \frac{2 \times 10}{1 \times 10} = \frac{20}{10}$
Now, five rational numbers between $\frac{10}{10}$ and $\frac{20}{10}$ can be:
$\frac{11}{10}, \frac{12}{10}, \frac{13}{10}, \frac{14}{10}, \frac{15}{10}$, which are equivalent to 1.1, 1.2, 1.3, 1.4, 1.5.
Exercise 1.1
Question 1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0?
Answer:
Yes, zero is a rational number.
A number is defined as a rational number if it can be expressed in the form $\frac{p}{q}$, where 'p' and 'q' are integers and the denominator 'q' is not equal to zero ($q \neq 0$).
Zero can be written in this form in many ways. Here are a few examples:
$\frac{0}{1}$, where p = 0 and q = 1 (both are integers, and q ≠ 0).
$\frac{0}{2}$, where p = 0 and q = 2 (both are integers, and q ≠ 0).
$\frac{0}{-5}$, where p = 0 and q = -5 (both are integers, and q ≠ 0).
In all these cases, the value of the fraction is 0, and the conditions for a rational number are satisfied. Therefore, zero is a rational number.
Question 2. Find six rational numbers between 3 and 4.
Answer:
There are infinitely many rational numbers between 3 and 4. We can find six of them using the following method.
Solution:
We will use the method of finding equivalent rational numbers with a common denominator.
Step 1: Express the given numbers, 3 and 4, as rational numbers with a denominator of 1.
$3 = \frac{3}{1}$
$4 = \frac{4}{1}$
Step 2: We need to find six rational numbers. To do this, we will multiply the numerator and denominator of both fractions by a number greater than 6. Let's use $6+1 = 7$.
Step 3: Convert the fractions to have a denominator of 7.
$3 = \frac{3 \times 7}{1 \times 7} = \frac{21}{7}$
$4 = \frac{4 \times 7}{1 \times 7} = \frac{28}{7}$
Step 4: Now, we can easily list six rational numbers between $\frac{21}{7}$ and $\frac{28}{7}$ by choosing numerators between 21 and 28.
The six rational numbers are:
$\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7}, \frac{27}{7}$
Alternate Solution
We can also multiply by a larger, more convenient number like 10.
Step 1: Express 3 and 4 as rational numbers.
$3 = \frac{3}{1}$ and $4 = \frac{4}{1}$
Step 2: Multiply the numerator and denominator by 10.
$3 = \frac{3 \times 10}{1 \times 10} = \frac{30}{10}$
$4 = \frac{4 \times 10}{1 \times 10} = \frac{40}{10}$
Step 3: List any six rational numbers between $\frac{30}{10}$ and $\frac{40}{10}$.
For example:
$\frac{31}{10}, \frac{32}{10}, \frac{33}{10}, \frac{34}{10}, \frac{35}{10}, \frac{36}{10}$
These can also be written in decimal form as 3.1, 3.2, 3.3, 3.4, 3.5, and 3.6, which are also rational numbers.
Question 3. Find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ .
Answer:
There are infinitely many rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$. We can find five of them by creating equivalent fractions with a larger common denominator.
Solution
The given numbers are $\frac{3}{5}$ and $\frac{4}{5}$.
Step 1: The numbers already have a common denominator, but there are no integers between the numerators 3 and 4. So, we need to find equivalent fractions.
Step 2: To find five rational numbers, we need to multiply the numerator and denominator of both fractions by a number greater than 5. A convenient choice is $5 + 1 = 6$.
Step 3: Convert both fractions into equivalent fractions with a new denominator ($5 \times 6 = 30$).
$\frac{3}{5} = \frac{3 \times 6}{5 \times 6} = \frac{18}{30}$
$\frac{4}{5} = \frac{4 \times 6}{5 \times 6} = \frac{24}{30}$
Step 4: Now we can easily list five rational numbers with the same denominator (30) and numerators between 18 and 24.
The five rational numbers are:
$\frac{19}{30}, \frac{20}{30}, \frac{21}{30}, \frac{22}{30}, \frac{23}{30}$
Note: These fractions can be simplified to $\frac{19}{30}, \frac{2}{3}, \frac{7}{10}, \frac{11}{15}, \frac{23}{30}$, but leaving them with a common denominator is also correct.
Alternate Solution
We can also multiply the numerator and denominator by 10, which is often an easy number to work with.
Step 1: Start with the fractions $\frac{3}{5}$ and $\frac{4}{5}$.
Step 2: Multiply the numerator and denominator of each fraction by 10.
$\frac{3}{5} = \frac{3 \times 10}{5 \times 10} = \frac{30}{50}$
$\frac{4}{5} = \frac{4 \times 10}{5 \times 10} = \frac{40}{50}$
Step 3: Now, list any five rational numbers between $\frac{30}{50}$ and $\frac{40}{50}$.
For example:
$\frac{31}{50}, \frac{32}{50}, \frac{33}{50}, \frac{34}{50}, \frac{35}{50}$
Question 4. State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Answer:
(i) Every natural number is a whole number.
True.
Reason: The set of natural numbers (counting numbers) is {1, 2, 3, 4, ...}. The set of whole numbers is {0, 1, 2, 3, 4, ...}. Since the collection of whole numbers includes all the natural numbers, this statement is true.
(ii) Every integer is a whole number.
False.
Reason: The set of integers includes negative numbers (e.g., -1, -2, -3, ...), zero, and positive numbers. The set of whole numbers only includes zero and positive numbers {0, 1, 2, ...}. Negative integers are not whole numbers. For example, -3 is an integer, but it is not a whole number.
(iii) Every rational number is a whole number.
False.
Reason: Rational numbers are numbers that can be expressed in the form $\frac{p}{q}$, where p and q are integers and q ≠ 0. This set includes fractions and decimals. While some rational numbers are whole numbers (e.g., $4 = \frac{4}{1}$), many are not. For example, $\frac{1}{2}$, $\frac{3}{4}$, and $-\frac{2}{5}$ are rational numbers, but they are not whole numbers.
Example 3 & 4 (Before Exercise 1.2)
Example 3: Locate $\sqrt{2}$ on the number line.
Answer:
Solution:
To locate $\sqrt{2}$ on the number line, we will use the concept of the Pythagorean theorem. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
If the two shorter sides (legs) of a right-angled triangle have lengths 'a' and 'b', and the hypotenuse has length 'c', then:
$c^2 = a^2 + b^2$
We want to construct a line segment of length $\sqrt{2}$. So, we need to find values for 'a' and 'b' such that $c^2=2$. A simple choice is to take $a=1$ and $b=1$.
Then, $c^2 = 1^2 + 1^2 = 1 + 1 = 2$.
This means $c = \sqrt{2}$.
So, if we construct a right-angled triangle where both perpendicular sides are 1 unit long, the hypotenuse will be $\sqrt{2}$ units long.
Steps of Construction:
1. Draw a number line. Mark the point O to represent 0 and the point A to represent 1. The distance OA is 1 unit.
2. At point A, draw a perpendicular line segment AB such that its length is also 1 unit.
3. Join the points O and B. Now, $\triangle OAB$ is a right-angled triangle with the right angle at A.
4. According to the Pythagorean theorem, the length of the hypotenuse OB can be calculated as:
$OB = \sqrt{OA^2 + AB^2}$
$OB = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2}$
5. We now have a line segment OB of length $\sqrt{2}$. To represent this length on the number line, we use a compass.
6. Place the pointed end of the compass at O and the pencil end at B. The radius of the compass is now equal to the length of OB, which is $\sqrt{2}$.
7. With the same radius and O as the center, draw an arc that intersects the number line at a point P.
8. The distance OP on the number line is equal to the length of OB. Therefore, the point P represents the number $\sqrt{2}$ on the number line.
Example 4: Locate $\sqrt{3}$ on the number line.
Answer:
Solution:
To locate $\sqrt{3}$ on the number line, we will again use the Pythagorean theorem. The construction for $\sqrt{3}$ builds upon the construction for $\sqrt{2}$.
Recall that in a right-angled triangle with sides 'a' and 'b', and hypotenuse 'c', we have $c^2 = a^2 + b^2$.
To get a hypotenuse of length $\sqrt{3}$, we need $c^2 = 3$. We can express 3 as the sum of two squares. A convenient way is $3 = 2 + 1$.
So, we can choose $a^2 = 2$ and $b^2 = 1$. This means we need sides of length $a = \sqrt{2}$ and $b = 1$.
The calculation would be:
$c = \sqrt{(\sqrt{2})^2 + 1^2} = \sqrt{2+1} = \sqrt{3}$
This tells us that if we construct a right-angled triangle with a base of length $\sqrt{2}$ units and a height of 1 unit, its hypotenuse will be $\sqrt{3}$ units long.
Steps of Construction:
First, we need to construct a line segment of length $\sqrt{2}$.
1. Draw a number line and mark point O for 0 and point A for 1.
2. At A, draw a perpendicular line segment AB of length 1 unit.
3. Join O and B. By the Pythagorean theorem, the length of OB is $\sqrt{1^2 + 1^2} = \sqrt{2}$.
Now that we have the length $\sqrt{2}$ (segment OB), we can proceed to construct $\sqrt{3}$.
4. Using the line segment OB as the base, draw a perpendicular line segment BC of length 1 unit at point B.
5. Join O and C. Now, $\triangle OBC$ is a right-angled triangle with the right angle at B.
6. The length of the hypotenuse OC can be calculated using the Pythagorean theorem:
$OC = \sqrt{OB^2 + BC^2}$
$OC = \sqrt{(\sqrt{2})^2 + 1^2} = \sqrt{2 + 1} = \sqrt{3}$
7. We now have a line segment OC of length $\sqrt{3}$. To represent this on the number line, we use a compass.
8. Place the pointed end of the compass at O and the pencil end at C. The radius of the compass is now equal to the length of OC, which is $\sqrt{3}$.
9. With O as the center and a radius of OC, draw an arc that intersects the number line at a point Q.
10. The distance OQ on the number line is equal to the length of OC. Therefore, the point Q represents the number $\sqrt{3}$ on the number line.
Exercise 1.2
Question 1. State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form $\sqrt{m}$ , where m is a natural number.
(iii) Every real number is an irrational number.
Answer:
(i) The provided statement is: Every irrational number is a real number.
The given statement is true.
- The set of Real Numbers is defined as the collection (union) of all Rational Numbers and all Irrational Numbers.
- Therefore, by definition, every irrational number falls within the category of real numbers.
(ii) The provided statement is: Every point on the number line is of the form $\sqrt{\mathbf{m}}$, where m is a natural number.
The given statement is false.
- The number line represents all real numbers, including negative numbers and positive numbers that are not perfect squares.
- The expression $\sqrt{m}$, where m is a natural number (m = 1, 2, 3, ...), can only represent non-negative numbers (e.g., $\sqrt{1}=1$, $\sqrt{2}$, $\sqrt{3}$, $\sqrt{4}=2$, etc.).
- Negative numbers, such as -1, -2, etc., are points on the number line but cannot be represented in the form $\sqrt{m}$ because the square root of a natural number is never negative.
- Furthermore, many positive real numbers like 0.5 or $\frac{3}{4}$ are on the number line, but they cannot be written as $\sqrt{m}$ where m is a natural number (e.g., if $\sqrt{m} = 0.5$, then $m = 0.25$, which is not natural).
- Since there are many points on the number line (negative numbers, certain positive fractions/decimals) that do not fit the form $\sqrt{m}$ (with m being natural), the statement is false.
(iii) The provided statement is: Every real number is an irrational number.
The given statement is false.
- The set of Real Numbers includes both Rational Numbers and Irrational Numbers.
- Rational numbers, such as 2 (which can be written as $\frac{2}{1}$) or $\frac{1}{2}$, are real numbers.
- However, these rational numbers are, by definition, "not" irrational numbers.
- Since there exist real numbers (the rationals) that are not irrational, the statement that "every real number is irrational" is false.
Question 2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Answer:
No, the statement that the square roots of all positive integers are irrational is false.
Reason:
The square root of a positive integer is rational if the integer is a perfect square. A perfect square is an integer that is the square of another integer (e.g., 1, 4, 9, 16, ...). If a positive integer is not a perfect square, then its square root is irrational.
Here is an example of the square root of a positive integer that is a rational number:
Consider the positive integer 4.
The square root of 4 is $\sqrt{4} = 2$.
The number 2 is a rational number because it can be expressed in the form $\frac{p}{q}$, where p and q are integers and $q \neq 0$. For instance, 2 can be written as $\frac{2}{1}$.
Other examples include:
- $\sqrt{9} = 3$, which is a rational number.
- $\sqrt{16} = 4$, which is a rational number.
- $\sqrt{25} = 5$, which is a rational number.
Question 3. Show how $\sqrt{5}$ can be represented on the number line.
Answer:
Solution:
To represent $\sqrt{5}$ on the number line, we will use the Pythagorean theorem. This theorem allows us to construct a line segment of a specific length, which we can then transfer to the number line.
The Pythagorean theorem states that in a right-angled triangle with perpendicular sides of length 'a' and 'b', and a hypotenuse of length 'c', the relationship is:
$c^2 = a^2 + b^2$
We want to construct a hypotenuse of length $\sqrt{5}$, so we need $c = \sqrt{5}$, which means $c^2 = 5$.
We need to find two numbers whose squares add up to 5. We can express 5 as the sum of two perfect squares: $4 + 1$.
$5 = 4 + 1 = 2^2 + 1^2$
This means we can construct a right-angled triangle with perpendicular sides of length $a = 2$ units and $b = 1$ unit. The length of its hypotenuse 'c' will be:
$c = \sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}$
Steps of Construction:
1. Draw a number line and mark the origin O at 0. Mark a point A at the position of 2. The length of the line segment OA is 2 units.
2. At point A, draw a line segment AB perpendicular to the number line, with a length of 1 unit.
3. Join the points O and B. This creates a right-angled triangle, $\triangle OAB$, with the right angle at A.
4. As calculated using the Pythagorean theorem, the length of the hypotenuse OB is:
$OB = \sqrt{OA^2 + AB^2} = \sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}$
5. Now we have a line segment OB of length $\sqrt{5}$. To mark this length on the number line, we use a compass.
6. Place the pointed tip of the compass at the origin O and extend the pencil tip to point B.
7. With this radius (equal to OB = $\sqrt{5}$), draw an arc that cuts the number line at a point P.
8. The distance from the origin O to the point P on the number line is equal to the length of OB. Therefore, the point P represents the number $\sqrt{5}$ on the number line.
Question 4. Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2, P3,...., Pn,... ., and joined them to create a beautiful spiral depicting $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{4}$ ,…..
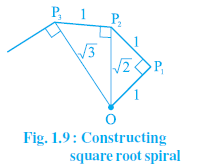
Answer:
Construction of the Square Root Spiral
The square root spiral is a spiral formed by a sequence of right-angled triangles, where the hypotenuse of each triangle becomes a leg of the next triangle. This activity visually represents the square roots of consecutive positive integers ($\sqrt{2}, \sqrt{3}, \sqrt{4}, \dots$).
The construction is based on the repeated application of the Pythagorean theorem, which states that for a right-angled triangle with perpendicular sides 'a' and 'b' and hypotenuse 'c', $c = \sqrt{a^2 + b^2}$.
Steps of Construction:
1. First Triangle (for $\sqrt{2}$):
- Take a point O as the center.
- Draw a horizontal line segment OP1 of 1 unit length.
- From point P1, draw a perpendicular line segment P1P2, also of 1 unit length.
- Join O and P2. $\triangle$OP1P2 is a right-angled triangle.
- By the Pythagorean theorem, the length of the hypotenuse OP2 is:
$OP_2 = \sqrt{OP_1^2 + P_1P_2^2} = \sqrt{1^2 + 1^2} = \sqrt{2}$
2. Second Triangle (for $\sqrt{3}$):
- Now, using OP2 as the base, draw a perpendicular line segment P2P3 of 1 unit length.
- Join O and P3. $\triangle$OP2P3 is a right-angled triangle.
- The length of the hypotenuse OP3 is:
$OP_3 = \sqrt{OP_2^2 + P_2P_3^2} = \sqrt{(\sqrt{2})^2 + 1^2} = \sqrt{2 + 1} = \sqrt{3}$
3. Third Triangle (for $\sqrt{4}$):
- Using OP3 as the base, draw a perpendicular line segment P3P4 of 1 unit length.
- Join O and P4. $\triangle$OP3P4 is a right-angled triangle.
- The length of the hypotenuse OP4 is:
$OP_4 = \sqrt{OP_3^2 + P_3P_4^2} = \sqrt{(\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2$
4. Continuing the Spiral:
- This process is repeated. For each new step, we draw a perpendicular line segment of 1 unit length from the last point (Pn) and join the new point (Pn+1) to the center O.
- The length of the hypotenuse OPn will always be $\sqrt{n}$.
By continuing this process, you will create a beautiful spiral shape. The lengths of the line segments OP1, OP2, OP3, OP4, ... will be 1, $\sqrt{2}, \sqrt{3}, \sqrt{4}, \dots$ respectively.
Example 5 to 10 (Before Exercise 1.3)
Example 5: Find the decimal expansions of $\frac{10}{3}$ , $\frac{7}{8}$ and $\frac{1}{7}$ .
Answer:
To find the decimal expansion of a rational number, we perform long division of the numerator by the denominator.
(i) Decimal expansion of $\frac{10}{3}$
We divide 10 by 3.
$\begin{array}{r} 3.33... \\ 3{\overline{\smash{\big)}\,10.000\phantom{)}}} \\ \underline{-~\phantom{(}9\phantom{....)}} \\ 1\ 0\phantom{...} \\ \underline{-~\phantom{()}9\phantom{...}} \\ 1\ 0\phantom{.} \\ \underline{-~\phantom{()}9\phantom{.}} \\ 1\phantom{)} \end{array}$
In this division, the remainder is always 1, and the digit 3 in the quotient repeats. We cannot get a remainder of 0.
Therefore, the decimal expansion of $\frac{10}{3}$ is $3.333...$ or $3.\overline{3}$.
This is a non-terminating repeating decimal expansion.
(ii) Decimal expansion of $\frac{7}{8}$
We divide 7 by 8.
$\begin{array}{r} 0.875\phantom{)} \\ 8{\overline{\smash{\big)}\,7.000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{.....)}} \\ 7\ 0\phantom{....} \\ \underline{-~\phantom{(}6\ 4\phantom{...}} \\ 6\ 0\phantom{..} \\ \underline{-~\phantom{(}5\ 6\phantom{..}} \\ 4\ 0\phantom{.} \\ \underline{-~\phantom{(}4\ 0\phantom{.}} \\ 0\phantom{)} \end{array}$
In this division, the remainders are 6, 4, and finally 0. Since the remainder becomes zero after a certain number of steps, the division process stops.
Therefore, the decimal expansion of $\frac{7}{8}$ is 0.875.
This is a terminating decimal expansion.
(iii) Decimal expansion of $\frac{1}{7}$
We divide 1 by 7.
$\begin{array}{r} 0.142857... \\ 7{\overline{\smash{\big)}\,1.000000\phantom{)}}} \\ \underline{-~\phantom{(}0\phantom{........)}} \\ 1\ 0\phantom{.......} \\ \underline{-~\phantom{(}7\phantom{......}} \\ 3\ 0\phantom{.....} \\ \underline{-~\phantom{(}2\ 8\phantom{....}} \\ 2\ 0\phantom{....} \\ \underline{-~\phantom{(}1\ 4\phantom{...}} \\ 6\ 0\phantom{...} \\ \underline{-~\phantom{(}5\ 6\phantom{..}} \\ 4\ 0\phantom{..} \\ \underline{-~\phantom{(}3\ 5\phantom{.}} \\ 5\ 0\phantom{.} \\ \underline{-~\phantom{(}4\ 9\phantom{.}} \\ 1\phantom{.} \end{array}$
In this division, the remainders are 3, 2, 6, 4, 5, and 1. After the remainder 1, the entire sequence of remainders and quotient digits will repeat. The division never ends.
Therefore, the decimal expansion of $\frac{1}{7}$ is $0.142857142857...$ or $0.\overline{142857}$.
This is a non-terminating repeating decimal expansion.
Example 6: Show that 3.142678 is a rational number. In other words, express 3.142678 in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0.
Answer:
Solution:
We are given the number 3.142678.
This is a terminating decimal because the digits after the decimal point end after a finite number of places (in this case, 6 places).
To express this decimal in the form of a fraction $\frac{p}{q}$, we can write the number without the decimal point as the numerator and 1 followed by the same number of zeros as there are decimal places for the denominator.
Number of decimal places = 6.
So, the denominator will be $10^6 = 1,000,000$.
Therefore, we can write:
$3.142678 = \frac{3142678}{1000000}$
Here, $p = 3142678$ and $q = 1000000$. Both $p$ and $q$ are integers, and $q \neq 0$.
Since 3.142678 can be expressed in the form $\frac{p}{q}$, it is a rational number.
Example 7: Show that $0.3333... = 0.\overline{3}$ can be expressed in the form $\frac{p}{q}$ ,, where p and q are integers and q ≠ 0.
Answer:
Solution:
We need to express the non-terminating repeating decimal $0.\overline{3}$ in the form $\frac{p}{q}$.
Let the number be $x$.
$x = 0.3333...$
... (i)
Since there is only one repeating digit (the digit 3), we will multiply both sides of equation (i) by 10.
$10x = 10 \times (0.3333...) = 3.3333...$
... (ii)
Now, we subtract equation (i) from equation (ii) to eliminate the repeating decimal part.
$10x - x = (3.3333...) - (0.3333...)$
$9x = 3$
Now, we solve for $x$:
$x = \frac{3}{9}$
Simplifying the fraction, we get:
$x = \frac{1}{3}$
Thus, $0.\overline{3} = \frac{1}{3}$. This is in the form $\frac{p}{q}$, where $p=1$ and $q=3$ are integers and $q \neq 0$.
Example 8: Show that $1.272727... = 1.\overline{27}$ can be expressed in the form $\frac{p}{q}$ , , where p and q are integers and q ≠ 0.
Answer:
Solution:
We want to express the non-terminating repeating decimal $1.\overline{27}$ in the form $\frac{p}{q}$.
Let the number be $x$.
$x = 1.272727...$
... (i)
Here, the block of repeating digits is '27', which has two digits. Therefore, we will multiply both sides of equation (i) by $10^2 = 100$.
$100x = 100 \times (1.272727...) = 127.2727...$
... (ii)
Now, subtract equation (i) from equation (ii).
$100x - x = (127.2727...) - (1.2727...)$
$99x = 126$
Solving for $x$:
$x = \frac{126}{99}$
We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 9.
$x = \frac{126 \div 9}{99 \div 9} = \frac{14}{11}$
Thus, $1.\overline{27} = \frac{14}{11}$. This is in the form $\frac{p}{q}$, where $p=14$ and $q=11$ are integers and $q \neq 0$.
Example 9: Show that $0.2353535... = 0.2\overline{35}$ can be expressed in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0.
Answer:
Solution:
We want to express the mixed repeating decimal $0.2\overline{35}$ in the form $\frac{p}{q}$.
Let the number be $x$.
$x = 0.2353535...$
... (i)
First, we need to shift the decimal point to the right so that only the repeating block remains after it. Since there is one non-repeating digit (2), we multiply equation (i) by 10.
$10x = 2.353535...$
... (ii)
Now we have a number where the decimal part is purely repeating. The repeating block '35' has two digits. So, we multiply equation (ii) by $10^2 = 100$.
$100 \times (10x) = 100 \times (2.353535...)$
$1000x = 235.3535...$
... (iii)
Now, we subtract equation (ii) from equation (iii) to eliminate the repeating part.
$1000x - 10x = (235.3535...) - (2.3535...)$
$990x = 233$
Solving for $x$:
$x = \frac{233}{990}$
Thus, $0.2\overline{35} = \frac{233}{990}$. This is in the form $\frac{p}{q}$, where $p=233$ and $q=990$ are integers and $q \neq 0$.
Example 10: Find an irrational number between $\frac{1}{7}$ and $\frac{2}{7}$ .
Answer:
Solution:
To find an irrational number between two rational numbers, we can first find their decimal expansions.
First, let's find the decimal expansion of $\frac{1}{7}$ by long division.
$\frac{1}{7} = 0.142857142857... = 0.\overline{142857}$
Now, we can find the decimal expansion of $\frac{2}{7}$ by multiplying the decimal for $\frac{1}{7}$ by 2.
$\frac{2}{7} = 2 \times \frac{1}{7} = 2 \times 0.\overline{142857} = 0.\overline{285714}$
So, we need to find an irrational number between $0.142857...$ and $0.285714...$
An irrational number has a decimal expansion that is both non-terminating and non-repeating.
We can construct such a number by choosing a starting value between the two given numbers and then creating a pattern that does not repeat.
For example, we can choose a number that starts with 0.15, which is clearly between 0.14... and 0.28.... To make it irrational, we can add digits in a non-repeating pattern.
One such number could be:
$0.15015001500015...$
This number is irrational because the pattern of zeros between the '15's keeps increasing, so the decimal expansion will never terminate and will never repeat. It is also greater than $\frac{1}{7}$ and less than $\frac{2}{7}$.
Many other answers are possible. For example:
$0.161161116...$
$0.2010010001...$
Exercise 1.3
Question 1. Write the following in decimal form and say what kind of decimal expansion each has :
(i) $\frac{36}{100}$
(ii) $\frac{1}{11}$
(iii) $4\frac{1}{8}$
(iv) $\frac{3}{13}$
(v) $\frac{2}{11}$
(vi) $\frac{329}{400}$
Answer:
(i) Here, we have $\frac{\mathbf{36}}{\mathbf{100}}$
So, $\frac{36}{100} = 0.36$
Thus, the decimal expansion of $\frac{36}{100}$ is terminating as there are finite number of digits after the decimal.
(ii) Here, we have $\frac{\mathbf{1}}{\mathbf{11}}$
Dividing 1 by 11, we have
$$\begin{array}{r} 0.0909\dots\phantom{)} \\ % Quotient shows repeating pattern 11{\overline{\smash{\big)}\,1.0000\phantom{)}}} \\ % Divisor 11, Dividend 1.0000 % Skip step for 10/11=0. Go directly to 100/11=9 \underline{-\phantom{(..)}9\;9\phantom{00)}} \\ % 11 * 9 = 99. Align under 1.00. Subtract from 100. \phantom{(...)}1\;00\phantom{)} \\ % Remainder 1. Bring down next two '0's to make 100. % Skip step for 10/11=0. Go directly to 100/11=9 \underline{-\phantom{(...)}9\;9\phantom{)}} \\ % 11 * 9 = 99. Align under the 100 above. Subtract. \underline{\phantom{(.....)}1\phantom{)}} % Remainder 1. Pattern repeats. \end{array}$$
$⸫ \ \frac{1}{11} = 0.090909 … = 0.\overline{09}$
Thus, the decimal expansion of $\frac{1}{11}$ is non-terminating and repeating as there are infinite number of digits after the decimal and the block of digits $09$ repeats itself.
(iii) Here, we have $4{\frac{\mathbf{1}}{\mathbf{8}}}$
So, $4{\frac{1}{8}} = \frac{33}{8}$
Dividing 33 by 8, we get
$$\begin{array}{r} 4.125\phantom{)} \\ % Quotient 8{\overline{\smash{\big)}\,33.000\phantom{)}}} \\ % Divisor 8, Dividend 33.000 \underline{-\phantom{(}32\phantom{.000)}} \\ % 8 * 4 = 32. Align under 33. \phantom{(-.)}1\;0\phantom{00)} \\ % Remainder 1, bring down 0 -> 10 \underline{-\phantom{(.)}\;8\phantom{00)}} \\ % 8 * 1 = 8. Align under 10. \phantom{(..)}2\;0\phantom{0)} \\ % Remainder 2, bring down 0 -> 20 \underline{-\phantom{(..)}16\phantom{0)}} \\ % 8 * 2 = 16. Align under 20. \phantom{(...)}4\;0\phantom{)} \\ % Remainder 4, bring down 0 -> 40 \underline{-\phantom{(...)}40\phantom{)}} \\ % 8 * 5 = 40. Align under 40. \underline{\phantom{(....)}0\phantom{)}} % Remainder 0. \end{array}$$
$⸫4{\frac{1}{8}} = 4.125$.
Thus, the decimal expansion of $4\frac{1}{8}$ is terminating as there are finite number of digits after the decimal.
(iv) Here, we have $\frac{\mathbf{3}}{\mathbf{13}}$
Dividing 3 by 13, we get
$$\begin{array}{r} 0.230769\dots\phantom{)} \\ % Quotient showing repeating cycle 13{\overline{\smash{\big)}\,3.000000\phantom{)}}} \\ % Divisor 13, Dividend 3.000000 \underline{-\phantom{(.}2\;6\phantom{00000)}} \\ % 13 * 2 = 26. Align under 3.0 \phantom{(..)}\;4\;0\phantom{0000)} \\ % Remainder 4, bring down 0 -> 40 \underline{-\phantom{(..)}3\;9\phantom{0000)}} \\ % 13 * 3 = 39. Align under 40 \phantom{(...)}1\;00\phantom{000)} \\ % Remainder 1, bring down 0 -> 10, bring down 0 -> 100 (Quotient digit 0) \underline{-\phantom{(....)}9\;1\phantom{000)}} \\ % 13 * 7 = 91. Align under 100 \phantom{(.....)}9\;0\phantom{00)} \\ % Remainder 9, bring down 0 -> 90 \underline{-\phantom{(.....)}7\;8\phantom{00)}} \\ % 13 * 6 = 78. Align under 90 \phantom{(......)}12\;0\phantom{0)} \\ % Remainder 12, bring down 0 -> 120 \underline{-\phantom{(......)}11\;7\phantom{0)}} \\ % 13 * 9 = 117. Align under 120 \underline{\phantom{(.......)}3\phantom{)}} % Remainder 3. Pattern repeats. \end{array}$$
$⸫ \frac{3}{13} = 0.23076923 … = 0.\overline{230769}$
Thus, the decimal expansion of $\frac{3}{13}$ is non-terminating and repeating as there are infinite number of digits after the decimal and the block of digits $230769$ repeats itself.
(v) Here, we have $\frac{\mathbf{2}}{\mathbf{11}}$
Dividing 2 by 11, we get
$$\begin{array}{r} 0.1818\dots\phantom{)} \\ % Quotient shows repeating pattern 11{\overline{\smash{\big)}\,2.0000\phantom{)}}} \\ % Divisor 11, Dividend 2.0000 \underline{-\phantom{(.}1\;1\phantom{000)}} \\ % 11 * 1 = 11. Align under 2.0 \phantom{(..)}\;9\;0\phantom{00)} \\ % Remainder 9, bring down 0 -> 90 \underline{-\phantom{(..)}8\;8\phantom{00)}} \\ % 11 * 8 = 88. Align under 90 \phantom{(...)}2\;0\phantom{0)} \\ % Remainder 2, bring down 0 -> 20 (start of repeat) \underline{-\phantom{(...)}1\;1\phantom{0)}} \\ % 11 * 1 = 11. Align under 20 \phantom{(....)}9\;0\phantom{)} \\ % Remainder 9, bring down 0 -> 90 \underline{-\phantom{(....)}8\;8\phantom{)}} \\ % 11 * 8 = 88. Align under 90 \underline{\phantom{(.....)}2\phantom{)}} % Remainder 2. Pattern repeats. \end{array}$$
$⸫ \ \frac{2}{11}=0.1818 …. = 0.\overline{18}$
Thus, the decimal expansion of $\frac{2}{11}$ is non-terminating and repeating as there are infinite number of digits after the decimal and the block of digits $18$ repeats itself.
(vi) Here, we have $\frac{\mathbf{329}}{\mathbf{400}}$
We can write $\frac{329}{400} = \frac{329}{4 \times 100} = \frac{329}{4} \times \frac{1}{100}$
First, dividing 329 by 4, we get
$$\begin{array}{r} 82.25\phantom{)} \\ % Quotient 4{\overline{\smash{\big)}\,329.00\phantom{)}}} \\ % Divisor 4, Dividend 329.00 \underline{-\phantom{(}32\phantom{9.00)}} \\ % 4 * 8 = 32. Align under 32. \phantom{(..)}09\phantom{.00)} \\ % Remainder 0, bring down 9 -> 9. Align 9 under 9 (col 3). Indent 2. \underline{-\phantom{(..)}8\phantom{.00)}} \\ % 4 * 2 = 8. Align 8 under 9 (col 3). Indent 2. \phantom{(..)}1\;0\phantom{0)} \\ % Remainder 1, bring down 0 -> 10. Align 1 under 8 (col 3). Indent 2. \underline{-\phantom{(...)}8\phantom{0)}} \\ % 4 * 2 = 8. Align 8 under 0 (col 4). Indent 3. \phantom{(...)}2\;0\phantom{)} \\ % Remainder 2, bring down 0 -> 20. Align 2 under 8 (col 4). Indent 3. \underline{-\phantom{(...)}2\;0\phantom{)}} \\ % 4 * 5 = 20. Align 20 under 20 (cols 4,5). Indent 3. \underline{\phantom{(....)}0\phantom{)}} % Remainder 0. Align 0 under 0 (col 5). Indent 4. \end{array}$$
$ \therefore \ \frac{329}{4} = 82.25 $
Now, $\frac{329}{400} = 82.25 \times \frac{1}{100} = \frac{82.25}{100}$
$ \Rightarrow \frac{329}{400} = 0.8225 $
Alternatively, notice that $400 = 4 \times 100 = 2^2 \times (10)^2 = 2^2 \times (2 \times 5)^2 = 2^2 \times 2^2 \times 5^2 = 2^4 \times 5^2$. Since the prime factors of the denominator are only 2s and 5s, the decimal expansion must be terminating.
Thus, the decimal expansion of $\frac{329}{400}$ is terminating as there are finite number of digits after the decimal.
Question 2. You know that $\frac{1}{7} = 0.\overline{142857}$ Can you predict what the decimal expansions of $\frac{2}{7}$ , $\frac{3}{7}$ , $\frac{4}{7}$ , $\frac{5}{7}$ , $\frac{6}{7}$ are, without actually doing the long division? If so, how?
[Hint : Study the remainders while finding the value of $\frac{1}{7}$ carefully.]
Answer:
We are given that $\frac{1}{7} = 0.\overline{142857}$.
The decimal expansion of $\frac{1}{7}$ is repeating and has a block of 6 digits (142857). When we perform the long division of $1 \div 7$, the sequence of remainders is $3, 2, 6, 4, 5, 1, ...$ before repeating.
To find the decimal expansion of $\frac{x}{7}$ (where $x = 2, 3, 4, 5, 6$), we can observe that the digits in the repeating block will be the same as for $\frac{1}{7}$, but they will start at a different point, corresponding to the first remainder encountered when dividing $x$ by $7$.
Alternatively, we can simply multiply the decimal expansion of $\frac{1}{7}$ by the numerator:
$\Rightarrow \frac{2}{7} = 2 \times \frac{1}{7} = 2 \times (0.\overline{142857}) = 0.\overline{285714}$
(Notice: $2 \times 142857 = 285714$. The digits are a cyclic permutation of 142857, starting with 2.)
$\Rightarrow \frac{3}{7} = 3 \times \frac{1}{7} = 3 \times (0.\overline{142857}) = 0.\overline{428571}$
(Notice: $3 \times 142857 = 428571$. The digits are a cyclic permutation, starting with 4.)
$\Rightarrow \frac{4}{7} = 4 \times \frac{1}{7} = 4 \times (0.\overline{142857}) = 0.\overline{571428}$
(Notice: $4 \times 142857 = 571428$. The digits are a cyclic permutation, starting with 5.)
$\Rightarrow \frac{5}{7} = 5 \times \frac{1}{7} = 5 \times (0.\overline{142857}) = 0.\overline{714285}$
(Notice: $5 \times 142857 = 714285$. The digits are a cyclic permutation, starting with 7.)
$\Rightarrow \frac{6}{7} = 6 \times \frac{1}{7} = 6 \times (0.\overline{142857}) = 0.\overline{857142}$
(Notice: $6 \times 142857 = 857142$. The digits are a cyclic permutation, starting with 8.)
Thus, without actually doing the long division for each fraction, we can predict the decimal expansions by multiplying the decimal expansion of $\frac{1}{7}$ by the respective numerators $2, 3, 4, 5, 6$. The resulting decimal expansions are cyclic permutations of the digits in $0.\overline{142857}$.
Question 3. Express the following in the form $\frac{p}{q}$ , where p and q are integers and q ≠ 0.
(i) $0.\overline{6}$
(ii) $0.4\overline{7}$
(iii) $0.\overline{001}$
Answer:
(i) Here, we have $0.\overline{\mathbf{6}}$
So, let $x = 0.\overline{6}$. So,
$x = 0.\overline{6}$
…(i)
$⇒ 10 × x = 10 × 0.\overline{6}$
[Multiply both side by 10]
$⇒ 10x = 6.\overline{6}$
…(ii)
Subtract eq (i) from (ii). So, we have.
$10x - x = 6.\overline{6} - 0.\overline{6}$
$⇒ 9x = 6$
$⇒ x = \frac{6}{9}$
$⸫x = \frac{2}{3}$
Hence, $0.\overline{\mathbf{6}}$ can be expressed in the form $\frac{\mathbf{p}}{\mathbf{q}}$ as $\frac{\mathbf{2}}{\mathbf{3}}$ , where p and q are integers and q ≠ 0.
(ii) Here, we have $0.4\overline{\mathbf{7}}$
So, let x = $0.4\overline{7}$. So,
$x = 0.4\overline{7}$
…(i)
$⇒ 10 × x = 10 × 0.4\overline{7}$
[Multiply both side by 10]
$⇒ 10x = 4.\overline{7}$
…(ii)
$⇒ 10 × 10x = 10 × 4.\overline{7}$
[Multiply both side by 10 again]
$⇒ 100x = 47.\overline{7}$
…(iii)
Subtract eq (ii) from (iii). So, we have.
$100x - 10x = 47.\overline{7} - 4.\overline{7}$
$⇒ 90x = 43$
$⸫x = \frac{43}{90}$
Hence, $0.4\overline{\mathbf{7}}$ can be expressed in the form $\frac{\mathbf{p}}{\mathbf{q}}$ as $\frac{\mathbf{43}}{\mathbf{90}}$ , where p and q are integers and q ≠ 0.
(iii) Here, we have $0.\overline{\mathbf{001}}$
So, let $x = 0.\overline{001}$. So,
$x = 0.\overline{001}$
…(i)
$⇒ 1000 × x = 1000 × 0.\overline{001}$
[Multiply both side by 1000]
$⇒ 1000x = 1.\overline{001}$
…(ii)
Subtract eq (i) from (ii). So, we have.
$1000x - x = 1.\overline{001} - 0.\overline{001}$
$⇒ 999x = 1$
$⸫x = \frac{1}{999}$
Hence, $0.\overline{\mathbf{001}}$ can be expressed in the form $\frac{\mathbf{p}}{\mathbf{q}}$ as $\frac{\mathbf{1}}{\mathbf{999}}$ , where p and q are integers and q ≠ 0.
Question 4. Express 0.99999 .... in the form $\frac{p}{q}$ . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Answer:
Here, let $x = 0.99999...$ or $0.\overline{9}$. So,
$x = 0.\overline{9}$
…(i)
$⇒ 10 × x = 10 × 0.\overline{9}$
[Multiply both side by 10]
$⇒ 10x = 9.\overline{9}$
…(ii)
Subtract eq (i) from (ii). So, we have.
$10x - 1x = 9.\overline{9} - 0.\overline{9}$
$⇒ 9x = 9$
$⇒ x = \frac{9}{9}$
$⸫x = 1 or \frac{1}{1}$ .
Hence, $0.\overline{\mathbf{9}}$ can be expressed in the form $\frac{\mathbf{p}}{\mathbf{q}}$ as $\frac{\mathbf{1}}{\mathbf{1}}$ , where p and q are integers and q ≠ 0.
Question 5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.
Answer:
When finding the decimal expansion of a rational number $\frac{p}{q}$ (where $p, q$ are integers, $q \neq 0$), the maximum number of digits in the repeating block of the decimal expansion is determined by the denominator $q$.
Specifically, the length of the repeating block (the period) must be less than the denominator $q$. This is because when performing the long division $p \div q$, the only possible remainders are $0, 1, 2, ..., q-1$. If the remainder becomes 0, the division terminates. If the remainder is never 0, it must eventually repeat one of the $q-1$ possible non-zero values. Once a remainder repeats, the sequence of quotients (digits in the decimal expansion) also starts repeating.
In the case of $\frac{1}{17}$, the denominator is $q = 17$. Therefore, the maximum number of digits in the repeating block is $q-1 = 17 - 1 = 16$.
Now, we perform the long division $1 \div 17$ to check the actual length of the repeating block:
$$\begin{array}{r} 0.0588235294117647\dots\phantom{)} \\ % Full repeating cycle quotient 17{\overline{\smash{\big)}\,1.0000000000000000\phantom{)}}} \\ % Divisor 17, Dividend 1. (16 zeros) % 100 / 17 = 5 rem 15 \underline{-\phantom{(..)}8\;5\phantom{00000000000000)}} \\ \phantom{(...)}1\;5\;0\phantom{0000000000000)} \\ % Rem 15, bring down 0 -> 150 % 150 / 17 = 8 rem 14 \underline{-\phantom{(...)}1\;3\;6\phantom{0000000000000)}} \\ \phantom{(....)}1\;4\;0\phantom{000000000000)} \\ % Rem 14, bring down 0 -> 140 % 140 / 17 = 8 rem 4 \underline{-\phantom{(....)}1\;3\;6\phantom{000000000000)}} \\ \phantom{(.....)}4\;0\phantom{00000000000)} \\ % Rem 4, bring down 0 -> 40 % 40 / 17 = 2 rem 6 \underline{-\phantom{(.....)}3\;4\phantom{00000000000)}} \\ \phantom{(......)}6\;0\phantom{0000000000)} \\ % Rem 6, bring down 0 -> 60 % 60 / 17 = 3 rem 9 \underline{-\phantom{(......)}5\;1\phantom{0000000000)}} \\ \phantom{(.......)}9\;0\phantom{000000000)} \\ % Rem 9, bring down 0 -> 90 % 90 / 17 = 5 rem 5 \underline{-\phantom{(.......)}8\;5\phantom{000000000)}} \\ \phantom{(........)}5\;0\phantom{00000000)} \\ % Rem 5, bring down 0 -> 50 % 50 / 17 = 2 rem 16 \underline{-\phantom{(........)}3\;4\phantom{00000000)}} \\ \phantom{(.........)}16\;0\phantom{0000000)} \\ % Rem 16, bring down 0 -> 160 % 160 / 17 = 9 rem 7 \underline{-\phantom{(.........)}15\;3\phantom{0000000)}} \\ \phantom{(..........)}7\;0\phantom{000000)} \\ % Rem 7, bring down 0 -> 70 % 70 / 17 = 4 rem 2 \underline{-\phantom{(..........)}6\;8\phantom{000000)}} \\ \phantom{(...........)}2\;0\phantom{00000)} \\ % Rem 2, bring down 0 -> 20 % 20 / 17 = 1 rem 3 \underline{-\phantom{(...........)}1\;7\phantom{00000)}} \\ \phantom{(............)}3\;0\phantom{0000)} \\ % Rem 3, bring down 0 -> 30 % 30 / 17 = 1 rem 13 \underline{-\phantom{(............)}1\;7\phantom{0000)}} \\ \phantom{(.............)}13\;0\phantom{000)} \\ % Rem 13, bring down 0 -> 130 % 130 / 17 = 7 rem 11 \underline{-\phantom{(.............)}11\;9\phantom{000)}} \\ \phantom{(..............)}11\;0\phantom{00)} \\ % Rem 11, bring down 0 -> 110 % 110 / 17 = 6 rem 8 \underline{-\phantom{(..............)}10\;2\phantom{00)}} \\ \phantom{(...............)}8\;0\phantom{0)} \\ % Rem 8, bring down 0 -> 80 % 80 / 17 = 4 rem 12 \underline{-\phantom{(...............)}6\;8\phantom{0)}} \\ \phantom{(................)}12\;0\phantom{)} \\ % Rem 12, bring down 0 -> 120 % 120 / 17 = 7 rem 1 \underline{-\phantom{(................)}11\;7\phantom{)}} \\ \underline{\phantom{(.................)}1\phantom{)}} % Remainder 1. Cycle complete. \end{array}$$
The sequence of remainders obtained during the division is $10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12, 1$. When the remainder $1$ reappears (the initial value we started dividing), the sequence of digits in the quotient starts repeating.
$ \therefore \ \frac{1}{17} = 0.\overline{0588235294117647} $
Counting the digits in the block $0588235294117647$, we find there are indeed 16 digits in the repeating block.
Thus, the maximum possible number of digits in the repeating block was 16, and the actual number of digits in the repeating block is 16.
Question 6. Look at several examples of rational numbers in the form $\frac{p}{q}$ (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Answer:
We consider rational numbers of the form $\frac{p}{q}$, where $p$ and $q$ are integers, $q \neq 0$, and $p, q$ have no common factors other than 1 (i.e., the fraction is in its simplest form).
A rational number $\frac{p}{q}$ has a terminating decimal expansion if and only if the prime factorization of the denominator $q$ consists solely of powers of 2 and/or powers of 5. That is, $q$ must be of the form $2^n \cdot 5^m$, where $n$ and $m$ are non-negative integers ($n \ge 0, m \ge 0$).
If the prime factorization of $q$ contains any prime factor other than 2 or 5, then the decimal expansion of $\frac{p}{q}$ will be non-terminating and repeating.
Let us look at some examples of rational numbers with terminating decimal expansions:
-
$\frac{3}{2} = 1.5$
Here, $q=2$. The prime factorization is $2 = 2^1 = 2^1 \cdot 5^0$. This fits the form $2^n \cdot 5^m$. -
$\frac{1}{5} = 0.2$
Here, $q=5$. The prime factorization is $5 = 5^1 = 2^0 \cdot 5^1$. This fits the form $2^n \cdot 5^m$. -
$\frac{7}{8} = 0.875$
Here, $q=8$. The prime factorization is $8 = 2 \times 2 \times 2 = 2^3 = 2^3 \cdot 5^0$. This fits the form $2^n \cdot 5^m$. -
$\frac{8}{125} = 0.064$
Here, $q=125$. The prime factorization is $125 = 5 \times 5 \times 5 = 5^3 = 2^0 \cdot 5^3$. This fits the form $2^n \cdot 5^m$. -
$\frac{13}{20} = 0.65$
Here, $q=20$. The prime factorization is $20 = 2 \times 2 \times 5 = 2^2 \cdot 5^1$. This fits the form $2^n \cdot 5^m$. -
$\frac{17}{16} = 1.0625$
Here, $q=16$. The prime factorization is $16 = 2 \times 2 \times 2 \times 2 = 2^4 = 2^4 \cdot 5^0$. This fits the form $2^n \cdot 5^m$. -
$\frac{36}{100} = 0.36$ (Simplify first: $\frac{36}{100} = \frac{9}{25}$)
Here, $q=25$. The prime factorization is $25 = 5 \times 5 = 5^2 = 2^0 \cdot 5^2$. This fits the form $2^n \cdot 5^m$. -
$\frac{329}{400} = 0.8225$
Here, $q=400$. The prime factorization is $400 = 4 \times 100 = 2^2 \times 10^2 = 2^2 \times (2 \times 5)^2 = 2^2 \times 2^2 \times 5^2 = 2^4 \cdot 5^2$. This fits the form $2^n \cdot 5^m$.
In all these examples where the decimal expansion terminates, the denominator $q$ (after simplifying the fraction) has only prime factors of 2 and/or 5.
Therefore, the property that $q$ must satisfy for $\frac{p}{q}$ (in simplest form) to have a terminating decimal expansion is that the prime factorization of $q$ must be of the form $2^n \cdot 5^m$, where $n$ and $m$ are non-negative integers.
Question 7. Write three numbers whose decimal expansions are non-terminating non-recurring.
Answer:
Numbers whose decimal expansions are non-terminating and non-recurring are known as irrational numbers.
A common way to find such numbers is to take the square root of any positive integer which is not a perfect square. The resulting decimal expansion will be non-terminating and non-recurring.
So, the examples of decimal expansions which are non-terminating and non-recurring are as follows:-
$$\sqrt2 = 1.414213562 …$$
$$\sqrt3 = 1.732050808 …$$
$$\sqrt5 = 2.23606797 …$$
Other examples include famous mathematical constants like $\pi = 3.14159...$ or numbers constructed to have non-repeating patterns like $0.12112111211112...$
Question 8. Find three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$ .
Answer:
To find different irrational numbers between $\frac{5}{7}$ and $\frac{9}{11}$, we first find the decimal expansions of $\frac{5}{7}$ and $\frac{9}{11}$.
We perform the long divisions:
$\begin{array}{r} 0.714285\dots\phantom{)} \\ % Quotient showing repeating cycle 7{\overline{\smash{\big)}\,5.000000\phantom{)}}} \\ % Divisor 7, Dividend 5.000000 \underline{-\phantom{(.}4\;9\phantom{00000)}} \\ % 7 * 7 = 49. Align under 5.0 \phantom{(..)}1\;0\phantom{0000)} \\ % Remainder 1, bring down 0 -> 10 \underline{-\phantom{(..)}\;7\phantom{0000)}} \\ % 7 * 1 = 7. Align under 10 \phantom{(...)}3\;0\phantom{000)} \\ % Remainder 3, bring down 0 -> 30 \underline{-\phantom{(...)}2\;8\phantom{000)}} \\ % 7 * 4 = 28. Align under 30 \phantom{(....)}2\;0\phantom{00)} \\ % Remainder 2, bring down 0 -> 20 \underline{-\phantom{(....)}1\;4\phantom{00)}} \\ % 7 * 2 = 14. Align under 20 \phantom{(.....)}6\;0\phantom{0)} \\ % Remainder 6, bring down 0 -> 60 \underline{-\phantom{(.....)}5\;6\phantom{0)}} \\ % 7 * 8 = 56. Align under 60 \phantom{(......)}4\;0\phantom{)} \\ % Remainder 4, bring down 0 -> 40 \underline{-\phantom{(......)}3\;5\phantom{)}} \\ % 7 * 5 = 35. Align under 40 \underline{\phantom{(.......)}5\phantom{)}} % Remainder 5. Cycle complete. \end{array}$
$\begin{array}{r} 0.81\dots\phantom{)} \\ % Quotient showing repeating cycle 11{\overline{\smash{\big)}\,9.00\phantom{)}}} \\ % Divisor 11, Dividend 9.00 \underline{-\phantom{(.}8\;8\phantom{0)}} \\ % 11 * 8 = 88. Align under 9.0 \phantom{(..)}2\;0\phantom{)} \\ % Remainder 2, bring down 0 -> 20 \underline{-\phantom{(..)}1\;1\phantom{)}} \\ % 11 * 1 = 11. Align under 20 \underline{\phantom{(...)}9\phantom{)}} % Remainder 9. Cycle complete. \end{array}$
$\therefore \ \frac{5}{7} = 0.714285714285... = 0.\overline{714285}$
$\therefore \ \frac{9}{11} = 0.818181... = 0.\overline{81}$
We need to find irrational numbers $x$ such that $0.\overline{714285} < x < 0.\overline{81}$. An irrational number has a decimal expansion that is non-terminating and non-recurring (non-repeating).
We can construct such numbers by choosing a starting sequence between $0.714...$ and $0.818...$ and then ensuring the rest of the digits do not repeat in a block.
Here are three different irrational numbers between $\frac{5}{7}$ and $\frac{9}{11}$:
(i) $0.750750075000750000...$
(Starts with $0.75$, which is between $0.714...$ and $0.818...$. The pattern of adding more zeros ensures it's non-repeating.)
(ii) $0.781781178111781111...$
(Starts with $0.781$, which is between the bounds. The pattern of adding more ones ensures it's non-repeating.)
(iii) $0.801001000100001...$
(Starts with $0.801$, which is between the bounds. The pattern of adding more zeros ensures it's non-repeating.)
Question 9. Classify the following numbers as rational or irrational :
(i) $\sqrt{23}$
(ii) $\sqrt{225}$
(iii) 0.3796
(iv) 7.478478…
(v) 1.101001000100001...
Answer:
(i) Here, we have $\sqrt{23}$
Since 23 is not a perfect square, its square root, $\sqrt{23}$, cannot be expressed as a ratio of two integers. The decimal expansion of the square root of a non-perfect square is non-terminating and non-recurring.
Therefore, $\sqrt{23}$ is an irrational number.
(ii) Here, we have $\sqrt{225}$
We check if 225 is a perfect square. Since $15 \times 15 = 15^2 = 225$, 225 is a perfect square.
Thus, $\sqrt{225} = 15$. Since 15 can be written as the ratio $\frac{15}{1}$, it is a rational number.
Therefore, $\sqrt{225}$ is a rational number.
(iii) Here, we have $0.3796$
The number $0.3796$ has a terminating decimal expansion (it ends after the digit 6). Any number with a terminating decimal expansion can be written as a fraction with a denominator that is a power of 10 (e.g., $0.3796 = \frac{3796}{10000}$).
Therefore, $0.3796$ is a rational number.
(iv) Here, we have $7.478478\dots$
The notation $\dots$ indicates that the pattern continues. We can see the block of digits '478' repeating. So, the number is $7.\overline{478}$.
Since $7.\overline{478}$ is a non-terminating but recurring (repeating) decimal number, it can be expressed as a ratio of two integers.
Therefore, $7.478478\dots$ is a rational number.
(v) Here, we have $1.101001000100001...$
The decimal expansion is $1.101001000100001\dots$. The pattern involves adding an extra '0' between the '1's each time ($1 \underline{0} 1 \underline{00} 1 \underline{000} 1 \underline{0000} 1 \dots$). This pattern ensures that the decimal expansion is non-terminating and does not have a repeating block of digits (non-recurring).
Therefore, $1.101001000100001...$ is an irrational number.
Example 11 (Before Exercise 1.4)
Example 11: Visualize the representation of $5.3\overline{7}$ on the number line upto 5 decimal places, that is, up to 5.37777.
Answer:
Solution:
We need to visualize the number $5.3\overline{7}$ up to 5 decimal places, which is $5.37777$. We will use the process of successive magnification to locate this number on the number line.
Step 1: Locate the number between two integers.
The number $5.37777$ is greater than 5 and less than 6. So, it lies somewhere between 5 and 6 on the number line. We divide the interval between 5 and 6 into 10 equal parts. We can see that $5.37777$ lies between 5.3 and 5.4.
Step 2: Magnify the interval [5.3, 5.4].
Now we focus on the interval between 5.3 and 5.4 and divide it into 10 equal parts. These parts will be 5.31, 5.32, 5.33, and so on. The number $5.37777$ is greater than 5.37 and less than 5.38. So, it lies in the interval [5.37, 5.38].
Step 3: Magnify the interval [5.37, 5.38].
Next, we magnify the interval between 5.37 and 5.38 and divide it into 10 equal parts. These parts will be 5.371, 5.372, etc. The number $5.37777$ is greater than 5.377 and less than 5.378. So, it lies in the interval [5.377, 5.378].
Step 4: Magnify the interval [5.377, 5.378].
We magnify the interval between 5.377 and 5.378 and divide it into 10 equal parts. The number $5.37777$ is greater than 5.3777 and less than 5.3778. So, it lies in the interval [5.3777, 5.3778].
Step 5: Magnify the interval [5.3777, 5.3778] and locate the point.
Finally, we magnify the interval between 5.3777 and 5.3778 and divide it into 10 equal parts. The markings will be 5.37771, 5.37772, ..., 5.37777, and so on. We can now precisely locate the point representing 5.37777.
This process of successive magnification allows us to visualize the position of a real number with a non-terminating decimal expansion on the number line to any desired level of accuracy.
Exercise 1.4
Question 1. Visualise 3.765 on the number line, using successive magnification.
Answer:
Solution:
We will locate the number 3.765 on the number line using the method of successive magnification.
Step 1: The number 3.765 lies between the integers 3 and 4. We start by dividing the interval [3, 4] on the number line into 10 equal parts. We observe that 3.765 lies between 3.7 and 3.8.
Step 2: Now, we magnify the interval [3.7, 3.8] and divide it into 10 equal parts. The markings will be 3.71, 3.72, 3.73, and so on. The number 3.765 lies between 3.76 and 3.77.
Step 3: Next, we magnify the interval [3.76, 3.77] and divide it into 10 equal parts. The markings will be 3.761, 3.762, ..., 3.765, ..., 3.769. We can now clearly locate the point 3.765 on this magnified number line.
By following these steps of successive magnification, we have successfully visualized the position of 3.765 on the number line.
Question 2. Visualise $4.\overline{26}$ on the number line, up to 4 decimal places.
Answer:
Solution:
We need to visualize the number $4.\overline{26}$ on the number line up to 4 decimal places. The number can be written as 4.2626.
We will use the method of successive magnification.
Step 1: The number 4.2626 lies between the integers 4 and 5. We divide the interval [4, 5] into 10 equal parts. We can see that 4.2626 lies between 4.2 and 4.3.
Step 2: We magnify the interval [4.2, 4.3] and divide it into 10 equal parts. The markings will be 4.21, 4.22, etc. The number 4.2626 lies between 4.26 and 4.27.
Step 3: Now, we magnify the interval [4.26, 4.27] and divide it into 10 equal parts. The markings will be 4.261, 4.262, etc. The number 4.2626 lies between 4.262 and 4.263.
Step 4: Finally, we magnify the interval [4.262, 4.263] and divide it into 10 equal parts. The markings will be 4.2621, 4.2622, ..., 4.2626, etc. We can now pinpoint the exact location of 4.2626 on this magnified number line.
Through this process of successive magnification, we have visualized the position of $4.\overline{26}$ up to four decimal places on the number line.
Example 12 & 20 (Before Exercise 1.5)
Example 12: Check whether $7\sqrt{5}$ , $\frac{7}{\sqrt{5}}$ , $\sqrt{2} + 21$, $π − 2$ are irrational numbers or not.
Answer:
We know the approximate values of the irrational numbers involved:
$$\sqrt5 = 2.236 ...,$$
$$\sqrt2 = 1.4142 ...,$$
$$π = 3.1415…$$
An irrational number is a number whose decimal expansion is non-terminating and non-recurring.
Therefore, $\sqrt{5}$, $\sqrt{2}$, and $\pi$ are known irrational numbers.
We use the following properties regarding operations between rational and irrational numbers:
- The sum or difference of a rational number and an irrational number is irrational.
- The product or quotient of a non-zero rational number and an irrational number is irrational.
Now let's check each number:
$$7\sqrt{5}$$
This is the product of a non-zero rational number (7) and an irrational number ($\sqrt{5}$). According to the properties, the result is irrational.
($7\sqrt{5} = 7 \times 2.236... = 15.652...$, which is non-terminating non-recurring).
$$\frac{7}{\sqrt{5}}$$
This is the quotient of a non-zero rational number (7) and an irrational number ($\sqrt{5}$). This can also be written as $\frac{7\sqrt{5}}{5} = \frac{7}{5}\sqrt{5}$. This is the product of a non-zero rational ($\frac{7}{5}$) and an irrational ($\sqrt{5}$). According to the properties, the result is irrational.
($\frac{7}{\sqrt{5}} = \frac{7}{2.236...} \approx 3.130...$, which is non-terminating non-recurring).
$$\sqrt{2} + 21$$
This is the sum of an irrational number ($\sqrt{2}$) and a rational number (21). According to the properties, the result is irrational.
($\sqrt{2} + 21 = 1.4142... + 21 = 22.4142...$, which is non-terminating non-recurring).
$$\pi - 2$$
This is the difference between an irrational number ($\pi$) and a rational number (2). According to the properties, the result is irrational.
($\pi - 2 = 3.1415... - 2 = 1.1415...$, which is non-terminating non-recurring).
Therefore, all the given numbers ($7\sqrt{5}$, $\frac{7}{\sqrt{5}}$, $\sqrt{2} + 21$, $\pi - 2$) are irrational numbers, as their decimal expansions are non-terminating and non-recurring.
Example 13: Add $2\sqrt{2} + 5\sqrt{3}$ and $\sqrt{2} − 3\sqrt{3}$ .
Answer:
We have, $\left(2\sqrt2+5\sqrt3\right)+\left(\sqrt2-3\sqrt3\right)$
$= \left(2\sqrt2+\sqrt2\right)+\left(5\sqrt3-3\sqrt3\right)$
$= \sqrt2 (2 + 1) + \sqrt3 (5 - 3)$
$= 3\sqrt2+2\sqrt3$
Example 14: Multiply $6\sqrt{5}$ by $2\sqrt{5}$ .
Answer:
We have, $6\sqrt5\times2\sqrt5$
$= 6\times2\times\sqrt5\times\sqrt5$
$= 12\times\left(\sqrt5\right)^2$
$= 12\times 5$
$= 60$
Example 15: Divide $8\sqrt{15}$ by $2\sqrt{3}$ .
Answer:
We have, $8\sqrt{15}\div2\sqrt3$
This can be written as a fraction:
$\frac{8\sqrt{15}}{2\sqrt{3}}$
$= \frac{\bcancel2\ \times\ 4\ \times\ \bcancel{\sqrt3}\ \times\ \sqrt5}{\bcancel2\ \times\ \bcancel{\sqrt3}}$
$= 4\ \times\ \sqrt5$
$= 4\sqrt5$
Example 16: Simplify the following expressions:
(i) $(5 + \sqrt{7}) (2 + \sqrt{5})$
(ii) $(5 + \sqrt{5})(5 - \sqrt{5})$
(iii) $(\sqrt{3} + \sqrt{7}^2$
(iv) $(\sqrt{11} - \sqrt{7})(\sqrt{11} + \sqrt{7})$
Answer:
(i) Here, we have $\left(\mathbf{5}+\sqrt{\mathbf{7}}\right)\left(\mathbf{2}+\sqrt{\mathbf{5}}\right)$
$= 5\left(2+\sqrt5\right)+\sqrt7\left(2+\sqrt5\right)$
$= 10+5\sqrt5\ +2\sqrt7\ +\sqrt7\times\sqrt5$
$= 10+5\sqrt5\ +2\sqrt7\ +\sqrt{35}$
(ii) Here, we have $\left(\mathbf{5}+\sqrt{\mathbf{5}}\right)\left(\mathbf{5}-\sqrt{\mathbf{5}}\right)$
$= \left(5\right)^2-\left(\sqrt5\right)^2$
$[⸪ (a + b)(a - b) = a^2 - b^2 ]$
$= 25-5$
$= 20$
(iii) Here, we have $\left(\sqrt{\mathbf{3}}+\sqrt{\mathbf{7}}\right)^\mathbf{2}$
$= \left(\sqrt3\right)^2+2\times\sqrt3\times\sqrt7+\left(\sqrt7\right)^2$
$[⸪ (a + b)^2 $$ = a^2 + 2ab + b^2 ]$
$= 3+2\sqrt{21}+7$
$= 10+2\sqrt{21}$
(iv) Here, we have $\left(\sqrt{\mathbf{11}}-\sqrt{\mathbf{7}}\right)\left(\sqrt{\mathbf{11}}+\sqrt{\mathbf{7}}\right)$
$= \left(\sqrt{11}\right)^2-\left(\sqrt7\right)^2$
$[⸪ (a + b)(a - b) = a^2 - b^2 ]$
$= 11-7$
$= 4$
Example 17: Rationalise the denominator of $\frac{1}{\sqrt{2}}$ .
Answer:
To rationalise the denominator means to eliminate the radical (in this case, the square root) from the denominator.
We can multiply the fraction $\frac{1}{\sqrt{2}}$ by $\frac{\sqrt{2}}{\sqrt{2}}$. This is equivalent to multiplying by $1$, so the value of the expression does not change.
$\frac{1}{\sqrt{2}}$
$= \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$
$= \frac{1 \ \times \ \sqrt{2}}{\sqrt{2} \ \times \ \sqrt{2}}$
Since $\sqrt{2} \times \sqrt{2} = (\sqrt{2})^2 = 2$:
$= \frac{\sqrt{2}}{2}$
The denominator is now $2$, which is a rational number. Thus, the expression is rationalised.
Example 18: Rationalise the denominator of $\frac{1}{2 \;+\; \sqrt{3}}$ .
Answer:
To rationalise the denominator $2 + \sqrt{3}$, we need to multiply both the numerator and the denominator by its conjugate.
The conjugate of $2 + \sqrt{3}$ is $2 - \sqrt{3}$.
We use the identity $(a + b)(a - b) = a^2 - b^2$ to simplify the denominator after multiplication.
Multiply the expression by $\frac{2 - \sqrt{3}}{2 - \sqrt{3}}$:
$\frac{1}{2 + \sqrt{3}}$
$= \frac{1}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}}$
$= \frac{1 \times (2 - \sqrt{3})}{(2 + \sqrt{3})(2 - \sqrt{3})}$
Apply the difference of squares identity to the denominator ($a=2, b=\sqrt{3}$):
$= \frac{2 - \sqrt{3}}{(2)^2 - (\sqrt{3})^2}$
$= \frac{2 - \sqrt{3}}{4 - 3}$
$= \frac{2 - \sqrt{3}}{1}$
$= 2 - \sqrt{3}$
The denominator is now $1$, which is a rational number. Thus, the expression is rationalised.
Example 19: Rationalise the denominator of $\frac{5}{\sqrt{3} \;-\; \sqrt{5}}$ .
Answer:
To rationalise the denominator $\sqrt{3} - \sqrt{5}$, we multiply both the numerator and the denominator by its conjugate, which is $\sqrt{3} + \sqrt{5}$.
We use the identity $(a - b)(a + b) = a^2 - b^2$ to simplify the denominator.
Multiply the expression by $\frac{\sqrt{3} + \sqrt{5}}{\sqrt{3} + \sqrt{5}}$:
$\frac{5}{\sqrt{3} - \sqrt{5}}$
$= \frac{5}{\sqrt{3} - \sqrt{5}} \times \frac{\sqrt{3} + \sqrt{5}}{\sqrt{3} + \sqrt{5}}$
$= \frac{5 (\sqrt{3} + \sqrt{5})}{(\sqrt{3} - \sqrt{5})(\sqrt{3} + \sqrt{5})}$
Apply the difference of squares identity to the denominator ($a=\sqrt{3}, b=\sqrt{5}$):
$= \frac{5(\sqrt{3} + \sqrt{5})}{(\sqrt{3})^2 - (\sqrt{5})^2}$
$= \frac{5(\sqrt{3} + \sqrt{5})}{3 - 5}$
$= \frac{5(\sqrt{3} + \sqrt{5})}{-2}$
It is conventional to write the negative sign in the numerator or in front of the fraction:
$= -\frac{5(\sqrt{3} + \sqrt{5})}{2}$ or $\frac{-5(\sqrt{3} + \sqrt{5})}{2}$
The denominator is now $-2$ (or $2$ if the negative is moved), which is a rational number. Thus, the expression is rationalised.
Example 20: Rationalise the denominator of $\frac{1}{7 \;+\; 3\sqrt{2}}$ .
Answer:
To rationalise the denominator $7 + 3\sqrt{2}$, we multiply both the numerator and the denominator by its conjugate, which is $7 - 3\sqrt{2}$.
We will use the identity $(a + b)(a - b) = a^2 - b^2$ to simplify the denominator.
Multiply the expression by $\frac{7 - 3\sqrt{2}}{7 - 3\sqrt{2}}$:
$\frac{1}{7 + 3\sqrt{2}}$
$= \frac{1}{7 + 3\sqrt{2}} \times \frac{7 - 3\sqrt{2}}{7 - 3\sqrt{2}}$
$= \frac{1 \times (7 - 3\sqrt{2})}{(7 + 3\sqrt{2})(7 - 3\sqrt{2})}$
Apply the difference of squares identity to the denominator ($a=7, b=3\sqrt{2}$):
$= \frac{7 - 3\sqrt{2}}{(7)^2 - (3\sqrt{2})^2}$
Simplify the denominator. Note that $(3\sqrt{2})^2 = 3^2 \times (\sqrt{2})^2 = 9 \times 2 = 18$.
$= \frac{7 - 3\sqrt{2}}{49 - 18}$
$= \frac{7 - 3\sqrt{2}}{31}$
The denominator is now $31$, which is a rational number. Thus, the expression is rationalised.
Exercise 1.5
Question 1. Classify the following numbers as rational or irrational:
(i) $2 − \sqrt{5}$
(ii) $(3 + \sqrt{23}) − \sqrt{23}$
(iii) $\frac{2\sqrt{7}}{7\sqrt{7}}$
(iv) $\frac{1}{\sqrt{2}}$
(v) $2π$
Answer:
Key Properties:
- A number is rational if it can be expressed as $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. Rational numbers have decimal expansions that are either terminating or non-terminating but repeating.
- A number is irrational if it cannot be expressed as $\frac{p}{q}$. Irrational numbers have decimal expansions that are non-terminating and non-repeating.
- The sum, difference, product, or quotient of a non-zero rational number and an irrational number is always irrational.
- Operations between two irrational numbers can result in either a rational or an irrational number (e.g., $\sqrt{2} \times \sqrt{2} = 2$ [rational], but $\sqrt{2} + \sqrt{3}$ [irrational]).
- $\sqrt{n}$ is irrational if $n$ is a positive integer that is not a perfect square. $\pi$ is a known irrational number.
(i) Here, we have $2 - \sqrt{5}$
This is the difference between a rational number (2) and an irrational number ($\sqrt{5}$, since 5 is not a perfect square).
Therefore, $2 - \sqrt{5}$ is irrational.
(ii) Here, we have $(3 + \sqrt{23}) - \sqrt{23}$
First, simplify the expression:
$= 3 + \sqrt{23} - \sqrt{23}$
$= 3$
The result is 3, which can be expressed as $\frac{3}{1}$.
Therefore, $(3 + \sqrt{23}) - \sqrt{23}$ is a rational number.
(iii) Here, we have $\frac{2\sqrt{7}}{7\sqrt{7}}$
Simplify the expression by cancelling the common factor $\sqrt{7}$ (assuming $\sqrt{7} \neq 0$, which is true):
$= \frac{2 \times \cancel{\sqrt{7}}}{7 \times \cancel{\sqrt{7}}}$
$= \frac{2}{7}$
The result is $\frac{2}{7}$, which is a ratio of two integers with a non-zero denominator.
Therefore, $\frac{2\sqrt{7}}{7\sqrt{7}}$ is a rational number.
(iv) Here, we have $\frac{1}{\sqrt{2}}$
This is the quotient of a rational number (1) and an irrational number ($\sqrt{2}$, since 2 is not a perfect square). Rationalising gives $\frac{\sqrt{2}}{2}$, which is still irrational (product of rational $\frac{1}{2}$ and irrational $\sqrt{2}$).
Therefore, $\frac{1}{\sqrt{2}}$ is irrational.
(v) Here, we have $2\pi$
This is the product of a non-zero rational number (2) and a known irrational number ($\pi$).
Therefore, $2\pi$ is irrational.
Question 2. Simplify each of the following expressions:
(i) $(3 + \sqrt{3})(2 + \sqrt{2})$
(ii) $(3 + \sqrt{3})(3 − \sqrt{3})$
(iii) $(\sqrt{5} + \sqrt{2})^2$
(iv) $(\sqrt{5}- \sqrt{2})(\sqrt{5} + \sqrt{2})$
Answer:
(i) Here, we have $(3 + \sqrt3)(2 + \sqrt2)$
$= 3(2 + \sqrt{2}) + \sqrt{3}(2 + \sqrt{2})$
$= (3 \times 2) + (3 \times \sqrt{2}) + (\sqrt{3} \times 2) + (\sqrt{3} \times \sqrt{2})$
$= 6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{3 \times 2}$
$= 6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{6}$
Thus, $(3 + \sqrt{3})(2 + \sqrt{2}) = 6 + 3\sqrt{2} + 2\sqrt{3} + \sqrt{6}$
(ii) Here, we have $(3 + \sqrt3)(3 − \sqrt3)$
$= 3^2 – \left(\sqrt3\right)^2$
$[⸪(a + b)(a - b) = a^2 - b^2]$
$= 9 \ – \ 3$
$= 6$
Thus, $(3 + \sqrt3)(3 – \sqrt3) = 6$
(iii) Here, we have $(\sqrt5 + \sqrt2)^2$
$= \left(\sqrt5\right)^2 + \left(\sqrt2\right)^2 + 2(\sqrt5)(\sqrt2)$
$[⸪(a + b)^2 $$ = a^2 - 2ab + b^2]$
$= 5 + 2 + 2\sqrt{10} $
$= 7 + 2\sqrt{10}$
Thus, $(\sqrt5 + \sqrt2)^2 = 7 + 2\sqrt{10}$
(iv) Here, we have $(\sqrt5 - \sqrt2)(\sqrt5 + \sqrt2)$
$= \left(\sqrt5\right)^2 – \left(\sqrt2\right)^2$
$[⸪(a + b)(a - b) = a^2 - b^2]$
$= 5 – 2$
$= 3$
Thus, $(\sqrt5 – \sqrt2)(\sqrt5 + \sqrt2) = 3$
Question 3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = $\frac{c}{d}$ . This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Answer:
This is an excellent question that touches on the difference between a mathematical definition and a real-world measurement. There is no actual contradiction, and here is how to resolve it.
The core of the issue lies in the definition of a rational number. A rational number is a number that can be expressed as a fraction $\frac{p}{q}$, where both p and q are integers and $q \neq 0$.
The formula for pi, $\pi = \frac{c}{d}$, looks like it fits this form. However, the key point is this:
For any given circle, it is mathematically impossible for both its circumference (c) and its diameter (d) to be rational numbers (including integers) at the same time.
Let's break this down:
1. The Mathematical Viewpoint:
- If you have a circle with a rational diameter (for example, a diameter of 1 unit), then its circumference must be irrational.
$c = \pi \times d = \pi \times 1 = \pi$. Since $\pi$ is irrational, the circumference 'c' is irrational. - Conversely, if you could somehow create a circle with a rational circumference (for example, a circumference of 6 units), then its diameter must be irrational.
$d = \frac{c}{\pi} = \frac{6}{\pi}$. Since $\pi$ is irrational, the diameter 'd' is also irrational.
Because at least one of the values (either c or d) must be irrational, their ratio $\frac{c}{d}$ does not fit the definition of a rational number, which requires a ratio of two integers.
2. The Practical Measurement Viewpoint:
When we measure the circumference and diameter of a real-world object (like a can lid) with a ruler or a piece of string, we are only getting an approximation. Our measuring tools have limited precision.
- We might measure the diameter as 7 cm and the circumference as approximately 22 cm.
- This gives us the fraction $\frac{22}{7}$. This fraction is a rational approximation of $\pi$, but it is not the exact value of $\pi$.
- No matter how precise our instruments are, any measurement we take will result in a terminating decimal (e.g., 7.01 cm), which is a rational number. This means our calculated ratio will always be a rational number that is close to, but not exactly, $\pi$.
Conclusion:
The "contradiction" is resolved when we understand that the definition of a rational number requires a ratio of two integers. The ratio $\frac{c}{d}$ is not a ratio of two integers. When we use measurements, we are only creating rational approximations of $\pi$, not expressing its true value. Therefore, the definition $\pi = \frac{c}{d}$ does not contradict the fact that $\pi$ is irrational.
Question 4. Represent $\sqrt{9.3}$ on the number line.
Answer:
Solution:
To represent $\sqrt{9.3}$ on the number line, we will use a geometric construction method. This method can be used to find the square root of any positive real number.
Steps of Construction:
- Draw a horizontal line and mark a starting point A.
- From point A, draw a line segment AB of length 9.3 units.
- From point B, extend the line to a point C such that the length of BC is 1 unit. The total length of AC is now $9.3 + 1 = 10.3$ units.
- Find the midpoint of the line segment AC. Let's call this midpoint O. The midpoint is at a distance of $\frac{10.3}{2} = 5.15$ units from A.
- With O as the center and OA (or OC) as the radius, draw a semicircle that starts at A and ends at C.
- From point B, draw a line perpendicular to AC that intersects the semicircle at a point D.
- The length of the line segment BD is exactly $\sqrt{9.3}$.
- To transfer this length onto the number line, consider the point B as the origin (0). Place the pointed end of a compass at B and the pencil end at D.
- Draw an arc that intersects the horizontal line at a point E.
- The point E on the number line represents the number $\sqrt{9.3}$.
Proof of Construction:
Let's prove why the length of the segment BD is equal to $\sqrt{9.3}$.
Consider the right-angled triangle $\triangle OBD$ formed during the construction.
The hypotenuse is OD, which is the radius of the semicircle.
Radius $= OD = OA = OC = \frac{AC}{2} = \frac{9.3 + 1}{2} = \frac{10.3}{2} = 5.15$ units
One leg of the triangle is OB. We can find its length:
Length of $OB = OC - BC = 5.15 - 1 = 4.15$ units
The other leg is BD, whose length we want to find.
By the Pythagorean theorem in $\triangle OBD$:
$OD^2 = OB^2 + BD^2$
$BD^2 = OD^2 - OB^2$
Substituting the values we found:
$BD^2 = (5.15)^2 - (4.15)^2$
Using the algebraic identity $a^2 - b^2 = (a+b)(a-b)$:
$BD^2 = (5.15 + 4.15)(5.15 - 4.15)$
$BD^2 = (9.30)(1.00)$
$BD^2 = 9.3$
$BD = \sqrt{9.3}$
Thus, the length of the line segment BD is indeed $\sqrt{9.3}$. By transferring this length to the number line, the point E correctly represents $\sqrt{9.3}$.
Question 5. Rationalise the denominators of the following:
(i) $\frac{1}{\sqrt{7}}$
(ii) $\frac{1}{\sqrt{7} \;-\; \sqrt{6}}$
(iii) $\frac{1}{\sqrt{5} \;+\; \sqrt{2}}$
(iv) $\frac{1}{\sqrt{7} \;-\; 2}$
Answer:
(i) Here, we have $\frac{1}{\sqrt{7}}$
To rationalise the denominator, we multiply the numerator and denominator by $\sqrt{7}$ (which is equivalent to multiplying by $\frac{\sqrt{7}}{\sqrt{7}} = 1$).
$\frac{1}{\sqrt{7}}$
$= \frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}$
$= \frac{1 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}}$
$= \frac{\sqrt{7}}{(\sqrt{7})^2}$
$= \frac{\sqrt{7}}{7}$
(ii) Here, we have $\frac{1}{\sqrt{7} - \sqrt{6}}$
To rationalise the denominator, we multiply the numerator and denominator by the conjugate of $\sqrt{7} - \sqrt{6}$, which is $\sqrt{7} + \sqrt{6}$. We use the identity $(a - b)(a + b) = a^2 - b^2$.
$\frac{1}{\sqrt{7} - \sqrt{6}}$
$= \frac{1}{\sqrt{7} - \sqrt{6}} \times \frac{\sqrt{7} + \sqrt{6}}{\sqrt{7} + \sqrt{6}}$
$= \frac{1 \times (\sqrt{7} + \sqrt{6})}{(\sqrt{7} - \sqrt{6})(\sqrt{7} + \sqrt{6})}$
$= \frac{\sqrt{7} + \sqrt{6}}{(\sqrt{7})^2 - (\sqrt{6})^2}$
$= \frac{\sqrt{7} + \sqrt{6}}{7 - 6}$
$= \frac{\sqrt{7} + \sqrt{6}}{1}$
$= \sqrt{7} + \sqrt{6}$
(iii) Here, we have $\frac{1}{\sqrt{5} + \sqrt{2}}$
To rationalise the denominator, we multiply the numerator and denominator by the conjugate of $\sqrt{5} + \sqrt{2}$, which is $\sqrt{5} - \sqrt{2}$. We use the identity $(a + b)(a - b) = a^2 - b^2$.
$\frac{1}{\sqrt{5} + \sqrt{2}}$
$= \frac{1}{\sqrt{5} + \sqrt{2}} \times \frac{\sqrt{5} - \sqrt{2}}{\sqrt{5} - \sqrt{2}}$
$= \frac{1 \times (\sqrt{5} - \sqrt{2})}{(\sqrt{5} + \sqrt{2})(\sqrt{5} - \sqrt{2})}$
$= \frac{\sqrt{5} - \sqrt{2}}{(\sqrt{5})^2 - (\sqrt{2})^2}$
$= \frac{\sqrt{5} - \sqrt{2}}{5 - 2}$
$= \frac{\sqrt{5} - \sqrt{2}}{3}$
(iv) Here, we have $\frac{1}{\sqrt{7} - 2}$
To rationalise the denominator, we multiply the numerator and denominator by the conjugate of $\sqrt{7} - 2$, which is $\sqrt{7} + 2$. We use the identity $(a - b)(a + b) = a^2 - b^2$.
$\frac{1}{\sqrt{7} - 2}$
$= \frac{1}{\sqrt{7} - 2} \times \frac{\sqrt{7} + 2}{\sqrt{7} + 2}$
$= \frac{1 \times (\sqrt{7} + 2)}{(\sqrt{7} - 2)(\sqrt{7} + 2)}$
$= \frac{\sqrt{7} + 2}{(\sqrt{7})^2 - (2)^2}$
$= \frac{\sqrt{7} + 2}{7 - 4}$
$= \frac{\sqrt{7} + 2}{3}$
Example 21 (Before Exercise 1.6)
Example 21: Simplify
(i) $2^{\frac{2}{3}}$ . $2^{\frac{1}{3}}$
(ii) $\left( 3^{\frac{1}{5}} \right)^4$
(iii) $\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}$
(iv) $13^{\frac{1}{5}}$ . $17^{\frac{1}{5}}$
Answer:
(i) Here, we have $\mathbf{2}^\frac{\mathbf{2}}{\mathbf{3}}.\mathbf{2}^\frac{\mathbf{1}}{\mathbf{3}}$
$= 2^{\left(\frac{2}{3}\ +\ \frac{1}{3}\right)}$
$[⸪ \ a^m . a^n = a^{m + n} ]$
$= 2^\frac{3}{3}$
$= 2^1$
$= 2$
(ii) Here, we have $\left(\mathbf{3}^\frac{\mathbf{1}}{\mathbf{5}}\right)^\mathbf{4}$
$= 3^{\frac{1}{5}\ \times\ 4}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 3^\frac{4}{5}$
(iii) Here, we have $\frac{\mathbf{7}^\frac{\mathbf{1}}{\mathbf{5}}}{\mathbf{7}^\frac{\mathbf{1}}{\mathbf{3}}}$
$= 7^{\left(\frac{1}{5}\ -\ \frac{1}{3}\right)}$
$[⸪ \ \frac{a^m}{a^n} = a^{m\ -\ n} ]$
$= 7^\frac{3\ -\ 5}{15}$
$= 7^\frac{-2}{15}$
(iv) Here, we have ${\mathbf{13}}^\frac{\mathbf{1}}{\mathbf{5}}.{\mathbf{17}}^\frac{\mathbf{1}}{\mathbf{5}}$
$= \left(13\times17\right)^\frac{1}{5}$
$[⸪ \ a^m.b^m = (ab)^m ]$
$= {221}^\frac{1}{5}$
Exercise 1.6
Question 1. Find:
(i) $64^{\frac{1}{2}}$
(ii) $32^{\frac{1}{5}}$
(iii) $125^{\frac{1}{3}}$
Answer:
(i) Here, we have $\left(\mathbf{64}\right)^\frac{\mathbf{1}}{\mathbf{2}}$
$= \left(8\ \times\ 8\right)^\frac{1}{2}$
$= \left(8^2\right)^\frac{1}{2}$
$= 8^{\frac{1}{2}\ \times\ 2}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 8$
(ii) Here, we have $\left(\mathbf{32}\right)^\frac{\mathbf{1}}{\mathbf{5}}$
$= \left(2\times2\times2\times2\times2\right)^\frac{1}{5}$
$= \left(2^5\right)^\frac{1}{5}$
$= 2^{\frac{1}{5}\ \times\ 5}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 2$
(iii) Here, we have $\left(\mathbf{125}\right)^\frac{\mathbf{1}}{\mathbf{3}}$
$= \left(5\ \times\ 5\times\ 5\right)^\frac{1}{3}$
$= \left(5^3\right)^\frac{1}{3}$
$= 5^{\frac{1}{3}\ \times\ 3}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 5$
Question 2. Find:
(i) $9^{\frac{3}{2}}$
(ii) $32^{\frac{2}{5}}$
(iii) $16^{\frac{3}{4}}$
(iv) $125^{\frac{-1}{3}}$
Answer:
(i) Here, we have $\left(\mathbf{9}\right)^\frac{\mathbf{3}}{\mathbf{2}}$
$= \left(3\ \times\ 3\right)^\frac{3}{2}$
$= \left(3^2\right)^\frac{3}{2}$
$= 3^{\frac{3}{2}\ \times\ 2}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 3^3$
$= 27$
(ii) Here, we have $\left(\mathbf{32}\right)^\frac{\mathbf{2}}{\mathbf{5}}$
$= \left(2\times2\times2\times2\times2\right)^\frac{2}{5}$
$= \left(2^5\right)^\frac{2}{5}$
$= 2^{\frac{2}{5}\ \times\ 5}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 2^2$
$= 4$
(iii) Here, we have $\left(\mathbf{16}\right)^\frac{\mathbf{3}}{\mathbf{4}}$
$= \left(2\times2\times2\times2\right)^\frac{3}{4}$
$= \left(2^4\right)^\frac{3}{4}$
$= 2^{\frac{3}{4}\ \times\ 4}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 2^3$
$= 8$
(iv) Here, we have $\left(\mathbf{125}\right)^{\left(-\ \frac{\mathbf{1}}{\mathbf{3}}\right)}$
$= \left(5\times5\times5\right)^{\left(-\ \frac{1}{3}\right)}$
$= \left(5^3\right)^{\left(-\ \frac{1}{3}\right)}$
$= 5^{\left(-\ \frac{1}{3}\right)\ \times\ 3}$
$[⸪ \ (a^m)^n = a^{m × n} ]$
$= 5^{-1}$
$= \frac{1}{5}$
$\left[ ⸪ \ a^{-n} =\frac{1}{a^n}\right]$
Question 3. Simplify:
(i) $2^{\frac{2}{3}}$ . $2^{\frac{1}{5}}$
(ii) $\left( \frac{1}{3^3}\right)^{7}$
(iii) $\frac{11^{\frac{1}{2}}}{11^{\frac{1}{4}}}$
(iv) $7^{\frac{1}{2}}$ . $8^{\frac{1}{2}}$
Answer:
(i) Here, we have $\mathbf{2}^\frac{\mathbf{2}}{\mathbf{3}}.\mathbf{2}^\frac{\mathbf{1}}{\mathbf{5}}$
$= 2^{\left(\frac{2}{3}\ +\ \frac{1}{5}\right)}$
$[⸪ a^m . a^n = a^{m + n} ]$
$= 2^{\left(\frac{10\ +\ 3}{15}\right)}$
$= 2^\frac{13}{15}$
(ii) Here, we have $\left(\frac{\mathbf{1}}{\mathbf{3}^\mathbf{3}}\right)^\mathbf{7}$
$= \left(3^{-3}\right)^7$
$\left[ ⸪a^{-n} =\frac{1}{a^n}\right]$
$= 3^{-3\times7}$
$[⸪ (a^m)^n = a^{m × n} ]$
$= 3^{-21}$
$= \frac{1}{3^{21}}$
(iii) Here, we have $\frac{{\mathbf{11}}^\frac{\mathbf{1}}{\mathbf{2}}}{{\mathbf{11}}^\frac{\mathbf{1}}{\mathbf{4}}}$
$= {11}^{\left(\frac{1}{2}\ -\ \frac{1}{4}\right)}$
$[⸪ \frac{a^m}{a^n} = a^{m\ -\ n} ]$
$= {11}^\frac{2\ -\ 1}{4}$
$= {11}^\frac{1}{4}$
(iv) Here, we have $\mathbf{7}^\frac{\mathbf{1}}{\mathbf{2}}.\mathbf{8}^\frac{\mathbf{1}}{\mathbf{2}}$
$= \left(7\times8\right)^\frac{1}{2}$
$[⸪ a^m.b^m = (ab)^m ]$
$= {56}^\frac{1}{2}$

