| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 12.1) | Exercise 12.1 | Example 4 to 6 (Before Exercise 12.2) |
| Exercise 12.2 | ||
Chapter 12 Heron's Formula
Welcome to the solutions guide for Chapter 12: Heron’s Formula. This chapter introduces a remarkably elegant and powerful tool in geometry for determining the area of any triangle when only the lengths of its three sides are known. Named after Hero of Alexandria, a Greek engineer and mathematician, Heron's Formula provides a method to calculate area without any reference to the triangle's altitude or height, which is often difficult or impossible to determine directly in practical scenarios. This makes it an invaluable asset in various fields, including surveying, engineering, and design, where side lengths are more readily measurable than perpendicular heights. The solutions presented here focus on elucidating this formula and demonstrating its wide range of applications through carefully worked examples.
The essence of this chapter revolves around understanding and applying Heron's Formula itself. It states that for any triangle with side lengths denoted by $a$, $b$, and $c$, the area can be calculated using the following expression:
$Area = \sqrt{s(s-a)(s-b)(s-c)}$
Here, the crucial variable '$s$' represents the semi-perimeter of the triangle. The semi-perimeter is simply half the total perimeter of the triangle, calculated as:
$s = \frac{a+b+c}{2}$
The solutions meticulously break down the process of applying this formula into a clear sequence of steps, ensuring students can follow along and replicate the calculation accurately:
- First, calculate the semi-perimeter '$s$' using the lengths of the three sides $a, b, c$.
- Next, compute the difference between the semi-perimeter and each side: $(s-a)$, $(s-b)$, and $(s-c)$.
- Substitute the values of $s$, $(s-a)$, $(s-b)$, and $(s-c)$ into Heron's formula: $\sqrt{s(s-a)(s-b)(s-c)}$.
- Calculate the product of these four terms inside the square root: $s(s-a)(s-b)(s-c)$.
- Finally, determine the square root of this product to obtain the triangle's Area.
The versatility of Heron's formula is highlighted through examples involving various triangle types – scalene, isosceles, and even equilateral. While simpler, specific formulas exist for isosceles and equilateral triangles, the solutions demonstrate that Heron's formula works universally, providing a single, consistent method regardless of the triangle's specific shape, as long as the three side lengths are known.
Furthermore, a significant focus of the solutions lies in extending the application of Heron's formula beyond simple triangles to calculate the area of more complex polygons, particularly quadrilaterals. The standard technique involves strategically dividing the quadrilateral (or other polygon) into constituent triangles using one or more diagonals. If the lengths of all sides and the chosen diagonal(s) are known (or can be calculated), Heron's formula can be applied to find the area of each resulting triangle. The total area of the polygon is then simply the sum of the areas of these individual triangles. Solutions tackle practical word problems, illustrating how to find the area of diverse shapes like parks or fields, sometimes involving calculating associated costs, such as leveling a field at a certain rate per square meter (e.g., $\textsf{₹} 5$ per $m^2$). Clear calculation steps, including the handling of square roots, are provided to ensure mastery of this powerful geometric tool.
Example 1 to 3 (Before Exercise 12.1)
Example 1. Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm (see Fig. 12.6).

Answer:
Given:
Let the sides of the triangle be $a$, $b$, and $c$.
Given two sides: $a = 8$ cm and $b = 11$ cm.
Given perimeter: $P = 32$ cm.
To Find:
The area of the triangle.
Solution:
The perimeter of a triangle is the sum of its three sides.
$P = a + b + c$
Substitute the given values:
$32 = 8 + 11 + c$
$32 = 19 + c$
Now, find the third side $c$:
$c = 32 - 19$
$c = 13$ cm
The third side of the triangle is 13 cm.
Now, calculate the semi-perimeter, $s$.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{32}{2}$
$s = 16$ cm
We can find the area of the triangle using Heron's formula:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values of $s$, $a$, $b$, and $c$:
$\text{Area} = \sqrt{16(16-8)(16-11)(16-13)}$
$\text{Area} = \sqrt{16(8)(5)(3)}$
$\text{Area} = \sqrt{16 \times 8 \times 15}$
$\text{Area} = \sqrt{128 \times 15}$
$\text{Area} = \sqrt{1920}$
To simplify the square root, find the prime factors of 1920:
$\begin{array}{c|cc} 2 & 1920 \\ \hline 2 & 960 \\ \hline 2 & 480 \\ \hline 2 & 240 \\ \hline 2 & 120 \\ \hline 2 & 60 \\ \hline 2 & 30 \\ \hline 3 & 15 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
$1920 = 2^2 \times 2^2 \times 2^2 \times 2 \times 3 \times 5$
$1920 = 16 \times 120 = 16 \times 4 \times 30 = 64 \times 30$
$\text{Area} = \sqrt{64 \times 30}$
$\text{Area} = \sqrt{64} \times \sqrt{30}$
$\text{Area} = 8\sqrt{30}$
The area of the triangle is $8\sqrt{30}$ cm$^2$.
The area of the triangle is $8\sqrt{30}$ cm$^2$.
Example 2. A triangular park ABC has sides 120m, 80m and 50m (see Fig. 12.7). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 20 per metre leaving a space 3m wide for a gate on one side.
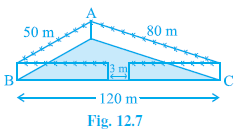
Answer:
Given:
Sides of the triangular park ABC are $a = 120$ m, $b = 80$ m, and $c = 50$ m.
Rate of fencing = $\textsf{₹}$ 20 per metre.
Space for a gate = 3 m.
To Find:
1. The area needed to plant grass.
2. The cost of fencing the park.
Solution:
1. Area to plant grass:
First, calculate the semi-perimeter of the triangle.
$\text{Perimeter} = a + b + c$
$\text{Perimeter} = 120 + 80 + 50 = 250$ m
Semi-perimeter, $s = \frac{\text{Perimeter}}{2}$
$s = \frac{250}{2} = 125$ m
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 125 - 120 = 5$ m
$(s-b) = 125 - 80 = 45$ m
$(s-c) = 125 - 50 = 75$ m
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
$\text{Area} = \sqrt{125 \times 5 \times 45 \times 75}$
Factorise the numbers under the square root:
$\text{Area} = \sqrt{(5^3) \times 5 \times (5 \times 3^2) \times (5^2 \times 3)}$
$\text{Area} = \sqrt{5^{3+1+1+2} \times 3^{2+1}}$
$\text{Area} = \sqrt{5^7 \times 3^3}$
Alternatively, group factors for easier extraction:
$\text{Area} = \sqrt{125 \times 5 \times 45 \times 75}$
$\text{Area} = \sqrt{(25 \times 5) \times 5 \times (9 \times 5) \times (25 \times 3)}$
$\text{Area} = \sqrt{(25 \times 25) \times (5 \times 5) \times 9 \times 3}$
$\text{Area} = \sqrt{25^2 \times 5^2 \times 3^2 \times 3}$
$\text{Area} = 25 \times 5 \times 3 \sqrt{3}$
$\text{Area} = 375\sqrt{3}$ m$^2$
The area needed to plant grass is $375\sqrt{3}$ m$^2$.
2. Cost of fencing:
The total perimeter of the park is 250 m.
A space of 3 m is left for a gate.
Length of wire required for fencing = Total Perimeter - Space for gate.
$\text{Length of fencing} = 250 \text{ m} - 3 \text{ m} = 247$ m
The rate of fencing is $\textsf{₹}$ 20 per metre.
Cost of fencing = Length of fencing $\times$ Rate per metre.
$\text{Cost} = 247 \times 20$
$\text{Cost} = 4940$
The cost of fencing is $\textsf{₹}$ 4940.
The area needed to plant grass is $375\sqrt{3}$ m$^2$.
The cost of fencing the park is $\textsf{₹}$ 4940.
Example 3. The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Answer:
Given:
The sides of a triangular plot are in the ratio 3 : 5 : 7.
The perimeter of the plot is 300 m.
To Find:
The area of the triangular plot.
Solution:
Let the sides of the triangular plot be $3x$, $5x$, and $7x$ metres, where $x$ is a positive constant.
The perimeter of the triangle is the sum of its sides.
$\text{Perimeter} = 3x + 5x + 7x$
We are given that the perimeter is 300 m.
$300 = (3+5+7)x$
$300 = 15x$
Now, solve for $x$:
$x = \frac{300}{15}$
$x = 20$
The actual lengths of the sides are:
Side 1 = $3x = 3 \times 20 = 60$ m
Side 2 = $5x = 5 \times 20 = 100$ m
Side 3 = $7x = 7 \times 20 = 140$ m
Let $a=60$ m, $b=100$ m, and $c=140$ m.
The semi-perimeter, $s$, is half of the perimeter.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{300}{2} = 150$ m
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 150 - 60 = 90$ m
$(s-b) = 150 - 100 = 50$ m
$(s-c) = 150 - 140 = 10$ m
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{150 \times 90 \times 50 \times 10}$
Factorise the numbers under the square root:
$\text{Area} = \sqrt{(15 \times 10) \times (9 \times 10) \times (5 \times 10) \times 10}$
$\text{Area} = \sqrt{15 \times 9 \times 5 \times 10^4}$
$\text{Area} = \sqrt{(3 \times 5) \times 3^2 \times 5 \times 10^4}$
$\text{Area} = \sqrt{3^{1+2} \times 5^{1+1} \times 10^4}$
$\text{Area} = \sqrt{3^3 \times 5^2 \times 10^4}$
Group perfect squares:
$\text{Area} = \sqrt{(3^2 \times 5^2 \times 10^4) \times 3}$
$\text{Area} = \sqrt{3^2} \times \sqrt{5^2} \times \sqrt{10^4} \times \sqrt{3}$
$\text{Area} = 3 \times 5 \times 10^2 \times \sqrt{3}$
$\text{Area} = 15 \times 100 \times \sqrt{3}$
$\text{Area} = 1500\sqrt{3}$ m$^2$
The area of the triangular plot is $1500\sqrt{3}$ m$^2$.
Exercise 12.1
Question 1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Answer:
Given:
A traffic signal board is an equilateral triangle with side 'a'.
To Find:
1. Area of the signal board using Heron’s formula in terms of 'a'.
2. Area of the signal board if its perimeter is 180 cm.
Solution:
For an equilateral triangle with side 'a', all sides are equal to 'a'.
Let the sides of the triangle be $a_1 = a$, $a_2 = a$, and $a_3 = a$.
The perimeter of the triangle is the sum of its sides:
Perimeter $= a + a + a = 3a$
The semi-perimeter, $s$, is half of the perimeter:
$s = \frac{3a}{2}$
Now, we calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$ using Heron's formula variables, where $a=b=c$ for an equilateral triangle:
$s - a = \frac{3a}{2} - a = \frac{3a - 2a}{2} = \frac{a}{2}$
$s - b = \frac{3a}{2} - a = \frac{a}{2}$
$s - c = \frac{3a}{2} - a = \frac{a}{2}$
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{\frac{3a}{2} \left(\frac{a}{2}\right) \left(\frac{a}{2}\right) \left(\frac{a}{2}\right)}$
$\text{Area} = \sqrt{\frac{3a \cdot a \cdot a \cdot a}{2 \cdot 2 \cdot 2 \cdot 2}}$
$\text{Area} = \sqrt{\frac{3a^4}{16}}$
$\text{Area} = \frac{\sqrt{3a^4}}{\sqrt{16}}$
$\text{Area} = \frac{\sqrt{3} \sqrt{a^4}}{4}$
Since $\sqrt{a^4} = a^2$:
$\text{Area} = \frac{\sqrt{3} a^2}{4}$
So, the area of the signal board with side 'a' using Heron's formula is $\frac{\sqrt{3}}{4} a^2$ square units.
Now, consider the second part where the perimeter is given as 180 cm.
For an equilateral triangle, Perimeter = 3 $\times$ side.
$180 \text{ cm} = 3a$
To find the side 'a':
$a = \frac{180}{3}$ cm
$a = 60$ cm
Now, use the formula for the area of an equilateral triangle derived above, with $a = 60$ cm:
$\text{Area} = \frac{\sqrt{3}}{4} a^2$
$\text{Area} = \frac{\sqrt{3}}{4} (60 \text{ cm})^2$
$\text{Area} = \frac{\sqrt{3}}{4} \times (60 \times 60) \text{ cm}^2$
$\text{Area} = \frac{\sqrt{3}}{4} \times 3600 \text{ cm}^2$
$\text{Area} = \sqrt{3} \times \frac{3600}{4} \text{ cm}^2$
$\text{Area} = 900\sqrt{3}$ cm$^2$
The area of the signal board using Heron's formula is $\frac{\sqrt{3}}{4} a^2$ square units.
If the perimeter is 180 cm, the area of the signal board is $900\sqrt{3}$ cm$^2$.
Question 2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
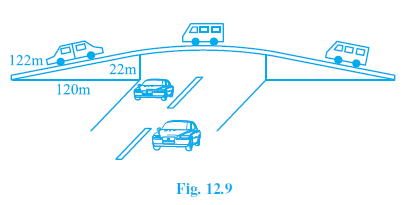
Answer:
Given:
The sides of the triangular side wall are $a = 122$ m, $b = 22$ m, and $c = 120$ m.
Earning rate from advertisement = $\textsf{₹}$ 5000 per m$^2$ per year.
Hiring period = 3 months.
To Find:
The amount of rent paid by the company for 3 months.
Solution:
First, we need to find the area of the triangular wall using Heron's formula.
The semi-perimeter of the triangle is $s = \frac{a+b+c}{2}$.
$\text{Perimeter} = 122 + 22 + 120 = 264$ m
$s = \frac{264}{2} = 132$ m
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 132 - 122 = 10$ m
$(s-b) = 132 - 22 = 110$ m
$(s-c) = 132 - 120 = 12$ m
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{132 \times 10 \times 110 \times 12}$
Factorise the numbers under the square root:
$\text{Area} = \sqrt{(12 \times 11) \times 10 \times (11 \times 10) \times 12}$
$\text{Area} = \sqrt{12 \times 11 \times 10 \times 11 \times 10 \times 12}$
$\text{Area} = \sqrt{12^2 \times 11^2 \times 10^2}$
Take the square root of the perfect squares:
$\text{Area} = 12 \times 11 \times 10$
$\text{Area} = 1320$ m$^2$
The area of the triangular wall is 1320 m$^2$.
Now, calculate the rent.
The earning rate is $\textsf{₹}$ 5000 per m$^2$ per year.
The rate per month is $\frac{\textsf{₹}\ 5000}{12}$.
The company hired the wall for 3 months.
Total rent = Area $\times$ Rate per m$^2$ per month $\times$ Number of months
$\text{Rent} = 1320 \times \frac{5000}{12} \times 3$
Simplify the calculation:
$\text{Rent} = 1320 \times 5000 \times \frac{\cancel{3}^{1}}{\cancel{12}_{4}}$
$\text{Rent} = 1320 \times \frac{5000}{4}$
$\text{Rent} = \cancel{1320}^{330} \times 1250$
$\text{Rent} = 330 \times 5000 = 1650000$
The rent paid by the company is $\textsf{₹}$ 1,650,000.
The area of the wall is 1320 m$^2$.
The rent paid for 3 months is $\textsf{₹}$ 1,650,000.
Question 3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.
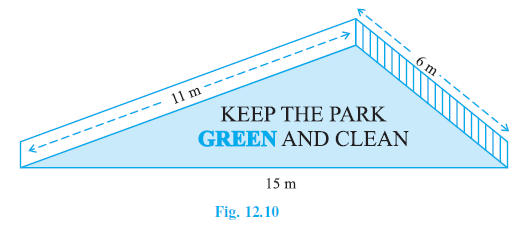
Answer:
Given:
The sides of the triangular side wall are $a = 15$ m, $b = 11$ m, and $c = 6$ m.
To Find:
The area painted in colour.
Solution:
We will use Heron's formula to find the area of the triangle.
First, calculate the semi-perimeter of the triangle, $s = \frac{a+b+c}{2}$.
$\text{Perimeter} = 15 + 11 + 6 = 32$ m
$s = \frac{32}{2} = 16$ m
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 16 - 15 = 1$ m
$(s-b) = 16 - 11 = 5$ m
$(s-c) = 16 - 6 = 10$ m
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{16 \times 1 \times 5 \times 10}$
Simplify the expression under the square root:
$\text{Area} = \sqrt{16 \times 50}$
$\text{Area} = \sqrt{16 \times 25 \times 2}$
$\text{Area} = \sqrt{16} \times \sqrt{25} \times \sqrt{2}$
$\text{Area} = 4 \times 5 \times \sqrt{2}$
$\text{Area} = 20\sqrt{2}$ m$^2$
The area painted in colour is $20\sqrt{2}$ m$^2$.
Question 4. Find the area of a triangle two sides of which are 18cm and 10cm and the perimeter is 42cm.
Answer:
Given:
Let the sides of the triangle be $a$, $b$, and $c$.
Given two sides: $a = 18$ cm and $b = 10$ cm.
Given perimeter: $P = 42$ cm.
To Find:
The area of the triangle.
Solution:
The perimeter of a triangle is the sum of its three sides.
$P = a + b + c$
Substitute the given values:
$42 = 18 + 10 + c$
$42 = 28 + c$
Now, find the third side $c$:
$c = 42 - 28$
$c = 14$ cm
The third side of the triangle is 14 cm.
Now, calculate the semi-perimeter, $s$.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{42}{2}$
$s = 21$ cm
We can find the area of the triangle using Heron's formula:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values of $s$, $a$, $b$, and $c$:
$\text{Area} = \sqrt{21(21-18)(21-10)(21-14)}$
$\text{Area} = \sqrt{21(3)(11)(7)}$
$\text{Area} = \sqrt{(3 \times 7) \times 3 \times 11 \times 7}$
$\text{Area} = \sqrt{3^2 \times 7^2 \times 11}$
Take the square root of the perfect squares:
$\text{Area} = \sqrt{3^2} \times \sqrt{7^2} \times \sqrt{11}$
$\text{Area} = 3 \times 7 \times \sqrt{11}$
$\text{Area} = 21\sqrt{11}$
The area of the triangle is $21\sqrt{11}$ cm$^2$.
The area of the triangle is $21\sqrt{11}$ cm$^2$.
Question 5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.
Answer:
Given:
The sides of a triangle are in the ratio 12 : 17 : 25.
The perimeter of the triangle is 540 cm.
To Find:
The area of the triangle.
Solution:
Let the sides of the triangle be $12x$, $17x$, and $25x$ cm, where $x$ is a positive constant.
The perimeter of the triangle is the sum of its sides.
$\text{Perimeter} = 12x + 17x + 25x$
We are given that the perimeter is 540 cm.
540 = $(12+17+25)x$
540 = $54x$
Now, solve for $x$:
$x = \frac{540}{54}$
$x = 10$
The actual lengths of the sides are:
Side 1 ($a$) = $12x = 12 \times 10 = 120$ cm
Side 2 ($b$) = $17x = 17 \times 10 = 170$ cm
Side 3 ($c$) = $25x = 25 \times 10 = 250$ cm
The semi-perimeter, $s$, is half of the perimeter.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{540}{2} = 270$ cm
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 270 - 120 = 150$ cm
$(s-b) = 270 - 170 = 100$ cm
$(s-c) = 270 - 250 = 20$ cm
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{270 \times 150 \times 100 \times 20}$
Factorise the numbers under the square root:
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times 100 \times (2 \times 10)}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10 \times 10 \times 100 \times 10}$
$\text{Area} = \sqrt{(3^3) \times (3 \times 5) \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 5^1 \times 2^1 \times 10^4}$
Group perfect squares and remaining factors:
$\text{Area} = \sqrt{(3^4) \times (10^4) \times (5 \times 2)}$
$\text{Area} = \sqrt{3^4} \times \sqrt{10^4} \times \sqrt{10}$
$\text{Area} = 3^2 \times 10^2 \times \sqrt{10}$
$\text{Area} = 9 \times 100 \times \sqrt{10}$
$\text{Area} = 900 \times \sqrt{10}$
Let's re-factorise $270 \times 150 \times 100 \times 20$ in a more systematic way:
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times (10 \times 10) \times (2 \times 10)}$
$\text{Area} = \sqrt{(3^3) \times (3 \times 5) \times 10 \times 10 \times 100 \times 2 \times 10}$
$\text{Area} = \sqrt{3^4 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10^1 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10^5}$
This factorisation seems incorrect. Let's try grouping terms to get perfect squares directly from $270 \times 150 \times 100 \times 20$:
$\text{Area} = \sqrt{270 \times 150 \times 100 \times 20}$
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times (10 \times 10) \times (2 \times 10)}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10 \times 10 \times 10 \times 10}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10^4}$
$\text{Area} = \sqrt{(3 \times 9) \times (3 \times 5) \times 2 \times 10^4}$
$\text{Area} = \sqrt{3 \times 3^2 \times 3 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10^5}$
There must be a simpler way to factor this. Let's pull out factors of 10 and look for squares.
$\text{Area} = \sqrt{27 \times 10 \times 15 \times 10 \times 100 \times 2 \times 10}$
$\text{Area} = \sqrt{(27 \times 15 \times 2) \times (10 \times 10 \times 100 \times 10)}$
$\text{Area} = \sqrt{810 \times 100000}$
This is getting complex. Let's factorise $s$, $(s-a)$, $(s-b)$, and $(s-c)$ first:
$\text{Area} = \sqrt{270 \times 150 \times 100 \times 20}$
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times 100 \times (2 \times 10)}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10 \times 10 \times 100 \times 10}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10^4}$
$\text{Area} = \sqrt{(3^3) \times (3 \times 5) \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10^5}$
Wait, let's group differently:
$\text{Area} = \sqrt{270 \times 150 \times 100 \times 20}$
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times (10 \times 10) \times (2 \times 10)}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10 \times 10 \times 10 \times 10}$
$\text{Area} = \sqrt{(3^3) \times (3 \times 5) \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 10^5}$
Let's go back to the product: $270 \times 150 \times 100 \times 20$
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times (100) \times (2 \times 10)}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10 \times 10 \times 100 \times 10}$
$\text{Area} = \sqrt{810 \times 10 \times 100 \times 10}$
$\text{Area} = \sqrt{81 \times 10 \times 10 \times 100 \times 10}$
$\text{Area} = \sqrt{81 \times 100 \times 100 \times 10}$
$\text{Area} = \sqrt{81 \times 100 \times 1000}$
$\text{Area} = \sqrt{81} \times \sqrt{100} \times \sqrt{1000}$
$\text{Area} = 9 \times 10 \times \sqrt{100 \times 10}$
$\text{Area} = 90 \times 10 \sqrt{10}$
$\text{Area} = 900\sqrt{10}$
Let's try factoring directly from the start:
$\text{Area} = \sqrt{270 \times 150 \times 100 \times 20}$
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times (10 \times 10) \times (2 \times 10)}$
$\text{Area} = \sqrt{(3^3 \times 2 \times 5) \times (3 \times 5 \times 2 \times 5) \times (2^2 \times 5^2) \times (2^2 \times 5)}$
No, let's stick to $270 \times 150 \times 100 \times 20$ and group terms with common factors, especially 10.
$\text{Area} = \sqrt{(27 \times 10) \times (15 \times 10) \times (10 \times 10) \times (2 \times 10)}$
$\text{Area} = \sqrt{27 \times 15 \times 2 \times 10^4}$
$\text{Area} = \sqrt{(3 \times 9) \times (3 \times 5) \times 2 \times 10^4}$
$\text{Area} = \sqrt{3 \times 3^2 \times 3 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4 \times 5 \times 2 \times 10^4}$
$\text{Area} = \sqrt{3^4} \times \sqrt{10} \times \sqrt{10^4}$
$\text{Area} = 3^2 \times \sqrt{10} \times 10^2$
$\text{Area} = 9 \times 100 \times \sqrt{10}$
$\text{Area} = 900\sqrt{10}$ cm$^2$
The area of the triangle is $900\sqrt{10}$ cm$^2$.
Question 6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Answer:
Given:
An isosceles triangle with perimeter = 30 cm.
Each of the equal sides = 12 cm.
To Find:
The area of the triangle.
Solution:
Let the sides of the isosceles triangle be $a$, $b$, and $c$. Since it is an isosceles triangle, two sides are equal. Let $a = 12$ cm and $b = 12$ cm.
The perimeter of a triangle is the sum of its three sides.
$\text{Perimeter} = a + b + c$
We are given that the perimeter is 30 cm.
30 cm = 12 cm + 12 cm + c
30 = 24 + c
Now, find the length of the third side, $c$:
c = 30 - 24
c = 6 cm
The sides of the triangle are 12 cm, 12 cm, and 6 cm.
Now, calculate the semi-perimeter, $s$.
s = $\frac{\text{Perimeter}}{2}$
s = $\frac{30}{2}$
s = 15 cm
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 15 - 12 = 3$ cm
$(s-b) = 15 - 12 = 3$ cm
$(s-c) = 15 - 6 = 9$ cm
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{15 \times 3 \times 3 \times 9}$
Simplify the expression under the square root:
$\text{Area} = \sqrt{(3 \times 5) \times 3^2 \times 3^2}$
$\text{Area} = \sqrt{3^1 \times 5^1 \times 3^2 \times 3^2}$
$\text{Area} = \sqrt{3^{1+2+2} \times 5}$
$\text{Area} = \sqrt{3^5 \times 5}$
Group the perfect squares:
$\text{Area} = \sqrt{(3^4 \times 3) \times 5}$
$\text{Area} = \sqrt{3^4} \times \sqrt{3 \times 5}$
$\text{Area} = 3^2 \times \sqrt{15}$
$\text{Area} = 9\sqrt{15}$ cm$^2$
The area of the isosceles triangle is $9\sqrt{15}$ cm$^2$.
Example 4 to 6 (Before Exercise 12.2)
Example 4. Kamla has a triangular field with sides 240 m, 200 m, 360 m, where she grew wheat. In another triangular field with sides 240 m, 320 m, 400 m adjacent to the previous field, she wanted to grow potatoes and onions (see Fig. 12.11). She divided the field in two parts by joining the mid-point of the longest side to the opposite vertex and grew patatoes in one part and onions in the other part. How much area (in hectares) has been used for wheat, potatoes and onions? (1 hectare = 10000 m2 )

Answer:
Given:
Kamla has two triangular fields.
Field 1 (for wheat) has sides $a_1 = 240$ m, $b_1 = 200$ m, and $c_1 = 360$ m.
Field 2 (for potatoes and onions) has sides $a_2 = 240$ m, $b_2 = 320$ m, and $c_2 = 400$ m.
Field 2 is divided into two equal parts by joining the mid-point of the longest side to the opposite vertex.
1 hectare = 10000 m$^2$.
To Find:
The area (in hectares) used for wheat, potatoes, and onions.
Solution:
Area for Wheat:
The sides of the wheat field are 240 m, 200 m, and 360 m.
First, calculate the semi-perimeter ($s_1$) of the wheat field.
$\text{Perimeter}_1 = 240 + 200 + 360 = 800$ m
$s_1 = \frac{\text{Perimeter}_1}{2} = \frac{800}{2} = 400$ m
Now, calculate the differences $(s_1-a_1)$, $(s_1-b_1)$, and $(s_1-c_1)$.
$(s_1-a_1) = 400 - 240 = 160$ m
$(s_1-b_1) = 400 - 200 = 200$ m
$(s_1-c_1) = 400 - 360 = 40$ m
Using Heron's formula for the area of the wheat field (Area$_1$):
$\text{Area}_1 = \sqrt{s_1(s_1-a_1)(s_1-b_1)(s_1-c_1)}$
$\text{Area}_1 = \sqrt{400 \times 160 \times 200 \times 40}$
Simplify the expression under the square root:
$\text{Area}_1 = \sqrt{(20^2) \times (16 \times 10) \times (2 \times 100) \times (4 \times 10)}$
$\text{Area}_1 = \sqrt{400 \times 160 \times 200 \times 40}$
$\text{Area}_1 = \sqrt{(400 \times 40) \times (160 \times 200)}$
$\text{Area}_1 = \sqrt{16000 \times 32000}$
$\text{Area}_1 = \sqrt{(16 \times 1000) \times (32 \times 1000)}$
$\text{Area}_1 = \sqrt{16 \times 32 \times 1000^2}$
$\text{Area}_1 = 1000 \times \sqrt{16 \times 32}$
$\text{Area}_1 = 1000 \times \sqrt{16 \times 16 \times 2}$
$\text{Area}_1 = 1000 \times \sqrt{16^2 \times 2}$
$\text{Area}_1 = 1000 \times 16 \sqrt{2} = 16000\sqrt{2}$ m$^2$
Convert Area$_1$ to hectares (1 hectare = 10000 m$^2$).
$\text{Area}_1 (\text{hectares}) = \frac{16000\sqrt{2}}{10000} = 1.6\sqrt{2}$ hectares
Area for Potatoes and Onions:
The sides of this field are 240 m, 320 m, and 400 m.
First, calculate the semi-perimeter ($s_2$) of this field.
$\text{Perimeter}_2 = 240 + 320 + 400 = 960$ m
$s_2 = \frac{\text{Perimeter}_2}{2} = \frac{960}{2} = 480$ m
Now, calculate the differences $(s_2-a_2)$, $(s_2-b_2)$, and $(s_2-c_2)$.
$(s_2-a_2) = 480 - 240 = 240$ m
$(s_2-b_2) = 480 - 320 = 160$ m
$(s_2-c_2) = 480 - 400 = 80$ m
Using Heron's formula for the area of this field (Area$_2$):
$\text{Area}_2 = \sqrt{s_2(s_2-a_2)(s_2-b_2)(s_2-c_2)}$
$\text{Area}_2 = \sqrt{480 \times 240 \times 160 \times 80}$
Simplify the expression under the square root:
$\text{Area}_2 = \sqrt{(48 \times 10) \times (24 \times 10) \times (16 \times 10) \times (8 \times 10)}$
$\text{Area}_2 = \sqrt{48 \times 24 \times 16 \times 8 \times 10^4}$
$\text{Area}_2 = 100 \sqrt{48 \times 24 \times 16 \times 8}$
$\text{Area}_2 = 100 \sqrt{(6 \times 8) \times (3 \times 8) \times (2 \times 8) \times 8}$
$\text{Area}_2 = 100 \sqrt{6 \times 3 \times 2 \times 8^4}$
$\text{Area}_2 = 100 \sqrt{36 \times 8^4}$
$\text{Area}_2 = 100 \sqrt{6^2 \times (8^2)^2}$
$\text{Area}_2 = 100 \times 6 \times 8^2 = 100 \times 6 \times 64$
$\text{Area}_2 = 38400$ m$^2$
The longest side of this field is 400 m. The field is divided into two parts by joining the mid-point of the longest side to the opposite vertex. This line segment is a median of the triangle. A median divides a triangle into two triangles of equal area.
$\text{Area}_{\text{Potatoes}} = \frac{1}{2} \text{Area}_2$
$\text{Area}_{\text{Potatoes}} = \frac{1}{2} \times 38400 = 19200$ m$^2$
$\text{Area}_{\text{Onions}} = \frac{1}{2} \text{Area}_2$
$\text{Area}_{\text{Onions}} = \frac{1}{2} \times 38400 = 19200$ m$^2$
Convert these areas to hectares (1 hectare = 10000 m$^2$).
$\text{Area}_{\text{Potatoes}} (\text{hectares}) = \frac{19200}{10000} = 1.92$ hectares
$\text{Area}_{\text{Onions}} (\text{hectares}) = \frac{19200}{10000} = 1.92$ hectares
Summary of Areas:
Area used for wheat = $1.6\sqrt{2}$ hectares.
Area used for potatoes = 1.92 hectares.
Area used for onions = 1.92 hectares.
Example 5. Students of a school staged a rally for cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes AB, BC and CA; while the other through AC, CD and DA (see Fig. 12.12). Then they cleaned the area enclosed within their lanes. If AB = 9 m, BC = 40 m, CD = 15 m, DA = 28 m and ∠B = 90º, which group cleaned more area and by how much? Find the total area cleaned by the students (neglecting the width of the lanes).
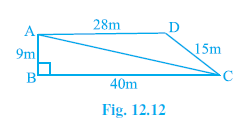
Answer:
Given:
Triangular lanes AB, BC, CA forming $\triangle$ABC with AB = 9 m, BC = 40 m, $\angle$B = $90^\circ$.
Triangular lanes AC, CD, DA forming $\triangle$ADC with CD = 15 m, DA = 28 m.
To Find:
1. Which group cleaned more area and by how much.
2. The total area cleaned by the students.
Solution:
The park is divided into two triangles, $\triangle$ABC and $\triangle$ADC, by the common side AC.
Area cleaned by the first group (Area of $\triangle$ABC):
In $\triangle$ABC, $\angle$B = $90^\circ$, AB = 9 m, and BC = 40 m.
Since it is a right-angled triangle, the area can be calculated as:
$\text{Area of } \triangle\text{ABC} = \frac{1}{2} \times \text{base} \times \text{height}$
$\text{Area of } \triangle\text{ABC} = \frac{1}{2} \times \text{BC} \times \text{AB}$
$\text{Area of } \triangle\text{ABC} = \frac{1}{2} \times 40 \text{ m} \times 9 \text{ m}$
$\text{Area of } \triangle\text{ABC} = 20 \times 9 = 180 \text{ m}^2$
Area cleaned by the first group is 180 m$^2$.
Area cleaned by the second group (Area of $\triangle$ADC):
To find the area of $\triangle$ADC, we first need the length of side AC. In $\triangle$ABC, AC is the hypotenuse.
Using the Pythagorean theorem in $\triangle$ABC:
$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$
$\text{AC}^2 = (9 \text{ m})^2 + (40 \text{ m})^2$
$\text{AC}^2 = 81 \text{ m}^2 + 1600 \text{ m}^2$
$\text{AC}^2 = 1681 \text{ m}^2$
$\text{AC} = \sqrt{1681} \text{ m} = 41 \text{ m}$
So, the sides of $\triangle$ADC are AD = 28 m, CD = 15 m, and AC = 41 m.
We use Heron's formula to find the area of $\triangle$ADC.
Let the sides be $a=41$ m, $b=15$ m, $c=28$ m.
The semi-perimeter, $s$, is:
$s = \frac{a+b+c}{2}$
$s = \frac{41 + 15 + 28}{2} = \frac{84}{2} = 42 \text{ m}$
Now, calculate $(s-a)$, $(s-b)$, and $(s-c)$:
$(s-a) = 42 - 41 = 1 \text{ m}$
$(s-b) = 42 - 15 = 27 \text{ m}$
$(s-c) = 42 - 28 = 14 \text{ m}$
Using Heron's formula for the area of $\triangle$ADC:
$\text{Area of } \triangle\text{ADC} = \sqrt{s(s-a)(s-b)(s-c)}$
$\text{Area of } \triangle\text{ADC} = \sqrt{42 \times 1 \times 27 \times 14}$
Simplify the expression under the square root:
$\text{Area of } \triangle\text{ADC} = \sqrt{(6 \times 7) \times 1 \times (3 \times 9) \times (2 \times 7)}$
$\text{Area of } \triangle\text{ADC} = \sqrt{(2 \times 3 \times 7) \times 3 \times 3^2 \times 2 \times 7}$
$\text{Area of } \triangle\text{ADC} = \sqrt{2^2 \times 3^4 \times 7^2}$
Take the square root of the perfect squares:
$\text{Area of } \triangle\text{ADC} = \sqrt{2^2} \times \sqrt{3^4} \times \sqrt{7^2}$
$\text{Area of } \triangle\text{ADC} = 2 \times 3^2 \times 7$
$\text{Area of } \triangle\text{ADC} = 2 \times 9 \times 7$
$\text{Area of } \triangle\text{ADC} = 18 \times 7 = 126 \text{ m}^2$
Area cleaned by the second group is 126 m$^2$.
Comparison of Areas:
Area cleaned by the first group = 180 m$^2$.
Area cleaned by the second group = 126 m$^2$.
Since $180 > 126$, the first group cleaned more area.
Difference in area = Area of $\triangle$ABC - Area of $\triangle$ADC
Difference = $180 \text{ m}^2 - 126 \text{ m}^2 = 54 \text{ m}^2$
The first group cleaned 54 m$^2$ more area than the second group.
Total Area Cleaned:
The total area cleaned is the sum of the areas of the two triangles.
$\text{Total Area} = \text{Area of } \triangle\text{ABC} + \text{Area of } \triangle\text{ADC}$
$\text{Total Area} = 180 \text{ m}^2 + 126 \text{ m}^2 = 306 \text{ m}^2$
The first group cleaned more area by 54 m$^2$.
The total area cleaned by the students is 306 m$^2$.
Example 6. Sanya has a piece of land which is in the shape of a rhombus (see Fig. 12.13). She wants her one daughter and one son to work on the land and produce different crops. She divided the land in two equal parts. If the perimeter of the land is 400 m and one of the diagonals is 160 m, how much area each of them will get for their crops?
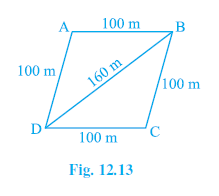
Answer:
Given:
The land is in the shape of a rhombus.
Perimeter of the rhombus = 400 m.
Length of one diagonal = 160 m.
To Find:
The area each child will get for their crops.
Solution:
A rhombus has all four sides equal in length.
Let the side of the rhombus be 'a'.
Perimeter of the rhombus = 4 $\times$ side
400 m = 4a
a = $\frac{400}{4}$ m
a = 100 m
So, each side of the rhombus is 100 m.
Let the rhombus be ABCD, and the given diagonal be AC = 160 m.
The land is divided into two equal parts by the diagonal AC. These parts are two triangles, $\triangle$ABC and $\triangle$ADC.
The diagonal of a rhombus divides it into two congruent triangles. Therefore, the area of $\triangle$ABC is equal to the area of $\triangle$ADC.
Each child gets one of these triangles.
Consider $\triangle$ABC. Its sides are AB, BC, and AC.
AB = 100 m (side of the rhombus)
BC = 100 m (side of the rhombus)
AC = 160 m (given diagonal)
We can find the area of $\triangle$ABC using Heron's formula.
Let the sides be $a' = 100$ m, $b' = 100$ m, and $c' = 160$ m.
The semi-perimeter, $s'$, of $\triangle$ABC is:
s' = $\frac{a' + b' + c'}{2}$
s' = $\frac{100 + 100 + 160}{2}$ m
s' = $\frac{360}{2}$ m = 180 m
Now, calculate the differences $(s'-a')$, $(s'-b')$, and $(s'-c')$.
$(s'-a') = 180 - 100 = 80$ m
$(s'-b') = 180 - 100 = 80$ m
$(s'-c') = 180 - 160 = 20$ m
Using Heron's formula for the area of $\triangle$ABC:
$\text{Area of } \triangle\text{ABC} = \sqrt{s'(s'-a')(s'-b')(s'-c')}$
Substitute the values:
$\text{Area of } \triangle\text{ABC} = \sqrt{180 \times 80 \times 80 \times 20}$
Simplify the expression under the square root:
$\text{Area} = \sqrt{(18 \times 10) \times (8 \times 10) \times (8 \times 10) \times (2 \times 10)}$
$\text{Area} = \sqrt{18 \times 8 \times 8 \times 2 \times 10^4}$
$\text{Area} = \sqrt{(2 \times 9) \times 8^2 \times 2 \times 10^4}$
$\text{Area} = \sqrt{2^2 \times 9 \times 8^2 \times 10^4}$
$\text{Area} = \sqrt{2^2} \times \sqrt{9} \times \sqrt{8^2} \times \sqrt{10^4}$
$\text{Area} = 2 \times 3 \times 8 \times 10^2$
$\text{Area} = 6 \times 8 \times 100$
$\text{Area} = 4800$ m$^2$
The area of $\triangle$ABC is 4800 m$^2$. Since the land is divided into two equal parts by the diagonal, each child gets an area equal to the area of one of these triangles.
$\text{Area each child gets} = 4800 \text{ m}^2$
Each child will get 4800 m$^2$ of area for their crops.
Exercise 12.2
Question 1. A park, in the shape of a quadrilateral ABCD, has ∠C = 90º, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Answer:
Given:
A quadrilateral park ABCD with sides AB = 9 m, BC = 12 m, CD = 5 m, and AD = 8 m.
Also, $\angle$C = $90^\circ$.
To Find:
The area occupied by the park ABCD.
Solution:
The quadrilateral ABCD can be divided into two triangles by joining the diagonal BD.
Since $\angle$C = $90^\circ$, $\triangle$BCD is a right-angled triangle.
The area of a right-angled triangle is given by $\frac{1}{2} \times \text{base} \times \text{height}$.
In $\triangle$BCD, base = BC = 12 m and height = CD = 5 m.
$\text{Area of } \triangle\text{BCD} = \frac{1}{2} \times \text{BC} \times \text{CD}$
$\text{Area of } \triangle\text{BCD} = \frac{1}{2} \times 12 \text{ m} \times 5 \text{ m}$
$\text{Area of } \triangle\text{BCD} = 6 \times 5 \text{ m}^2 = 30 \text{ m}^2$
To find the area of $\triangle$ABD, we need the lengths of all three sides. We are given AB = 9 m and AD = 8 m. We need to find the length of the diagonal BD.
In the right-angled $\triangle$BCD, we can use the Pythagorean theorem to find BD (the hypotenuse):
$\text{BD}^2 = \text{BC}^2 + \text{CD}^2$
$\text{BD}^2 = (12 \text{ m})^2 + (5 \text{ m})^2$
$\text{BD}^2 = 144 \text{ m}^2 + 25 \text{ m}^2$
$\text{BD}^2 = 169 \text{ m}^2$
$\text{BD} = \sqrt{169} \text{ m} = 13 \text{ m}$
Now, the sides of $\triangle$ABD are AB = 9 m, AD = 8 m, and BD = 13 m.
We can find the area of $\triangle$ABD using Heron's formula.
Let the sides be $a'=9$, $b'=8$, and $c'=13$. The semi-perimeter ($s'$) is:
$s' = \frac{a' + b' + c'}{2}$
$s' = \frac{9 + 8 + 13}{2} \text{ m} = \frac{30}{2} \text{ m} = 15 \text{ m}$
Now, calculate $(s'-a')$, $(s'-b')$, and $(s'-c')$:
$(s'-a') = 15 - 9 = 6 \text{ m}$
$(s'-b') = 15 - 8 = 7 \text{ m}$
$(s'-c') = 15 - 13 = 2 \text{ m}$
Using Heron's formula for the area of $\triangle$ABD:
$\text{Area of } \triangle\text{ABD} = \sqrt{s'(s'-a')(s'-b')(s'-c')}$
$\text{Area of } \triangle\text{ABD} = \sqrt{15 \times 6 \times 7 \times 2}$
Simplify the expression under the square root:
$\text{Area of } \triangle\text{ABD} = \sqrt{(3 \times 5) \times (2 \times 3) \times 7 \times 2}$
$\text{Area of } \triangle\text{ABD} = \sqrt{2^2 \times 3^2 \times 5 \times 7}$
$\text{Area of } \triangle\text{ABD} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{5 \times 7}$
$\text{Area of } \triangle\text{ABD} = 2 \times 3 \times \sqrt{35}$
$\text{Area of } \triangle\text{ABD} = 6\sqrt{35} \text{ m}^2$
The total area of the quadrilateral ABCD is the sum of the areas of the two triangles $\triangle$BCD and $\triangle$ABD.
$\text{Area of ABCD} = \text{Area of } \triangle\text{BCD} + \text{Area of } \triangle\text{ABD}$
$\text{Area of ABCD} = (30 + 6\sqrt{35}) \text{ m}^2$
The area occupied by the park ABCD is $(30 + 6\sqrt{35})$ m$^2$.
Question 2. Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Answer:
Given:
A quadrilateral ABCD with side lengths AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm, and diagonal AC = 5 cm.
To Find:
The area of the quadrilateral ABCD.
Solution:
The quadrilateral ABCD can be divided into two triangles by the diagonal AC: $\triangle$ABC and $\triangle$ADC.
Let's first find the area of $\triangle$ABC. The sides are AB = 3 cm, BC = 4 cm, and AC = 5 cm.
We check if $\triangle$ABC is a right-angled triangle using the Pythagorean theorem: $3^2 + 4^2 = 9 + 16 = 25$, and $5^2 = 25$.
Since $AB^2 + BC^2 = AC^2$, $\triangle$ABC is a right-angled triangle with the right angle at B ($\angle$B = $90^\circ$).
The area of a right-angled triangle is given by $\frac{1}{2} \times \text{base} \times \text{height}$.
$\text{Area of } \triangle\text{ABC} = \frac{1}{2} \times \text{AB} \times \text{BC}$
$\text{Area of } \triangle\text{ABC} = \frac{1}{2} \times 3 \text{ cm} \times 4 \text{ cm}$
$\text{Area of } \triangle\text{ABC} = 6 \text{ cm}^2$
Now, let's find the area of $\triangle$ADC. The sides are AD = 5 cm, CD = 4 cm, and AC = 5 cm.
We use Heron's formula for $\triangle$ADC.
Let the sides be $a=5$, $b=4$, and $c=5$. The semi-perimeter ($s$) is:
s = $\frac{a+b+c}{2}$
s = $\frac{5 + 4 + 5}{2}$ cm = $\frac{14}{2}$ cm = 7 cm
Now, calculate $(s-a)$, $(s-b)$, and $(s-c)$:
$(s-a) = 7 - 5 = 2$ cm
$(s-b) = 7 - 4 = 3$ cm
$(s-c) = 7 - 5 = 2$ cm
Using Heron's formula for the area of $\triangle$ADC:
$\text{Area of } \triangle\text{ADC} = \sqrt{s(s-a)(s-b)(s-c)}$
$\text{Area of } \triangle\text{ADC} = \sqrt{7 \times 2 \times 3 \times 2}$
Simplify the expression under the square root:
$\text{Area of } \triangle\text{ADC} = \sqrt{4 \times 21}$
$\text{Area of } \triangle\text{ADC} = \sqrt{4} \times \sqrt{21}$
$\text{Area of } \triangle\text{ADC} = 2\sqrt{21} \text{ cm}^2$
The total area of the quadrilateral ABCD is the sum of the areas of the two triangles $\triangle$ABC and $\triangle$ADC.
$\text{Area of ABCD} = \text{Area of } \triangle\text{ABC} + \text{Area of } \triangle\text{ADC}$
$\text{Area of ABCD} = (6 + 2\sqrt{21}) \text{ cm}^2$
The area of the quadrilateral ABCD is $(6 + 2\sqrt{21})$ cm$^2$.
Question 3. Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.

Answer:
Given:
A picture of an aeroplane made with coloured paper, divided into five regions (I, II, III, IV, V) with the given dimensions.
To Find:
The total area of the paper used.
Solution:
We will calculate the area of each region separately and then sum them up to find the total area.
Region I:
This is a triangle with sides 5 cm, 5 cm, and 1 cm.
We use Heron's formula to find its area.
Let the sides be $a = 5$, $b = 5$, and $c = 1$.
The semi-perimeter, $s_1$, is:
s$_1$ = $\frac{a+b+c}{2} = \frac{5+5+1}{2} = \frac{11}{2} = 5.5$ cm
Area of Region I = $\sqrt{s_1(s_1-a)(s_1-b)(s_1-c)}$
Area$_1$ = $\sqrt{5.5(5.5-5)(5.5-5)(5.5-1)}$
Area$_1$ = $\sqrt{5.5 \times 0.5 \times 0.5 \times 4.5}$
Area$_1$ = $\sqrt{\frac{11}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{9}{2}} = \sqrt{\frac{99}{16}} = \frac{\sqrt{99}}{4} = \frac{\sqrt{9 \times 11}}{4} = \frac{3\sqrt{11}}{4}$ cm$^2$
Using $\sqrt{11} \approx 3.317$:
Area$_1 \approx \frac{3 \times 3.317}{4} = \frac{9.951}{4} \approx 2.488$ cm$^2$
Region II:
This is a rectangle with length 6.5 cm and width 1 cm.
Area$_2$ = length $\times$ width
Area$_2$ = $6.5 \text{ cm} \times 1 \text{ cm} = 6.5$ cm$^2$
Region III:
This is an isosceles trapezium with parallel sides 1 cm and 2 cm, and non-parallel sides 1 cm each.
To find the area, we need the height of the trapezium. Draw perpendiculars from the endpoints of the shorter parallel side to the longer parallel side. This forms two right triangles at the ends and a rectangle in the middle.
The base of each right triangle is $\frac{2-1}{2} = \frac{1}{2} = 0.5$ cm.
Using the Pythagorean theorem, the height (h) is:
h$^2$ + $(0.5)^2 = 1^2$
h$^2$ + 0.25 = 1
h$^2$ = 1 - 0.25 = 0.75
h = $\sqrt{0.75} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}$ cm
Area of Trapezium = $\frac{1}{2} \times$ (sum of parallel sides) $\times$ height
Area$_3$ = $\frac{1}{2} \times (1 \text{ cm} + 2 \text{ cm}) \times \frac{\sqrt{3}}{2} \text{ cm}$
Area$_3$ = $\frac{1}{2} \times 3 \times \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{4}$ cm$^2$
Using $\sqrt{3} \approx 1.732$:
Area$_3 \approx \frac{3 \times 1.732}{4} = \frac{5.196}{4} \approx 1.299$ cm$^2$
Region IV and V:
These are two identical triangles (wings) with sides 1.5 cm, 6 cm, and 6 cm.
We use Heron's formula to find the area of one of these triangles (Area$_4$).
Let the sides be $a' = 6$, $b' = 6$, and $c' = 1.5$.
The semi-perimeter, $s_4$, is:
s$_4$ = $\frac{a'+b'+c'}{2} = \frac{6+6+1.5}{2} = \frac{13.5}{2} = 6.75$ cm
Area of Region IV = $\sqrt{s_4(s_4-a')(s_4-b')(s_4-c')}$
Area$_4$ = $\sqrt{6.75(6.75-6)(6.75-6)(6.75-1.5)}$
Area$_4$ = $\sqrt{6.75 \times 0.75 \times 0.75 \times 5.25}$
Area$_4$ = $\sqrt{\frac{27}{4} \times \frac{3}{4} \times \frac{3}{4} \times \frac{21}{4}} = \sqrt{\frac{27 \times 3 \times 3 \times 21}{256}}$
Area$_4$ = $\sqrt{\frac{(3^3) \times 3^2 \times (3 \times 7)}{16^2}} = \sqrt{\frac{3^6 \times 7}{16^2}} = \frac{\sqrt{3^6 \times 7}}{16} = \frac{3^3 \sqrt{7}}{16} = \frac{27\sqrt{7}}{16}$ cm$^2$
Using $\sqrt{7} \approx 2.646$:
Area$_4 \approx \frac{27 \times 2.646}{16} = \frac{71.442}{16} \approx 4.465$ cm$^2$
Area of Region V = Area of Region IV $\approx 4.465$ cm$^2$
Total Area:
Total Area = Area$_1$ + Area$_2$ + Area$_3$ + Area$_4$ + Area$_5$
Total Area $\approx 2.488 + 6.5 + 1.299 + 4.465 + 4.465$
Total Area $\approx 19.217$ cm$^2$
Rounding to one decimal place, the total area is approximately 19.3 cm$^2$.
The total area of the paper used is approximately 19.3 cm$^2$.
Question 4. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram
Answer:
Given:
A triangle with sides $a = 26$ cm, $b = 28$ cm, and $c = 30$ cm.
A parallelogram standing on the base 28 cm.
The area of the triangle is equal to the area of the parallelogram.
To Find:
The height of the parallelogram.
Solution:
First, we find the area of the triangle using Heron's formula.
The semi-perimeter of the triangle is $s = \frac{a+b+c}{2}$.
s = $\frac{26 + 28 + 30}{2}$
s = $\frac{84}{2}$
s = 42 cm
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 42 - 26 = 16$ cm
$(s-b) = 42 - 28 = 14$ cm
$(s-c) = 42 - 30 = 12$ cm
Using Heron's formula for the area of the triangle:
$\text{Area of Triangle} = \sqrt{s(s-a)(s-b)(s-c)}$
$\text{Area of Triangle} = \sqrt{42 \times 16 \times 14 \times 12}$
Simplify the expression under the square root:
$\text{Area of Triangle} = \sqrt{(2 \times 3 \times 7) \times (4^2) \times (2 \times 7) \times (3 \times 4)}$
$\text{Area of Triangle} = \sqrt{2 \times 3 \times 7 \times 16 \times 2 \times 7 \times 3 \times 4}$
$\text{Area of Triangle} = \sqrt{(2 \times 2) \times (3 \times 3) \times (7 \times 7) \times 16 \times 4}$
$\text{Area of Triangle} = \sqrt{2^2 \times 3^2 \times 7^2 \times 4^2 \times 2^2}$
$\text{Area of Triangle} = 2 \times 3 \times 7 \times 4$
$\text{Area of Triangle} = 6 \times 28 = 168$
Let's simplify again: $\sqrt{42 \times 16 \times 14 \times 12} = \sqrt{(6 \times 7) \times 16 \times (2 \times 7) \times (2 \times 6)}$
$\text{Area of Triangle} = \sqrt{6^2 \times 7^2 \times 2^2 \times 16}$
$\text{Area of Triangle} = 6 \times 7 \times 2 \times \sqrt{16}$
$\text{Area of Triangle} = 84 \times 4 = 336$ cm$^2$
The area of the triangle is 336 cm$^2$.
Given that the area of the parallelogram is equal to the area of the triangle:
$\text{Area of Parallelogram} = 336 \text{ cm}^2$
The formula for the area of a parallelogram is Base $\times$ Height.
The base of the parallelogram is given as 28 cm.
Base $\times$ Height = 336
28 cm $\times$ Height = 336 cm$^2$
Now, solve for the Height:
Height = $\frac{336}{28}$ cm
Height = 12 cm
The height of the parallelogram is 12 cm.
Question 5. A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Answer:
Given:
A rhombus shaped field with side length = 30 m.
Length of the longer diagonal = 48 m.
Number of cows to graze = 18.
To Find:
The area of grass field each cow will get.
Solution:
Let the rhombus be ABCD. Let the diagonals AC and BD intersect at point O.
All sides of a rhombus are equal, so AB = BC = CD = DA = 30 m.
Let the longer diagonal be AC = 48 m.
The diagonals of a rhombus bisect each other at right angles.
So, AO = OC = $\frac{1}{2} \times \text{AC} = \frac{1}{2} \times 48 \text{ m} = 24$ m.
Also, $\angle$AOB = $90^\circ$.
Consider the right-angled triangle $\triangle$AOB. By the Pythagorean theorem, we have:
$\text{AB}^2 = \text{AO}^2 + \text{BO}^2$
Substitute the known values:
$(30)^2 = (24)^2 + \text{BO}^2$
900 = 576 + BO$^2$
Solve for BO$^2$:
BO$^2$ = 900 - 576 = 324
Find BO:
BO = $\sqrt{324} = 18$ m
The other diagonal BD is twice the length of BO:
BD = 2 $\times$ BO = 2 $\times$ 18 m = 36 m
The area of a rhombus is given by the formula $\frac{1}{2} \times d_1 \times d_2$, where $d_1$ and $d_2$ are the lengths of the diagonals.
$\text{Area of Rhombus} = \frac{1}{2} \times \text{AC} \times \text{BD}$
$\text{Area} = \frac{1}{2} \times 48 \text{ m} \times 36 \text{ m}$
$\text{Area} = 24 \times 36 \text{ m}^2$
$\text{Area} = 864 \text{ m}^2$
The total area of the grass field is 864 m$^2$.
This area is for 18 cows to graze. To find the area each cow will get, divide the total area by the number of cows.
$\text{Area per cow} = \frac{\text{Total Area}}{\text{Number of Cows}}$
$\text{Area per cow} = \frac{864 \text{ m}^2}{18}$
Perform the division:
$\frac{864}{18} = 48$
$\text{Area per cow} = 48 \text{ m}^2$
Each cow will get 48 m$^2$ of grass field to graze.
Question 6. An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Fig. 12.16), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
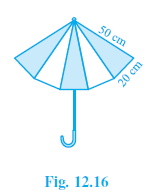
Answer:
Given:
Total number of triangular pieces in the umbrella = 10.
Number of different colours = 2.
Dimensions of each triangular piece: sides of length 20 cm, 50 cm, and 50 cm.
To Find:
The amount of cloth of each colour required for the umbrella.
Solution:
The umbrella is made of 10 triangular pieces of two different colours. Since the total number of pieces is 10 and there are two colours, there are $10 \div 2 = 5$ pieces of each colour.
We need to find the area of one triangular piece and then multiply it by the number of pieces of each colour (which is 5).
The sides of one triangular piece are $a = 20$ cm, $b = 50$ cm, and $c = 50$ cm.
We use Heron's formula to find the area of this triangle.
First, calculate the semi-perimeter ($s$) of the triangle:
s = $\frac{a+b+c}{2}$
s = $\frac{20 + 50 + 50}{2}$ cm
s = $\frac{120}{2}$ cm
s = 60 cm
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 60 - 20 = 40$ cm
$(s-b) = 60 - 50 = 10$ cm
$(s-c) = 60 - 50 = 10$ cm
Area of one triangular piece = $\sqrt{s(s-a)(s-b)(s-c)}$
Area = $\sqrt{60 \times 40 \times 10 \times 10}$
Simplify the expression under the square root:
Area = $\sqrt{(6 \times 10) \times (4 \times 10) \times 10 \times 10}$
Area = $\sqrt{6 \times 4 \times 10 \times 10 \times 10 \times 10}$
Area = $\sqrt{24 \times 10^4}$
Area = $\sqrt{(4 \times 6) \times 10^4}$
Area = $\sqrt{4} \times \sqrt{6} \times \sqrt{10^4}$
Area = $2 \times \sqrt{6} \times 10^2$
Area = $200\sqrt{6}$ cm$^2$
The area of one triangular piece is $200\sqrt{6}$ cm$^2$.
Since there are 5 pieces of each colour, the total area of cloth of one colour is:
Area of cloth of one colour = Area of one piece $\times$ Number of pieces of one colour
Area per colour = $200\sqrt{6} \text{ cm}^2 \times 5$
Area per colour = $1000\sqrt{6}$ cm$^2$
The amount of cloth of each colour required for the umbrella is $1000\sqrt{6}$ cm$^2$.
Question 7. A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Fig. 12.17. How much paper of each shade has been used in it?

Answer:
Given:
A kite composed of three parts:
Part 1: A square with a diagonal of 32 cm (divided into two equal parts by the diagonal).
Part 3: An isosceles triangle with base 8 cm and equal sides 6 cm each.
The square part is divided into two shades (Shade 1 and Shade 2), and the triangular part is the third shade (Shade 3).
To Find:
The amount of paper of each shade used.
Solution:
Area of the square part (Shade 1 and Shade 2):
A square is a rhombus, and its diagonals are perpendicular bisectors of each other. The area of a rhombus is $\frac{1}{2} \times d_1 \times d_2$. For a square, the diagonals are equal ($d_1 = d_2 = 32$ cm).
Area of Square = $\frac{1}{2} \times \text{diagonal}_1 \times \text{diagonal}_2$
Area of Square = $\frac{1}{2} \times 32 \text{ cm} \times 32 \text{ cm}$
Area of Square = $\cancel{16}^{16} \times 32$ cm$^2$
Area of Square = $16 \times 32 = 512$ cm$^2$
The square part is divided into two equal triangles by a diagonal (assuming the diagonal shown divides the shaded regions). These two triangles represent Shade 1 and Shade 2.
Area of Shade 1 = $\frac{1}{2} \times$ Area of Square
Area of Shade 1 = $\frac{1}{2} \times 512 \text{ cm}^2 = 256 \text{ cm}^2$
Area of Shade 2 = $\frac{1}{2} \times$ Area of Square
Area of Shade 2 = $\frac{1}{2} \times 512 \text{ cm}^2 = 256 \text{ cm}^2$
Area of the triangular part (Shade 3):
This is an isosceles triangle with base $b = 8$ cm and equal sides $a = 6$ cm and $c = 6$ cm.
We use Heron's formula to find the area.
First, calculate the semi-perimeter ($s$) of this triangle:
s = $\frac{a+b+c}{2}$
s = $\frac{6 + 8 + 6}{2}$ cm
s = $\frac{20}{2}$ cm
s = 10 cm
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 10 - 6 = 4$ cm
$(s-b) = 10 - 8 = 2$ cm
$(s-c) = 10 - 6 = 4$ cm
Area of Shade 3 = $\sqrt{s(s-a)(s-b)(s-c)}$
Area$_3$ = $\sqrt{10 \times 4 \times 2 \times 4}$
Simplify the expression under the square root:
Area$_3$ = $\sqrt{(2 \times 5) \times 4 \times 2 \times 4}$
Area$_3$ = $\sqrt{2 \times 5 \times 2^2 \times 2 \times 2^2}$
Area$_3$ = $\sqrt{2^4 \times 5 \times 2^2}$
Area$_3$ = $\sqrt{2^4 \times 5 \times 2^2}$
Let's simplify again: $\sqrt{10 \times 4 \times 2 \times 4} = \sqrt{10 \times 32} = \sqrt{320}$
Area$_3$ = $\sqrt{64 \times 5}$
Area$_3$ = $\sqrt{64} \times \sqrt{5}$
Area$_3$ = $8\sqrt{5}$ cm$^2$
Amount of paper of Shade 1 = 256 cm$^2$.
Amount of paper of Shade 2 = 256 cm$^2$.
Amount of paper of Shade 3 = $8\sqrt{5}$ cm$^2$.
Question 8. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50p per cm2.

Answer:
Given:
Number of triangular tiles = 16.
Sides of each triangular tile are $a = 9$ cm, $b = 28$ cm, and $c = 35$ cm.
Cost of polishing = 50 paise per cm$^2$ = $\textsf{₹}\ 0.50$ per cm$^2$.
To Find:
The total cost of polishing all the tiles.
Solution:
First, we find the area of one triangular tile using Heron's formula.
The sides of one tile are 9 cm, 28 cm, and 35 cm.
The semi-perimeter ($s$) of the triangle is:
s = $\frac{a+b+c}{2}$
s = $\frac{9 + 28 + 35}{2}$ cm
s = $\frac{72}{2}$ cm
s = 36 cm
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 36 - 9 = 27$ cm
$(s-b) = 36 - 28 = 8$ cm
$(s-c) = 36 - 35 = 1$ cm
Area of one triangular tile = $\sqrt{s(s-a)(s-b)(s-c)}$
Area of one tile = $\sqrt{36 \times 27 \times 8 \times 1}$
Simplify the expression under the square root:
Area of one tile = $\sqrt{(6^2) \times (3^3) \times (2^3)}$
Area of one tile = $\sqrt{(6^2) \times (3 \times 3^2) \times (2 \times 2^2)}$
Area of one tile = $\sqrt{6^2 \times 3^2 \times 2^2 \times 3 \times 2}$
Area of one tile = $\sqrt{(6^2 \times 3^2 \times 2^2) \times 6}$
Area of one tile = $\sqrt{6^2} \times \sqrt{3^2} \times \sqrt{2^2} \times \sqrt{6}$
Area of one tile = $6 \times 3 \times 2 \times \sqrt{6}$
Area of one tile = $36\sqrt{6}$ cm$^2$
The total area of 16 tiles is the area of one tile multiplied by 16.
Total Area = Area of one tile $\times$ Number of tiles
Total Area = $36\sqrt{6} \text{ cm}^2 \times 16$
Total Area = 576$\sqrt{6}$ cm$^2$
The cost of polishing is 50 paise per cm$^2$, which is $\textsf{₹}\ 0.50$ per cm$^2$.
Total cost of polishing = Total Area $\times$ Rate per cm$^2$
Total Cost = $576\sqrt{6} \text{ cm}^2 \times \textsf{₹}\ 0.50 / \text{cm}^2$
Total Cost = $576\sqrt{6} \times 0.50 \textsf{₹}$
Total Cost = $576\sqrt{6} \times \frac{1}{2} \textsf{₹}$
Total Cost = $288\sqrt{6}$ $\textsf{₹}$
The total cost of polishing the tiles is $288\sqrt{6}$ $\textsf{₹}$.
Question 9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Answer:
Given:
A field in the shape of a trapezium ABCD, with parallel sides AB and DC.
Length of parallel sides: AB = 25 m, DC = 10 m.
Length of non-parallel sides: AD = 13 m, BC = 14 m.
To Find:
The area of the trapezium ABCD.
Solution:
To find the area of the trapezium, we need its height. We can find the height by drawing a line parallel to one of the non-parallel sides from a vertex of the shorter parallel side, forming a parallelogram and a triangle.
Draw a line CE parallel to AD, where E is a point on AB.
Since AECD is a parallelogram (AD $\parallel$ CE and AE $\parallel$ DC), we have:
AE = DC = 10 m
CE = AD = 13 m
Now, consider $\triangle$BCE. The side BE = AB - AE = 25 m - 10 m = 15 m.
The sides of $\triangle$BCE are BE = 15 m, BC = 14 m, and CE = 13 m.
We can find the area of $\triangle$BCE using Heron's formula.
Let the sides of $\triangle$BCE be $a=15$, $b=14$, and $c=13$.
The semi-perimeter ($s$) of $\triangle$BCE is:
s = $\frac{a+b+c}{2}$
s = $\frac{15 + 14 + 13}{2}$ m = $\frac{42}{2}$ m = 21 m
Now, calculate the differences $(s-a)$, $(s-b)$, and $(s-c)$.
$(s-a) = 21 - 15 = 6$ m
$(s-b) = 21 - 14 = 7$ m
$(s-c) = 21 - 13 = 8$ m
Area of $\triangle$BCE = $\sqrt{s(s-a)(s-b)(s-c)}$
Area of $\triangle$BCE = $\sqrt{21 \times 6 \times 7 \times 8}$
Simplify the expression under the square root:
Area of $\triangle$BCE = $\sqrt{(3 \times 7) \times (2 \times 3) \times 7 \times (2^3)}$
Area of $\triangle$BCE = $\sqrt{2^4 \times 3^2 \times 7^2}$
Area of $\triangle$BCE = $\sqrt{2^4} \times \sqrt{3^2} \times \sqrt{7^2}$
Area of $\triangle$BCE = $2^2 \times 3 \times 7$
Area of $\triangle$BCE = $4 \times 21 = 84$ m$^2$
Now, we know the area of $\triangle$BCE and its base BE = 15 m. We can find the height (h) of $\triangle$BCE corresponding to the base BE. This height is also the height of the trapezium.
Area of $\triangle$BCE = $\frac{1}{2} \times \text{base} \times \text{height}$
84 m$^2$ = $\frac{1}{2} \times 15 \text{ m} \times h$
Solve for $h$:
$h = \frac{2 \times 84}{15}$ m
$h = \frac{168}{15}$ m
$h = \frac{56}{5}$ m = 11.2 m
The height of the trapezium is 11.2 m.
The area of a trapezium is given by the formula:
Area of Trapezium = $\frac{1}{2} \times$ (sum of parallel sides) $\times$ height
Area = $\frac{1}{2} \times (\text{AB} + \text{DC}) \times h$
Substitute the values:
Area = $\frac{1}{2} \times (25 \text{ m} + 10 \text{ m}) \times 11.2 \text{ m}$
Area = $\frac{1}{2} \times 35 \text{ m} \times 11.2 \text{ m}$
Area = $35 \times 5.6$ m$^2$
Area = 196 m$^2$
The area of the field is 196 m$^2$.

