| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 6.1) | Exercise 6.1 | Example 4 to 6 (Before Exercise 6.2) |
| Exercise 6.2 | Example 7 & 8 (Before Exercise 6.3) | Exercise 6.3) |
Chapter 6 Lines And Angles
Welcome to the solutions for Chapter 6, "Lines And Angles." This crucial chapter represents a significant step forward from foundational geometric concepts typically introduced in Classes 7 and 8. It acts as a vital bridge, transitioning learners from intuitive understanding and basic calculations towards the more rigorous world of geometric proofs and deductive reasoning. The solutions provided here are designed not just to give answers, but to meticulously explain the underlying principles, axioms, and theorems that govern the behavior of lines and angles. Mastering this chapter is absolutely essential, as it lays the indispensable groundwork for subsequent chapters dealing with triangles, quadrilaterals, and circles, where the properties explored here are constantly applied. Think of this as learning the fundamental grammar of geometry, enabling you to construct logical arguments and solve complex spatial problems.
The journey begins by revisiting and reinforcing core definitions to ensure absolute clarity and precision, which is paramount in formal geometry. The solutions carefully define and illustrate concepts such as:
- Line segment: A part of a line with two distinct endpoints.
- Ray: A part of a line starting at a particular point and extending infinitely in one direction.
- Collinear points: Points that lie on the same straight line ($\ge 3$ points).
- Non-collinear points: Points that do not all lie on the same straight line.
- Types of Angles: Including acute ($< 90^\circ$), obtuse ($> 90^\circ$ but $< 180^\circ$), right ($= 90^\circ$), straight ($= 180^\circ$), and reflex ($> 180^\circ$ but $< 360^\circ$).
- Adjacent angles: Two angles sharing a common vertex and a common arm, but with non-common arms on opposite sides of the common arm.
- Linear pair of angles: A pair of adjacent angles whose non-common arms form a straight line. Their sum is always $180^\circ$.
- Vertically opposite angles: Angles formed by the intersection of two lines, positioned opposite to each other. They are proven to be equal.
Building upon these definitions, the solutions extensively demonstrate the application of the Linear Pair Axiom. This axiom states that if a ray stands on a line, the sum of the two adjacent angles formed is $180^\circ$. For instance, if $\angle 1$ and $\angle 2$ form a linear pair, then $\angle 1 + \angle 2 = 180^\circ$. Coupled with this is the crucial theorem stating that vertically opposite angles are equal. Solutions provide step-by-step procedures showing how knowing just one angle in a setup of intersecting lines allows for the determination of all other angles using these two principles. A major focus is then shifted towards the scenario of parallel lines intersected by a transversal line. The solutions meticulously dissect the various pairs of angles formed – corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles (also known as co-interior angles).
Central to this section are key axioms and theorems connecting parallel lines and transversals. The solutions emphasize:
- If two parallel lines are cut by a transversal, then pairs of corresponding angles are equal (This is treated as an axiom).
- If two parallel lines are cut by a transversal, then pairs of alternate interior angles are equal (This is a theorem derived from the axiom).
- If two parallel lines are cut by a transversal, then pairs of consecutive interior angles are supplementary, meaning their sum is $180^\circ$ (This is also a theorem).
Finally, the chapter and its solutions culminate in applying these line and angle properties within triangles. Two cornerstone theorems are covered: the Angle Sum Property of a Triangle, which states that the sum of the three interior angles of any triangle is always $180^\circ$ (i.e., $\angle A + \angle B + \angle C = 180^\circ$), and the Exterior Angle Theorem, stating that if a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles. The solutions often include formal proofs for these theorems, frequently utilizing constructions involving parallel lines, thereby reinforcing earlier concepts. Extensive practice problems involving finding unknown angles in various triangular configurations are solved, always stressing the importance of logical reasoning and the explicit justification of each step using the appropriate definition, axiom, or theorem.
Example 1 to 3 (Before Exercise 6.1)
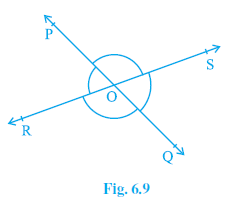
Example 1. In Fig. 6.9, lines PQ and RS intersect each other at point O. If ∠ POR : ∠ ROQ = 5 : 7, find all the angles.
Answer:
Given: Lines PQ and RS intersect at point O. $∠ POR : ∠ ROQ = 5 : 7$.
To Find: All the angles: $∠ POR$, $∠ ROQ$, $∠ QOS$, $∠ POS$.
Solution:
Since ray OR stands on line PQ, $∠ POR$ and $∠ ROQ$ form a linear pair.
By the Linear Pair Axiom:
$∠ POR + ∠ ROQ = 180°$
Given the ratio $∠ POR : ∠ ROQ = 5 : 7$.
Let $∠ POR = 5x$ and $∠ ROQ = 7x$.
Substituting these into the linear pair equation:
$5x + 7x = 180°$
$12x = 180°$
$x = \frac{180°}{12}$
$x = 15°$
Now, find the angles:
$∠ POR = 5x = 5 \times 15° = 75°$
$∠ ROQ = 7x = 7 \times 15° = 105°$
Since lines PQ and RS intersect at O, vertically opposite angles are equal:
$∠ QOS = ∠ POR$ (Vertically opposite angles)
$∠ QOS = 75°$
$∠ POS = ∠ ROQ$ (Vertically opposite angles)
$∠ POS = 105°$
Therefore, the angles are: $∠ POR = 75°$, $∠ ROQ = 105°$, $∠ QOS = 75°$, and $∠ POS = 105°$.
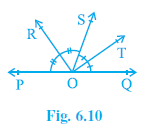
Example 2. In Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠ POS and ∠ SOQ, respectively. If ∠ POS = x, find ∠ROT.
Answer:
Given:
- POQ is a straight line.
- Ray OS stands on the line POQ.
- Ray OR bisects $\angle POS$.
- Ray OT bisects $\angle SOQ$.
- $\angle POS = x$.
To Find:
The measure of $\angle ROT$.
Solution:
Since ray OS stands on the line POQ, the angles $\angle POS$ and $\angle SOQ$ form a linear pair. The sum of angles in a linear pair is $180^\circ$.
$\angle POS + \angle SOQ = 180^\circ$
(Linear Pair Axiom)
We are given that $\angle POS = x$. Substituting this into the equation:
$x + \angle SOQ = 180^\circ$
$\angle SOQ = 180^\circ - x$
... (i)
We are also given that ray OR is the angle bisector of $\angle POS$. An angle bisector divides an angle into two equal halves.
$\angle ROS = \frac{1}{2}\angle POS = \frac{1}{2}x$
... (ii)
Similarly, ray OT is the angle bisector of $\angle SOQ$.
$\angle SOT = \frac{1}{2}\angle SOQ$
(Definition of angle bisector)
Substituting the value of $\angle SOQ$ from equation (i):
$\angle SOT = \frac{1}{2}(180^\circ - x)$
... (iii)
From the figure, we can see that $\angle ROT$ is the sum of $\angle ROS$ and $\angle SOT$.
$\angle ROT = \angle ROS + \angle SOT$
Now, we substitute the values from equations (ii) and (iii):
$\angle ROT = \frac{1}{2}x + \frac{1}{2}(180^\circ - x)$
$\angle ROT = \frac{1}{2}x + \frac{180^\circ}{2} - \frac{1}{2}x$
$\angle ROT = \frac{1}{2}x + 90^\circ - \frac{1}{2}x$
$\angle ROT = 90^\circ$
Therefore, the measure of $\angle ROT$ is $90^\circ$, regardless of the value of $x$.
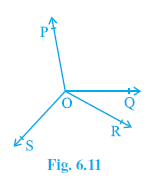
Example 3. In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠ POQ + ∠ QOR + ∠ SOR + ∠ POS = 360°.
Answer:
Given:
Four rays OP, OQ, OR, and OS originate from the same point O, forming four angles around the point.
To Prove:
$\angle POQ + \angle QOR + \angle SOR + \angle POS = 360^\circ$.
Construction Required:
We need to introduce a straight line to use the linear pair axiom. We can do this by extending one of the rays in the opposite direction. Let's extend the ray OQ backwards to a point T, which forms the straight line TOQ.
Proof:
From our construction, TOQ is a straight line.
The sum of all angles on one side of the line is $180^\circ$. The angles on the side of ray OP are $\angle POQ$ and $\angle POT$. Therefore:
$\angle POQ + \angle POT = 180^\circ$
(Linear Pair Axiom) ... (i)
The sum of all angles on the other side of the line TOQ is also $180^\circ$. The angles that form the straight angle are $\angle TOS$ and $\angle SOQ$. So,
$\angle TOS + \angle SOR + \angle QOR = 180^\circ$
(Linear Pair Axiom) ... (ii)
Now, adding equation (i) and (ii)):
$(\angle POQ + \angle POT) + (\angle TOS + \angle SOR + \angle QOR) = 180^\circ + 180^\circ = 360^\circ$
From the figure, we can combine the angles $\angle POT$ and $\angle TOS$ to form the original angle $\angle POS$.
$\angle POT + \angle TOS = \angle POS$.
Substituting this back into our sum:
$\angle POQ + (\angle POT + \angle TOS) + \angle SOR + \angle QOR = 360^\circ$
$\angle POQ + \angle POS + \angle SOR + \angle QOR = 360^\circ$
Rearranging the terms to match the required format:
$\angle POQ + \angle QOR + \angle SOR + \angle POS = 360^\circ$
Hence, proved.
Exercise 6.1
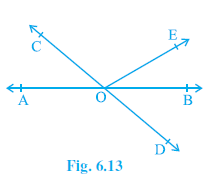
Question 1. In Fig. 6.13, lines AB and CD intersect at O. If ∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find ∠ BOE and reflex ∠ COE.
Answer:
Given: Lines AB and CD intersect at O. $∠ AOC + ∠ BOE = 70°$. $∠ BOD = 40°$.
To Find: $∠ BOE$ and reflex $∠ COE$.
Solution:
Lines AB and CD intersect at O.
Therefore, $∠ AOC = ∠ BOD$ (Vertically opposite angles).
Since $∠ BOD = 40°$, we have $∠ AOC = 40°$.
Now, use the given sum:
$∠ AOC + ∠ BOE = 70°$
Substitute $∠ AOC = 40°$:
$40° + ∠ BOE = 70°$
$∠ BOE = 70° - 40°$
$∠ BOE = 30°$
Since AB is a straight line and rays OC and OE stand on it:
$∠ AOC + ∠ COE + ∠ BOE = 180°$ (Angles on a straight line)
We know $∠ AOC + ∠ BOE = 70°$. Substitute this sum into the equation:
$70° + ∠ COE = 180°$
$∠ COE = 180° - 70°$
$∠ COE = 110°$
We need to find reflex $∠ COE$.
Reflex $∠ COE = 360° - ∠ COE$
Reflex $∠ COE = 360° - 110°$
Reflex $∠ COE = 250°$
Therefore, $∠ BOE = 30°$ and reflex $∠ COE = 250°$.
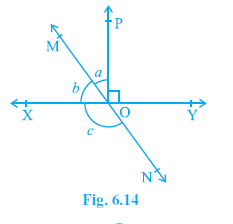
Question 2. In Fig. 6.14, lines XY and MN intersect at O. If ∠ POY = 90° and a : b = 2 : 3, find c.
Answer:
Given: Lines XY and MN intersect at O. $∠ POY = 90°$. $a : b = 2 : 3$. (Where $a = ∠ POM$, $b = ∠ MOX$).
To Find: Angle $c$ (where $c = ∠ XON$).
Solution:
Ray OP stands on line XY.
Therefore, $∠ POX + ∠ POY = 180°$ (Linear Pair Axiom)
$∠ POX + 90° = 180°$
$∠ POX = 180° - 90° = 90°$
From the figure, $∠ POX = ∠ POM + ∠ MOX = a + b$.
So, $a + b = 90°$.
Given the ratio $a : b = 2 : 3$.
Let $a = 2k$ and $b = 3k$.
Substitute these into the sum equation:
$2k + 3k = 90°$
$5k = 90°$
$k = \frac{90°}{5} = 18°$
So, $a = 2k = 2 \times 18° = 36°$
And $b = 3k = 3 \times 18° = 54°$.
Now, consider the line MN. Ray OX stands on it.
Therefore, $∠ MOX + ∠ XON = 180°$ (Linear Pair Axiom)
$b + c = 180°$
Substitute the value of $b = 54°$:
$54° + c = 180°$
$c = 180° - 54°$
$c = 126°$
Therefore, $c = 126°$.
Question 3. In Fig. 6.15, ∠ PQR = ∠ PRQ, then prove that ∠ PQS = ∠ PRT.
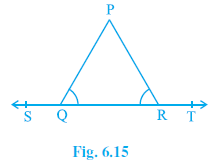
Answer:
Given: In Figure 6.15, ST is a straight line and $∠ PQR = ∠ PRQ$.
To Prove: $∠ PQS = ∠ PRT$.
Proof:
Ray QP stands on the straight line ST.
Therefore, $∠ PQS$ and $∠ PQR$ form a linear pair.
$∠ PQS + ∠ PQR = 180°$ (Linear Pair Axiom)
$∠ PQS = 180° - ∠ PQR$
$∠ PQS = 180° - ∠ PQR$
...(1)
Ray RP stands on the straight line ST.
Therefore, $∠ PRT$ and $∠ PRQ$ form a linear pair.
$∠ PRT + ∠ PRQ = 180°$ (Linear Pair Axiom)
$∠ PRT = 180° - ∠ PRQ$
$∠ PRT = 180° - ∠ PRQ$
...(2)
We are given that $∠ PQR = ∠ PRQ$
$∠ PQR = ∠ PRQ$
...(3)
Using equation (3) in equation (1):
$∠ PQS = 180° - ∠ PRQ$
...(4)
Comparing equations (2) and (4):
The right-hand sides are equal ($180° - ∠ PRQ$).
Therefore, the left-hand sides must be equal.
$∠ PQS = ∠ PRT$
Hence, proved.
Question 4. In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
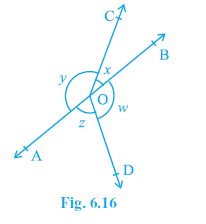
Answer:
Given: Angles $x, y, z, w$ around point O such that $x + y = w + z$.
To Prove: AOB is a straight line.
Proof:
The sum of all angles around a point is $360°$.
$x + y + w + z = 360°$
$x + y + w + z = 360°$
...(1)
We are given that $x + y = w + z$
$x + y = w + z$
...(2)
Substitute (2) into (1):
$(x + y) + (x + y) = 360°$
$2(x + y) = 360°$
$x + y = \frac{360°}{2}$
$x + y = 180°$
Alternatively, substituting (2) into (1):
$(w + z) + (w + z) = 360°$
$2(w + z) = 360°$
$w + z = \frac{360°}{2}$
$w + z = 180°$
From the figure, $x$ ($∠ BOC$) and $y$ ($∠ AOC$) are adjacent angles with non-common arms OB and OA. Since their sum ($x + y$) is $180°$, the non-common arms OA and OB form a straight line.
Similarly, $w$ ($∠ AOD$) and $z$ ($∠ BOD$) are adjacent angles whose sum is $180°$, so their non-common arms OA and OB form a straight line.
By the axiom (Converse of Linear Pair Axiom): If the sum of two adjacent angles is $180°$, then their non-common arms form a straight line.
Since $x + y = 180°$ (or $w + z = 180°$), AOB is a straight line.
Hence, proved.
Question 5. In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
∠ ROS = $\frac{1}{2}$ (∠ QOS – ∠ POS).
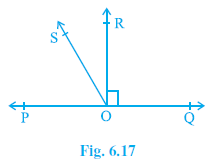
Answer:
Given:
- POQ is a straight line.
- Ray OR is perpendicular to line PQ. This means $\angle ROQ = 90^\circ$.
- Ray OS lies between rays OP and OR.
To Prove:
$\angle ROS = \frac{1}{2} (\angle QOS - \angle POS)$
Proof:
Since ray OR is perpendicular to the line PQ, we know that the angle it makes with the line is $90^\circ$.
$\angle ROQ = 90^\circ$
(Given)
Also, since POQ is a straight line, the angles on one side form a linear pair, summing to $180^\circ$.
$\angle POR + \angle ROQ = 180^\circ$
$\angle POR + 90^\circ = 180^\circ$
$\angle POR = 90^\circ$
... (i)
From the figure, we can express $\angle POR$ in terms of other angles. Ray OS lies within $\angle POR$.
$\angle POR = \angle POS + \angle ROS$
Substituting the value of $\angle POR$ from equation (i):
$90^\circ = \angle POS + \angle ROS$
We can rearrange this to express $\angle ROS$ in terms of $\angle POS$:
$\angle ROS = 90^\circ - \angle POS$
... (ii)
Now, let's look at the angles on the other side of ray OR. From the figure, we can see that:
$\angle QOS = \angle ROQ + \angle ROS$
Substituting $\angle ROQ = 90^\circ$:
$\angle QOS = 90^\circ + \angle ROS$
This gives us another expression for $\angle ROS$, but let's try a different path. We want to prove something involving $(\angle QOS - \angle POS)$. Let's construct this expression.
From the figure, we can write:
$\angle QOS = \angle ROQ + \angle ROS = 90^\circ + \angle ROS$
$\angle POS = \angle POR - \angle ROS = 90^\circ - \angle ROS$
Now, let's subtract the second equation from the first:
$\angle QOS - \angle POS = (90^\circ + \angle ROS) - (90^\circ - \angle ROS)$
$\angle QOS - \angle POS = 90^\circ + \angle ROS - 90^\circ + \angle ROS$
$\angle QOS - \angle POS = 2 \angle ROS$
Now, we can isolate $\angle ROS$ by dividing both sides by 2:
$\frac{1}{2}(\angle QOS - \angle POS) = \angle ROS$
Rearranging this gives the desired result:
$\angle ROS = \frac{1}{2}(\angle QOS - \angle POS)$
Hence, proved.
Question 6. It is given that ∠ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP.
Answer:
Given:
- $\angle XYZ = 64^\circ$.
- Line segment XY is produced (extended) to a point P, which means PYX is a straight line.
- Ray YQ bisects $\angle ZYP$.
To Find:
- $\angle XYQ$
- reflex $\angle QYP$
Figure:
First, we draw a figure based on the given information.
Solution:
Since PYX is a straight line, the angles on the line at point Y form a linear pair and their sum is $180^\circ$.
$\angle XYZ + \angle ZYP = 180^\circ$ (Linear Pair)
We are given $\angle XYZ = 64^\circ$.
$64^\circ + \angle ZYP = 180^\circ$
$\angle ZYP = 180^\circ - 64^\circ$
$\angle ZYP = 116^\circ$
Now, we are told that ray YQ bisects $\angle ZYP$. This means it divides $\angle ZYP$ into two equal angles: $\angle ZYQ$ and $\angle QYP$.
$\angle ZYQ = \angle QYP = \frac{1}{2} \angle ZYP$
$\angle QYP = \frac{1}{2} (116^\circ) = 58^\circ$
Finding $\angle XYQ$:
From the figure, we can see that $\angle XYQ$ is the sum of $\angle XYZ$ and $\angle ZYQ$.
$\angle XYQ = \angle XYZ + \angle ZYQ$
Since $\angle ZYQ = \angle QYP = 58^\circ$, we have:
$\angle XYQ = 64^\circ + 58^\circ$
$\angle XYQ = 122^\circ$
Finding reflex $\angle QYP$:
A reflex angle is an angle that is greater than $180^\circ$ and less than $360^\circ$. The reflex angle of any angle $\theta$ is calculated as $360^\circ - \theta$.
We found that $\angle QYP = 58^\circ$.
Reflex $\angle QYP = 360^\circ - \angle QYP$
Reflex $\angle QYP = 360^\circ - 58^\circ$
Reflex $\angle QYP = 302^\circ$
Final Answers:
- $\angle XYQ = \bf{122^\circ}$
- Reflex $\angle QYP = \bf{302^\circ}$
Example 4 to 6 (Before Exercise 6.2)
Example 4. In Fig. 6.24, if PQ || RS, ∠ MXQ = 135° and ∠ MYR = 40°, find ∠XMY
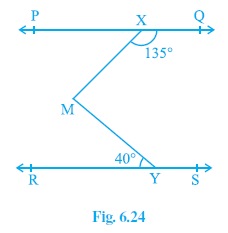
Answer:
Given:
- Line PQ is parallel to line RS (PQ || RS).
- $\angle MXQ = 135^\circ$
- $\angle MYR = 40^\circ$
To Find:
The measure of $\angle XMY$.
Construction Required:
To find $\angle XMY$, we need to relate it to the given angles. We can do this by drawing a line through point M that is parallel to both PQ and RS. Let's draw a line AB through M such that AB || PQ.
Solution:
Since we have constructed AB || PQ, and it is given that PQ || RS, it follows that all three lines are parallel to each other.
AB || RS
(Lines parallel to the same line are parallel to each other)
Now, we can find the two parts of $\angle XMY$ separately.
1. Finding $\angle XMB$:
Consider the parallel lines PQ and AB intersected by the transversal XM. The angles $\angle QXM$ and $\angle XMB$ are consecutive interior angles (or co-interior angles).
The sum of consecutive interior angles is $180^\circ$.
$\angle QXM + \angle XMB = 180^\circ$
(Consecutive interior angles)
We are given $\angle MXQ = 135^\circ$, which is the same as $\angle QXM$.
$135^\circ + \angle XMB = 180^\circ$
$\angle XMB = 180^\circ - 135^\circ$
$\angle XMB = 45^\circ$
... (i)
2. Finding $\angle YMB$:
Consider the parallel lines RS and AB intersected by the transversal YM. The angles $\angle MYR$ and $\angle YMB$ are alternate interior angles.
Alternate interior angles are equal.
$\angle YMB = \angle MYR$
(Alternate interior angles)
We are given $\angle MYR = 40^\circ$.
$\angle YMB = 40^\circ$
... (ii)
3. Finding $\angle XMY$:
From the figure, it is clear that $\angle XMY$ is the sum of the two angles we just found.
$\angle XMY = \angle XMB + \angle YMB$
Substituting the values from (i) and (ii):
$\angle XMY = 45^\circ + 40^\circ$
$\angle XMY = 85^\circ$
Therefore, the measure of $\angle XMY$ is $85^\circ$.
Example 5. If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
Answer:
Given:
- A transversal AD intersects two lines PQ and RS at points B and C, respectively.
- Ray BE is the bisector of $\angle ABQ$.
- Ray CG is the bisector of $\angle BCS$.
- The bisectors are parallel, i.e., BE || CG.
To Prove:
The two lines are parallel, i.e., PQ || RS.
Proof:
We are given that ray BE is the bisector of $\angle ABQ$. This means:
$\angle ABQ = 2 \angle ABE$
... (i)
Similarly, ray CG is the bisector of $\angle BCS$. This means:
$\angle BCS = 2 \angle BCG$
... (ii)
Now, we are also given that the bisectors BE and CG are parallel (BE || CG), and the line AD acts as a transversal for them.
When a transversal intersects two parallel lines, the corresponding angles are equal.
In this case, $\angle ABE$ and $\angle BCG$ are corresponding angles.
$\angle ABE = \angle BCG$
(Corresponding angles axiom, since BE || CG) ... (iii)
Now, we can use equations (i), (ii), and (iii) to establish a relationship between $\angle ABQ$ and $\angle BCS$.
From (iii), we know that $\angle ABE = \angle BCG$.
Multiplying both sides of this equation by 2:
$2 \angle ABE = 2 \angle BCG$
From (i), we can substitute $2 \angle ABE$ with $\angle ABQ$.
From (ii), we can substitute $2 \angle BCG$ with $\angle BCS$.
This gives us:
$\angle ABQ = \angle BCS$
Now, let's consider the lines PQ and RS with the transversal AD.
We have just shown that the corresponding angles, $\angle ABQ$ and $\angle BCS$, are equal.
According to the Converse of the Corresponding Angles Axiom, if a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel.
Since $\angle ABQ = \angle BCS$, it must be that:
PQ || RS
Hence, proved.
Example 6. In Fig. 6.27, AB || CD and CD || EF. Also EA⊥AB. If ∠BEF = 55°, find the values of x, y and z.

Answer:
Given:
- AB || CD and CD || EF, which implies AB || CD || EF.
- EA ⊥ AB, which means $\angle EAB = 90^\circ$.
- $\angle BEF = 55^\circ$.
To Find:
The values of x, y, and z.
Solution:
We will find the values of x, y, and z one by one using the properties of parallel lines and transversals.
Finding the value of x:
Consider the parallel lines AB and EF, with BE as the transversal.
The angles $x$ and $\angle BEF$ are consecutive interior angles (or co-interior angles). The sum of consecutive interior angles is $180^\circ$.
$x + \angle BEF = 180^\circ$
(Consecutive interior angles)
Substituting the given values:
$x + 55^\circ = 180^\circ$
$x = 180^\circ - 55^\circ$
$x = 125^\circ$
Finding the value of y:
The angles $x$ and $y$ are corresponding angles. Therefore, they are equal.
$y = x = 125^\circ$
(Corresponding angles)
$y = 125^\circ$
Finding the value of z:
We are given that EA ⊥ AB. Since AB || EF, the transversal EA must also be perpendicular to EF.
$\angle AEF = 90^\circ$
$90^\circ = z + 55^\circ$
$z = 90^\circ - 55^\circ$
$z = 35^\circ$
Final Answer:
$x = 125^\circ$
$y = 125^\circ$
$z = 35^\circ$
Exercise 6.2
Question 1. In Fig. 6.28, find the values of x and y and then show that AB || CD.
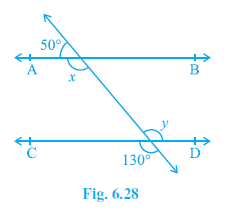
Answer:
Given: Two lines AB and CD intersected by a transversal. Specific angles are marked as 50°, x, y, and 130°.
To Find: Values of x and y.
To Show: AB || CD.
Solution:
Finding x:
The angle 50° and angle x form a linear pair on the transversal line where it intersects AB.
$50° + x = 180°$ (Linear Pair Axiom)
$x = 180° - 50°$
$\mathbf{x = 130°}$
Finding y:
The angle y and the angle 130° are vertically opposite angles formed by the intersection of line CD and the transversal.
$y = 130°$ (Vertically opposite angles are equal)
$\mathbf{y = 130°}$
Showing AB || CD:
We found $x = 130°$ and $y = 130°$.
From the figure, x and y are a pair of alternate interior angles.
By the Converse of the Alternate Interior Angles Theorem: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
Since $x = y = 130°$, we conclude that AB || CD.
Hence, x = 130°, y = 130°, and AB || CD is shown.
Question 2. In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.
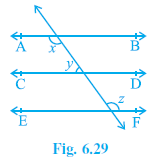
Answer:
Given: AB || CD, CD || EF. $y : z = 3 : 7$.
To Find: Value of x.
Solution:
Since AB || CD and CD || EF, we have AB || EF (Lines parallel to the same line are parallel to each other).
Consider AB || EF and the transversal intersecting them.
$x = z$ (Alternate interior angles are equal, as AB || EF)
$x = z$
...(1)
Consider AB || CD and the transversal intersecting them.
$x + y = 180°$ (Consecutive interior angles are supplementary)
$x + y = 180°$
...(2)
Substitute $x = z$ from (1) into (2):
$z + y = 180°$
Given $y : z = 3 : 7$.
Let $y = 3k$ and $z = 7k$.
Substitute these into the sum equation:
$7k + 3k = 180°$
$10k = 180°$
$k = \frac{180°}{10} = 18°$
Now find y and z:
$y = 3k = 3 \times 18° = 54°$
$z = 7k = 7 \times 18° = 126°$
Since $x = z$ (from step 1):
$\mathbf{x = 126°}$
Alternate Solution:
Let the angle vertically opposite to y on line CD be angle 'a'. So, $a = y$.
Since CD || EF, angle 'a' and angle z are consecutive interior angles.
$a + z = 180°$
Since $a = y$, we have $y + z = 180°$.
Given $y : z = 3 : 7$. Let $y = 3k$ and $z = 7k$.
$3k + 7k = 180°$
$10k = 180° \implies k = 18°$.
So, $y = 3 \times 18° = 54°$ and $z = 7 \times 18° = 126°$.
Since AB || CD, x and y are consecutive interior angles.
$x + y = 180°$
$x + 54° = 180°$
$x = 180° - 54°$
$\mathbf{x = 126°}$
Therefore, x = 126°.
Question 3. In Fig. 6.30, if AB || CD, EF⊥CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
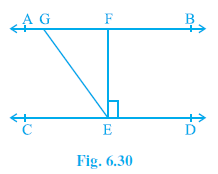
Answer:
Given: AB || CD, EF ⊥ CD, $∠ GED = 126°$.
To Find: $∠ AGE$, $∠ GEF$, $∠ FGE$.
Solution:
Finding $∠ AGE$:
Since AB || CD and GE is a transversal:
$∠ AGE = ∠ GED$ (Alternate interior angles are equal)
Given $∠ GED = 126°$.
Therefore, $\mathbf{∠ AGE = 126°}$.
Finding $∠ GEF$:
We are given $∠ GED = 126°$.
From the figure, $∠ GED = ∠ GEF + ∠ FED$.
Since EF ⊥ CD, $∠ FED = 90°$.
So, $126° = ∠ GEF + 90°$
$∠ GEF = 126° - 90°$
Therefore, $\mathbf{∠ GEF = 36°}$.
Finding $∠ FGE$:
Since AB || CD and GE is a transversal:
Consider the linear pair on line CD at point E. Let $∠CEG$ be the angle adjacent to $∠GED$.
$∠ CEG + ∠ GED = 180°$ (Linear Pair Axiom)
$∠ CEG + 126° = 180°$
$∠ CEG = 180° - 126° = 54°$.
Now, $∠ FGE$ and $∠ CEG$ are alternate interior angles formed by the transversal GE intersecting the parallel lines AB and CD.
$∠ FGE = ∠ CEG$ (Alternate interior angles)
Therefore, $\mathbf{∠ FGE = 54°}$.
(Alternatively: Using linear pair on line AB. $∠ AGE + ∠ FGE = 180°$. $126° + ∠ FGE = 180°$. $∠ FGE = 54°$. This assumes AGE and FGE form a linear pair on AB, which they do as G lies on AB and F is just a point defining the ray.)
Final Answer: $∠ AGE = 126°$, $∠ GEF = 36°$, $∠ FGE = 54°$.
Question 4. In Fig. 6.31, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint: Draw a line parallel to ST through point R.]
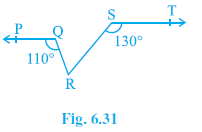
Answer:
Given:
In the given figure, we have:
PQ || ST
$\angle$PQR = 110°
$\angle$RST = 130°
To Find:
The measure of $\angle$QRS.
Construction:
As per the hint, we draw a line XY passing through point R, such that XY is parallel to ST.
Solution:
We are given that PQ || ST.
By construction, we have XY || ST.
Since lines parallel to the same line are parallel to each other, we have:
PQ || XY
Now, let's consider the parallel lines PQ and XY with QR as the transversal.
The sum of consecutive interior angles is 180°.
$\angle$PQR + $\angle$QRX = 180°
(Consecutive interior angles)
Substituting the given value of $\angle$PQR:
$110^\circ + \angle QRX = 180^\circ$
$\angle QRX = 180^\circ - 110^\circ$
$\angle QRX = 70^\circ$
... (i)
Next, let's consider the parallel lines ST and XY with SR as the transversal.
Again, the sum of consecutive interior angles is 180°.
$\angle$RST + $\angle$SRY = 180°
(Consecutive interior angles)
Substituting the given value of $\angle$RST:
$130^\circ + \angle SRY = 180^\circ$
$\angle SRY = 180^\circ - 130^\circ$
$\angle SRY = 50^\circ$
... (ii)
Now, XY is a straight line. The angles on the line XY at point R are $\angle$QRX, $\angle$QRS, and $\angle$SRY.
The angles on the straight line XY at point R are:
$\angle XRQ + \angle QRS + \angle SRY = 180^\circ$
Here, $\angle XRQ$ is the same as $\angle QRX$, and $\angle SRY$ is the angle between RS and RY.
So, $180^\circ = 70^\circ + \angle QRS + 50^\circ$
$180^\circ = 120^\circ + \angle QRS$
$\angle QRS = 180^\circ - 120^\circ$
$\angle QRS = 60^\circ$
Thus, the measure of $\angle$QRS is 60°.
Question 5. In Fig. 6.32, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y.

Answer:
Given: AB || CD, $∠ APQ = 50°$, $∠ PRD = 127°$. (In the figure, $∠PQR = x$, $∠QPR = y$).
To Find: Values of x and y.
Solution:
Finding x:
Since AB || CD and PQ is a transversal:
$∠ APQ = ∠ PQR$ (Alternate interior angles are equal)
Given $∠ APQ = 50°$ and $∠ PQR = x$.
Therefore, $\mathbf{x = 50°}$.
Finding y:
Since AB || CD and PR is a transversal:
$∠ APR = ∠ PRD$ (Alternate interior angles are equal)
From the figure, $∠ APR = ∠ APQ + ∠ QPR = 50° + y$.
Given $∠ PRD = 127°$.
So, $50° + y = 127°$
$y = 127° - 50°$
$\mathbf{y = 77°}$
Alternate method for y:
Consider triangle PQR. The exterior angle at R, which is $∠ PRD$, is equal to the sum of the two opposite interior angles ($∠ PQR + ∠ QPR$).
$∠ PRD = ∠ PQR + ∠ QPR$
$∠ PRD = x + y$
$127° = 50° + y$ (Substituting known values)
$y = 127° - 50°$
$\mathbf{y = 77°}$.
Therefore, x = 50° and y = 77°.
Question 6. In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
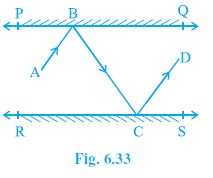
Answer:
Given:
Two plane mirrors PQ and RS are placed parallel to each other, i.e., PQ || RS.
An incident ray AB strikes the mirror PQ at point B.
The ray reflects along BC and strikes the mirror RS at point C.
The ray reflects again from mirror RS along CD.
To Prove:
The incident ray AB is parallel to the final reflected ray CD, i.e., AB || CD.
Construction:
Draw a normal BM to the mirror PQ at point B. (A normal is a line perpendicular to the surface).
Draw a normal CN to the mirror RS at point C.
So, BM ⊥ PQ and CN ⊥ RS.
Proof:
According to the laws of reflection, the angle of incidence is equal to the angle of reflection.
For the reflection at point B on mirror PQ:
Angle of incidence = $\angle$ABM
Angle of reflection = $\angle$MBC
$\angle$ABM = $\angle$MBC
... (i)
For the reflection at point C on mirror RS:
Angle of incidence = $\angle$BCN
Angle of reflection = $\angle$NCD
$\angle$BCN = $\angle$NCD
... (ii)
Now, we know that the mirrors PQ and RS are parallel (PQ || RS).
The normals BM and CN are perpendicular to the parallel lines PQ and RS respectively.
Since the lines perpendicular to two parallel lines are themselves parallel, we have:
BM || CN
Now, consider the parallel lines BM and CN, with the line segment BC as the transversal.
The alternate interior angles must be equal.
$\angle$MBC = $\angle$BCN
[Alternate interior angles] ... (iii)
From equations (i), (ii), and (iii), we can relate all four angles:
From (i) and (iii): $\angle$ABM = $\angle$BCN
From (ii) and (iii): $\angle$MBC = $\angle$NCD
Combining all, we get:
$\angle$ABM = $\angle$MBC = $\angle$BCN = $\angle$NCD
Now let's consider the angles $\angle$ABC and $\angle$BCD.
From the figure, we can write:
$\angle$ABC = $\angle$ABM + $\angle$MBC
Using equation (i), we can write this as:
$\angle$ABC = $\angle$MBC + $\angle$MBC = 2$\angle$MBC
Similarly, from the figure:
$\angle$BCD = $\angle$BCN + $\angle$NCD
Using equation (ii), we can write this as:
$\angle$BCD = $\angle$BCN + $\angle$BCN = 2$\angle$BCN
From equation (iii), we know that $\angle$MBC = $\angle$BCN.
Therefore, 2$\angle$MBC = 2$\angle$BCN.
This implies:
$\angle$ABC = $\angle$BCD
For the lines AB and CD, the line segment BC acts as a transversal. We have just proved that the pair of alternate interior angles, $\angle$ABC and $\angle$BCD, are equal.
By the converse of the alternate interior angles theorem, if the alternate interior angles are equal, then the lines are parallel.
Hence, AB || CD.
Proved.
Example 7 & 8 (Before Exercise 6.3)
Example 7. In Fig. 6.37, if QT⊥PR, ∠TQR = 40° and ∠SPR = 30°, find x and y.
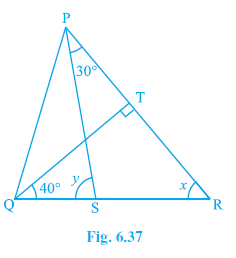
Answer:
Given: In ΔPQR, QT ⊥ PR, $∠ TQR = 40°$, $∠ SPR = 30°$. In the figure, $∠ TRQ = x$, $∠ PSR = y$.
To Find: Values of x and y.
Solution:
Finding x:
Consider ΔTQR.
Given QT ⊥ PR, so $∠ QTR = 90°$.
The sum of angles in a triangle is $180°$ (Angle Sum Property of a triangle).
In ΔTQR: $∠ TQR + ∠ TRQ + ∠ QTR = 180°$
$40° + x + 90° = 180°$
$x + 130° = 180°$
$x = 180° - 130°$
$\mathbf{x = 50°}$ (So, $∠ TRQ = 50°$).
Finding y:
Consider ΔPSR.
The exterior angle of a triangle is equal to the sum of the two opposite interior angles (Exterior Angle Theorem).
Exterior angle $∠ PSQ$ ($y$) = Interior opposite angles ($∠ SPR + ∠ SRP$)
Note that $∠ SRP$ is the same as $∠ TRQ$, which we found to be $x = 50°$.
So, $y = ∠ SPR + ∠ SRP$
$y = 30° + 50°$
$\mathbf{y = 80°}$
Therefore, x = 50° and y = 80°.
Example 8. In Fig. 6.38, the sides AB and AC of ∆ABC are produced to points E and D respectively. If bisectors BO and CO of ∠ CBE and ∠ BCD respectively meet at point O, then prove that
∠BOC = 90° – $\frac{1}{2}$ ∠BAC.

Answer:
Given: Sides AB and AC of ΔABC are produced to E and D. BO bisects $∠ CBE$. CO bisects $∠ BCD$. BO and CO meet at O.
To Prove: $∠ BOC = 90° – \frac{1}{2} ∠ BAC$.
Proof:
Ray BO bisects $∠ CBE$.
Therefore, $∠ CBO = \frac{1}{2} ∠ CBE$.
Since $∠ CBE$ and $∠ ABC$ form a linear pair: $∠ CBE = 180° - ∠ ABC$. Let $∠ ABC = y$.
$∠ CBE = 180° - y$.
So, $∠ CBO = \frac{1}{2} (180° - y) = 90° - \frac{y}{2}$
$∠ CBO = 90° - \frac{y}{2}$
...(1)
Ray CO bisects $∠ BCD$.
Therefore, $∠ BCO = \frac{1}{2} ∠ BCD$.
Since $∠ BCD$ and $∠ ACB$ form a linear pair: $∠ BCD = 180° - ∠ ACB$. Let $∠ ACB = z$.
$∠ BCD = 180° - z$.
So, $∠ BCO = \frac{1}{2} (180° - z) = 90° - \frac{z}{2}$
$∠ BCO = 90° - \frac{z}{2}$
...(2)
Now, consider ΔBOC. The sum of angles is $180°$ (Angle Sum Property).
$∠ BOC + ∠ CBO + ∠ BCO = 180°$
Substitute expressions from (1) and (2):
$∠ BOC + (90° - \frac{y}{2}) + (90° - \frac{z}{2}) = 180°$
$∠ BOC + 180° - \frac{1}{2}(y + z) = 180°$
Subtract $180°$ from both sides:
$∠ BOC - \frac{1}{2}(y + z) = 0$
$∠ BOC = \frac{1}{2}(y + z)$
$∠ BOC = \frac{1}{2}(y + z)$
...(3)
Now, consider ΔABC. Let $∠ BAC = x$.
The sum of angles is $180°$ (Angle Sum Property).
$∠ BAC + ∠ ABC + ∠ ACB = 180°$
$x + y + z = 180°$
$y + z = 180° - x$
$y + z = 180° - x$
...(4)
Substitute the value of $(y + z)$ from (4) into (3):
$∠ BOC = \frac{1}{2} (180° - x)$
$∠ BOC = 90° - \frac{x}{2}$
Replace x with $∠ BAC$:
$∠ BOC = 90° – \frac{1}{2} ∠ BAC$.
Hence, proved.
Exercise 6.3
Question 1. In Fig. 6.39, sides QP and RQ of ∆ PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
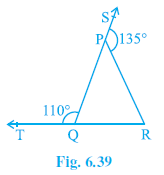
Answer:
Given: In ΔPQR, QP is produced to S, RQ is produced to T. $∠ SPR = 135°$, $∠ PQT = 110°$.
To Find: $∠ PRQ$.
Solution:
Angle $∠ PQT$ and $∠ PQR$ form a linear pair on the line TRQ.
$∠ PQT + ∠ PQR = 180°$ (Linear Pair Axiom)
$110° + ∠ PQR = 180°$
$∠ PQR = 180° - 110° = 70°$
Angle $∠ SPR$ and $∠ QPR$ form a linear pair on the line SPQ.
$∠ SPR + ∠ QPR = 180°$ (Linear Pair Axiom)
$135° + ∠ QPR = 180°$
$∠ QPR = 180° - 135° = 45°$
Now, consider ΔPQR. The sum of angles in a triangle is $180°$ (Angle Sum Property).
$∠ PQR + ∠ QPR + ∠ PRQ = 180°$
Substitute the values found:
$70° + 45° + ∠ PRQ = 180°$
$115° + ∠ PRQ = 180°$
$∠ PRQ = 180° - 115°$
$\mathbf{∠ PRQ = 65°}$
Alternative Method (Using Exterior Angle Theorem):
First find $∠PQR$ using the linear pair with $∠PQT$:
$∠ PQR = 180° - ∠ PQT = 180° - 110° = 70°$.
Now, consider the exterior angle $∠ SPR$ of ΔPQR.
$∠ SPR = ∠ PQR + ∠ PRQ$ (Exterior Angle Theorem)
$135° = 70° + ∠ PRQ$
$∠ PRQ = 135° - 70°$
$\mathbf{∠ PRQ = 65°}$.
Therefore, $∠ PRQ = 65°$.
Question 2. In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆ XYZ, find ∠OZY and ∠YOZ.

Answer:
Given: In ΔXYZ, $∠ X = 62°$, $∠ XYZ = 54°$. YO bisects $∠ XYZ$. ZO bisects $∠ XZY$.
To Find: $∠ OZY$ and $∠ YOZ$.
Solution:
Consider ΔXYZ. Sum of angles is $180°$ (Angle Sum Property).
$∠ X + ∠ XYZ + ∠ XZY = 180°$
$62° + 54° + ∠ XZY = 180°$
$116° + ∠ XZY = 180°$
$∠ XZY = 180° - 116° = 64°$
Now, consider the angle bisectors.
YO bisects $∠ XYZ$.
Therefore, $∠ OYZ = \frac{1}{2} ∠ XYZ = \frac{1}{2} \times 54° = 27°$.
ZO bisects $∠ XZY$.
Therefore, $∠ OZY = \frac{1}{2} ∠ XZY = \frac{1}{2} \times 64° = 32°$.
$\mathbf{So, ∠ OZY = 32°}$.
Now, consider ΔOYZ. Sum of angles is $180°$ (Angle Sum Property).
$∠ OYZ + ∠ OZY + ∠ YOZ = 180°$
Substitute the values found:
$27° + 32° + ∠ YOZ = 180°$
$59° + ∠ YOZ = 180°$
$∠ YOZ = 180° - 59°$
$\mathbf{∠ YOZ = 121°}$
Therefore, $∠ OZY = 32°$ and $∠ YOZ = 121°$.
Question 3. In Fig. 6.41, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
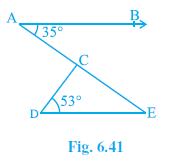
Answer:
Given: AB || DE, $∠ BAC = 35°$, $∠ CDE = 53°$.
To Find: $∠ DCE$.
Solution:
Since AB || DE and AE is a transversal:
$∠ BAC = ∠ CED$ (Alternate interior angles are equal)
Given $∠ BAC = 35°$.
Therefore, $∠ CED = 35°$.
Now, consider ΔCDE. The sum of angles is $180°$ (Angle Sum Property).
$∠ CDE + ∠ CED + ∠ DCE = 180°$
Substitute the known values:
$53° + 35° + ∠ DCE = 180°$
$88° + ∠ DCE = 180°$
$∠ DCE = 180° - 88°$
$\mathbf{∠ DCE = 92°}$
Therefore, $∠ DCE = 92°$.
Question 4. In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
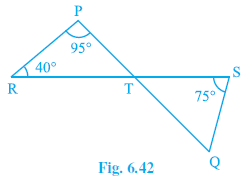
Answer:
Given: Lines PQ and RS intersect at T. In ΔPRT, $∠ PRT = 40°$, $∠ RPT = 95°$. In ΔTSQ, $∠ TSQ = 75°$.
To Find: $∠ SQT$.
Solution:
Consider ΔPRT. Sum of angles is $180°$ (Angle Sum Property).
$∠ PRT + ∠ RPT + ∠ PTR = 180°$
$40° + 95° + ∠ PTR = 180°$
$135° + ∠ PTR = 180°$
$∠ PTR = 180° - 135° = 45°$
Since lines PQ and RS intersect at T, vertically opposite angles are equal.
$∠ STQ = ∠ PTR$ (Vertically opposite angles)
Therefore, $∠ STQ = 45°$.
Now, consider ΔSTQ. Sum of angles is $180°$ (Angle Sum Property).
$∠ STQ + ∠ TSQ + ∠ SQT = 180°$
Substitute the known values:
$45° + 75° + ∠ SQT = 180°$
$120° + ∠ SQT = 180°$
$∠ SQT = 180° - 120°$
$\mathbf{∠ SQT = 60°}$
Therefore, $∠ SQT = 60°$.
Question 5. In Fig. 6.43, if PQ⊥PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
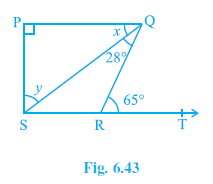
Answer:
Given: PQ ⊥ PS (so $∠ QPS = 90°$), PQ || SR, $∠ SQR = 28°$, $∠ QRT = 65°$. In the figure, $∠ PQS = x$, $∠ PSQ = y$.
To Find: Values of x and y.
Solution:
Finding x:
Since PQ || SR and QR is a transversal:
$∠ PQR = ∠ QRT$ (Alternate interior angles are equal).
From the figure, $∠ PQR = ∠ PQS + ∠ SQR = x + 28°$.
Given $∠ QRT = 65°$.
So, $x + 28° = 65°$
$x = 65° - 28°$
$\mathbf{x = 37°}$
Finding y:
Consider the right-angled triangle ΔPQS (since PQ ⊥ PS, $∠ QPS = 90°$).
The sum of angles in ΔPQS is $180°$ (Angle Sum Property).
$∠ QPS + ∠ PQS + ∠ PSQ = 180°$
Substitute the known values ($∠ QPS = 90°$, $∠ PQS = x = 37°$, $∠ PSQ = y$):
$90° + 37° + y = 180°$
$127° + y = 180°$
$y = 180° - 127°$
$\mathbf{y = 53°}$
Therefore, x = 37° and y = 53°.
Question 6. In Fig. 6.44, the side QR of ∆ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = $\frac{1}{2}$ ∠QPR.

Answer:
Given: In ΔPQR, side QR is produced to S. QT bisects $∠ PQR$. RT bisects $∠ PRS$. QT and RT meet at T.
To Prove: $∠ QTR = \frac{1}{2} ∠ QPR$.
Proof:
Consider ΔTQR. The exterior angle $∠ TRS$ is equal to the sum of the two opposite interior angles (Exterior Angle Theorem).
$∠ TRS = ∠ QTR + ∠ TQR$
$∠ TRS = ∠ QTR + ∠ TQR$
...(1)
Consider ΔPQR. The exterior angle $∠ PRS$ is equal to the sum of the two opposite interior angles (Exterior Angle Theorem).
$∠ PRS = ∠ QPR + ∠ PQR$
$∠ PRS = ∠ QPR + ∠ PQR$
...(2)
Since RT bisects $∠ PRS$:
$∠ TRS = \frac{1}{2} ∠ PRS$
$∠ TRS = \frac{1}{2} ∠ PRS$
...(3)
Since QT bisects $∠ PQR$:
$∠ TQR = \frac{1}{2} ∠ PQR$
$∠ TQR = \frac{1}{2} ∠ PQR$
...(4)
Substitute $∠ TRS$ from (3) and $∠ TQR$ from (4) into equation (1):
$\frac{1}{2} ∠ PRS = ∠ QTR + \frac{1}{2} ∠ PQR$
Multiply the entire equation by 2:
$∠ PRS = 2 ∠ QTR + ∠ PQR$
$∠ PRS = 2 ∠ QTR + ∠ PQR$
...(5)
Now we have two expressions for $∠ PRS$ (equation 2 and equation 5). Equate them:
$∠ QPR + ∠ PQR = 2 ∠ QTR + ∠ PQR$
Subtract $∠ PQR$ from both sides:
$∠ QPR = 2 ∠ QTR$
Divide by 2:
$\frac{1}{2} ∠ QPR = ∠ QTR$
Rearranging gives:
$∠ QTR = \frac{1}{2} ∠ QPR$.
Hence, proved.

