| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 7 Triangles
Welcome to an in-depth exploration of Chapter 7: Triangles. This section serves as a crucial cornerstone in geometry, building upon foundational concepts likely introduced in earlier studies, such as Class 7, but now diving into more rigorous applications, particularly focusing on the fundamental idea of congruence. We will navigate through the essential properties, theorems, and problem-solving techniques associated with triangles, emphasizing logical reasoning and structured proofs. Understanding triangles is not just about recognizing shapes; it's about analyzing relationships between sides, angles, and the conditions under which two triangles can be considered identical in form and size.
At the heart of this chapter lies the concept of congruence. Two geometric figures, specifically triangles in our case, are congruent if they possess the exact same shape and the exact same size. This implies a perfect overlap if one were placed upon the other. A critical consequence of congruence is that all corresponding parts – the sides and angles that match up between the two triangles – must be equal. This principle is widely known by the acronym CPCTC, which stands for Corresponding Parts of Congruent Triangles are Congruent. Mastering the identification of these corresponding parts and understanding CPCTC is paramount for solving proofs and problems within this chapter.
To establish congruence between two triangles without measuring every single side and angle, we rely on specific sets of conditions known as the congruence criteria or postulates. These provide shortcuts based on proving the equality of only three specific corresponding parts. The core criteria meticulously explained and applied throughout this chapter's solutions include:
- SAS (Side-Angle-Side): Two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding parts of another triangle.
- ASA (Angle-Side-Angle): Two angles and the included side (the side between those two angles) of one triangle are equal to the corresponding parts of another triangle.
- SSS (Side-Side-Side): All three sides of one triangle are equal to the corresponding three sides of another triangle.
- RHS (Right angle-Hypotenuse-Side): In two right-angled triangles, the hypotenuses and one corresponding side are equal.
Solutions within this chapter demonstrate extensively how to dissect given information, whether from diagrams or textual statements, to identify the necessary equal sides and angles. Applying the correct criterion allows us to formally declare two triangles congruent, always ensuring the congruence relation is written with the vertices in the correct corresponding order, for instance, $\triangle ABC \cong \triangle PQR$. This symbolic representation is crucial for clarity and accuracy.
Furthermore, a significant focus is placed on utilizing congruence as a powerful tool within geometric proofs. Many exercises require proving triangles congruent as an intermediate step to deduce the equality of other specific sides or angles (using CPCTC). Classic theorems, such as those related to isosceles triangles (e.g., proving that angles opposite equal sides are equal, often using an auxiliary line like an angle bisector or median to facilitate SAS or SSS proof), and their converses (e.g., sides opposite equal angles are equal, often using ASA) are thoroughly addressed, showcasing the practical application of congruence criteria in establishing broader geometric truths.
Beyond congruence, the chapter delves into the vital concept of triangle inequalities. Key theorems governing the relationships between sides and angles within a single triangle are explored. Solutions explain and apply principles such as: the sum of the lengths of any two sides of a triangle must be greater than the length of the third side (e.g., $a + b > c$); the angle opposite the longer side is necessarily larger; and conversely, the side opposite the larger angle is longer. These inequalities are essential for comparing sides and angles and for determining whether a triangle with given side lengths can even be constructed. Throughout, the emphasis remains firmly on logical deduction, the structure of formal proofs, and the precise application of theorems.
Example 1 to 3 (Before Exercise 7.1)
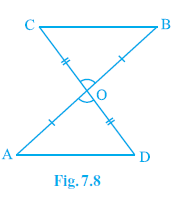
Example 1. In Fig. 7.8, OA = OB and OD = OC. Show that
(i) ∆ AOD ≅ ∆ BOC and
(ii) AD || BC.
Answer:
Given:
In Fig. 7.8, we are given that:
OA = OB
(Given)
OD = OC
(Given)
To Prove:
(i) $\triangle$ AOD $\cong$ $\triangle$ BOC
(ii) AD $||$ BC
Proof:
(i) Proving $\triangle$ AOD $\cong$ $\triangle$ BOC:
Consider $\triangle$ AOD and $\triangle$ BOC.
OA = OB
(Given)
$\angle$ AOD = $\angle$ BOC
(Vertically Opposite Angles)
OD = OC
(Given)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ AOD $\cong$ $\triangle$ BOC
Hence, part (i) is proved.
(ii) Proving AD $||$ BC:
Since $\triangle$ AOD $\cong$ $\triangle$ BOC (proved above), we can use CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
So, $\angle$ OAD = $\angle$ OBC
Also, $\angle$ ODA = $\angle$ OCB
Now, consider the lines AD and BC with transversal AC. We have $\angle$ OCB = $\angle$ ODA. These are alternate interior angles.
Similarly, consider the lines AD and BC with transversal BD. We have $\angle$ OBC = $\angle$ OAD. These are also alternate interior angles.
Since a pair of alternate interior angles are equal, the lines AD and BC must be parallel.
Therefore, AD $||$ BC.
Hence, part (ii) is proved.
Example 2. AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
Answer:
Given:
AB is a line segment.
Line $l$ is the perpendicular bisector of the line segment AB.
A point P lies on the line $l$.
To Prove:
Point P is equidistant from points A and B, i.e., PA = PB.
Construction:
Let the line $l$ intersect the line segment AB at point C. Join P to A and P to B.
Proof:
Since line $l$ is the perpendicular bisector of AB, it means:
1. Line $l$ is perpendicular to AB. Therefore, $\angle PCA = \angle PCB = 90^\circ$.
2. Line $l$ bisects AB. Therefore, AC = CB.
Now, let's consider the triangles $\Delta PAC$ and $\Delta PBC$.
AC = CB
(Line $l$ bisects AB)
$\angle PCA = \angle PCB$
(Each is $90^\circ$)
PC = PC
(Common side)
By the SAS (Side-Angle-Side) congruence criterion, we can conclude that:
$\Delta PAC \cong \Delta PBC$
Since the triangles are congruent, their corresponding parts are equal (by C.P.C.T. - Corresponding Parts of Congruent Triangles).
Therefore, PA = PB.
This proves that the point P is equidistant from points A and B.
Hence, proved.
Alternate Solution (Using Pythagoras Theorem):
Proof:
From the construction, we have two right-angled triangles, $\Delta PAC$ and $\Delta PBC$, as $\angle PCA = \angle PCB = 90^\circ$.
In the right-angled triangle $\Delta PAC$, by Pythagoras theorem:
$PA^2 = AC^2 + PC^2$
... (i)
In the right-angled triangle $\Delta PBC$, by Pythagoras theorem:
$PB^2 = CB^2 + PC^2$
... (ii)
Since line $l$ is the bisector of AB, we know that:
AC = CB
(Given)
Squaring both sides, we get:
$AC^2 = CB^2$
Now, substituting $CB^2$ with $AC^2$ in equation (ii):
$PB^2 = AC^2 + PC^2$
... (iii)
Comparing equation (i) and equation (iii), we see that the right-hand sides are identical.
$PA^2 = PB^2$
Taking the square root on both sides (since length cannot be negative):
PA = PB
This proves that the point P is equidistant from points A and B.
Hence, proved.
Example 3. Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid-point of BC.

Answer:
Given:
AB $||$ CD.
O is the mid-point of AD, which means AO = OD.
To Prove:
(i) $\triangle$AOB $\cong$ $\triangle$DOC
(ii) O is also the mid-point of BC (i.e., BO = OC).
Proof:
(i) Proving $\triangle$AOB $\cong$ $\triangle$DOC:
Consider $\triangle$AOB and $\triangle$DOC.
Since AB $||$ CD and AD is a transversal:
$\angle$ OAB = $\angle$ ODC
(Alternate Interior Angles)
AO = OD
(O is the midpoint of AD, Given)
Also, AD and BC are lines intersecting at O.
$\angle$ AOB = $\angle$ DOC
(Vertically Opposite Angles)
Therefore, by ASA (Angle-Side-Angle) congruence rule:
$\triangle$AOB $\cong$ $\triangle$DOC
Hence, part (i) is proved.
Alternate Method using AAS:
Consider $\triangle$AOB and $\triangle$DOC.
Since AB $||$ CD and BC is a transversal:
$\angle$ OBA = $\angle$ OCD
(Alternate Interior Angles)
Since AB $||$ CD and AD is a transversal:
$\angle$ OAB = $\angle$ ODC
(Alternate Interior Angles)
AO = OD
(O is the midpoint of AD, Given)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle$AOB $\cong$ $\triangle$DOC
(ii) Proving O is the mid-point of BC:
Since $\triangle$AOB $\cong$ $\triangle$DOC (proved in part (i)), we can use CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
Therefore, BO = OC.
Since BO = OC, O is the mid-point of the line segment BC.
Hence, part (ii) is proved.
Exercise 7.1
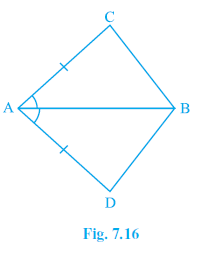
Question 1. In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see Fig. 7.16). Show that ∆ ABC ≅ ∆ ABD. What can you say about BC and BD?
Answer:
Given:
In quadrilateral ACBD:
AC = AD
(Given)
AB bisects $\angle$ A, which means $\angle$ CAB = $\angle$ DAB.
To Prove:
$\triangle$ ABC $\cong$ $\triangle$ ABD
Also, determine the relationship between BC and BD.
Proof:
Consider $\triangle$ ABC and $\triangle$ ABD.
AC = AD
(Given)
$\angle$ CAB = $\angle$ DAB
(AB bisects $\angle$ A)
AB = AB
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ ABC $\cong$ $\triangle$ ABD
Hence, proved.
Conclusion about BC and BD:
Since $\triangle$ ABC $\cong$ $\triangle$ ABD, their corresponding parts must be equal (CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
Therefore, BC = BD.
We can say that BC and BD are equal in length.
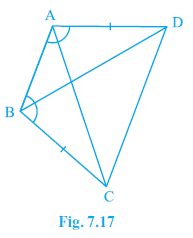
Question 2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Answer:
Given:
In quadrilateral ABCD:
AD = BC
(Given)
$\angle$DAB = $\angle$CBA
(Given)
To Prove:
(i) $\triangle$ABD $\cong$ $\triangle$BAC
(ii) BD = AC
(iii) $\angle$ABD = $\angle$BAC
Proof:
(i) Proving $\triangle$ABD $\cong$ $\triangle$BAC:
Consider $\triangle$ABD and $\triangle$BAC.
AD = BC
(Given)
$\angle$DAB = $\angle$CBA
(Given)
AB = BA
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ABD $\cong$ $\triangle$BAC
Hence, part (i) is proved.
(ii) Proving BD = AC:
Since $\triangle$ABD $\cong$ $\triangle$BAC (proved in part (i)), their corresponding parts are equal (CPCTC).
Therefore, BD = AC.
Hence, part (ii) is proved.
(iii) Proving $\angle$ABD = $\angle$BAC:
Since $\triangle$ABD $\cong$ $\triangle$BAC (proved in part (i)), their corresponding parts are equal (CPCTC).
Therefore, $\angle$ABD = $\angle$BAC.
Hence, part (iii) is proved.
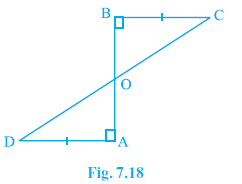
Question 3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
Answer:
Given:
AD and BC are perpendiculars to line segment AB.
This means $\angle$OAD = $90^\circ$ and $\angle$OBC = $90^\circ$.
AD = BC
(Given)
CD intersects AB at point O.
To Prove:
CD bisects AB. (This means we need to show that O is the mid-point of AB, i.e., AO = OB).
Proof:
Consider $\triangle$OAD and $\triangle$OBC.
$\angle$OAD = $\angle$OBC
($90^\circ$ each, Given)
$\angle$AOD = $\angle$BOC
(Vertically Opposite Angles)
AD = BC
(Given)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle$OAD $\cong$ $\triangle$OBC
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, AO = OB.
Since AO = OB, O is the mid-point of AB.
This means that the line segment CD bisects the line segment AB.
Hence, proved.
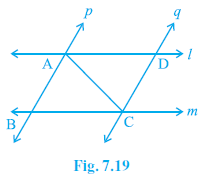
Question 4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ∆ABC ≅ ∆CDA.
Answer:
Given:
Line l $||$ line m.
Line p $||$ line q.
Lines l and m intersect lines p and q, forming points A, B, C, D and the diagonal AC as shown in Fig. 7.19.
Specifically, AB lies on line p, DC lies on line p, AD lies on line l, BC lies on line m. So, AB $||$ DC and AD $||$ BC, which means ABCD is a parallelogram.
To Prove:
$\triangle$ABC $\cong$ $\triangle$CDA
Proof:
Consider $\triangle$ABC and $\triangle$CDA.
Since line p $||$ line q (i.e., AB $||$ DC) and AC is a transversal:
$\angle$BAC = $\angle$DCA
(Alternate Interior Angles)
AC = CA
(Common side)
Since line l $||$ line m (i.e., AD $||$ BC) and AC is a transversal:
$\angle$BCA = $\angle$DAC
(Alternate Interior Angles)
Therefore, by ASA (Angle-Side-Angle) congruence rule:
$\triangle$ABC $\cong$ $\triangle$CDA
Hence, proved.
Alternate Solution (using properties of parallelogram):
Since l $||$ m and p $||$ q, the quadrilateral ABCD formed is a parallelogram.
In a parallelogram, opposite sides are equal.
So, AB = CD and BC = DA.
Consider $\triangle$ABC and $\triangle$CDA.
AB = CD
(Opposite sides of parallelogram)
BC = DA
(Opposite sides of parallelogram)
AC = CA
(Common side)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle$ABC $\cong$ $\triangle$CDA
Hence, proved.
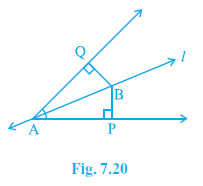
Question 5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.
Answer:
Given:
Line l bisects $\angle$A, so $\angle$PAB = $\angle$QAB.
B is a point on line l.
BP $\perp$ arm AP (containing P), so $\angle$BPA = $90^\circ$.
BQ $\perp$ arm AQ (containing Q), so $\angle$BQA = $90^\circ$.
To Prove:
(i) $\triangle$APB $\cong$ $\triangle$AQB
(ii) BP = BQ (B is equidistant from the arms of $\angle$ A)
Proof:
(i) Proving $\triangle$APB $\cong$ $\triangle$AQB:
Consider $\triangle$APB and $\triangle$AQB.
$\angle$PAB = $\angle$QAB
(Line l bisects $\angle$A, Given)
$\angle$BPA = $\angle$BQA
($90^\circ$ each, Given)
AB = AB
(Common side)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle$APB $\cong$ $\triangle$AQB
Hence, part (i) is proved.
(ii) Proving BP = BQ:
Since $\triangle$APB $\cong$ $\triangle$AQB (proved in part (i)), their corresponding parts are equal (CPCTC).
Therefore, BP = BQ.
This means that the point B is equidistant from the arms of $\angle$ A.
Hence, part (ii) is proved.
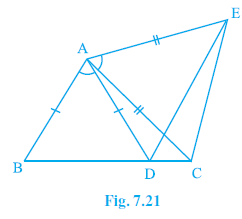
Question 6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Answer:
Given:
AC = AE
(Given)
AB = AD
(Given)
$\angle$BAD = $\angle$EAC
(Given)
To Prove:
BC = DE
Proof:
We are given $\angle$BAD = $\angle$EAC.
Add $\angle$DAC to both sides of this equation:
$\angle$BAD + $\angle$DAC = $\angle$EAC + $\angle$DAC
From the figure, $\angle$BAD + $\angle$DAC = $\angle$BAC.
Also, from the figure, $\angle$EAC + $\angle$DAC = $\angle$DAE (or $\angle$EAD).
Therefore, $\angle$BAC = $\angle$DAE.
Now, consider $\triangle$ABC and $\triangle$ADE.
AB = AD
(Given)
$\angle$BAC = $\angle$DAE
(Proved above)
AC = AE
(Given)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ABC $\cong$ $\triangle$ADE
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, BC = DE.
Hence, proved.
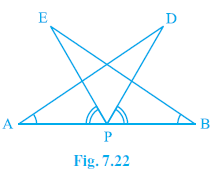
Question 7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE
Answer:
Given:
AB is a line segment.
P is the mid-point of AB, so AP = BP.
D and E are points on the same side of AB.
$\angle$BAD = $\angle$ABE
(Given)
(This is the same as $\angle$DAP = $\angle$EBP)
$\angle$EPA = $\angle$DPB
(Given)
To Prove:
(i) $\triangle$DAP $\cong$ $\triangle$EBP
(ii) AD = BE
Proof:
(i) Proving $\triangle$DAP $\cong$ $\triangle$EBP:
We are given $\angle$EPA = $\angle$DPB.
Add $\angle$EPD to both sides of this equation:
$\angle$EPA + $\angle$EPD = $\angle$DPB + $\angle$EPD
From the figure, $\angle$EPA + $\angle$EPD = $\angle$APD.
Also, from the figure, $\angle$DPB + $\angle$EPD = $\angle$BPE (or $\angle$EPB).
Therefore, $\angle$APD = $\angle$BPE.
Now, consider $\triangle$DAP and $\triangle$EBP.
$\angle$DAP = $\angle$EBP
($\angle$BAD = $\angle$ABE, Given)
AP = BP
(P is the mid-point of AB)
$\angle$APD = $\angle$BPE
(Proved above)
Therefore, by ASA (Angle-Side-Angle) congruence rule:
$\triangle$DAP $\cong$ $\triangle$EBP
Hence, part (i) is proved.
(ii) Proving AD = BE:
Since $\triangle$DAP $\cong$ $\triangle$EBP (proved in part (i)), their corresponding parts are equal (CPCTC).
Therefore, AD = BE.
Hence, part (ii) is proved.
Question 8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle.
(iii) ∆DBC ≅ ∆ACB
(iv) CM = $\frac{1}{2}$ AB
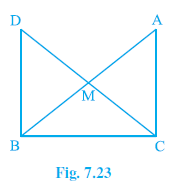
Answer:
Given:
In $\triangle$ABC, $\angle$C = $90^\circ$.
M is the mid-point of hypotenuse AB. So, AM = BM.
C is joined to M and produced to D such that DM = CM.
Point D is joined to point B.
To Prove:
(i) $\triangle$AMC $\cong$ $\triangle$BMD
(ii) $\angle$DBC is a right angle ($90^\circ$).
(iii) $\triangle$DBC $\cong$ $\triangle$ACB
(iv) CM = $\frac{1}{2}$ AB
Proof:
(i) Proving $\triangle$AMC $\cong$ $\triangle$BMD:
Consider $\triangle$AMC and $\triangle$BMD.
AM = BM
(M is the mid-point of AB)
$\angle$AMC = $\angle$BMD
(Vertically Opposite Angles)
CM = DM
(Given)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$AMC $\cong$ $\triangle$BMD
Hence, part (i) is proved.
(ii) Proving $\angle$DBC is a right angle:
Since $\triangle$AMC $\cong$ $\triangle$BMD (from part (i)), their corresponding parts are equal (CPCTC).
So, AC = DB.
And, $\angle$MAC = $\angle$MBD (or $\angle$CAB = $\angle$DBA).
These angles ($\angle$CAB and $\angle$DBA) are alternate interior angles formed by the transversal AB intersecting lines AC and DB.
Since the alternate interior angles are equal, the lines AC and DB must be parallel.
AC $||$ DB.
Now, consider AC $||$ DB and BC as the transversal.
The sum of consecutive interior angles is $180^\circ$.
$\angle$DBC + $\angle$ACB = $180^\circ$
We are given that $\angle$ACB = $90^\circ$.
$\angle$DBC + $90^\circ$ = $180^\circ$
$\angle$DBC = $180^\circ - 90^\circ$
$\angle$DBC = $90^\circ$.
Thus, $\angle$DBC is a right angle.
Hence, part (ii) is proved.
(iii) Proving $\triangle$DBC $\cong$ $\triangle$ACB:
Consider $\triangle$DBC and $\triangle$ACB.
DB = AC
(From CPCTC in part (i))
$\angle$DBC = $\angle$ACB
($90^\circ$ each, Given and Proved in part (ii))
BC = CB
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$DBC $\cong$ $\triangle$ACB
Hence, part (iii) is proved.
(iv) Proving CM = $\frac{1}{2}$ AB:
Since $\triangle$DBC $\cong$ $\triangle$ACB (from part (iii)), their corresponding parts are equal (CPCTC).
So, DC = AB.
From the construction, we know that D, M, C are collinear and M is between D and C.
So, DC = DM + MC.
We are given that DM = CM.
Substituting DM = CM in the equation for DC:
DC = CM + CM
DC = 2 CM.
Now, substitute DC = AB into this equation:
AB = 2 CM
Dividing both sides by 2:
CM = $\frac{1}{2}$ AB
Hence, part (iv) is proved.
Example 4 to 6 (Before Exercise 7.2)
Example 4. In ∆ ABC, the bisector AD of ∠A is perpendicular to side BC (see Fig. 7.27). Show that AB = AC and ∆ ABC is isosceles.

Answer:
Given:
In $\triangle$ABC:
AD bisects $\angle$A, which means $\angle$BAD = $\angle$CAD.
AD is perpendicular to BC, which means $\angle$ADB = $90^\circ$ and $\angle$ADC = $90^\circ$.
To Prove:
AB = AC
$\triangle$ ABC is isosceles.
Proof:
Consider $\triangle$ABD and $\triangle$ACD.
$\angle$BAD = $\angle$CAD
(AD bisects $\angle$A, Given)
AD = AD
(Common side)
$\angle$ADB = $\angle$ADC
($90^\circ$ each, as AD $\perp$ BC, Given)
Therefore, by ASA (Angle-Side-Angle) congruence rule:
$\triangle$ABD $\cong$ $\triangle$ACD
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, AB = AC.
A triangle with two equal sides is an isosceles triangle.
Since AB = AC, $\triangle$ ABC is an isosceles triangle.
Hence, proved.
Example 5. E and F are respectively the mid-points of equal sides AB and AC of ∆ ABC (see Fig. 7.28). Show that BF = CE.
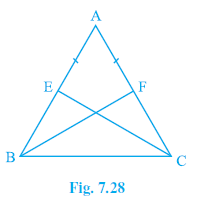
Answer:
Given:
In $\triangle$ABC:
AB = AC
(Given)
E is the mid-point of AB, so AE = EB = $\frac{1}{2}$ AB.
F is the mid-point of AC, so AF = FC = $\frac{1}{2}$ AC.
To Prove:
BF = CE.
Proof:
Since AB = AC, their halves must also be equal.
$\frac{1}{2}$ AB = $\frac{1}{2}$ AC
Therefore, AE = AF and EB = FC.
Consider $\triangle$ABF and $\triangle$ACE.
AB = AC
(Given)
$\angle$A = $\angle$A
(Common angle)
AF = AE
(Halves of equal sides AB and AC)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ABF $\cong$ $\triangle$ACE
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, BF = CE.
Hence, proved.
Alternate Solution:
Consider $\triangle$BCF and $\triangle$CBE.
Since AB = AC, the angles opposite to these sides are equal.
$\angle$ABC = $\angle$ACB
(Angles opposite equal sides)
Also, since AB = AC, their halves are equal.
EB = FC
(Halves of equal sides AB and AC)
BC = CB
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$BCF $\cong$ $\triangle$CBE
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, BF = CE.
Hence, proved.
Example 6. In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see Fig. 7.29). Show that AD = AE.

Answer:
Given:
Isosceles $\triangle$ABC with AB = AC.
D and E are points on BC such that BE = CD.
To Prove:
AD = AE.
Proof:
Since $\triangle$ABC is isosceles with AB = AC, the angles opposite to these sides are equal.
$\angle$ABC = $\angle$ACB
(Angles opposite equal sides)
Let's denote these as $\angle$B = $\angle$C.
We are given BE = CD.
From the figure (assuming B-D-E-C as shown), we can write:
BE = BD + DE
CD = CE + DE
Since BE = CD:
BD + DE = CE + DE
Subtracting DE from both sides gives:
BD = CE
Now, consider $\triangle$ABD and $\triangle$ACE.
AB = AC
(Given)
$\angle$ABD = $\angle$ACE
($\angle$B = $\angle$C, Proved above)
BD = CE
(Proved above)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ABD $\cong$ $\triangle$ACE
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, AD = AE.
Hence, proved.
Exercise 7.2
Question 1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A
Answer:
Given:
An isosceles triangle $\Delta ABC$ in which AB = AC.
The bisectors of $\angle B$ and $\angle C$ intersect each other at O.
To Prove:
(i) OB = OC
(ii) AO bisects $\angle A$
Proof:
(i) To prove OB = OC
In $\Delta ABC$, we are given that:
AB = AC
(Given)
Since the angles opposite to equal sides of a triangle are equal, we have:
$\angle ACB = \angle ABC$
Now, dividing both sides of the equation by 2, we get:
$\frac{1}{2}\angle ACB = \frac{1}{2}\angle ABC$
It is given that BO and CO are the bisectors of $\angle ABC$ and $\angle ACB$ respectively. This means:
$\angle OBC = \frac{1}{2}\angle ABC$
and
$\angle OCB = \frac{1}{2}\angle ACB$
From the above relations, we can conclude that:
$\angle OCB = \angle OBC$
Now, consider the triangle $\Delta OBC$.
Since the sides opposite to equal angles in a triangle are equal, we have:
OB = OC
Hence, the first part is proved.
(ii) To prove AO bisects $\angle A$
To prove this, we will show that $\Delta ABO$ and $\Delta ACO$ are congruent.
Consider the triangles $\Delta ABO$ and $\Delta ACO$:
AB = AC
(Given)
AO = AO
(Common side)
OB = OC
(Proved in part (i))
By the SSS (Side-Side-Side) congruence criterion, we have:
$\Delta ABO \cong \Delta ACO$
Since the triangles are congruent, their corresponding parts must be equal (C.P.C.T. - Corresponding Parts of Congruent Triangles).
Therefore,
$\angle BAO = \angle CAO$
(By C.P.C.T.)
This shows that the line segment AO divides $\angle A$ into two equal angles.
Hence, AO bisects $\angle A$. The second part is proved.
Question 2. In ∆ABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ∆ABC is an isosceles triangle in which AB = AC.

Answer:
Given:
In $\triangle$ABC, AD is the perpendicular bisector of BC.
This means AD $\perp$ BC, so $\angle$ADB = $\angle$ADC = $90^\circ$.
Also, AD bisects BC, so BD = CD.
To Prove:
$\triangle$ABC is an isosceles triangle with AB = AC.
Proof:
Consider $\triangle$ADB and $\triangle$ADC.
BD = CD
(AD bisects BC, Given)
$\angle$ADB = $\angle$ADC
($90^\circ$ each, AD $\perp$ BC, Given)
AD = AD
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ADB $\cong$ $\triangle$ADC
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, AB = AC.
A triangle with two equal sides is an isosceles triangle.
Hence, $\triangle$ABC is an isosceles triangle.
Hence, proved.
Question 3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
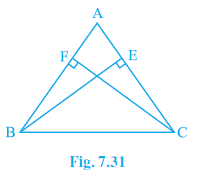
Answer:
Given:
Isosceles $\triangle$ABC with AB = AC.
BE is altitude to AC, so BE $\perp$ AC ($\angle$BEA = $90^\circ$).
CF is altitude to AB, so CF $\perp$ AB ($\angle$CFA = $90^\circ$).
To Prove:
The altitudes are equal, i.e., BE = CF.
Proof:
Consider $\triangle$ABE and $\triangle$ACF.
$\angle$A = $\angle$A
(Common angle)
$\angle$BEA = $\angle$CFA
($90^\circ$ each, Given altitudes)
AB = AC
(Given)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle$ABE $\cong$ $\triangle$ACF
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, BE = CF.
Hence, the altitudes are equal.
Hence, proved.
Alternate Solution (using RHS):
Since AB = AC, the angles opposite are equal: $\angle$ABC = $\angle$ACB.
Consider $\triangle$BCF and $\triangle$CBE.
$\angle$BFC = $\angle$CEB
($90^\circ$ each, Given altitudes)
$\angle$FBC = $\angle$ECB
($\angle$ABC = $\angle$ACB, angles opposite equal sides)
BC = CB
(Common side)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
(Note: We used AAS here again. To use RHS, we would need to compare $\triangle$BCF and $\triangle$CBE using hypotenuse BC, right angles $\angle$BFC = $\angle$CEB = 90°, but we need one more side (BF=CE or CF=BE), which is what we want to prove. So AAS or the first method using $\triangle$ABE and $\triangle$ACF is more direct).
$\triangle$BCF $\cong$ $\triangle$CBE (using AAS)
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, CF = BE.
Hence, the altitudes are equal.
Hence, proved.
Question 4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ∆ ABE ≅ ∆ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
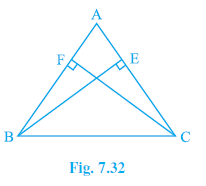
Answer:
Given:
In $\triangle$ABC:
BE is altitude to AC ($\angle$BEA = $90^\circ$).
CF is altitude to AB ($\angle$CFA = $90^\circ$).
BE = CF
(Given)
To Prove:
(i) $\triangle$ ABE $\cong$ $\triangle$ ACF
(ii) AB = AC (i.e., $\triangle$ABC is isosceles)
Proof:
(i) Proving $\triangle$ ABE $\cong$ $\triangle$ ACF:
Consider $\triangle$ABE and $\triangle$ACF.
$\angle$A = $\angle$A
(Common angle)
$\angle$BEA = $\angle$CFA
($90^\circ$ each, Given altitudes)
BE = CF
(Given)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle$ABE $\cong$ $\triangle$ACF
Hence, part (i) is proved.
(ii) Proving AB = AC:
Since $\triangle$ABE $\cong$ $\triangle$ACF (proved in part (i)), their corresponding parts are equal (CPCTC).
Therefore, AB = AC.
Since two sides of $\triangle$ABC are equal, $\triangle$ABC is an isosceles triangle.
Hence, part (ii) is proved.
Alternate Solution (using RHS for part (i)):
Consider right-angled triangles $\triangle$BCF and $\triangle$CBE.
$\angle$BFC = $\angle$CEB
($90^\circ$ each, Given altitudes)
BC = CB
(Common hypotenuse)
CF = BE
(Given)
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle$BCF $\cong$ $\triangle$CBE
By CPCTC, $\angle$FBC = $\angle$ECB (i.e., $\angle$ABC = $\angle$ACB).
In $\triangle$ABC, since $\angle$ABC = $\angle$ACB, the sides opposite to these angles must be equal.
Therefore, AC = AB.
Thus, $\triangle$ABC is an isosceles triangle.
Now, to prove $\triangle$ ABE $\cong$ $\triangle$ ACF using this approach:
In $\triangle$ABE and $\triangle$ACF:
$\angle$A = $\angle$A
(Common angle)
$\angle$AEB = $\angle$AFC
($90^\circ$ each)
AB = AC
(Proved above)
By AAS congruence rule:
$\triangle$ ABE $\cong$ $\triangle$ ACF
(Note: This alternate proof first proves (ii) using RHS on different triangles, then proves (i) using AAS).
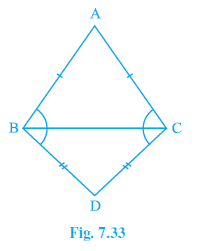
Question 5. ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.
Answer:
Given:
$\triangle$ABC and $\triangle$DBC are isosceles triangles on the same base BC.
In $\triangle$ABC, AB = AC.
In $\triangle$DBC, DB = DC.
To Prove:
$\angle$ABD = $\angle$ACD.
Proof:
In $\triangle$ABC:
AB = AC
(Given)
Since sides are equal, the angles opposite to them are equal.
$\angle$ABC = $\angle$ACB
[Angles opposite equal sides] ... (i)
In $\triangle$DBC:
DB = DC
(Given)
Since sides are equal, the angles opposite to them are equal.
$\angle$DBC = $\angle$DCB
[Angles opposite equal sides] ... (ii)
Adding equation (i) and equation (ii):
$\angle$ABC + $\angle$DBC = $\angle$ACB + $\angle$DCB
From the figure, $\angle$ABC + $\angle$DBC = $\angle$ABD.
From the figure, $\angle$ACB + $\angle$DCB = $\angle$ACD.
Therefore, $\angle$ABD = $\angle$ACD.
Hence, proved.
Alternate Solution (using Congruence):
Construction: Join A to D.
Proof:
Consider $\triangle$ABD and $\triangle$ACD.
AB = AC
(Given)
DB = DC
(Given)
AD = AD
(Common side)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle$ABD $\cong$ $\triangle$ACD
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, $\angle$ABD = $\angle$ACD.
Hence, proved.
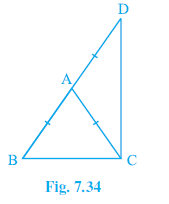
Question 6. ∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠ BCD is a right angle.
Answer:
Given:
Isosceles $\triangle$ABC with AB = AC.
Side BA is produced to D such that AD = AB.
To Prove:
$\angle$BCD = $90^\circ$.
Proof:
In $\triangle$ABC:
AB = AC
(Given)
Therefore, angles opposite equal sides are equal:
$\angle$ACB = $\angle$ABC
[Angles opposite equal sides] ... (i)
We are also given AD = AB.
Since AB = AC and AD = AB, we have AD = AC.
Now consider $\triangle$ADC.
AD = AC
(Proved above)
Therefore, angles opposite equal sides are equal:
$\angle$ACD = $\angle$ADC
[Angles opposite equal sides] ... (ii)
Note that $\angle$ABC can be written as $\angle$DBC and $\angle$ADC can be written as $\angle$BDC.
Now, consider the large triangle $\triangle$DBC.
The sum of angles in $\triangle$DBC is $180^\circ$.
$\angle$DBC + $\angle$BDC + $\angle$BCD = $180^\circ$
From the figure, $\angle$BCD = $\angle$ACB + $\angle$ACD.
Substitute $\angle$DBC = $\angle$ACB (from (i)) and $\angle$BDC = $\angle$ACD (from (ii)) into the angle sum equation:
$\angle$ACB + $\angle$ACD + ($\angle$ACB + $\angle$ACD) = $180^\circ$
$\angle$ACB + $\angle$ACD + $\angle$BCD = $180^\circ$
Substitute $\angle$ACB + $\angle$ACD = $\angle$BCD:
$\angle$BCD + $\angle$BCD = $180^\circ$
2 $\angle$BCD = $180^\circ$
$\angle$BCD = $\frac{180^\circ}{2}$
$\angle$BCD = $90^\circ$.
Hence, $\angle$BCD is a right angle.
Hence, proved.
Question 7. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Answer:
Given:
Right angled $\triangle$ABC with $\angle$A = $90^\circ$.
AB = AC.
To Find:
The values of $\angle$B and $\angle$C.
Solution:
In $\triangle$ABC, we are given AB = AC.
Since sides AB and AC are equal, the angles opposite to these sides must be equal.
$\angle$C = $\angle$B
(Angles opposite equal sides)
The sum of angles in a triangle is $180^\circ$.
$\angle$A + $\angle$B + $\angle$C = $180^\circ$
Substitute the given value $\angle$A = $90^\circ$ and $\angle$C = $\angle$B:
$90^\circ$ + $\angle$B + $\angle$B = $180^\circ$
$90^\circ$ + 2 $\angle$B = $180^\circ$
2 $\angle$B = $180^\circ - 90^\circ$
2 $\angle$B = $90^\circ$
$\angle$B = $\frac{90^\circ}{2}$
$\angle$B = $45^\circ$
Since $\angle$C = $\angle$B:
$\angle$C = $45^\circ$
Therefore, the required angles are $\angle$B = $45^\circ$ and $\angle$C = $45^\circ$.
Question 8. Show that the angles of an equilateral triangle are 60° each.
Answer:
Given:
An equilateral triangle, let's call it $\triangle$ABC.
In an equilateral triangle, all sides are equal: AB = BC = CA.
To Prove:
Each angle is $60^\circ$, i.e., $\angle$A = $\angle$B = $\angle$C = $60^\circ$.
Proof:
Consider $\triangle$ABC.
Since AB = AC, the angles opposite to these sides are equal.
$\angle$C = $\angle$B
(Angles opposite equal sides) ... (i)
Since BC = AC (or AC = BC), the angles opposite to these sides are equal.
$\angle$A = $\angle$B
(Angles opposite equal sides) ... (ii)
From (i) and (ii), we can conclude that all three angles are equal:
$\angle$A = $\angle$B = $\angle$C
Let $\angle$A = $\angle$B = $\angle$C = $x$.
The sum of angles in a triangle is $180^\circ$.
$\angle$A + $\angle$B + $\angle$C = $180^\circ$
Substitute $x$ for each angle:
$x + x + x = 180^\circ$
3$x$ = $180^\circ$
$x = \frac{180^\circ}{3}$
$x = 60^\circ$
Therefore, $\angle$A = $\angle$B = $\angle$C = $60^\circ$.
Thus, each angle of an equilateral triangle is $60^\circ$.
Hence, proved.
Example 7 & 8 (Before Exercise 7.3)
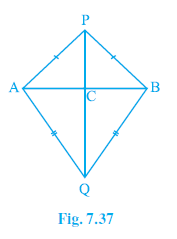
Example 7. AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB.
Answer:
Given:
AB is a line segment.
P and Q are points on opposite sides of AB.
P is equidistant from A and B, so PA = PB.
Q is equidistant from A and B, so QA = QB.
Line PQ intersects AB at point C (as shown in the figure).
To Prove:
Line PQ is the perpendicular bisector of AB.
(This requires proving two things: (1) PQ $\perp$ AB, i.e., $\angle$PCA = $90^\circ$, and (2) PQ bisects AB, i.e., AC = CB).
Proof:
Step 1: Prove $\triangle$PAQ $\cong$ $\triangle$PBQ
Consider $\triangle$PAQ and $\triangle$PBQ.
PA = PB
(Given)
QA = QB
(Given)
PQ = PQ
(Common side)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle$PAQ $\cong$ $\triangle$PBQ
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent):
$\angle$APQ = $\angle$BPQ
(This means $\angle$APC = $\angle$BPC as C lies on PQ).
Step 2: Prove $\triangle$PAC $\cong$ $\triangle$PBC
Consider $\triangle$PAC and $\triangle$PBC.
PA = PB
(Given)
$\angle$APC = $\angle$BPC
(Proved in Step 1)
PC = PC
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$PAC $\cong$ $\triangle$PBC
By CPCTC:
AC = CB ... (i)
And $\angle$PCA = $\angle$PCB ... (ii)
Step 3: Show PQ $\perp$ AB
Since AB is a straight line, $\angle$PCA and $\angle$PCB form a linear pair.
$\angle$PCA + $\angle$PCB = $180^\circ$ (Linear Pair Axiom)
From (ii), we know $\angle$PCA = $\angle$PCB.
Substituting this into the linear pair equation:
$\angle$PCA + $\angle$PCA = $180^\circ$
2 $\angle$PCA = $180^\circ$
$\angle$PCA = $\frac{180^\circ}{2} = 90^\circ$
Since $\angle$PCA = $90^\circ$, PQ is perpendicular to AB.
Step 4: Conclusion
From (i), we have AC = CB, which means PQ bisects AB.
From Step 3, we have PQ $\perp$ AB.
Since PQ bisects AB and is perpendicular to AB, PQ is the perpendicular bisector of AB.
Hence, proved.
Example 8. P is a point equidistant from two lines l and m intersecting at point A (see Fig. 7.38). Show that the line AP bisects the angle between them.

Answer:
Given:
Two lines l and m intersecting at point A.
P is a point such that it is equidistant from lines l and m.
Let PB be the perpendicular distance from P to line l (so PB $\perp$ l, $\angle$PBA = $90^\circ$).
Let PC be the perpendicular distance from P to line m (so PC $\perp$ m, $\angle$PCA = $90^\circ$).
Since P is equidistant, PB = PC.
Line AP is drawn.
To Prove:
Line AP bisects the angle between lines l and m.
(This means we need to prove $\angle$PAB = $\angle$PAC).
Construction:
Draw perpendiculars PB from P to line l and PC from P to line m.
(This is implied by the definition of "equidistant" from lines and shown in the figure).
Proof:
Consider the right-angled triangles $\triangle$PAB and $\triangle$PAC.
$\angle$PBA = $\angle$PCA
($90^\circ$ each, by construction/definition)
PA = PA
(Common hypotenuse)
PB = PC
(P is equidistant from l and m, Given)
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle$PAB $\cong$ $\triangle$PAC
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, $\angle$PAB = $\angle$PAC.
This shows that the line AP bisects the angle between lines l and m ($\angle$BAC).
Hence, proved.
Exercise 7.3
Question 1. ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.

Answer:
Given:
$\triangle$ABC and $\triangle$DBC are isosceles triangles on the same base BC.
Vertices A and D are on the same side of BC.
In $\triangle$ABC, AB = AC.
In $\triangle$DBC, DB = DC.
AD is extended to intersect BC at P.
To Prove:
(i) $\triangle$ABD $\cong$ $\triangle$ACD
(ii) $\triangle$ABP $\cong$ $\triangle$ACP
(iii) AP bisects $\angle$A as well as $\angle$D
(iv) AP is the perpendicular bisector of BC
Proof:
(i) Proving $\triangle$ABD $\cong$ $\triangle$ACD:
Consider $\triangle$ABD and $\triangle$ACD.
AB = AC
(Given)
DB = DC
(Given)
AD = AD
(Common side)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle$ABD $\cong$ $\triangle$ACD
Hence, part (i) is proved.
By CPCTC, we get: $\angle$BAD = $\angle$CAD ... (1)
And $\angle$BDA = $\angle$CDA ... (2)
(ii) Proving $\triangle$ABP $\cong$ $\triangle$ACP:
Consider $\triangle$ABP and $\triangle$ACP.
AB = AC
(Given)
$\angle$BAP = $\angle$CAP
($\angle$BAD = $\angle$CAD from (1), P lies on AD extended)
AP = AP
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ABP $\cong$ $\triangle$ACP
Hence, part (ii) is proved.
By CPCTC, we get: BP = CP ... (3)
And $\angle$APB = $\angle$APC ... (4)
(iii) Proving AP bisects $\angle$A as well as $\angle$D:
From equation (1) ($\angle$BAD = $\angle$CAD), since P lies on AD extended, $\angle$BAP = $\angle$CAP.
Therefore, AP bisects $\angle$A.
Now consider $\triangle$BDP and $\triangle$CDP.
DB = DC
(Given)
BP = CP
(From (3))
DP = DP
(Common side)
Therefore, by SSS congruence rule:
$\triangle$BDP $\cong$ $\triangle$CDP
By CPCTC, $\angle$BDP = $\angle$CDP.
Since $\angle$BDA and $\angle$CDA are parts of angles on a straight line formed by extending AD, and $\angle$BDP = $\angle$CDP, this confirms that AD (and hence AP) bisects $\angle$D (more precisely, $\angle$BDC).
Therefore, AP bisects $\angle$D.
Hence, AP bisects $\angle$A as well as $\angle$D.
Hence, part (iii) is proved.
(iv) Proving AP is the perpendicular bisector of BC:
From equation (3), we have BP = CP. This means P is the midpoint of BC, so AP bisects BC.
From equation (4), we have $\angle$APB = $\angle$APC.
Since BC is a straight line, $\angle$APB and $\angle$APC form a linear pair.
$\angle$APB + $\angle$APC = $180^\circ$
Substituting $\angle$APB = $\angle$APC:
$\angle$APB + $\angle$APB = $180^\circ$
2 $\angle$APB = $180^\circ$
$\angle$APB = $90^\circ$
Since $\angle$APB = $90^\circ$, AP is perpendicular to BC.
Since AP bisects BC (BP = CP) and AP is perpendicular to BC, AP is the perpendicular bisector of BC.
Hence, part (iv) is proved.
Question 2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Answer:
Given:
Isosceles $\triangle$ABC with AB = AC.
AD is an altitude, so AD $\perp$ BC.
This means $\angle$ADB = $\angle$ADC = $90^\circ$.
To Prove:
(i) AD bisects BC (i.e., BD = CD)
(ii) AD bisects $\angle$A (i.e., $\angle$BAD = $\angle$CAD)
Proof:
Consider the right-angled triangles $\triangle$ABD and $\triangle$ACD.
$\angle$ADB = $\angle$ADC
($90^\circ$ each, AD is altitude)
AB = AC
(Given, Hypotenuse)
AD = AD
(Common side)
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle$ABD $\cong$ $\triangle$ACD
Proof of (i):
By CPCTC, corresponding sides are equal.
BD = CD.
Therefore, AD bisects BC.
Hence, part (i) is proved.
Proof of (ii):
By CPCTC, corresponding angles are equal.
$\angle$BAD = $\angle$CAD.
Therefore, AD bisects $\angle$A.
Hence, part (ii) is proved.
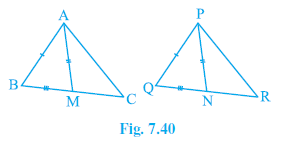
Question 3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆ PQR (see Fig. 7.40). Show that:
(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR
Answer:
Given:
In $\triangle$ABC and $\triangle$PQR:
AB = PQ
(Given)
BC = QR
(Given)
AM is the median of $\triangle$ABC, so M is the midpoint of BC ($BM = MC = \frac{1}{2} BC$).
PN is the median of $\triangle$PQR, so N is the midpoint of QR ($QN = NR = \frac{1}{2} QR$).
AM = PN
(Given)
To Prove:
(i) $\triangle$ ABM $\cong$ $\triangle$ PQN
(ii) $\triangle$ ABC $\cong$ $\triangle$ PQR
Proof:
(i) Proving $\triangle$ ABM $\cong$ $\triangle$ PQN:
Since BC = QR and M, N are midpoints:
$\frac{1}{2} BC = \frac{1}{2} QR$
Therefore, BM = QN.
Now, consider $\triangle$ABM and $\triangle$PQN.
AB = PQ
(Given)
BM = QN
(Proved above)
AM = PN
(Given)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle$ ABM $\cong$ $\triangle$ PQN
Hence, part (i) is proved.
By CPCTC, we get: $\angle$ABM = $\angle$PQN (or $\angle$B = $\angle$Q) ... (1)
(ii) Proving $\triangle$ ABC $\cong$ $\triangle$ PQR:
Consider $\triangle$ABC and $\triangle$PQR.
AB = PQ
(Given)
$\angle$ABC = $\angle$PQR
($\angle$B = $\angle$Q from (1))
BC = QR
(Given)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle$ ABC $\cong$ $\triangle$ PQR
Hence, part (ii) is proved.
Question 4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Answer:
Given:
In $\triangle$ABC:
BE is an altitude to AC, so BE $\perp$ AC ($\angle$BEC = $90^\circ$).
CF is an altitude to AB, so CF $\perp$ AB ($\angle$BFC = $90^\circ$).
The altitudes are equal: BE = CF.
To Prove:
$\triangle$ABC is isosceles (i.e., AB = AC), using RHS congruence rule.
Proof:
Consider the right-angled triangles $\triangle$BEC and $\triangle$CFB.
$\angle$BEC = $\angle$CFB
($90^\circ$ each, Given altitudes)
BC = CB
(Common hypotenuse)
BE = CF
(Given equal altitudes, Side)
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle$BEC $\cong$ $\triangle$CFB
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, $\angle$BCE = $\angle$CBF.
This means $\angle$ACB = $\angle$ABC (or $\angle$C = $\angle$B).
Now, in $\triangle$ABC, since $\angle$ACB = $\angle$ABC, the sides opposite to these equal angles must also be equal.
Side opposite $\angle$ACB is AB.
Side opposite $\angle$ABC is AC.
Therefore, AB = AC.
Since two sides of $\triangle$ABC are equal, $\triangle$ABC is an isosceles triangle.
Hence, proved using RHS rule.
Question 5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Answer:
Given:
Isosceles $\triangle$ABC with AB = AC.
Construction:
Draw AP $\perp$ BC, where P is a point on BC.
This means $\angle$APB = $\angle$APC = $90^\circ$.
To Prove:
$\angle$B = $\angle$C (i.e., $\angle$ABC = $\angle$ACB)
Proof:
Consider the right-angled triangles $\triangle$APB and $\triangle$APC.
$\angle$APB = $\angle$APC
($90^\circ$ each, by construction)
AB = AC
(Given, Hypotenuse)
AP = AP
(Common side)
Therefore, by RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle$APB $\cong$ $\triangle$APC
Since the triangles are congruent, their corresponding parts are equal (CPCTC).
Therefore, $\angle$ABP = $\angle$ACP.
This means $\angle$B = $\angle$C.
Hence, proved.
Example 9 (Before Exercise 7.4)
Example 9. D is a point on side BC of ∆ABC such that AD = AC (see Fig. 7.47). Show that AB > AD.

Answer:
Given:
In $\triangle$ABC, D is a point on side BC.
AD = AC.
To Prove:
AB > AD.
Proof:
In $\triangle$ADC, we are given AD = AC.
Since sides are equal, the angles opposite to them are equal.
$\angle$ADC = $\angle$ACD
(Angles opposite equal sides are equal)
Now, consider $\triangle$ABD. The angle $\angle$ADC is an exterior angle to $\triangle$ABD.
The exterior angle of a triangle is greater than either of the interior opposite angles.
Therefore, $\angle$ADC > $\angle$ABD (which is the same as $\angle$ABC).
Substituting $\angle$ADC = $\angle$ACD from the first step:
$\angle$ACD > $\angle$ABC
Now consider the entire $\triangle$ABC.
We have shown that $\angle$ACD > $\angle$ABC.
Since $\angle$ACD is a part of $\angle$ACB (or equal to it if D coincides with B, which is not the case from the diagram), we have $\angle$ACB $\geq$ $\angle$ACD.
Therefore, $\angle$ACB > $\angle$ABC.
In $\triangle$ABC, the side opposite the greater angle is longer.
Side opposite $\angle$ACB is AB.
Side opposite $\angle$ABC is AC.
Since $\angle$ACB > $\angle$ABC, we have AB > AC.
But we are given that AC = AD.
Substituting AC = AD into the inequality AB > AC, we get:
AB > AD.
Hence, proved.
Exercise 7.4
Question 1. Show that in a right angled triangle, the hypotenuse is the longest side.
Answer:
Given:
A right-angled triangle, let's call it $\triangle$ABC, right-angled at B.
So, $\angle$B = $90^\circ$.
The side opposite the right angle, AC, is the hypotenuse.
To Prove:
The hypotenuse is the longest side (i.e., AC > AB and AC > BC).
Proof:
In $\triangle$ABC, the sum of angles is $180^\circ$.
$\angle$A + $\angle$B + $\angle$C = $180^\circ$
Since $\angle$B = $90^\circ$:
$\angle$A + $90^\circ$ + $\angle$C = $180^\circ$
$\angle$A + $\angle$C = $180^\circ - 90^\circ = 90^\circ$
Since angles in a triangle are positive, this means $\angle$A < $90^\circ$ and $\angle$C < $90^\circ$.
Therefore, $\angle$B ($90^\circ$) is the largest angle in $\triangle$ABC.
$\angle$B > $\angle$A and $\angle$B > $\angle$C.
In a triangle, the side opposite the larger angle is longer.
Since $\angle$B > $\angle$C, the side opposite $\angle$B (AC) is longer than the side opposite $\angle$C (AB).
So, AC > AB.
Since $\angle$B > $\angle$A, the side opposite $\angle$B (AC) is longer than the side opposite $\angle$A (BC).
So, AC > BC.
Since AC is longer than both AB and BC, the hypotenuse AC is the longest side in the right-angled triangle ABC.
Hence, proved.
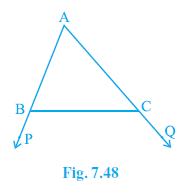
Question 2. In Fig. 7.48, sides AB and AC of ∆ ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
Answer:
Given:
In $ \triangle $ABC, side AB is extended to P and side AC is extended to Q.
$ \angle $PBC < $ \angle $QCB.
To Prove:
AC > AB.
Proof:
Angles $ \angle $ABC and $ \angle $PBC form a linear pair on the line segment PB.
$ \angle $ABC + $ \angle $PBC = $ 180^\circ $
$ \angle $ABC = $ 180^\circ $ - $ \angle $PBC
... (i)
Angles $ \angle $ACB and $ \angle $QCB form a linear pair on the line segment QC.
$ \angle $ACB + $ \angle $QCB = $ 180^\circ $
$ \angle $ACB = $ 180^\circ $ - $ \angle $QCB
... (ii)
We are given $ \angle $PBC < $ \angle $QCB.
Multiply both sides by -1 (this reverses the inequality sign):
$-$ $ \angle $PBC > $-$ $ \angle $QCB
Add $ 180^\circ $ to both sides:
$ 180^\circ $ - $ \angle $PBC > $ 180^\circ $ - $ \angle $QCB
Using equations (i) and (ii), substitute the equivalent angles:
$ \angle $ABC > $ \angle $ACB
Now, in $ \triangle $ABC, we have $ \angle $ABC > $ \angle $ACB.
The side opposite the larger angle is longer.
Side opposite $ \angle $ABC is AC.
Side opposite $ \angle $ACB is AB.
Therefore, AC > AB.
Hence, proved.
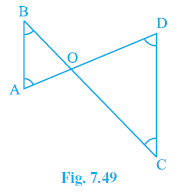
Question 3. In Fig. 7.49, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
Answer:
Given:
Figure shows lines AD and BC intersected by AB and CD, with AD and BC intersecting at O (implicitly).
In $ \triangle $OAB (formed by intersection), $ \angle $B < $ \angle $A (which means $ \angle $OBA < $ \angle $OAB).
In $ \triangle $OCD (formed by intersection), $ \angle $C < $ \angle $D (which means $ \angle $OCD < $ \angle $ODC).
To Prove:
AD < BC.
Proof:
Consider $ \triangle $OAB.
We are given $ \angle $OBA < $ \angle $OAB.
In a triangle, the side opposite the smaller angle is shorter.
Side opposite $ \angle $OBA is OA.
Side opposite $ \angle $OAB is OB.
OA < OB
... (i)
Consider $ \triangle $OCD.
We are given $ \angle $OCD < $ \angle $ODC.
In a triangle, the side opposite the smaller angle is shorter.
Side opposite $ \angle $OCD is OD.
Side opposite $ \angle $ODC is OC.
OD < OC
... (ii)
Adding the inequalities (i) and (ii):
(OA + OD) < (OB + OC)
From the figure, OA + OD = AD.
From the figure, OB + OC = BC.
Substituting these into the inequality:
AD < BC.
Hence, proved.
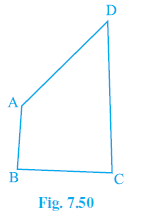
Question 4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that ∠A > ∠C and ∠B > ∠D.
Answer:
Given:
Quadrilateral ABCD.
AB is the smallest side (AB < BC, AB < CD, AB < DA).
CD is the longest side (CD > AB, CD > BC, CD > DA).
To Prove:
(i) $ \angle $A > $ \angle $C
(ii) $ \angle $B > $ \angle $D
Construction:
Join A to C and B to D.
Proof:
(i) Proving $ \angle $A > $ \angle $C:
Consider $ \triangle $ABC.
Since AB is the smallest side, AB < BC.
The angle opposite the longer side is greater.
Angle opposite BC is $ \angle $BAC.
Angle opposite AB is $ \angle $BCA (or $ \angle $ACB).
$ \angle $BAC > $ \angle $BCA
... (1)
Consider $ \triangle $ADC.
Since CD is the longest side, CD > AD.
The angle opposite the longer side is greater.
Angle opposite CD is $ \angle $CAD.
Angle opposite AD is $ \angle $ACD.
$ \angle $CAD > $ \angle $ACD
... (2)
Adding inequalities (1) and (2):
($ \angle $BAC + $ \angle $CAD) > ($ \angle $BCA + $ \angle $ACD)
From the figure, $ \angle $BAC + $ \angle $CAD = $ \angle $BAD = $ \angle $A.
From the figure, $ \angle $BCA + $ \angle $ACD = $ \angle $BCD = $ \angle $C.
Therefore, $ \angle $A > $ \angle $C.
Hence, part (i) is proved.
(ii) Proving $ \angle $B > $ \angle $D:
Consider $ \triangle $ABD.
Since AB is the smallest side, AB < AD.
The angle opposite the longer side is greater.
Angle opposite AD is $ \angle $ABD.
Angle opposite AB is $ \angle $ADB.
$ \angle $ABD > $ \angle $ADB
... (3)
Consider $ \triangle $BCD.
Since CD is the longest side, CD > BC.
The angle opposite the longer side is greater.
Angle opposite CD is $ \angle $CBD.
Angle opposite BC is $ \angle $BDC.
$ \angle $CBD > $ \angle $BDC
... (4)
Adding inequalities (3) and (4):
($ \angle $ABD + $ \angle $CBD) > ($ \angle $ADB + $ \angle $BDC)
From the figure, $ \angle $ABD + $ \angle $CBD = $ \angle $ABC = $ \angle $B.
From the figure, $ \angle $ADB + $ \angle $BDC = $ \angle $ADC = $ \angle $D.
Therefore, $ \angle $B > $ \angle $D.
Hence, part (ii) is proved.
Question 5. In Fig 7.51, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

Answer:
Given:
In $ \triangle $PQR:
PR > PQ.
PS bisects $ \angle $QPR, so $ \angle $QPS = $ \angle $RPS.
To Prove:
$ \angle $PSR > $ \angle $PSQ.
Proof:
In $ \triangle $PQR, we are given PR > PQ.
The angle opposite the longer side is greater.
Angle opposite PR is $ \angle $PQR.
Angle opposite PQ is $ \angle $PRQ.
Therefore, $ \angle $PQR > $ \angle $PRQ.
We are given that PS bisects $ \angle $QPR, so $ \angle $QPS = $ \angle $RPS.
Let $ \angle $QPS = $ \angle $RPS = $ x $.
Consider $ \triangle $PQS.
The sum of angles is $ 180^\circ $.
$ \angle $PQS + $ \angle $QPS + $ \angle $PSQ = $ 180^\circ $
$ \angle $PQR + $ x $ + $ \angle $PSQ = $ 180^\circ $
$ \angle $PQR = $ 180^\circ $ - $ x $ - $ \angle $PSQ
... (i)
Consider $ \triangle $PRS.
The sum of angles is $ 180^\circ $.
$ \angle $PRS + $ \angle $RPS + $ \angle $PSR = $ 180^\circ $
$ \angle $PRQ + $ x $ + $ \angle $PSR = $ 180^\circ $
$ \angle $PRQ = $ 180^\circ $ - $ x $ - $ \angle $PSR
... (ii)
Substitute (i) and (ii) into the inequality $ \angle $PQR > $ \angle $PRQ:
($ 180^\circ $ - $ x $ - $ \angle $PSQ) > ($ 180^\circ $ - $ x $ - $ \angle $PSR)
Subtract $ 180^\circ $ from both sides:
$-$ $ x $ - $ \angle $PSQ > $-$ $ x $ - $ \angle $PSR
Add $ x $ to both sides:
$-$ $ \angle $PSQ > $-$ $ \angle $PSR
Multiply both sides by -1 (this reverses the inequality sign):
$ \angle $PSQ < $ \angle $PSR
Or, $ \angle $PSR > $ \angle $PSQ.
Hence, proved.
Alternate Solution (using Exterior Angle Theorem):
In $ \triangle $PQR, since PR > PQ, the angle opposite PR ($ \angle $PQR) is greater than the angle opposite PQ ($ \angle $PRQ).
$ \angle $PQR > $ \angle $PRQ.
Given PS bisects $ \angle $QPR, so $ \angle $QPS = $ \angle $RPS.
In $ \triangle $PQS, the exterior angle $ \angle $PSR = $ \angle $PQS + $ \angle $QPS (i.e., $ \angle $PSR = $ \angle $PQR + $ \angle $QPS).
In $ \triangle $PRS, the exterior angle $ \angle $PSQ = $ \angle $PRS + $ \angle $RPS (i.e., $ \angle $PSQ = $ \angle $PRQ + $ \angle $RPS).
We know $ \angle $PQR > $ \angle $PRQ.
We also know $ \angle $QPS = $ \angle $RPS.
Adding these two statements (inequality and equality):
$ \angle $PQR + $ \angle $QPS > $ \angle $PRQ + $ \angle $RPS
Substituting the exterior angles:
$ \angle $PSR > $ \angle $PSQ
Hence, proved.
Question 6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Answer:
Given:
A line l and a point P not on l.
PM is the perpendicular line segment from P to l (so PM $ \perp $ l).
N is any point on l other than M.
PN is a line segment joining P to N.
To Prove:
PM is the shortest line segment from P to l (i.e., PM < PN).
Proof:
Consider the triangle $ \triangle $PMN formed by the points P, M, and N.
Since PM $ \perp $ l, the angle $ \angle $PMN is a right angle.
$ \angle $PMN = $ 90^\circ $.
Therefore, $ \triangle $PMN is a right-angled triangle, with the right angle at M.
In a right-angled triangle, the sum of the other two angles is $ 90^\circ $.
$ \angle $MPN + $ \angle $PNM = $ 90^\circ $.
This implies that both $ \angle $MPN and $ \angle $PNM are acute angles (less than $ 90^\circ $).
So, $ \angle $PMN ($ 90^\circ $) is the largest angle in $ \triangle $PMN.
In any triangle, the side opposite the largest angle is the longest side.
The side opposite the largest angle $ \angle $PMN is PN (the hypotenuse).
The side opposite the angle $ \angle $PNM is PM.
Since $ \angle $PMN > $ \angle $PNM, the side opposite $ \angle $PMN (PN) is longer than the side opposite $ \angle $PNM (PM).
Therefore, PN > PM, or PM < PN.
Since N was any point on l other than M, this shows that the perpendicular line segment PM is shorter than any other line segment drawn from P to the line l.
Hence, the perpendicular line segment is the shortest.
Hence, proved.
Exercise 7.5 (Optional)
Question 1. ABC is a triangle. Locate a point in the interior of ∆ ABC which is equidistant from all the vertices of ∆ ABC.
Answer:
The point in the interior of a triangle that is equidistant from all its vertices is called the circumcenter of the triangle. The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect.
To Locate:
A point O in the interior of $\triangle$ABC such that it is equidistant from all the vertices, i.e., OA = OB = OC.
Steps of Construction:
1. Draw the triangle $\triangle$ABC.
2. Construct the perpendicular bisector of the side AB. Let's call this line $l_1$.
3. Construct the perpendicular bisector of the side BC. Let's call this line $l_2$.
4. Let the point where these two perpendicular bisectors, $l_1$ and $l_2$, intersect be named O.
5. Join OA, OB, and OC.
6. The point O is the required point which is equidistant from the vertices A, B, and C.
Justification (Proof):
The fundamental property we use is that any point on the perpendicular bisector of a line segment is equidistant from the endpoints of the segment.
From our construction:
Point O lies on the perpendicular bisector of the side AB.
OA = OB
[Property of perpendicular bisector] ... (i)
Similarly, point O also lies on the perpendicular bisector of the side BC.
OB = OC
[Property of perpendicular bisector] ... (ii)
From equation (i) and equation (ii), we can conclude that:
OA = OB = OC
This shows that the point O is equidistant from all three vertices of the triangle ABC.
Therefore, O is the required point.
Note: The perpendicular bisector of the third side, AC, will also pass through this same point O.
Question 2. In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Answer:
The point in the interior of a triangle that is equidistant from all its sides is called the incenter of the triangle. The incenter is the point where the bisectors of the interior angles of the triangle intersect.
To Locate:
A point O in the interior of $\triangle$ABC such that it is equidistant from all the sides AB, BC, and CA.
Steps of Construction:
1. Draw the triangle $\triangle$ABC.
2. Construct the angle bisector of $\angle B$.
3. Construct the angle bisector of $\angle C$.
4. Let the point where these two angle bisectors intersect be named O.
5. The point O is the required point which is equidistant from the sides of the triangle.
Justification (Proof):
The fundamental property we use is that any point on the bisector of an angle is equidistant from the two arms of the angle.
Let's draw perpendiculars from the point O to the sides of the triangle. Let OD $\perp$ BC, OE $\perp$ AC, and OF $\perp$ AB.
From our construction:
Point O lies on the angle bisector of $\angle B$. Therefore, its distance from the arms BA and BC is equal.
OF = OD
[Property of angle bisector] ... (i)
Similarly, point O also lies on the angle bisector of $\angle C$. Therefore, its distance from the arms CB and CA is equal.
OD = OE
[Property of angle bisector] ... (ii)
From equation (i) and equation (ii), we can conclude that:
OF = OD = OE
This shows that the point O is equidistant from all three sides of the triangle ABC.
Therefore, O is the required point.
Note: The angle bisector of the third angle, $\angle A$, will also pass through this same point O.
Question 3. In a huge park, people are concentrated at three points (see Fig. 7.52):
A : where there are different slides and swings for children,
B : near which a man-made lake is situated,
C : which is near to a large parking and exit.
Where should an icecream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlour should be equidistant from A, B and C)

Answer:
The problem asks for a location for an icecream parlour that is equally accessible to the maximum number of people concentrated at three different points: A, B, and C. As suggested by the hint, this means the parlour should be located at a point that is equidistant from A, B, and C.
In geometry, the point that is equidistant from the three vertices of a triangle is known as the circumcenter of the triangle. The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect.
To Locate the Position of the Icecream Parlour:
The ideal location for the icecream parlour is the circumcenter of the triangle formed by joining the points A, B, and C. Let's call this point O.
Steps of Construction:
1. Join the points A, B, and C to form a triangle, $\triangle$ABC.
2. Construct the perpendicular bisector of the side AB.
3. Construct the perpendicular bisector of the side BC.
4. The point where these two perpendicular bisectors intersect is the required location. Let's name this point O.
5. The point O is the circumcenter of $\triangle$ABC and is the ideal location for the icecream parlour.
Justification:
We need to show that the point O is equidistant from A, B, and C (i.e., OA = OB = OC).
We use the property that any point on the perpendicular bisector of a line segment is equidistant from the endpoints of that segment.
Since point O lies on the perpendicular bisector of the line segment AB:
OA = OB
[Property of perpendicular bisector] ... (i)
Similarly, since point O lies on the perpendicular bisector of the line segment BC:
OB = OC
[Property of perpendicular bisector] ... (ii)
From equations (i) and (ii), we can conclude that:
OA = OB = OC
This proves that the point O is equidistant from A, B, and C. Therefore, the icecream parlour should be set up at the circumcenter O of the triangle ABC to be equally accessible to people at points A, B, and C.
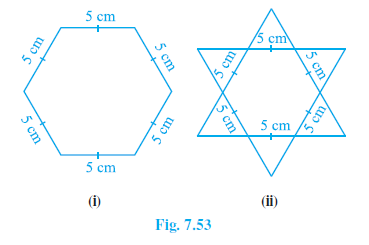
Question 4. Complete the hexagonal and star shaped Rangolies [see Fig. 7.53 (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
Answer:
To solve this problem, we will determine the area of each Rangoli shape in terms of the number of small equilateral triangles of side 1 cm that can fit inside it. We can do this by first decomposing each large shape into simpler, congruent equilateral triangles with a side length of 5 cm.
The number of small equilateral triangles (side 1 cm) that can fit into a larger equilateral triangle (side 'a' cm) is given by $a^2$.
In our case, the larger constituent triangles have a side length of 5 cm. So, the number of small 1 cm triangles in one such triangle is:
Number of triangles = $5^2 = 25$
Case (i): Hexagonal Rangoli
The hexagonal Rangoli is a regular hexagon with each side of length 5 cm.
A regular hexagon can be divided into 6 congruent equilateral triangles, with the side of each triangle being equal to the side of the hexagon (5 cm).
The total number of 1 cm equilateral triangles in the hexagon is the number of large triangles multiplied by the number of small triangles in each large triangle.
Total triangles in hexagon = (Number of large triangles) $\times$ (Number of small triangles per large triangle)
Total triangles in hexagon = $6 \times 25$
Total triangles in hexagon = 150
Case (ii): Star-shaped Rangoli
The star-shaped Rangoli is a hexagram. This shape can be divided into 12 congruent equilateral triangles, each with a side length of 5 cm (6 triangles form the points of the star, and 6 triangles form the central hexagon).
The total number of 1 cm equilateral triangles in the star is the number of large triangles multiplied by the number of small triangles in each large triangle.
Total triangles in star = (Number of large triangles) $\times$ (Number of small triangles per large triangle)
Total triangles in star = $12 \times 25$
Total triangles in star = 300
Conclusion
By comparing the number of triangles in each case:
Number of triangles in Hexagonal Rangoli = 150
Number of triangles in Star-shaped Rangoli = 300
Since $300 > 150$, the star-shaped Rangoli has more triangles.

