| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 9.1 | Example 1 & 2 (Before Exercise 9.2) | Exercise 9.2 |
| Example 3 & 4 (Before Exercise 9.3) | Exercise 9.3 | Exercise 9.4 (Optional) |
Chapter 9 Areas of Parallelograms and Triangles
We now venture into Chapter 9: Areas Of Parallelograms And Triangles, a fascinating section of geometry that shifts our perspective on area. Instead of solely focusing on computational formulas like length times width or half-base-times-height, this chapter emphasizes the relative areas of geometric figures, specifically parallelograms and triangles, based on their spatial relationships. The core concepts revolve around figures sharing common bases and being situated between the same parallel lines. Understanding these relationships allows us to deduce equalities and proportions between areas without necessarily calculating their exact numerical values, establishing several fundamental geometric theorems crucial for deeper analysis.
A foundational idea explored in the solutions is that geometric figures can possess the exact same area even if they are not congruent (i.e., they might not have the same shape). The chapter systematically builds upon this, presenting key theorems that form the bedrock of comparing areas under specific conditions. The solutions meticulously guide users through the understanding, proof (where applicable), and application of these vital principles.
The central theorems and concepts covered, often demonstrated with clear proofs and application examples in the solutions, include:
- Parallelograms on the same base (or on equal bases) and positioned between the same parallel lines are definitively equal in area. Solutions focus on identifying these configurations in diagrams and using this theorem rigorously to prove area equalities. The underlying proof, often involving triangle congruence, is frequently detailed to ensure a thorough understanding.
- While the formula for the area of a parallelogram as base times height is acknowledged, it's contextualized within the framework of the first theorem, highlighting why parallelograms under the specified conditions share the same area (same base, same height).
- Similarly, triangles constructed on the same base (or on equal bases) and lying between the same parallel lines are also proven to be equal in area. Solutions provide guidance on recognizing these setups and applying the theorem effectively. The proof often connects the triangle's area to half the area of a related parallelogram sharing the same base and height.
- The standard formula for the area of a triangle, $Area = \frac{1}{2} \times \text{base} \times \text{height}$, is intrinsically linked to the third theorem, explaining why triangles under those conditions have equal areas (sharing the same base and height).
- A crucial property derived from area principles is that a median of a triangle divides the triangle into two smaller triangles of precisely equal areas. The solutions demonstrate the straightforward proof (using the area formula $Area = \frac{1}{2} \times b \times h$, noting shared height and equal bases created by the median) and showcase its application in various problems, sometimes involving intricate figures with multiple medians or centroids.
Exercises within this chapter frequently challenge students to establish relationships between the areas of different components within a complex figure. This often requires the strategic combination of the theorems mentioned above. The solutions excel in providing clear, logical, step-by-step proofs, consistently emphasizing the critical conditions of figures sharing the same base and lying between the same parallels. This reinforces a robust understanding of these area-related geometric principles and their practical application in deductive reasoning.
Exercise 9.1
Question 1. Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
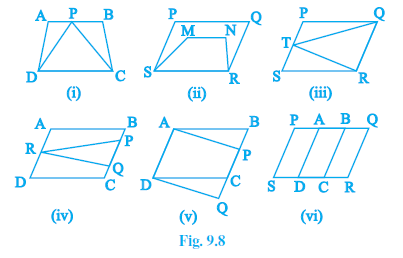
Answer:
To determine if figures lie on the same base and between the same parallels, we must check two conditions:
1. The figures must share a common side (the common base).
2. The vertices of each figure that are opposite to the common base must all lie on a single straight line that is parallel to the base (the parallels).
(i) Trapezium ABCD and $\triangle$PDC
Yes. These figures lie on the same base and between the same parallels.
Common Base: DC
Parallels: DC and AB
(The vertices A and B of the trapezium and the vertex P of the triangle all lie on the line AB, which is parallel to the base DC.)
(ii) Parallelogram PQRS and Trapezium MNRS
No. Although they share a common base SR and are between the same parallels (SR and PQ), the condition is typically applied to compare two distinct figures. Here, the trapezium MNRS is a part of the parallelogram PQRS, not a separate figure being compared to it.
(iii) Parallelogram PQRS and $\triangle$TQR
Yes. These figures lie on the same base and between the same parallels.
Common Base: QR
Parallels: QR and PS
(The vertices P and S of the parallelogram and the vertex T of the triangle all lie on the line PS, which is parallel to the base QR.)
(iv) Parallelogram ABCD and $\triangle$PQR
No. The figures lie between the same parallels (AD and BC), but they do not share a common base. The base of the triangle, QR, is only a part of the side BC.
(v) Trapezium ABCD and Trapezium APQD
Yes. These figures lie on the same base and between the same parallels.
Common Base: AD
Parallels: AD and BQ
(The vertices B and C of the first trapezium and the vertices P and Q of the second trapezium all lie on the single straight line BQ, which is parallel to the base AD.)
(vi) Parallelogram PQRS and the smaller parallelograms inside it
No. While the figures lie between the same parallels PQ and SR, they are on different, adjacent bases (such as PA, AD, DC, etc.) and do not share a single common base.
Example 1 & 2 (Before Exercise 9.2)
Example 1. In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle.
Also, AL ⊥ DC. Prove that
(i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC × AL
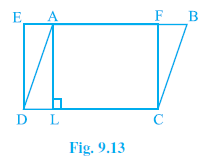
Answer:
Given:
ABCD is a parallelogram.
EFCD is a rectangle.
AL $\perp$ DC.
To Prove:
(i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC $\times$ AL
Proof:
We are given that ABCD is a parallelogram and EFCD is a rectangle.
(i) To prove ar (ABCD) = ar (EFCD)
Parallelogram ABCD and rectangle EFCD are on the same base DC.
AB $\parallel$ DC
(Opposite sides of parallelogram ABCD)
EF $\parallel$ DC
(Opposite sides of rectangle EFCD)
From the figure, it is clear that the vertices A and B of parallelogram ABCD lie on the line BE.
Also, the vertices E and F of rectangle EFCD lie on the same line BE.
Since AB $\parallel$ DC and EF $\parallel$ DC, the line BE must be parallel to DC.
Thus, parallelogram ABCD and rectangle EFCD are on the same base DC and between the same parallels DC and BE.
We know that two parallelograms (or a parallelogram and a rectangle) on the same base and between the same parallels are equal in area.
Therefore,
ar (ABCD) = ar (EFCD)
(ii) To prove ar (ABCD) = DC $\times$ AL
We know that the area of a parallelogram is given by the product of its base and the corresponding altitude.
For parallelogram ABCD, we can take DC as the base.
The corresponding altitude from vertex A to the base DC is AL.
AL $\perp$ DC
(Given)
Therefore, the area of parallelogram ABCD is given by:
ar (ABCD) = Base $\times$ Height
ar (ABCD) = DC $\times$ AL
This proves the second part.
Example 2. If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
Answer:
Given:
A parallelogram ABCD and a triangle $\triangle$PBC are on the same base BC and lie between the same parallel lines BC and AP.
To Prove:
The area of the triangle is equal to half the area of the parallelogram, i.e.,
ar($\triangle$PBC) = $\frac{1}{2}$ ar(ABCD)
Construction:
Draw a line segment CQ such that it is parallel to BP (CQ $||$ BP), where Q is a point on the line AP.
Proof:
Let's consider the quadrilateral PBCQ.
We have:
BP $||$ CQ
(By construction)
BC $||$ PQ
(Since BC $||$ AP and Q lies on the line AP)
Since both pairs of opposite sides are parallel, the quadrilateral PBCQ is a parallelogram.
Now, the parallelogram ABCD and the parallelogram PBCQ are on the same base BC and between the same parallel lines BC and AQ.
According to the theorem, parallelograms on the same base and between the same parallels are equal in area.
ar(parallelogram ABCD) = ar(parallelogram PBCQ)
... (i)
Now, let's consider the parallelogram PBCQ. The line segment PC is a diagonal of this parallelogram.
We know that a diagonal of a parallelogram divides it into two triangles of equal area.
Therefore,
ar($\triangle$PBC) = $\frac{1}{2}$ ar(parallelogram PBCQ)
... (ii)
Now, substituting the value from equation (i) into equation (ii), we get:
ar($\triangle$PBC) = $\frac{1}{2}$ ar(parallelogram ABCD)
Hence, it is proved that if a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is equal to half the area of the parallelogram.
Exercise 9.2
Question 1. In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
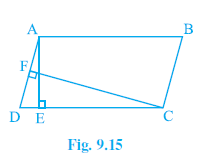
Answer:
Given:
ABCD is a parallelogram.
AB = 16 cm.
AE $\perp$ DC, AE = 8 cm.
CF $\perp$ AD, CF = 10 cm.
To Find:
The length of side AD.
Solution:
In a parallelogram, opposite sides are equal in length.
DC = AB
(Opposite sides of parallelogram)
Given AB = 16 cm, so DC = 16 cm.
The area of a parallelogram can be calculated by the product of a base and its corresponding altitude.
Using base DC and altitude AE:
ar (ABCD) = Base $\times$ Altitude
ar (ABCD) = DC $\times$ AE
... (i)
Substitute the given values into equation (i):
ar (ABCD) = 16 cm $\times$ 8 cm
ar (ABCD) = 128 cm$^2$
... (ii)
Now, consider AD as the base and CF as the corresponding altitude.
ar (ABCD) = AD $\times$ CF
... (iii)
Substitute the known values (from equation (ii) and given CF) into equation (iii):
128 cm$^2$ = AD $\times$ 10 cm
To find AD, rearrange the equation:
AD = $\frac{128 \text{ cm}^2}{10 \text{ cm}}$
AD = 12.8 cm
Thus, the length of AD is 12.8 cm.
Question 2. If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = $\frac{1}{2}$ ar (ABCD).
Answer:
Given:
ABCD is a parallelogram.
E, F, G, and H are respectively the mid-points of the sides AB, BC, CD, and DA.
To Prove:
ar (EFGH) = $\frac{1}{2}$ ar (ABCD).
Construction:
Join H to F.
Proof:
In parallelogram ABCD, AD $\parallel$ BC and AD = BC (Opposite sides of a parallelogram).
H is the mid-point of AD and F is the mid-point of BC.
Since H and F are the mid-points of opposite sides AD and BC in parallelogram ABCD, the line segment HF is parallel to AB and DC, and its length is equal to AB (or DC).
HF $\parallel$ AB
... (i)
HF $\parallel$ DC
... (ii)
HF = AB = DC
... (iii)
Consider the quadrilateral ABFH.
Since H and F are mid-points of AD and BC respectively, AH = $\frac{1}{2}$ AD and BF = $\frac{1}{2}$ BC.
As AD = BC, AH = BF.
AH $\parallel$ BF
($\because$ AD $\parallel$ BC)
Since AH = BF and AH $\parallel$ BF, ABFH is a parallelogram.
Alternatively, since AB $\parallel$ HF (from (i)) and AH $\parallel$ BF, ABFH is a parallelogram.
Similarly, consider the quadrilateral HFCD.
HD = $\frac{1}{2}$ AD and FC = $\frac{1}{2}$ BC.
As AD = BC, HD = FC.
HD $\parallel$ FC
($\because$ AD $\parallel$ BC)
Since HD = FC and HD $\parallel$ FC, HFCD is a parallelogram.
Alternatively, since DC $\parallel$ HF (from (ii)) and HD $\parallel$ FC, HFCD is a parallelogram.
Let 'h' be the perpendicular distance between the parallel sides AB and DC.
Since HF is parallel to AB and DC and passes through the mid-points H and F, the perpendicular distance between AB and HF is $\frac{h}{2}$, and the perpendicular distance between HF and DC is $\frac{h}{2}$.
Area of parallelogram ABFH = Base $\times$ Height = AB $\times$ $\frac{h}{2}$.
Area of parallelogram HFCD = Base $\times$ Height = DC $\times$ $\frac{h}{2}$.
Since AB = DC (from (iii)), ar (ABFH) = ar (HFCD).
Also, ar (ABCD) = Base $\times$ Height = DC $\times$ h = DC $\times$ ($\frac{h}{2} + \frac{h}{2}$) = DC $\times$ $\frac{h}{2}$ + DC $\times$ $\frac{h}{2}$.
ar (ABCD) = ar (HFCD) + ar (ABFH)
Since ar (ABFH) = ar (HFCD), we have ar (ABCD) = ar (HFCD) + ar (HFCD) = 2 $\times$ ar (HFCD).
ar (HFCD) = $\frac{1}{2}$ ar (ABCD)
... (iv)
Also, ar (ABFH) = $\frac{1}{2}$ ar (ABCD).
Now, consider $\triangle$EFH and parallelogram ABFH.
They lie on the same base HF and between the same parallels AB and HF (from (i)).
By the theorem stating that if a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram (as proved in Example 2):
ar ($\triangle$EFH) = $\frac{1}{2}$ ar (ABFH)
... (v)
Similarly, consider $\triangle$HGF and parallelogram HFCD.
They lie on the same base HF and between the same parallels DC and HF (from (ii)).
ar ($\triangle$HGF) = $\frac{1}{2}$ ar (HFCD)
... (vi)
Parallelogram EFGH is formed by the union of $\triangle$EFH and $\triangle$HGF.
ar (EFGH) = ar ($\triangle$EFH) + ar ($\triangle$HGF)
... (vii)
Substitute the results from (v) and (vi) into (vii):
ar (EFGH) = $\frac{1}{2}$ ar (ABFH) + $\frac{1}{2}$ ar (HFCD)
ar (EFGH) = $\frac{1}{2}$ [ar (ABFH) + ar (HFCD)]
From the area addition property, ar (ABFH) + ar (HFCD) = ar (ABCD).
ar (EFGH) = $\frac{1}{2}$ ar (ABCD)
Hence Proved.
Question 3. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
Answer:
Given:
ABCD is a parallelogram.
P is any point lying on the side DC.
Q is any point lying on the side AD.
To Prove:
ar (APB) = ar (BQC).
Proof:
Consider $\triangle$APB and parallelogram ABCD.
They lie on the same base AB.
AB $\parallel$ DC
(Opposite sides of parallelogram ABCD)
Since P is a point on DC, AB is parallel to AP, BP lies on the line DC.
Thus, $\triangle$APB and parallelogram ABCD lie on the same base AB and between the same parallels AB and DC.
By the theorem, the area of a triangle is half the area of a parallelogram if they are on the same base and between the same parallels.
ar ($\triangle$APB) = $\frac{1}{2}$ ar (ABCD)
... (i)
Now, consider $\triangle$BQC and parallelogram ABCD.
They lie on the same base BC.
BC $\parallel$ AD
(Opposite sides of parallelogram ABCD)
Since Q is a point on AD, BQ, CQ lies on the line AD.
Thus, $\triangle$BQC and parallelogram ABCD lie on the same base BC and between the same parallels BC and AD.
By the same theorem:
ar ($\triangle$BQC) = $\frac{1}{2}$ ar (ABCD)
... (ii)
From equations (i) and (ii), we see that both ar ($\triangle$APB) and ar ($\triangle$BQC) are equal to half the area of parallelogram ABCD.
Therefore,
ar (APB) = ar (BQC)
Hence Proved.
Question 4. In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = $\frac{1}{2}$ ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through P, draw a line parallel to AB.]
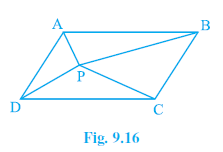
Answer:
Given:
ABCD is a parallelogram.
P is a point in the interior of parallelogram ABCD.
To Prove:
(i) ar (APB) + ar (PCD) = $\frac{1}{2}$ ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
Construction:
Draw a line segment EF passing through point P, parallel to AB and DC, such that E lies on AD and F lies on BC.
Proof:
(i) To prove ar (APB) + ar (PCD) = $\frac{1}{2}$ ar (ABCD)
Since EF $\parallel$ AB and E is on AD, F is on BC, and ABCD is a parallelogram, the quadrilateral ABEF is a parallelogram.
AB $\parallel$ EF
(By construction)
AE $\parallel$ BF
(Parts of parallel sides AD and BC)
Therefore, ABEF is a parallelogram.
Similarly, the quadrilateral EFCD is a parallelogram.
DC $\parallel$ EF
(By construction)
ED $\parallel$ FC
(Parts of parallel sides AD and BC)
Therefore, EFCD is a parallelogram.
Consider $\triangle$APB and parallelogram ABEF.
They are on the same base AB and between the same parallels AB and EF.
By the theorem, the area of a triangle is half the area of a parallelogram on the same base and between the same parallels.
ar ($\triangle$APB) = $\frac{1}{2}$ ar (ABEF)
... (1)
Consider $\triangle$PCD and parallelogram EFCD.
They are on the same base DC and between the same parallels DC and EF.
ar ($\triangle$PCD) = $\frac{1}{2}$ ar (EFCD)
... (2)
Adding equations (1) and (2):
ar (APB) + ar (PCD) = $\frac{1}{2}$ ar (ABEF) + $\frac{1}{2}$ ar (EFCD)
ar (APB) + ar (PCD) = $\frac{1}{2}$ [ar (ABEF) + ar (EFCD)]
The sum of the areas of parallelograms ABEF and EFCD is the area of parallelogram ABCD.
ar (ABEF) + ar (EFCD) = ar (ABCD)
Therefore,
ar (APB) + ar (PCD) = $\frac{1}{2}$ ar (ABCD)
This proves part (i).
(ii) To prove ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
Draw another line segment GH passing through point P, parallel to AD and BC, such that G lies on AB and H lies on DC.
Since GH $\parallel$ AD and G is on AB, H is on DC, and ABCD is a parallelogram, the quadrilateral AGHD is a parallelogram.
AD $\parallel$ GH
(By construction)
AG $\parallel$ DH
(Parts of parallel sides AB and DC)
Therefore, AGHD is a parallelogram.
Similarly, the quadrilateral GBCH is a parallelogram.
BC $\parallel$ GH
(By construction)
GB $\parallel$ HC
(Parts of parallel sides AB and DC)
Therefore, GBCH is a parallelogram.
Consider $\triangle$APD and parallelogram AGHD.
They are on the same base AD and between the same parallels AD and GH.
ar ($\triangle$APD) = $\frac{1}{2}$ ar (AGHD)
... (3)
Consider $\triangle$PBC and parallelogram GBCH.
They are on the same base BC and between the same parallels BC and GH.
ar ($\triangle$PBC) = $\frac{1}{2}$ ar (GBCH)
... (4)
Adding equations (3) and (4):
ar (APD) + ar (PBC) = $\frac{1}{2}$ ar (AGHD) + $\frac{1}{2}$ ar (GBCH)
ar (APD) + ar (PBC) = $\frac{1}{2}$ [ar (AGHD) + ar (GBCH)]
The sum of the areas of parallelograms AGHD and GBCH is the area of parallelogram ABCD.
ar (AGHD) + ar (GBCH) = ar (ABCD)
Therefore,
ar (APD) + ar (PBC) = $\frac{1}{2}$ ar (ABCD)
... (5)
From the result of part (i), we have:
ar (APB) + ar (PCD) = $\frac{1}{2}$ ar (ABCD)
... (6)
Comparing equations (5) and (6), we get:
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
This proves part (ii).
Question 5. In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = $\frac{1}{2}$ ar (PQRS)

Answer:
Given:
PQRS is a parallelogram.
ABRS is a parallelogram.
X is any point on side BR.
To Prove:
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = $\frac{1}{2}$ ar (PQRS)
Proof:
(i) To prove ar (PQRS) = ar (ABRS)
Parallelogram PQRS and parallelogram ABRS share a common base RS.
In parallelogram PQRS, PS $\parallel$ QR and PQ $\parallel$ RS.
In parallelogram ABRS, AS $\parallel$ BR and AB $\parallel$ RS.
Since PQRS and ABRS are both parallelograms sharing the base RS, the side PQ of PQRS lies on the line PB and the side AB of ABRS lies on the same line PB.
Since PQ $\parallel$ RS and AB $\parallel$ RS, the line containing P, Q, A, B must be parallel to RS.
Thus, parallelogram PQRS and parallelogram ABRS lie on the same base RS and between the same parallels RS and PB.
We know that two parallelograms on the same base and between the same parallels are equal in area.
Therefore,
ar (PQRS) = ar (ABRS)
... (1)
This proves part (i).
(ii) To prove ar (AXS) = $\frac{1}{2}$ ar (PQRS)
Consider $\triangle$AXS and parallelogram ABRS.
They share a common base AS.
In parallelogram ABRS, AS $\parallel$ BR.
The vertex X of $\triangle$AXS lies on the line segment BR, which is parallel to AS.
Thus, $\triangle$AXS and parallelogram ABRS lie on the same base AS and between the same parallels AS and BR.
By the theorem, the area of a triangle is half the area of a parallelogram if they are on the same base and between the same parallels.
Therefore,
ar ($\triangle$AXS) = $\frac{1}{2}$ ar (ABRS)
... (2)
From equation (1), we know that ar (ABRS) = ar (PQRS).
Substitute this into equation (2):
ar (AXS) = $\frac{1}{2}$ ar (PQRS)
This proves part (ii).
Hence Proved.
Question 6. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Answer:
Analysis of the problem:
The farmer has a parallelogram-shaped field PQRS. She chooses a point A on the side RS and joins it to the vertices P and Q.
1. In how many parts is the field divided? What are their shapes?
As shown in the figure, the field is divided into three parts.
The shapes of all three parts are triangles. The three triangular parts are:
- $\triangle$PSA
- $\triangle$PAQ
- $\triangle$QRA
2. How should the farmer sow wheat and pulses in equal portions?
To solve this, we need to find the relationship between the areas of these three triangles.
Consider the middle triangle, $\triangle$PAQ, and the original parallelogram, PQRS.
- Both the triangle and the parallelogram lie on the same base, which is PQ.
- They also lie between the same parallel lines, PQ and RS (since PQRS is a parallelogram, PQ $||$ RS, and the vertex A of the triangle lies on the line RS).
There is a theorem which states that if a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.
Applying this theorem, we get:
ar($\triangle$PAQ) = $\frac{1}{2}$ ar(PQRS)
... (i)
The total area of the field is the sum of the areas of the three triangles:
ar(PQRS) = ar($\triangle$PSA) + ar($\triangle$PAQ) + ar($\triangle$QRA)
The area of the other two triangles combined is:
ar($\triangle$PSA) + ar($\triangle$QRA) = ar(PQRS) - ar($\triangle$PAQ)
Substituting the result from equation (i):
ar($\triangle$PSA) + ar($\triangle$QRA) = ar(PQRS) - $\frac{1}{2}$ ar(PQRS)
ar($\triangle$PSA) + ar($\triangle$QRA) = $\frac{1}{2}$ ar(PQRS)
... (ii)
From equations (i) and (ii), we can see that the area of the central triangle ($\triangle$PAQ) is exactly half the area of the field, and the sum of the areas of the two side triangles ($\triangle$PSA and $\triangle$QRA) is also exactly half the area of the field.
To sow wheat and pulses in equal portions, the farmer has two choices:
- Option 1: Sow wheat in the central triangular part $\triangle$PAQ and sow pulses in the other two triangular parts, $\triangle$PSA and $\triangle$QRA.
- Option 2: Sow pulses in the central triangular part $\triangle$PAQ and sow wheat in the other two triangular parts, $\triangle$PSA and $\triangle$QRA.
In either case, both crops will be sown in equal portions of the field.
Example 3 & 4 (Before Exercise 9.3)
Example 3. Show that a median of a triangle divides it into two triangles of equal areas.
Answer:
Given:
A $\triangle$ABC and a median AD, where D is the mid-point of BC.
To Prove:
ar ($\triangle$ABD) = ar ($\triangle$ACD).
Construction:
Draw an altitude AM from vertex A to the side BC.
AM $\perp$ BC
Proof:
In $\triangle$ABC, AD is the median to the side BC.
This means that D is the mid-point of BC.
BD = CD
(Definition of median)
The area of a triangle is given by the formula:
Area of triangle = $\frac{1}{2} \times$ base $\times$ height
Consider $\triangle$ABD. The base is BD and the corresponding height (altitude from A to the line containing BD) is AM.
ar ($\triangle$ABD) = $\frac{1}{2} \times$ BD $\times$ AM
... (i)
Consider $\triangle$ACD. The base is CD and the corresponding height (altitude from A to the line containing CD) is AM.
ar ($\triangle$ACD) = $\frac{1}{2} \times$ CD $\times$ AM
... (ii)
Since BD = CD, we can substitute BD for CD in equation (ii):
ar ($\triangle$ACD) = $\frac{1}{2} \times$ BD $\times$ AM
... (iii)
Comparing equations (i) and (iii), we see that:
ar ($\triangle$ABD) = ar ($\triangle$ACD)
Thus, the median AD divides the $\triangle$ABC into two triangles ($\triangle$ABD and $\triangle$ACD) of equal areas.
Hence Proved.
Example 4. In Fig. 9.22, ABCD is a quadrilateral and BE || AC and also BE meets DC produced at E. Show that area of ∆ ADE is equal to the area of thequadrilateral ABCD.

Answer:
Given:
ABCD is a quadrilateral.
BE $\parallel$ AC, and BE meets DC produced at E.
To Prove:
ar ($\triangle$ ADE) = ar (quadrilateral ABCD).
Proof:
Consider $\triangle$ABC and $\triangle$AEC.
Both triangles are on the same base AC.
BE $\parallel$ AC
(Given)
Since BE is parallel to AC, and the vertices B and E lie on the line BE, $\triangle$ABC and $\triangle$AEC are between the same parallels AC and BE.
We know that triangles on the same base and between the same parallels have equal areas.
ar ($\triangle$ABC) = ar ($\triangle$AEC)
... (1)
Now, consider the area of the quadrilateral ABCD.
The quadrilateral ABCD can be divided into two triangles, $\triangle$ABC and $\triangle$ADC.
ar (quadrilateral ABCD) = ar ($\triangle$ABC) + ar ($\triangle$ADC)
... (2)
Next, consider the area of $\triangle$ADE.
The triangle $\triangle$ADE can be expressed as the sum of the areas of $\triangle$ADC and $\triangle$AEC.
ar ($\triangle$ADE) = ar ($\triangle$ADC) + ar ($\triangle$AEC)
... (3)
Substitute the result from equation (1) into equation (3):
ar ($\triangle$ADE) = ar ($\triangle$ADC) + ar ($\triangle$ABC)
... (4)
Comparing equation (2) and equation (4), we can see that the expressions on the right-hand side are the same.
Therefore,
ar ($\triangle$ ADE) = ar (quadrilateral ABCD)
Hence Proved.
Exercise 9.3
Question 1. In Fig.9.23, E is any point on median AD of a ∆ ABC. Show that ar (ABE) = ar (ACE).
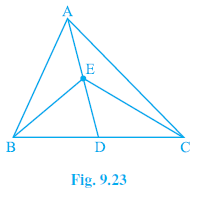
Answer:
Given:
$\triangle$ ABC, where AD is a median.
E is any point on the median AD.
To Prove:
ar (ABE) = ar (ACE).
Proof:
In $\triangle$ ABC, AD is the median.
A median divides a triangle into two triangles of equal areas.
ar ($\triangle$ ABD) = ar ($\triangle$ ACD)
... (1)
Now, consider $\triangle$ EBC.
Since AD is the median of $\triangle$ ABC, D is the mid-point of BC.
Since E is a point on AD, ED is the median of $\triangle$ EBC.
Applying the same property of the median to $\triangle$ EBC:
ar ($\triangle$ EBD) = ar ($\triangle$ ECD)
... (2)
Now, consider the area of $\triangle$ ABE.
ar ($\triangle$ ABE) = ar ($\triangle$ ABD) - ar ($\triangle$ EBD)
And consider the area of $\triangle$ ACE.
ar ($\triangle$ ACE) = ar ($\triangle$ ACD) - ar ($\triangle$ ECD)
Subtracting equation (2) from equation (1):
ar ($\triangle$ ABD) - ar ($\triangle$ EBD) = ar ($\triangle$ ACD) - ar ($\triangle$ ECD)
Substituting the expressions for ar ($\triangle$ ABE) and ar ($\triangle$ ACE):
ar (ABE) = ar (ACE)
Hence Proved.
Question 2. In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = $\frac{1}{4}$ ar(ABC).
Answer:
Given:
$\triangle$ ABC, where AD is the median.
E is the mid-point of median AD.
To Prove:
ar (BED) = $\frac{1}{4}$ ar(ABC).
Proof:
In $\triangle$ ABC, AD is the median to the side BC.
A median divides a triangle into two triangles of equal areas.
ar ($\triangle$ ABD) = ar ($\triangle$ ACD)
... (1)
Also, the sum of the areas of these two triangles is the area of the original triangle.
ar ($\triangle$ ABD) + ar ($\triangle$ ACD) = ar ($\triangle$ ABC)
Using equation (1), we can write:
ar ($\triangle$ ABD) + ar ($\triangle$ ABD) = ar ($\triangle$ ABC)
2 $\times$ ar ($\triangle$ ABD) = ar ($\triangle$ ABC)
ar ($\triangle$ ABD) = $\frac{1}{2}$ ar ($\triangle$ ABC)
... (2)
Now, consider $\triangle$ ABD.
E is the mid-point of AD (Given).
Therefore, BE is a median in $\triangle$ ABD.
Applying the same property of the median to $\triangle$ ABD and median BE:
ar ($\triangle$ BED) = ar ($\triangle$ ABE)
... (3)
Also, the sum of the areas of these two triangles is the area of $\triangle$ ABD.
ar ($\triangle$ BED) + ar ($\triangle$ ABE) = ar ($\triangle$ ABD)
Using equation (3), we can write:
ar ($\triangle$ BED) + ar ($\triangle$ BED) = ar ($\triangle$ ABD)
2 $\times$ ar ($\triangle$ BED) = ar ($\triangle$ ABD)
ar ($\triangle$ BED) = $\frac{1}{2}$ ar ($\triangle$ ABD)
... (4)
Now, substitute the result from equation (2) into equation (4):
ar ($\triangle$ BED) = $\frac{1}{2} \times \left( \frac{1}{2} \text{ ar} (\triangle \text{ ABC}) \right)$
ar (BED) = $\frac{1}{4}$ ar(ABC)
Hence Proved.
Question 3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer:
Given:
A parallelogram ABCD.
Diagonals AC and BD intersect at point O.
To Prove:
ar ($\triangle$ AOB) = ar ($\triangle$ BOC) = ar ($\triangle$ COD) = ar ($\triangle$ DOA).
Proof:
We know that the diagonals of a parallelogram bisect each other.
Therefore, O is the mid-point of the diagonal AC, and also O is the mid-point of the diagonal BD.
Consider $\triangle$ ABC.
Since O is the mid-point of AC, BO is the median of $\triangle$ ABC.
A median of a triangle divides it into two triangles of equal area.
ar ($\triangle$ AOB) = ar ($\triangle$ BOC)
... (1)
Consider $\triangle$ ADC.
Since O is the mid-point of AC, DO is the median of $\triangle$ ADC.
Applying the same property of the median:
ar ($\triangle$ AOD) = ar ($\triangle$ COD)
... (2)
Consider $\triangle$ ABD.
Since O is the mid-point of BD, AO is the median of $\triangle$ ABD.
Applying the same property of the median:
ar ($\triangle$ AOB) = ar ($\triangle$ AOD)
... (3)
Consider $\triangle$ BCD.
Since O is the mid-point of BD, CO is the median of $\triangle$ BCD.
Applying the same property of the median:
ar ($\triangle$ BOC) = ar ($\triangle$ COD)
... (4)
From equations (1), (2), (3), and (4), we can combine the equalities:
From (1) and (3): ar ($\triangle$ AOB) = ar ($\triangle$ BOC) and ar ($\triangle$ AOB) = ar ($\triangle$ AOD).
This implies ar ($\triangle$ BOC) = ar ($\triangle$ AOD).
From (2) and (4): ar ($\triangle$ AOD) = ar ($\triangle$ COD) and ar ($\triangle$ BOC) = ar ($\triangle$ COD).
This implies ar ($\triangle$ AOD) = ar ($\triangle$ BOC).
Combining all these results, we get:
ar ($\triangle$ AOB) = ar ($\triangle$ BOC) = ar ($\triangle$ COD) = ar ($\triangle$ DOA)
Thus, the diagonals of a parallelogram divide it into four triangles of equal area.
Hence Proved.
Question 4. In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
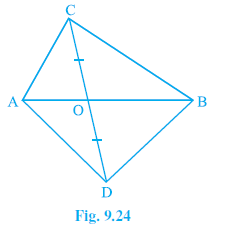
Answer:
Given:
$\triangle$ ABC and $\triangle$ ABD are two triangles on the same base AB.
Line segment CD is bisected by AB at O, which means O is the mid-point of CD.
To Prove:
ar (ABC) = ar (ABD).
Proof:
In $\triangle$ ACD, O is the mid-point of CD (Given).
Therefore, AO is the median of $\triangle$ ACD.
We know that a median of a triangle divides it into two triangles of equal area.
ar ($\triangle$ AOC) = ar ($\triangle$ AOD)
... (1)
In $\triangle$ BCD, O is the mid-point of CD (Given).
Therefore, BO is the median of $\triangle$ BCD.
Applying the same property of the median to $\triangle$ BCD:
ar ($\triangle$ BOC) = ar ($\triangle$ BOD)
... (2)
Now, consider the area of $\triangle$ ABC.
ar ($\triangle$ ABC) = ar ($\triangle$ AOC) + ar ($\triangle$ BOC)
Consider the area of $\triangle$ ABD.
ar ($\triangle$ ABD) = ar ($\triangle$ AOD) + ar ($\triangle$ BOD)
Substitute ar ($\triangle$ AOC) with ar ($\triangle$ AOD) from equation (1) and ar ($\triangle$ BOC) with ar ($\triangle$ BOD) from equation (2) into the expression for ar ($\triangle$ ABC):
ar ($\triangle$ ABC) = ar ($\triangle$ AOD) + ar ($\triangle$ BOD)
This is the same as the expression for ar ($\triangle$ ABD).
Therefore,
ar (ABC) = ar (ABD)
Hence Proved.
Question 5. D, E and F are respectively the mid-points of the sides BC, CA and AB of a ∆ ABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = $\frac{1}{4}$ ar (ABC)
(iii) ar (BDEF) = $\frac{1}{2}$ ar (ABC)
Answer:
Given:
$\triangle$ ABC.
D, E, and F are respectively the mid-points of the sides BC, CA, and AB.
To Prove:
(i) BDEF is a parallelogram.
(ii) ar (DEF) = $\frac{1}{4}$ ar (ABC).
(iii) ar (BDEF) = $\frac{1}{2}$ ar (ABC).
Proof:
(i) To prove BDEF is a parallelogram.
In $\triangle$ ABC, E and F are the mid-points of AC and AB respectively (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of the third side.
EF $\parallel$ BC
... (1)
EF = $\frac{1}{2}$ BC
... (2)
Since D is the mid-point of BC (Given), BD = $\frac{1}{2}$ BC.
BD = $\frac{1}{2}$ BC
... (3)
From (2) and (3), we get:
EF = BD
... (4)
From (1), EF $\parallel$ BC. Since D is a point on BC, EF is also parallel to BD.
EF $\parallel$ BD
... (5)
From (4) and (5), in quadrilateral BDEF, one pair of opposite sides (EF and BD) is equal and parallel. Therefore, BDEF is a parallelogram.
(ii) To prove ar (DEF) = $\frac{1}{4}$ ar (ABC).
Similarly, using the Mid-point Theorem for the other pairs of sides:
In $\triangle$ ABC, D and F are mid-points of BC and AB.
DF $\parallel$ AC and DF = $\frac{1}{2}$ AC
In $\triangle$ ABC, D and E are mid-points of BC and AC.
DE $\parallel$ AB and DE = $\frac{1}{2}$ AB
Consider the four triangles formed by joining the mid-points: $\triangle$ AFE, $\triangle$ BDF, $\triangle$ CDE, and $\triangle$ DEF.
Sides of $\triangle$ DEF are DE, EF, DF.
Sides of $\triangle$ AFE are AF, FE, AE.
Sides of $\triangle$ BDF are BD, DF, BF.
Sides of $\triangle$ CDE are CD, DE, CE.
Since F is the mid-point of AB, AF = BF = $\frac{1}{2}$ AB. By Mid-point Theorem, DE = $\frac{1}{2}$ AB. So, AF = BF = DE.
Since E is the mid-point of AC, AE = CE = $\frac{1}{2}$ AC. By Mid-point Theorem, DF = $\frac{1}{2}$ AC. So, AE = CE = DF.
Since D is the mid-point of BC, BD = CD = $\frac{1}{2}$ BC. By Mid-point Theorem, EF = $\frac{1}{2}$ BC. So, BD = CD = EF.
Comparing the side lengths of the four triangles:
$\triangle$ AFE has sides AF, AE, EF with lengths $\frac{1}{2}$ AB, $\frac{1}{2}$ AC, $\frac{1}{2}$ BC.
$\triangle$ BDF has sides BF, BD, DF with lengths $\frac{1}{2}$ AB, $\frac{1}{2}$ BC, $\frac{1}{2}$ AC.
$\triangle$ CDE has sides CD, CE, DE with lengths $\frac{1}{2}$ BC, $\frac{1}{2}$ AC, $\frac{1}{2}$ AB.
$\triangle$ DEF has sides DE, EF, DF with lengths $\frac{1}{2}$ AB, $\frac{1}{2}$ BC, $\frac{1}{2}$ AC.
By SSS congruence criterion, $\triangle$ AFE $\cong$ $\triangle$ BDF $\cong$ $\triangle$ CDE $\cong$ $\triangle$ DEF.
Congruent triangles have equal areas. Thus,
ar (AFE) = ar (BDF) = ar (CDE) = ar (DEF)
... (6)
The area of $\triangle$ ABC is the sum of the areas of these four triangles:
ar (ABC) = ar (AFE) + ar (BDF) + ar (CDE) + ar (DEF)
Using equation (6):
ar (ABC) = ar (DEF) + ar (DEF) + ar (DEF) + ar (DEF)
ar (ABC) = 4 $\times$ ar (DEF)
Rearranging, we get:
ar (DEF) = $\frac{1}{4}$ ar (ABC)
This proves part (ii).
(iii) To prove ar (BDEF) = $\frac{1}{2}$ ar (ABC).
From part (i), we know that BDEF is a parallelogram.
The area of parallelogram BDEF is the sum of the areas of the two triangles formed by its diagonal FD, which are $\triangle$ BDF and $\triangle$ DEF.
ar (BDEF) = ar (BDF) + ar (DEF)
From equation (6), we know that ar (BDF) = ar (DEF).
ar (BDEF) = ar (DEF) + ar (DEF)
ar (BDEF) = 2 $\times$ ar (DEF)
... (7)
From part (ii), we have ar (DEF) = $\frac{1}{4}$ ar (ABC).
Substitute this into equation (7):
ar (BDEF) = 2 $\times$ $\left( \frac{1}{4} \text{ ar} (\text{ABC}) \right)$
ar (BDEF) = $\frac{2}{4}$ ar (ABC)
ar (BDEF) = $\frac{1}{2}$ ar (ABC)
This proves part (iii).
Hence Proved.
Question 6. In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]
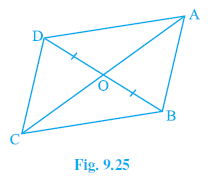
Answer:
Given:
ABCD is a quadrilateral.
Diagonals AC and BD intersect at O.
OB = OD.
AB = CD.
To Prove:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA $\parallel$ CB or ABCD is a parallelogram.
Construction:
Draw DN $\perp$ AC from D and BM $\perp$ AC from B.
Proof:
Consider right-angled $\triangle$ DON and $\triangle$ BOM.
$\angle$ DNO = $\angle$ BMO = $90^\circ$
(Construction)
$\angle$ DON = $\angle$ BOM
(Vertically opposite angles)
OD = OB
(Given)
By AAS congruence criterion:
$\triangle$ DON $\cong$ $\triangle$ BOM
From congruence, corresponding parts are equal:
DN = BM
(CPCT) ... (1)
ON = OM
(CPCT) ... (2)
Now consider right-angled $\triangle$ DNC and $\triangle$ BMA.
Hypotenuse DC = Hypotenuse AB
(Given)
Side DN = Side BM
(From (1))
By RHS congruence criterion:
$\triangle$ DNC $\cong$ $\triangle$ BMA
From congruence, corresponding parts are equal:
NC = MA
(CPCT) ... (3)
Consider the lengths along the line AC.
AO = AM + MO
OC = ON + NC
Substitute from (2) and (3):
OC = OM + MA
Thus,
AO = OC
... (4)
So, O is the mid-point of AC.
(i) To prove ar (DOC) = ar (AOB)
The area of $\triangle$ DOC = $\frac{1}{2} \times$ base OC $\times$ altitude DN.
ar ($\triangle$ DOC) = $\frac{1}{2} \times$ OC $\times$ DN
... (5)
The area of $\triangle$ AOB = $\frac{1}{2} \times$ base AO $\times$ altitude BM.
ar ($\triangle$ AOB) = $\frac{1}{2} \times$ AO $\times$ BM
... (6)
From (4), AO = OC, and from (1), DN = BM.
Substitute these into equation (5):
ar ($\triangle$ DOC) = $\frac{1}{2} \times$ AO $\times$ BM
... (7)
Comparing (6) and (7), we get:
ar (DOC) = ar (AOB)
This proves part (i).
(ii) To prove ar (DCB) = ar (ACB)
We know that O is the mid-point of AC (from (4)).
In $\triangle$ ABC, BO is the median to the side AC.
A median divides a triangle into two triangles of equal areas.
ar ($\triangle$ AOB) = ar ($\triangle$ BOC)
... (8)
In $\triangle$ ADC, DO is the median to the side AC.
ar ($\triangle$ AOD) = ar ($\triangle$ DOC)
... (9)
From part (i), ar ($\triangle$ AOB) = ar ($\triangle$ DOC).
Combining (8) and (9) with this result:
ar ($\triangle$ AOB) = ar ($\triangle$ BOC) = ar ($\triangle$ DOC) = ar ($\triangle$ AOD)
Now, consider the area of $\triangle$ DCB:
ar (DCB) = ar ($\triangle$ DOC) + ar ($\triangle$ BOC)
Consider the area of $\triangle$ ACB:
ar (ACB) = ar ($\triangle$ AOC) + ar ($\triangle$ AOB)
Since ar ($\triangle$ DOC) = ar ($\triangle$ AOB) and ar ($\triangle$ BOC) = ar ($\triangle$ AOC) (from the result that all four small triangles have equal area), we can write:
ar (DCB) = ar ($\triangle$ AOB) + ar ($\triangle$ AOC)
Comparing with the expression for ar (ACB):
ar (DCB) = ar (ACB)
This proves part (ii).
(iii) To prove DA $\parallel$ CB or ABCD is a parallelogram.
From part (ii), we have ar (DCB) = ar (ACB).
Consider $\triangle$ DCB and $\triangle$ ACB.
These two triangles share the same base BC.
They also have equal areas.
We know that if two triangles have the same base and equal areas, their vertices opposite to the common base must lie on a line parallel to the base.
The vertex opposite to base BC in $\triangle$ DCB is D.
The vertex opposite to base BC in $\triangle$ ACB is A.
Therefore, the line segment AD must be parallel to the base BC.
AD $\parallel$ BC
This shows that DA $\parallel$ CB.
Now we consider the quadrilateral ABCD. We have shown that its diagonals bisect each other (AO=OC and OB=OD).
A quadrilateral whose diagonals bisect each other is a parallelogram.
Therefore, ABCD is a parallelogram.
Since ABCD is a parallelogram, its opposite sides are parallel by definition.
Thus, AD $\parallel$ BC (or DA $\parallel$ CB) and AB $\parallel$ DC.
The condition DA $\parallel$ CB is proven. Proving that ABCD is a parallelogram is a stronger conclusion that implies DA $\parallel$ CB.
Hence Proved.
Question 7. D and E are points on sides AB and AC respectively of ∆ABC such that ar (DBC) = ar (EBC). Prove that DE || BC.
Answer:
Given:
$\triangle$ ABC.
D is a point on side AB.
E is a point on side AC.
ar (DBC) = ar (EBC).
To Prove:
DE $\parallel$ BC.
Proof:
We are given that ar ($\triangle$ DBC) = ar ($\triangle$ EBC).
Observe that $\triangle$ DBC and $\triangle$ EBC share the same base BC.
We know that if two triangles have the same base and equal areas, then their vertices opposite to the common base lie on a line parallel to the base.
In $\triangle$ DBC and $\triangle$ EBC, the common base is BC.
The vertex opposite to the base BC in $\triangle$ DBC is D.
The vertex opposite to the base BC in $\triangle$ EBC is E.
Since ar ($\triangle$ DBC) = ar ($\triangle$ EBC) and they are on the same base BC, the vertices D and E must lie on a line that is parallel to BC.
Therefore, the line segment joining D and E must be parallel to BC.
DE $\parallel$ BC
Hence Proved.
Question 8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF).
Answer:
Given:
$\triangle$ ABC.
XY is a line parallel to side BC.
BE $\parallel$ AC, where E is on XY.
CF $\parallel$ AB, where F is on XY.
To Prove:
ar (ABE) = ar (ACF).
Proof:
We are given that XY is a line parallel to BC.
Consider $\triangle$ BCE and $\triangle$ BCF.
Both triangles share the same base BC.
They are also between the same parallel lines BC and XY (since E and F are on XY).
We know that triangles on the same base and between the same parallels have equal areas.
ar ($\triangle$ BCE) = ar ($\triangle$ BCF)
... (1)
Now, let h be the perpendicular distance between the parallel lines BC and XY. This height is constant for any point on XY with respect to the line BC.
Area of $\triangle$ BCE can also be considered with base CE which lies on the line XY. The corresponding height is the perpendicular distance from B to the line XY. Let this height be $h_B$.
ar ($\triangle$ BCE) = $\frac{1}{2} \times$ CE $\times$ $h_B$
... (2)
Similarly, area of $\triangle$ BCF can be considered with base BF which lies on the line XY. The corresponding height is the perpendicular distance from C to the line XY. Let this height be $h_C$.
ar ($\triangle$ BCF) = $\frac{1}{2} \times$ BF $\times$ $h_C$
... (3)
Since BC $\parallel$ XY, the perpendicular distance from any point on BC to the line XY is the same. Therefore, the height from B to XY is equal to the height from C to XY.
$h_B$ = $h_C$
(Distance between parallel lines BC and XY)
From (1), ar ($\triangle$ BCE) = ar ($\triangle$ BCF). Substituting from (2) and (3):
$\frac{1}{2} \times$ CE $\times$ $h_B$ = $\frac{1}{2} \times$ BF $\times$ $h_C$
Since $h_B = h_C$ (and $h_B \neq 0$ as XY is distinct from BC), we can cancel $\frac{1}{2}$ and $h_B$ (or $h_C$) from both sides:
CE = BF
... (4)
Now, consider $\triangle$ ACE and $\triangle$ ABF.
Their bases CE and BF lie on the same line XY. From (4), we know that these bases are equal in length.
The vertex opposite to the base CE in $\triangle$ ACE is A.
The vertex opposite to the base BF in $\triangle$ ABF is A.
The perpendicular distance from A to the line XY is the height for both triangles when taking bases on XY. Let this height be $h_A$.
ar ($\triangle$ ACE) = $\frac{1}{2} \times$ CE $\times$ $h_A$
ar ($\triangle$ ABF) = $\frac{1}{2} \times$ BF $\times$ $h_A$
Since CE = BF and $h_A$ is common, we have:
ar ($\triangle$ ACE) = ar ($\triangle$ ABF)
... (5)
Consider the area of the quadrilateral ABCE. It can be seen as the sum of ar ($\triangle$ ABC) and ar ($\triangle$ ACE), or as the sum of ar ($\triangle$ ABE) and ar ($\triangle$ BCE).
ar (quad ABCE) = ar ($\triangle$ ABC) + ar ($\triangle$ ACE)
ar (quad ABCE) = ar ($\triangle$ ABE) + ar ($\triangle$ BCE)
Equating the two expressions for ar (quad ABCE):
ar ($\triangle$ ABC) + ar ($\triangle$ ACE) = ar ($\triangle$ ABE) + ar ($\triangle$ BCE)
... (6)
Consider the area of the quadrilateral ABCF. It can be seen as the sum of ar ($\triangle$ ABC) and ar ($\triangle$ ABF), or as the sum of ar ($\triangle$ ACF) and ar ($\triangle$ BCF).
ar (quad ABCF) = ar ($\triangle$ ABC) + ar ($\triangle$ ABF)
ar (quad ABCF) = ar ($\triangle$ ACF) + ar ($\triangle$ BCF)
Equating the two expressions for ar (quad ABCF):
ar ($\triangle$ ABC) + ar ($\triangle$ ABF) = ar ($\triangle$ ACF) + ar ($\triangle$ BCF)
... (7)
From (1), ar ($\triangle$ BCE) = ar ($\triangle$ BCF). Let's substitute ar ($\triangle$ BCF) with ar ($\triangle$ BCE) in equation (7):
ar ($\triangle$ ABC) + ar ($\triangle$ ABF) = ar ($\triangle$ ACF) + ar ($\triangle$ BCE)
... (8)
Now we have two equations (6) and (8) involving ar ($\triangle$ ABC), ar ($\triangle$ BCE), ar ($\triangle$ ACE), ar ($\triangle$ ABF), ar ($\triangle$ ABE), and ar ($\triangle$ ACF).
Equation (6): ar ($\triangle$ ABC) + ar ($\triangle$ ACE) = ar ($\triangle$ ABE) + ar ($\triangle$ BCE)
Equation (8): ar ($\triangle$ ABC) + ar ($\triangle$ ABF) = ar ($\triangle$ ACF) + ar ($\triangle$ BCE)
Subtract equation (8) from equation (6):
[ar (ABC) + ar (ACE)] - [ar (ABC) + ar (ABF)] = [ar (ABE) + ar (BCE)] - [ar (ACF) + ar (BCE)]
ar (ABC) + ar (ACE) - ar (ABC) - ar (ABF) = ar (ABE) + ar (BCE) - ar (ACF) - ar (BCE)
ar (ACE) - ar (ABF) = ar (ABE) - ar (ACF)
From (5), we know that ar ($\triangle$ ACE) = ar ($\triangle$ ABF). So, ar (ACE) - ar (ABF) = 0.
0 = ar (ABE) - ar (ACF)
ar (ABE) = ar (ACF)
Hence Proved.
Question 9. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see Fig. 9.26). Show that ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare ar (ACQ) and ar (APQ).]
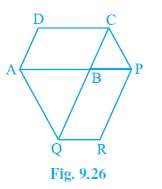
Answer:
Given:
ABCD is a parallelogram.
The side AB is produced to any point P.
A line through A parallel to CP meets CB produced at Q.
PBQR is a parallelogram.
To Prove:
ar (ABCD) = ar (PBQR).
Construction:
Join AC and PQ.
Proof:
We are given that a line through A is parallel to CP and meets CB produced at Q. This means the line segment AQ is parallel to the line segment CP.
AQ $\parallel$ CP
(Given construction)
Consider $\triangle$ ACQ and $\triangle$ APQ.
These two triangles are on the same base AQ.
Since AQ $\parallel$ CP, the vertices C and P lie on the line CP which is parallel to AQ.
Therefore, $\triangle$ ACQ and $\triangle$ APQ lie on the same base AQ and between the same parallels AQ and CP.
By the theorem that triangles on the same base and between the same parallels are equal in area:
ar ($\triangle$ ACQ) = ar ($\triangle$ APQ)
... (1)
From the figure, since Q is on CB produced, B lies on the line segment CQ.
Also, since A, B, P are collinear and P is on AB produced, B lies on the line segment AP.
Consider $\triangle$ ACQ. Since B lies on CQ, the area of $\triangle$ ACQ can be written as the sum of the areas of $\triangle$ ABQ and $\triangle$ ABC.
ar ($\triangle$ ACQ) = ar ($\triangle$ ABQ) + ar ($\triangle$ ABC)
... (2)
Consider $\triangle$ APQ. Since B lies on AP, the area of $\triangle$ APQ can be written as the sum of the areas of $\triangle$ ABQ and $\triangle$ BPQ.
ar ($\triangle$ APQ) = ar ($\triangle$ ABQ) + ar ($\triangle$ BPQ)
... (3)
Substitute the expressions from equations (2) and (3) into equation (1):
ar ($\triangle$ ABQ) + ar ($\triangle$ ABC) = ar ($\triangle$ ABQ) + ar ($\triangle$ BPQ)
Subtract ar ($\triangle$ ABQ) from both sides of the equation:
ar ($\triangle$ ABC) = ar ($\triangle$ BPQ)
... (4)
Now, consider parallelogram ABCD.
The diagonal AC divides the parallelogram into two triangles of equal area.
ar ($\triangle$ ABC) = $\frac{1}{2}$ ar (ABCD)
... (5)
Consider parallelogram PBQR.
The diagonal PQ divides the parallelogram into two triangles of equal area.
ar ($\triangle$ PBQ) = $\frac{1}{2}$ ar (PBQR)
... (6)
From equation (4), we have ar ($\triangle$ ABC) = ar ($\triangle$ BPQ).
Substitute the expressions for ar ($\triangle$ ABC) and ar ($\triangle$ BPQ) from equations (5) and (6) into equation (4):
$\frac{1}{2}$ ar (ABCD) = $\frac{1}{2}$ ar (PBQR)
Multiply both sides by 2:
ar (ABCD) = ar (PBQR)
Hence Proved.
Question 10. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
Answer:
Given:
A trapezium ABCD in which AB || DC.
The diagonals AC and BD intersect each other at point O.
To Prove:
ar (AOD) = ar (BOC)
Proof:
Consider triangles $\triangle$ADC and $\triangle$BDC.
These triangles lie on the same base DC.
They are between the same parallel lines AB and DC.
(Given AB || DC)
We know that triangles on the same base and between the same parallels are equal in area.
$\therefore$ ar ($\triangle$ADC) = ar ($\triangle$BDC)
...(i)
From the figure, we can see:
ar ($\triangle$ADC) = ar ($\triangle$AOD) + ar ($\triangle$DOC)
ar ($\triangle$BDC) = ar ($\triangle$BOC) + ar ($\triangle$DOC)
Substituting these into equation (i):
ar ($\triangle$AOD) + ar ($\triangle$DOC) = ar ($\triangle$BOC) + ar ($\triangle$DOC)
Subtracting ar ($\triangle$DOC) from both sides:
ar ($\triangle$AOD) = ar ($\triangle$BOC)
Hence, proved.
Question 11. In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
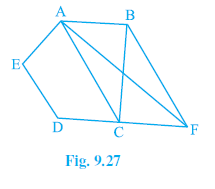
Answer:
Given:
ABCDE is a pentagon.
A line through B parallel to AC (BF || AC) meets DC produced at F.
To Prove:
(i) $ar (\triangle ACB) = ar (\triangle ACF)$
(ii) $ar (AEDF) = ar (ABCDE)$
Proof:
(i)
Consider $\triangle$ACB and $\triangle$ACF.
These two triangles lie on the same base AC.
They also lie between the same parallel lines AC and BF. (Given BF || AC)
We know that triangles on the same base and between the same parallel lines are equal in area.
$\therefore ar (\triangle ACB) = ar (\triangle ACF)$
...(i)
(ii)
From part (i), we have proved that:
$ar (\triangle ACB) = ar (\triangle ACF)$
Adding $ar (ACDE)$ to both sides of the equation:
$ar (\triangle ACB) + ar (ACDE) = ar (\triangle ACF) + ar (ACDE)$
From the figure, we can see that:
$ar (\triangle ACB) + ar (ACDE) = ar (ABCDE)$
(Area of pentagon ABCDE)
$ar (\triangle ACF) + ar (ACDE) = ar (AEDF)$
(Area of quadrilateral AEDF)
Therefore, substituting these into the equation above:
$ar (ABCDE) = ar (AEDF)$
Or,
$ar (AEDF) = ar (ABCDE)$
Hence, proved.
Question 12. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Answer:
The problem is to replace a quadrilateral plot with a triangular plot of the same area, while exchanging a piece of land from a corner for an adjacent piece of equal size. This can be implemented using the geometric principle that triangles on the same base and between the same parallels are equal in area.
Here is a step-by-step explanation of how the proposal can be implemented.
Steps of Implementation:
Let the original quadrilateral plot of land be represented by ABCD. Suppose the Gram Panchayat wants to take a portion of land from the corner at vertex C.
1. Join the Diagonal: First, join the diagonal BD.
2. Draw a Parallel Line: From the vertex C, draw a line parallel to the diagonal BD (CE $||$ BD).
3. Extend the Side: Extend the side AD of the plot until it intersects the parallel line drawn in the previous step. Let the point of intersection be E.
4. Form the New Plot: Join the point B to the new point E. The new triangular plot for Itwaari will be the triangle $\triangle$ABE.
5. The Exchange: Let the line segment CD intersect the new boundary BE at point O. The portion of land Itwaari gives to the Panchayat is $\triangle$OCB. In return, he receives the adjacent land portion $\triangle$ODE.
Justification and Explanation:
We need to show that this implementation satisfies Itwaari's conditions: (a) the new plot is triangular, (b) the total area of his land remains the same, and (c) the land he gives is equal in area to the land he receives.
(a) The New Plot is a Triangle:
By construction, the new plot ABE is clearly a triangle.
(b) and (c) The Areas are Equal:
Consider the triangles $\triangle$BCD and $\triangle$BED.
- They lie on the same base BD.
- They lie between the same parallel lines BD and CE (by construction).
Therefore, according to the theorem, their areas are equal.
ar($\triangle$BCD) = ar($\triangle$BED)
... (i)
Now, to show that the exchanged portions are equal, we can subtract the common area of $\triangle$OBD from both sides of equation (i).
ar($\triangle$BCD) - ar($\triangle$OBD) = ar($\triangle$BED) - ar($\triangle$OBD)
From the figure, this simplifies to:
ar($\triangle$OCB) = ar($\triangle$ODE)
This proves that the area of the land Itwaari gives to the Panchayat ($\triangle$OCB) is exactly equal to the area of the new land he receives ($\triangle$ODE).
To prove that the total area of his plot remains unchanged, we can add the area of quadrilateral ABOD to both sides of the above equation:
ar($\triangle$OCB) + ar(ABOD) = ar($\triangle$ODE) + ar(ABOD)
From the figure, this simplifies to:
ar(ABCD) = ar($\triangle$ABE)
This proves that the area of the original quadrilateral plot is equal to the area of the new triangular plot.
Conclusion:
By following these steps, the Panchayat can take the land area of $\triangle$OCB from the corner of Itwaari's plot. In return, Itwaari receives an adjacent plot of land, $\triangle$ODE, which is of the exact same area. His new plot, the triangle ABE, is now a single triangular piece of land with a total area equal to his original plot. Thus, the proposal is implemented successfully.
Question 13. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
[Hint: Join CX.]
Answer:
Given:
ABCD is a trapezium with AB || DC.
A line segment XY is parallel to the diagonal AC (XY || AC).
This line intersects AB at X and BC at Y.
To Prove:
$ar (\triangle ADX) = ar (\triangle ACY)$
Construction:
Join CX.
Proof:
Consider $\triangle$ADX and $\triangle$ACX.
These two triangles lie on the same base AX.
They are also between the same parallel lines AB and DC.
(Since X lies on AB, AX is part of AB, and AB || DC is given)
We know that triangles on the same base and between the same parallel lines are equal in area.
$\therefore ar (\triangle ADX) = ar (\triangle ACX)$
...(i)
Now, consider $\triangle$ACY and $\triangle$ACX.
These two triangles lie on the same base AC.
They are also between the same parallel lines AC and XY.
(Given XY || AC)
Again, using the property that triangles on the same base and between the same parallel lines are equal in area:
$\therefore ar (\triangle ACY) = ar (\triangle ACX)$
...(ii)
From equations (i) and (ii), we can equate the areas:
$ar (\triangle ADX) = ar (\triangle ACY)$
Hence, proved.
Question 14. In Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Answer:
Given:
Three lines AP, BQ, and CR are parallel to each other.
AP || BQ || CR
To Prove:
$ar (\triangle AQC) = ar (\triangle PBR)$
Proof:
Consider the triangles $\triangle ABQ$ and $\triangle PBQ$.
These triangles lie on the same base BQ.
They are between the same parallel lines AP and BQ. (Given AP || BQ)
We know that triangles on the same base and between the same parallel lines are equal in area.
$\therefore ar (\triangle ABQ) = ar (\triangle PBQ)$
...(i)
Now, consider the triangles $\triangle CBQ$ and $\triangle RBQ$.
These triangles lie on the same base BQ.
They are between the same parallel lines BQ and CR. (Given BQ || CR)
Using the same theorem:
$\therefore ar (\triangle CBQ) = ar (\triangle RBQ)$
...(ii)
Adding equation (i) and equation (ii):
$ar (\triangle ABQ) + ar (\triangle CBQ) = ar (\triangle PBQ) + ar (\triangle RBQ)$
From the figure, we can see that:
$ar (\triangle ABQ) + ar (\triangle CBQ) = ar (\triangle AQC)$
$ar (\triangle PBQ) + ar (\triangle RBQ) = ar (\triangle PBR)$
Substituting these into the combined equation:
$ar (\triangle AQC) = ar (\triangle PBR)$
Hence, proved.
Question 15. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
Answer:
Given:
A quadrilateral ABCD where diagonals AC and BD intersect at point O.
$ar (\triangle AOD) = ar (\triangle BOC)$
...(i)
To Prove:
ABCD is a trapezium.
(A quadrilateral is a trapezium if one pair of opposite sides is parallel. We need to prove either AB || DC or AD || BC).
Proof:
We are given that:
$ar (\triangle AOD) = ar (\triangle BOC)$
[From (i)]
Add the area of $\triangle DOC$ to both sides of this equation:
$ar (\triangle AOD) + ar (\triangle DOC) = ar (\triangle BOC) + ar (\triangle DOC)$
By observing the figure formed by the quadrilateral and its diagonals, we can combine the areas:
$ar (\triangle AOD) + ar (\triangle DOC) = ar (\triangle ADC)$
$ar (\triangle BOC) + ar (\triangle DOC) = ar (\triangle BDC)$
Therefore, the equation becomes:
$ar (\triangle ADC) = ar (\triangle BDC)$
...(ii)
Now, consider the triangles $\triangle ADC$ and $\triangle BDC$.
These two triangles lie on the same base DC.
Their areas are equal, as established in equation (ii).
A key theorem states that triangles on the same base (or equal bases) and having equal areas lie between the same parallel lines.
Applying this theorem to $\triangle ADC$ and $\triangle BDC$, which share the base DC and have equal areas, we can conclude that they must lie between the same parallel lines.
The line connecting the vertices opposite the common base DC is AB.
Therefore, the line AB must be parallel to the line DC.
$\therefore AB || DC$
Since one pair of opposite sides (AB and DC) of the quadrilateral ABCD is parallel, by definition, ABCD is a trapezium.
Hence, proved.
Question 16. In Fig.9.29, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

Answer:
Given:
In Fig. 9.29, we are given two area equalities:
$ar (\triangle DRC) = ar (\triangle DPC)$
...(i)
$ar (\triangle BDP) = ar (\triangle ARC)$
...(ii)
To Prove:
1. Quadrilateral DCPR is a trapezium.
2. Quadrilateral ABCD is a trapezium.
Proof:
Part 1: Proving DCPR is a trapezium
We are given from (i):
$ar (\triangle DRC) = ar (\triangle DPC)$
[Given] ... (i)
Consider the triangles $\triangle DRC$ and $\triangle DPC$.
These two triangles lie on the same base DC.
Their areas are equal, as given in equation (i).
We know that triangles on the same base and having equal areas lie between the same parallel lines.
Applying this theorem to $\triangle DRC$ and $\triangle DPC$, since they are on the same base DC and have equal areas, they must lie between the same parallel lines.
Therefore, the line segment RP must be parallel to the line segment DC.
$\therefore DC || RP$
Since one pair of opposite sides (DC and RP) of the quadrilateral DCPR are parallel, DCPR is a trapezium.
Part 2: Proving ABCD is a trapezium
We are given from (ii):
$ar (\triangle BDP) = ar (\triangle ARC)$
[Given] ... (ii)
From equation (i), we know $ar (\triangle DRC) = ar (\triangle DPC)$.
Subtracting $ar (\triangle DPC)$ from the left side of equation (ii) and $ar (\triangle DRC)$ from the right side of equation (ii). Since these subtracted areas are equal, the equality holds:
$ar (\triangle BDP) - ar (\triangle DPC) = ar (\triangle ARC) - ar (\triangle DRC)$
Observing the figure:
$ar (\triangle BDP) - ar (\triangle DPC) = ar (\triangle BDC)$
$ar (\triangle ARC) - ar (\triangle DRC) = ar (\triangle ADC)$
Substituting these into the previous equation, we get:
$ar (\triangle BDC) = ar (\triangle ADC)$
...(iii)
Now consider the triangles $\triangle BDC$ and $\triangle ADC$.
These two triangles lie on the same base DC.
Their areas are equal, as shown in equation (iii).
Again, using the theorem that triangles on the same base and having equal areas lie between the same parallel lines.
Applying this theorem to $\triangle BDC$ and $\triangle ADC$, since they are on the same base DC and have equal areas, they must lie between the same parallel lines.
Therefore, the line segment AB must be parallel to the line segment DC.
$\therefore AB || DC$
Since one pair of opposite sides (AB and DC) of the quadrilateral ABCD are parallel, ABCD is a trapezium.
Thus, we have proved that both quadrilaterals ABCD and DCPR are trapeziums.
Hence, proved.
Exercise 9.4 (Optional)
Question 1. Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Answer:
Given:
A parallelogram ABCD and a rectangle ABEF are on the same base AB.
$ar (ABCD) = ar (ABEF)$
To Prove:
Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF.
Proof:
Since the parallelogram ABCD and the rectangle ABEF are on the same base AB and have equal areas, they must lie between the same parallel lines.
Therefore, the line FC containing the vertices F, E, D, and C must be parallel to the base AB.
Now, let's compare the sides of the two figures.
In parallelogram ABCD, the opposite sides are equal:
AB = CD
AD = BC
In rectangle ABEF, the opposite sides are equal:
AB = EF
AE = BF
So, we have AB = CD = EF.
Now, consider the side AD of the parallelogram and the side AE of the rectangle.
Consider the right-angled triangle $\triangle AEF$. Wait, this is not a triangle. Let's consider the right-angled triangle formed by the perpendicular from A to the line FC. Since ABEF is a rectangle, AE is perpendicular to EF. So, $\triangle AEF$ is not helpful.
Let's consider the right-angled triangle $\triangle ADE$. This is not necessarily right-angled.
Let's focus on the side AD and the perpendicular distance between the parallel lines AB and FC. The side AE of the rectangle is the perpendicular distance between these parallel lines, since $\angle AEF = 90^\circ$ is incorrect, but $\angle EAB=90^\circ$. Let's assume the rectangle is ABEF where AB is the base, so AE and BF are perpendicular to AB.
In the right-angled triangle $\triangle ADE$ (if E lies between F and D), the hypotenuse AD is the longest side. This is not guaranteed.
The simplest argument is: Of all line segments that can be drawn from a point to a line, the perpendicular line segment is the shortest.
Here, the parallel lines are AB and FC. The line segment AD connects the point A on line AB to the point D on line FC. The line segment AE connects the same point A on line AB to the point E on line FC.
Since ABEF is a rectangle, AE is perpendicular to the base AB and thus perpendicular to the parallel line FC.
Therefore, AE is the perpendicular distance between the parallel lines AB and FC.
AD is a slant line segment connecting the same parallel lines from point A.
Thus, the slant segment AD must be longer than the perpendicular segment AE.
AD > AE
(The hypotenuse is longer than the perpendicular side in a right triangle formed by dropping a perpendicular from A to line FC, which is AE itself.)
Now, let's compare the perimeters:
Perimeter of parallelogram ABCD = $AB + BC + CD + DA \ $$ = AB + AD + \ $$ AB + AD = 2(AB + AD)$.
Perimeter of rectangle ABEF = $AB + BE + EF + FA \ $$ = AB + AE + AB + AE = 2(AB + AE)$.
We need to compare $2(AB + AD)$ and $2(AB + AE)$.
Since we have established that $AD > AE$, we can add the common length AB to both sides of the inequality:
$AB + AD > AB + AE$
Multiplying both sides by 2:
$2(AB + AD) > 2(AB + AE)$
Substituting the expressions for the perimeters:
Perimeter(ABCD) > Perimeter(ABEF)
Hence, the perimeter of the parallelogram is greater than that of the rectangle.
Hence, proved.
Question 2. In Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide DABC into n triangles of equal areas.]
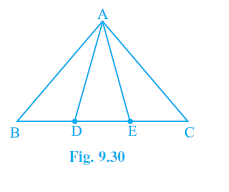
Answer:
Given:
In $\triangle ABC$, D and E are points on the side BC such that $BD = DE = EC$.
To Prove:
$ar (\triangle ABD) = ar (\triangle ADE) = ar (\triangle AEC)$
Construction:
Draw a perpendicular AM from vertex A to the base BC. Let $AM = h$.
Proof:
We know that the area of a triangle is given by the formula:
$Area = \frac{1}{2} \times \text{base} \times \text{height}$
Consider $\triangle ABD$. Its base is BD and its height is AM = $h$.
$ar (\triangle ABD) = \frac{1}{2} \times BD \times AM = \frac{1}{2} \times BD \times h$
...(i)
Consider $\triangle ADE$. Its base is DE and its height is AM = $h$.
$ar (\triangle ADE) = \frac{1}{2} \times DE \times AM = \frac{1}{2} \times DE \times h$
...(ii)
Consider $\triangle AEC$. Its base is EC and its height is AM = $h$.
$ar (\triangle AEC) = \frac{1}{2} \times EC \times AM = \frac{1}{2} \times EC \times h$
...(iii)
We are given that:
$BD = DE = EC$
...(iv)
Using the condition (iv) in equations (i), (ii), and (iii), we get:
$\frac{1}{2} \times BD \times h = \frac{1}{2} \times DE \times h = \frac{1}{2} \times EC \times h$
Therefore,
$ar (\triangle ABD) = ar (\triangle ADE) = ar (\triangle AEC)$
Hence, proved.
Answer to the Question from the Introduction (Budhia's Field):
Yes, based on the proof above, the field of Budhia has been actually divided into three parts of equal area.
The method involved dividing the base of the triangular field into three equal segments (like BD = DE = EC) and connecting the points of division (D and E) to the opposite vertex (A). As demonstrated, this divides the triangle into three smaller triangles ($\triangle ABD$, $\triangle ADE$, $\triangle AEC$) which all share the same height (the altitude from A) and have equal bases (BD = DE = EC). Consequently, their areas are equal.
Therefore, Budhia's method of dividing the field ensures that her son and two daughters receive parts of the field with equal areas.
Question 3. In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

Answer:
Given:
ABCD, DCFE and ABFE are parallelograms.
To Prove:
$ar (\triangle ADE) = ar (\triangle BCF)$
Proof:
Since ABCD is a parallelogram, we know that opposite sides are equal in length.
$\therefore AD = BC$
(Opposite sides of parallelogram ABCD)
Since DCFE is a parallelogram, we know that opposite sides are equal in length.
$\therefore DE = CF$
(Opposite sides of parallelogram DCFE)
Since ABFE is a parallelogram, we know that opposite sides are equal in length.
$\therefore AE = BF$
(Opposite sides of parallelogram ABFE)
Now, consider the triangles $\triangle ADE$ and $\triangle BCF$.
We have established that:
$AD = BC$
$DE = CF$
$AE = BF$
By the SSS (Side-Side-Side) congruence rule, if the three sides of one triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent.
$\therefore \triangle ADE \cong \triangle BCF$
(SSS Congruence Rule)
Since congruent figures have equal areas, we can conclude that:
$ar (\triangle ADE) = ar (\triangle BCF)$
Hence, proved.
Question 4. In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
[Hint: Join AC.]

Answer:
Given:
ABCD is a parallelogram.
BC is produced to Q such that AD = CQ.
AQ intersects DC at P.
To Prove:
$ar (\triangle BPC) = ar (\triangle DPQ)$
Construction:
Join AC.
Proof:
Since ABCD is a parallelogram,
$AD = BC$
(Opposite sides of a parallelogram)
We are given:
$AD = CQ$
(Given)
From these two equations, we get:
$BC = CQ$
Also, since ABCD is a parallelogram, $AD || BC$. As BC is produced to Q, we have $AD || BQ$.
Now, consider $\triangle ADP$ and $\triangle QCP$.
$\angle PAD = \angle PQC$
(Alternate interior angles, as $AD || BQ$ and AQ is transversal)
$\angle APD = \angle QPC$
(Vertically opposite angles)
$AD = CQ$
(Given)
By AAS (Angle-Angle-Side) congruence rule:
$\triangle ADP \cong \triangle QCP$
Since the triangles are congruent, their corresponding parts are equal.
$\therefore DP = CP$
(CPCT - Corresponding Parts of Congruent Triangles)
And $AP = PQ$
(CPCT)
Since $AP = PQ$, P is the midpoint of AQ. Therefore, DP is a median of $\triangle ADQ$.
We know that a median divides a triangle into two triangles of equal areas.
$\therefore ar(\triangle ADP) = ar(\triangle DPQ)$
...(i)
Now, consider $\triangle ADP$ and $\triangle BPC$.
Base $DP = CP$
(Proved above)
Also, since ABCD is a parallelogram, $AB || DC$.
The perpendicular distance between the parallel lines AB and DC represents the height of $\triangle ADP$ from vertex A to base DP (on line DC) and the height of $\triangle BPC$ from vertex B to base CP (on line DC).
Therefore, $\triangle ADP$ and $\triangle BPC$ have equal bases ($DP=CP$) and lie between the same parallel lines AB and DC (meaning they have equal heights relative to bases DP and CP).
Alternatively, triangles having equal bases and equal heights have equal areas.
$\therefore ar(\triangle ADP) = ar(\triangle BPC)$
...(ii)
From equations (i) and (ii):
$ar (\triangle BPC) = ar (\triangle DPQ)$
Hence, proved.
Alternate Approach (Using Hint):
Join AC.
Given $AD = CQ$ and $AD = BC$ (opposite sides of parallelogram ABCD). Thus, $BC = CQ$.
In $\triangle ABQ$, since $BC=CQ$, C is the midpoint of BQ. AC is the line joining vertex A to the midpoint C of the opposite side BQ. Therefore, AC is a median of $\triangle ABQ$.
A median divides a triangle into two triangles of equal area.
$ar(\triangle ABC) = ar(\triangle ACQ)$
...(iii)
Also, the diagonal AC divides the parallelogram ABCD into two triangles of equal area.
$ar(\triangle ABC) = ar(\triangle ADC)$
...(iv)
From (iii) and (iv):
$ar(\triangle ACQ) = ar(\triangle ADC)$
Subtracting $ar(\triangle APC)$ from both sides:
$ar(\triangle ACQ) - ar(\triangle APC) = ar(\triangle ADC) - ar(\triangle APC)$
$ar(\triangle PQC) = ar(\triangle DPC)$
...(v)
From the main proof (using congruence $\triangle ADP \cong \triangle QCP$), we established $DP=CP$.
Since $DP=CP$, P is the midpoint of DC. In $\triangle ADQ$, we also know $AP=PQ$, so P is midpoint of AQ. DP is the median to side AQ in $\triangle ADQ$.
$ar(\triangle ADP) = ar(\triangle DPQ)$
...(vi)
Consider $\triangle ADC$. AC is the diagonal. We showed $ar(\triangle ABC) = ar(\triangle ADC)$.
$ar(\triangle ABC) = ar(\triangle APC) + ar(\triangle BPC)$
$ar(\triangle ADC) = ar(\triangle APC) + ar(\triangle DPC)$
Equating them gives:
$ar(\triangle BPC) = ar(\triangle DPC)$
...(vii)
From (v) and (vii):
$ar(\triangle BPC) = ar(\triangle PQC)$
From congruence $\triangle ADP \cong \triangle QCP$, we have $ar(\triangle ADP) = ar(\triangle QCP)$.
So, $ar(\triangle BPC) = ar(\triangle ADP)$.
Using equation (vi), $ar(\triangle ADP) = ar(\triangle DPQ)$.
Therefore, $ar(\triangle BPC) = ar(\triangle DPQ)$.
Hence, proved.
Question 5. In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(i) ar (BDE) = $\frac{1}{4}$ ar (ABC)
(ii) ar (BDE) = $\frac{1}{2}$ ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = $\frac{1}{8}$ ar (AFC)
[Hint: Join EC and AD. Show that BE || AC and DE || AB, etc.]
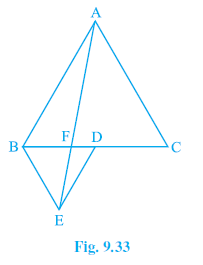
Answer:
Given:
$\triangle$ ABC and $\triangle$ BDE are equilateral triangles.
D is the mid-point of BC.
AE intersects BC at F.
To Prove:
(i) ar (BDE) = $\frac{1}{4}$ ar (ABC)
(ii) ar (BDE) = $\frac{1}{2}$ ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = $\frac{1}{8}$ ar (AFC)
Construction:
Join AD and EC.
Proof:
Let the side length of equilateral triangle ABC be $s$.
Area of an equilateral triangle with side length $a$ is given by $\frac{\sqrt{3}}{4} a^2$.
ar (ABC) = $\frac{\sqrt{3}}{4} s^2$
...(1)
Since D is the mid-point of BC, $BD = \frac{1}{2} BC = \frac{s}{2}$.
$\triangle$ BDE is an equilateral triangle with side length BD = $\frac{s}{2}$.
ar (BDE) = $\frac{\sqrt{3}}{4} (\frac{s}{2})^2 = \frac{\sqrt{3}}{4} \frac{s^2}{4} = \frac{1}{4} (\frac{\sqrt{3}}{4} s^2)$
...(2)
Comparing (1) and (2):
ar (BDE) = $\frac{1}{4}$ ar (ABC)
[From (1) and (2)] ... (i)
Thus, part (i) is Proved.
In $\triangle$ BEC, D is the mid-point of BC. Thus, ED is the median of $\triangle$ BEC.
A median of a triangle divides it into two triangles of equal area.
ar (BDE) = ar (CDE)
[ED is median of $\triangle$ BEC]
ar (BEC) = ar (BDE) + ar (CDE) = ar (BDE) + ar (BDE) = 2 ar (BDE).
From (i), ar (BDE) = $\frac{1}{4}$ ar (ABC).
So, ar (BEC) = 2 $\times \frac{1}{4}$ ar (ABC) = $\frac{1}{2}$ ar (ABC).
ar (ABC) = 2 ar (BEC)
... (iii)
Thus, part (iii) is Proved.
As per the hint, we assume that DE || AB.
DE || AB
[Hint]
Triangles on the same base and between the same parallels have equal areas.
Consider $\triangle$ ABD and $\triangle$ ABE. They share the base AB and are between the parallel lines AB and DE.
ar (ABD) = ar (ABE)
[Triangles on same base AB, between AB || DE]
In $\triangle$ ABC, since D is the mid-point of BC, AD is the median.
ar (ABD) = $\frac{1}{2}$ ar (ABC)
[AD is median of $\triangle$ ABC]
So, ar (ABE) = ar (ABD) = $\frac{1}{2}$ ar (ABC).
ar (BAE) = $\frac{1}{2}$ ar (ABC)
...(3)
We need to prove ar (BDE) = $\frac{1}{2}$ ar (BAE) [part (ii)].
Substitute ar (BDE) = $\frac{1}{4}$ ar (ABC) [from (i)] and ar (BAE) = $\frac{1}{2}$ ar (ABC) [from (3)] into the expression:
$\frac{1}{2}$ ar (BAE) = $\frac{1}{2} \times (\frac{1}{2}$ ar (ABC)) = $\frac{1}{4}$ ar (ABC)
[Using (3)]
Comparing this with ar (BDE) from (i):
ar (BDE) = $\frac{1}{4}$ ar (ABC) = $\frac{1}{2}$ ar (BAE)
[Using (i)] ... (ii)
Thus, part (ii) is Proved.
From the result ar (ABE) = ar (ABD) [from step 4 in thought process]:
Subtract the area of the common triangle $\triangle$ ABF from both sides:
ar (ABE) - ar (ABF) = ar (ABD) - ar (ABF)
[Subtracting ar(ABF)]
ar (BFE) = ar (AFD)
... (iv)
Thus, part (iv) is Proved.
Since DE || AB, and AE is a transversal intersecting AB and DE, consider $\triangle$ FAB and $\triangle$ FED.
$\angle$ FAB = $\angle$ FED
[Alternate Interior Angles, AB || DE]
$\angle$ FBA = $\angle$ FDE
[Alternate Interior Angles, AB || DE]
$\angle$ AFB = $\angle$ DFE
[Vertically Opposite Angles]
Thus, $\triangle$ FAB is similar to $\triangle$ FED (AAA similarity).
The ratio of corresponding sides is equal:
$\frac{FA}{FE} = \frac{FB}{FD} = \frac{AB}{ED}$
...(4)
We know $AB = s$ and $ED = BD = s/2$ (side of equilateral $\triangle$ BDE).
$\frac{AB}{ED} = \frac{s}{s/2} = 2$
...(5)
From (4) and (5), we get $\frac{FA}{FE} = 2$ and $\frac{FB}{FD} = 2$.
$FA = 2 FE$ and $FB = 2 FD$.
Consider $\triangle$ AFD and $\triangle$ FED. They share the same altitude from vertex D to the line AE.
The ratio of their areas is equal to the ratio of their bases on AE:
$\frac{\text{ar (AFD)}}{\text{ar (FED)}} = \frac{FA}{FE}$
...(6)
Substitute $\frac{FA}{FE} = 2$ from the similarity result:
$\frac{\text{ar (AFD)}}{\text{ar (FED)}} = 2$
[Using (6)]
ar (AFD) = 2 ar (FED).
From part (iv), ar (BFE) = ar (AFD).
Therefore, ar (BFE) = 2 ar (FED). Hence Proved (v).
Now, we need to prove part (vi) ar (FED) = $\frac{1}{8}$ ar (AFC).
From the similarity result, we have $FB = 2 FD$.
Since D is the mid-point of BC, $BD = DC = s/2$. F lies on BC.
Given $FB = 2 FD$, F must lie between B and D (otherwise if D were between B and F, $BF = BD + DF \implies 2FD = s/2 + FD \implies FD = s/2$, then $FB = s$, which means F coincides with C, which is not possible as AE intersects BC at F, not necessarily C).
Since F is between B and D, $BD = BF + FD$.
$s/2 = BF + FD$
[D is midpoint of BC]
Substitute $BF = 2 FD$ into the equation:
$s/2 = 2 FD + FD = 3 FD$
$FD = \frac{s}{6}$
Then $BF = 2 FD = 2 \times \frac{s}{6} = \frac{s}{3}$.
So, F is on BC such that $BF = s/3$.
$FC = BC - BF = s - \frac{s}{3} = \frac{3s - s}{3} = \frac{2s}{3}$.
Thus, $BF = s/3$ and $FC = 2s/3$. The ratio $\frac{BF}{FC} = \frac{s/3}{2s/3} = \frac{1}{2}$.
Consider $\triangle$ ABF and $\triangle$ AFC. They share the same altitude from vertex A to the line BC.
The ratio of their areas is equal to the ratio of their bases on BC:
$\frac{\text{ar (ABF)}}{\text{ar (AFC)}} = \frac{BF}{FC} = \frac{s/3}{2s/3} = \frac{1}{2}$
...(7)
ar (AFC) = 2 ar (ABF).
Also, ar (ABC) = ar (ABF) + ar (AFC).
Substitute ar (AFC) = 2 ar (ABF):
ar (ABC) = ar (ABF) + 2 ar (ABF) = 3 ar (ABF).
ar (ABF) = $\frac{1}{3}$ ar (ABC)
...(8)
And ar (AFC) = 2 ar (ABF) = 2 $\times \frac{1}{3}$ ar (ABC) = $\frac{2}{3}$ ar (ABC).
ar (AFC) = $\frac{2}{3}$ ar (ABC)
...(9)
We know ar (ABD) = $\frac{1}{2}$ ar (ABC) [AD is median].
Also, ar (ABD) = ar (ABF) + ar (AFD).
Substitute ar (ABD) = $\frac{1}{2}$ ar (ABC) and ar (ABF) = $\frac{1}{3}$ ar (ABC) [from (8)]:
$\frac{1}{2}$ ar (ABC) = $\frac{1}{3}$ ar (ABC) + ar (AFD)
[Using (8)]
ar (AFD) = $\frac{1}{2}$ ar (ABC) - $\frac{1}{3}$ ar (ABC) = $(\frac{3 - 2}{6})$ ar (ABC) = $\frac{1}{6}$ ar (ABC).
ar (AFD) = $\frac{1}{6}$ ar (ABC)
...(10)
From the proof of part (v), we established ar (AFD) = 2 ar (FED).
So, ar (FED) = $\frac{1}{2}$ ar (AFD).
Substitute ar (AFD) = $\frac{1}{6}$ ar (ABC) [from (10)]:
ar (FED) = $\frac{1}{2} \times \frac{1}{6}$ ar (ABC) = $\frac{1}{12}$ ar (ABC)
...(11)
Now we check if ar (FED) = $\frac{1}{8}$ ar (AFC) [part (vi)].
Substitute ar (FED) = $\frac{1}{12}$ ar (ABC) [from (11)] and ar (AFC) = $\frac{2}{3}$ ar (ABC) [from (9)] into the equation:
$\frac{1}{12}$ ar (ABC) = $\frac{1}{8} \times (\frac{2}{3}$ ar (ABC))
[Using (11) and (9)]
Check the numerical part: $\frac{1}{12} = \frac{1}{8} \times \frac{2}{3} = \frac{2}{24} = \frac{1}{12}$.
The equality holds.
ar (FED) = $\frac{1}{8}$ ar (AFC)
... (vi)
Thus, part (vi) is Proved.
Question 6. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint: From A and C, draw perpendiculars to BD.]
Answer:
Given:
A quadrilateral ABCD whose diagonals AC and BD intersect at P.
To Prove:
ar (APB) $\times$ ar (CPD) = ar (APD) $\times$ ar (BPC)
Construction Required:
Draw AL $\perp$ BD and CM $\perp$ BD.
Proof:
The area of a triangle is given by the formula: Area $= \frac{1}{2} \times \text{base} \times \text{height}$.
Using this formula for the triangles formed with base on BD and heights AL and CM:
ar (APB) = $\frac{1}{2} \times$ PB $\times$ AL
... (i)
ar (APD) = $\frac{1}{2} \times$ PD $\times$ AL
... (ii)
ar (BPC) = $\frac{1}{2} \times$ PB $\times$ CM
... (iii)
ar (CPD) = $\frac{1}{2} \times$ PD $\times$ CM
... (iv)
Now, let's find the product of ar (APB) and ar (CPD) from equations (i) and (iv):
ar (APB) $\times$ ar (CPD) = $\left(\frac{1}{2} \times \text{PB} \times \text{AL}\right) \times \left(\frac{1}{2} \times \text{PD} \times \text{CM}\right)$
ar (APB) $\times$ ar (CPD) = $\frac{1}{4} \times \text{PB} \times \text{PD} \times \text{AL} \times \text{CM}$
ar (APB) $\times$ ar (CPD) = $\frac{1}{4} \times \text{PB} \times \text{PD} \times \text{AL} \times \text{CM}
... (v)
Next, let's find the product of ar (APD) and ar (BPC) from equations (ii) and (iii):
ar (APD) $\times$ ar (BPC) = $\left(\frac{1}{2} \times \text{PD} \times \text{AL}\right) \times \left(\frac{1}{2} \times \text{PB} \times \text{CM}\right)$
ar (APD) $\times$ ar (BPC) = $\frac{1}{4} \times \text{PD} \times \text{AL} \times \text{PB} \times \text{CM}$
ar (APD) $\times$ ar (BPC) = $\frac{1}{4} \times \text{PB} \times \text{PD} \times \text{AL} \times \text{CM}
... (vi)
Comparing equation (v) and equation (vi), we can see that the right-hand sides are equal.
Therefore, the left-hand sides must also be equal.
ar (APB) $\times$ ar (CPD) = ar (APD) $\times$ ar (BPC)
Hence proved.
Question 7. P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar (PRQ) = $\frac{1}{2}$ ar (ARC)
(ii) ar (RQC) = $\frac{3}{8}$ ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Answer:
Given:
$\triangle$ ABC is a triangle.
P is the mid-point of side AB.
Q is the mid-point of side BC.
R is the mid-point of AP.
To Prove:
(i) ar (PRQ) = $\frac{1}{2}$ ar (ARC)
(ii) ar (RQC) = $\frac{3}{8}$ ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Proof:
We know that a median of a triangle divides it into two triangles of equal area.
In $\triangle$ ABC, Q is the mid-point of BC.
Therefore, AQ is the median of $\triangle$ ABC.
ar (AQB) = ar (AQC)
... (1)
ar (AQB) = ar (AQC) = $\frac{1}{2}$ ar (ABC)
... (2)
In $\triangle$ AQB, P is the mid-point of AB.
Therefore, QP is the median of $\triangle$ AQB.
ar (APQ) = ar (BPQ)
... (3)
Using (2) and (3):
ar (APQ) = ar (BPQ) = $\frac{1}{2}$ ar (AQB)
[QP is median of $\triangle$ AQB] ... (4)
From (2) and (4):
ar (APQ) = ar (BPQ) = $\frac{1}{2} \times \frac{1}{2}$ ar (ABC) = $\frac{1}{4}$ ar (ABC)
... (5)
In $\triangle$ APQ, R is the mid-point of AP.
Therefore, QR is the median of $\triangle$ APQ.
ar (PRQ) = ar (ARQ)
[QR is median of $\triangle$ APQ] ... (6)
Using (5) and (6):
ar (PRQ) = ar (ARQ) = $\frac{1}{2}$ ar (APQ)
... (7)
From (5) and (7):
ar (PRQ) = ar (ARQ) = $\frac{1}{2} \times \frac{1}{4}$ ar (ABC) = $\frac{1}{8}$ ar (ABC)
... (8)
Now consider $\triangle$ ABC again. P is the mid-point of AB.
Therefore, CP is the median of $\triangle$ ABC.
ar (APC) = ar (BPC)
[CP is median of $\triangle$ ABC] ... (9)
ar (APC) = $\frac{1}{2}$ ar (ABC)
... (10)
In $\triangle$ APC, R is the mid-point of AP.
Therefore, CR is the median of $\triangle$ APC.
ar (ARC) = ar (PRC)
[CR is median of $\triangle$ APC] ... (11)
ar (ARC) = $\frac{1}{2}$ ar (APC)
... (12)
From (10) and (12):
ar (ARC) = $\frac{1}{2} \times \frac{1}{2}$ ar (ABC) = $\frac{1}{4}$ ar (ABC)
... (13)
(i) To Prove: ar (PRQ) = $\frac{1}{2}$ ar (ARC)
From (8), ar (PRQ) = $\frac{1}{8}$ ar (ABC).
From (13), ar (ARC) = $\frac{1}{4}$ ar (ABC).
Consider $\frac{1}{2}$ ar (ARC):
$\frac{1}{2}$ ar (ARC) = $\frac{1}{2} \times \frac{1}{4}$ ar (ABC)
[Using (13)]
$\frac{1}{2}$ ar (ARC) = $\frac{1}{8}$ ar (ABC)
Comparing this with ar (PRQ) from (8):
ar (PRQ) = $\frac{1}{8}$ ar (ABC) = $\frac{1}{2}$ ar (ARC)
[Using (8)]
Thus, ar (PRQ) = $\frac{1}{2}$ ar (ARC). Hence Proved (i).
(ii) To Prove: ar (RQC) = $\frac{3}{8}$ ar (ABC)
We know that ar (AQC) = $\frac{1}{2}$ ar (ABC) from (2).
Also, ar (AQC) is the sum of areas of $\triangle$ ARQ and $\triangle$ RQC.
ar (AQC) = ar (ARQ) + ar (RQC)
... (14)
From (8), ar (ARQ) = $\frac{1}{8}$ ar (ABC).
Substitute the values of ar (AQC) and ar (ARQ) into (14):
$\frac{1}{2}$ ar (ABC) = $\frac{1}{8}$ ar (ABC) + ar (RQC)
[Using (2) and (8)]
Rearrange the equation to find ar (RQC):
ar (RQC) = $\frac{1}{2}$ ar (ABC) - $\frac{1}{8}$ ar (ABC)
ar (RQC) = $(\frac{1}{2} - \frac{1}{8})$ ar (ABC)
ar (RQC) = $(\frac{4}{8} - \frac{1}{8})$ ar (ABC)
ar (RQC) = $\frac{3}{8}$ ar (ABC)
Thus, ar (RQC) = $\frac{3}{8}$ ar (ABC). Hence Proved (ii).
(iii) To Prove: ar (PBQ) = ar (ARC)
From (5), we have ar (PBQ) = $\frac{1}{4}$ ar (ABC).
From (13), we have ar (ARC) = $\frac{1}{4}$ ar (ABC).
Comparing the expressions for ar (PBQ) and ar (ARC):
ar (PBQ) = $\frac{1}{4}$ ar (ABC)
[From (5)]
ar (ARC) = $\frac{1}{4}$ ar (ABC)
[From (13)]
Since both are equal to $\frac{1}{4}$ ar (ABC), we can conclude that:
ar (PBQ) = ar (ARC)
Thus, ar (PBQ) = ar (ARC). Hence Proved (iii).
Question 8. In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
(i) ∆ MBC ≅ ∆ ABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆ FCB ≅∆ ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Answer:
Given:
1. ABC is a right triangle, right-angled at A ($\angle BAC = 90^\circ$).
2. BCED, ACFG, and ABMN are squares on sides BC, CA, and AB respectively.
3. Line segment AX $\perp$ DE and meets BC at Y.
To Prove:
(i) $\triangle MBC \cong \triangle ABD$
(ii) $ar (BYXD) = 2 ar (MBC)$
(iii) $ar (BYXD) = ar (ABMN)$
(iv) $\triangle FCB \cong \triangle ACE$
(v) $ar (CYXE) = 2 ar (FCB)$
(vi) $ar (CYXE) = ar (ACFG)$
(vii) $ar (BCED) = ar (ABMN) + ar (ACFG)$
Proof:
(i) Prove $\triangle MBC \cong \triangle ABD$
In $\triangle MBC$ and $\triangle ABD$:
MB = AB
(Sides of square ABMN)
BC = BD
(Sides of square BCED)
We know that $\angle ABM = 90^\circ$ (Angle of square ABMN) and $\angle DBC = 90^\circ$ (Angle of square BCED).
$\angle MBC = \angle ABM + \angle ABC$
$\angle MBC = 90^\circ + \angle ABC$
$\angle ABD = \angle DBC + \angle ABC$
$\angle ABD = 90^\circ + \angle ABC$
Therefore,
$\angle MBC = \angle ABD$
By SAS congruence rule:
$\triangle MBC \cong \triangle ABD$
Hence proved (i).
(ii) Prove $ar (BYXD) = 2 ar (MBC)$
From (i), we have $\triangle MBC \cong \triangle ABD$.
Therefore, $ar (\triangle MBC) = ar (\triangle ABD)$.
Now, consider $\triangle ABD$ and rectangle BYXD.
They lie on the same base BD and between the same parallels BD and AX (as AX $\perp$ DE and BD is part of DE).
Theorem: If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram.
So, $ar (\triangle ABD) = \frac{1}{2} ar (BYXD)$.
$\implies ar (BYXD) = 2 ar (\triangle ABD)$.
Since $ar (\triangle ABD) = ar (\triangle MBC)$, we have:
$ar (BYXD) = 2 ar (\triangle MBC)$.
Hence proved (ii).
(iii) Prove $ar (BYXD) = ar (ABMN)$
Consider $\triangle MBC$ and square ABMN.
They lie on the same base MB.
We need to show they lie between the same parallels MB and NC.
$\angle NAB = 90^\circ$
(Angle of square ABMN)
$\angle BAC = 90^\circ$
(Given)
Adding these, $\angle NAB + \angle BAC = 90^\circ + 90^\circ = 180^\circ$.
So, $\angle NAC = 180^\circ$, which means N, A, C form a straight line.
Thus, $\triangle MBC$ and square ABMN are on the same base MB and between the same parallels MB and NC.
Using the theorem from part (ii):
$ar (\triangle MBC) = \frac{1}{2} ar (ABMN)$.
$\implies ar (ABMN) = 2 ar (\triangle MBC)$.
From part (ii), we have $ar (BYXD) = 2 ar (\triangle MBC)$.
Therefore, $ar (BYXD) = ar (ABMN)$.
Hence proved (iii).
(iv) Prove $\triangle FCB \cong \triangle ACE$
In $\triangle FCB$ and $\triangle ACE$:
FC = AC
(Sides of square ACFG)
CB = CE
(Sides of square BCED)
We know that $\angle ACF = 90^\circ$ (Angle of square ACFG) and $\angle BCE = 90^\circ$ (Angle of square BCED).
$\angle FCB = \angle FCA + \angle ACB$
$\angle FCB = 90^\circ + \angle ACB$
$\angle ACE = \angle BCE + \angle ACB$
$\angle ACE = 90^\circ + \angle ACB$
Therefore,
$\angle FCB = \angle ACE$
By SAS congruence rule:
$\triangle FCB \cong \triangle ACE$
Hence proved (iv).
(v) Prove $ar (CYXE) = 2 ar (FCB)$
From (iv), we have $\triangle FCB \cong \triangle ACE$.
Therefore, $ar (\triangle FCB) = ar (\triangle ACE)$.
Now, consider $\triangle ACE$ and rectangle CYXE.
They lie on the same base CE and between the same parallels CE and AX (as AX $\perp$ DE and CE is part of DE).
Using the theorem: If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram.
So, $ar (\triangle ACE) = \frac{1}{2} ar (CYXE)$.
$\implies ar (CYXE) = 2 ar (\triangle ACE)$.
Since $ar (\triangle ACE) = ar (\triangle FCB)$, we have:
$ar (CYXE) = 2 ar (\triangle FCB)$.
Hence proved (v).
(vi) Prove $ar (CYXE) = ar (ACFG)$
Consider $\triangle FCB$ and square ACFG.
They lie on the same base FC.
We need to show they lie between the same parallels FC and GB.
$\angle GAC = 90^\circ$
(Angle of square ACFG)
$\angle CAB = 90^\circ$
(Given)
Adding these, $\angle GAC + \angle CAB = 90^\circ + 90^\circ = 180^\circ$.
So, $\angle GAB = 180^\circ$, which means G, A, B form a straight line.
Thus, $\triangle FCB$ and square ACFG are on the same base FC and between the same parallels FC and GB.
Using the theorem from part (ii):
$ar (\triangle FCB) = \frac{1}{2} ar (ACFG)$.
$\implies ar (ACFG) = 2 ar (\triangle FCB)$.
From part (v), we have $ar (CYXE) = 2 ar (\triangle FCB)$.
Therefore, $ar (CYXE) = ar (ACFG)$.
Hence proved (vi).
(vii) Prove $ar (BCED) = ar (ABMN) + ar (ACFG)$
From the figure, the square BCED is composed of two rectangles BYXD and CYXE.
$ar (BCED) = ar (BYXD) + ar (CYXE)$.
From part (iii), we proved $ar (BYXD) = ar (ABMN)$.
From part (vi), we proved $ar (CYXE) = ar (ACFG)$.
Substituting these results into the equation for the area of BCED:
$ar (BCED) = ar (ABMN) + ar (ACFG)$.
Hence proved (vii).
This result is the Pythagoras Theorem.

