| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 13 Statistics And Probability
Welcome to this comprehensive resource dedicated to providing detailed, step-by-step solutions for the Class 10 NCERT Exemplar problems encompassing both Statistics and Probability. These Exemplar questions are meticulously crafted to push beyond standard textbook exercises, demanding a significantly deeper level of analytical skill, more complex calculations, nuanced interpretations of data and outcomes, and the application of core concepts within non-routine, often challenging scenarios. Mastering these problems is crucial for developing a robust understanding of data analysis and the principles of chance, essential skills for further studies and real-world applications.
Within the realm of Statistics, the Exemplar problems predominantly focus on the analysis of grouped data, requiring proficiency in handling data presented in frequency distribution tables. Our solutions provide exhaustive calculations and explanations for the key measures of central tendency, tackling the complexities often introduced at the Exemplar level:
- Mean: Solutions demonstrate the application of the Direct Method, the Assumed Mean Method, and the Step-Deviation Method. Exemplar challenges might include finding missing frequencies within a distribution given the mean, or dealing with distributions having unequal class sizes or other complexities requiring careful handling of the chosen method.
- Median: The calculation relies on the formula: Median $= l + [\frac{(\frac{n}{2})-cf}{f}]\times h$, where $l$ is the lower limit of the median class, $n$ is the total frequency, $cf$ is the cumulative frequency of the class preceding the median class, $f$ is the frequency of the median class, and $h$ is the class size. Solutions guide through identifying the median class and applying the formula accurately, even for complex frequency tables.
- Mode: Calculated using the formula: Mode $= l + [\frac{f_1-f_0}{2f_1-f_0-f_2}]\times h$, where $l$ is the lower limit of the modal class, $f_1$ is the frequency of the modal class, $f_0$ is the frequency of the preceding class, $f_2$ is the frequency of the succeeding class, and $h$ is the class size. Exemplar problems might present challenges in correctly identifying the modal class, especially in distributions with irregular frequency patterns.
Furthermore, the interpretation and construction of graphical representations, particularly cumulative frequency curves (ogives), are explored in depth. Solutions cover both 'less than' type and 'more than' type ogives, demonstrating their construction and, critically, their use in determining the median graphically. The Exemplar often demands deeper analysis, such as interpreting the shape of the ogive or comparing different datasets based on their respective ogives.
Transitioning to Probability, the solutions focus squarely on theoretical probability, grounded in the fundamental definition $P(E) = \frac{\text{Number of outcomes favorable to E}}{\text{Total number of possible outcomes}} = \frac{n(E)}{n(S)}$. However, the Exemplar elevates the complexity of the random experiments considered. You will find detailed analyses for scenarios involving:
- Multiple coin tosses or dice rolls, requiring careful enumeration of the sample space ($S$) and identification of favorable outcomes ($E$) for complex events (e.g., getting a specific sum, prime numbers on both dice).
- Intricate problems based on drawing cards from a standard 52-card deck, potentially involving multiple draws or conditions related to specific suits, colours, face cards, or combinations thereof.
- Selection problems from groups (e.g., selecting balls from a bag, students from a class) where careful listing or basic combinatorial thinking is implicitly needed to determine $n(E)$ and $n(S)$.
The solutions also demonstrate the application of concepts like complementary events, using the relationship $P(E') = 1 - P(E)$ to simplify calculations, and may touch upon scenarios implicitly involving mutually exclusive or independent events, or even basic geometric probability in challenging contexts. All question formats are addressed, from conceptual MCQs and precise Fill-in-the-Blanks/True-False to demanding Short/Long Answer questions requiring detailed statistical calculations, accurate ogive construction, or systematic probability determination. This resource is designed to equip students with the skills needed for advanced statistical analysis and sophisticated probability problem-solving.
Sample Question 1 to 6 (Before Exercise 13.1)
Choose the correct answer from the given four options:
Sample Question 1: Construction of a cumulative frequency table is useful in determining the
(A) mean
(B) median
(C) mode
(D) all the above three measures
Answer:
The correct option is (B).
The correct answer is median.
A cumulative frequency table helps in determining the cumulative frequency of different classes, which is essential for locating the median class (the class containing the $\left(\frac{N}{2}\right)^{\text{th}}$ observation) and subsequently calculating the median.
Sample Question 2: In the following distribution :
| Monthly income range (in Rs) | Number of families |
|---|---|
| Income more than Rs 10000 | 100 |
| Income more than Rs 13000 | 85 |
| Income more than Rs 16000 | 69 |
| Income more than Rs 19000 | 50 |
| Income more than Rs 22000 | 33 |
| Income more than Rs 25000 | 15 |
the number of families having income range (in Rs) 16000 – 19000 is
(A) 15
(B) 16
(C) 17
(D) 19
Answer:
The correct option is (D).
The number of families having income range (in $\textsf{₹}$) 16000 – 19000 is the difference between the number of families having income more than $\textsf{₹}$ 16000 and the number of families having income more than $\textsf{₹}$ 19000.
From the given table:
Number of families with income more than $\textsf{₹}$ 16000 = 69
Number of families with income more than $\textsf{₹}$ 19000 = 50
Number of families in the income range $\textsf{₹}$ 16000 – 19000 = (Number of families with income > $\textsf{₹}$ 16000) - (Number of families with income > $\textsf{₹}$ 19000)
Number of families = $69 - 50$
Number of families = $19$
Sample Question 3: Consider the following frequency distribution of the heights of 60 students of a class :
| Height (in cm) | Number of students |
|---|---|
| 150-155 | 15 |
| 155-160 | 13 |
| 160-165 | 10 |
| 165-170 | 8 |
| 170-175 | 9 |
| 175-180 | 5 |
The sum of the lower limit of the modal class and upper limit of the median class is
(A) 310
(B) 315
(C) 320
(D) 330
Answer:
The correct option is (B).
To find the sum of the lower limit of the modal class and the upper limit of the median class, we first need to identify these classes from the given frequency distribution.
Finding the Modal Class:
The modal class is the class interval with the highest frequency.
Looking at the table, the frequencies are 15, 13, 10, 8, 9, and 5.
The highest frequency is 15, which corresponds to the height range 150-155 cm.
Thus, the modal class is 150-155.
The lower limit of the modal class is 150.
Finding the Median Class:
The median class is the class interval where the cumulative frequency is greater than or equal to $\frac{N}{2}$, where $N$ is the total number of observations (students).
Total number of students $N = 15 + 13 + 10 + 8 + 9 + 5 = 60$.
So, $\frac{N}{2} = \frac{60}{2} = 30$.
Now, let's construct the cumulative frequency table:
| Height (in cm) | Number of students (f) | Cumulative Frequency (cf) |
| 150-155 | 15 | 15 |
| 155-160 | 13 | $15 + 13 = 28$ |
| 160-165 | 10 | $28 + 10 = 38$ |
| 165-170 | 8 | $38 + 8 = 46$ |
| 170-175 | 9 | $46 + 9 = 55$ |
| 175-180 | 5 | $55 + 5 = 60$ |
We are looking for the class where the cumulative frequency is 30 or more. The first cumulative frequency that is greater than or equal to 30 is 38, which corresponds to the class interval 160-165.
Thus, the median class is 160-165.
The upper limit of the median class is 165.
Calculating the Sum:
Sum of the lower limit of the modal class and the upper limit of the median class = Lower limit of modal class + Upper limit of median class
Sum = $150 + 165 = 315$
Sample Question 4: Which of the the following can be the probability of an event?
(A) – 0.04
(B) 1.004
(C) $\frac{18}{23}$
(D) $\frac{8}{7}$
Answer:
The correct option is (C).
The probability of any event E, denoted by $P(E)$, must satisfy the condition $0 \leq P(E) \leq 1$. That is, the probability of an event must be a value between 0 and 1, inclusive.
Let's examine each option:
(A) – 0.04: This value is negative. Probability cannot be negative.
(B) 1.004: This value is greater than 1. Probability cannot be greater than 1.
(C) $\frac{18}{23}$: To check if this value is between 0 and 1, we can compare the numerator and the denominator. Since $18 < 23$, the fraction $\frac{18}{23}$ is less than 1. Also, since both 18 and 23 are positive, the fraction is greater than 0. Thus, $0 < \frac{18}{23} < 1$. This is a valid probability.
(D) $\frac{8}{7}$: Since $8 > 7$, the fraction $\frac{8}{7}$ is greater than 1. This is not a valid probability.
Therefore, the only value that can be the probability of an event is $\frac{18}{23}$.
Sample Question 5: A card is selected at random from a well shuffled deck of 52 playing cards. The probability of its being a face card is
(A) $\frac{3}{13}$
(B) $\frac{4}{13}$
(C) $\frac{6}{13}$
(D) $\frac{9}{13}$
Answer:
The correct option is (A).
In a standard deck of 52 playing cards, there are 4 suits: Hearts, Diamonds, Clubs, and Spades.
Each suit has 13 cards: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King.
The face cards are the Jack, Queen, and King.
Number of face cards in each suit = 3.
Since there are 4 suits, the total number of face cards in a deck = $3 \times 4 = 12$.
The total number of possible outcomes when selecting a card at random is the total number of cards in the deck, which is 52.
The number of favourable outcomes (selecting a face card) is 12.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of being a face card = $\frac{\text{Number of face cards}}{\text{Total number of cards}}$
Probability = $\frac{12}{52}$
Simplify the fraction:
$\frac{12}{52} = \frac{\cancel{12}^{3}}{\cancel{52}_{13}}$
Probability = $\frac{3}{13}$
Sample Question 6: A bag contains 3 red balls, 5 white balls and 7 black balls. What is the probability that a ball drawn from the bag at random will be neither red nor black?
(A) $\frac{1}{5}$
(B) $\frac{1}{3}$
(C) $\frac{7}{15}$
(D) $\frac{8}{15}$
Answer:
The correct option is (B).
We are given the number of balls of different colours in the bag:
Number of red balls = 3
Number of white balls = 5
Number of black balls = 7
The total number of balls in the bag is the sum of the number of balls of each colour.
Total number of balls = $3 + 5 + 7 = 15$
We want to find the probability that a ball drawn from the bag is neither red nor black.
A ball that is neither red nor black must be a white ball.
The number of favourable outcomes (drawing a white ball) is the number of white balls, which is 5.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of drawing a ball that is neither red nor black = Probability of drawing a white ball
$P(\text{neither red nor black}) = \frac{\text{Number of white balls}}{\text{Total number of balls}}$
$P(\text{neither red nor black}) = \frac{5}{15}$
Simplify the fraction:
$\frac{5}{15} = \frac{\cancel{5}^{1}}{\cancel{15}_{3}}$
$P(\text{neither red nor black}) = \frac{1}{3}$
Exercise 13.1
Choose the correct answer from the given four options:
Question 1. In the formula
$\overline{x} = a + \frac{f_{i}d_{i}}{f_{i}}$
for finding the mean of grouped data di ’s are deviations from a of
(A) lower limits of the classes
(B) upper limits of the classes
(C) mid points of the classes
(D) frequencies of the class marks
Answer:
The correct option is (C).
The formula given for finding the mean of grouped data is a variation of the assumed mean method, which is typically written as:
$\overline{x} = a + \frac{\sum f_{i}d_{i}}{\sum f_{i}}$
where $\overline{x}$ is the mean, $a$ is the assumed mean, $f_i$ is the frequency of the $i$-th class, and $d_i$ is the deviation of the class mark (or midpoint) of the $i$-th class from the assumed mean $a$.
The deviations $d_i$ are calculated as $d_i = x_i - a$, where $x_i$ represents the class mark or midpoint of the $i$-th class interval.
Therefore, $d_i$'s are deviations from $a$ of the mid points of the classes.
Question 2. While computing mean of grouped data, we assume that the frequencies are
(A) evenly distributed over all the classes
(B) centred at the classmarks of the classes
(C) centred at the upper limits of the classes
(D) centred at the lower limits of the classes
Answer:
The correct option is (B).
While computing the mean of grouped data, we use the class mark (midpoint) of each class interval as the representative value for all observations falling within that interval.
This method implicitly assumes that the frequency of each class is centred at the classmark of that class.
In other words, we assume that the data values within each interval are evenly distributed around the classmark, or that the classmark represents the average value for that interval.
Question 3. If xi’s are the mid points of the class intervals of grouped data, fi’s are the corresponding frequencies and $\overline{x}$ is the mean, then $\sum (f_{i}x_{i} - \overline{x})$ is equal to
(A) 0
(B) –1
(C) 1
(D) 2
Answer:
The correct option is (A).
To Find: The value of $\sum (f_{i}x_{i} - \overline{x})$.
Solution:
We are given that $x_i$'s are the midpoints of the class intervals, $f_i$'s are the corresponding frequencies, and $\overline{x}$ is the mean of the grouped data.
The formula for the mean of grouped data is:
$\overline{x} = \frac{\sum f_{i}x_{i}}{\sum f_{i}}$
From the definition of the mean, we can write:
$\overline{x} \sum f_{i} = \sum f_{i}x_{i}$
Now, let's evaluate the given expression $\sum (f_{i}x_{i} - \overline{x})$.
We can distribute the summation:
$\sum (f_{i}x_{i} - \overline{x}) = \sum (f_{i}x_{i}) - \sum (\overline{x})$
The term $\overline{x}$ is a constant with respect to the index $i$ of the summation. So, $\sum (\overline{x})$ means adding $\overline{x}$ for each term in the summation. The number of terms is the total number of observations, which is $\sum f_i$.
Therefore, $\sum (\overline{x})$ is not correct. The $\overline{x}$ is constant with respect to $i$, but it is multiplied by $f_i$ inside the bracket. Let's correct this.
The expression is $\sum (f_{i}x_{i} - \overline{x})$. We can write this as:
$\sum (f_{i}x_{i} - f_{i}\overline{x} + f_{i}\overline{x} - \overline{x})$
Let's go back to $\sum (f_{i}x_{i} - \overline{x})$. We can split the sum only if $\overline{x}$ is multiplied by $f_i$. The correct way to distribute is:
$\sum (f_{i}x_{i} - \overline{x}) = \sum (f_{i}x_{i}) - \sum (\overline{x})$
This is also not correct. The $\overline{x}$ is not multiplied by $f_i$ inside the bracket $\sum (f_i x_i - \overline{x})$.
Let's rethink the expression. It should be $\sum f_i (x_i - \overline{x})$ for the property $\sum f_i d_i = 0$. However, the question asks for $\sum (f_i x_i - \overline{x})$. Let's assume there is a typo and it is $\sum (f_i x_i - f_i \overline{x})$ or $\sum f_i (x_i - \overline{x})$. Based on the options and common statistical properties, the sum of deviations from the mean, weighted by frequency, is zero.
Let's evaluate the given expression $\sum (f_{i}x_{i} - \overline{x})$. This expression seems unusual. Let's assume the expression is $\sum f_i (x_i - \overline{x})$.
$\sum f_i (x_i - \overline{x}) = \sum (f_i x_i - f_i \overline{x})$
$= \sum f_i x_i - \sum f_i \overline{x}$
Since $\overline{x}$ is a constant with respect to the summation index $i$, we can factor it out from the second term:
$= \sum f_i x_i - \overline{x} \sum f_i$
We know that $\overline{x} = \frac{\sum f_i x_i}{\sum f_i}$, which implies $\sum f_i x_i = \overline{x} \sum f_i$.
Substituting this into the expression:
$= (\overline{x} \sum f_i) - \overline{x} \sum f_i$
$= 0$
If the question is strictly asking for $\sum (f_{i}x_{i} - \overline{x})$, then:
$\sum (f_{i}x_{i} - \overline{x}) = \sum f_{i}x_{i} - \sum \overline{x}$
The summation $\sum \overline{x}$ depends on the number of terms being summed. If the summation is over the different classes (indexed by $i$), and there are $n$ such classes, then $\sum \overline{x} = n \overline{x}$.
So, $\sum (f_{i}x_{i} - \overline{x}) = \sum f_{i}x_{i} - n \overline{x}$.
We know $\sum f_{i}x_{i} = \overline{x} \sum f_{i}$. Let $N = \sum f_i$ (total frequency).
So, $\sum (f_{i}x_{i} - \overline{x}) = \overline{x} N - n \overline{x} = \overline{x} (N - n)$.
This value is generally not 0 unless $N=n$ or $\overline{x}=0$. $N$ is the total frequency (sum of frequencies), and $n$ is the number of classes. $N$ is usually much larger than $n$.
Given the options (0, -1, 1, 2) and the standard statistical properties, it is highly probable that the question intends to ask for $\sum f_i (x_i - \overline{x})$ or $\sum (f_i x_i - f_i \overline{x})$, which is always 0.
Assuming the standard property related to the mean (sum of weighted deviations from the mean is zero), the intended expression was likely $\sum f_i (x_i - \overline{x})$. Under this assumption, the value is 0.
Question 4. In the formula $\overline{x} = a + h\frac{\sum f_{i}u_{i}}{\sum f_{i}}$ , for finding the mean of grouped frequency distribution, ui =
(A) $\frac{x_{i} \;+\; a}{h}$
(B) $h(x_i - a)$
(C) $\frac{x_{i} \;-\; a}{h}$
(D) $\frac{a \;-\; x_{i}}{h}$
Answer:
The correct option is (C).
The formula given, $\overline{x} = a + h\frac{\sum f_{i}u_{i}}{\sum f_{i}}$, is the formula for finding the mean of grouped frequency distribution using the step-deviation method.
In this method:
- $\overline{x}$ is the mean.
- $a$ is the assumed mean, which is usually taken from the class marks ($x_i$).
- $h$ is the class size (assuming uniform class size).
- $f_i$ is the frequency of the $i$-th class.
- $x_i$ is the class mark (midpoint) of the $i$-th class.
- $u_i$ is the step deviation for the $i$-th class.
The step deviation $u_i$ is obtained by dividing the deviation of the class mark from the assumed mean by the class size $h$. The deviation of the class mark from the assumed mean is $d_i = x_i - a$.
So, the definition of $u_i$ is:
$u_i = \frac{x_i - a}{h}$
Question 5. The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its
(A) mean
(B) median
(C) mode
(D) all the three above
Answer:
The correct option is (B).
The graph of a cumulative frequency distribution is called an ogive.
There are two types of cumulative frequency ogives: the less than ogive and the more than ogive.
When both the less than type and the more than type cumulative frequency curves are drawn on the same graph, their point of intersection is significant.
The abscissa (x-coordinate) of this point of intersection represents the median of the grouped data.
The ordinate (y-coordinate) of this point represents half of the total frequency, i.e., $\frac{\sum f_i}{2}$.
Question 6. For the following distribution
| Class | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 |
|---|---|---|---|---|---|
| Frequency | 10 | 15 | 12 | 20 | 9 |
the sum of lower limits of the median class and modal class is
(A) 15
(B) 25
(C) 30
(D) 35
Answer:
The correct option is (B).
To find the sum of the lower limits of the median class and the modal class, we need to identify these classes from the given frequency distribution.
Finding the Modal Class:
The modal class is the class interval with the highest frequency.
Looking at the frequencies (10, 15, 12, 20, 9), the highest frequency is 20.
The class interval corresponding to the highest frequency (20) is 15-20.
Thus, the modal class is 15-20.
The lower limit of the modal class is 15.
Finding the Median Class:
The median class is the class interval where the cumulative frequency is greater than or equal to $\frac{N}{2}$, where $N$ is the total frequency.
Total frequency $N = 10 + 15 + 12 + 20 + 9 = 66$.
So, $\frac{N}{2} = \frac{66}{2} = 33$.
Now, let's construct the cumulative frequency table:
| Class | Frequency (f) | Cumulative Frequency (cf) |
| 0-5 | 10 | 10 |
| 5-10 | 15 | $10 + 15 = 25$ |
| 10-15 | 12 | $25 + 12 = 37$ |
| 15-20 | 20 | $37 + 20 = 57$ |
| 20-25 | 9 | $57 + 9 = 66$ |
We are looking for the class where the cumulative frequency is 33 or more. The first cumulative frequency that is greater than or equal to 33 is 37, which corresponds to the class interval 10-15.
Thus, the median class is 10-15.
The lower limit of the median class is 10.
Calculating the Sum:
Sum of the lower limits of the median class and modal class = Lower limit of median class + Lower limit of modal class
Sum = $10 + 15 = 25$
Question 7. Consider the following frequency distribution :
| Class | 0 - 5 | 6 - 11 | 12 - 17 | 18 - 23 | 24 - 29 |
|---|---|---|---|---|---|
| Frequency | 13 | 10 | 15 | 8 | 11 |
The upper limit of the median class is
(A) 17
(B) 17.5
(C) 18
(D) 18.5
Answer:
The correct option is (B).
The given class intervals are discontinuous (e.g., 0-5, 6-11). To find the median, we need to convert them into continuous class intervals.
We do this by finding the difference between the upper limit of a class and the lower limit of the next class, dividing by 2, and then subtracting this value from the lower limits and adding it to the upper limits.
The difference between the upper limit of the first class and the lower limit of the second class is $6 - 5 = 1$.
Half of this difference is $\frac{1}{2} = 0.5$.
Now, we form the continuous class intervals and find the cumulative frequencies:
| Continuous Class | Frequency (f) | Cumulative Frequency (cf) |
| $0 - 0.5$ to $5 + 0.5$ i.e., 0.5 - 5.5 | 13 | 13 |
| $6 - 0.5$ to $11 + 0.5$ i.e., 5.5 - 11.5 | 10 | $13 + 10 = 23$ |
| $12 - 0.5$ to $17 + 0.5$ i.e., 11.5 - 17.5 | 15 | $23 + 15 = 38$ |
| $18 - 0.5$ to $23 + 0.5$ i.e., 17.5 - 23.5 | 8 | $38 + 8 = 46$ |
| $24 - 0.5$ to $29 + 0.5$ i.e., 23.5 - 29.5 | 11 | $46 + 11 = 57$ |
The total frequency is $N = \sum f_i = 57$.
For the median class, we need to find the class interval containing the $\left(\frac{N}{2}\right)^{\text{th}}$ observation.
$\frac{N}{2} = \frac{57}{2} = 28.5$
We look for the cumulative frequency that is just greater than or equal to 28.5.
From the cumulative frequency column, 38 is the first value greater than 28.5.
The class interval corresponding to the cumulative frequency 38 is 11.5 - 17.5.
This is the median class.
The upper limit of the median class (11.5 - 17.5) is 17.5.
Question 8. For the following distribution :
| Marks | Number of students |
|---|---|
| Below 10 | 3 |
| Below 20 | 12 |
| Below 30 | 27 |
| Below 40 | 57 |
| Below 50 | 75 |
| Below 60 | 80 |
the modal class is
(A) 10-20
(B) 20-30
(C) 30-40
(D) 50-60
Answer:
The correct option is (C).
The given distribution is a "less than" cumulative frequency distribution. To find the modal class, we need to convert this into a simple frequency distribution.
Let's create the frequency distribution table:
| Marks | Number of students (Cumulative Frequency) | Class Interval | Frequency (f) |
| Below 10 | 3 | 0-10 | 3 |
| Below 20 | 12 | 10-20 | $12 - 3 = 9$ |
| Below 30 | 27 | 20-30 | $27 - 12 = 15$ |
| Below 40 | 57 | 30-40 | $57 - 27 = 30$ |
| Below 50 | 75 | 40-50 | $75 - 57 = 18$ |
| Below 60 | 80 | 50-60 | $80 - 75 = 5$ |
The modal class is the class interval with the highest frequency.
Looking at the frequencies (3, 9, 15, 30, 18, 5), the highest frequency is 30.
The class interval corresponding to the frequency 30 is 30-40.
Therefore, the modal class is 30-40.
Question 9. Consider the data :
| Class | 65 - 85 | 85 - 105 | 105 - 125 | 125 - 145 | 145 -165 | 165 -185 | 185 - 205 |
|---|---|---|---|---|---|---|---|
| Frequency | 4 | 5 | 13 | 20 | 14 | 7 | 4 |
The difference of the upper limit of the median class and the lower limit of the modal class is
(A) 0
(B) 19
(C) 20
(D) 38
Answer:
The correct option is (C).
To find the difference of the upper limit of the median class and the lower limit of the modal class, we need to identify these classes from the given frequency distribution.
Finding the Modal Class:
The modal class is the class interval with the highest frequency.
Looking at the frequencies (4, 5, 13, 20, 14, 7, 4), the highest frequency is 20.
The class interval corresponding to the highest frequency (20) is 125-145.
Thus, the modal class is 125-145.
The lower limit of the modal class is 125.
Finding the Median Class:
The median class is the class interval where the cumulative frequency is greater than or equal to $\frac{N}{2}$, where $N$ is the total frequency.
Total frequency $N = 4 + 5 + 13 + 20 + 14 + 7 + 4 = 67$.
So, $\frac{N}{2} = \frac{67}{2} = 33.5$.
Now, let's construct the cumulative frequency table:
| Class | Frequency (f) | Cumulative Frequency (cf) |
| 65-85 | 4 | 4 |
| 85-105 | 5 | $4 + 5 = 9$ |
| 105-125 | 13 | $9 + 13 = 22$ |
| 125-145 | 20 | $22 + 20 = 42$ |
| 145-165 | 14 | $42 + 14 = 56$ |
| 165-185 | 7 | $56 + 7 = 63$ |
| 185-205 | 4 | $63 + 4 = 67$ |
We are looking for the class where the cumulative frequency is 33.5 or more. The first cumulative frequency that is greater than or equal to 33.5 is 42, which corresponds to the class interval 125-145.
Thus, the median class is 125-145.
The upper limit of the median class is 145.
Calculating the Difference:
Difference = Upper limit of median class - Lower limit of modal class
Difference = $145 - 125 = 20$
Question 10. The times, in seconds, taken by 150 atheletes to run a 110 m hurdle race are tabulated below
| Class | 13.8 - 14 | 14 - 14.2 | 14.2 - 14.4 | 14.4 - 14.6 | 14.6 - 14.8 | 14.8 - 15 |
|---|---|---|---|---|---|---|
| Frequency | 2 | 4 | 5 | 71 | 48 | 20 |
The number of atheletes who completed the race in less then 14.6 seconds is :
(A) 11
(B) 71
(C) 82
(D) 130
Answer:
The correct option is (C).
We need to find the number of athletes who completed the race in less than 14.6 seconds.
This corresponds to the sum of frequencies for all class intervals whose upper limit is less than or equal to 14.6 seconds.
From the given table, the class intervals with upper limit less than or equal to 14.6 are:
- 13.8 - 14 (Frequency: 2)
- 14 - 14.2 (Frequency: 4)
- 14.2 - 14.4 (Frequency: 5)
- 14.4 - 14.6 (Frequency: 71)
Note that since the classes are continuous, 'less than 14.6' includes all athletes in the 14.4-14.6 class.
The number of athletes who completed the race in less than 14.6 seconds is the sum of the frequencies of these classes:
Number of athletes = Frequency(13.8-14) + Frequency(14-14.2) + Frequency(14.2-14.4) + Frequency(14.4-14.6)
Number of athletes = $2 + 4 + 5 + 71$
Number of athletes = $6 + 5 + 71$
Number of athletes = $11 + 71$
Number of athletes = $82$
Question 11. Consider the following distribution :
| Marks obtained | Number of students |
|---|---|
| More than or equal to 0 | 63 |
| More than or equal to 10 | 58 |
| More than or equal to 20 | 55 |
| More than or equal to 30 | 51 |
| More than or equal to 40 | 48 |
| More than or equal to 50 | 42 |
the frequency of the class 30-40 is
(A) 3
(B) 4
(C) 48
(D) 51
Answer:
The correct option is (A).
The given distribution is a "more than or equal to" cumulative frequency distribution. To find the frequency of a specific class interval, we use the provided cumulative frequencies.
The frequency of the class 30-40 represents the number of students who scored marks greater than or equal to 30 but less than 40.
From the table:
- Number of students with marks more than or equal to 30 = 51
- Number of students with marks more than or equal to 40 = 48
The number of students in the class interval 30-40 is the difference between the number of students who scored more than or equal to 30 and the number of students who scored more than or equal to 40.
Frequency of class 30-40 = (Number of students with marks $\geq 30$) - (Number of students with marks $\geq 40$)
Frequency = $51 - 48 = 3$
Question 12. If an event cannot occur, then its probability is
(A) 1
(B) $\frac{3}{4}$
(C) $\frac{1}{2}$
(D) 0
Answer:
The correct option is (D).
An event that cannot occur is called an impossible event.
The probability of an impossible event is 0.
The probability of any event E must satisfy $0 \leq P(E) \leq 1$.
A probability of 1 indicates a certain event (an event that is sure to occur).
Values between 0 and 1 represent events that are possible but not certain.
Question 13. Which of the following cannot be the probability of an event?
(A) $\frac{1}{3}$
(B) 0.1
(C) 3%
(D) $\frac{17}{16}$
Answer:
The correct option is (D).
The probability of any event E, denoted by $P(E)$, must satisfy the condition $0 \leq P(E) \leq 1$. This means the probability of an event must be a value between 0 and 1, inclusive.
Let's examine each option:
(A) $\frac{1}{3}$: This is a fraction where the numerator (1) is less than the denominator (3), and both are positive. So, $0 < \frac{1}{3} < 1$. This can be a probability.
(B) 0.1: This is a decimal number between 0 and 1 ($0 < 0.1 < 1$). This can be a probability.
(C) 3%: This is a percentage probability. To convert to a decimal or fraction, we divide by 100: $3\% = \frac{3}{100} = 0.03$. This value is between 0 and 1 ($0 < 0.03 < 1$). This can be a probability.
(D) $\frac{17}{16}$: This is a fraction where the numerator (17) is greater than the denominator (16). This means the value is greater than 1: $\frac{17}{16} = 1.0625$. Since this value is greater than 1, it cannot be the probability of an event.
Therefore, the only option that cannot be the probability of an event is $\frac{17}{16}$.
Question 14. An event is very unlikely to happen. Its probability is closest to
(A) 0.0001
(B) 0.001
(C) 0.01
(D) 0.1
Answer:
The correct option is (A).
The probability of an event indicates how likely it is to occur. A probability value ranges from 0 to 1.
- A probability of 0 means the event is impossible.
- A probability of 1 means the event is certain.
- Probabilities between 0 and 1 represent events that are possible but not certain.
An event that is "very unlikely to happen" has a probability that is very close to 0.
Let's compare the given options:
- (A) 0.0001
- (B) 0.001
- (C) 0.01
- (D) 0.1
We want to find the value that is closest to 0 among these options.
Comparing the values, $0.0001 < 0.001 < 0.01 < 0.1$.
The smallest positive value is the closest to 0.
Therefore, 0.0001 is the probability value closest to 0 among the given options.
Question 15. If the probability of an event is p, the probability of its complementary event will be
(A) p – 1
(B) p
(C) 1 – p
(D) 1 - $\frac{1}{p}$
Answer:
The correct option is (C).
Let E be an event and E' be its complementary event. The complementary event E' is the event that E does not occur.
The sum of the probability of an event and the probability of its complementary event is always equal to 1.
This relationship is expressed as:
$P(E) + P(E') = 1$
We are given that the probability of the event is $p$, so $P(E) = p$.
Substituting this into the formula:
$p + P(E') = 1$
To find the probability of the complementary event $P(E')$, we subtract $p$ from both sides of the equation:
$P(E') = 1 - p$
Therefore, the probability of its complementary event will be $1 - p$.
Question 16. The probability expressed as a percentage of a particular occurrence can never be
(A) less than 100
(B) less than 0
(C) greater than 1
(D) anything but a whole number
Answer:
The correct option is (B).
The probability of any event must be a value between 0 and 1, inclusive. That is, if P is the probability of an event, then $0 \leq P \leq 1$.
When the probability is expressed as a percentage, it is obtained by multiplying the probability value by 100. So, the percentage probability is $P \times 100\%$.
Since $0 \leq P \leq 1$, the probability expressed as a percentage must be between $0 \times 100\% = 0\%$ and $1 \times 100\% = 100\%$.
Thus, the probability expressed as a percentage must be in the range $[0\%, 100\%]$.
Let's examine the given options in light of this range:
(A) less than 100: A percentage probability can be less than 100% (e.g., 50%). So, this is possible.
(B) less than 0: A percentage probability cannot be less than 0% because the probability value cannot be negative. So, this is impossible.
(C) greater than 1: A percentage probability can be greater than 1 (e.g., 50% is numerically 50, which is greater than 1). So, this is possible.
(D) anything but a whole number: A percentage probability can be a non-whole number (e.g., 33.3% or 12.5%). So, it is possible for it to be something other than a whole number. The phrasing is awkward, but it does not describe an impossibility.
Therefore, the probability expressed as a percentage of a particular occurrence can never be less than 0.
Question 17. If P(A) denotes the probability of an event A, then
(A) P(A) < 0
(B) P(A) > 1
(C) 0 ≤ P(A) ≤ 1
(D) –1 ≤ P(A) ≤ 1
Answer:
The correct option is (C).
The probability of any event A, denoted by $P(A)$, is a measure of the likelihood of the event occurring.
By definition, the probability of any event must lie between 0 and 1, inclusive.
This fundamental property can be stated as:
$0 \leq P(A) \leq 1$
This means that the probability of an event can be:
- 0, if the event is impossible.
- 1, if the event is certain to occur.
- Any value between 0 and 1, if the event is possible but not certain.
Let's look at the options:
- (A) $P(A) < 0$: Probability cannot be negative.
- (B) $P(A) > 1$: Probability cannot be greater than 1.
- (C) $0 \leq P(A) \leq 1$: This correctly states that the probability is between 0 and 1, inclusive.
- (D) $-1 \leq P(A) \leq 1$: Probability cannot be negative, so the lower bound must be 0, not -1.
Therefore, the correct range for the probability of an event A is $0 \leq P(A) \leq 1$.
Question 18. A card is selected from a deck of 52 cards. The probability of its being a red face card is
(A) $\frac{3}{26}$
(B) $\frac{3}{13}$
(C) $\frac{2}{13}$
(D) $\frac{1}{2}$
Answer:
The correct option is (A).
In a standard deck of 52 playing cards, there are 4 suits: Hearts, Diamonds, Clubs, and Spades.
Each suit has 13 cards.
The deck is divided into two colours: Red (Hearts and Diamonds) and Black (Clubs and Spades).
Number of red suits = 2 (Hearts, Diamonds)
Number of black suits = 2 (Clubs, Spades)
The face cards in each suit are Jack, Queen, and King.
Number of face cards per suit = 3.
We are interested in red face cards. Red suits are Hearts and Diamonds.
Number of red face cards = (Number of face cards in Hearts) + (Number of face cards in Diamonds)
Number of red face cards = 3 (Jack, Queen, King of Hearts) + 3 (Jack, Queen, King of Diamonds)
Number of red face cards = $3 + 3 = 6$.
The total number of possible outcomes when selecting a card at random is the total number of cards in the deck, which is 52.
The number of favourable outcomes (selecting a red face card) is 6.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of being a red face card = $\frac{\text{Number of red face cards}}{\text{Total number of cards}}$
Probability = $\frac{6}{52}$
Simplify the fraction:
$\frac{6}{52} = \frac{\cancel{6}^{3}}{\cancel{52}_{26}}$
Probability = $\frac{3}{26}$
Question 19. The probability that a non leap year selected at random will contain 53 sundays is
(A) $\frac{1}{7}$
(B) $\frac{2}{7}$
(C) $\frac{3}{7}$
(D) $\frac{5}{7}$
Answer:
The correct option is (A).
Solution:
A non-leap year has 365 days.
There are 7 days in a week.
To find the number of full weeks and the remaining days in a non-leap year, we divide the total number of days by 7:
$365 \div 7 = 52$ weeks and $1$ day remainder
This means a non-leap year contains exactly 52 full weeks and one extra day.
The 52 full weeks will always contain 52 Sundays.
For the non-leap year to contain 53 Sundays, the extra day must be a Sunday.
The extra day can be any one of the 7 days of the week: Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, or Saturday.
Total number of possible outcomes for the extra day = 7.
The favourable outcome (the extra day being a Sunday) has only 1 possibility.
The probability of an event is given by the formula:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability that the extra day is a Sunday = $\frac{\text{Number of ways the extra day is Sunday}}{\text{Total number of possible days for the extra day}}$
Probability = $\frac{1}{7}$
Thus, the probability that a non-leap year selected at random will contain 53 Sundays is $\frac{1}{7}$.
Question 20. When a die is thrown, the probability of getting an odd number less than 3 is
(A) $\frac{1}{6}$
(B) $\frac{1}{3}$
(C) $\frac{1}{2}$
(D) 0
Answer:
The correct option is (A).
When a standard six-sided die is thrown, the possible outcomes are the integers from 1 to 6.
The sample space (S) is $\{1, 2, 3, 4, 5, 6\}$.
The total number of possible outcomes is $n(S) = 6$.
We are interested in the event E of getting an odd number less than 3.
The odd numbers in the sample space are $\{1, 3, 5\}$.
The numbers in the sample space that are less than 3 are $\{1, 2\}$.
We need numbers that are both odd AND less than 3.
The numbers satisfying both conditions is the set $\{1\}$.
The number of favourable outcomes is $n(E) = 1$.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of getting an odd number less than 3 = $\frac{n(E)}{n(S)}$
$P(\text{odd number less than 3}) = \frac{1}{6}$
Question 21. A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is
(A) 4
(B) 13
(C) 48
(D) 51
Answer:
The correct option is (D).
The total number of cards in a well-shuffled deck is 52.
So, the total number of possible outcomes when a card is drawn is 52.
The event E is that the card drawn is not an ace of hearts.
This means that the outcomes favourable to E are all the cards in the deck except the ace of hearts.
There is only one ace of hearts in a deck of 52 cards.
Number of outcomes favourable to E = (Total number of cards) - (Number of aces of hearts)
Number of outcomes favourable to E = $52 - 1 = 51$
Question 22. The probability of getting a bad egg in a lot of 400 is 0.035. The number of bad eggs in the lot is
(A) 7
(B) 14
(C) 21
(D) 28
Answer:
The correct option is (B).
We are given the total number of eggs in a lot and the probability of selecting a bad egg.
Total number of eggs in the lot = 400
Probability of getting a bad egg = 0.035
The probability of an event is defined as:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
In this case, the event is getting a bad egg.
Number of favourable outcomes = Number of bad eggs
Total number of possible outcomes = Total number of eggs in the lot
So, we have:
$0.035 = \frac{\text{Number of bad eggs}}{400}$
To find the number of bad eggs, we can rearrange the equation:
$\text{Number of bad eggs} = 0.035 \times 400$
Calculate the product:
$0.035 \times 400 = \frac{35}{1000} \times 400 = \frac{35 \times 400}{1000} = \frac{35 \times \cancel{400}^{4}}{\cancel{1000}_{10}}$
$= \frac{35 \times 4}{10} = \frac{140}{10} = 14$
The number of bad eggs in the lot is 14.
Question 23. A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets has she bought?
(A) 40
(B) 240
(C) 480
(D) 750
Answer:
The correct option is (C).
Given:
Probability of winning the first prize = 0.08
Total number of lottery tickets sold = 6000
To Find:
The number of tickets the girl bought.
Solution:
The probability of an event is calculated as:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
In this case:
The event is the girl winning the first prize.
The number of favourable outcomes is the number of tickets the girl bought (assuming each ticket has an equal chance of winning).
The total number of possible outcomes is the total number of tickets sold.
Let $N$ be the number of tickets the girl bought.
We can write the equation:
$0.08 = \frac{N}{6000}$
To find $N$, we multiply both sides of the equation by 6000:
$N = 0.08 \times 6000$
Calculate the product:
$N = \frac{8}{100} \times 6000$
$N = 8 \times \frac{\cancel{6000}^{60}}{\cancel{100}_{1}}$
$N = 8 \times 60$
$N = 480$
The number of tickets she has bought is 480.
Question 24. One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 5 is
(A) $\frac{1}{5}$
(B) $\frac{3}{5}$
(C) $\frac{4}{5}$
(D) $\frac{1}{3}$
Answer:
The correct option is (A).
The tickets are numbered from 1 to 40. The total number of possible outcomes when drawing one ticket at random is the total number of tickets.
Total number of possible outcomes = 40.
We are interested in the event that the selected ticket has a number which is a multiple of 5.
The multiples of 5 between 1 and 40 are: 5, 10, 15, 20, 25, 30, 35, 40.
The set of favourable outcomes is $\{5, 10, 15, 20, 25, 30, 35, 40\}$.
The number of favourable outcomes is the count of these numbers, which is 8.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of getting a multiple of 5 = $\frac{\text{Number of multiples of 5 between 1 and 40}}{\text{Total number of tickets}}$
Probability = $\frac{8}{40}$
Simplify the fraction:
$\frac{8}{40} = \frac{\cancel{8}^{1}}{\cancel{40}_{5}}$
Probability = $\frac{1}{5}$
Question 25. Someone is asked to take a number from 1 to 100. The probability that it is a prime is
(A) $\frac{1}{5}$
(B) $\frac{6}{25}$
(C) $\frac{1}{4}$
(D) $\frac{13}{50}$
Answer:
The correct option is (C).
We are selecting a number from 1 to 100 at random.
The total number of possible outcomes is the total number of integers from 1 to 100.
Total number of possible outcomes = 100.
We are interested in the event that the selected number is a prime number.
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Let's list the prime numbers between 1 and 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
The number of favourable outcomes is the count of these prime numbers.
Number of favourable outcomes = 25.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of selecting a prime number = $\frac{\text{Number of prime numbers between 1 and 100}}{\text{Total number of integers between 1 and 100}}$
Probability = $\frac{25}{100}$
Simplify the fraction:
$\frac{25}{100} = \frac{\cancel{25}^{1}}{\cancel{100}_{4}}$
Probability = $\frac{1}{4}$
Question 26. A school has five houses A, B, C, D and E. A class has 23 students, 4 from house A, 8 from house B, 5 from house C, 2 from house D and rest from house E. A single student is selected at random to be the class monitor. The probability that the selected student is not from A, B and C is
(A) $\frac{4}{23}$
(B) $\frac{6}{23}$
(C) $\frac{8}{23}$
(D) $\frac{17}{23}$
Answer:
The correct option is (B).
Given:
Total number of students in the class = 23.
Number of students from House A = 4
Number of students from House B = 8
Number of students from House C = 5
Number of students from House D = 2
Number of students from House E = rest
To Find:
The probability that the selected student is not from A, B and C.
Solution:
First, let's find the number of students from House E.
Total number of students = (Students from A) + (Students from B) + (Students from C) + (Students from D) + (Students from E)
$23 = 4 + 8 + 5 + 2 + \text{(Students from E)}$
$23 = 12 + 5 + 2 + \text{(Students from E)}$
$23 = 17 + 2 + \text{(Students from E)}$
$23 = 19 + \text{(Students from E)}$
Number of students from House E = $23 - 19 = 4$.
The event of interest is that the selected student is not from houses A, B, and C.
This means the selected student must be from either House D or House E.
Number of favourable outcomes = (Number of students from D) + (Number of students from E)
Number of favourable outcomes = $2 + 4 = 6$.
The total number of possible outcomes is the total number of students in the class, which is 23.
The probability of an event is given by the formula:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability that the selected student is not from A, B and C = $\frac{\text{Number of students from D or E}}{\text{Total number of students}}$
Probability = $\frac{6}{23}$
The fraction $\frac{6}{23}$ cannot be simplified further as 23 is a prime number and 6 is not a multiple of 23.
Sample Question 1 to 3 (Before Exercise 13.2)
Sample Question 1: The mean of ungrouped data and the mean calculated when the same data is grouped are always the same. Do you agree with this statement? Give reason for your answer.
Answer:
No, I do not agree with the statement that the mean of ungrouped data and the mean calculated when the same data is grouped are always the same.
Reason:
When calculating the mean for ungrouped data, the actual values of each observation are used in the calculation. The formula for the mean of ungrouped data is:
$\overline{x} = \frac{\sum x_i}{n}$
where $x_i$ are the individual data values and $n$ is the total number of observations.
When calculating the mean for grouped data, the actual values of the observations within each class interval are not used. Instead, we assume that the frequency of each class is concentrated at its class mark (midpoint).
The formula for the mean of grouped data is typically:
$\overline{x}_{\text{grouped}} = \frac{\sum f_i x_i}{\sum f_i}$
where $f_i$ is the frequency of the $i$-th class and $x_i$ is the class mark of the $i$-th class.
This assumption that all values within a class are equal to the class mark introduces an approximation. Unless all observations within each class interval happen to be exactly equal to the class mark, the mean calculated from grouped data will generally be slightly different from the true mean of the original ungrouped data.
Therefore, the mean of ungrouped data and the mean calculated from the same data after grouping are not always the same; the mean of grouped data is an approximation of the mean of the ungrouped data.
Sample Question 2: Is it correct to say that an ogive is a graphical representation of a frequency distribution? Give reason.
Answer:
No, it is not correct to say that an ogive is a graphical representation of a frequency distribution.
Reason:
A frequency distribution shows how often each value or range of values occurs in a dataset. It typically involves listing class intervals and their corresponding frequencies.
A cumulative frequency distribution, on the other hand, shows the running total of frequencies up to the upper boundary of each class interval. It indicates the number or proportion of observations that fall below (for 'less than' type) or above (for 'more than' type) a particular value.
An ogive is a graphical representation of a cumulative frequency distribution, not a simple frequency distribution.
There are two types of ogives:
- 'Less than' ogive: It plots the upper class boundaries on the x-axis and the corresponding cumulative frequencies on the y-axis.
- 'More than' ogive: It plots the lower class boundaries on the x-axis and the corresponding cumulative frequencies on the y-axis.
While a frequency distribution is the data used to construct an ogive, the ogive itself visually represents the cumulative frequencies.
Sample Question 3: In any situation that has only two possible outcomes, each outcome will have probability $\frac{1}{2}$ . True or false? Why?
Answer:
False.
Reason:
The statement is incorrect because having only two possible outcomes does not guarantee that each outcome is equally likely.
For the probability of each of the two outcomes to be $\frac{1}{2}$, the outcomes must be equally likely or equiprobable.
For example, when flipping a fair coin, there are two outcomes (Heads and Tails), and each has a probability of $\frac{1}{2}$ because they are equally likely.
However, consider a situation where a biased coin is flipped, or drawing a ball from a bag containing 1 red ball and 9 blue balls. There are only two outcomes (drawing a red ball or drawing a blue ball), but they are not equally likely. The probability of drawing a red ball is $\frac{1}{10}$ and the probability of drawing a blue ball is $\frac{9}{10}$. In this case, the probabilities are not $\frac{1}{2}$ for each outcome.
Exercise 13.2
Question 1. The median of an ungrouped data and the median calculated when the same data is grouped are always the same. Do you think that this is a correct statement? Give reason.
Answer:
No, I do not think that this is a correct statement.
Reason:
When calculating the median of ungrouped data, we arrange the data in ascending or descending order and find the middle value (or the average of the two middle values if the number of observations is even). This calculation uses the exact values of the data points.
When calculating the median of grouped data, we use a formula:
$\text{Median} = L + \frac{\left(\frac{N}{2} - CF\right)}{f} \times h$
where $L$ is the lower limit of the median class, $N$ is the total frequency, $CF$ is the cumulative frequency of the class preceding the median class, $f$ is the frequency of the median class, and $h$ is the class size.
This formula for grouped data provides an approximate value for the median. It assumes that the observations within the median class are uniformly distributed, which is generally not the case in real-world data.
Because the grouped median relies on this approximation (using the class mark or assuming uniform distribution within the median class), it will often differ from the exact median calculated from the original ungrouped data.
Therefore, the median calculated from grouped data is an estimate and is not always the same as the true median of the ungrouped data.
Question 2. In calculating the mean of grouped data, grouped in classes of equal width, we may use the formula
$\overline{x} = a + \frac{\sum f_{i}d_{i}}{\sum f_{i}}$
where a is the assumed mean. a must be one of the mid-points of the classes. Is the last statement correct? Justify your answer.
Answer:
No, the last statement is not correct.
Reason:
In the formula for the mean of grouped data using the assumed mean method:
$\overline{x} = a + \frac{\sum f_{i}d_{i}}{\sum f_{i}}$
where $a$ is the assumed mean, $f_i$ is the frequency of the $i$-th class, and $d_i = x_i - a$ is the deviation of the class mark ($x_i$) of the $i$-th class from the assumed mean $a$.
The value chosen for the assumed mean ($a$) does not necessarily have to be one of the mid-points of the classes. While choosing a midpoint, especially the midpoint of a class near the centre of the distribution, is a common and convenient practice because it simplifies calculations by keeping the values of $d_i$ relatively small, it is not a mathematical requirement for the formula to be valid.
The formula is derived from the direct method $\overline{x} = \frac{\sum f_{i}x_{i}}{\sum f_{i}}$ by substituting $x_i = a + d_i$. This algebraic substitution is valid for any constant value of $a$.
$\overline{x} = \frac{\sum f_{i}(a + d_i)}{\sum f_{i}} = \frac{\sum f_{i}a + \sum f_{i}d_i}{\sum f_{i}} = \frac{a \sum f_{i}}{\sum f_{i}} + \frac{\sum f_{i}d_i}{\sum f_{i}} = a + \frac{\sum f_{i}d_i}{\sum f_{i}}$
This derivation holds true for any arbitrary constant $a$.
Therefore, while choosing a midpoint for $a$ is a practical choice for ease of calculation, it is not a necessary condition for the formula itself.
Question 3. Is it true to say that the mean, mode and median of grouped data will always be different? Justify your answer.
Answer:
No, it is not true to say that the mean, mode and median of grouped data will always be different.
Reason:
The relationship between the mean, median, and mode depends on the shape or skewness of the distribution of the data.
- For a symmetrical distribution (like a normal distribution), the mean, median, and mode are ideally equal. While grouping introduces approximations, it is possible for the calculated values of the mean, median, and mode from grouped data to be equal or very close if the underlying distribution is symmetrical and the grouping is appropriate.
- For a skewed distribution (either positively or negatively skewed), the mean, median, and mode are generally different.
For example, for a moderately skewed distribution, there is an empirical relationship:
Mode $\approx$ 3 Median $-$ 2 Mean
This shows that they are related, and for skewed distributions, they will typically have different values.
However, the statement claims they will always be different, which is false because in cases of symmetry (even when grouped, allowing for the approximations), they can be the same or very close.
Question 4. Will the median class and modal class of grouped data always be different? Justify your answer.
Answer:
No, the median class and modal class of grouped data will not always be different.
Reason:
The modal class is defined as the class interval with the highest frequency.
The median class is defined as the class interval in which the $\left(\frac{N}{2}\right)^{\text{th}}$ observation (where $N$ is the total frequency) falls, determined by looking at the cumulative frequencies.
These two classes are determined by different criteria:
- Modal class depends solely on the maximum frequency.
- Median class depends on the position of the middle observation in the cumulative frequency distribution.
It is possible for the class interval that has the maximum frequency (modal class) to also be the class interval where the cumulative frequency crosses or reaches $\frac{N}{2}$ for the first time (median class).
Consider a dataset where the frequencies are highest in the middle classes, and the cumulative frequency up to the start of this middle class is less than $\frac{N}{2}$, but the cumulative frequency up to the end of this class is greater than or equal to $\frac{N}{2}$. In such a case, the median class will be the same as the modal class.
For example, in a perfectly symmetrical unimodal distribution, both the mode and the median coincide at the center, and thus their respective classes in grouped data are likely to be the same.
Question 5. In a family having three children, there may be no girl, one girl, two girls or three girls. So, the probability of each is $\frac{1}{4}$ . Is this correct? Justify your answer.
Answer:
False.
Reason:
The statement assumes that the four possible outcomes (no girl, one girl, two girls, three girls) are equally likely, which is not correct in this scenario.
Let's consider the possible gender combinations for three children, assuming each child's gender is independent and has an equal probability of being a Boy (B) or a Girl (G).
The sample space consists of all possible combinations of B and G for three children. The possible outcomes are:
BBB, BBG, BGB, GBB, BGG, GBG, GGB, GGG
There are $2^3 = 8$ possible outcomes in the sample space.
Now, let's find the number of outcomes favourable to each event mentioned:
- No girl: This corresponds to the outcome BBB. Number of outcomes = 1.
- One girl: This corresponds to the outcomes BBG, BGB, GBB. Number of outcomes = 3.
- Two girls: This corresponds to the outcomes BGG, GBG, GGB. Number of outcomes = 3.
- Three girls: This corresponds to the outcome GGG. Number of outcomes = 1.
The probability of an event is the ratio of the number of favourable outcomes to the total number of possible outcomes.
Probability (No girl) = $\frac{1}{8}$
Probability (One girl) = $\frac{3}{8}$
Probability (Two girls) = $\frac{3}{8}$
Probability (Three girls) = $\frac{1}{8}$
Since the probabilities of the events "no girl", "one girl", "two girls", and "three girls" are $\frac{1}{8}$, $\frac{3}{8}$, $\frac{3}{8}$, and $\frac{1}{8}$ respectively, and not all equal to $\frac{1}{4}$, the original statement is incorrect.
Question 6. A game consists of spinning an arrow which comes to rest pointing at one of the regions (1, 2 or 3) (Fig. 13.1). Are the outcomes 1, 2 and 3 equally likely to occur? Give reasons.
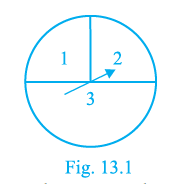
Answer:
No, the outcomes 1, 2 and 3 are not equally likely to occur.
Reason:
In a game of chance involving a spinner, the probability of the arrow coming to rest in a particular region is proportional to the area of that region (or the angle of the sector it covers) compared to the total area (or total angle) of the spinner.
From Figure 13.1 (which is not provided for viewing, but based on the context of this question in the NCERT Exemplar), the regions labelled 1, 2, and 3 occupy sectors of the circle that have unequal areas or angles at the centre. For the outcomes to be equally likely, each region must have the same area or cover the same angle.
Since the areas/angles corresponding to regions 1, 2, and 3 are not equal, the probability of the arrow pointing to each region is different.
For example, if Region 1 covers a larger area than Region 2, the probability of the arrow pointing to 1 will be greater than the probability of the arrow pointing to 2.
Question 7. Apoorv throws two dice once and computes the product of the numbers appearing on the dice. Peehu throws one die and squares the number that appears on it. Who has the better chance of getting the number 36? Why?
Answer:
Peehu has a better chance of getting the number 36.
Reason:
Let's analyse the possible outcomes and probabilities for both Apoorv and Peehu.
Apoorv's Experiment:
Apoorv throws two dice and computes the product of the numbers appearing on them.
When two dice are thrown, the total number of possible outcomes is $6 \times 6 = 36$. Each outcome is an ordered pair $(d_1, d_2)$, where $d_1$ is the number on the first die and $d_2$ is the number on the second die, and $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$.
The event of interest for Apoorv is getting a product of 36.
We need to find pairs $(d_1, d_2)$ from the sample space such that $d_1 \times d_2 = 36$. The possible integer values for $d_1$ and $d_2$ from 1 to 6 are only 6.
The only pair $(d_1, d_2)$ such that $d_1 \times d_2 = 36$ and $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$ is $(6, 6)$.
Number of favourable outcomes for Apoorv = 1 (the outcome (6, 6)).
Total number of possible outcomes for Apoorv = 36.
The probability of Apoorv getting 36 is:
$P(\text{Apoorv gets 36}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{1}{36}$
Peehu's Experiment:
Peehu throws one die and squares the number that appears on it.
When one die is thrown, the total number of possible outcomes is 6. The sample space is $\{1, 2, 3, 4, 5, 6\}$.
The event of interest for Peehu is getting a square of the number equal to 36.
We need to find a number $x$ from the sample space $\{1, 2, 3, 4, 5, 6\}$ such that $x^2 = 36$.
Solving $x^2 = 36$, we get $x = \sqrt{36} = \pm 6$. Since the number on a die must be positive, the only possible value is $x = 6$.
The only favourable outcome for Peehu is getting a 6 on the die.
Number of favourable outcomes for Peehu = 1 (the outcome 6).
Total number of possible outcomes for Peehu = 6.
The probability of Peehu getting 36 is:
$P(\text{Peehu gets 36}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{1}{6}$
Comparison:
Apoorv's probability of getting 36 is $\frac{1}{36}$.
Peehu's probability of getting 36 is $\frac{1}{6}$.
To compare $\frac{1}{36}$ and $\frac{1}{6}$, we can note that $\frac{1}{6} = \frac{6}{36}$.
Since $\frac{6}{36} > \frac{1}{36}$, Peehu's probability is greater than Apoorv's probability.
Therefore, Peehu has a better chance of getting the number 36.
Question 8. When we toss a coin, there are two possible outcomes - Head or Tail. Therefore, the probability of each outcome is $\frac{1}{2}$ . Justify your answer.
Answer:
The statement is correct, provided that the coin is a fair coin.
Justification:
When we toss a coin, the two possible outcomes are Head (H) and Tail (T).
The total number of possible outcomes is 2.
For the probability of each outcome to be $\frac{1}{2}$, the outcomes must be equally likely or equiprobable.
Equally likely outcomes are those that have the same chance of occurring.
In the case of a fair coin, there is no reason to expect one outcome (Head) to occur more or less often than the other outcome (Tail). The symmetry of a fair coin implies that both outcomes are equally likely.
Using the formula for probability when outcomes are equally likely:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
For the event of getting a Head, the number of favourable outcomes is 1 (Head).
$P(\text{Head}) = \frac{1}{2}$
For the event of getting a Tail, the number of favourable outcomes is 1 (Tail).
$P(\text{Tail}) = \frac{1}{2}$
Therefore, for a fair coin, the probability of each outcome (Head or Tail) is indeed $\frac{1}{2}$. However, if the coin were biased (not fair), the outcomes would not be equally likely, and their probabilities would not be $\frac{1}{2}$. The statement holds true specifically for a fair coin.
Question 9. A student says that if you throw a die, it will show up 1 or not 1. Therefore, the probability of getting 1 and the probability of getting ‘not 1’ each is equal to $\frac{1}{2}$ . Is this correct? Give reasons.
Answer:
No, the student's statement is not correct.
Reason:
When a standard six-sided die is thrown, there are six possible outcomes, which are the integers from 1 to 6: $\{1, 2, 3, 4, 5, 6\}$.
Assuming the die is fair, each of these six outcomes is equally likely to occur.
The probability of any single outcome (like getting a 1, 2, 3, 4, 5, or 6) is $\frac{1}{6}$.
The event "getting 1" consists of only one outcome: $\{1\}$.
The number of favourable outcomes for getting 1 is 1.
The probability of getting 1 is $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{1}{6}$.
The event "getting not 1" consists of all outcomes except 1: $\{2, 3, 4, 5, 6\}$.
The number of favourable outcomes for getting not 1 is 5.
The probability of getting not 1 is $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{5}{6}$.
Since the probability of getting 1 is $\frac{1}{6}$ and the probability of getting not 1 is $\frac{5}{6}$, neither is equal to $\frac{1}{2}$. The student's logic is flawed because it assumes that simply partitioning the sample space into two categories makes those categories equally likely, which is only true if the number of elementary outcomes within each category is the same.
Question 10. I toss three coins together. The possible outcomes are no heads, 1 head, 2 heads and 3 heads. So, I say that probability of no heads is $\frac{1}{4}$ . What is wrong with this conclusion?
Answer:
The conclusion that the probability of no heads is $\frac{1}{4}$ is wrong.
Reason:
When tossing three coins together, the possible outcomes are not just defined by the number of heads (0, 1, 2, or 3). To correctly determine probabilities, we need to consider all the individual outcomes for each coin toss, assuming the coins are fair and the tosses are independent.
The sample space of tossing three coins simultaneously consists of the following equally likely outcomes:
HHH, HHT, HTH, THH, HTT, THT, TTH, TTT
where H represents Head and T represents Tail. The order matters when listing these elementary outcomes.
The total number of possible outcomes is $2 \times 2 \times 2 = 8$. Each of these 8 outcomes is equally likely, with a probability of $\frac{1}{8}$ for each.
Now let's look at the event "no heads". This event occurs when all three coins are Tails.
The outcome corresponding to "no heads" is TTT.
There is only 1 outcome favourable to the event "no heads".
The probability of an event is calculated as:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of no heads = $\frac{\text{Number of outcomes with no heads}}{\text{Total number of possible outcomes}}$
$P(\text{no heads}) = \frac{1}{8}$
The student's mistake was assuming that the events categorized by the number of heads (0 heads, 1 head, 2 heads, 3 heads) are equally likely. These events are not equally likely because they contain different numbers of elementary outcomes from the sample space:
- 0 heads (TTT): 1 outcome
- 1 head (HTT, THT, TTH): 3 outcomes
- 2 heads (HHT, HTH, THH): 3 outcomes
- 3 heads (HHH): 1 outcome
The sum of these outcomes is $1 + 3 + 3 + 1 = 8$, which matches the total number of equally likely elementary outcomes.
Question 11. If you toss a coin 6 times and it comes down heads on each occasion. Can you say that the probability of getting a head is 1? Give reasons.
Answer:
No, you cannot say that the probability of getting a head is 1 based on tossing a coin 6 times and getting heads each time.
Reason:
Probability is a measure of the likelihood of an event occurring in the long run, or theoretically based on the nature of the experiment.
The observation of getting heads in 6 consecutive tosses is the result of a specific set of experiments (6 trials). The observed relative frequency of getting a head in these 6 trials is $\frac{6}{6} = 1$. However, this is an experimental probability based on a very small sample size.
The true probability of getting a head on a single toss of a fair coin is $\frac{1}{2}$. Even with a fair coin, it is possible, though unlikely, to get heads several times in a row.
According to the Law of Large Numbers, the experimental probability (relative frequency) tends to get closer to the theoretical probability as the number of trials increases.
Concluding that the probability is 1 after only 6 successful trials would be an incorrect inference. A probability of 1 means that the event is absolutely certain to happen every single time, which is not the case for a standard coin toss.
Question 12. Sushma tosses a coin 3 times and gets tail each time. Do you think that the outcome of next toss will be a tail? Give reasons.
Answer:
No, the outcome of the next toss is not necessarily a tail. While it is a possible outcome, the probability of getting a tail on the next toss remains the same as that of getting a head.
Reason:
Each toss of a coin is an independent event. This means that the outcome of one toss does not influence or depend on the outcomes of previous tosses.
The fact that Sushma got tails in the first three tosses is simply a sequence of results that occurred. It does not change the inherent probability of the coin landing on heads or tails for any future toss.
Assuming the coin is a fair coin, the probability of getting a head on any single toss is $\frac{1}{2}$, and the probability of getting a tail on any single toss is also $\frac{1}{2}$.
The outcome of the previous tosses (getting three tails in a row) has no memory or influence on the physical process of the next toss.
Therefore, for the fourth toss, the probability of getting a tail is still $\frac{1}{2}$, and the probability of getting a head is also still $\frac{1}{2}$. The past results do not alter these probabilities.
Question 13. If I toss a coin 3 times and get head each time, should I expect a tail to have a higher chance in the 4th toss? Give reason in support of your answer.
Answer:
No, you should not expect a tail to have a higher chance in the 4th toss.
Reason:
Each toss of a coin is an independent event. This means that the outcome of any particular toss is not influenced by the outcomes of the previous tosses.
The fact that you got heads in the first three tosses does not affect the physical properties of the coin or the conditions of the toss for the fourth throw.
Assuming the coin is a fair coin, the probability of getting a head on any single toss is $\frac{1}{2}$, and the probability of getting a tail on any single toss is also $\frac{1}{2}$. These probabilities remain constant for each toss, regardless of the results of previous tosses.
The feeling that a tail is "due" after a sequence of heads is a common misconception known as the Gambler's Fallacy. In reality, the coin has no memory of past results.
Therefore, the probability of getting a tail on the 4th toss is still $\frac{1}{2}$, just as the probability of getting a head on the 4th toss is still $\frac{1}{2}$.
Question 14. A bag contains slips numbered from 1 to 100. If Fatima chooses a slip at random from the bag, it will either be an odd number or an even number. Since this situation has only two possible outcomes, so, the probability of each is $\frac{1}{2}$ . Justify.
Answer:
Yes, the conclusion that the probability of each is $\frac{1}{2}$ is correct in this specific situation, but the reason given is not universally correct.
Justification:
The statement says that since there are only two possible types of outcomes (odd number or even number), the probability of each is $\frac{1}{2}$. This reasoning is flawed in general, as simply having two categories of outcomes does not make them equally likely (as shown in previous questions, e.g., tossing three coins and counting the number of heads).
However, let's consider the specific case of drawing a slip numbered from 1 to 100 at random from the bag.
The total number of possible outcomes is the number of slips, which is 100.
Let's count the number of odd numbers and even numbers between 1 and 100:
- Odd numbers: 1, 3, 5, ..., 99. There are 50 odd numbers from 1 to 100.
- Even numbers: 2, 4, 6, ..., 100. There are 50 even numbers from 1 to 100.
Since a slip is chosen at random, each slip has an equal probability of being chosen.
The probability of drawing an odd number is the number of odd slips divided by the total number of slips:
$P(\text{Odd}) = \frac{\text{Number of odd numbers}}{\text{Total number of slips}} = \frac{50}{100} = \frac{1}{2}$
The probability of drawing an even number is the number of even slips divided by the total number of slips:
$P(\text{Even}) = \frac{\text{Number of even numbers}}{\text{Total number of slips}} = \frac{50}{100} = \frac{1}{2}$
In this particular scenario (numbers from 1 to 100), the number of odd outcomes is equal to the number of even outcomes. Therefore, the events "drawing an odd number" and "drawing an even number" are indeed equally likely, and the probability of each is $\frac{1}{2}$.
So, the conclusion $P(\text{Odd}) = \frac{1}{2}$ and $P(\text{Even}) = \frac{1}{2}$ is correct for this specific problem, but it is correct because the number of odd and even numbers happens to be equal (50 each), not simply because there are only two types of outcomes.
Sample Question 1 to 4 (Before Exercise 13.3)
Sample Question 1: Construct the cumulative frequency distribution of the following distribution :
| Class | 12.5 - 17.5 | 17.5 - 22.5 | 22.5 - 27.5 | 27.5 - 32.5 | 32.5 - 37.5 |
|---|---|---|---|---|---|
| Frequency | 2 | 22 | 19 | 14 | 13 |
Answer:
Given:
A frequency distribution with class intervals and their corresponding frequencies.
To Construct:
The cumulative frequency distribution.
Solution:
To construct the cumulative frequency distribution, we add the frequency of each class to the cumulative frequency of the preceding class. The cumulative frequency of the first class is the frequency of that class itself.
We can construct the table as follows:
| Class | Frequency | Cumulative Frequency |
| 12.5 - 17.5 | 2 | 2 |
| 17.5 - 22.5 | 22 | 2 + 22 = 24 |
| 22.5 - 27.5 | 19 | 24 + 19 = 43 |
| 27.5 - 32.5 | 14 | 43 + 14 = 57 |
| 32.5 - 37.5 | 13 | 57 + 13 = 70 |
The cumulative frequency distribution is shown in the table above.
Sample Question 2: Daily wages of 110 workers, obtained in a survey, are tabulated below :
| Daily wages (in Rs) | Number of workers |
|---|---|
| 100 - 120 | 10 |
| 120 - 140 | 15 |
| 140 - 160 | 20 |
| 160 - 180 | 22 |
| 180 - 200 | 18 |
| 200 - 220 | 12 |
| 220 - 240 | 13 |
Compute the mean daily wages of these workers.
Answer:
Given:
The daily wages and the number of workers corresponding to each wage group.
To Find:
The mean daily wages of the workers.
Solution:
To compute the mean daily wages for this grouped data, we will use the direct method. We need to find the class mark ($x_i$) for each class interval, then multiply it by the corresponding frequency ($f_i$), sum these products ($\sum f_i x_i$), and finally divide by the total frequency ($\sum f_i$).
The class mark ($x_i$) is the midpoint of a class interval, calculated as: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
First, let's construct a table with the class intervals, frequencies, class marks, and the product of frequency and class mark:
| Daily wages (in $\textsf{₹}$) | Number of workers ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 100 - 120 | 10 | $\frac{100+120}{2} = 110$ | $10 \times 110 = 1100$ |
| 120 - 140 | 15 | $\frac{120+140}{2} = 130$ | $15 \times 130 = 1950$ |
| 140 - 160 | 20 | $\frac{140+160}{2} = 150$ | $20 \times 150 = 3000$ |
| 160 - 180 | 22 | $\frac{160+180}{2} = 170$ | $22 \times 170 = 3740$ |
| 180 - 200 | 18 | $\frac{180+200}{2} = 190$ | $18 \times 190 = 3420$ |
| 200 - 220 | 12 | $\frac{200+220}{2} = 210$ | $12 \times 210 = 2520$ |
| 220 - 240 | 13 | $\frac{220+240}{2} = 230$ | $13 \times 230 = 2990$ |
| Total | $\sum\limits f_i = 10 + 15 + 20 + 22 + 18 + 12 + 13 = 110$ | $\sum\limits f_i x_i = 1100 + 1950 + 3000 + 3740 + 3420 + 2520 + 2990 = 18720$ |
The formula for the mean ($\bar{x}$) of grouped data using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substituting the calculated values from the table:
$\bar{x} = \frac{18720}{110}$
$\bar{x} = \frac{1872}{11}$
Performing the division:
$\bar{x} \approx 170.1818...$
Rounding to two decimal places, the mean daily wages is approximately $\textsf{₹} 170.18$.
Sample Question 3: The percentage of marks obtained by 100 students in an examination are given below:
| Marks | 30-35 | 35-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
| Frequency | 14 | 16 | 18 | 23 | 18 | 8 | 3 |
Determine the median percentage of marks
Answer:
Given:
The percentage of marks obtained by 100 students in different class intervals and the corresponding frequencies.
To Find:
The median percentage of marks.
Solution:
To find the median of grouped data, we first need to calculate the cumulative frequencies. Then, we find the median class, which is the class interval containing the $(\frac{N}{2})^{\text{th}}$ observation, where $N$ is the total number of observations.
Let's construct the cumulative frequency distribution table:
| Marks | Frequency ($f_i$) | Cumulative Frequency (CF) |
| 30-35 | 14 | 14 |
| 35-40 | 16 | $14 + 16 = 30$ |
| 40-45 | 18 | $30 + 18 = 48$ |
| 45-50 | 23 | $48 + 23 = 71$ |
| 50-55 | 18 | $71 + 18 = 89$ |
| 55-60 | 8 | $89 + 8 = 97$ |
| 60-65 | 3 | $97 + 3 = 100$ |
| Total | $\sum\limits f_i = N = 100$ |
Total number of observations, $N = 100$.
We need to find the $(\frac{N}{2})^{\text{th}}$ observation.
$\frac{N}{2} = \frac{100}{2} = 50^{\text{th}}$ observation
Now, we look for the cumulative frequency that is greater than or equal to 50. From the table, the cumulative frequency 71 is the first cumulative frequency greater than 50, and it corresponds to the class interval 45-50.
Thus, the median class is 45-50.
The formula for the median of grouped data is:
$Median = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
Where:
$L$ = lower boundary of the median class = 45
$N$ = total number of observations = 100
$CF$ = cumulative frequency of the class preceding the median class = 48 (CF of class 40-45)
$f$ = frequency of the median class = 23
$h$ = class size = $50 - 45 = 5$
Substitute these values into the formula:
$Median = 45 + \left(\frac{\frac{100}{2} - 48}{23}\right) \times 5$
$Median = 45 + \left(\frac{50 - 48}{23}\right) \times 5$
$Median = 45 + \left(\frac{2}{23}\right) \times 5$
$Median = 45 + \frac{10}{23}$
$Median = 45 + 0.4347...$
Rounding to two decimal places:
$Median \approx 45.43$
The median percentage of marks is approximately 45.43%.
Sample Question 4: The frequency distribution table of agricultural holdings in a village is given below :
| Area of land (in hectares) | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Number of families | 20 | 45 | 80 | 55 | 40 | 12 |
Find the modal agricultural holdings of the village.
Answer:
Given:
The frequency distribution table of agricultural holdings in a village.
To Find:
The modal agricultural holdings of the village.
Solution:
The mode for grouped data is given by the formula:
$Mode = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h$
Where:
- $L$ is the lower limit of the modal class.
- $f_1$ is the frequency of the modal class.
- $f_0$ is the frequency of the class preceding the modal class.
- $f_2$ is the frequency of the class succeeding the modal class.
- $h$ is the class size.
First, we need to identify the modal class. The modal class is the class interval with the highest frequency.
From the given table, the frequencies are 20, 45, 80, 55, 40, and 12. The highest frequency is 80, which corresponds to the class interval 5-7.
So, the modal class is 5-7.
Now, we extract the values from the modal class and its neighbours:
- $L$ = Lower limit of the modal class = 5
- $f_1$ = Frequency of the modal class = 80
- $f_0$ = Frequency of the class preceding the modal class (3-5) = 45
- $f_2$ = Frequency of the class succeeding the modal class (7-9) = 55
- $h$ = Class size = Upper limit - Lower limit = $7 - 5 = 2$
Substitute these values into the mode formula:
$Mode = 5 + \left(\frac{80 - 45}{2(80) - 45 - 55}\right) \times 2$
$Mode = 5 + \left(\frac{35}{160 - 100}\right) \times 2$
$Mode = 5 + \left(\frac{35}{60}\right) \times 2$
$Mode = 5 + \frac{35}{30}$
$Mode = 5 + \frac{7}{6}$
$Mode = 5 + 1.1666...$
$Mode \approx 6.17$
The modal agricultural holdings of the village is approximately 6.17 hectares.
Exercise 13.3
Question 1. Find the mean of the distribution :
| Class | 1 - 3 | 3 - 5 | 5 - 7 | 7 - 10 |
|---|---|---|---|---|
| Frequency | 9 | 22 | 27 | 17 |
Answer:
Given:
A frequency distribution table with class intervals and frequencies.
To Find:
The mean of the distribution.
Solution:
To find the mean of grouped data, we can use the direct method. We need to calculate the class mark ($x_i$) for each class interval, multiply it by the corresponding frequency ($f_i$), sum the products ($\sum f_i x_i$), and divide by the total frequency ($\sum f_i$).
The class mark ($x_i$) is the midpoint of the class interval: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
Let's create a table to organize the calculations:
| Class | Frequency ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 1 - 3 | 9 | $\frac{1+3}{2} = 2$ | $9 \times 2 = 18$ |
| 3 - 5 | 22 | $\frac{3+5}{2} = 4$ | $22 \times 4 = 88$ |
| 5 - 7 | 27 | $\frac{5+7}{2} = 6$ | $27 \times 6 = 162$ |
| 7 - 10 | 17 | $\frac{7+10}{2} = 8.5$ | $17 \times 8.5 = 144.5$ |
| Total | $\sum\limits f_i = 9 + 22 + 27 + 17 = 75$ | $\sum\limits f_i x_i = 18 + 88 + 162 + 144.5 = 412.5$ |
The formula for the mean ($\bar{x}$) is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the values from the table:
$\bar{x} = \frac{412.5}{75}$
To simplify the division, we can multiply the numerator and denominator by 10:
$\bar{x} = \frac{4125}{750}$
Divide both by 25:
$\bar{x} = \frac{\cancel{4125}^{165}}{\cancel{750}_{30}}$
Divide both by 15:
$\bar{x} = \frac{\cancel{165}^{11}}{\cancel{30}_{2}}$
$\bar{x} = \frac{11}{2}$
$\bar{x} = 5.5$
The mean of the distribution is 5.5.
Question 2. Calculate the mean of the scores of 20 students in a mathematics test :
| Marks | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 |
|---|---|---|---|---|---|
| Number of students | 2 | 4 | 7 | 6 | 1 |
Answer:
Given:
The marks obtained by 20 students in a mathematics test and the frequency distribution.
To Find:
The mean of the scores.
Solution:
To compute the mean of the grouped data, we will use the direct method. We first find the class mark ($x_i$) for each class interval, then calculate the product of the frequency ($f_i$) and the class mark ($x_i$), sum these products ($\sum f_i x_i$), and finally divide by the total frequency ($\sum f_i$).
The class mark ($x_i$) for a class interval is the midpoint, calculated as: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
Let's create a table to facilitate the calculation:
| Marks (Class Interval) | Number of students ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 10 - 20 | 2 | $\frac{10+20}{2} = 15$ | $2 \times 15 = 30$ |
| 20 - 30 | 4 | $\frac{20+30}{2} = 25$ | $4 \times 25 = 100$ |
| 30 - 40 | 7 | $\frac{30+40}{2} = 35$ | $7 \times 35 = 245$ |
| 40 - 50 | 6 | $\frac{40+50}{2} = 45$ | $6 \times 45 = 270$ |
| 50 - 60 | 1 | $\frac{50+60}{2} = 55$ | $1 \times 55 = 55$ |
| Total | $\sum\limits f_i = 2 + 4 + 7 + 6 + 1 = 20$ | $\sum\limits f_i x_i = 30 + 100 + 245 + 270 + 55 = 700$ |
The total number of students is $\sum\limits f_i = 20$, which matches the given information.
The sum of the products of frequency and class mark is $\sum\limits f_i x_i = 700$.
The formula for the mean ($\bar{x}$) of grouped data using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the calculated values:
$\bar{x} = \frac{700}{20}$
$\bar{x} = \frac{70}{2}$
$\bar{x} = 35$
The mean of the scores is 35.
Question 3. Calculate the mean of the following data :
| Class | 4 - 7 | 8 - 11 | 12 - 15 | 16 - 19 |
|---|---|---|---|---|
| Frequency | 5 | 4 | 9 | 10 |
Answer:
Given:
A frequency distribution with discrete class intervals and their corresponding frequencies.
To Find:
The mean of the given data.
Solution:
To calculate the mean for this grouped data, we can use the direct method. This involves finding the class mark ($x_i$) for each interval, multiplying it by its frequency ($f_i$), summing these products ($\sum f_i x_i$), and dividing by the total frequency ($\sum f_i$).
The class mark ($x_i$) is the midpoint of each class interval, calculated as $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$. Since the classes are discrete, we calculate the midpoints of the given intervals.
Let's set up a table to compute the necessary values:
| Class | Frequency ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 4 - 7 | 5 | $\frac{4+7}{2} = 5.5$ | $5 \times 5.5 = 27.5$ |
| 8 - 11 | 4 | $\frac{8+11}{2} = 9.5$ | $4 \times 9.5 = 38.0$ |
| 12 - 15 | 9 | $\frac{12+15}{2} = 13.5$ | $9 \times 13.5 = 121.5$ |
| 16 - 19 | 10 | $\frac{16+19}{2} = 17.5$ | $10 \times 17.5 = 175.0$ |
| Total | $\sum\limits f_i = 5 + 4 + 9 + 10 = 28$ | $\sum\limits f_i x_i = 27.5 + 38.0 + 121.5 + 175.0 = 362.0$ |
The formula for the mean ($\bar{x}$) using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the total values from the table:
$\bar{x} = \frac{362.0}{28}$
$\bar{x} = \frac{362}{28}$
We can simplify the fraction by dividing the numerator and the denominator by 2:
$\bar{x} = \frac{\cancel{362}^{181}}{\cancel{28}_{14}}$
$\bar{x} = \frac{181}{14}$
Now, perform the division:
$\bar{x} \approx 12.92857...$
Rounding to two decimal places, the mean is approximately 12.93.
The mean of the given data is approximately 12.93.
Question 4. The following table gives the number of pages written by Sarika for completing her own book for 30 days :
| Number of pages written per day | 16 - 18 | 19 - 21 | 22 - 24 | 25 - 27 | 28 - 30 |
|---|---|---|---|---|---|
| Number of days | 1 | 3 | 4 | 9 | 13 |
Find the mean number of pages written per day.
Answer:
Given:
The number of pages written by Sarika per day for 30 days in different ranges, along with the number of days for each range.
To Find:
The mean number of pages written per day.
Solution:
To calculate the mean for this grouped data, we will use the direct method. We need to find the class mark ($x_i$) for each interval, multiply it by its frequency ($f_i$), sum these products ($\sum f_i x_i$), and divide by the total frequency ($\sum f_i$).
The class mark ($x_i$) is the midpoint of each class interval. For intervals like 16-18, the class mark is $\frac{16+18}{2}$.
Let's create a table to organize the data and calculations:
| Number of pages written per day (Class) | Number of days ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 16 - 18 | 1 | $\frac{16+18}{2} = 17$ | $1 \times 17 = 17$ |
| 19 - 21 | 3 | $\frac{19+21}{2} = 20$ | $3 \times 20 = 60$ |
| 22 - 24 | 4 | $\frac{22+24}{2} = 23$ | $4 \times 23 = 92$ |
| 25 - 27 | 9 | $\frac{25+27}{2} = 26$ | $9 \times 26 = 234$ |
| 28 - 30 | 13 | $\frac{28+30}{2} = 29$ | $13 \times 29 = 377$ |
| Total | $\sum\limits f_i = 1 + 3 + 4 + 9 + 13 = 30$ | $\sum\limits f_i x_i = 17 + 60 + 92 + 234 + 377 = 780$ |
The total number of days (total frequency) is $\sum\limits f_i = 30$, which matches the information given in the question.
The sum of the products of frequency and class mark is $\sum\limits f_i x_i = 780$.
The formula for the mean ($\bar{x}$) using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the calculated values into the formula:
$\bar{x} = \frac{780}{30}$
$\bar{x} = \frac{78}{3}$
$\bar{x} = 26$
The mean number of pages written per day is 26.
Question 5. The daily income of a sample of 50 employees are tabulated as follows :
| Income (in Rs) | 1 - 200 | 201 - 400 | 401 - 600 | 601 - 800 |
|---|---|---|---|---|
| Number of employees | 14 | 15 | 14 | 7 |
Find the mean daily income of employees.
Answer:
Given:
The daily income of 50 employees and the frequency distribution.
To Find:
The mean daily income of the employees.
Solution:
To calculate the mean of the grouped data, we will use the direct method. This requires us to find the class mark ($x_i$) for each income interval, multiply it by the corresponding number of employees ($f_i$), sum these products ($\sum f_i x_i$), and divide by the total number of employees ($\sum f_i$).
The class mark ($x_i$) is the midpoint of the class interval, calculated as: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$. Since the classes are inclusive, the midpoints are calculated directly from the given limits.
Let's create a table to organize the data and perform the calculations:
| Income (in $\textsf{₹}$) (Class) | Number of employees ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 1 - 200 | 14 | $\frac{1+200}{2} = 100.5$ | $14 \times 100.5 = 1407.0$ |
| 201 - 400 | 15 | $\frac{201+400}{2} = 300.5$ | $15 \times 300.5 = 4507.5$ |
| 401 - 600 | 14 | $\frac{401+600}{2} = 500.5$ | $14 \times 500.5 = 7007.0$ |
| 601 - 800 | 7 | $\frac{601+800}{2} = 700.5$ | $7 \times 700.5 = 4903.5$ |
| Total | $\sum\limits f_i = 14 + 15 + 14 + 7 = 50$ | $\sum\limits f_i x_i = 1407.0 + 4507.5 + 7007.0 + 4903.5 = 17825.0$ |
The total number of employees is $\sum\limits f_i = 50$, which is given in the question.
The sum of the products of frequency and class mark is $\sum\limits f_i x_i = 17825.0$.
The formula for the mean ($\bar{x}$) using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the calculated values into the formula:
$\bar{x} = \frac{17825.0}{50}$
$\bar{x} = \frac{17825}{50}$
$\bar{x} = \frac{\cancel{17825}^{3565}}{\cancel{50}_{10}}$
$\bar{x} = \frac{3565}{10}$
$\bar{x} = 356.5$
The mean daily income of the employees is $\textsf{₹} 356.50$.
Question 6. An aircraft has 120 passenger seats. The number of seats occupied during 100 flights is given in the following table :
| Number of seats | 100 - 104 | 104 - 108 | 108 - 112 | 112 - 116 | 116 - 120 |
|---|---|---|---|---|---|
| Frequency | 15 | 20 | 32 | 18 | 15 |
Determine the mean number of seats occupied over the flights.
Answer:
Given:
The number of seats occupied during 100 flights and the frequency distribution.
To Determine:
The mean number of seats occupied over the flights.
Solution:
To find the mean of the grouped data, we will use the direct method. This involves calculating the class mark ($x_i$) for each class interval, multiplying it by the corresponding frequency ($f_i$), summing these products ($\sum f_i x_i$), and dividing by the total frequency ($\sum f_i$).
The class mark ($x_i$) is the midpoint of the class interval, calculated as: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
Let's set up a table to perform the calculations:
| Number of seats (Class) | Number of flights ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 100 - 104 | 15 | $\frac{100+104}{2} = 102$ | $15 \times 102 = 1530$ |
| 104 - 108 | 20 | $\frac{104+108}{2} = 106$ | $20 \times 106 = 2120$ |
| 108 - 112 | 32 | $\frac{108+112}{2} = 110$ | $32 \times 110 = 3520$ |
| 112 - 116 | 18 | $\frac{112+116}{2} = 114$ | $18 \times 114 = 2052$ |
| 116 - 120 | 15 | $\frac{116+120}{2} = 118$ | $15 \times 118 = 1770$ |
| Total | $\sum\limits f_i = 15 + 20 + 32 + 18 + 15 = 100$ | $\sum\limits f_i x_i = 1530 + 2120 + 3520 + 2052 + 1770 = 10992$ |
The total number of flights (total frequency) is $\sum\limits f_i = 100$.
The sum of the products of frequency and class mark is $\sum\limits f_i x_i = 10992$.
The formula for the mean ($\bar{x}$) using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the calculated values into the formula:
$\bar{x} = \frac{10992}{100}$
$\bar{x} = 109.92$
The mean number of seats occupied over the flights is 109.92.
Question 7. The weights (in kg) of 50 wrestlers are recorded in the following table :
| Weight (in kg) | 100 - 110 | 110 - 120 | 120 - 130 | 130 - 140 | 140 - 150 |
|---|---|---|---|---|---|
| Number of wrestlers | 4 | 14 | 21 | 8 | 3 |
Find the mean weight of the wrestlers.
Answer:
Given:
The weights (in kg) of 50 wrestlers and the frequency distribution.
To Find:
The mean weight of the wrestlers.
Solution:
To calculate the mean of this grouped data, we will use the direct method. This involves finding the class mark ($x_i$) for each class interval, multiplying it by the corresponding number of wrestlers ($f_i$), summing these products ($\sum f_i x_i$), and dividing by the total number of wrestlers ($\sum f_i$).
The class mark ($x_i$) is the midpoint of the class interval, calculated as: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
Let's create a table to organize the data and perform the calculations:
| Weight (in kg) (Class) | Number of wrestlers ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 100 - 110 | 4 | $\frac{100+110}{2} = 105$ | $4 \times 105 = 420$ |
| 110 - 120 | 14 | $\frac{110+120}{2} = 115$ | $14 \times 115 = 1610$ |
| 120 - 130 | 21 | $\frac{120+130}{2} = 125$ | $21 \times 125 = 2625$ |
| 130 - 140 | 8 | $\frac{130+140}{2} = 135$ | $8 \times 135 = 1080$ |
| 140 - 150 | 3 | $\frac{140+150}{2} = 145$ | $3 \times 145 = 435$ |
| Total | $\sum\limits f_i = 4 + 14 + 21 + 8 + 3 = 50$ | $\sum\limits f_i x_i = 420 + 1610 + 2625 + 1080 + 435 = 6170$ |
The total number of wrestlers is $\sum\limits f_i = 50$, which is given in the question.
The sum of the products of frequency and class mark is $\sum\limits f_i x_i = 6170$.
The formula for the mean ($\bar{x}$) using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the calculated values into the formula:
$\bar{x} = \frac{6170}{50}$
$\bar{x} = \frac{617}{5}$
$\bar{x} = 123.4$
The mean weight of the wrestlers is 123.4 kg.
Question 8. The mileage (km per litre) of 50 cars of the same model was tested by a manufacturer and details are tabulated as given below :
| Mileage (km/l) | 10 - 12 | 12 - 14 | 14 - 16 | 16 - 18 |
|---|---|---|---|---|
| Number of cars | 7 | 12 | 18 | 13 |
Find the mean mileage.
The manufacturer claimed that the mileage of the model was 16 km/litre. Do you agree with this claim?
Answer:
Given:
The mileage of 50 cars and the frequency distribution.
To Find:
The mean mileage and to comment on the manufacturer's claim.
Solution:
To find the mean mileage for this grouped data, we will use the direct method. We need to calculate the class mark ($x_i$) for each class interval, multiply it by the corresponding number of cars ($f_i$), sum these products ($\sum f_i x_i$), and divide by the total number of cars ($\sum f_i$).
The class mark ($x_i$) is the midpoint of the class interval, calculated as: $x_i = \frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
Let's set up a table to perform the calculations:
| Mileage (km/l) (Class) | Number of cars ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 10 - 12 | 7 | $\frac{10+12}{2} = 11$ | $7 \times 11 = 77$ |
| 12 - 14 | 12 | $\frac{12+14}{2} = 13$ | $12 \times 13 = 156$ |
| 14 - 16 | 18 | $\frac{14+16}{2} = 15$ | $18 \times 15 = 270$ |
| 16 - 18 | 13 | $\frac{16+18}{2} = 17$ | $13 \times 17 = 221$ |
| Total | $\sum\limits f_i = 7 + 12 + 18 + 13 = 50$ | $\sum\limits f_i x_i = 77 + 156 + 270 + 221 = 724$ |
The total number of cars (total frequency) is $\sum\limits f_i = 50$.
The sum of the products of frequency and class mark is $\sum\limits f_i x_i = 724$.
The formula for the mean ($\bar{x}$) using the direct method is:
$\bar{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
Substitute the calculated values into the formula:
$\bar{x} = \frac{724}{50}$
$\bar{x} = \frac{724 \times 2}{50 \times 2} = \frac{1448}{100}$
$\bar{x} = 14.48$
The mean mileage is 14.48 km/litre.
Comment on the claim:
The manufacturer claimed that the mileage of the model was 16 km/litre.
Our calculated mean mileage based on the test of 50 cars is 14.48 km/litre.
Since the calculated mean mileage (14.48 km/litre) is less than the manufacturer's claimed mileage (16 km/litre), based on this data, we do not agree with the manufacturer's claim.
Question 9. The following is the distribution of weights (in kg) of 40 persons :
| Weight (in kg) | 40 - 45 | 45 - 50 | 50 - 55 | 55 - 60 | 60 - 65 | 65 - 70 | 70 - 75 | 75 - 80 |
|---|---|---|---|---|---|---|---|---|
| Number of persons | 4 | 4 | 13 | 5 | 6 | 5 | 2 | 1 |
Construct a cumulative frequency distribution (of the less than type) table for the data above.
Answer:
Given:
The frequency distribution of weights (in kg) of 40 persons.
To Construct:
A cumulative frequency distribution table of the less than type.
Solution:
To construct a cumulative frequency distribution of the less than type, we need to consider the upper limit of each class interval. The cumulative frequency for each class represents the total number of observations less than the upper limit of that class.
We add the frequencies sequentially, starting from the first class.
Let's construct the cumulative frequency distribution table:
| Weight (in kg) (Less than) | Number of persons (Cumulative Frequency) |
| Less than 45 | 4 |
| Less than 50 | 4 + 4 = 8 |
| Less than 55 | 8 + 13 = 21 |
| Less than 60 | 21 + 5 = 26 |
| Less than 65 | 26 + 6 = 32 |
| Less than 70 | 32 + 5 = 37 |
| Less than 75 | 37 + 2 = 39 |
| Less than 80 | 39 + 1 = 40 |
The cumulative frequency distribution table (less than type) is shown above. The last cumulative frequency (40) equals the total number of persons, which confirms the calculation is correct.
Question 10. The following table shows the cumulative frequency distribution of marks of 800 students in an examination:
| Marks | Number of students |
|---|---|
| Below 10 | 10 |
| Below 20 | 50 |
| Below 30 | 130 |
| Below 40 | 270 |
| Below 50 | 440 |
| Below 60 | 570 |
| Below 70 | 670 |
| Below 80 | 740 |
| Below 90 | 780 |
| Below 100 | 800 |
Construct a frequency distribution table for the data above.
Answer:
Given:
A cumulative frequency distribution table (less than type) of marks of 800 students.
To Construct:
A frequency distribution table for the given data.
Solution:
The given table is a cumulative frequency distribution of the less than type. Each entry "Below X" represents the upper limit of a class interval, and the corresponding number of students is the cumulative frequency up to that upper limit.
To convert this into a standard frequency distribution table, we need to determine the class intervals and their corresponding frequencies.
The class intervals can be formed by taking the difference between successive "Below" values. For example, "Below 20" and "Below 10" imply the class interval 10-20. The first class is typically assumed to start from 0 if the marks are percentages or scores from zero.
The frequency of a class interval is obtained by subtracting the cumulative frequency of the preceding class from the cumulative frequency of the current class.
Let's construct the frequency distribution table:
| Marks (Class Interval) | Number of students (Frequency) |
| 0 - 10 | 10 (Cumulative frequency for Below 10) |
| 10 - 20 | 50 - 10 = 40 |
| 20 - 30 | 130 - 50 = 80 |
| 30 - 40 | 270 - 130 = 140 |
| 40 - 50 | 440 - 270 = 170 |
| 50 - 60 | 570 - 440 = 130 |
| 60 - 70 | 670 - 570 = 100 |
| 70 - 80 | 740 - 670 = 70 |
| 80 - 90 | 780 - 740 = 40 |
| 90 - 100 | 800 - 780 = 20 |
| Total | $10 + 40 + 80 + 140 + 170 + 130 + 100 + 70 + 40 + 20 = 800$ |
The frequency distribution table is shown above. The sum of frequencies is 800, which matches the total number of students.
Question 11. Form the frequency distribution table from the following data
| Marks (Out of 90) | Number of candidates |
|---|---|
| More than or equal to 80 | 4 |
| More than or equal to 70 | 6 |
| More than or equal to 60 | 11 |
| More than or equal to 50 | 17 |
| More than or equal to 40 | 23 |
| More than or equal to 30 | 27 |
| More than or equal to 20 | 30 |
| More than or equal to 10 | 32 |
| More than or equal to 0 | 34 |
Answer:
Given:
A cumulative frequency distribution table (more than or equal to type) of marks of candidates.
To Form:
The frequency distribution table from the given data.
Solution:
The given table shows the cumulative frequency distribution of the 'more than or equal to' type. Each entry represents the lower limit of a class interval, and the corresponding number of candidates is the cumulative frequency (number of candidates scoring more than or equal to that lower limit).
To convert this into a standard frequency distribution table, we need to determine the class intervals and their frequencies. The class intervals can be formed using the "More than or equal to" values as the lower limits. The upper limit of a class will be the lower limit of the next class.
The frequency of a class interval (say $L_1 - L_2$, where $L_1$ is the lower limit and $L_2$ is the next lower limit) is the difference between the cumulative frequency of "More than or equal to $L_1$" and the cumulative frequency of "More than or equal to $L_2$".
Let's construct the frequency distribution table:
| Marks (Class Interval) | Number of candidates (Frequency) |
| 0 - 10 | (More than or equal to 0) - (More than or equal to 10) = $34 - 32 = 2$ |
| 10 - 20 | (More than or equal to 10) - (More than or equal to 20) = $32 - 30 = 2$ |
| 20 - 30 | (More than or equal to 20) - (More than or equal to 30) = $30 - 27 = 3$ |
| 30 - 40 | (More than or equal to 30) - (More than or equal to 40) = $27 - 23 = 4$ |
| 40 - 50 | (More than or equal to 40) - (More than or equal to 50) = $23 - 17 = 6$ |
| 50 - 60 | (More than or equal to 50) - (More than or equal to 60) = $17 - 11 = 6$ |
| 60 - 70 | (More than or equal to 60) - (More than or equal to 70) = $11 - 6 = 5$ |
| 70 - 80 | (More than or equal to 70) - (More than or equal to 80) = $6 - 4 = 2$ |
| 80 - 90 | (More than or equal to 80). Since maximum marks are 90, this includes those scoring 80 up to 90. The cumulative frequency of "More than or equal to 80" is 4. Assuming no one scored exactly 90 or more, the frequency for 80-90 is 4. (Alternatively, if there was a "More than or equal to 90" entry, we would subtract it). |
| Total | $2 + 2 + 3 + 4 + 6 + 6 + 5 + 2 + 4 = 34$ |
The frequency distribution table is shown above. The sum of frequencies is 34, which matches the total number of candidates scoring more than or equal to 0.
Question 12. Find the unknown entries a, b, c, d, e, f in the following distribution of heights of students in a class :
| Height (in cm) | Frequency | Cumulative Frequency |
|---|---|---|
| 150 - 155 | 12 | a |
| 155 - 160 | b | 25 |
| 160 - 165 | 10 | c |
| 165 - 170 | d | 43 |
| 170 - 175 | e | 48 |
| 175 - 180 | 2 | f |
| Total | 50 |
Answer:
Given:
A frequency distribution table with some unknown frequencies and cumulative frequencies.
To Find:
The unknown entries a, b, c, d, e, and f in the table.
Solution:
The cumulative frequency (CF) of a class is the sum of the frequency of that class and the cumulative frequency of the preceding class. The cumulative frequency of the first class is equal to its frequency. The cumulative frequency of the last class is equal to the total frequency.
Using these relationships, we can find the unknown entries:
1. **Find 'a'**: 'a' is the cumulative frequency of the first class (150-155). The cumulative frequency of the first class is equal to its frequency.
$a = \text{Frequency of 150-155} = 12$
2. **Find 'b'**: The cumulative frequency of the second class (155-160) is given as 25. This is the sum of the cumulative frequency of the first class (a) and the frequency of the second class (b).
$25 = a + b$
Substitute the value of a:
$25 = 12 + b$
$b = 25 - 12 = 13$
3. **Find 'c'**: 'c' is the cumulative frequency of the third class (160-165). This is the sum of the cumulative frequency of the second class (25) and the frequency of the third class (10).
$c = 25 + 10 = 35$
4. **Find 'd'**: The cumulative frequency of the fourth class (165-170) is given as 43. This is the sum of the cumulative frequency of the third class (c) and the frequency of the fourth class (d).
$43 = c + d$
Substitute the value of c:
$43 = 35 + d$
$d = 43 - 35 = 8$
5. **Find 'e'**: The cumulative frequency of the fifth class (170-175) is given as 48. This is the sum of the cumulative frequency of the fourth class (43) and the frequency of the fifth class (e).
$48 = 43 + e$
$e = 48 - 43 = 5$
6. **Find 'f'**: 'f' is the cumulative frequency of the last class (175-180). This is the sum of the cumulative frequency of the fifth class (48) and the frequency of the sixth class (2).
$f = 48 + 2 = 50$
Alternatively, the cumulative frequency of the last class must be equal to the total frequency, which is given as 50. This confirms $f=50$.
The unknown entries are:
$a = 12$
$b = 13$
$c = 35$
$d = 8$
$e = 5$
$f = 50$
The completed table is:
| Height (in cm) | Frequency | Cumulative Frequency |
| 150 - 155 | 12 | 12 |
| 155 - 160 | 13 | 25 |
| 160 - 165 | 10 | 35 |
| 165 - 170 | 8 | 43 |
| 170 - 175 | 5 | 48 |
| 175 - 180 | 2 | 50 |
| Total | 50 |
Question 13. The following are the ages of 300 patients getting medical treatment in a hospital on a particular day :
| Age (in years) | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
|---|---|---|---|---|---|---|
| Number of patients | 60 | 42 | 55 | 70 | 53 | 20 |
Form:
(i) Less than type cumulative frequency distribution.
(ii) More than type cumulative frequency distribution.
Answer:
Given:
The frequency distribution of ages of 300 patients in a hospital.
To Form:
(i) Less than type cumulative frequency distribution.
(ii) More than type cumulative frequency distribution.
Solution:
We are given a frequency distribution table. To form the cumulative frequency distributions, we will calculate the running totals of frequencies in two different ways.
(i) Less than type cumulative frequency distribution:
For the 'less than' type cumulative frequency, we consider the upper limit of each class. The cumulative frequency for a class is the sum of frequencies of all classes with upper limits less than or equal to the upper limit of the current class. We start with the frequency of the first class and add subsequent frequencies.
| Age (in years) (Less than) | Number of patients (Cumulative Frequency) |
| Less than 20 | 60 |
| Less than 30 | $60 + 42 = 102$ |
| Less than 40 | $102 + 55 = 157$ |
| Less than 50 | $157 + 70 = 227$ |
| Less than 60 | $227 + 53 = 280$ |
| Less than 70 | $280 + 20 = 300$ |
The less than type cumulative frequency distribution is shown in the table above.
(ii) More than type cumulative frequency distribution:
For the 'more than' type cumulative frequency, we consider the lower limit of each class (or "More than or equal to" the lower limit). The cumulative frequency for a class is the sum of frequencies of all classes with lower limits greater than or equal to the lower limit of the current class. We start with the total frequency and subtract the frequencies of preceding classes.
The total number of patients is $60 + 42 + 55 + 70 + 53 + 20 = 300$.
| Age (in years) (More than or equal to) | Number of patients (Cumulative Frequency) |
| More than or equal to 10 | 300 |
| More than or equal to 20 | $300 - 60 = 240$ |
| More than or equal to 30 | $240 - 42 = 198$ |
| More than or equal to 40 | $198 - 55 = 143$ |
| More than or equal to 50 | $143 - 70 = 73$ |
| More than or equal to 60 | $73 - 53 = 20$ |
The more than type cumulative frequency distribution is shown in the table above.
Question 14. Given below is a cumulative frequency distribution showing the marks secured by 50 students of a class :
| Marks | Below 20 | Below 40 | Below 60 | Below 80 | Below 100 |
|---|---|---|---|---|---|
| Number of students | 17 | 22 | 29 | 37 | 50 |
Form the frequency distribution table for the data.
Answer:
Given:
A cumulative frequency distribution table (less than type) showing marks secured by 50 students.
To Form:
The frequency distribution table for the given data.
Solution:
The given table is a cumulative frequency distribution of the 'less than' type. The "Marks Below X" entries indicate the upper limits of the class intervals, and the "Number of students" entries are the cumulative frequencies.
To convert this to a standard frequency distribution, we need to define the class intervals and calculate the frequency for each interval. The class intervals will be formed using the consecutive upper limits provided.
The frequency of a class interval (say $U_1 - U_2$, where $U_1$ is the upper limit of the previous class and $U_2$ is the upper limit of the current class) is the difference between the cumulative frequency of "Below $U_2$" and the cumulative frequency of "Below $U_1$". The first class will start from 0, as marks are typically scored from 0.
Let's construct the frequency distribution table:
| Marks (Class Interval) | Number of students (Frequency) |
| 0 - 20 | 17 (Cumulative frequency for Below 20) |
| 20 - 40 | (Cumulative frequency for Below 40) - (Cumulative frequency for Below 20) = $22 - 17 = 5$ |
| 40 - 60 | (Cumulative frequency for Below 60) - (Cumulative frequency for Below 40) = $29 - 22 = 7$ |
| 60 - 80 | (Cumulative frequency for Below 80) - (Cumulative frequency for Below 60) = $37 - 29 = 8$ |
| 80 - 100 | (Cumulative frequency for Below 100) - (Cumulative frequency for Below 80) = $50 - 37 = 13$ |
| Total | $17 + 5 + 7 + 8 + 13 = 50$ |
The frequency distribution table is shown above. The sum of the frequencies is 50, which matches the total number of students given.
Question 15. Weekly income of 600 families is tabulated below :
| Weekly income (in Rs) | Number of families |
|---|---|
| 0 - 1000 | 250 |
| 1000 - 2000 | 190 |
| 2000 - 3000 | 100 |
| 3000 - 4000 | 40 |
| 4000 - 5000 | 15 |
| 5000 - 6000 | 5 |
| Total | 600 |
Compute the median income.
Answer:
Given:
The frequency distribution of weekly income of 600 families.
To Compute:
The median income.
Solution:
To find the median of grouped data, we first need to construct the cumulative frequency distribution. The median class is the class interval containing the $(\frac{N}{2})^{\text{th}}$ observation, where $N$ is the total number of observations (families).
Let's add a column for cumulative frequency to the table:
| Weekly income (in $\textsf{₹}$) | Number of families ($f_i$) | Cumulative Frequency (CF) |
| 0 - 1000 | 250 | 250 |
| 1000 - 2000 | 190 | $250 + 190 = 440$ |
| 2000 - 3000 | 100 | $440 + 100 = 540$ |
| 3000 - 4000 | 40 | $540 + 40 = 580$ |
| 4000 - 5000 | 15 | $580 + 15 = 595$ |
| 5000 - 6000 | 5 | $595 + 5 = 600$ |
| Total | $N = 600$ |
Total number of families, $N = 600$.
The median position is $\frac{N}{2}$.
$\frac{N}{2} = \frac{600}{2} = 300^{\text{th}}$ observation
Now, we locate the class interval whose cumulative frequency is greater than or equal to 300 for the first time. From the table, the cumulative frequency 440 is the first one greater than or equal to 300, and it corresponds to the class interval 1000 - 2000.
Thus, the median class is 1000 - 2000.
The formula for the median of grouped data is:
$Median = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
Where:
- $L$ = lower boundary of the median class = 1000
- $N$ = total number of observations = 600
- $CF$ = cumulative frequency of the class preceding the median class (0-1000) = 250
- $f$ = frequency of the median class (1000-2000) = 190
- $h$ = class size = $2000 - 1000 = 1000$
Substitute these values into the formula:
$Median = 1000 + \left(\frac{\frac{600}{2} - 250}{190}\right) \times 1000$
$Median = 1000 + \left(\frac{300 - 250}{190}\right) \times 1000$
$Median = 1000 + \left(\frac{50}{190}\right) \times 1000$
$Median = 1000 + \frac{5}{19} \times 1000$
$Median = 1000 + \frac{5000}{19}$
Perform the division:
$\frac{5000}{19} \approx 263.1578...$
$Median \approx 1000 + 263.1578...$
$Median \approx 1263.1578...$
Rounding to two decimal places, the median income is approximately $\textsf{₹} 1263.16$.
The median income is approximately $\textsf{₹} 1263.16$.
Question 16. The maximum bowling speeds, in km per hour, of 33 players at a cricket coaching centre are given as follows :
| Speed (km/h) | 85 - 100 | 100 - 115 | 115 - 130 | 130 - 145 |
|---|---|---|---|---|
| Number of players | 11 | 9 | 8 | 5 |
Calculate the median bowling speed.
Answer:
Given:
The frequency distribution of bowling speeds of 33 players.
To Calculate:
The median bowling speed.
Solution:
To find the median of grouped data, we first need to construct the cumulative frequency distribution. The median class is the class interval containing the $(\frac{N}{2})^{\text{th}}$ observation, where $N$ is the total number of observations (players).
Let's add a column for cumulative frequency (CF) to the table:
| Speed (km/h) | Number of players ($f_i$) | Cumulative Frequency (CF) |
| 85 - 100 | 11 | 11 |
| 100 - 115 | 9 | $11 + 9 = 20$ |
| 115 - 130 | 8 | $20 + 8 = 28$ |
| 130 - 145 | 5 | $28 + 5 = 33$ |
| Total | $N = 33$ |
Total number of players, $N = 33$.
The median position is $\frac{N}{2}$.
$\frac{N}{2} = \frac{33}{2} = 16.5^{\text{th}}$ observation
Now, we locate the class interval whose cumulative frequency is greater than or equal to 16.5 for the first time. From the table, the cumulative frequency 20 is the first one greater than or equal to 16.5, and it corresponds to the class interval 100 - 115.
Thus, the median class is 100 - 115.
The formula for the median of grouped data is:
$Median = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
Where:
- $L$ = lower boundary of the median class = 100
- $N$ = total number of observations = 33
- $CF$ = cumulative frequency of the class preceding the median class (85-100) = 11
- $f$ = frequency of the median class (100-115) = 9
- $h$ = class size = $115 - 100 = 15$
Substitute these values into the formula:
$Median = 100 + \left(\frac{\frac{33}{2} - 11}{9}\right) \times 15$
$Median = 100 + \left(\frac{16.5 - 11}{9}\right) \times 15$
$Median = 100 + \left(\frac{5.5}{9}\right) \times 15$
$Median = 100 + \frac{5.5 \times 15}{9}$
$Median = 100 + \frac{82.5}{9}$
$Median = 100 + \frac{825}{90}$
Simplify the fraction:
$Median = 100 + \frac{\cancel{825}^{55}}{\cancel{90}_{6}}$
$Median = 100 + \frac{55}{6}$
Performing the division $\frac{55}{6}$:
$\frac{55}{6} = 9.166...$
$Median \approx 100 + 9.17$
$Median \approx 109.17$
The median bowling speed is approximately 109.17 km/h.
Question 17. The monthly income of 100 families are given as below :
| Income (in Rs) | Number of families |
|---|---|
| 0 - 5000 | 8 |
| 5000 - 10000 | 26 |
| 10000 - 15000 | 41 |
| 15000 - 20000 | 16 |
| 20000 - 25000 | 3 |
| 25000 - 30000 | 3 |
| 30000 - 35000 | 2 |
| 35000 - 40000 | 1 |
Calculate the modal income.
Answer:
Given:
The frequency distribution of monthly income of 100 families.
To Calculate:
The modal income.
Solution:
To find the mode of grouped data, we first need to identify the modal class. The modal class is the class interval with the highest frequency.
From the given table, the frequencies are 8, 26, 41, 16, 3, 3, 2, and 1. The highest frequency is 41, which corresponds to the class interval 10000 - 15000.
Thus, the modal class is 10000 - 15000.
Now, we use the formula for the mode of grouped data:
$Mode = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h$
Where:
- $L$ = lower limit of the modal class = 10000
- $f_1$ = frequency of the modal class = 41
- $f_0$ = frequency of the class preceding the modal class (5000-10000) = 26
- $f_2$ = frequency of the class succeeding the modal class (15000-20000) = 16
- $h$ = class size = Upper limit - Lower limit = $15000 - 10000 = 5000$
Substitute these values into the formula:
$Mode = 10000 + \left(\frac{41 - 26}{2(41) - 26 - 16}\right) \times 5000$
$Mode = 10000 + \left(\frac{15}{82 - 42}\right) \times 5000$
$Mode = 10000 + \left(\frac{15}{40}\right) \times 5000$
$Mode = 10000 + \frac{15}{40} \times 5000$
$Mode = 10000 + \frac{15}{\cancel{40}_1} \times \cancel{5000}^{125}$
$Mode = 10000 + 15 \times 125$
$Mode = 10000 + 1875$
$Mode = 11875$
The modal income is $\textsf{₹} 11875$.
Question 18. The weight of coffee in 70 packets are shown in the following table :
| Weight (in g) | Number of packets |
|---|---|
| 200 - 201 | 12 |
| 201 - 202 | 26 |
| 202 - 203 | 20 |
| 203 - 204 | 9 |
| 204 - 205 | 2 |
| 205 - 206 | 1 |
Determine the modal weight.
Answer:
Given:
The frequency distribution of the weight of coffee in 70 packets.
To Determine:
The modal weight.
Solution:
To find the mode of grouped data, we first need to identify the modal class. The modal class is the class interval with the highest frequency.
From the given table, the frequencies are 12, 26, 20, 9, 2, and 1. The highest frequency is 26, which corresponds to the class interval 201 - 202.
Thus, the modal class is 201 - 202.
Now, we use the formula for the mode of grouped data:
$Mode = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h$
Where:
- $L$ = lower limit of the modal class = 201
- $f_1$ = frequency of the modal class = 26
- $f_0$ = frequency of the class preceding the modal class (200-201) = 12
- $f_2$ = frequency of the class succeeding the modal class (202-203) = 20
- $h$ = class size = Upper limit - Lower limit = $202 - 201 = 1$
Substitute these values into the formula:
$Mode = 201 + \left(\frac{26 - 12}{2(26) - 12 - 20}\right) \times 1$
$Mode = 201 + \left(\frac{14}{52 - 32}\right) \times 1$
$Mode = 201 + \left(\frac{14}{20}\right) \times 1$
$Mode = 201 + \frac{14}{20}$
$Mode = 201 + \frac{7}{10}$
$Mode = 201 + 0.7$
$Mode = 201.7$
The modal weight is 201.7 g.
Question 19. Two dice are thrown at the same time. Find the probability of getting
(i) same number on both dice.
(ii) different numbers on both dice.
Answer:
Given:
Two fair dice are thrown simultaneously.
To Find:
(i) The probability of getting the same number on both dice.
(ii) The probability of getting different numbers on both dice.
Solution:
When two fair dice are thrown, the total number of possible outcomes is the product of the number of outcomes for each die. Each die has 6 faces (1, 2, 3, 4, 5, 6).
The sample space $S$ consists of pairs of numbers $(d_1, d_2)$, where $d_1$ is the outcome on the first die and $d_2$ is the outcome on the second die.
The total number of possible outcomes is $n(S) = 6 \times 6 = 36$.
The sample space is:
$S = \{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),$
$\phantom{S = } (2,1), (2,2), (2,3), (2,4), (2,5), (2,6),$
$\phantom{S = } (3,1), (3,2), (3,3), (3,4), (3,5), (3,6),$
$\phantom{S = } (4,1), (4,2), (4,3), (4,4), (4,5), (4,6),$
$\phantom{S = } (5,1), (5,2), (5,3), (5,4), (5,5), (5,6),$
$\phantom{S = } (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)\}$
(i) Probability of getting the same number on both dice:
Let $A$ be the event of getting the same number on both dice. The outcomes for this event are the pairs where both numbers are identical.
$A = \{(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)\}$
The number of favourable outcomes for event $A$ is $n(A) = 6$.
The probability of event $A$, $P(A)$, is given by:
$P(A) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{n(A)}{n(S)}$
$P(\text{same number}) = \frac{6}{36}$
$P(\text{same number}) = \frac{\cancel{6}^1}{\cancel{36}_6}$
$P(\text{same number}) = \frac{1}{6}$
The probability of getting the same number on both dice is $\frac{1}{6}$.
(ii) Probability of getting different numbers on both dice:
Let $B$ be the event of getting different numbers on both dice. The outcomes for this event are all the outcomes in the sample space except those where the numbers are the same.
The number of favourable outcomes for event $B$ is $n(B) = n(S) - n(A) = 36 - 6 = 30$.
The probability of event $B$, $P(B)$, is given by:
$P(B) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{n(B)}{n(S)}$
$P(\text{different numbers}) = \frac{30}{36}$
$P(\text{different numbers}) = \frac{\cancel{30}^5}{\cancel{36}_6}$
$P(\text{different numbers}) = \frac{5}{6}$
The probability of getting different numbers on both dice is $\frac{5}{6}$.
Alternate Solution (for part ii):
The event of getting different numbers on both dice is the complement of the event of getting the same number on both dice.
Let $A$ be the event of getting the same number on both dice.
Let $A'$ be the event of getting different numbers on both dice (the complement of $A$).
The probability of the complement event is $P(A') = 1 - P(A)$.
From part (i), we found $P(A) = \frac{1}{6}$.
So, $P(\text{different numbers}) = 1 - P(\text{same number})$
$P(\text{different numbers}) = 1 - \frac{1}{6}$
$P(\text{different numbers}) = \frac{6}{6} - \frac{1}{6} = \frac{6-1}{6}$
$P(\text{different numbers}) = \frac{5}{6}$
This confirms the result obtained earlier.
Question 20. Two dice are thrown simultaneously. What is the probability that the sum of the numbers appearing on the dice is
(i) 7?
(ii) a prime number?
(iii) 1?
Answer:
Given:
Two fair dice are thrown simultaneously.
To Find:
The probability that the sum of the numbers appearing on the dice is:
(i) 7
(ii) a prime number
(iii) 1
Solution:
When two fair dice are thrown, the total number of possible outcomes is $6 \times 6 = 36$.
The sample space $S$ consists of 36 ordered pairs $(d_1, d_2)$, where $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$.
The sum of the numbers on the two dice can range from $1+1=2$ to $6+6=12$.
(i) Probability that the sum is 7:
Let $A$ be the event that the sum of the numbers is 7. We need to find the pairs $(d_1, d_2)$ such that $d_1 + d_2 = 7$.
The favourable outcomes are:
$A = \{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}$
The number of favourable outcomes is $n(A) = 6$.
The probability of event $A$ is $P(A) = \frac{n(A)}{n(S)}$.
$P(\text{sum is 7}) = \frac{6}{36}$
$P(\text{sum is 7}) = \frac{\cancel{6}^1}{\cancel{36}_6}$
$P(\text{sum is 7}) = \frac{1}{6}$
The probability that the sum of the numbers is 7 is $\frac{1}{6}$.
(ii) Probability that the sum is a prime number:
Let $B$ be the event that the sum of the numbers is a prime number. The possible sums range from 2 to 12. The prime numbers within this range are 2, 3, 5, 7, and 11.
We find the pairs $(d_1, d_2)$ for each prime sum:
- Sum = 2: $(1,1)$ (1 outcome)
- Sum = 3: $(1,2), (2,1)$ (2 outcomes)
- Sum = 5: $(1,4), (2,3), (3,2), (4,1)$ (4 outcomes)
- Sum = 7: $(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)$ (6 outcomes)
- Sum = 11: $(5,6), (6,5)$ (2 outcomes)
The favourable outcomes for event $B$ are the union of these sets of pairs.
$B = \{(1,1), (1,2), (2,1), (1,4), (2,3), (3,2), (4,1), (1,6), (2,5), (3,4), (4,3), (5,2), (6,1), (5,6), (6,5)\}$
The number of favourable outcomes is $n(B) = 1 + 2 + 4 + 6 + 2 = 15$.
The probability of event $B$ is $P(B) = \frac{n(B)}{n(S)}$.
$P(\text{sum is a prime number}) = \frac{15}{36}$
$P(\text{sum is a prime number}) = \frac{\cancel{15}^5}{\cancel{36}_{12}}$
$P(\text{sum is a prime number}) = \frac{5}{12}$
The probability that the sum of the numbers is a prime number is $\frac{5}{12}$.
(iii) Probability that the sum is 1:
Let $C$ be the event that the sum of the numbers is 1. The minimum possible sum when rolling two dice is $1+1 = 2$.
There are no pairs $(d_1, d_2)$ in the sample space $S$ such that $d_1 + d_2 = 1$.
The number of favourable outcomes for event $C$ is $n(C) = 0$.
The probability of event $C$ is $P(C) = \frac{n(C)}{n(S)}$.
$P(\text{sum is 1}) = \frac{0}{36}$
$P(\text{sum is 1}) = 0$
The probability that the sum of the numbers is 1 is 0. This is an impossible event.
Question 21. Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is
(i) 6
(ii) 12
(iii) 7
Answer:
Given:
Two fair dice are thrown simultaneously.
To Find:
The probability that the product of the numbers on the top of the dice is:
(i) 6
(ii) 12
(iii) 7
Solution:
When two fair dice are thrown, the total number of possible outcomes is $6 \times 6 = 36$.
The sample space $S$ consists of 36 ordered pairs $(d_1, d_2)$, where $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$.
(i) Probability that the product is 6:
Let $A$ be the event that the product of the numbers is 6. We need to find the pairs $(d_1, d_2)$ such that $d_1 \times d_2 = 6$.
The possible pairs are:
- $1 \times 6 = 6 \implies (1,6)$
- $2 \times 3 = 6 \implies (2,3)$
- $3 \times 2 = 6 \implies (3,2)$
- $6 \times 1 = 6 \implies (6,1)$
The favourable outcomes are:
$A = \{(1,6), (2,3), (3,2), (6,1)\}$
The number of favourable outcomes is $n(A) = 4$.
The probability of event $A$ is $P(A) = \frac{n(A)}{n(S)}$.
$P(\text{product is 6}) = \frac{4}{36}$
$P(\text{product is 6}) = \frac{\cancel{4}^1}{\cancel{36}_9}$
$P(\text{product is 6}) = \frac{1}{9}$
The probability that the product of the numbers is 6 is $\frac{1}{9}$.
(ii) Probability that the product is 12:
Let $B$ be the event that the product of the numbers is 12. We need to find the pairs $(d_1, d_2)$ such that $d_1 \times d_2 = 12$, where $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$.
The possible pairs are:
- $2 \times 6 = 12 \implies (2,6)$
- $3 \times 4 = 12 \implies (3,4)$
- $4 \times 3 = 12 \implies (4,3)$
- $6 \times 2 = 12 \implies (6,2)$
The favourable outcomes are:
$B = \{(2,6), (3,4), (4,3), (6,2)\}$
The number of favourable outcomes is $n(B) = 4$.
The probability of event $B$ is $P(B) = \frac{n(B)}{n(S)}$.
$P(\text{product is 12}) = \frac{4}{36}$
$P(\text{product is 12}) = \frac{\cancel{4}^1}{\cancel{36}_9}$
$P(\text{product is 12}) = \frac{1}{9}$
The probability that the product of the numbers is 12 is $\frac{1}{9}$.
(iii) Probability that the product is 7:
Let $C$ be the event that the product of the numbers is 7. We need to find the pairs $(d_1, d_2)$ such that $d_1 \times d_2 = 7$, where $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$.
The only integer factors of 7 are 1 and 7. Since the maximum number on a die is 6, we cannot get a product of 7 using the numbers 1 through 6 on two dice.
There are no pairs $(d_1, d_2)$ in the sample space $S$ such that $d_1 \times d_2 = 7$.
The number of favourable outcomes for event $C$ is $n(C) = 0$.
The probability of event $C$ is $P(C) = \frac{n(C)}{n(S)}$.
$P(\text{product is 7}) = \frac{0}{36}$
$P(\text{product is 7}) = 0$
The probability that the product of the numbers is 7 is 0. This is an impossible event.
Question 22. Two dice are thrown at the same time and the product of numbers appearing on them is noted. Find the probability that the product is less than 9.
Answer:
Given:
Two fair dice are thrown simultaneously, and the product of the numbers is noted.
To Find:
The probability that the product is less than 9.
Solution:
When two fair dice are thrown, the total number of possible outcomes is $6 \times 6 = 36$.
The sample space $S$ consists of 36 ordered pairs $(d_1, d_2)$, where $d_1, d_2 \in \{1, 2, 3, 4, 5, 6\}$.
Let $A$ be the event that the product of the numbers is less than 9. This means $d_1 \times d_2 < 9$.
We need to list all pairs $(d_1, d_2)$ from the sample space whose product is less than 9.
- If $d_1 = 1$, then $d_2$ can be 1, 2, 3, 4, 5, 6. Products are $1 \times 1 = 1, 1 \times 2 = 2, ..., 1 \times 6 = 6$. All are less than 9. Pairs: $(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)$. (6 outcomes)
- If $d_1 = 2$, then $d_2$ can be 1, 2, 3, 4. Products are $2 \times 1 = 2, 2 \times 2 = 4, 2 \times 3 = 6, 2 \times 4 = 8$. $2 \times 5 = 10 \geq 9$. Pairs: $(2,1), (2,2), (2,3), (2,4)$. (4 outcomes)
- If $d_1 = 3$, then $d_2$ can be 1, 2. Products are $3 \times 1 = 3, 3 \times 2 = 6$. $3 \times 3 = 9 \geq 9$. Pairs: $(3,1), (3,2)$. (2 outcomes)
- If $d_1 = 4$, then $d_2$ can be 1, 2. Products are $4 \times 1 = 4, 4 \times 2 = 8$. $4 \times 3 = 12 \geq 9$. Pairs: $(4,1), (4,2)$. (2 outcomes)
- If $d_1 = 5$, then $d_2$ can be 1. Product is $5 \times 1 = 5$. $5 \times 2 = 10 \geq 9$. Pair: $(5,1)$. (1 outcome)
- If $d_1 = 6$, then $d_2$ can be 1. Product is $6 \times 1 = 6$. $6 \times 2 = 12 \geq 9$. Pair: $(6,1)$. (1 outcome)
The favourable outcomes for event $A$ are:
$A = \{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),$
$\phantom{A = } (2,1), (2,2), (2,3), (2,4),$
$\phantom{A = } (3,1), (3,2),$
$\phantom{A = } (4,1), (4,2),$
$\phantom{A = } (5,1),$
$\phantom{A = } (6,1)\}$
The number of favourable outcomes is $n(A) = 6 + 4 + 2 + 2 + 1 + 1 = 16$.
The probability of event $A$ is $P(A) = \frac{n(A)}{n(S)}$.
$P(\text{product is less than 9}) = \frac{16}{36}$
$P(\text{product is less than 9}) = \frac{\cancel{16}^4}{\cancel{36}_9}$
$P(\text{product is less than 9}) = \frac{4}{9}$
The probability that the product of the numbers is less than 9 is $\frac{4}{9}$.
Question 23. Two dice are numbered 1, 2, 3, 4, 5, 6 and 1, 1, 2, 2, 3, 3, respectively. They are thrown and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.
Answer:
Given:
Two dice are thrown. The first die is numbered 1, 2, 3, 4, 5, 6. The second die is numbered 1, 1, 2, 2, 3, 3.
To Find:
The probability of getting each sum from 2 to 9 separately.
Solution:
Let Die 1 be the standard die with faces {1, 2, 3, 4, 5, 6}.
Let Die 2 be the special die with faces {1, 1, 2, 2, 3, 3}.
When two dice are thrown, the total number of possible outcomes is the product of the number of faces on each die.
Total number of outcomes = (Number of faces on Die 1) $\times$ (Number of faces on Die 2)
Total number of outcomes = $6 \times 6 = 36$.
To find the probability of each sum, we need to identify the pairs of outcomes from the two dice that result in the specific sum and count how many ways each sum can occur, considering the repeated numbers on the second die.
Let $(d_1, d_2)$ represent the outcome where $d_1$ is the number on Die 1 and $d_2$ is the number on Die 2. We can list the number of ways to obtain each sum:
- Sum = 2: The only way to get a sum of 2 is $1 + 1$. Die 1 must show 1 (1 way). Die 2 must show 1 (2 faces have 1).
- Sum = 3: Possible pairs are $1 + 2$ or $2 + 1$.
- Sum = 4: Possible pairs are $1 + 3$, $2 + 2$, or $3 + 1$.
- Sum = 5: Possible pairs are $2 + 3$, $3 + 2$, or $4 + 1$.
- Sum = 6: Possible pairs are $3 + 3$, $4 + 2$, or $5 + 1$.
- Sum = 7: Possible pairs are $4 + 3$, $5 + 2$, or $6 + 1$.
- Sum = 8: Possible pairs are $5 + 3$ or $6 + 2$.
- Sum = 9: The only way to get a sum of 9 is $6 + 3$. Die 1 must show 6 (1 way). Die 2 must show 3 (2 faces have 3).
Number of ways for Sum = 2: $1 \times 2 = 2$.
- Die 1 shows 1 (1 way), Die 2 shows 2 (2 faces have 2): $1 \times 2 = 2$ ways.
- Die 1 shows 2 (1 way), Die 2 shows 1 (2 faces have 1): $1 \times 2 = 2$ ways.
Number of ways for Sum = 3: $2 + 2 = 4$.
- Die 1 shows 1 (1 way), Die 2 shows 3 (2 faces have 3): $1 \times 2 = 2$ ways.
- Die 1 shows 2 (1 way), Die 2 shows 2 (2 faces have 2): $1 \times 2 = 2$ ways.
- Die 1 shows 3 (1 way), Die 2 shows 1 (2 faces have 1): $1 \times 2 = 2$ ways.
Number of ways for Sum = 4: $2 + 2 + 2 = 6$.
- Die 1 shows 2 (1 way), Die 2 shows 3 (2 faces have 3): $1 \times 2 = 2$ ways.
- Die 1 shows 3 (1 way), Die 2 shows 2 (2 faces have 2): $1 \times 2 = 2$ ways.
- Die 1 shows 4 (1 way), Die 2 shows 1 (2 faces have 1): $1 \times 2 = 2$ ways.
Number of ways for Sum = 5: $2 + 2 + 2 = 6$.
- Die 1 shows 3 (1 way), Die 2 shows 3 (2 faces have 3): $1 \times 2 = 2$ ways.
- Die 1 shows 4 (1 way), Die 2 shows 2 (2 faces have 2): $1 \times 2 = 2$ ways.
- Die 1 shows 5 (1 way), Die 2 shows 1 (2 faces have 1): $1 \times 2 = 2$ ways.
Number of ways for Sum = 6: $2 + 2 + 2 = 6$.
- Die 1 shows 4 (1 way), Die 2 shows 3 (2 faces have 3): $1 \times 2 = 2$ ways.
- Die 1 shows 5 (1 way), Die 2 shows 2 (2 faces have 2): $1 \times 2 = 2$ ways.
- Die 1 shows 6 (1 way), Die 2 shows 1 (2 faces have 1): $1 \times 2 = 2$ ways.
Number of ways for Sum = 7: $2 + 2 + 2 = 6$.
- Die 1 shows 5 (1 way), Die 2 shows 3 (2 faces have 3): $1 \times 2 = 2$ ways.
- Die 1 shows 6 (1 way), Die 2 shows 2 (2 faces have 2): $1 \times 2 = 2$ ways.
Number of ways for Sum = 8: $2 + 2 = 4$.
Number of ways for Sum = 9: $1 \times 2 = 2$.
The probability of getting a specific sum is the number of ways to get that sum divided by the total number of outcomes (36).
- Probability of Sum = 2: $P(2) = \frac{2}{36} = \frac{1}{18}$
- Probability of Sum = 3: $P(3) = \frac{4}{36} = \frac{1}{9}$
- Probability of Sum = 4: $P(4) = \frac{6}{36} = \frac{1}{6}$
- Probability of Sum = 5: $P(5) = \frac{6}{36} = \frac{1}{6}$
- Probability of Sum = 6: $P(6) = \frac{6}{36} = \frac{1}{6}$
- Probability of Sum = 7: $P(7) = \frac{6}{36} = \frac{1}{6}$
- Probability of Sum = 8: $P(8) = \frac{4}{36} = \frac{1}{9}$
- Probability of Sum = 9: $P(9) = \frac{2}{36} = \frac{1}{18}$
The probabilities for each sum from 2 to 9 are:
$P(\text{Sum}=2) = \frac{1}{18}$
$P(\text{Sum}=3) = \frac{1}{9}$
$P(\text{Sum}=4) = \frac{1}{6}$
$P(\text{Sum}=5) = \frac{1}{6}$
$P(\text{Sum}=6) = \frac{1}{6}$
$P(\text{Sum}=7) = \frac{1}{6}$
$P(\text{Sum}=8) = \frac{1}{9}$
$P(\text{Sum}=9) = \frac{1}{18}$
Question 24. A coin is tossed two times. Find the probability of getting at most one head.
Answer:
Given:
A fair coin is tossed two times.
To Find:
The probability of getting at most one head.
Solution:
When a fair coin is tossed two times, the possible outcomes are:
Head on the first toss and Head on the second toss (HH)
Head on the first toss and Tail on the second toss (HT)
Tail on the first toss and Head on the second toss (TH)
Tail on the first toss and Tail on the second toss (TT)
The sample space $S$ consists of all possible outcomes:
$S = \{HH, HT, TH, TT\}$
The total number of possible outcomes is $n(S) = 4$.
We are interested in the event of getting "at most one head". This means the number of heads obtained is less than or equal to one. This includes the outcomes with zero heads or exactly one head.
Let $E$ be the event of getting at most one head.
Outcomes with zero heads: TT
Outcomes with exactly one head: HT, TH
The favourable outcomes for event $E$ are:
$E = \{HT, TH, TT\}$
The number of favourable outcomes is $n(E) = 3$.
The probability of an event is calculated using the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{n(E)}{n(S)}$
Substitute the number of favourable outcomes and the total number of outcomes into the formula:
$P(\text{at most one head}) = \frac{3}{4}$
The probability of getting at most one head is $\frac{3}{4}$.
Question 25. A coin is tossed 3 times. List the possible outcomes. Find the probability of getting
(i) all heads
(ii) at least 2 heads
Answer:
Given:
A fair coin is tossed 3 times.
To Find:
List the possible outcomes. Find the probability of getting:
(i) all heads
(ii) at least 2 heads
Solution:
When a fair coin is tossed 3 times, each toss has two possible outcomes: Head (H) or Tail (T). The total number of possible outcomes is $2 \times 2 \times 2 = 2^3 = 8$.
The possible outcomes can be listed by considering all combinations of H and T for the three tosses.
The sample space $S$ is:
- HHH
- HHT
- HTH
- THH
- HTT
- THT
- TTH
- TTT
The total number of outcomes is $n(S) = 8$.
(i) Probability of getting all heads:
Let $A$ be the event of getting all heads. This means getting H on all three tosses.
The favourable outcome for event $A$ is:
- HHH
The number of favourable outcomes is $n(A) = 1$.
The probability of event $A$ is given by:
$P(A) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{n(A)}{n(S)}$
$P(\text{all heads}) = \frac{1}{8}$
The probability of getting all heads is $\frac{1}{8}$.
(ii) Probability of getting at least 2 heads:
Let $B$ be the event of getting at least 2 heads. This means getting exactly 2 heads or exactly 3 heads.
Outcomes with exactly 2 heads: HHT, HTH, THH
Outcomes with exactly 3 heads: HHH
The favourable outcomes for event $B$ are:
- HHT
- HTH
- THH
- HHH
The number of favourable outcomes is $n(B) = 4$.
The probability of event $B$ is given by:
$P(B) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{n(B)}{n(S)}$
$P(\text{at least 2 heads}) = \frac{4}{8}$
Simplify the fraction:
$P(\text{at least 2 heads}) = \frac{\cancel{4}^1}{\cancel{8}_2}$
$P(\text{at least 2 heads}) = \frac{1}{2}$
The probability of getting at least 2 heads is $\frac{1}{2}$.
Question 26. Two dice are thrown at the same time. Determine the probabiity that the difference of the numbers on the two dice is 2.
Answer:
Given:
Two fair dice are thrown simultaneously.
To Determine:
The probability that the difference of the numbers on the two dice is 2.
Solution:
When two fair dice are thrown, the total number of possible outcomes is $6 \times 6 = 36$.
The sample space $S$ consists of 36 ordered pairs $(d_1, d_2)$, where $d_1$ is the number on the first die ($d_1 \in \{1, 2, 3, 4, 5, 6\}$) and $d_2$ is the number on the second die ($d_2 \in \{1, 2, 3, 4, 5, 6\}$).
Let $E$ be the event that the difference of the numbers on the two dice is 2. This means the absolute difference between the numbers is 2, i.e., $|d_1 - d_2| = 2$.
We need to list the pairs $(d_1, d_2)$ such that $|d_1 - d_2| = 2$:
- If the first die is 1, the second must be $1+2=3$. Pair: (1, 3).
- If the first die is 2, the second must be $2+2=4$. Pair: (2, 4).
- If the first die is 3, the second can be $3-2=1$ or $3+2=5$. Pairs: (3, 1), (3, 5).
- If the first die is 4, the second can be $4-2=2$ or $4+2=6$. Pairs: (4, 2), (4, 6).
- If the first die is 5, the second must be $5-2=3$. Pair: (5, 3).
- If the first die is 6, the second must be $6-2=4$. Pair: (6, 4).
The favourable outcomes for event $E$ are:
$E = \{(1,3), (2,4), (3,1), (3,5), (4,2), (4,6), (5,3), (6,4)\}$
The number of favourable outcomes is $n(E) = 8$.
The probability of event $E$ is calculated using the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{n(E)}{n(S)}$
Substitute the number of favourable outcomes and the total number of outcomes into the formula:
$P(\text{difference is 2}) = \frac{8}{36}$
Simplify the fraction:
$P(\text{difference is 2}) = \frac{\cancel{8}^2}{\cancel{36}_9}$
$P(\text{difference is 2}) = \frac{2}{9}$
The probability that the difference of the numbers on the two dice is 2 is $\frac{2}{9}$.
Question 27. A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a
(i) red ball
(ii) green ball
(iii) not a blue ball
Answer:
Given:
A bag contains 10 red balls, 5 blue balls, and 7 green balls.
A ball is drawn at random from the bag.
To Find:
The probability of the ball being:
(i) a red ball
(ii) a green ball
(iii) not a blue ball
Solution:
First, calculate the total number of balls in the bag.
Total number of balls = Number of red balls + Number of blue balls + Number of green balls
Total number of balls = $10 + 5 + 7 = 22$
The total number of possible outcomes when drawing one ball at random is the total number of balls in the bag, which is 22.
The probability of an event $E$ is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of being a red ball:
Let $R$ be the event that the drawn ball is red.
The number of favourable outcomes (drawing a red ball) is the number of red balls, which is 10.
$n(R) = 10$
Total number of outcomes = 22.
$P(\text{red ball}) = \frac{n(R)}{\text{Total number of balls}} = \frac{10}{22}$
Simplify the fraction:
$P(\text{red ball}) = \frac{\cancel{10}^5}{\cancel{22}_{11}}$
$P(\text{red ball}) = \frac{5}{11}$
The probability of the ball being a red ball is $\frac{5}{11}$.
(ii) Probability of being a green ball:
Let $G$ be the event that the drawn ball is green.
The number of favourable outcomes (drawing a green ball) is the number of green balls, which is 7.
$n(G) = 7$
Total number of outcomes = 22.
$P(\text{green ball}) = \frac{n(G)}{\text{Total number of balls}} = \frac{7}{22}$
The probability of the ball being a green ball is $\frac{7}{22}$.
(iii) Probability of not being a blue ball:
Let $B$ be the event that the drawn ball is blue.
Let $B'$ be the event that the drawn ball is not blue.
The event "not a blue ball" means the ball is either red or green.
Number of balls that are not blue = Number of red balls + Number of green balls
Number of balls that are not blue = $10 + 7 = 17$.
$n(B') = 17$
Total number of outcomes = 22.
$P(\text{not a blue ball}) = \frac{n(B')}{\text{Total number of balls}} = \frac{17}{22}$
The probability of the ball not being a blue ball is $\frac{17}{22}$.
Alternate Solution (for part iii):
The event "not a blue ball" is the complement of the event "being a blue ball".
Let $B$ be the event of drawing a blue ball.
Number of blue balls = 5.
Total number of balls = 22.
$P(B) = \frac{\text{Number of blue balls}}{\text{Total number of balls}} = \frac{5}{22}$
The probability of not being a blue ball is $P(B') = 1 - P(B)$.
$P(\text{not a blue ball}) = 1 - \frac{5}{22}$
$P(\text{not a blue ball}) = \frac{22}{22} - \frac{5}{22} = \frac{22-5}{22}$
$P(\text{not a blue ball}) = \frac{17}{22}$
This confirms the result obtained earlier.
Question 28. The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. Determine the probability that the card is
(i) a heart
(ii) a king
Answer:
Given:
A standard deck of 52 playing cards. The king, queen, and jack of clubs are removed. One card is drawn at random from the remaining cards.
To Determine:
The probability that the card drawn is:
(i) a heart
(ii) a king
Solution:
A standard deck of 52 cards has 4 suits: Hearts, Diamonds, Clubs, and Spades. Each suit has 13 cards: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King.
The king, queen, and jack of clubs are removed from the deck.
Initial number of cards = 52.
Number of cards removed = 3 (King of clubs, Queen of clubs, Jack of clubs).
Number of remaining cards = $52 - 3 = 49$.
The total number of possible outcomes when drawing one card from the remaining deck is 49.
The remaining cards consist of:
- Hearts: 13 cards
- Diamonds: 13 cards
- Clubs: 13 - 3 = 10 cards (excluding K, Q, J)
- Spades: 13 cards
Check: $13 + 13 + 10 + 13 = 49$. This matches the number of remaining cards.
(i) Probability that the card is a heart:
Let $H$ be the event that the drawn card is a heart.
The number of favourable outcomes (drawing a heart) is the number of heart cards in the remaining deck, which is 13.
$n(H) = 13$
Total number of outcomes = 49.
$P(\text{a heart}) = \frac{n(H)}{\text{Total number of remaining cards}} = \frac{13}{49}$
The probability that the card is a heart is $\frac{13}{49}$.
(ii) Probability that the card is a king:
Let $K$ be the event that the drawn card is a king.
A standard deck has 4 kings (one of each suit: Hearts, Diamonds, Clubs, Spades).
The king of clubs was removed. So, the kings remaining in the deck are the King of Hearts, King of Diamonds, and King of Spades.
The number of favourable outcomes (drawing a king) is the number of kings remaining, which is 3.
$n(K) = 3$
Total number of outcomes = 49.
$P(\text{a king}) = \frac{n(K)}{\text{Total number of remaining cards}} = \frac{3}{49}$
The probability that the card is a king is $\frac{3}{49}$.
Question 29. Refer to Q.28. What is the probability that the card is
(i) a club
(ii) 10 of hearts
Answer:
Given:
A deck of 52 playing cards from which the king, queen, and jack of clubs have been removed.
One card is drawn at random from the remaining cards.
From Question 28, the total number of remaining cards is $52 - 3 = 49$.
The remaining cards consist of:
- Hearts: 13 cards
- Diamonds: 13 cards
- Clubs: 10 cards (Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10)
- Spades: 13 cards
To Determine:
The probability that the card drawn is:
(i) a club
(ii) 10 of hearts
Solution:
The total number of possible outcomes when drawing one card from the remaining deck is 49.
The probability of an event $E$ is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the card is a club:
Let $C$ be the event that the drawn card is a club.
From the given information, the number of club cards remaining after removing the King, Queen, and Jack is 10.
$n(C) = 10$
Total number of outcomes = 49.
$P(\text{a club}) = \frac{n(C)}{\text{Total number of remaining cards}} = \frac{10}{49}$
The probability that the card is a club is $\frac{10}{49}$.
(ii) Probability that the card is 10 of hearts:
Let $T_H$ be the event that the drawn card is the 10 of hearts.
The King, Queen, and Jack of clubs were removed. The heart cards were not affected. There is exactly one card that is the 10 of hearts in a standard deck.
Since the heart suit was not modified, the 10 of hearts is still in the remaining deck.
The number of favourable outcomes (drawing the 10 of hearts) is 1.
$n(T_H) = 1$
Total number of outcomes = 49.
$P(\text{10 of hearts}) = \frac{n(T_H)}{\text{Total number of remaining cards}} = \frac{1}{49}$
The probability that the card is the 10 of hearts is $\frac{1}{49}$.
Question 30. All the jacks, queens and kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value
(i) 7
(ii) greater than 7
(iii) less than 7
Answer:
Given:
A standard deck of 52 playing cards. All jacks, queens, and kings are removed. One card is drawn at random from the remaining cards.
Ace is given a value of 1, and other cards have their face value (2 to 10).
To Find:
The probability that the card drawn has a value:
(i) 7
(ii) greater than 7
(iii) less than 7
Solution:
A standard deck of 52 cards has 4 suits (Hearts, Diamonds, Clubs, Spades). Each suit has 13 cards: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack (J), Queen (Q), King (K).
The jacks, queens, and kings from all four suits are removed.
Number of jacks removed = 4 (one from each suit).
Number of queens removed = 4 (one from each suit).
Number of kings removed = 4 (one from each suit).
Total number of cards removed = $4 + 4 + 4 = 12$.
Number of remaining cards = $52 - 12 = 40$.
The total number of possible outcomes when drawing one card from the remaining deck is 40.
The remaining cards in each suit are: Ace (value 1), 2, 3, 4, 5, 6, 7, 8, 9, 10.
There are 10 cards in each of the 4 suits, totalling $10 \times 4 = 40$ cards.
The possible values of the remaining cards are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
For each value, there are 4 cards (one from each suit).
The probability of an event $E$ is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the card has a value 7:
Let $E_1$ be the event that the drawn card has a value of 7.
The cards with value 7 are the four 7s (7 of Hearts, 7 of Diamonds, 7 of Clubs, 7 of Spades). These cards were not removed.
The number of favourable outcomes is $n(E_1) = 4$.
Total number of outcomes = 40.
$P(\text{value is 7}) = \frac{n(E_1)}{\text{Total number of remaining cards}} = \frac{4}{40}$
$P(\text{value is 7}) = \frac{\cancel{4}^1}{\cancel{40}_{10}}$
$P(\text{value is 7}) = \frac{1}{10}$
The probability that the card has a value 7 is $\frac{1}{10}$.
(ii) Probability that the card has a value greater than 7:
Let $E_2$ be the event that the drawn card has a value greater than 7.
The values greater than 7 among the remaining cards are 8, 9, and 10.
Number of cards with value 8 = 4 (one for each suit)
Number of cards with value 9 = 4 (one for each suit)
Number of cards with value 10 = 4 (one for each suit)
The number of favourable outcomes is $n(E_2) = 4 + 4 + 4 = 12$.
Total number of outcomes = 40.
$P(\text{value > 7}) = \frac{n(E_2)}{\text{Total number of remaining cards}} = \frac{12}{40}$
$P(\text{value > 7}) = \frac{\cancel{12}^3}{\cancel{40}_{10}}$
$P(\text{value > 7}) = \frac{3}{10}$
The probability that the card has a value greater than 7 is $\frac{3}{10}$.
(iii) Probability that the card has a value less than 7:
Let $E_3$ be the event that the drawn card has a value less than 7.
The values less than 7 among the remaining cards are Ace (value 1), 2, 3, 4, 5, and 6.
Number of cards with value 1 (Ace) = 4
Number of cards with value 2 = 4
Number of cards with value 3 = 4
Number of cards with value 4 = 4
Number of cards with value 5 = 4
Number of cards with value 6 = 4
The number of favourable outcomes is $n(E_3) = 4 + 4 + 4 + 4 + 4 + 4 = 6 \times 4 = 24$.
Total number of outcomes = 40.
$P(\text{value < 7}) = \frac{n(E_3)}{\text{Total number of remaining cards}} = \frac{24}{40}$
$P(\text{value < 7}) = \frac{\cancel{24}^3}{\cancel{40}_5}$
$P(\text{value < 7}) = \frac{3}{5}$
The probability that the card has a value less than 7 is $\frac{3}{5}$.
Question 31. An integer is chosen between 0 and 100. What is the probability that it is
(i) divisible by 7?
(ii) not divisible by 7?
Answer:
Given:
An integer is chosen between 0 and 100.
To Find:
The probability that the integer is:
(i) divisible by 7
(ii) not divisible by 7
Solution:
The phrase "between 0 and 100" implies that the integers are greater than 0 and less than 100. Thus, the possible integers are 1, 2, 3, ..., 99.
The total number of possible outcomes is the number of integers from 1 to 99, inclusive.
Total number of outcomes = $99 - 1 + 1 = 99$.
$n(S) = 99$
The probability of an event $E$ is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the integer is divisible by 7:
Let $E_1$ be the event that the chosen integer is divisible by 7.
The integers between 0 and 100 (i.e., from 1 to 99) that are divisible by 7 are the multiples of 7 in this range.
Multiples of 7: $7 \times 1 = 7, 7 \times 2 = 14, ..., 7 \times k$.
We need to find the largest integer $k$ such that $7k \leq 99$.
$k \leq \frac{99}{7}$
$k \leq 14.14...$
The largest integer $k$ is 14. So the multiples are $7 \times 1, 7 \times 2, ..., 7 \times 14$.
The integers divisible by 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98.
The number of favourable outcomes is $n(E_1) = 14$.
Total number of outcomes = 99.
$P(\text{divisible by 7}) = \frac{n(E_1)}{n(S)} = \frac{14}{99}$
The probability that the integer is divisible by 7 is $\frac{14}{99}$.
(ii) Probability that the integer is not divisible by 7:
Let $E_2$ be the event that the chosen integer is not divisible by 7.
The number of integers that are not divisible by 7 is the total number of integers minus the number of integers that are divisible by 7.
Number of favourable outcomes $n(E_2) = n(S) - n(E_1) = 99 - 14 = 85$.
Total number of outcomes = 99.
$P(\text{not divisible by 7}) = \frac{n(E_2)}{n(S)} = \frac{85}{99}$
The probability that the integer is not divisible by 7 is $\frac{85}{99}$.
Alternate Solution (for part ii):
The event that the integer is not divisible by 7 is the complement of the event that the integer is divisible by 7.
Let $E_1$ be the event that the integer is divisible by 7.
Let $E_2$ be the event that the integer is not divisible by 7.
$E_2 = E_1'$
The probability of the complement event is $P(E_2) = 1 - P(E_1)$.
From part (i), we have $P(E_1) = \frac{14}{99}$.
$P(\text{not divisible by 7}) = 1 - \frac{14}{99}$
$P(\text{not divisible by 7}) = \frac{99}{99} - \frac{14}{99} = \frac{99-14}{99}$
$P(\text{not divisible by 7}) = \frac{85}{99}$
This confirms the result obtained earlier.
Question 32. Cards with numbers 2 to 101 are placed in a box. A card is selected at random. Find the probability that the card has
(i) an even number
(ii) a square number
Answer:
Given:
A box contains cards with numbers from 2 to 101. A card is selected at random.
To Find:
The probability that the card has:
(i) an even number
(ii) a square number
Solution:
The cards in the box are numbered 2, 3, 4, ..., 101.
The total number of possible outcomes is the number of integers from 2 to 101, inclusive.
Total number of outcomes = $101 - 2 + 1 = 100$.
$n(S) = 100$
The probability of an event $E$ is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the card has an even number:
Let $E_1$ be the event that the chosen card has an even number.
The even numbers between 2 and 101 (inclusive) are 2, 4, 6, ..., 100.
These are of the form $2k$. We need to find the number of such integers where $2 \leq 2k \leq 100$.
Divide by 2: $1 \leq k \leq 50$.
The values of $k$ are 1, 2, ..., 50. The number of such values is 50.
The even numbers are $2 \times 1, 2 \times 2, ..., 2 \times 50$.
The number of favourable outcomes is $n(E_1) = 50$.
Total number of outcomes = 100.
$P(\text{an even number}) = \frac{n(E_1)}{n(S)} = \frac{50}{100}$
$P(\text{an even number}) = \frac{\cancel{50}^1}{\cancel{100}_2}$
$P(\text{an even number}) = \frac{1}{2}$
The probability that the card has an even number is $\frac{1}{2}$.
(ii) Probability that the card has a square number:
Let $E_2$ be the event that the chosen card has a square number.
The square numbers are numbers that are the square of an integer ($k^2$). We need to find the square numbers between 2 and 101 (inclusive).
- $1^2 = 1$ (not in the range 2-101)
- $2^2 = 4$ (in the range)
- $3^2 = 9$ (in the range)
- $4^2 = 16$ (in the range)
- $5^2 = 25$ (in the range)
- $6^2 = 36$ (in the range)
- $7^2 = 49$ (in the range)
- $8^2 = 64$ (in the range)
- $9^2 = 81$ (in the range)
- $10^2 = 100$ (in the range)
- $11^2 = 121$ (not in the range)
The square numbers in the range 2 to 101 are 4, 9, 16, 25, 36, 49, 64, 81, 100.
The number of favourable outcomes is $n(E_2) = 9$.
Total number of outcomes = 100.
$P(\text{a square number}) = \frac{n(E_2)}{n(S)} = \frac{9}{100}$
The probability that the card has a square number is $\frac{9}{100}$.
Question 33. A letter of English alphabets is chosen at random. Determine the probability that the letter is a consonant.
Answer:
Given:
A letter of the English alphabet is chosen at random.
To Determine:
The probability that the letter is a consonant.
Solution:
The English alphabet consists of 26 letters.
The total number of possible outcomes when choosing one letter is 26.
$n(S) = 26$
The English alphabet is divided into vowels and consonants.
The vowels are A, E, I, O, U.
Number of vowels = 5.
The consonants are all the letters that are not vowels.
Number of consonants = Total number of letters - Number of vowels
Number of consonants = $26 - 5 = 21$.
Let $C$ be the event that the chosen letter is a consonant.
The number of favourable outcomes (choosing a consonant) is the number of consonants, which is 21.
$n(C) = 21$
The probability of an event is calculated using the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{a consonant}) = \frac{n(C)}{n(S)} = \frac{21}{26}$
The probability that the letter chosen is a consonant is $\frac{21}{26}$.
Question 34. There are 1000 sealed envelopes in a box, 10 of them contain a cash prize of Rs 100 each, 100 of them contain a cash prize of Rs 50 each and 200 of them contain a cash prize of Rs 10 each and rest do not contain any cash prize. If they are well shuffled and an envelope is picked up out, what is the probability that it contains no cash prize?
Answer:
Given:
Total number of sealed envelopes in a box = 1000.
Number of envelopes with $\textsf{₹} 100$ prize = 10.
Number of envelopes with $\textsf{₹} 50$ prize = 100.
Number of envelopes with $\textsf{₹} 10$ prize = 200.
The rest contain no cash prize.
An envelope is picked at random.
To Find:
The probability that the picked envelope contains no cash prize.
Solution:
First, find the total number of envelopes that contain a cash prize.
Number of envelopes with prize = (Number with $\textsf{₹} 100$) + (Number with $\textsf{₹} 50$) + (Number with $\textsf{₹} 10$)
Number of envelopes with prize = $10 + 100 + 200 = 310$
Next, find the number of envelopes that do not contain any cash prize.
Number of envelopes with no prize = Total number of envelopes - Number of envelopes with prize
Number of envelopes with no prize = $1000 - 310 = 690$
The total number of possible outcomes when picking one envelope at random is the total number of envelopes in the box.
Total number of possible outcomes = 1000.
The number of favourable outcomes for the event "contains no cash prize" is the number of envelopes with no cash prize, which is 690.
The probability of an event is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Let $N$ be the event that the picked envelope contains no cash prize.
$P(N) = \frac{\text{Number of envelopes with no prize}}{\text{Total number of envelopes}}$
$P(\text{no cash prize}) = \frac{690}{1000}$
Simplify the fraction:
$P(\text{no cash prize}) = \frac{\cancel{690}^{69}}{\cancel{1000}_{100}}$
$P(\text{no cash prize}) = \frac{69}{100}$
The probability that the envelope contains no cash prize is $\frac{69}{100}$.
Question 35. Box A contains 25 slips of which 19 are marked Re 1 and other are marked Rs 5 each. Box B contains 50 slips of which 45 are marked Re 1 each and others are marked Rs 13 each. Slips of both boxes are poured into a third box and resuffled. A slip is drawn at random. What is the probability that it is marked other than Re 1?
Answer:
Given:
Box A contains 25 slips: 19 marked $\textsf{₹} 1$ and the rest marked $\textsf{₹} 5$.
Box B contains 50 slips: 45 marked $\textsf{₹} 1$ and the rest marked $\textsf{₹} 13$.
All slips from both boxes are poured into a third box and reshuffled. A slip is drawn at random from the third box.
To Find:
The probability that the drawn slip is marked other than $\textsf{₹} 1$.
Solution:
First, determine the composition of each box and the third box.
Box A:
- Total slips = 25
- Slips marked $\textsf{₹} 1$ = 19
- Slips marked $\textsf{₹} 5$ = Total slips in A - Slips marked $\textsf{₹} 1$ in A = $25 - 19 = 6$
Box B:
- Total slips = 50
- Slips marked $\textsf{₹} 1$ = 45
- Slips marked $\textsf{₹} 13$ = Total slips in B - Slips marked $\textsf{₹} 1$ in B = $50 - 45 = 5$
Third Box:
When slips from both boxes are poured into the third box, the total number of slips is the sum of the slips in Box A and Box B.
Total number of slips in the third box = Total slips in A + Total slips in B = $25 + 50 = 75$.
These 75 slips constitute the total number of possible outcomes when drawing a slip from the third box. $n(S) = 75$.
We want to find the probability that the slip is marked "other than $\textsf{₹} 1$". This means the slip is marked either $\textsf{₹} 5$ or $\textsf{₹} 13$.
Number of slips marked $\textsf{₹} 5$ in the third box = 6 (from Box A)
Number of slips marked $\textsf{₹} 13$ in the third box = 5 (from Box B)
The number of favourable outcomes (slips marked other than $\textsf{₹} 1$) is the sum of the slips marked $\textsf{₹} 5$ and $\textsf{₹} 13$ in the third box.
Number of slips marked other than $\textsf{₹} 1 = 6 + 5 = 11$.
Let $E$ be the event that the drawn slip is marked other than $\textsf{₹} 1$.
The number of favourable outcomes is $n(E) = 11$.
Total number of possible outcomes = 75.
The probability of event $E$ is given by:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{n(E)}{n(S)}$
$P(\text{marked other than } \textsf{₹} 1) = \frac{11}{75}$
The probability that the drawn slip is marked other than $\textsf{₹} 1$ is $\frac{11}{75}$.
Alternate Solution:
The event "marked other than $\textsf{₹} 1$" is the complement of the event "marked $\textsf{₹} 1$".
Total number of slips in the third box = 75.
Number of slips marked $\textsf{₹} 1$ in the third box = (Slips marked $\textsf{₹} 1$ in A) + (Slips marked $\textsf{₹} 1$ in B) = $19 + 45 = 64$.
Let $R_1$ be the event that the drawn slip is marked $\textsf{₹} 1$.
$P(R_1) = \frac{\text{Number of slips marked } \textsf{₹} 1}{\text{Total number of slips}} = \frac{64}{75}$
The probability of the slip being marked other than $\textsf{₹} 1$ is $1 - P(R_1)$.
$P(\text{marked other than } \textsf{₹} 1) = 1 - \frac{64}{75}$
$P(\text{marked other than } \textsf{₹} 1) = \frac{75}{75} - \frac{64}{75} = \frac{75-64}{75}$
$P(\text{marked other than } \textsf{₹} 1) = \frac{11}{75}$
This confirms the result obtained earlier.
Question 36. A carton of 24 bulbs contain 6 defective bulbs. One bulbs is drawn at random. What is the probability that the bulb is not defective? If the bulb selected is defective and it is not replaced and a second bulb is selected at random from the rest, what is the probability that the second bulb is defective?
Answer:
Given:
A carton contains 24 bulbs.
Number of defective bulbs = 6.
Number of non-defective bulbs = Total bulbs - Defective bulbs = $24 - 6 = 18$.
To Find:
1. Probability that a randomly drawn bulb is not defective.
2. If the first bulb drawn is defective and not replaced, the probability that a second randomly drawn bulb is defective.
Solution:
Total number of bulbs in the carton = 24.
Number of defective bulbs = 6.
Number of non-defective bulbs = 18.
Total number of possible outcomes when drawing one bulb = 24.
The probability of an event $E$ is given by: $P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$.
Part 1: Probability that the first bulb is not defective
Let $ND_1$ be the event that the first bulb drawn is not defective.
The number of favourable outcomes (drawing a non-defective bulb) is the number of non-defective bulbs, which is 18.
$n(ND_1) = 18$.
$P(ND_1) = \frac{\text{Number of non-defective bulbs}}{\text{Total number of bulbs}}$
$P(\text{not defective}) = \frac{18}{24}$
Simplify the fraction:
$P(\text{not defective}) = \frac{\cancel{18}^3}{\cancel{24}_4}$
$P(\text{not defective}) = \frac{3}{4}$
The probability that the first bulb drawn is not defective is $\frac{3}{4}$.
Part 2: Probability that the second bulb is defective, given the first was defective and not replaced
Assume the first bulb drawn was defective and it was not replaced.
Now, the total number of bulbs remaining in the carton is $24 - 1 = 23$.
Since one defective bulb was removed, the number of defective bulbs remaining is $6 - 1 = 5$.
The number of non-defective bulbs remaining is 18 (as none were removed in the first step).
Total number of outcomes for the second draw = 23.
Let $D_2$ be the event that the second bulb drawn is defective.
The number of favourable outcomes for the second draw (drawing a defective bulb) is the number of defective bulbs remaining, which is 5.
$n(D_2 \text{ after } D_1) = 5$.
The probability of the second bulb being defective, given the first was defective and not replaced, is:
$P(D_2 \mid D_1) = \frac{\text{Number of remaining defective bulbs}}{\text{Total number of remaining bulbs}}$
$P(\text{second defective } \mid \text{ first defective}) = \frac{5}{23}$
The probability that the second bulb drawn is defective, given the first was defective and not replaced, is $\frac{5}{23}$.
Question 37. A child’s game has 8 triangles of which 3 are blue and rest are red, and 10 squares of which 6 are blue and rest are red. One piece is lost at random. Find the probability that it is a
(i) triangle
(ii) square
(iii) square of blue colour
(iv) triangle of red colour
Answer:
Given:
A child's game has 8 triangles and 10 squares.
Among the triangles: 3 are blue, the rest are red. So, red triangles = $8 - 3 = 5$.
Among the squares: 6 are blue, the rest are red. So, red squares = $10 - 6 = 4$.
One piece is lost at random.
To Find:
The probability that the lost piece is a:
(i) triangle
(ii) square
(iii) square of blue colour
(iv) triangle of red colour
Solution:
First, find the total number of pieces in the game.
Total number of pieces = Number of triangles + Number of squares
Total number of pieces = $8 + 10 = 18$.
The total number of possible outcomes when one piece is lost is 18.
$n(S) = 18$.
The probability of an event $E$ is given by: $P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$.
(i) Probability that the lost piece is a triangle:
Let $T$ be the event that the lost piece is a triangle.
The number of favourable outcomes (lost piece is a triangle) is the total number of triangles, which is 8.
$n(T) = 8$.
$P(\text{a triangle}) = \frac{\text{Number of triangles}}{\text{Total number of pieces}} = \frac{8}{18}$
Simplify the fraction:
$P(\text{a triangle}) = \frac{\cancel{8}^4}{\cancel{18}_9}$
$P(\text{a triangle}) = \frac{4}{9}$
The probability that the lost piece is a triangle is $\frac{4}{9}$.
(ii) Probability that the lost piece is a square:
Let $Q$ be the event that the lost piece is a square.
The number of favourable outcomes (lost piece is a square) is the total number of squares, which is 10.
$n(Q) = 10$.
$P(\text{a square}) = \frac{\text{Number of squares}}{\text{Total number of pieces}} = \frac{10}{18}$
Simplify the fraction:
$P(\text{a square}) = \frac{\cancel{10}^5}{\cancel{18}_9}$
$P(\text{a square}) = \frac{5}{9}$
The probability that the lost piece is a square is $\frac{5}{9}$.
(iii) Probability that the lost piece is a square of blue colour:
Let $QB$ be the event that the lost piece is a blue square.
The number of blue squares is given as 6.
$n(QB) = 6$.
$P(\text{blue square}) = \frac{\text{Number of blue squares}}{\text{Total number of pieces}} = \frac{6}{18}$
Simplify the fraction:
$P(\text{blue square}) = \frac{\cancel{6}^1}{\cancel{18}_3}$
$P(\text{blue square}) = \frac{1}{3}$
The probability that the lost piece is a square of blue colour is $\frac{1}{3}$.
(iv) Probability that the lost piece is a triangle of red colour:
Let $TR$ be the event that the lost piece is a red triangle.
The number of red triangles is the total number of triangles minus the number of blue triangles = $8 - 3 = 5$.
$n(TR) = 5$.
$P(\text{red triangle}) = \frac{\text{Number of red triangles}}{\text{Total number of pieces}} = \frac{5}{18}$
The probability that the lost piece is a triangle of red colour is $\frac{5}{18}$.
Question 38. In a game, the entry fee is Rs 5. The game consists of a tossing a coin 3 times. If one or two heads show, Sweta gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise she will lose. For tossing a coin three times, find the probability that she
(i) loses the entry fee.
(ii) gets double entry fee.
(iii) just gets her entry fee.
Answer:
Given:
Entry fee for a game is $\textsf{₹} 5$. The game involves tossing a coin 3 times.
Rules for winning/losing:
- One or two heads: Entry fee back ($\textsf{₹} 5$).
- Three heads: Double entry fee ($\textsf{₹} 10$).
- Otherwise (zero heads): Loses the entry fee.
To Find:
For tossing a coin three times, find the probability that Sweta:
(i) loses the entry fee.
(ii) gets double entry fee.
(iii) just gets her entry fee back.
Solution:
When a fair coin is tossed 3 times, the possible outcomes are:
Sample space $S = \{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT\}$
The total number of possible outcomes is $n(S) = 8$.
Let's analyze the number of heads in each outcome:
- HHH: 3 heads
- HHT: 2 heads
- HTH: 2 heads
- THH: 2 heads
- HTT: 1 head
- THT: 1 head
- TTH: 1 head
- TTT: 0 heads
Now, let's relate these outcomes to the game rules and define events for each scenario.
(i) Probability that she loses the entry fee:
Sweta loses the entry fee if she gets "otherwise", which means zero heads.
Let $L$ be the event that Sweta loses the entry fee (gets 0 heads).
The outcome with 0 heads is TTT.
Favourable outcomes for event $L$: $\{TTT\}$
Number of favourable outcomes, $n(L) = 1$.
Probability $P(L) = \frac{n(L)}{n(S)} = \frac{1}{8}$.
The probability that she loses the entry fee is $\frac{1}{8}$.
(ii) Probability that she gets double entry fee:
Sweta gets double entry fee if she throws 3 heads.
Let $D$ be the event that Sweta gets double entry fee (gets 3 heads).
The outcome with 3 heads is HHH.
Favourable outcomes for event $D$: $\{HHH\}$
Number of favourable outcomes, $n(D) = 1$.
Probability $P(D) = \frac{n(D)}{n(S)} = \frac{1}{8}$.
The probability that she gets double entry fee is $\frac{1}{8}$.
(iii) Probability that she just gets her entry fee back:
Sweta gets her entry fee back if she throws one or two heads.
Let $E$ be the event that Sweta just gets her entry fee back (gets 1 or 2 heads).
Outcomes with 1 head: HTT, THT, TTH
Outcomes with 2 heads: HHT, HTH, THH
Favourable outcomes for event $E$: $\{HHT, HTH, THH, HTT, THT, TTH\}$
Number of favourable outcomes, $n(E) = 3 + 3 = 6$.
Probability $P(E) = \frac{n(E)}{n(S)} = \frac{6}{8}$.
Simplify the fraction:
$P(E) = \frac{\cancel{6}^3}{\cancel{8}_4}$
$P(E) = \frac{3}{4}$
The probability that she just gets her entry fee back is $\frac{3}{4}$.
Verification: The sum of probabilities of all possible outcomes should be 1. The possible outcomes regarding heads are 0 heads, 1 head, 2 heads, or 3 heads.
Probability of 0 heads (Losing) = $P(L) = \frac{1}{8}$
Probability of 1 or 2 heads (Getting fee back) = $P(E) = \frac{6}{8}$
Probability of 3 heads (Getting double fee) = $P(D) = \frac{1}{8}$
Sum of probabilities = $P(L) + P(E) + P(D) = \frac{1}{8} + \frac{6}{8} + \frac{1}{8} = \frac{1+6+1}{8} = \frac{8}{8} = 1$. This confirms the calculations are correct.
Question 39. A die has its six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded.
(i) How many different scores are possible?
(ii) What is the probability of getting a total of 7?
Answer:
Given:
Two dice are thrown together. Each die has its six faces marked 0, 1, 1, 1, 6, 6.
To Find:
(i) The number of different possible scores (sums).
(ii) The probability of getting a total score of 7.
Solution:
Each die has 6 faces with the numbers $\{0, 1, 1, 1, 6, 6\}$. The possible outcomes for a single throw of one die are the values on the faces: 0, 1, or 6.
When two such dice are thrown, the total score is the sum of the numbers shown on the top faces of the two dice.
Let the outcome of the first die be $d_1$ and the outcome of the second die be $d_2$, where $d_1, d_2 \in \{0, 1, 6\}$.
(i) How many different scores are possible?
The possible sums are obtained by adding any possible outcome from the first die to any possible outcome from the second die. The possible outcomes for each die are 0, 1, and 6.
Let's list the possible sums:
- Sum of 0 and 0: $0 + 0 = 0$
- Sum of 0 and 1: $0 + 1 = 1$
- Sum of 0 and 6: $0 + 6 = 6$
- Sum of 1 and 1: $1 + 1 = 2$
- Sum of 1 and 6: $1 + 6 = 7$
- Sum of 6 and 6: $6 + 6 = 12$
The possible sums (scores) are 0, 1, 2, 6, 7, and 12.
These are 6 distinct values.
The number of different possible scores is 6.
(ii) What is the probability of getting a total of 7?
The total number of possible outcomes when throwing two dice is the product of the number of faces on each die. Since each die has 6 faces, the total number of outcomes is $6 \times 6 = 36$.
The sample space consists of 36 ordered pairs $(d_1, d_2)$, where $d_1$ is the number on the first die and $d_2$ is the number on the second die, considering the specific faces marked on each die: $\{0, 1, 1, 1, 6, 6\}$.
We want to find the number of outcomes where the sum of the numbers on the two dice is 7 ($d_1 + d_2 = 7$).
We need to find pairs of faces from the two dice that add up to 7. The possible face values are 0, 1, or 6.
A sum of 7 can be obtained by adding 1 and 6.
- Case 1: First die shows 1, Second die shows 6.
- Case 2: First die shows 6, Second die shows 1.
The number '1' appears on 3 faces of the first die.
The number '6' appears on 2 faces of the second die.
Number of ways for this case = (Number of '1' faces on Die 1) $\times$ (Number of '6' faces on Die 2) $= 3 \times 2 = 6$.
The number '6' appears on 2 faces of the first die.
The number '1' appears on 3 faces of the second die.
Number of ways for this case = (Number of '6' faces on Die 1) $\times$ (Number of '1' faces on Die 2) $= 2 \times 3 = 6$.
The total number of favourable outcomes for getting a sum of 7 is the sum of the ways in Case 1 and Case 2.
Number of favourable outcomes for sum = 7 is $6 + 6 = 12$.
The probability of getting a total of 7 is given by:
$P(\text{total of 7}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{12}{36}$
Simplify the fraction:
$P(\text{total of 7}) = \frac{\cancel{12}^1}{\cancel{36}_3}$
$P(\text{total of 7}) = \frac{1}{3}$
The probability of getting a total score of 7 is $\frac{1}{3}$.
Question 40. A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone if it is good but the trader will only buy a mobile if it has no major defect. One phone is selected at random from the lot. What is the probability that it is
(i) acceptable to Varnika?
(ii) acceptable to the trader?
Answer:
Given:
Total number of mobile phones in a lot = 48.
Number of good phones = 42.
Number of phones with minor defects = 3.
Number of phones with major defects = 3.
Total number of phones = $42 + 3 + 3 = 48$. This matches the given total.
Varnika buys a phone if it is good.
The trader buys a phone if it has no major defect.
One phone is selected at random from the lot.
To Find:
The probability that the selected phone is:
(i) acceptable to Varnika
(ii) acceptable to the trader
Solution:
Total number of possible outcomes when selecting one phone is 48.
$n(S) = 48$.
The probability of an event $E$ is given by: $P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$.
(i) Probability that the phone is acceptable to Varnika:
Varnika will buy a phone if it is good.
Let $A_V$ be the event that the selected phone is acceptable to Varnika (i.e., it is good).
The number of favourable outcomes (good phones) is 42.
$n(A_V) = 42$.
$P(\text{acceptable to Varnika}) = \frac{\text{Number of good phones}}{\text{Total number of phones}} = \frac{42}{48}$
Simplify the fraction by dividing numerator and denominator by their greatest common divisor, which is 6:
$P(\text{acceptable to Varnika}) = \frac{\cancel{42}^7}{\cancel{48}_8}$
$P(\text{acceptable to Varnika}) = \frac{7}{8}$
The probability that the phone is acceptable to Varnika is $\frac{7}{8}$.
(ii) Probability that the phone is acceptable to the trader:
The trader will buy a mobile if it has no major defect.
This means the phone can be good or have only minor defects. The phones the trader will NOT buy are those with major defects.
Number of phones with major defects = 3.
Number of phones with no major defect = Total number of phones - Number of phones with major defects
Number of phones with no major defect = $48 - 3 = 45$.
Alternatively, Number of phones with no major defect = Number of good phones + Number of phones with minor defects = $42 + 3 = 45$.
Let $A_T$ be the event that the selected phone is acceptable to the trader (i.e., has no major defect).
The number of favourable outcomes is 45.
$n(A_T) = 45$.
$P(\text{acceptable to trader}) = \frac{\text{Number of phones with no major defect}}{\text{Total number of phones}} = \frac{45}{48}$
Simplify the fraction by dividing numerator and denominator by their greatest common divisor, which is 3:
$P(\text{acceptable to trader}) = \frac{\cancel{45}^{15}}{\cancel{48}_{16}}$
$P(\text{acceptable to trader}) = \frac{15}{16}$
The probability that the phone is acceptable to the trader is $\frac{15}{16}$.
Question 41. A bag contains 24 balls of which x are red, 2x are white and 3x are blue. A ball is selected at random. What is the probability that it is
(i) not red?
(ii) white?
Answer:
Given:
A bag contains 24 balls.
Number of red balls = $x$
Number of white balls = $2x$
Number of blue balls = $3x$
A ball is selected at random.
To Find:
The probability that the selected ball is:
(i) not red
(ii) white
Solution:
First, find the total number of balls in terms of $x$ and equate it to the given total number of balls to find the value of $x$.
Total number of balls = (Number of red balls) + (Number of white balls) + (Number of blue balls)
$24 = x + 2x + 3x$
$24 = 6x$
Divide both sides by 6:
$x = \frac{24}{6} = 4$
Now we can find the actual number of balls of each colour:
Number of red balls = $x = 4$
Number of white balls = $2x = 2 \times 4 = 8$
Number of blue balls = $3x = 3 \times 4 = 12$
Check the total: $4 + 8 + 12 = 24$. This matches the given total number of balls.
The total number of possible outcomes when selecting one ball at random is 24.
$n(S) = 24$.
The probability of an event $E$ is given by: $P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$.
(i) Probability that the ball is not red:
Let $NR$ be the event that the selected ball is not red. This means the ball is either white or blue.
Number of balls that are not red = Number of white balls + Number of blue balls
Number of balls that are not red = $8 + 12 = 20$.
$n(NR) = 20$.
$P(\text{not red}) = \frac{\text{Number of balls that are not red}}{\text{Total number of balls}} = \frac{20}{24}$
Simplify the fraction:
$P(\text{not red}) = \frac{\cancel{20}^5}{\cancel{24}_6}$
$P(\text{not red}) = \frac{5}{6}$
The probability that the ball is not red is $\frac{5}{6}$.
Alternate Solution (for part i):
The event "not red" is the complement of the event "red".
Let $R$ be the event that the selected ball is red.
Number of red balls = 4.
$P(R) = \frac{\text{Number of red balls}}{\text{Total number of balls}} = \frac{4}{24} = \frac{1}{6}$.
$P(\text{not red}) = 1 - P(R) = 1 - \frac{1}{6} = \frac{6}{6} - \frac{1}{6} = \frac{5}{6}$.
This confirms the result.
(ii) Probability that the ball is white:
Let $W$ be the event that the selected ball is white.
The number of favourable outcomes (drawing a white ball) is the number of white balls, which is 8.
$n(W) = 8$.
$P(\text{white}) = \frac{\text{Number of white balls}}{\text{Total number of balls}} = \frac{8}{24}$
Simplify the fraction:
$P(\text{white}) = \frac{\cancel{8}^1}{\cancel{24}_3}$
$P(\text{white}) = \frac{1}{3}$
The probability that the ball is white is $\frac{1}{3}$.
Question 42. At a fete, cards bearing numbers 1 to 1000, one number on one card, are put in a box. Each player selects one card at random and that card is not replaced. If the selected card has a perfect square greater than 500, the player wins a prize. What is the probability that
(i) the first player wins a prize?
(ii) the second player wins a prize, if the first has won?
Answer:
Given:
A box contains cards numbered from 1 to 1000.
Total number of cards = 1000.
A player wins a prize if the selected card has a perfect square greater than 500.
The selected card is not replaced.
To Find:
(i) The probability that the first player wins a prize.
(ii) The probability that the second player wins a prize, if the first has won.
Solution:
The total number of possible outcomes for the first draw is 1000.
$n(S_1) = 1000$.
A player wins a prize if the card drawn is a perfect square greater than 500.
Let's find the perfect squares in the range 1 to 1000.
We need to find integers $k$ such that $k^2 \leq 1000$.
$k \leq \sqrt{1000}$.
Since $31^2 = 961$ and $32^2 = 1024$, the possible values for $k$ are from 1 to 31.
The perfect squares are $1^2, 2^2, ..., 31^2$, which are 1, 4, ..., 961.
Now we need to identify which of these perfect squares are greater than 500.
We need $k^2 > 500$.
$k > \sqrt{500}$.
Since $22^2 = 484$ and $23^2 = 529$, the perfect squares greater than 500 are $23^2, 24^2, ..., 31^2$.
The square numbers greater than 500 are: $23^2=529, 24^2=576, 25^2=625, 26^2=676, 27^2=729, 28^2=784, 29^2=841, 30^2=900, 31^2=961$.
The number of perfect squares greater than 500 is 9.
(i) Probability that the first player wins a prize:
Let $W_1$ be the event that the first player wins a prize (draws a perfect square greater than 500).
The number of favourable outcomes is the number of perfect squares greater than 500, which is 9.
$n(W_1) = 9$.
$P(W_1) = \frac{\text{Number of perfect squares > 500}}{\text{Total number of cards}}$
$P(\text{first player wins}) = \frac{9}{1000}$
The probability that the first player wins a prize is $\frac{9}{1000}$.
(ii) Probability that the second player wins a prize, if the first has won:
This is a conditional probability. We are given that the first player won a prize, which means the first player drew a perfect square greater than 500.
Since the selected card is not replaced, the total number of cards remaining in the box for the second player is $1000 - 1 = 999$.
Also, since the first player drew one of the perfect squares greater than 500, the number of perfect squares greater than 500 remaining in the box is $9 - 1 = 8$.
Let $W_2$ be the event that the second player wins a prize.
We want to find the probability of $W_2$ given $W_1$ has occurred, denoted as $P(W_2 \mid W_1)$.
The number of favourable outcomes for the second player to win (drawing a perfect square greater than 500) is the number of remaining perfect squares greater than 500, which is 8.
The total number of possible outcomes for the second draw is the number of remaining cards, which is 999.
$P(W_2 \mid W_1) = \frac{\text{Number of remaining perfect squares > 500}}{\text{Total number of remaining cards}}$
$P(\text{second wins } \mid \text{ first won}) = \frac{8}{999}$
The probability that the second player wins a prize, if the first has won, is $\frac{8}{999}$.
Sample Question 1 to 3 (Before Exercise 13.4)
Sample Question 1: The following is the cumulative frequency distribution (of less than type) of 1000 persons each of age 20 years and above. Determine the mean age.
| Age below (in years) | 30 | 40 | 50 | 60 | 70 | 80 |
| Number of persons | 100 | 220 | 350 | 750 | 950 | 1000 |
Answer:
The given distribution is a cumulative frequency distribution of the less than type. We need to convert this into a simple frequency distribution (class intervals and corresponding frequencies) to calculate the mean age. The age is given as 20 years and above.
Let's construct the frequency distribution table. The class intervals will be formed based on the 'Age below' values. Since the age is 20 years and above, the first class interval will be 20-30.
| Age (in years) | Number of Persons (Cumulative Frequency) | Class Interval | Number of Persons (Frequency, $f_i$) |
| Below 30 | 100 | 20-30 | 100 |
| Below 40 | 220 | 30-40 | $220 - 100 = 120$ |
| Below 50 | 350 | 40-50 | $350 - 220 = 130$ |
| Below 60 | 750 | 50-60 | $750 - 350 = 400$ |
| Below 70 | 950 | 60-70 | $950 - 750 = 200$ |
| Below 80 | 1000 | 70-80 | $1000 - 950 = 50$ |
Now, we will calculate the midpoint ($x_i$) for each class interval and the product $f_i x_i$.
| Class Interval (Age) | Frequency ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 20-30 | 100 | $(20+30)/2 = 25$ | $100 \times 25 = 2500$ |
| 30-40 | 120 | $(30+40)/2 = 35$ | $120 \times 35 = 4200$ |
| 40-50 | 130 | $(40+50)/2 = 45$ | $130 \times 45 = 5850$ |
| 50-60 | 400 | $(50+60)/2 = 55$ | $400 \times 55 = 22000$ |
| 60-70 | 200 | $(60+70)/2 = 65$ | $200 \times 65 = 13000$ |
| 70-80 | 50 | $(70+80)/2 = 75$ | $50 \times 75 = 3750$ |
| Total | $\sum f_i = 1000$ | $\sum f_i x_i = 2500 + 4200 + 5850 + 22000 + 13000 + 3750 = 51300$ |
The formula for calculating the mean ($\overline{x}$) for grouped data using the direct method is:
$\overline{x} = \frac{\sum f_i x_i}{\sum f_i}$
... (i)
Substituting the values we calculated from the table:
$\sum f_i = 1000$
$\sum f_i x_i = 51300$
Mean age $\overline{x} = \frac{51300}{1000}$
$\overline{x} = 51.3$
Therefore, the mean age is 51.3 years.
Sample Question 2: The mean of the following distribution is 18. The frequency f in the class interval 19-21 is missing. Determine f.
| Class interval | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| Frequency | 3 | 6 | 9 | 13 | f | 5 | 4 |
Answer:
We are given a frequency distribution and its mean. We need to find the missing frequency 'f'.
We will use the direct method to calculate the mean. First, we need to find the midpoint ($x_i$) for each class interval and then the product $f_i x_i$.
| Class Interval | Frequency ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 11-13 | 3 | $(11+13)/2 = 12$ | $3 \times 12 = 36$ |
| 13-15 | 6 | $(13+15)/2 = 14$ | $6 \times 14 = 84$ |
| 15-17 | 9 | $(15+17)/2 = 16$ | $9 \times 16 = 144$ |
| 17-19 | 13 | $(17+19)/2 = 18$ | $13 \times 18 = 234$ |
| 19-21 | f | $(19+21)/2 = 20$ | $f \times 20 = 20f$ |
| 21-23 | 5 | $(21+23)/2 = 22$ | $5 \times 22 = 110$ |
| 23-25 | 4 | $(23+25)/2 = 24$ | $4 \times 24 = 96$ |
| Total | $\sum f_i = 3 + 6 + 9 + 13 + f + 5 + 4 = 40 + f$ | $\sum f_i x_i = 36 + 84 + 144 + 234 + 20f + 110 + 96 = 704 + 20f$ |
The formula for the mean ($\overline{x}$) of grouped data is:
$\overline{x} = \frac{\sum f_i x_i}{\sum f_i}$
... (i)
We are given that the mean $\overline{x} = 18$.
Substituting the values of $\sum f_i x_i$ and $\sum f_i$ from the table and the given mean into the formula (i):
$18 = \frac{704 + 20f}{40 + f}$
Now, we solve this equation for f:
$18(40 + f) = 704 + 20f$
$720 + 18f = 704 + 20f$
$720 - 704 = 20f - 18f$
$16 = 2f$
$f = \frac{16}{2}$
$f = 8$
Thus, the missing frequency f is 8.
Sample Question 3: The median of the distribution given below is 14.4. Find the values of x and y, if the total frequency is 20.
| Class interval | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
| Frequency | 4 | x | 5 | y | 1 |
Answer:
Given:
Median = 14.4
Total Frequency ($N$) = 20
First, let's construct the cumulative frequency distribution table.
| Class Interval | Frequency ($f_i$) | Cumulative Frequency (CF) |
| 0-6 | 4 | 4 |
| 6-12 | x | $4 + x$ |
| 12-18 | 5 | $4 + x + 5 = 9 + x$ |
| 18-24 | y | $9 + x + y$ |
| 24-30 | 1 | $9 + x + y + 1 = 10 + x + y$ |
The total frequency is given as 20. From the table, the total frequency is also the last cumulative frequency, which is $10 + x + y$.
$10 + x + y = 20$
... (1)
$x + y = 20 - 10$
$x + y = 10$
... (2)
The median is given as 14.4. This value lies in the class interval 12-18.
Therefore, the median class is 12-18.
For the median class:
Lower limit ($L$) = 12
Frequency of the median class ($f$) = 5
Cumulative frequency of the class preceding the median class (CF) = $4 + x$
Class size ($h$) = $18 - 12 = 6$
Total frequency ($N$) = 20, so $\frac{N}{2} = \frac{20}{2} = 10$.
The formula for the median of a grouped frequency distribution is:
$\text{Median} = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
... (3)
Substitute the known values into the median formula (3):
$14.4 = 12 + \left(\frac{10 - (4 + x)}{5}\right) \times 6$
$14.4 - 12 = \left(\frac{10 - 4 - x}{5}\right) \times 6$
$2.4 = \left(\frac{6 - x}{5}\right) \times 6$
$2.4 = \frac{6(6 - x)}{5}$
$2.4 \times 5 = 6(6 - x)$
$12 = 6(6 - x)$
$\frac{12}{6} = 6 - x$
$2 = 6 - x$
$x = 6 - 2$
$x = 4$
Now substitute the value of x into equation (2) to find y:
$x + y = 10$
$4 + y = 10$
$y = 10 - 4$
$y = 6$
So, the values of the missing frequencies are $x = 4$ and $y = 6$.
Exercise 13.4
Question 1. Find the mean marks of students for the following distribution :
| Marks | Number of students |
|---|---|
| 0 and above | 80 |
| 10 and above | 77 |
| 20 and above | 72 |
| 30 and above | 65 |
| 40 and above | 55 |
| 50 and above | 43 |
| 60 and above | 28 |
| 70 and above | 16 |
| 80 and above | 10 |
| 90 and above | 8 |
| 100 and above | 0 |
Answer:
The given distribution is a cumulative frequency distribution of the 'more than' type. We need to convert this into a simple frequency distribution (class intervals and corresponding frequencies) to calculate the mean. The marks are given in intervals of 10.
Let's construct the frequency distribution table from the given cumulative frequencies.
| Marks (More than) | Number of Students (Cumulative Frequency) | Class Interval (Marks) | Number of Students (Frequency, $f_i$) |
| 0 and above | 80 | 0-10 | $80 - 77 = 3$ |
| 10 and above | 77 | 10-20 | $77 - 72 = 5$ |
| 20 and above | 72 | 20-30 | $72 - 65 = 7$ |
| 30 and above | 65 | 30-40 | $65 - 55 = 10$ |
| 40 and above | 55 | 40-50 | $55 - 43 = 12$ |
| 50 and above | 43 | 50-60 | $43 - 28 = 15$ |
| 60 and above | 28 | 60-70 | $28 - 16 = 12$ |
| 70 and above | 16 | 70-80 | $16 - 10 = 6$ |
| 80 and above | 10 | 80-90 | $10 - 8 = 2$ |
| 90 and above | 8 | 90-100 | $8 - 0 = 8$ |
Now, we will calculate the midpoint ($x_i$) for each class interval and the product $f_i x_i$ to find the mean using the direct method.
| Class Interval (Marks) | Frequency ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 0-10 | 3 | $(0+10)/2 = 5$ | $3 \times 5 = 15$ |
| 10-20 | 5 | $(10+20)/2 = 15$ | $5 \times 15 = 75$ |
| 20-30 | 7 | $(20+30)/2 = 25$ | $7 \times 25 = 175$ |
| 30-40 | 10 | $(30+40)/2 = 35$ | $10 \times 35 = 350$ |
| 40-50 | 12 | $(40+50)/2 = 45$ | $12 \times 45 = 540$ |
| 50-60 | 15 | $(50+60)/2 = 55$ | $15 \times 55 = 825$ |
| 60-70 | 12 | $(60+70)/2 = 65$ | $12 \times 65 = 780$ |
| 70-80 | 6 | $(70+80)/2 = 75$ | $6 \times 75 = 450$ |
| 80-90 | 2 | $(80+90)/2 = 85$ | $2 \times 85 = 170$ |
| 90-100 | 8 | $(90+100)/2 = 95$ | $8 \times 95 = 760$ |
| Total | $\sum f_i = 80$ | $\sum f_i x_i = 15 + 75 + 175 + 350 + 540 + 825 + 780 + 450 + 170 + 760 = 4140$ |
The formula for calculating the mean ($\overline{x}$) for grouped data using the direct method is:
$\overline{x} = \frac{\sum f_i x_i}{\sum f_i}$
... (i)
Substituting the values from the table into the formula (i):
$\overline{x} = \frac{4140}{80}$
$\overline{x} = \frac{\cancel{4140}^{414}}{\cancel{80}_{8}}$
$\overline{x} = \frac{414}{8} = \frac{\cancel{414}^{207}}{\cancel{8}_{4}}$
$\overline{x} = \frac{207}{4}$
$\overline{x} = 51.75$
The mean marks of the students are 51.75.
Question 2. Determine the mean of the following distribution :
| Marks | Number of students |
|---|---|
| Below 10 | 5 |
| Below 20 | 9 |
| Below 30 | 17 |
| Below 40 | 29 |
| Below 50 | 45 |
| Below 60 | 60 |
| Below 70 | 70 |
| Below 80 | 78 |
| Below 90 | 83 |
| Below 100 | 85 |
Answer:
The given distribution is a cumulative frequency distribution of the 'less than' type. To find the mean, we first need to convert it into a simple frequency distribution.
Let's create the frequency distribution table:
| Marks (Below) | Number of Students (Cumulative Frequency) | Class Interval (Marks) | Number of Students (Frequency, $f_i$) |
| Below 10 | 5 | 0-10 | 5 |
| Below 20 | 9 | 10-20 | $9 - 5 = 4$ |
| Below 30 | 17 | 20-30 | $17 - 9 = 8$ |
| Below 40 | 29 | 30-40 | $29 - 17 = 12$ |
| Below 50 | 45 | 40-50 | $45 - 29 = 16$ |
| Below 60 | 60 | 50-60 | $60 - 45 = 15$ |
| Below 70 | 70 | 60-70 | $70 - 60 = 10$ |
| Below 80 | 78 | 70-80 | $78 - 70 = 8$ |
| Below 90 | 83 | 80-90 | $83 - 78 = 5$ |
| Below 100 | 85 | 90-100 | $85 - 83 = 2$ |
Now, we calculate the midpoint ($x_i$) for each class and the product $f_i x_i$.
| Class Interval (Marks) | Frequency ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 0-10 | 5 | 5 | $5 \times 5 = 25$ |
| 10-20 | 4 | 15 | $4 \times 15 = 60$ |
| 20-30 | 8 | 25 | $8 \times 25 = 200$ |
| 30-40 | 12 | 35 | $12 \times 35 = 420$ |
| 40-50 | 16 | 45 | $16 \times 45 = 720$ |
| 50-60 | 15 | 55 | $15 \times 55 = 825$ |
| 60-70 | 10 | 65 | $10 \times 65 = 650$ |
| 70-80 | 8 | 75 | $8 \times 75 = 600$ |
| 80-90 | 5 | 85 | $5 \times 85 = 425$ |
| 90-100 | 2 | 95 | $2 \times 95 = 190$ |
| Total | $\sum\limits f_i = 85$ | $\sum\limits f_i x_i = 25 + 60 + 200 + 420 + 720 + 825 + 650 + 600 + 425 + 190 = 4115$ |
The formula for the mean ($\overline{x}$) using the direct method is:
$\overline{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
... (i)
Substitute the values from the table into formula (i):
$\overline{x} = \frac{4115}{85}$
We can simplify the fraction by dividing both numerator and denominator by 5:
$\overline{x} = \frac{\cancel{4115}^{823}}{\cancel{85}_{17}}$
$\overline{x} = \frac{823}{17}$
Now, perform the division:
$823 \div 17 \approx 48.41$
The mean marks of the students are approximately 48.41.
Question 3. Find the mean age of 100 residents of a town from the following data :
| Age equal and above (in years) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Number of Persons | 100 | 90 | 75 | 50 | 25 | 15 | 5 | 0 |
Answer:
The given distribution is a cumulative frequency distribution of the 'more than or equal to' type. To find the mean age, we need to convert this into a simple frequency distribution.
Let's construct the frequency distribution table:
| Age equal and above | Number of Persons (Cumulative Frequency) | Class Interval (Age in years) | Number of Persons (Frequency, $f_i$) |
| 0 | 100 | 0-10 | $100 - 90 = 10$ |
| 10 | 90 | 10-20 | $90 - 75 = 15$ |
| 20 | 75 | 20-30 | $75 - 50 = 25$ |
| 30 | 50 | 30-40 | $50 - 25 = 25$ |
| 40 | 25 | 40-50 | $25 - 15 = 10$ |
| 50 | 15 | 50-60 | $15 - 5 = 10$ |
| 60 | 5 | 60-70 | $5 - 0 = 5$ |
| 70 | 0 | 70-80 | $0 - 0 = 0$ (Note: The last category '70 and above' implies the upper limit could be considered 80 for calculation convenience based on the pattern, although it's not explicitly stated. The last frequency is 0, so this interval contributes nothing to the sum $f_i x_i$.) |
Note: The total frequency is given as 100, which matches the cumulative frequency for 'Age equal and above 0'. The class interval 70-80 is formed following the pattern, but its frequency is 0.
Now, we calculate the midpoint ($x_i$) for each class interval and the product $f_i x_i$.
| Class Interval (Age) | Frequency ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 0-10 | 10 | $(0+10)/2 = 5$ | $10 \times 5 = 50$ |
| 10-20 | 15 | $(10+20)/2 = 15$ | $15 \times 15 = 225$ |
| 20-30 | 25 | $(20+30)/2 = 25$ | $25 \times 25 = 625$ |
| 30-40 | 25 | $(30+40)/2 = 35$ | $25 \times 35 = 875$ |
| 40-50 | 10 | $(40+50)/2 = 45$ | $10 \times 45 = 450$ |
| 50-60 | 10 | $(50+60)/2 = 55$ | $10 \times 55 = 550$ |
| 60-70 | 5 | $(60+70)/2 = 65$ | $5 \times 65 = 325$ |
| Total | $\sum\limits f_i = 10 + 15 + 25 + 25 + 10 + 10 + 5 = 100$ | $\sum\limits f_i x_i = 50 + 225 + 625 + 875 + 450 + 550 + 325 = 3100$ |
The formula for the mean ($\overline{x}$) of grouped data using the direct method is:
$\overline{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
... (i)
Substitute the values from the table into formula (i):
$\overline{x} = \frac{3100}{100}$
$\overline{x} = \frac{\cancel{3100}}{\cancel{100}}$
$\overline{x} = 31$
The mean age of the 100 residents is 31 years.
Question 4. The weights of tea in 70 packets are shown in the following table :
| Weight (in gram) | Number of packets |
|---|---|
| 200-201 | 13 |
| 201-202 | 27 |
| 202-203 | 18 |
| 203-204 | 10 |
| 204-205 | 1 |
| 205-206 | 1 |
Find the mean weight of packets.
Answer:
We are given the frequency distribution of the weights of 70 tea packets. We need to find the mean weight. We can use the direct method for calculating the mean.
We will calculate the midpoint ($x_i$) for each class interval and the product of frequency and midpoint ($f_i x_i$).
| Class Interval (Weight in gram) | Number of Packets (Frequency, $f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 200-201 | 13 | $(200+201)/2 = 200.5$ | $13 \times 200.5 = 2606.5$ |
| 201-202 | 27 | $(201+202)/2 = 201.5$ | $27 \times 201.5 = 5440.5$ |
| 202-203 | 18 | $(202+203)/2 = 202.5$ | $18 \times 202.5 = 3645.0$ |
| 203-204 | 10 | $(203+204)/2 = 203.5$ | $10 \times 203.5 = 2035.0$ |
| 204-205 | 1 | $(204+205)/2 = 204.5$ | $1 \times 204.5 = 204.5$ |
| 205-206 | 1 | $(205+206)/2 = 205.5$ | $1 \times 205.5 = 205.5$ |
| Total | $\sum\limits f_i = 13 + 27 + 18 + 10 + 1 + 1 = 70$ | $\sum\limits f_i x_i = 2606.5 + 5440.5 + 3645.0 + 2035.0 + 204.5 + 205.5 = 14137.0$ |
The formula for the mean ($\overline{x}$) of grouped data using the direct method is:
$\overline{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
... (i)
Substitute the values from the table into formula (i):
$\overline{x} = \frac{14137.0}{70}$
$\overline{x} \approx 201.957$
The mean weight of the packets is approximately 201.96 grams (rounded to two decimal places).
Question 5. Refer to Q.4 above.
Draw the less than type ogive for this data and use it to find the median weight
Answer:
To draw the 'less than' type ogive, we first need to convert the given frequency distribution from Question 4 into a 'less than' cumulative frequency distribution.
The frequency distribution from Question 4 is:
| Weight (in gram) | Number of packets ($f_i$) |
| 200-201 | 13 |
| 201-202 | 27 |
| 202-203 | 18 |
| 203-204 | 10 |
| 204-205 | 1 |
| 205-206 | 1 |
Now, let's prepare the 'less than' cumulative frequency table:
| Weight (less than) | Cumulative Frequency (CF) |
| Less than 201 | 13 |
| Less than 202 | $13 + 27 = 40$ |
| Less than 203 | $40 + 18 = 58$ |
| Less than 204 | $58 + 10 = 68$ |
| Less than 205 | $68 + 1 = 69$ |
| Less than 206 | $69 + 1 = 70$ |
To draw the 'less than' ogive, we plot the points with coordinates given by (upper class limit, cumulative frequency). The points to be plotted are:
(201, 13), (202, 40), (203, 58), (204, 68), (205, 69), (206, 70).
We can also include the point corresponding to the lower limit of the first class with cumulative frequency 0, which is (200, 0).
Plot these points on a graph paper, taking the upper class limits on the x-axis and the cumulative frequencies on the y-axis. Join these points with a smooth curve. This curve is the 'less than' ogive.
To find the median from the ogive:
The total frequency is $N = 70$.
The median corresponds to the value on the x-axis at the cumulative frequency $\frac{N}{2}$.
$\frac{N}{2} = \frac{70}{2} = 35$
... (i)
Steps to find the median graphically:
1. Locate the value 35 on the y-axis.
2. From the point corresponding to 35 on the y-axis, draw a horizontal line to the right to intersect the ogive.
3. From the point of intersection on the ogive, draw a vertical line down to the x-axis.
4. The point where this vertical line meets the x-axis gives the median value.
By following these steps on the drawn ogive, the value on the x-axis corresponding to a cumulative frequency of 35 will be approximately 201.81.
Thus, the median weight from the ogive is approximately 201.81 grams.
Question 6. Refer to Q.4 above.
Draw the less than type and more than type ogives for the data and use them to find the median weight.
Answer:
To draw both the 'less than' and 'more than' type ogives, we need to prepare their respective cumulative frequency tables from the given frequency distribution in Question 4.
The frequency distribution from Question 4 is:
| Weight (in gram) | Number of packets ($f_i$) |
| 200-201 | 13 |
| 201-202 | 27 |
| 202-203 | 18 |
| 203-204 | 10 |
| 204-205 | 1 |
| 205-206 | 1 |
| Total | $\sum f_i = 70$ |
'Less Than' Cumulative Frequency Distribution:
| Weight (less than) | Cumulative Frequency (CF) |
| Less than 201 | 13 |
| Less than 202 | $13 + 27 = 40$ |
| Less than 203 | $40 + 18 = 58$ |
| Less than 204 | $58 + 10 = 68$ |
| Less than 205 | $68 + 1 = 69$ |
| Less than 206 | $69 + 1 = 70$ |
Points for 'less than' ogive: (Upper Class Limit, CF) -> (201, 13), (202, 40), (203, 58), (204, 68), (205, 69), (206, 70). We can also include (200, 0).
'More Than' Cumulative Frequency Distribution:
| Weight (more than or equal to) | Cumulative Frequency (CF) |
| More than or equal to 200 | 70 |
| More than or equal to 201 | $70 - 13 = 57$ |
| More than or equal to 202 | $57 - 27 = 30$ |
| More than or equal to 203 | $30 - 18 = 12$ |
| More than or equal to 204 | $12 - 10 = 2$ |
| More than or equal to 205 | $2 - 1 = 1$ |
| More than or equal to 206 | $1 - 1 = 0$ |
Points for 'more than' ogive: (Lower Class Limit, CF) -> (200, 70), (201, 57), (202, 30), (203, 12), (204, 2), (205, 1), (206, 0).
Drawing the Ogives:
1. Draw the x-axis representing the Weight (in grams) and the y-axis representing the Cumulative Frequency.
2. Plot the points for the 'less than' ogive and join them with a smooth curve.
3. Plot the points for the 'more than' ogive on the same graph and join them with a smooth curve.
Finding the Median from the Intersection:
The median is the x-coordinate of the point of intersection of the 'less than' ogive and the 'more than' ogive.
To find this graphically, locate the point where the two curves intersect. From this point, draw a vertical line down to the x-axis. The value on the x-axis where this vertical line meets is the median.
Alternatively, the intersection point's y-coordinate should be equal to $\frac{N}{2}$.
$\frac{N}{2} = \frac{70}{2} = 35$
... (i)
The intersection of the two ogives will have a y-coordinate of 35. The x-coordinate of this intersection point represents the median weight.
By drawing the ogives accurately on graph paper and finding their intersection point, you will observe that the x-coordinate is approximately 201.81.
(Note: Calculating the median using the formula gives $201 + \frac{35-13}{27} \times 1 \approx 201.8148$, which validates the graphical result).
Thus, the median weight from the ogives is approximately 201.81 grams.
Question 7. The table below shows the salaries of 280 persons.
| Salary (in thousand $\textsf{₹}$) | Number of persons |
|---|---|
| 5-10 | 49 |
| 10-15 | 133 |
| 15-20 | 63 |
| 20-25 | 15 |
| 25-30 | 6 |
| 30-35 | 7 |
| 35-40 | 4 |
| 40-45 | 2 |
| 45-50 | 1 |
Calculate the median and mode of the data.
Answer:
We are given the frequency distribution of the salaries of 280 persons. We need to calculate the median and the mode.
Calculation of Median
To find the median, we first need to calculate the cumulative frequencies.
| Salary (in thousand $\textsf{₹}$) | Number of Persons ($f_i$) | Cumulative Frequency (CF) |
| 5-10 | 49 | 49 |
| 10-15 | 133 | $49 + 133 = 182$ |
| 15-20 | 63 | $182 + 63 = 245$ |
| 20-25 | 15 | $245 + 15 = 260$ |
| 25-30 | 6 | $260 + 6 = 266$ |
| 30-35 | 7 | $266 + 7 = 273$ |
| 35-40 | 4 | $273 + 4 = 277$ |
| 40-45 | 2 | $277 + 2 = 279$ |
| 45-50 | 1 | $279 + 1 = 280$ |
| Total | $\sum\limits f_i = N = 280$ |
The total frequency is $N = 280$.
We need to find the class interval where the $\frac{N}{2}$th observation lies.
$\frac{N}{2} = \frac{280}{2} = 140$
... (1)
The cumulative frequency just greater than or equal to 140 is 182, which corresponds to the class interval 10-15.
So, the median class is 10-15.
For the median class:
Lower limit ($L$) = 10
Frequency of the median class ($f$) = 133
Cumulative frequency of the class preceding the median class (CF) = 49
Class size ($h$) = $15 - 10 = 5$
The formula for the median of a grouped frequency distribution is:
$\text{Median} = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
... (2)
Substitute the values into the formula (2):
$\text{Median} = 10 + \left(\frac{140 - 49}{133}\right) \times 5$
$\text{Median} = 10 + \left(\frac{91}{133}\right) \times 5$
$\text{Median} = 10 + \frac{455}{133}$
$\text{Median} \approx 10 + 3.42105$
$\text{Median} \approx 13.42$ (rounded to two decimal places)
Calculation of Mode
To find the mode, we need to identify the modal class, which is the class with the highest frequency.
From the frequency distribution table, the highest frequency is 133, which corresponds to the class interval 10-15.
So, the modal class is 10-15.
For the modal class:
Lower limit ($L$) = 10
Frequency of the modal class ($f_1$) = 133
Frequency of the class preceding the modal class ($f_0$) = 49
Frequency of the class succeeding the modal class ($f_2$) = 63
Class size ($h$) = $15 - 10 = 5$
The formula for the mode of a grouped frequency distribution is:
$\text{Mode} = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h$
... (3)
Substitute the values into the formula (3):
$\text{Mode} = 10 + \left(\frac{133 - 49}{2 \times 133 - 49 - 63}\right) \times 5$
$\text{Mode} = 10 + \left(\frac{84}{266 - 49 - 63}\right) \times 5$
$\text{Mode} = 10 + \left(\frac{84}{266 - 112}\right) \times 5$
$\text{Mode} = 10 + \left(\frac{84}{154}\right) \times 5$
$\text{Mode} = 10 + \frac{420}{154}$
Simplify the fraction $\frac{420}{154}$ by dividing both numerator and denominator by 14:
$\text{Mode} = 10 + \frac{\cancel{420}^{30}}{\cancel{154}_{11}}$
$\text{Mode} = 10 + \frac{30}{11}$
$\text{Mode} \approx 10 + 2.72727$
$\text{Mode} \approx 12.73$ (rounded to two decimal places)
The median salary is approximately $\textsf{₹}$ 13.42 thousand.
The mode salary is approximately $\textsf{₹}$ 12.73 thousand.
Question 8. The mean of the following frequency distribution is 50, but the frequencies f1 and f2 in classes 20-40 and 60-80, respectively are not known. Find these frequencies, if the sum of all the frequencies is 120.
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 17 | $f_1$ | 32 | $f_2$ | 19 |
Answer:
Given:
Mean ($\overline{x}$) = 50
Total frequency ($\sum\limits f_i$) = 120
We need to find the missing frequencies, $f_1$ and $f_2$. First, let's calculate the midpoints ($x_i$) for each class and the product $f_i x_i$.
| Class Interval | Frequency ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 0-20 | 17 | $(0+20)/2 = 10$ | $17 \times 10 = 170$ |
| 20-40 | $f_1$ | $(20+40)/2 = 30$ | $f_1 \times 30 = 30f_1$ |
| 40-60 | 32 | $(40+60)/2 = 50$ | $32 \times 50 = 1600$ |
| 60-80 | $f_2$ | $(60+80)/2 = 70$ | $f_2 \times 70 = 70f_2$ |
| 80-100 | 19 | $(80+100)/2 = 90$ | $19 \times 90 = 1710$ |
| Total | $\sum\limits f_i = 17 + f_1 + 32 + f_2 + 19 = 68 + f_1 + f_2$ | $\sum\limits f_i x_i = 170 + 30f_1 + 1600 + 70f_2 + 1710 = 3480 + 30f_1 + 70f_2$ |
We are given that the total frequency is 120.
$68 + f_1 + f_2 = 120$
... (1)
From equation (1), we get:
$f_1 + f_2 = 120 - 68$
(Subtracting 68 from both sides)
$f_1 + f_2 = 52$
... (2)
The formula for the mean ($\overline{x}$) of grouped data is:
$\overline{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
... (3)
We are given $\overline{x} = 50$, $\sum\limits f_i = 120$, and $\sum\limits f_i x_i = 3480 + 30f_1 + 70f_2$.
Substitute these values into formula (3):
$50 = \frac{3480 + 30f_1 + 70f_2}{120}$
Multiply both sides by 120:
$50 \times 120 = 3480 + 30f_1 + 70f_2$
$6000 = 3480 + 30f_1 + 70f_2$
Subtract 3480 from both sides:
$6000 - 3480 = 30f_1 + 70f_2$
$2520 = 30f_1 + 70f_2$
Divide the entire equation by 10:
$252 = 3f_1 + 7f_2$
... (4)
Now we have a system of two linear equations with two variables $f_1$ and $f_2$:
Equation (2): $f_1 + f_2 = 52$
Equation (4): $3f_1 + 7f_2 = 252$
From equation (2), we can express $f_1$ in terms of $f_2$:
$f_1 = 52 - f_2$
... (5)
Substitute the expression for $f_1$ from equation (5) into equation (4):
$3(52 - f_2) + 7f_2 = 252$
$156 - 3f_2 + 7f_2 = 252$
$156 + 4f_2 = 252$
Subtract 156 from both sides:
$4f_2 = 252 - 156$
$4f_2 = 96$
Divide by 4:
$f_2 = \frac{96}{4}$
$f_2 = 24$
Now substitute the value of $f_2 = 24$ into equation (5) to find $f_1$:
$f_1 = 52 - f_2$
$f_1 = 52 - 24$
$f_1 = 28$
The missing frequencies are $f_1 = 28$ and $f_2 = 24$.
Question 9. The median of the following data is 50. Find the values of p and q, if the sum of all the frequencies is 90.
| Marks | Frequency |
|---|---|
| 20-30 | p |
| 30-40 | 15 |
| 40-50 | 25 |
| 50-60 | 20 |
| 60-70 | q |
| 70-80 | 8 |
| 80-90 | 10 |
Answer:
Given:
Median = 50
Total Frequency ($N$) = 90
First, let's construct the cumulative frequency distribution table.
| Class Interval (Marks) | Frequency ($f_i$) | Cumulative Frequency (CF) |
| 20-30 | p | p |
| 30-40 | 15 | $p + 15$ |
| 40-50 | 25 | $p + 15 + 25 = p + 40$ |
| 50-60 | 20 | $p + 40 + 20 = p + 60$ |
| 60-70 | q | $p + 60 + q$ |
| 70-80 | 8 | $p + 60 + q + 8 = p + q + 68$ |
| 80-90 | 10 | $p + q + 68 + 10 = p + q + 78$ |
The total frequency is given as 90. From the table, the total frequency is also the last cumulative frequency, which is $p + q + 78$.
$p + q + 78 = 90$
... (1)
From equation (1), we get:
$p + q = 90 - 78$
(Subtracting 78 from both sides)
$p + q = 12$
... (2)
The median is given as 50. This value lies in the class interval 50-60.
Therefore, the median class is 50-60.
For the median class:
Lower limit ($L$) = 50
Frequency of the median class ($f$) = 20
Cumulative frequency of the class preceding the median class (CF) = $p + 40$
Class size ($h$) = $60 - 50 = 10$
Total frequency ($N$) = 90, so $\frac{N}{2} = \frac{90}{2} = 45$.
The formula for the median of a grouped frequency distribution is:
$\text{Median} = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
... (3)
Substitute the known values into the median formula (3):
$50 = 50 + \left(\frac{45 - (p + 40)}{20}\right) \times 10$
Subtract 50 from both sides:
$50 - 50 = \left(\frac{45 - p - 40}{20}\right) \times 10$
$0 = \left(\frac{5 - p}{20}\right) \times 10$
$0 = \frac{10(5 - p)}{20}$
$0 = \frac{5 - p}{2}$
Multiply both sides by 2:
$0 \times 2 = 5 - p$
$0 = 5 - p$
$p = 5$
Now substitute the value of $p = 5$ into equation (2) to find q:
$p + q = 12$
$5 + q = 12$
$q = 12 - 5$
$q = 7$
So, the values of the missing frequencies are $p = 5$ and $q = 7$.
Question 10. The distribution of heights (in cm) of 96 children is given below :
| Height (in cm) | Number of children |
|---|---|
| 124-128 | 5 |
| 128-132 | 8 |
| 132-136 | 17 |
| 136-140 | 24 |
| 140-144 | 16 |
| 144-148 | 12 |
| 148-152 | 6 |
| 152-156 | 4 |
| 156-160 | 3 |
| 160-164 | 1 |
Draw a less than type cumulative frequency curve for this data and use it to compute median height of the children.
Answer:
To draw the 'less than' type cumulative frequency curve (ogive), we first need to prepare the 'less than' cumulative frequency distribution table.
'Less Than' Cumulative Frequency Distribution:
| Height (less than) | Number of Children (Cumulative Frequency) |
| Less than 128 | 5 |
| Less than 132 | $5 + 8 = 13$ |
| Less than 136 | $13 + 17 = 30$ |
| Less than 140 | $30 + 24 = 54$ |
| Less than 144 | $54 + 16 = 70$ |
| Less than 148 | $70 + 12 = 82$ |
| Less than 152 | $82 + 6 = 88$ |
| Less than 156 | $88 + 4 = 92$ |
| Less than 160 | $92 + 3 = 95$ |
| Less than 164 | $95 + 1 = 96$ |
To draw the 'less than' ogive, we plot the points with coordinates given by (upper class limit, cumulative frequency).
The points to be plotted are:
(128, 5), (132, 13), (136, 30), (140, 54), (144, 70), (148, 82), (152, 88), (156, 92), (160, 95), (164, 96).
We can also include the point corresponding to the lower limit of the first class with cumulative frequency 0, which is (124, 0).
Plot these points on a graph paper, taking the upper class limits on the x-axis (representing Height in cm) and the cumulative frequencies on the y-axis (representing Number of children). Join these points with a smooth curve. This curve is the 'less than' ogive.
To find the median from the ogive:
The total frequency is $N = 96$.
The median corresponds to the value on the x-axis at the cumulative frequency $\frac{N}{2}$.
$\frac{N}{2} = \frac{96}{2} = 48$
... (i)
Steps to find the median graphically:
1. Locate the value 48 on the y-axis.
2. From the point corresponding to 48 on the y-axis, draw a horizontal line to the right to intersect the ogive.
3. From the point of intersection on the ogive, draw a vertical line down to the x-axis.
4. The point where this vertical line meets the x-axis gives the median height.
Let's calculate the median using the formula to verify the graphical method result.
$\frac{N}{2} = 48$. The cumulative frequency just greater than 48 is 54, which corresponds to the class interval 136-140.
So, the median class is 136-140.
Lower limit ($L$) = 136
Frequency of the median class ($f$) = 24
Cumulative frequency of the class preceding the median class (CF) = 30
Class size ($h$) = $140 - 136 = 4$
Median $= L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
Median $= 136 + \left(\frac{48 - 30}{24}\right) \times 4$
Median $= 136 + \left(\frac{18}{24}\right) \times 4$
Median $= 136 + \left(\frac{3}{4}\right) \times 4$
Median $= 136 + 3$
Median $= 139$
By following the graphical steps on the drawn ogive, the value on the x-axis corresponding to a cumulative frequency of 48 should be 139 cm.
Thus, the median height of the children is 139 cm.
Question 11. Size of agricultural holdings in a survey of 200 families is given in the following table:
| Size of agricultural holdings (in ha) | Number of families |
|---|---|
| 0-5 | 10 |
| 5-10 | 15 |
| 10-15 | 30 |
| 15-20 | 80 |
| 20-25 | 40 |
| 25-30 | 20 |
| 30-35 | 5 |
Compute median and mode size of the holdings.
Answer:
We are given the frequency distribution of the size of agricultural holdings for 200 families. We need to calculate the median and the mode.
Calculation of Median
To find the median, we first need to calculate the cumulative frequencies.
| Size of agricultural holdings (in ha) | Number of Families ($f_i$) | Cumulative Frequency (CF) |
| 0-5 | 10 | 10 |
| 5-10 | 15 | $10 + 15 = 25$ |
| 10-15 | 30 | $25 + 30 = 55$ |
| 15-20 | 80 | $55 + 80 = 135$ |
| 20-25 | 40 | $135 + 40 = 175$ |
| 25-30 | 20 | $175 + 20 = 195$ |
| 30-35 | 5 | $195 + 5 = 200$ |
| Total | $\sum\limits f_i = N = 200$ |
The total frequency is given as $N = 200$.
We need to find the class interval where the $\frac{N}{2}$th observation lies.
$\frac{N}{2} = \frac{200}{2} = 100$
... (1)
The cumulative frequency just greater than or equal to 100 is 135, which corresponds to the class interval 15-20.
So, the median class is 15-20.
For the median class:
Lower limit ($L$) = 15
Frequency of the median class ($f$) = 80
Cumulative frequency of the class preceding the median class (CF) = 55
Class size ($h$) = $20 - 15 = 5$
The formula for the median of a grouped frequency distribution is:
$\text{Median} = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
... (2)
Substitute the values into the formula (2):
$\text{Median} = 15 + \left(\frac{100 - 55}{80}\right) \times 5$
$\text{Median} = 15 + \left(\frac{45}{80}\right) \times 5$
Simplify the fraction $\frac{45}{80}$:
$\text{Median} = 15 + \left(\frac{\cancel{45}^{9}}{\cancel{80}_{16}}\right) \times 5$
$\text{Median} = 15 + \frac{9 \times 5}{16}$
$\text{Median} = 15 + \frac{45}{16}$
$\text{Median} = 15 + 2.8125$
$\text{Median} = 17.8125$
Calculation of Mode
To find the mode, we need to identify the modal class, which is the class with the highest frequency.
From the frequency distribution table, the highest frequency is 80, which corresponds to the class interval 15-20.
So, the modal class is 15-20.
For the modal class:
Lower limit ($L$) = 15
Frequency of the modal class ($f_1$) = 80
Frequency of the class preceding the modal class ($f_0$) = 30 (frequency of 10-15)
Frequency of the class succeeding the modal class ($f_2$) = 40 (frequency of 20-25)
Class size ($h$) = $20 - 15 = 5$
The formula for the mode of a grouped frequency distribution is:
$\text{Mode} = L + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h$
... (3)
Substitute the values into the formula (3):
$\text{Mode} = 15 + \left(\frac{80 - 30}{2 \times 80 - 30 - 40}\right) \times 5$
$\text{Mode} = 15 + \left(\frac{50}{160 - 30 - 40}\right) \times 5$
$\text{Mode} = 15 + \left(\frac{50}{160 - 70}\right) \times 5$
$\text{Mode} = 15 + \left(\frac{50}{90}\right) \times 5$
Simplify the fraction $\frac{50}{90}$:
$\text{Mode} = 15 + \left(\frac{\cancel{50}^{5}}{\cancel{90}_{9}}\right) \times 5$
$\text{Mode} = 15 + \frac{5 \times 5}{9}$
$\text{Mode} = 15 + \frac{25}{9}$
$\text{Mode} \approx 15 + 2.777...$
$\text{Mode} \approx 17.78$ (rounded to two decimal places)
The median size of the holdings is 17.8125 ha.
The mode size of the holdings is approximately 17.78 ha.
Question 12. The annual rainfall record of a city for 66 days is given in the following table.
| Rainfall (in cm) | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Number of days | 22 | 10 | 8 | 15 | 5 | 6 |
Calculate the median rainfall using ogives (of more than type and of less than type)
Answer:
To calculate the median rainfall using ogives, we need to draw both the 'less than' and 'more than' cumulative frequency curves. First, let's construct the cumulative frequency tables.
'Less Than' Cumulative Frequency Distribution:
| Rainfall (less than) | Number of Days (Cumulative Frequency) |
| Less than 10 | 22 |
| Less than 20 | $22 + 10 = 32$ |
| Less than 30 | $32 + 8 = 40$ |
| Less than 40 | $40 + 15 = 55$ |
| Less than 50 | $55 + 5 = 60$ |
| Less than 60 | $60 + 6 = 66$ |
Points to plot for 'less than' ogive (Upper Class Limit, CF): (10, 22), (20, 32), (30, 40), (40, 55), (50, 60), (60, 66). Include (0, 0) to start the curve.
'More Than' Cumulative Frequency Distribution:
Total Frequency ($N$) = 66.
| Rainfall (more than or equal to) | Number of Days (Cumulative Frequency) |
| More than or equal to 0 | 66 |
| More than or equal to 10 | $66 - 22 = 44$ |
| More than or equal to 20 | $44 - 10 = 34$ |
| More than or equal to 30 | $34 - 8 = 26$ |
| More than or equal to 40 | $26 - 15 = 11$ |
| More than or equal to 50 | $11 - 5 = 6$ |
| More than or equal to 60 | $6 - 6 = 0$ |
Points to plot for 'more than' ogive (Lower Class Limit, CF): (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6), (60, 0).
Drawing the Ogives:
1. Draw the x-axis representing the Rainfall (in cm) and the y-axis representing the Cumulative Frequency (Number of Days).
2. Plot the points for the 'less than' ogive ((0,0), (10, 22), ..., (60, 66)) and join them with a smooth curve.
3. Plot the points for the 'more than' ogive ((0,66), (10, 44), ..., (60, 0)) on the same graph and join them with a smooth curve.
Finding the Median from the Intersection:
The median is the x-coordinate of the point of intersection of the 'less than' ogive and the 'more than' ogive.
To find this graphically, locate the point where the two curves intersect. From this point, draw a vertical line down to the x-axis. The value on the x-axis where this vertical line meets is the median.
The intersection point's y-coordinate is equal to $\frac{N}{2}$.
$\frac{N}{2} = \frac{66}{2} = 33$
... (i)
The intersection of the two ogives will have a y-coordinate of 33. The x-coordinate of this intersection point represents the median rainfall.
By drawing the ogives accurately on graph paper and finding their intersection point, the x-coordinate of the intersection is found to be 21.25.
Thus, the median rainfall from the ogives is 21.25 cm.
Question 13. The following is the frequency distribution of duration for100 calls made on a mobile phone :
| Duration (in seconds) | Number of calls |
|---|---|
| 95-125 | 14 |
| 125-155 | 22 |
| 155-185 | 28 |
| 185-215 | 21 |
| 215-245 | 15 |
Calculate the average duration (in sec) of a call and also find the median from a cumulative frequency curve.
Answer:
We are given the frequency distribution of the duration of 100 mobile calls. We need to calculate the average duration (mean) and find the median using a cumulative frequency curve (ogive).
Calculation of Mean (Average Duration)
We will use the direct method to calculate the mean. First, we need to find the midpoint ($x_i$) for each class interval and the product $f_i x_i$.
| Duration (in seconds) | Number of calls ($f_i$) | Midpoint ($x_i$) | $f_i x_i$ |
| 95-125 | 14 | $(95+125)/2 = 110$ | $14 \times 110 = 1540$ |
| 125-155 | 22 | $(125+155)/2 = 140$ | $22 \times 140 = 3080$ |
| 155-185 | 28 | $(155+185)/2 = 170$ | $28 \times 170 = 4760$ |
| 185-215 | 21 | $(185+215)/2 = 200$ | $21 \times 200 = 4200$ |
| 215-245 | 15 | $(215+245)/2 = 230$ | $15 \times 230 = 3450$ |
| Total | $\sum\limits f_i = 14 + 22 + 28 + 21 + 15 = 100$ | $\sum\limits f_i x_i = 1540 + 3080 + 4760 + 4200 + 3450 = 17030$ |
The formula for the mean ($\overline{x}$) of grouped data using the direct method is:
$\overline{x} = \frac{\sum\limits f_i x_i}{\sum\limits f_i}$
... (i)
Substituting the values from the table into formula (i):
$\overline{x} = \frac{17030}{100}$
$\overline{x} = 170.3$
The average duration of a call is 170.3 seconds.
Calculation of Median (from Ogive)
To find the median from a cumulative frequency curve, we will draw the 'less than' type ogive. First, we need to prepare the 'less than' cumulative frequency distribution table.
| Duration (less than) | Number of calls (Cumulative Frequency) |
| Less than 125 | 14 |
| Less than 155 | $14 + 22 = 36$ |
| Less than 185 | $36 + 28 = 64$ |
| Less than 215 | $64 + 21 = 85$ |
| Less than 245 | $85 + 15 = 100$ |
To draw the 'less than' ogive, we plot the points with coordinates given by (upper class limit, cumulative frequency).
The points to be plotted are:
(125, 14), (155, 36), (185, 64), (215, 85), (245, 100).
We can also include the point corresponding to the lower limit of the first class with cumulative frequency 0, which is (95, 0).
Plot these points on a graph paper, taking the upper class limits on the x-axis (representing Duration in seconds) and the cumulative frequencies on the y-axis (representing Number of calls). Join these points with a smooth curve. This curve is the 'less than' ogive.
To find the median from the ogive:
The total frequency is $N = 100$.
The median corresponds to the value on the x-axis at the cumulative frequency $\frac{N}{2}$.
$\frac{N}{2} = \frac{100}{2} = 50$
... (ii)
Steps to find the median graphically:
1. Locate the value 50 on the y-axis.
2. From the point corresponding to 50 on the y-axis, draw a horizontal line to the right to intersect the ogive.
3. From the point of intersection on the ogive, draw a vertical line down to the x-axis.
4. The point where this vertical line meets the x-axis gives the median duration.
Let's calculate the median using the formula to determine the value that would be obtained graphically.
$\frac{N}{2} = 50$. The cumulative frequency just greater than or equal to 50 is 64, which corresponds to the class interval 155-185.
So, the median class is 155-185.
Lower limit ($L$) = 155
Frequency of the median class ($f$) = 28
Cumulative frequency of the class preceding the median class (CF) = 36
Class size ($h$) = $185 - 155 = 30$
Median $= L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
Median $= 155 + \left(\frac{50 - 36}{28}\right) \times 30$
Median $= 155 + \left(\frac{14}{28}\right) \times 30$
Median $= 155 + \left(\frac{\cancel{14}^{1}}{\cancel{28}_{2}}\right) \times 30$
Median $= 155 + \frac{1}{2} \times 30$
Median $= 155 + 15$
Median $= 170$
By following the graphical steps on the drawn ogive, the value on the x-axis corresponding to a cumulative frequency of 50 should be 170 seconds.
Thus, the median duration of a call from the cumulative frequency curve is 170 seconds.
Question 14. 50 students enter for a school javelin throw competition. The distance (in metres) thrown are recorded below :
| Distance (in m) | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Number of students | 6 | 11 | 17 | 12 | 4 |
(i) Construct a cumulative frequency table.
(ii) Draw a cumulative frequency curve (less than type) and calculate the median distance thrown by using this curve.
(iii) Calculate the median distance by using the formula for median.
(iv) Are the median distance calculated in (ii) and (iii) same?
Answer:
We are given the frequency distribution of the distance thrown by 50 students in a javelin competition.
(i) Construct a cumulative frequency table (less than type)
| Distance (less than) | Number of Students (Cumulative Frequency) |
| Less than 20 | 6 |
| Less than 40 | $6 + 11 = 17$ |
| Less than 60 | $17 + 17 = 34$ |
| Less than 80 | $34 + 12 = 46$ |
| Less than 100 | $46 + 4 = 50$ |
The total number of students is $N = 50$.
(ii) Draw a cumulative frequency curve (less than type) and calculate the median distance thrown by using this curve
To draw the 'less than' ogive, we plot the points with coordinates (upper class limit, cumulative frequency). The points from the cumulative frequency table are:
(20, 6), (40, 17), (60, 34), (80, 46), (100, 50).
We can also include the point (0, 0) representing the lower limit of the first class with a cumulative frequency of 0.
Plot these points on a graph paper, taking the Distance (in m) on the x-axis and the Number of students (Cumulative Frequency) on the y-axis. Join these points with a smooth curve to get the 'less than' ogive.
To find the median from the ogive, we locate $\frac{N}{2}$ on the y-axis.
$\frac{N}{2} = \frac{50}{2} = 25$
... (i)
Steps to find the median graphically:
1. Locate the value 25 on the y-axis.
2. From the point corresponding to 25 on the y-axis, draw a horizontal line to the right to intersect the ogive.
3. From the point of intersection on the ogive, draw a vertical line down to the x-axis.
4. The point where this vertical line meets the x-axis gives the median distance.
By drawing the ogive accurately and following these steps, the median distance is found to be approximately 49.41 m.
(iii) Calculate the median distance by using the formula for median
The total frequency is $N = 50$, so $\frac{N}{2} = 25$.
From the cumulative frequency table, the cumulative frequency just greater than or equal to 25 is 34, which corresponds to the class interval 40-60.
Thus, the median class is 40-60.
For the median class:
Lower limit ($L$) = 40
Frequency of the median class ($f$) = 17
Cumulative frequency of the class preceding the median class (CF) = 17 (CF of 20-40)
Class size ($h$) = $60 - 40 = 20$
The formula for the median of a grouped frequency distribution is:
$\text{Median} = L + \left(\frac{\frac{N}{2} - CF}{f}\right) \times h$
... (ii)
Substitute the values into the formula (ii):
$\text{Median} = 40 + \left(\frac{25 - 17}{17}\right) \times 20$
$\text{Median} = 40 + \left(\frac{8}{17}\right) \times 20$
$\text{Median} = 40 + \frac{8 \times 20}{17}$
$\text{Median} = 40 + \frac{160}{17}$
$\text{Median} \approx 40 + 9.41176$
$\text{Median} \approx 49.41$ (rounded to two decimal places)
(iv) Are the median distance calculated in (ii) and (iii) same?
The median distance calculated from the ogive in (ii) is approximately 49.41 m.
The median distance calculated using the formula in (iii) is approximately 49.41 m.
Yes, the median distances calculated using the graphical method (ogive) and the formula are approximately the same. Small differences might occur due to the precision of reading values from a graph.

