| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 Triangles
Welcome to this essential resource providing comprehensive solutions for the Class 10 NCERT Exemplar problems dedicated to the fundamental geometric chapter on Triangles. These Exemplar questions are meticulously designed to move significantly beyond standard textbook exercises, demanding a deeper conceptual understanding and the ability to construct rigorous proofs and solve complex problems involving triangle properties. The primary focus lies on two critical areas: the detailed exploration of triangle similarity and the powerful applications of the Pythagoras theorem. Mastering the challenges presented in the Exemplar is crucial for developing advanced geometric reasoning and problem-solving skills.
A substantial portion of these solutions delves into the concept of similarity of triangles. We explore the necessary and sufficient criteria for establishing similarity:
- AA (Angle-Angle) Similarity: If two angles of one triangle are respectively equal to two angles of another triangle, the triangles are similar.
- SAS (Side-Angle-Side) Similarity: If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in proportion (e.g., $\frac{AB}{DE} = \frac{AC}{DF}$ and $\angle A = \angle D$), then the triangles are similar.
- SSS (Side-Side-Side) Similarity: If the corresponding sides of two triangles are in proportion (e.g., $\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$), then the triangles are similar.
Another critical theorem extensively covered is the Basic Proportionality Theorem (BPT), also known as Thales Theorem, and its converse. The BPT states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio (e.g., if $DE \parallel BC$ in $\triangle ABC$, then $\frac{AD}{DB} = \frac{AE}{EC}$). The solutions tackle problems where applying the BPT or its converse involves multiple steps or requires combining it with other geometric principles. Closely related, and often proven using similarity, is the theorem regarding the areas of similar triangles: the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. That is, if $\triangle ABC \sim \triangle DEF$, then $\frac{\text{ar}(\triangle ABC)}{\text{ar}(\triangle DEF)} = (\frac{AB}{DE})^2 = (\frac{BC}{EF})^2 = (\frac{AC}{DF})^2$. The Exemplar problems frequently leverage this theorem for complex area comparisons or to find side ratios when area ratios are known.
The timeless Pythagoras Theorem ($a^2 + b^2 = c^2$ for a right triangle with legs $a, b$ and hypotenuse $c$) and its converse form the final major pillar of this chapter's Exemplar solutions. Often, the proof of the theorem itself utilizes concepts of triangle similarity. The solutions demonstrate the rigorous application of this theorem and its converse to solve challenging problems. These often involve right-angled triangles embedded within more complex figures, requiring the calculation of lengths, altitudes, or proving specific geometric relationships. Success frequently hinges on employing strategic constructions or skillfully combining the Pythagoras theorem with similarity criteria or the BPT.
These solutions address the full spectrum of Exemplar question formats, from conceptual MCQs and precise Fill-in-the-Blanks/True/False statements to demanding Short and Long Answer questions requiring well-structured, logically sound proofs with explicit justification citing relevant theorems, or multi-step solutions to complex geometric calculations. With clear diagrams, methodical arguments, and precise theorem application highlighted throughout, this resource is indispensable for students seeking to achieve mastery over advanced triangle geometry and excel in rigorous mathematical assessments.
Sample Question 1 & 2 (Before Exercise 6.1)
Choose the correct answer from the given four options:
Sample Question 1: If in Fig 6.1, O is the point of intersection of two chords AB and CD such that OB = OD, then triangles OAC and ODB are
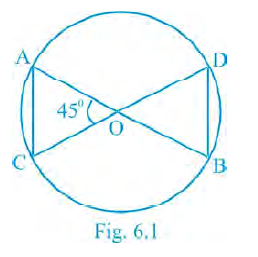
(A) equilateral but not similar
(B) isosceles but not similar
(C) equilateral and similar
(D) isosceles and similar
Answer:
Given:
Chords AB and CD intersect at point O.
OB = OD.
Solution:
In $\triangle$ODB,
OB = OD
(Given)
Since two sides are equal, $\triangle$ODB is an **isosceles** triangle.
The angles opposite the equal sides are equal.
$\angle$OBD = $\angle$ODB
... (i)
Now consider $\triangle$OAC.
We know that angles subtended by the same arc in a circle are equal.
$\angle$OAC = $\angle$ODB
(Angles subtended by arc BC)
$\angle$OCA = $\angle$OBD
(Angles subtended by arc AD)
From (i), we have $\angle$OBD = $\angle$ODB.
Comparing the angle equalities:
Since $\angle$OAC = $\angle$ODB and $\angle$ODB = $\angle$OBD, we get $\angle$OAC = $\angle$OBD.
Since $\angle$OCA = $\angle$OBD and $\angle$OBD = $\angle$ODB, we get $\angle$OCA = $\angle$ODB.
Therefore, $\angle$OAC = $\angle$OCA.
In $\triangle$OAC, since $\angle$OAC = $\angle$OCA, the sides opposite these angles are equal.
OA = OC
Thus, $\triangle$OAC is also an **isosceles** triangle.
Now let's check for similarity between $\triangle$OAC and $\triangle$ODB.
Consider $\triangle$OAC and $\triangle$ODB.
$\angle$AOC = $\angle$BOD
(Vertically Opposite Angles)
$\angle$OAC = $\angle$ODB
(Proved above, angles in the same segment)
$\angle$OCA = $\angle$OBD
(Proved above, angles in the same segment)
Since all three corresponding angles are equal, $\triangle$OAC is **similar** to $\triangle$ODB by AAA similarity criterion.
Thus, both triangles OAC and ODB are **isosceles and similar**.
Conclusion:
The triangles OAC and ODB are isosceles and similar.
The correct option is **(D) isosceles and similar**.
Sample Question 2: D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is
(A) 2.5
(B) 3
(C) 5
(D) 6
Answer:
Given:
In $\triangle$ABC, D is on AB and E is on AC.
AD = 2 cm
BD = 3 cm
BC = 7.5 cm
DE || BC
To Find:
Length of DE.
Solution:
Since DE || BC, by the Basic Proportionality Theorem (BPT) or Thales' Theorem, the triangle ADE is similar to triangle ABC.
Consider $\triangle$ADE and $\triangle$ABC.
Since DE || BC, we have:
$\angle$ADE = $\angle$ABC
(Corresponding angles)
$\angle$AED = $\angle$ACB
(Corresponding angles)
$\angle$DAE = $\angle$BAC
(Common angle)
Thus, by AAA similarity criterion,
$\triangle$ADE $\sim$ $\triangle$ABC
When two triangles are similar, the ratio of their corresponding sides is equal.
Therefore,
$\frac{AD}{AB} = \frac{DE}{BC} = \frac{AE}{AC}$
... (i)
We know AD = 2 cm and BD = 3 cm.
So, AB = AD + BD.
AB = 2 cm + 3 cm = 5 cm
... (ii)
We are given BC = 7.5 cm.
Using the ratio from (i) and substituting the values from (ii) and the given information:
$\frac{AD}{AB} = \frac{DE}{BC}$
... (iii)
$\frac{2}{5} = \frac{DE}{7.5}$
... (iv)
To find DE, we cross-multiply:
$5 \times DE = 2 \times 7.5$
... (v)
$5 \times DE = 15$
... (vi)
Now, divide both sides by 5:
$\text{DE} = \frac{15}{5}$
... (vii)
$\text{DE} = 3$ cm
... (viii)
Conclusion:
The length of DE is 3 cm.
The correct option is **(B) 3**.
Exercise 6.1
Choose the correct answer from the given four options:
Question 1. In Fig. 6.2, ∠BAC = 90° and AD ⊥ BC. Then
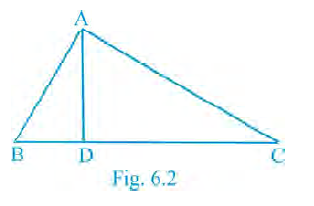
(A) BD . CD = BC2
(B) AB . AC = BC2
(C) BD . CD = AD2
(D) AB . AC = AD2
Answer:
Given:
In $\triangle$ABC,
$\angle$BAC = $90^\circ$
AD $\perp$ BC
Solution:
In $\triangle$ABC, AD is the altitude to the hypotenuse BC.
When an altitude is drawn to the hypotenuse of a right-angled triangle, the triangles on each side of the altitude are similar to the whole triangle and also to each other.
Thus, we have:
$\triangle$DBA $\sim$ $\triangle$ABC
$\triangle$DAC $\sim$ $\triangle$ABC
$\triangle$DBA $\sim$ $\triangle$DAC
... (i)
Let's consider the similarity between $\triangle$DBA and $\triangle$DAC from (i).
The corresponding angles are:
$\angle$ADB = $\angle$ADC = $90^\circ$
(Given AD $\perp$ BC)
$\angle$B = $\angle$DAC
(Angles complementary to $\angle$C in $\triangle$ABC)
$\angle$BAD = $\angle$C
(Angles complementary to $\angle$B in $\triangle$ABC)
Since $\triangle$DBA $\sim$ $\triangle$DAC, the ratio of corresponding sides is equal:
$\frac{DB}{DA} = \frac{BA}{AC} = \frac{DA}{DC}$
... (ii)
Taking the first and third ratios from (ii):
$\frac{DB}{DA} = \frac{DA}{DC}$
... (iii)
Cross-multiplying equation (iii):
$\text{DB} \times \text{DC} = \text{DA} \times \text{DA}$
... (iv)
$\text{BD} \cdot \text{CD} = \text{AD}^2$
... (v)
This relationship is often referred to as the Altitude Theorem or Geometric Mean Theorem for right triangles.
Conclusion:
The relationship between BD, CD, and AD is BD . CD = AD$^2$.
The correct option is **(C) BD . CD = AD2**.
Question 2. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(A) 9 cm
(B) 10 cm
(C) 8 cm
(D) 20 cm
Answer:
Given:
Length of the diagonals of a rhombus are 16 cm and 12 cm.
Let the diagonals be $d_1 = 16$ cm and $d_2 = 12$ cm.
To Find:
The length of the side of the rhombus.
Solution:
We know that the diagonals of a rhombus bisect each other at right angles.
Let the rhombus be ABCD, and let the diagonals AC and BD intersect at point O.
In $\triangle$AOB, which is a right-angled triangle at O, the legs OA and OB are half the lengths of the diagonals AC and BD, respectively.
$\text{OA} = \frac{d_1}{2} = \frac{16}{2}$ cm = 8 cm
$\text{OB} = \frac{d_2}{2} = \frac{12}{2}$ cm = 6 cm
The side of the rhombus AB is the hypotenuse of the right-angled triangle $\triangle$AOB.
By the Pythagorean theorem in $\triangle$AOB:
$\text{AB}^2 = \text{OA}^2 + \text{OB}^2$
... (i)
Substitute the values of OA and OB into equation (i):
$\text{AB}^2 = (8 \text{ cm})^2 + (6 \text{ cm})^2$
... (ii)
$\text{AB}^2 = 64 \text{ cm}^2 + 36 \text{ cm}^2$
... (iii)
$\text{AB}^2 = 100 \text{ cm}^2$
... (iv)
Taking the square root of both sides:
$\text{AB} = \sqrt{100 \text{ cm}^2}$
... (v)
$\text{AB} = 10$ cm
... (vi)
The length of the side of the rhombus is 10 cm.
Conclusion:
The length of the side of the rhombus is 10 cm.
The correct option is **(B) 10 cm**.
Question 3. If Δ ABC ~ Δ EDF and Δ ABC is not similar to Δ DEF, then which of the following is not true?
(A) BC . EF = AC. FD
(B) AB . EF = AC . DE
(C) BC . DE = AB . EF
(D) BC . DE = AB . FD
Answer:
Given:
$\triangle$ ABC $\sim$ $\triangle$ EDF
$\triangle$ ABC is not similar to $\triangle$ DEF
To Find:
Which of the given statements is not true.
Solution:
Since $\triangle$ ABC $\sim$ $\triangle$ EDF, the corresponding vertices are in the order A $\leftrightarrow$ E, B $\leftrightarrow$ D, and C $\leftrightarrow$ F.
The ratio of the corresponding sides of similar triangles is equal. Thus, we have:
$\frac{\text{AB}}{\text{ED}} = \frac{\text{BC}}{\text{DF}} = \frac{\text{AC}}{\text{EF}}$
... (i)
Let's examine each option based on the ratios in equation (i):
**(A) BD . CD = BC2**
This option seems to be related to Question 1 and does not directly involve the sides of $\triangle$ ABC and $\triangle$ EDF in proportion. This must be a typo in the options provided in the input for Question 3, as it does not fit the context of similar triangles ABC and EDF. Assuming the options were intended to test the properties of the similarity $\triangle$ ABC $\sim$ $\triangle$ EDF, let's re-examine the options provided in the input image for Question 3, which are (A) BC . EF = AC. FD, (B) AB . EF = AC . DE, (C) BC . DE = AB . EF, (D) BC . DE = AB . FD. We will proceed using these options.
Let's check the intended options based on $\frac{\text{AB}}{\text{ED}} = \frac{\text{BC}}{\text{DF}} = \frac{\text{AC}}{\text{EF}}$.
**(A) BC . EF = AC . FD**
From the ratios, we can write $\frac{\text{BC}}{\text{DF}} = \frac{\text{AC}}{\text{EF}}$.
Cross-multiplying gives $\text{BC} \times \text{EF} = \text{AC} \times \text{DF}$. This matches option (A). So, statement (A) is **true**.
**(B) AB . EF = AC . DE**
From the ratios, we can write $\frac{\text{AB}}{\text{ED}} = \frac{\text{AC}}{\text{EF}}$. Note that ED is the same as DE.
Cross-multiplying gives $\text{AB} \times \text{EF} = \text{AC} \times \text{ED}$. This matches option (B). So, statement (B) is **true**.
**(C) BC . DE = AB . EF**
This statement can be rewritten as $\frac{\text{BC}}{\text{EF}} = \frac{\text{AB}}{\text{DE}}$. Let's check if this ratio is equal from our original similarity ratios $\frac{\text{AB}}{\text{ED}} = \frac{\text{BC}}{\text{DF}} = \frac{\text{AC}}{\text{EF}}$. The denominator for BC is DF, not EF. The denominator for AB is ED (or DE), not EF. This ratio does not directly follow from the similarity statement $\triangle$ ABC $\sim$ $\triangle$ EDF. So, statement (C) is likely **not true**.
**(D) BC . DE = AB . FD**
This statement can be rewritten as $\frac{\text{BC}}{\text{FD}} = \frac{\text{AB}}{\text{DE}}$. From the original similarity ratios $\frac{\text{AB}}{\text{ED}} = \frac{\text{BC}}{\text{DF}} = \frac{\text{AC}}{\text{EF}}$, we have $\frac{\text{BC}}{\text{DF}} = \frac{\text{AB}}{\text{ED}}$. Since DF = FD and ED = DE, this means $\frac{\text{BC}}{\text{FD}} = \frac{\text{AB}}{\text{DE}}$. Cross-multiplying gives $\text{BC} \times \text{DE} = \text{AB} \times \text{FD}$. This matches option (D). So, statement (D) is **true**.
Based on the similarity $\triangle$ ABC $\sim$ $\triangle$ EDF, options (A), (B), and (D) are true. Option (C) is not true.
Conclusion:
The statement that is not true is BC . DE = AB . EF.
The correct option is **(C) BC . DE = AB . EF**.
Question 4. If in two triangles ABC and PQR, $\frac{AB}{QR}$ = $\frac{BC}{PR}$ = $\frac{CA}{PQ}$, then,
(A) ΔPQR ~ ΔCAB
(B) ΔPQR ~ ΔABC
(C) ΔCBA ~ ΔPQR
(D) ΔBCA ~ ΔPQR
Answer:
Given:
In $\triangle$ABC and $\triangle$PQR,
$\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}$
... (i)
Solution:
The similarity of two triangles is determined by the correspondence between their vertices such that the ratios of corresponding sides are equal and corresponding angles are equal.
From the given ratio of sides $\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}$, we can establish the correspondence between the vertices of $\triangle$ABC and $\triangle$PQR.
The side AB corresponds to QR.
The side BC corresponds to PR.
The side CA corresponds to PQ.
Let's find the vertex correspondence:
Vertex A is the intersection of sides AB and CA. The corresponding sides in $\triangle$PQR are QR and PQ. The common vertex is Q. Thus, A corresponds to Q (A $\leftrightarrow$ Q).
Vertex B is the intersection of sides AB and BC. The corresponding sides in $\triangle$PQR are QR and PR. The common vertex is R. Thus, B corresponds to R (B $\leftrightarrow$ R).
Vertex C is the intersection of sides BC and CA. The corresponding sides in $\triangle$PQR are PR and PQ. The common vertex is P. Thus, C corresponds to P (C $\leftrightarrow$ P).
So, the similarity statement for $\triangle$ABC is $\triangle$ABC $\sim$ $\triangle$QRP.
This means the ratio of corresponding sides is $\frac{AB}{QR} = \frac{BC}{RP} = \frac{CA}{QP}$. This is consistent with the given ratio, since RP is the same as PR and QP is the same as PQ.
Now let's check the given options to see which one matches this similarity or an equivalent form.
**(A) $\triangle$PQR ~ $\triangle$CAB**
This statement implies the vertex correspondence P $\leftrightarrow$ C, Q $\leftrightarrow$ A, R $\leftrightarrow$ B.
The ratio of corresponding sides would be $\frac{PQ}{CA} = \frac{QR}{AB} = \frac{PR}{CB}$.
Let's rewrite the given ratio: $\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}$.
Taking the reciprocal of the given ratios, we get $\frac{QR}{AB} = \frac{PR}{BC} = \frac{PQ}{CA}$.
Rearranging the terms in the reciprocal equation: $\frac{PQ}{CA} = \frac{QR}{AB} = \frac{PR}{BC}$.
Since BC is the same segment as CB, this matches the ratio derived from option (A): $\frac{PQ}{CA} = \frac{QR}{AB} = \frac{PR}{CB}$.
Thus, $\triangle$PQR ~ $\triangle$CAB is a correct similarity statement based on the given information.
Let's quickly check other options to confirm they are incorrect:
**(B) $\triangle$PQR ~ $\triangle$ABC** implies $\frac{PQ}{AB} = \frac{QR}{BC} = \frac{PR}{AC}$. This does not match the given ratio.
**(C) $\triangle$CBA ~ $\triangle$PQR** implies $\frac{CB}{PQ} = \frac{BA}{QR} = \frac{CA}{PR}$. From the given, $\frac{BA}{QR} = \frac{CB}{PR} = \frac{CA}{PQ}$. Comparing these, $\frac{CB}{PQ} = \frac{CB}{PR}$ implies PQ=PR, which is not generally true. So this is incorrect.
**(D) $\triangle$BCA ~ $\triangle$PQR** implies $\frac{BC}{PQ} = \frac{CA}{QR} = \frac{BA}{PR}$. From the given, $\frac{BA}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}$. Comparing these, $\frac{BC}{PQ} = \frac{BC}{PR}$ implies PQ=PR, which is not generally true. Also $\frac{CA}{QR} = \frac{CA}{PQ}$ implies QR=PQ, not generally true. So this is incorrect.
Conclusion:
Based on the given ratio of sides, the correct similarity statement is $\triangle$PQR ~ $\triangle$CAB.
The correct option is **(A) ΔPQR ~ ΔCAB**.
Question 5. In Fig.6.3, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to
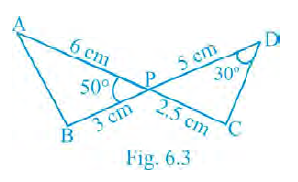
(A) 50°
(B) 30°
(C) 60°
(D) 100°
Answer:
Given:
Line segments AC and BD intersect at point P.
PA = 6 cm
PB = 3 cm
PC = 2.5 cm
PD = 5 cm
$\angle$APB = $50^\circ$
$\angle$CDP = $30^\circ$
To Find:
The measure of $\angle$PBA.
Solution:
Consider triangles $\triangle$APB and $\triangle$DPC.
Check the ratios of the sides around the vertically opposite angles $\angle$APB and $\angle$DPC.
$\frac{\text{PA}}{\text{PD}} = \frac{6 \text{ cm}}{5 \text{ cm}} = \frac{6}{5}$
... (i)
$\frac{\text{PB}}{\text{PC}} = \frac{3 \text{ cm}}{2.5 \text{ cm}} = \frac{30}{25} = \frac{6}{5}$
... (ii)
From (i) and (ii), we have:
$\frac{\text{PA}}{\text{PD}} = \frac{\text{PB}}{\text{PC}} = \frac{6}{5}$
... (iii)
Also, the angles between these sides are vertically opposite:
$\angle$APB = $\angle$DPC
(Vertically opposite angles)
$\angle$APB = $50^\circ$
(Given)
Since the ratio of two pairs of sides is equal, and the included angles are equal, by the SAS similarity criterion:
$\triangle$APB $\sim$ $\triangle$DPC
... (iv)
The corresponding vertices are A $\leftrightarrow$ D, P $\leftrightarrow$ P, B $\leftrightarrow$ C.
Since the triangles are similar, their corresponding angles are equal.
$\angle$PAB = $\angle$PDC
... (v)
$\angle$PBA = $\angle$PCD
... (vi)
$\angle$APB = $\angle$DPC = $50^\circ$
... (vii)
We are given $\angle$CDP = $30^\circ$. This is the same as $\angle$PDC.
From (v), $\angle$PAB = $\angle$PDC = $30^\circ$.
Now, consider $\triangle$APB. The sum of angles in a triangle is $180^\circ$.
$\angle$PAB + $\angle$APB + $\angle$PBA = $180^\circ$
(Sum of angles in $\triangle$APB)
Substitute the known values:
$30^\circ + 50^\circ + \angle$PBA = $180^\circ$
... (viii)
$80^\circ + \angle$PBA = $180^\circ$
... (ix)
Subtract $80^\circ$ from both sides:
$\angle$PBA = $180^\circ - 80^\circ$
... (x)
$\angle$PBA = $100^\circ$
... (xi)
Conclusion:
The measure of $\angle$PBA is $100^\circ$.
The correct option is **(D) 100°**.
Question 6. If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
(A) $\frac{EF}{PR}$ = $\frac{DF}{PQ}$
(B) $\frac{DE}{PQ}$ = $\frac{EF}{RP}$
(C) $\frac{DE}{QR}$ = $\frac{DE}{PQ}$
(D) $\frac{EF}{RP}$ = $\frac{DE}{QR}$
Answer:
Solution:
Given $\angle$D = $\angle$Q and $\angle$E = $\angle$R.
By AAA similarity criterion, $\triangle$DEF $\sim$ $\triangle$QRP.
The ratio of corresponding sides is:
$\frac{\text{DE}}{\text{QR}} = \frac{\text{EF}}{\text{RP}} = \frac{\text{DF}}{\text{QP}}$
... (i)
Let's examine option (C): $\frac{DE}{QR}$ = $\frac{DE}{PQ}$.
From equation (i), $\frac{DE}{QR}$ is a correct ratio of corresponding sides.
The ratio $\frac{DE}{PQ}$ involves side DE from $\triangle$DEF and side PQ from $\triangle$PQR. The corresponding side to DE (D $\leftrightarrow$ Q, E $\leftrightarrow$ R) is QR, not PQ.
The statement $\frac{DE}{QR}$ = $\frac{DE}{PQ}$ implies $\frac{1}{QR} = \frac{1}{PQ}$ (assuming DE $\neq$ 0), which means QR = PQ.
The similarity $\triangle$DEF $\sim$ $\triangle$QRP does not imply that sides QR and PQ in $\triangle$PQR are equal. Therefore, the statement $\frac{DE}{QR}$ = $\frac{DE}{PQ}$ is not true in general based on the given similarity.
Let's quickly check other options against $\frac{DE}{QR} = \frac{EF}{RP} = \frac{DF}{QP}$:
(A) $\frac{EF}{PR} = \frac{DF}{PQ} \implies \frac{EF}{RP} = \frac{DF}{QP}$. This is true.
(D) $\frac{EF}{RP}$ = $\frac{DE}{QR}$. This is true.
Option (B) $\frac{DE}{PQ} = \frac{EF}{RP}$ is also not true in general, as it implies PQ = QR.
However, option (C) directly equates a correct ratio to a ratio using a non-corresponding side from the same triangle (second triangle PQR), leading to a specific condition on the sides of $\triangle$PQR that is not implied by the similarity.
Conclusion:
The statement that is not true is $\frac{DE}{QR}$ = $\frac{DE}{PQ}$.
The correct option is **(C) $\frac{DE}{QR}$ = $\frac{DE}{PQ}$**.
Question 7. In triangles ABC and DEF, ∠B = ∠E, ∠F =∠C and AB = 3 DE. Then, the two triangles are
(A) congruent but not similar
(B) similar but not congruent
(C) neither congruent nor similar
(D) congruent as well as similar
Answer:
Given:
In $\triangle$ABC and $\triangle$DEF:
$\angle$B = $\angle$E
... (i)
$\angle$F = $\angle$C
... (ii)
AB = 3 DE
... (iii)
Solution:
Consider $\triangle$ABC and $\triangle$DEF.
From (i) and (ii), we have two pairs of corresponding angles equal.
By the Angle-Angle (AA) similarity criterion, if two angles of one triangle are equal to two corresponding angles of another triangle, then the triangles are similar.
Thus, $\triangle$ABC $\sim$ $\triangle$DEF.
The correspondence of vertices is A $\leftrightarrow$ D, B $\leftrightarrow$ E, C $\leftrightarrow$ F.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{AB}}{\text{DE}} = \frac{\text{BC}}{\text{EF}} = \frac{\text{AC}}{\text{DF}}$
... (iv)
From (iii), we are given AB = 3 DE.
Dividing both sides by DE (assuming DE $\neq$ 0), we get:
$\frac{\text{AB}}{\text{DE}} = 3$
... (v)
Substituting (v) into (iv), we get the ratio of corresponding sides:
$\frac{\text{AB}}{\text{DE}} = \frac{\text{BC}}{\text{EF}} = \frac{\text{AC}}{\text{DF}} = 3$
... (vi)
For triangles to be congruent, they must be similar and the ratio of their corresponding sides must be 1.
In this case, the ratio of corresponding sides is 3, not 1.
Therefore, the triangles are not congruent.
However, they are similar as established by the AA criterion.
Conclusion:
The two triangles are similar but not congruent.
The correct option is **(B) similar but not congruent**.
Question 8. It is given that ΔABC ~ ΔPQR, with $\frac{BC}{QR}$ = $\frac{1}{3}$ . Then, $\frac{ar (PRQ)}{ar (BCA)}$ is equal to
(A) 9
(B) 3
(C) $\frac{1}{3}$
(D) $\frac{1}{9}$
Answer:
Given:
$\triangle$ABC ~ $\triangle$PQR
$\frac{\text{BC}}{\text{QR}} = \frac{1}{3}$
... (i)
To Find:
The value of $\frac{ar (PRQ)}{ar (BCA)}$.
Solution:
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given $\triangle$ABC ~ $\triangle$PQR, the corresponding sides are AB and PQ, BC and QR, AC and PR.
So, the ratio of areas is:
$\frac{\text{ar (ABC)}}{\text{ar (PQR)}} = \left(\frac{\text{AB}}{\text{PQ}}\right)^2 = \left(\frac{\text{BC}}{\text{QR}}\right)^2 = \left(\frac{\text{AC}}{\text{PR}}\right)^2$
... (ii)
We are given $\frac{\text{BC}}{\text{QR}} = \frac{1}{3}$.
Using the ratio of areas property from (ii):
$\frac{\text{ar (ABC)}}{\text{ar (PQR)}} = \left(\frac{1}{3}\right)^2$
... (iii)
$\frac{\text{ar (ABC)}}{\text{ar (PQR)}} = \frac{1}{9}$
... (iv)
We need to find $\frac{ar (PRQ)}{ar (BCA)}$.
The area of a triangle is independent of the order of vertices in the name, so $ar(PRQ) = ar(PQR)$ and $ar(BCA) = ar(ABC)$.
Thus, we need to find $\frac{ar (PQR)}{ar (ABC)}$.
This is the reciprocal of $\frac{ar (ABC)}{ar (PQR)}$.
$\frac{\text{ar (PQR)}}{\text{ar (ABC)}} = \frac{1}{\frac{\text{ar (ABC)}}{\text{ar (PQR)}}}$
... (v)
Substitute the value from (iv) into (v):
$\frac{\text{ar (PQR)}}{\text{ar (ABC)}} = \frac{1}{\frac{1}{9}}$
... (vi)
$\frac{\text{ar (PQR)}}{\text{ar (ABC)}} = 9$
... (vii)
Therefore, $\frac{ar (PRQ)}{ar (BCA)} = 9$.
Conclusion:
The value of $\frac{ar (PRQ)}{ar (BCA)}$ is 9.
The correct option is **(A) 9**.
Question 9. It is given that ΔABC ~ ΔDFE,∠A = 30°∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true:
(A) DE = 12 cm,∠F = 50°
(B) DE = 12 cm, ∠F = 100°
(C) EF = 12 cm, ∠D = 100°
(D) EF = 12 cm, ∠D = 30°
Answer:
Given:
$\triangle$ABC ~ $\triangle$DFE
$\angle$A = $30^\circ$
$\angle$C = $50^\circ$
AB = 5 cm
AC = 8 cm
DF = 7.5 cm
To Find:
Which of the given statements is true.
Solution:
Since $\triangle$ABC ~ $\triangle$DFE, the corresponding vertices are A $\leftrightarrow$ D, B $\leftrightarrow$ F, C $\leftrightarrow$ E.
The corresponding angles are equal:
$\angle$A = $\angle$D = $30^\circ$
... (i)
$\angle$B = $\angle$F
... (ii)
$\angle$C = $\angle$E = $50^\circ$
... (iii)
In $\triangle$ABC, the sum of angles is $180^\circ$.
$\angle$A + $\angle$B + $\angle$C = $180^\circ$
... (iv)
Substitute the known values into (iv):
$30^\circ + \angle$B + $50^\circ$ = $180^\circ$
... (v)
$\angle$B + $80^\circ$ = $180^\circ$
... (vi)
$\angle$B = $180^\circ - 80^\circ = 100^\circ$
... (vii)
From (ii), $\angle$F = $\angle$B = $100^\circ$.
The corresponding sides are proportional:
$\frac{\text{AB}}{\text{DF}} = \frac{\text{BC}}{\text{FE}} = \frac{\text{AC}}{\text{DE}}$
... (viii)
Substitute the given side lengths into (viii):
$\frac{5 \text{ cm}}{7.5 \text{ cm}} = \frac{\text{BC}}{\text{FE}} = \frac{8 \text{ cm}}{\text{DE}}$
... (ix)
Simplify the ratio of known sides:
$\frac{5}{7.5} = \frac{50}{75} = \frac{2 \times 25}{3 \times 25} = \frac{2}{3}$
... (x)
So, the ratio of corresponding sides is $\frac{2}{3}$.
$\frac{\text{AB}}{\text{DF}} = \frac{5}{7.5} = \frac{2}{3}$
... (xi)
$\frac{\text{AC}}{\text{DE}} = \frac{8}{\text{DE}} = \frac{2}{3}$
... (xii)
From (xii), cross-multiply to find DE:
$2 \times \text{DE} = 8 \times 3$
... (xiii)
$2 \times \text{DE} = 24$
... (xiv)
$\text{DE} = \frac{24}{2} = 12$ cm
... (xv)
We found $\angle$F = $100^\circ$ and DE = 12 cm.
Let's check the options:
(A) DE = 12 cm, $\angle$F = 50°. Incorrect ($\angle$F = 100°).
(B) DE = 12 cm, $\angle$F = 100°. Correct.
(C) EF = 12 cm, $\angle$D = 100°. Incorrect ($\angle$D = 30°, and we haven't calculated EF yet).
(D) EF = 12 cm, $\angle$D = 30°. Incorrect ($\angle$D = 30° is correct, but we haven't confirmed EF = 12 cm).
To be thorough, let's find EF if possible. We need BC. We know $\frac{\text{BC}}{\text{FE}} = \frac{2}{3}$. Without BC, we cannot find EF.
However, we have definitively found DE = 12 cm and $\angle$F = $100^\circ$.
Conclusion:
The true statement is DE = 12 cm and $\angle$F = $100^\circ$.
The correct option is **(B) DE = 12 cm, ∠F = 100°**.
Question 10. If in triangles ABC and DEF, $\frac{AB}{DE}$ = $\frac{BC}{FD}$ , then they will be similar, when
(A) ∠B = ∠E
(B) ∠A = ∠D
(C) ∠B = ∠D
(D) ∠A = ∠F
Answer:
Given:
In $\triangle$ABC and $\triangle$DEF,
$\frac{\text{AB}}{\text{DE}} = \frac{\text{BC}}{\text{FD}}$
... (i)
To Find:
The condition for $\triangle$ABC and $\triangle$DEF to be similar.
Solution:
We are given the ratio of two pairs of sides of $\triangle$ABC and $\triangle$DEF. For the triangles to be similar based on this information, we can use the SAS similarity criterion.
The SAS (Side-Angle-Side) similarity criterion states that if the ratio of two sides of one triangle is equal to the ratio of the corresponding two sides of another triangle, and the included angles between these sides are equal, then the two triangles are similar.
From the given ratio $\frac{\text{AB}}{\text{DE}} = \frac{\text{BC}}{\text{FD}}$:
In $\triangle$ABC, the two sides mentioned in the ratio are AB and BC. The angle included between sides AB and BC is $\angle$B.
In $\triangle$DEF, the two sides mentioned in the ratio (corresponding to AB and BC in the given pairing) are DE and FD. The angle included between sides DE and FD is $\angle$D.
For similarity by SAS criterion, the included angles must be equal.
Therefore, the condition for $\triangle$ABC and $\triangle$DEF to be similar is that the angle included between sides AB and BC ($\angle$B) must be equal to the angle included between sides DE and FD ($\angle$D).
$\angle$B = $\angle$D
... (ii)
If $\frac{\text{AB}}{\text{DE}} = \frac{\text{BC}}{\text{FD}}$ and $\angle$B = $\angle$D, then by SAS similarity, $\triangle$ABC $\sim$ $\triangle$EDF.
Let's check the ratio for $\triangle$ABC $\sim$ $\triangle$EDF:
$\frac{\text{AB}}{\text{ED}} = \frac{\text{BC}}{\text{DF}} = \frac{\text{AC}}{\text{EF}}$
... (iii)
Since ED = DE and DF = FD, equation (iii) is $\frac{\text{AB}}{\text{DE}} = \frac{\text{BC}}{\text{FD}} = \frac{\text{AC}}{\text{EF}}$. This matches the given ratio of sides.
So the correct condition is $\angle$B = $\angle$D.
Conclusion:
The triangles will be similar when $\angle$B = $\angle$D.
The correct option is **(C) ∠B = ∠D**.
Question 11. If ΔABC ~ ΔQRP, $\frac{ar (ABC)}{ar (PQR)}$ = $\frac{9}{4}$ , AB = 18 cm and BC = 15 cm, then PR is equal to
(A) 10 cm
(B) 12 cm
(C) $\frac{20}{3}$ cm
(D) 8 cm
Answer:
Given:
$\triangle$ABC ~ $\triangle$QRP
$\frac{\text{ar (ABC)}}{\text{ar (PQR)}} = \frac{9}{4}$
... (i)
AB = 18 cm
BC = 15 cm
To Find:
The length of PR.
Solution:
Since $\triangle$ABC $\sim$ $\triangle$QRP, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
The correspondence of vertices is A $\leftrightarrow$ Q, B $\leftrightarrow$ R, C $\leftrightarrow$ P.
The ratio of corresponding sides is:
$\frac{\text{AB}}{\text{QR}} = \frac{\text{BC}}{\text{RP}} = \frac{\text{AC}}{\text{QP}}$
... (ii)
The ratio of areas is:
$\frac{\text{ar (ABC)}}{\text{ar (QRP)}} = \left(\frac{\text{AB}}{\text{QR}}\right)^2 = \left(\frac{\text{BC}}{\text{RP}}\right)^2 = \left(\frac{\text{AC}}{\text{QP}}\right)^2$
... (iii)
We are given $\frac{\text{ar (ABC)}}{\text{ar (PQR)}} = \frac{9}{4}$. Since $ar(PQR) = ar(QRP)$, we have:
$\frac{\text{ar (ABC)}}{\text{ar (QRP)}} = \frac{9}{4}$
... (iv)
From (iii) and (iv), we can find the ratio of corresponding sides:
$\left(\frac{\text{BC}}{\text{RP}}\right)^2 = \frac{9}{4}$
... (v)
Take the square root of both sides of (v):
$\frac{\text{BC}}{\text{RP}} = \sqrt{\frac{9}{4}} = \frac{3}{2}$
... (vi)
We are given BC = 15 cm and we need to find PR (which is the same as RP).
Substitute the value of BC into (vi):
$\frac{15 \text{ cm}}{\text{RP}} = \frac{3}{2}$
... (vii)
Cross-multiply:
3 $\times$ RP = 15 $\times$ 2
... (viii)
3 $\times$ RP = 30
... (ix)
Divide both sides by 3:
$\text{RP} = \frac{30}{3} = 10$ cm
... (x)
So, PR = 10 cm.
Note: We were given AB = 18 cm as extra information, which is not needed to find PR.
Conclusion:
The length of PR is 10 cm.
The correct option is **(A) 10 cm**.
Question 12. If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then
(A) PR . QR = RS2
(B) QS2 + RS2 = QR2
(C) PR2 + QR2 = PQ2
(D) PS2 + RS2 = PR2
Answer:
Given:
S is a point on side PQ of $\triangle$PQR.
PS = QS = RS
... (i)
To Find:
The true relationship among the sides of $\triangle$PQR.
Solution:
From equation (i), PS = QS. Since S is a point on the side PQ, this means that S is the **midpoint** of the side PQ.
Also from equation (i), RS = PS and RS = QS.
The fact that the distance from S (the midpoint of PQ) to vertex R is equal to the distance from S to vertices P and Q (i.e., RS = PS = QS = $\frac{1}{2}$PQ) implies a special property about $\triangle$PQR.
A well-known geometric theorem states that in a triangle, if the length of the median to one side is half the length of that side, then the angle opposite that side is a right angle.
Here, RS is the median to the side PQ, and its length RS is equal to half the length of PQ (since PS = QS = RS = $\frac{1}{2}$PQ).
Therefore, the angle opposite the side PQ, which is $\angle$PRQ (or $\angle$R), must be a **right angle** ($90^\circ$).
$\angle$PRQ = $90^\circ$
... (ii)
So, $\triangle$PQR is a right-angled triangle with the right angle at R.
By the **Pythagorean theorem** in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
In $\triangle$PQR, the hypotenuse is PQ (opposite to $\angle$R), and the other two sides are PR and QR.
Applying the Pythagorean theorem:
$\text{PR}^2 + \text{QR}^2 = \text{PQ}^2$
... (iii)
This is the relationship between the sides of $\triangle$PQR.
Now, let's compare this with the given options.
Option (C) matches equation (iii): $\text{PR}^2 + \text{QR}^2 = \text{PQ}^2$.
Conclusion:
If S is a point on side PQ of a $\triangle$PQR such that PS = QS = RS, then $\triangle$PQR is right-angled at R, and the Pythagorean theorem $\text{PR}^2 + \text{QR}^2 = \text{PQ}^2$ holds true.
The correct option is **(C) PR2 + QR2 = PQ2**.
Sample Question 1 to 3 (Before Exercise 6.2)
Sample Question 1: In ΔABC, AB = 24 cm, BC = 10 cm and AC = 26 cm. Is this triangle a right triangle? Give reasons for your answer.
Answer:
Given the sides of $\Delta$ABC are:
AB = $24$ cm
BC = $10$ cm
AC = $26$ cm
To determine if $\Delta$ABC is a right triangle, we can use the Pythagorean theorem.
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs).
The longest side in $\Delta$ABC is AC = $26$ cm. This would be the hypotenuse if it is a right triangle.
Let's calculate the square of the longest side and the sum of the squares of the other two sides:
Square of the longest side:
$AC^2 = 26^2 = 26 \times 26 = 676$
Sum of the squares of the other two sides:
$AB^2 + BC^2 = 24^2 + 10^2$
$24^2 = 24 \times 24 = 576$
$10^2 = 10 \times 10 = 100$
$AB^2 + BC^2 = 576 + 100 = 676$
Now we check if the square of the longest side is equal to the sum of the squares of the other two sides:
$AC^2 = AB^2 + BC^2$
(Checking the Pythagorean condition)
$676 = 676$
Since the condition $AC^2 = AB^2 + BC^2$ is satisfied, the triangle $\Delta$ABC is a right triangle.
The reason is the converse of the Pythagorean theorem, which states that if in a triangle, the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
In this case, the angle opposite the side AC is $\angle$ABC, which must be $90^\circ$.
Sample Question 2: P and Q are the points on the sides DE and DF of a triangle DEF such that DP = 5 cm, DE = 15 cm, DQ= 6 cm and QF = 18 cm. Is PQ || EF? Give reasons for your answer
Answer:
Given:
In $\Delta$DEF, P is a point on side DE and Q is a point on side DF.
$DP = 5$ cm
$DE = 15$ cm
$DQ = 6$ cm
$QF = 18$ cm
To check:
Is PQ || EF?
Solution:
To determine if PQ is parallel to EF, we can use the Converse of the Basic Proportionality Theorem (BPT).
The converse of BPT states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
For PQ to be parallel to EF, the line segment PQ must divide the sides DE and DF in the same ratio. That is, we must check if $\frac{DP}{PE} = \frac{DQ}{QF}$.
First, we need to find the length of the segment PE on side DE. Since P is on DE, PE is the remaining part of DE after DP.
$DE = DP + PE$
$15 = 5 + PE$
$PE = 15 - 5 = 10$ cm
Now, we calculate the ratio of the segments on side DE:
$\frac{DP}{PE} = \frac{5}{10} = \frac{1}{2}$
Next, we calculate the ratio of the segments on side DF. We are given DQ and QF directly.
$\frac{DQ}{QF} = \frac{6}{18} = \frac{1}{3}$
Now, we compare the two ratios:
Ratio on side DE is $\frac{DP}{PE} = \frac{1}{2}$.
Ratio on side DF is $\frac{DQ}{QF} = \frac{1}{3}$.
We observe that $\frac{1}{2} \neq \frac{1}{3}$.
Since the line segment PQ does not divide the sides DE and DF in the same ratio ($\frac{DP}{PE} \neq \frac{DQ}{QF}$), by the Converse of the Basic Proportionality Theorem, PQ is not parallel to EF.
Sample Question 3: It is given that Δ FED ~ Δ STU . Is it true to say that $\frac{DE}{ST}$ = $\frac{EF}{TU}$ ? Why?
Answer:
Given:
Two triangles $\Delta$ FED and $\Delta$ STU are similar.
We are given the similarity statement as $\Delta$ FED ~ $\Delta$ STU.
To check:
Is the statement $\frac{DE}{ST} = \frac{EF}{TU}$ true?
Why or why not?
Solution:
When two triangles are similar, their corresponding angles are equal and the ratio of their corresponding sides is constant.
The order of the vertices in the similarity statement is crucial as it defines which vertices and sides correspond to each other.
Given $\Delta$ FED ~ $\Delta$ STU, the correspondence of vertices is:
- F corresponds to S
- E corresponds to T
- D corresponds to U
Based on this correspondence, the corresponding sides are:
- Side FE corresponds to side ST
- Side ED corresponds to side TU
- Side FD corresponds to side SU
Therefore, the ratios of the corresponding sides are:
$\frac{FE}{ST} = \frac{ED}{TU} = \frac{FD}{SU}$
Or, using the side names as given in the question:
$\frac{EF}{ST} = \frac{DE}{TU} = \frac{FD}{SU}$
The statement we are asked to check is $\frac{DE}{ST} = \frac{EF}{TU}$.
Let's compare this with the correct ratios from the similarity:
The correct ratio involving DE is $\frac{DE}{TU}$.
The correct ratio involving EF is $\frac{EF}{ST}$.
So, the correct relationship from the similarity $\Delta$ FED ~ $\Delta$ STU is:
$\frac{EF}{ST} = \frac{DE}{TU}$
... (i)
The statement $\frac{DE}{ST} = \frac{EF}{TU}$ implies $\frac{DE}{EF} = \frac{ST}{TU}$.
However, the similarity $\Delta$ FED ~ $\Delta$ STU implies $\frac{DE}{TU} = \frac{EF}{ST}$.
Comparing the given statement $\frac{DE}{ST} = \frac{EF}{TU}$ with the correct ratio equality $\frac{DE}{TU} = \frac{EF}{ST}$, we see that they are generally not the same unless the sides happen to have specific lengths that make this equality hold coincidentally.
The correspondence requires that the ratio of the first two letters of $\Delta$ FED (FE) to the first two letters of $\Delta$ STU (ST) is equal to the ratio of the second two letters of $\Delta$ FED (ED) to the second two letters of $\Delta$ STU (TU), and so on for the first and third letters (FD and SU).
Therefore, based on the correspondence in $\Delta$ FED ~ $\Delta$ STU, the correct ratio equality is $\frac{FE}{ST} = \frac{ED}{TU} = \frac{FD}{SU}$.
The statement $\frac{DE}{ST} = \frac{EF}{TU}$ rearranges the denominators compared to the correct ratios.
Conclusion:
It is false to say that $\frac{DE}{ST} = \frac{EF}{TU}$.
Reason:
Because the ratios of corresponding sides are determined by the order of vertices in the similarity statement. Given $\Delta$ FED ~ $\Delta$ STU, the correct ratios of corresponding sides are $\frac{FE}{ST} = \frac{ED}{TU} = \frac{FD}{SU}$, not $\frac{DE}{ST} = \frac{EF}{TU}$. The side DE corresponds to TU, and the side EF (or FE) corresponds to ST.
Exercise 6.2
Question 1. Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
Answer:
Given the lengths of the sides of a triangle are:
$a = 25$ cm
$b = 5$ cm
$c = 24$ cm
To determine if this triangle is a right triangle, we can use the Pythagorean theorem or its converse.
The longest side is $25$ cm. If the triangle is a right triangle, this side must be the hypotenuse.
Let's check if the square of the longest side is equal to the sum of the squares of the other two sides.
Square of the longest side:
$25^2 = 25 \times 25 = 625$
Sum of the squares of the other two sides:
$5^2 + 24^2$
$5^2 = 5 \times 5 = 25$
$24^2 = 24 \times 24 = 576$
$5^2 + 24^2 = 25 + 576 = 601$
Now, let's compare the results:
$25^2$ vs $5^2 + 24^2$
(Checking Pythagorean condition)
$625$ vs $601$
We see that $625 \neq 601$.
Thus, the condition $25^2 = 5^2 + 24^2$ is not satisfied.
Conclusion:
No, the triangle with sides 25 cm, 5 cm, and 24 cm is not a right triangle.
Reason:
According to the converse of the Pythagorean theorem, if the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. In this case, the square of the longest side ($25^2 = 625$) is not equal to the sum of the squares of the other two sides ($5^2 + 24^2 = 601$). Therefore, the triangle does not satisfy the condition for being a right triangle.
Question 2. It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
Answer:
Given:
Two triangles $\Delta$DEF and $\Delta$RPQ are similar.
We are given the similarity statement as $\Delta$ DEF ~ $\Delta$ RPQ.
To check:
Is the statement $\angle$D = $\angle$R and $\angle$F = $\angle$P true?
Why or why not?
Solution:
When two triangles are similar, their corresponding angles are equal and the ratio of their corresponding sides is constant.
The order of the vertices in the similarity statement $\Delta$ DEF ~ $\Delta$ RPQ tells us which angles and sides correspond.
The correspondence of vertices is:
- First vertex D in $\Delta$ DEF corresponds to the first vertex R in $\Delta$ RPQ.
- Second vertex E in $\Delta$ DEF corresponds to the second vertex P in $\Delta$ RPQ.
- Third vertex F in $\Delta$ DEF corresponds to the third vertex Q in $\Delta$ RPQ.
Based on this vertex correspondence, the corresponding angles are:
- $\angle$D corresponds to $\angle$R. Therefore, $\angle$D = $\angle$R.
- $\angle$E corresponds to $\angle$P. Therefore, $\angle$E = $\angle$P.
- $\angle$F corresponds to $\angle$Q. Therefore, $\angle$F = $\angle$Q.
Now let's look at the statement we are asked to check: $\angle$D = $\angle$R and $\angle$F = $\angle$P.
From our analysis of the correspondence:
- $\angle$D = $\angle$R is true because D and R are corresponding vertices.
- $\angle$F = $\angle$P is false because F corresponds to Q, and E corresponds to P. The correct angle equality involving $\angle$F is $\angle$F = $\angle$Q, and the correct angle equality involving $\angle$P is $\angle$P = $\angle$E.
Since one part of the statement ($\angle$F = $\angle$P) is false, the entire statement "$\angle$D = $\angle$R and $\angle$F = $\angle$P" is false.
Conclusion:
It is false to say that $\angle$D = $\angle$R and $\angle$F = $\angle$P.
Reason:
In similar triangles, corresponding angles are equal. The similarity statement $\Delta$ DEF ~ $\Delta$ RPQ establishes the vertex correspondence as D $\leftrightarrow$ R, E $\leftrightarrow$ P, and F $\leftrightarrow$ Q. This means $\angle$D = $\angle$R, $\angle$E = $\angle$P, and $\angle$F = $\angle$Q. The statement $\angle$F = $\angle$P is incorrect based on this correspondence; angle F corresponds to angle Q, and angle P corresponds to angle E.
Question 3. A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR= 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Answer:
Given:
In $\Delta$PQR, A is a point on side PQ and B is a point on side PR.
$PQ = 12.5$ cm
$PA = 5$ cm
$BR = 6$ cm
$PB = 4$ cm
To check:
Is AB || QR?
Solution:
To determine if AB is parallel to QR, we can use the Converse of the Basic Proportionality Theorem (BPT).
The converse of BPT states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
For AB to be parallel to QR, the line segment AB must divide the sides PQ and PR in the same ratio. That is, we must check if $\frac{PA}{AQ} = \frac{PB}{BR}$.
First, we need to find the length of the segment AQ on side PQ. Since A is on PQ, AQ is the remaining part of PQ after PA.
$PQ = PA + AQ$
$12.5 = 5 + AQ$
$AQ = 12.5 - 5 = 7.5$ cm
Now, we calculate the ratio of the segments on side PQ:
$\frac{PA}{AQ} = \frac{5}{7.5} = \frac{50}{75}$
Simplifying the fraction by dividing numerator and denominator by 25:
$\frac{50 \div 25}{75 \div 25} = \frac{2}{3}$
So, $\frac{PA}{AQ} = \frac{2}{3}$.
Next, we calculate the ratio of the segments on side PR. We are given PB and BR directly.
$\frac{PB}{BR} = \frac{4}{6}$
Simplifying the fraction by dividing numerator and denominator by 2:
$\frac{4 \div 2}{6 \div 2} = \frac{2}{3}$
So, $\frac{PB}{BR} = \frac{2}{3}$.
Now, we compare the two ratios:
Ratio on side PQ is $\frac{PA}{AQ} = \frac{2}{3}$.
Ratio on side PR is $\frac{PB}{BR} = \frac{2}{3}$.
We observe that $\frac{PA}{AQ} = \frac{PB}{BR} = \frac{2}{3}$.
Conclusion:
Yes, AB is parallel to QR.
Reason:
Since the line segment AB divides the sides PQ and PR in the same ratio ($\frac{PA}{AQ} = \frac{PB}{BR}$), by the Converse of the Basic Proportionality Theorem, AB is parallel to QR.
Question 4. In Fig 6.4, BD and CE intersect each other at the point P. Is Δ PBC ~ Δ PDE? Why?
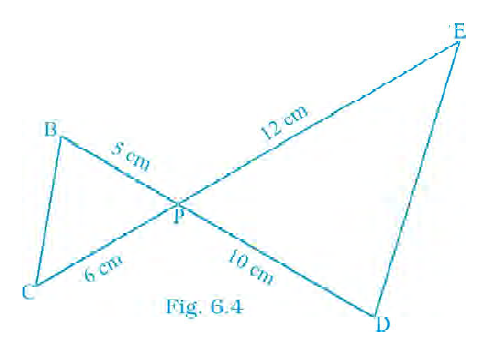
Answer:
Given:
Lines BD and CE intersect at point P, forming $\Delta$PBC and $\Delta$PDE.
To check:
Is $\Delta$ PBC ~ $\Delta$ PDE?
Why or why not?
Solution:
We are considering triangles $\Delta$ PBC and $\Delta$ PDE.
From the figure, we can observe the angles formed by the intersection of lines BD and CE at P.
$\angle$BPC and $\angle$DPE are a pair of vertically opposite angles.
Vertically opposite angles are always equal.
$\angle$BPC = $\angle$DPE
(Vertically opposite angles)
To prove that two triangles are similar, we need to satisfy one of the similarity criteria (AA, SAS, or SSS).
We have found one pair of equal angles ($\angle$BPC = $\angle$DPE).
For AA similarity, we would need another pair of equal angles, such as $\angle$PBC = $\angle$PDE or $\angle$PCB = $\angle$PED. However, there is no information given in the problem statement or indicated in the figure (like parallel lines BC and DE) to suggest that any other angles are equal.
For SAS similarity, we would need the ratio of the sides including the equal angles to be proportional, i.e., $\frac{PB}{PD} = \frac{PC}{PE}$. No side lengths are given to check this proportionality.
For SSS similarity, we would need the ratios of all three pairs of corresponding sides to be equal, i.e., $\frac{PB}{PD} = \frac{PC}{PE} = \frac{BC}{DE}$. Again, no side lengths are provided.
Conclusion:
It is false to say that $\Delta$ PBC ~ $\Delta$ PDE based solely on the given information.
Reason:
We only have one pair of equal angles, $\angle$BPC = $\angle$DPE (vertically opposite angles). This is not sufficient to prove similarity. We would need additional information, such as another pair of equal angles or the proportionality of corresponding sides, to satisfy any of the similarity criteria (AA, SAS, SSS). Without such information, we cannot conclude that $\Delta$ PBC is similar to $\Delta$ PDE.
Question 5. In triangles PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ΔQPR ~ ΔTSM? Why?
Answer:
Given:
In $\Delta$PQR, $\angle$P = $55^\circ$ and $\angle$Q = $25^\circ$.
In $\Delta$MST, $\angle$M = $100^\circ$ and $\angle$S = $25^\circ$.
To check:
Is $\Delta$QPR ~ $\Delta$TSM?
Why or why not?
Solution:
First, let's find the measure of the third angle in each triangle using the Angle Sum Property of a triangle.
In $\Delta$PQR:
$\angle$P + $\angle$Q + $\angle$R = $180^\circ$
$55^\circ + 25^\circ + \angle$R = $180^\circ$
$80^\circ + \angle$R = $180^\circ$
$\angle$R = $180^\circ - 80^\circ$
$\angle$R = $100^\circ$
In $\Delta$MST:
$\angle$M + $\angle$S + $\angle$T = $180^\circ$
$100^\circ + 25^\circ + \angle$T = $180^\circ$
$125^\circ + \angle$T = $180^\circ$
$\angle$T = $180^\circ - 125^\circ$
$\angle$T = $55^\circ$
So, the angles of $\Delta$PQR are $\angle$P=$55^\circ$, $\angle$Q=$25^\circ$, $\angle$R=$100^\circ$.
And the angles of $\Delta$MST are $\angle$M=$100^\circ$, $\angle$S=$25^\circ$, $\angle$T=$55^\circ$.
We are asked if $\Delta$QPR ~ $\Delta$TSM is true. For this similarity statement to be true, the corresponding angles must be equal based on the order of the vertices.
The correspondence is:
- Q $\leftrightarrow$ T
- P $\leftrightarrow$ S
- R $\leftrightarrow$ M
Let's check if the corresponding angles are equal:
Is $\angle$Q = $\angle$T?
$\angle$Q = $25^\circ$ and $\angle$T = $55^\circ$.
$25^\circ \neq 55^\circ$. So, $\angle$Q $\neq$ $\angle$T.
Is $\angle$P = $\angle$S?
$\angle$P = $55^\circ$ and $\angle$S = $25^\circ$.
$55^\circ \neq 25^\circ$. So, $\angle$P $\neq$ $\angle$S.
Is $\angle$R = $\angle$M?
$\angle$R = $100^\circ$ and $\angle$M = $100^\circ$.
$100^\circ = 100^\circ$. So, $\angle$R = $\angle$M.
Conclusion:
No, it is false to say that $\Delta$QPR ~ $\Delta$TSM.
Reason:
For the similarity statement $\Delta$QPR ~ $\Delta$TSM to be true, the corresponding angles must be equal. This means $\angle$Q should be equal to $\angle$T, $\angle$P should be equal to $\angle$S, and $\angle$R should be equal to $\angle$M. We found that $\angle$Q = $25^\circ$ and $\angle$T = $55^\circ$, so $\angle$Q $\neq$ $\angle$T. Also, $\angle$P = $55^\circ$ and $\angle$S = $25^\circ$, so $\angle$P $\neq$ $\angle$S. Although $\angle$R = $\angle$M = $100^\circ$, the lack of equality in the other two pairs of corresponding angles (as per the given vertex order) means the statement $\Delta$QPR ~ $\Delta$TSM is not true.
The triangles $\Delta$PQR and $\Delta$MST are similar because their angles ($25^\circ, 55^\circ, 100^\circ$) are the same. However, the correct similarity statement requires the vertices to be in corresponding order, such as $\Delta$PQR ~ $\Delta$TSM or $\Delta$QPR ~ $\Delta$STM.
Question 6. Is the following statement true? Why?
“Two quadrilaterals are similar, if their corresponding angles are equal”.
Answer:
Given statement:
“Two quadrilaterals are similar, if their corresponding angles are equal”.
To check:
Is the statement true? Why or why not?
Solution:
For any two polygons (with the same number of sides) to be considered similar, they must satisfy two conditions:
- Their corresponding angles must be equal.
- The ratio of their corresponding sides must be constant (i.e., their corresponding sides must be in proportion).
The given statement only mentions the first condition: "if their corresponding angles are equal". It does not include the second condition about the proportionality of corresponding sides.
For polygons with more than three sides (like quadrilaterals, pentagons, etc.), having corresponding angles equal is necessary for similarity, but it is not sufficient on its own.
Consider a counterexample:
Let's take a square with side length $2$ cm and a rectangle with sides $2$ cm and $3$ cm (that is not a square).
- In the square, all four angles are $90^\circ$.
- In the rectangle, all four angles are also $90^\circ$.
So, the corresponding angles of the square and this rectangle are all equal ($90^\circ$).
Now let's check the ratio of corresponding sides:
- For the square, all sides are $2$ cm.
- For the rectangle, two sides are $2$ cm and two sides are $3$ cm.
Let's try to match sides. If a side of length $2$ cm from the square corresponds to a side of length $2$ cm from the rectangle, the ratio is $\frac{2}{2} = 1$.
If a side of length $2$ cm from the square corresponds to a side of length $3$ cm from the rectangle, the ratio is $\frac{2}{3}$.
Since $1 \neq \frac{2}{3}$, the ratio of corresponding sides is not constant.
Conclusion:
No, the statement is false.
Reason:
Having corresponding angles equal is not sufficient for two quadrilaterals to be similar. For quadrilaterals (and other polygons with more than 3 sides), both conditions - equality of corresponding angles and proportionality of corresponding sides - must be satisfied for similarity. The counterexample of a square and a non-square rectangle shows that two quadrilaterals can have all corresponding angles equal ($90^\circ$), but still not be similar because their sides are not in proportion.
(Note: For triangles, the AA (Angle-Angle) similarity criterion exists, which states that if two angles of one triangle are respectively equal to two angles of another triangle, then the triangles are similar. This is because if two angles are equal, the third angle must also be equal by the angle sum property, and this angle equality automatically guarantees the proportionality of sides. However, this special property only applies to triangles, not to quadrilaterals or polygons with more sides).
Question 7. Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Answer:
Given:
Let the two triangles be $\Delta$ ABC and $\Delta$ PQR.
Let their sides be AB, BC, AC and PQ, QR, PR respectively.
Given that two sides of $\Delta$ ABC are three times the corresponding sides of $\Delta$ PQR.
Let's assume, without loss of generality, that AB and BC are the sides of $\Delta$ ABC which are three times the corresponding sides PQ and QR of $\Delta$ PQR.
AB = 3 $\times$ PQ
... (i)
BC = 3 $\times$ QR
... (ii)
Given that the perimeter of $\Delta$ ABC is three times the perimeter of $\Delta$ PQR.
Perimeter($\Delta$ ABC) = 3 $\times$ Perimeter($\Delta$ PQR)
... (iii)
The perimeter of a triangle is the sum of its sides.
Perimeter($\Delta$ ABC) = AB + BC + AC
Perimeter($\Delta$ PQR) = PQ + QR + PR
To check:
Are $\Delta$ ABC and $\Delta$ PQR similar?
Why?
Solution:
Substitute the expressions for the perimeters into equation (iii):
AB + BC + AC = 3 $\times$ (PQ + QR + PR)
AB + BC + AC = 3PQ + 3QR + 3PR
Now substitute the values from equations (i) and (ii) into this equation:
(3 $\times$ PQ) + (3 $\times$ QR) + AC = 3PQ + 3QR + 3PR
3PQ + 3QR + AC = 3PQ + 3QR + 3PR
Subtract 3PQ and 3QR from both sides of the equation:
AC = 3PR
AC = 3 $\times$ PR
... (iv)
Now let's examine the ratios of the corresponding sides:
From equation (i), $\frac{AB}{PQ} = 3$
From equation (ii), $\frac{BC}{QR} = 3$
From equation (iv), $\frac{AC}{PR} = 3$
We have found that the ratio of all three pairs of corresponding sides is equal:
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR} = 3$
This means that the corresponding sides of $\Delta$ ABC and $\Delta$ PQR are in the same proportion (the ratio is 3).
Conclusion:
Yes, the two triangles are similar.
Reason:
According to the SSS (Side-Side-Side) similarity criterion, if the corresponding sides of two triangles are in the same ratio, then the triangles are similar. We are given that two pairs of corresponding sides are in a ratio of 3:1, and the perimeters are also in a ratio of 3:1. We used this information to show that the third pair of corresponding sides must also be in the same ratio of 3:1. Since all three pairs of corresponding sides are in the same ratio, the triangles satisfy the SSS similarity criterion and are therefore similar.
Question 8. If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
Answer:
Given:
Two triangles are right triangles. Let them be $\Delta$ ABC and $\Delta$ PQR.
In $\Delta$ ABC, let $\angle$C = $90^\circ$. The acute angles are $\angle$A and $\angle$B.
In $\Delta$ PQR, let $\angle$R = $90^\circ$. The acute angles are $\angle$P and $\angle$Q.
Given that one acute angle of $\Delta$ ABC is equal to one acute angle of $\Delta$ PQR.
Let's assume, without loss of generality, that $\angle$A is the acute angle in $\Delta$ ABC and $\angle$P is the acute angle in $\Delta$ PQR, such that $\angle$A = $\angle$P.
To check:
Are the two triangles, $\Delta$ ABC and $\Delta$ PQR, similar?
Why?
Solution:
Consider the two triangles $\Delta$ ABC and $\Delta$ PQR.
We have the following information:
$\angle$C = $90^\circ$
(Given, as $\Delta$ ABC is a right triangle)
$\angle$R = $90^\circ$
(Given, as $\Delta$ PQR is a right triangle)
From the above two points, we have $\angle$C = $\angle$R.
We are also given that one acute angle of one triangle is equal to one acute angle of the other triangle. Let's assume $\angle$A = $\angle$P.
$\angle$A = $\angle$P
(Given)
Now, consider the two triangles $\Delta$ ABC and $\Delta$ PQR. We have two pairs of corresponding angles that are equal:
1. $\angle$A = $\angle$P
2. $\angle$C = $\angle$R (both are $90^\circ$)
According to the AA (Angle-Angle) similarity criterion, if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
Since we have shown that two pairs of corresponding angles ($\angle$A and $\angle$P, and $\angle$C and $\angle$R) are equal, the triangles $\Delta$ ABC and $\Delta$ PQR are similar.
Conclusion:
Yes, the two triangles will be similar.
Reason:
In two right triangles, one angle in each triangle is $90^\circ$. If one acute angle of one right triangle is equal to an acute angle of the other right triangle, then we have two pairs of corresponding equal angles: the right angles ($90^\circ$) and the given equal acute angles. By the AA similarity criterion, if two angles of one triangle are equal to two angles of another triangle, the triangles are similar. Therefore, the two right triangles are similar.
Question 9. The ratio of the corresponding altitudes of two similar triangles is $\frac{3}{5}$ . Is it correct to say that ratio of their areas is $\frac{6}{5}$ ? Why?
Answer:
Given:
Two triangles are similar.
The ratio of their corresponding altitudes is $\frac{3}{5}$.
To check:
Is it correct to say that the ratio of their areas is $\frac{6}{5}$?
Why?
Solution:
Let the two similar triangles be $\Delta_1$ and $\Delta_2$.
Let $h_1$ and $h_2$ be the lengths of their corresponding altitudes.
We are given that the ratio of corresponding altitudes is $\frac{h_1}{h_2} = \frac{3}{5}$.
There is a theorem regarding the relationship between the areas of two similar triangles and the ratio of their corresponding sides, altitudes, medians, or angle bisectors.
The theorem states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
It also states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding altitudes.
Mathematically, if $\Delta_1 \sim \Delta_2$, then:
$\frac{\text{Area}(\Delta_1)}{\text{Area}(\Delta_2)} = \left(\frac{\text{Corresponding side 1}}{\text{Corresponding side 2}}\right)^2 = \left(\frac{\text{Corresponding altitude 1}}{\text{Corresponding altitude 2}}\right)^2$
Using the given ratio of corresponding altitudes, we can find the ratio of their areas:
$\frac{\text{Area}(\Delta_1)}{\text{Area}(\Delta_2)} = \left(\frac{h_1}{h_2}\right)^2$
Substitute the given ratio $\frac{h_1}{h_2} = \frac{3}{5}$:
$\frac{\text{Area}(\Delta_1)}{\text{Area}(\Delta_2)} = \left(\frac{3}{5}\right)^2$
$\frac{\text{Area}(\Delta_1)}{\text{Area}(\Delta_2)} = \frac{3^2}{5^2} = \frac{9}{25}$
The calculated ratio of the areas is $\frac{9}{25}$.
The statement in the question claims the ratio of the areas is $\frac{6}{5}$.
Comparing the calculated ratio with the claimed ratio:
$\frac{9}{25} \neq \frac{6}{5}$
(Note that $\frac{6}{5} = \frac{30}{25}$)
Conclusion:
No, it is not correct to say that the ratio of their areas is $\frac{6}{5}$.
Reason:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding altitudes. Since the ratio of the corresponding altitudes is $\frac{3}{5}$, the ratio of their areas is $\left(\frac{3}{5}\right)^2 = \frac{9}{25}$, not $\frac{6}{5}$. The statement is based on an incorrect application of the theorem.
Question 10. D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
Answer:
Given:
In $\Delta$PQR, D is a point on side QR.
PD $\perp$ QR.
To check:
Is $\Delta$PQD ~ $\Delta$RPD?
Why or why not?
Solution:
We are asked to determine if $\Delta$PQD is similar to $\Delta$RPD.
Given that PD $\perp$ QR, this means that PD is perpendicular to the line segment QR at point D.
Therefore, the angles formed by PD and QR at point D are right angles.
$\angle$PDQ = $90^\circ$
(Since PD $\perp$ QR)
$\angle$PDR = $90^\circ$
(Since PD $\perp$ QR)
So, we have one pair of corresponding angles equal in $\Delta$PQD and $\Delta$RPD: $\angle$PDQ = $\angle$PDR.
For two triangles to be similar, they must satisfy one of the similarity criteria: AA, SAS, or SSS.
We have one pair of equal angles ($\angle$PDQ and $\angle$PDR).
For AA similarity, we would need another pair of corresponding angles to be equal.
We would need either:
- $\angle$PQD = $\angle$PRD (i.e., $\angle$PQR = $\angle$PRQ), which means $\Delta$PQR must be an isosceles triangle with PQ = PR, or
- $\angle$QPD = $\angle$RPD, which means PD must be the angle bisector of $\angle$QPR.
However, the problem statement only provides that PD is an altitude. There is no information given about the angles of $\Delta$PQR or whether PD bisects $\angle$QPR.
For SAS similarity, we would need $\frac{PQ}{RP} = \frac{QD}{PD}$ and the included angles $\angle$PDQ = $\angle$PDR. We only have the angle equality, but no information on the side lengths to check the proportionality.
For SSS similarity, we would need $\frac{PQ}{RP} = \frac{QD}{RD} = \frac{PD}{PD}$. This implies $\frac{PQ}{RP} = \frac{QD}{RD} = 1$, meaning PQ=RP and QD=RD. Again, no side lengths are provided to check this.
Without additional information that provides another equal pair of corresponding angles or the proportionality of corresponding sides, we cannot conclude similarity.
Conclusion:
No, it is not correct to say that $\Delta$PQD ~ $\Delta$RPD based on the given information.
Reason:
We are only given that PD is an altitude, which provides one pair of equal corresponding angles ($\angle$PDQ = $\angle$PDR = $90^\circ$). This information alone is not sufficient to prove similarity between $\Delta$PQD and $\Delta$RPD. For similarity, we would require either another pair of corresponding angles to be equal (like $\angle$PQR = $\angle$PRQ or $\angle$QPD = $\angle$RPD) or the ratio of corresponding sides to be proportional. Since this additional information is not provided, we cannot apply any of the similarity criteria to conclude that the triangles are similar.
Question 11. In Fig. 6.5, if ∠D =∠C, then is it true that ΔADE ~ ΔACB? Why?
Answer:
Given:
In the given figure (Fig. 6.5), $\Delta$ADE and $\Delta$ACB are shown.
Point D is on AC and point E is on AB.
$\angle$D = $\angle$C.
To check:
Is $\Delta$ADE ~ $\Delta$ACB?
Why?
Solution:
Consider the two triangles, $\Delta$ADE and $\Delta$ACB.
We are given that $\angle$D = $\angle$C.
$\angle$ADE = $\angle$ACB
(Given)
Observe that $\Delta$ADE and $\Delta$ACB share a common angle at vertex A.
$\angle$DAE = $\angle$CAB
(Common angle)
We have found two pairs of corresponding angles that are equal in $\Delta$ADE and $\Delta$ACB:
1. $\angle$DAE = $\angle$CAB (Common angle at A)
2. $\angle$ADE = $\angle$ACB (Given)
According to the AA (Angle-Angle) similarity criterion, if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
Since $\angle$DAE = $\angle$CAB and $\angle$ADE = $\angle$ACB, the triangles $\Delta$ADE and $\Delta$ACB satisfy the AA similarity criterion.
Conclusion:
Yes, it is true that $\Delta$ADE ~ $\Delta$ACB.
Reason:
The triangles $\Delta$ADE and $\Delta$ACB are similar by the AA (Angle-Angle) similarity criterion because they have two pairs of corresponding angles equal: the common angle at A ($\angle$DAE = $\angle$CAB) and the given angles ($\angle$ADE = $\angle$ACB).
Question 12. Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer
Answer:
Given statement:
“If in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar.”
To check:
Is the statement true?
Give reasons.
Solution:
This statement describes a condition for similarity that is similar to the SAS (Side-Angle-Side) similarity criterion, but it lacks a crucial detail.
The SAS similarity criterion states: "If one angle of a triangle is equal to one angle of the other triangle, and the sides including these angles are proportional, then the two triangles are similar."
The given statement does not specify that the equal angle must be the angle included between the two proportional sides.
Let's examine if the statement holds true when the equal angle is not included between the proportional sides.
Consider two triangles, $\Delta$ABC and $\Delta$PQR.
Let's assume that $\angle$A = $\angle$P.
Let's assume that two sides are proportional, for example, $\frac{AB}{PQ} = \frac{BC}{QR}$. Note that the equal angle $\angle$A (or $\angle$P) is not included between sides AB and BC (or PQ and QR).
We can construct a counterexample where this condition is met, but the triangles are not similar.
Consider $\Delta$ABC with $\angle$A = $30^\circ$, side AB = $10$ cm and side BC = $6$ cm.
Using the Sine Rule in $\Delta$ABC:
$\frac{BC}{\sin A} = \frac{AB}{\sin C}$
$\frac{6}{\sin 30^\circ} = \frac{10}{\sin C}$
$\frac{6}{0.5} = \frac{10}{\sin C}$
$12 = \frac{10}{\sin C}$
$\sin C = \frac{10}{12} = \frac{5}{6}$
There are two possible angles C for which $\sin C = \frac{5}{6}$. One acute ($\approx 56.44^\circ$) and one obtuse ($\approx 123.56^\circ$). Let's choose the obtuse angle for $\Delta$ABC.
Let $\angle$C $\approx 123.56^\circ$. Then $\angle$B = $180^\circ - 30^\circ - 123.56^\circ = 26.44^\circ$.
So $\Delta$ABC has angles approximately $30^\circ$, $26.44^\circ$, and $123.56^\circ$.
Now, consider $\Delta$PQR with $\angle$P = $30^\circ$, side PQ = $5$ cm and side QR = $3$ cm.
Here, we have $\angle$A = $\angle$P = $30^\circ$.
Let's check the ratio of sides: $\frac{AB}{PQ} = \frac{10}{5} = 2$ and $\frac{BC}{QR} = \frac{6}{3} = 2$. So, $\frac{AB}{PQ} = \frac{BC}{QR}$.
Now, using the Sine Rule in $\Delta$PQR:
$\frac{QR}{\sin P} = \frac{PQ}{\sin R}$
$\frac{3}{\sin 30^\circ} = \frac{5}{\sin R}$
$\frac{3}{0.5} = \frac{5}{\sin R}$
$6 = \frac{5}{\sin R}$
$\sin R = \frac{5}{6}$
Again, there are two possible angles R. Let's choose the acute angle for $\Delta$PQR.
Let $\angle$R $\approx 56.44^\circ$. Then $\angle$Q = $180^\circ - 30^\circ - 56.44^\circ = 93.56^\circ$.
So $\Delta$PQR has angles approximately $30^\circ$, $93.56^\circ$, and $56.44^\circ$.
We have constructed two triangles $\Delta$ABC (angles $\approx$ 30, 26.44, 123.56) and $\Delta$PQR (angles $\approx$ 30, 93.56, 56.44) such that:
- An angle of one triangle is equal to an angle of the other ($\angle$A = $\angle$P = $30^\circ$).
- Two sides of one triangle are proportional to two sides of the other triangle ($\frac{AB}{PQ} = \frac{BC}{QR} = 2$).
However, the triangles are clearly not similar because their sets of angles are different. ($\{30^\circ, 26.44^\circ, 123.56^\circ\} \neq \{30^\circ, 93.56^\circ, 56.44^\circ\}$).
Conclusion:
No, it is false to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar.
Reason:
For the similarity criterion involving two sides and an angle (SAS criterion), the equal angle must be the included angle between the two proportional sides. If the equal angle is not the included angle, it is possible to construct triangles that satisfy the given condition but are not similar. This situation is analogous to the SSA case in triangle congruence, which does not guarantee congruence. The counterexample above illustrates this point.
Sample Question 1 to 3 (Before Exercise 6.3)
Sample Question 1: Legs (sides other than the hypotenuse) of a right triangle are of lengths 16cm and 8 cm. Find the length of the side of the largest square that can be inscribed in the triangle.
Answer:
Given the legs of a right triangle are $a = 16$ cm and $b = 8$ cm.
To Find:
The side length of the largest inscribed square.
Solution:
There are two main cases for the largest inscribed square in a right triangle:
Case 1: One vertex of the square is at the right angle.
Let the side length of this square be $s_1$. Using the formula for this case:
$s_1 = \frac{ab}{a+b}$
Substituting the given values:
$s_1 = \frac{16 \times 8}{16 + 8} = \frac{128}{24} = \frac{16}{3}$ cm.
$s_1 = \frac{16}{3}$ cm
... (1)
Case 2: One side of the square lies on the hypotenuse.
Let the side length of this square be $s_2$. First, calculate the length of the hypotenuse $c$ and the altitude to the hypotenuse $h$.
$c = \sqrt{a^2 + b^2} = \sqrt{16^2 + 8^2} = \sqrt{256 + 64} = \sqrt{320} = \sqrt{64 \times 5} = 8\sqrt{5}$ cm.
The altitude to the hypotenuse is $h = \frac{ab}{c} = \frac{16 \times 8}{8\sqrt{5}} = \frac{16}{\sqrt{5}}$ cm.
Using the formula for the side length of the square in this case:
$s_2 = \frac{ch}{c+h}$
Substituting the calculated values:
$s_2 = \frac{8\sqrt{5} \times \frac{16}{\sqrt{5}}}{8\sqrt{5} + \frac{16}{\sqrt{5}}} = \frac{8 \times 16}{\frac{8\sqrt{5} \times \sqrt{5} + 16}{\sqrt{5}}} = \frac{128}{\frac{40 + 16}{\sqrt{5}}} = \frac{128}{\frac{56}{\sqrt{5}}} = \frac{128\sqrt{5}}{56}$
Simplifying the fraction:
$s_2 = \frac{\cancel{128}^{16}\sqrt{5}}{\cancel{56}_{7}} = \frac{16\sqrt{5}}{7}$ cm.
$s_2 = \frac{16\sqrt{5}}{7}$ cm
... (2)
To find the largest square, we compare $s_1$ and $s_2$.
Compare $\frac{16}{3}$ and $\frac{16\sqrt{5}}{7}$.
Since $16$ is positive, compare $\frac{1}{3}$ and $\frac{\sqrt{5}}{7}$.
Square both values: $(\frac{1}{3})^2 = \frac{1}{9}$ and $(\frac{\sqrt{5}}{7})^2 = \frac{5}{49}$.
Compare $\frac{1}{9}$ and $\frac{5}{49}$. Find a common denominator ($9 \times 49 = 441$):
$\frac{1}{9} = \frac{1 \times 49}{9 \times 49} = \frac{49}{441}$
$\frac{5}{49} = \frac{5 \times 9}{49 \times 9} = \frac{45}{441}$
Since $\frac{49}{441} > \frac{45}{441}$, we have $\frac{1}{9} > \frac{5}{49}$.
Taking the square root (since values are positive), $\frac{1}{3} > \frac{\sqrt{5}}{7}$.
Multiplying by 16, $\frac{16}{3} > \frac{16\sqrt{5}}{7}$.
So, $s_1 > s_2$.
Conclusion:
The side length of the largest square is the greater of $s_1$ and $s_2$, which is $s_1 = \frac{16}{3}$ cm.
Final Answer: The length of the side of the largest square that can be inscribed in the triangle is $\frac{16}{3}$ cm.
Sample Question 2: Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is longer than the other by 5 cm. Find the lengths of the other two sides.
Answer:
Given:
In a right triangle, the length of the hypotenuse is $25$ cm.
One leg is $5$ cm longer than the other leg.
To Find:
The lengths of the other two sides (the legs).
Solution:
Let the length of one leg of the right triangle be $x$ cm.
According to the problem, the other leg is $5$ cm longer than this leg.
So, the length of the other leg is $(x+5)$ cm.
The length of the hypotenuse is given as $25$ cm.
In a right triangle, the relationship between the lengths of the legs and the hypotenuse is given by the Pythagorean theorem:
$(\text{Leg } 1)^2 + (\text{Leg } 2)^2 = (\text{Hypotenuse})^2$
Substitute the expressions and values into the Pythagorean theorem:
$(x)^2 + (x+5)^2 = 25^2$
(By Pythagorean theorem)
Expand and simplify the equation:
$x^2 + (x^2 + 2 \times x \times 5 + 5^2) = 25 \times 25$
$x^2 + x^2 + 10x + 25 = 625$
$2x^2 + 10x + 25 = 625$
Move all terms to one side to form a quadratic equation:
$2x^2 + 10x + 25 - 625 = 0$
$2x^2 + 10x - 600 = 0$
Divide the entire equation by 2 to simplify:
$\frac{2x^2}{2} + \frac{10x}{2} - \frac{600}{2} = \frac{0}{2}$
$x^2 + 5x - 300 = 0$
Now, solve the quadratic equation $x^2 + 5x - 300 = 0$ for $x$. We can factor the quadratic expression.
We need two numbers that multiply to -300 and add up to +5.
Let's consider the factors of 300. The pair 20 and 15 has a difference of 5. To get a product of -300 and a sum of +5, the numbers must be +20 and -15.
So, the quadratic equation can be factored as:
$(x + 20)(x - 15) = 0$
Set each factor equal to zero to find the possible values for $x$:
$x + 20 = 0$ or $x - 15 = 0$
$x = -20$ or $x = 15$
Since $x$ represents the length of a side of a triangle, it must be a positive value.
Therefore, $x = -20$ is not a valid solution.
The valid value for $x$ is $15$.
$x = 15$ cm.
Now find the lengths of the two legs using $x = 15$:
Length of the first leg = $x = 15$ cm.
Length of the second leg = $x + 5 = 15 + 5 = 20$ cm.
Let's verify these lengths using the Pythagorean theorem:
$15^2 + 20^2 = 225 + 400 = 625$
Hypotenuse squared $= 25^2 = 625$
Since $15^2 + 20^2 = 25^2$, the lengths are correct.
Conclusion:
The lengths of the other two sides of the right triangle are $15$ cm and $20$ cm.
Sample Question 3: In Fig 6.7,
∠D =∠E and $\frac{AD}{DB}$ = $\frac{AE}{EC}$ . Prove that BAC is an isosceles triangle.
Answer:
Given:
In a triangle BAC (assuming D is on AB and E is on AC based on the context of the question asking to prove $\Delta$BAC is isosceles, despite the potentially mismatched figure):
$\frac{AD}{DB} = \frac{AE}{EC}$
... (i)
$\angle$ADE = $\angle$AED
... (ii)
To Prove:
$\Delta$BAC is an isosceles triangle.
Proof:
Consider $\Delta$BAC.
From the given condition (i):
$\frac{AD}{DB} = \frac{AE}{EC}$
(Given)
By the Converse of the Basic Proportionality Theorem (BPT), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Since the line segment DE divides the sides AB and AC in the same ratio, we can conclude that DE is parallel to BC.
So, DE || BC.
Now, consider the parallel lines DE and BC intersected by transversals AB and AC.
When a transversal intersects two parallel lines, the corresponding angles are equal.
Therefore, we have:
$\angle$ADE = $\angle$ABC
(Corresponding angles, since DE || BC)
$\angle$AED = $\angle$ACB
(Corresponding angles, since DE || BC)
We are also given the condition (ii):
$\angle$ADE = $\angle$AED
(Given)
Now, we can use the property of transitivity of equality.
Since $\angle$ADE = $\angle$ABC and $\angle$AED = $\angle$ACB, and we know that $\angle$ADE = $\angle$AED, it follows that:
$\angle$ABC = $\angle$ACB
(By substituting equal angles)
Now, consider $\Delta$BAC. We have shown that two of its angles, $\angle$ABC and $\angle$ACB, are equal.
In any triangle, the sides opposite to equal angles are equal in length.
The side opposite to $\angle$ACB is AB.
The side opposite to $\angle$ABC is AC.
Therefore, since $\angle$ABC = $\angle$ACB, we have AB = AC.
By definition, a triangle with two equal sides is an isosceles triangle.
Since AB = AC, $\Delta$BAC is an isosceles triangle.
Hence Proved.
Exercise 6.3
Question 1. In a ΔPQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR.
Prove that QM2 = PM × MR.
Answer:
Given:
$\triangle PQR$ with $PR^2 - PQ^2 = QR^2$.
M is a point on side PR such that $QM \perp PR$.
To Prove:
$QM^2 = PM \times MR$.
Proof:
We are given that $PR^2 - PQ^2 = QR^2$.
Rearranging the equation, we get:
$PR^2 = PQ^2 + QR^2$
By the converse of the Pythagorean theorem, if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
In $\triangle PQR$, the side opposite to PR is the angle $\angle PQR$. Since $PR^2 = PQ^2 + QR^2$, $\triangle PQR$ is a right-angled triangle with the right angle at Q.
So, $\angle PQR = 90^\circ$.
We are also given that $QM \perp PR$. This means QM is the altitude from the vertex Q to the hypotenuse PR.
In a right-angled triangle, the altitude from the vertex of the right angle to the hypotenuse divides the triangle into two triangles that are similar to the original triangle and also similar to each other.
Consider $\triangle QMP$ and $\triangle QMR$.
In $\triangle PQR$, $\angle P + \angle R = 90^\circ$ (since $\angle PQR = 90^\circ$).
In $\triangle QMP$:
$\angle PMQ = 90^\circ$ (Given $QM \perp PR$).
$\angle MPQ = \angle RPQ = \angle P$ (Common angle).
Therefore, $\angle MQP = 180^\circ - 90^\circ - \angle P = 90^\circ - \angle P = \angle R$.
In $\triangle QMR$:
$\angle QMR = 90^\circ$ (Given $QM \perp PR$).
$\angle MRQ = \angle PRQ = \angle R$ (Common angle).
Therefore, $\angle MQR = 180^\circ - 90^\circ - \angle R = 90^\circ - \angle R = \angle P$.
Comparing $\triangle QMP$ and $\triangle QMR$:
$\angle PMQ = \angle QMR = 90^\circ$
$\angle MQP = \angle MRQ$ (Both equal to $\angle R$)
$\angle MPQ = \angle MQR$ (Both equal to $\angle P$)
By AAA similarity criterion, $\triangle QMP \sim \triangle QMR$.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{PM}{QM} = \frac{MQ}{MR} = \frac{QP}{QR}$
Taking the first two ratios:
$\frac{PM}{QM} = \frac{MQ}{MR}$
Cross-multiplying gives:
$PM \times MR = QM \times MQ$
Since $MQ = QM$, we have:
$PM \times MR = QM^2$
Hence, $QM^2 = PM \times MR$.
Hence Proved.
Question 2. Find the value of x for which DE || AB in Fig. 6.8.
Answer:
Given:
In $\triangle CAB$, points D and E are on sides CA and CB respectively.
The lengths of the segments are:
$CD = (x+3)$ cm
$DA = (3x+19)$ cm
$CE = x$ cm
$EB = (3x+4)$ cm
To Find:
The value of x for which $DE || AB$.
Solution:
For $DE$ to be parallel to $AB$ in $\triangle CAB$, the Basic Proportionality Theorem (BPT) must hold.
According to the converse of the BPT, if a line divides any two sides of a triangle proportionally, then it is parallel to the third side.
Therefore, for $DE || AB$, we must have:
$\frac{CD}{DA} = \frac{CE}{EB}$
Substitute the given expressions for the segment lengths:
$\frac{x+3}{3x+19} = \frac{x}{3x+4}$
Cross-multiply the equation:
$(x+3)(3x+4) = x(3x+19)$
Expand both sides:
$x(3x) + x(4) + 3(3x) + 3(4) = x(3x) + x(19)$
$3x^2 + 4x + 9x + 12 = 3x^2 + 19x$
Combine like terms on the left side:
$3x^2 + 13x + 12 = 3x^2 + 19x$
Subtract $3x^2$ from both sides:
$13x + 12 = 19x$
Subtract $13x$ from both sides:
$12 = 19x - 13x$
$12 = 6x$
Divide by 6:
$x = \frac{12}{6}$
$x = 2$
We should verify that this value of x results in positive lengths for all segments:
$CD = 2+3 = 5 > 0$
$DA = 3(2)+19 = 6+19 = 25 > 0$
$CE = 2 > 0$
$EB = 3(2)+4 = 6+4 = 10 > 0$
Since all lengths are positive, the value $x=2$ is valid.
Thus, for $DE || AB$, the value of x is 2.
Question 3. In Fig. 6.9, if ∠1 =∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
Answer:
Given:
In $\triangle PQR$, $\angle 1 = \angle 2$.
$\triangle NSQ \cong \triangle MTR$.
To Prove:
$\triangle PTS \sim \triangle PRQ$.
Proof:
We are given that $\angle 1 = \angle 2$.
In $\triangle PQR$, $\angle 1$ is $\angle PQR$ and $\angle 2$ is $\angle PRQ$.
So, $\angle PQR = \angle PRQ$.
In a triangle, sides opposite to equal angles are equal.
Therefore, $PQ = PR$.
We are given that $\triangle NSQ \cong \triangle MTR$.
Since the triangles are congruent, their corresponding parts are equal (CPCT).
Thus, we have:
$NS = MT$
$SQ = TR$
$NQ = MR$
And the corresponding angles are equal:
$\angle SNQ = \angle TMR$
$\angle NSQ = \angle MTR$
$\angle NQS = \angle MRT$
Consider the angles $\angle PQR$ and $\angle PRQ$. We know $\angle PQR = \angle PRQ$.
We can write these angles as:
$\angle PQR = \angle PQS + \angle NQS$
$\angle PRQ = \angle PRT + \angle MRT$
Since $\angle PQR = \angle PRQ$ and $\angle NQS = \angle MRT$, we can write:
$\angle PQS + \angle NQS = \angle PRT + \angle MRT$
$\angle PQS + \angle NQS = \angle PRT + \angle NQS$ (since $\angle MRT = \angle NQS$)
Subtracting $\angle NQS$ from both sides gives:
$\angle PQS = \angle PRT$.
Now, consider $\triangle PQS$ and $\triangle PRT$.
$\angle QPS = \angle RPT = \angle P$ (Common angle to both triangles).
$\angle PQS = \angle PRT$ (Proved above).
By AA similarity criterion, $\triangle PQS \sim \triangle PRT$.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{PQ}{PR} = \frac{PS}{PT} = \frac{QS}{RT}$
We know that $PQ = PR$. So, $\frac{PQ}{PR} = 1$.
Therefore, $\frac{PS}{PT} = 1$, which implies $PS = PT$.
Also, $\frac{QS}{RT} = 1$, which implies $QS = RT$. (Note that $QS=RT$ is also consistent with $SQ=TR$ from congruence, just written with vertices in a different order).
Now, consider $\triangle PTS$ and $\triangle PRQ$.
$\angle TPS = \angle RPQ = \angle P$ (Common angle to both triangles).
Consider the ratio of sides adjacent to $\angle P$ in both triangles:
Ratio of sides involving PT and PQ: $\frac{PT}{PQ}$.
Ratio of sides involving PS and PR: $\frac{PS}{PR}$.
We have proved that $PT = PS$ and $PQ = PR$.
So, $\frac{PT}{PQ} = \frac{PS}{PR}$ (since both ratios are equal, e.g., $\frac{a}{b} = \frac{a}{b}$).
Thus, by SAS similarity criterion, $\triangle PTS \sim \triangle PRQ$.
Hence Proved.
Question 4. Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
Answer:
Given:
Trapezium PQRS with diagonals PR and QS intersecting at O.
$PQ || RS$
$PQ = 3 RS$
To Find:
The ratio of the areas of $\triangle POQ$ and $\triangle ROS$, i.e., $\frac{\text{Area}(\triangle POQ)}{\text{Area}(\triangle ROS)}$.
Solution:
Consider $\triangle POQ$ and $\triangle ROS$.
Since $PQ || RS$, we can use the properties of parallel lines and transversals.
$\angle OPQ = \angle ORS$ (Alternate interior angles, as PR is a transversal)
$\angle OQP = \angle OSR$ (Alternate interior angles, as QS is a transversal)
$\angle POQ = \angle ROS$ (Vertically opposite angles)
Since all three corresponding angles are equal, $\triangle POQ$ is similar to $\triangle ROS$ by AAA similarity criterion.
$\triangle POQ \sim \triangle ROS$
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
The corresponding sides opposite to the vertically opposite angles $\angle POQ$ and $\angle ROS$ are PQ and RS.
So, the ratio of areas is:
$\frac{\text{Area}(\triangle POQ)}{\text{Area}(\triangle ROS)} = \left(\frac{PQ}{RS}\right)^2$
We are given that $PQ = 3 RS$.
Substituting this into the ratio of sides:
$\frac{PQ}{RS} = \frac{3 RS}{RS} = 3$
Now, substitute the ratio of sides into the ratio of areas formula:
$\frac{\text{Area}(\triangle POQ)}{\text{Area}(\triangle ROS)} = (3)^2 = 9$
The ratio of the areas of triangles POQ and ROS is 9:1.
The ratio of the areas of triangles POQ and ROS is 9:1.
Question 5. In Fig. 6.10, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
Answer:
Given:
In the given figure, $AB || DC$.
AC and PQ intersect each other at the point O.
P is a point on AB and Q is a point on DC.
To Prove:
$OA \cdot CQ = OC \cdot AP$.
Proof:
Consider $\triangle PAO$ and $\triangle QCO$.
Since $AB || DC$, and AC is a transversal, the alternate interior angles are equal.
$\angle PAO = \angle QCO$
$\angle OAP = \angle OCQ$
(Alternate interior angles, since $AB || DC$)
The lines AC and PQ intersect at O. The angles opposite to each other at the intersection are vertically opposite angles, which are equal.
$\angle AOP = \angle COQ$
$\angle AOP = \angle COQ$
(Vertically opposite angles)
Now, in $\triangle PAO$ and $\triangle QCO$, we have two pairs of corresponding angles that are equal ($\angle OAP = \angle OCQ$ and $\angle AOP = \angle COQ$).
Therefore, by AA similarity criterion, $\triangle PAO \sim \triangle QCO$.
When two triangles are similar, the ratio of their corresponding sides is equal.
Thus, we have:
$\frac{OA}{OC} = \frac{AP}{CQ} = \frac{PO}{QO}$
Taking the first two ratios:
$\frac{OA}{OC} = \frac{AP}{CQ}$
Cross-multiplying the terms, we get:
$OA \cdot CQ = OC \cdot AP$
This is the required equation to prove.
Hence Proved.
Question 6. Find the altitude of an equilateral triangle of side 8 cm.
Answer:
Given:
An equilateral triangle with side length 8 cm.
To Find:
The altitude of the equilateral triangle.
Solution:
Let the equilateral triangle be $\triangle ABC$, with side length $a = 8$ cm.
Let AD be the altitude from vertex A to the base BC, where D is a point on BC.
In an equilateral triangle, the altitude from a vertex to the opposite side is also the median and the angle bisector. Therefore, the altitude AD bisects the base BC.
So, $BD = DC = \frac{1}{2} BC = \frac{1}{2} \times 8 = 4$ cm.
Also, the altitude is perpendicular to the base, so $\angle ADB = 90^\circ$.
Now, consider the right-angled triangle $\triangle ABD$. By the Pythagorean theorem, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AD and BD).
$AB^2 = AD^2 + BD^2$
Substitute the known values:
$8^2 = AD^2 + 4^2$
$64 = AD^2 + 16$
Subtract 16 from both sides to find $AD^2$:
$AD^2 = 64 - 16$
$AD^2 = 48$
Take the square root of both sides to find AD:
$AD = \sqrt{48}$
We can simplify $\sqrt{48}$:
$48 = 16 \times 3$
$AD = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3} = 4\sqrt{3}$
So, the altitude $AD = 4\sqrt{3}$ cm.
Alternatively, we can use the formula for the altitude of an equilateral triangle with side length $a$, which is $h = \frac{\sqrt{3}}{2} a$.
Using this formula with $a = 8$ cm:
$h = \frac{\sqrt{3}}{2} \times 8$
$h = 4\sqrt{3}$ cm
The altitude of the equilateral triangle is $4\sqrt{3}$ cm.
Question 7. If ΔABC ~ ΔDEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ABC.
Answer:
Given:
$\triangle ABC \sim \triangle DEF$
Side lengths of $\triangle ABC$: $AB = 4$ cm
Side lengths of $\triangle DEF$: $DE = 6$ cm, $EF = 9$ cm, $FD = 12$ cm.
To Find:
The perimeter of $\triangle ABC$.
Solution:
We are given that $\triangle ABC \sim \triangle DEF$.
When two triangles are similar, the ratio of their corresponding sides is equal.
Based on the similarity statement $\triangle ABC \sim \triangle DEF$, the corresponding sides are:
AB corresponds to DE
BC corresponds to EF
AC corresponds to DF
So, the ratio of corresponding sides is:
$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$
Substitute the given values into the equation:
$\frac{4}{6} = \frac{BC}{9} = \frac{AC}{12}$
First, let's find the length of side BC using the first part of the ratio:
$\frac{4}{6} = \frac{BC}{9}$
Simplify the ratio on the left side:
$\frac{\cancel{4}^{2}}{\cancel{6}_{3}} = \frac{2}{3}$
So, $\frac{2}{3} = \frac{BC}{9}$
Multiply both sides by 9:
$BC = \frac{2}{3} \times 9$
$BC = 2 \times \cancel{9}^{3}/\cancel{3}_{1}$
$BC = 2 \times 3$
$BC = 6$ cm.
Next, let's find the length of side AC using the ratio $\frac{2}{3}$ and the third part of the ratio:
$\frac{4}{6} = \frac{AC}{12}$
Using the simplified ratio $\frac{2}{3}$:
$\frac{2}{3} = \frac{AC}{12}$
Multiply both sides by 12:
$AC = \frac{2}{3} \times 12$
$AC = 2 \times \cancel{12}^{4}/\cancel{3}_{1}$
$AC = 2 \times 4$
$AC = 8$ cm.
The sides of $\triangle ABC$ are $AB = 4$ cm, $BC = 6$ cm, and $AC = 8$ cm.
The perimeter of $\triangle ABC$ is the sum of its side lengths:
Perimeter of $\triangle ABC = AB + BC + AC$
Perimeter of $\triangle ABC = 4 + 6 + 8$
Perimeter of $\triangle ABC = 18$ cm.
The perimeter of triangle ABC is 18 cm.
Question 8. In Fig. 6.11, if DE || BC, find the ratio of ar (ADE) and ar (DECB).
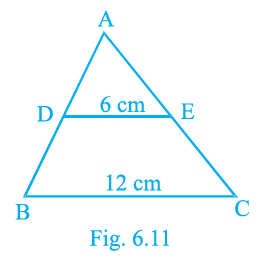
Answer:
Given:
In $\triangle ABC$, $DE || BC$, where D is on AB and E is on AC.
$AD = 2$ cm
$BD = 3$ cm
To Find:
The ratio of area($\triangle ADE$) to area(Trapezium DECB).
Solution:
We are given that $DE || BC$.
Consider $\triangle ADE$ and $\triangle ABC$.
Since $DE || BC$, and AB is a transversal, $\angle ADE = \angle ABC$ (Corresponding angles).
Since $DE || BC$, and AC is a transversal, $\angle AED = \angle ACB$ (Corresponding angles).
$\angle DAE = \angle BAC$ (Common angle).
Thus, by AAA similarity criterion, $\triangle ADE \sim \triangle ABC$.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
The corresponding side to AD in $\triangle ABC$ is AB.
The length of AB is $AB = AD + BD$.
$AB = 2 + 3 = 5$ cm.
The ratio of corresponding sides $\frac{AD}{AB} = \frac{2}{5}$.
So, the ratio of areas is:
$\frac{\text{Area}(\triangle ADE)}{\text{Area}(\triangle ABC)} = \left(\frac{AD}{AB}\right)^2 = \left(\frac{2}{5}\right)^2 = \frac{4}{25}$
This ratio means that if the area of $\triangle ADE$ is $4k$ for some constant $k$, then the area of $\triangle ABC$ is $25k$.
The area of the trapezium DECB is the difference between the area of $\triangle ABC$ and the area of $\triangle ADE$.
Area(Trapezium DECB) = Area($\triangle ABC$) - Area($\triangle ADE$)
Area(Trapezium DECB) = $25k - 4k = 21k$
We need to find the ratio of area($\triangle ADE$) and area(Trapezium DECB).
Ratio = $\frac{\text{Area}(\triangle ADE)}{\text{Area}(\text{Trapezium DECB})} = \frac{4k}{21k}$
Cancel out the common factor $k$:
Ratio = $\frac{4}{21}$
Alternatively, from the ratio of areas $\frac{\text{Area}(\triangle ADE)}{\text{Area}(\triangle ABC)} = \frac{4}{25}$, we can write:
Area($\triangle ABC$) = $\frac{25}{4}$ Area($\triangle ADE$)
Area(Trapezium DECB) = Area($\triangle ABC$) - Area($\triangle ADE$)
Area(Trapezium DECB) = $\frac{25}{4}$ Area($\triangle ADE$) - Area($\triangle ADE$)
Area(Trapezium DECB) = $\left(\frac{25}{4} - 1\right)$ Area($\triangle ADE$)
Area(Trapezium DECB) = $\left(\frac{25-4}{4}\right)$ Area($\triangle ADE$)
Area(Trapezium DECB) = $\frac{21}{4}$ Area($\triangle ADE$)
Now, form the required ratio:
$\frac{\text{Area}(\triangle ADE)}{\text{Area}(\text{Trapezium DECB})} = \frac{\text{Area}(\triangle ADE)}{\frac{21}{4} \text{Area}(\triangle ADE)}$
$\frac{\text{Area}(\triangle ADE)}{\text{Area}(\text{Trapezium DECB})} = \frac{1}{\frac{21}{4}} = \frac{4}{21}$
The ratio of ar(ADE) and ar(DECB) is 4:21.
Question 9. ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
Answer:
Given:
ABCD is a trapezium in which $AB || DC$.
P and Q are points on AD and BC, respectively, such that $PQ || DC$.
$PD = 18$ cm
$BQ = 35$ cm
$QC = 15$ cm
To Find:
The length of AD.
Solution:
We are given that in trapezium ABCD, $AB || DC$.
We are also given that $PQ || DC$, where P is on AD and Q is on BC.
Since $AB || DC$ and $PQ || DC$, it follows that $AB || PQ || DC$.
When a line parallel to the parallel sides of a trapezium intersects the non-parallel sides, it divides the non-parallel sides proportionally.
Therefore, according to this property (which is a consequence of Basic Proportionality Theorem), we have:
$\frac{AP}{PD} = \frac{BQ}{QC}$
Substitute the given values into the equation:
$\frac{AP}{18} = \frac{35}{15}$
Simplify the fraction on the right side by dividing the numerator and denominator by 5:
$\frac{AP}{18} = \frac{\cancel{35}^{7}}{\cancel{15}_{3}}$
$\frac{AP}{18} = \frac{7}{3}$
Now, multiply both sides by 18 to solve for AP:
$AP = \frac{7}{3} \times 18$
$AP = 7 \times \frac{18}{3}$
Simplify the fraction $\frac{18}{3}$:
$AP = 7 \times \cancel{18}^{6}/\cancel{3}_{1}$
$AP = 7 \times 6$
$AP = 42$ cm
The length of the side AD is the sum of the lengths of AP and PD.
$AD = AP + PD$
Substitute the values of AP and PD:
$AD = 42 + 18$
$AD = 60$ cm
The length of AD is 60 cm.
Question 10. Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2 , find the area of the larger triangle.
Answer:
Given:
Two similar triangles.
Ratio of corresponding sides = $2:3$.
Area of the smaller triangle = $48$ cm$^2$.
To Find:
The area of the larger triangle.
Solution:
Let the two similar triangles be $\triangle_1$ and $\triangle_2$.
Let the ratio of their corresponding sides be $\frac{s_1}{s_2}$.
We are given $\frac{s_1}{s_2} = \frac{2}{3}$. Since the ratio is 2:3, $\triangle_1$ is the smaller triangle and $\triangle_2$ is the larger triangle.
We are given that the area of the smaller triangle, Area($\triangle_1$) = $48$ cm$^2$.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
This can be stated as:
$\frac{\text{Area}(\triangle_1)}{\text{Area}(\triangle_2)} = \left(\frac{s_1}{s_2}\right)^2$
Substitute the given values into this equation:
$\frac{48}{\text{Area}(\triangle_2)} = \left(\frac{2}{3}\right)^2$
Calculate the square of the ratio of sides:
$\left(\frac{2}{3}\right)^2 = \frac{2^2}{3^2} = \frac{4}{9}$
So the equation becomes:
$\frac{48}{\text{Area}(\triangle_2)} = \frac{4}{9}$
Now, we need to solve for Area($\triangle_2$). We can cross-multiply:
$4 \times \text{Area}(\triangle_2) = 48 \times 9$
Divide both sides by 4:
$\text{Area}(\triangle_2) = \frac{48 \times 9}{4}$
Simplify the expression. We can divide 48 by 4:
$\text{Area}(\triangle_2) = \frac{\cancel{48}^{12} \times 9}{\cancel{4}_{1}}$
$\text{Area}(\triangle_2) = 12 \times 9$
Calculate the product:
$12 \times 9 = 108$
So, Area($\triangle_2$) = $108$ cm$^2$.
The area of the larger triangle is $108$ cm$^2$.
Question 11. In a triangle PQR, N is a point on PR such that QN ⊥ PR . If PN. NR = QN2 , prove that∠PQR = 90° .
Answer:
Given:
In $\triangle PQR$, N is a point on PR such that $QN \perp PR$.
$PN \cdot NR = QN^2$.
To Prove:
$\angle PQR = 90^\circ$.
Proof:
We are given that $QN \perp PR$. This implies that $\angle QNP = 90^\circ$ and $\angle QNR = 90^\circ$.
Thus, $\triangle QNP$ and $\triangle QNR$ are right-angled triangles with the right angle at N.
In the right-angled triangle $\triangle QNP$, by the Pythagorean theorem, we have:
$PQ^2 = PN^2 + QN^2$
In the right-angled triangle $\triangle QNR$, by the Pythagorean theorem, we have:
$QR^2 = NR^2 + QN^2$
Add the equations for $PQ^2$ and $QR^2$:
$PQ^2 + QR^2 = (PN^2 + QN^2) + (NR^2 + QN^2)$
$PQ^2 + QR^2 = PN^2 + NR^2 + 2 QN^2$
We are given the relation $PN \cdot NR = QN^2$.
Substitute $QN^2$ with $PN \cdot NR$ in the equation for $PQ^2 + QR^2$:
$PQ^2 + QR^2 = PN^2 + NR^2 + 2 (PN \cdot NR)$
The expression on the right side, $PN^2 + NR^2 + 2 PN \cdot NR$, is in the form of $(a+b)^2 = a^2 + b^2 + 2ab$, where $a=PN$ and $b=NR$.
So, $PN^2 + NR^2 + 2 PN \cdot NR = (PN + NR)^2$.
Since N is a point on the line segment PR, the length of PR is the sum of the lengths of PN and NR.
$PR = PN + NR$
Therefore, $(PN + NR)^2 = PR^2$.
Substituting this back into the equation for $PQ^2 + QR^2$, we get:
$PQ^2 + QR^2 = PR^2$
This equation shows that in $\triangle PQR$, the square of side PR is equal to the sum of the squares of the other two sides, PQ and QR.
By the converse of the Pythagorean theorem, if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
In $\triangle PQR$, the angle opposite the side PR is $\angle PQR$.
Therefore, $\angle PQR$ must be a right angle.
$\angle PQR = 90^\circ$.
Hence Proved.
Question 12. Areas of two similar triangles are 36 cm2 and 100 cm2 . If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
Answer:
Given:
Two similar triangles.
Area of the smaller triangle ($\text{Area}_1$) = $36$ cm$^2$.
Area of the larger triangle ($\text{Area}_2$) = $100$ cm$^2$.
Length of a side of the larger triangle ($s_2$) = $20$ cm.
To Find:
The length of the corresponding side of the smaller triangle ($s_1$).
Solution:
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Let $\triangle_1$ be the smaller triangle and $\triangle_2$ be the larger triangle.
Let $s_1$ be the length of a side of $\triangle_1$ and $s_2$ be the length of the corresponding side of $\triangle_2$.
The ratio of their areas is given by:
$\frac{\text{Area}_1}{\text{Area}_2} = \left(\frac{s_1}{s_2}\right)^2$
Substitute the given values into this equation:
$\frac{36}{100} = \left(\frac{s_1}{20}\right)^2$
Simplify the fraction on the left side:
$\frac{36}{100} = \frac{9 \times 4}{25 \times 4} = \frac{9}{25}$
So, the equation becomes:
$\frac{9}{25} = \left(\frac{s_1}{20}\right)^2$
To find $\frac{s_1}{20}$, take the square root of both sides of the equation:
$\sqrt{\frac{9}{25}} = \sqrt{\left(\frac{s_1}{20}\right)^2}$
$\frac{\sqrt{9}}{\sqrt{25}} = \frac{s_1}{20}$
$\frac{3}{5} = \frac{s_1}{20}$
Now, solve for $s_1$ by multiplying both sides by 20:
$s_1 = \frac{3}{5} \times 20$
$s_1 = 3 \times \frac{20}{5}$
$s_1 = 3 \times 4$
$s_1 = 12$
The length of the corresponding side of the smaller triangle is 12 cm.
The length of the corresponding side of the smaller triangle is 12 cm.
Question 13. In Fig. 6.12, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.
Answer:
Given:
In $\triangle ABC$, D is a point on AB.
$\angle ACB = \angle CDA$.
$AC = 8$ cm.
$AD = 3$ cm.
To Find:
The length of BD.
Solution:
Consider $\triangle ABC$ and $\triangle ACD$.
We are given that $\angle ACB = \angle CDA$.
$\angle ACB = \angle CDA$
(Given)
Both triangles share the common angle $\angle CAB$ (or $\angle DAC$).
$\angle CAB = \angle DAC$
(Common angle)
By AA similarity criterion, if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
Therefore, $\triangle ABC \sim \triangle ACD$.
When two triangles are similar, the ratio of their corresponding sides is equal.
The corresponding sides are identified by the order of vertices in the similarity statement:
AB corresponds to AC
BC corresponds to CD
AC corresponds to AD
So, we have the ratio:
$\frac{AB}{AC} = \frac{BC}{CD} = \frac{AC}{AD}$
We are given the lengths of AC and AD. We can use the ratio involving these sides to find AB.
$\frac{AB}{AC} = \frac{AC}{AD}$
Substitute the given values $AC = 8$ cm and $AD = 3$ cm:
$\frac{AB}{8} = \frac{8}{3}$
Multiply both sides by 8 to find AB:
$AB = \frac{8}{3} \times 8$
$AB = \frac{64}{3}$ cm.
The point D lies on the line segment AB. Therefore, $AB = AD + BD$.
We need to find BD. Rearranging the equation, we get $BD = AB - AD$.
Substitute the values of AB and AD:
$BD = \frac{64}{3} - 3$
To subtract, find a common denominator, which is 3.
$BD = \frac{64}{3} - \frac{3 \times 3}{3}$
$BD = \frac{64}{3} - \frac{9}{3}$
$BD = \frac{64 - 9}{3}$
$BD = \frac{55}{3}$ cm.
The length of BD is $\frac{55}{3}$ cm.
Question 14. A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Answer:
Given:
Height of the tower ($H_T$) = $15$ metres.
Length of the tower's shadow ($S_T$) = $24$ metres.
Length of the telephone pole's shadow ($S_P$) = $16$ metres.
To Find:
The height of the telephone pole ($H_P$).
Solution:
At the same time of the day, the angle of elevation of the sun is the same for both the tower and the telephone pole.
We can consider the tower and its shadow as forming a right-angled triangle, and the telephone pole and its shadow as forming another right-angled triangle.
Let the height of the tower be AB and its shadow be BC. So $\triangle ABC$ is a right-angled triangle at B.
Let the height of the telephone pole be PQ and its shadow be QR. So $\triangle PQR$ is a right-angled triangle at Q.
The angle of elevation of the sun is $\angle ACB$ in the first triangle and $\angle PRQ$ in the second triangle.
Since the angle of elevation is the same at the same time, $\angle ACB = \angle PRQ$.
In $\triangle ABC$ and $\triangle PQR$:
$\angle ABC = \angle PQR = 90^\circ$ (Assuming vertical objects)
$\angle ACB = \angle PRQ$ (Same angle of elevation of the sun)
Therefore, by AA similarity criterion, $\triangle ABC \sim \triangle PQR$.
For similar triangles, the ratio of corresponding sides is equal.
$\frac{AB}{PQ} = \frac{BC}{QR}$
Using our defined variables:
$\frac{H_T}{H_P} = \frac{S_T}{S_P}$
Substitute the given values:
$\frac{15}{H_P} = \frac{24}{16}$
We can simplify the fraction on the right side:
$\frac{24}{16} = \frac{\cancel{24}^{3 \times 8}}{\cancel{16}^{2 \times 8}} = \frac{3}{2}$
So the equation becomes:
$\frac{15}{H_P} = \frac{3}{2}$
To solve for $H_P$, we can cross-multiply:
$15 \times 2 = 3 \times H_P$
$30 = 3 H_P$
Divide both sides by 3:
$H_P = \frac{30}{3}$
$H_P = 10$
The height of the telephone pole is 10 metres.
The height of the telephone pole is 10 metres.
Question 15. Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
Answer:
Given:
Length of the ladder = $10$ m.
Distance of the foot of the ladder from the base of the wall = $6$ m.
To Find:
The height on the wall where the top of the ladder reaches.
Solution:
Let the vertical wall be represented by a line segment and the ground by a horizontal line segment. The ladder leaning against the wall forms the hypotenuse of a right-angled triangle.
Let the height on the wall where the ladder reaches be $h$ metres.
The distance from the base of the wall to the foot of the ladder is the base of the triangle, which is $6$ metres.
The length of the ladder is the hypotenuse of the triangle, which is $10$ metres.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Let $h$ be the height on the wall and $d$ be the distance from the base of the wall. Let $l$ be the length of the ladder.
The relationship is given by:
$l^2 = h^2 + d^2$
Substitute the given values: $l = 10$ m and $d = 6$ m.
$10^2 = h^2 + 6^2$
Calculate the squares:
$100 = h^2 + 36$
To find $h^2$, subtract 36 from both sides of the equation:
$h^2 = 100 - 36$
$h^2 = 64$
To find $h$, take the square root of both sides:
$h = \sqrt{64}$
$h = 8$
The height on the wall where the top of the ladder reaches is 8 metres.
The height of the point on the wall is 8 m.
Sample Question 1 to 4 (Before Exercise 6.4)
Sample Question 1: In Fig 6.13, OB is the perpendicular bisector of the line segment DE, FA ⊥OB and F E intersects OB at the point C. Prove that $\frac{1}{OA}$ + $\frac{1}{OB}$ = $\frac{2}{OC}$ .
Answer:
Sample Question 2: Prove that if in a triangle square on one side is equal to the sum of the squares on the other two sides, then the angle opposite the first side is a right angle.
Answer:
This theorem is the converse of the Pythagorean Theorem.
Given:
In $\triangle ABC$, we are given that the square on one side $AC$ is equal to the sum of the squares on the other two sides $AB$ and $BC$.
$AC^2 = AB^2 + BC^2$
... (i)
To Prove:
The angle opposite the first side $AC$ is a right angle, i.e., $\angle B = 90^\circ$.
Construction Required:
Construct a triangle $PQR$ such that $PQ = AB$, $QR = BC$, and $\angle Q = 90^\circ$.
PQ = AB
(By construction)
QR = BC
(By construction)
$\angle Q = 90^\circ$
(By construction)
Proof:
In the constructed triangle $PQR$, $\angle Q = 90^\circ$.
By the Pythagorean Theorem, the square on the hypotenuse $PR$ is equal to the sum of the squares on the other two sides $PQ$ and $QR$.
$\underbrace{PR^2 = PQ^2 + QR^2}_{\text{By Pythagorean Theorem}}$
... (ii)
From our construction, we have $PQ = AB$ and $QR = BC$. Substituting these into equation (ii):
$\underbrace{PR^2 = AB^2 + BC^2}_{\text{Substituting construction values}}$
... (iii)
From the given information in equation (i), we have $AC^2 = AB^2 + BC^2$.
Comparing equation (i) and equation (iii), we see that both $AC^2$ and $PR^2$ are equal to $AB^2 + BC^2$.
$\underbrace{AC^2 = PR^2}_{\text{From (i) and (iii)}}$
... (iv)
Taking the positive square root of both sides of equation (iv) (since lengths are positive):
AC = PR
... (v)
Now, consider triangles $\triangle ABC$ and $\triangle PQR$.
We have:
AB = PQ
(By construction)
BC = QR
(By construction)
AC = PR
(From equation (v))
Since all three sides of $\triangle ABC$ are equal to the corresponding three sides of $\triangle PQR$, the two triangles are congruent by the SSS (Side-Side-Side) Congruence Criterion.
$\triangle ABC \cong \triangle PQR$
[By SSS congruence] ... (vi)
Since the triangles are congruent, their corresponding angles are equal (CPCT - Corresponding Parts of Congruent Triangles).
$\underbrace{\angle B = \angle Q}_{\text{CPCT}}$
... (vii)
From our construction, we know that $\angle Q = 90^\circ$.
Substituting the value of $\angle Q$ into equation (vii):
$\angle B = 90^\circ$
[Since $\angle Q = 90^\circ$] ... (viii)
Thus, the angle opposite the side $AC$ (which is $\angle B$) is a right angle.
Hence, Proved.
Sample Question 3: An aeroplane leaves an Airport and flies due North at 300 km/h. At the same time, another aeroplane leaves the same Airport and flies due West at 400 km/h. How far apart the two aeroplanes would be after $1\frac{1}{2}$ hours?
Answer:
Given:
Speed of the first aeroplane (flying due North) = 300 km/h
Speed of the second aeroplane (flying due West) = 400 km/h
Time taken = $1\frac{1}{2}$ hours = $\frac{3}{2}$ hours = 1.5 hours
To Find:
The distance between the two aeroplanes after $1\frac{1}{2}$ hours.
Solution:
Let the Airport be denoted by point O.
The first aeroplane flies due North from O. Let its position after 1.5 hours be point A.
The second aeroplane flies due West from O. Let its position after 1.5 hours be point B.
The distance covered by an object is given by the formula: Distance = Speed $\times$ Time.
Distance covered by the first aeroplane (OA) in 1.5 hours:
$OA = 300 \text{ km/h} \times 1.5 \text{ hours}$
$OA = 300 \times \frac{3}{2} \text{ km}$
$OA = 150 \times 3 \text{ km}$
$OA = 450 \text{ km}$
Distance covered by the second aeroplane (OB) in 1.5 hours:
$OB = 400 \text{ km/h} \times 1.5 \text{ hours}$
$OB = 400 \times \frac{3}{2} \text{ km}$
$OB = 200 \times 3 \text{ km}$
$OB = 600 \text{ km}$
Since the aeroplanes fly due North and due West, the path OA is perpendicular to the path OB. This means that the angle $\angle AOB$ is $90^\circ$.
The points O, A, and B form a right-angled triangle $\triangle OAB$, with the right angle at O. The distance between the two aeroplanes after 1.5 hours is the length of the hypotenuse AB.
According to the Pythagorean Theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
$\underbrace{AB^2 = OA^2 + OB^2}_{\text{By Pythagorean Theorem}}$
... (i)
Substitute the calculated values of OA and OB into the equation (i):
$AB^2 = (450)^2 + (600)^2$
Calculate the squares:
$450^2 = 450 \times 450 = 202500$
$600^2 = 600 \times 600 = 360000$
Now, substitute these values back into the equation:
$AB^2 = 202500 + 360000$
$AB^2 = 562500$
To find AB, take the square root of $562500$:
$AB = \sqrt{562500}$
$AB = \sqrt{5625 \times 100}$
$AB = \sqrt{5625} \times \sqrt{100}$
We know that $\sqrt{5625} = 75$ and $\sqrt{100} = 10$.
$AB = 75 \times 10$
$AB = 750 \text{ km}$
The distance between the two aeroplanes after $1\frac{1}{2}$ hours is 750 km.
Sample Question 4: In Fig. 6.15, if ΔABC ~ ΔDEF and their sides are of lengths (in cm) as marked along them, then find the lengths of the sides of each triangle.
Answer:
Given:
$\triangle ABC \sim \triangle DEF$
Side lengths of $\triangle ABC$: AB = $2x - 1$, BC = $2x + 2$, AC = $3x$.
Side lengths of $\triangle DEF$: DE = $18$, EF = $3x + 9$, DF = $6x$.
To Find:
The lengths of the sides of $\triangle ABC$ and $\triangle DEF$.
Solution:
Since $\triangle ABC \sim \triangle DEF$, the ratio of their corresponding sides is equal.
$\underbrace{\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}}_{\text{Property of similar triangles}}$
Substitute the given side lengths into the ratio:
$\frac{2x - 1}{18} = \frac{2x + 2}{3x + 9} = \frac{3x}{6x}$
Let's simplify the third ratio $\frac{3x}{6x}$. Assuming $x \neq 0$, we get:
$\frac{3x}{6x} = \frac{\cancel{3x}}{\cancel{6x}^2} = \frac{1}{2}$
Now, we can equate any of the first two ratios to $\frac{1}{2}$ to find the value of $x$. Let's use the first ratio:
$\frac{2x - 1}{18} = \frac{1}{2}$
Multiply both sides by 18:
$(2x - 1) = \frac{1}{2} \times 18$
$2x - 1 = 9$
Add 1 to both sides:
$2x = 9 + 1$
$2x = 10$
Divide by 2:
$x = \frac{10}{2}$
$x = 5$
Now, substitute the value of $x=5$ into the expressions for the side lengths of both triangles.
Sides of $\triangle ABC$:
AB = $2x - 1 = 2(5) - 1 = 10 - 1 = 9$ cm
BC = $2x + 2 = 2(5) + 2 = 10 + 2 = 12$ cm
AC = $3x = 3(5) = 15$ cm
Sides of $\triangle DEF$:
DE = $18$ cm
EF = $3x + 9 = 3(5) + 9 = 15 + 9 = 24$ cm
DF = $6x = 6(5) = 30$ cm
The lengths of the sides of $\triangle ABC$ are 9 cm, 12 cm, and 15 cm.
The lengths of the sides of $\triangle DEF$ are 18 cm, 24 cm, and 30 cm.
Exercise 6.4
Question 1. In Fig. 6.16, if∠A =∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.
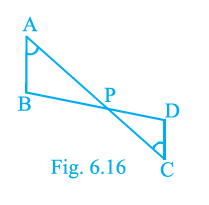
Answer:
Given:
In the given figure, we have two triangles $\triangle APB$ and $\triangle CPD$.
$\angle A = \angle C$
AB = 6 cm
BP = 15 cm
AP = 12 cm
CP = 4 cm
To Find:
The lengths of PD and CD.
Solution:
Consider triangles $\triangle APB$ and $\triangle CPD$.
$\angle A = \angle C$
(Given)
$\angle APB = \angle CPD$
(Vertically Opposite Angles)
Since two angles of $\triangle APB$ are equal to two corresponding angles of $\triangle CPD$, by the AA (Angle-Angle) Similarity Criterion, we can say that $\triangle APB$ is similar to $\triangle CPD$.
Note the order of vertices in the similarity statement corresponds to the equal angles: A maps to C, P maps to P, and B maps to D.
So, we have $\triangle APB \sim \triangle CPD$.
When two triangles are similar, the ratio of their corresponding sides is equal.
$\underbrace{\frac{AP}{CP} = \frac{PB}{PD} = \frac{AB}{CD}}_{\text{Corresponding sides of similar triangles are proportional}}$
Substitute the given values into the ratios:
$\frac{12}{4} = \frac{15}{PD} = \frac{6}{CD}$
Simplify the first ratio:
$\frac{12}{4} = 3$
Now equate the ratios involving the unknowns to the simplified ratio 3.
For PD:
$\frac{15}{PD} = 3$
$15 = 3 \times PD$
$PD = \frac{15}{3}$
$PD = 5$ cm
For CD:
$\frac{6}{CD} = 3$
$6 = 3 \times CD$
$CD = \frac{6}{3}$
$CD = 2$ cm
The length of PD is 5 cm and the length of CD is 2 cm.
Question 2. It is given that ΔABC ~ ΔEDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Answer:
Given:
$\triangle ABC \sim \triangle EDF$
AB = 5 cm
AC = 7 cm
DF = 15 cm
DE = 12 cm
To Find:
The lengths of the remaining sides, BC (of $\triangle ABC$) and EF (of $\triangle EDF$).
Solution:
Since $\triangle ABC \sim \triangle EDF$, the ratio of their corresponding sides is equal.
The similarity statement $\triangle ABC \sim \triangle EDF$ tells us the corresponding vertices:
- A corresponds to E
- B corresponds to D
- C corresponds to F
Therefore, the corresponding sides are AB and ED, BC and DF, and AC and EF.
The ratio of corresponding sides is:
$\frac{AB}{ED} = \frac{BC}{DF} = \frac{AC}{EF}$
... (i)
Substitute the given side lengths into the proportionality from equation (i):
$\frac{5}{12} = \frac{BC}{15} = \frac{7}{EF}$
Now, we can use these equalities to find the unknown side lengths.
Finding BC:
Equate the first ratio to the second ratio:
$\frac{5}{12} = \frac{BC}{15}$
To solve for BC, cross-multiply:
$12 \times BC = 5 \times 15$
$12 \times BC = 75$
$BC = \frac{75}{12}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 3:
$BC = \frac{\cancel{75}^{25}}{\cancel{12}_{4}}$
$BC = \frac{25}{4}$
$BC = 6.25$ cm
Finding EF:
Equate the first ratio to the third ratio:
$\frac{5}{12} = \frac{7}{EF}$
To solve for EF, cross-multiply:
$5 \times EF = 12 \times 7$
$5 \times EF = 84$
$EF = \frac{84}{5}$
$EF = 16.8$ cm
The lengths of the remaining sides are BC = 6.25 cm and EF = 16.8 cm.
Question 3. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Answer:
This theorem is the Basic Proportionality Theorem (BPT), also known as Thales's Theorem.
Given:
In $\triangle ABC$, a line DE is drawn parallel to side BC, intersecting AB at D and AC at E.
DE || BC
(Given)
To Prove:
The line DE divides the other two sides AB and AC in the same ratio, i.e.,
$\frac{AD}{DB} = \frac{AE}{EC}$
Construction Required:
Join BE and CD. Draw $EM \perp AB$ and $DN \perp AC$.
Proof:
The area of a triangle is given by the formula:
$Area = \frac{1}{2} \times base \times height$
Consider $\triangle ADE$. Using AD as the base and EM as the height:
$Area(\triangle ADE) = \frac{1}{2} \times AD \times EM$
Consider $\triangle BDE$. Using DB as the base and EM as the height (since EM is the perpendicular distance from E to the line AB):
$Area(\triangle BDE) = \frac{1}{2} \times DB \times EM$
Take the ratio of the areas of $\triangle ADE$ and $\triangle BDE$:
$\frac{Area(\triangle ADE)}{Area(\triangle BDE)} = \frac{\frac{1}{2} \times AD \times EM}{\frac{1}{2} \times DB \times EM}$
Cancel out the common terms $\frac{1}{2}$ and EM:
$\frac{Area(\triangle ADE)}{Area(\triangle BDE)} = \frac{AD}{DB}$
... (i)
Now, consider $\triangle ADE$ again. Using AE as the base and DN as the height:
$Area(\triangle ADE) = \frac{1}{2} \times AE \times DN$
Consider $\triangle CED$. Using EC as the base and DN as the height (since DN is the perpendicular distance from D to the line AC):
$Area(\triangle CED) = \frac{1}{2} \times EC \times DN$
Take the ratio of the areas of $\triangle ADE$ and $\triangle CED$:
$\frac{Area(\triangle ADE)}{Area(\triangle CED)} = \frac{\frac{1}{2} \times AE \times DN}{\frac{1}{2} \times EC \times DN}$
Cancel out the common terms $\frac{1}{2}$ and DN:
$\frac{Area(\triangle ADE)}{Area(\triangle CED)} = \frac{AE}{EC}$
... (ii)
Now, consider $\triangle BDE$ and $\triangle CED$. These two triangles lie on the same base DE and between the same parallel lines DE and BC (since DE || BC is given).
Triangles on the same base and between the same parallels are equal in area.
$\underbrace{Area(\triangle BDE) = Area(\triangle CED)}_{\text{Triangles on the same base and between same parallels}}$
... (iii)
From equation (iii), we can say that $\frac{1}{Area(\triangle BDE)} = \frac{1}{Area(\triangle CED)}$.
Multiply both sides by $Area(\triangle ADE)$:
$\frac{Area(\triangle ADE)}{Area(\triangle BDE)} = \frac{Area(\triangle ADE)}{Area(\triangle CED)}$
Now, substitute the results from equations (i) and (ii) into this equality:
$\frac{AD}{DB} = \frac{AE}{EC}$
[From (i) and (ii)]
This proves that the line DE divides the sides AB and AC in the same ratio.
Hence, Proved.
Question 4. In Fig 6.17, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
Answer:
Question 5. A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Answer:
Given:
Length of the ladder = $5$ m.
Initial height reached on the wall = $4$ m.
Distance the foot of the ladder is moved towards the wall = $1.6$ m.
To Find:
The distance by which the top of the ladder would slide upwards on the wall.
Solution:
Let the initial position of the ladder be represented by a right-angled triangle ABC, where AB is the wall, BC is the ground, and AC is the ladder. Here, $\angle{\text{ABC}} = 90^\circ$.
Initial length of the ladder, AC = $5$ m.
Initial height reached on the wall, AB = $4$ m.
Let the initial distance of the foot of the ladder from the wall be BC = $x$ m.
By the Pythagorean theorem in $\triangle{\text{ABC}}$:
$AB^2 + BC^2 = AC^2$
$4^2 + x^2 = 5^2$
$16 + x^2 = 25$
$x^2 = 25 - 16$
$x^2 = 9$
$x = \sqrt{9}$
$x = 3$ m
So, the initial distance of the foot of the ladder from the wall is $3$ m.
Now, the foot of the ladder is moved $1.6$ m towards the wall.
New distance of the foot of the ladder from the wall = Initial distance - Distance moved
= $3$ m - $1.6$ m = $1.4$ m.
Let the new position of the ladder be represented by triangle A'BC', where A'B is the new height reached on the wall, BC' is the new distance from the wall, and A'C' is the ladder. Here, $\angle{\text{A'BC'}} = 90^\circ$.
New distance from the wall, BC' = $1.4$ m.
Length of the ladder remains the same, A'C' = $5$ m.
Let the new height reached on the wall be A'B = $y$ m.
By the Pythagorean theorem in $\triangle{\text{A'BC'}}$:
$(A'B)^2 + (BC')^2 = (A'C')^2$
$y^2 + (1.4)^2 = 5^2$
$y^2 + 1.96 = 25$
$y^2 = 25 - 1.96$
$y^2 = 23.04$
$y = \sqrt{23.04}$
$y = 4.8$ m
So, the new height reached on the wall is $4.8$ m.
The distance by which the top of the ladder slides upwards is the difference between the new height and the initial height.
Distance slided upwards = New height - Initial height
= $4.8$ m - $4$ m = $0.8$ m.
Answer:
The top of the ladder would slide upwards by $0.8$ m.
Question 6. For going to a city B from city A, there is a route via city C such that AC⊥CB, AC = 2 x km and CB = 2 (x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway
Answer:
Given:
Route from city A to city B is via city C.
AC $\perp$ CB, forming a right-angled triangle ACB with the right angle at C.
Distance AC = $2x$ km.
Distance CB = $2(x+7)$ km.
Length of the direct highway connecting A and B (hypotenuse AB) = $26$ km.
To Find:
The distance saved in reaching city B from city A after the construction of the highway.
Solution:
In the right-angled triangle ACB, according to the Pythagorean theorem:
$AC^2 + CB^2 = AB^2$
Substitute the given values:
$(2x)^2 + (2(x+7))^2 = 26^2$
$4x^2 + 4(x+7)^2 = 676$
$4x^2 + 4(x^2 + 14x + 49) = 676$
$4x^2 + 4x^2 + 56x + 196 = 676$
$8x^2 + 56x + 196 - 676 = 0$
$8x^2 + 56x - 480 = 0$
Divide the entire equation by 8:
$\frac{8x^2}{8} + \frac{56x}{8} - \frac{480}{8} = 0$
$x^2 + 7x - 60 = 0$
Now, we need to solve this quadratic equation for $x$. We can factor the quadratic equation:
Find two numbers that multiply to -60 and add up to 7. These numbers are 12 and -5.
$x^2 + 12x - 5x - 60 = 0$
$x(x + 12) - 5(x + 12) = 0$
$(x - 5)(x + 12) = 0$
This gives two possible values for $x$: $x - 5 = 0$ or $x + 12 = 0$.
So, $x = 5$ or $x = -12$.
Since distance cannot be negative, we take the positive value $x = 5$ km.
Now, calculate the distances AC and CB using $x=5$:
AC = $2x = 2(5) = 10$ km.
CB = $2(x+7) = 2(5+7) = 2(12) = 24$ km.
The distance from city A to city B via city C is AC + CB.
Distance via C = $10$ km + $24$ km = $34$ km.
The distance of the direct highway connecting A and B is given as $26$ km.
Distance saved = Distance via C - Distance via highway
Distance saved = $34$ km - $26$ km = $8$ km.
Answer:
The distance saved in reaching city B from city A after the construction of the highway is $8$ km.
Question 7. A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Answer:
Given:
Height of the flag pole = $18$ m.
Length of the shadow cast by the flag pole = $9.6$ m.
To Find:
The distance of the top of the pole from the far end of the shadow.
Solution:
Consider the flag pole, its shadow, and the line connecting the top of the pole to the far end of the shadow. These three form a right-angled triangle.
The height of the flag pole is perpendicular to the ground, so it forms one leg of the right triangle.
The length of the shadow lies on the ground and forms the other leg of the right triangle.
The distance from the top of the pole to the far end of the shadow is the hypotenuse of the right triangle.
Let the height of the pole be $h = 18$ m.
Let the length of the shadow be $s = 9.6$ m.
Let the distance of the top of the pole from the far end of the shadow be $d$.
By the Pythagorean theorem:
$h^2 + s^2 = d^2$
$18^2 + (9.6)^2 = d^2$
$324 + 92.16 = d^2$
$416.16 = d^2$
$d = \sqrt{416.16}$
To find the square root of 416.16:
$d = 20.4$ m
Answer:
The distance of the top of the pole from the far end of the shadow is $20.4$ m.
Question 8. A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3m, find how far she is away from the base of the pole.
Answer:
Given:
Height of the street light pole = $6$ m.
Height of the woman = $1.5$ m.
Length of the shadow cast by the woman = $3$ m.
To Find:
The distance of the woman from the base of the pole.
Solution:
Let the height of the street light pole be AB, where A is the top (light bulb) and B is the base. So, AB = $6$ m.
Let the position of the woman be CD, where C is her head and D is her feet. So, CD = $1.5$ m.
Let the far end of the woman's shadow be E. The shadow is DE = $3$ m.
The light from the bulb A passes over the woman's head C and falls at point E, forming the shadow DE.
This setup forms two right-angled triangles: $\triangle{\text{ABE}}$ (formed by the pole, the ground, and the line from the light to the end of the shadow) and $\triangle{\text{CDE}}$ (formed by the woman, her shadow, and the line from her head to the end of the shadow).
Both the pole (AB) and the woman (CD) are perpendicular to the ground (BE).
Thus, $\angle{\text{ABE}} = 90^\circ$ and $\angle{\text{CDE}} = 90^\circ$.
Also, $\angle{\text{AEB}} = \angle{\text{CED}}$ as they are the same angle (common angle at the end of the shadow).
Therefore, $\triangle{\text{ABE}}$ is similar to $\triangle{\text{CDE}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{AB}}{\text{CD}} = \frac{\text{BE}}{\text{DE}}$
We know AB = $6$ m, CD = $1.5$ m, and DE = $3$ m.
Let the distance of the woman from the base of the pole be BD. We need to find BD.
The distance BE is the sum of the distance from the pole to the woman and the length of the shadow.
BE = BD + DE = BD + $3$ m.
Substitute the values into the ratio equation:
$\frac{6}{1.5} = \frac{\text{BD} + 3}{3}$
$4 = \frac{\text{BD} + 3}{3}$
Multiply both sides by 3:
$4 \times 3 = \text{BD} + 3$
$12 = \text{BD} + 3$
Subtract 3 from both sides:
$\text{BD} = 12 - 3$
$\text{BD} = 9$ m.
So, the woman is $9$ m away from the base of the pole.
Answer:
The woman is $9$ m away from the base of the pole.
Question 9. In Fig. 6.18, ABC is a triangle right angled at B and BD ⊥AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.
Answer:
Given:
In $\triangle{\text{ABC}}$, $\angle{\text{B}} = 90^\circ$.
BD $\perp$ AC.
AD = $4$ cm.
CD = $5$ cm.
To Find:
Length of BD.
Length of AB.
Solution:
In a right-angled triangle, the altitude to the hypotenuse divides the triangle into two triangles that are similar to the original triangle and to each other.
Thus, $\triangle{\text{ADB}} \sim \triangle{\text{BDC}} \sim \triangle{\text{ABC}}$.
Considering the similarity between $\triangle{\text{ADB}}$ and $\triangle{\text{BDC}}$, the ratio of corresponding sides is equal:
$\frac{\text{AD}}{\text{BD}} = \frac{\text{BD}}{\text{CD}}$
Cross-multiplying, we get the geometric mean theorem for the altitude:
$BD^2 = AD \times CD$
Substitute the given values of AD and CD:
$BD^2 = 4 \times 5$
$BD^2 = 20$
$BD = \sqrt{20}$
$BD = \sqrt{4 \times 5}$
$BD = 2\sqrt{5}$ cm.
Now, we need to find the length of AB.
The length of the hypotenuse AC is the sum of AD and CD:
AC = AD + CD
AC = $4 + 5 = 9$ cm.
Considering the similarity between $\triangle{\text{ADB}}$ and $\triangle{\text{ABC}}$, the ratio of corresponding sides is equal:
$\frac{\text{AB}}{\text{AC}} = \frac{\text{AD}}{\text{AB}}$
Cross-multiplying, we get the geometric mean theorem for the leg:
$AB^2 = AD \times AC$
Substitute the values of AD and AC:
$AB^2 = 4 \times 9$
$AB^2 = 36$
$AB = \sqrt{36}$
$AB = 6$ cm.
Answer:
The length of BD is $2\sqrt{5}$ cm.
The length of AB is $6$ cm.
Question 10. In Fig. 6.19, PQR is a right triangle right angled at Q and QS ⊥ PR . If PQ = 6 cm and PS = 4 cm, find QS, RS and QR
Answer:
Given:
In $\triangle{\text{PQR}}$, $\angle{\text{Q}} = 90^\circ$.
QS $\perp$ PR.
PQ = $6$ cm.
PS = $4$ cm.
To Find:
Length of QS.
Length of RS.
Length of QR.
Solution:
In a right-angled triangle, the altitude to the hypotenuse divides the triangle into two triangles that are similar to the original triangle and to each other.
Thus, $\triangle{\text{PQS}} \sim \triangle{\text{RQS}} \sim \triangle{\text{PQR}}$.
Consider the similarity between $\triangle{\text{PQS}}$ and $\triangle{\text{PQR}}$. The ratio of corresponding sides is equal:
$\frac{\text{PQ}}{\text{PR}} = \frac{\text{PS}}{\text{PQ}}$
This gives $PQ^2 = PS \times PR$.
Substitute the given values PQ = $6$ and PS = $4$:
$6^2 = 4 \times PR$
$36 = 4 \times PR$
$PR = \frac{36}{4}$
$PR = 9$ cm.
Now that we have PR and PS, we can find RS:
RS = PR - PS
RS = $9 - 4$
RS = $5$ cm.
Now, consider the similarity between $\triangle{\text{PQS}}$ and $\triangle{\text{RQS}}$. The ratio of corresponding sides is equal:
$\frac{\text{QS}}{\text{RS}} = \frac{\text{PS}}{\text{QS}}$
This gives $QS^2 = PS \times RS$.
Substitute the values PS = $4$ and RS = $5$:
$QS^2 = 4 \times 5$
$QS^2 = 20$
$QS = \sqrt{20}$
$QS = \sqrt{4 \times 5}$
$QS = 2\sqrt{5}$ cm.
Finally, we need to find QR. Consider the similarity between $\triangle{\text{RQS}}$ and $\triangle{\text{PQR}}$. The ratio of corresponding sides is equal:
$\frac{\text{QR}}{\text{PR}} = \frac{\text{RS}}{\text{QR}}$
This gives $QR^2 = RS \times PR$.
Substitute the values RS = $5$ and PR = $9$:
$QR^2 = 5 \times 9$
$QR^2 = 45$
$QR = \sqrt{45}$
$QR = \sqrt{9 \times 5}$
$QR = 3\sqrt{5}$ cm.
Alternatively, QR can be found using the Pythagorean theorem in $\triangle{\text{RQS}}$:
$QS^2 + RS^2 = QR^2$
$(2\sqrt{5})^2 + 5^2 = QR^2$
$20 + 25 = QR^2$
$45 = QR^2$
$QR = \sqrt{45} = 3\sqrt{5}$ cm. (This confirms the result)
Answer:
The length of QS is $2\sqrt{5}$ cm.
The length of RS is $5$ cm.
The length of QR is $3\sqrt{5}$ cm.
Question 11. In PQR, PD ⊥ QR such that D lies on QR . If PQ = a, PR = b, QD = c and DR = d, prove that (a + b) (a – b) = (c + d) (c – d).
Answer:
Given:
In $\triangle{\text{PQR}}$, PD $\perp$ QR such that D lies on QR.
PQ = $a$, PR = $b$, QD = $c$, and DR = $d$.
To Prove:
$(a + b) (a – b) = (c + d) (c – d)$.
Proof:
Consider the triangle PQR with altitude PD to the side QR.
Since PD $\perp$ QR, $\triangle{\text{PQD}}$ and $\triangle{\text{PRD}}$ are right-angled triangles at D.
In the right-angled triangle $\triangle{\text{PQD}}$, by the Pythagorean theorem:
$PQ^2 = PD^2 + QD^2$
Substituting the given values:
$a^2 = PD^2 + c^2$
From this equation, we can express $PD^2$:
$PD^2 = a^2 - c^2$
In the right-angled triangle $\triangle{\text{PRD}}$, by the Pythagorean theorem:
$PR^2 = PD^2 + DR^2$
Substituting the given values:
$b^2 = PD^2 + d^2$
From this equation, we can express $PD^2$:
$PD^2 = b^2 - d^2$
Since both expressions are equal to $PD^2$, we can equate them:
$a^2 - c^2 = b^2 - d^2$
Rearrange the terms by bringing the terms with 'a' and 'b' to one side and 'c' and 'd' to the other side:
$a^2 - b^2 = c^2 - d^2$
Using the difference of squares formula, $x^2 - y^2 = (x - y)(x + y)$, we can factor both sides of the equation:
$(a - b)(a + b) = (c - d)(c + d)$
This is the required equation to prove.
Thus, $(a + b) (a – b) = (c + d) (c – d)$ is proven.
Hence Proved.
Question 12. In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
Answer:
Given:
A quadrilateral ABCD such that $\angle{\text{A}} + \angle{\text{D}} = 90^\circ$.
To Prove:
$AC^2 + BD^2 = AD^2 + BC^2$.
Construction Required:
Produce side AB and side DC to meet at a point E.
Proof:
Since AB and DC are produced to meet at E, consider the $\triangle{\text{ADE}}$.
The angles of $\triangle{\text{ADE}}$ are $\angle{\text{EAD}}$ (which is the same as $\angle{\text{A}}$ of quadrilateral ABCD), $\angle{\text{EDA}}$ (which is the same as $\angle{\text{D}}$ of quadrilateral ABCD), and $\angle{\text{AED}}$.
The sum of angles in $\triangle{\text{ADE}}$ is $180^\circ$.
$\angle{\text{EAD}} + \angle{\text{EDA}} + \angle{\text{AED}} = 180^\circ$
$\angle{\text{A}} + \angle{\text{D}} + \angle{\text{AED}} = 180^\circ$
We are given that $\angle{\text{A}} + \angle{\text{D}} = 90^\circ$.
$90^\circ + \angle{\text{AED}} = 180^\circ$
$\angle{\text{AED}} = 180^\circ - 90^\circ = 90^\circ$.
Thus, $\triangle{\text{ADE}}$ is a right-angled triangle at E.
Since AB is extended to E, AE is a straight line, and BE is a part of AE.
Since DC is extended to E, DE is a straight line, and CE is a part of DE.
In right-angled $\triangle{\text{ADE}}$, by Pythagorean theorem:
$AD^2 = AE^2 + DE^2$
In right-angled $\triangle{\text{BCE}}$ (since $\angle{\text{E}} = 90^\circ$), by Pythagorean theorem:
$BC^2 = BE^2 + CE^2$
In right-angled $\triangle{\text{ACE}}$ (since $\angle{\text{E}} = 90^\circ$), by Pythagorean theorem:
$AC^2 = AE^2 + CE^2$
In right-angled $\triangle{\text{BDE}}$ (since $\angle{\text{E}} = 90^\circ$), by Pythagorean theorem:
$BD^2 = BE^2 + DE^2$
We want to prove $AC^2 + BD^2 = AD^2 + BC^2$. Let's substitute the expressions we found using the Pythagorean theorem:
Left Hand Side (LHS): $AC^2 + BD^2 = (AE^2 + CE^2) + (BE^2 + DE^2)$
Right Hand Side (RHS): $AD^2 + BC^2 = (AE^2 + DE^2) + (BE^2 + CE^2)$
Comparing LHS and RHS:
$AE^2 + CE^2 + BE^2 + DE^2 = AE^2 + DE^2 + BE^2 + CE^2$
Rearranging terms on the RHS:
$AE^2 + BE^2 + CE^2 + DE^2 = AE^2 + BE^2 + CE^2 + DE^2$
Both sides of the equation are equal.
Thus, $AC^2 + BD^2 = AD^2 + BC^2$ is proven.
Hence Proved.
Question 13. In fig. 6.20, l || m and line segments AB, CD and EF are concurrent at point P. Prove that $\frac{AE}{BF}$ = $\frac{AC}{BD}$ = $\frac{CE}{FD}$ .
Answer:
Given:
Lines l and m are parallel ($l || m$).
Line segments AB, CD, and EF intersect at point P.
Points A, C, E lie on line l, and points B, D, F lie on line m.
To Prove:
$\frac{AE}{BF} = \frac{AC}{BD} = \frac{CE}{FD}$.
Proof:
Consider the triangles $\triangle{\text{PAC}}$ and $\triangle{\text{PBD}}$.
$\angle{\text{APC}} = \angle{\text{BPD}}$ (Vertically opposite angles)
Since line l || line m and AB is a transversal, $\angle{\text{PAC}} = \angle{\text{PBD}}$ (Alternate interior angles)
Therefore, $\triangle{\text{PAC}} \sim \triangle{\text{PBD}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{PA}}{\text{PB}} = \frac{\text{PC}}{\text{PD}} = \frac{\text{AC}}{\text{BD}}$
Consider the triangles $\triangle{\text{PAE}}$ and $\triangle{\text{PBF}}$.
$\angle{\text{APE}} = \angle{\text{BPF}}$ (Vertically opposite angles)
Since line l || line m and EF is a transversal, $\angle{\text{PAE}} = \angle{\text{PBF}}$ (Alternate interior angles)
Therefore, $\triangle{\text{PAE}} \sim \triangle{\text{PBF}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{PA}}{\text{PB}} = \frac{\text{PE}}{\text{PF}} = \frac{\text{AE}}{\text{BF}}$
Consider the triangles $\triangle{\text{PCE}}$ and $\triangle{\text{PFD}}$.
$\angle{\text{CPE}} = \angle{\text{DPF}}$ (Vertically opposite angles)
Since line l || line m and CD is a transversal, $\angle{\text{PCE}} = \angle{\text{PFD}}$ (Alternate interior angles)
Therefore, $\triangle{\text{PCE}} \sim \triangle{\text{PFD}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{PC}}{\text{PD}} = \frac{\text{PE}}{\text{PF}} = \frac{\text{CE}}{\text{FD}}$
From the similarity of $\triangle{\text{PAC}}$ and $\triangle{\text{PBD}}$, we have $\frac{\text{AC}}{\text{BD}} = \frac{\text{PA}}{\text{PB}}$.
From the similarity of $\triangle{\text{PAE}}$ and $\triangle{\text{PBF}}$, we have $\frac{\text{AE}}{\text{BF}} = \frac{\text{PA}}{\text{PB}}$.
Equating the ratios involving $\frac{\text{PA}}{\text{PB}}$ from these two similarities, we get:
$\frac{\text{AE}}{\text{BF}} = \frac{\text{AC}}{\text{BD}}$
From the similarity of $\triangle{\text{PAC}}$ and $\triangle{\text{PBD}}$, we have $\frac{\text{AC}}{\text{BD}} = \frac{\text{PC}}{\text{PD}}$.
From the similarity of $\triangle{\text{PCE}}$ and $\triangle{\text{PFD}}$, we have $\frac{\text{CE}}{\text{FD}} = \frac{\text{PC}}{\text{PD}}$.
Equating the ratios involving $\frac{\text{PC}}{\text{PD}}$ from these two similarities, we get:
$\frac{\text{AC}}{\text{BD}} = \frac{\text{CE}}{\text{FD}}$
Combining the two results:
$\frac{\text{AE}}{\text{BF}} = \frac{\text{AC}}{\text{BD}}$ and $\frac{\text{AC}}{\text{BD}} = \frac{\text{CE}}{\text{FD}}$.
Therefore, we can conclude that:
$\frac{AE}{BF} = \frac{AC}{BD} = \frac{CE}{FD}$
This proves the required relationship between the line segments.
Hence Proved.
Question 14. In Fig. 6.21, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
Answer:
Given:
PA $\perp$ line l, QB $\perp$ line l, RC $\perp$ line l, SD $\perp$ line l.
This implies that PA || QB || RC || SD.
Segments on line l: AB = $6$ cm, BC = $9$ cm, CD = $12$ cm.
Total segment on the other transversal: SP = $36$ cm.
To Find:
The lengths of the segments PQ, QR, and RS.
Solution:
We have four parallel lines PA, QB, RC, and SD intersected by two transversals (the line l and the line passing through P, Q, R, S).
According to the property of transversals intersecting three or more parallel lines (also known as the Intercept Theorem), they cut off the segments on the transversals in the same ratio.
This means that the ratio of the segments on line l is equal to the ratio of the corresponding segments on the line containing P, Q, R, S.
So, we can write the proportion:
$\frac{\text{PQ}}{\text{AB}} = \frac{\text{QR}}{\text{BC}} = \frac{\text{RS}}{\text{CD}}$
Let this common ratio be $m$.
$\frac{\text{PQ}}{6} = \frac{\text{QR}}{9} = \frac{\text{RS}}{12} = m$
From this equality, we can express PQ, QR, and RS in terms of $m$:
PQ = $6m$
QR = $9m$
RS = $12m$
The total length of the segment SP on the second transversal is the sum of the individual segments PQ, QR, and RS.
SP = PQ + QR + RS
We are given that SP = $36$ cm. Substitute the expressions for PQ, QR, and RS:
$36 = 6m + 9m + 12m$
Combine the terms on the right side:
$36 = (6 + 9 + 12)m$
$36 = 27m$
To find the value of $m$, divide both sides of the equation by 27:
$m = \frac{36}{27}$
Simplify the fraction $\frac{36}{27}$ by dividing both the numerator and the denominator by their greatest common divisor, which is 9:
$m = \frac{\cancel{36}^{4}}{\cancel{27}_{3}}$
$m = \frac{4}{3}$
Now that we have the value of $m$, we can find the lengths of PQ, QR, and RS by substituting $m = \frac{4}{3}$ into their expressions:
PQ = $6m = 6 \times \frac{4}{3} = \frac{6 \times 4}{3} = \frac{24}{3} = 8$ cm.
QR = $9m = 9 \times \frac{4}{3} = \frac{9 \times 4}{3} = \frac{36}{3} = 12$ cm.
RS = $12m = 12 \times \frac{4}{3} = \frac{12 \times 4}{3} = \frac{48}{3} = 16$ cm.
Let's verify if the sum of these lengths equals SP: PQ + QR + RS = $8 + 12 + 16 = 36$ cm, which matches the given SP.
Answer:
The length of PQ is $8$ cm.
The length of QR is $12$ cm.
The length of RS is $16$ cm.
Question 15. O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
Answer:
Given:
ABCD is a trapezium with AB || DC.
Diagonals AC and BD intersect at O.
A line segment PQ is drawn through O such that P is on AD, Q is on BC, and PQ || AB.
Since PQ || AB and AB || DC, it follows that PQ || DC.
To Prove:
PO = QO.
Proof:
Consider the triangles $\triangle{\text{ABO}}$ and $\triangle{\text{CDO}}$.
Since AB || DC, and AC is a transversal:
$\angle{\text{OAB}} = \angle{\text{OCD}}$ (Alternate interior angles)
Since AB || DC, and BD is a transversal:
$\angle{\text{OBA}} = \angle{\text{ODC}}$ (Alternate interior angles)
Also, $\angle{\text{AOB}} = \angle{\text{COD}}$ (Vertically opposite angles)
Therefore, $\triangle{\text{ABO}} \sim \triangle{\text{CDO}}$ by AAA similarity criterion.
From the similarity of these triangles, the ratio of corresponding sides is equal:
$\frac{\text{AO}}{\text{CO}} = \frac{\text{BO}}{\text{DO}} = \frac{\text{AB}}{\text{CD}}$
Now consider $\triangle{\text{DAB}}$. The line segment PO is within this triangle, and we are given that PQ || AB, which means PO || AB.
In $\triangle{\text{DAB}}$, since PO || AB, by the property of similar triangles formed by a line parallel to one side (or by Basic Proportionality Theorem applied to $\triangle{\text{DAB}}$ intersected by PO):
$\triangle{\text{DPO}} \sim \triangle{\text{DAB}}$
The ratio of corresponding sides is:
$\frac{\text{DO}}{\text{DB}} = \frac{\text{PO}}{\text{AB}}$
From the ratio $\frac{\text{BO}}{\text{DO}} = \frac{\text{AO}}{\text{CO}}$, let $\frac{\text{BO}}{\text{DO}} = k$. Then $\frac{\text{DO}}{\text{BO}} = \frac{1}{k}$.
$\frac{\text{DO}}{\text{DB}} = \frac{\text{DO}}{\text{DO} + \text{BO}} = \frac{\text{DO}}{\text{DO}(1 + \frac{\text{BO}}{\text{DO}})} = \frac{1}{1 + \frac{\text{BO}}{\text{DO}}} = \frac{1}{1+k}$.
So, $\frac{\text{PO}}{\text{AB}} = \frac{1}{1+k}$
This gives $\text{PO} = \frac{\text{AB}}{1+k}$.
Next, consider $\triangle{\text{CAB}}$. The line segment QO is within this triangle, and we are given that PQ || AB, which means QO || AB.
In $\triangle{\text{CAB}}$, since QO || AB, by the property of similar triangles formed by a line parallel to one side (or by Basic Proportionality Theorem applied to $\triangle{\text{CAB}}$ intersected by QO):
$\triangle{\text{CQO}} \sim \triangle{\text{CAB}}$
The ratio of corresponding sides is:
$\frac{\text{CO}}{\text{CA}} = \frac{\text{QO}}{\text{AB}}$
From the ratio $\frac{\text{AO}}{\text{CO}} = k$, we have $\frac{\text{CO}}{\text{AO}} = \frac{1}{k}$.
$\frac{\text{CO}}{\text{CA}} = \frac{\text{CO}}{\text{CO} + \text{AO}} = \frac{\text{CO}}{\text{CO}(1 + \frac{\text{AO}}{\text{CO}})} = \frac{1}{1 + \frac{\text{AO}}{\text{CO}}} = \frac{1}{1+k}$.
So, $\frac{\text{QO}}{\text{AB}} = \frac{1}{1+k}$
This gives $\text{QO} = \frac{\text{AB}}{1+k}$.
Comparing the expressions for PO and QO:
$\text{PO} = \frac{\text{AB}}{1+k}$
$\text{QO} = \frac{\text{AB}}{1+k}$
Since both PO and QO are equal to the same expression $\frac{\text{AB}}{1+k}$, we can conclude that PO = QO.
Hence Proved.
Question 16. In Fig. 6.22, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE . Prove that $\frac{BD}{CD}$ = $\frac{BF}{CE}$ .
[Hint: Take point G on AB such that CG || DF.]
Answer:
Given:
In $\triangle{\text{ABC}}$, E is the midpoint of side AC.
A line segment DF intersects AC at E, where D is on BC and F is on the line containing AB.
$\angle{\text{AEF}} = \angle{\text{AFE}}$.
To Prove:
$\frac{BD}{CD} = \frac{BF}{CE}$.
Construction Required:
Draw a line segment CG parallel to DF, such that G is a point on AB.
Proof:
In $\triangle{\text{AEF}}$, we are given that $\angle{\text{AEF}} = \angle{\text{AFE}}$.
According to the property of triangles, if two angles in a triangle are equal, then the sides opposite to these angles are also equal.
The side opposite to $\angle{\text{AEF}}$ is AF.
The side opposite to $\angle{\text{AFE}}$ is AE.
Thus, AF = AE.
We are given that E is the midpoint of AC.
Therefore, AE = CE.
From the above two results (AF = AE and AE = CE), we can conclude that:
AF = AE = CE.
Now consider the construction. We have drawn CG || DF, where G is on AB.
Since E is a point on DF, it means CG || EF.
Consider $\triangle{\text{ACG}}$. E is the midpoint of AC, and the line segment EF is parallel to CG.
The line segment EF intersects the line AB at F. By the Basic Proportionality Theorem (BPT) applied to $\triangle{\text{ACG}}$ with transversal ABF cutting parallel lines CG and EF, we have:
$\frac{\text{AE}}{\text{EC}} = \frac{\text{AF}}{\text{FG}}$
Since E is the midpoint of AC, AE = EC, which means $\frac{\text{AE}}{\text{EC}} = 1$.
Substituting this into the equation:
$1 = \frac{\text{AF}}{\text{FG}}$
This implies AF = FG.
Now consider $\triangle{\text{BCG}}$. D is a point on BC, and G is a point on AB.
The line segment DF is parallel to CG (by construction).
This line DF intersects the side BC at D and the side BG (which is part of AB) extended at F.
By the Basic Proportionality Theorem (BPT) applied to $\triangle{\text{BCG}}$ with line segment DF parallel to CG, we have:
$\frac{\text{BD}}{\text{DC}} = \frac{\text{BF}}{\text{FG}}$
We have shown that FG = AF and AF = CE.
Therefore, FG = CE.
Substitute FG = CE into the BPT equation $\frac{\text{BD}}{\text{DC}} = \frac{\text{BF}}{\text{FG}}$:
$\frac{\text{BD}}{\text{DC}} = \frac{\text{BF}}{\text{CE}}$
This matches the expression we needed to prove.
Hence Proved.
Question 17. Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Answer:
Given:
A right-angled triangle ABC, with the right angle at B.
Let the lengths of the sides be AB, BC, and AC (hypotenuse).
Semicircles are drawn on the sides AB, BC, and AC as diameters.
To Prove:
Area of the semicircle on hypotenuse AC = Area of the semicircle on side AB + Area of the semicircle on side BC.
Proof:
Let the lengths of the sides of the right-angled triangle ABC be:
AB = $c_1$
BC = $c_2$
AC = $h$ (hypotenuse)
By the Pythagorean theorem in the right-angled $\triangle{\text{ABC}}$:
$AB^2 + BC^2 = AC^2$
$c_1^2 + c_2^2 = h^2$
Now, consider the semicircles drawn on each side as the diameter.
For the semicircle on side AB:
Diameter = $c_1$
Radius, $r_1 = \frac{c_1}{2}$
Area of the semicircle, $A_1 = \frac{1}{2} \pi r_1^2 = \frac{1}{2} \pi \left(\frac{c_1}{2}\right)^2 = \frac{1}{2} \pi \frac{c_1^2}{4} = \frac{\pi c_1^2}{8}$
For the semicircle on side BC:
Diameter = $c_2$
Radius, $r_2 = \frac{c_2}{2}$
Area of the semicircle, $A_2 = \frac{1}{2} \pi r_2^2 = \frac{1}{2} \pi \left(\frac{c_2}{2}\right)^2 = \frac{1}{2} \pi \frac{c_2^2}{4} = \frac{\pi c_2^2}{8}$
For the semicircle on hypotenuse AC:
Diameter = $h$
Radius, $r_h = \frac{h}{2}$
Area of the semicircle, $A_h = \frac{1}{2} \pi r_h^2 = \frac{1}{2} \pi \left(\frac{h}{2}\right)^2 = \frac{1}{2} \pi \frac{h^2}{4} = \frac{\pi h^2}{8}$
We want to check if $A_1 + A_2 = A_h$.
Substitute the area expressions into the equation:
$A_1 + A_2 = \frac{\pi c_1^2}{8} + \frac{\pi c_2^2}{8}$
Factor out $\frac{\pi}{8}$:
$A_1 + A_2 = \frac{\pi}{8} (c_1^2 + c_2^2)$
From the Pythagorean theorem, we know that $c_1^2 + c_2^2 = h^2$. Substitute this into the equation:
$A_1 + A_2 = \frac{\pi}{8} (h^2)$
$A_1 + A_2 = \frac{\pi h^2}{8}$
We also found that $A_h = \frac{\pi h^2}{8}$.
Thus, we have $A_1 + A_2 = A_h$.
This proves that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Hence Proved.
Question 18. Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Answer:
Given:
A right-angled triangle ABC, with the right angle at B.
Equilateral triangles are drawn on the sides AB, BC, and AC as bases.
To Prove:
Area of the equilateral triangle on hypotenuse AC = Area of the equilateral triangle on side AB + Area of the equilateral triangle on side BC.
Proof:
Let the lengths of the sides of the right-angled triangle ABC be:
Length of side AB = $a$
Length of side BC = $b$}
Length of hypotenuse AC = $c$
Since $\triangle{\text{ABC}}$ is a right-angled triangle at B, by the Pythagorean theorem:
$AB^2 + BC^2 = AC^2$
$a^2 + b^2 = c^2$
Now, consider the equilateral triangles drawn on each side as the base.
The formula for the area of an equilateral triangle with side length $s$ is $Area = \frac{\sqrt{3}}{4} s^2$.
Area of the equilateral triangle on side AB (with side length $a$):
$Area_{\text{AB}} = \frac{\sqrt{3}}{4} a^2$
Area of the equilateral triangle on side BC (with side length $b$):
$Area_{\text{BC}} = \frac{\sqrt{3}}{4} b^2$
Area of the equilateral triangle on side AC (with side length $c$):
$Area_{\text{AC}} = \frac{\sqrt{3}}{4} c^2$
We need to prove that $Area_{\text{AB}} + Area_{\text{BC}} = Area_{\text{AC}}$.
Substitute the area expressions into the equation:
$\frac{\sqrt{3}}{4} a^2 + \frac{\sqrt{3}}{4} b^2 = \frac{\sqrt{3}}{4} c^2$
Factor out $\frac{\sqrt{3}}{4}$ from the left side:
$\frac{\sqrt{3}}{4} (a^2 + b^2) = \frac{\sqrt{3}}{4} c^2$
From the Pythagorean theorem, we know that $a^2 + b^2 = c^2$. Substitute this into the equation:
$\frac{\sqrt{3}}{4} (c^2) = \frac{\sqrt{3}}{4} c^2$
Both sides of the equation are equal. This confirms the relationship between the areas.
Thus, the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Hence Proved.

