| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 9 Circles
Welcome to this vital resource providing comprehensive solutions and detailed explanations for the Class 10 NCERT Exemplar problems centered on the geometry of Circles, with a primary emphasis on the properties and applications of tangents. The Exemplar questions in this domain are specifically designed to challenge students beyond standard textbook exercises, presenting more intricate geometric scenarios and demanding the construction of rigorous proofs. These problems often require a deeper understanding of tangent properties and necessitate the skillful integration of concepts learned in Class 9 circle theorems, pushing students towards a more advanced level of geometric reasoning.
This solutions page begins by revisiting the fundamental definitions of tangents (lines that touch a circle at exactly one point) and secants (lines that intersect a circle at two distinct points). However, the core focus lies in the thorough exploration and application of the two pivotal theorems governing tangents in Class 10:
- Theorem 10.1: This fundamental theorem states that the tangent at any point of a circle is perpendicular to the radius through the point of contact. The solutions extensively demonstrate how this theorem is applied – establishing right angles (e.g., if $P$ is the point of contact and $O$ is the center, then the radius $OP \perp$ tangent at $P$, meaning $\angle OPT = 90^\circ$ where $T$ is a point on the tangent). This perpendicularity is crucial for solving problems involving angles and often leads to the application of the Pythagoras theorem in right-angled triangles formed by the radius, tangent segment, and line joining the center to an external point.
- Theorem 10.2: This equally important theorem states that the lengths of tangents drawn from an external point to a circle are equal. The solutions showcase the power of this theorem in solving numerous problems involving finding unknown lengths, proving relationships in figures with multiple tangents from the same point, and establishing properties of figures related to circles.
The true challenge of the NCERT Exemplar lies in applying these theorems within complex diagrams that might involve one or more circles, multiple tangents originating from various external points, chords, and secants interacting within the same figure. The solutions guide students through finding unknown angles, often requiring the use of Theorem 10.1 in conjunction with angle sum properties of triangles and quadrilaterals, or potentially integrating Class 9 circle theorems like angles in the same segment or the relationship between the angle subtended by an arc at the center and at the circumference. Similarly, calculating unknown lengths frequently involves combining Theorem 10.2 with the Pythagoras theorem or properties of similar triangles if they arise.
A significant portion of the Exemplar problems demands the construction of rigorous geometric proofs. These solutions provide detailed, step-by-step proofs for challenging propositions, such as:
- Demonstrating properties of quadrilaterals circumscribing a circle (e.g., proving that opposite sides subtend supplementary angles at the center, or showing that a parallelogram circumscribing a circle must be a rhombus).
- Establishing specific geometric relationships between tangents drawn under particular conditions.
- Solving problems involving concentric circles where tangents to the inner circle act as chords to the outer circle.
These solutions cater to all Exemplar question formats, including probing MCQs, specific Fill-in-the-Blanks, conceptual True/False statements, and comprehensive Short/Long Answer questions. For the latter, the solutions emphasize detailed calculations with clear justifications citing the relevant theorems (like Theorem 10.1 or 10.2) at each step, alongside well-structured, logical deductive arguments for proofs. Featuring clear diagrams, precise theorem referencing, and methodical problem-solving strategies, this resource is invaluable for any student aiming to master advanced geometric problems involving tangents to circles.
Sample Question 1 to 3 (Before Exercise 9.1)
Choose the correct answer from the given four options:
Sample Question 1: If angle between two radii of a circle is 130º, the angle between the tangents at the ends of the radii is :
(A) 90º
(B) 50º
(C) 70º
(D) 40º
Answer:
Given:
A circle with two radii.
The angle between the two radii is $130^\circ$.
Tangents are drawn at the ends of these two radii.
To Find:
The angle between the tangents at the ends of the radii.
Solution:
Let O be the centre of the circle.
Let OA and OB be the two radii of the circle such that the angle between them is $130^\circ$.
$\angle AOB = 130^\circ$
(Given)
Let PA and PB be the tangents to the circle at points A and B respectively. These tangents intersect at an external point P.
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
According to this theorem, the radius OA is perpendicular to the tangent PA, and the radius OB is perpendicular to the tangent PB.
$\angle OAP = 90^\circ$
$\angle OBP = 90^\circ$
Now, consider the quadrilateral OAPB. The sum of the interior angles of a quadrilateral is $360^\circ$.
$\angle OAP + \angle APB + \angle OBP + \angle AOB = 360^\circ$
Substituting the known values into the equation:
$90^\circ + \angle APB + 90^\circ + 130^\circ = 360^\circ$
$\Rightarrow \angle APB + 310^\circ = 360^\circ$
$\Rightarrow \angle APB = 360^\circ - 310^\circ$
$\Rightarrow \angle APB = 50^\circ$
The angle between the tangents at the ends of the radii is $50^\circ$.
Hence, the correct option is (B).
Sample Question 2: In Fig. 9.1, the pair of tangents AP and AQ drawn from an external point A to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm. Then the radius of the circle is
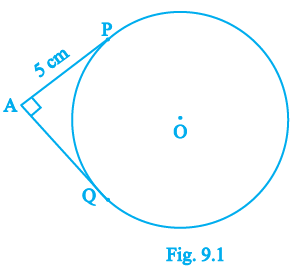
(A) 10 cm
(B) 7.5 cm
(C) 5 cm
(D) 2.5 cm
Answer:
Given:
A circle with centre O.
AP and AQ are a pair of tangents drawn from an external point A to the circle.
The tangents AP and AQ are perpendicular to each other, which means $\angle PAQ = 90^\circ$.
The length of each tangent is 5 cm, so $AP = AQ = 5$ cm.
To Find:
The radius of the circle.
Construction:
Join the centre O to the points of contact P and Q. This forms the radii OP and OQ.
Solution:
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Therefore, the radius OP is perpendicular to the tangent AP, and the radius OQ is perpendicular to the tangent AQ.
$\angle OPA = 90^\circ$
$\angle OQA = 90^\circ$
Now, let's consider the quadrilateral OPAQ.
We have the following information about its angles:
$\angle OPA = 90^\circ$ (Proved above)
$\angle OQA = 90^\circ$ (Proved above)
$\angle PAQ = 90^\circ$ (Given)
Since the sum of the interior angles of a quadrilateral is $360^\circ$, the fourth angle, $\angle POQ$, must be:
$\angle POQ = 360^\circ - (90^\circ + 90^\circ + 90^\circ) = 360^\circ - 270^\circ = 90^\circ$.
Since all four angles of the quadrilateral OPAQ are $90^\circ$, it is a rectangle.
Now, let's consider the sides of this rectangle:
$OP$ and $OQ$ are the radii of the circle, so $OP = OQ = r$.
Since adjacent sides of the rectangle are equal ($OP=OQ$), the rectangle OPAQ must be a square.
In a square, all four sides are equal in length.
Therefore, $OP = OQ = AP = AQ$.
We are given that the length of the tangent AP is 5 cm.
So, $AP = 5$ cm.
The radius of the circle is the length of OP. Since $OP = AP$, we have:
Radius = $OP = 5$ cm.
Hence, the correct option is (C).
Sample Question 3: In Fig. 9.2, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT = 60°. Then ∠PRQ is equal to
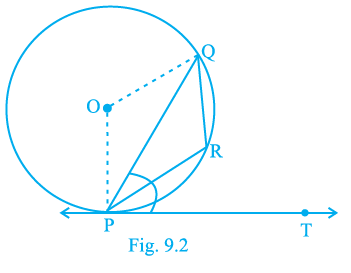
(A) 135°
(B) 150°
(C) 120°
(D) 110°
Answer:
Given:
In the given figure, PQ is a chord of a circle.
PT is the tangent to the circle at the point of contact P.
R is a point on the minor arc PQ.
The angle between the tangent PT and the chord PQ is $60^\circ$, i.e., $\angle QPT = 60^\circ$.
To Find:
The measure of the angle $\angle PRQ$.
Solution:
Step 1: Find the angle $\angle OPQ$.
We know the theorem that the radius of a circle is perpendicular to the tangent at the point of contact.
Since OP is the radius and PT is the tangent at point P, we have:
$OP \perp PT$
This means the angle between the radius and the tangent is $90^\circ$.
$\angle OPT = 90^\circ$
From the figure, we can see that the angle $\angle OPT$ is the sum of $\angle OPQ$ and $\angle QPT$.
$\angle OPT = \angle OPQ + \angle QPT$
Substituting the known values:
$90^\circ = \angle OPQ + 60^\circ$
$\Rightarrow \angle OPQ = 90^\circ - 60^\circ = 30^\circ$
Step 2: Find the central angle $\angle POQ$.
Now, consider the triangle $\triangle OPQ$.
The sides OP and OQ are both radii of the same circle, so their lengths are equal.
OP = OQ
[Radii of the same circle]
Therefore, $\triangle OPQ$ is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are also equal.
$\angle OQP = \angle OPQ = 30^\circ$
Using the angle sum property of a triangle for $\triangle OPQ$:
$\angle POQ + \angle OPQ + \angle OQP = 180^\circ$
$\angle POQ + 30^\circ + 30^\circ = 180^\circ$
$\angle POQ + 60^\circ = 180^\circ$
$\Rightarrow \angle POQ = 180^\circ - 60^\circ = 120^\circ$
Step 3: Find the angle $\angle PRQ$.
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
The angle $\angle PRQ$ is subtended by the major arc PQ at a point R on the minor arc.
The angle subtended by the major arc PQ at the centre is the reflex angle $\angle POQ$.
Reflex $\angle POQ = 360^\circ - \angle POQ$
Reflex $\angle POQ = 360^\circ - 120^\circ = 240^\circ$
Now, applying the theorem:
Reflex $\angle POQ = 2 \times \angle PRQ$
$240^\circ = 2 \times \angle PRQ$
$\Rightarrow \angle PRQ = \frac{240^\circ}{2} = 120^\circ$
Hence, the measure of $\angle PRQ$ is $120^\circ$.
This corresponds to option (C).
Exercise 9.1
Choose the correct answer from the given four options:
Question 1. If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is
(A) 3 cm
(B) 6 cm
(C) 9 cm
(D) 1 cm
Answer:
Given:
Two concentric circles (circles with the same center) with radii 4 cm and 5 cm.
A chord of the larger circle is a tangent to the smaller circle.
To Find:
The length of this chord.
Solution:
Let the two concentric circles have their center at point O.
Let the radius of the inner circle be $r_1 = 4$ cm.
Let the radius of the outer circle be $r_2 = 5$ cm.
Let AB be a chord of the outer circle which is tangent to the inner circle at a point P.
Now, let's join the center O to the point of tangency P and to the endpoint A of the chord.
So, we have:
$OP = r_1 = 4$ cm (Radius of the inner circle)
$OA = r_2 = 5$ cm (Radius of the outer circle)
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Since AB is a tangent to the inner circle at point P, the radius OP must be perpendicular to the chord AB.
Therefore, $\angle OPA = 90^\circ$.
This makes the triangle $\triangle OPA$ a right-angled triangle, with the hypotenuse being OA.
By applying the Pythagorean theorem to $\triangle OPA$, we have:
$OA^2 = OP^2 + AP^2$
Substituting the known values:
$5^2 = 4^2 + AP^2$
$25 = 16 + AP^2$
$AP^2 = 25 - 16$
$AP^2 = 9$
$AP = \sqrt{9} = 3$ cm.
Now, we know another theorem: "A perpendicular drawn from the centre of a circle to a chord bisects the chord."
Since OP is perpendicular to the chord AB of the outer circle, it must bisect the chord AB. This means P is the midpoint of AB.
Therefore, the length of the chord AB is twice the length of AP.
$AB = 2 \times AP$
$AB = 2 \times 3$ cm
$AB = 6$ cm.
Hence, the correct option is (B).
Question 2. In Fig. 9.3, if ∠AOB = 125°, then ∠COD is equal to

(A) 62.5°
(B) 45°
(C) 35°
(D) 55°
Answer:
Given:
In the given figure, a quadrilateral ABCD circumscribes a circle with centre O.
The angle subtended by the side AB at the centre O is $125^\circ$, i.e., $\angle AOB = 125^\circ$.
To Find:
The measure of the angle $\angle COD$.
Solution:
We will use the theorem which states: "The opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle."
This means that the sum of the angles subtended by the opposite sides of the circumscribed quadrilateral at the centre is $180^\circ$.
In the given quadrilateral ABCD, the pair of opposite sides are (AB, CD) and (AD, BC).
According to the theorem, we have two relationships:
1. $\angle AOB + \angle COD = 180^\circ$
2. $\angle AOD + \angle BOC = 180^\circ$
We are given the value of $\angle AOB$ and we need to find the value of $\angle COD$. We will use the first relationship.
$\angle AOB + \angle COD = 180^\circ$
Substituting the given value of $\angle AOB = 125^\circ$ into the equation:
$125^\circ + \angle COD = 180^\circ$
$\Rightarrow \angle COD = 180^\circ - 125^\circ$
$\Rightarrow \angle COD = 55^\circ$
Hence, the measure of $\angle COD$ is $55^\circ$.
Comparing this result with the given options, we find that option (D) is correct.
Question 3. In Fig. 9.4, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
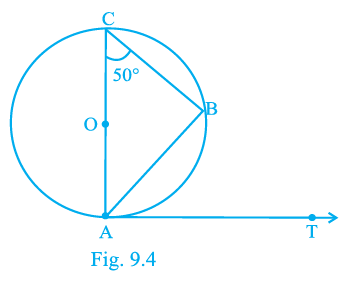
(A) 65°
(B) 60°
(C) 50°
(D) 40°
Answer:
Given:
In the given figure, AB is a chord of the circle with centre O.
AOC is a diameter of the circle.
The measure of angle $\angle ACB = 50^\circ$.
AT is the tangent to the circle at point A.
To Find:
The measure of the angle $\angle BAT$.
Solution:
We are given that AOC is a diameter of the circle.
We know the theorem: "The angle in a semicircle is a right angle."
The angle subtended by the diameter AOC at any point on the circumference is $90^\circ$. Therefore, the angle at point B, $\angle ABC$, is a right angle.
$\angle ABC = 90^\circ$
[Angle in a semicircle]
Now, let's consider the triangle $\triangle ABC$.
By the angle sum property of a triangle, the sum of all its interior angles is $180^\circ$.
$\angle CAB + \angle ABC + \angle BCA = 180^\circ$
We know $\angle ABC = 90^\circ$ and we are given $\angle ACB = 50^\circ$ (which is the same as $\angle BCA$).
Substituting these values into the equation:
$\angle CAB + 90^\circ + 50^\circ = 180^\circ$
$\Rightarrow \angle CAB + 140^\circ = 180^\circ$
$\Rightarrow \angle CAB = 180^\circ - 140^\circ = 40^\circ$
The angle $\angle CAB$ represents the angle between the chord AB and the diameter AC.
Now, we use the Alternate Segment Theorem. This theorem states that the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Here, the angle between the tangent AT and the chord AB is $\angle BAT$.
The angle in the alternate segment is the angle subtended by the chord AB at any point on the major arc AC B. The point C is on this arc.
Therefore, according to the Alternate Segment Theorem:
$\angle BAT = \angle ACB$
We are given that $\angle ACB = 50^\circ$.
So, $\angle BAT = 50^\circ$.
Hence, the correct option is (C).
Alternate Solution:
We know the theorem that the radius (or diameter) is perpendicular to the tangent at the point of contact.
Since AOC is the diameter and AT is the tangent at point A, we have:
$AC \perp AT$
This means the angle between the diameter and the tangent is $90^\circ$.
$\angle CAT = 90^\circ$
From the figure, we can see that the angle $\angle CAT$ is composed of two adjacent angles, $\angle CAB$ and $\angle BAT$.
$\angle CAT = \angle CAB + \angle BAT$
In the first part of the solution, we found the value of $\angle CAB$ using the angle sum property of $\triangle ABC$.
$\angle CAB = 40^\circ$
Now, substitute the known values into the equation for $\angle CAT$:
$90^\circ = 40^\circ + \angle BAT$
$\Rightarrow \angle BAT = 90^\circ - 40^\circ$
$\Rightarrow \angle BAT = 50^\circ$
This confirms the result from the first method.
Question 4. From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(A) 60 cm2
(B) 65 cm2
(C) 30 cm2
(D) 32.5 cm2
Given:
A circle with centre O and radius 5 cm.
An external point P is at a distance of 13 cm from the centre O, so $OP = 13$ cm.
PQ and PR are the two tangents from point P to the circle.
The radius is $OQ = OR = 5$ cm.
To Find:
The area of the quadrilateral PQOR.
Solution:
The quadrilateral PQOR is formed by two triangles, $\triangle POQ$ and $\triangle POR$.
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Therefore, the radius OQ is perpendicular to the tangent PQ at the point of contact Q.
$\angle OQP = 90^\circ$
This means that $\triangle POQ$ is a right-angled triangle with the right angle at Q. The hypotenuse is the side opposite the right angle, which is OP.
We can find the length of the tangent PQ using the Pythagorean theorem in $\triangle POQ$:
$OP^2 = OQ^2 + PQ^2$
Substituting the given values:
$13^2 = 5^2 + PQ^2$
$169 = 25 + PQ^2$
$PQ^2 = 169 - 25 = 144$
$PQ = \sqrt{144} = 12$ cm.
Now we can find the area of the right-angled triangle $\triangle POQ$.
Area($\triangle POQ$) = $\frac{1}{2} \times \text{base} \times \text{height}$
The two legs of the right triangle, OQ and PQ, can be taken as the base and height.
Area($\triangle POQ$) = $\frac{1}{2} \times OQ \times PQ$
Area($\triangle POQ$) = $\frac{1}{2} \times 5 \text{ cm} \times 12 \text{ cm} = 30 \text{ cm}^2$.
The quadrilateral PQOR is composed of two congruent right-angled triangles, $\triangle POQ$ and $\triangle POR$. (They are congruent by RHS criterion: OQ=OR, OP=OP, $\angle OQP=\angle ORP=90^\circ$).
Therefore, the area of the quadrilateral PQOR is twice the area of one of these triangles.
Area(PQOR) = Area($\triangle POQ$) + Area($\triangle POR$)
Area(PQOR) = $2 \times$ Area($\triangle POQ$)
Area(PQOR) = $2 \times 30 \text{ cm}^2 = 60 \text{ cm}^2$.
Conclusion:
The area of the quadrilateral PQOR is 60 cm2.
The correct option is (A) 60 cm$^2$.
Question 5. At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
(A) 4 cm
(B) 5 cm
(C) 6 cm
(D) 8 cm
Given:
A circle with centre O and radius $r = 5$ cm.
AB is a diameter of the circle.
XAY is a tangent to the circle at point A.
CD is a chord of the circle that is parallel to the tangent XAY ($CD \parallel XY$).
The distance of the chord CD from the point A is 8 cm.
To Find:
The length of the chord CD.
Solution:
Since AB is a diameter and XAY is a tangent at point A, the diameter is perpendicular to the tangent at the point of contact.
$AB \perp XY$
We are given that the chord CD is parallel to the tangent XY.
$CD \parallel XY$
Since AB is perpendicular to XY, and CD is parallel to XY, it follows that AB must also be perpendicular to the chord CD.
$AB \perp CD$
Let the point of intersection of the diameter AB and the chord CD be M. Thus, $\angle OMD = 90^\circ$.
We are given that the distance from point A to the chord CD is 8 cm. Since AB is perpendicular to CD, this distance is the length of the segment AM.
$AM = 8$ cm
We know that the radius of the circle is 5 cm. Since A is a point on the circle and O is the centre, the distance $OA = 5$ cm.
The points A, O, and M lie on the same straight line (the diameter AB). We have $OA = 5$ cm and $AM = 8$ cm. The distance of the chord CD from the centre O is the length of the perpendicular segment OM.
From the collinear points, we can find the length of OM:
$OM = AM - OA$
$OM = 8 \text{ cm} - 5 \text{ cm} = 3$ cm
Now, consider the right-angled triangle $\triangle OMD$.
The hypotenuse is the radius OD, so $OD = 5$ cm.
One leg is the perpendicular distance from the centre to the chord, $OM = 3$ cm.
The other leg is MD, which is half the length of the chord CD (since the perpendicular from the centre bisects the chord).
Using the Pythagorean theorem in $\triangle OMD$:
$OD^2 = OM^2 + MD^2$
$5^2 = 3^2 + MD^2$
$25 = 9 + MD^2$
$MD^2 = 25 - 9 = 16$
$MD = \sqrt{16} = 4$ cm.
The full length of the chord CD is twice the length of MD.
$CD = 2 \times MD = 2 \times 4 = 8$ cm.
Conclusion:
The length of the chord CD is 8 cm.
The correct option is (D) 8 cm.
Question 6. In Fig. 9.5, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to

(A) 4 cm
(B) 2 cm
(C) 2$\sqrt{3}$ cm
(D) 4$\sqrt{3}$ cm
Answer:
Given:
In the given figure, AT is a tangent to the circle with centre O.
The distance from the centre to the external point T is $OT = 4$ cm.
The angle formed by the tangent and the line segment OT is $\angle OTA = 30^\circ$.
To Find:
The length of the tangent AT.
Solution:
Let's join the centre of the circle O to the point of tangency A. The line segment OA is the radius of the circle.
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
According to this theorem, the radius OA is perpendicular to the tangent AT at the point of contact A.
Therefore, $\angle OAT = 90^\circ$.
This means that the triangle $\triangle OAT$ is a right-angled triangle with the right angle at vertex A.
In the right-angled triangle $\triangle OAT$:
- The side opposite the right angle, OT, is the hypotenuse. $OT = 4$ cm.
- We are given the angle $\angle OTA = 30^\circ$.
- The side AT is the side adjacent to the angle $\angle OTA$.
We can use trigonometric ratios to find the length of the adjacent side AT. The cosine function relates the adjacent side, the hypotenuse, and the angle.
$\cos(\theta) = \frac{\text{Adjacent Side}}{\text{Hypotenuse}}$
Applying this to our triangle:
$\cos(\angle OTA) = \frac{AT}{OT}$
Substituting the known values:
$\cos(30^\circ) = \frac{AT}{4}$
We know that the value of $\cos(30^\circ)$ is $\frac{\sqrt{3}}{2}$.
$\frac{\sqrt{3}}{2} = \frac{AT}{4}$
To solve for AT, we can multiply both sides by 4:
$AT = 4 \times \frac{\sqrt{3}}{2}$
$AT = 2\sqrt{3}$ cm.
Hence, the length of the tangent AT is $2\sqrt{3}$ cm.
This corresponds to option (C).
Question 7. In Fig. 9.6, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to

(A) 100°
(B) 80°
(C) 90°
(D) 75°
Answer:
Given:
In the given figure, O is the centre of the circle.
PQ is a chord of the circle.
PR is the tangent to the circle at the point of contact P.
The angle between the tangent PR and the chord PQ is $50^\circ$, i.e., $\angle QPR = 50^\circ$.
To Find:
The measure of the central angle $\angle POQ$.
Solution:
We know the theorem that states: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Here, OP is the radius and PR is the tangent at point P. Therefore, the radius OP is perpendicular to the tangent PR.
$OP \perp PR$
This means the angle between the radius and the tangent is $90^\circ$.
$\angle OPR = 90^\circ$
From the figure, we can see that the angle $\angle OPR$ is the sum of the angles $\angle OPQ$ and $\angle QPR$.
$\angle OPR = \angle OPQ + \angle QPR$
Substituting the known values:
$90^\circ = \angle OPQ + 50^\circ$
$\Rightarrow \angle OPQ = 90^\circ - 50^\circ = 40^\circ$
Now, let's consider the triangle $\triangle OPQ$.
The sides OP and OQ are both radii of the same circle, so their lengths are equal.
OP = OQ
[Radii of the same circle]
Therefore, $\triangle OPQ$ is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are also equal.
$\angle OQP = \angle OPQ$
Since we found that $\angle OPQ = 40^\circ$, we have:
$\angle OQP = 40^\circ$
Finally, we can find the angle $\angle POQ$ by applying the angle sum property of a triangle to $\triangle OPQ$. The sum of the interior angles of a triangle is $180^\circ$.
$\angle POQ + \angle OPQ + \angle OQP = 180^\circ$
$\angle POQ + 40^\circ + 40^\circ = 180^\circ$
$\angle POQ + 80^\circ = 180^\circ$
$\Rightarrow \angle POQ = 180^\circ - 80^\circ$
$\Rightarrow \angle POQ = 100^\circ$
Hence, the measure of $\angle POQ$ is $100^\circ$.
This corresponds to option (A).
Question 8. In Fig. 9.7, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to
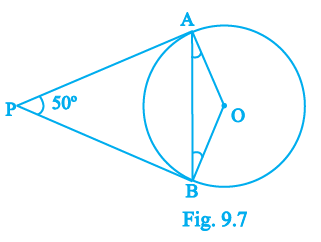
(A) 25°
(B) 30°
(C) 40°
(D) 50°
Answer:
Given:
In the given figure, PA and PB are tangents from an external point P to a circle with centre O.
The angle between the two tangents is $50^\circ$, i.e., $\angle APB = 50^\circ$.
To Find:
The measure of the angle $\angle OAB$.
Solution:
We know the theorem: "The lengths of tangents drawn from an external point to a circle are equal."
Therefore, the lengths of the tangents PA and PB are equal.
PA = PB
Now, consider the triangle $\triangle PAB$.
Since two of its sides are equal (PA = PB), $\triangle PAB$ is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are also equal.
The angle opposite side PB is $\angle PAB$.
The angle opposite side PA is $\angle PBA$.
Therefore, $\angle PAB = \angle PBA$.
By applying the angle sum property of a triangle to $\triangle PAB$, we have:
$\angle PAB + \angle PBA + \angle APB = 180^\circ$
Substituting $\angle PBA$ with $\angle PAB$ and the given value of $\angle APB$:
$\angle PAB + \angle PAB + 50^\circ = 180^\circ$
$2\angle PAB = 180^\circ - 50^\circ$
$2\angle PAB = 130^\circ$
$\angle PAB = \frac{130^\circ}{2} = 65^\circ$.
Now, we use another theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Here, PA is the tangent at point A, and OA is the radius through the point of contact.
Therefore, the radius OA is perpendicular to the tangent PA.
$OA \perp PA$
This means the angle between the radius and the tangent is $90^\circ$.
$\angle OAP = 90^\circ$
From the figure, we can see that the angle $\angle OAP$ is the sum of the angles $\angle OAB$ and $\angle PAB$.
$\angle OAP = \angle OAB + \angle PAB$
Substituting the known values:
$90^\circ = \angle OAB + 65^\circ$
$\Rightarrow \angle OAB = 90^\circ - 65^\circ$
$\Rightarrow \angle OAB = 25^\circ$
Hence, the measure of $\angle OAB$ is $25^\circ$.
This corresponds to option (A).
Question 9. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to
(A) $\frac{3}{2}\sqrt{3}$ cm
(B) 6 cm
(C) 3 cm
(D) $3\sqrt{3}$ cm
Answer:
Given:
A circle with a radius of 3 cm.
Two tangents are drawn to the circle from an external point, and they are inclined at an angle of $60^\circ$ to each other.
To Find:
The length of each tangent.
Solution:
Let O be the centre of the circle and let P be the external point from which the tangents PA and PB are drawn to the circle.
The points A and B are the points of contact on the circle.
We are given:
Radius, $OA = OB = 3$ cm.
Angle between the tangents, $\angle APB = 60^\circ$.
Join the centre O to the external point P.
We know that the line segment joining the centre of the circle to the external point from which tangents are drawn bisects the angle between the two tangents.
Therefore, the line OP bisects the angle $\angle APB$.
$\angle OPA = \angle OPB = \frac{1}{2} \angle APB = \frac{1}{2} \times 60^\circ = 30^\circ$
Now, consider the triangle $\triangle OAP$.
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
So, the radius OA is perpendicular to the tangent PA.
$\angle OAP = 90^\circ$
This means that $\triangle OAP$ is a right-angled triangle.
We can now use trigonometric ratios to find the length of the tangent PA.
In the right-angled triangle $\triangle OAP$:
$\tan(\angle OPA) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{OA}{PA}$
Substituting the known values:
$\tan(30^\circ) = \frac{3}{PA}$
We know that the value of $\tan(30^\circ)$ is $\frac{1}{\sqrt{3}}$.
$\frac{1}{\sqrt{3}} = \frac{3}{PA}$
By cross-multiplication, we get:
$PA = 3 \times \sqrt{3}$
$PA = 3\sqrt{3}$ cm.
We also know that the lengths of tangents drawn from an external point to a circle are equal. So, $PA = PB$.
Hence, the length of each tangent is $3\sqrt{3}$ cm.
This corresponds to option (D).
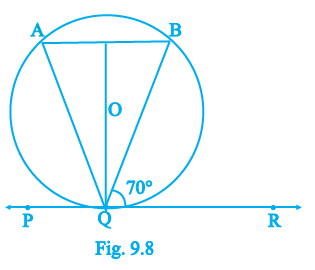
Question 10. In Fig. 9.8, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
(A) 20°
(B) 40°
(C) 35°
(D) 45°
Answer:
Given:
In the given figure, PQR is the tangent to a circle with centre O at the point of contact Q.
AB is a chord of the circle which is parallel to the tangent PR ($AB \parallel PR$).
The angle $\angle BQR = 70^\circ$.
To Find:
The measure of the angle $\angle AQB$.
Solution:
This problem can be solved by using the properties of parallel lines and the properties of chords and arcs in a circle.
Step 1: Use the property of parallel lines.
We are given that the chord AB is parallel to the tangent PR. The line segment BQ acts as a transversal intersecting these two parallel lines.
$AB \parallel PR$
(Given)
The angles $\angle ABQ$ and $\angle BQR$ are alternate interior angles. For parallel lines, alternate interior angles are equal.
$\angle ABQ = \angle BQR$
[Alternate interior angles]
Since we are given $\angle BQR = 70^\circ$, it follows that:
$\angle ABQ = 70^\circ$
... (i)
Step 2: Use the property of parallel tangent and chord.
There is a theorem in circle geometry which states that if a tangent is parallel to a chord, then the arcs intercepted between the point of tangency and the endpoints of the chord are equal.
Here, the tangent is PR (with point of tangency Q) and the parallel chord is AB. The intercepted arcs are arc AQ and arc BQ.
Therefore, according to the theorem:
arc AQ = arc BQ
Step 3: Relate equal arcs to angles in $\triangle AQB$.
Another theorem states that in a circle, equal arcs are subtended by equal chords. Since arc AQ = arc BQ, their corresponding chords must be equal.
chord AQ = chord BQ
Now, consider the triangle $\triangle AQB$. Since two of its sides are equal (AQ = BQ), it is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are also equal. The angle opposite side BQ is $\angle QAB$, and the angle opposite side AQ is $\angle ABQ$.
$\angle QAB = \angle ABQ$
From Step 1 (equation i), we found that $\angle ABQ = 70^\circ$. Therefore:
$\angle QAB = 70^\circ$
... (ii)
Step 4: Find $\angle AQB$ using the angle sum property of a triangle.
In $\triangle AQB$, the sum of the interior angles is $180^\circ$.
$\angle AQB + \angle QAB + \angle ABQ = 180^\circ$
Substituting the values from equations (i) and (ii):
$\angle AQB + 70^\circ + 70^\circ = 180^\circ$
$\angle AQB + 140^\circ = 180^\circ$
$\Rightarrow \angle AQB = 180^\circ - 140^\circ$
$\Rightarrow \angle AQB = 40^\circ$
Hence, the measure of $\angle AQB$ is $40^\circ$.
This corresponds to option (B).
Sample Question 1 & 2 (Before Exercise 9.2)
Write ‘True’ or ‘False’ and give reasons for your answer.
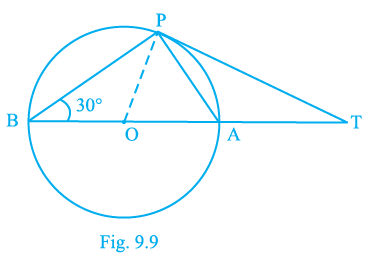
Sample Question 1: In Fig. 9.9, BOA is a diameter of a circle and the tangent at a point P meets BA extended at T. If ∠PBO = 30°, then ∠PTA is equal to 30°.
Answer:
Given:
In the given figure, BOA is a diameter of a circle with centre O.
A tangent to the circle at point P intersects the extended diameter BA at point T.
The measure of angle $\angle PBO = 30^\circ$.
To Determine:
Whether the statement "$\angle PTA = 30^\circ$" is true or false.
Solution:
Let's find the actual measure of $\angle PTA$ and compare it with the given value.
Step 1: Analyze $\triangle OPB$.
Consider the triangle $\triangle OPB$. The sides OP and OB are both radii of the same circle.
OP = OB
[Radii of the same circle]
Therefore, $\triangle OPB$ is an isosceles triangle. The angles opposite the equal sides are also equal.
$\angle OPB = \angle OBP$ (which is the same as $\angle PBO$).
Since we are given $\angle PBO = 30^\circ$, we have:
$\angle OPB = 30^\circ$.
Step 2: Find the exterior angle $\angle AOP$.
Now, consider the side BT of the triangle $\triangle OPT$. The angle $\angle AOP$ is an exterior angle to the triangle $\triangle OPB$ at vertex O.
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
$\angle AOP = \angle OBP + \angle OPB$
$\angle AOP = 30^\circ + 30^\circ = 60^\circ$.
Step 3: Analyze the right-angled triangle $\triangle OPT$.
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Here, PT is the tangent and OP is the radius at the point of contact P. Therefore, $OP \perp PT$.
$\angle OPT = 90^\circ$
This means that $\triangle OPT$ is a right-angled triangle with the right angle at P.
Step 4: Find $\angle PTA$ using the angle sum property of $\triangle OPT$.
In the right-angled triangle $\triangle OPT$, the sum of the interior angles is $180^\circ$.
$\angle POT + \angle OPT + \angle PTO = 180^\circ$
The angle $\angle POT$ is the same as the angle $\angle AOP$ which we found to be $60^\circ$.
The angle $\angle PTO$ is the same as the angle $\angle PTA$.
Substituting the known values:
$60^\circ + 90^\circ + \angle PTA = 180^\circ$
$150^\circ + \angle PTA = 180^\circ$
$\Rightarrow \angle PTA = 180^\circ - 150^\circ$
$\Rightarrow \angle PTA = 30^\circ$
The calculated value of $\angle PTA$ is $30^\circ$, which matches the value given in the statement.
Conclusion:
The statement is true.
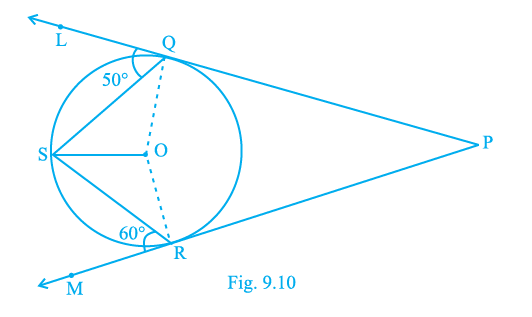
Sample Question 2: In Fig. 9.10, PQL and PRM are tangents to the circle with centre O at the points Q and R, respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then ∠QSR is equal to 40°.
Answer:
Given:
In the given figure, PQL and PRM are tangents to the circle with centre O at points Q and R respectively.
S is a point on the circle.
The angle $\angle SQL = 50^\circ$.
The angle $\angle SRM = 60^\circ$.
To Determine:
Whether the statement "$\angle QSR = 40^\circ$" is true or false.
Solution:
We will find the actual measure of $\angle QSR$ and compare it with the given value.
We will use the Alternate Segment Theorem. This theorem states that the angle between a tangent and a chord through the point of contact is equal to the angle subtended by the chord in the alternate segment.
Step 1: Apply the theorem for tangent PQL and chord SQ.
The angle between the tangent PQL and the chord SQ is $\angle SQL = 50^\circ$.
The alternate segment is the one containing the point R. The angle subtended by the chord SQ in this segment is $\angle SRQ$.
Therefore, by the Alternate Segment Theorem:
$\angle SRQ = \angle SQL = 50^\circ$
... (i)
Step 2: Apply the theorem for tangent PRM and chord SR.
The angle between the tangent PRM and the chord SR is $\angle SRM = 60^\circ$.
The alternate segment is the one containing the point Q. The angle subtended by the chord SR in this segment is $\angle SQR$.
Therefore, by the Alternate Segment Theorem:
$\angle SQR = \angle SRM = 60^\circ$
... (ii)
Step 3: Find $\angle QSR$ using the angle sum property of $\triangle QSR$.
Now, consider the triangle $\triangle QSR$. We have found two of its interior angles from the steps above:
$\angle SRQ = 50^\circ$
$\angle SQR = 60^\circ$
The sum of the interior angles of a triangle is $180^\circ$.
$\angle QSR + \angle SQR + \angle SRQ = 180^\circ$
Substituting the known values:
$\angle QSR + 60^\circ + 50^\circ = 180^\circ$
$\angle QSR + 110^\circ = 180^\circ$
$\Rightarrow \angle QSR = 180^\circ - 110^\circ$
$\Rightarrow \angle QSR = 70^\circ$
The calculated value of $\angle QSR$ is $70^\circ$.
The statement claims that $\angle QSR = 40^\circ$.
Since $70^\circ \neq 40^\circ$, the statement is incorrect.
Conclusion:
The statement is false.
Exercise 9.2
Write ‘True’ or ‘False’ and justify your answer in each of the following:
Question 1. If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
To Determine:
Whether the following statement is true or false: "If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°."
Justification:
Let O be the center of the circle and AB be the chord.
We are given that the angle subtended by the chord at the center is $\angle AOB = 60^\circ$.
Let the tangents to the circle at points A and B intersect at an external point P.
We know the theorem: "The tangent at any point of a circle is perpendicular to the radius through the point of contact."
Therefore, the radius OA is perpendicular to the tangent PA, and the radius OB is perpendicular to the tangent PB.
$\angle OAP = 90^\circ$
$\angle OBP = 90^\circ$
Now, consider the quadrilateral OAPB. The sum of the interior angles of a quadrilateral is $360^\circ$.
$\angle AOB + \angle OBP + \angle BPA + \angle OAP = 360^\circ$
Substituting the known values:
$60^\circ + 90^\circ + \angle BPA + 90^\circ = 360^\circ$
$240^\circ + \angle BPA = 360^\circ$
$\angle BPA = 360^\circ - 240^\circ = 120^\circ$
The angle between the tangents at A and B is $120^\circ$.
The statement claims the angle is $60^\circ$. Since $120^\circ \neq 60^\circ$, the statement is false.
Conclusion:
The statement is False.
Question 2. The length of tangent from an external point on a circle is always greater than the radius of the circle.
To Determine:
Whether the following statement is true or false: "The length of tangent from an external point on a circle is always greater than the radius of the circle."
Justification:
Let O be the centre of a circle with radius $r$. Let P be an external point and let PA be the tangent from P to the circle, where A is the point of contact.
The length of the tangent is PA, and the radius is $OA = r$.
We know that the radius is perpendicular to the tangent at the point of contact, so $\angle OAP = 90^\circ$. This makes $\triangle OAP$ a right-angled triangle.
By the Pythagorean theorem:
$OP^2 = OA^2 + PA^2$
$OP^2 = r^2 + PA^2$
Rearranging for the tangent length PA:
$PA^2 = OP^2 - r^2$
The statement claims that $PA > r$ is always true. This is equivalent to checking if $PA^2 > r^2$ is always true.
$OP^2 - r^2 > r^2$
$OP^2 > 2r^2$
$OP > \sqrt{2}r$
This shows that the length of the tangent (PA) is greater than the radius ($r$) only if the distance of the external point from the centre (OP) is greater than $\sqrt{2}$ times the radius. It is not always true.
Counterexample:
Let the radius of the circle be $r = 3$ cm.
Let the external point P be at a distance $OP = 4$ cm from the centre. (Note that $r < OP < \sqrt{2}r$, since $3 < 4 < 3\sqrt{2} \approx 4.24$).
Using the Pythagorean theorem, the length of the tangent is:
$PA^2 = OP^2 - r^2 = 4^2 - 3^2 = 16 - 9 = 7$
$PA = \sqrt{7} \approx 2.65$ cm.
In this case, the length of the tangent ($PA \approx 2.65$ cm) is less than the radius ($r = 3$ cm).
Since we have found a case where the tangent length is not greater than the radius, the statement is false.
Conclusion:
The statement is False.
Question 3. The length of tangent from an external point P on a circle with centre O is always less than OP.
To Determine:
Whether the following statement is true or false: "The length of tangent from an external point P on a circle with centre O is always less than OP."
Justification:
Let O be the centre of the circle and P be an external point.
Let A be the point of contact of the tangent drawn from P to the circle. The length of the tangent is PA.
OP is the distance from the centre to the external point.
We know that the radius (OA) is perpendicular to the tangent (PA) at the point of contact (A). This means that $\triangle OAP$ is a right-angled triangle, with the right angle at vertex A.
In any right-angled triangle, the side opposite the right angle is the hypotenuse, and the hypotenuse is always the longest side of the triangle.
In $\triangle OAP$, the side opposite the right angle $\angle OAP$ is OP. Therefore, OP is the hypotenuse.
Since the hypotenuse is the longest side, its length must be greater than the length of either of the other two sides (the legs).
Therefore, $OP > PA$.
This means that the length of the tangent (PA) is always less than the distance of the external point from the centre (OP).
Conclusion:
The statement is True.
Question 4. The angle between two tangents to a circle may be 0°.
To Determine:
Whether the following statement is true or false: "The angle between two tangents to a circle may be 0°."
Justification:
Let's consider the different ways two tangents can be drawn to a single circle.
Case 1: Tangents from an external point.
If two tangents are drawn from a single external point P, they intersect at P. For the angle of intersection to be $0^\circ$, the two tangent lines would have to be the same line. However, from any external point, two distinct tangents can be drawn to a circle. Since the tangents are distinct, they cannot be the same line, and the angle between them must be greater than $0^\circ$.
Case 2: Parallel tangents.
A circle can have two tangents that are parallel to each other. These tangents touch the circle at the opposite ends of a diameter. Parallel lines never intersect in Euclidean geometry. The angle between two non-intersecting parallel lines is often defined as $0^\circ$. However, the phrase "angle between two tangents" usually implies the angle at their point of intersection. Since parallel tangents do not intersect, there is no point of intersection to form an angle.
If we interpret the question in the context of tangents drawn from a single point, the angle can never be $0^\circ$. As the external point moves farther away from the circle, the angle between the tangents approaches $0^\circ$, but it never reaches it for any finite distance.
Therefore, it is not possible for the angle between two distinct intersecting tangents to be $0^\circ$.
Conclusion:
The statement is False.
Question 5. If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = a$\sqrt{2}$ .
To Determine:
Whether the following statement is true or false: "If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = a$\sqrt{2}$."
Justification:
Let the two tangents from the external point P be PA and PB, where A and B are the points of contact on the circle.
We are given:
Radius of the circle, $OA = a$.
Angle between the tangents, $\angle APB = 90^\circ$.
We know that the radius is perpendicular to the tangent at the point of contact. Therefore:
$\angle OAP = 90^\circ$
$\angle OBP = 90^\circ$
Now, consider the quadrilateral OAPB. The sum of its interior angles is $360^\circ$.
$\angle AOB + \angle OBP + \angle APB + \angle OAP = 360^\circ$
$\angle AOB + 90^\circ + 90^\circ + 90^\circ = 360^\circ$
$\angle AOB + 270^\circ = 360^\circ \implies \angle AOB = 90^\circ$
Since all four angles of the quadrilateral OAPB are $90^\circ$, it is a rectangle. Furthermore, since the adjacent sides OA and OB are both radii of length $a$, the rectangle is a square.
In the square OAPB, all sides are equal: $OA = AP = PB = BO = a$.
Now, consider the right-angled triangle $\triangle OAP$. The sides are $OA = a$ and $AP = a$. The hypotenuse is OP.
Using the Pythagorean theorem:
$OP^2 = OA^2 + AP^2$
$OP^2 = a^2 + a^2$
$OP^2 = 2a^2$
$OP = \sqrt{2a^2} = a\sqrt{2}$
The result matches the statement.
Conclusion:
The statement is True.
Question 6. If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = a$\sqrt{3}$ .
To Determine:
Whether the following statement is true or false: "If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = a$\sqrt{3}$."
Justification:
Let PA and PB be the two tangents from an external point P to a circle with centre O and radius $a$.
We are given:
Radius, $OA = a$.
Angle between the tangents, $\angle APB = 60^\circ$.
The line segment OP, which connects the centre O to the external point P, bisects the angle between the tangents, $\angle APB$.
$\angle OPA = \frac{1}{2} \angle APB = \frac{1}{2} \times 60^\circ = 30^\circ$
We also know that the radius is perpendicular to the tangent at the point of contact. Therefore, $OA \perp PA$.
$\angle OAP = 90^\circ$
Now, consider the right-angled triangle $\triangle OAP$. We can use trigonometric ratios to find the length of the hypotenuse OP.
In $\triangle OAP$:
$\sin(\angle OPA) = \frac{\text{Opposite Side}}{\text{Hypotenuse}} = \frac{OA}{OP}$
Substituting the known values:
$\sin(30^\circ) = \frac{a}{OP}$
We know that $\sin(30^\circ) = \frac{1}{2}$.
$\frac{1}{2} = \frac{a}{OP}$
By cross-multiplication, we get:
$OP = 2a$
The calculated value is $OP = 2a$. The statement claims that $OP = a\sqrt{3}$. Since $2a \neq a\sqrt{3}$, the statement is false.
(Note: The length of the tangent PA would be $a\sqrt{3}$, which can be found using $\tan(30^\circ) = \frac{OA}{PA}$.)
Conclusion:
The statement is False.
Question 7. The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
To Determine:
Whether the following statement is true or false: "The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC."
Justification:
Let XAY be the tangent to the circumcircle of $\triangle ABC$ at the vertex A.
We are given that $\triangle ABC$ is an isosceles triangle with $AB = AC$.
In $\triangle ABC$, since the sides AB and AC are equal, the angles opposite to these sides must also be equal.
$\angle ABC = \angle ACB$
[Angles opposite to equal sides] ... (i)
By the Alternate Segment Theorem, the angle between the tangent (XAY) and a chord (AC) through the point of contact (A) is equal to the angle in the alternate segment.
The angle between tangent XAY and chord AC is $\angle YAC$. The angle in the alternate segment subtended by chord AC is $\angle ABC$.
$\angle YAC = \angle ABC$
[Alternate Segment Theorem] ... (ii)
From equations (i) and (ii), we can conclude that:
$\angle YAC = \angle ACB$
Now, consider the line BC and the tangent line XAY, with AC as a transversal.
The angles $\angle YAC$ and $\angle ACB$ are a pair of alternate interior angles. Since we have proved that these angles are equal, the lines XAY and BC must be parallel.
$XAY \parallel BC$
Conclusion:
The statement is True.
Question 8. If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
To Determine:
Whether the following statement is true or false: "If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ."
Justification:
Let PQ be a given line segment and let A be a point on PQ.
Consider any circle that touches the line PQ at the point A. For this circle, the line segment PQ is a tangent at the point of contact A.
We know the theorem: "The radius of a circle is perpendicular to the tangent at the point of contact."
This means that for any circle touching PQ at A, its center must lie on the line that is perpendicular to PQ and passes through the point A.
The statement in the question claims that the centers lie on the perpendicular bisector of PQ.
The perpendicular bisector of PQ is the line that is perpendicular to PQ and passes through the midpoint of PQ.
The line on which the centers lie (the perpendicular to PQ at A) is the same as the perpendicular bisector of PQ only in the special case where the point of tangency A is also the midpoint of the line segment PQ.
Since the point A can be any point on the line segment PQ (not necessarily the midpoint), the statement is not always true.
Conclusion:
The statement is False.
Question 9. If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
To Determine:
Whether the following statement is true or false: "If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ."
Justification:
Let P and Q be the endpoints of a line segment PQ.
Consider any circle that passes through both points P and Q. Let the center of this circle be C.
Since both P and Q are points on the circle, the distance from the center C to P and the distance from the center C to Q are both equal to the radius of the circle.
Therefore, $CP = CQ$.
This means that the center C is equidistant from the two points P and Q.
The geometric definition of a perpendicular bisector of a line segment is the locus of all points that are equidistant from the two endpoints of the segment.
Since the center C of any circle passing through P and Q must be equidistant from P and Q, the center C must lie on the perpendicular bisector of the line segment PQ.
This holds true for all such circles.
Conclusion:
The statement is True.
Question 10. AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
To Determine:
Whether the statement "BC = BD" is true or false.
Justification:
Let O be the centre of the circle.
Step 1: Find the angles in $\triangle ABC$.
Since AB is a diameter, the angle subtended by it at any point on the circumference is a right angle.
$\angle ACB = 90^\circ$
[Angle in a semicircle]
In $\triangle ABC$, by the angle sum property:
$\angle ABC = 180^\circ - \angle BAC - \angle ACB = 180^\circ - 30^\circ - 90^\circ = 60^\circ$.
Step 2: Find the angles related to the tangent.
By the Alternate Segment Theorem, the angle between the tangent at C (line CD) and the chord BC is equal to the angle in the alternate segment, which is $\angle BAC$.
$\angle BCD = \angle BAC = 30^\circ$
... (i)
Step 3: Find the angles of $\triangle BCD$.
To prove that $BC = BD$, we need to show that the angles opposite to these sides in $\triangle BCD$ are equal, i.e., $\angle BDC = \angle BCD$.
Let's find the third angle of $\triangle BCD$, which is $\angle BDC$.
The angle $\angle ABC = 60^\circ$ is an exterior angle to the triangle $\triangle BCD$ at vertex B. This is incorrect. The angle inside $\triangle BCD$ is $\angle CBD$. Since A, B, and D are collinear with B between A and D, the angle $\angle CBD$ and $\angle ABC$ form a linear pair, summing to $180^\circ$.
$\angle CBD = 180^\circ - \angle ABC = 180^\circ - 60^\circ = 120^\circ$.
Now, using the angle sum property in $\triangle BCD$:
$\angle BDC = 180^\circ - \angle CBD - \angle BCD$
$\angle BDC = 180^\circ - 120^\circ - 30^\circ = 30^\circ$.
Step 4: Compare the angles and sides.
In $\triangle BCD$, we have found that:
$\angle BCD = 30^\circ$ (from Step 2)
$\angle BDC = 30^\circ$ (from Step 3)
Since two angles of the triangle are equal, the sides opposite these angles must also be equal.
The side opposite $\angle BDC$ is BC.
The side opposite $\angle BCD$ is BD.
Therefore, $BC = BD$.
Conclusion:
The statement is True.
Sample Question 1 & 2 (Before Exercise 9.3)
Sample Question 1: If d1 , d2 (d2 > d1 ) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, prove that $d_2^2 = c^2 + d_1^2$
Answer:
Given:
Two concentric circles, $C_1$ (inner) and $C_2$ (outer), with a common center O.
The diameter of the inner circle $C_1$ is $d_1$.
The diameter of the outer circle $C_2$ is $d_2$.
AB is a chord of the outer circle $C_2$ with length $c$, which is tangent to the inner circle $C_1$ at a point P.
To Prove:
$d_2^2 = c^2 + d_1^2$
Construction:
Join OA and OP.
Proof:
Let $r_1$ and $r_2$ be the radii of the inner circle ($C_1$) and the outer circle ($C_2$) respectively.
The radius is half of the diameter, so:
$r_1 = \frac{d_1}{2}$
$r_2 = \frac{d_2}{2}$
We are given that AB is a tangent to the inner circle $C_1$ at point P.
We know that the radius to the point of tangency is perpendicular to the tangent. Therefore:
$OP \perp AB$
This means that $\triangle OPA$ is a right-angled triangle with the right angle at P.
Also, the perpendicular drawn from the center of a circle to a chord bisects the chord. Since AB is a chord of the outer circle $C_2$ and $OP \perp AB$, P is the midpoint of AB.
$AP = PB = \frac{1}{2} AB = \frac{c}{2}$
Now, applying the Pythagorean theorem to the right-angled triangle $\triangle OPA$:
$OA^2 = OP^2 + AP^2$
In $\triangle OPA$:
$OA = r_2$ (radius of the outer circle)
$OP = r_1$ (radius of the inner circle)
$AP = \frac{c}{2}$
Substituting these values into the Pythagorean theorem:
$r_2^2 = r_1^2 + \left(\frac{c}{2}\right)^2$
Now, substitute the radii with their equivalent diameter expressions:
$\left(\frac{d_2}{2}\right)^2 = \left(\frac{d_1}{2}\right)^2 + \left(\frac{c}{2}\right)^2$
$\frac{d_2^2}{4} = \frac{d_1^2}{4} + \frac{c^2}{4}$
Multiply the entire equation by 4 to eliminate the denominators:
$d_2^2 = d_1^2 + c^2$
Rearranging the terms to match the statement to be proved:
$d_2^2 = c^2 + d_1^2$
Hence, Proved.
Sample Question 2: If a, b, c are the sides of a right triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r = $\frac{a \;+\; b \;-\; c}{2}$ .
Answer:
Given:
A right-angled triangle with sides $a$ and $b$, and hypotenuse $c$.
An incircle with radius $r$ touches all three sides of the triangle.
To Prove:
The inradius $r$ is given by the formula:
$r = \frac{a + b - c}{2}$
Proof:
Let the right-angled triangle be $\triangle ABC$, with the right angle at vertex C. Let the side lengths be $BC = a$, $AC = b$, and the hypotenuse $AB = c$.
Let the incircle touch the sides BC, AC, and AB at points D, E, and F respectively. Let I be the center of the incircle (the incenter).
The radius of the incircle is $r$. Thus, $ID = IE = IF = r$.
The radius to the point of tangency is perpendicular to the tangent. Therefore, $ID \perp BC$ and $IE \perp AC$.
Now, consider the quadrilateral CDIE.
$\angle C = 90^\circ$
(Given)
$\angle IDC = 90^\circ$
(Radius is perpendicular to tangent)
$\angle IEC = 90^\circ$
(Radius is perpendicular to tangent)
Since three angles are $90^\circ$, the fourth angle $\angle DIE$ must also be $90^\circ$. Also, the adjacent sides are equal ($CD=CE=r$ is shown below, but more directly $ID=IE=r$). Therefore, CDIE is a square with side length $r$.
This implies $CD = r$ and $CE = r$.
A key property of circles is that the lengths of the two tangents drawn from an external point to a circle are equal.
From vertex A: $AE = AF$.
From vertex B: $BD = BF$.
Now we can express the lengths of the sides in terms of these segments:
Side $a = BC = BD + CD = BD + r \implies BD = a - r$.
Side $b = AC = AE + CE = AE + r \implies AE = b - r$.
The hypotenuse $c = AB = AF + BF$.
Substituting $AF = AE$ and $BF = BD$ into the equation for the hypotenuse:
$c = AE + BD$
Now substitute the expressions for AE and BD in terms of $a, b,$ and $r$:
$c = (b - r) + (a - r)$
$c = a + b - 2r$
Rearranging this equation to solve for $r$:
$2r = a + b - c$
$r = \frac{a + b - c}{2}$
Hence, Proved.
Alternate Solution
This can also be proved using the area of the triangle.
The area of a right-angled triangle with legs $a$ and $b$ is:
Area = $\frac{1}{2}ab$
... (i)
The area of any triangle can also be expressed in terms of its inradius $r$ and semi-perimeter $s$, where $s = \frac{a+b+c}{2}$.
Area = $r \cdot s = r \left( \frac{a+b+c}{2} \right)$
... (ii)
Equating the two expressions for the area from (i) and (ii):
$\frac{1}{2}ab = r \left( \frac{a+b+c}{2} \right)$
Multiply both sides by 2:
$ab = r(a+b+c)$
$r = \frac{ab}{a+b+c}$
To show this is equivalent to the required expression, we multiply the numerator and denominator by $(a+b-c)$:
$r = \frac{ab(a+b-c)}{(a+b+c)(a+b-c)} = \frac{ab(a+b-c)}{(a+b)^2 - c^2}$
$r = \frac{ab(a+b-c)}{a^2 + b^2 + 2ab - c^2}$
By the Pythagorean theorem, $a^2 + b^2 = c^2$, so $a^2 + b^2 - c^2 = 0$.
$r = \frac{ab(a+b-c)}{2ab} = \frac{\cancel{ab}(a+b-c)}{2\cancel{ab}}$
$r = \frac{a+b-c}{2}$
Hence, Proved.
Exercise 9.3
Question 1. Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Answer:
Given:
Two concentric circles with a common center, let's say O.
Radius of the outer circle, $R = 5$ cm.
A chord of the outer circle, AC, has a length of $8$ cm.
This chord AC is a tangent to the inner circle.
To Find:
The radius of the inner circle, let's call it $r$.
Solution:
Let the chord AC touch the inner circle at point M.
According to the properties of circles, the radius to the point of tangency is perpendicular to the tangent. Therefore, the radius of the inner circle, OM, is perpendicular to the chord AC.
$OM \perp AC$
Another property of circles is that a perpendicular drawn from the center of a circle to a chord bisects the chord. Since OM is perpendicular to the chord AC of the outer circle, M must be the midpoint of AC.
$AM = MC = \frac{1}{2} AC$
Given that the length of the chord AC is 8 cm:
$AM = \frac{1}{2} \times 8 = 4$ cm
Now, consider the triangle $\triangle OMA$.
OA is the radius of the outer circle, so $OA = R = 5$ cm.
OM is the radius of the inner circle, so $OM = r$.
AM is half the length of the chord, so $AM = 4$ cm.
Since $OM \perp AC$, $\triangle OMA$ is a right-angled triangle with the right angle at M.
By applying the Pythagorean theorem to $\triangle OMA$:
$OA^2 = OM^2 + AM^2$
Substitute the known values:
$5^2 = r^2 + 4^2$
$25 = r^2 + 16$
Solve for $r^2$:
$r^2 = 25 - 16 = 9$
Take the square root to find $r$ (radius must be a positive value):
$r = \sqrt{9} = 3$ cm
Final Answer:
The radius of the inner circle is 3 cm.
Question 2. Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Answer:
Given:
A circle with centre O.
An external point P from which two tangents, PQ and PR, are drawn to the circle.
Q and R are the points of tangency on the circle.
To Prove:
The quadrilateral QORP is a cyclic quadrilateral.
Proof:
A quadrilateral is cyclic if the sum of a pair of its opposite angles is $180^\circ$.
OQ is the radius of the circle at the point of tangency Q. According to the tangent-radius theorem, the radius at the point of contact is perpendicular to the tangent.
$OQ \perp PQ$
Therefore, the angle between the radius and the tangent is $90^\circ$.
$\angle OQP = 90^\circ$
... (i)
Similarly, OR is the radius of the circle at the point of tangency R.
$OR \perp PR$
Therefore, the angle between the radius and the tangent is $90^\circ$.
$\angle ORP = 90^\circ$
... (ii)
Now, consider the quadrilateral QORP. The sum of its interior angles is $360^\circ$.
$\angle QOR + \angle ORP + \angle RPQ + \angle PQO = 360^\circ$
Substituting the values from (i) and (ii):
$\angle QOR + 90^\circ + \angle RPQ + 90^\circ = 360^\circ$
$\angle QOR + \angle RPQ + 180^\circ = 360^\circ$
$\angle QOR + \angle RPQ = 360^\circ - 180^\circ$
$\angle QOR + \angle RPQ = 180^\circ$
Since the sum of the pair of opposite angles ($\angle QOR$ and $\angle RPQ$) of the quadrilateral QORP is $180^\circ$, the quadrilateral is cyclic.
Hence Proved.
Question 3. If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
Answer:
Given:
A circle with centre O.
An external point B from which two tangents, BC and BD, are drawn to the circle.
The angle between the tangents, $\angle DBC = 120^\circ$.
To Prove:
$BC + BD = BO$, which is equivalent to proving $BO = 2BC$.
Proof:
First, we use the property that tangents drawn from an external point to a circle are equal in length.
$BC = BD$
... (i)
Next, the line segment joining the centre of the circle to the external point (BO) bisects the angle between the two tangents.
$\angle OBC = \angle OBD = \frac{1}{2} \angle DBC$
Substituting the given value $\angle DBC = 120^\circ$:
$\angle OBC = \frac{1}{2} \times 120^\circ = 60^\circ$
Now, consider the triangle $\triangle OBC$. OC is the radius at the point of tangency C. The radius is perpendicular to the tangent at the point of contact.
$OC \perp BC$
Therefore, $\triangle OBC$ is a right-angled triangle with $\angle OCB = 90^\circ$.
In the right-angled $\triangle OBC$, we can use trigonometric ratios. We want to relate the side BC (adjacent to the $60^\circ$ angle) and the hypotenuse BO.
$\cos(\angle OBC) = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{BC}{BO}$
Substitute the value of the angle:
$\cos(60^\circ) = \frac{BC}{BO}$
We know that $\cos(60^\circ) = \frac{1}{2}$.
$\frac{1}{2} = \frac{BC}{BO}$
By cross-multiplication, we get:
$BO = 2BC$
... (ii)
This proves the second part of the statement.
Now, let's prove the first part, $BC + BD = BO$.
From (i), we know $BC = BD$. So, we can write:
$BC + BD = BC + BC = 2BC$
From (ii), we have proved that $BO = 2BC$.
Therefore, by substituting $2BC$ with $BO$, we get:
$BC + BD = BO$
Hence Proved.
Question 4. Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
Answer:
Given:
Two lines, $l_1$ and $l_2$, intersect at a point P.
A circle with centre O touches the line $l_1$ at point A and the line $l_2$ at point B.
To Prove:
The centre of the circle, O, lies on the angle bisector of the angle formed by the intersection of lines $l_1$ and $l_2$.
Construction:
Join OA, OB, and OP.
Proof:
Since the circle is tangent to line $l_1$ at point A, the radius OA is perpendicular to the tangent line $l_1$ at the point of contact.
$OA \perp l_1 \implies \angle OAP = 90^\circ$
Similarly, since the circle is tangent to line $l_2$ at point B, the radius OB is perpendicular to the tangent line $l_2$ at the point of contact.
$OB \perp l_2 \implies \angle OBP = 90^\circ$
Now, consider the two triangles $\triangle OAP$ and $\triangle OBP$.
$OA = OB$
(Radii of the same circle)
$OP = OP$
(Common hypotenuse)
$\angle OAP = \angle OBP = 90^\circ$
(Proved above)
By the RHS (Right angle-Hypotenuse-Side) congruence criterion, the two triangles are congruent.
$\triangle OAP \cong \triangle OBP$
Since the triangles are congruent, their corresponding parts must be equal (CPCTC).
Therefore, the angle $\angle OPA$ is equal to the angle $\angle OPB$.
$\angle OPA = \angle OPB$
(By CPCTC)
This means that the line segment OP bisects the angle $\angle APB$, which is the angle formed by the intersection of lines $l_1$ and $l_2$.
Since the centre O lies on the line OP, it lies on the angle bisector of the two intersecting lines.
Hence Proved.
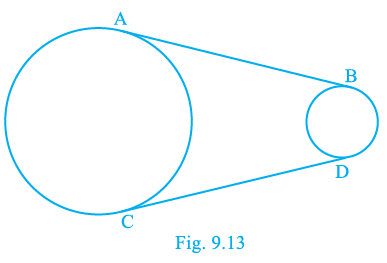
Question 5. In Fig. 9.13, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
Answer:
Given:
Two circles with unequal radii.
AB and CD are two common tangents to these circles.
To Prove:
The lengths of the two common tangents are equal, i.e., $AB = CD$.
Construction:
Produce the non-parallel tangents AB and CD to intersect at a point P.
Proof:
We know that the lengths of the two tangents drawn from an external point to a circle are equal.
Let's consider the larger circle. From the external point P, two tangents PA and PC are drawn to this circle.
Therefore, their lengths must be equal.
$PA = PC$
(Tangents from P to the larger circle) ... (i)
Now, let's consider the smaller circle. From the same external point P, two tangents PB and PD are drawn to this circle.
Therefore, their lengths must also be equal.
$PB = PD$
(Tangents from P to the smaller circle) ... (ii)
We want to prove that $AB = CD$.
From the figure, we can express the length of the segment AB as the difference between PA and PB.
$AB = PA - PB$
Similarly, we can express the length of the segment CD as the difference between PC and PD.
$CD = PC - PD$
We can prove the required statement by subtracting equation (ii) from equation (i).
Subtracting the corresponding sides:
$PA - PB = PC - PD$
From our observations from the figure, $PA - PB = AB$ and $PC - PD = CD$.
Substituting these into the equation:
$AB = CD$
Thus, the lengths of the two common tangents are equal.
Hence, Proved.
Question 6. In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Answer:
Given:
Two circles with equal radii.
AB and CD are two common tangents to these circles.
To Prove:
$AB = CD$.
Construction:
Let the centers of the two circles be $O_1$ and $O_2$, and let the equal radius be $r$.
Join the centers to the points of contact. That is, join $O_1$ to A and C, and join $O_2$ to B and D.
Proof:
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
For the tangent AB:
$O_1A \perp AB \implies \angle O_1AB = 90^\circ$
$O_2B \perp AB \implies \angle O_2BA = 90^\circ$
Since both $O_1A$ and $O_2B$ are perpendicular to the same line AB, they are parallel to each other.
$O_1A \parallel O_2B$.
Now, consider the quadrilateral $ABO_2O_1$.
We have $O_1A \parallel O_2B$ (proved above) and $O_1A = O_2B = r$ (given that radii are equal).
A quadrilateral with one pair of opposite sides that are both equal and parallel is a parallelogram.
Furthermore, since this parallelogram has a right angle ($\angle O_1AB = 90^\circ$), it must be a rectangle.
In a rectangle, opposite sides are equal in length. Therefore:
$AB = O_1O_2$
(Distance between the centers) ... (i)
Now, we apply the same logic to the common tangent CD.
For the tangent CD:
$O_1C \perp CD \implies \angle O_1CD = 90^\circ$
$O_2D \perp CD \implies \angle O_2DC = 90^\circ$
Consider the quadrilateral $CDO_2O_1$.
We have $O_1C \parallel O_2D$ (both perpendicular to CD) and $O_1C = O_2D = r$.
Therefore, $CDO_2O_1$ is also a parallelogram with a right angle, which makes it a rectangle.
In this rectangle, the opposite sides are equal:
$CD = O_1O_2$
(Distance between the centers) ... (ii)
From equations (i) and (ii), we can see that both AB and CD are equal to the distance between the centers, $O_1O_2$.
Therefore, $AB = CD$.
Note on the method used in Question 5:
When the radii of the two circles are equal, the direct common tangents (AB and CD) become parallel to the line segment joining the centers ($O_1O_2$). Consequently, the tangents AB and CD are parallel to each other and will never intersect. The proof used in Question 5, which involves producing the tangents to meet at an external point P, is only valid for circles with unequal radii where the tangents are not parallel.
Hence, Proved.
Question 7. In Fig. 9.14, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.

Answer:
Given:
Two circles with common tangents AB and CD.
The tangents intersect at an external point E.
To Prove:
The lengths of the chords formed by the points of tangency are equal, i.e., $AB = CD$.
Proof:
We will use the theorem that states that the lengths of the two tangents drawn from an external point to a single circle are equal.
Let's consider the first circle (the one on the left in the figure).
From the external point E, two tangents are drawn to this circle: EA and EC.
According to the theorem, their lengths must be equal.
$EA = EC$
(Tangents from E to the first circle) ... (i)
Now, let's consider the second circle (the one on the right).
From the same external point E, two tangents are drawn to this circle: EB and ED.
According to the same theorem, their lengths must also be equal.
$EB = ED$
(Tangents from E to the second circle) ... (ii)
We are asked to prove that $AB = CD$.
From the figure, we can see that the length of the tangent segment AB is the sum of the lengths of AE and EB.
$AB = AE + EB$
Similarly, the length of the tangent segment CD is the sum of the lengths of CE and ED.
$CD = CE + ED$
From our results in equations (i) and (ii), we know that $AE = CE$ and $EB = ED$.
Let's start with the expression for AB:
$AB = AE + EB$
Substitute $AE$ with $CE$ (from eq. i) and $EB$ with $ED$ (from eq. ii):
$AB = CE + ED$
We know that $CE + ED = CD$.
Therefore, we can conclude that:
$AB = CD$
Hence, Proved.
Question 8. A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Answer:
Given:
A circle with a chord PQ.
A tangent, let's call it $L$, is drawn at a point R on the circle.
The chord PQ is parallel to the tangent $L$.
To Prove:
The point R bisects the arc PRQ. This means that arc PR is equal to arc RQ.
($\text{arc } PR = \text{arc } RQ$)
Construction:
Join the points P and R to form the chord PR. Join the points Q and R to form the chord QR.
Proof:
Let the tangent line at R be denoted by XY.
We are given that the chord PQ is parallel to the tangent XY.
$PQ \parallel XY$
Consider the transversal line PR that intersects the parallel lines PQ and XY.
The alternate interior angles are equal.
$\angle PQR = \angle QRY$
(Alternate interior angles)
Now, we use the Alternate Segment Theorem. This theorem states that the angle between a tangent and a chord through the point of contact is equal to the angle subtended by the chord in the alternate segment.
The angle between the tangent XY and the chord QR at the point of contact R is $\angle QRY$. The angle subtended by the chord QR in the alternate segment is $\angle QPR$.
$\angle QRY = \angle QPR$
(Alternate Segment Theorem)
From the two equations above, we have:
$\angle PQR = \angle QPR$
Now, consider the triangle $\triangle PQR$. We have shown that two of its angles, $\angle PQR$ and $\angle QPR$, are equal.
In a triangle, the sides opposite to equal angles are equal in length.
The side opposite to $\angle QPR$ is QR.
The side opposite to $\angle PQR$ is PR.
Therefore, $PR = QR$.
A property of circles is that equal chords subtend equal arcs. Since the chords PR and QR are equal, the corresponding minor arcs PR and QR are also equal.
$\text{arc } PR = \text{arc } QR$
This shows that the point R bisects the arc PRQ.
Hence Proved.
Question 9. Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Answer:
Given:
A circle with a chord AB.
Two tangents are drawn at the endpoints of the chord, A and B. Let these tangents intersect at a point P.
To Prove:
The tangents at A and B make equal angles with the chord AB.
We need to prove that $\angle PAB = \angle PBA$.
Proof 1: Using Properties of Tangents and Triangles
Consider the triangle $\triangle PAB$ formed by the chord and the two tangents.
We know that the lengths of the two tangents drawn from an external point to a circle are equal.
In this case, PA and PB are tangents from the external point P.
$PA = PB$
Since two sides of $\triangle PAB$ are equal, it is an isosceles triangle.
In an isosceles triangle, the angles opposite to the equal sides are also equal.
The angle opposite to side PB is $\angle PAB$.
The angle opposite to side PA is $\angle PBA$.
Therefore:
$\angle PAB = \angle PBA$
This proves that the angles made by the tangents with the chord are equal.
Proof 2: Using the Alternate Segment Theorem
Let the tangent at A be $L_1$ and the tangent at B be $L_2$.
By the Alternate Segment Theorem, the angle between the tangent at A ($L_1$) and the chord AB is equal to the angle subtended by the chord AB in the alternate (major) segment.
Let C be any point on the major arc AB.
Angle between $L_1$ and AB = $\angle ACB$
Similarly, the angle between the tangent at B ($L_2$) and the chord AB is also equal to the angle subtended by the chord AB in the alternate (major) segment.
Angle between $L_2$ and AB = $\angle ACB$
Since both angles are equal to $\angle ACB$, they are equal to each other.
Angle between $L_1$ and AB = Angle between $L_2$ and AB
Hence Proved.
Question 10. Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Answer:
Given:
A circle with centre O and diameter AB.
A tangent line, let's call it $L$, is drawn to the circle at point A.
A chord CD is drawn in the circle such that it is parallel to the tangent $L$.
To Prove:
The diameter AB bisects the chord CD. (i.e., $CM = MD$).
Proof:
The tangent $L$ touches the circle at point A.
The line segment OA is the radius at the point of contact A, and it lies on the diameter AB.
According to the tangent-radius theorem, the radius at the point of contact is perpendicular to the tangent.
$OA \perp L$
Since OA is part of the diameter AB, we can say:
$AB \perp L$
We are given that the chord CD is parallel to the tangent $L$.
$CD \parallel L$
Since AB is perpendicular to $L$ and CD is parallel to $L$, it follows that AB must also be perpendicular to CD.
$AB \perp CD$
Let the point of intersection of the diameter AB and the chord CD be M.
The line segment OM, which is part of the diameter AB, is a line from the center O that is perpendicular to the chord CD.
A fundamental property of circles states that a perpendicular line drawn from the center of a circle to a chord bisects the chord.
Therefore, the line OM bisects the chord CD at point M.
This means $CM = MD$.
Since CD was an arbitrary chord parallel to the tangent at A, this property holds for all such chords.
Hence Proved.
Sample Question 1 & 2 (Before Exercise 9.4)
Sample Question 1: In Fig. 9.15, from an external point P, a tangent PT and a line segment PAB is drawn to a circle with centre O. ON is perpendicular on the chord AB. Prove that :
(i) PA . PB = PN2 – AN2
(ii) PN2 – AN2 = OP2 – OT2
(iii) PA.PB = PT2

Answer:
Given:
A circle with centre O.
An external point P.
A tangent PT from P to the circle at point T.
A secant PAB intersecting the circle at points A and B.
$ON \perp AB$.
To Prove:
(i) $PA \cdot PB = PN^2 – AN^2$
(ii) $PN^2 – AN^2 = OP^2 – OT^2$
(iii) $PA \cdot PB = PT^2$
Proof:
(i) Prove that $PA \cdot PB = PN^2 – AN^2$
From the figure, we can express PA and PB in terms of PN and AN/BN.
$PA = PN - AN$
$PB = PN + BN$
Since ON is a perpendicular from the center to the chord AB, it bisects the chord.
$AN = BN$
(Perpendicular from center bisects the chord)
Substitute BN with AN in the expression for PB:
$PB = PN + AN$
Now, let's find the product $PA \cdot PB$:
$PA \cdot PB = (PN - AN)(PN + AN)$
Using the algebraic identity $(x-y)(x+y) = x^2 - y^2$, we get:
$PA \cdot PB = PN^2 - AN^2$
Hence, part (i) is proved.
(ii) Prove that $PN^2 – AN^2 = OP^2 – OT^2$
Consider the right-angled triangle $\triangle ONP$ (since $ON \perp AB$, hence $ON \perp PN$).
By the Pythagorean theorem:
$OP^2 = ON^2 + PN^2 \implies PN^2 = OP^2 - ON^2$
Now, consider the right-angled triangle $\triangle ONA$ (since $ON \perp AB$, hence $ON \perp AN$).
By the Pythagorean theorem:
$OA^2 = ON^2 + AN^2$
Let's evaluate the expression $PN^2 - AN^2$ by substituting the expression for $PN^2$:
$PN^2 - AN^2 = (OP^2 - ON^2) - AN^2$
$PN^2 - AN^2 = OP^2 - (ON^2 + AN^2)$
From the Pythagorean theorem on $\triangle ONA$, we know $ON^2 + AN^2 = OA^2$.
$PN^2 - AN^2 = OP^2 - OA^2$
OA and OT are both radii of the same circle, so $OA = OT$.
$PN^2 - AN^2 = OP^2 - OT^2$
Hence, part (ii) is proved.
(iii) Prove that $PA \cdot PB = PT^2$
This is the Tangent-Secant Theorem.
From the result of part (i), we have:
$PA \cdot PB = PN^2 - AN^2$
From the result of part (ii), we have:
$PN^2 - AN^2 = OP^2 - OT^2$
Combining these two results, we get:
$PA \cdot PB = OP^2 - OT^2$
Now, consider the triangle $\triangle OTP$.
Since PT is a tangent to the circle at point T, the radius OT is perpendicular to the tangent PT.
$\angle OTP = 90^\circ$
By applying the Pythagorean theorem to the right-angled $\triangle OTP$:
$OP^2 = OT^2 + PT^2$
Rearranging this to get an expression for $PT^2$:
$PT^2 = OP^2 - OT^2$
Comparing this with our expression for $PA \cdot PB$, we see they are equal.
$PA \cdot PB = PT^2$
Hence, part (iii) is proved.
Sample Question 2: If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively, prove that AQ = $\frac{1}{2}$ (BC + CA + AB)
Answer:
Given:
A triangle $\triangle ABC$.
A circle touches the side BC at point P.
The same circle touches the extended side AB at point Q and the extended side AC at point R.
To Prove:
The length of the tangent from vertex A to the circle is half the perimeter of the triangle ABC.
$AQ = \frac{1}{2} (BC + CA + AB)$
Proof:
We will use the theorem that states: "The lengths of the two tangents drawn from an external point to a circle are equal."
Applying this theorem to the given figure:
1. From the external point A, the tangents to the circle are AQ and AR.
$AQ = AR$
... (i)
2. From the external point B, the tangents to the circle are BQ and BP.
$BQ = BP$
... (ii)
3. From the external point C, the tangents to the circle are CR and CP.
$CR = CP$
... (iii)
Now, let's consider the perimeter of the triangle $\triangle ABC$.
Perimeter of $\triangle ABC = AB + BC + CA$
From the figure, we can write the side BC as the sum of BP and PC.
Perimeter = $AB + (BP + PC) + CA$
Using the results from (ii) and (iii), we can substitute $BP$ with $BQ$ and $PC$ with $CR$.
Perimeter = $AB + BQ + CR + CA$
Rearranging the terms:
Perimeter = $(AB + BQ) + (CA + CR)$
From the figure, we can see that $AB + BQ = AQ$ and $CA + CR = AR$.
Perimeter = $AQ + AR$
From our first result (i), we know that $AQ = AR$. So we can replace AR with AQ.
Perimeter = $AQ + AQ$
Perimeter = $2 \cdot AQ$
Substituting the full expression for the perimeter:
$AB + BC + CA = 2 \cdot AQ$
Dividing both sides by 2, we get the desired result:
$AQ = \frac{1}{2} (AB + BC + CA)$
Hence, Proved.
Exercise 9.4
Question 1. If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
Answer:
Given:
A hexagon ABCDEF circumscribes a circle. This means each side of the hexagon is tangent to the circle.
To Prove:
The sum of alternate sides are equal.
$AB + CD + EF = BC + DE + FA$
Proof:
Let the points of tangency on the sides AB, BC, CD, DE, EF, and FA be P, Q, R, S, T, and U, respectively.
According to the theorem that states the lengths of tangents drawn from an external point to a circle are equal, we can write the following relationships:
$AP = AU$
... (i)
$BP = BQ$
... (ii)
$CR = CQ$
... (iii)
$DR = DS$
... (iv)
$ET = ES$
... (v)
$FT = FU$
... (vi)
Now, let's consider the Left Hand Side (LHS) of the equation we need to prove:
LHS = $AB + CD + EF$
We can express each side as the sum of its tangent segments:
LHS = $(AP + PB) + (CR + RD) + (ET + TF)$
Now, substitute the equal tangent segments using the equations (i) to (vi):
LHS = $(AU + BQ) + (CQ + DS) + (ES + FU)$
Rearrange the terms to group them in a way that forms the sides on the Right Hand Side (RHS):
LHS = $(BQ + CQ) + (DS + ES) + (FU + AU)$
Now, recognize these grouped segments as the sides of the hexagon:
$BQ + CQ = BC$
$DS + ES = DE$
$FU + AU = FA$
Substituting these back into the expression for the LHS:
LHS = $BC + DE + FA$
This is exactly the Right Hand Side (RHS) of the equation.
Therefore, $AB + CD + EF = BC + DE + FA$.
Hence Proved.
Question 2. Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
Answer:
Given:
A triangle $\triangle ABC$ with side lengths $BC = a$, $CA = b$, and $AB = c$.
The semi-perimeter of the triangle is $s = \frac{a+b+c}{2}$.
An incircle (a circle inscribed within the triangle) touches the sides BC, CA, and AB at points D, E, and F, respectively.
To Prove:
The length of the tangent segment from vertex B to the incircle is equal to the semi-perimeter minus the length of the side opposite to B.
$BD = s – b$
Proof:
According to the theorem that tangents from an external point to a circle are equal in length, we have:
$AF = AE$
... (i)
$BF = BD$
... (ii)
$CD = CE$
... (iii)
The perimeter of the triangle is the sum of its sides:
Perimeter = $AB + BC + CA$
We can express the sides as the sum of the tangent segments:
Perimeter = $(AF + FB) + (BD + DC) + (CE + EA)$
Using the equalities from (i), (ii), and (iii), we can group the like terms:
Perimeter = $(AF + AE) + (BF + BD) + (CD + CE)$
Perimeter = $2AE + 2BD + 2CD$
The semi-perimeter, $s$, is half of the perimeter:
$s = \frac{2AE + 2BD + 2CD}{2} = AE + BD + CD$
... (iv)
We want to find an expression for BD. From equation (iv), we can write:
$BD = s - (AE + CD)$
From the equalities of tangents (i) and (iii), we know $AE = AF$ and $CD = CE$. We need to relate $(AE+CD)$ to side $b$. Let's use $CD = CE$.
$BD = s - (AE + CE)$
From the figure, the side $CA$ (with length $b$) is the sum of the segments $AE$ and $CE$.
$AC = AE + CE = b$
Substituting this into our expression for BD:
$BD = s - AC = s - b$
Hence Proved.
Question 3. From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
Answer:
Given:
A circle with centre O.
An external point P from which two tangents, PA and PB, are drawn to the circle.
The length of the tangent $PA = 10$ cm.
A third tangent is drawn at a point E on the circle, intersecting PA at C and PB at D.
To Find:
The perimeter of the triangle $\triangle PCD$.
Solution:
The perimeter of $\triangle PCD$ is the sum of the lengths of its three sides: $PC + CD + DP$.
Perimeter($\triangle PCD$) = $PC + CD + DP$
The side CD can be expressed as the sum of the segments CE and ED.
$CD = CE + ED$
So, the perimeter becomes:
Perimeter($\triangle PCD$) = $PC + (CE + ED) + DP$
We use the property that the lengths of tangents from an external point to a circle are equal.
1. For the external point C, the tangents are CA and CE.
$CA = CE$
... (i)
2. For the external point D, the tangents are DB and DE.
$DB = DE$
... (ii)
Substitute these into the perimeter equation:
Perimeter($\triangle PCD$) = $PC + (CA + DB) + DP$
Now, rearrange the terms:
Perimeter($\triangle PCD$) = $(PC + CA) + (DP + DB)$
From the figure, we can see that:
$PC + CA = PA$
$DP + DB = PB$
So, the perimeter is:
Perimeter($\triangle PCD$) = $PA + PB$
3. For the external point P, the tangents are PA and PB.
$PA = PB$
We are given that $PA = 10$ cm. Therefore, $PB = 10$ cm.
Now, substitute the lengths of PA and PB into the perimeter formula:
Perimeter($\triangle PCD$) = $10 \text{ cm} + 10 \text{ cm} = 20$ cm
Final Answer:
The perimeter of the triangle PCD is 20 cm.
Question 4. If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in Fig. 9.17. Prove that ∠BAT = ∠ACB
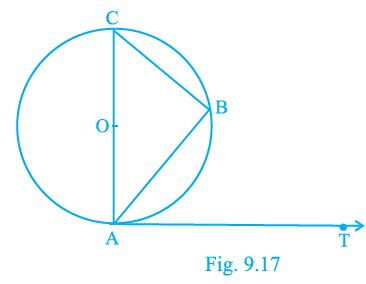
Answer:
Given:
A circle with centre O.
AB is a chord of the circle.
AOC is a diameter of the circle.
AT is the tangent to the circle at point A.
To Prove:
$\angle BAT = \angle ACB$
Proof:
We are given that AOC is a diameter and AT is the tangent at point A.
We know that the radius (or diameter) is perpendicular to the tangent at the point of contact.
$OA \perp AT$
Therefore, the angle between the diameter and the tangent is $90^\circ$.
$\angle CAT = 90^\circ$
From the figure, we can express $\angle CAT$ as the sum of two angles:
$\angle CAT = \angle CAB + \angle BAT$
Substituting $\angle CAT = 90^\circ$:
$90^\circ = \angle CAB + \angle BAT$
Rearranging this equation to find an expression for $\angle BAT$:
$\angle BAT = 90^\circ - \angle CAB$
... (i)
Now, consider the triangle $\triangle ABC$.
Since AOC is a diameter, the angle subtended by the diameter at any point on the circumference is a right angle ($90^\circ$).
Therefore, the angle at vertex B is $90^\circ$.
$\angle ABC = 90^\circ$
(Angle in a semicircle)
The sum of the angles in any triangle is $180^\circ$.
In $\triangle ABC$:
$\angle CAB + \angle ABC + \angle BCA = 180^\circ$
Substitute $\angle ABC = 90^\circ$:
$\angle CAB + 90^\circ + \angle ACB = 180^\circ$
Rearranging this equation to find an expression for $\angle ACB$:
$\angle ACB = 180^\circ - 90^\circ - \angle CAB$
$\angle ACB = 90^\circ - \angle CAB$
... (ii)
Now, comparing the expressions for $\angle BAT$ from equation (i) and for $\angle ACB$ from equation (ii), we see that they are identical.
From (i) and (ii), we can conclude that:
$\angle BAT = \angle ACB$
This is a specific case of the Alternate Segment Theorem.
Hence, Proved.
Question 5. Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
Answer:
Given:
Two circles with centres O and O' intersect at two points P and Q.
Radius of the circle with centre O, $r_1 = 3$ cm.
Radius of the circle with centre O', $r_2 = 4$ cm.
The radius of the first circle, OP, is a tangent to the second circle at point P.
The radius of the second circle, O'P, is a tangent to the first circle at point P.
To Find:
The length of the common chord PQ.
Solution:
Since OP is a tangent to the circle with centre O' at point P, the radius O'P must be perpendicular to the tangent OP at the point of contact.
$\text{O'P} \perp \text{OP}$
This means that the angle between the two radii at the point of intersection is $90^\circ$.
$\angle OPO' = 90^\circ$
Therefore, the triangle $\triangle OPO'$ is a right-angled triangle, with the right angle at P.
The sides of this triangle are OP (radius of first circle), O'P (radius of second circle), and OO' (the distance between the centers).
We are given:
$OP = r_1 = 3$ cm
$O'P = r_2 = 4$ cm
We can find the distance between the centers, OO', using the Pythagorean theorem in $\triangle OPO'$:
$(OO')^2 = OP^2 + (O'P)^2$
$(OO')^2 = 3^2 + 4^2 = 9 + 16 = 25$
$OO' = \sqrt{25} = 5$ cm
Now, we need to find the length of the common chord PQ. A property of intersecting circles is that the line segment connecting their centers (OO') is the perpendicular bisector of their common chord (PQ).
Let the intersection point of OO' and PQ be M. Then, $OM \perp PQ$ and $PM = MQ$.
The length of the common chord is $PQ = 2 \times PM$.
In the right-angled triangle $\triangle OPO'$, PM is the altitude from the right-angle vertex P to the hypotenuse OO'.
The area of $\triangle OPO'$ can be calculated in two ways:
Area = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times OP \times O'P$
Area = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times OO' \times PM$
Equating these two expressions for the area:
$OP \times O'P = OO' \times PM$
Substitute the known lengths:
$3 \times 4 = 5 \times PM$
$12 = 5 \times PM$
$PM = \frac{12}{5} = 2.4$ cm
The length of the common chord PQ is twice the length of PM:
$PQ = 2 \times PM = 2 \times 2.4 = 4.8$ cm
Final Answer:
The length of the common chord PQ is 4.8 cm.
Question 6. In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
Answer:
Given:
A right-angled triangle $\triangle ABC$ with $\angle B = 90^\circ$.
A circle is drawn with side AB as its diameter.
This circle intersects the hypotenuse AC at a point P.
A tangent is drawn to the circle at point P, and it intersects the side BC at a point Q.
To Prove:
The tangent at P bisects the side BC. That is, Q is the midpoint of BC ($BQ = QC$).
Construction:
Join B and P.
Proof:
Since AB is the diameter of the circle, the angle subtended by the diameter at any point on the circumference is a right angle ($90^\circ$).
Therefore, the angle at P, $\angle APB$, must be $90^\circ$.
$BP \perp AC$
(Angle in a semicircle)
Now, consider the tangent PQ and the chord PB of the circle.
From the property of tangents, the length of tangents from an external point to a circle are equal.
From the external point Q, the tangents to the circle are QP and QB (since $\triangle ABC$ is right-angled at B, BC is tangent to the circle at B).
$QB = QP$
(Tangents from Q) ... (i)
Since $QB = QP$, the triangle $\triangle QBP$ is an isosceles triangle. Therefore, the angles opposite to these equal sides are equal.
$\angle QPB = \angle QBP$
... (ii)
In the right-angled triangle $\triangle ABC$, the sum of the acute angles is $90^\circ$.
$\angle BAC + \angle BCA = 90^\circ$
... (iii)
Also, in the right-angled triangle $\triangle BPC$ (since $BP \perp AC$), the sum of the acute angles is $90^\circ$.
$\angle PBC + \angle PCB = 90^\circ$
Since $\angle PCB$ is the same as $\angle BCA$, we have:
$\angle PBC + \angle BCA = 90^\circ$
... (iv)
Comparing equations (iii) and (iv), we get:
$\angle BAC = \angle PBC$
Also, $\angle QBP$ is the same as $\angle PBC$. So, $\angle QBP = \angle BAC$.
From (ii), we have $\angle QPB = \angle QBP$. Therefore, $\angle QPB = \angle BAC$.
Now consider $\triangle QPC$. We have $\angle QCP = \angle BCA$.
The exterior angle $\angle BQP$ of $\triangle QPC$ is equal to the sum of the interior opposite angles.
$\angle BQP = \angle QCP + \angle QPC$. (This approach is complex)
Let's use the angles in $\triangle QPC$.
We know $\angle QCP = \angle BCA$. From (iv), $\angle BCA = 90^\circ - \angle PBC$.
From (ii), $\angle PBC = \angle QBP = \angle QPB$. So, $\angle BCA = 90^\circ - \angle QPB$.
Also, $\angle BPC = 90^\circ$, so $\angle QPC = 90^\circ - \angle QPB$.
Therefore, we have $\angle QCP = \angle QPC$.
Since two angles of $\triangle QPC$ are equal, it is an isosceles triangle. The sides opposite these equal angles are also equal.
$QC = QP$
(Sides opposite equal angles) ... (v)
From equations (i) and (v), we have $QB = QP$ and $QC = QP$.
Therefore, $QB = QC$.
This shows that Q is the midpoint of the side BC.
Hence Proved.
Question 7. In Fig. 9.18, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]

Answer:
Given:
Tangents PQ and PR are drawn from an external point P to a circle.
$\angle RPQ = 30^\circ$
A chord RS is drawn parallel to the tangent PQ.
$RS \parallel PQ$
To Find:
The measure of the angle $\angle RQS$.
Solution:
We know that the lengths of tangents drawn from an external point to a circle are equal.
Therefore, for tangents from point P:
$PQ = PR$
This means that $\triangle PQR$ is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are also equal.
$\angle PQR = \angle PRQ$
Using the angle sum property in $\triangle PQR$ (sum of angles is $180^\circ$):
$\angle RPQ + \angle PQR + \angle PRQ = 180^\circ$
$30^\circ + \angle PQR + \angle PQR = 180^\circ$
$2\angle PQR = 180^\circ - 30^\circ$
$2\angle PQR = 150^\circ$
$\angle PQR = 75^\circ$
Since the chord RS is parallel to the tangent PQ ($RS \parallel PQ$), and QR is a transversal line intersecting them, the alternate interior angles are equal.
$\angle SRQ = \angle PQR$
(Alternate interior angles)
$\angle SRQ = 75^\circ$
... (i)
Now, by the Alternate Segment Theorem, the angle between the tangent PQ and the chord QR through the point of contact Q is equal to the angle in the alternate segment, which is $\angle QSR$.
$\angle QSR = \angle PQR$
(Alternate Segment Theorem)
$\angle QSR = 75^\circ$
... (ii)
Now, consider the triangle $\triangle QRS$. The sum of its interior angles is $180^\circ$.
$\angle RQS + \angle QSR + \angle SRQ = 180^\circ$
Substituting the values from (i) and (ii):
$\angle RQS + 75^\circ + 75^\circ = 180^\circ$
$\angle RQS + 150^\circ = 180^\circ$
$\angle RQS = 180^\circ - 150^\circ$
$\angle RQS = 30^\circ$
Final Answer:
The measure of $\angle RQS$ is $30^\circ$.
Question 8. AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Answer:
Given:
A circle with centre O and diameter AB.
AC is a chord of the circle.
$\angle BAC = 30^\circ$.
The tangent to the circle at point C intersects the extended diameter AB at point D.
To Prove:
BC = BD.
Proof:
To prove that BC = BD, we need to show that the triangle $\triangle BCD$ is an isosceles triangle by proving that the angles opposite to these sides are equal, i.e., $\angle BDC = \angle BCD$.
Since AB is the diameter of the circle, the angle subtended by the diameter at any point on the circumference is a right angle ($90^\circ$).
$\angle ACB = 90^\circ$
(Angle in a semicircle)
Now, in $\triangle ABC$, the sum of angles is $180^\circ$.
$\angle ABC + \angle BAC + \angle ACB = 180^\circ$
Substitute the known values:
$\angle ABC + 30^\circ + 90^\circ = 180^\circ$
$\angle ABC = 180^\circ - 120^\circ = 60^\circ$
According to the Alternate Segment Theorem, the angle between the tangent (CD) and a chord (BC) through the point of contact (C) is equal to the angle subtended by the chord in the alternate segment ($\angle BAC$).
$\angle BCD = \angle BAC$
(Alternate Segment Theorem)
$\angle BCD = 30^\circ$
... (i)
Now, consider the triangle $\triangle BCD$. We need to find its angles.
Since ABD is a straight line (extended diameter):
$\angle ABC + \angle CBD = 180^\circ$ (Linear pair)
$60^\circ + \angle CBD = 180^\circ$
$\angle CBD = 120^\circ$
In $\triangle BCD$, the sum of angles is $180^\circ$.
$\angle BDC + \angle BCD + \angle CBD = 180^\circ$
Substitute the known angles:
$\angle BDC + 30^\circ + 120^\circ = 180^\circ$
$\angle BDC + 150^\circ = 180^\circ$
$\angle BDC = 30^\circ$
... (ii)
From (i) and (ii), we see that in $\triangle BCD$:
$\angle BCD = \angle BDC = 30^\circ$
Since two angles of $\triangle BCD$ are equal, it is an isosceles triangle. The sides opposite to the equal angles must also be equal.
BC = BD
(Sides opposite to equal angles)
Hence Proved.
Question 9. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Answer:
Given:
A circle with an arc PAQ.
Point A is the midpoint of the arc PAQ.
PQ is the chord joining the endpoints of the arc.
A tangent, let's call it XY, is drawn to the circle at point A.
To Prove:
The tangent XY is parallel to the chord PQ.
Construction:
Join the points A, P, and Q to form the chords AP and AQ.
Proof:
We are given that A is the midpoint of the arc PAQ.
This means that the arc PA is equal to the arc AQ.
arc PA = arc AQ
A property of circles is that equal arcs correspond to equal chords. Therefore:
Chord AP = Chord AQ
(Chords corresponding to equal arcs)
Now, consider the triangle $\triangle APQ$. Since two of its sides, AP and AQ, are equal, it is an isosceles triangle.
In an isosceles triangle, the angles opposite to the equal sides are also equal.
$\angle AQP = \angle APQ$
... (i)
Now, we use the Alternate Segment Theorem. This theorem states that the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
The angle between the tangent XY and the chord AP at point A is $\angle XAP$. The angle in the alternate segment is $\angle AQP$.
$\angle XAP = \angle AQP$
(Alternate Segment Theorem) ... (ii)
From equations (i) and (ii), we can conclude:
$\angle XAP = \angle APQ$
The angles $\angle XAP$ and $\angle APQ$ are a pair of alternate interior angles formed by the transversal line AP intersecting the lines XY and PQ.
Since the alternate interior angles are equal, the lines XY and PQ must be parallel.
XY $\parallel$ PQ
Hence Proved.
Question 10. In Fig. 9.19, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
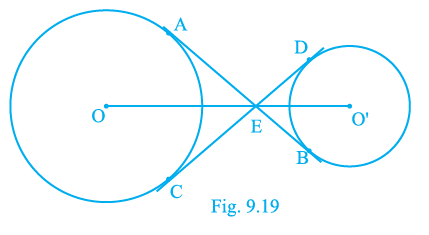
Answer:
Given:
Two circles with centres O and O'.
Two common tangents, AB and CD, to these circles, which intersect at a point E.
To Prove:
The points O, E, and O' are collinear (lie on the same straight line).
Proof:
We know that the center of a circle that is touched by two intersecting lines lies on the angle bisector of the angle formed by those lines.
Consider the first circle with centre O. The two intersecting lines are the tangents AB and CD, which intersect at point E.
Since the circle with centre O is tangent to both lines AB and CD, its centre O must lie on the angle bisector of the angle $\angle AEC$ (and also $\angle AED$).
Therefore, OE is the angle bisector of $\angle AEC$.
$\angle AEO = \angle CEO$
... (i)
Now, consider the second circle with centre O'. The two intersecting lines are the same tangents AB and CD, intersecting at E.
Since the circle with centre O' is tangent to both lines AB and CD, its centre O' must also lie on the angle bisector of the angle $\angle DEB$ (and also $\angle CEB$).
Therefore, O'E is the angle bisector of $\angle DEB$.
$\angle DEO' = \angle BEO'$
... (ii)
The lines AB and CD intersect at E, forming two pairs of vertically opposite angles.
The pair of angles $\angle AEC$ and $\angle DEB$ are vertically opposite angles. Therefore, they are equal.
$\angle AEC = \angle DEB$
(Vertically opposite angles)
The line OE is the bisector of $\angle AEC$, and the line O'E is the bisector of $\angle DEB$.
Since the angles $\angle AEC$ and $\angle DEB$ are the same (vertically opposite), their angle bisectors (OE and O'E) must lie on the same straight line.
When two lines intersect, the bisectors of the vertically opposite angles form a single straight line.
Thus, the line segment OEO' is a straight line.
This means that the points O, E, and O' are collinear.
Hence, Proved.
Question 11. In Fig. 9.20. O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.
Answer:
Given:
A circle with centre O and radius 5 cm. So, $OP = OE = 5$ cm.
T is a point such that the distance from the centre is $OT = 13$ cm.
The line segment OT intersects the circle at point E.
AB is a tangent to the circle at point E.
TP is a tangent to the circle from point T at point P.
The tangent AB intersects the tangent TP at A and another tangent TQ at B.
To Find:
The length of the segment AB.
Solution:
Join the point O to the point of tangency P. Since the radius is perpendicular to the tangent at the point of contact, we have:
$OP \perp TP$
Therefore, $\triangle OPT$ is a right-angled triangle with the right angle at P.
By applying the Pythagorean theorem in $\triangle OPT$:
$OT^2 = OP^2 + TP^2$
Substitute the given values $OT = 13$ cm and $OP = 5$ cm:
$13^2 = 5^2 + TP^2$
$169 = 25 + TP^2$
$TP^2 = 169 - 25 = 144$
$TP = \sqrt{144} = 12$ cm
Now, AB is the tangent to the circle at point E. Since OE is the radius at the point of contact, OE is perpendicular to the tangent AB.
$OE \perp AB$
Since O, E, T are collinear, the line OT is perpendicular to AB. This means $\angle AET = 90^\circ$.
Thus, $\triangle AET$ is a right-angled triangle.
The lengths of tangents drawn from an external point to a circle are equal. From the external point A, tangents AP and AE are drawn.
$AP = AE$
... (i)
Now, we apply the Pythagorean theorem in the right-angled $\triangle AET$:
$AT^2 = AE^2 + ET^2$
We can express AT and ET in terms of known quantities:
$AT = TP - AP = 12 - AP$
$ET = OT - OE = 13 - 5 = 8$ cm
Substitute these expressions and $AE = AP$ into the Pythagorean theorem:
$(12 - AP)^2 = AP^2 + 8^2$
Expand the left side:
$144 - 24 \cdot AP + AP^2 = AP^2 + 64$
Cancel $AP^2$ from both sides and solve for AP:
$144 - 64 = 24 \cdot AP$
$80 = 24 \cdot AP$
$AP = \frac{80}{24} = \frac{10}{3}$ cm
From (i), $AE = AP$, so $AE = \frac{10}{3}$ cm.
By symmetry of the figure, the calculation for point B on tangent TQ will be identical. The tangents from external point B are BE and BQ.
$BE = BQ$
Also, by symmetry, $BE = AE$.
$BE = \frac{10}{3}$ cm
The length of AB is the sum of the lengths of AE and BE.
$AB = AE + BE$
$AB = \frac{10}{3} + \frac{10}{3} = \frac{20}{3}$ cm
Final Answer:
The length of AB is $\frac{20}{3}$ cm.
Question 12. The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA =110º , find CBA [see Fig. 9.21].
[Hint: Join C with centre O.]

Answer:
Given:
A circle with centre O and diameter AB.
The diameter AB is extended to a point P.
A tangent is drawn from P, touching the circle at point C.
The angle $\angle PCA = 110^\circ$.
To Find:
The measure of the angle $\angle CBA$.
Construction:
Join the centre O to the point of tangency C.
Solution:
Since OC is the radius of the circle at the point of contact C, and PC is the tangent, the radius is perpendicular to the tangent.
$OC \perp PC \implies \angle OCP = 90^\circ$
We are given that $\angle PCA = 110^\circ$. From the figure, we can see that:
$\angle PCA = \angle OCP + \angle OCA$
Substitute the known values:
$110^\circ = 90^\circ + \angle OCA$
$\angle OCA = 110^\circ - 90^\circ = 20^\circ$
Now, consider the triangle $\triangle OAC$.
The sides OA and OC are both radii of the same circle, so their lengths are equal.
$OA = OC$
(Radii of the same circle)
Since $\triangle OAC$ is an isosceles triangle, the angles opposite the equal sides are also equal.
$\angle OAC = \angle OCA = 20^\circ$
The angle $\angle OAC$ is the same as $\angle CAB$. So, $\angle CAB = 20^\circ$.
By the Alternate Segment Theorem, the angle between the tangent (PC) and a chord (AC) through the point of contact is equal to the angle in the alternate segment. The angle in the alternate segment for chord AC is $\angle ABC$ (or $\angle CBA$).
However, the angle given is $\angle PCA$, not the angle between the tangent and chord AC inside the triangle. Let's use another approach.
Consider the straight line PAB. The angle $\angle PCA$ and $\angle ACB$ are not directly related. Let's use the sum of angles in $\triangle ABC$.
Since AB is a diameter, the angle subtended by the diameter at any point on the circumference is $90^\circ$.
$\angle ACB = 90^\circ$
(Angle in a semicircle)
In $\triangle ABC$, the sum of angles is $180^\circ$.
$\angle CAB + \angle ABC + \angle BCA = 180^\circ$
Substitute the known angles:
$20^\circ + \angle CBA + 90^\circ = 180^\circ$
$\angle CBA + 110^\circ = 180^\circ$
$\angle CBA = 180^\circ - 110^\circ = 70^\circ$
Final Answer:
The measure of $\angle CBA$ is $70^\circ$.
Question 13. If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
Answer:
Given:
An isosceles triangle ABC is inscribed in a circle with center O.
The lengths of the equal sides are $AB = AC = 6$ cm.
The radius of the circle is $R = 9$ cm.
To Find:
The area of the triangle ABC.
Construction:
Join the vertices of the triangle to the center of the circle: OA, OB, and OC. Draw a line from A to the midpoint M of BC.
Proof:
In $\triangle ABO$ and $\triangle ACO$:
$AB = AC$
(Given)
$BO = CO$
(Radii of the same circle)
$AO = AO$
(Common side)
By SSS (Side-Side-Side) congruence criterion, $\triangle ABO \cong \triangle ACO$.
Therefore, $\angle BAO = \angle CAO$ (by CPCT). Let's call this $\angle 1 = \angle 2$.
Now, in $\triangle ABM$ and $\triangle ACM$:
$AB = AC$
(Given)
$\angle 1 = \angle 2$
(Proved above)
$AM = AM$
(Common side)
By SAS (Side-Angle-Side) congruence criterion, $\triangle AMB \cong \triangle AMC$.
Therefore, $\angle AMB = \angle AMC$ (by CPCT). Since these form a linear pair, $\angle AMB + \angle AMC = 180^\circ$, which means $\angle AMB = \angle AMC = 90^\circ$.
This proves that AM is the altitude to the base BC. Since the perpendicular from the center of a circle bisects a chord, the center O must lie on the perpendicular bisector AM.
Let the altitude $AM = x$. Since OA is the radius, $OA = 9$ cm.
From the figure, $OM = OA - AM = 9 - x$.
Now, consider the right-angled triangle $\triangle AMC$. By the Pythagorean theorem:
$AC^2 = AM^2 + MC^2$
$6^2 = x^2 + MC^2$
$MC^2 = 36 - x^2$
... (i)
Next, consider the right-angled triangle $\triangle OMC$. By the Pythagorean theorem:
$OC^2 = OM^2 + MC^2$
Here, $OC = 9$ cm (radius) and $OM = 9 - x$.
$9^2 = (9 - x)^2 + MC^2$
$MC^2 = 81 - (9 - x)^2$
... (ii)
From equations (i) and (ii), we can equate the expressions for $MC^2$:
$36 - x^2 = 81 - (9 - x)^2$
$36 - x^2 = 81 - (81 + x^2 - 18x)$
$36 - x^2 = 81 - 81 - x^2 + 18x$
$36 = 18x$
$x = \frac{36}{18} = 2$ cm.
So, the altitude of the triangle is $AM = 2$ cm.
Now, substitute $x=2$ into equation (i) to find MC:
$MC^2 = 36 - 2^2 = 36 - 4 = 32$
$MC = \sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}$ cm.
The base of the triangle is $BC = 2 \times MC = 2 \times 4\sqrt{2} = 8\sqrt{2}$ cm.
Finally, the area of $\triangle ABC$ is:
Area = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times BC \times AM$
Area = $\frac{1}{2} \times 8\sqrt{2} \times 2 = 8\sqrt{2}$ cm$^2$.
Final Answer:
The area of the triangle ABC is $8\sqrt{2}$ cm$^2$.
Question 14. A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ΔABC.
Answer:
Given:
A circle with centre O and radius $r = 5$ cm.
A point A is at a distance of $13$ cm from the centre O ($OA = 13$ cm).
AP and AQ are tangents drawn from point A to the circle at points P and Q.
A tangent BC is drawn at a point R on the minor arc PQ, which intersects AP at B and AQ at C.
To Find:
The perimeter of $\triangle ABC$.
Solution:
First, let's find the length of the tangent AP. Consider the triangle $\triangle OPA$.
The radius OP is perpendicular to the tangent AP at the point of contact P.
Therefore, $\triangle OPA$ is a right-angled triangle with $\angle OPA = 90^\circ$.
By the Pythagorean theorem:
$OA^2 = OP^2 + AP^2$
Substitute the given values $OA = 13$ cm and $OP = 5$ cm:
$13^2 = 5^2 + AP^2$
$169 = 25 + AP^2$
$AP^2 = 169 - 25 = 144$
$AP = \sqrt{144} = 12$ cm
Now, let's find the perimeter of $\triangle ABC$.
Perimeter($\triangle ABC$) = $AB + BC + CA$.
The side BC can be expressed as the sum of the segments BR and RC.
Perimeter = $AB + (BR + RC) + CA$.
We use the property that tangents from an external point to a circle are equal in length.
1. From point B, the tangents are BP and BR. So, $BP = BR$.
2. From point C, the tangents are CQ and CR. So, $CQ = CR$.
Substitute these into the perimeter equation:
Perimeter = $AB + (BP + CQ) + CA$.
Rearrange the terms:
Perimeter = $(AB + BP) + (CA + CQ)$.
From the figure, we see that:
$AB + BP = AP$
$CA + CQ = AQ$
So, the perimeter becomes:
Perimeter = $AP + AQ$.
3. From point A, the tangents are AP and AQ. So, $AP = AQ$.
Since we calculated $AP = 12$ cm, we have $AQ = 12$ cm.
Therefore, the perimeter is:
Perimeter($\triangle ABC$) = $12 \text{ cm} + 12 \text{ cm} = 24$ cm
Final Answer:
The perimeter of the $\triangle ABC$ is 24 cm.

