| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Class 6th Chapters | ||
|---|---|---|
| 1. Number System | 2. Geometry | 3. Integers |
| 4. Fractions & Decimals | 5. Data Handling | 6. Mensuration |
| 7. Algebra | 8. Ratio & Proportion | 9. Symmetry & Practical Geometry |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 5) | Question 1 to 5 (Multiple Choice Questions) | Question 6 to 13 (True or False) |
| Question 14 to 21 (Fill in the Blanks) | Question 22 to 55 | |
Chapter 5 Data Handling (Examples 1 to 5)
This solutions page is meticulously designed to offer comprehensive guidance and detailed answers for the NCERT Exemplar problems specifically related to Class 6 Mathematics, Chapter 5: Data Handling. It is essential to understand that the Exemplar questions in this domain aim higher than typical textbook exercises. They are specifically crafted to strengthen students' core abilities in organizing raw information, representing data sets clearly and accurately, and interpreting the presented data with a discerning eye. Often, these problems involve more complex datasets or demand a deeper level of analysis than students might have previously encountered, pushing them towards greater data literacy.
The provided solutions thoroughly cover the fundamental concepts central to data handling at this level. These key areas include:
- The initial step of collecting data relevant to a specific query or investigation.
- Techniques for organizing raw data systematically. This prominently features the use of tally marks, where each data point is recorded with a vertical stroke ($|$) and groups of five are bundled for efficient counting (e.g., four marks are $||||$, and the fifth completes the bundle as $\bcancel{||||}$). This process leads directly to the creation of informative frequency distribution tables, which summarize how often each value or category appears.
- Interpreting existing visual representations, such as pictographs. Exemplar problems might challenge students with pictographs using non-standard scales (where one symbol represents multiple units) or even fractional symbols requiring careful calculation.
- Constructing clear and accurate pictographs from given data.
- Interpreting information presented in bar graphs, focusing on reading values from the axes and comparing bar heights.
- Constructing well-defined bar graphs, which involves critical decisions like choosing an appropriate scale for the axes, ensuring uniform width of bars and equal spacing between them, and labeling both axes and the graph title correctly.
A significant focus of the Exemplar problems, and consequently these solutions, is testing not just the procedural skill of drawing a graph but also the crucial ability to critically analyze the information presented graphically or in tables. The solutions address the diverse question formats used:
- Multiple Choice Questions (MCQs): These often require careful reading and precise interpretation of given pictographs, bar graphs, or frequency tables to select the correct answer among closely related options.
- Fill-in-the-Blanks: Testing the correct usage of essential terminology like 'frequency', 'scale', 'pictograph', 'bar graph', or 'tally marks'.
- True/False Statements: Probing the understanding of underlying principles of graphical representation and the validity of interpretations drawn from data.
- Short and Long Answer Questions: These demand the accurate construction of frequency tables (using tally marks like $\bcancel{||||}$ for 5), pictographs, or bar graphs from provided raw data. They also require students to extract specific information, make meaningful comparisons between data points or categories, and draw logical inferences or conclusions based on complex data representations.
For instance, challenging problems might involve interpreting a bar graph depicting data over several time periods and asking about trends, calculating total frequencies, or finding differences – tasks that require careful reading of the scale. Constructing a bar graph where the data range necessitates choosing a non-obvious but appropriate scale is another common task. The solutions provide crystal-clear explanations for interpretations, offer detailed step-by-step instructions for constructing tables and graphs (always emphasizing accuracy in scaling, labeling, and drawing elements), and articulate the logical reasoning behind any conclusions drawn from the data. By engaging with these comprehensive solutions, students can significantly enhance their data literacy, refine their skills in visualizing and representing data effectively, and develop the critical thinking necessary to interpret statistical information encountered in various contexts.
Solved Examples (Examples 1 to 5)
Write the correct answer from the given four options:
Example 1: Using tally marks which one of the following represents the number five?
(A) $|||||$
(B) $\sqrt{} \sqrt{} \sqrt{} \sqrt{} \sqrt{}$
(C) $\bcancel{|||}|$
(D) $\bcancel{||||}$
Answer:
Given:
Different representations, and asked to identify the one representing the number five using tally marks.
To Find:
The correct tally mark representation for the number five from the given options.
Solution:
In the standard system of tally marks, groups of five are typically represented by four vertical lines crossed by a diagonal line.
This is shown as $\bcancel{||||}$.
Let's examine the given options:
(A) $|||||$ represents five individual strokes.
(B) $\sqrt{} \sqrt{} \sqrt{} \sqrt{} \sqrt{}$ represents five check marks, which are not standard tally marks.
(C) $\bcancel{||||}$ followed by $|||$ represents a group of five plus three individual strokes, totaling $5 + 3 = 8$.
(D) $\bcancel{||||}$ represents a group of four vertical lines crossed by a diagonal line, which is the standard tally mark representation for the number five.
Therefore, option (D) correctly represents the number five using tally marks.
Final Answer:
The correct option is (D).
(D) $\bcancel{||||}$
Example 2: State whether the following statements are true or false:
(a) A tabular form of data is also a pictorial representation of the data.
(b) A pictograph represents data in the form of pictures of objects or parts of objects.
Answer:
Given:
Two statements regarding the representation of data.
To State:
Whether each given statement is true or false.
Solution:
Let's analyze each statement.
(a) A tabular form of data is also a pictorial representation of the data.
A tabular form of data, or a table, organizes data into rows and columns. It presents data in a structured way using numbers and text.
A pictorial representation of data uses pictures or symbols to represent the data, such as a pictograph or a bar graph. A table itself does not use pictures or symbols to represent the quantity of data; it lists the data numerically or textually.
Therefore, a tabular form of data is not considered a pictorial representation.
This statement is false.
(b) A pictograph represents data in the form of pictures of objects or parts of objects.
A pictograph is a way of displaying data using images or symbols. Each image or symbol represents a specific quantity of the data being represented. The number of times the picture or symbol appears indicates the total quantity for a particular category.
This description accurately defines how a pictograph works.
Therefore, this statement is true.
Final Answer:
(a) False
(b) True
Example 3: The blood groups of 25 students are recorded as under:
| A | B | O | A | AB | O | A | O | B | A |
| O | B | A | AB | AB | A | A | B | B | O |
| B | AB | O | A | B |
Arrange the information in a table using tally marks.
Answer:
Given:
The blood groups of 25 students are given: A, B, O, A, AB, O, A, O, B, A, O, B, A, AB, AB, A, A, B, B, O, B, AB, O, A, B.
To Arrange:
Arrange the given information in a table using tally marks.
Solution:
We need to count the frequency of each blood group using tally marks. The blood groups are A, B, O, and AB.
We will go through the list of blood groups and make a tally mark for each occurrence in the corresponding row of the table.
List: A, B, O, A, AB, O, A, O, B, A, O, B, A, AB, AB, A, A, B, B, O, B, AB, O, A, B
Counting the occurrences:
A: |||| | | (7 times)
B: |||| | | (6 times)
O: |||| | (5 times)
AB: |||| (4 times)
Let's recount carefully using tally marks as we go through the list:
A ($||$): A, B, O, A
AB ($|||$): AB, O, A, O, B, A
O ($||$): O, B, A, AB, AB, A, A, B, B, O
A ($||||$): A, A, B, B, O, B, AB, O, A
AB ($||||$): AB, AB, B, AB
B ($||||$): B, B, B, B
O ($||||$): O, O, O
Let's make the table by going through the list sequentially:
| Blood Group | Tally Marks | Number of Students (Frequency) |
| A | ||
| B | ||
| O | ||
| AB |
Going through the list: A, B, O, A, AB, O, A, O, B, A, O, B, A, AB, AB, A, A, B, B, O, B, AB, O, A, B
- A: $||$ (Count: 1)
- B: $||$ (Count: 1)
- O: $||$ (Count: 1)
- A: $||$ (Count: 2)
- AB: $||$ (Count: 1)
- O: $||$ (Count: 2)
- A: $||$ (Count: 3)
- O: $||$ (Count: 3)
- B: $||$ (Count: 2)
- A: $||||$ (Count: 4)
- O: $||||$ (Count: 4)
- B: $||||$ (Count: 3)
- A: $\bcancel{||||}$ (Count: 5)
- AB: $||$ (Count: 2)
- AB: $||$ (Count: 3)
- A: $\bcancel{||||} |$ (Count: 6)
- A: $\bcancel{||||} ||$ (Count: 7)
- B: $||||$ (Count: 4)
- B: $\bcancel{||||}$ (Count: 5)
- O: $|||| |$ (Count: 5)
- B: $\bcancel{||||} |$ (Count: 6)
- AB: $||||$ (Count: 4)
- O: $\bcancel{||||}$ (Count: 5). Correction: O count was 5 already, so this is the 6th O. Let's restart the tallying to be precise.
Let's create the table and fill it row by row as we read the blood groups.
| Blood Group | Tally Marks | Number of Students (Frequency) |
| A | ||
| B | ||
| O | ||
| AB |
A: $||$
B: $||$
O: $||$
A: $||$
AB: $||$
O: $||$
A: $||$
O: $||$
B: $||$
A: $||||$
O: $||||$
B: $||||$
A: $\bcancel{||||}$
AB: $||$
AB: $||$
A: $\bcancel{||||} |$
A: $\bcancel{||||} ||$
B: $||||$
B: $\bcancel{||||}$
O: $|||| |$
B: $\bcancel{||||} |$
AB: $||||$
O: $|||| |$
A: $\bcancel{||||} |||$
B: $\bcancel{||||} ||$
Let's count the tallies for each blood group:
A: $\bcancel{||||} |||$ represents $5 + 3 = 8$ students.
B: $\bcancel{||||} ||$ represents $5 + 2 = 7$ students.
O: $|||| |$ represents $5 + 1 = 6$ students.
AB: $||||$ represents 4 students.
Total students = $8 + 7 + 6 + 4 = 25$. This matches the given number of students.
Now, we put this information into the table.
Final Answer:
| Blood Group | Tally Marks | Number of Students (Frequency) |
| A | $\bcancel{||||} |||$ | 8 |
| B | $\bcancel{||||} ||$ | 7 |
| O | $\bcancel{||||} |$ | 6 |
| AB | $||||$ | 4 |
Example 4: In a school, there are five sections of Class VI. The number of students in each section is given below:
| Section | A | B | C | D | E |
|---|---|---|---|---|---|
| Number of students | 40 | 44 | 42 | 36 | 32 |
Represent the above data using a bar graph.
Answer:
Given:
The number of students in five sections of Class VI are provided in a table.
| Section | A | B | C | D | E |
| Number of students | 40 | 44 | 42 | 36 | 32 |
To Represent:
Represent the given data using a bar graph.
Construction Required:
To represent the given data using a bar graph, follow these steps:
1. Draw two perpendicular lines, one horizontal and one vertical. These are the axes.
2. Label the horizontal axis. This axis will represent the 'Section of Class VI'. Mark points at equal intervals along this axis to represent each section (A, B, C, D, E).
3. Label the vertical axis. This axis will represent the 'Number of Students'. Choose a suitable scale for this axis. Look at the number of students: 40, 44, 42, 36, 32. The numbers range from 32 to 44. A scale starting from 0 and going up to 50, with intervals of 2 or 4, would be appropriate. For example, let 1 unit length on the vertical axis represent 4 students.
4. Draw bars for each section. For each section marked on the horizontal axis, draw a rectangular bar vertically upwards. The height of each bar should be proportional to the number of students in that section, according to the scale chosen on the vertical axis.
- For Section A (40 students): Draw a bar up to the mark representing 40 on the vertical axis.
- For Section B (44 students): Draw a bar up to the mark representing 44 on the vertical axis.
- For Section C (42 students): Draw a bar up to the mark representing 42 on the vertical axis.
- For Section D (36 students): Draw a bar up to the mark representing 36 on the vertical axis.
- For Section E (32 students): Draw a bar up to the mark representing 32 on the vertical axis.
5. Ensure the bars are of uniform width and the spacing between consecutive bars is equal.
6. Give an appropriate title to the bar graph, such as "Number of Students in Class VI Sections".
Final Representation (Description):
The bar graph will show five bars of equal width, separated by equal gaps. The bars will be labelled A, B, C, D, and E on the horizontal axis. The heights of the bars will correspond to 40, 44, 42, 36, and 32 units respectively on the vertical axis, according to the chosen scale. The vertical axis will represent the frequency (number of students), and the horizontal axis will represent the categories (sections).
Example 5: The number of vistors in a science exhibition on different days of a week is shown below:
Look at the above pictograph and answer the following questions:

(a) What is the total number of visitors from Monday to Saturday?
(b) On which day was the number of visitors maximum? What was their total number?
(c) On which day was the number of visitors minimum?
(d) On which day was the number of visitors same as the number of visitors on two days taken together?
Answer:
Given:
A pictograph showing the number of visitors to a science exhibition from Monday to Saturday.
Key: 1 picture of a person represents 100 visitors.
To Find:
Answers to the questions (a), (b), (c), and (d) based on the pictograph.
Solution:
First, let's determine the number of visitors for each day by counting the symbols and multiplying by the key value (100).
- Monday: 5 symbols $\times$ 100 visitors/symbol = 500 visitors
- Tuesday: 4 symbols $\times$ 100 visitors/symbol = 400 visitors
- Wednesday: 3 symbols $\times$ 100 visitors/symbol = 300 visitors
- Thursday: 6 symbols $\times$ 100 visitors/symbol = 600 visitors
- Friday: 5 symbols $\times$ 100 visitors/symbol = 500 visitors
- Saturday: 7 symbols $\times$ 100 visitors/symbol = 700 visitors
Now, we answer the questions:
(a) What is the total number of visitors from Monday to Saturday?
Total visitors = Visitors on Monday + Tuesday + Wednesday + Thursday + Friday + Saturday
Total visitors = $500 + 400 + 300 + 600 + 500 + 700$
Total visitors = $900 + 300 + 600 + 500 + 700$
Total visitors = $1200 + 600 + 500 + 700$
Total visitors = $1800 + 500 + 700$
Total visitors = $2300 + 700$
Total visitors = $3000$
(b) On which day was the number of visitors maximum? What was their total number?
Comparing the number of visitors for each day (500, 400, 300, 600, 500, 700), the maximum number is 700.
The day with the maximum number of visitors is Saturday.
The total number of visitors on Saturday was 700.
(c) On which day was the number of visitors minimum?
Comparing the number of visitors for each day (500, 400, 300, 600, 500, 700), the minimum number is 300.
The day with the minimum number of visitors is Wednesday.
(d) On which day was the number of visitors same as the number of visitors on two days taken together?
We need to find if the sum of visitors on any two days equals the number of visitors on a single day.
Let's check combinations:
Visitors on Tuesday (400) + Visitors on Wednesday (300) = $400 + 300 = 700$.
The number 700 corresponds to the number of visitors on Saturday.
So, the number of visitors on Saturday is the same as the number of visitors on Tuesday and Wednesday taken together.
The day is Saturday.
Final Answer:
(a) The total number of visitors from Monday to Saturday is 3000.
(b) The number of visitors was maximum on Saturday, and their total number was 700.
(c) The number of visitors was minimum on Wednesday.
(d) The number of visitors on Saturday was the same as the number of visitors on Tuesday and Wednesday taken together.
Exercise
Question 1 to 5 (Multiple Choice Questions)
In questions 1 to 5, out of the four options, only one is correct. write the correct answer.
Question 1. Using tally marks, which one of the following represents the number eight:
(A) $|||||$ $|||$
(B) $\bcancel{|||}$ $\bcancel{|||}$
(C) $\bcancel{|||||}$ $||$
(D) $\bcancel{||||}$ $|||$
Answer:
To represent a number using tally marks, we use vertical strokes. A group of five is commonly represented by four vertical strokes crossed by a diagonal stroke.
To represent the number eight, we need one group of five and three additional strokes.
The standard representation for five using tally marks is $\bcancel{||||}$.
The standard representation for three using tally marks is $|||$.
Therefore, the number eight is represented as $\bcancel{||||}$ $|||$.
Comparing this with the given options:
(A) $|||||$ $|||$ represents $5 + 3 = 8$, but the representation of five is not standard.
(B) $\bcancel{|||}$ $\bcancel{|||}$ is not a standard representation of tally marks.
(C) $\bcancel{|||||}$ $||$ is not a standard representation of tally marks.
(D) $\bcancel{||||}$ $|||$ represents $5 + 3 = 8$, using the standard representation for five and three.
Thus, the correct option representing the number eight using standard tally marks is (D).
The correct answer is (D) $\bcancel{||||}$ $|||$.
Question 2. The marks (out of 10) obtained by 28 students in a Mathematics test are listed as below:
| 8 | 1 | 2 | 6 | 5 | 5 | 5 | 0 | 1 | 9 |
| 7 | 8 | 0 | 5 | 8 | 3 | 0 | 8 | 10 | 10 |
| 3 | 4 | 8 | 7 | 8 | 9 | 2 | 0 |
The number of students who obtained marks more than or equal to 5 is
(A) 13
(B) 15
(C) 16
(D) 17
Answer:
We need to find the number of students who obtained marks more than or equal to 5. This means we need to count the students whose marks are 5, 6, 7, 8, 9, or 10.
Let's list the marks obtained by the 28 students:
8, 1, 2, 6, 5, 5, 5, 0, 1, 9,
7, 8, 0, 5, 8, 3, 0, 8, 10, 10,
3, 4, 8, 7, 8, 9, 2, 0
Now, let's identify the marks that are $\geq 5$ from the list:
Marks $\geq 5$ are: 8, 6, 5, 5, 5, 9, 7, 8, 5, 8, 10, 10, 8, 7, 8, 9.
Counting these identified marks, we get:
1 (8), 2 (6), 3 (5), 4 (5), 5 (5), 6 (9), 7 (7), 8 (8), 9 (5), 10 (8), 11 (10), 12 (10), 13 (8), 14 (7), 15 (8), 16 (9).
There are a total of 16 students who obtained marks more than or equal to 5.
Comparing this count with the given options, we find that the number 16 corresponds to option (C).
The correct answer is (C) 16.
Question 3. In question 2 above, the number of students who scored marks less than 4 is
(A) 15
(B) 13
(C) 12
(D) 10
Answer:
We need to find the number of students who scored marks less than 4. This means we need to count the students whose marks are 0, 1, 2, or 3 from the list provided in Question 2.
The marks obtained by the 28 students are:
8, 1, 2, 6, 5, 5, 5, 0, 1, 9,
7, 8, 0, 5, 8, 3, 0, 8, 10, 10,
3, 4, 8, 7, 8, 9, 2, 0
Now, let's identify the marks that are strictly less than 4 from the list:
Marks $< 4$ are: 1, 2, 0, 1, 0, 3, 0, 3, 2, 0.
Counting these identified marks, we get:
1 (1), 2 (2), 3 (0), 4 (1), 5 (0), 6 (3), 7 (0), 8 (3), 9 (2), 10 (0).
Let's re-list the marks $< 4$ and count them carefully:
1, 2, 0, 1, 0, 3, 0, 3, 2, 0.
Count = 10.
There are a total of 10 students who scored marks less than 4.
Comparing this count with the given options, we find that the number 10 corresponds to option (D).
The correct answer is (D) 10.
Question 4. The choices of the fruits of 42 students in a class are as follows:
| A | O | B | M | A | G | B | G | A | G |
| B | M | A | G | M | A | B | G | M | B |
| A | O | M | O | G | B | O | M | G | A |
| A | B | M | O | M | G | B | A | M | O |
| M | O |
where A, B, G, M and O stand for the fruits Apple, Banana, Grapes, Mango and Orange respectively.
Which two fruits are liked by an equal number of students?
(A) A and M
(B) M and B
(C) B and O
(D) B and G
Answer:
We are given the fruit choices of 42 students and need to find which two fruits are liked by an equal number of students. We need to count the frequency of each fruit choice.
The fruit codes are: A (Apple), B (Banana), G (Grapes), M (Mango), O (Orange).
Let's count the occurrences of each code in the given list:
A: Count the number of 'A's.
O: Count the number of 'O's.
B: Count the number of 'B's.
M: Count the number of 'M's.
G: Count the number of 'G's.
Let's count:
A: A (1), A (2), A (3), A (4), A (5), A (6), A (7), A (8), A (9)
Number of students who like Apple (A) = 9.
B: B (1), B (2), B (3), B (4), B (5), B (6), B (7), B (8)
Number of students who like Banana (B) = 8.
G: G (1), G (2), G (3), G (4), G (5), G (6), G (7), G (8)
Number of students who like Grapes (G) = 8.
M: M (1), M (2), M (3), M (4), M (5), M (6), M (7), M (8), M (9)
Number of students who like Mango (M) = 9.
O: O (1), O (2), O (3), O (4), O (5), O (6)
Number of students who like Orange (O) = 6.
Let's summarize the counts:
Apple (A): 9
Banana (B): 8
Grapes (G): 8
Mango (M): 9
Orange (O): 6
We are looking for two fruits liked by an equal number of students. Comparing the counts, we see that:
Apple (A) count is 9.
Banana (B) count is 8.
Grapes (G) count is 8.
Mango (M) count is 9.
Orange (O) count is 6.
The fruits with equal counts are Apple (A) and Mango (M), both liked by 9 students, and Banana (B) and Grapes (G), both liked by 8 students.
Now, let's check the given options:
(A) A and M: Apple (A) count is 9, Mango (M) count is 9. They are equal.
(B) M and B: Mango (M) count is 9, Banana (B) count is 8. They are not equal.
(C) B and O: Banana (B) count is 8, Orange (O) count is 6. They are not equal.
(D) B and G: Banana (B) count is 8, Grapes (G) count is 8. They are equal.
Options (A) and (D) both list pairs of fruits liked by an equal number of students based on our counts (A & M = 9, B & G = 8). Let's re-verify the count to ensure no error.
Total number of students = 9 (A) + 8 (B) + 8 (G) + 9 (M) + 6 (O) = 40.
The question states there are 42 students. Let's recount carefully.
Row 1: A, O, B, M, A, G, B, G, A, G (3 A, 2 B, 3 G, 1 M, 1 O)
Row 2: B, M, A, G, M, A, B, G, M, B (2 A, 3 B, 2 G, 3 M, 0 O)
Row 3: A, O, M, O, G, B, O, M, G, A (2 A, 1 B, 2 G, 2 M, 3 O)
Row 4: A, B, M, O, M, G, B, A, M, O (2 A, 2 B, 1 G, 3 M, 2 O)
Row 5: M, O (0 A, 0 B, 0 G, 1 M, 1 O)
Total counts:
A: 3 + 2 + 2 + 2 + 0 = 9
B: 2 + 3 + 1 + 2 + 0 = 8
G: 3 + 2 + 2 + 1 + 0 = 8
M: 1 + 3 + 2 + 3 + 1 = 10
O: 1 + 0 + 3 + 2 + 1 = 7
Sum of counts = 9 + 8 + 8 + 10 + 7 = 42. This matches the total number of students.
Revised counts:
Apple (A): 9
Banana (B): 8
Grapes (G): 8
Mango (M): 10
Orange (O): 7
Now let's compare the counts to find pairs of fruits with equal numbers:
Apple (9) is not equal to any other count.
Banana (8) is equal to Grapes (8).
Mango (10) is not equal to any other count.
Orange (7) is not equal to any other count.
The only pair of fruits liked by an equal number of students based on the revised counts is Banana (B) and Grapes (G), both liked by 8 students.
Let's check the options again with the revised counts:
(A) A and M: Apple (9) and Mango (10). Not equal.
(B) M and B: Mango (10) and Banana (8). Not equal.
(C) B and O: Banana (8) and Orange (7). Not equal.
(D) B and G: Banana (8) and Grapes (8). They are equal.
Based on the accurate count, the fruits liked by an equal number of students are Banana and Grapes.
The correct answer is (D) B and G.
Question 5. According to data of question 4, which fruit is liked by most of the students?
(A) O
(B) G
(C) M
(D) A
Answer:
We need to determine which fruit is liked by the most students based on the data from Question 4. We will use the frequency counts calculated in the solution for Question 4.
The frequency counts for each fruit are:
Apple (A): 9 students
Banana (B): 8 students
Grapes (G): 8 students
Mango (M): 10 students
Orange (O): 7 students
To find the fruit liked by most students, we need to identify the fruit with the highest frequency count.
Comparing the counts (9, 8, 8, 10, 7), the maximum count is 10.
The fruit corresponding to the count of 10 is Mango (M).
Therefore, Mango is the fruit liked by most of the students.
Comparing this result with the given options:
(A) O (Orange) has a count of 7.
(B) G (Grapes) has a count of 8.
(C) M (Mango) has a count of 10.
(D) A (Apple) has a count of 9.
The highest count is 10, which corresponds to Mango (M).
The correct answer is (C) M.
Question 6 to 13 (True or False)
In questions 6 to 13, state whether the given statements are true (T) or false (F).
Question 6. In a bar graph, the width of bars may be unequal.
Answer:
A bar graph is a visual representation of data using bars. In a bar graph, the bars represent categories, and their heights (or lengths) correspond to the frequency or value of each category.
A fundamental characteristic of a standard bar graph is that all bars have the same width. The spaces between the bars are also typically equal.
The width of the bars does not represent any value; only the height or length does. Unequal widths would misrepresent the data and make the graph difficult to interpret correctly.
Therefore, the statement "In a bar graph, the width of bars may be unequal" is incorrect.
The given statement is False (F).
Question 7. In a bar graph, bars of uniform width are drawn vertically only.
Answer:
A bar graph uses bars of uniform width (or height) to represent data. The orientation of the bars can be either vertical or horizontal.
In a vertical bar graph, the bars are drawn upwards from the horizontal axis, with the length (height) of the bars representing the frequency or value of the data.
In a horizontal bar graph, the bars are drawn sideways from the vertical axis, with the length (width) of the bars representing the frequency or value of the data.
Since bar graphs can be drawn horizontally as well as vertically, the statement that bars are drawn vertically only is incorrect.
The given statement is False (F).
Question 8. In a bar graph, the gap between two consecutive bars may not be thesame.
Answer:
A standard practice in constructing a bar graph is to keep the gap between any two consecutive bars uniform. This uniformity helps in clearly distinguishing between the categories and maintaining a consistent visual representation of the data.
While it is technically possible to draw a graph with unequal gaps, this is not the convention for a standard bar graph and would typically lead to a misleading or poorly constructed graph.
For a proper bar graph, the gaps between consecutive bars should be equal.
Therefore, the statement "In a bar graph, the gap between two consecutive bars may not be the same" is incorrect for a properly constructed standard bar graph.
The given statement is False (F).
Question 9. In a bar graph, each bar (rectangle) represents only one value of thenumerical data.
Answer:
In a bar graph, each individual bar represents a specific category or discrete value. The height or length of that bar corresponds to the frequency or magnitude of the data associated with that category.
For instance, if a bar graph shows the number of students who like different fruits, each bar represents one fruit (e.g., Apple, Banana, Grapes), and its height represents the number of students who like that specific fruit. So, each bar is linked to a single numerical value (the count or frequency) for its corresponding category.
Therefore, each bar (rectangle) in a bar graph indeed represents a single value of the numerical data for the category it represents.
The given statement is True (T).
Question 10. To represent the population of different towns using bar graph, it isconvenient to take one unit length to represent one person.
Answer:
When constructing a bar graph, a suitable scale must be chosen for the axis that represents the numerical data (frequency or value). The scale relates the length of the bar to the numerical value it represents.
If we are representing the population of different towns, the population numbers are likely to be very large (hundreds, thousands, millions, etc.). If we were to take one unit length to represent just one person, the bars would need to be extremely long to represent the populations of even small towns. For example, a town with a population of 10,000 would require a bar 10,000 units long, which would be impractical to draw and display.
For large datasets like population figures, it is much more convenient and necessary to choose a scale where one unit length represents a larger number of people (e.g., 100 people, 1000 people, 10,000 people, etc.), depending on the range of the population data.
Therefore, taking one unit length to represent one person is not convenient for representing the population of different towns.
The given statement is False (F).
Question 11. Pictographs and bar graphs are pictorial representations of the numerical data.
Answer:
Data can be represented visually using various graphical methods. Pictographs use symbols or pictures to represent units of data, while bar graphs use bars (rectangles) to represent quantities.
Both pictographs and bar graphs aim to provide a visual summary and comparison of numerical data, making it easier to understand and interpret trends or differences.
A pictograph uses pictures to show the frequency of items, with each picture representing a certain number of units. For example, if one car symbol represents 5 cars sold, then 3 car symbols would represent 15 cars sold.
A bar graph uses bars of varying heights or lengths to show the frequency or value of different categories. The length of the bar is proportional to the numerical data it represents.
Since both methods use graphical elements (pictures or bars) to display numerical information, they are considered pictorial or visual representations of numerical data.
Therefore, the statement is correct.
The given statement is True (T).
Question 12. An observation occurring five times in a data is recorded as | | | | | , using tally marks.
Answer:
Tally marks are used for counting occurrences of observations. The standard way to represent counts using tally marks is to draw a vertical stroke for each observation up to four, and then draw a diagonal stroke across the four vertical strokes to represent a group of five.
The representation for one is $|$.
The representation for two is $||$.
The representation for three is $|||$.
The representation for four is $||||$.
The standard representation for five is $\bcancel{||||}$.
The statement says that an observation occurring five times is recorded as $| | | | |$. This is incorrect according to the standard method of using tally marks for grouping in fives.
Therefore, the given statement is false.
The given statement is False (F).
Question 13. In a pictograph, if a symbol  represents 50 books in a library shelf, then the symbol
represents 50 books in a library shelf, then the symbol  represents 25 books.
represents 25 books.
Answer:
In a pictograph, a symbol is used to represent a certain quantity. If a full symbol represents a specific number of units, then a fraction of that symbol represents the same fraction of the number of units.
According to the statement, the symbol  represents 50 books.
represents 50 books.
The symbol  appears to be a representation of half of the full symbol
appears to be a representation of half of the full symbol  .
.
If the full symbol represents 50 books, then a half symbol should represent half of that quantity.
Value represented by half symbol = $\frac{1}{2} \times \text{Value represented by full symbol}$
Value represented by half symbol = $\frac{1}{2} \times 50$ books
Value represented by half symbol = 25 books.
The statement claims that the symbol  represents 25 books, which matches our calculation.
represents 25 books, which matches our calculation.
Therefore, the given statement is correct.
The given statement is True (T).
Question 14 to 21 (Fill in the Blanks)
In questions 14 to 21, fill in the blanks to make the statements true:
Question 14. A _______ is a collection of numbers gathered to give some meaningful information.
Answer:
The definition provided, "a collection of numbers gathered to give some meaningful information," precisely describes data.
Data can be numerical or categorical, and when collected and organized, it provides insights or information about a particular phenomenon or subject.
The blank should be filled with the word 'data'.
The complete statement is: A data is a collection of numbers gathered to give some meaningful information.
Question 15. The data can be arranged in a tabular form using _______ marks.
Answer:
When arranging raw data into a frequency distribution table, it is common practice to use tally marks to count the number of times each observation occurs.
Tally marks provide a quick and systematic way to keep track of counts as you go through the data. After using tally marks to count the frequency of each category or value, these counts are then written as numbers in the frequency column of the table.
The blank should be filled with the word 'tally'.
The complete statement is: The data can be arranged in a tabular form using tally marks.
Question 16. A _______ represents data through pictures of objects.
Answer:
There are different ways to visually represent data. One common method uses pictures or symbols to denote quantities.
A pictograph is a statistical graph that uses pictures or symbols to represent the frequency of data. Each picture or symbol represents a specific number of items. For example, a picture of a tree might represent 10 trees planted.
The blank should be filled with the word 'pictograph'.
The complete statement is: A pictograph represents data through pictures of objects.
Question 17. In a bar graph, ________ can be drawn horizontally or vertically.
Answer:
A bar graph uses rectangular bars to represent data. These bars are the primary visual elements of the graph.
As discussed in Question 7, bar graphs can have their bars oriented either vertically (extending upwards) or horizontally (extending sideways). Both orientations are valid forms of a bar graph.
The blank should be filled with the word 'bars'.
The complete statement is: In a bar graph, bars can be drawn horizontally or vertically.
Question 18. In a bar graph, bars of ________ width can be drawn horizontally or vertically with ________ spacing between them.
Answer:
As discussed in previous questions about bar graphs, standard bar graphs have bars that share certain characteristics regarding their dimensions and the space between them.
All bars in a standard bar graph have the same width. This ensures that the length or height is the sole indicator of the value being represented, preventing visual distortion.
Also, the gaps between consecutive bars are kept uniform. This consistent spacing makes the graph easy to read and compare the values of different categories.
The first blank should be filled with 'uniform' or 'equal'. 'Uniform' is a common term used in this context.
The second blank should be filled with 'equal' or 'uniform'. 'Equal' is a common term for spacing.
The complete statement is: In a bar graph, bars of uniform width can be drawn horizontally or vertically with equal spacing between them.
Question 19. An observation occurring seven times in a data is represented as ________ using tally marks.
Answer:
We need to represent the count of seven using tally marks according to the standard method.
The standard method involves grouping in fives:
Count 1: $|$
Count 2: $||$
Count 3: $|||$
Count 4: $||||$
Count 5: $\bcancel{||||}$
To represent seven, we need one group of five and two additional strokes.
Seven = Five + Two
Seven in tally marks = $\bcancel{||||}$ $||$.
The blank should be filled with the tally mark representation for seven.
The complete statement is: An observation occurring seven times in a data is represented as $\bcancel{||||}$ $||$ using tally marks.
Question 20. In a pictograph, if a symbol  represents 20 flowers in a basket then
represents 20 flowers in a basket then  stands for ________ flowers.
stands for ________ flowers.
Answer:
In a pictograph, symbols represent quantities. The given information provides the value represented by a full symbol and asks for the value represented by a combination of symbols.
We are given that the symbol  represents 20 flowers.
represents 20 flowers.
The symbol  appears to be three instances of the symbol
appears to be three instances of the symbol  placed side by side.
placed side by side.
If one symbol represents 20 flowers, then three such symbols represent three times that quantity.
Value represented by  = $3 \times \text{Value represented by one symbol}$
= $3 \times \text{Value represented by one symbol}$
Value represented by  = $3 \times 20$ flowers
= $3 \times 20$ flowers
Value represented by  = 60 flowers.
= 60 flowers.
The blank should be filled with the number 60.
The complete statement is: In a pictograph, if a symbol  represents 20 flowers in a basket then
represents 20 flowers in a basket then  stands for 60 flowers.
stands for 60 flowers.
Question 21. On the scale of 1 unit length = 10 crore, the bar of length 6 units will represent ________ crore and of ______ units will represent 75 crore.
Answer:
We are given a scale for a bar graph where 1 unit length represents 10 crore.
We need to find the value represented by a bar of length 6 units. Using the given scale:
1 unit length = 10 crore
6 units length = $6 \times 10$ crore
6 units length = 60 crore.
So, a bar of length 6 units will represent 60 crore.
Next, we need to find the number of units that will represent 75 crore. Let the required number of units be $x$.
Using the scale:
$x$ units length = 75 crore
Since 1 unit length = 10 crore, we can write:
$\text{Number of units} = \frac{\text{Value}}{\text{Value per unit}}$
... (i)
Substituting the given values into Equation (i):
$x = \frac{75 \text{ crore}}{10 \text{ crore/unit}}$
$x = 7.5$ units
... (ii)
So, a bar of length 7.5 units will represent 75 crore.
The first blank should be filled with '60'.
The second blank should be filled with '7.5'.
The complete statement is: On the scale of 1 unit length = 10 crore, the bar of length 6 units will represent 60 crore and of 7.5 units will represent 75 crore.
Question 22 to 55
Question 22. In an examination, the grades achieved by 30 students of a class are given below. Arrange these grades in a table using tally marks:
| B | C | C | E | A | C | B | B | D | D |
| D | D | B | C | C | C | A | C | B | E |
| A | D | C | B | E | C | B | E | C | D |
Answer:
To arrange the grades in a table using tally marks, we first list the distinct grades obtained by the students. The grades are A, B, C, D, and E.
Next, we count the frequency of each grade by going through the given list of grades and marking one tally stroke ($|$) for each occurrence. For every fifth occurrence, we draw a diagonal stroke across the previous four strokes to form a group of five ($\bcancel{||||}$).
Let's count the occurrences of each grade:
Grade A: Appears 3 times.
Grade B: Appears 7 times.
Grade C: Appears 10 times.
Grade D: Appears 6 times.
Grade E: Appears 4 times.
Now, we represent these counts using tally marks:
Grade A: $|||$
Grade B: $\bcancel{||||}$ $||$
Grade C: $\bcancel{||||}$ $\bcancel{||||}$
Grade D: $\bcancel{||||}$ $|$
Grade E: $||||$
Finally, we construct the frequency distribution table with columns for Grade, Tally Marks, and Frequency.
| Grade | Tally Marks | Number of Students (Frequency) |
| A | $|||$ | 3 |
| B | $\bcancel{||||}$ $||$ | 7 |
| C | $\bcancel{||||}$ $\bcancel{||||}$ | 10 |
| D | $\bcancel{||||}$ $|$ | 6 |
| E | $||||$ | 4 |
| Total | 30 |
The table above shows the distribution of grades among the 30 students using tally marks.
Question 23. The number of two wheelers owned individually by each of 50 families are listed below. Make a table using tally marks.
| 1 | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 1 |
| 0 | 1 | 1 | 2 | 3 | 1 | 2 | 1 | 1 | 2 |
| 1 | 2 | 3 | 1 | 0 | 2 | 1 | 0 | 2 | 1 |
| 2 | 1 | 2 | 1 | 1 | 4 | 1 | 3 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | 2 | 3 | 2 | 1 | 1 |
Find the number of families having two or more, two wheelers.
Answer:
First, we need to create a frequency distribution table for the number of two-wheelers owned by 50 families using tally marks. The distinct values for the number of two-wheelers are 0, 1, 2, 3, and 4.
We will count the frequency of each value by going through the list and using tally marks:
0: Appears 3 times.
1: Appears 23 times.
2: Appears 14 times.
3: Appears 4 times.
4: Appears 1 time.
Now, we represent these counts using tally marks:
0: $|||$
1: $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $|||$
2: $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $||||$
3: $||||$
4: $|$
Here is the frequency distribution table:
| Number of Two-wheelers | Tally Marks | Number of Families (Frequency) |
| 0 | $|||$ | 3 |
| 1 | $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $|||$ | 23 |
| 2 | $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $||||$ | 14 |
| 3 | $||||$ | 4 |
| 4 | $|$ | 1 |
| Total | 50 |
Next, we need to find the number of families having two or more two-wheelers. This includes families who own 2, 3, or 4 two-wheelers.
From the table, the number of families with:
2 two-wheelers is 14.
3 two-wheelers is 4.
4 two-wheelers is 1.
The total number of families having two or more two-wheelers is the sum of these frequencies:
Number of families ($\geq 2$ two-wheelers) = (Freq. of 2) + (Freq. of 3) + (Freq. of 4)
Number of families ($\geq 2$ two-wheelers) = $14 + 4 + 1$
Number of families ($\geq 2$ two-wheelers) = 19
... (i)
Thus, 19 families have two or more two-wheelers.
Question 24. The lengths in centimetres (to the nearest centimetre) of 30 carrots are given as follows:
| 15 | 22 | 21 | 20 | 22 | 15 | 15 | 20 | 20 | 15 |
| 20 | 18 | 20 | 22 | 21 | 20 | 21 | 18 | 21 | 18 |
| 20 | 18 | 21 | 18 | 22 | 20 | 15 | 21 | 18 | 20 |
Arrange the data given above in a table using tally marks and answerthe following questions.
(a) What is the number of carrots which have length more than 20 cm?
(b) Which length of the carrots occur maximum number of times? Minimum number of times?
Answer:
First, we need to arrange the given data in a table using tally marks. The distinct lengths of the carrots are 15 cm, 18 cm, 20 cm, 21 cm, and 22 cm.
We will count the frequency of each length by going through the list and using tally marks:
Length 15 cm: Appears 5 times.
Length 18 cm: Appears 6 times.
Length 20 cm: Appears 9 times.
Length 21 cm: Appears 6 times.
Length 22 cm: Appears 4 times.
Now, we represent these counts using tally marks:
15 cm: $\bcancel{||||}$
18 cm: $\bcancel{||||}$ $|$
20 cm: $\bcancel{||||}$ $\bcancel{||||}$ $|$
21 cm: $\bcancel{||||}$ $|$
22 cm: $||||$
Here is the frequency distribution table:
| Length (in cm) | Tally Marks | Number of Carrots (Frequency) |
| 15 | $\bcancel{||||}$ | 5 |
| 18 | $\bcancel{||||}$ $|$ | 6 |
| 20 | $\bcancel{||||}$ $\bcancel{||||}$ $|$ | 9 |
| 21 | $\bcancel{||||}$ $|$ | 6 |
| 22 | $||||$ | 4 |
| Total | 30 |
Now, we answer the questions based on the table:
(a) What is the number of carrots which have length more than 20 cm?
We need to find the number of carrots with lengths greater than 20 cm. From the table, the lengths greater than 20 cm are 21 cm and 22 cm.
Number of carrots with length 21 cm = 6
Number of carrots with length 22 cm = 4
The total number of carrots with length more than 20 cm is the sum of these frequencies:
Number of carrots ($> 20$ cm) = (Freq. of 21 cm) + (Freq. of 22 cm)
Number of carrots ($> 20$ cm) = $6 + 4$
Number of carrots ($> 20$ cm) = 10
... (i)
There are 10 carrots with a length of more than 20 cm.
(b) Which length of the carrots occur maximum number of times? Minimum number of times?
To find the length that occurs the maximum number of times, we look for the highest frequency in the table. The frequencies are 5, 6, 9, 6, and 4.
The maximum frequency is 9, which corresponds to the length 20 cm.
To find the length that occurs the minimum number of times, we look for the lowest frequency in the table. The frequencies are 5, 6, 9, 6, and 4.
The minimum frequency is 4, which corresponds to the length 22 cm.
The length that occurs the maximum number of times is 20 cm.
The length that occurs the minimum number of times is 22 cm.
Question 25. Thirty students were interviewed to find out what they want to be in future. Their responses are listed as below:
| doctor | engineer | doctor | pilot | officer | doctor |
| engineer | doctor | pilot | officer | pilot | engineer |
| officer | pilot | doctor | engineer | pilot | officer |
| doctor | officer | doctor | pilot | engineer | doctor |
| pilot | officer | doctor | pilot | doctor | engineer |
Arrange the data in a table using tally marks.
Answer:
To arrange the data in a table using tally marks, we first identify the different future professions chosen by the students. The professions are doctor, engineer, pilot, and officer.
Next, we will count the frequency of each profession by going through the list of responses and marking one tally stroke ($|$) for each occurrence. For every fifth occurrence, we draw a diagonal stroke across the previous four strokes ($\bcancel{||||}$).
Let's count the occurrences of each profession:
Doctor: Appears 10 times.
Engineer: Appears 6 times.
Pilot: Appears 7 times.
Officer: Appears 7 times.
Now, we represent these counts using tally marks:
Doctor: $\bcancel{||||}$ $\bcancel{||||}$
Engineer: $\bcancel{||||}$ $|$
Pilot: $\bcancel{||||}$ $||$
Officer: $\bcancel{||||}$ $||$
Finally, we construct the frequency distribution table with columns for Profession, Tally Marks, and Number of Students (Frequency).
| Profession | Tally Marks | Number of Students (Frequency) |
| doctor | $\bcancel{||||}$ $\bcancel{||||}$ | 10 |
| engineer | $\bcancel{||||}$ $|$ | 6 |
| pilot | $\bcancel{||||}$ $||$ | 7 |
| officer | $\bcancel{||||}$ $||$ | 7 |
| Total | 30 |
The table above shows the distribution of desired future professions among the 30 students using tally marks.
Question 26. Following are the choices of games of 40 students of Class VI:
| football | cricket | football | kho-kho | hockey | cricket |
| hockey | kho-kho | tennis | tennis | cricket | football |
| football | hockey | kho-kho | football | cricket | tennis |
| football | hockey | kho-kho | football | cricket | cricket |
| football | hockey | kho-kho | tennis | football | hockey |
| cricket | football | hockey | cricket | football | kho-kho |
| football | cricket | hockey | football |
(a) Arrange the choices of games in a table using tally marks.
(b) Which game is liked by most of the students?
(c) Which game is liked by minimum number of students?
Answer:
(a) Arrange the choices of games in a table using tally marks.
To arrange the choices of games in a table using tally marks, we first identify the distinct games. The games mentioned are football, cricket, kho-kho, hockey, and tennis.
Next, we count the frequency of each game by going through the given list of choices and marking one tally stroke ($|$) for each occurrence. For every fifth occurrence, we draw a diagonal stroke across the previous four strokes ($\bcancel{||||}$).
Let's count the occurrences of each game:
Football: Appears 12 times.
Cricket: Appears 10 times.
Kho-kho: Appears 6 times.
Hockey: Appears 8 times.
Tennis: Appears 4 times.
Now, we represent these counts using tally marks:
Football: $\bcancel{||||}$ $\bcancel{||||}$ $||$
Cricket: $\bcancel{||||}$ $\bcancel{||||}$
Kho-kho: $\bcancel{||||}$ $|$
Hockey: $\bcancel{||||}$ $|||$
Tennis: $||||$
Here is the frequency distribution table:
| Game | Tally Marks | Number of Students (Frequency) |
| football | $\bcancel{||||}$ $\bcancel{||||}$ $||$ | 12 |
| cricket | $\bcancel{||||}$ $\bcancel{||||}$ | 10 |
| kho-kho | $\bcancel{||||}$ $|$ | 6 |
| hockey | $\bcancel{||||}$ $|||$ | 8 |
| tennis | $||||$ | 4 |
| Total | 40 |
(b) Which game is liked by most of the students?
To find the game liked by most students, we look for the game with the highest frequency in the table. The frequencies are 12, 10, 6, 8, and 4.
The maximum frequency is 12, which corresponds to the game 'football'.
The game liked by most of the students is football.
(c) Which game is liked by minimum number of students?
To find the game liked by the minimum number of students, we look for the game with the lowest frequency in the table. The frequencies are 12, 10, 6, 8, and 4.
The minimum frequency is 4, which corresponds to the game 'tennis'.
The game liked by minimum number of students is tennis.
Question 27. Fill in the blanks in the following table which represents shirt size of 40 students of a school.
| Shirt size | Tally Marks | Number of students |
|---|---|---|
| 30 | $|||$ | 3 |
| 32 | $\bcancel{||||}$ | __ |
| 34 | __ | 8 |
| 36 | $\bcancel{||||} ||$ | __ |
| 38 | $\bcancel{||||}$ ___ | 10 |
| 40 | ___ | 7 |
Answer:
We are given a frequency distribution table with some missing entries for the number of students and tally marks. We need to fill in the blanks based on the provided information in each row.
Let's go through each row with missing information:
For Shirt size 32:
The tally marks are $\bcancel{||||}$. This represents one group of five.
Number of students = 5.
For Shirt size 34:
The number of students is 8. To represent 8 using tally marks, we use one group of five and three additional strokes.
Tally marks for 8 = $\bcancel{||||}$ $|||$.
For Shirt size 36:
The tally marks are $\bcancel{||||}$ $||$. This represents one group of five ($\bcancel{||||}$) plus two additional strokes ($||$).
Number of students = $5 + 2 = 7$.
For Shirt size 38:
The number of students is 10. The tally marks shown are $\bcancel{||||}$ ___. This is one group of five. To reach a total of 10, we need another group of five.
The missing tally marks should be $\bcancel{||||}$. The complete tally marks for 10 are $\bcancel{||||}$ $\bcancel{||||}$.
For Shirt size 40:
The number of students is 7. To represent 7 using tally marks, we use one group of five and two additional strokes.
Tally marks for 7 = $\bcancel{||||}$ $||$.
Now we can fill in the blanks in the table.
| Shirt size | Tally Marks | Number of Students |
| 30 | $|||$ | 3 |
| 32 | $\bcancel{||||}$ | 5 |
| 34 | $\bcancel{||||}$ $|||$ | 8 |
| 36 | $\bcancel{||||}$ $||$ | 7 |
| 38 | $\bcancel{||||}$ $\bcancel{||||}$ | 10 |
| 40 | $\bcancel{||||}$ $||$ | 7 |
| Total | 40 |
The completed table shows the distribution of shirt sizes among the 40 students.
Question 28. Following pictograph represents some surnames of people listed in the telephone directory of a city

Observe the pictograph and answer the following questions:
(a) How many people have surname ‘Roy’?
(b) Which surname appears the maximum number of times in the telephone directory?
(c) Which surname appears the least number of times in the directory?
(d) Which two surnames appear an equal number of times?
Answer:
To answer the questions, we need to observe the given pictograph. The pictograph shows different surnames and uses a symbol to represent a certain number of people.
First, let's find the key of the pictograph. The key states that  represents 10 people.
represents 10 people.
Also, it appears that the symbol  represents half of the full symbol, so it represents $\frac{1}{2} \times 10 = 5$ people.
represents half of the full symbol, so it represents $\frac{1}{2} \times 10 = 5$ people.
Now, let's find the number of people for each surname by counting the symbols:
Surname: Gupta
Symbols: 





Number of people with surname Gupta = $5 \times 10 + 1 \times 5 = 50 + 5 = 55$.
Surname: Sharma
Symbols: 





Number of people with surname Sharma = $6 \times 10 = 60$.
Surname: Roy
Symbols: 


Number of people with surname Roy = $3 \times 10 = 30$.
Surname: Mehta
Symbols: 



Number of people with surname Mehta = $4 \times 10 = 40$.
Surname: Arora
Symbols: 



Number of people with surname Arora = $4 \times 10 = 40$.
Now we can answer the questions:
(a) How many people have surname ‘Roy’?
From our count, the number of people with surname Roy is 30.
Answer (a): 30
(b) Which surname appears the maximum number of times in the telephone directory?
Comparing the counts: Gupta (55), Sharma (60), Roy (30), Mehta (40), Arora (40).
The maximum count is 60, which corresponds to the surname Sharma.
Answer (b): Sharma
(c) Which surname appears the least number of times in the directory?
Comparing the counts: Gupta (55), Sharma (60), Roy (30), Mehta (40), Arora (40).
The minimum count is 30, which corresponds to the surname Roy.
Answer (c): Roy
(d) Which two surnames appear an equal number of times?
Comparing the counts: Gupta (55), Sharma (60), Roy (30), Mehta (40), Arora (40).
We can see that the surnames Mehta and Arora both have a count of 40.
Answer (d): Mehta and Arora
Question 29. Students of Class VI in a school were given a task to count the number of articles made of different materials in the school. The information collected by them is represented as follows:

Observe the pictograph and answer the following questions:
(a) Which material is used in maximum number of articles?
(b) Which material is used in minimum number of articles?
(c) Which material is used in exactly half the number of articles as those made up of metal?
(d) What is the total number of articles counted by the students?
Answer:
To answer the questions, we need to observe the given pictograph. The pictograph shows the number of articles made of different materials and uses a key to represent the quantity.
The key of the pictograph states that the symbol  represents 20 articles. The half symbol
represents 20 articles. The half symbol  represents half of the value of the full symbol, which is $\frac{1}{2} \times 20 = 10$ articles.
represents half of the value of the full symbol, which is $\frac{1}{2} \times 20 = 10$ articles.
Now, let's find the number of articles made of each material by counting the symbols:
Material: Wood
Symbols: 4 full symbols (


 )
)
Number of Wood articles = $4 \times 20 = 80$.
Material: Glass
Symbols: 3 full symbols (

 ) and 1 half symbol (
) and 1 half symbol ( )
)
Number of Glass articles = $3 \times 20 + 1 \times 10 = 60 + 10 = 70$.
Material: Metal
Symbols: 6 full symbols (




 )
)
Number of Metal articles = $6 \times 20 = 120$.
Material: Plastic
Symbols: 5 full symbols (



 )
)
Number of Plastic articles = $5 \times 20 = 100$.
Material: Paper
Symbols: 2 full symbols (
 )
)
Number of Paper articles = $2 \times 20 = 40$.
Summary of the number of articles for each material:
Wood: 80
Glass: 70
Metal: 120
Plastic: 100
Paper: 40
Now we answer the questions:
(a) Which material is used in maximum number of articles?
Comparing the number of articles (80, 70, 120, 100, 40), the maximum number is 120.
The material corresponding to 120 articles is Metal.
Answer (a): Metal
(b) Which material is used in minimum number of articles?
Comparing the number of articles (80, 70, 120, 100, 40), the minimum number is 40.
The material corresponding to 40 articles is Paper.
Answer (b): Paper
(c) Which material is used in exactly half the number of articles as those made up of metal?
The number of articles made up of metal is 120.
Half the number of articles made up of metal is $\frac{1}{2} \times 120 = 60$.
We need to check if any material has exactly 60 articles.
Looking at the counts (80, 70, 120, 100, 40), none of the materials has exactly 60 articles.
Answer (c): None (Based on the provided data, no material has exactly 60 articles)
(d) Which two surnames appear an equal number of times?
This question seems to be from the previous problem (Question 28) regarding surnames, not the current problem (Question 29) regarding materials.
Assuming the question intends to ask about materials instead of surnames: "Which two materials appear an equal number of times?"
Comparing the number of articles for each material (80, 70, 120, 100, 40), all the numbers are distinct.
Therefore, based on the provided data, no two materials appear an equal number of times.
If the question is indeed asking about surnames from Question 28, the answer would be Mehta and Arora (both 40).
Assuming the question is a copy-paste error and intended to ask about materials in this pictograph:
Answer (d): None (Based on the provided data, no two materials appear an equal number of times)
There is usually a part (e) in such questions asking for the total number of articles. Let's calculate that as well, although it is not explicitly asked here.
Total number of articles = $80 + 70 + 120 + 100 + 40 = 410$.
Question 30. The number of scouts in a school is depicted by the following pictograph:

Observe the pictograph and answer the following questions:
(a) Which class has the minimum number of scouts?
(b) Which class has the maximum number of scouts?
(c) How many scouts are there in Class VI?
(d) Which class has exactly four times the scouts as that of Class X?
(e) What is the total number of scouts in the Classes VI to X?
Answer:
To answer the questions, we need to observe the given pictograph and determine the number of scouts in each class based on the key.
The key of the pictograph states that one symbol  represents 10 scouts.
represents 10 scouts.
The half symbol 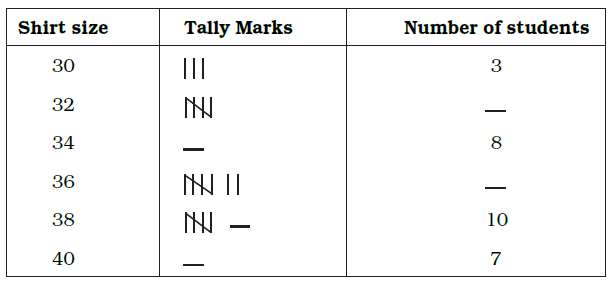 represents $\frac{1}{2}$ of the full symbol, which is $\frac{1}{2} \times 10 = 5$ scouts.
represents $\frac{1}{2}$ of the full symbol, which is $\frac{1}{2} \times 10 = 5$ scouts.
Let's count the number of scouts for each class:
Class VI: There are 4 full symbols. Number of scouts = $4 \times 10 = 40$.
Class VII: There are 5 full symbols. Number of scouts = $5 \times 10 = 50$.
Class VIII: There are 6 full symbols. Number of scouts = $6 \times 10 = 60$.
Class IX: There are 4 full symbols and 1 half symbol. Number of scouts = $4 \times 10 + 1 \times 5 = 40 + 5 = 45$.
Class X: There are 3 full symbols. Number of scouts = $3 \times 10 = 30$.
Here is a summary of the number of scouts in each class:
| Class | Number of Scouts |
| VI | 40 |
| VII | 50 |
| VIII | 60 |
| IX | 45 |
| X | 30 |
Now we answer the questions based on the calculated numbers:
(a) Which class has the minimum number of scouts?
Comparing the number of scouts in each class (40, 50, 60, 45, 30), the minimum number is 30.
The class with the minimum number of scouts is Class X.
Answer (a): Class X
(b) Which class has the maximum number of scouts?
Comparing the number of scouts in each class (40, 50, 60, 45, 30), the maximum number is 60.
The class with the maximum number of scouts is Class VIII.
Answer (b): Class VIII
(c) How many scouts are there in Class VI?
From our calculation, the number of scouts in Class VI is 40.
Answer (c): 40
(d) Which class has exactly four times the scouts as that of Class X?
The number of scouts in Class X is 30.
Four times the number of scouts in Class X is $4 \times 30 = 120$.
Looking at the number of scouts in each class (40, 50, 60, 45, 30), none of the classes have exactly 120 scouts.
Answer (d): None
(e) What is the total number of scouts in the Classes VI to X?
To find the total number of scouts, we sum the number of scouts in each class:
Total Scouts = (Scouts in VI) + (Scouts in VII) + (Scouts in VIII) + (Scouts in IX) + (Scouts in X)
Total Scouts = $40 + 50 + 60 + 45 + 30$
Total Scouts = $90 + 60 + 45 + 30$
Total Scouts = $150 + 45 + 30$
Total Scouts = $195 + 30$
Total Scouts = 225
... (i)
The total number of scouts in Classes VI to X is 225.
Answer (e): 225
Question 31. A survey was carried out in a certain school to find out the popular school subjects among students of Classes VI to VIII. The data in this regard is displayed as pictograph given below:

(a) Which subject is most popular among the students?
(b) How many students like Mathematics?
(c) Find the number of students who like subjects other than Mathematics and Science.
Answer:
To answer the questions, we need to interpret the given pictograph which shows the popularity of school subjects among students of Classes VI to VIII.
First, we identify the key of the pictograph. The key states that the symbol  represents 30 students.
represents 30 students.
Now, we count the number of symbols for each subject and calculate the number of students who like each subject:
English: There are 3 full symbols. Number of students = $3 \times 30 = 90$.
Hindi: There are 4 full symbols. Number of students = $4 \times 30 = 120$.
Mathematics: There are 5 full symbols. Number of students = $5 \times 30 = 150$.
Science: There are 4 full symbols. Number of students = $4 \times 30 = 120$.
Social Science: There are 3 full symbols. Number of students = $3 \times 30 = 90$.
Here is a summary of the number of students who like each subject:
| Subject | Number of Students |
| English | 90 |
| Hindi | 120 |
| Mathematics | 150 |
| Science | 120 |
| Social Science | 90 |
Now, we answer the questions based on the calculated numbers:
(a) Which subject is most popular among the students?
To find the most popular subject, we look for the subject with the highest number of students. Comparing the numbers (90, 120, 150, 120, 90), the maximum number is 150.
The subject corresponding to the maximum number is Mathematics.
Answer (a): Mathematics
(b) How many students like Mathematics?
From our calculation, the number of students who like Mathematics is 150.
Answer (b): 150
(c) Find the number of students who like subjects other than Mathematics and Science.
The subjects other than Mathematics and Science are English, Hindi, and Social Science.
Number of students who like English = 90.
Number of students who like Hindi = 120.
Number of students who like Social Science = 90.
The total number of students who like subjects other than Mathematics and Science is the sum of these numbers:
Total = (Students for English) + (Students for Hindi) + (Students for Social Science)
Total = $90 + 120 + 90$
Total = $210 + 90$
Total = 300
... (i)
The number of students who like subjects other than Mathematics and Science is 300.
Answer (c): 300
Question 32. The following pictograph depicts the information about the areas in sqkm (to nearest hundred) of some districts of Chhattisgarh State:

(a) What is the area of Koria district?
(b) Which two districts have the same area?
(c) How many districts have area more than 5000 square kilometres?
Answer:
To answer these questions, we need to refer to the provided pictograph and its key. However, the image link provided appears to be for a different pictograph, likely from a previous question (Question 31), representing student popularity for subjects, not district areas. The correct pictograph for the areas of Chhattisgarh districts is missing or incorrectly linked.
Assuming a standard pictograph format where a symbol represents a certain number of square kilometres, we would need to:
1. Identify the key of the pictograph (the value represented by one symbol).
2. Count the number of symbols shown for each district (Bilaspur, Surguja, Rajnandgaon, Durg, Koria, Raigarh, Bastar).
3. Multiply the number of symbols for each district by the value of one symbol (from the key) to find the area of that district.
Based on the structure of the question asking for areas in "sqkm (to nearest hundred)", it is likely that the key symbol represents a value like 100, 500, 1000, or some other multiple of 100.
(a) What is the area of Koria district?
To find the area of Koria district, we would count the number of symbols shown next to 'Koria' in the pictograph and multiply this count by the value of one symbol (as given in the key). Without the correct pictograph image and key, we cannot determine the specific area.
(b) Which two districts have the same area?
To find which two districts have the same area, we would calculate the area for each district (as described above) and then compare the calculated areas to see if any two districts have the exact same value. Without the correct pictograph, we cannot identify these districts.
(c) How many districts have area more than 5000 square kilometres?
To answer this question, we would first calculate the area for each district. Then, we would count how many of these calculated areas are strictly greater than 5000 square kilometres. Without the correct pictograph and the areas it represents, we cannot determine the number of such districts.
Due to the absence of the correct pictograph image and its key, the specific numerical answers to questions (a), (b), and (c) cannot be provided.
Question 33. The number of bottles of cold drinks sold by a shopkeeper on six consecutive days is as follows:
| Day | Sunday | Monday | Tuesday | Wednesday | Thursday | Friday |
|---|---|---|---|---|---|---|
| Number of bottles | 350 | 200 | 300 | 250 | 100 | 150 |
Prepare a pictograph of the data using one symbol to represent 50 bottles.
Answer:
Given:
The number of cold drinks bottles sold by a shopkeeper on six consecutive days is provided in the table in the question.
To Prepare:
A pictograph of the given data using one symbol to represent 50 bottles.
Solution:
Let us use the symbol '$\cup$' to represent 50 bottles of cold drinks.
Now, we calculate the number of symbols needed for each day by dividing the number of bottles sold by 50.
Number of symbols for Sunday = $350 \div 50 = 7$
Number of symbols for Monday = $200 \div 50 = 4$
Number of symbols for Tuesday = $300 \div 50 = 6$
Number of symbols for Wednesday = $250 \div 50 = 5$
Number of symbols for Thursday = $100 \div 50 = 2$
Number of symbols for Friday = $150 \div 50 = 3$
Pictograph:
| Day | Number of Bottles Sold |
| Sunday | $\cup$ $\cup$ $\cup$ $\cup$ $\cup$ $\cup$ $\cup$ |
| Monday | $\cup$ $\cup$ $\cup$ $\cup$ |
| Tuesday | $\cup$ $\cup$ $\cup$ $\cup$ $\cup$ $\cup$ |
| Wednesday | $\cup$ $\cup$ $\cup$ $\cup$ $\cup$ |
| Thursday | $\cup$ $\cup$ |
| Friday | $\cup$ $\cup$ $\cup$ |
Key:
$\cup$ = 50 bottles
Question 34. The following table gives information about the circulation of newspapers (dailies) in a town in five languages.
| Language | English | Hindi | Tamil | Punjabi | Gujrati |
|---|---|---|---|---|---|
| Number of newspapers | 5000 | 8500 | 500 | 2500 | 1000 |
Prepare a pictograph of the above data, using a symbol of your choice, each representing 1000 newspapers.
Answer:
Given:
The circulation of newspapers in five languages is provided in the table in the question.
To Prepare:
A pictograph of the given data, using a symbol of choice, where each symbol represents 1000 newspapers.
Solution:
Let us use the symbol '$\clubsuit$' to represent 1000 newspapers.
Since one symbol represents 1000 newspapers, a half symbol will represent 500 newspapers.
Number of symbols for English = $5000 \div 1000 = 5$ symbols.
Number of symbols for Hindi = $8500 \div 1000 = 8.5$ symbols, which is 8 full symbols and 1 half symbol.
Number of symbols for Tamil = $500 \div 1000 = 0.5$ symbols, which is 1 half symbol.
Number of symbols for Punjabi = $2500 \div 1000 = 2.5$ symbols, which is 2 full symbols and 1 half symbol.
Number of symbols for Gujrati = $1000 \div 1000 = 1$ symbol.
Pictograph:
| Language | Number of Newspapers |
| English | $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ |
| Hindi | $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ $\clubsuit$ $\frac{1}{2}\clubsuit$ |
| Tamil | $\frac{1}{2}\clubsuit$ |
| Punjabi | $\clubsuit$ $\clubsuit$ $\frac{1}{2}\clubsuit$ |
| Gujrati | $\clubsuit$ |
Key:
$\clubsuit$ = 1000 newspapers
$\frac{1}{2}\clubsuit$ = 500 newspapers
Question 35. Annual expenditure of a company in the year 2007-2008 is given below:
| Items | Expenditure (RS in lakh) |
|---|---|
| Salaries of employees | 65 |
| Advertisement | 10 |
| Purchase of machinery | 85 |
| Electricity and water | 15 |
| Transport | 25 |
| Other expenses | 30 |
Prepare a pictograph of the above data using an appropriate symbol to represent Rs 10 lakh.
Answer:
Given:
The annual expenditure of a company in the year 2007-2008 on various items is provided in the table in the question.
To Prepare:
A pictograph of the given data using an appropriate symbol to represent $\textsf{₹}$ 10 lakh.
Solution:
Let us use the symbol '$\circledast$' to represent $\textsf{₹}$ 10 lakh of expenditure.
Since one symbol represents $\textsf{₹}$ 10 lakh, a half symbol will represent $\textsf{₹}$ 5 lakh.
Number of symbols for Salaries of employees = $65 \div 10 = 6.5$ symbols, which is 6 full symbols and 1 half symbol.
Number of symbols for Advertisement = $10 \div 10 = 1$ symbol.
Number of symbols for Purchase of machinery = $85 \div 10 = 8.5$ symbols, which is 8 full symbols and 1 half symbol.
Number of symbols for Electricity and water = $15 \div 10 = 1.5$ symbols, which is 1 full symbol and 1 half symbol.
Number of symbols for Transport = $25 \div 10 = 2.5$ symbols, which is 2 full symbols and 1 half symbol.
Number of symbols for Other expenses = $30 \div 10 = 3$ symbols.
Pictograph:
| Items | Expenditure ($\textsf{₹}$ in lakh) |
| Salaries of employees | $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\frac{1}{2}\circledast$ |
| Advertisement | $\circledast$ |
| Purchase of machinery | $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\circledast$ $\frac{1}{2}\circledast$ |
| Electricity and water | $\circledast$ $\frac{1}{2}\circledast$ |
| Transport | $\circledast$ $\circledast$ $\frac{1}{2}\circledast$ |
| Other expenses | $\circledast$ $\circledast$ $\circledast$ |
Key:
$\circledast$ = $\textsf{₹}$ 10 lakh
$\frac{1}{2}\circledast$ = $\textsf{₹}$ 5 lakh
Question 36. The following bar graph shows the number of houses (out of 100) in a town using different types of fuels for cooking.
Read the bar graph and answer the following questions:
Scale: 1 unit length = 5 houses
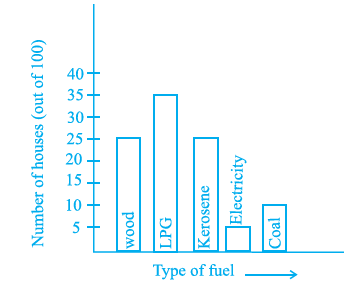
(a) Which fuel is used in maximum number of houses?
(b) How many houses are using coal as fuel?
(c) Suppose that the total number of houses in the town is 1 lakh. From the above graph estimate the number of houses using electricity.
Answer:
Given:
A bar graph showing the number of houses (out of 100) in a town using different types of fuels for cooking.
Scale: 1 unit length = 5 houses.
To Answer:
The questions asked based on the given bar graph.
Solution:
From the bar graph, we can read the number of houses using each type of fuel by using the given scale (1 unit length = 5 houses).
Number of houses using LPG = 8 unit lengths $\times$ 5 houses/unit length = 40 houses.
Number of houses using Kerosene = 3 unit lengths $\times$ 5 houses/unit length = 15 houses.
Number of houses using Coal = 4 unit lengths $\times$ 5 houses/unit length = 20 houses.
Number of houses using Electricity = 1 unit length $\times$ 5 houses/unit length = 5 houses.
Number of houses using Wood = 4 unit lengths $\times$ 5 houses/unit length = 20 houses.
Answering the questions:
(a) To find the fuel used in the maximum number of houses, we compare the number of houses for each fuel type. The maximum number of houses is 40, which corresponds to LPG.
So, LPG is used in the maximum number of houses.
(b) From the data read from the graph, the number of houses using coal as fuel is 20.
So, 20 houses are using coal as fuel.
(c) The bar graph shows the data for 100 houses. Out of 100 houses, 5 houses use electricity.
This means the proportion of houses using electricity is $\frac{5}{100}$.
The total number of houses in the town is 1 lakh, which is 100,000 houses.
To estimate the number of houses using electricity in the town, we multiply the total number of houses by the proportion of houses using electricity from the graph.
Estimated number of houses using electricity = (Proportion of houses using electricity) $\times$ (Total number of houses in town)
Estimated number of houses using electricity = $\frac{5}{100} \times 100000$
Estimated number of houses using electricity = $0.05 \times 100000$
Estimated number of houses using electricity = $5000$
So, the estimated number of houses using electricity is 5000.
Question 37. The following bar graph represents the data for different sizes of shoes worn by the students in a school. Read the graph and answer the following questions.
Scale : 1 unit length = 50 students
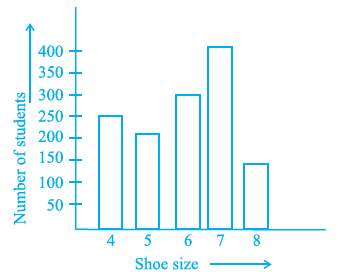
(a) Find the number of students whose shoe sizes have been collected.
(b) What is the number of students wearing shoe size 6?
(c) What are the different sizes of the shoes worn by the students?
(d) Which shoe size is worn by the maximum number of students?
(e) Which shoe size is worn by minimum number of students?
(f) State whether true or false:
The total number of students wearing shoe sizes 5 and 8 is the same as the number of students wearing shoe size 6.
Answer:
Given:
A bar graph showing the number of students wearing different shoe sizes in a school.
Scale: 1 unit length = 50 students.
To Answer:
The questions asked based on the given bar graph.
Solution:
From the bar graph, we read the number of students for each shoe size using the given scale (1 unit length = 50 students).
Number of students wearing size 4 = 2 unit lengths $\times$ 50 students/unit length = 100 students.
Number of students wearing size 5 = 4 unit lengths $\times$ 50 students/unit length = 200 students.
Number of students wearing size 6 = 5 unit lengths $\times$ 50 students/unit length = 250 students.
Number of students wearing size 7 = 3 unit lengths $\times$ 50 students/unit length = 150 students.
Number of students wearing size 8 = 2 unit lengths $\times$ 50 students/unit length = 100 students.
Answering the questions:
(a) To find the total number of students whose shoe sizes have been collected, we sum the number of students for each shoe size.
Total number of students = (Students of size 4) + (Students of size 5) + (Students of size 6) + (Students of size 7) + (Students of size 8)
Total number of students = 100 + 200 + 250 + 150 + 100
Total number of students = 800
So, the number of students whose shoe sizes have been collected is 800.
(b) From the data read from the graph, the number of students wearing shoe size 6 is 250.
So, the number of students wearing shoe size 6 is 250.
(c) The different shoe sizes represented in the bar graph are listed on the horizontal axis (x-axis).
The different sizes of shoes worn by the students are 4, 5, 6, 7, and 8.
(d) To find which shoe size is worn by the maximum number of students, we compare the number of students for each size. The maximum number of students is 250, which corresponds to shoe size 6.
So, shoe size 6 is worn by the maximum number of students.
(e) To find which shoe size is worn by the minimum number of students, we compare the number of students for each size. The minimum number of students is 100, which corresponds to shoe sizes 4 and 8.
So, shoe sizes 4 and 8 are worn by the minimum number of students.
(f) We need to compare the total number of students wearing shoe sizes 5 and 8 with the number of students wearing shoe size 6.
Number of students wearing shoe size 5 = 200
Number of students wearing shoe size 8 = 100
Total number of students wearing shoe sizes 5 and 8 = 200 + 100 = 300
Number of students wearing shoe size 6 = 250
Comparing the two values: $300 \ne 250$.
The statement says that the total number of students wearing shoe sizes 5 and 8 is the same as the number of students wearing shoe size 6, which is false.
So, the statement is False.
Question 38. The following graph gives the information about the number of railway tickets sold for different cities on a railway ticket counter between 6.00 am to 10.00 am. Read the bar graph and answer the following questions.
Scale : 1 unit length = 10 tickets
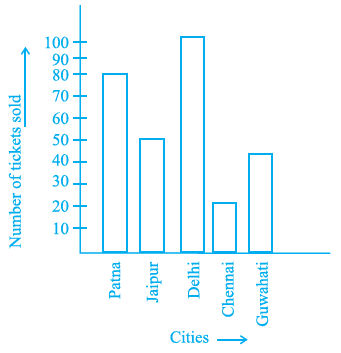
(a) How many tickets were sold in all?
(b) For which city were themaximum number oftickets sold?
(c) For which city were the minimum number of tickets sold?
(d) Name the cities for which the number of tickets sold is more than 20.
(e) Fill in the blanks:
Number of tickets sold for Delhi and Jaipur together exceeds the total number of tickets sold for Patna and Chennai by ______.
Answer:
Given:
A bar graph showing the number of railway tickets sold for different cities.
Time duration: 6:00 am to 10:00 am.
Scale: 1 unit length = 10 tickets.
To Answer:
The questions asked based on the given bar graph.
Solution:
From the bar graph, we read the number of tickets sold for each city using the given scale (1 unit length = 10 tickets).
Number of tickets sold for Delhi = 5 unit lengths $\times$ 10 tickets/unit length = 50 tickets.
Number of tickets sold for Patna = 2 unit lengths $\times$ 10 tickets/unit length = 20 tickets.
Number of tickets sold for Kolkata = 4 unit lengths $\times$ 10 tickets/unit length = 40 tickets.
Number of tickets sold for Jaipur = 6 unit lengths $\times$ 10 tickets/unit length = 60 tickets.
Number of tickets sold for Chennai = 3 unit lengths $\times$ 10 tickets/unit length = 30 tickets.
Answering the questions:
(a) To find the total number of tickets sold, we sum the number of tickets sold for all cities.
Total tickets sold = (Tickets for Delhi) + (Tickets for Patna) + (Tickets for Kolkata) + (Tickets for Jaipur) + (Tickets for Chennai)
Total tickets sold = 50 + 20 + 40 + 60 + 30
Total tickets sold = 200
So, 200 tickets were sold in all.
(b) To find the city for which the maximum number of tickets were sold, we compare the number of tickets for each city. The maximum number of tickets is 60, which corresponds to Jaipur.
So, the maximum number of tickets were sold for Jaipur.
(c) To find the city for which the minimum number of tickets were sold, we compare the number of tickets for each city. The minimum number of tickets is 20, which corresponds to Patna.
So, the minimum number of tickets were sold for Patna.
(d) We need to find the cities for which the number of tickets sold is more than 20. Comparing the numbers: 50 (Delhi) > 20, 20 (Patna) is not > 20, 40 (Kolkata) > 20, 60 (Jaipur) > 20, 30 (Chennai) > 20.
The cities for which the number of tickets sold is more than 20 are Delhi, Kolkata, Jaipur, and Chennai.
(e) We need to calculate the number of tickets sold for Delhi and Jaipur together and the number of tickets sold for Patna and Chennai together, and then find the difference.
Tickets sold for Delhi and Jaipur together = (Tickets for Delhi) + (Tickets for Jaipur) = 50 + 60 = 110.
Tickets sold for Patna and Chennai together = (Tickets for Patna) + (Tickets for Chennai) = 20 + 30 = 50.
Difference = (Tickets for Delhi and Jaipur) - (Tickets for Patna and Chennai)
Difference = 110 - 50 = 60.
So, the number of tickets sold for Delhi and Jaipur together exceeds the total number of tickets sold for Patna and Chennai by 60.
Question 39. The bar graph given below represents approximate length (in kilometres) of some National Highways in India. Study the bar graph and answer the following questions:
Scale : 1 unit length = 200km
(a) Which National Highway (N.H.) is the longest among the above?
(b) Which National Highway is the shortest among the above?
(c) What is the length of National Highway 9?
(d) Length of which National Highway is about three times the National Highway10?
Answer:
Given:
A bar graph showing the approximate length (in kilometres) of some National Highways in India.
Scale: 1 unit length = 200 km.
To Answer:
The questions asked based on the given bar graph.
Solution:
From the bar graph, we read the length of each National Highway using the given scale (1 unit length = 200 km).
Length of NH 2 = 7.5 unit lengths $\times$ 200 km/unit length = $7.5 \times 200 = 1500$ km.
Length of NH 8 = 7 unit lengths $\times$ 200 km/unit length = $7 \times 200 = 1400$ km.
Length of NH 3 = 5 unit lengths $\times$ 200 km/unit length = $5 \times 200 = 1000$ km.
Length of NH 9 = 2 unit lengths $\times$ 200 km/unit length = $2 \times 200 = 400$ km.
Length of NH 10 = 1 unit length $\times$ 200 km/unit length = $1 \times 200 = 200$ km.
Length of NH 6 = 8.5 unit lengths $\times$ 200 km/unit length = $8.5 \times 200 = 1700$ km.
Answering the questions:
(a) To find the longest National Highway, we compare the lengths: 1500 km (NH 2), 1400 km (NH 8), 1000 km (NH 3), 400 km (NH 9), 200 km (NH 10), 1700 km (NH 6). The maximum length is 1700 km, which corresponds to NH 6.
So, National Highway 6 is the longest among the above.
(b) To find the shortest National Highway, we compare the lengths. The minimum length is 200 km, which corresponds to NH 10.
So, National Highway 10 is the shortest among the above.
(c) From our calculation, the length of National Highway 9 is 400 km.
The length of National Highway 9 is 400 km.
(d) We need to find the National Highway whose length is about three times the length of National Highway 10.
Length of National Highway 10 = 200 km.
Three times the length of National Highway 10 = $3 \times 200$ km = 600 km.
Now we look for a highway among the given list whose length is approximately 600 km.
The lengths are: 1500 km, 1400 km, 1000 km, 400 km, 200 km, 1700 km.
Comparing these lengths to 600 km:
$|1500 - 600| = 900$
$|1400 - 600| = 800$
$|1000 - 600| = 400$
$|400 - 600| = 200$
$|200 - 600| = 400$
$|1700 - 600| = 1100$
The length closest to 600 km is 400 km, which is the length of NH 9. While 400 km is exactly twice 200 km, it is the length provided in the graph that is nearest to 600 km.
Alternatively, let's look at the ratio of each highway's length to the length of NH 10:
NH 2: $1500 \div 200 = 7.5$
NH 8: $1400 \div 200 = 7$
NH 3: $1000 \div 200 = 5$
NH 9: $400 \div 200 = 2$
NH 10: $200 \div 200 = 1$
NH 6: $1700 \div 200 = 8.5$
The ratio closest to 3 among these values (1, 2, 5, 7, 7.5, 8.5) is 2, which corresponds to NH 9.
Based on both interpretations (closest length to 600 km and closest ratio to 3), National Highway 9 is the answer, despite its length being exactly twice that of NH 10 as per the graph.
So, the length of National Highway 9 is about three times the National Highway 10 (based on the provided data being closest to the expected value/ratio).
Question 40. The bar graph given below represents the circulation of newspapers in different languages in a town. Study the bar graph and answer the following questions:
Scale : 1 unit length = 200 Newspapers
(a) What is the circulation of English newspaper?
(b) Name the two languages in which circulation of newspaper is the same.
(c) By how much is the circulation of newspaper in Hindi more than the newspaper in Bengali?
Answer:
Given:
A bar graph representing the circulation of newspapers in different languages in a town.
Scale: 1 unit length = 200 Newspapers.
To Answer:
The questions asked based on the given bar graph.
Solution:
From the bar graph, we read the circulation of newspapers for each language using the given scale (1 unit length = 200 Newspapers).
Circulation of English newspaper = 4 unit lengths $\times$ 200 Newspapers/unit length = $4 \times 200 = 800$ Newspapers.
Circulation of Hindi newspaper = 6.5 unit lengths $\times$ 200 Newspapers/unit length = $6.5 \times 200 = 1300$ Newspapers.
Circulation of Punjabi newspaper = 3 unit lengths $\times$ 200 Newspapers/unit length = $3 \times 200 = 600$ Newspapers.
Circulation of Urdu newspaper = 2 unit lengths $\times$ 200 Newspapers/unit length = $2 \times 200 = 400$ Newspapers.
Circulation of Bengali newspaper = 4 unit lengths $\times$ 200 Newspapers/unit length = $4 \times 200 = 800$ Newspapers.
Circulation of Telugu newspaper = 3.5 unit lengths $\times$ 200 Newspapers/unit length = $3.5 \times 200 = 700$ Newspapers.
Answering the questions:
(a) From our calculation, the circulation of English newspaper is 800.
The circulation of English newspaper is 800.
(b) Comparing the circulation numbers (800, 1300, 600, 400, 800, 700), we see that the circulation is the same for English (800) and Bengali (800).
The two languages in which the circulation of newspaper is the same are English and Bengali.
(c) We need to find the difference between the circulation of Hindi and Bengali newspapers.
Circulation of Hindi newspaper = 1300.
Circulation of Bengali newspaper = 800.
Difference = Circulation of Hindi - Circulation of Bengali
Difference = $1300 - 800 = 500$.
The circulation of newspaper in Hindi is more than the newspaper in Bengali by 500.
Question 41. Read the bar graph given below and answer the following questions:
Scale : 1 unit = 50 students
(a) What information is given by the bar graph?
(b) In which year is the number of students maximum?
(c) In which year is the number of students twice as that of 2001-02?
(d) In which year did the number of students decrease as compared to previous year?
(e) In which year is the increase in number of students maximum as compared to the previous year?
Answer:
Given:
A bar graph showing the number of students in a school over different academic years.
Scale: 1 unit length = 50 students.
To Answer:
The questions asked based on the given bar graph.
Solution:
From the bar graph, we read the number of students for each academic year using the given scale (1 unit length = 50 students).
Number of students in 2001-02 = 3 unit lengths $\times$ 50 students/unit length = $3 \times 50 = 150$ students.
Number of students in 2002-03 = 3.5 unit lengths $\times$ 50 students/unit length = $3.5 \times 50 = 175$ students.
Number of students in 2003-04 = 5 unit lengths $\times$ 50 students/unit length = $5 \times 50 = 250$ students.
Number of students in 2004-05 = 4.5 unit lengths $\times$ 50 students/unit length = $4.5 \times 50 = 225$ students.
Number of students in 2005-06 = 6 unit lengths $\times$ 50 students/unit length = $6 \times 50 = 300$ students.
Answering the questions:
(a) The bar graph gives information about the number of students in a school over different academic years from 2001-02 to 2005-06.
(b) Comparing the number of students each year (150, 175, 250, 225, 300), the maximum number is 300, which occurred in the year 2005-06.
The year in which the number of students is maximum is 2005-06.
(c) The number of students in 2001-02 is 150. Twice this number is $2 \times 150 = 300$. Looking at the number of students each year, 300 students were in the year 2005-06.
The year in which the number of students is twice as that of 2001-02 is 2005-06.
(d) We check the change in the number of students compared to the previous year:
Change in 2002-03: $175 - 150 = 25$ (Increase)
Change in 2003-04: $250 - 175 = 75$ (Increase)
Change in 2004-05: $225 - 250 = -25$ (Decrease)
Change in 2005-06: $300 - 225 = 75$ (Increase)
The number of students decreased in the year 2004-05.
The year in which the number of students decreased as compared to the previous year is 2004-05.
(e) We look at the increases calculated in part (d): 25 (2002-03), 75 (2003-04), 75 (2005-06). The maximum increase is 75, which occurred in the years 2003-04 and 2005-06.
The years in which the increase in the number of students is maximum as compared to the previous year are 2003-04 and 2005-06.
Question 42. The lengths in km (rounded to nearest hundred) of some major rivers of India is given below:
| River | Length (in km) |
|---|---|
| Narmada | 1300 |
| Mahanadi | 900 |
| Brahmputra | 2900 |
| Ganga | 2500 |
| Kaveri | 800 |
| Krishna | 1300 |
Draw a bar graph to represent the above information.
Answer:
Given:
The lengths (in km) of some major rivers of India are provided in the table in the question.
To Draw:
A bar graph to represent the given information.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Rivers' on the horizontal axis (x-axis) and the 'Length (in km)' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The lengths range from 800 km to 2900 km. Let's choose the scale as 1 unit length = 200 km.
Now, we calculate the height of the bars (in unit lengths) for each river by dividing its length by the scale value (200 km).
Height for Narmada = $1300 \div 200 = 6.5$ units.
Height for Mahanadi = $900 \div 200 = 4.5$ units.
Height for Brahmputra = $2900 \div 200 = 14.5$ units.
Height for Ganga = $2500 \div 200 = 12.5$ units.
Height for Kaveri = $800 \div 200 = 4$ units.
Height for Krishna = $1300 \div 200 = 6.5$ units.
Now, we can draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis and a vertical axis.
2. Mark points on the horizontal axis for each river (Narmada, Mahanadi, Brahmputra, Ganga, Kaveri, Krishna).
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the scale 1 unit length = 200 km (e.g., 0, 200, 400, 600, ..., 3000).
5. Draw rectangular bars corresponding to each river up to the calculated height (in units) or the corresponding length (in km) on the vertical axis.
The heights of the bars will be:
- Narmada: 6.5 units (representing 1300 km)
- Mahanadi: 4.5 units (representing 900 km)
- Brahmputra: 14.5 units (representing 2900 km)
- Ganga: 12.5 units (representing 2500 km)
- Kaveri: 4 units (representing 800 km)
- Krishna: 6.5 units (representing 1300 km)
Draw the bars accordingly to create the bar graph.
Question 43. The number of ATMs of different banks in a city is shown below:
| Bank | Number of ATMs |
|---|---|
| Syndicate Bank | 5 |
| Dena Bank | 15 |
| Indian Bank | 20 |
| State Bank of India | 25 |
| Vijya Bank | 10 |
Draw a bar graph to represent the above information by choosing the scale of your choice.
Answer:
Given:
The number of ATMs of different banks in a city is provided in the table in the question.
To Draw:
A bar graph to represent the given information by choosing an appropriate scale.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Banks' on the horizontal axis (x-axis) and the 'Number of ATMs' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The numbers of ATMs are 5, 10, 15, 20, and 25. Since all these numbers are multiples of 5, we can choose the scale as 1 unit length = 5 ATMs.
Now, we calculate the height of the bars (in unit lengths) for each bank by dividing the number of ATMs by the scale value (5 ATMs).
Height for Syndicate Bank = $5 \div 5 = 1$ unit.
Height for Dena Bank = $15 \div 5 = 3$ units.
Height for Indian Bank = $20 \div 5 = 4$ units.
Height for State Bank of India = $25 \div 5 = 5$ units.
Height for Vijya Bank = $10 \div 5 = 2$ units.
Now, we can draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis and a vertical axis.
2. Mark points on the horizontal axis for each bank (Syndicate Bank, Dena Bank, Indian Bank, State Bank of India, Vijya Bank).
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the chosen scale 1 unit length = 5 ATMs (e.g., 0, 5, 10, 15, 20, 25).
5. Draw rectangular bars corresponding to each bank up to the calculated height (in units) or the corresponding number of ATMs on the vertical axis.
The heights of the bars will be:
- Syndicate Bank: 1 unit (representing 5 ATMs)
- Dena Bank: 3 units (representing 15 ATMs)
- Indian Bank: 4 units (representing 20 ATMs)
- State Bank of India: 5 units (representing 25 ATMs)
- Vijya Bank: 2 units (representing 10 ATMs)
Draw the bars accordingly to create the bar graph.
Question 44. Number of mobile phone users in various age groups in a city is listed below:
| Age group (in years) | Number of mobile users |
|---|---|
| 1 - 20 | 25000 |
| 21 - 40 | 40000 |
| 41 - 50 | 35000 |
| 61 - 80 | 10000 |
Draw a bar graph to represent the above information.
Answer:
Given:
The number of mobile phone users in various age groups in a city is provided in the table in the question.
To Draw:
A bar graph to represent the given information.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Age group (in years)' on the horizontal axis (x-axis) and the 'Number of mobile users' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The number of users are 25000, 40000, 35000, and 10000. All these numbers are multiples of 5000.
Let's choose the scale as 1 unit length = 5000 mobile users.
Now, we calculate the height of the bars (in unit lengths) for each age group by dividing the number of users by the scale value (5000 users).
Height for age group 1 - 20 = $25000 \div 5000 = 5$ units.
Height for age group 21 - 40 = $40000 \div 5000 = 8$ units.
Height for age group 41 - 60 (Assuming this should be 41-60, as 51-60 is missing from the table, or perhaps the table meant 41-50 and 51-60. Based on the standard age grouping and the jump from 41-50 to 61-80, let's assume the 35000 corresponds to 41-60 for drawing the graph, though the table says 41-50.) Let's stick to the table's headings exactly for the bars.
Height for age group 41 - 50 = $35000 \div 5000 = 7$ units.
Height for age group 61 - 80 = $10000 \div 5000 = 2$ units.
Now, we can draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis and a vertical axis.
2. Label the horizontal axis as 'Age group (in years)' and mark points for each age group (1-20, 21-40, 41-50, 61-80).
3. Label the vertical axis as 'Number of mobile users'.
4. Choose a uniform width for the bars and a uniform gap between the bars.
5. Mark points on the vertical axis according to the chosen scale 1 unit length = 5000 mobile users (e.g., 0, 5000, 10000, ..., 40000).
6. Draw rectangular bars corresponding to each age group up to the calculated height (in units) or the corresponding number of mobile users on the vertical axis.
The heights of the bars will be:
- Age group 1 - 20: 5 units (representing 25000 users)
- Age group 21 - 40: 8 units (representing 40000 users)
- Age group 41 - 50: 7 units (representing 35000 users)
- Age group 61 - 80: 2 units (representing 10000 users)
Draw the bars accordingly to create the bar graph.
Question 45. The following table gives the number of vehicles passing through a toll gate, every hour from 8.00 am. to 1.00 pm:
| Time Interval | 8.00 to 9.00 | 9.00 to 10.00 | 10.00 to 11.00 | 11.00 to 12.00 | 12.00 to 1.00 |
|---|---|---|---|---|---|
| Number of vehicles | 250 | 450 | 300 | 250 | 150 |
Draw a bar graph representing the above data.
Answer:
Given:
The number of vehicles passing through a toll gate every hour from 8.00 am to 1.00 pm is provided in the table in the question.
To Draw:
A bar graph representing the given data.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Time Interval' on the horizontal axis (x-axis) and the 'Number of vehicles' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The number of vehicles are 250, 450, 300, 250, and 150. All these numbers are multiples of 50.
Let's choose the scale as 1 unit length = 50 vehicles.
Now, we calculate the height of the bars (in unit lengths) for each time interval by dividing the number of vehicles by the scale value (50 vehicles).
Height for 8.00 to 9.00 = $250 \div 50 = 5$ units.
Height for 9.00 to 10.00 = $450 \div 50 = 9$ units.
Height for 10.00 to 11.00 = $300 \div 50 = 6$ units.
Height for 11.00 to 12.00 = $250 \div 50 = 5$ units.
Height for 12.00 to 1.00 = $150 \div 50 = 3$ units.
Now, we can draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis and a vertical axis.
2. Label the horizontal axis as 'Time Interval' and mark points for each interval (8.00 to 9.00, 9.00 to 10.00, 10.00 to 11.00, 11.00 to 12.00, 12.00 to 1.00).
3. Label the vertical axis as 'Number of vehicles'.
4. Choose a uniform width for the bars and a uniform gap between the bars.
5. Mark points on the vertical axis according to the chosen scale 1 unit length = 50 vehicles (e.g., 0, 50, 100, 150, ..., 450).
6. Draw rectangular bars corresponding to each time interval up to the calculated height (in units) or the corresponding number of vehicles on the vertical axis.
The heights of the bars will be:
- 8.00 to 9.00: 5 units (representing 250 vehicles)
- 9.00 to 10.00: 9 units (representing 450 vehicles)
- 10.00 to 11.00: 6 units (representing 300 vehicles)
- 11.00 to 12.00: 5 units (representing 250 vehicles)
- 12.00 to 1.00: 3 units (representing 150 vehicles)
Draw the bars accordingly to create the bar graph.
Question 46. The following table represents income of a Gram Panchayat from different sources in a particular year:
| Source | Income |
|---|---|
| Income from local taxes | 75000 |
| Funds received from government | 150000 |
| Donations | 25000 |
| Income from other resources | 50000 |
Draw a bar graph to represent the above information.
Answer:
Given:
The income of a Gram Panchayat from different sources in a particular year is provided in the table in the question.
To Draw:
A bar graph to represent the given information.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Source' on the horizontal axis (x-axis) and the 'Income ($\textsf{₹}$)' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The income values are 75000, 150000, 25000, and 50000. All these numbers are multiples of 25000.
Let's choose the scale as 1 unit length = $\textsf{₹}$ 25000.
Now, we calculate the height of the bars (in unit lengths) for each source by dividing the income by the scale value ($\textsf{₹}$ 25000).
Height for Income from local taxes = $75000 \div 25000 = 3$ units.
Height for Funds received from government = $150000 \div 25000 = 6$ units.
Height for Donations = $25000 \div 25000 = 1$ unit.
Height for Income from other resources = $50000 \div 25000 = 2$ units.
Now, we can describe how to draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis (for Source) and a vertical axis (for Income).
2. Mark points on the horizontal axis for each source of income.
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the chosen scale 1 unit length = $\textsf{₹}$ 25000 (e.g., 0, 25000, 50000, 75000, 100000, 125000, 150000).
5. Draw rectangular bars corresponding to each income source up to the calculated height (in units) or the corresponding income value on the vertical axis.
The heights of the bars representing the income from each source will be:
- Income from local taxes: 3 units (representing $\textsf{₹}$ 75000)
- Funds received from government: 6 units (representing $\textsf{₹}$ 150000)
- Donations: 1 unit (representing $\textsf{₹}$ 25000)
- Income from other resources: 2 units (representing $\textsf{₹}$ 50000)
Draw the bars accordingly to create the bar graph.
Question 47. The following table gives the data of number of schools (stage-wise) of a country in the year 2002.
| Stage | Number of schools (in thousands) |
|---|---|
| Primary | 80 |
| Upper Primary | 55 |
| Secondary | 30 |
| Higher Secondary | 20 |
Draw a bar graph to represent the above data:
Answer:
Given:
The number of schools (stage-wise) of a country in the year 2002 is provided in the table in the question.
To Draw:
A bar graph to represent the given data.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Stage' on the horizontal axis (x-axis) and the 'Number of schools (in thousands)' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The numbers are 80, 55, 30, and 20. We can choose a scale that allows us to represent these values accurately.
Let's choose the scale as 1 unit length = 10 thousand schools.
Now, we calculate the height of the bars (in unit lengths) for each stage by dividing the number of schools (in thousands) by the scale value (10 thousand schools).
Height for Primary = $80 \div 10 = 8$ units.
Height for Upper Primary = $55 \div 10 = 5.5$ units.
Height for Secondary = $30 \div 10 = 3$ units.
Height for Higher Secondary = $20 \div 10 = 2$ units.
Now, we can describe how to draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis (for Stage) and a vertical axis (for Number of schools).
2. Mark points on the horizontal axis for each stage (Primary, Upper Primary, Secondary, Higher Secondary).
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the chosen scale 1 unit length = 10 thousand schools (e.g., 0, 10, 20, 30, ..., 90). Remember that the numbers on the vertical axis represent 'Number of schools (in thousands)'.
5. Draw rectangular bars corresponding to each stage up to the calculated height (in units) or the corresponding number of schools (in thousands) on the vertical axis.
The heights of the bars representing the number of schools for each stage will be:
- Primary: 8 units (representing 80 thousand schools)
- Upper Primary: 5.5 units (representing 55 thousand schools)
- Secondary: 3 units (representing 30 thousand schools)
- Higher Secondary: 2 units (representing 20 thousand schools)
Draw the bars accordingly to create the bar graph.
Question 48. Home appliances sold by a shop in one month are given as below:
| Home appliance | Number of home appliances |
|---|---|
| Refrigerator | 75 |
| Television | 45 |
| Washing Machine | 30 |
| Cooler | 60 |
| DVD Player | 30 |
Draw a bar graph to represent the above information.
Answer:
Given:
The number of home appliances sold by a shop in one month is provided in the table in the question.
To Draw:
A bar graph to represent the given information.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Home appliance' on the horizontal axis (x-axis) and the 'Number of home appliances sold' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The numbers of appliances sold are 75, 45, 30, 60, and 30. All these numbers are multiples of 15.
Let's choose the scale as 1 unit length = 15 home appliances.
Now, we calculate the height of the bars (in unit lengths) for each appliance by dividing the number sold by the scale value (15 appliances).
Height for Refrigerator = $75 \div 15 = 5$ units.
Height for Television = $45 \div 15 = 3$ units.
Height for Washing Machine = $30 \div 15 = 2$ units.
Height for Cooler = $60 \div 15 = 4$ units.
Height for DVD Player = $30 \div 15 = 2$ units.
Now, we can describe how to draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis (for Home appliance) and a vertical axis (for Number of home appliances).
2. Mark points on the horizontal axis for each type of home appliance.
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the chosen scale 1 unit length = 15 home appliances (e.g., 0, 15, 30, 45, 60, 75).
5. Draw rectangular bars corresponding to each appliance up to the calculated height (in units) or the corresponding number sold on the vertical axis.
The heights of the bars representing the number of home appliances sold will be:
- Refrigerator: 5 units (representing 75 appliances)
- Television: 3 units (representing 45 appliances)
- Washing Machine: 2 units (representing 30 appliances)
- Cooler: 4 units (representing 60 appliances)
- DVD Player: 2 units (representing 30 appliances)
Draw the bars accordingly to create the bar graph.
Question 49. In a botanical garden, the number of different types of plants are found as follows:
| Type of the plant | Number of plants |
|---|---|
| Herb | 50 |
| Shrub | 60 |
| Creeper | 20 |
| Climber | 45 |
| Tree | 95 |
Draw a bar graph to represent the above information and answer the following questions:
(a) Which type of plant is maximum in number in the garden?
(b) Which type of plant is minimum in number in the garden?
Answer:
Given:
The number of different types of plants in a botanical garden is provided in the table in the question.
To Draw and Answer:
To draw a bar graph to represent the given information and answer the questions asked based on the graph.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Type of the plant' on the horizontal axis (x-axis) and the 'Number of plants' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The numbers of plants are 50, 60, 20, 45, and 95. These numbers have common factors like 5.
Let's choose the scale as 1 unit length = 5 plants.
Now, we calculate the height of the bars (in unit lengths) for each type of plant by dividing the number of plants by the scale value (5 plants).
Height for Herb = $50 \div 5 = 10$ units.
Height for Shrub = $60 \div 5 = 12$ units.
Height for Creeper = $20 \div 5 = 4$ units.
Height for Climber = $45 \div 5 = 9$ units.
Height for Tree = $95 \div 5 = 19$ units.
Now, we can describe how to draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis (for Type of the plant) and a vertical axis (for Number of plants).
2. Mark points on the horizontal axis for each type of plant (Herb, Shrub, Creeper, Climber, Tree).
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the chosen scale 1 unit length = 5 plants (e.g., 0, 5, 10, ..., 100).
5. Draw rectangular bars corresponding to each plant type up to the calculated height (in units) or the corresponding number of plants on the vertical axis.
The heights of the bars representing the number of each type of plant will be:
- Herb: 10 units (representing 50 plants)
- Shrub: 12 units (representing 60 plants)
- Creeper: 4 units (representing 20 plants)
- Climber: 9 units (representing 45 plants)
- Tree: 19 units (representing 95 plants)
Draw the bars accordingly to create the bar graph.
Answering the questions:
(a) To find which type of plant is maximum in number, we compare the number of plants for each type: 50 (Herb), 60 (Shrub), 20 (Creeper), 45 (Climber), 95 (Tree). The maximum number is 95, which corresponds to Tree.
So, Tree is the type of plant that is maximum in number in the garden.
(b) To find which type of plant is minimum in number, we compare the number of plants for each type. The minimum number is 20, which corresponds to Creeper.
So, Creeper is the type of plant that is minimum in number in the garden.
Question 50. Prepare a bar graph of the data given in question 28.
Answer:
Given:
The request is to prepare a bar graph for the data provided in Question 28.
To Draw:
A bar graph representing the data from Question 28.
Note:
The specific data from Question 28 regarding the number of students who like to play different games is not provided in the current input. To draw the exact bar graph, the data from Question 28 is required.
General Steps to Draw the Bar Graph (Based on typical Q28 data structure):
Assuming the data from Question 28 lists different games and the number of students who like each game, we would follow these steps to create a bar graph:
1. Draw two perpendicular axes: a horizontal axis (x-axis) to represent the 'Games' and a vertical axis (y-axis) to represent the 'Number of students'.
2. Label the horizontal axis clearly with the names of the games mentioned in Question 28. Mark points on this axis for each game.
3. Label the vertical axis as 'Number of Students'.
4. Choose an appropriate scale for the vertical axis. The scale should be selected such that the highest number of students from the data fits comfortably on the axis. For example, if the numbers are in tens or twenties, a scale like 1 unit length = 2 students might be suitable. If the numbers are larger, a larger scale would be chosen.
5. Mark points on the vertical axis according to the chosen scale (e.g., 0, 2, 4, 6, ... or 0, 5, 10, 15, ... depending on the scale).
6. Choose a uniform width for the bars and maintain a uniform gap between the bars.
7. For each game listed on the horizontal axis, draw a rectangular bar upwards from the axis. The height of each bar must be proportional to the number of students who like that game, as read from the vertical axis according to the chosen scale.
Example Illustration (using hypothetical data for Q28):
Suppose the data from Question 28 was as follows:
| Game | Number of Students |
| Cricket | 30 |
| Badminton | 20 |
| Football | 45 |
| Tennis | 15 |
| Volleyball | 25 |
We would choose a scale, for example, 1 unit length = 5 students.
The heights of the bars would then be calculated as:
- Cricket: $30 \div 5 = 6$ units
- Badminton: $20 \div 5 = 4$ units
- Football: $45 \div 5 = 9$ units
- Tennis: $15 \div 5 = 3$ units
- Volleyball: $25 \div 5 = 5$ units
The bar graph would then consist of bars of these calculated heights above the respective labels on the horizontal axis.
Question 51. Refer to question 39. Prepare a pictograph of the data by taking a suitable symbol to represent 200 kilometers.
Answer:
Given:
The lengths (in km) of some major rivers of India from Question 39 are:
NH 2: 1500 km
NH 8: 1400 km
NH 3: 1000 km
NH 9: 400 km
NH 10: 200 km
NH 6: 1700 km
To Prepare:
A pictograph of the given data using a suitable symbol to represent 200 kilometers.
Solution:
Let us use the symbol '$\leftarrow\mkern-10mu\Rightarrow$' (representing a road/highway) to represent 200 kilometers.
Since one symbol represents 200 km, a half symbol will represent $200 \div 2 = 100$ km.
Now, we calculate the number of symbols needed for each National Highway by dividing its length by 200 km.
Number of symbols for NH 2 = $1500 \div 200 = 7.5$ symbols, which is 7 full symbols and 1 half symbol.
Number of symbols for NH 8 = $1400 \div 200 = 7$ symbols.
Number of symbols for NH 3 = $1000 \div 200 = 5$ symbols.
Number of symbols for NH 9 = $400 \div 200 = 2$ symbols.
Number of symbols for NH 10 = $200 \div 200 = 1$ symbol.
Number of symbols for NH 6 = $1700 \div 200 = 8.5$ symbols, which is 8 full symbols and 1 half symbol.
Pictograph:
| National Highway | Length (in km) |
| NH 2 | $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\frac{1}{2}\leftarrow\mkern-10mu\Rightarrow$ |
| NH 8 | $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ |
| NH 3 | $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ |
| NH 9 | $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ |
| NH 10 | $\leftarrow\mkern-10mu\Rightarrow$ |
| NH 6 | $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\leftarrow\mkern-10mu\Rightarrow$ $\frac{1}{2}\leftarrow\mkern-10mu\Rightarrow$ |
Key:
$\leftarrow\mkern-10mu\Rightarrow$ = 200 km
$\frac{1}{2}\leftarrow\mkern-10mu\Rightarrow$ = 100 km
Question 52. Prepare a pictograph of the information given in question 38.
Answer:
Given:
The number of railway tickets sold for different cities on a railway ticket counter from Question 38:
Delhi: 50 tickets
Patna: 20 tickets
Kolkata: 40 tickets
Jaipur: 60 tickets
Chennai: 30 tickets
Scale from Question 38: 1 unit length = 10 tickets.
To Prepare:
A pictograph of the given data using a suitable symbol to represent 10 tickets.
Solution:
Let us use the symbol '$\odot$' (representing a ticket) to represent 10 tickets.
Now, we calculate the number of symbols needed for each city by dividing the number of tickets sold by 10 tickets.
Number of symbols for Delhi = $50 \div 10 = 5$ symbols.
Number of symbols for Patna = $20 \div 10 = 2$ symbols.
Number of symbols for Kolkata = $40 \div 10 = 4$ symbols.
Number of symbols for Jaipur = $60 \div 10 = 6$ symbols.
Number of symbols for Chennai = $30 \div 10 = 3$ symbols.
Pictograph:
| City | Number of Tickets Sold |
| Delhi | $\odot$ $\odot$ $\odot$ $\odot$ $\odot$ |
| Patna | $\odot$ $\odot$ |
| Kolkata | $\odot$ $\odot$ $\odot$ $\odot$ |
| Jaipur | $\odot$ $\odot$ $\odot$ $\odot$ $\odot$ $\odot$ |
| Chennai | $\odot$ $\odot$ $\odot$ |
Key:
$\odot$ = 10 tickets
Question 53. Refer to question 23. Prepare a bar graph of the data.
Answer:
Given:
The request is to prepare a bar graph for the data provided in Question 23.
To Draw:
A bar graph representing the data from Question 23.
Note:
The specific data from Question 23 regarding the number of absentees in a class during a week is not provided in the current input. To draw the exact bar graph, the data from Question 23 is required. The following steps outline how to draw the bar graph based on the general structure of such data.
General Steps to Draw the Bar Graph (Based on typical Q23 data structure):
Assuming the data from Question 23 lists the days of the week and the corresponding number of absentees for each day, we would follow these steps to create a bar graph:
1. Draw two perpendicular axes: a horizontal axis (x-axis) to represent the 'Day' and a vertical axis (y-axis) to represent the 'Number of absentees'.
2. Label the horizontal axis clearly with the days of the week mentioned in Question 23 (e.g., Monday, Tuesday, Wednesday, etc.). Mark points on this axis for each day.
3. Label the vertical axis as 'Number of Absentees'.
4. Choose an appropriate scale for the vertical axis. The scale should be selected such that the highest number of absentees from the data fits comfortably on the axis. Since the number of absentees is likely a relatively small integer, a scale like 1 unit length = 1 student or 1 unit length = 2 students would be suitable.
5. Mark points on the vertical axis according to the chosen scale (e.g., 0, 1, 2, 3, ... or 0, 2, 4, 6, ... depending on the scale).
6. Choose a uniform width for the bars and maintain a uniform gap between the bars.
7. For each day listed on the horizontal axis, draw a rectangular bar upwards from the axis. The height of each bar must be proportional to the number of absentees on that specific day, as read from the vertical axis according to the chosen scale.
Example Illustration (using hypothetical data for Q23):
Suppose the data from Question 23 was as follows:
| Day | Number of Absentees |
| Monday | 4 |
| Tuesday | 6 |
| Wednesday | 3 |
| Thursday | 5 |
| Friday | 2 |
We could choose a scale, for example, 1 unit length = 1 student.
The heights of the bars would then correspond directly to the number of absentees:
- Monday: 4 units (representing 4 absentees)
- Tuesday: 6 units (representing 6 absentees)
- Wednesday: 3 units (representing 3 absentees)
- Thursday: 5 units (representing 5 absentees)
- Friday: 2 units (representing 2 absentees)
The bar graph would then consist of bars of these calculated heights above the respective day labels on the horizontal axis.
Question 54. The following table shows the area of the land on which different crops were grown.
| Crop | Area of land (in million hectrares) |
|---|---|
| Rice | 50 |
| Wheat | 30 |
| Pulses | 20 |
| Sugarcane | 25 |
| Cotton | 15 |
Prepare a pictograph by choosing a suitable symbol to represent 10 million hectares.
Answer:
Given:
The area of land on which different crops were grown is provided in the table in the question.
To Prepare:
A pictograph representing the given data, using a suitable symbol to represent 10 million hectares.
Solution:
Let us use the symbol '$\blacksquare$' (representing an area of land) to represent 10 million hectares.
Since one symbol represents 10 million hectares, a half symbol will represent $10 \div 2 = 5$ million hectares.
Now, we calculate the number of symbols needed for each crop's area by dividing the area by 10 million hectares.
Number of symbols for Rice = $50 \div 10 = 5$ symbols.
Number of symbols for Wheat = $30 \div 10 = 3$ symbols.
Number of symbols for Pulses = $20 \div 10 = 2$ symbols.
Number of symbols for Sugarcane = $25 \div 10 = 2.5$ symbols, which is 2 full symbols and 1 half symbol.
Number of symbols for Cotton = $15 \div 10 = 1.5$ symbols, which is 1 full symbol and 1 half symbol.
Pictograph:
| Crop | Area of land (in million hectares) |
| Rice | $\blacksquare$ $\blacksquare$ $\blacksquare$ $\blacksquare$ $\blacksquare$ |
| Wheat | $\blacksquare$ $\blacksquare$ $\blacksquare$ |
| Pulses | $\blacksquare$ $\blacksquare$ |
| Sugarcane | $\blacksquare$ $\blacksquare$ $\frac{1}{2}\blacksquare$ |
| Cotton | $\blacksquare$ $\frac{1}{2}\blacksquare$ |
Key:
$\blacksquare$ = 10 million hectares
$\frac{1}{2}\blacksquare$ = 5 million hectares
Question 55. Refer to question 54. Prepare a bar graph of the data.
Answer:
Given:
The area of land on which different crops were grown, as given in Question 54:
| Crop | Area of land (in million hectares) |
| Rice | 50 |
| Wheat | 30 |
| Pulses | 20 |
| Sugarcane | 25 |
| Cotton | 15 |
To Draw:
A bar graph to represent the above information.
Solution:
We will draw a bar graph to represent the given data.
Let's take the 'Crop' on the horizontal axis (x-axis) and the 'Area of land (in million hectares)' on the vertical axis (y-axis).
We need to choose an appropriate scale for the vertical axis. The area values are 50, 30, 20, 25, and 15. All these numbers are multiples of 5.
Let's choose the scale as 1 unit length = 5 million hectares.
Now, we calculate the height of the bars (in unit lengths) for each crop by dividing the area by the scale value (5 million hectares).
Height for Rice = $50 \div 5 = 10$ units.
Height for Wheat = $30 \div 5 = 6$ units.
Height for Pulses = $20 \div 5 = 4$ units.
Height for Sugarcane = $25 \div 5 = 5$ units.
Height for Cotton = $15 \div 5 = 3$ units.
Now, we can describe how to draw the bar graph:
1. Draw two perpendicular axes, a horizontal axis (for Crop) and a vertical axis (for Area of land).
2. Mark points on the horizontal axis for each type of crop (Rice, Wheat, Pulses, Sugarcane, Cotton).
3. Choose a uniform width for the bars and a uniform gap between the bars.
4. Mark points on the vertical axis according to the chosen scale 1 unit length = 5 million hectares (e.g., 0, 5, 10, 15, ..., 50).
5. Draw rectangular bars corresponding to each crop up to the calculated height (in units) or the corresponding area on the vertical axis.
The heights of the bars representing the area of land for each crop will be:
- Rice: 10 units (representing 50 million hectares)
- Wheat: 6 units (representing 30 million hectares)
- Pulses: 4 units (representing 20 million hectares)
- Sugarcane: 5 units (representing 25 million hectares)
- Cotton: 3 units (representing 15 million hectares)
Draw the bars accordingly to create the bar graph.

