| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 16) | Question 1 to 16 (Multiple Choice Questions) | Question 17 to 32 (Fill in the Blanks) |
| Question 33 to 52 (True or False) | Question 53 to 100 | |
Chapter 10 Algebraic Expressions
Welcome to this comprehensive resource providing detailed solutions for the NCERT Exemplar problems tailored for Class 7 Mathematics, specifically focusing on Chapter 12: Algebraic Expressions. These Exemplar questions are intentionally designed to significantly strengthen students' foundational algebraic skills, pushing them beyond the standard textbook exercises. They achieve this by presenting more complex expressions to manipulate, challenging simplification tasks, and fostering a deeper conceptual exploration of fundamental ideas like terms, coefficients, and the evaluation of expressions, thereby ensuring a more robust understanding.
The solutions provided here meticulously cover the essential building blocks of elementary algebra. Key concepts addressed include:
- Identifying Components: Breaking down expressions into their constituent terms (parts separated by '+' or '-' signs). Within each term, identifying the factors, distinguishing between numerical factors and literal factors (variables, possibly with exponents, like $x^2$). Precisely identifying the coefficient, which is the numerical factor of a term (e.g., in the term $-5xy^2$, the coefficient is $-5$).
- Classifying Expressions: Categorizing expressions based on the number of terms they contain after simplification: Monomial (one term), Binomial (two terms), Trinomial (three terms), and more generally, Polynomial (one or more terms with non-negative integer exponents on variables).
- Like and Unlike Terms: Mastering the crucial skill of identifying like terms – terms that have the exact same literal factors (variable parts, including exponents, e.g., $3x^2y$ and $-7x^2y$ are like terms). Differentiating them from unlike terms (e.g., $3x^2y$ and $3xy^2$). This distinction is fundamental for performing operations.
A major focus of this chapter, heavily emphasized in the Exemplar problems, is performing arithmetic operations on algebraic expressions:
- Addition and Subtraction: Learning the process of combining expressions. The core principle is that only like terms can be added or subtracted. Solutions demonstrate combining the coefficients of like terms while keeping the literal factors unchanged. Special attention is given to subtraction, emphasizing the critical step of changing the sign of every term in the expression being subtracted before combining like terms. Both horizontal and vertical methods of addition/subtraction are often illustrated.
Exemplar problems frequently involve more complex scenarios, such as:
- Simplifying elaborate expressions that contain multiple sets of brackets (parentheses, curly braces, square brackets), requiring careful application of removal rules and sign changes.
- Performing combined addition and subtraction operations in a single problem.
- Evaluating expressions: Substituting given numerical values for the variables within an expression and calculating the resulting numerical value. Exemplar questions often increase the difficulty by using negative integers or fractional values for substitution, demanding careful attention to sign rules and the order of operations (BODMAS/PEMDAS).
- Solving application problems like finding "what should be added to expression A to get expression B?" (requiring $B - A$) or "what should be subtracted from expression C to get expression D?" (requiring $C - D$).
The solutions address diverse question formats (MCQs, Fill-ins, T/F, Short/Long Answer), providing meticulous step-by-step simplification processes. They clearly show how like terms are identified, grouped, and combined, explicitly illustrate sign changes during subtraction, demonstrate careful substitution techniques and evaluation procedures, and offer clear explanations for conceptual points. Mastering the manipulation of algebraic expressions is not just about this chapter; it is an absolutely vital skill underpinning success in virtually all subsequent mathematical topics, including solving equations, functions, calculus, and beyond. Engaging with these Exemplar solutions is crucial for building the necessary accuracy and confidence.
Solved Examples (Examples 1 to 16)
In Examples 1 to 3, there are four options, out of which one is correct. Write the correct answer.
Example 1: The like terms in 3x (3 – 2y) and 2 (xy + x2) are
(a) 9x and 2x2
(b) – 6xy and 2xy
(c) 9x and 2xy
(d) – 6xy and 2x2
Answer:
Solution:
We are given two algebraic expressions: $3x(3 - 2y)$ and $2(xy + x^2)$.
To find the like terms, we first need to expand these expressions by removing the parentheses.
Expanding the first expression:
$3x(3 - 2y) = 3x \times 3 - 3x \times 2y$
$= 9x - 6xy$.
The terms in this expression are $9x$ and $-6xy$.
Expanding the second expression:
$2(xy + x^2) = 2 \times xy + 2 \times x^2$
$= 2xy + 2x^2$.
The terms in this expression are $2xy$ and $2x^2$.
Now we list all the terms from both expressions:
$9x$, $-6xy$, $2xy$, $2x^2$.
Like terms are terms that have the same variables raised to the same power.
Let's examine the variables and powers for each term:
Term 1: $9x$ (variable is $x$ with power 1)
Term 2: $-6xy$ (variables are $x$ and $y$ with power 1 each)
Term 3: $2xy$ (variables are $x$ and $y$ with power 1 each)
Term 4: $2x^2$ (variable is $x$ with power 2)
Comparing the terms, we can see that the terms $-6xy$ and $2xy$ have the same variables ($x$ and $y$) raised to the same powers (1 for $x$ and 1 for $y$). Therefore, they are like terms.
Looking at the given options:
(a) $9x$ and $2x^2$ (Variables/powers are different: $x^1$ and $x^2$) - Not like terms.
(b) $-6xy$ and $2xy$ (Variables/powers are the same: $xy$) - Like terms.
(c) $9x$ and $2xy$ (Variables are different: $x$ and $xy$) - Not like terms.
(d) $-6xy$ and $2x^2$ (Variables/powers are different: $xy$ and $x^2$) - Not like terms.
The correct option is (b).
The final answer is (b) – 6xy and 2xy.
Example 2: The coefficient of xy in 3x2zy + 7xyz – 2z2x is
(a) 3z
(b) – 2
(c) 7yz
(d) 7z
Answer:
Solution:
The given algebraic expression is $3x^2zy + 7xyz – 2z^2x$.
The terms in this expression are $3x^2zy$, $7xyz$, and $-2z^2x$.
The coefficient of a term with respect to a variable part is the remaining factor of the term when the variable part is removed.
We are asked to find the coefficient of $xy$ in the given expression.
Let's examine each term to see if it contains the variable part $xy$ (meaning $x$ raised to the power 1 and $y$ raised to the power 1).
Term 1: $3x^2zy$. This term contains $x^2$, $z$, and $y$. It does not contain $xy$ as a factor with $x$ and $y$ each having power 1.
Term 2: $7xyz$. This term contains $x$, $y$, and $z$. We can rewrite this term as $7z \times (xy)$. This term contains $xy$ as a factor.
Term 3: $-2z^2x$. This term contains $z^2$ and $x$. It does not contain $y$, so it does not contain $xy$ as a factor.
The term in the expression which contains the variable part $xy$ is $7xyz$.
We can write the term $7xyz$ as $7z \times xy$.
When the variable part $xy$ is removed from the term $7xyz$, the remaining factor is $7z$.
Therefore, the coefficient of $xy$ in the expression $3x^2zy + 7xyz – 2z^2x$ is $7z$.
Comparing this with the given options:
(a) $3z$
(b) $-2$
(c) $7yz$
(d) $7z$
The correct option is (d).
The final answer is (d) 7z.
Example 3: The factors of the term –xy2 are
(a) x × y × y
(b) – 1 × y × y
(c) – 1 × x × y
(d) – 1 × x × y × y
Answer:
Solution:
The given term is $-xy^2$.
A term in an algebraic expression is a product of factors.
We can break down the term $-xy^2$ into its constituent factors.
The term consists of a numerical part and a variable part.
The numerical coefficient is the number multiplying the variables. In $-xy^2$, the numerical coefficient is $-1$ (since $-xy^2 = -1 \times xy^2$).
The variable part is $xy^2$. This means $x$ multiplied by $y^2$.
$y^2$ means $y$ multiplied by itself, i.e., $y \times y$.
So, the term $-xy^2$ can be written as the product of its factors:
$-xy^2 = -1 \times x \times y^2$
$-xy^2 = -1 \times x \times (y \times y)$
The factors of the term $-xy^2$ are $-1$, $x$, $y$, and $y$.
Expressing this as a product of these factors gives: $-1 \times x \times y \times y$.
Now, let's compare this factorization with the given options:
(a) $x \times y \times y$: This is equal to $xy^2$. It is missing the numerical coefficient $-1$. Thus, it is not the correct set of factors for $-xy^2$.
(b) $-1 \times y \times y$: This is equal to $-y^2$. It is missing the variable factor $x$. Thus, it is not the correct set of factors for $-xy^2$.
(c) $-1 \times x \times y$: This is equal to $-xy$. It is missing one factor of $y$ (the term is $-xy^2$). Thus, it is not the correct set of factors for $-xy^2$.
(d) $-1 \times x \times y \times y$: This is equal to $-1 \times x \times y^2 = -xy^2$. This matches the given term. Thus, this is the correct set of factors.
The correct option is (d).
The final answer is (d) – 1 $\times$ x $\times$ y $\times$ y.
In Examples 4 to 7, fill in the blanks to make the statements true.
Example 4: An algebraic expression having one or more terms with non-negative integral exponents of the variables is called ___________.
Answer:
Solution:
An algebraic expression is a combination of variables and constants connected by mathematical operations.
Terms in an algebraic expression are separated by addition or subtraction signs.
The exponent (or power) of a variable indicates how many times the variable is multiplied by itself.
When an algebraic expression has one or more terms, and the exponents of the variables in each term are non-negative integers (i.e., 0, 1, 2, 3, ...), such an expression is specifically called a polynomial.
Examples of such expressions include $2x$, $3x+5$, $x^2-4y+7$, $5x^3y^2+2xy-1$, etc.
Expressions like $\sqrt{x}$ (which is $x^{1/2}$), $\frac{1}{x}$ (which is $x^{-1}$), or $y^{-2}$ are not polynomials because they have fractional or negative exponents.
The blank should be filled with the term "polynomial".
The final answer is polynomial.
Example 5: Numerical factor in any term of a polynomial is called ___________ of the term.
Answer:
Solution:
A term in a polynomial is a product of factors.
For example, in the polynomial $5x^2y - 3xy + 7$, the terms are $5x^2y$, $-3xy$, and $7$.
Let's look at the factors of each term:
The term $5x^2y$ can be written as $5 \times x^2 \times y$. Here, 5 is the numerical factor, and $x^2y$ is the variable factor.
The term $-3xy$ can be written as $-3 \times x \times y$. Here, $-3$ is the numerical factor, and $xy$ is the variable factor.
The term $7$ can be written as $7 \times 1$. Here, 7 is the numerical factor, and the variable factor is absent (or can be considered as 1). This is a constant term.
The definition states that the numerical factor in any term of a polynomial is called the coefficient of the term.
For example, the numerical coefficient of $5x^2y$ is 5.
The numerical coefficient of $-3xy$ is $-3$.
The numerical coefficient of the constant term 7 is 7.
The blank should be filled with the term "coefficient".
The final answer is coefficient.
Example 6: The terms with different algebraic factors are called ______.
Answer:
Solution:
In algebra, terms in an expression consist of a numerical coefficient and one or more variables (algebraic factors) raised to certain powers.
Terms are classified based on their algebraic factors:
- Terms that have the same algebraic factors (i.e., the same variables raised to the same powers) are called like terms.
Examples of like terms: $3x^2y$ and $-5x^2y$; $7ab$ and $2ab$; $9$ and $-4$ (constant terms are like terms).
- Terms that have different algebraic factors are called unlike terms.
Examples of unlike terms: $3x$ and $3y$ (different variables); $2a^2b$ and $2ab^2$ (same variables but different powers); $5xy$ and $5x$ (different variables).
The statement describes terms that have "different algebraic factors". By definition, such terms are called unlike terms.
The blank should be filled with the term "unlike terms".
The final answer is unlike terms.
Example 7: The terms with same algebraic factors are called _______.
Answer:
Solution:
In algebraic expressions, terms consist of a numerical part (coefficient) and a variable part (algebraic factors).
Terms are classified as either like terms or unlike terms based on their variable parts.
Terms that have exactly the same variables raised to the same powers are called like terms. The numerical coefficients can be different.
Examples: $2x^2y$ and $-7x^2y$ are like terms because both have the variable factors $x^2y$.
Examples: $5ab$ and $9ab$ are like terms because both have the variable factors $ab$.
Examples: $4$ and $-10$ are like terms because they are both constant terms (no variable factors, or variable factor can be considered as $x^0y^0$, which is the same for both).
Terms that have different variable factors are called unlike terms.
Examples: $3x$ and $5y$ are unlike terms (different variables).
Examples: $2a^2b$ and $2ab^2$ are unlike terms (same variables, but different powers).
The statement "The terms with same algebraic factors are called _______" refers to terms where the variable parts are identical.
Based on the definition, such terms are called like terms.
The blank should be filled with the term "like terms".
The final answer is like terms.
In Examples 8 to 10, state whether the statements are True or False.
Example 8: An expression with two terms is called a binomial.
Answer:
Solution:
An algebraic expression is classified based on the number of terms it contains.
If an expression has only one term, it is called a monomial (e.g., $5x$, $-3y^2$).
If an expression has exactly two terms, it is called a binomial (e.g., $2x + 3$, $a^2 - b^2$).
If an expression has exactly three terms, it is called a trinomial (e.g., $x^2 + 2x + 1$).
An expression with one or more terms with non-negative integral exponents is generally called a polynomial.
The statement says that an expression with two terms is called a binomial.
This matches the definition of a binomial.
Therefore, the statement is True.
The final answer is True.
Example 9: Every polynomial is a monomial.
Answer:
Solution:
A polynomial is an algebraic expression consisting of one or more terms, where the variables have only non-negative integer exponents.
A monomial is an algebraic expression that consists of exactly one term.
Based on these definitions:
- A polynomial can have one term (e.g., $5x$, $7y^2$, $10$), two terms (e.g., $x+y$, $2m-5$), three terms (e.g., $a^2+b^2-c^2$), or more terms.
- A monomial must have only one term.
While a monomial is a type of polynomial (specifically, a polynomial with one term), not all polynomials are monomials.
For example, the expression $x+y$ is a polynomial because it has two terms and the exponents (1) are non-negative integers. However, it is not a monomial because it has two terms.
The statement "Every polynomial is a monomial" implies that any expression that is a polynomial must also be a monomial. This is incorrect because polynomials can have more than one term.
Therefore, the statement is False.
The final answer is False.
Example 10: The value of a variable is fixed.
Answer:
Solution:
In algebra, a variable is a symbol, usually a letter like $x$, $y$, $a$, $b$, etc., that represents a quantity that can take on different values.
For example, in the expression $x + 5$, the value of the expression changes depending on the value of $x$. If $x=1$, the value is $1+5=6$. If $x=10$, the value is $10+5=15$. Here, $x$ is a variable, and its value is not fixed; it can vary.
In an equation like $2x = 10$, the value of the variable $x$ that satisfies the equation is specific ($x=5$), but the variable itself is still defined as a symbol that *can* represent different quantities. The context of the equation gives it a particular value that makes the equation true, but the nature of a variable is that its value is not inherently fixed in all situations or expressions.
A quantity with a fixed value is called a constant (e.g., numbers like 5, $-3$, $\pi$ are constants).
Since a variable can take on different values (is not fixed), the statement "The value of a variable is fixed" is incorrect.
Therefore, the statement is False.
The final answer is False.
Example 11: Twice the sum of length x and breadth y of a rectangle is the perimeter of a rectangle. Write the expression for perimeter.
Answer:
Given:
Length of the rectangle $= x$.
Breadth of the rectangle $= y$.
Perimeter of the rectangle is twice the sum of its length and breadth.
To Find:
The algebraic expression for the perimeter of the rectangle.
Solution:
Let the length of the rectangle be $l$ and the breadth be $b$.
According to the problem, $l = x$ and $b = y$.
The sum of the length and breadth is $l + b = x + y$.
The problem states that the perimeter is "twice the sum of length x and breadth y".
So, Perimeter $= 2 \times (\text{Sum of length and breadth})$
Perimeter $= 2 \times (x + y)$.
The formula for the perimeter of a rectangle is also known to be $2(l+b)$. Substituting $l=x$ and $b=y$, we get $2(x+y)$.
Thus, the expression for the perimeter of the rectangle is $2(x+y)$.
The final answer is $2(x+y)$.
Example 12: Identify the term containing u2 in the expression u3 + 3u2v + 3uv2 + v3 and write its coefficient.
Answer:
Solution:
Given:
The algebraic expression is $u^3 + 3u^2v + 3uv^2 + v^3$.
To Find:
The term containing $u^2$ and its coefficient.
Solution:
The given expression is $u^3 + 3u^2v + 3uv^2 + v^3$.
This expression has four terms: $u^3$, $3u^2v$, $3uv^2$, and $v^3$.
We need to identify the term that contains $u^2$. Let's look at each term:
- The first term is $u^3$. This term contains $u$ raised to the power of 3, not 2.
- The second term is $3u^2v$. This term contains $u$ raised to the power of 2, along with the variable $v$ and the numerical factor 3. This is the term containing $u^2$.
- The third term is $3uv^2$. This term contains $u$ raised to the power of 1 and $v$ raised to the power of 2. It does not contain $u^2$.
- The fourth term is $v^3$. This term contains only the variable $v$. It does not contain $u^2$.
So, the term containing $u^2$ is $3u^2v$.
Now we need to find the coefficient of $u^2$ in this term.
The term is $3u^2v$. The coefficient of a specific part of a term is the remaining factor(s) when that specific part is separated.
We can write the term as $3 \times u^2 \times v$, or $(3v) \times u^2$.
When we isolate $u^2$, the remaining factors are $3$ and $v$. Their product is $3v$.
Therefore, the coefficient of $u^2$ in the term $3u^2v$ is $3v$.
The term containing $u^2$ is $3u^2v$.
The coefficient of $u^2$ in this term is $3v$.
Example 13: Simplify the expression by combining the like terms:
7x3 – 3x2y + xy2 + x2y – y3
Answer:
Given:
The algebraic expression: $7x^3 – 3x^2y + xy^2 + x^2y – y^3$.
To Simplify:
Simplify the given expression by combining like terms.
Solution:
The given expression is $7x^3 – 3x^2y + xy^2 + x^2y – y^3$.
The terms in the expression are $7x^3$, $-3x^2y$, $xy^2$, $x^2y$, and $-y^3$.
Like terms are terms that have the same variables raised to the same powers.
We need to identify terms with identical variable parts.
Let's examine the variable part of each term:
1. $7x^3$: Variable part is $x^3$.
2. $-3x^2y$: Variable part is $x^2y$.
3. $xy^2$: Variable part is $xy^2$.
4. $x^2y$: Variable part is $x^2y$. Note that $x^2y$ is the same as $x^2y$.
5. $-y^3$: Variable part is $y^3$.
Comparing the variable parts, we can see that the terms $-3x^2y$ and $x^2y$ have the same variable part $x^2y$. These are like terms.
The terms $7x^3$, $xy^2$, and $-y^3$ have unique variable parts among themselves, so they do not have any other like terms in this expression.
Now, we group the like terms together:
$(7x^3) + (-3x^2y + x^2y) + (xy^2) + (-y^3)$
Next, we combine the like terms by adding or subtracting their numerical coefficients.
The term $7x^3$ remains as is.
For the like terms $-3x^2y$ and $x^2y$ (which is $1x^2y$), we combine their coefficients:
$-3x^2y + x^2y = (-3 + 1)x^2y = -2x^2y$.
The term $xy^2$ remains as is.
The term $-y^3$ remains as is.
Putting the combined terms back together, we get the simplified expression:
$7x^3 - 2x^2y + xy^2 - y^3$.
The simplified expression is $7x^3 - 2x^2y + xy^2 - y^3$.
Example 14: Subtract the sum of – 3x3y2 + 2x2y3 and – 3x2y3 – 5y4 from x4 + x3y2 + x2y3 + y4.
Answer:
Given:
Expression 1: $-3x^3y^2 + 2x^2y^3$
Expression 2: $-3x^2y^3 - 5y^4$
Expression from which to subtract: $x^4 + x^3y^2 + x^2y^3 + y^4$
To Find:
Subtract (Expression 1 + Expression 2) from (Expression from which to subtract).
Solution:
First, we find the sum of the first two expressions: $(-3x^3y^2 + 2x^2y^3) + (-3x^2y^3 - 5y^4)$.
Sum $= -3x^3y^2 + 2x^2y^3 - 3x^2y^3 - 5y^4$.
Identify and combine like terms. The like terms are $2x^2y^3$ and $-3x^2y^3$.
Sum $= -3x^3y^2 + (2x^2y^3 - 3x^2y^3) - 5y^4$
Sum $= -3x^3y^2 + (2 - 3)x^2y^3 - 5y^4$
Sum $= -3x^3y^2 - 1x^2y^3 - 5y^4$
Sum $= -3x^3y^2 - x^2y^3 - 5y^4$.
Now, we need to subtract this sum from the third expression: $(x^4 + x^3y^2 + x^2y^3 + y^4) - (-3x^3y^2 - x^2y^3 - 5y^4)$.
Subtracting an expression is the same as adding the additive inverse of the expression. We change the sign of each term in the expression being subtracted.
$-(-3x^3y^2 - x^2y^3 - 5y^4) = +3x^3y^2 + x^2y^3 + 5y^4$.
So, the subtraction becomes:
$(x^4 + x^3y^2 + x^2y^3 + y^4) + (3x^3y^2 + x^2y^3 + 5y^4)$
$= x^4 + x^3y^2 + x^2y^3 + y^4 + 3x^3y^2 + x^2y^3 + 5y^4$.
Now, identify and combine the like terms:
- Terms with $x^4$: $x^4$ (only one term)
- Terms with $x^3y^2$: $x^3y^2$ and $3x^3y^2$. Combining them: $x^3y^2 + 3x^3y^2 = (1+3)x^3y^2 = 4x^3y^2$.
- Terms with $x^2y^3$: $x^2y^3$ and $x^2y^3$. Combining them: $x^2y^3 + x^2y^3 = (1+1)x^2y^3 = 2x^2y^3$.
- Terms with $y^4$: $y^4$ and $5y^4$. Combining them: $y^4 + 5y^4 = (1+5)y^4 = 6y^4$.
Combining all the simplified terms:
The result is $x^4 + 4x^3y^2 + 2x^2y^3 + 6y^4$.
The final answer is $x^4 + 4x^3y^2 + 2x^2y^3 + 6y^4$.
Example 15: Find the value of the following expressions at a = 1 and b = –2:
(i) a2 + b2 + 3ab
(ii) a3 + a2b + ab2 + b3
Answer:
Given:
Value of $a = 1$.
Value of $b = -2$.
To Find:
The value of the given expressions at $a = 1$ and $b = -2$.
Solution:
We need to substitute $a=1$ and $b=-2$ into each expression and evaluate.
(i) Evaluate $a^2 + b^2 + 3ab$:
Substitute $a=1$ and $b=-2$ into the expression:
$a^2 + b^2 + 3ab = (1)^2 + (-2)^2 + 3(1)(-2)$
Calculate the squares:
$(1)^2 = 1 \times 1 = 1$
$(-2)^2 = (-2) \times (-2) = 4$
Calculate the product $3(1)(-2)$:
$3(1)(-2) = 3 \times 1 \times (-2) = 3 \times (-2) = -6$
Substitute these values back into the expression:
$1 + 4 + (-6)$
Combine the numbers:
$1 + 4 - 6 = 5 - 6 = -1$
The value of the expression $a^2 + b^2 + 3ab$ at $a=1$ and $b=-2$ is $-1$.
(ii) Evaluate $a^3 + a^2b + ab^2 + b^3$:
Substitute $a=1$ and $b=-2$ into the expression:
$a^3 + a^2b + ab^2 + b^3 = (1)^3 + (1)^2(-2) + (1)(-2)^2 + (-2)^3$
Calculate the powers:
$(1)^3 = 1 \times 1 \times 1 = 1$
$(1)^2(-2) = (1)(-2) = -2$
$(1)(-2)^2 = (1)(4) = 4$
$(-2)^3 = (-2) \times (-2) \times (-2) = 4 \times (-2) = -8$
Substitute these values back into the expression:
$1 + (-2) + 4 + (-8)$
$= 1 - 2 + 4 - 8$
Combine the positive terms and the negative terms separately:
$(1 + 4) + (-2 - 8)$
$= 5 + (-10)$
$= 5 - 10 = -5$
The value of the expression $a^3 + a^2b + ab^2 + b^3$ at $a=1$ and $b=-2$ is $-5$.
The values of the expressions are:
(i) $a^2 + b^2 + 3ab = -1$.
(ii) $a^3 + a^2b + ab^2 + b^3 = -5$.
Example 16: Find each side of an equilateral triangle given below, if it’s perimeter is 240 cm.

Answer:
Given:
The figure shows an equilateral triangle.
The perimeter of the equilateral triangle is 240 cm.
From the figure, the length of each side is represented by $x$ cm.
To Find:
The length of each side of the equilateral triangle (the value of $x$).
Solution:
An equilateral triangle is a triangle in which all three sides are equal in length.
The perimeter of any triangle is the sum of the lengths of its three sides.
For an equilateral triangle with side length $x$, the perimeter is the sum of the three equal sides:
Perimeter $= \text{Side 1} + \text{Side 2} + \text{Side 3}$
Perimeter $= x + x + x$
Perimeter $= 3x$.
We are given that the perimeter of the equilateral triangle is 240 cm.
So, we can set up the equation:
$3x = 240$
... (i)
Perimeter $= 240$ cm
(Given)
To find the value of $x$, we need to solve the equation $3x = 240$.
Divide both sides of the equation by 3:
$\frac{3x}{3} = \frac{240}{3}$
$x = 80$.
The length of each side of the equilateral triangle is 80 cm.
The final answer is 80 cm.
Exercise
Question 1 to 16 (Multiple Choice Questions)
In each of the questions 1 to 16, out of the four options, only one is correct. Write the correct answer.
Question 1. An algebraic expression containing three terms is called a
(a) monomial
(b) binomial
(c) trinomial
(d) All of these
Answer:
An algebraic expression containing three terms is called a trinomial.
Therefore, the correct option is (c) trinomial.
Question 2. Number of terms in the expression 3x2y – 2y2z – z2x + 5 is
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
The given algebraic expression is $3x^2y - 2y^2z - z^2x + 5$.
The terms in this expression are separated by addition or subtraction signs.
The terms are:
1. $3x^2y$
2. $-2y^2z$
3. $-z^2x$
4. $5$
There are four terms in the given expression.
Therefore, the correct option is (c) 4.
Question 3. The terms of expression 4x2 – 3xy are:
(a) 4x2 and –3xy
(b) 4x2 and 3xy
(c) 4x2 and –xy
(d) x2 and xy
Answer:
The given algebraic expression is $4x^2 - 3xy$.
The terms in this expression are separated by the subtraction sign.
The terms are:
1. $4x^2$
2. $-3xy$
Therefore, the correct option is (a) 4x2 and –3xy.
Question 4. Factors of –5x2y2z are
(a) – 5 × x × y × z
(b) – 5 × x2 × y × z
(c) – 5 × x × x × y × y × z
(d) – 5 × x × y × z2
Answer:
The given expression is $-5x^2y^2z$.
To find the factors of an expression, we break it down into its prime numerical factors and the literal factors (variables) in their expanded form.
In the given expression, we have:
Numerical factor: $-5$
Variable factors: $x^2$, $y^2$, $z$.
We can write $x^2$ as $x \times x$ and $y^2$ as $y \times y$.
So, the expression $-5x^2y^2z$ can be written as the product of its factors:
$-5 \times x \times x \times y \times y \times z$
Comparing this with the given options, we see that option (c) matches the factors.
Therefore, the correct option is (c) – 5 × x × x × y × y × z.
Question 5. Coefficient of x in – 9xy2z is
(a) 9yz
(b) – 9yz
(c) 9y2z
(d) – 9y2z
Answer:
The given algebraic expression is $-9xy^2z$.
In a term, the coefficient of a variable is the factor by which the variable is multiplied.
In the term $-9xy^2z$, we are looking for the coefficient of $x$.
We can write the term as $x \times (-9y^2z)$.
So, the coefficient of $x$ is $-9y^2z$.
Therefore, the correct option is (d) – 9y2z.
Question 6. Which of the following is a pair of like terms?
(a) –7xy2z, – 7x2yz
(b) –10xyz2, 3xyz2
(c) 3xyz, 3x2y2z2
(d) 4xyz2, 4x2yz
Answer:
Like terms are terms that have the same variables raised to the same power. The numerical coefficients can be different.
Let's examine the options:
(a) $-7xy^2z$ and $-7x^2yz$. The variables are $x, y, z$. In the first term, the powers are $x^1y^2z^1$. In the second term, the powers are $x^2y^1z^1$. The powers of $x$ and $y$ are different. So, these are not like terms.
(b) $-10xyz^2$ and $3xyz^2$. The variables are $x, y, z$. In the first term, the powers are $x^1y^1z^2$. In the second term, the powers are $x^1y^1z^2$. The variables and their powers are the same. So, these are like terms.
(c) $3xyz$ and $3x^2y^2z^2$. The variables are $x, y, z$. In the first term, the powers are $x^1y^1z^1$. In the second term, the powers are $x^2y^2z^2$. The powers are different. So, these are not like terms.
(d) $4xyz^2$ and $4x^2yz$. The variables are $x, y, z$. In the first term, the powers are $x^1y^1z^2$. In the second term, the powers are $x^2y^1z^1$. The powers of $x$ and $z$ are different. So, these are not like terms.
Therefore, the correct option is (b) –10xyz2, 3xyz2.
Question 7. Identify the binomial out of the following:
(a) 3xy2 + 5y – x2y
(b) x2y – 5y – x2y
(c) xy + yz + zx
(d) 3xy2 + 5y – xy2
Answer:
A binomial is an algebraic expression that contains exactly two terms.
Let's analyze each option:
(a) $3xy^2 + 5y - x^2y$: The terms are $3xy^2$, $5y$, and $-x^2y$. There are 3 terms. This is a trinomial.
(b) $x^2y - 5y - x^2y$: This expression can be simplified by combining like terms ($x^2y$ and $-x^2y$).
$x^2y - x^2y - 5y = (1-1)x^2y - 5y = 0x^2y - 5y = -5y$
The simplified expression is $-5y$, which has only 1 term. This is a monomial.
(c) $xy + yz + zx$: The terms are $xy$, $yz$, and $zx$. There are 3 terms. This is a trinomial.
(d) $3xy^2 + 5y - xy^2$: This expression can be simplified by combining like terms ($3xy^2$ and $-xy^2$).
$3xy^2 - xy^2 + 5y = (3-1)xy^2 + 5y = 2xy^2 + 5y$
The simplified expression is $2xy^2 + 5y$. The terms are $2xy^2$ and $5y$. There are 2 terms. This is a binomial.
Therefore, the correct option is (d) 3xy2 + 5y – xy2.
Question 8. The sum of x4 – xy + 2y2 and –x4 + xy + 2y2 is
(a) Monomial and polynomial in y
(b) Binomial and Polynomial
(c) Trinomial and polynomial
(d) Monomial and polynomial in x
Answer:
To find the sum, we add the two given expressions:
$(x^4 - xy + 2y^2) + (-x^4 + xy + 2y^2)$
Combine like terms:
$(x^4 - x^4) + (-xy + xy) + (2y^2 + 2y^2)$
$0 + 0 + 4y^2$
$= 4y^2$
The resulting expression is $4y^2$.
Let's analyze the resulting expression $4y^2$:
1. It contains only one term ($4y^2$). An algebraic expression with only one term is called a monomial.
2. It contains only the variable $y$. An expression is a polynomial in a variable if it involves only that variable with non-negative integer exponents. Since $4y^2$ only has the variable $y$ with exponent 2 (which is a non-negative integer), it is a polynomial in y.
Based on this analysis, the sum is a monomial and a polynomial in y.
Comparing with the given options:
(a) Monomial and polynomial in y - This matches our result.
(b) Binomial and Polynomial - Incorrect, it's a monomial.
(c) Trinomial and polynomial - Incorrect, it's a monomial.
(d) Monomial and polynomial in x - Incorrect, it is a polynomial in y, not x (as there is no x term other than implicitly $x^0$).
Therefore, the correct option is (a) Monomial and polynomial in y.
Question 9. The subtraction of 5 times of y from x is
(a) 5x – y
(b) y – 5x
(c) x – 5y
(d) 5y – x
Answer:
The phrase "5 times of y" means $5 \times y$, which is $5y$.
The phrase "subtraction of $5y$ from x" means that $5y$ is being subtracted from $x$.
So, the algebraic expression is $x - 5y$.
Comparing this with the given options, we see that option (c) matches our expression.
Therefore, the correct option is (c) x – 5y.
Question 10. – b – 0 is equal to
(a) –1 × b
(b) 1 – b – 0
(c) 0 – (–1) × b
(d) – b – 0 – 1
Answer:
The given expression is $-b - 0$.
Subtracting 0 from any number or expression does not change its value.
So, $-b - 0 = -b$.
Now let's evaluate each option:
(a) $-1 \times b = -b$
(b) $1 - b - 0 = 1 - b$
(c) $0 - (-1) \times b = 0 - (-b) = 0 + b = b$
(d) $-b - 0 - 1 = -b - 1$
Comparing the simplified form of the given expression $(-b)$ with the options, we see that option (a) is equal to $-b$.
Therefore, the correct option is (a) –1 × b.
Question 11. The side length of the top of square table is x. The expression for perimeter is:
(a) 4 + x
(b) 2x
(c) 4x
(d) 8x
Answer:
The top of the table is square-shaped.
The side length of the square is given as $x$.
The perimeter of a square is the sum of the lengths of its four sides. Since all sides of a square are equal in length, the perimeter is 4 times the side length.
Perimeter of square = $4 \times \text{(side length)}$
Perimeter = $4 \times x$
Perimeter = $4x$
Comparing this with the given options, we see that option (c) matches our expression.
Therefore, the correct option is (c) 4x.
Question 12. The number of scarfs of length half metre that can be made from y metres of cloth is :
(a) 2y
(b) $\frac{y}{2}$
(c) y + 2
(d) y + $\frac{1}{2}$
Answer:
The total length of cloth is $y$ metres.
The length of each scarf is half a metre, which is $\frac{1}{2}$ metre.
To find the number of scarfs that can be made, we divide the total length of cloth by the length of one scarf.
Number of scarfs = $\frac{\text{Total length of cloth}}{\text{Length of one scarf}}$
Number of scarfs = $\frac{y}{\frac{1}{2}}$
Dividing by a fraction is the same as multiplying by its reciprocal.
Number of scarfs = $y \times \frac{2}{1}$
Number of scarfs = $2y$
Therefore, the correct option is (a) 2y.
Question 13. 123x2y – 138x2y is a like term of :
(a) 10xy
(b) –15xy
(c) –15xy2
(d) 10x2y
Answer:
First, let's simplify the given expression: $123x^2y - 138x^2y$.
These are like terms because they have the same variables ($x, y$) with the same powers ($x^2, y^1$).
We can combine their coefficients:
$(123 - 138)x^2y$
$-15x^2y$
So, the expression simplifies to $-15x^2y$.
Now, we need to find which of the given options is a like term to $-15x^2y$.
Like terms must have the same variables raised to the same powers.
Let's examine the variables and powers in each option:
The expression is $-15x^2y$ (variables $x, y$ with powers $x^2, y^1$).
(a) $10xy$ (variables $x, y$ with powers $x^1, y^1$). Powers are different.
(b) $-15xy$ (variables $x, y$ with powers $x^1, y^1$). Powers are different.
(c) $-15xy^2$ (variables $x, y$ with powers $x^1, y^2$). Powers are different.
(d) $10x^2y$ (variables $x, y$ with powers $x^2, y^1$). Variables and their powers are the same.
Therefore, $10x^2y$ is a like term of $123x^2y - 138x^2y$.
The correct option is (d) 10x2y.
Question 14. The value of 3x2 – 5x + 3 when x = 1 is
(a) 1
(b) 0
(c) –1
(d) 11
Answer:
We are given the expression $3x^2 - 5x + 3$.
We need to find the value of this expression when $x = 1$.
Substitute $x = 1$ into the expression:
$3(1)^2 - 5(1) + 3$
First, evaluate the power: $(1)^2 = 1 \times 1 = 1$.
$3(1) - 5(1) + 3$
Perform the multiplications:
$3 \times 1 = 3$
$5 \times 1 = 5$
So the expression becomes:
$3 - 5 + 3$
Perform the addition and subtraction from left to right:
$3 - 5 = -2$
$-2 + 3 = 1$
So, the value of the expression when $x = 1$ is 1.
Comparing this result with the given options, we see that option (a) matches our value.
Therefore, the correct option is (a) 1.
Question 15. The expression for the number of diagonals that we can make from one vertex of a n sided polygon is:
(a) 2n + 1
(b) n – 2
(c) 5n + 2
(d) n – 3
Answer:
Consider a polygon with $n$ sides. Let's pick one vertex.
From this vertex, we can draw lines to all other vertices. There are $n-1$ other vertices.
However, two of these lines will be the sides of the polygon connected to the chosen vertex (the two adjacent vertices). These are not diagonals.
The number of diagonals from a single vertex is the total number of other vertices minus the two adjacent vertices.
Number of diagonals from one vertex = (Total number of vertices - 1) - 2
Number of diagonals from one vertex = $n - 1 - 2$
Number of diagonals from one vertex = $n - 3$
Let's check with a few examples:
For a triangle ($n=3$), number of diagonals from one vertex = $3 - 3 = 0$. Correct.
For a quadrilateral ($n=4$), number of diagonals from one vertex = $4 - 3 = 1$. Correct (a quadrilateral has 2 diagonals in total, one from each of two non-adjacent vertices).
For a pentagon ($n=5$), number of diagonals from one vertex = $5 - 3 = 2$. Correct.
Comparing this with the given options, we see that option (d) matches our expression.
Therefore, the correct option is (d) n – 3.
Question 16. The length of a side of square is given as 2x + 3. Which expression represents the perimeter of the square?
(a) 2x + 16
(b) 6x + 9
(c) 8x + 3
(d) 8x + 12
Answer:
The given shape is a square.
The length of a side of the square is given as $2x + 3$.
The perimeter of a square is calculated by the formula:
Perimeter = $4 \times \text{(side length)}$
Substitute the given side length into the formula:
Perimeter = $4 \times (2x + 3)$
Apply the distributive property to multiply 4 by each term inside the parenthesis:
Perimeter = $(4 \times 2x) + (4 \times 3)$
Perimeter = $8x + 12$
So, the expression representing the perimeter of the square is $8x + 12$.
Compare this result with the given options:
(a) $2x + 16$
(b) $6x + 9$
(c) $8x + 3$
(d) $8x + 12$
Option (d) matches our calculated expression for the perimeter.
Therefore, the correct option is (d) 8x + 12.
Question 17 to 32 (Fill in the Blanks)
In questions 17 to 32, fill in the blanks to make the statements true.
Question 17. Sum or difference of two like terms is ________.
Answer:
When we add or subtract two like terms, we combine their coefficients while keeping the variable part the same.
For example, if we add $3x$ and $5x$, we get $(3+5)x = 8x$.
If we subtract $5y^2$ from $7y^2$, we get $(7-5)y^2 = 2y^2$.
In both cases, the result is a single term which has the same variable part as the original terms. Such a term is a like term to the original terms.
The sum or difference of two like terms is a like term.
Question 18. In the formula, area of circle = πr2, the numerical constant of the expression πr2 is ________.
Answer:
The given formula is Area of circle = $\pi r^2$.
The expression is $\pi r^2$.
In an algebraic expression, the numerical coefficient (or constant) is the number that multiplies the variable part.
In the term $\pi r^2$, $r$ is the variable, and $\pi$ is the constant that multiplies $r^2$.
Although $\pi$ is a mathematical constant (approximately 3.14159...), in the context of algebraic expressions involving variables like $r$, $\pi$ acts as the numerical coefficient of the term $r^2$.
The numerical constant (coefficient) of the expression $\pi r^2$ is $\pi$.
Question 19. 3a2b and –7ba2 are ________ terms.
Answer:
We are given two terms: $3a^2b$ and $-7ba^2$.
To determine if they are like terms, we need to check if they have the same variables raised to the same powers. The order of multiplication of variables does not matter, so $ba^2$ is the same as $a^2b$.
In the first term, $3a^2b$, the variables are $a$ and $b$, with powers $a^2$ and $b^1$.
In the second term, $-7ba^2$, which is equivalent to $-7a^2b$, the variables are $a$ and $b$, with powers $a^2$ and $b^1$.
Since both terms have the same variables ($a$ and $b$) raised to the same powers ($a^2$ and $b^1$), they are like terms.
$3a^2b$ and $-7ba^2$ are like terms.
Question 20. –5a2b and –5b2a are ________ terms.
Answer:
We are given two terms: $-5a^2b$ and $-5b^2a$.
To determine if they are like terms, we check if they have the same variables raised to the same powers.
In the first term, $-5a^2b$, the variables are $a$ and $b$, with powers $a^2$ and $b^1$.
In the second term, $-5b^2a$, which is equivalent to $-5ab^2$, the variables are $a$ and $b$, with powers $a^1$ and $b^2$.
The powers of the variables are different ($a^2$ vs $a^1$ and $b^1$ vs $b^2$).
Since the variables are not raised to the same powers in both terms, they are unlike terms.
$-5a^2b$ and $-5b^2a$ are unlike terms.
Question 21. In the expression 2πr, the algebraic variable is ________.
Answer:
The given expression is $2\pi r$. This expression often represents the circumference of a circle, where $r$ is the radius.
In this expression, $2$ is a numerical constant and $\pi$ is a mathematical constant (approximately 3.14159...).
The quantity that can change or vary is the radius, represented by the symbol $r$.
An algebraic variable is a symbol (usually a letter) that represents a quantity that may vary.
In the expression $2\pi r$, the algebraic variable is $r$.
In the expression 2πr, the algebraic variable is r.
Question 22. Number of terms in a monomial is ________.
Answer:
By definition, a monomial is an algebraic expression that contains exactly one term.
Examples of monomials are $5$, $3x$, $-7y^2$, $2ab$. Each of these expressions consists of a single term.
Number of terms in a monomial is one.
Question 23. Like terms in the expression n (n + 1) + 6 (n – 1) are ___________and ________.
Answer:
The given expression is $n(n+1) + 6(n-1)$.
To find the like terms, we first need to expand and simplify the expression.
Expand the first part: $n(n+1) = n \times n + n \times 1 = n^2 + n$.
Expand the second part: $6(n-1) = 6 \times n - 6 \times 1 = 6n - 6$.
Now, add the expanded parts:
$(n^2 + n) + (6n - 6)$
$n^2 + n + 6n - 6$
Identify the terms in the expression: $n^2$, $n$, $6n$, and $-6$.
Like terms are terms that have the same variable raised to the same power.
The term $n^2$ has the variable $n$ raised to the power 2. There are no other terms with $n^2$.
The term $n$ has the variable $n$ raised to the power 1 ($n^1$). The term $6n$ also has the variable $n$ raised to the power 1. So, $n$ and $6n$ are like terms.
The term $-6$ is a constant term (it does not have a variable). There are no other constant terms.
The like terms in the expanded expression are $n$ and $6n$.
Like terms in the expression n (n + 1) + 6 (n – 1) are $n$ and $6n$.
Question 24. The expression 13 + 90 is a ________.
Answer:
The expression $13 + 90$ consists of two numbers being added together.
Since there are no variables involved, this is a purely numerical expression.
When we evaluate it, $13 + 90 = 103$.
This result is a single number. An expression consisting of a single number is a numerical constant.
The expression 13 + 90 is a numerical expression (or a constant).
Question 25. The speed of car is 55 km/hrs. The distance covered in y hours is ________.
Answer:
We are given the speed of the car and the time taken.
Speed = 55 km/hr
Time = $y$ hours
The relationship between distance, speed, and time is given by the formula:
Distance = Speed $\times$ Time
Substitute the given values into the formula:
Distance = $55 \text{ km/hr} \times y \text{ hours}$
Distance = $55y$ km
The expression for the distance covered in $y$ hours is $55y$.
The distance covered in y hours is $55y$ km.
Question 26. x + y + z is an expression which is neither monomial nor ________.
Answer:
The given expression is $x + y + z$.
The terms in this expression are $x$, $y$, and $z$.
There are 3 terms in the expression.
An expression with 1 term is a monomial.
An expression with 2 terms is a binomial.
An expression with 3 terms is a trinomial.
An expression with one or more terms is generally called a polynomial.
Since the expression $x+y+z$ has 3 terms, it is a trinomial.
The question states that the expression is neither monomial (1 term) nor ________. It is a trinomial (3 terms).
Therefore, it is neither a monomial nor a binomial.
x + y + z is an expression which is neither monomial nor binomial.
Question 27. If (x2y + y2 + 3) is subtracted from (3x2y + 2y2 + 5), then coefficient of y in the result is ________.
Answer:
We subtract the first expression from the second:
$(3x^2y + 2y^2 + 5) - (x^2y + y^2 + 3)$
$= 3x^2y + 2y^2 + 5 - x^2y - y^2 - 3$
Combine like terms:
$= (3x^2y - x^2y) + (2y^2 - y^2) + (5 - 3)$
$= 2x^2y + y^2 + 2$
The resulting expression is $2x^2y + y^2 + 2$.
We need to find the coefficient of the term with $y$ (i.e., $y^1$) where the coefficient is a constant.
The terms are $2x^2y$, $y^2$, and $2$.
There is no term of the form (constant) $\times y$.
Therefore, the coefficient of $y$ is 0.
If (x2y + y2 + 3) is subtracted from (3x2y + 2y2 + 5), then coefficient of y in the result is 0.
Question 28. – a – b – c is same as – a – ( ________ ).
Answer:
The given expression is $-a - b - c$.
We want to rewrite it in the form $-a - (\text{expression})$.
Consider the part of the expression after $-a$, which is $-b - c$.
We can factor out a minus sign from these terms:
$-b - c = -(b + c)$
So, the original expression can be written as:
$-a - (b + c)$
Comparing this with $-a - (\text{________})$, the expression in the blank is $b + c$.
– a – b – c is same as – a – ( b + c ).
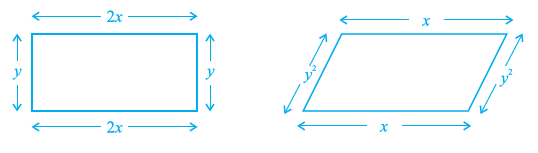
Question 29. The unlike terms in perimeters of following figures are___________ and __________.
Answer:
Let's find the perimeter of each figure:
1. Square with side $x$: Perimeter = $x + x + x + x = 4x$. The term is $4x$.
2. Equilateral triangle with side $y$: Perimeter = $y + y + y = 3y$. The term is $3y$.
3. Rectangle with sides $a$ and $2b$: Perimeter = $a + 2b + a + 2b = 2a + 4b$. The terms are $2a$ and $4b$.
4. Regular pentagon with side $m$: Perimeter = $m + m + m + m + m = 5m$. The term is $5m$.
5. Circle with radius $r$: Perimeter (Circumference) = $2\pi r$. The term is $2\pi r$.
6. Trapezium with sides $p, q, r, s$: Perimeter = $p + q + r + s$. The terms are $p, q, r, s$.
The terms from all the perimeters are: $4x, 3y, 2a, 4b, 5m, 2\pi r, p, q, r, s$.
Like terms have the same variable part (variables and their powers).
Let's look at the variable parts: $4x$ has variable part $x$. $3y$ has variable part $y$. $2a$ has variable part $a$. $4b$ has variable part $b$. $5m$ has variable part $m$. $2\pi r$ has variable part $r$. $p$ has variable part $p$. $q$ has variable part $q$. $r$ has variable part $r$. $s$ has variable part $s$.
The terms $2\pi r$ and $r$ both have the variable part $r$, so they are like terms.
All other terms ($4x, 3y, 2a, 4b, 5m, p, q, s$) have different variable parts from each other and from the terms involving $r$.
Therefore, any two terms from the set $\{4x, 3y, 2a, 4b, 5m, p, q, s\}$, or any term from this set and a term from $\{r, 2\pi r\}$, are unlike terms.
We need to provide two unlike terms. We can pick any two terms from the list that do not have the same variable part. Let's choose terms from different figures.
For example, $4x$ (from the square) and $3y$ (from the equilateral triangle) are unlike terms because their variable parts ($x$ and $y$) are different.
The unlike terms in perimeters of following figures are $4x$ and $3y$.
Note: Other correct answers for the blank would be any pair of terms from the list $\{4x, 3y, 2a, 4b, 5m, p, q, s\}$ or a pair consisting of one term from this set and one term from $\{r, 2\pi r\}$. For example, $2a$ and $5m$ are also unlike terms.
Question 30. On adding a monomial _____________ to – 2x + 4y2 + z, the resulting expression becomes a binomial.
Answer:
The given expression is $-2x + 4y^2 + z$. This expression has 3 terms: $-2x$, $4y^2$, and $z$. It is a trinomial.
We are adding a monomial to this expression, and the result is a binomial, which has 2 terms.
Let the monomial be $M$. The sum is $(-2x + 4y^2 + z) + M$.
For the resulting expression to be a binomial, one of the terms in the original trinomial must be cancelled out when combined with the monomial $M$.
This happens if the monomial $M$ is a like term to one of the terms in the trinomial, and its coefficient is the additive inverse of the coefficient of that term.
The terms in the trinomial are: 1. $-2x$ 2. $4y^2$ 3. $z$
Let's consider adding a monomial that is the additive inverse of one of these terms:
- If $M = 2x$ (additive inverse of $-2x$), then:
$(-2x + 4y^2 + z) + 2x = (-2x + 2x) + 4y^2 + z = 0 + 4y^2 + z = 4y^2 + z$.
This result, $4y^2 + z$, has two terms, $4y^2$ and $z$. It is a binomial.
- If $M = -4y^2$ (additive inverse of $4y^2$), then:
$(-2x + 4y^2 + z) + (-4y^2) = -2x + (4y^2 - 4y^2) + z = -2x + 0 + z = -2x + z$.
This result, $-2x + z$, has two terms, $-2x$ and $z$. It is a binomial.
- If $M = -z$ (additive inverse of $z$), then:
$(-2x + 4y^2 + z) + (-z) = -2x + 4y^2 + (z - z) = -2x + 4y^2 + 0 = -2x + 4y^2$.
This result, $-2x + 4y^2$, has two terms, $-2x$ and $4y^2$. It is a binomial.
Any of these monomials ($2x$, $-4y^2$, or $-z$) can be added to the trinomial to result in a binomial. The question asks for "a monomial", implying there might be more than one possibility, and any valid one will fill the blank.
Let's choose one of the possible monomials, for example, $2x$.
On adding a monomial $2x$ to – 2x + 4y2 + z, the resulting expression becomes a binomial.
Alternate Answers: $-4y^2$ or $-z$.
Question 31. 3x + 23x2 + 6y2 + 2x + y2 + ____________ = 5x + 7y2.
Answer:
Let the unknown term be $M$. The equation is:
$3x + 23x^2 + 6y^2 + 2x + y^2 + M = 5x + 7y^2$
First, simplify the left side of the equation by combining like terms.
Identify the terms: $3x$, $23x^2$, $6y^2$, $2x$, $y^2$, and $M$.
Like terms are: - Terms with $x$: $3x$ and $2x$. Their sum is $3x + 2x = (3+2)x = 5x$. - Terms with $x^2$: $23x^2$. - Terms with $y^2$: $6y^2$ and $y^2$. Their sum is $6y^2 + y^2 = (6+1)y^2 = 7y^2$.
The simplified left side (excluding $M$) is:
$23x^2 + 5x + 7y^2$
So, the equation becomes:
$23x^2 + 5x + 7y^2 + M = 5x + 7y^2$
To find $M$, we need to isolate it. We can subtract the terms from the left side (except $M$) from both sides of the equation.
$M = (5x + 7y^2) - (23x^2 + 5x + 7y^2)$
Remove the parenthesis on the right side, changing the signs of the terms being subtracted:
$M = 5x + 7y^2 - 23x^2 - 5x - 7y^2$
Group the like terms on the right side:
$M = (5x - 5x) + (7y^2 - 7y^2) - 23x^2$
Combine the like terms:
$M = 0 + 0 - 23x^2$
$M = -23x^2$
The unknown term is $-23x^2$.
Let's verify by substituting $-23x^2$ back into the original equation:
$3x + 23x^2 + 6y^2 + 2x + y^2 + (-23x^2)$
$= (3x + 2x) + (23x^2 - 23x^2) + (6y^2 + y^2)$
$= 5x + 0 + 7y^2$
$= 5x + 7y^2$
This matches the right side of the given equation.
3x + 23x2 + 6y2 + 2x + y2 + $-23x^2$ = 5x + 7y2.
Question 32. If Rohit has 5xy toffees and Shantanu has 20yx toffees, then Shantanu has _____ more toffees.
Answer:
Rohit has $5xy$ toffees.
Shantanu has $20yx$ toffees.
The terms $5xy$ and $20yx$ are like terms because the order of multiplication of variables does not matter, so $xy = yx$.
To find how many more toffees Shantanu has than Rohit, we subtract Rohit's toffees from Shantanu's toffees:
Number of more toffees = Shantanu's toffees - Rohit's toffees
Number of more toffees = $20yx - 5xy$
Since $yx = xy$, we can write this as:
Number of more toffees = $20xy - 5xy$
Combine the like terms by subtracting their coefficients:
Number of more toffees = $(20 - 5)xy$
Number of more toffees = $15xy$
So, Shantanu has $15xy$ more toffees than Rohit.
If Rohit has 5xy toffees and Shantanu has 20yx toffees, then Shantanu has $15xy$ more toffees.
Question 33 to 52 (True or False)
In questions 33 to 52, state whether the statements given are True or False.
Question 33. 1 + $\frac{x}{2}$ + x3 is a polynomial.
Answer:
The given expression is $1 + \frac{x}{2} + x^3$.
An algebraic expression is called a polynomial if the exponents of the variables are non-negative integers.
In the given expression, the terms are $1$, $\frac{x}{2}$, and $x^3$.
The exponents of the variable $x$ in these terms are:
For the term $1$, we can write it as $1 \cdot x^0$. The exponent is $0$, which is a non-negative integer.
For the term $\frac{x}{2}$, we can write it as $\frac{1}{2} \cdot x^1$. The exponent is $1$, which is a non-negative integer.
For the term $x^3$, the exponent is $3$, which is a non-negative integer.
Since all the exponents of the variable $x$ in the expression are non-negative integers, the expression $1 + \frac{x}{2} + x^3$ is a polynomial.
Therefore, the given statement is True.
Question 34. (3a – b + 3) – (a + b) is a binomial.
Answer:
The given expression is $(3a – b + 3) – (a + b)$.
To determine if the expression is a binomial, we first need to simplify it.
Remove the parentheses:
$(3a – b + 3) – (a + b) = 3a – b + 3 – a – b$
Combine the like terms:
$3a - a = 2a$
$-b - b = -2b$
The constant term is $3$.
So, the simplified expression is $2a - 2b + 3$.
A polynomial is classified based on the number of terms it contains.
A polynomial with one term is a monomial.
A polynomial with two terms is a binomial.
A polynomial with three terms is a trinomial.
The simplified expression $2a - 2b + 3$ has three distinct terms: $2a$, $-2b$, and $3$.
Therefore, the expression is a trinomial.
The statement "(3a – b + 3) – (a + b) is a binomial" is False.
Question 35. A trinomial can be a polynomial.
Answer:
A polynomial is an algebraic expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables.
A trinomial is a polynomial that contains exactly three terms.
For example, $x^2 + 2x + 1$ is a trinomial because it has three terms ($x^2$, $2x$, and $1$). It also fits the definition of a polynomial because the exponents of the variable ($2$, $1$, and $0$ for the constant term) are non-negative integers.
Since a trinomial is defined as a polynomial with a specific number of terms, every trinomial is a type of polynomial.
Therefore, the statement "A trinomial can be a polynomial" is True.
Question 36. A polynomial with more than two terms is a trinomial.
Answer:
A polynomial is classified by the number of terms it contains:
A monomial has exactly one term (e.g., $5x$).
A binomial has exactly two terms (e.g., $2x - 7$).
A trinomial has exactly three terms (e.g., $x^2 + 3x - 4$).
The statement says that any polynomial with more than two terms is a trinomial.
This means it claims that polynomials with three terms, four terms, five terms, and so on, are all trinomials.
However, a trinomial specifically refers to a polynomial with *exactly* three terms.
For example, a polynomial with four terms, such as $a^3 + b^3 + c^3 - 3abc$, has more than two terms, but it is not a trinomial; it is a quadrinomial or simply a polynomial with four terms.
Therefore, the statement is incorrect because polynomials can have more than three terms (e.g., 4, 5, 6 terms), and these are not classified as trinomials.
The statement "A polynomial with more than two terms is a trinomial" is False.
Question 37. Sum of x and y is x + y.
Answer:
In mathematics, the term "sum" refers to the result obtained by adding two or more numbers or quantities.
The quantities given are $x$ and $y$.
The operation of addition is represented by the '+' symbol.
Therefore, the sum of $x$ and $y$ is written as the expression formed by placing the addition symbol between $x$ and $y$, which is $x + y$.
The statement directly matches the definition of the sum of two variables.
The statement "Sum of x and y is x + y" is True.
Question 38. Sum of 2 and p is 2p.
Answer:
The sum of two quantities is the result of adding them together.
The quantities given are the number $2$ and the variable $p$.
The sum of $2$ and $p$ is represented by the expression $2 + p$.
The expression $2p$ represents the product of $2$ and $p$, which means $2 \times p$.
Unless $p$ is equal to $0$, $2 + p$ is generally not equal to $2p$. For example, if $p=1$, $2+p = 2+1 = 3$, and $2p = 2 \times 1 = 2$. Here $3 \neq 2$.
The statement claims that the sum of 2 and p is 2p, which is incorrect as 2p represents the product.
The statement "Sum of 2 and p is 2p" is False.
Question 39. A binomial has more than two terms.
Answer:
In the classification of polynomials based on the number of terms:
A monomial has exactly one term.
A binomial has exactly two terms.
A trinomial has exactly three terms.
The prefix "bi-" means two. A binomial is specifically defined as a polynomial consisting of two terms.
The statement "A binomial has more than two terms" contradicts this definition, as it implies a binomial could have 3, 4, or more terms, which is incorrect.
The statement "A binomial has more than two terms" is False.
Question 40. A trinomial has exactly three terms.
Answer:
In the classification of polynomials based on the number of terms:
A monomial has exactly one term.
A binomial has exactly two terms.
A trinomial has exactly three terms.
The prefix "tri-" means three. A trinomial is specifically defined as a polynomial consisting of exactly three terms.
Examples of trinomials include $x^2 + 2x + 1$, $a + b - c$, $3y^5 - 7y + 10$. Each of these expressions has exactly three distinct terms.
The statement aligns perfectly with the mathematical definition of a trinomial.
The statement "A trinomial has exactly three terms" is True.
Question 41. In like terms, variables and their powers are the same.
Answer:
In algebra, like terms are terms that have the same variables raised to the same power.
The coefficients of like terms can be different.
For example, $2x^2y$ and $-5x^2y$ are like terms because they both have the variables $x$ and $y$, where $x$ is raised to the power of $2$ and $y$ is raised to the power of $1$ (since $y = y^1$). The coefficients $2$ and $-5$ are different, but that does not affect whether the terms are like terms.
Conversely, $2xy^2$ and $2x^2y$ are not like terms because the powers of $x$ and $y$ are not the same in both terms ($x^1y^2$ vs $x^2y^1$).
The statement "In like terms, variables and their powers are the same" accurately describes the condition for terms to be considered like terms.
The statement "In like terms, variables and their powers are the same" is True.
Question 42. The expression x + y + 5x is a trinomial.
Answer:
The given expression is $x + y + 5x$.
To determine the number of terms, we should first simplify the expression by combining like terms.
The terms in the expression are $x$, $y$, and $5x$.
The terms $x$ and $5x$ are like terms because they have the same variable ($x$) raised to the same power ($1$).
Combine the like terms: $x + 5x = (1+5)x = 6x$.
The simplified expression is $6x + y$.
The simplified expression has two distinct terms: $6x$ and $y$.
A polynomial with two terms is called a binomial.
A trinomial is a polynomial with exactly three terms.
Since the simplified expression has only two terms, it is a binomial, not a trinomial.
The statement "The expression x + y + 5x is a trinomial" is False.
Question 43. 4p is the numerical coefficient of q2 in – 4pq2.
Answer:
In a term of an algebraic expression, the coefficient is the numerical or literal factor that multiplies the variable part.
The given term is $-4pq^2$.
We want to find the coefficient of $q^2$. This means we should consider $q^2$ as the variable part and everything else as the coefficient.
The term can be written as $(-4p) \times q^2$.
Here, $-4p$ is the factor that is multiplying $q^2$.
So, the coefficient of $q^2$ in $-4pq^2$ is $-4p$.
The statement says that the numerical coefficient of $q^2$ is $4p$. This is incorrect for two reasons:
1. The coefficient is $-4p$, not $4p$. The sign must be included.
2. The coefficient $-4p$ contains a variable ($p$), so it is a literal coefficient (or algebraic coefficient), not a purely numerical coefficient.
The numerical coefficient of the entire term $-4pq^2$ is $-4$.
The statement "4p is the numerical coefficient of q2 in – 4pq2" is False.
Question 44. 5a and 5b are unlike terms.
Answer:
Like terms are terms that have the same variables raised to the same power.
Unlike terms are terms that do not have the same variables or have the same variables but raised to different powers.
The given terms are $5a$ and $5b$.
In the term $5a$, the variable is $a$ and its power is $1$.
In the term $5b$, the variable is $b$ and its power is $1$.
The variables in the two terms are different ($a$ vs $b$).
Since the variables are different, the terms are unlike terms, regardless of their coefficients or the powers of the variables.
The statement claims that $5a$ and $5b$ are unlike terms, which is consistent with the definition of unlike terms.
The statement "5a and 5b are unlike terms" is True.
Question 45. Sum of x2 + x and y + y2 is 2x2 + 2y2.
Answer:
We need to find the sum of the two expressions: $(x^2 + x)$ and $(y + y^2)$.
Sum = $(x^2 + x) + (y + y^2)$
Remove the parentheses:
Sum = $x^2 + x + y + y^2$
To simplify the sum, we look for like terms. Like terms have the same variables raised to the same powers.
The terms are $x^2$, $x$, $y$, and $y^2$.
The term $x^2$ has variable $x$ with power $2$.
The term $x$ has variable $x$ with power $1$. These are unlike terms.
The term $y$ has variable $y$ with power $1$.
The term $y^2$ has variable $y$ with power $2$. These are unlike terms.
Also, terms involving $x$ and terms involving $y$ are unlike terms ($x^2$, $x$ are unlike $y$, $y^2$).
Since there are no like terms in the expression $x^2 + x + y + y^2$, it cannot be simplified further.
The sum of $x^2 + x$ and $y + y^2$ is $x^2 + x + y + y^2$.
The statement claims that the sum is $2x^2 + 2y^2$. This would imply that $x^2 + x + y + y^2 = 2x^2 + 2y^2$. This equation is generally false. For example, if $x=1$ and $y=1$, the sum is $1^2 + 1 + 1 + 1^2 = 1 + 1 + 1 + 1 = 4$. The claimed sum is $2(1)^2 + 2(1)^2 = 2(1) + 2(1) = 2 + 2 = 4$. However, let's try another example. If $x=2$ and $y=3$, the sum is $2^2 + 2 + 3 + 3^2 = 4 + 2 + 3 + 9 = 18$. The claimed sum is $2(2)^2 + 2(3)^2 = 2(4) + 2(9) = 8 + 18 = 26$. Since $18 \neq 26$, the statement is false.
The statement "Sum of x2 + x and y + y2 is 2x2 + 2y2" is False.
Question 46. Subtracting a term from a given expression is the same as adding its additive inverse to the given expression.
Answer:
Let the given expression be $E$ and the term to be subtracted be $T$.
Subtracting the term $T$ from the expression $E$ is written as $E - T$.
The additive inverse of a term $T$ is the term which, when added to $T$, results in zero. The additive inverse of $T$ is $-T$.
Adding the additive inverse of $T$ to the given expression $E$ is written as $E + (-T)$.
According to the properties of arithmetic and algebra, subtracting a number or an expression is equivalent to adding its additive inverse.
That is, for any quantities $a$ and $b$, $a - b = a + (-b)$.
In this case, $E - T$ is indeed equal to $E + (-T)$.
For example, consider the expression $5x + 3$ and the term $2x$.
Subtracting the term $2x$: $(5x + 3) - 2x = 5x - 2x + 3 = 3x + 3$.
The additive inverse of the term $2x$ is $-2x$.
Adding the additive inverse: $(5x + 3) + (-2x) = 5x - 2x + 3 = 3x + 3$.
Both operations yield the same result.
Therefore, the statement is correct.
The statement "Subtracting a term from a given expression is the same as adding its additive inverse to the given expression" is True.
Question 47. The total number of planets of Sun can be denoted by the variable n.
Answer:
A variable is a symbol, typically a letter, that represents a quantity that may change or is unknown.
A constant is a value that does not change.
The total number of planets orbiting the Sun in our solar system is a fixed, known number (currently 8). This number is a constant.
However, it is possible to assign a constant value to a variable. For example, in an algebraic problem, we might say "Let $C$ be the cost of an item, where $C = \textsf{₹}10$". Here, $C$ is a variable used to denote a constant value.
Similarly, we can define a variable $n$ and state that it represents the number of planets of the Sun. In this specific context, $n$ would take the value 8.
So, while the number of planets is a constant, it can still be denoted by a variable symbol for convenience in algebraic expressions or equations, especially if this number were to be used in calculations or formulas.
Therefore, the statement is correct.
The statement "The total number of planets of Sun can be denoted by the variable n" is True.
Question 48. In like terms, the numerical coefficients should also be the same.
Answer:
Like terms are terms that have the same variables raised to the same power.
The definition of like terms focuses on the variable part of the term, not the numerical coefficient.
For example, consider the terms $3x^2$ and $-7x^2$.
The variable part is $x^2$ in both terms, which is the same.
The numerical coefficient of $3x^2$ is $3$.
The numerical coefficient of $-7x^2$ is $-7$.
Since the variable parts are the same ($x^2$), the terms $3x^2$ and $-7x^2$ are considered like terms, even though their numerical coefficients ($3$ and $-7$) are different.
The ability to combine like terms depends only on the variable part being identical, not the numerical coefficient.
Therefore, the statement is incorrect.
The statement "In like terms, the numerical coefficients should also be the same" is False.
Question 49. If we add a monomial and binomial, then answer can never be a monomial.
Answer:
Let's consider the definitions of a monomial and a binomial.
A monomial is a polynomial with exactly one term.
A binomial is a polynomial with exactly two unlike terms.
Let the monomial be $M$.
Let the binomial be $B_1 + B_2$, where $B_1$ and $B_2$ are unlike terms.
The sum of the monomial and the binomial is $M + (B_1 + B_2)$.
We want to determine if this sum can result in a monomial (a single term).
Consider the case where the monomial $M$ is the additive inverse of one of the terms in the binomial, say $B_1$.
If $M = -B_1$, then the sum becomes:
Sum = $(-B_1) + (B_1 + B_2)$
Sum = $-B_1 + B_1 + B_2$
Sum = $( -B_1 + B_1) + B_2$
Sum = $0 + B_2$
Sum = $B_2$
Since $B_1 + B_2$ is a binomial, $B_1$ and $B_2$ must be non-zero unlike terms. Therefore, $B_2$ is a single non-zero term.
A single non-zero term is a monomial.
Let's look at a specific example:
Let the monomial be $3x$.
Let the binomial be $-3x + 5y$. Note that $-3x$ and $5y$ are unlike terms.
The sum is $(3x) + (-3x + 5y)$.
Sum = $3x - 3x + 5y$
Sum = $(3x - 3x) + 5y$
Sum = $0 + 5y$
Sum = $5y$
The result, $5y$, is a single term and is therefore a monomial.
This example shows that when we add a monomial and a binomial, the result can indeed be a monomial.
The statement claims that the answer can never be a monomial.
Since we have found a case where the answer is a monomial, the statement is false.
The statement "If we add a monomial and binomial, then answer can never be a monomial" is False.
Question 50. If we subtract a monomial from a binomial, then answer is atleast a binomial.
Answer:
Let a binomial be an expression with two unlike terms, for example, $a + b$, where $a$ and $b$ are unlike terms.
Let a monomial be an expression with one term, for example, $m$.
We are subtracting the monomial $m$ from the binomial $a + b$. The expression is $(a + b) - m$.
Simplifying this gives $a + b - m$.
The number of terms in the result depends on whether $m$ is a like term with either $a$ or $b$.
Consider an example:
Let the binomial be $3x + 5y$. Here $3x$ and $5y$ are unlike terms.
Let the monomial be $3x$. This is a like term with one of the terms in the binomial.
Subtract the monomial from the binomial:
$(3x + 5y) - (3x)$
Remove parentheses:
$3x + 5y - 3x$
Combine like terms:
$(3x - 3x) + 5y$
$0 + 5y$
$5y$
The result is $5y$. This expression has only one term.
An expression with one term is a monomial.
The statement says the answer is "at least a binomial", meaning it must have 2 or more terms.
Our example resulted in a monomial, which has only 1 term.
Therefore, the statement is false.
The statement "If we subtract a monomial from a binomial, then answer is atleast a binomial" is False.
Question 51. When we subtract a monomial from a trinomial, then answer can be a polynomial.
Answer:
Let a trinomial be an expression with exactly three unlike terms. For example, $ax^2 + bx + c$, where $a, b, c$ are coefficients and the terms $ax^2$, $bx$, and $c$ are unlike terms (assuming $x$ is the variable). Other examples include $x+y+z$ or $m^3 - 2m^2 + 5$.
Let a monomial be an expression with exactly one term. For example, $m$ or $kx^2$ or $5$.
We are subtracting a monomial from a trinomial.
Let the trinomial be $T_1 + T_2 + T_3$, where $T_1, T_2, T_3$ are unlike terms.
Let the monomial be $M$.
The subtraction is $(T_1 + T_2 + T_3) - M$, which simplifies to $T_1 + T_2 + T_3 - M$.
Let's consider possible scenarios based on whether the monomial $M$ is a like term with any of the terms in the trinomial:
1. If $M$ is not a like term with any of $T_1, T_2, T_3$.
Example: Trinomial $x^2 + 2x + 3$, Monomial $y$.
Subtraction: $(x^2 + 2x + 3) - y = x^2 + 2x + 3 - y$.
This result has four terms ($x^2$, $2x$, $3$, $-y$). An expression with four terms, where variables have non-negative integer exponents, is a polynomial.
2. If $M$ is a like term with one of the terms in the trinomial, say $T_1$.
Example: Trinomial $x^2 + 2x + 3$, Monomial $4x^2$. Here $4x^2$ is a like term with $x^2$.
Subtraction: $(x^2 + 2x + 3) - 4x^2 = x^2 - 4x^2 + 2x + 3 = -3x^2 + 2x + 3$.
This result has three terms ($-3x^2$, $2x$, $3$). An expression with three terms is a trinomial, and a trinomial is a type of polynomial.
Example: Trinomial $x^2 + 2x + 3$, Monomial $2x$. Here $2x$ is a like term with $2x$.
Subtraction: $(x^2 + 2x + 3) - 2x = x^2 + (2x - 2x) + 3 = x^2 + 0 + 3 = x^2 + 3$.
This result has two terms ($x^2$, $3$). An expression with two terms is a binomial, and a binomial is a type of polynomial.
In all these cases, the result of subtracting a monomial from a trinomial is a polynomial (it could be a polynomial with 4 terms, a trinomial, or a binomial).
The statement says that the answer *can be* a polynomial. Since the answer is *always* a polynomial in these cases, it certainly *can be* a polynomial.
The statement "When we subtract a monomial from a trinomial, then answer can be a polynomial" is True.
Question 52. When we add a monomial and a trinomial, then answer can be a monomial.
Answer:
Let $M$ be a monomial and $T$ be a trinomial.
A monomial has exactly one term.
A trinomial has exactly three unlike terms.
Let the monomial be $m$.
Let the trinomial be $t_1 + t_2 + t_3$, where $t_1$, $t_2$, and $t_3$ are unlike terms.
The sum of the monomial and the trinomial is $m + (t_1 + t_2 + t_3) = m + t_1 + t_2 + t_3$.
For the sum to be a monomial (have exactly one term), all the terms in the simplified expression $m + t_1 + t_2 + t_3$ must be able to combine into a single term.
Since $t_1$, $t_2$, and $t_3$ are unlike terms, they cannot be combined with each other.
The monomial $m$ can only be combined with one of the terms $t_1$, $t_2$, or $t_3$ if it is a like term with that specific term.
Let's consider the possibilities after combining like terms:
1. If $m$ is not a like term with any of $t_1$, $t_2$, or $t_3$. In this case, none of the terms can be combined. The sum is $m + t_1 + t_2 + t_3$, which consists of four unlike terms. This is a polynomial with 4 terms, not a monomial.
2. If $m$ is a like term with exactly one of the terms in the trinomial, say $t_1$. Then $m$ and $t_1$ can be combined into a single term $(m+t_1)$. The sum becomes $(m+t_1) + t_2 + t_3$. Since $t_2$ and $t_3$ are unlike terms (from the original trinomial definition), and they are unlike $(m+t_1)$ (unless $(m+t_1)$ is zero and $t_2, t_3$ were constants or some edge case), the result will typically have two or three terms.
If $(m+t_1) \neq 0$, the terms are $(m+t_1)$, $t_2$, and $t_3$. These are three terms (a trinomial), unless $(m+t_1)$ is like $t_2$ or $t_3$, which contradicts the assumption that $t_1, t_2, t_3$ are unlike terms and $m$ is only like $t_1$.
If $(m+t_1) = 0$, which happens when $m$ is the additive inverse of $t_1$ (i.e., $m = -t_1$), the sum becomes $0 + t_2 + t_3 = t_2 + t_3$. Since $t_2$ and $t_3$ are unlike terms (as they were part of the original trinomial), the result is a binomial (two terms).
In all cases, the sum of a monomial and a trinomial results in either four terms, three terms (a trinomial), or two terms (a binomial). It never results in a single term (a monomial).
Therefore, the statement that the answer can be a monomial is incorrect.
The statement "When we add a monomial and a trinomial, then answer can be a monomial" is False.
Question 53 to 100
Question 53. Write the following statements in the form of algebraic expressions and write whether it is monomial, binomial or trinomial.
(a) x is multiplied by itself and then added to the product of x and y.
(b) Three times of p and two times of q are multiplied and then subtracted from r.
(c) Product of p, twice of q and thrice of r .
(d) Sum of the products of a and b, b and c and c and a.
(e) Perimeter of an equilateral triangle of side x.
(f) Perimeter of a rectangle with length p and breadth q.
(g) Area of a triangle with base m and height n.
(h) Area of a square with side x.
(i) Cube of s subtracted from cube of t.
(j) Quotient of x and 15 multiplied by x.
(k) The sum of square of x and cube of z.
(l) Two times q subtracted from cube of q.
Answer:
(a) x is multiplied by itself and then added to the product of x and y.
Expression: $x \times x + x \times y = x^2 + xy$
Number of terms: 2 ($x^2$ and $xy$ are unlike terms)
Classification: Binomial
(b) Three times of p and two times of q are multiplied and then subtracted from r.
Expression: $r - (3 \times p) \times (2 \times q) = r - (3p) \times (2q) = r - 6pq$
Number of terms: 2 ($r$ and $-6pq$ are unlike terms)
Classification: Binomial
(c) Product of p, twice of q and thrice of r.
Expression: $p \times (2 \times q) \times (3 \times r) = p \times 2q \times 3r = 6pqr$
Number of terms: 1 ($6pqr$ is a single term)
Classification: Monomial
(d) Sum of the products of a and b, b and c and c and a.
Expression: $(a \times b) + (b \times c) + (c \times a) = ab + bc + ca$
Number of terms: 3 ($ab$, $bc$, and $ca$ are unlike terms)
Classification: Trinomial
(e) Perimeter of an equilateral triangle of side x.
Expression: $x + x + x = 3x$
Number of terms: 1 ($3x$ is a single term)
Classification: Monomial
(f) Perimeter of a rectangle with length p and breadth q.
Expression: $2 \times (\text{length} + \text{breadth}) = 2 \times (p + q) = 2p + 2q$
Number of terms: 2 ($2p$ and $2q$ are unlike terms)
Classification: Binomial
(g) Area of a triangle with base m and height n.
Expression: $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times m \times n = \frac{1}{2}mn$
Number of terms: 1 ($\frac{1}{2}mn$ is a single term)
Classification: Monomial
(h) Area of a square with side x.
Expression: $\text{side} \times \text{side} = x \times x = x^2$
Number of terms: 1 ($x^2$ is a single term)
Classification: Monomial
(i) Cube of s subtracted from cube of t.
Expression: $t^3 - s^3$
Number of terms: 2 ($t^3$ and $-s^3$ are unlike terms)
Classification: Binomial
(j) Quotient of x and 15 multiplied by x.
Expression: $\frac{x}{15} \times x = \frac{x^2}{15}$ or $\frac{1}{15}x^2$
Number of terms: 1 ($\frac{1}{15}x^2$ is a single term)
Classification: Monomial
(k) The sum of square of x and cube of z.
Expression: $x^2 + z^3$
Number of terms: 2 ($x^2$ and $z^3$ are unlike terms)
Classification: Binomial
(l) Two times q subtracted from cube of q.
Expression: $q^3 - 2 \times q = q^3 - 2q$
Number of terms: 2 ($q^3$ and $-2q$ are unlike terms)
Classification: Binomial
Question 54. Write the coefficient of x2 in the following:
(i) x2 – x + 4
(ii) x3 – 2x2 + 3x + 1
(iii) 1 + 2x + 3x2 + 4x3
(iv) y + y2x + y3x2 + y4x3
Answer:
To find the coefficient of $x^2$ in an expression, we identify the term containing $x^2$ and state the factor multiplying $x^2$.
(i) $x^2 – x + 4$
The term with $x^2$ is $x^2$. This can be written as $1 \cdot x^2$.
The coefficient of $x^2$ is $\mathbf{1}$.
(ii) $x^3 – 2x^2 + 3x + 1$
The term with $x^2$ is $-2x^2$. This can be written as $-2 \cdot x^2$.
The coefficient of $x^2$ is $\mathbf{-2}$.
(iii) $1 + 2x + 3x^2 + 4x^3$
The term with $x^2$ is $3x^2$. This can be written as $3 \cdot x^2$.
The coefficient of $x^2$ is $\mathbf{3}$.
(iv) $y + y^2x + y^3x^2 + y^4x^3$
The term with $x^2$ is $y^3x^2$. This can be written as $y^3 \cdot x^2$.
The coefficient of $x^2$ is $\mathbf{y^3}$.
Question 55. Find the numerical coefficient of each of the terms :
(i) x3y2z, xy2z3, –3xy2z3, 5x3y2z, –7x2y2z2
(ii) 10xyz, –7xy2z, –9xyz, 2xy2z, 2x2y2z2
Answer:
The numerical coefficient of a term is the constant factor that multiplies the variable part.
(i) Terms: $x^3y^2z$, $xy^2z^3$, $-3xy^2z^3$, $5x^3y^2z$, $-7x^2y^2z^2$
For $x^3y^2z$: This can be written as $1 \cdot x^3y^2z$. The numerical coefficient is $\mathbf{1}$.
For $xy^2z^3$: This can be written as $1 \cdot xy^2z^3$. The numerical coefficient is $\mathbf{1}$.
For $-3xy^2z^3$: The numerical coefficient is $\mathbf{-3}$.
For $5x^3y^2z$: The numerical coefficient is $\mathbf{5}$.
For $-7x^2y^2z^2$: The numerical coefficient is $\mathbf{-7}$.
(ii) Terms: $10xyz$, $-7xy^2z$, $-9xyz$, $2xy^2z$, $2x^2y^2z^2$
For $10xyz$: The numerical coefficient is $\mathbf{10}$.
For $-7xy^2z$: The numerical coefficient is $\mathbf{-7}$.
For $-9xyz$: The numerical coefficient is $\mathbf{-9}$.
For $2xy^2z$: The numerical coefficient is $\mathbf{2}$.
For $2x^2y^2z^2$: The numerical coefficient is $\mathbf{2}$.
Question 56. Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.
(a) 3x2yz2 – 3xy2z + x2yz2 + 7xy2z
(b) x4 + 3x3y + 3x2y2 – 3x3y – 3xy3 + y4 – 3x2y2
(c) p3q2r + pq2r3 + 3p2qr2 – 9p2qr2
(d) 2a + 2b + 2c – 2a – 2b – 2c – 2b + 2c + 2a
(e) 50x3 – 21x + 107 + 41x3 – x + 1 – 93 + 71x – 31x3
Answer:
To simplify the expressions, we combine the terms that have the exact same variables raised to the same powers (like terms).
(a) $3x^2yz^2 – 3xy^2z + x^2yz^2 + 7xy^2z$
Group like terms:
$(3x^2yz^2 + x^2yz^2) + (-3xy^2z + 7xy^2z)$
Combine coefficients of like terms:
$(3 + 1)x^2yz^2 + (-3 + 7)xy^2z$
$4x^2yz^2 + 4xy^2z$
The simplified expression is $4x^2yz^2 + 4xy^2z$.
This expression has two distinct terms: $4x^2yz^2$ and $4xy^2z$.
Classification: Binomial
(b) $x^4 + 3x^3y + 3x^2y^2 – 3x^3y – 3xy^3 + y^4 – 3x^2y^2$
Group like terms:
$x^4 + (3x^3y – 3x^3y) + (3x^2y^2 – 3x^2y^2) – 3xy^3 + y^4$
Combine coefficients of like terms:
$x^4 + (3 - 3)x^3y + (3 - 3)x^2y^2 – 3xy^3 + y^4$
$x^4 + 0x^3y + 0x^2y^2 – 3xy^3 + y^4$
$x^4 – 3xy^3 + y^4$
The simplified expression is $x^4 – 3xy^3 + y^4$.
This expression has three distinct terms: $x^4$, $-3xy^3$, and $y^4$.
Classification: Trinomial
(c) $p^3q^2r + pq^2r^3 + 3p^2qr^2 – 9p^2qr^2$
Group like terms:
$p^3q^2r + pq^2r^3 + (3p^2qr^2 – 9p^2qr^2)$
Combine coefficients of like terms:
$p^3q^2r + pq^2r^3 + (3 - 9)p^2qr^2$
$p^3q^2r + pq^2r^3 – 6p^2qr^2$
The simplified expression is $p^3q^2r + pq^2r^3 – 6p^2qr^2$.
This expression has three distinct terms: $p^3q^2r$, $pq^2r^3$, and $-6p^2qr^2$.
Classification: Trinomial
(d) $2a + 2b + 2c – 2a – 2b – 2c – 2b + 2c + 2a$
Group like terms:
$(2a – 2a + 2a) + (2b – 2b – 2b) + (2c – 2c + 2c)$
Combine coefficients of like terms:
$(2 – 2 + 2)a + (2 – 2 – 2)b + (2 – 2 + 2)c$
$2a + (-2)b + 2c$
$2a – 2b + 2c$
The simplified expression is $2a – 2b + 2c$.
This expression has three distinct terms: $2a$, $-2b$, and $2c$.
Classification: Trinomial
(e) $50x^3 – 21x + 107 + 41x^3 – x + 1 – 93 + 71x – 31x^3$
Group like terms (terms with $x^3$, terms with $x$, and constant terms):
$(50x^3 + 41x^3 – 31x^3) + (-21x – x + 71x) + (107 + 1 – 93)$
Combine coefficients of like terms:
$(50 + 41 – 31)x^3 + (-21 – 1 + 71)x + (107 + 1 – 93)$
$(91 – 31)x^3 + (-22 + 71)x + (108 – 93)$
$60x^3 + 49x + 15$
The simplified expression is $60x^3 + 49x + 15$.
This expression has three distinct terms: $60x^3$, $49x$, and $15$.
Classification: Trinomial
Question 57. Add the following expressions:
(a) p2 – 7pq – q2 and – 3p2 – 2pq + 7q2
(b) x3 – x2y – xy2 – y3 and x3 – 2x2y + 3xy2 + 4y
(c) ab + bc + ca and – bc – ca – ab
(d) p2 – q + r, q2 – r + p and r2 – p + q
(e) x3y2 + x2y3 +3y4 and x4 + 3x2y3 + 4y4
(f) p2qr + pq2r + pqr2 and – 3pq2r –2pqr2
(g) uv – vw, vw – wu and wu – uv
(h) a2 + 3ab – bc, b2 + 3bc – ca and c2 + 3ca – ab
(i) $\frac{5}{8}$p4 + 2p2 + $\frac{5}{8}$ ; $\frac{1}{8}$ - 17p + $\frac{9}{8}$p2 and p5 - p3 + 7
(j) t – t2 – t3 – 14; 15t3 + 13 + 9t – 8t2; 12t2 – 19 – 24t and 4t – 9t2 + 19t3
Answer:
(a) Add $p^2 - 7pq - q^2$ and $-3p^2 - 2pq + 7q^2$.
Sum $= (p^2 - 7pq - q^2) + (-3p^2 - 2pq + 7q^2)$
Sum $= p^2 - 3p^2 - 7pq - 2pq - q^2 + 7q^2$
Sum $= (1-3)p^2 + (-7-2)pq + (-1+7)q^2$
Sum $= -2p^2 - 9pq + 6q^2$
(b) Add $x^3 - x^2y - xy^2 - y^3$ and $x^3 - 2x^2y + 3xy^2 + 4y$.
Sum $= (x^3 - x^2y - xy^2 - y^3) + (x^3 - 2x^2y + 3xy^2 + 4y)$
Sum $= x^3 + x^3 - x^2y - 2x^2y - xy^2 + 3xy^2 - y^3 + 4y$
Sum $= (1+1)x^3 + (-1-2)x^2y + (-1+3)xy^2 - y^3 + 4y$
Sum $= 2x^3 - 3x^2y + 2xy^2 - y^3 + 4y$
(c) Add $ab + bc + ca$ and $-bc - ca - ab$.
Sum $= (ab + bc + ca) + (-bc - ca - ab)$
Sum $= ab - ab + bc - bc + ca - ca$
Sum $= (1-1)ab + (1-1)bc + (1-1)ca$
Sum $= 0 \cdot ab + 0 \cdot bc + 0 \cdot ca$
Sum $= 0$
(d) Add $p^2 - q + r$, $q^2 - r + p$ and $r^2 - p + q$.
Sum $= (p^2 - q + r) + (q^2 - r + p) + (r^2 - p + q)$
Sum $= p^2 + q^2 + r^2 - q + q - r + r + p - p$
Sum $= p^2 + q^2 + r^2 + (-q+q) + (-r+r) + (p-p)$
Sum $= p^2 + q^2 + r^2 + 0 + 0 + 0$
Sum $= p^2 + q^2 + r^2$
(e) Add $x^3y^2 + x^2y^3 + 3y^4$ and $x^4 + 3x^2y^3 + 4y^4$.
Sum $= (x^3y^2 + x^2y^3 + 3y^4) + (x^4 + 3x^2y^3 + 4y^4)$
Sum $= x^4 + x^3y^2 + x^2y^3 + 3x^2y^3 + 3y^4 + 4y^4$
Sum $= x^4 + x^3y^2 + (1+3)x^2y^3 + (3+4)y^4$
Sum $= x^4 + x^3y^2 + 4x^2y^3 + 7y^4$
(f) Add $p^2qr + pq^2r + pqr^2$ and $-3pq^2r - 2pqr^2$.
Sum $= (p^2qr + pq^2r + pqr^2) + (-3pq^2r - 2pqr^2)$
Sum $= p^2qr + pq^2r - 3pq^2r + pqr^2 - 2pqr^2$
Sum $= p^2qr + (1-3)pq^2r + (1-2)pqr^2$
Sum $= p^2qr - 2pq^2r - pqr^2$
(g) Add $uv - vw$, $vw - wu$ and $wu - uv$.
Sum $= (uv - vw) + (vw - wu) + (wu - uv)$
Sum $= uv - uv - vw + vw - wu + wu$
Sum $= (1-1)uv + (-1+1)vw + (-1+1)wu$
Sum $= 0 \cdot uv + 0 \cdot vw + 0 \cdot wu$
Sum $= 0$
(h) Add $a^2 + 3ab - bc$, $b^2 + 3bc - ca$ and $c^2 + 3ca - ab$.
Sum $= (a^2 + 3ab - bc) + (b^2 + 3bc - ca) + (c^2 + 3ca - ab)$
Sum $= a^2 + b^2 + c^2 + 3ab - ab - bc + 3bc - ca + 3ca$
Sum $= a^2 + b^2 + c^2 + (3-1)ab + (-1+3)bc + (-1+3)ca$
Sum $= a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$
(i) Add $\frac{5}{8}p^4 + 2p^2 + \frac{5}{8}$, $\frac{1}{8} - 17p + \frac{9}{8}p^2$ and $p^5 - p^3 + 7$.
Sum $= (\frac{5}{8}p^4 + 2p^2 + \frac{5}{8}) + (\frac{1}{8} - 17p + \frac{9}{8}p^2) + (p^5 - p^3 + 7)$
Sum $= p^5 + \frac{5}{8}p^4 - p^3 + 2p^2 + \frac{9}{8}p^2 - 17p + \frac{5}{8} + \frac{1}{8} + 7$
Sum $= p^5 + \frac{5}{8}p^4 - p^3 + (2 + \frac{9}{8})p^2 - 17p + (\frac{5}{8} + \frac{1}{8} + 7)$
Sum $= p^5 + \frac{5}{8}p^4 - p^3 + (\frac{16}{8} + \frac{9}{8})p^2 - 17p + (\frac{6}{8} + \frac{56}{8})$
Sum $= p^5 + \frac{5}{8}p^4 - p^3 + \frac{25}{8}p^2 - 17p + \frac{62}{8}$
Sum $= p^5 + \frac{5}{8}p^4 - p^3 + \frac{25}{8}p^2 - 17p + \frac{31}{4}$
(j) Add $t - t^2 - t^3 - 14$, $15t^3 + 13 + 9t - 8t^2$, $12t^2 - 19 - 24t$ and $4t - 9t^2 + 19t^3$.
Sum $= (t - t^2 - t^3 - 14) + (15t^3 + 13 + 9t - 8t^2) + (12t^2 - 19 - 24t) + (4t - 9t^2 + 19t^3)$
Sum $= (-t^3 + 15t^3 + 19t^3) + (-t^2 - 8t^2 + 12t^2 - 9t^2) + (t + 9t - 24t + 4t) + (-14 + 13 - 19)$
Sum $= (-1 + 15 + 19)t^3 + (-1 - 8 + 12 - 9)t^2 + (1 + 9 - 24 + 4)t + (-14 + 13 - 19)$
Sum $= (14 + 19)t^3 + (-9 + 12 - 9)t^2 + (10 - 24 + 4)t + (-1 - 19)$
Sum $= 33t^3 + (3 - 9)t^2 + (-14 + 4)t - 20$
Sum $= 33t^3 - 6t^2 - 10t - 20$
Question 58. Subtract
(a) – 7p2qr from – 3p2qr.
(b) –a2 – ab from b2 + ab.
(c) –4x2y – y3 from x3 + 3xy2 – x2y.
(d) x4 + 3x3y3 + 5y4 from 2x4 – x3y3 + 7y4.
(e) ab – bc – ca from – ab + bc + ca.
(f) –2a2 – 2b2 from – a2 – b2 + 2ab.
(g) x3y2 + 3x2y2 – 7xy3 from x4 + y4 + 3x2y2 – xy3.
(h) 2 (ab + bc + ca) from –ab – bc – ca.
(i) 4.5x5 – 3.4x2 + 5.7 from 5x4 – 3.2x2 – 7.3x.
(j) 11 – 15y2 from y3 – 15y2 – y – 11.
Answer:
(a) Subtract $-7p^2qr$ from $-3p^2qr$.
Difference $= (-3p^2qr) - (-7p^2qr)$
Difference $= -3p^2qr + 7p^2qr$
Difference $= (-3+7)p^2qr$
Difference $= 4p^2qr$
(b) Subtract $-a^2 - ab$ from $b^2 + ab$.
Difference $= (b^2 + ab) - (-a^2 - ab)$
Difference $= b^2 + ab + a^2 + ab$
Difference $= a^2 + b^2 + ab + ab$
Difference $= a^2 + b^2 + 2ab$
(c) Subtract $-4x^2y - y^3$ from $x^3 + 3xy^2 - x^2y$.
Difference $= (x^3 + 3xy^2 - x^2y) - (-4x^2y - y^3)$
Difference $= x^3 + 3xy^2 - x^2y + 4x^2y + y^3$
Difference $= x^3 + y^3 + 3xy^2 - x^2y + 4x^2y$
Difference $= x^3 + y^3 + 3xy^2 + (-1+4)x^2y$
Difference $= x^3 + y^3 + 3xy^2 + 3x^2y$
(d) Subtract $x^4 + 3x^3y^3 + 5y^4$ from $2x^4 - x^3y^3 + 7y^4$.
Difference $= (2x^4 - x^3y^3 + 7y^4) - (x^4 + 3x^3y^3 + 5y^4)$
Difference $= 2x^4 - x^3y^3 + 7y^4 - x^4 - 3x^3y^3 - 5y^4$
Difference $= 2x^4 - x^4 - x^3y^3 - 3x^3y^3 + 7y^4 - 5y^4$
Difference $= (2-1)x^4 + (-1-3)x^3y^3 + (7-5)y^4$
Difference $= x^4 - 4x^3y^3 + 2y^4$
(e) Subtract $ab - bc - ca$ from $-ab + bc + ca$.
Difference $= (-ab + bc + ca) - (ab - bc - ca)$
Difference $= -ab + bc + ca - ab + bc + ca$
Difference $= -ab - ab + bc + bc + ca + ca$
Difference $= (-1-1)ab + (1+1)bc + (1+1)ca$
Difference $= -2ab + 2bc + 2ca$
(f) Subtract $-2a^2 - 2b^2$ from $-a^2 - b^2 + 2ab$.
Difference $= (-a^2 - b^2 + 2ab) - (-2a^2 - 2b^2)$
Difference $= -a^2 - b^2 + 2ab + 2a^2 + 2b^2$
Difference $= -a^2 + 2a^2 - b^2 + 2b^2 + 2ab$
Difference $= (-1+2)a^2 + (-1+2)b^2 + 2ab$
Difference $= a^2 + b^2 + 2ab$
(g) Subtract $x^3y^2 + 3x^2y^2 - 7xy^3$ from $x^4 + y^4 + 3x^2y^2 - xy^3$.
Difference $= (x^4 + y^4 + 3x^2y^2 - xy^3) - (x^3y^2 + 3x^2y^2 - 7xy^3)$
Difference $= x^4 + y^4 + 3x^2y^2 - xy^3 - x^3y^2 - 3x^2y^2 + 7xy^3$
Difference $= x^4 + y^4 - x^3y^2 + (3x^2y^2 - 3x^2y^2) + (-xy^3 + 7xy^3)$
Difference $= x^4 + y^4 - x^3y^2 + 0 + (-1+7)xy^3$
Difference $= x^4 + y^4 - x^3y^2 + 6xy^3$
(h) Subtract $2(ab + bc + ca)$ from $-ab - bc - ca$.
$2(ab + bc + ca) = 2ab + 2bc + 2ca$
Difference $= (-ab - bc - ca) - (2ab + 2bc + 2ca)$
Difference $= -ab - bc - ca - 2ab - 2bc - 2ca$
Difference $= (-1-2)ab + (-1-2)bc + (-1-2)ca$
Difference $= -3ab - 3bc - 3ca$
Difference $= -3(ab + bc + ca)$
(i) Subtract $4.5x^5 - 3.4x^2 + 5.7$ from $5x^4 - 3.2x^2 - 7.3x$.
Difference $= (5x^4 - 3.2x^2 - 7.3x) - (4.5x^5 - 3.4x^2 + 5.7)$
Difference $= 5x^4 - 3.2x^2 - 7.3x - 4.5x^5 + 3.4x^2 - 5.7$
Difference $= -4.5x^5 + 5x^4 + (-3.2 + 3.4)x^2 - 7.3x - 5.7$
Difference $= -4.5x^5 + 5x^4 + 0.2x^2 - 7.3x - 5.7$
(j) Subtract $11 - 15y^2$ from $y^3 - 15y^2 - y - 11$.
Difference $= (y^3 - 15y^2 - y - 11) - (11 - 15y^2)$
Difference $= y^3 - 15y^2 - y - 11 - 11 + 15y^2$
Difference $= y^3 + (-15y^2 + 15y^2) - y + (-11 - 11)$
Difference $= y^3 + 0 - y - 22$
Difference $= y^3 - y - 22$
Question 59.
(a) What should be added to x3 + 3x2y + 3xy2 + y3 to get x3 + y3?
(b) What should be added to 3pq + 5p2q2 + p3 to get p3 + 2p2q2 + 4pq ?
Answer:
(a) To find what should be added to $x^3 + 3x^2y + 3xy^2 + y^3$ to get $x^3 + y^3$, we subtract the first expression from the second expression.
Required expression $= (x^3 + y^3) - (x^3 + 3x^2y + 3xy^2 + y^3)$
Required expression $= x^3 + y^3 - x^3 - 3x^2y - 3xy^2 - y^3$
Required expression $= (x^3 - x^3) + (y^3 - y^3) - 3x^2y - 3xy^2$
Required expression $= 0 + 0 - 3x^2y - 3xy^2$
Required expression $= -3x^2y - 3xy^2$
(b) To find what should be added to $3pq + 5p^2q^2 + p^3$ to get $p^3 + 2p^2q^2 + 4pq$, we subtract the first expression from the second expression.
Required expression $= (p^3 + 2p^2q^2 + 4pq) - (3pq + 5p^2q^2 + p^3)$
Required expression $= p^3 + 2p^2q^2 + 4pq - 3pq - 5p^2q^2 - p^3$
Required expression $= (p^3 - p^3) + (2p^2q^2 - 5p^2q^2) + (4pq - 3pq)$
Required expression $= 0 + (2-5)p^2q^2 + (4-3)pq$
Required expression $= -3p^2q^2 + pq$
Question 60.
(a) What should be subtracted from 2x3 – 3x2y + 2xy2 + 3y3 to get x3 – 2x2y + 3xy2 + 4y3?
(b) What should be subtracted from –7mn + 2m2 + 3n2 to get m2 + 2mn + n2 ?
Answer:
(a) Let the expression that should be subtracted be $E$.
According to the question:
$(2x^3 - 3x^2y + 2xy^2 + 3y^3) - E = x^3 - 2x^2y + 3xy^2 + 4y^3$
To find $E$, we rearrange the equation:
$E = (2x^3 - 3x^2y + 2xy^2 + 3y^3) - (x^3 - 2x^2y + 3xy^2 + 4y^3)$
$E = 2x^3 - 3x^2y + 2xy^2 + 3y^3 - x^3 + 2x^2y - 3xy^2 - 4y^3$
Combine like terms:
$E = (2x^3 - x^3) + (-3x^2y + 2x^2y) + (2xy^2 - 3xy^2) + (3y^3 - 4y^3)$
$E = (2-1)x^3 + (-3+2)x^2y + (2-3)xy^2 + (3-4)y^3$
$E = 1x^3 - 1x^2y - 1xy^2 - 1y^3$
$E = x^3 - x^2y - xy^2 - y^3$
Thus, $x^3 - x^2y - xy^2 - y^3$ should be subtracted.
(b) Let the expression that should be subtracted be $E$.
According to the question:
$(-7mn + 2m^2 + 3n^2) - E = m^2 + 2mn + n^2$
To find $E$, we rearrange the equation:
$E = (-7mn + 2m^2 + 3n^2) - (m^2 + 2mn + n^2)$
$E = -7mn + 2m^2 + 3n^2 - m^2 - 2mn - n^2$
Combine like terms:
$E = (2m^2 - m^2) + (3n^2 - n^2) + (-7mn - 2mn)$
$E = (2-1)m^2 + (3-1)n^2 + (-7-2)mn$
$E = 1m^2 + 2n^2 - 9mn$
$E = m^2 + 2n^2 - 9mn$
Thus, $m^2 + 2n^2 - 9mn$ should be subtracted.
Question 61. How much is 21a3 – 17a2 less than 89a3 – 64a2 + 6a + 16?
Answer:
To find how much $21a^3 - 17a^2$ is less than $89a^3 - 64a^2 + 6a + 16$, we need to subtract the first expression from the second expression.
Difference $= (89a^3 - 64a^2 + 6a + 16) - (21a^3 - 17a^2)$
Difference $= 89a^3 - 64a^2 + 6a + 16 - 21a^3 + 17a^2$
Group like terms:
Difference $= (89a^3 - 21a^3) + (-64a^2 + 17a^2) + 6a + 16$
Combine the coefficients:
Difference $= (89 - 21)a^3 + (-64 + 17)a^2 + 6a + 16$
Difference $= 68a^3 - 47a^2 + 6a + 16$
So, $21a^3 - 17a^2$ is $68a^3 - 47a^2 + 6a + 16$ less than $89a^3 - 64a^2 + 6a + 16$.
Question 62. How much is y4 – 12y2 + y + 14 greater than 17y3 + 34y2 – 51y + 68?
Answer:
To find how much $y^4 - 12y^2 + y + 14$ is greater than $17y^3 + 34y^2 - 51y + 68$, we need to subtract the second expression from the first expression.
Difference $= (y^4 - 12y^2 + y + 14) - (17y^3 + 34y^2 - 51y + 68)$
Difference $= y^4 - 12y^2 + y + 14 - 17y^3 - 34y^2 + 51y - 68$
Group like terms, arranging in descending order of powers of $y$:
Difference $= y^4 - 17y^3 + (-12y^2 - 34y^2) + (y + 51y) + (14 - 68)$
Combine the coefficients of like terms:
Difference $= y^4 - 17y^3 + (-12 - 34)y^2 + (1 + 51)y + (14 - 68)$
Difference $= y^4 - 17y^3 - 46y^2 + 52y - 54$
So, $y^4 - 12y^2 + y + 14$ is $y^4 - 17y^3 - 46y^2 + 52y - 54$ greater than $17y^3 + 34y^2 - 51y + 68$.
Question 63. How much does 93p2 – 55p + 4 exceed 13p3 – 5p2 + 17p – 90?
Answer:
To find how much $93p^2 - 55p + 4$ exceeds $13p^3 - 5p^2 + 17p - 90$, we need to subtract the second expression from the first expression.
Expression 1: $93p^2 - 55p + 4$
Expression 2: $13p^3 - 5p^2 + 17p - 90$
Difference $= (93p^2 - 55p + 4) - (13p^3 - 5p^2 + 17p - 90)$
Remove parentheses and change signs of the terms being subtracted:
Difference $= 93p^2 - 55p + 4 - 13p^3 + 5p^2 - 17p + 90$
Group like terms:
Difference $= -13p^3 + (93p^2 + 5p^2) + (-55p - 17p) + (4 + 90)$
Combine coefficients of like terms:
Difference $= -13p^3 + (93+5)p^2 + (-55-17)p + (4+90)$
Difference $= -13p^3 + 98p^2 - 72p + 94$
Thus, $93p^2 - 55p + 4$ exceeds $13p^3 - 5p^2 + 17p - 90$ by $98p^2 - 72p + 94 - 13p^3$.
We can also write the result as $-13p^3 + 98p^2 - 72p + 94$.
Question 64. To what expression must 99x3 – 33x2 – 13x – 41 be added to make the sum zero?
Answer:
Let the expression that must be added be $E$.
According to the question, when $E$ is added to $99x^3 - 33x^2 - 13x - 41$, the sum is zero.
So, we have the equation:
$(99x^3 - 33x^2 - 13x - 41) + E = 0$
To find the expression $E$, we subtract $(99x^3 - 33x^2 - 13x - 41)$ from $0$:
$E = 0 - (99x^3 - 33x^2 - 13x - 41)$
$E = - (99x^3 - 33x^2 - 13x - 41)$
Distribute the negative sign to each term inside the parentheses:
$E = -99x^3 - (-33x^2) - (-13x) - (-41)$
$E = -99x^3 + 33x^2 + 13x + 41$
Thus, the expression that must be added is $-99x^3 + 33x^2 + 13x + 41$.
Question 65. Subtract 9a2 – 15a + 3 from unity.
Answer:
Unity means the number $1$.
To subtract the expression $9a^2 - 15a + 3$ from unity, we write:
Difference $= 1 - (9a^2 - 15a + 3)$
Remove the parentheses by distributing the negative sign to each term inside:
Difference $= 1 - 9a^2 - (-15a) - (+3)$
Difference $= 1 - 9a^2 + 15a - 3$
Combine the constant terms $1$ and $-3$:
Difference $= -9a^2 + 15a + (1 - 3)$
Difference $= -9a^2 + 15a - 2$
Thus, the result of subtracting $9a^2 - 15a + 3$ from unity is $-9a^2 + 15a - 2$.
Question 66. Find the values of the following polynomials at a = – 2 and b = 3:
(a) a2 + 2ab + b2
(b) a2 – 2ab + b2
(c) a3 + 3a2b + 3ab2 + b3
(d) a3 – 3a2b + 3ab2 – b3
(e) $\frac{a^2 + b^2}{2}$
(f) $\frac{a^2 - b^2}{2}$
(g) $\frac{a}{b}$ + $\frac{b}{a}$
(h) a2 + b2 – ab – b2 – a2
Answer:
We are given $a = -2$ and $b = 3$. We need to find the value of each expression by substituting these values.
(a) $a^2 + 2ab + b^2$
Substitute $a=-2$ and $b=3$:
$(-2)^2 + 2(-2)(3) + (3)^2$
$= 4 + 2(-6) + 9$
$= 4 - 12 + 9$
$= -8 + 9$
$= 1$
(b) $a^2 - 2ab + b^2$
Substitute $a=-2$ and $b=3$:
$(-2)^2 - 2(-2)(3) + (3)^2$
$= 4 - 2(-6) + 9$
$= 4 + 12 + 9$
$= 16 + 9$
$= 25$
(c) $a^3 + 3a^2b + 3ab^2 + b^3$
This is the expansion of $(a+b)^3$.
Substitute $a=-2$ and $b=3$:
$(-2+3)^3 = (1)^3 = 1$
Alternatively, substitute directly:
$(-2)^3 + 3(-2)^2(3) + 3(-2)(3)^2 + (3)^3$
$= -8 + 3(4)(3) + 3(-2)(9) + 27$
$= -8 + 36 - 54 + 27$
$= 63 - 62 = 1$
(d) $a^3 - 3a^2b + 3ab^2 - b^3$
This is the expansion of $(a-b)^3$.
Substitute $a=-2$ and $b=3$:
$(-2-3)^3 = (-5)^3 = -125$
Alternatively, substitute directly:
$(-2)^3 - 3(-2)^2(3) + 3(-2)(3)^2 - (3)^3$
$= -8 - 3(4)(3) + 3(-2)(9) - 27$
$= -8 - 36 - 54 - 27$
$= -125$
(e) $\frac{a^2 + b^2}{2}$
Substitute $a=-2$ and $b=3$:
$\frac{(-2)^2 + (3)^2}{2} = \frac{4 + 9}{2} = \frac{13}{2}$
(f) $\frac{a^2 - b^2}{2}$
Substitute $a=-2$ and $b=3$:
$\frac{(-2)^2 - (3)^2}{2} = \frac{4 - 9}{2} = \frac{-5}{2}$
(g) $\frac{a}{b} + \frac{b}{a}$
Substitute $a=-2$ and $b=3$:
$\frac{-2}{3} + \frac{3}{-2} = -\frac{2}{3} - \frac{3}{2}$
Find a common denominator:
$-\frac{2}{3} - \frac{3}{2} = -\frac{2 \times 2}{3 \times 2} - \frac{3 \times 3}{2 \times 3} = -\frac{4}{6} - \frac{9}{6} = \frac{-4-9}{6} = \frac{-13}{6}$
(h) $a^2 + b^2 - ab - b^2 - a^2$
First, simplify the expression:
$a^2 + b^2 - ab - b^2 - a^2 = (a^2 - a^2) + (b^2 - b^2) - ab = 0 + 0 - ab = -ab$
Now, substitute $a=-2$ and $b=3$ into the simplified expression:
$-(-2)(3) = -(-6) = 6$
Question 67. Find the values of following polynomials at m = 1, n = –1 and p = 2:
(a) m + n + p
(b) m2 + n2 + p2
(c) m3 + n3 + p3
(d) mn + np + pm
(e) m3 + n3 + p3 – 3mnp
(f) m2n2 + n2p2 + p2m2
Answer:
We are given $m = 1$, $n = -1$, and $p = 2$. We will substitute these values into each expression.
(a) $m + n + p$
Substitute $m=1$, $n=-1$, $p=2$:
$1 + (-1) + 2$
$= 1 - 1 + 2$
$= 0 + 2$
$= 2$
(b) $m^2 + n^2 + p^2$
Substitute $m=1$, $n=-1$, $p=2$:
$(1)^2 + (-1)^2 + (2)^2$
$= 1 + 1 + 4$
$= 2 + 4$
$= 6$
(c) $m^3 + n^3 + p^3$
Substitute $m=1$, $n=-1$, $p=2$:
$(1)^3 + (-1)^3 + (2)^3$
$= 1 + (-1) + 8$
$= 1 - 1 + 8$
$= 0 + 8$
$= 8$
(d) $mn + np + pm$
Substitute $m=1$, $n=-1$, $p=2$:
$(1)(-1) + (-1)(2) + (2)(1)$
$= -1 + (-2) + 2$
$= -1 - 2 + 2$
$= -3 + 2$
$= -1$
(e) $m^3 + n^3 + p^3 - 3mnp$
From part (c), $m^3 + n^3 + p^3 = 8$.
Calculate $3mnp$:
$3(1)(-1)(2)$
$= 3(-2)$
$= -6$
Now substitute these values into the expression:
$(m^3 + n^3 + p^3) - 3mnp = 8 - (-6)$
$= 8 + 6$
$= 14$
Alternatively, substitute directly into the expression:
$(1)^3 + (-1)^3 + (2)^3 - 3(1)(-1)(2)$
$= 1 + (-1) + 8 - 3(-2)$
$= 1 - 1 + 8 + 6$
$= 0 + 8 + 6$
$= 14$
(f) $m^2n^2 + n^2p^2 + p^2m^2$
Substitute $m=1$, $n=-1$, $p=2$:
$(1)^2(-1)^2 + (-1)^2(2)^2 + (2)^2(1)^2$
$= (1)(1) + (1)(4) + (4)(1)$
$= 1 + 4 + 4$
$= 9$
Question 68. If A = 3x2 – 4x + 1, B = 5x2 + 3x – 8 and C = 4x2 – 7x + 3, then find:
(i) (A + B) – C
(ii) B + C – A
(iii) A + B + C
Answer:
Given the expressions:
$A = 3x^2 - 4x + 1$
$B = 5x^2 + 3x - 8$
$C = 4x^2 - 7x + 3$
(i) Find $(A + B) - C$
First, calculate $A + B$:
$A + B = (3x^2 - 4x + 1) + (5x^2 + 3x - 8)$
$A + B = 3x^2 + 5x^2 - 4x + 3x + 1 - 8$
$A + B = (3+5)x^2 + (-4+3)x + (1-8)$
$A + B = 8x^2 - x - 7$
Now, subtract $C$ from $A + B$:
$(A + B) - C = (8x^2 - x - 7) - (4x^2 - 7x + 3)$
$(A + B) - C = 8x^2 - x - 7 - 4x^2 + 7x - 3$
$(A + B) - C = 8x^2 - 4x^2 - x + 7x - 7 - 3$
$(A + B) - C = (8-4)x^2 + (-1+7)x + (-7-3)$
$(A + B) - C = 4x^2 + 6x - 10$
(ii) Find $B + C - A$
First, calculate $B + C$:
$B + C = (5x^2 + 3x - 8) + (4x^2 - 7x + 3)$
$B + C = 5x^2 + 4x^2 + 3x - 7x - 8 + 3$
$B + C = (5+4)x^2 + (3-7)x + (-8+3)$
$B + C = 9x^2 - 4x - 5$
Now, subtract $A$ from $B + C$:
$(B + C) - A = (9x^2 - 4x - 5) - (3x^2 - 4x + 1)$
$(B + C) - A = 9x^2 - 4x - 5 - 3x^2 + 4x - 1$
$(B + C) - A = 9x^2 - 3x^2 - 4x + 4x - 5 - 1$
$(B + C) - A = (9-3)x^2 + (-4+4)x + (-5-1)$
$(B + C) - A = 6x^2 + 0x - 6$
$(B + C) - A = 6x^2 - 6$
(iii) Find $A + B + C$
Add the three expressions:
$A + B + C = (3x^2 - 4x + 1) + (5x^2 + 3x - 8) + (4x^2 - 7x + 3)$
$A + B + C = 3x^2 + 5x^2 + 4x^2 - 4x + 3x - 7x + 1 - 8 + 3$
$A + B + C = (3+5+4)x^2 + (-4+3-7)x + (1-8+3)$
$A + B + C = (8+4)x^2 + (-1-7)x + (-7+3)$
$A + B + C = 12x^2 - 8x - 4$
Question 69. If P = –(x – 2), Q = –2(y + 1) and R = –x + 2y, find a, when P + Q + R = ax.
Answer:
Given the expressions:
$P = -(x - 2)$
$Q = -2(y + 1)$
$R = -x + 2y$
Simplify expressions P and Q:
$P = -x + 2$
$Q = -2y - 2$
$R = -x + 2y$
Calculate the sum $P + Q + R$:
$P + Q + R = (-x + 2) + (-2y - 2) + (-x + 2y)$
Group like terms:
$P + Q + R = (-x - x) + (-2y + 2y) + (2 - 2)$
Combine coefficients:
$P + Q + R = (-1 - 1)x + (-2 + 2)y + (2 - 2)$
$P + Q + R = -2x + 0y + 0$
$P + Q + R = -2x$
We are given that $P + Q + R = ax$.
Substitute the calculated sum into the given equation:
$-2x = ax$
To find the value of $a$, compare the coefficients of $x$ on both sides of the equation.
The coefficient of $x$ on the left side is $-2$.
The coefficient of $x$ on the right side is $a$.
Equating the coefficients:
$-2 = a$
Thus, the value of $a$ is $-2$.
Question 70. From the sum of x2 – y2 – 1, y2 – x2 – 1 and 1 – x2 – y2 subtract – (1 + y2).
Answer:
First, find the sum of the three expressions: $x^2 - y^2 - 1$, $y^2 - x^2 - 1$, and $1 - x^2 - y^2$.
Sum $= (x^2 - y^2 - 1) + (y^2 - x^2 - 1) + (1 - x^2 - y^2)$
Sum $= x^2 - y^2 - 1 + y^2 - x^2 - 1 + 1 - x^2 - y^2$
Group the like terms:
Sum $= (x^2 - x^2 - x^2) + (-y^2 + y^2 - y^2) + (-1 - 1 + 1)$
Combine the coefficients:
Sum $= (1 - 1 - 1)x^2 + (-1 + 1 - 1)y^2 + (-1 - 1 + 1)$
Sum $= (-1)x^2 + (-1)y^2 + (-1)$
Sum $= -x^2 - y^2 - 1$
Next, identify the expression to be subtracted: $-(1 + y^2)$.
Simplify the expression to be subtracted:
$-(1 + y^2) = -1 - y^2$
Now, subtract the simplified expression from the sum obtained above.
Result $= (\text{Sum}) - (-1 - y^2)$
Result $= (-x^2 - y^2 - 1) - (-1 - y^2)$
Remove the parentheses and change the sign of each term being subtracted:
Result $= -x^2 - y^2 - 1 + 1 + y^2$
Group the like terms:
Result $= -x^2 + (-y^2 + y^2) + (-1 + 1)$
Combine the like terms:
Result $= -x^2 + 0 + 0$
Result $= -x^2$
The final result is $-x^2$.
Question 71. Subtract the sum of 12ab – 10b2 – 18a2 and 9ab + 12b2 + 14a2 from the sum of ab + 2b2 and 3b2 – a2.
Answer:
First, find the sum of the expressions $12ab - 10b^2 - 18a^2$ and $9ab + 12b^2 + 14a^2$.
Sum 1 $= (12ab - 10b^2 - 18a^2) + (9ab + 12b^2 + 14a^2)$
Sum 1 $= 12ab + 9ab - 10b^2 + 12b^2 - 18a^2 + 14a^2$
Sum 1 $= (12+9)ab + (-10+12)b^2 + (-18+14)a^2$
Sum 1 $= 21ab + 2b^2 - 4a^2$
Rearranging in terms of descending powers of a (and b):
Sum 1 $= -4a^2 + 2b^2 + 21ab$
Next, find the sum of the expressions $ab + 2b^2$ and $3b^2 - a^2$.
Sum 2 $= (ab + 2b^2) + (3b^2 - a^2)$
Sum 2 $= ab + 2b^2 + 3b^2 - a^2$
Sum 2 $= -a^2 + (2+3)b^2 + ab$
Sum 2 $= -a^2 + 5b^2 + ab$
Now, subtract Sum 1 from Sum 2.
Result $= \text{Sum 2} - \text{Sum 1}$
Result $= (-a^2 + 5b^2 + ab) - (-4a^2 + 2b^2 + 21ab)$
Remove parentheses and change signs of the terms being subtracted:
Result $= -a^2 + 5b^2 + ab + 4a^2 - 2b^2 - 21ab$
Group the like terms:
Result $= (-a^2 + 4a^2) + (5b^2 - 2b^2) + (ab - 21ab)$
Combine the coefficients:
Result $= (-1+4)a^2 + (5-2)b^2 + (1-21)ab$
Result $= 3a^2 + 3b^2 - 20ab$
Question 72. Each symbol given below represents an algebraic expression:
.png) = 2x2 + 3y ,
= 2x2 + 3y ,
.png) = 5x2 + 3x ,
= 5x2 + 3x ,
.png) = 8y2 - 3x2 + 2x + 3y
= 8y2 - 3x2 + 2x + 3y
The symbols are then represented in the expression:

Find the expression which is represented by the above symbols.
Answer:
Given the symbols represent the following algebraic expressions:
.png) $ = 2x^2 + 3y$
$ = 2x^2 + 3y$
.png) $ = 5x^2 + 3x$
$ = 5x^2 + 3x$
.png) $ = 8y^2 - 3x^2 + 2x + 3y$
$ = 8y^2 - 3x^2 + 2x + 3y$
The given symbolic expression is:

This can be written in terms of symbols as:
$\text{Triangle} - \text{Circle} + \text{Square}$
Substituting the corresponding algebraic expressions:
$(2x^2 + 3y) - (5x^2 + 3x) + (8y^2 - 3x^2 + 2x + 3y)$
Now, we simplify the expression by removing the parentheses. Remember to change the sign of each term inside the second parenthesis because of the subtraction:
$2x^2 + 3y - 5x^2 - 3x + 8y^2 - 3x^2 + 2x + 3y$
Group the like terms together:
$(2x^2 - 5x^2 - 3x^2) + (8y^2) + (-3x + 2x) + (3y + 3y)$
Combine the like terms:
$(2 - 5 - 3)x^2 + 8y^2 + (-3 + 2)x + (3 + 3)y$
$-6x^2 + 8y^2 - x + 6y$
Thus, the expression represented by the given symbols is:
$\mathbf{-6x^2 + 8y^2 - x + 6y}$
Question 73. Observe the following nutritional chart carefully:
Food Item (Per Unit = 100g)
Rajma
Cabbage
Potato
Carrot
Tomato
Apples
Carbohydrates
60g
5g
22g
11g
4g
14g
Write an algebraic expression for the amount of carbohydrates in ‘g’ for
(a) y units of potatoes and 2 units of rajma
(b) 2x units tomatoes and y units apples.
Answer:
From the given chart, the amount of carbohydrates per unit (100g) is:
Potatoes: 22g
Rajma: 60g
Tomatoes: 4g
Apples: 14g
(a) y units of potatoes and 2 units of rajma
Amount of carbohydrates in y units of potatoes = $y \times 22\text{g} = 22y\text{g}$
Amount of carbohydrates in 2 units of rajma = $2 \times 60\text{g} = 120\text{g}$
Total amount of carbohydrates = (Carbs from potatoes) + (Carbs from rajma)
Total amount of carbohydrates = $22y + 120\text{g}$
The algebraic expression for the amount of carbohydrates is $\mathbf{22y + 120}$.
(b) 2x units tomatoes and y units apples
Amount of carbohydrates in 2x units of tomatoes = $2x \times 4\text{g} = 8x\text{g}$
Amount of carbohydrates in y units of apples = $y \times 14\text{g} = 14y\text{g}$
Total amount of carbohydrates = (Carbs from tomatoes) + (Carbs from apples)
Total amount of carbohydrates = $8x + 14y\text{g}$
The algebraic expression for the amount of carbohydrates is $\mathbf{8x + 14y}$.
Question 74. Arjun bought a rectangular plot with length x and breadth y and then sold a triangular part of it whose base is y and height is z. Find the area of the remaining part of the plot.
Answer:
Given:
Length of the rectangular plot = x
Breadth of the rectangular plot = y
Base of the triangular part sold = y
Height of the triangular part sold = z
To Find:
The area of the remaining part of the plot.
Solution:
The area of a rectangle is given by the formula: Area = length $\times$ breadth.
Area of the rectangular plot = $x \times y = xy$
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times$ base $\times$ height.
Area of the triangular part sold = $\frac{1}{2} \times y \times z = \frac{1}{2}yz$
The area of the remaining part of the plot is the area of the rectangular plot minus the area of the triangular part sold.
Area of remaining part = (Area of rectangle) - (Area of triangle)
Area of remaining part = $xy - \frac{1}{2}yz$
The area of the remaining part of the plot is $\mathbf{xy - \frac{1}{2}yz}$.
Question 75. Amisha has a square plot of side m and another triangular plot with base and height each equal to m. What is the total area of both plots?
Answer:
Given:
Side of the square plot = m
Base of the triangular plot = m
Height of the triangular plot = m
To Find:
The total area of both plots.
Solution:
The area of a square is given by the formula: Area = side $\times$ side.
Area of the square plot = $m \times m = m^2$
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times$ base $\times$ height.
Area of the triangular plot = $\frac{1}{2} \times m \times m = \frac{1}{2}m^2$
The total area of both plots is the sum of the area of the square plot and the area of the triangular plot.
Total Area = (Area of square plot) + (Area of triangular plot)
Total Area = $m^2 + \frac{1}{2}m^2$
Total Area = $(1 + \frac{1}{2})m^2$
Total Area = $(\frac{2}{2} + \frac{1}{2})m^2$
Total Area = $\frac{3}{2}m^2$
The total area of both plots is $\mathbf{\frac{3}{2}m^2}$.
Question 76. A taxi service charges ₹ 8 per km and levies a fixed charge of ₹ 50. Write an algebraic expression for the above situation, if the taxi is hired for x km.
Answer:
Given:
Charge per km = $\textsf{₹}$ 8
Fixed charge = $\textsf{₹}$ 50
Distance covered = x km
To Find:
An algebraic expression for the total charge if the taxi is hired for x km.
Solution:
The total charge consists of two parts:
1. The fixed charge.
2. The variable charge which depends on the distance covered.
Fixed charge = $\textsf{₹}$ 50
Variable charge = (Charge per km) $\times$ (Number of km)
Variable charge = $\textsf{₹}$ 8 $\times$ x = $\textsf{₹}$ $8x$
Total charge = Fixed charge + Variable charge
Total charge = $\textsf{₹}$ 50 + $\textsf{₹}$ $8x$
Total charge = $\textsf{₹}$ $(50 + 8x)$
The algebraic expression for the total charge in $\textsf{₹}$ is $\mathbf{50 + 8x}$.
Question 77. Shiv works in a mall and gets paid ₹ 50 per hour. Last week he worked for 7 hours and this week he will work for x hours. Write an algebraic expression for the money paid to him for both the weeks.
Answer:
Given:
Hourly pay rate = $\textsf{₹}$ 50
Hours worked last week = 7 hours
Hours to work this week = x hours
To Find:
An algebraic expression for the total money paid to him for both the weeks.
Solution:
Money earned last week = Hourly pay $\times$ Hours worked last week
Money earned last week = $\textsf{₹ }50 \times 7$
Money earned last week = $\textsf{₹ }350$
Money earned this week = Hourly pay $\times$ Hours worked this week
Money earned this week = $\textsf{₹ }50 \times x$
Money earned this week = $\textsf{₹ }50x$
Total money paid for both weeks = (Money earned last week) + (Money earned this week)
Total money paid = $\textsf{₹ }350 + \textsf{₹ }50x$
Total money paid = $\textsf{₹ }(350 + 50x)$
The algebraic expression for the money paid to him for both the weeks is $\mathbf{350 + 50x}$.
Question 78. Sonu and Raj have to collect different kinds of leaves for science project. They go to a park where Sonu collects 12 leaves and Raj collects x leaves. After some time Sonu loses 3 leaves and Raj collects 2x leaves. Write an algebraic expression to find the total number of leaves collected by both of them.
Answer:
Given:
Initially, Sonu collects 12 leaves.
Initially, Raj collects x leaves.
Sonu loses 3 leaves.
Raj collects an additional 2x leaves.
To Find:
An algebraic expression for the total number of leaves collected by both Sonu and Raj.
Solution:
First, let's find the number of leaves Sonu has after losing some.
Number of leaves Sonu has = (Initial leaves) - (Leaves lost)
Number of leaves Sonu has = $12 - 3 = 9$
Next, let's find the total number of leaves Raj has.
Number of leaves Raj has = (Initial leaves) + (Additional leaves collected)
Number of leaves Raj has = $x + 2x$
Number of leaves Raj has = $3x$
The total number of leaves collected by both of them is the sum of the leaves Sonu has and the leaves Raj has.
Total number of leaves = (Leaves Sonu has) + (Leaves Raj has)
Total number of leaves = $9 + 3x$
The algebraic expression for the total number of leaves collected by both of them is $\mathbf{9 + 3x}$.
Question 79. A school has a rectangular play ground with length x and breadth y and a square lawn with side x as shown in the figure given below. What is the total perimeter of both of them combined together?
Answer:
Given:
Length of the rectangular playground = x
Breadth of the rectangular playground = y
Side of the square lawn = x
To Find:
The total perimeter of both the rectangular playground and the square lawn combined together.
Solution:
The perimeter of a rectangle is given by the formula: Perimeter = 2 $\times$ (length + breadth).
Perimeter of the rectangular playground = $2 \times (x + y)$
Perimeter of the rectangular playground = $2x + 2y$
The perimeter of a square is given by the formula: Perimeter = 4 $\times$ side.
Perimeter of the square lawn = $4 \times x = 4x$
The total perimeter of both of them combined together is the sum of the individual perimeters of the rectangular playground and the square lawn.
Total Perimeter = (Perimeter of rectangle) + (Perimeter of square)
Total Perimeter = $(2x + 2y) + 4x$
Now, combine the like terms:
Total Perimeter = $(2x + 4x) + 2y$
Total Perimeter = $(2 + 4)x + 2y$
Total Perimeter = $6x + 2y$
The total perimeter of both the rectangular playground and the square lawn combined together is $\mathbf{6x + 2y}$.
Question 80. The rate of planting the grass is ₹ x per square metre. Find the cost of planting the grass on a triangular lawn whose base is y metres and height is z metres.
Answer:
Given:
Rate of planting grass = $\textsf{₹}$ x per square metre
Base of the triangular lawn = y metres
Height of the triangular lawn = z metres
To Find:
The cost of planting the grass on the triangular lawn.
Solution:
First, we need to find the area of the triangular lawn.
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times$ base $\times$ height.
Area of the triangular lawn = $\frac{1}{2} \times y \times z$ square metres
Area of the triangular lawn = $\frac{1}{2}yz$ square metres
Next, we need to find the total cost of planting the grass.
Cost of planting grass = Area $\times$ Rate per square metre
Cost of planting grass = $(\frac{1}{2}yz) \times x$
Cost of planting grass = $\frac{1}{2}xyz$
The cost is in Rupees ($\textsf{₹}$).
The cost of planting the grass on the triangular lawn is $\mathbf{\textsf{₹} \frac{1}{2}xyz}$.
Question 81. Find the perimeter of the figure given below:
Answer:
Given:
A polygon with side lengths as shown in the figure. The side lengths are p, p, r, r, q, and q.
To Find:
The perimeter of the given figure.
Solution:
The perimeter of a polygon is the sum of the lengths of all its sides.
In the given figure, the sides have lengths p, p, r, r, q, and q.
Perimeter = Sum of all side lengths
Perimeter = $p + p + r + r + q + q$
Combine the like terms:
Perimeter = $(p + p) + (r + r) + (q + q)$
Perimeter = $2p + 2r + 2q$
We can also factor out the common factor, 2:
Perimeter = $2(p + r + q)$
The perimeter of the figure is $\mathbf{2p + 2r + 2q}$ or $\mathbf{2(p + r + q)}$.
Question 82. In a rectangular plot, 5 square flower beds of side (x + 2) metres each have been laid (see figure given below). Find the total cost of fencing the flower beds at the cost of ₹ 50 per 100 metres:

Answer:
Given:
Number of square flower beds = 5
Side of each square flower bed = $(x + 2)$ metres
Cost of fencing = $\textsf{₹}$ 50 per 100 metres
To Find:
The total cost of fencing the flower beds.
Solution:
Fencing is done around the perimeter of each flower bed. The perimeter of a square is given by the formula: Perimeter = 4 $\times$ side.
Perimeter of one square flower bed = $4 \times (x + 2)$ metres
Perimeter of one square flower bed = $(4x + 8)$ metres
There are 5 such flower beds, and each needs to be fenced. So, we need to find the total length of fencing required.
Total length of fencing = Number of flower beds $\times$ Perimeter of one flower bed
Total length of fencing = $5 \times (4x + 8)$ metres
Total length of fencing = $(20x + 40)$ metres
The cost of fencing is given as $\textsf{₹}$ 50 per 100 metres.
Cost per metre = $\frac{\textsf{₹} 50}{100 \text{ metres}} = \textsf{₹} \frac{1}{2}$ per metre or $\textsf{₹} 0.50$ per metre.
Now, calculate the total cost of fencing:
Total cost = Total length of fencing $\times$ Cost per metre
Total cost = $(20x + 40) \times \textsf{₹} \frac{1}{2}$
Total cost = $\frac{1}{2} \times (20x + 40)$
Total cost = $\frac{1}{2} \times 20x + \frac{1}{2} \times 40$
Total cost = $10x + 20$
The total cost of fencing the flower beds is $\mathbf{\textsf{₹}(10x + 20)}$.
Question 83. A wire is (7x – 3) metres long. A length of (3x – 4) metres is cut for use. Now, answer the following questions:
(a) How much wire is left?
(b) If this left out wire is used for making an equilateral triangle.
What is the length of each side of the triangle so formed?
Answer:
Given:
Initial length of the wire = $(7x - 3)$ metres
Length of wire cut = $(3x - 4)$ metres
(a) How much wire is left?
The length of the wire left is the initial length minus the length cut for use.
Length of wire left = (Initial length) - (Length cut)
Length of wire left = $(7x - 3) - (3x - 4)$
Remove the parentheses. Remember to distribute the negative sign to both terms inside the second parenthesis:
Length of wire left = $7x - 3 - 3x + 4$
Combine the like terms:
Length of wire left = $(7x - 3x) + (-3 + 4)$
Length of wire left = $(7 - 3)x + (4 - 3)$
Length of wire left = $4x + 1$
The length of wire left is $\mathbf{(4x + 1)}$ metres.
(b) What is the length of each side of the triangle so formed?
The wire left is used to make an equilateral triangle. An equilateral triangle has three sides of equal length.
The perimeter of the equilateral triangle is equal to the length of the wire left.
Perimeter of equilateral triangle = $(4x + 1)$ metres
Let the length of each side of the equilateral triangle be 's'.
Perimeter of equilateral triangle = $3 \times s$
So, $3s = 4x + 1$
To find the length of each side, divide the perimeter by 3:
$s = \frac{4x + 1}{3}$
$s = \frac{4x}{3} + \frac{1}{3}$
The length of each side of the equilateral triangle is $\mathbf{\frac{4x + 1}{3}}$ metres or $\mathbf{(\frac{4}{3}x + \frac{1}{3})}$ metres.
Question 84. Rohan's mother gave him ₹ 3xy2 and his father gave him ₹ 5(xy2 + 2). Out of this total money he spent ₹ (10 – 3xy2) on his birthday party. How much money is left with him?
Answer:
Given:
Money given by mother = $\textsf{₹ }3xy^2$
Money given by father = $\textsf{₹ }5(xy^2 + 2)$
Money spent on birthday party = $\textsf{₹ }(10 - 3xy^2)$
To Find:
The amount of money left with Rohan.
Solution:
First, calculate the money given by the father:
Money from father = $5(xy^2 + 2) = 5 \times xy^2 + 5 \times 2 = 5xy^2 + 10$
So, money from father is $\textsf{₹ }(5xy^2 + 10)$.
Next, calculate the total money Rohan has before spending:
Total money = Money from mother + Money from father
Total money = $\textsf{₹ }3xy^2 + \textsf{₹ }(5xy^2 + 10)$
Total money = $\textsf{₹ }(3xy^2 + 5xy^2 + 10)$
Total money = $\textsf{₹ }(8xy^2 + 10)$
Now, calculate the money left with Rohan by subtracting the money spent from the total money:
Money left = Total money - Money spent
Money left = $\textsf{₹ }(8xy^2 + 10) - \textsf{₹ }(10 - 3xy^2)$
Money left = $8xy^2 + 10 - (10 - 3xy^2)$
Remove the parentheses, distributing the negative sign:
Money left = $8xy^2 + 10 - 10 + 3xy^2$
Combine the like terms:
Money left = $(8xy^2 + 3xy^2) + (10 - 10)$
Money left = $(8 + 3)xy^2 + 0$
Money left = $11xy^2$
The money left with Rohan is $\mathbf{\textsf{₹ }11xy^2}$.
Question 85.
(i) A triangle is made up of 2 red sticks and 1 blue sticks 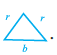 . The length of a red stick is given by r and that of a blue stick is given by b. Using this information, write an expression for the total length of sticks in the pattern given below:
. The length of a red stick is given by r and that of a blue stick is given by b. Using this information, write an expression for the total length of sticks in the pattern given below:
(ii) In the given figure, the length of a green side is given by g and that of the red side is given by p.
Write an expression for the following pattern. Also write an expression if 100 such shapes are joined together.
Answer:
(i)
Given:
A triangle is made of 2 red sticks and 1 blue stick.
Length of a red stick = r
Length of a blue stick = b
To Find:
The total length of sticks in the given pattern.
Solution:
The given pattern shows 3 triangles joined together horizontally. Each triangle consists of 2 red sticks and 1 blue stick.
Length of sticks in one triangle = (Length of 2 red sticks) + (Length of 1 blue stick)
Length of sticks in one triangle = $2 \times r + 1 \times b = 2r + b$
The pattern consists of 3 such triangles. Based on the visual representation in the pattern image  , it appears that the triangles are distinct units placed side-by-side, without sharing sticks in a way that reduces the total count. The image shows 3 horizontal blue sticks and 6 slanted red sticks.
, it appears that the triangles are distinct units placed side-by-side, without sharing sticks in a way that reduces the total count. The image shows 3 horizontal blue sticks and 6 slanted red sticks.
Total number of red sticks in the pattern = 3 triangles $\times$ 2 red sticks/triangle = 6 red sticks
Total number of blue sticks in the pattern = 3 triangles $\times$ 1 blue stick/triangle = 3 blue sticks
Total length of sticks in the pattern = (Total length of red sticks) + (Total length of blue sticks)
Total length = $6 \times r + 3 \times b = 6r + 3b$
The expression for the total length of sticks in the pattern is $\mathbf{6r + 3b}$.
(ii)
Given:
Length of a green side = g
Length of a red side = p
The basic shape is a pentagon with 1 red side and 4 green sides  .
.
To Find:
An expression for the perimeter of the given pattern (3 shapes joined).
An expression for the perimeter if 100 such shapes are joined together.
Solution:
The given pattern  shows 3 basic shapes (pentagons) joined together. From the clarifying image
shows 3 basic shapes (pentagons) joined together. From the clarifying image  , it is clear that the shapes are joined by sharing one vertical green side.
, it is clear that the shapes are joined by sharing one vertical green side.
Let N be the number of shapes joined together in a line.
Consider the perimeter of the combined shape:
Each original shape has one red side (p) and four green sides (4g). When two shapes are joined along a green side, that shared green side is no longer part of the outer perimeter.
For N shapes joined in a line, there are N red sides on the outer boundary, each with length p. Total length from red sides = Np.
For the green sides forming the outer boundary:
There are two vertical green sides at the two ends of the line of shapes, each with length g. Total length from end green sides = $2g$.
For each of the N shapes, there is a top horizontal green side and a bottom horizontal green side on the outer boundary, each with length g. Total length from top and bottom green sides = $N \times (g + g) = 2Ng$.
Total perimeter for N shapes joined = (Length of red sides) + (Length of green sides)
Total perimeter = $Np + 2g + 2Ng = Np + (2N + 2)g$
For the given pattern, there are 3 shapes joined (N = 3).
Expression for the pattern = $3p + (2 \times 3 + 2)g$
Expression for the pattern = $3p + (6 + 2)g$
Expression for the pattern = $3p + 8g$
The expression for the given pattern is $\mathbf{3p + 8g}$.
If 100 such shapes are joined together (N = 100):
Expression for 100 shapes = $100p + (2 \times 100 + 2)g$
Expression for 100 shapes = $100p + (200 + 2)g$
Expression for 100 shapes = $100p + 202g$
The expression if 100 such shapes are joined together is $\mathbf{100p + 202g}$.
Questino 86. The sum of first n natural numbers is given by $\frac{1}{2}$n2 + $\frac{1}{2}$n. Find
(i) The sum of first 5 natural numbers.
(ii) The sum of first 11 natural numbers.
(iii) The sum of natural numbers from 11 to 30.
Answer:
Given:
The sum of the first n natural numbers is given by the formula: $S_n = \frac{1}{2}n^2 + \frac{1}{2}n$
(i) The sum of first 5 natural numbers.
Here, we need to find the sum of the first 5 natural numbers, so n = 5.
Substitute $n=5$ into the formula:
$S_5 = \frac{1}{2}(5)^2 + \frac{1}{2}(5)$
$S_5 = \frac{1}{2}(25) + \frac{1}{2}(5)$
$S_5 = \frac{25}{2} + \frac{5}{2}$
$S_5 = \frac{25 + 5}{2}$
$S_5 = \frac{30}{2}$
$S_5 = 15$
The sum of the first 5 natural numbers is $\mathbf{15}$.
(ii) The sum of first 11 natural numbers.
Here, we need to find the sum of the first 11 natural numbers, so n = 11.
Substitute $n=11$ into the formula:
$S_{11} = \frac{1}{2}(11)^2 + \frac{1}{2}(11)$
$S_{11} = \frac{1}{2}(121) + \frac{1}{2}(11)$
$S_{11} = \frac{121}{2} + \frac{11}{2}$
$S_{11} = \frac{121 + 11}{2}$
$S_{11} = \frac{132}{2}$
$S_{11} = 66$
The sum of the first 11 natural numbers is $\mathbf{66}$.
(iii) The sum of natural numbers from 11 to 30.
To find the sum of natural numbers from 11 to 30, we subtract the sum of the first 10 natural numbers from the sum of the first 30 natural numbers.
Sum (11 to 30) = Sum (1 to 30) - Sum (1 to 10)
First, find the sum of the first 30 natural numbers (n = 30):
$S_{30} = \frac{1}{2}(30)^2 + \frac{1}{2}(30)$
$S_{30} = \frac{1}{2}(900) + \frac{1}{2}(30)$
$S_{30} = 450 + 15$
$S_{30} = 465$
Next, find the sum of the first 10 natural numbers (n = 10):
$S_{10} = \frac{1}{2}(10)^2 + \frac{1}{2}(10)$
$S_{10} = \frac{1}{2}(100) + \frac{1}{2}(10)$
$S_{10} = 50 + 5$
$S_{10} = 55$
Now, subtract the sum of the first 10 numbers from the sum of the first 30 numbers:
Sum (11 to 30) = $S_{30} - S_{10}$
Sum (11 to 30) = $465 - 55$
Sum (11 to 30) = $410$
The sum of natural numbers from 11 to 30 is $\mathbf{410}$.
Question 87. The sum of squares of first n natural numbers is given by $\frac{1}{6}$n (n + 1) (2n + 1) or $\frac{1}{6}$ (2n3 + 3n2 + n). Find the sum of squares of the first 10 natural numbers.
Answer:
Given:
The sum of squares of the first n natural numbers is given by the formula:
$S_n = \frac{1}{6}n(n + 1)(2n + 1)$ or $S_n = \frac{1}{6}(2n^3 + 3n^2 + n)$
To Find:
The sum of squares of the first 10 natural numbers.
Solution:
We need to find the sum of squares of the first 10 natural numbers, so we set $n = 10$ in the formula $S_n = \frac{1}{6}n(n + 1)(2n + 1)$.
Substitute $n = 10$ into the formula:
$S_{10} = \frac{1}{6}(10)(10 + 1)(2 \times 10 + 1)$
$S_{10} = \frac{1}{6}(10)(11)(20 + 1)$
$S_{10} = \frac{1}{6}(10)(11)(21)$
$S_{10} = \frac{10 \times 11 \times 21}{6}$
Perform the calculation by cancelling common factors:
$S_{10} = \frac{\cancel{10}^{5} \times 11 \times \cancel{21}^{7}}{\cancel{6}_{1}}$
$S_{10} = 5 \times 11 \times 7$
$S_{10} = 55 \times 7$
$S_{10} = 385$
The sum of squares of the first 10 natural numbers is $\mathbf{385}$.
Question 88. The sum of the multiplication table of natural number ‘n’ is given by 55 × n. Find the sum of
(a) Table of 7
(b) Table of 10
(c) Table of 19
Answer:
Given:
The sum of the multiplication table of a natural number 'n' is given by the formula: Sum $= 55 \times n$
To Find:
The sum of the multiplication table of 7, 10, and 19.
Solution:
We use the given formula $Sum = 55 \times n$ for each part.
(a) Table of 7
Here, $n = 7$.
Sum of table of 7 $= 55 \times 7$
Sum $= 385$
The sum of the table of 7 is $\mathbf{385}$.
(b) Table of 10
Here, $n = 10$.
Sum of table of 10 $= 55 \times 10$
Sum $= 550$
The sum of the table of 10 is $\mathbf{550}$.
(c) Table of 19
Here, $n = 19$.
Sum of table of 19 $= 55 \times 19$
Sum $= 55 \times (20 - 1)$
Sum $= 55 \times 20 - 55 \times 1$
Sum $= 1100 - 55$
Sum $= 1045$
The sum of the table of 19 is $\mathbf{1045}$.
Question 89. If
 ,
,
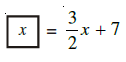 and
and
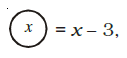
then find the value of :
(i)
.png)
(ii)
.png)
Answer:
Given:
 represents $a^2$
represents $a^2$
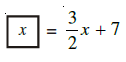 represents $b^2$
represents $b^2$
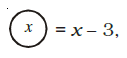 represents $ab$
represents $ab$
To Find:
The value of the given symbolic expressions.
(i) The symbolic expression is .png)
Observing the image, this expression represents the sum of three terms:
Term 1:  which is $a^2$
which is $a^2$
Term 2: 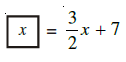 which is $b^2$
which is $b^2$
Term 3: 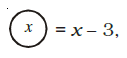 +
+ 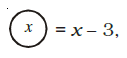 which is $ab + ab = 2ab$
which is $ab + ab = 2ab$
So, the expression is equivalent to:
$a^2 + b^2 + 2ab$
This is a well-known algebraic identity:
$a^2 + b^2 + 2ab = (a + b)^2$
The value of the first symbolic expression is $\mathbf{(a + b)^2}$.
(ii) The symbolic expression is .png)
Observing the image, this expression represents the sum/difference of three terms:
Term 1:  which is $a^2$
which is $a^2$
Term 2: 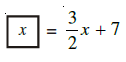 which is $b^2$
which is $b^2$
Term 3: - 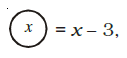 -
- 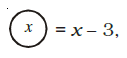 which is $-ab - ab = -2ab$
which is $-ab - ab = -2ab$
So, the expression is equivalent to:
$a^2 + b^2 - 2ab$
This is also a well-known algebraic identity:
$a^2 + b^2 - 2ab = (a - b)^2$
The value of the second symbolic expression is $\mathbf{(a - b)^2}$.
Question 90. If  then find the value of:
then find the value of:
(i)
.png)
(ii)
.png)
Answer:
Given:
The symbol containing a value 'A' above and a value 'B' below is given. The problem states that if the symbol contains 'x' above and '3y' below  , its value is $5x + 7y$.
, its value is $5x + 7y$.
Let the symbol with 'A' above and 'B' below represent an expression $f(A, B)$. Based on the given information:
$f(x, 3y) = 5x + 7y$
Assuming a linear relationship in the form $f(A, B) = c_1 A + c_2 B$, we substitute A=x and B=3y:
$c_1 (x) + c_2 (3y) = 5x + 7y$
$c_1 x + 3c_2 y = 5x + 7y$
Comparing the coefficients of x and y on both sides of the equation:
$c_1 = 5$
$3c_2 = 7$
Solving for $c_2$ from the second equation:
$c_2 = \frac{7}{3}$
Therefore, the rule represented by the symbol is that the symbol with value 'A' above and value 'B' below represents the expression $5A + \frac{7}{3}B$.
To Find:
The value of the symbolic expression for the given inputs.
Solution:
We use the derived rule: Symbol with (A, B) represents $5A + \frac{7}{3}B$.
(i) The symbolic expression is .png) which has 2 above and 5 below. Here, we have $A = 2$ and $B = 5$.
which has 2 above and 5 below. Here, we have $A = 2$ and $B = 5$.
Substitute these values into the rule:
Value $= 5A + \frac{7}{3}B$
Value $= 5(2) + \frac{7}{3}(5)$
Value $= 10 + \frac{35}{3}$
To add these, we find a common denominator, which is 3:
Value $= \frac{10 \times 3}{3} + \frac{35}{3}$
Value $= \frac{30}{3} + \frac{35}{3}$
Value $= \frac{30 + 35}{3}$
Value $= \frac{65}{3}$
The value of the expression in (i) is $\mathbf{\frac{65}{3}}$.
(ii) The symbolic expression is .png) which has -1 above and 0 below. Here, we have $A = -1$ and $B = 0$.
which has -1 above and 0 below. Here, we have $A = -1$ and $B = 0$.
Substitute these values into the rule:
Value $= 5A + \frac{7}{3}B$
Value $= 5(-1) + \frac{7}{3}(0)$
Value $= -5 + 0$
Value $= -5$
The value of the expression in (ii) is $\mathbf{-5}$.
Translate each of the following algebraic expressions Question 91 to 94 into words.
Question 91. 4b – 3
Answer:
The expression is $4b - 3$.
This expression involves multiplication (4 multiplied by b) and subtraction (3 is subtracted from the result).
We can translate this into words in several ways:
1. Three subtracted from four times b.
2. The product of 4 and b, reduced by 3.
3. 3 less than the product of 4 and b.
A common translation is: Three subtracted from four times b.
Question 92. 8 (m + 5)
Answer:
The expression is $8(m + 5)$.
This expression involves the sum of m and 5, and then the result is multiplied by 8.
We can translate this into words as:
1. 8 times the sum of m and 5.
2. The product of 8 and the sum of m and 5.
3. 8 multiplied by the quantity m plus 5.
A common and clear translation is: 8 times the sum of m and 5.
Question 93. $\frac{7}{ 8 - x}$
Answer:
The expression is $\frac{7}{8 - x}$.
This expression is a fraction, which represents division. The numerator is 7 and the denominator is $(8 - x)$. The denominator involves subtraction.
First, translate the denominator $(8 - x)$: This can be expressed as "the difference between 8 and x", or "x subtracted from 8".
Now, translate the entire expression (7 divided by the denominator):
Using "the difference between 8 and x" for the denominator, the expression can be translated as:
7 divided by the difference between 8 and x.
Alternatively, we could say:
The quotient of 7 and the difference between 8 and x.
Question 94. 7 $\left( \frac{16}{w} \right)$
Answer:
The expression is $7 \left( \frac{16}{w} \right)$.
This expression involves division (16 divided by w) inside parentheses, and then the result is multiplied by 7.
First, consider the part inside the parentheses: $\frac{16}{w}$.
This can be translated as "16 divided by w" or "the quotient of 16 and w".
Now, the entire expression means 7 multiplied by the result of the division.
Using "16 divided by w" for the inner part, the expression can be translated as:
7 times 16 divided by w.
Alternatively, using "the quotient of 16 and w":
7 times the quotient of 16 and w.
Or:
The product of 7 and the quotient of 16 and w.
Question 95.
(i) Critical Thinking Write two different algebraic expressions for the word phrase “ $\left( \frac{1}{4} \right)$ of the sum of x and 7.”
(ii) What’s the Error? A student wrote an algebraic expression for “5 less than a number n divided by 3” as $\frac{n}{3}$ - 5 What error did the student make?
(iii) Write About it Shashi used addition to solve a word problem about the weekly cost of commuting by toll tax for ₹ 15 each day. Ravi solved the same problem by multiplying. They both got the correct answer. How is this possible?
Answer:
(i)
Given Phrase: $\left( \frac{1}{4} \right)$ of the sum of x and 7.
Solution:
The phrase "the sum of x and 7" translates to the algebraic expression $(x + 7)$.
The phrase "$\left( \frac{1}{4} \right)$ of" means multiplying by $\frac{1}{4}$.
So, we are multiplying $\frac{1}{4}$ by the quantity $(x + 7)$.
Two different algebraic expressions for this phrase are:
1. $\mathbf{\frac{1}{4}(x + 7)}$
2. Since multiplying by $\frac{1}{4}$ is the same as dividing by 4, another expression is $\mathbf{\frac{x + 7}{4}}$.
(ii)
Given Phrase: 5 less than a number n divided by 3.
Student's Expression: $\frac{n}{3} - 5$
Error Analysis:
The phrase "a number n divided by 3" translates to $\frac{n}{3}$.
The phrase "5 less than" a quantity means that 5 is subtracted *from* that quantity.
So, "5 less than ($\frac{n}{3}$)" translates to $\frac{n}{3} - 5$.
Based on the typical phrasing and order of operations, the student's expression $\frac{n}{3} - 5$ correctly translates "5 less than (n divided by 3)".
However, if the intended meaning of the phrase was "(5 less than a number n) divided by 3", then the phrase "5 less than a number n" should be calculated first, which is $(n - 5)$. Then this entire quantity should be divided by 3, resulting in $\frac{n - 5}{3}$.
Given that the question asks "What error did the student make?", it is likely that the intended phrase was the latter. The student made the error of applying the division by 3 only to 'n' and then subtracting 5, rather than first finding "5 less than a number n" and then dividing the result by 3.
The student interpreted "a number n divided by 3" as $\frac{n}{3}$ and then applied "5 less than" to that result. The error is assuming the division by 3 applies only to 'n' before the "5 less than" operation on the quantity (n-5).
Error: The student performed the division of n by 3 before subtracting 5. The phrase likely intended the subtraction of 5 from n to be performed first, and then the result divided by 3.
(iii)
Given:
Cost of toll tax per day = $\textsf{₹}$ 15
Weekly cost is calculated for 7 days (assuming a standard week).
Shashi used addition and Ravi used multiplication to find the total weekly cost. Both got the correct answer.
Explanation:
The weekly cost is the sum of the cost for each day of the week.
Shashi calculated the total cost by adding the daily cost for each of the 7 days:
Weekly Cost = $\textsf{₹} 15 + \textsf{₹} 15 + \textsf{₹} 15 + \textsf{₹} 15 + \textsf{₹} 15 + \textsf{₹} 15 + \textsf{₹} 15$
Shashi calculated Weekly Cost = $\textsf{₹} (15 \times 7)$
Ravi calculated the total cost by multiplying the daily cost by the number of days in a week:
Weekly Cost = Cost per day $\times$ Number of days
Weekly Cost = $\textsf{₹} 15 \times 7$
Both Shashi and Ravi got the correct answer because multiplication is a shorthand way of representing repeated addition. Adding 15 to itself 7 times is equivalent to multiplying 15 by 7. They used different operations, but one (multiplication) is a direct result of the other (repeated addition), leading to the same correct total cost.
Question 96. Challenge Write an expression for the sum of 1 and twice a number n. If you let n be any odd number, will the result always be an odd number?
Answer:
Part 1: Write an expression for the sum of 1 and twice a number n.
Given:
A number is represented by 'n'.
We need to find an expression for the sum of 1 and twice the number n.
Solution:
"Twice a number n" means multiplying the number n by 2, which is $2 \times n = 2n$.
"The sum of 1 and twice a number n" means adding 1 to the expression for twice a number n.
Expression = $1 + 2n$ or $2n + 1$
The expression for the sum of 1 and twice a number n is $\mathbf{2n + 1}$.
Part 2: If n is any odd number, will the result always be an odd number?
Analysis:
We want to know if the expression $2n + 1$ always results in an odd number when 'n' is an odd number.
An odd number can be represented in the form $2k + 1$, where k is any integer (0, 1, 2, 3, ... for positive odd numbers 1, 3, 5, 7, ...).
Let's substitute $n = 2k + 1$ into the expression $2n + 1$:
Result $= 2(2k + 1) + 1$
Apply the distributive property:
Result $= (2 \times 2k) + (2 \times 1) + 1$
Result $= 4k + 2 + 1$
Result $= 4k + 3$
Now, let's analyze the expression $4k + 3$.
The term $4k$ is always an even number because it is a multiple of 4 (and any multiple of an even number is even).
When we add an odd number (3) to an even number ($4k$), the result is always an odd number.
Even number + Odd number = Odd number
Let's test with a few odd values for n:
If n = 1 (which is $2(0)+1$, so k=0), result = $2(1) + 1 = 2 + 1 = 3$ (Odd)
If n = 3 (which is $2(1)+1$, so k=1), result = $2(3) + 1 = 6 + 1 = 7$ (Odd)
If n = 5 (which is $2(2)+1$, so k=2), result = $2(5) + 1 = 10 + 1 = 11$ (Odd)
Conclusion:
Based on the algebraic analysis and examples, when 'n' is any odd number, the expression $2n + 1$ will always result in an odd number.
The answer is Yes, the result will always be an odd number.
Question 97. Critical Thinking Will the value of 11x for x = –5 be greater than 11 or less than 11? Explain.
Answer:
Given:
The expression is $11x$.
The value of x is $-5$.
To Find:
Whether the value of $11x$ for $x = -5$ is greater than 11 or less than 11.
Solution and Explanation:
We need to calculate the value of the expression $11x$ when $x = -5$.
Substitute $x = -5$ into the expression $11x$:
Value $= 11 \times (-5)$
When a positive number is multiplied by a negative number, the result is a negative number.
$11 \times (-5) = -55$
Now, we compare the calculated value ($-55$) with 11.
We need to determine if $-55 > 11$ or $-55 < 11$.
$-55$ is a negative number, and 11 is a positive number.
Any negative number is always less than any positive number.
Therefore, $-55$ is less than 11.
$-55 < 11$
The value of $11x$ for $x = -5$ will be less than 11.
Explanation: When a positive number (11) is multiplied by a negative number ($-5$), the product is negative ($-55$). Since $-55$ is a negative number and 11 is a positive number, $-55$ is less than 11.
Question 98. Match Column I with Column II in the following:
Column I
1. The difference of 3 and a number squared
2. 5 less than twice a number squared
3. Five minus twice the square of a number
4. Four minus a number multiplied by 2
5. Seven times the sum of a number and 1
6. A number squared plus 6
7. 2 times the sum of a number and 6
8. Three less than the square of a number
Column II
(a) 4 – 2x
(b) n2 – 3
(c) 2n2 – 5
(d) 5 – 2n2
(e) 3 – n2
(f) 2 (n + 6)
(g) 7 (n + 1)
(h) n2 + 6
Answer:
Let the number be represented by the variable 'n' or 'x' as shown in Column II.
Let's translate each phrase from Column I into an algebraic expression:
1. "The difference of 3 and a number squared": This means 3 minus the square of the number. If the number is n, its square is $n^2$. The difference is $3 - n^2$. This matches expression (e).
2. "5 less than twice a number squared": "A number squared" is $n^2$. "Twice a number squared" is $2n^2$. "5 less than $2n^2$" means $2n^2 - 5$. This matches expression (c).
3. "Five minus twice the square of a number": "The square of a number" is $n^2$. "Twice the square of a number" is $2n^2$. "Five minus $2n^2$" means $5 - 2n^2$. This matches expression (d).
4. "Four minus a number multiplied by 2": "A number multiplied by 2". If we use the variable 'x' as in (a), this is $2x$. "Four minus $2x$" means $4 - 2x$. This matches expression (a).
5. "Seven times the sum of a number and 1": "The sum of a number and 1". If the number is n, the sum is $(n + 1)$. "Seven times $(n+1)$" means $7(n + 1)$. This matches expression (g).
6. "A number squared plus 6": "A number squared" is $n^2$. "$n^2$ plus 6" means $n^2 + 6$. This matches expression (h).
7. "2 times the sum of a number and 6": "The sum of a number and 6". If the number is n, the sum is $(n + 6)$. "2 times $(n+6)$" means $2(n + 6)$. This matches expression (f).
8. "Three less than the square of a number": "The square of a number" is $n^2$. "Three less than $n^2$" means $n^2 - 3$. This matches expression (b).
The correct matches are:
1. The difference of 3 and a number squared $\to$ (e) $3 - n^2$
2. 5 less than twice a number squared $\to$ (c) $2n^2 - 5$
3. Five minus twice the square of a number $\to$ (d) $5 - 2n^2$
4. Four minus a number multiplied by 2 $\to$ (a) $4 - 2x$
5. Seven times the sum of a number and 1 $\to$ (g) $7 (n + 1)$
6. A number squared plus 6 $\to$ (h) $n^2 + 6$
7. 2 times the sum of a number and 6 $\to$ (f) $2 (n + 6)$
8. Three less than the square of a number $\to$ (b) $n^2 - 3$
Question 99. At age of 2 years, a cat or a dog is considered 24 “human” years old.
Each year, after age 2 is equivalent to 4 “human” years. Fill in the expression [24 + (a – 2)] so that it represents the age of a cat or dog in human years. Also, you need to determine for what ‘a’ stands for. Copy the chart and use your expression to complete it.
| Age | [24 + (a – 2)] | Age (Human Years) |
|---|---|---|
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Answer:
Given Information:
Age at 2 human years = 24 human years.
Each year after age 2 is equivalent to 4 human years.
Expression form: $[24 + \text{__} (a – 2)]$
Determine the missing number and what 'a' stands for:
The expression $[24 + \text{__} (a – 2)]$ calculates the total human years.
The $24$ represents the human years accumulated by age 2.
The term $(a - 2)$ represents the number of years the cat/dog has lived after reaching the age of 2, where 'a' is the current age of the cat/dog in years.
Each of these $(a - 2)$ years adds 4 human years.
So, the total human years added after age 2 is $4 \times (a - 2)$.
Therefore, the missing number in the expression is 4.
The completed expression is $\mathbf{24 + 4(a – 2)}$.
The variable 'a' stands for the actual age of the cat or dog in years.
Complete the chart using the expression $24 + 4(a – 2)$:
| Age (a) | $[24 + 4(a – 2)]$ | Age (Human Years) |
| 2 | $24 + 4(2 – 2) = 24 + 4(0) = 24 + 0 = 24$ | 24 |
| 3 | $24 + 4(3 – 2) = 24 + 4(1) = 24 + 4 = 28$ | 28 |
| 4 | $24 + 4(4 – 2) = 24 + 4(2) = 24 + 8 = 32$ | 32 |
| 5 | $24 + 4(5 – 2) = 24 + 4(3) = 24 + 12 = 36$ | 36 |
| 6 | $24 + 4(6 – 2) = 24 + 4(4) = 24 + 16 = 40$ | 40 |
The completed expression is $\mathbf{24 + 4(a – 2)}$, where 'a' is the actual age of the cat or dog in years. The completed table is shown above.
Question 100. Express the following properties with variables x, y and z.
(i) Commutative property of addition
(ii) Commutative property of multiplication
(iii) Associative property of addition
(iv) Associative property of multiplication
(v) Distributive property of multiplication over addition
Answer:
Here are the expressions for the given properties using variables x, y, and z:
(i) Commutative property of addition
This property states that changing the order of the addends does not change the sum.
Algebraic expression:
$x + y = y + x$
(ii) Commutative property of multiplication
This property states that changing the order of the factors does not change the product.
Algebraic expression:
$x \times y = y \times x$
or
$xy = yx$
(iii) Associative property of addition
This property states that changing the grouping of the addends does not change the sum.
Algebraic expression:
$(x + y) + z = x + (y + z)$
(iv) Associative property of multiplication
This property states that changing the grouping of the factors does not change the product.
Algebraic expression:
$(x \times y) \times z = x \times (y \times z)$
or
$(xy)z = x(yz)$
(v) Distributive property of multiplication over addition
This property states that multiplying a sum by a number is the same as multiplying each addend by the number and then adding the products.
Algebraic expression:
$x \times (y + z) = (x \times y) + (x \times z)$
or
$x(y + z) = xy + xz$

