| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 10 Circles
Welcome to this essential resource offering detailed and meticulously crafted solutions for the NCERT Exemplar problems tailored for Class 9 students, focusing specifically on the intricate chapter of Circles. The Exemplar questions represent a significant step up in difficulty compared to standard textbook exercises. They are deliberately designed to rigorously test and deepen your understanding of fundamental circle theorems, often presenting you with complex geometric figures that demand sophisticated proofs and the skillful application of multiple theorems working in concert. Engaging with these problems and their solutions is crucial for developing a robust command of circle geometry.
The scope of theorems covered within these Exemplar problems is comprehensive, touching upon nearly every critical aspect of circle properties taught at this level. You will need a firm grasp of the following key concepts, as the solutions provided will extensively reference and apply them:
- Properties of Chords: This includes understanding that the perpendicular drawn from the center of a circle bisects the chord, the converse (the line joining the center to the mid-point of a chord is perpendicular to it), the fact that equal chords are equidistant from the center, the converse (chords equidistant from the center are equal), and that equal chords subtend equal angles at the center (and its converse).
- Properties of Arcs: The fundamental relationship that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle is frequently tested.
- Angles in Segments: Key theorems here are that angles in the same segment of a circle are equal, and the special case that the angle in a semicircle is always a right angle ($90^\circ$).
- Cyclic Quadrilaterals: Understanding their unique properties is vital, namely that the sum of either pair of opposite angles is $180^\circ$, that an exterior angle is equal to the interior opposite angle, and the converses of these theorems which help identify cyclic quadrilaterals.
The Exemplar problems often weave these theorems together in challenging ways. You will frequently encounter tasks that involve finding unknown angles within complex diagrams, often requiring a sequential application of several circle theorems, potentially combined with properties of triangles (like the angle sum property or identifying isosceles triangles formed by radii). Many problems demand the construction of rigorous geometric proofs establishing relationships between chords, arcs, tangents (even if only implicitly), and cyclic quadrilaterals. Some questions might even require proving concepts like collinearity of points or concurrency of lines using circle properties as justification.
To assess understanding thoroughly, the Exemplar employs various question formats. Expect challenging Multiple Choice Questions (MCQs) that necessitate careful angle calculations or precise theorem application, Fill-in-the-Blanks reinforcing definitions, True/False statements probing the nuances and conditions of theorems, and, crucially, Short and Long Answer questions. These longer questions demand formal, step-by-step proofs or multi-stage angle calculations, always requiring detailed justification that accurately cites the relevant theorems at each logical step. The solutions provided here feature clearly labeled diagrams, meticulous logical deductions, precise theorem referencing, and strategic approaches, making this resource invaluable for mastering circle theorems and elevating your geometric reasoning capabilities.
Sample Question 1 & 2 (Before Exercise 10.1)
Write the correct answer :
Sample Question 1: In Fig. 10.1, two congruent circles have centres O and O′. Arc AXB subtends an angle of 75º at the centre O and arc A′ Y B′ subtends an angle of 25º at the centre O′. Then the ratio of arcs A X B and A′ Y B′ is:
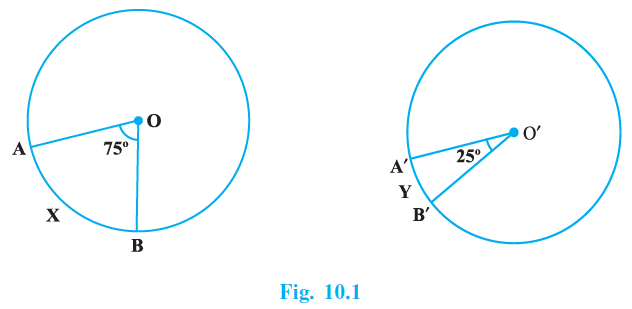
(A) 2 : 1
(B) 1 : 2
(C) 3 : 1
(D) 1 : 3
Answer:
Given:
Two congruent circles with centres O and O'.
Angle subtended by arc AXB at centre O is $\angle$AOB $= 75^\circ$.
Angle subtended by arc A'YB' at centre O' is $\angle$A'O'B' $= 25^\circ$.
To Find:
Ratio of the length of arc AXB to the length of arc A'YB'.
Solution:
Since the two circles are congruent, their radii are equal. Let the radius of both circles be $r$.
The formula for the length of an arc subtending an angle $\theta$ (in degrees) at the centre of a circle with radius $r$ is given by:
$L = \frac{\theta}{360^\circ} \times 2\pi r$
Length of arc AXB ($L_1$) is:
$L_1 = \frac{75^\circ}{360^\circ} \times 2\pi r$
Length of arc A'YB' ($L_2$) is:
$L_2 = \frac{25^\circ}{360^\circ} \times 2\pi r$
Now, we find the ratio of the lengths of arc AXB and arc A'YB':
$\frac{L_1}{L_2} = \frac{\frac{75^\circ}{360^\circ} \times 2\pi r}{\frac{25^\circ}{360^\circ} \times 2\pi r}$
We can cancel out the common terms $\frac{1}{360^\circ} \times 2\pi r$ from the numerator and the denominator (assuming $r \neq 0$):
$\frac{L_1}{L_2} = \frac{75^\circ}{25^\circ}$
$\frac{L_1}{L_2} = 3$
So, the ratio of the lengths of arc AXB and arc A'YB' is $3:1$.
The correct option is (C).
Answer: (C) 3 : 1
Sample Question 2: In Fig. 10.2, AB and CD are two equal chords of a circle with centre O. OP and OQ are perpendiculars on chords AB and CD, respectively. If ∠POQ = 150º, then ∠APQ is equal to
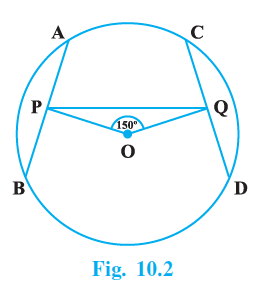
(A) 30º
(B) 75º
(C) 15º
(D) 60º
Answer:
Given:
AB and CD are two equal chords of a circle with centre O.
OP $\perp$ AB and OQ $\perp$ CD.
$\angle$POQ = $150^\circ$.
To Find:
The measure of $\angle$APQ.
Solution:
Since AB and CD are equal chords of the circle, they are equidistant from the centre O.
OP = OQ
(Equal chords are equidistant from the centre)
In $\triangle$OPQ, we have OP = OQ. Therefore, $\triangle$OPQ is an isosceles triangle.
$\angle$OPQ = $\angle$OQP
(Angles opposite to equal sides are equal)
The sum of angles in $\triangle$OPQ is $180^\circ$.
$\angle$OPQ + $\angle$OQP + $\angle$POQ = $180^\circ$
... (i)
Substituting the given value $\angle$POQ = $150^\circ$ and $\angle$OQP = $\angle$OPQ into equation (i):
$\angle$OPQ + $\angle$OPQ + $150^\circ = 180^\circ$
$2\angle$OPQ = $180^\circ - 150^\circ$
$2\angle$OPQ = $30^\circ$
$\angle$OPQ = $\frac{30^\circ}{2}$
$\angle$OPQ = $15^\circ$.
Given that OP $\perp$ AB, the angle between the line AB (containing AP) and the line segment PO is $90^\circ$.
$\angle$APO = $90^\circ$
(OP $\perp$ AB)
The angle $\angle$APQ is the angle between the line AB and the line segment PQ. From the diagram, it is clear that $\angle$APQ and $\angle$OPQ are parts of the right angle $\angle$APO such that $\angle$APQ + $\angle$OPQ = $\angle$APO is not the configuration. Instead, think about lines AB and PO being perpendicular. The angle between AB and PO is 90°. The angle between PO and PQ is $\angle$OPQ = 15°. The angle between AB and PQ ($\angle$APQ) is therefore $90^\circ - \angle$OPQ.
$\angle$APQ = $\angle$APO - $\angle$OPQ
$\angle$APQ = $90^\circ - 15^\circ$
$\angle$APQ = $75^\circ$.
The correct option is (B).
Answer: (B) $75^\circ$
Exercise 10.1
Question 1. AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is :
(A) 17 cm
(B) 15 cm
(C) 4 cm
(D) 8 cm
Answer:
Solution: The correct option is (D) 8 cm.
Given:
A circle with a diameter AD = 34 cm.
A chord AB = 30 cm.
To Find:
The distance of the chord AB from the centre of the circle.
Construction:
Let O be the centre of the circle. Draw a perpendicular line segment OM from the centre O to the chord AB. Join OA.
Solution:
Since AD is the diameter, the radius of the circle is half the length of the diameter.
Radius (OA) = $\frac{\text{Diameter (AD)}}{2} = \frac{34}{2} = 17$ cm.
We know that the perpendicular drawn from the centre of a circle to a chord bisects the chord.
Since OM $\perp$ AB, M is the mid-point of AB.
Therefore, $AM = \frac{1}{2} AB = \frac{30}{2} = 15$ cm.
Now, consider the right-angled triangle $\triangle OMA$.
By the Pythagorean theorem, we have:
$OA^2 = OM^2 + AM^2$
Substituting the known values:
$17^2 = OM^2 + 15^2$
$289 = OM^2 + 225$
$OM^2 = 289 - 225$
$OM^2 = 64$
$OM = \sqrt{64}$
$OM = 8$ cm.
The distance of the chord AB from the centre of the circle is the length of the perpendicular OM, which is 8 cm.
Hence, the correct option is (D).
Question 2. In Fig. 10.3, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to:
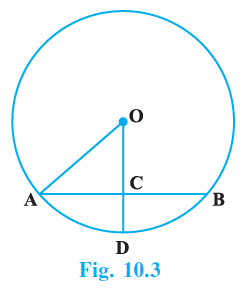
(A) 2 cm
(B) 3 cm
(C) 4 cm
(D) 5 cm
Answer:
Given:
OA is the radius of the circle, OA = $5 \text{ cm}$.
AB is a chord, AB = $8 \text{ cm}$.
OD is perpendicular to AB, with O being the centre and D a point on the circle.
To Find:
The length of CD.
Solution:
Since OA is the radius, the radius of the circle is $r = OA = 5 \text{ cm}$.
OD is also a radius of the circle, so OD = $5 \text{ cm}$.
Let M be the point where OD intersects AB. Since OD is perpendicular to AB, OM is the perpendicular distance from the centre O to the chord AB.
The perpendicular from the centre of a circle to a chord bisects the chord.
Therefore, M is the midpoint of AB.
AM = MB = $\frac{1}{2} \times AB = \frac{1}{2} \times 8 \text{ cm} = 4 \text{ cm}$.
In the right-angled triangle $\triangle$OMA (since OM $\perp$ AB), by the Pythagorean theorem:
$OA^2 = OM^2 + AM^2$
Substitute the known values:
$(5)^2 = OM^2 + (4)^2$
$25 = OM^2 + 16$
$OM^2 = 25 - 16$
$OM^2 = 9$
$OM = \sqrt{9} = 3 \text{ cm}$ (Since distance must be positive)
From the figure, the points O, M, and D are collinear, and M lies between O and D. Also, OD is the radius and CD is the remaining part of the radius after OM.
CD = OD - OM
Substitute the values of OD and OM:
CD = $5 \text{ cm} - 3 \text{ cm}$
CD = $2 \text{ cm}$.
The correct option is (A).
Answer: (A) $2 \text{ cm}$
Question 3. If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is :
(A) 6 cm
(B) 8 cm
(C) 10 cm
(D) 12 cm
Answer:
Solution: The correct option is (C) 10 cm.
Given:
A circle passes through the points A, B, and C.
Length of the side, $AB = 12$ cm.
Length of the side, $BC = 16$ cm.
The side AB is perpendicular to BC, which means $\angle ABC = 90^\circ$.
To Find:
The radius of the circle passing through the points A, B, and C.
Construction:
Draw a circle passing through the points A, B, and C. Join A and C.
Solution:
We are given that the points A, B, and C lie on a circle and that the angle formed at vertex B is a right angle ($\angle ABC = 90^\circ$).
We know a key property of circles: the angle subtended by a diameter at any point on the circumference is a right angle ($90^\circ$).
The converse of this theorem is also true: if a chord subtends a right angle at any point on the circumference, then the chord must be the diameter of the circle.
In our case, the chord AC subtends an angle of $90^\circ$ at point B on the circumference. Therefore, the chord AC must be the diameter of the circle.
Now, we can find the length of the diameter AC by applying the Pythagorean theorem to the right-angled triangle $\triangle ABC$.
$AC^2 = AB^2 + BC^2$
(By Pythagorean theorem)
Substituting the given values, $AB = 12$ cm and $BC = 16$ cm:
$AC^2 = 12^2 + 16^2$
$AC^2 = 144 + 256$
$AC^2 = 400$
$AC = \sqrt{400}$
$AC = 20$ cm.
So, the diameter of the circle is 20 cm.
The radius of a circle is half of its diameter.
Radius = $\frac{\text{Diameter}}{2} = \frac{AC}{2}$
Radius = $\frac{20}{2} = 10$ cm.
Hence, the radius of the circle is 10 cm.
Question 4. In Fig.10.4, if ∠ABC = 20º, then ∠AOC is equal to:
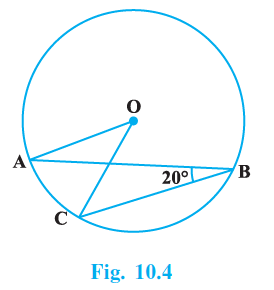
(A) 20º
(B) 40º
(C) 60º
(D) 10º
Answer:
Given:
In the given figure, O is the centre of the circle.
A, B, and C are points on the circumference of the circle.
$\angle$ABC $= 20^\circ$.
To Find:
The measure of $\angle$AOC.
Solution:
$\angle$AOC is the angle subtended by the arc AC at the centre O.
$\angle$ABC is the angle subtended by the same arc AC at a point B on the remaining part of the circle.
According to the theorem which states that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle:
$\angle$AOC $= 2 \times \angle$ABC
... (i)
Substitute the given value $\angle$ABC $= 20^\circ$ into equation (i):
$\angle$AOC $= 2 \times 20^\circ$
$\angle$AOC $= 40^\circ$.
The correct option is (B).
Answer: (B) $40^\circ$
Question 5. In Fig.10.5, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to:

(A) 30º
(B) 60º
(C) 90º
(D) 45º
Answer:
Given:
AOB is the diameter of the circle.
AC = BC.
To Find:
The measure of $\angle$CAB.
Solution:
Since AOB is the diameter of the circle, the angle subtended by the diameter at any point on the circumference is $90^\circ$.
$\angle$ACB $= 90^\circ$
(Angle in a semicircle)
In $\triangle$ABC, we are given that AC = BC.
This means that $\triangle$ABC is an isosceles triangle with the base AB.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$CAB = $\angle$CBA
(Angles opposite to equal sides)
Let $\angle$CAB $= \angle$CBA $= x$.
The sum of the angles in a triangle is $180^\circ$. In $\triangle$ABC:
$\angle$CAB + $\angle$CBA + $\angle$ACB $= 180^\circ$
Substitute the values:
$x + x + 90^\circ = 180^\circ$
$2x + 90^\circ = 180^\circ$
$2x = 180^\circ - 90^\circ$
$2x = 90^\circ$
$x = \frac{90^\circ}{2}$
$x = 45^\circ$
Therefore, $\angle$CAB $= 45^\circ$.
The correct option is (D).
Answer: (D) $45^\circ$
Question 6. In Fig. 10.6, if ∠OAB = 40º, then ∠ACB is equal to :

(A) 50º
(B) 40º
(C) 60º
(D) 70°
Answer:
Given:
In the given figure, O is the centre of the circle.
A, B, and C are points on the circumference of the circle.
$\angle$OAB $= 40^\circ$.
To Find:
The measure of $\angle$ACB.
Solution:
In $\triangle$OAB, OA and OB are radii of the same circle.
OA = OB
(Radii of the same circle)
Therefore, $\triangle$OAB is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$OBA = $\angle$OAB
(Angles opposite to equal sides)
Given $\angle$OAB $= 40^\circ$, so $\angle$OBA $= 40^\circ$.
Now, consider the sum of angles in $\triangle$OAB:
$\angle$AOB + $\angle$OAB + $\angle$OBA $= 180^\circ$
Substitute the known values:
$\angle$AOB + $40^\circ + 40^\circ = 180^\circ$
$\angle$AOB + $80^\circ = 180^\circ$
$\angle$AOB $= 180^\circ - 80^\circ$
$\angle$AOB $= 100^\circ$
... (i)
The angle subtended by an arc at the centre is double the angle subtended by the same arc at any point on the remaining part of the circle.
Arc AB subtends $\angle$AOB at the centre and $\angle$ACB at the circumference.
$\angle$AOB $= 2 \times \angle$ACB
... (ii)
Substitute the value of $\angle$AOB from equation (i) into equation (ii):
$100^\circ = 2 \times \angle$ACB
$\angle$ACB $= \frac{100^\circ}{2}$
$\angle$ACB $= 50^\circ$.
The correct option is (A).
Answer: (A) $50^\circ$
Question 7. In Fig. 10.7, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to:
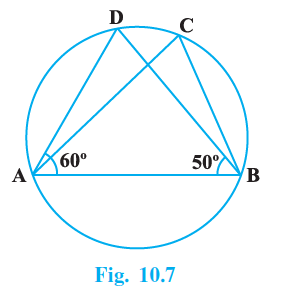
(A) 60º
(B) 50º
(C) 70º
(D) 80º
Answer:
Given:
In the given figure, A, B, C, and D are points on the circle.
$\angle$DAB $= 60^\circ$.
$\angle$ABD $= 50^\circ$.
To Find:
The measure of $\angle$ACB.
Solution:
Consider $\triangle$ABD.
The sum of angles in a triangle is $180^\circ$.
So, in $\triangle$ABD:
$\angle$ADB + $\angle$DAB + $\angle$ABD $= 180^\circ$
Substitute the given values:
$\angle$ADB + $60^\circ + 50^\circ = 180^\circ$
$\angle$ADB + $110^\circ = 180^\circ$
$\angle$ADB $= 180^\circ - 110^\circ$
$\angle$ADB $= 70^\circ$
... (i)
Now, observe that $\angle$ACB and $\angle$ADB are angles subtended by the same arc AB on the circumference of the circle.
According to the theorem that states angles in the same segment of a circle are equal:
$\angle$ACB = $\angle$ADB
(Angles in the same segment)
From equation (i), we know that $\angle$ADB $= 70^\circ$.
Therefore, $\angle$ACB $= 70^\circ$.
The correct option is (C).
Answer: (C) $70^\circ$
Question 8. ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to:
(A) 80º
(B) 50º
(C) 40º
(D) 30º
Answer:
Solution: The correct option is (B) 50º.
Given:
ABCD is a cyclic quadrilateral.
AB is the diameter of the circumscribing circle.
$\angle ADC = 140^\circ$.
To Find:
The measure of $\angle BAC$.
Construction:
Draw a circle with diameter AB. Mark points C and D on the circumference to form the cyclic quadrilateral ABCD.
Solution:
We know that in a cyclic quadrilateral, the sum of the opposite angles is $180^\circ$.
Therefore, for the cyclic quadrilateral ABCD:
$\angle ABC + \angle ADC = 180^\circ$
(Opposite angles of a cyclic quadrilateral)
Substituting the given value of $\angle ADC = 140^\circ$:
$\angle ABC + 140^\circ = 180^\circ$
$\angle ABC = 180^\circ - 140^\circ$
$\angle ABC = 40^\circ$
... (i)
We are also given that AB is the diameter of the circle. The angle subtended by a diameter at any point on the circumference is a right angle ($90^\circ$).
Therefore, the angle $\angle ACB$, which is subtended by the diameter AB at point C on the circumference, is $90^\circ$.
$\angle ACB = 90^\circ$
(Angle in a semicircle)
Now, consider the triangle $\triangle ABC$. The sum of the angles in a triangle is $180^\circ$.
$\angle BAC + \angle ABC + \angle ACB = 180^\circ$
Substituting the values we have found for $\angle ABC$ and $\angle ACB$:
$\angle BAC + 40^\circ + 90^\circ = 180^\circ$
$\angle BAC + 130^\circ = 180^\circ$
$\angle BAC = 180^\circ - 130^\circ$
$\angle BAC = 50^\circ$.
Hence, the measure of $\angle BAC$ is 50º.
Question 9. In Fig. 10.8, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to :
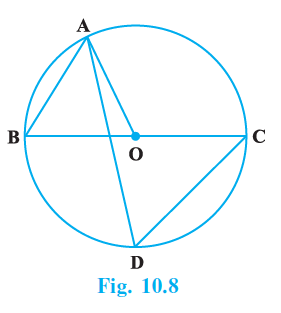
(A) 30º
(B) 45º
(C) 60º
(D) 120º
Answer:
Solution: The correct option is (C) 60º.
Given:
A circle with center O and BC as its diameter.
The points A, B, C, and D lie on the circle.
$\angle BAO = 60^\circ$.
To Find:
The measure of $\angle ADC$.
Solution:
Consider the triangle $\triangle AOB$.
The sides OA and OB are radii of the same circle.
OA = OB
(Radii of the same circle)
Since two sides of $\triangle AOB$ are equal, it is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are also equal.
$\angle OBA = \angle OAB$
We are given that $\angle BAO = 60^\circ$ (which is the same as $\angle OAB$).
Therefore, $\angle OBA = 60^\circ$.
Since two angles of $\triangle AOB$ are $60^\circ$, the third angle, $\angle AOB$, must also be $60^\circ$ (since the sum of angles in a triangle is $180^\circ$). So, $\triangle AOB$ is an equilateral triangle.
Now, consider the angle $\angle AOC$. Since BC is a diameter, it is a straight line. The angles on this straight line at the center O must add up to $180^\circ$.
$\angle AOB + \angle AOC = 180^\circ$
$60^\circ + \angle AOC = 180^\circ$
$\angle AOC = 180^\circ - 60^\circ = 120^\circ$.
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
The arc AC subtends the angle $\angle AOC$ at the center O and the angle $\angle ADC$ at point D on the remaining part of the circle.
$\angle AOC = 2 \times \angle ADC$
Substituting the value of $\angle AOC$ we found:
$120^\circ = 2 \times \angle ADC$
$\angle ADC = \frac{120^\circ}{2}$
$\angle ADC = 60^\circ$.
Hence, the measure of $\angle ADC$ is 60º.
Question 10. In Fig. 10.9, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to:
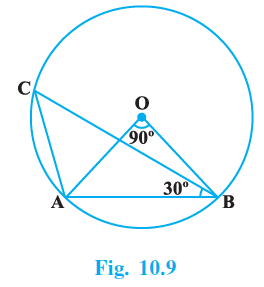
(A) 30º
(B) 45º
(C) 90º
(D) 60º
Answer:
Solution: The correct option is (D) 60º.
Given:
In the circle with centre O:
$\angle AOB = 90^\circ$.
$\angle ABC = 30^\circ$.
To Find:
The measure of $\angle CAO$.
Solution:
First, consider the triangle $\triangle OAB$.
The sides OA and OB are radii of the same circle, so $OA = OB$.
Therefore, $\triangle OAB$ is an isosceles triangle, and the angles opposite the equal sides are equal.
$\angle OAB = \angle OBA$.
Using the angle sum property for $\triangle OAB$:
$\angle OAB + \angle OBA + \angle AOB = 180^\circ$
$\angle OAB + \angle OAB + 90^\circ = 180^\circ$
$2 \angle OAB = 180^\circ - 90^\circ$
$2 \angle OAB = 90^\circ$
$\angle OAB = 45^\circ$
... (i)
Next, we find the measure of $\angle ACB$.
The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
The arc AB subtends $\angle AOB$ at the center and $\angle ACB$ at the circumference.
$\angle ACB = \frac{1}{2} \angle AOB = \frac{1}{2} \times 90^\circ = 45^\circ$.
Now, consider the larger triangle $\triangle ABC$. The sum of its angles is $180^\circ$.
$\angle CAB + \angle ABC + \angle ACB = 180^\circ$
Substituting the known values:
$\angle CAB + 30^\circ + 45^\circ = 180^\circ$
$\angle CAB + 75^\circ = 180^\circ$
$\angle CAB = 180^\circ - 75^\circ = 105^\circ$.
From the figure, we can see that the angle $\angle CAB$ is the sum of $\angle CAO$ and $\angle OAB$.
$\angle CAB = \angle CAO + \angle OAB$
Substituting the values of $\angle CAB$ and $\angle OAB$ from equation (i):
$105^\circ = \angle CAO + 45^\circ$
$\angle CAO = 105^\circ - 45^\circ$
$\angle CAO = 60^\circ$.
Hence, the measure of $\angle CAO$ is 60º.
Sample Question 1 & 2 (Before Exercise 10.2)
Write True or False and justify your answer.
Sample Question 1: The angles subtended by a chord at any two points of a circle are equal.
Answer:
The given statement is False.
Justification:
The statement is only true if the two points lie on the same segment of the circle (either both in the major segment or both in the minor segment). The correct theorem is: Angles in the same segment of a circle are equal.
If the two points are in different segments, the angles are not equal. In fact, they are supplementary (they add up to $180^\circ$).
Example:
Let AB be a chord of a circle. Let C be a point on the major arc and D be a point on the minor arc.
In this case, ACBD forms a cyclic quadrilateral. The angles subtended by the chord AB at points C and D are $\angle ACB$ and $\angle ADB$ respectively.
Since the sum of opposite angles in a cyclic quadrilateral is $180^\circ$:
$\angle ACB + \angle ADB = 180^\circ$
As $\angle ACB$ and $\angle ADB$ are supplementary and not equal (unless both are $90^\circ$, which happens only when AB is a diameter), the original statement that the angles subtended by a chord at *any* two points are equal is false.
Sample Questions 2: Two chords of a circle of lengths 10 cm and 8 cm are at the distances 8.0 cm and 3.5 cm, respectively from the centre.
Answer:
The given statement is False.
Justification:
A fundamental property of circles is that the longer a chord is, the closer it is to the centre of the circle. Conversely, the shorter a chord is, the farther it is from the centre.
Let's analyze the given information:
Chord 1: Length = 10 cm, Distance from centre = 8.0 cm.
Chord 2: Length = 8 cm, Distance from centre = 3.5 cm.
Here, the 10 cm chord is longer than the 8 cm chord. According to the property, the 10 cm chord should be closer to the centre than the 8 cm chord. This means its distance from the centre should be less.
However, the given distances are 8.0 cm for the 10 cm chord and 3.5 cm for the 8 cm chord. Since 8.0 cm > 3.5 cm, the statement claims that the longer chord is farther from the centre. This is a contradiction of the established property of circles.
Mathematical Verification:
We can also verify this by calculating the radius of the circle required for each case. In a single circle, the radius must be the same.
The relationship between the radius (r), the length of a chord (L), and its distance from the centre (d) is given by the Pythagorean theorem: $r^2 = d^2 + (\frac{L}{2})^2$.
For the first chord:
L = 10 cm, d = 8.0 cm.
$r^2 = (8.0)^2 + (\frac{10}{2})^2 = 8^2 + 5^2$
$r^2 = 64 + 25 = 89$.
For the second chord:
L = 8 cm, d = 3.5 cm.
$r^2 = (3.5)^2 + (\frac{8}{2})^2 = (3.5)^2 + 4^2$
$r^2 = 12.25 + 16 = 28.25$.
Since the calculated value of $r^2$ is different for both chords (89 ≠ 28.25), it is impossible for these two chords to exist in the same circle with the given dimensions. Thus, the statement is false.
Exercise 10.2
Write True or False and justify your answer in each of the following:
Question 1. Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Answer:
The given statement is True.
Justification:
This is a direct application of a fundamental theorem of circles which states that: Chords of a circle that are equidistant from the centre are equal in length.
In this problem, we are given:
Distance of chord AB from the centre = 4 cm.
Distance of chord CD from the centre = 4 cm.
Since both chords are at the same distance from the centre, they are equidistant. Therefore, according to the theorem, their lengths must be equal.
Hence, AB = CD.
Mathematical Proof:
Let O be the centre of the circle and let $r$ be its radius.
Let OM be the perpendicular from the centre O to the chord AB. Then, OM = 4 cm.
Let ON be the perpendicular from the centre O to the chord CD. Then, ON = 4 cm.
In the right-angled triangle $\triangle OMA$, by the Pythagorean theorem:
$OA^2 = OM^2 + AM^2$
Since OA is the radius, $r^2 = 4^2 + AM^2$.
We know the perpendicular from the centre bisects the chord, so $AB = 2 \times AM$, which means $AM = \frac{AB}{2}$.
$r^2 = 16 + \left(\frac{AB}{2}\right)^2$
... (i)
Similarly, in the right-angled triangle $\triangle ONC$, by the Pythagorean theorem:
$OC^2 = ON^2 + CN^2$
Since OC is the radius, $r^2 = 4^2 + CN^2$.
The perpendicular from the centre bisects the chord CD, so $CD = 2 \times CN$, which means $CN = \frac{CD}{2}$.
$r^2 = 16 + \left(\frac{CD}{2}\right)^2$
... (ii)
From equations (i) and (ii), we can equate the expressions for $r^2$:
$16 + \left(\frac{AB}{2}\right)^2 = 16 + \left(\frac{CD}{2}\right)^2$
$\left(\frac{AB}{2}\right)^2 = \left(\frac{CD}{2}\right)^2$
Taking the square root on both sides (since lengths are positive):
$\frac{AB}{2} = \frac{CD}{2}$
$AB = CD$.
This confirms that the statement is true.
Question 2. Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .
Answer:
The given statement is False.
Justification:
The statement claims that for any two chords AB and AC on opposite sides of the radius OA, the angles $\angle OAB$ and $\angle OAC$ will be equal. This is not necessarily true. This condition only holds if the two chords, AB and AC, are equal in length.
If the chords have different lengths, the triangles they form with the centre ( $\triangle OAB$ and $\triangle OAC$) will not be congruent, and consequently, the angles $\angle OAB$ and $\angle OAC$ will not be equal.
Mathematical Proof:
Let's consider the triangles $\triangle OAB$ and $\triangle OAC$.
In $\triangle OAB$:
OA and OB are radii of the same circle, so $OA = OB$.
This means $\triangle OAB$ is an isosceles triangle.
Therefore, the angles opposite the equal sides are equal: $\angle OAB = \angle OBA$.
In $\triangle OAC$:
OA and OC are radii of the same circle, so $OA = OC$.
This means $\triangle OAC$ is an isosceles triangle.
Therefore, the angles opposite the equal sides are equal: $\angle OAC = \angle OCA$.
For the statement $\angle OAB = \angle OAC$ to be true, the two isosceles triangles, $\triangle OAB$ and $\triangle OAC$, must have the same base angles.
This would only happen if the triangles were congruent (by SAS congruence, since OA is a common side, OB=OC, and we would need $\angle AOB = \angle AOC$).
The condition $\angle AOB = \angle AOC$ (equal angles at the centre) is only true if the chords subtending these angles are equal, i.e., $AB = AC$.
Since the problem statement does not specify that the chords AB and AC must be equal in length, we cannot assume that $\angle OAB = \angle OAC$. As shown in the diagram above where AB < AC, it is clear that $\angle OAB > \angle OAC$.
Therefore, the statement is false.
Question 3. Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
Answer:
The given statement is True.
Justification:
When two circles are congruent, they have the same radius. The common chord AB will subtend an angle at the center of each circle. The triangles formed by this chord and the radii in each circle ( $\triangle AOB$ and $\triangle AO'B$) are congruent by the Side-Side-Side (SSS) criterion, because all the radii are equal and the chord is common. Since the triangles are congruent, their corresponding angles, including the angles at the centers ($\angle AOB$ and $\angle AO'B$), must be equal.
Mathematical Proof:
Let the two congruent circles have centres O and O′ and a common radius $r$.
The circles intersect at points A and B, so AB is the common chord.
Consider the triangle $\triangle AOB$ formed in the first circle and the triangle $\triangle AO'B$ formed in the second circle.
In $\triangle AOB$ and $\triangle AO'B$:
OA = O'A
(Radii of congruent circles, both equal to $r$)
OB = O'B
(Radii of congruent circles, both equal to $r$)
AB = AB
(Common chord)
By the Side-Side-Side (SSS) congruence criterion, the two triangles are congruent.
$\triangle AOB \cong \triangle AO'B$
Since the triangles are congruent, their corresponding parts must be equal (CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
Therefore, the angles at the vertices O and O′ are equal:
$\angle AOB = \angle AO'B$
This proves that the statement is true.
Question 4. Through three collinear points a circle can be drawn.
Answer:
Answer: False
Justification:
A circle is defined as the set of all points in a plane that are at a fixed distance (the radius) from a fixed point (the centre).
If three points are collinear, it means they lie on the same straight line.
Consider a circle and a straight line.
A straight line can intersect a circle at most at two distinct points.
If a circle were to pass through three distinct collinear points, it would mean that the straight line containing these three points intersects the circle at three distinct points.
This contradicts the property that a straight line can intersect a circle at a maximum of two points.
Therefore, it is not possible to draw a circle that passes through three distinct collinear points.
A circle can only be drawn through three non-collinear points.
Question 5. A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm
Answer:
Answer: True
Justification:
We are given two points A and B such that the distance between them is $AB = 6$ cm.
We are asked if a circle of radius $r = 3$ cm can be drawn through these two points.
The diameter of a circle with radius $r$ is $d = 2r$.
For a circle with radius $r = 3$ cm, the diameter is $d = 2 \times 3 = 6$ cm.
The distance between points A and B is given as $AB = 6$ cm.
Since the distance between points A and B is equal to the diameter of the proposed circle, this implies that the line segment AB can be a diameter of the circle.
The endpoints of a diameter always lie on the circle.
Therefore, a circle with radius 3 cm (and diameter 6 cm) can indeed be drawn such that it passes through points A and B, where AB forms the diameter of this circle.
The center of such a circle would be the midpoint of the segment AB.
Hence, the statement is true.
Question 6. If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2 .
Answer:
The given statement is True.
Justification:
The statement is a direct application of the Pythagorean theorem to a triangle inscribed in a semicircle, which is always a right-angled triangle.
Proof:
We are given that AOB is a diameter of a circle and C is a point on the circle.
A key theorem in circle geometry states that the angle in a semicircle is a right angle. This means that the angle subtended by a diameter at any point on the circumference is always $90^\circ$.
In this case, the diameter AB subtends the angle $\angle ACB$ at the point C on the circumference.
Therefore, according to the theorem:
$\angle ACB = 90^\circ$
This means that the triangle $\triangle ABC$ is a right-angled triangle, with the right angle at vertex C.
The side opposite the right angle is the hypotenuse. In $\triangle ABC$, the side opposite $\angle ACB$ is the diameter AB.
According to the Pythagorean theorem, in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Applying the Pythagorean theorem to $\triangle ABC$, we get:
$AC^2 + BC^2 = AB^2$
This is exactly the statement given in the question. Therefore, the statement is true.
Question 7. ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
Answer:
Answer: False
Justification:
For a quadrilateral to be cyclic, the sum of opposite angles must be $180^\circ$.
In the given quadrilateral ABCD, the angles are $\angle A = 90^\circ$, $\angle B = 70^\circ$, $\angle C = 95^\circ$, and $\angle D = 105^\circ$.
Let's check the sum of opposite angles:
Sum of $\angle A$ and $\angle C$:
$\angle A + \angle C = 90^\circ + 95^\circ = 185^\circ$
Sum of $\angle B$ and $\angle D$:
$\angle B + \angle D = 70^\circ + 105^\circ = 175^\circ$
Since $\angle A + \angle C \neq 180^\circ$ and $\angle B + \angle D \neq 180^\circ$, the condition for a quadrilateral to be cyclic is not met.
Also, the sum of all angles in any quadrilateral must be $360^\circ$. Let's check this:
$90^\circ + 70^\circ + 95^\circ + 105^\circ = 360^\circ$. This confirms that ABCD is a valid quadrilateral, but not necessarily cyclic.
Because the sums of opposite angles are not $180^\circ$, the quadrilateral ABCD with these angle measures cannot be cyclic.
Hence, the statement is false.
Question 8. If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
Answer:
The given statement is True.
Justification:
The relationship between the angle subtended by an arc at the centre of a circle and the angle subtended by the same arc at the circumference is a key theorem in circle geometry.
The theorem states: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Let's analyze the given information in the context of this theorem.
Consider the circle passing through the points A, B, and C.
The angle $\angle BAC = 30^\circ$ is the angle subtended by the arc BC at a point A on the circumference.
If D were the centre of this circle, then the angle $\angle BDC = 60^\circ$ would be the angle subtended by the same arc BC at the centre.
According to the theorem, for D to be the centre, the following condition must hold:
$\angle BDC = 2 \times \angle BAC$
Let's check if the given values satisfy this condition:
Given: $\angle BDC = 60^\circ$ and $\angle BAC = 30^\circ$.
Substituting these values into the equation:
$60^\circ = 2 \times 30^\circ$
$60^\circ = 60^\circ$
Since the condition is perfectly satisfied, the point D must be the centre of the circle passing through the points A, B, and C.
Therefore, the statement is true.
Question 9. If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
Answer:
The given statement is True.
Justification:
This statement is a direct application of the converse of the "Angles in the same segment" theorem.
The theorem states: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, then the four points lie on a circle (i.e., they are concyclic).
Let's apply this theorem to the given problem:
1. The line segment in question is BC.
2. The two other points are A and D.
3. The problem states that the angles subtended by the line segment BC at points A and D are equal:
$\angle BAC = \angle BDC = 45^\circ$
4. Since the line segment BC subtends equal angles at points A and D (assuming they are on the same side of BC), the conditions of the theorem are met.
Therefore, we can conclude that the four points A, B, C, and D are concyclic.
Question 10. In Fig. 10.10, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.

Answer:
The given statement is True.
Given:
A circle with center O and diameter AOB.
Points A, B, C, and D are on the circle, forming a cyclic quadrilateral ABCD.
$\angle ADC = 120^\circ$.
To Prove:
The statement "$\angle CAB = 30^\circ$" is true.
Construction:
The figure is as given. We will use the properties of the cyclic quadrilateral ABCD and the inscribed triangle ABC.
Proof:
Since ABCD is a cyclic quadrilateral, the sum of its opposite angles is $180^\circ$.
$\angle ABC + \angle ADC = 180^\circ$
(Opposite angles of a cyclic quadrilateral)
Substituting the given value of $\angle ADC = 120^\circ$:
$\angle ABC + 120^\circ = 180^\circ$
$\angle ABC = 180^\circ - 120^\circ$
$\angle ABC = 60^\circ$
... (i)
We are given that AOB is the diameter of the circle. The angle subtended by a diameter at any point on the circumference is a right angle ($90^\circ$).
Therefore, the angle $\angle ACB$, which is subtended by the diameter AB at point C, is $90^\circ$.
$\angle ACB = 90^\circ$
(Angle in a semicircle)
Now, let's consider the triangle $\triangle ABC$. The sum of the angles in a triangle is $180^\circ$.
$\angle CAB + \angle ABC + \angle ACB = 180^\circ$
Substituting the values we have found for $\angle ABC$ and $\angle ACB$:
$\angle CAB + 60^\circ + 90^\circ = 180^\circ$
$\angle CAB + 150^\circ = 180^\circ$
$\angle CAB = 180^\circ - 150^\circ$
$\angle CAB = 30^\circ$.
The calculated value of $\angle CAB$ is $30^\circ$, which matches the value given in the statement.
Hence, the statement is true.
Sample Question 1 & 2 (Before Exercise 10.3)
Sample Question 1: In Fig. 10.11, AOC is a diameter of the circle and arc AXB = $\frac{1}{2}$ arc BYC. Find ∠BOC.
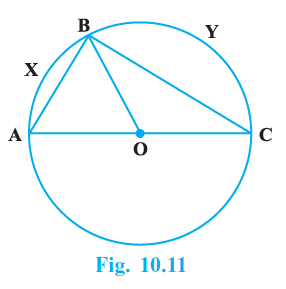
Answer:
Given:
In the given figure, AOC is a diameter of the circle with center O.
Also, it is given that the length of arc AXB is half the length of arc BYC.
i.e., arc AXB = $\frac{1}{2}$ arc BYC
To Find:
The measure of $\angle$BOC.
Solution:
We know that the angle subtended by an arc at the centre of a circle is proportional to the length of the arc.
The angle subtended by arc AXB at the centre is $\angle AOB$.
The angle subtended by arc BYC at the centre is $\angle BOC$.
Given the relation between the arcs:
arc AXB = $\frac{1}{2}$ arc BYC
(Given)
Therefore, the relation between the angles subtended by these arcs at the centre is:
$\angle AOB = \frac{1}{2} \angle BOC$
... (i)
Since AOC is the diameter of the circle, it is a straight line.
Therefore, $\angle AOB$ and $\angle BOC$ form a linear pair.
$\angle AOB + \angle BOC = 180^\circ$
[Linear Pair] ... (ii)
Substituting the value of $\angle AOB$ from equation (i) into equation (ii), we get:
$\frac{1}{2} \angle BOC + \angle BOC = 180^\circ$
$\Rightarrow \left(\frac{1}{2} + 1\right) \angle BOC = 180^\circ$
$\Rightarrow \frac{3}{2} \angle BOC = 180^\circ$
$\Rightarrow \angle BOC = 180^\circ \times \frac{2}{3}$
$\Rightarrow \angle BOC = 60^\circ \times 2$
$\Rightarrow \angle BOC = 120^\circ$
Hence, the measure of $\angle$BOC is $120^\circ$.
Sample Question 2: In Fig. 10.12, ∠ABC = 45º, prove that OA ⊥ OC.

Answer:
Given:
In the given figure, O is the centre of the circle and A, B, C are points on the circle.
$\angle ABC = 45^\circ$
(Given)
To Prove:
OA is perpendicular to OC, which means we have to prove that $\angle AOC = 90^\circ$.
Proof:
We know the theorem: "The angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle."
In the given figure, the arc AC subtends $\angle AOC$ at the centre O and $\angle ABC$ at point B on the remaining part of the circle.
Therefore, by the theorem, we have:
$\angle AOC = 2 \times \angle ABC$
Substituting the given value of $\angle ABC = 45^\circ$ into the above relation, we get:
$\angle AOC = 2 \times 45^\circ$
$\angle AOC = 90^\circ$
Since the angle between the radii OA and OC is $90^\circ$, they are perpendicular to each other.
Thus, $OA \perp OC$.
Hence, proved.
Exercise 10.3
Question 1. If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
Answer:
Given:
In a circle, there are two arcs, AXB and CYD, which are congruent.
arc AXB ≅ arc CYD
To Find:
The ratio of the lengths of the corresponding chords AB and CD.
Solution:
Let's visualize the given situation with a figure.
We have a theorem in circle geometry which states that: "In the same circle, or in congruent circles, if two arcs are congruent, then their corresponding chords are equal."
Here, we are given that arc AXB is congruent to arc CYD.
arc AXB ≅ arc CYD
(Given)
The chord corresponding to arc AXB is AB.
The chord corresponding to arc CYD is CD.
Applying the theorem, we can conclude that the lengths of the corresponding chords are equal.
$AB = CD$
We are asked to find the ratio of AB and CD, which is expressed as $AB : CD$ or $\frac{AB}{CD}$.
To find the ratio, we can divide both sides of the equation $AB = CD$ by CD (assuming $CD \neq 0$, which is true as it's a chord).
$\frac{AB}{CD} = \frac{CD}{CD}$
$\frac{AB}{CD} = 1$
This can also be written as a ratio:
$AB : CD = 1 : 1$
Hence, the ratio of AB and CD is 1:1.
Question 2. If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA ≅ arc PYB.
Answer:
Given:
A circle with a chord AB.
A line segment PQ is the perpendicular bisector of the chord AB, and it intersects the circle at points P and Q.
To Prove:
arc PXA ≅ arc PYB.
Construction:
Join PA and PB. Let the perpendicular bisector PQ intersect the chord AB at point M.
Proof:
Since the line PQ is the perpendicular bisector of the chord AB, it intersects AB at M such that:
AM = MB
(PQ bisects AB)
$\angle PMA = \angle PMB = 90^\circ$
(PQ $\perp$ AB)
Now, let's consider the triangles $\triangle PMA$ and $\triangle PMB$.
AM = MB
(Proved above)
$\angle PMA = \angle PMB$
(Each $90^\circ$)
PM = PM
(Common side)
Therefore, by the Side-Angle-Side (SAS) congruence criterion, we have:
$\triangle PMA \cong \triangle PMB$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$PA = PB$
We know a theorem which states that: "In a circle, if two chords are equal, then their corresponding arcs are congruent."
Since the chord PA is equal to the chord PB, their corresponding minor arcs must also be congruent.
The arc PXA is the minor arc corresponding to chord PA, and arc PYB is the minor arc corresponding to chord PB.
Therefore, arc PA ≅ arc PB.
Hence, arc PXA ≅ arc PYB.
Hence, proved.
Question 3. A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
Answer:
Given:
A, B, and C are three non-collinear points on a circle, forming the vertices of a triangle $\triangle ABC$.
To Prove:
The perpendicular bisectors of the sides AB, BC, and CA are concurrent.
Construction:
Let's draw the perpendicular bisectors of the sides AB and BC. Let these perpendicular bisectors be named $l_1$ and $l_2$ respectively. Since AB and BC are non-parallel sides of a triangle, their perpendicular bisectors $l_1$ and $l_2$ are also not parallel and will intersect at a point. Let this point of intersection be O.
Join OA, OB, and OC.
Proof:
We know that any point lying on the perpendicular bisector of a line segment is equidistant from the endpoints of that segment.
The point O lies on the perpendicular bisector $l_1$ of the chord AB.
Therefore, O is equidistant from A and B.
$OA = OB$
... (i)
The point O also lies on the perpendicular bisector $l_2$ of the chord BC.
Therefore, O is equidistant from B and C.
$OB = OC$
... (ii)
From equations (i) and (ii), we can conclude that:
$OA = OB = OC$
This implies that the point O is equidistant from the points A and C.
Now, we use the converse of the perpendicular bisector theorem, which states that any point equidistant from the endpoints of a line segment must lie on its perpendicular bisector.
Since $OA = OC$, the point O must lie on the perpendicular bisector of the line segment CA.
Thus, the perpendicular bisector of the third side CA also passes through the same point O.
Since all three perpendicular bisectors of the sides AB, BC, and CA pass through the common point O, they are concurrent.
Hence, it is proved that the perpendicular bisectors of AB, BC, and CA are concurrent.
(Note: This point of concurrency O is the center of the circle that passes through the points A, B, and C, and is called the circumcenter of the triangle ABC.)
Question 4. AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
Answer:
Given:
A circle with center O, in which AB and AC are two equal chords.
$AB = AC$
To Prove:
The bisector of the angle $\angle BAC$ passes through the centre O of the circle.
Construction:
Join the centre O to the points A, B, and C. Draw perpendiculars from O to the chords AB and AC. Let these be OM and ON respectively, so that $OM \perp AB$ and $ON \perp AC$.
Proof:
We consider the two triangles $\triangle OMA$ and $\triangle ONA$.
We are given that the chords AB and AC are equal.
$AB = AC$
(Given)
We know that equal chords of a circle are equidistant from the centre.
Therefore, the perpendicular distance from O to AB is equal to the perpendicular distance from O to AC.
$OM = ON$
... (i)
Now, in the right-angled triangles $\triangle OMA$ and $\triangle ONA$:
$OM = ON$
[From (i)]
$\angle OMA = \angle ONA$
[Each $90^\circ$, by construction]
OA = OA
[Common hypotenuse]
Therefore, by the Right angle-Hypotenuse-Side (RHS) congruence criterion, we have:
$\triangle OMA \cong \triangle ONA$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$\angle MAO = \angle NAO$
This implies that $\angle BAO = \angle CAO$.
This shows that the line segment OA is the bisector of the angle $\angle BAC$.
Since OA passes through the centre O, we can conclude that the bisector of $\angle BAC$ passes through the centre of the circle.
Hence, proved.
Alternate Solution:
Construction: Join OB and OC.
Proof:
In $\triangle AOB$ and $\triangle AOC$, we have:
AB = AC
(Given)
OB = OC
[Radii of the same circle]
OA = OA
[Common side]
Therefore, by the Side-Side-Side (SSS) congruence criterion, we have:
$\triangle AOB \cong \triangle AOC$
By CPCTC, we get:
$\angle BAO = \angle CAO$
This means that OA is the bisector of $\angle BAC$. Since the line segment OA passes through the centre O, it is proved that the bisector of $\angle BAC$ passes through the centre of the circle.
Hence, proved.
Question 5. If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Answer:
Given:
A circle with centre O.
AB and CD are two chords of the circle.
M is the midpoint of chord AB and N is the midpoint of chord CD.
The line segment MN passes through the centre O.
To Prove:
The chords AB and CD are parallel (AB || CD).
Construction:
Draw a circle with center O. Draw two chords AB and CD with midpoints M and N respectively, such that the line segment MN passes through O. Join OM and ON.
Proof:
We know the theorem: "The line segment joining the centre of a circle to the midpoint of a chord is perpendicular to the chord."
Since M is the midpoint of the chord AB, the line segment OM is perpendicular to AB.
$OM \perp AB$
This implies that the angle formed by OM and AB is $90^\circ$.
$\angle OMA = 90^\circ$
... (i)
Similarly, since N is the midpoint of the chord CD, the line segment ON is perpendicular to CD.
$ON \perp CD$
This implies that the angle formed by ON and CD is $90^\circ$.
$\angle ONC = 90^\circ$
... (ii)
It is given that the line segment joining M and N passes through the centre O. This means that M, O, and N are collinear, and the line MON acts as a transversal intersecting the chords AB and CD.
From the figure, the angles $\angle AMN$ (which is the same as $\angle OMA$) and $\angle CNM$ (which is the same as $\angle ONC$) are a pair of interior angles on the same side of the transversal MN.
Let's find the sum of these interior angles:
$\angle AMN + \angle CNM = \angle OMA + \angle ONC$
Using the results from (i) and (ii):
$\angle AMN + \angle CNM = 90^\circ + 90^\circ = 180^\circ$
According to the property of parallel lines, if a transversal intersects two lines such that the sum of the interior angles on the same side of the transversal is $180^\circ$, then the two lines are parallel.
Since the sum of the consecutive interior angles is $180^\circ$, the chords AB and CD must be parallel.
Hence, AB || CD.
Question 6. ABCD is such a quadrilateral that A is the centre of the circle passing through B, C and D. Prove that ∠CBD + ∠CDB = $\frac{1}{2}$ ∠BAD
Answer:
Given:
A quadrilateral ABCD such that A is the centre of a circle that passes through the points B, C, and D.
To Prove:
$\angle CBD + \angle CDB = \frac{1}{2} \angle BAD$
Construction:
Join the points B, C and D to the center A. Also, join B to C, C to D, and B to D.
Proof:
We know the theorem: "The angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle."
Let's consider the arc BC. The angle subtended by this arc at the centre is $\angle BAC$. The angle subtended by it at point D on the remaining part of the circle is $\angle BDC$ (which is the same as $\angle CDB$).
Therefore, according to the theorem:
$\angle BAC = 2 \angle CDB$
... (i)
Now, let's consider the arc CD. The angle subtended by this arc at the centre is $\angle CAD$. The angle subtended by it at point B on the remaining part of the circle is $\angle CBD$.
Therefore, according to the same theorem:
$\angle CAD = 2 \angle CBD$
... (ii)
Adding equation (i) and equation (ii), we get:
$\angle BAC + \angle CAD = 2 \angle CDB + 2 \angle CBD$
From the figure, it is clear that the sum of the angles $\angle BAC$ and $\angle CAD$ is equal to the angle $\angle BAD$.
$\angle BAC + \angle CAD = \angle BAD$
Substituting this into our equation, we get:
$\angle BAD = 2 \angle CDB + 2 \angle CBD$
Taking 2 as a common factor on the right-hand side:
$\angle BAD = 2 (\angle CDB + \angle CBD)$
Dividing both sides by 2, we get:
$\frac{1}{2} \angle BAD = \angle CDB + \angle CBD$
Rearranging the terms, we have:
$\angle CBD + \angle CDB = \frac{1}{2} \angle BAD$
Hence, proved.
Question 7. O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
Answer:
Given:
O is the circumcentre of the triangle ABC.
D is the mid-point of the base BC.
To Prove:
$\angle BOD = \angle A$.
Construction:
Join OB and OC.
Proof:
Let's consider the triangles $\triangle OBD$ and $\triangle OCD$.
OB = OC
[Radii of the same circle]
OD = OD
[Common side]
BD = CD
[D is the midpoint of BC]
Therefore, by the Side-Side-Side (SSS) congruence criterion, we have:
$\triangle OBD \cong \triangle OCD$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$\angle BOD = \angle COD$
This means that:
$\angle BOC = \angle BOD + \angle COD = \angle BOD + \angle BOD = 2 \angle BOD$
$\angle BOC = 2 \angle BOD$
... (i)
Now, we know the theorem: "The angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle."
The arc BC subtends $\angle BOC$ at the centre O and $\angle BAC$ (or $\angle A$) at point A on the remaining part of the circle.
Therefore, according to the theorem:
$\angle BOC = 2 \angle BAC$
or, $\angle BOC = 2 \angle A$
$\angle BOC = 2 \angle A$
... (ii)
From equation (i) and equation (ii), we can equate the expressions for $\angle BOC$:
$2 \angle BOD = 2 \angle A$
Dividing both sides by 2, we get:
$\angle BOD = \angle A$
Hence, proved.
Question 8. On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
Answer:
Given:
Two right-angled triangles, $\triangle ACB$ and $\triangle ADB$, are situated on opposite sides of a common hypotenuse AB.
This means $\angle ACB = 90^\circ$ and $\angle ADB = 90^\circ$.
To Prove:
$\angle BAC = \angle BDC$.
Construction:
Draw a circle with the common hypotenuse AB as its diameter.
Proof:
We know that the angle in a semicircle is a right angle ($90^\circ$).
For the triangle $\triangle ACB$, we are given:
$\angle ACB = 90^\circ$
(Given)
Since $\angle ACB$ is a right angle, the point C must lie on the circumference of a circle with AB as its diameter.
Similarly, for the triangle $\triangle ADB$, we are given:
$\angle ADB = 90^\circ$
(Given)
Since $\angle ADB$ is also a right angle, the point D must also lie on the circumference of the same circle with AB as its diameter.
From this, we can conclude that the four points A, C, B, and D lie on the same circle. In other words, the points A, C, B, and D are concyclic.
Now, let's consider the chord BC of this circle. The angles $\angle BAC$ and $\angle BDC$ are subtended by the same arc BPC (or the same chord BC) in the same segment of the circle.
We know the theorem: "Angles in the same segment of a circle are equal."
Therefore, by applying this theorem, we get:
$\angle BAC = \angle BDC$
Hence, proved.
Question 9. Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
Answer:
Given:
A circle with centre O.
Two chords AB and AC are drawn from the point A.
The angle subtended by chord AB at the centre is $90^\circ$, i.e., $\angle AOB = 90^\circ$.
The angle subtended by chord AC at the centre is $150^\circ$, i.e., $\angle AOC = 150^\circ$.
The chords AB and AC lie on the opposite sides of the centre.
To Find:
The measure of $\angle BAC$.
Solution:
Let's consider the triangle $\triangle AOB$.
In $\triangle AOB$, the sides OA and OB are the radii of the same circle.
OA = OB
[Radii of the same circle]
Since two sides of the triangle are equal, $\triangle AOB$ is an isosceles triangle.
In an isosceles triangle, the angles opposite to the equal sides are also equal.
$\angle OAB = \angle OBA$
By the angle sum property of a triangle, the sum of all angles in $\triangle AOB$ is $180^\circ$.
$\angle OAB + \angle OBA + \angle AOB = 180^\circ$
$\Rightarrow \angle OAB + \angle OAB + 90^\circ = 180^\circ$
$\Rightarrow 2\angle OAB = 180^\circ - 90^\circ$
$\Rightarrow 2\angle OAB = 90^\circ$
$\Rightarrow \angle OAB = \frac{90^\circ}{2} = 45^\circ$
Now, let's consider the triangle $\triangle AOC$.
In $\triangle AOC$, the sides OA and OC are the radii of the same circle.
OA = OC
[Radii of the same circle]
Therefore, $\triangle AOC$ is an isosceles triangle.
The angles opposite to the equal sides are equal.
$\angle OAC = \angle OCA$
By the angle sum property of a triangle, the sum of all angles in $\triangle AOC$ is $180^\circ$.
$\angle OAC + \angle OCA + \angle AOC = 180^\circ$
$\Rightarrow \angle OAC + \angle OAC + 150^\circ = 180^\circ$
$\Rightarrow 2\angle OAC = 180^\circ - 150^\circ$
$\Rightarrow 2\angle OAC = 30^\circ$
$\Rightarrow \angle OAC = \frac{30^\circ}{2} = 15^\circ$
Since it is given that AB and AC lie on opposite sides of the centre, the angle $\angle BAC$ is the sum of $\angle OAB$ and $\angle OAC$.
$\angle BAC = \angle OAB + \angle OAC$
$\angle BAC = 45^\circ + 15^\circ$
$\angle BAC = 60^\circ$
Hence, the measure of $\angle BAC$ is $60^\circ$.
Question 10. If BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC, prove that the points B, C, M and N are concyclic.
Answer:
Given:
A triangle ABC.
BM and CN are the perpendiculars drawn on the sides AC and AB respectively.
This means $BM \perp AC$ and $CN \perp AB$.
To Prove:
The points B, C, M, and N are concyclic (i.e., they lie on the same circle).
Construction:
Draw a triangle ABC and draw the perpendiculars BM from B to AC and CN from C to AB.
Proof:
Since BM is perpendicular to AC, the angle formed at M is a right angle.
$\angle BMC = 90^\circ$
... (i)
Similarly, since CN is perpendicular to AB, the angle formed at N is a right angle.
$\angle BNC = 90^\circ$
... (ii)
From equations (i) and (ii), we can see that:
$\angle BMC = \angle BNC = 90^\circ$
Now, let's consider the line segment BC. The points M and N are on the same side of the line segment BC.
We observe that the line segment BC subtends equal angles at points M and N on the same side of BC.
We know the theorem: "If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the segment, then the four points are concyclic."
Since the conditions of the theorem are satisfied for the points B, C, M, and N with respect to the line segment BC, we can conclude that these four points are concyclic.
In fact, the circle on which these points lie will have BC as its diameter, as the angles subtended at the circumference ($\angle BMC$ and $\angle BNC$) are right angles.
Hence, the points B, C, M and N are concyclic.
Question 11. If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
Answer:
Given:
An isosceles triangle ABC with equal sides AB and AC ($AB = AC$).
A line DE is drawn parallel to the base BC, intersecting the equal sides AB at D and AC at E.
This forms a quadrilateral BCED.
To Prove:
The quadrilateral BCED is a cyclic quadrilateral.
Construction:
Draw an isosceles triangle ABC with AB = AC. Draw a line DE parallel to BC such that D is on AB and E is on AC.
Proof:
A quadrilateral is cyclic if the sum of either pair of its opposite angles is $180^\circ$. We will prove that $\angle BDE + \angle BCE = 180^\circ$.
In the given isosceles triangle ABC, we have:
AB = AC
(Given)
Since angles opposite to equal sides of a triangle are equal, we get:
$\angle ABC = \angle ACB$
... (i)
Now, it is given that the line DE is parallel to BC, and AB is a transversal line intersecting them.
DE || BC
(Given)
Therefore, the corresponding angles are equal:
$\angle ADE = \angle ABC$
[Corresponding angles] ... (ii)
The angles $\angle ADE$ and $\angle BDE$ form a linear pair on the straight line AB.
$\angle ADE + \angle BDE = 180^\circ$
[Linear pair axiom] ... (iii)
Substituting the value of $\angle ADE$ from equation (ii) into equation (iii), we get:
$\angle ABC + \angle BDE = 180^\circ$
From equation (i), we can replace $\angle ABC$ with $\angle ACB$:
$\angle ACB + \angle BDE = 180^\circ$
The angle $\angle ACB$ is the same as the angle $\angle BCE$. So, we can write:
$\angle BCE + \angle BDE = 180^\circ$
This shows that the sum of a pair of opposite angles ($\angle BDE$ and $\angle BCE$) of the quadrilateral BCED is $180^\circ$.
Since the sum of opposite angles is supplementary, the quadrilateral BCED is cyclic.
Hence, proved.
Alternate Solution:
We will first prove that the quadrilateral BCED is an isosceles trapezium, and then use the property that an isosceles trapezium is always cyclic.
In quadrilateral BCED, we are given that DE || BC. A quadrilateral with one pair of parallel sides is a trapezium. So, BCED is a trapezium.
Now, in $\triangle ABC$, we have DE || BC. By the property of similar triangles (or Basic Proportionality Theorem), we have:
$\triangle ADE \sim \triangle ABC$
Therefore, the ratio of corresponding sides is equal:
$\frac{AD}{AB} = \frac{AE}{AC}$
It is given that the triangle ABC is isosceles with $AB = AC$.
$\Rightarrow \frac{AD}{AB} = \frac{AE}{AB}$
$\Rightarrow AD = AE$
Now, we subtract this from the given equal sides:
$AB - AD = AC - AE$
From the figure, $AB - AD = DB$ and $AC - AE = EC$.
Therefore, $DB = EC$.
Since the non-parallel sides (DB and EC) of the trapezium BCED are equal, it is an isosceles trapezium.
We know that every isosceles trapezium is a cyclic quadrilateral.
Hence, the quadrilateral BCED is cyclic.
Question 12. If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
Answer:
Given:
A cyclic quadrilateral ABCD in which a pair of opposite sides are equal.
Let's assume $AD = BC$.
To Prove:
The diagonals of the quadrilateral are equal, i.e., $AC = BD$.
Construction:
Draw the cyclic quadrilateral ABCD and join its diagonals AC and BD.
Proof:
We know the theorem: "In a circle, equal chords correspond to congruent arcs."
We are given that the chords AD and BC are equal.
$AD = BC$
(Given)
Therefore, their corresponding arcs are also equal.
arc AD = arc BC
Now, let's add the arc DC to both sides of the equation.
arc AD + arc DC = arc BC + arc DC
From the figure, the sum of arc AD and arc DC is the arc ADC.
Similarly, the sum of arc BC and arc DC is the arc BCD.
So, we have:
arc ADC = arc BCD
We also know the theorem: "In a circle, congruent arcs have corresponding equal chords."
The chord corresponding to the arc ADC is AC.
The chord corresponding to the arc BCD is BD.
Therefore, since the arcs are equal, their corresponding chords must also be equal.
$AC = BD$
Hence, it is proved that the diagonals of the cyclic quadrilateral are equal.
Alternate Solution:
Proof:
Let's consider the triangles $\triangle ABC$ and $\triangle BAD$.
We know that angles subtended by the same arc at any point on the remaining part of the circle are equal.
Angle $\angle ADB$ and angle $\angle ACB$ are subtended by the same arc AB.
$\angle ADB = \angle ACB$
... (i)
Angle $\angle BAC$ and angle $\angle BDC$ are subtended by the same arc BC.
$\angle BAC = \angle BDC$
... (ii)
Now, consider the triangles $\triangle ADC$ and $\triangle BCD$.
AD = BC
(Given)
DC = DC
(Common side)
Since equal chords subtend equal arcs (arc AD = arc BC), these arcs will also subtend equal angles at the circumference.
Angle subtended by arc AD is $\angle ACD$.
Angle subtended by arc BC is $\angle BDC$.
So, $\angle ACD = \angle BDC$.
From (ii), we know $\angle BDC = \angle BAC$. Therefore, $\angle ACD = \angle BAC$.
Let's reconsider using a different pair of triangles, $\triangle ADC$ and $\triangle BCD$.
In $\triangle ADC$ and $\triangle BCD$:
AD = BC
(Given)
DC = CD
(Common)
In the cyclic quadrilateral ABCD, since $AD=BC$, it forms an isosceles trapezium. Thus, the base angles are equal. The angles between the parallel sides and one of the non-parallel sides are equal. Let's prove that $\angle ADC = \angle BCD$.
We have arc AD = arc BC. Adding arc AB to both sides, we get arc DAB = arc CBA. The angles subtended by these arcs at the circumference are $\angle DCB$ and $\angle ADC$ respectively.
$\angle ADC = \angle BCD$ [Angles subtended by equal arcs are equal]
Now, by SAS congruence criterion in $\triangle ADC$ and $\triangle BCD$:
$\triangle ADC \cong \triangle BCD$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$AC = BD$
Hence, proved.
Question 13. The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
Answer:
Given:
O is the circumcentre of the triangle ABC.
To Prove:
$\angle OBC + \angle BAC = 90^\circ$.
Construction:
Join OB and OC.
Proof:
Let's consider the triangle $\triangle OBC$.
Since O is the circumcentre of $\triangle ABC$, the points A, B, and C lie on the circumference of the circle with centre O. Therefore, OB and OC are the radii of this circle.
OB = OC
[Radii of the same circle]
Since two sides of the triangle $\triangle OBC$ are equal, it is an isosceles triangle.
In an isosceles triangle, the angles opposite to the equal sides are also equal.
$\angle OBC = \angle OCB$
By the angle sum property of a triangle, the sum of all angles in $\triangle OBC$ is $180^\circ$.
$\angle BOC + \angle OBC + \angle OCB = 180^\circ$
Substituting $\angle OCB = \angle OBC$ into the equation, we get:
$\angle BOC + \angle OBC + \angle OBC = 180^\circ$
$\angle BOC + 2\angle OBC = 180^\circ$
$\angle BOC = 180^\circ - 2\angle OBC$
$\angle BOC = 180^\circ - 2\angle OBC$
... (i)
Now, we know the theorem: "The angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle."
The arc BC subtends $\angle BOC$ at the centre O and $\angle BAC$ at point A on the remaining part of the circle.
Therefore, according to the theorem:
$\angle BOC = 2\angle BAC$
... (ii)
From equation (i) and equation (ii), we can equate the expressions for $\angle BOC$:
$180^\circ - 2\angle OBC = 2\angle BAC$
Rearranging the terms, we get:
$180^\circ = 2\angle BAC + 2\angle OBC$
$180^\circ = 2(\angle BAC + \angle OBC)$
Dividing both sides by 2:
$\frac{180^\circ}{2} = \angle BAC + \angle OBC$
$90^\circ = \angle BAC + \angle OBC$
Or,
$\angle OBC + \angle BAC = 90^\circ$
Hence, proved.
Question 14. A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
Answer:
Given:
A circle with centre O and radius r.
A chord AB such that its length is equal to the radius of the circle.
$AB = r$
To Find:
The angle subtended by the chord AB at a point in the major segment.
Solution:
Let's draw a diagram to represent the given information. Let O be the centre of the circle and AB be the chord.
Join the endpoints of the chord, A and B, to the centre O.
Now, consider the triangle $\triangle AOB$.
OA = r
[Radius of the circle]
OB = r
[Radius of the circle]
It is given that the length of the chord AB is equal to the radius.
AB = r
(Given)
From the above three relations, we can see that all three sides of the triangle $\triangle AOB$ are equal.
$OA = OB = AB = r$
Therefore, $\triangle AOB$ is an equilateral triangle.
We know that all angles in an equilateral triangle are equal to $60^\circ$.
So, the angle subtended by the chord AB at the centre O is:
$\angle AOB = 60^\circ$
Now, let C be any point on the major segment of the circle. We need to find the angle subtended by the chord AB at this point, which is $\angle ACB$.
We know the theorem: "The angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle."
Here, the arc AB subtends $\angle AOB$ at the centre and $\angle ACB$ at a point on the remaining part of the circle.
Therefore, by the theorem, we have:
$\angle AOB = 2 \times \angle ACB$
Substituting the value of $\angle AOB$, we get:
$60^\circ = 2 \times \angle ACB$
$\angle ACB = \frac{60^\circ}{2}$
$\angle ACB = 30^\circ$
Hence, the angle subtended by the chord at a point in the major segment is $30^\circ$.
Question 15. In Fig.10.13, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.
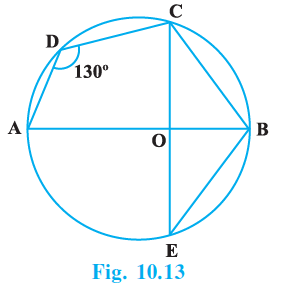
Answer:
Given:
ABCD is a cyclic quadrilateral in a circle with centre O.
AB is the diameter.
$\angle ADC = 130^\circ$
chord BC = chord BE.
To Find:
The measure of $\angle CBE$.
Solution:
We are given that ABCD is a cyclic quadrilateral.
The sum of opposite angles of a cyclic quadrilateral is $180^\circ$.
Therefore, $\angle ABC + \angle ADC = 180^\circ$
$\Rightarrow \angle ABC + 130^\circ = 180^\circ$
$\Rightarrow \angle ABC = 180^\circ - 130^\circ$
$\Rightarrow \angle ABC = 50^\circ$
Since AB is a diameter, the line passing through A, O, and B is a straight line. The angle $\angle ABC$ is the same as the angle $\angle OBC$.
Therefore, $\angle OBC = 50^\circ$.
Now, let's consider the triangles $\triangle BOC$ and $\triangle BOE$.
BC = BE
[Given equal chords]
OC = OE
[Radii of the same circle]
OB = OB
[Common side]
By the Side-Side-Side (SSS) congruence criterion, we have:
$\triangle BOC \cong \triangle BOE$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$\angle OBC = \angle OBE$
[by CPCTC]
Since we found that $\angle OBC = 50^\circ$, it follows that:
$\angle OBE = 50^\circ$
From the figure, the angle $\angle CBE$ is the sum of $\angle OBC$ and $\angle OBE$.
$\angle CBE = \angle OBC + \angle OBE$
$\angle CBE = 50^\circ + 50^\circ$
$\angle CBE = 100^\circ$
Hence, the measure of $\angle CBE$ is $100^\circ$.
Question 16. In Fig.10.14, ∠ACB = 40º. Find ∠OAB.

Answer:
Given:
In a circle with center O, $\angle$ACB = $40^\circ$.
To Find:
$\angle$OAB.
Solution:
The angle subtended by an arc at the center is double the angle subtended by the same arc at any point on the remaining part of the circle.
Arc AB subtends $\angle$AOB at the center O and $\angle$ACB at point C on the circumference.
$\angle$AOB = 2$\angle$ACB
... (i)
Substitute the given value $\angle$ACB = $40^\circ$ into equation (i):
$\angle$AOB = 2 $\times$ $40^\circ$
$\angle$AOB = $80^\circ$
Now consider $\triangle$OAB.
OA and OB are the radii of the same circle.
OA = OB
(Radii of the same circle)
Since OA = OB, $\triangle$OAB is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$OAB = $\angle$OBA
The sum of angles in a triangle is $180^\circ$. In $\triangle$OAB:
$\angle$OAB + $\angle$OBA + $\angle$AOB = $180^\circ$
Substitute $\angle$OBA = $\angle$OAB and $\angle$AOB = $80^\circ$:
$\angle$OAB + $\angle$OAB + $80^\circ$ = $180^\circ$
2$\angle$OAB = $180^\circ - 80^\circ$
2$\angle$OAB = $100^\circ$
$\angle$OAB = $\frac{100^\circ}{2}$
$\angle$OAB = $50^\circ$
The angle $\angle$OAB is $50^\circ$.
Question 17. A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
Answer:
Given:
A quadrilateral ABCD is inscribed in a circle (it is a cyclic quadrilateral).
AB is a diameter of the circle.
The measure of angle $\angle ADC = 130^\circ$.
To Find:
The measure of the angle $\angle BAC$.
Construction:
Join the points A, C and B to form the triangle $\triangle ABC$.
Solution:
Since ABCD is a cyclic quadrilateral, the sum of its opposite angles is $180^\circ$.
Therefore, we have:
$\angle ABC + \angle ADC = 180^\circ$
Substituting the given value of $\angle ADC = 130^\circ$ into the equation:
$\angle ABC + 130^\circ = 180^\circ$
$\Rightarrow \angle ABC = 180^\circ - 130^\circ$
$\angle ABC = 50^\circ$
... (i)
Now, it is given that AB is a diameter of the circle.
We know the theorem: "The angle in a semicircle is a right angle."
The angle subtended by the diameter AB at any point on the circumference is $90^\circ$. Therefore, the angle at point C is:
$\angle ACB = 90^\circ$
[Angle in a semicircle] ... (ii)
Now, let's consider the triangle $\triangle ABC$.
By the angle sum property of a triangle, the sum of all its interior angles is $180^\circ$.
$\angle BAC + \angle ABC + \angle ACB = 180^\circ$
Substituting the values from equations (i) and (ii) into this equation:
$\angle BAC + 50^\circ + 90^\circ = 180^\circ$
$\Rightarrow \angle BAC + 140^\circ = 180^\circ$
$\Rightarrow \angle BAC = 180^\circ - 140^\circ$
$\Rightarrow \angle BAC = 40^\circ$
Hence, the measure of $\angle BAC$ is $40^\circ$.
Question 18. Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′.
Answer:
Given:
Two circles with centres O and O′ intersect at points A and B.
A line PQ is drawn through point A, parallel to the line of centres OO′.
The line PQ intersects the circle with centre O at P and the circle with centre O′ at Q.
To Prove:
$PQ = 2 OO'$.
Construction:
From the centre O, draw a perpendicular OM to the chord AP.
From the centre O′, draw a perpendicular O′N to the chord AQ.
Proof:
We know that the perpendicular drawn from the centre of a circle to a chord bisects the chord.
For the circle with centre O, since $OM \perp AP$, M is the midpoint of AP.
$PA = 2 AM$
... (i)
Similarly, for the circle with centre O′, since $O'N \perp AQ$, N is the midpoint of AQ.
$AQ = 2 AN$
... (ii)
The total length of the line segment PQ is the sum of PA and AQ.
$PQ = PA + AQ$
Substituting the values from equations (i) and (ii):
$PQ = 2 AM + 2 AN$
$PQ = 2 (AM + AN)$
From the figure, $AM + AN = MN$. Therefore,
$PQ = 2 MN$
... (iii)
Now, let's consider the quadrilateral OO′NM.
By construction, $OM \perp PQ$ and $O'N \perp PQ$. This means that $\angle OMN = 90^\circ$ and $\angle O'NM = 90^\circ$.
It is given that the line PQ is parallel to OO′.
So, we have a quadrilateral OO'NM where:
1. $MN \parallel OO'$ (Since MN is part of line PQ)
2. $OM \perp MN$ and $O'N \perp MN$
The lines OM and O'N are perpendiculars between the two parallel lines PQ and OO'. This means that the distance between the parallel lines is constant, and the quadrilateral OO'NM is a rectangle.
In a rectangle, opposite sides are equal in length. Therefore,
$MN = OO'$
... (iv)
Substituting the result from equation (iv) into equation (iii), we get:
$PQ = 2 OO'$
Hence, proved.
Question 19. In Fig.10.15, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
Answer:
Given:
In the given figure, AOB is a diameter of a circle with centre O.
C, D, and E are any three points on the semi-circle.
To Find:
The value of $\angle ACD + \angle BED$.
Construction:
Join the points A and E.
Solution:
Consider the points A, C, D, and E on the circle. Since these four points lie on the circle, the quadrilateral ACDE is a cyclic quadrilateral.
We know that the sum of opposite angles in a cyclic quadrilateral is $180^\circ$.
Therefore, for the cyclic quadrilateral ACDE, we have:
$\angle ACD + \angle AED = 180^\circ$
[Sum of opposite angles in a cyclic quadrilateral] ... (i)
Now, it is given that AOB is a diameter of the circle.
The angle subtended by a diameter at any point on the circumference is a right angle ($90^\circ$). This is also known as the angle in a semicircle.
Therefore, the angle subtended by the diameter AB at point E is:
$\angle AEB = 90^\circ$
[Angle in a semicircle] ... (ii)
Adding equation (i) and equation (ii), we get:
$(\angle ACD + \angle AED) + \angle AEB = 180^\circ + 90^\circ$
By grouping the angles on the left side, we get:
$\angle ACD + (\angle AED + \angle AEB) = 270^\circ$
From the figure, it is clear that $\angle AED + \angle AEB = \angle BED$.
Substituting this into the equation, we get:
$\angle ACD + \angle BED = 270^\circ$
Hence, the value of $\angle ACD + \angle BED$ is $270^\circ$.
Question 20. In Fig. 10.16, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.
Answer:
Given:
In the circle with centre O, we have:
$\angle OAB = 30^\circ$
$\angle OCB = 57^\circ$
To Find:
The measure of the angles $\angle BOC$ and $\angle AOC$.
Solution:
First, let's consider the triangle $\triangle OAB$.
OA = OB
[Radii of the same circle]
Since $\triangle OAB$ has two equal sides, it is an isosceles triangle. In an isosceles triangle, angles opposite to the equal sides are also equal.
Therefore, $\angle OBA = \angle OAB = 30^\circ$.
Now, applying the angle sum property to $\triangle OAB$:
$\angle AOB + \angle OBA + \angle OAB = 180^\circ$
$\Rightarrow \angle AOB + 30^\circ + 30^\circ = 180^\circ$
$\Rightarrow \angle AOB + 60^\circ = 180^\circ$
$\Rightarrow \angle AOB = 180^\circ - 60^\circ$
$\angle AOB = 120^\circ$
... (i)
Next, let's consider the triangle $\triangle OCB$.
OC = OB
[Radii of the same circle]
Since $\triangle OCB$ has two equal sides, it is an isosceles triangle. Therefore, angles opposite to the equal sides are equal.
Therefore, $\angle OBC = \angle OCB = 57^\circ$.
Now, applying the angle sum property to $\triangle OCB$:
$\angle BOC + \angle OBC + \angle OCB = 180^\circ$
$\Rightarrow \angle BOC + 57^\circ + 57^\circ = 180^\circ$
$\Rightarrow \angle BOC + 114^\circ = 180^\circ$
$\Rightarrow \angle BOC = 180^\circ - 114^\circ$
$\Rightarrow \angle BOC = 66^\circ$
From the figure, it is clear that the angle $\angle AOB$ is the sum of the angles $\angle AOC$ and $\angle BOC$.
$\angle AOB = \angle AOC + \angle BOC$
Substituting the values of $\angle AOB$ and $\angle BOC$ from our calculations:
$120^\circ = \angle AOC + 66^\circ$
$\Rightarrow \angle AOC = 120^\circ - 66^\circ$
$\Rightarrow \angle AOC = 54^\circ$
Hence, the measures of the angles are $\angle BOC = 66^\circ$ and $\angle AOC = 54^\circ$.
Sample Question 1 & 2 (Before Exercise 10.4)
Sample Question 1: Prove that two circles cannot intersect at more than two points.
Answer:
Given:
Two circles, let's call them C1 and C2, with centres O and O′ respectively.
To Prove:
The circles C1 and C2 cannot intersect at more than two points.
Proof:
We will use the method of proof by contradiction.
Assumption: Let us assume that it is possible for the two circles to intersect at three distinct points, say A, B, and C.
Since the points A, B, and C lie on the circle C1 with centre O, they must be equidistant from O. This distance is the radius of circle C1.
$OA = OB = OC$
[Radii of the same circle C1]
Similarly, since the points A, B, and C also lie on the circle C2 with centre O′, they must be equidistant from O′. This distance is the radius of circle C2.
$O'A = O'B = O'C$
[Radii of the same circle C2]
We know that any point equidistant from two given points must lie on the perpendicular bisector of the line segment joining those two points.
Since $OA = OB$ and $O'A = O'B$, both centres O and O′ must lie on the perpendicular bisector of the line segment AB.
This implies that the line joining the centres, OO′, is the perpendicular bisector of the chord AB.
By the same logic, since $OB = OC$ and $O'B = O'C$, both centres O and O′ must also lie on the perpendicular bisector of the line segment BC. This implies that the line OO′ is also the perpendicular bisector of the chord BC.
However, since A, B, and C are three distinct points of intersection, they cannot be collinear (a straight line can intersect a circle at a maximum of two points). Therefore, A, B, and C form the vertices of a triangle.
This leads to a contradiction: The single straight line OO′ cannot be the perpendicular bisector of two different non-parallel line segments AB and BC.
This is impossible because A, B, and C are not on the same line. The only way the line OO' could be the perpendicular bisector of both AB and BC is if A, B, and C were collinear, which they are not.
Since our initial assumption leads to a logical contradiction, the assumption must be false.
Hence, two circles cannot intersect at more than two points.
Sample Question 2: Prove that among all the chords of a circle passing through a given point inside the circle that one is smallest which is perpendicular to the diameter passing through the point.
Answer:
Given:
A circle with centre O.
A point P inside the circle.
A chord AB passing through P and perpendicular to the diameter that also passes through P.
Any other chord CD passing through the same point P.
To Prove:
The chord AB is the smallest of all chords passing through P.
That is, $AB < CD$.
Construction:
Let MN be the diameter of the circle passing through the point P.
Draw the chord AB such that it passes through P and is perpendicular to the diameter MN. So, $AB \perp MN$.
Draw another chord CD passing through P.
From the centre O, draw a perpendicular to the chord CD, meeting it at point K. So, $OK \perp CD$.
Join OC.
Proof:
We know that the perpendicular distance from the centre of a circle to a chord determines its length. Specifically, the theorem states: "Of any two chords of a circle, the one which is farther from the centre is smaller in length."
The distance of the chord AB from the centre O is the length of the perpendicular from O to AB. Since AB is perpendicular to the diameter MN at P, the distance of chord AB from the centre O is OP.
By construction, the distance of the chord CD from the centre O is the length of the perpendicular OK.
Now, let's consider the right-angled triangle $\triangle OKP$.
$\angle OKP = 90^\circ$
[By construction]
In a right-angled triangle, the hypotenuse is the longest side. Here, the side opposite to the right angle, OP, is the hypotenuse.
Therefore, in $\triangle OKP$, we have:
$OP > OK$
This inequality shows that the distance of the chord AB from the centre (OP) is greater than the distance of the chord CD from the centre (OK).
Since the chord AB is farther from the centre than the chord CD, according to the theorem, the length of chord AB must be smaller than the length of chord CD.
$AB < CD$
As CD was any arbitrary chord passing through P, this relationship holds true for all chords passing through P (other than AB itself).
Hence, it is proved that among all the chords of a circle passing through a given point inside the circle, the one which is perpendicular to the diameter passing through the point is the smallest.
Alternate Solution:
The length of a chord in a circle can be calculated using the formula: $Length = 2 \sqrt{r^2 - d^2}$, where 'r' is the radius of the circle and 'd' is the perpendicular distance of the chord from the centre.
For the chord AB, its distance from the centre is $d_1 = OP$.
So, the length of AB is given by: $AB = 2 \sqrt{r^2 - (OP)^2}$
For the chord CD, its distance from the centre is $d_2 = OK$.
So, the length of CD is given by: $CD = 2 \sqrt{r^2 - (OK)^2}$
As established in the previous proof, in the right-angled triangle $\triangle OKP$, the hypotenuse OP is greater than the side OK.
$OP > OK$
Squaring both sides of the inequality (since both lengths are positive):
$(OP)^2 > (OK)^2$
Multiplying both sides by -1 reverses the inequality sign:
$-(OP)^2 < -(OK)^2$
Adding $r^2$ to both sides of the inequality:
$r^2 - (OP)^2 < r^2 - (OK)^2$
Taking the square root on both sides (the terms are positive as the point P is inside the circle):
$\sqrt{r^2 - (OP)^2} < \sqrt{r^2 - (OK)^2}$
Multiplying both sides by 2:
$2 \sqrt{r^2 - (OP)^2} < 2 \sqrt{r^2 - (OK)^2}$
This implies:
$AB < CD$
Hence, proved.
Exercise 10.4
Question 1. If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.
Answer:
Given:
A circle with centre O.
Two equal chords, AB and CD, intersect at a point P inside the circle.
$AB = CD$
To Prove:
The parts of one chord are separately equal to the parts of the other chord.
That is, $AP = DP$ and $BP = CP$.
Construction:
From the centre O, draw perpendiculars to the chords AB and CD. Let these be OM and ON respectively, so that $OM \perp AB$ and $ON \perp CD$.
Join the point of intersection P to the centre O.
Proof:
We are given that the chords are equal in length.
$AB = CD$
(Given)
We know the theorem: "Equal chords of a circle are equidistant from the centre."
Therefore, the perpendicular distances from the centre to these chords are equal.
$OM = ON$
... (i)
Now, let's consider the right-angled triangles $\triangle OMP$ and $\triangle ONP$.
$OM = ON$
[From equation (i)]
OP = OP
[Common hypotenuse]
$\angle OMP = \angle ONP$
[Each $90^\circ$, by construction]
Therefore, by the Right angle-Hypotenuse-Side (RHS) congruence criterion, we have:
$\triangle OMP \cong \triangle ONP$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$PM = PN$
... (ii)
We also know another theorem: "The perpendicular from the centre of a circle to a chord bisects the chord."
Since $OM \perp AB$, M is the midpoint of AB. So, $AM = MB = \frac{1}{2}AB$.
Since $ON \perp CD$, N is the midpoint of CD. So, $CN = ND = \frac{1}{2}CD$.
As it is given that $AB = CD$, their halves must also be equal.
$AM = ND$
... (iii)
and
$MB = CN$
... (iv)
Now, let's prove the required parts.
From the figure, $AP = AM + PM$.
Using equations (ii) and (iii), we can substitute $AM$ with $ND$ and $PM$ with $PN$.
$AP = ND + PN$
From the figure, $ND + PN = DP$.
Therefore, $AP = DP$.
Next, from the figure, $BP = MB - PM$.
Using equations (ii) and (iv), we can substitute $MB$ with $CN$ and $PM$ with $PN$.
$BP = CN - PN$
From the figure, $CN - PN = CP$.
Therefore, $BP = CP$.
Hence, it is proved that the parts of one chord are separately equal to the parts of the other chord.
Question 2. If non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
Given:
A trapezium ABCD in which one pair of opposite sides is parallel (AB || DC) and the non-parallel sides are equal in length ($AD = BC$).
To Prove:
The trapezium ABCD is a cyclic quadrilateral.
Construction:
From the vertices D and C, draw perpendiculars to the side AB. Let these perpendiculars be DM and CN respectively. So, $DM \perp AB$ and $CN \perp AB$.
Proof:
We know that a quadrilateral is cyclic if the sum of either pair of its opposite angles is $180^\circ$. We will prove that $\angle A + \angle C = 180^\circ$ or $\angle B + \angle D = 180^\circ$.
Let's consider the right-angled triangles $\triangle DMA$ and $\triangle CNB$.
AD = BC
(Given)
$\angle DMA = \angle CNB$
(Each $90^\circ$, by construction)
Since DM and CN are perpendiculars between the same pair of parallel lines (AB and DC), their lengths are equal.
DM = CN
[Distance between parallel lines]
Therefore, by the Right angle-Hypotenuse-Side (RHS) congruence criterion, we have:
$\triangle DMA \cong \triangle CNB$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$\angle DAM = \angle CBN$
This means, $\angle A = \angle B$
$\angle A = \angle B$
... (i)
Now, since AB is parallel to DC and BC is a transversal intersecting them, the sum of the consecutive interior angles on the same side of the transversal is $180^\circ$.
$\angle ABC + \angle BCD = 180^\circ$
or, $\angle B + \angle C = 180^\circ$
$\angle B + \angle C = 180^\circ$
... (ii)
From equation (i), we can substitute $\angle B$ with $\angle A$ in equation (ii):
$\angle A + \angle C = 180^\circ$
This shows that the sum of a pair of opposite angles ($\angle A$ and $\angle C$) of the trapezium ABCD is $180^\circ$.
Since the sum of a pair of opposite angles of the quadrilateral is supplementary, the quadrilateral is cyclic.
Hence, the trapezium ABCD is cyclic.
Question 3. If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
Answer:
Given:
A triangle $\triangle ABC$.
P, Q, and R are the mid-points of the sides BC, CA, and AB respectively.
AD is the perpendicular from vertex A to the side BC, i.e., $AD \perp BC$.
To Prove:
The four points P, Q, R, and D are concyclic.
Construction:
Join the points RQ, QP, PR, and RD.
Proof:
Our goal is to prove that the quadrilateral RQPD is a cyclic quadrilateral.
First, we apply the Mid-point Theorem in $\triangle ABC$.
Since R and Q are the mid-points of sides AB and AC respectively,
$RQ \parallel BC$
The points D and P both lie on the side BC. Thus, the line segment DP is part of the line BC.
Therefore, $RQ \parallel DP$.
Since one pair of opposite sides (RQ and DP) of the quadrilateral RQPD is parallel, RQPD is a trapezium.
code CodeNow, we will show that this trapezium is an isosceles trapezium by proving that its non-parallel sides are equal.
In $\triangle ABC$, since Q and P are the mid-points of sides AC and BC respectively,
By the Mid-point Theorem,
$QP = \frac{1}{2}AB$
... (i)
Next, consider the right-angled triangle $\triangle ADB$.
Since $AD \perp BC$, we have $\angle ADB = 90^\circ$.
R is the mid-point of the hypotenuse AB of $\triangle ADB$.
We know a property of right-angled triangles: the median to the hypotenuse is half the length of the hypotenuse. Here, RD is the median to the hypotenuse AB.
Therefore,
$RD = \frac{1}{2}AB$
... (ii)
From equation (i) and equation (ii), we can conclude that:
$QP = RD$
Since the non-parallel sides of the trapezium RQPD are equal, it is an isosceles trapezium.
We know that an isosceles trapezium is always a cyclic quadrilateral.
Therefore, the quadrilateral RQPD is cyclic.
This means that all its four vertices, P, Q, R, and D, lie on the same circle.
Hence, it is proved that the points P, Q, R, and D are concyclic.
Question 4. ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
Answer:
Given:
ABCD is a parallelogram.
A circle passes through the vertices A and B, and intersects the side AD at point P and the side BC at point Q.
To Prove:
The points P, Q, C, and D are concyclic (i.e., the quadrilateral PQCD is cyclic).
Construction:
Join PQ. The given information forms two quadrilaterals: ABQP and PQCD.
Proof:
We are given that the points A, B, Q, and P lie on a circle. Therefore, ABQP is a cyclic quadrilateral.
We know that the sum of opposite angles in a cyclic quadrilateral is supplementary ($180^\circ$).
For the cyclic quadrilateral ABQP, we have:
$\angle APQ + \angle ABQ = 180^\circ$
... (i)
Since AD is a side of the parallelogram, it is a straight line segment. Therefore, the angles $\angle APQ$ and $\angle DPQ$ form a linear pair.
$\angle APQ + \angle DPQ = 180^\circ$
[Linear pair axiom] ... (ii)
From equation (i) and equation (ii), we can equate the expressions for $180^\circ$ or simply observe that:
$\angle ABQ = \angle DPQ$
Since $\angle ABQ$ is the same as the angle $\angle ABC$ of the parallelogram, we can write:
$\angle ABC = \angle DPQ$
... (iii)
Now, let's use the properties of the parallelogram ABCD. We know that consecutive angles of a parallelogram are supplementary.
Considering the consecutive angles $\angle ABC$ and $\angle BCD$, we have:
$\angle ABC + \angle BCD = 180^\circ$
The angle $\angle BCD$ is the same as the angle $\angle DCQ$. So, we can write:
$\angle ABC + \angle DCQ = 180^\circ$
... (iv)
Now, substitute the value of $\angle ABC$ from equation (iii) into equation (iv):
$\angle DPQ + \angle DCQ = 180^\circ$
This equation shows that the sum of a pair of opposite angles ($\angle DPQ$ and $\angle DCQ$) of the quadrilateral PQCD is $180^\circ$.
By the theorem which states, "If the sum of a pair of opposite angles of a quadrilateral is $180^\circ$, then the quadrilateral is cyclic", we can conclude that the quadrilateral PQCD is cyclic.
Since PQCD is a cyclic quadrilateral, its four vertices P, Q, C, and D lie on the same circle.
Hence, it is proved that the points P, Q, C, and D are concyclic.
Question 5. Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
Answer:
Given:
A triangle $\triangle ABC$ and its circumcircle.
An angle bisector of one of its angles (let's say $\angle A$).
The perpendicular bisector of the opposite side (BC).
To Prove:
The point of intersection of the angle bisector of $\angle A$ and the perpendicular bisector of the side BC lies on the circumcircle of $\triangle ABC$.
Construction:
Let AP be the bisector of the angle $\angle A$.
Let this angle bisector AP intersect the circumcircle of $\triangle ABC$ at the point P.
Join the points P to B and P to C, forming the chords PB and PC.
Proof:
Our strategy is to show that the point P, where the angle bisector of $\angle A$ meets the circumcircle, also lies on the perpendicular bisector of the side BC. If this is true, then the intersection of the two lines must be on the circumcircle.
Since AP is the bisector of $\angle A$, it divides the angle into two equal parts.
$\angle BAP = \angle CAP$
... (i)
We know the theorem: "Angles subtended by the same arc at the circumference are equal." The converse is also true: "Equal angles subtended at the circumference of a circle correspond to equal arcs."
In the circumcircle, the angle $\angle BAP$ subtends the arc BP.
The angle $\angle CAP$ subtends the arc CP.
Since $\angle BAP = \angle CAP$ (from equation i), their corresponding arcs must also be equal.
arc BP = arc CP
We also know another theorem: "In a circle, equal arcs have corresponding equal chords."
Since the arcs are equal, their corresponding chords must also be equal in length.
PB = PC
... (ii)
This result shows that the point P is equidistant from the vertices B and C.
Now, we use the property of a perpendicular bisector. The perpendicular bisector of a line segment is the locus of all points that are equidistant from the two endpoints of the segment.
Since the point P is equidistant from B and C (as shown in equation ii), the point P must lie on the perpendicular bisector of the line segment BC.
So, we have established two facts about the point P:
1. P lies on the angle bisector of $\angle A$ (by construction).
2. P lies on the perpendicular bisector of the side BC (as proved above).
This means that the intersection of the angle bisector of $\angle A$ and the perpendicular bisector of BC is the point P.
And since we initially defined P as the point where the angle bisector intersects the circumcircle, it follows that the intersection point lies on the circumcircle.
Hence, it is proved that the angle bisector of any angle of a triangle and the perpendicular bisector of the opposite side will intersect on the circumcircle of the triangle.
Question 6. If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see Fig.10.18), prove that arc CXA + arc DZB = arc AYD + arc BWC = semicircle.
Answer:
Given:
A circle with two chords, AB and CD, intersecting at a point P inside the circle. The chords are perpendicular to each other, so $\angle APC = 90^\circ$.
To Prove:
The sum of the opposite arcs are equal to a semicircle.
1. arc CXA + arc DZB = semicircle
2. arc AYD + arc BWC = semicircle
Construction:
Join the points A and D to form the triangle $\triangle APD$.
Proof:
Let P be the point of intersection of the chords AB and CD.
It is given that the chords are perpendicular, so in the triangle $\triangle APD$, we have:
$\angle APD = 90^\circ$
(Given)
By the angle sum property of a triangle, the sum of the interior angles of $\triangle APD$ is $180^\circ$.
$\angle PAD + \angle PDA + \angle APD = 180^\circ$
Substituting the value of $\angle APD$:
$\angle PAD + \angle PDA + 90^\circ = 180^\circ$
$\Rightarrow \angle PAD + \angle PDA = 180^\circ - 90^\circ$
$\angle PAD + \angle PDA = 90^\circ$
... (i)
We know that the measure of an arc is twice the angle subtended by it at any point on the remaining part of the circle.
The inscribed angle $\angle PDA$ (which is the same as $\angle CDA$) is subtended by the arc CXA.
Therefore, $m(\text{arc CXA}) = 2 \times \angle PDA$
The inscribed angle $\angle PAD$ (which is the same as $\angle DAB$) is subtended by the arc DZB.
Therefore, $m(\text{arc DZB}) = 2 \times \angle PAD$
Now, let's find the sum of the measures of these two arcs:
$m(\text{arc CXA}) + m(\text{arc DZB}) = (2 \times \angle PDA) + (2 \times \angle PAD)$
$m(\text{arc CXA}) + m(\text{arc DZB}) = 2(\angle PDA + \angle PAD)$
Using the result from equation (i):
$m(\text{arc CXA}) + m(\text{arc DZB}) = 2(90^\circ) = 180^\circ$
An arc measure of $180^\circ$ corresponds to a semicircle.
Hence, arc CXA + arc DZB = semicircle.
The sum of all four arcs makes up the complete circle, which has a measure of $360^\circ$ (or two semicircles).
(arc CXA + arc DZB) + (arc AYD + arc BWC) = Full Circle
Since we have proved that (arc CXA + arc DZB) is a semicircle, the sum of the remaining two arcs must also be a semicircle.
semicircle + (arc AYD + arc BWC) = 2 semicircles
Hence, arc AYD + arc BWC = semicircle.
Thus, it is proved that arc CXA + arc DZB = arc AYD + arc BWC = semicircle.
Question 7. If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Answer:
Given:
An equilateral triangle ABC is inscribed in a circle.
P is any point on the minor arc BC, where P is not the same as B or C.
To Prove:
PA is the angle bisector of the angle $\angle BPC$.
That is, we need to prove that $\angle BPA = \angle CPA$.
Construction:
Join the points P to A, P to B, and P to C.
Proof:
It is given that the triangle ABC is an equilateral triangle.
Therefore, all the sides of the triangle are equal in length.
$AB = BC = CA$
[Sides of an equilateral triangle]
These sides of the triangle are also chords of the circumscribed circle.
We know the theorem: "Equal chords of a circle subtend equal angles at any point on the remaining part of the circle."
Now, let's consider the equal chords AB and AC.
AB = AC
[Proved above]
The chord AB subtends the angle $\angle APB$ at point P on the circumference.
The chord AC subtends the angle $\angle APC$ at the same point P on the circumference.
Since the chords AB and AC are equal, the angles they subtend at point P must also be equal.
Therefore, we can conclude that:
$\angle APB = \angle APC$
This shows that the line segment PA divides the angle $\angle BPC$ into two equal angles.
Thus, PA is the angle bisector of $\angle BPC$.
Hence, proved.
Question 8. In Fig. 10.19, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = $\frac{1}{2}$ (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre)
Answer:
Given:
In the given figure, AB and CD are two chords of a circle with centre O, intersecting each other at point E.
To Prove:
$\angle AEC = \frac{1}{2}$ (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre)
In other words, we need to prove that $\angle AEC = \frac{1}{2}(\angle AOC + \angle BOD)$.
Construction:
Join the points A and D to form the line segment AD.
Proof:
Let's consider the triangle $\triangle ADE$.
The angle $\angle AEC$ is an exterior angle to the triangle $\triangle ADE$ when the side DE is extended to C.
By the Exterior Angle Theorem of a triangle, an exterior angle is equal to the sum of the two opposite interior angles.
Therefore, we can write:
$\angle AEC = \angle DAE + \angle ADE$
... (i)
Now, we will use the theorem: "The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle."
The inscribed angle $\angle DAE$ (which is the same as $\angle DAB$) is subtended by the arc DYB. The angle subtended by this arc at the centre is $\angle BOD$.
Therefore, according to the theorem:
$\angle DAE = \frac{1}{2}\angle BOD$
... (ii)
Similarly, the inscribed angle $\angle ADE$ (which is the same as $\angle ADC$) is subtended by the arc CXA. The angle subtended by this arc at the centre is $\angle AOC$.
Therefore, according to the same theorem:
$\angle ADE = \frac{1}{2}\angle AOC$
... (iii)
Now, substitute the expressions for $\angle DAE$ and $\angle ADE$ from equations (ii) and (iii) into equation (i):
$\angle AEC = \left(\frac{1}{2}\angle BOD\right) + \left(\frac{1}{2}\angle AOC\right)$
Taking $\frac{1}{2}$ as a common factor, we get:
$\angle AEC = \frac{1}{2}(\angle BOD + \angle AOC)$
Rearranging the terms inside the bracket:
$\angle AEC = \frac{1}{2}(\angle AOC + \angle BOD)$
This proves that $\angle AEC = \frac{1}{2}$ (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).
Hence, proved.
Question 9. If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
Answer:
Given:
A cyclic quadrilateral ABCD.
The bisector of angle $\angle A$ intersects the circumscribing circle at point P.
The bisector of angle $\angle C$ intersects the circumscribing circle at point Q.
To Prove:
The line segment PQ is a diameter of the circle.
Construction:
Draw the cyclic quadrilateral ABCD and its circumscribing circle. Draw the angle bisectors AP and CQ intersecting the circle at P and Q respectively. Join the points P and Q.
Proof:
To prove that PQ is a diameter, we need to show that the arc PAQ or the arc PDQ is a semicircle, which means its measure is $180^\circ$.
Since AP is the bisector of angle $\angle A$, we have:
$\angle DAP = \frac{1}{2} \angle DAB$
... (i)
Similarly, since CQ is the bisector of angle $\angle C$, we have:
$\angle DCQ = \frac{1}{2} \angle DCB$
... (ii)
We know that the measure of an arc of a circle is twice the measure of the inscribed angle that subtends it.
The inscribed angle $\angle DAP$ subtends the arc DP at the circumference.
Therefore, $m(\text{arc DP}) = 2 \times \angle DAP$
Using equation (i), we get:
$m(\text{arc DP}) = 2 \times \left(\frac{1}{2} \angle DAB\right) = \angle DAB$
... (iii)
Similarly, the inscribed angle $\angle DCQ$ subtends the arc DQ at the circumference.
Therefore, $m(\text{arc DQ}) = 2 \times \angle DCQ$
Using equation (ii), we get:
$m(\text{arc DQ}) = 2 \times \left(\frac{1}{2} \angle DCB\right) = \angle DCB$
... (iv)
Now, let's consider the measure of the arc PDQ. It is the sum of the measures of arc PD and arc DQ.
$m(\text{arc PDQ}) = m(\text{arc PD}) + m(\text{arc DQ})$
Substituting the values from equations (iii) and (iv):
$m(\text{arc PDQ}) = \angle DAB + \angle DCB$
Since ABCD is a cyclic quadrilateral, the sum of its opposite angles is $180^\circ$.
$\angle DAB + \angle DCB = 180^\circ$
Therefore, the measure of the arc PDQ is:
$m(\text{arc PDQ}) = 180^\circ$
An arc that measures $180^\circ$ is a semicircle.
Since arc PDQ is a semicircle, the chord joining its endpoints P and Q must be a diameter of the circle.
Hence, it is proved that PQ is a diameter of the circle.
Question 10. A circle has radius $\sqrt{2}$ cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45º.
Answer:
Given:
A circle with radius, $r = \sqrt{2}$ cm.
A chord of length 2 cm, let's call it AB.
To Prove:
The angle subtended by the chord at a point in the major segment is $45^\circ$.
Construction:
Let O be the centre of the circle. Join the endpoints of the chord, A and B, to the centre O. This forms the triangle $\triangle AOB$.
Proof:
Our strategy is to first find the angle subtended by the chord AB at the centre of the circle ($\angle AOB$) and then use it to find the angle subtended at a point on the major segment.
Let's consider the triangle $\triangle AOB$. The lengths of its sides are:
$OA = \sqrt{2}$ cm
[Radius of the circle]
$OB = \sqrt{2}$ cm
[Radius of the circle]
$AB = 2$ cm
(Given)
Now, let's check if the triangle satisfies the Pythagorean theorem. We calculate the sum of the squares of the two smaller sides:
$OA^2 + OB^2 = (\sqrt{2})^2 + (\sqrt{2})^2$
$OA^2 + OB^2 = 2 + 2 = 4$
Now, we calculate the square of the longest side:
$AB^2 = (2)^2 = 4$
Since we found that $OA^2 + OB^2 = AB^2$, by the converse of the Pythagorean theorem, the triangle $\triangle AOB$ is a right-angled triangle, with the right angle at the vertex O.
Therefore, the angle subtended by the chord AB at the centre is:
$\angle AOB = 90^\circ$
Now, let P be any point on the major segment of the circle. We need to find the angle subtended by the chord AB at this point, which is $\angle APB$.
We know the theorem: "The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle."
Applying this theorem, we get:
$\angle AOB = 2 \times \angle APB$
Substituting the value of $\angle AOB$ we found:
$90^\circ = 2 \times \angle APB$
$\Rightarrow \angle APB = \frac{90^\circ}{2}$
$\Rightarrow \angle APB = 45^\circ$
Hence, it is proved that the angle subtended by the chord at a point in the major segment is $45^\circ$.
Question 11. Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD.
Answer:
Given:
A circle with centre O.
Two equal chords, AB and CD, which when produced, intersect at an external point P.
$AB = CD$
To Prove:
$PB = PD$.
Construction:
From the centre O, draw perpendiculars to the lines containing the chords AB and CD. Let these be OM and ON respectively, so that $OM \perp AP$ and $ON \perp CP$.
Join the point of intersection P to the centre O.
Proof:
We are given that the chords are equal in length.
$AB = CD$
(Given)
We know the theorem: "Equal chords of a circle are equidistant from the centre."
Therefore, the perpendicular distances from the centre to these chords are equal.
$OM = ON$
... (i)
Now, let's consider the right-angled triangles $\triangle OMP$ and $\triangle ONP$.
$OM = ON$
[From equation (i)]
$OP = OP$
[Common hypotenuse]
$\angle OMP = \angle ONP$
[Each $90^\circ$, by construction]
By the Right angle-Hypotenuse-Side (RHS) congruence criterion, we have:
$\triangle OMP \cong \triangle ONP$
By the property of Corresponding Parts of Congruent Triangles are Corresponding (CPCTC), we get:
$PM = PN$
... (ii)
We also know that the perpendicular from the centre of a circle to a chord bisects the chord.
So, $AM = MB = \frac{1}{2}AB$
And, $CN = ND = \frac{1}{2}CD$
Since it is given that $AB = CD$, their halves must also be equal.
$MB = ND$
... (iii)
From the figure, we can express PB as:
$PB = PM - MB$
And PD as:
$PD = PN - ND$
Since we have proved that $PM = PN$ (from equation ii) and $MB = ND$ (from equation iii), we can subtract the equal quantities from the equal quantities.
$PM - MB = PN - ND$
Therefore, $PB = PD$.
Hence, proved.
Alternate Solution:
We can prove this result using the Power of a Point Theorem (also known as the Tangent-Secant Theorem for two secants from an external point).
The theorem states that if two secant lines are drawn from a point P outside a circle, intersecting the circle at points A, B, C, and D, then the following relationship holds:
$PA \times PB = PC \times PD$
From the figure, we can express the lengths PA and PC as:
$PA = PB + AB$
$PC = PD + CD$
Substituting these expressions into the theorem's equation:
$(PB + AB) \times PB = (PD + CD) \times PD$
We are given that the chords are equal in length, $AB = CD$.
Let's substitute CD with AB in the equation:
$(PB + AB) \times PB = (PD + AB) \times PD$
Expanding both sides of the equation:
$(PB)^2 + AB \cdot PB = (PD)^2 + AB \cdot PD$
Rearranging the terms to one side:
$(PB)^2 - (PD)^2 + AB \cdot PB - AB \cdot PD = 0$
Factoring the terms:
$(PB - PD)(PB + PD) + AB(PB - PD) = 0$
Taking out the common factor $(PB - PD)$:
$(PB - PD)(PB + PD + AB) = 0$
Since PB, PD, and AB are all lengths, their sum $(PB + PD + AB)$ must be a positive value and cannot be equal to zero.
Therefore, for the product of the two factors to be zero, the other factor must be zero.
$PB - PD = 0$
$\Rightarrow PB = PD$
Hence, proved.
Question 12. AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2 .
Answer:
Given:
A circle with centre O and radius r.
AB and AC are two chords of the circle such that $AB = 2AC$.
The distance of chord AB from the centre O is $p$.
The distance of chord AC from the centre O is $q$.
To Prove:
$4q^2 = p^2 + 3r^2$.
Construction:
Draw a perpendicular from the centre O to the chord AB at point M. So, $OM = p$.
Draw a perpendicular from the centre O to the chord AC at point N. So, $ON = q$.
Join the point A to the centre O. So, $OA = r$.
Proof:
We know that the perpendicular from the centre of a circle to a chord bisects the chord.
Since $OM \perp AB$, M is the midpoint of AB. Therefore,
$AM = \frac{1}{2}AB$
Now, consider the right-angled triangle $\triangle OMA$. By the Pythagorean theorem, we have:
$OA^2 = OM^2 + AM^2$
$r^2 = p^2 + \left(\frac{1}{2}AB\right)^2$
$r^2 = p^2 + \frac{AB^2}{4}$
Multiplying the entire equation by 4, we get:
$4r^2 = 4p^2 + AB^2$
Rearranging the terms to find an expression for $AB^2$:
$AB^2 = 4r^2 - 4p^2 = 4(r^2 - p^2)$
... (i)
Similarly, since $ON \perp AC$, N is the midpoint of AC. Therefore,
$AN = \frac{1}{2}AC$
Now, consider the right-angled triangle $\triangle ONA$. By the Pythagorean theorem, we have:
$OA^2 = ON^2 + AN^2$
$r^2 = q^2 + \left(\frac{1}{2}AC\right)^2$
$r^2 = q^2 + \frac{AC^2}{4}$
Multiplying the entire equation by 4, we get:
$4r^2 = 4q^2 + AC^2$
Rearranging the terms to find an expression for $AC^2$:
$AC^2 = 4r^2 - 4q^2 = 4(r^2 - q^2)$
... (ii)
We are given the relationship between the lengths of the chords:
$AB = 2AC$
(Given)
Squaring both sides of this equation, we get:
$AB^2 = 4AC^2$
... (iii)
Now, substitute the expressions for $AB^2$ from equation (i) and $AC^2$ from equation (ii) into equation (iii):
$4(r^2 - p^2) = 4 \times [4(r^2 - q^2)]$
$4(r^2 - p^2) = 16(r^2 - q^2)$
Divide both sides by 4:
$r^2 - p^2 = 4(r^2 - q^2)$
$r^2 - p^2 = 4r^2 - 4q^2$
Rearranging the terms to bring $4q^2$ to the left side and other terms to the right side:
$4q^2 = 4r^2 - r^2 + p^2$
$4q^2 = 3r^2 + p^2$
Or, writing it in the required format:
$4q^2 = p^2 + 3r^2$
Hence, proved.
Question 13. In Fig. 10.20, O is the centre of the circle, ∠BCO = 30°. Find x and y.
Answer:
Given:
In the given figure, O is the centre of the circle.
From the figure markings, we can infer the following:
1. The line from O is perpendicular to the chord BC. Let's call the intersection point M. So, $OM \perp BC$.
2. The line segment OD is perpendicular to the line segment AO. This means $\angle AOD = 90^\circ$.
3. $\angle BCO = 30^\circ$.
To Find:
The values of x and y, where $x = \angle OAB$ and $y = \angle CBD$.
Solution:
Finding the value of x:
First, consider the triangle $\triangle OAC$.
OA = OC
[Radii of the same circle]
Since $\triangle OAC$ has two equal sides, it is an isosceles triangle. Therefore, the angles opposite to the equal sides are equal.
$\angle OAC = \angle OCA$
Given that $\angle OCA$ (same as $\angle BCO$) is $30^\circ$, we have:
$\angle OAC = 30^\circ$
... (i)
Now, consider the triangle $\triangle OBC$.
OB = OC
[Radii of the same circle]
Therefore, $\triangle OBC$ is also an isosceles triangle. This means $\angle OBC = \angle OCB = 30^\circ$.
By the angle sum property of a triangle, in $\triangle OBC$:
$\angle BOC = 180^\circ - (\angle OBC + \angle OCB)$
$\angle BOC = 180^\circ - (30^\circ + 30^\circ) = 180^\circ - 60^\circ = 120^\circ$
The angle subtended by the arc BC at the centre is $\angle BOC = 120^\circ$. The angle subtended by the same arc at the circumference is $\angle BAC$.
$\angle BAC = \frac{1}{2}\angle BOC = \frac{1}{2}(120^\circ) = 60^\circ$
From the figure, we can see that $\angle BAC = \angle OAB + \angle OAC$.
Substituting the known values:
$60^\circ = x + 30^\circ$
$\Rightarrow x = 60^\circ - 30^\circ$
$\Rightarrow x = 30^\circ$
Finding the value of y:
We know that angles subtended by the same arc at any point on the remaining part of the circle are equal.
The angles $\angle CBD$ (which is y) and $\angle CAD$ are both subtended by the arc CD.
Therefore, $y = \angle CAD$.
Now, we need to find the measure of $\angle CAD$. From the given information, we have $\angle AOD = 90^\circ$.
Consider the triangle $\triangle AOD$.
OA = OD
[Radii of the same circle]
Since $\triangle AOD$ is an isosceles triangle with $\angle AOD = 90^\circ$, the other two angles are equal.
By the angle sum property of a triangle:
$\angle OAD = \angle ODA = \frac{180^\circ - 90^\circ}{2} = \frac{90^\circ}{2} = 45^\circ$
From the figure, we can see that $\angle OAD = \angle OAC + \angle CAD$.
Substituting the known values:
$45^\circ = 30^\circ + \angle CAD$
$\Rightarrow \angle CAD = 45^\circ - 30^\circ = 15^\circ$
Since $y = \angle CAD$, we have:
$y = 15^\circ$
Hence, the required values are $x = 30^\circ$ and $y = 15^\circ$.
Question 14. In Fig. 10.21, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.

Answer:
Given:
In the given figure, O is the centre of the circle.
From the figure, it is clear that AB is a diameter passing through the centre O.
It is given that the length of the chord BD is equal to the length of the radius OD, i.e., $BD = OD$.
The chord CD is perpendicular to the diameter AB, i.e., $CD \perp AB$.
To Find:
The measure of the angle $\angle CAB$.
Solution:
Let's consider the triangle $\triangle OBD$.
The sides OB and OD are both radii of the same circle.
OB = OD
[Radii of the same circle]
It is given that the chord BD is equal to the radius OD.
BD = OD
(Given)
From the above two relations, we can conclude that all three sides of the triangle $\triangle OBD$ are equal.
$OB = OD = BD$
Therefore, $\triangle OBD$ is an equilateral triangle.
We know that all angles in an equilateral triangle are equal to $60^\circ$.
So, the angle at vertex B is:
$\angle OBD = 60^\circ$
The angle $\angle OBD$ is the same as the angle $\angle CBA$.
Therefore, $\angle CBA = 60^\circ$.
Now, it is given that AB is a diameter of the circle.
We know the theorem: "The angle in a semicircle is a right angle."
The angle subtended by the diameter AB at any point on the circumference is $90^\circ$. Therefore, the angle at point C is:
$\angle ACB = 90^\circ$
[Angle in a semicircle]
Now, let's consider the triangle $\triangle ACB$.
By the angle sum property of a triangle, the sum of all its interior angles is $180^\circ$.
$\angle CAB + \angle CBA + \angle ACB = 180^\circ$
Substituting the values we have found:
$\angle CAB + 60^\circ + 90^\circ = 180^\circ$
$\Rightarrow \angle CAB + 150^\circ = 180^\circ$
$\Rightarrow \angle CAB = 180^\circ - 150^\circ$
$\Rightarrow \angle CAB = 30^\circ$
Hence, the measure of $\angle CAB$ is $30^\circ$.

