| Classwise Concept with Examples | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 1 Knowing Our Numbers (Concepts)
Welcome to this exciting exploration of Chapter 1: Knowing Our Numbers! Numbers are all around us, from counting toys to measuring distances and understanding time. But have you ever thought about numbers that are really, really big? This chapter is our starting point for understanding the amazing world of numbers, especially those large numbers that help us describe huge quantities, like the population of a country or the distance to the stars. We will learn how to confidently handle these large numbers, understand their value, estimate calculations, and even explore an ancient system of writing numbers. Think of this chapter as building a strong foundation for all the exciting mathematics you will learn in the future. It's about becoming comfortable and confident with numbers, no matter how big or small.
Our first adventure will be into the realm of large numbers. We often use numbers like 10, 100, or 1000, but what happens when we need to talk about thousands of thousands, or even more? We will introduce Indian units like Lakhs and Crores, which are commonly used to talk about large quantities in India. Alongside this, we will explore the International System of Numeration, using terms like Millions and Billions, which are used globally. You'll learn not just how to read and write these large numbers accurately, but also crucial skills like comparing them to see which is bigger or smaller, and how to form the greatest or smallest possible number using a given set of digits. This will help us make sense of large figures we encounter in news, books, and everyday discussions.
Understanding large numbers goes hand-in-hand with understanding Place Value. The position of a digit in a number dramatically changes its value – a '7' in the tens place means 70, but in the thousands place, it means 7000! We will dive deep into the place value chart for both the Indian System and the International System. This knowledge is key to correctly reading numbers, writing them in expanded form (like $345 = 300 + 40 + 5$), and using commas appropriately to make large numbers easier to read and comprehend according to standard conventions in both systems.
Sometimes, we don't need an exact answer, but a good guess or estimate is enough. This chapter introduces the practical skill of Estimation through Rounding Off. We will learn systematic ways to round numbers off to the nearest tens, hundreds, thousands, and beyond. Why is this useful? Estimation helps us make quick mental calculations and check if our exact answers are reasonable. We'll practice estimating sums, differences, and products in various real-life situations, showing how rounding off can simplify calculations significantly while still providing a useful approximate result.
To ensure calculations are done correctly, especially when multiple operations are involved, we use Brackets. You might have seen expressions like $(2+3) \times 4$. Brackets tell us the order in which operations must be performed, ensuring everyone gets the same answer. We will learn the rules for using brackets and practice simplifying numerical expressions involving them. Finally, we'll take a fascinating look back in time at Roman Numerals. We will learn the basic symbols used by the ancient Romans – I (1), V (5), X (10), L (50), C (100), D (500), M (1000) – and the rules for combining them to form numbers. You'll practice converting numbers between the familiar Hindu-Arabic system and the Roman numeral system.
Natural Numbers
In mathematics, when we talk about counting things like apples, books, or students, we use numbers like 1, 2, 3, 4, and so on. These are the numbers we use in our everyday life for counting. These counting numbers are called Natural Numbers.
The term "natural numbers" comes from the fact that they are the numbers that arise naturally from the act of counting.
So, the collection of natural numbers starts with 1 and continues indefinitely (never ends). Every natural number is followed by a unique next natural number which is one greater than the previous one.
The set of natural numbers is usually denoted by the symbol $\mathbb{N}$ or $\mathbf{N}$.
$\mathbb{N} = \{1, 2, 3, 4, 5, 6, ...\}$
Smallest Natural Number
By definition, the natural numbers begin with 1. Therefore, the smallest natural number is 1.
Largest Natural Number
There is no largest natural number. For any natural number you can think of, no matter how big, you can always find a larger natural number by simply adding 1 to it (e.g., if you think of 1000, 1000 + 1 = 1001 is a larger natural number). Natural numbers form an infinite set, meaning they go on endlessly without a limit.
Indian System of Numeration
The Indian System of Numeration, also known as the Indo-Arabic System, is a numerical system widely used in India, Pakistan, Bangladesh, and Nepal. This system organises digits of a number into groups called periods to make reading and writing large numbers easier. These periods are based on powers of 10, but the grouping pattern differs from the International System, especially for larger numbers.
In this system, the places for digits from right to left are arranged as: Ones, Tens, Hundreds, Thousands, Ten Thousands, Lakhs, Ten Lakhs, Crores, Ten Crores, Arab, Ten Arab, and so on.
Basic Concepts: Numerals, Numeration, Place Value and Face Value
Numerals and Numeration
- Digits: The symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 are called digits.
- Numeral: A numeral is a symbol or a group of symbols (digits) that represents a number. For example, '7', '45', and '913' are numerals.
- Numeration: Numeration is the method of expressing a number in words. For example, writing '45' as "Forty-five" is numeration.
Face Value and Place Value
Every digit in a numeral has two kinds of values: a face value and a place value.
- Face Value: The face value of a digit is the value of the digit itself, regardless of its position in the number. The face value of '8' in the number 5,834 is simply 8.
- Place Value: The place value of a digit is its value determined by its position or place within the number. It is calculated as:
Place Value = Face Value × Value of the Place
Example 1. Find the face value and place value of each digit in the number 9,47,235.
Answer:
| Digit | Face Value | Place in the Number | Value of the Place | Place Value (Face Value × Value of Place) |
|---|---|---|---|---|
| 5 | 5 | Ones | 1 | $5 \times 1 = 5$ |
| 3 | 3 | Tens | 10 | $3 \times 10 = 30$ |
| 2 | 2 | Hundreds | 100 | $2 \times 100 = 200$ |
| 7 | 7 | Thousands | 1,000 | $7 \times 1,000 = 7,000$ |
| 4 | 4 | Ten Thousands | 10,000 | $4 \times 10,000 = 40,000$ |
| 9 | 9 | Lakhs | 1,00,000 | $9 \times 1,00,000 = 9,00,000$ |
Place Value Chart (Indian System)
The place value of a digit in a number is the value of the place it occupies in the place value chart. As we move from right to left in the place value chart, the place value of each position becomes ten times the place value of the position to its immediate right.
The place values, starting from the rightmost digit, are:
Ones (or Units), Tens, Hundreds, Thousands, Ten Thousands, Lakhs, Ten Lakhs, Crores, Ten Crores, etc.
The value of these places are 1, 10, 100, 1,000, 10,000, 1,00,000, 10,00,000, 1,00,00,000, 10,00,00,000, and so on, respectively.
Periods (Indian System)
To read large numbers conveniently, the place values are grouped into periods in the Indian System. These periods help in chunking the number into readable parts. The grouping is done from right to left.
- The first period is the Ones period. It consists of the first three place values from the right: Ones, Tens, and Hundreds.
- The second period is the Thousands period. It consists of the next two place values: Thousands and Ten Thousands.
- The third period is the Lakhs period. It consists of the next two place values: Lakhs and Ten Lakhs.
- The fourth period is the Crores period. It consists of the next two place values: Crores and Ten Crores.
- Subsequent periods (Arab, Ten Arab, etc.) also consist of two place values each.
The use of periods simplifies the process of reading and writing large numbers.
Using Commas (Indian System)
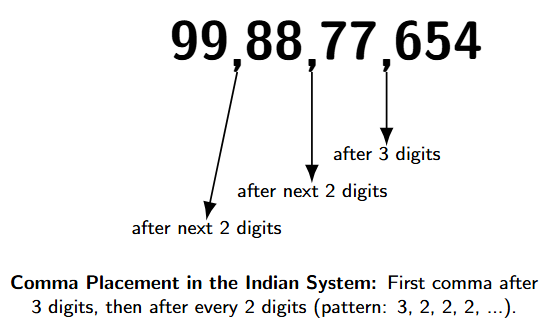
Commas (,) are used to separate the periods in a number written in the Indian System. This helps in identifying the periods easily and makes the number readable. The commas are placed from the right side of the number.
- The first comma is placed after the first period (Ones period), which means after the Hundreds place (3 digits from the right).
- The second comma is placed after the second period (Thousands period), which is after the Ten Thousands place (2 digits after the first comma, or 5 digits from the right).
- The third comma is placed after the third period (Lakhs period), which is after the Ten Lakhs place (2 digits after the second comma, or 7 digits from the right).
- This pattern of placing commas continues, with a comma after every two digits for the subsequent periods (Lakhs, Crores, Arab, etc.). The pattern of comma placement from the right is $3, 2, 2, 2, ...$
How to Read and Write Numbers
To read a number:
- First, place commas from the right according to the 3, 2, 2... pattern.
- Read the digits in each period together (from left to right).
- After reading the number in a period, say the name of that period (e.g., "Crore", "Lakh", "Thousand").
- Do not say the name of the Ones period.
Table: Indian Place Value Chart
| Period | Place Value | Value |
|---|---|---|
| Crores | Ten Crores | $10,00,00,000$ |
| Crores | $1,00,00,000$ | |
| Lakhs | Ten Lakhs | $10,00,000$ |
| Lakhs | $1,00,000$ | |
| Thousands | Ten Thousands | $10,000$ |
| Thousands | $1,000$ | |
| Ones | Hundreds | $100$ |
| Tens | $10$ | |
| Ones | $1$ |
Example 2. Write the number 78921092 in the Indian System using commas and write its number name.
Answer:
Let's place the digits in the Indian place value chart from right to left:
$7 \quad 8 \quad 9 \quad 2 \quad 1 \quad 0 \quad 9 \quad 2$
Crores Lakhs Thousands Ones
Ten Crores Crores Ten Lakhs Lakhs Ten Thousands Thousands Hundreds Tens Ones
To use commas, we group the digits into periods:
- Ones period (first 3 digits from right): 092
- Thousands period (next 2 digits): 21
- Lakhs period (next 2 digits): 89
- Crores period (remaining digit): 7
Placing commas according to the periods (after 3, 2, 2 digits from the right):
The number is written as $7,89,21,092$.
Now, let's write the number name by reading the number in each period followed by the period name (except for the Ones period):
- Crores period: 7 $\to$ Seven crore
- Lakhs period: 89 $\to$ Eighty-nine lakh
- Thousands period: 21 $\to$ Twenty-one thousand
- Ones period: 092 $\to$ Ninety-two (We read 092 as ninety-two)
Combining these, the number name is: Seven crore eighty-nine lakh twenty-one thousand ninety-two.
Example 3. Write the number name "Nine crore five lakh forty-one" as a numeral in the Indian System.
Answer:
Let's identify the digits for each period based on the number name:
- "Nine crore": This means 9 is in the Crores period. Since the Crores period has two places (Ten Crores and Crores), and only 'nine' is mentioned, it corresponds to 9 in the Crores place. So the Crores period is $09$.
- "five lakh": This means 5 is in the Lakhs period. The Lakhs period also has two places (Ten Lakhs and Lakhs). 'Five lakh' means 0 in the Ten Lakhs place and 5 in the Lakhs place. So the Lakhs period is $05$.
- The name does not mention 'Thousands'. The Thousands period has two places (Ten Thousands and Thousands). Since it's not mentioned, we put 00 in the Thousands period.
- "forty-one": This is the value in the Ones period (Hundreds, Tens, Ones). Forty-one is written as $041$. The Ones period always has three places.
Now, let's arrange the digits for each period from left to right (Crores, Lakhs, Thousands, Ones) and place the commas:
Crores period: $09$
Lakhs period: $05$
Thousands period: $00$
Ones period: $041$
Combining the digits: $090500041$.
Placing commas (after 3 digits, then 2, then 2 from the right): $9,05,00,041$. The leading zero in the crores period is usually dropped unless it is the only digit.
The numeral for "Nine crore five lakh forty-one" is $9,05,00,041$.
International System of Numeration
The International System of Numeration is a system used globally to read and write large numbers. In this system, digits are grouped into periods, typically consisting of three places each.
Place Value Chart (International System)
In the International System, the place values are arranged from right to left, increasing in value. The place values are:
Ones, Tens, Hundreds, Thousands, Ten Thousands, Hundred Thousands, Millions, Ten Millions, Hundred Millions, Billions, Ten Billions, Hundred Billions, and so on.
Periods (International System)
The place values are grouped into periods to make large numbers easier to read. Each period in the International System consists of three place values. The periods are:
- The first period is the Ones period. It includes the Ones, Tens, and Hundreds places.
- The second period is the Thousands period. It includes the Thousands, Ten Thousands, and Hundred Thousands places.
- The third period is the Millions period. It includes the Millions, Ten Millions, and Hundred Millions places.
- The fourth period is the Billions period. It includes the Billions, Ten Billions, and Hundred Billions places, and so on for Trillions, Quadrillions, etc.
A key feature of the International System is that each period consistently contains three place values.
Using Commas (International System)
To read numbers conveniently in the International System, commas are used to separate the periods.
Commas are inserted after every three digits, starting from the rightmost digit (the Ones place).
- The first comma comes after the Hundreds place, marking the end of the Ones period (after the $3^\text{rd}$ digit from the right).
- The second comma comes after the Hundred Thousands place, marking the end of the Thousands period (after the $6^\text{th}$ digit from the right, or $3$ digits after the first comma).
- The third comma comes after the Hundred Millions place, marking the end of the Millions period (after the $9^\text{th}$ digit from the right, or $3$ digits after the second comma), and so on.
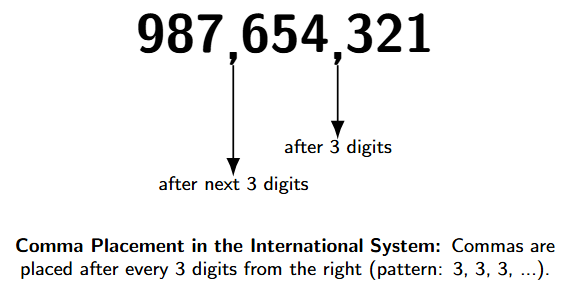
Table: International Place Value Chart
| Period | Place Value | Value |
|---|---|---|
| Billions | Hundred Billions | $100,000,000,000$ |
| Ten Billions | $10,000,000,000$ | |
| Billions | $1,000,000,000$ | |
| Millions | Hundred Millions | $100,000,000$ |
| Ten Millions | $10,000,000$ | |
| Millions | $1,000,000$ | |
| Thousands | Hundred Thousands | $100,000$ |
| Ten Thousands | $10,000$ | |
| Thousands | $1,000$ | |
| Ones | Hundreds | $100$ |
| Tens | $10$ | |
| Ones | $1$ |
How to Read and Write Numbers
To read a number:
- First, place commas after every three digits, starting from the right.
- Read the three-digit number in each period together (from left to right).
- After reading the number in a period, say the name of that period (e.g., "Billion", "Million", "Thousand").
- Do not say the name of the Ones period.
Example 1. Write the number $78921092$ in the International System using commas and write its number name.
Answer:
Step 1: Write the numeral and place commas from the right.
$78921092$
- Place the first comma after 3 digits: $78921,092$
- Place the second comma after the next 3 digits: $78,921,092$
Step 2: Identify the periods.
$$\underbrace{78}_{\text{Millions}} , \underbrace{921}_{\text{Thousands}} , \underbrace{092}_{\text{Ones}}$$
Step 3: Read each period and write the number name.
- 78 in Millions period $\to$ Seventy-eight million
- 921 in Thousands period $\to$ Nine hundred twenty-one thousand
- 092 in Ones period $\to$ Ninety-two
Combining these, the number name is: Seventy-eight million nine hundred twenty-one thousand ninety-two.
Example 2. Write the numeral for "Five hundred eighty-two million six hundred three thousand nine".
Answer:
Step 1: Set up the period slots with commas.
$$\underbrace{ \_ \ \_ \ \_}_{\text{Millions}} , \underbrace{ \_ \ \_ \ \_}_{\text{Thousands}} , \underbrace{\_ \ \_ \ \_}_{\text{Ones}}$$
Step 2: Fill in the three slots for each period mentioned.
- "Five hundred eighty-two million": Fill the Millions period with 582.
- "six hundred three thousand": Fill the Thousands period with 603.
- "nine": This is the Ones period. We must use three digits, so we write it as 009.
Step 3: Combine the digits.
$$\underline{5} \ \underline{8} \ \underline{2} , \underline{6} \ \underline{0} \ \underline{3} , \underline{0} \ \underline{0} \ \underline{9}$$
The numeral is $582,603,009$.
Comparing Indian and International Systems
The main difference between the two systems appears after the Ten Thousands place. The Indian system introduces Lakhs and Crores, while the International system continues with Hundred Thousands and then Millions.
| Numeral | Indian System Name | International System Name |
|---|---|---|
| $1,00,000$ | 1 Lakh | 100 Thousand |
| $10,00,000$ | 10 Lakh | 1 Million |
| $1,00,00,000$ | 1 Crore | 10 Million |
| $10,00,00,000$ | 10 Crore | 100 Million |
| $1,00,00,00,000$ | 1 Arab | 1 Billion |
Comparison of Numbers
Comparing numbers means determining which number is larger, which is smaller, or if they are equal in value. We use comparison symbols:
- $>$ (greater than)
- $<$ (less than)
- $=$ (equal to)
Rule 1: Comparing numbers with different number of digits
The simplest way to compare numbers is by looking at the number of digits they have. The number with more digits is always greater than a number with fewer digits.
For example, let's compare $456$ and $1234$.
$456$ has $3$ digits.
$1234$ has $4$ digits.
Since $1234$ has more digits ($4$) than $456$ ($3$), $1234$ is greater than $456$.
We write this as: $1234 > 456$.
Rule 2: Comparing numbers with the same number of digits
When two numbers have the same number of digits, we need to compare their digits starting from the leftmost place value (the highest place value).
Follow these steps:
- Start comparing the digits at the leftmost (highest) place value.
- If the digits at this place are different, the number with the larger digit is the greater number.
- If the digits at the leftmost place are the same, move to the next place value to the right and compare those digits.
- Continue this process digit by digit from left to right until you find a pair of digits that are different. The number with the larger digit at that specific place value is the greater number.
- If all the digits in both numbers are the same, then the numbers are equal.
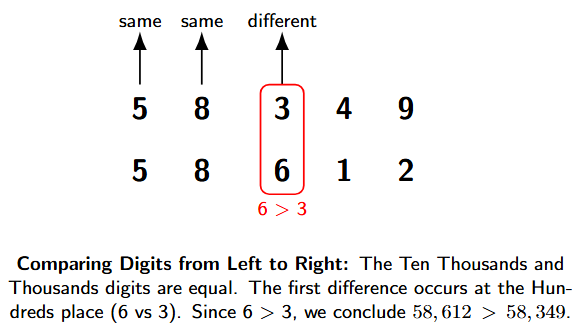
Example 1. Compare $87,654$ and $87,591$. Use the symbols $>$ or $<$.
Answer:
Both numbers have 5 digits. We will compare them from left to right.
| Place | $87,654$ | $87,591$ | Comparison |
|---|---|---|---|
| Ten Thousands | 8 | 8 | Same |
| Thousands | 7 | 7 | Same |
| Hundreds | 6 | 5 | Different ($6 > 5$) |
| Tens | 5 | 9 | - |
| Ones | 4 | 1 | - |
The first point of difference is in the hundreds place. Since $6$ is greater than $5$, the first number is greater.
So, $87,654 > 87,591$.
Example 2. Arrange the following numbers in ascending order (smallest to largest): $345$, $1,234$, $99$, $5,000$.
Answer:
Step 1: Compare based on the number of digits.
- $99$ has 2 digits (Smallest).
- $345$ has 3 digits.
- $1,234$ and $5,000$ both have 4 digits (Largest).
Step 2: Order the numbers with different digit counts.
The smallest is $99$, followed by $345$.
Step 3: Compare the numbers with the same number of digits.
We need to compare $1,234$ and $5,000$.
- Compare the leftmost (Thousands) digit: $1$ in $1,234$ and $5$ in $5,000$.
- Since $1 < 5$, we have $1,234 < 5,000$.
Step 4: Combine the results to get the final order.
The ascending order is: $99, 345, 1,234, 5,000$.
Example 3. Arrange the following numbers in descending order (largest to smallest): $7,865$; $7,901$; $7,880$; $7,910$.
Answer:
All four numbers have 4 digits. We will compare them from left to right.
Step 1: Compare the leftmost (Thousands) place.
All numbers have a 7 in the thousands place. So we move to the next place.
Step 2: Compare the Hundreds place.
- $7,865$
- $7,901$
- $7,880$
- $7,910$
The numbers with 9 in the hundreds place ($7,901$ and $7,910$) are greater than the numbers with 8 in the hundreds place ($7,865$ and $7,880$).
Step 3: Compare the larger group ($7,901$ and $7,910$).
- Compare the Tens place: $7,901$ vs $7,910$.
- Since $1 > 0$, we have $7,910 > 7,901$. These are the two largest numbers.
Step 4: Compare the smaller group ($7,865$ and $7,880$).
- Compare the Tens place: $7,865$ vs $7,880$.
- Since $8 > 6$, we have $7,880 > 7,865$.
Step 5: Combine the results for the final descending order.
The descending order is: $7,910, 7,901, 7,880, 7,865$.
Formation of Numbers
Using a given set of digits, we can build different numbers by arranging the digits in various orders. This section explains the simple rules for forming the greatest and the smallest possible numbers from a given set of digits, both with and without repeating them.
Forming Numbers without Repetition
This is the most common type of problem, where each given digit must be used exactly once.
Rule for the Greatest Number
To form the greatest possible number, we want the largest digits in the most valuable places. The rule is to arrange the given digits in descending order (from largest to smallest).
Rule for the Smallest Number
To form the smallest possible number, we want the smallest digits in the most valuable places. The general rule is to arrange the given digits in ascending order (from smallest to largest).
The Special Case of Zero (0)
When forming the smallest number, the digit 0 is a special case. If we place 0 at the beginning of a number, it has no value and reduces the number of digits (e.g., $045$ is a 2-digit number, not a 3-digit number).
To form the smallest N-digit number when 0 is one of the digits:
- Arrange the digits in ascending order.
- Swap the first two digits. (This places the smallest non-zero digit at the beginning and the 0 in the second position).
- The rest of the digits remain in ascending order.
Example 1. Use the digits $4, 9, 2, 7$ to form the greatest and smallest $4$-digit numbers without repetition.
Answer:
The given digits are $4, 9, 2, 7$.
To form the greatest number: Arrange the digits in descending order.
Descending order: $9, 7, 4, 2$.
The greatest number is $9,742$.
To form the smallest number: Arrange the digits in ascending order.
Ascending order: $2, 4, 7, 9$.
The smallest number is $2,479$.
Example 2. Use the digits $5, 0, 8, 3$ to form the greatest and smallest $4$-digit numbers without repetition.
Answer:
The given digits are $5, 0, 8, 3$.
To form the greatest number: Arrange the digits in descending order.
Descending order: $8, 5, 3, 0$.
The greatest number is $8,530$.
To form the smallest number (with a '0'):
- Arrange in ascending order: $0, 3, 5, 8$.
- Since we cannot start with 0 for a 4-digit number, swap the first two digits (0 and 3).
- The new arrangement is: $3, 0, 5, 8$.
The smallest 4-digit number is $3,058$.
Smallest and Greatest N-Digit Numbers
We can also determine the smallest and greatest numbers for a given number of digits in general.
| Number of Digits | Smallest Number | Greatest Number |
|---|---|---|
| 1-digit | 1 (0 is not a natural counting number) | 9 |
| 2-digits | 10 | 99 |
| 3-digits | 100 | 999 |
| 4-digits | 1,000 | 9,999 |
| 5-digits | 10,000 | 99,999 |
Pattern for the smallest N-digit number: The digit 1 followed by (N-1) zeros.
Pattern for the greatest N-digit number: The digit 9 repeated N times.
Forming Numbers with Repetition
If digits can be repeated, the rules are slightly different.
Rule for the Greatest Number
To form the greatest number with repetition, find the largest digit among the given options and use it for all the places.
Rule for the Smallest Number
To form the smallest number with repetition:
- For the leftmost place, use the smallest non-zero digit.
- For all other places, use the absolute smallest digit (which can be 0).
Example 3. Form the greatest and smallest $5$-digit numbers using the digits $2, 8, 0, 7, 4$, allowing repetition of digits.
Answer:
The given digits are $2, 8, 0, 7, 4$.
To form the greatest $5$-digit number:
The largest digit available is 8. Since we can repeat digits, we fill all five places with 8.
The greatest number is $88,888$.
To form the smallest $5$-digit number:
The smallest digit is 0 and the smallest non-zero digit is 2.
- The first (leftmost) place must be the smallest non-zero digit, which is 2.
- The remaining four places should be filled with the absolute smallest digit, which is 0.
The smallest number is $20,000$.
Conversion of Units
In our daily lives, we measure quantities like length, mass (weight), and capacity (volume). Each quantity can be expressed using different units. For instance, we might measure the length of a pencil in centimetres but the distance between cities in kilometres.
Conversion of units is the process of changing a measurement from one unit to another (e.g., metres to centimetres) without changing its actual value. Understanding how to do this is essential for solving practical problems.
The metric system, which includes most of the units we use, is based on powers of 10. This makes conversions straightforward.
The Golden Rule of Conversion
There is a simple rule to remember for all metric conversions:
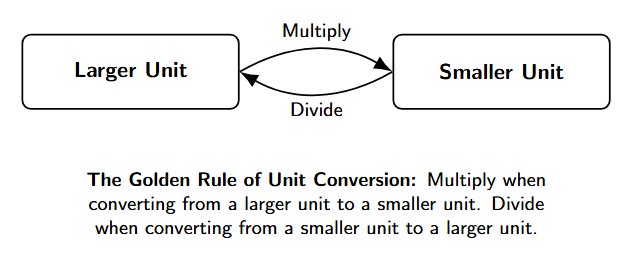
- To convert from a larger unit to a smaller unit, you multiply. (Because you will need more of the smaller units).
- To convert from a smaller unit to a larger unit, you divide. (Because you will need fewer of the larger units).
Units of Length
Length is a measure of distance. Common units used to measure length are:
- Millimetre ($\text{mm}$)
- Centimetre ($\text{cm}$)
- Metre ($\text{m}$)
- Kilometre ($\text{km}$)
Here are the relationships between these units:
- $1 \text{ cm} = 10 \text{ mm}$
- $1 \text{ m} = 100 \text{ cm}$
- $1 \text{ km} = 1000 \text{ m}$
From these basic relations, we can also find other relationships:
- $1 \text{ m} = 100 \text{ cm} = 100 \times 10 \text{ mm} = 1000 \text{ mm}$
- $1 \text{ km} = 1000 \text{ m} = 1000 \times 100 \text{ cm} = 100,000 \text{ cm}$
- $1 \text{ km} = 1000 \text{ m} = 1000 \times 1000 \text{ mm} = 1,000,000 \text{ mm}$
Rule for Conversion:
- To convert a larger unit to a smaller unit, you multiply by the conversion factor (the number of smaller units in one larger unit).
- To convert a smaller unit to a larger unit, you divide by the conversion factor.
For example, to convert metres to centimetres (larger to smaller), you multiply by $100$ because $1 \text{ m} = 100 \text{ cm}$. To convert centimetres to metres (smaller to larger), you divide by $100$.
Units of Mass (Weight)
Mass is the measure of the amount of matter in an object, often called weight in everyday language. Common units used to measure mass are:
- Milligram ($\text{mg}$)
- Gram ($\text{g}$)
- Kilogram ($\text{kg}$)
Here are the relationships between these units:
- $1 \text{ g} = 1000 \text{ mg}$
- $1 \text{ kg} = 1000 \text{ g}$
From these, we also get:
- $1 \text{ kg} = 1000 \text{ g} = 1000 \times 1000 \text{ mg} = 1,000,000 \text{ mg}$
Rule for Conversion:
- To convert a larger unit to a smaller unit, you multiply.
- To convert a smaller unit to a larger unit, you divide.
Units of Capacity (Volume)
Capacity is the amount of liquid a container can hold. Common units used to measure capacity are:
- Millilitre ($\text{mL}$ or $\text{ml}$)
- Litre ($\text{L}$ or $\text{l}$)
Here is the relationship between these units:
- $1 \text{ L} = 1000 \text{ mL}$
Rule for Conversion:
- To convert a larger unit to a smaller unit, you multiply.
- To convert a smaller unit to a larger unit, you divide.
Table: Common Unit Conversions
| From Unit | To Unit | Relationship | To Convert (Multiply/Divide) |
|---|---|---|---|
| Kilometre ($\text{km}$) | Metre ($\text{m}$) | $1 \text{ km} = 1000 \text{ m}$ | Multiply by $1000$ |
| Metre ($\text{m}$) | Centimetre ($\text{cm}$) | $1 \text{ m} = 100 \text{ cm}$ | Multiply by $100$ |
| Centimetre ($\text{cm}$) | Millimetre ($\text{mm}$) | $1 \text{ cm} = 10 \text{ mm}$ | Multiply by $10$ |
| Metre ($\text{m}$) | Millimetre ($\text{mm}$) | $1 \text{ m} = 1000 \text{ mm}$ | Multiply by $1000$ |
| Kilogram ($\text{kg}$) | Gram ($\text{g}$) | $1 \text{ kg} = 1000 \text{ g}$ | Multiply by $1000$ |
| Gram ($\text{g}$) | Milligram ($\text{mg}$) | $1 \text{ g} = 1000 \text{ mg}$ | Multiply by $1000$ |
| Litre ($\text{L}$) | Millilitre ($\text{mL}$) | $1 \text{ L} = 1000 \text{ mL}$ | Multiply by $1000$ |
Example 1. Convert $5$ kilometres into metres.
Answer:
Identify the units: We are converting from kilometres (km) to metres (m).
Compare the units: Kilometre is a larger unit than metre.
Find the relationship: $1 \text{ km} = 1000 \text{ m}$.
Apply the rule: To convert from a larger unit to a smaller unit, we multiply.
$5 \text{ km} = 5 \times 1000 \text{ m} = 5,000 \text{ m}$.
So, $5$ kilometres is equal to $5,000$ metres.
Example 2. Convert $7,500$ grams into kilograms.
Answer:
Identify the units: We are converting from grams (g) to kilograms (kg).
Compare the units: Gram is a smaller unit than kilogram.
Find the relationship: $1 \text{ kg} = 1000 \text{ g}$.
Apply the rule: To convert from a smaller unit to a larger unit, we divide.
$7,500 \text{ g} = \frac{7500}{1000} \text{ kg} = 7.5 \text{ kg}$.
So, $7,500$ grams is equal to $7.5$ kilograms.
Example 3. A medicine bottle contains $120 \text{ mL}$ of syrup. How many litres is this?
Answer:
Identify the units: We are converting from millilitres (mL) to litres (L).
Compare the units: Millilitre is a smaller unit than litre.
Find the relationship: $1 \text{ L} = 1000 \text{ mL}$.
Apply the rule: To convert from a smaller unit to a larger unit, we divide.
$120 \text{ mL} = \frac{120}{1000} \text{ L} = 0.12 \text{ L}$.
The bottle contains $0.12$ litres of syrup.
Estimation
Estimation is the process of finding a value that is close enough to the correct value, instead of the exact value. It is a very useful skill for quick calculations in everyday situations. We often estimate numbers by rounding off.
Rounding off makes numbers simpler to work with and helps us get a quick idea of the answer without doing precise calculations.
The General Rule of Rounding Off
The core idea of rounding is the same no matter which place value you are rounding to.
- Identify the rounding place: Determine the place value you need to round to (e.g., Ten, Hundred, Thousand).
- Look at the digit to its right: This is the "deciding" digit.
- Apply the rule:
- If the deciding digit is 4 or less (0, 1, 2, 3, 4), you round down. This means the digit in the rounding place stays the same, and all digits to its right become zero.
- If the deciding digit is 5 or more (5, 6, 7, 8, 9), you round up. This means you add 1 to the digit in the rounding place, and all digits to its right become zero.
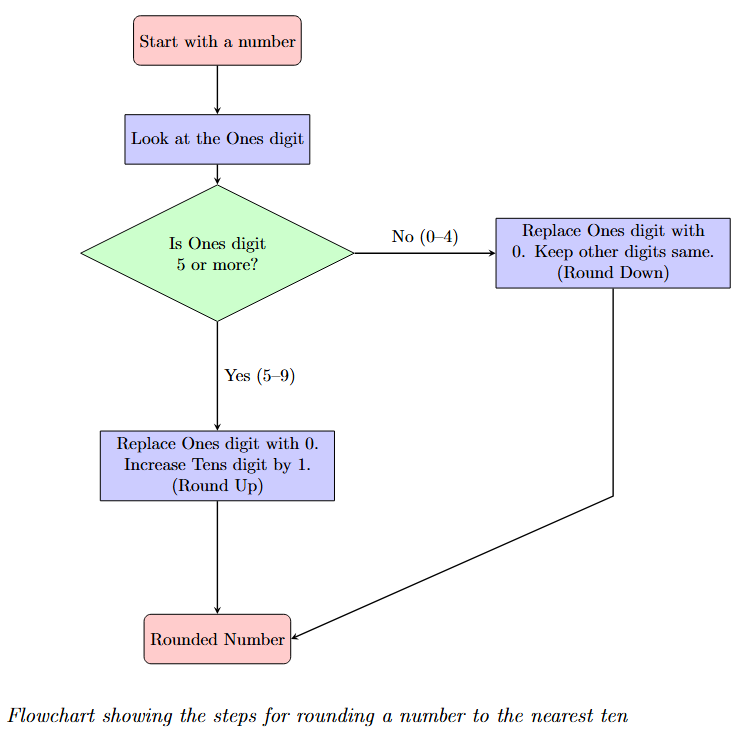
Rounding off to the Nearest Ten
To round off a given number to the nearest ten, we look at the digit in the Ones place.
- If the digit in the Ones place is $0, 1, 2, 3,$ or $4$ (i.e., less than $5$), we replace the Ones digit with $0$ and keep the Tens digit and all digits to its left as they are. This is called rounding down.
- If the digit in the Ones place is $5, 6, 7, 8,$ or $9$ (i.e., $5$ or greater), we replace the Ones digit with $0$ and increase the Tens digit by $1$. If the Tens digit becomes $10$, we carry over $1$ to the Hundreds place and make the Tens digit $0$. This is called rounding up.
Example 1. Round off $53$ and $68$ to the nearest ten.
Answer:
For the number $53$:
The digit in the Ones place is $3$.
Since $3$ is less than $5$, we round down. Replace the Ones digit ($3$) with $0$. The Tens digit ($5$) remains the same.
So, $53$ rounded to the nearest ten is $50$.
For the number $68$:
The digit in the Ones place is $8$.
Since $8$ is $5$ or greater, we round up. Replace the Ones digit ($8$) with $0$ and increase the Tens digit ($6$) by $1$ ($6+1=7$).
So, $68$ rounded to the nearest ten is $70$.
Rounding off to the Nearest Hundred
To round off a given number to the nearest hundred, we look at the digit in the Tens place.
- If the digit in the Tens place is $0, 1, 2, 3,$ or $4$ (i.e., less than $5$), we replace the Ones and Tens digits with $0$s and keep the Hundreds digit and all digits to its left as they are. This is rounding down.
- If the digit in the Tens place is $5, 6, 7, 8,$ or $9$ (i.e., $5$ or greater), we replace the Ones and Tens digits with $0$s and increase the Hundreds digit by $1$. If the Hundreds digit becomes $10$, we carry over $1$ to the Thousands place and make the Hundreds digit $0$. This is rounding up.
Example 2. Round off $437$ and $871$ to the nearest hundred.
Answer:
For the number $437$:
The digit in the Tens place is $3$.
Since $3$ is less than $5$, we round down. Replace the Tens digit ($3$) and Ones digit ($7$) with $0$s. The Hundreds digit ($4$) remains the same.
So, $437$ rounded to the nearest hundred is $400$.
For the number $871$:
The digit in the Tens place is $7$.
Since $7$ is $5$ or greater, we round up. Replace the Tens digit ($7$) and Ones digit ($1$) with $0$s and increase the Hundreds digit ($8$) by $1$ ($8+1=9$).
So, $871$ rounded to the nearest hundred is $900$.
Rounding off to the Nearest Thousand
To round off a given number to the nearest thousand, we look at the digit in the Hundreds place.
- If the digit in the Hundreds place is $0, 1, 2, 3,$ or $4$ (i.e., less than $5$), we replace the Ones, Tens, and Hundreds digits with $0$s and keep the Thousands digit and all digits to its left as they are. This is rounding down.
- If the digit in the Hundreds place is $5, 6, 7, 8,$ or $9$ (i.e., $5$ or greater), we replace the Ones, Tens, and Hundreds digits with $0$s and increase the Thousands digit by $1$. If the Thousands digit becomes $10$, we carry over $1$ to the Ten Thousands place and make the Thousands digit $0$. This is rounding up.
Example 3. Round off $6250$ and $7814$ to the nearest thousand.
Answer:
For the number $6250$:
The digit in the Hundreds place is $2$.
Since $2$ is less than $5$, we round down. Replace the Hundreds digit ($2$), Tens digit ($5$), and Ones digit ($0$) with $0$s. The Thousands digit ($6$) remains the same.
So, $6250$ rounded to the nearest thousand is $6000$.
For the number $7814$:
The digit in the Hundreds place is $8$.
Since $8$ is $5$ or greater, we round up. Replace the Hundreds digit ($8$), Tens digit ($1$), and Ones digit ($4$) with $0$s and increase the Thousands digit ($7$) by $1$ ($7+1=8$).
So, $7814$ rounded to the nearest thousand is $8000$.
Estimating Sums, Differences, and Products
We can use rounding off to estimate the result of operations like addition, subtraction, and multiplication. The process involves rounding off the numbers first and then performing the operation on the rounded numbers.
The place value to which you round off depends on the required level of accuracy for the estimate. Rounding to a higher place value (like nearest thousand or ten thousand) gives a rougher estimate, while rounding to a lower place value (like nearest hundred or ten) gives a closer estimate.
Example 4. Estimate $5290 + 17986$ by rounding off to the nearest thousand.
Answer:
Given:
Numbers to be added: $5290$ and $17986$.
Rounding required: Nearest thousand.
To Find:
Estimated sum.
Solution:
Round off $5290$ to the nearest thousand:
The Hundreds digit is $2$. Since $2 < 5$, round down.
$5290 \approx 5000$.
Round off $17986$ to the nearest thousand:
The Hundreds digit is $9$. Since $9 \ge 5$, round up. Increase the Thousands digit ($7$) by $1$ ($7+1=8$).
$17986 \approx 18000$.
Now, estimate the sum by adding the rounded numbers:
Estimated sum $= 5000 + 18000$
$\begin{array}{cc} & \small{1} \\ & & 5 & 0 & 0 & 0 \\ + & 1 & 8 & 0 & 0 & 0 \\ \hline & 2 & 3 & 0 & 0 & 0 \\ \hline \end{array}$
The estimated sum is $23000$.
Example 5. Estimate $5673 - 436$ by rounding off to the nearest hundred.
Answer:
Given:
Numbers for subtraction: $5673$ and $436$.
Rounding required: Nearest hundred.
To Find:
Estimated difference.
Solution:
Round off $5673$ to the nearest hundred:
The Tens digit is $7$. Since $7 \ge 5$, round up. Increase the Hundreds digit ($6$) by $1$ ($6+1=7$).
$5673 \approx 5700$.
Round off $436$ to the nearest hundred:
The Tens digit is $3$. Since $3 < 5$, round down.
$436 \approx 400$.
Now, estimate the difference by subtracting the rounded numbers:
Estimated difference $= 5700 - 400$
$\begin{array}{ccccc} & 5 & 7 & 0 & 0 \\ - & & 4 & 0 & 0 \\ \hline & 5 & 3 & 0 & 0 \\ \hline \end{array}$
The estimated difference is $5300$.
Roman Numerals
Besides the Hindu-Arabic system (using digits $0, 1, 2, ..., 9$) that we use every day, there is another ancient system for writing numbers called Roman numerals. This system was developed in ancient Rome and is still used today on clock faces, for chapter numbers in books, in the names of monarchs (like Queen Elizabeth II), and for marking dates on buildings.

It is based on seven basic symbols from the Latin alphabet.
Basic Roman Numerals and their Values
| Roman Numeral | Hindu-Arabic Value |
|---|---|
| I | $1$ |
| V | $5$ |
| X | $10$ |
| L | $50$ |
| C | $100$ |
| D | $500$ |
| M | $1000$ |
These seven symbols are combined according to specific rules to form other numbers.
Rules for Writing Roman Numerals
To write a number in Roman numerals or to convert a Roman numeral back to a Hindu-Arabic number, we follow these important rules.
Rule 1: Repetition means Addition
When a symbol is repeated in a row, its value is added as many times as it appears.
- Examples:
II $= 1 + 1 = 2$
XXX $= 10 + 10 + 10 = 30$
CC $= 100 + 100 = 200$ - Restrictions:
- Only the symbols I, X, C, and M (the "powers of 10") can be repeated.
- These symbols can be repeated a maximum of three times. (e.g., III is 3, but IIII for 4 is incorrect).
- The symbols V, L, and D (the "fives") are never repeated.
Rule 2: Smaller Value After Larger Value means Addition
If a symbol of smaller value is written to the right of a symbol of larger value, their values are added.
- Examples:
VI $= 5 + 1 = 6$
LX $= 50 + 10 = 60$
MCC $= 1000 + 100 + 100 = 1200$
Rule 3: Smaller Value Before Larger Value means Subtraction
If a symbol of smaller value is written to the left of a symbol of larger value, the smaller value is subtracted from the larger value. This is how numbers like 4 and 9 are formed.
- Examples:
IV $= 5 - 1 = 4$
IX $= 10 - 1 = 9$
XL $= 50 - 10 = 40$
XC $= 100 - 10 = 90$
CD $= 500 - 100 = 400$
CM $= 1000 - 100 = 900$ - Restrictions:
- The symbols V, L, and D are never subtracted.
- I can only be subtracted from V and X.
- X can only be subtracted from L and C.
- C can only be subtracted from D and M.
Rule 4: A smaller value between two larger values
When a symbol of a smaller value is placed between two symbols of larger values, its value is subtracted from the symbol immediately following it.
- Example: In XIX, the I is between two Xs. It is subtracted from the second X.
XIX $= 10 + (10 - 1) = 10 + 9 = 19$.
Rule 5: The Vinculum (Bar) for Large Numbers
To write very large numbers (typically 4,000 and above), a bar, known as a vinculum, is placed above a Roman numeral. The bar multiplies the value of the numeral(s) beneath it by 1,000.
- Examples:
$\overline{V} = 5 \times 1000 = 5,000$
$\overline{X} = 10 \times 1000 = 10,000$
$\overline{L} = 50 \times 1000 = 50,000$
This bar can be used with any numeral and is combined with other numerals using the addition rule.
Example Combination: To write the number 12,435:
Break it down: $12,000 + 400 + 30 + 5$.
- $12,000$: Write 12 as XII, then place a bar over it: $\overline{XII}$.
- $400$: Write 400 as CD.
- $30$: Write 30 as XXX.
- $5$: Write 5 as V.
Combine them: $\overline{XII}CDXXXV$.
General Method: The easiest way to write a large number is to break it down into its expanded form and convert each part separately.
Example 1. Write the Hindu-Arabic numeral for XXXVIII.
Answer:
Let's break down the Roman numeral into its parts from left to right.
XXX + V + III
- XXX $= 10 + 10 + 10 = 30$ (Rule 1: Repetition)
- V $= 5$
- III $= 1 + 1 + 1 = 3$ (Rule 1: Repetition)
Since the values are arranged from largest to smallest, we add them together.
XXXVIII $= 30 + 5 + 3 = 38$.
So, the Hindu-Arabic numeral for XXXVIII is $38$.
Example 2. Write the Hindu-Arabic numeral for XCIX.
Answer:
Let's break the numeral into groups where subtraction occurs.
XCIX can be read as XC + IX.
- For XC, X (10) is before C (100). This means subtraction.
XC $= 100 - 10 = 90$. - For IX, I (1) is before X (10). This also means subtraction.
IX $= 10 - 1 = 9$.
Now we add the values of the groups.
XCIX $= 90 + 9 = 99$.
So, the Hindu-Arabic numeral for XCIX is $99$.
Example 3. Write the Roman numeral for $67$.
Answer:
Step 1: Expand the number.
$67 = 60 + 7$.
Step 2: Convert each part to Roman numerals.
- To write 60, we use addition: $50 + 10 \to$ L followed by X $\to$ LX.
- To write 7, we use addition: $5 + 1 + 1 \to$ V followed by II $\to$ VII.
Step 3: Combine the Roman numerals.
$67 = $ LXVII.
So, $67$ in Roman numerals is LXVII.
Example 4. Write the Roman numeral for $49$.
Answer:
Step 1: Expand the number.
$49 = 40 + 9$.
Step 2: Convert each part to Roman numerals using subtraction.
- To write 40, we use subtraction: $50 - 10 \to$ X before L $\to$ XL.
- To write 9, we use subtraction: $10 - 1 \to$ I before X $\to$ IX.
Step 3: Combine the Roman numerals.
$49 = $ XLIX.
So, $49$ in Roman numerals is XLIX.

