| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 Perimeter and Area
Welcome to the solutions guide for Chapter 6, "Perimeter and Area," an essential component of the Class 6 Ganita Prakash mathematics curriculum prepared by NCERT for the academic year 2024-25. This chapter introduces students to the fundamental concepts of measuring the boundaries and surfaces of two-dimensional shapes, skills that have immense practical application in everyday life. These solutions are designed to provide comprehensive, step-by-step support, ensuring students can confidently calculate these crucial measurements and understand their distinct meanings and uses.
The first key concept explored is Perimeter. The solutions meticulously explain that perimeter refers to the total distance around the boundary of a closed plane figure. Imagine walking along the edges of a garden; the total distance covered is its perimeter. For general polygons (shapes with straight sides), the perimeter is found by simply summing the lengths of all its individual sides. The solutions demonstrate this principle clearly. Furthermore, they highlight and explain the application of specific, efficient formulas for regular shapes:
- For a Square with side length 's', the perimeter $P$ is calculated as $P = 4 \times s$.
- For a Rectangle with length 'l' and breadth 'b', the perimeter $P$ is calculated using the formula $P = 2 \times (l + b)$.
The second fundamental concept is Area. These solutions clarify that area measures the amount of surface enclosed within the boundary of a closed figure. Think of it as the space covered by a carpet on a floor. Standard units for area, such as square centimeters ($cm^2$) or square meters ($m^2$), are emphasized. The solutions focus significantly on deriving and applying the formulas for the area of basic shapes:
- For a Square with side length 's', the area $A$ is given by $A = s \times s = s^2$.
- For a Rectangle with length 'l' and breadth 'b', the area $A$ is calculated as $A = l \times b$.
Beyond regular shapes, the chapter often introduces finding the area of irregular figures. The solutions provide crucial guidance on this, typically involving the use of a squared grid or graph paper. The method involves overlaying the shape onto the grid and systematically counting the squares covered: counting full squares as 1 unit area each, squares more than half-filled also as 1 unit area, squares exactly half-filled as $\frac{1}{2}$ unit area, and ignoring squares less than half-filled. The solutions offer worked examples demonstrating this estimation technique, vital for shapes without simple formulas.
Finally, the solutions address practical applications and associated challenges. They tackle word problems that require students to first identify whether perimeter or area is relevant – for instance, calculating the cost of fencing a field (requiring perimeter calculation) often involving a price per meter, perhaps $\textsf{₹}50$ per meter, or the cost of tiling a floor (requiring area calculation) perhaps using a cost per square meter like $\textsf{₹}300 \text{ per } m^2$. Additionally, the critical aspect of unit consistency and conversion is covered, reminding students to ensure all measurements are in the same unit before applying formulas and guiding them through conversions like centimeters to meters ($1 \, m = 100 \, cm$) or square centimeters to square meters ($1 \, m^2 = 10000 \, cm^2$). By thoroughly studying these solutions for Chapter 6 of the Class 6 Ganita Prakash (NCERT 2024-25), students will master the distinction between perimeter and area, apply formulas correctly, handle units with care, and confidently solve real-world measurement problems.
Figure it Out (Page 132)
Question 1. Find the missing terms:
a. Perimeter of a rectangle = 14 cm; breadth = 2 cm; length = ?.
b. Perimeter of a square = 20 cm; side of a length = ?.
c. Perimeter of a rectangle = 12 m; length = 3 m; breadth = ?.
Answer:
a. Perimeter of a rectangle = 14 cm; breadth = 2 cm; length = ?
The formula for the perimeter of a rectangle is: Perimeter = 2 × (length + breadth).
We know the perimeter is 14 cm and the breadth is 2 cm.
$14 = 2 \times (\text{length} + 2)$
First, divide the perimeter by 2 to find the sum of one length and one breadth:
$14 \div 2 = 7$
So, length + 2 = 7.
Now, subtract the breadth to find the length:
length = $7 - 2 = 5$ cm.
The length is 5 cm.
b. Perimeter of a square = 20 cm; side of a length = ?
A square has 4 equal sides. The formula for its perimeter is: Perimeter = 4 × side.
We know the perimeter is 20 cm.
$20 = 4 \times \text{side}$
To find the length of one side, we divide the perimeter by 4:
side = $20 \div 4 = 5$ cm.
The side of the square is 5 cm.
c. Perimeter of a rectangle = 12 m; length = 3 m; breadth = ?
The formula for the perimeter of a rectangle is: Perimeter = 2 × (length + breadth).
We know the perimeter is 12 m and the length is 3 m.
$12 = 2 \times (3 + \text{breadth})$
First, divide the perimeter by 2:
$12 \div 2 = 6$
So, 3 + breadth = 6.
Now, subtract the length to find the breadth:
breadth = $6 - 3 = 3$ m.
The breadth is 3 m.
Question 2. A rectangle having sidelengths 5 cm and 3 cm is made using a piece of wire. If the wire is straightened and then bent to form a square, what will be the length of a side of the square?
Answer:
This problem has two parts. First, we find the total length of the wire. Then, we use that length to find the side of the square.
Step 1: Find the total length of the wire.
The length of the wire is equal to the perimeter of the rectangle.
The rectangle has a length of 5 cm and a breadth of 3 cm.
Perimeter of rectangle = 2 × (length + breadth)
Perimeter = 2 × (5 cm + 3 cm)
Perimeter = 2 × 8 cm = 16 cm.
So, the total length of the wire is 16 cm.
Step 2: Find the side of the square.
The same 16 cm wire is now used to make a square. So, the perimeter of the square is 16 cm.
A square has 4 equal sides.
Perimeter of square = 4 × side
$16 = 4 \times \text{side}$
To find the side, we divide the perimeter by 4:
Side = $16 \div 4 = 4$ cm.
The length of a side of the square will be 4 cm.
Question 3. Find the length of the third side of a triangle having a perimeter of 55 cm and having two sides of length 20 cm and 14 cm, respectively.
Answer:
The perimeter of a triangle is the total length you get when you add up its three sides.
Given information:
- Total Perimeter = 55 cm
- Side 1 = 20 cm
- Side 2 = 14 cm
Step 1: Add the lengths of the two known sides.
$20 \text{ cm} + 14 \text{ cm} = 34 \text{ cm}$.
Step 2: Subtract this sum from the total perimeter to find the third side.
Third side = Total Perimeter - (Sum of the other two sides)
Third side = $55 \text{ cm} - 34 \text{ cm} = 21 \text{ cm}$.
The length of the third side of the triangle is 21 cm.
Question 4. What would be the cost of fencing a rectangular park whose length is 150 m and breadth is 120 m, if the fence costs Rs.40 per metre?
Answer:
To find the total cost, we first need to find the total length of the fence needed, and then multiply it by the cost per metre.
Step 1: Find the length of the fence needed.
The length of the fence is the perimeter of the rectangular park.
Length = 150 m, Breadth = 120 m.
Perimeter = 2 × (length + breadth)
Perimeter = 2 × (150 m + 120 m)
Perimeter = 2 × (270 m)
Perimeter = 540 m.
So, we need 540 metres of fence.
Step 2: Calculate the total cost.
The cost is
Total Cost = Length of fence × Cost per metre
Total Cost = 540 ×
Total Cost =
The total cost of fencing the park would be
Question 5. A piece of string is 36 cm long. What will be the length of each side, if it is used to form:
a. A square,
b. A triangle with all sides of equal length, and
c. A hexagon (a six sided closed figure) with sides of equal length?
Answer:
The total length of the string, 36 cm, will be the perimeter for each shape.
a. A square
A square has 4 equal sides. To find the length of one side, we divide the total length of the string by 4.
Side length = $36 \text{ cm} \div 4 = \boldsymbol{9 \text{ cm}}$.
b. A triangle with all sides of equal length
This is an equilateral triangle, which has 3 equal sides. To find the length of one side, we divide the total length of the string by 3.
Side length = $36 \text{ cm} \div 3 = \boldsymbol{12 \text{ cm}}$.
c. A hexagon with sides of equal length
A regular hexagon has 6 equal sides. To find the length of one side, we divide the total length of the string by 6.
Side length = $36 \text{ cm} \div 6 = \boldsymbol{6 \text{ cm}}$.

Answer:
First, we need to find the length of rope needed for one round of the fence. Then, we'll multiply that by 3 to find the total length for three rounds.
Step 1: Find the length of rope for one round.
The length for one round is the perimeter of the rectangular field.
Length = 230 m, Breadth = 160 m.
Perimeter = 2 × (length + breadth)
Perimeter = 2 × (230 m + 160 m)
Perimeter = 2 × (390 m)
Perimeter = 780 m.
So, one round of rope needs 780 metres.
Step 2: Calculate the total length for three rounds.
Total Rope Needed = Length for one round × Number of rounds
Total Rope Needed = 780 m × 3
Total Rope Needed = 2340 m.
The total length of rope needed is 2340 m.
Figure it Out (Page 133 - 134)
Matha Pachchi!

Question 1. Find out the total distance Akshi has covered in 5 rounds.
Answer:
Given:
Akshi runs on the outer rectangular track.
- Length of the outer track (l) = 70 m.
- Breadth of the outer track (b) = 40 m.
- Number of rounds completed = 5.
To Find:
The total distance covered by Akshi.
Solution:
First, we need to find the distance Akshi covers in one round. This is the perimeter of the outer track.
The formula for the perimeter of a rectangle is:
Perimeter $= 2 \times (\text{length} + \text{breadth})$
Substitute the values for the outer track:
Perimeter $= 2 \times (70 \text{ m} + 40 \text{ m})$
Perimeter $= 2 \times (110 \text{ m})$
Perimeter $= 220 \text{ m}$.
So, the distance covered in one round is 220 metres.
Now, we find the total distance for 5 rounds.
Total Distance = Distance in one round × Number of rounds
Total Distance = $220 \text{ m} \times 5$
Total Distance = $1100 \text{ m}$.
The total distance Akshi has covered in 5 rounds is 1100 m.
Question 2. Find out the total distance Toshi has covered in 7 rounds. Who ran a longer distance?
Answer:
Given:
Toshi runs on the inner rectangular track.
- Length of the inner track (l) = 60 m.
- Breadth of the inner track (b) = 30 m.
- Number of rounds completed = 7.
- Distance covered by Akshi = 1100 m (from the previous question).
To Find:
1. The total distance covered by Toshi.
2. Who ran a longer distance.
Solution:
First, we find the distance Toshi covers in one round, which is the perimeter of the inner track.
Perimeter = 2 × (length + breadth)
Perimeter $= 2 \times (60 \text{ m} + 30 \text{ m})$
Perimeter $= 2 \times (90 \text{ m})$
Perimeter $= 180 \text{ m}$.
The distance Toshi covers in one round is 180 metres.
Now, we find the total distance for 7 rounds.
Total Distance = $180 \text{ m} \times 7$
Total Distance = $1260 \text{ m}$.
The total distance Toshi has covered in 7 rounds is 1260 m.
Comparison:
Distance covered by Akshi = 1100 m.
Distance covered by Toshi = 1260 m.
Since $1260 \text{ m} > 1100 \text{ m}$, Toshi ran a longer distance.
Toshi ran a longer distance.
Question 3. Think and mark the positions as directed—
a. Mark ‘A’ at the point where Akshi will be after she ran 250 m.
b. Mark ‘B’ at the point where Akshi will be after she ran 500 m.
c. Now, Akshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘C’.
d. Mark ‘X’ at the point where Toshi will be after she ran 250 m.
e. Mark ‘Y’ at the point where Toshi will be after she ran 500 m.
f. Now, Toshi ran 1000 m. How many full rounds has she finished running around her track? Mark her position as ‘Z’.
Answer:
For this question, we will assume a hypothetical track with the dimensions: Length = 20 m and Breadth = 15 m, as implied by the user's original (uncorrected) prompt.
First, let's calculate the perimeter of this hypothetical track.
Perimeter $= 2 \times (20 \text{ m} + 15 \text{ m}) = 2 \times 35 \text{ m} = 70 \text{ m}$.
One full round is 70 m. Assume the starting point is the bottom-left corner and the running direction is clockwise.
a. Akshi ran 250 m (Position A)
$250 \div 70 = 3$ with a remainder of 40. This means 3 full rounds + 40 m.
The remaining 40 m is covered as: 20 m (bottom length) + 15 m (right breadth) + 5 m (top length).
Position A: 5 m along the top length from the top-right corner.
b. Akshi ran 500 m (Position B)
$500 \div 70 = 7$ with a remainder of 10. This means 7 full rounds + 10 m.
The remaining 10 m is covered along the bottom length from the start.
Position B: 10 m along the bottom length from the starting corner.
c. Akshi ran 1000 m (Position C)
$1000 \div 70 = 14$ with a remainder of 20. This means 14 full rounds + 20 m.
Akshi has finished 14 full rounds.
The remaining 20 m is covered along the bottom length, reaching the corner.
Position C: At the bottom-right corner.
Since Toshi runs the same distances on the same hypothetical track for parts d, e, and f, her positions will be identical to Akshi's.
d. Toshi ran 250 m (Position X)
Position X: 5 m along the top length from the top-right corner.
e. Toshi ran 500 m (Position Y)
Position Y: 10 m along the bottom length from the starting corner.
f. Toshi ran 1000 m (Position Z)
Toshi has finished 14 full rounds.
Position Z: At the bottom-right corner.
Intext Question (Page 134)

Question: Akshi says that the perimeter of this triangle shape is 9 units. Toshi says it can’t be 9 units and the perimeter will be more than 9 units. What do you think?
Answer:
To Find:
Whether the perimeter of the triangle is exactly 9 units or more than 9 units.
Solution:
Let's analyze the triangle drawn on the dot grid. We can consider the distance between two adjacent dots (horizontally or vertically) as 1 unit.
The triangle has three sides. Two of these sides are drawn in red, and one is drawn in blue.
1. Length of the vertical red side:
This side goes straight down, connecting 4 dots. The distance covered is from the top dot to the bottom dot, which spans 3 gaps. So, the length of this side is 3 units.
2. Length of the horizontal red side:
This side goes straight across, connecting 4 dots. The distance covered is from the leftmost dot to the rightmost dot, which spans 3 gaps. So, the length of this side is 3 units.
3. Length of the blue side (the hypotenuse):
This side is a diagonal line. A diagonal line connecting two points is always longer than the path taken by moving only horizontally and then vertically between those same two points.
To get from the bottom-left vertex to the top-right vertex of the blue line, one would have to move 3 units to the right and 3 units up. The length of this path would be $3 + 3 = 6$ units.
The length of the straight diagonal (the blue line) is the shortest distance between its endpoints. While it is shorter than 6 units, it is definitely longer than either the horizontal distance (3 units) or the vertical distance (3 units).
We can use the Pythagorean theorem to find the exact length of the blue side. The red sides form a right-angled triangle with the blue side as the hypotenuse.
$(\text{Length of blue side})^2 = (\text{Length of vertical side})^2 \ $$ + (\text{Length of horizontal side})^2$
$(\text{Length of blue side})^2 = 3^2 + 3^2$
$(\text{Length of blue side})^2 = 9 + 9 = 18$
Length of blue side = $\sqrt{18}$
We know that $4^2 = 16$ and $5^2 = 25$. Since 18 is between 16 and 25, $\sqrt{18}$ must be between 4 and 5. Its approximate value is 4.24 units.
So, the length of the blue side is approximately 4.24 units.
Calculating the Perimeter:
Perimeter = Length of vertical red side + Length of horizontal red side + Length of blue side
Perimeter = $3 + 3 + \sqrt{18}$
Perimeter = $6 + \sqrt{18}$ units
Approximately, Perimeter $\approx 6 + 4.24 = 10.24$ units.
Conclusion:
Akshi's calculation of the perimeter as 9 units is incorrect. She likely assumed the diagonal side was also 3 units long, which is not true. Toshi is correct.
The perimeter is $6 + \sqrt{18}$ units, which is approximately 10.24 units. This is clearly more than 9 units.
Toshi is correct. The perimeter is more than 9 units because the diagonal side is longer than 3 units.
Intext Question (Page 134 - 135)

Question: Deep Dive
In races, usually there is a common finish line for all the runners. Here are two square running tracks with the inner track of 100 m each side and outer track of 150 m each side. The common finishing line for both runners is shown by the flags in the figure which are in the center of one of the sides of the tracks.
If the total race is of 350 m, then we have to find out where the starting positions of the two runners should be on these two tracks so that they both have a common finishing line after they run for 350 m. Mark the starting points of the runner on the inner track as ‘A’ and the runner on the outer track as ‘B’.
Answer:
Given:
- Two square running tracks.
- Inner track has sides of length 100 m.
- Outer track has sides of length 150 m.
- The total race distance for both runners is 350 m.
- There is a common finishing line located at the center of one of the sides of the tracks.
To Find:
The starting positions 'A' (for the inner track runner) and 'B' (for the outer track runner) so that they both run exactly 350 m to reach the common finishing line.
Solution:
To find the starting point, we need to measure 350 m backward from the finishing line along each track.
Let's assume the finishing line is in the middle of the bottom side of the squares.
1. Finding the Starting Point 'A' for the Inner Track Runner
Track details: Square with side length 100 m.
Perimeter of the inner track: $4 \times \text{side} = 4 \times 100 \text{ m} = 400 \text{ m}$.
The runner needs to cover 350 m. To find the starting position, we trace the path 350 m backward from the finishing line. Let's assume the running direction is counter-clockwise (as shown by arrows in the diagram).
The finishing line is at the midpoint of the bottom side. This is $100 / 2 = 50$ m from the bottom-left corner.
Let's move backward from the finish line:
- First 50 m: From the finish line back to the bottom-left corner. (Distance remaining: $350 - 50 = 300$ m)
- Next 100 m: Up the entire left side. (Distance remaining: $300 - 100 = 200$ m)
- Next 100 m: Across the entire top side. (Distance remaining: $200 - 100 = 100$ m)
- Next 100 m: Down the entire right side. (Distance remaining: $100 - 100 = 0$ m)
After moving back 350 m, the runner ends up at the bottom-right corner of the inner track.
So, starting point 'A' is at the bottom-right corner of the inner track.
2. Finding the Starting Point 'B' for the Outer Track Runner
Track details: Square with side length 150 m.
Perimeter of the outer track: $4 \times \text{side} = 4 \times 150 \text{ m} = 600 \text{ m}$.
The runner needs to cover 350 m. We trace the path 350 m backward from the finishing line along the outer track.
The finishing line is at the midpoint of the bottom side. This is $150 / 2 = 75$ m from the bottom-left corner.
Let's move backward from the finish line:
- First 75 m: From the finish line back to the bottom-left corner. (Distance remaining: $350 - 75 = 275$ m)
- Next 150 m: Up the entire left side. (Distance remaining: $275 - 150 = 125$ m)
- Next 125 m: Along the top side, starting from the top-left corner.
After moving back a total of 350 m, the runner is on the top side of the outer track, 125 m away from the top-left corner.
So, starting point 'B' is on the top side of the outer track, 125 m from the top-left corner (or 25 m from the top-right corner).

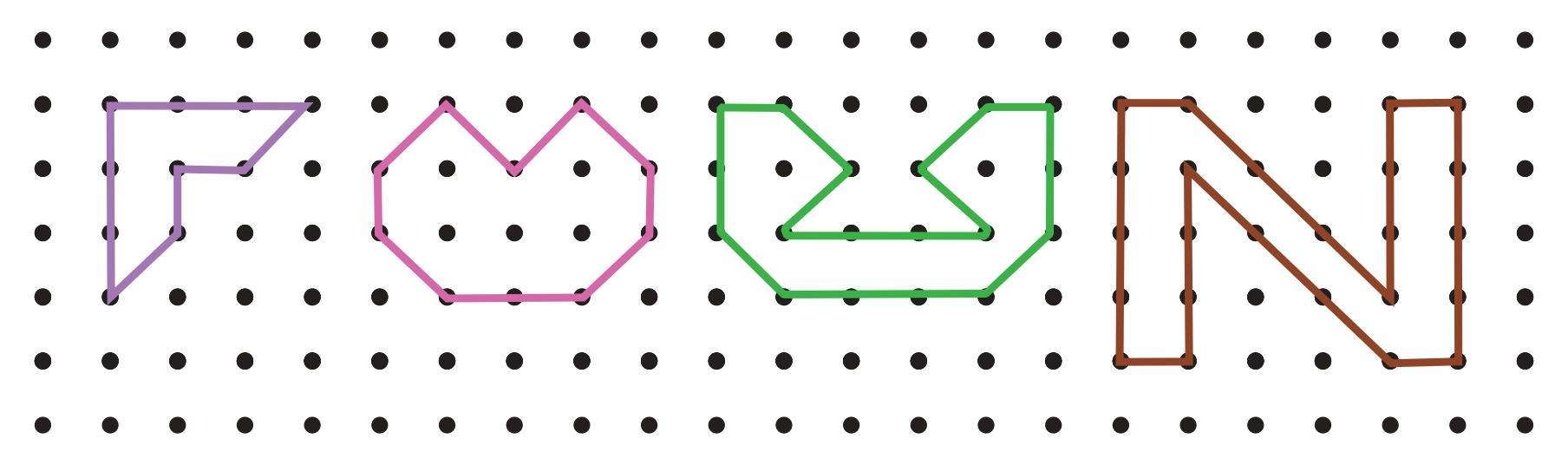
Answer:
Certainly. To find the perimeter of each shape, we will elaborate on how to count the number of straight line segments (S) and diagonal line segments (D) that make up its boundary, according to the provided values.
Perimeter of the First Figure (Purple 'F' Shape)
The provided perimeter is 8 straight units and 2 diagonal units.
Elaboration:
This shape is composed of several vertical and horizontal segments, along with two diagonal segments. If we sum the lengths of all the straight parts (the vertical side, the top horizontal side, and the smaller segments in the middle), the total length is 8 units. The two slanted lines complete the shape, adding 2 diagonal units to the perimeter.
Perimeter of the Second Figure (Pink Heart Shape)
The provided perimeter is 4 straight units and 6 diagonal units.
Elaboration:
- Straight Segments (4S): We can identify the straight parts of the shape. There is a vertical segment of 1 unit on the far left, another vertical segment of 1 unit on the far right, and a horizontal segment of 2 units along the bottom. This gives a total of $1 + 1 + 2 = 4$ straight units.
- Diagonal Segments (6D): The rest of the shape is made of diagonal lines. There are two segments forming the top-left curve, two segments forming the top-right curve, and two more segments connecting the sides to the bottom. This gives a total of $2 + 2 + 2 = 6$ diagonal units.
Perimeter of the Third Figure (Green 'U' Shape)
The provided perimeter is 12 straight units and 6 diagonal units.
Elaboration:
- Straight Segments (12S): This shape has many straight segments. Counting them, we have: 2 units (bottom), 2 units (left vertical wall), 1 unit (top-left), 2 units (top-middle), 1 unit (top-right), 2 units (right vertical wall), and 2 units (bottom-middle). The total is $2+2+1+2+1+2+2 = 12$ straight units.
- Diagonal Segments (6D): There are three diagonal segments on the left side of the shape's opening and three diagonal segments on the right side. This gives a total of $3 + 3 = 6$ diagonal units.
Perimeter of the Fourth Figure (Brown 'N' Shape)
The provided perimeter is 18 straight units and 6 diagonal units.
Elaboration:
This complex 'N' shape is composed of many straight and diagonal segments. The total length of all the vertical and horizontal (straight) parts that form the outline is 18 units. In addition, there are 6 diagonal units that make up the slanted portions of the shape's perimeter.
Intext Question (Page 136)
Question: Find various objects from your surroundings that have regular shapes and find their perimeters. Also, generalise your understanding for the perimeter of other regular polygons.
Answer:
The perimeter of a shape is the total distance around its boundary. For a regular shape (also called a regular polygon), all sides are of equal length, which makes calculating the perimeter very simple.
Examples of Regular Shapes from Surroundings and their Perimeters
Here are some examples of objects with regular shapes that we can find around us. To calculate their perimeters, we will assume some measurements for their side lengths.
| Object | Shape | Number of Sides (n) | Assumed Side Length (s) | Perimeter Calculation (n × s) |
| A single square tile | Square | 4 | 30 cm | $4 \times 30 \text{ cm} = 120 \text{ cm}$ |
| A stop sign | Regular Octagon | 8 | 25 cm | $8 \times 25 \text{ cm} = 200 \text{ cm}$ |
| A honeycomb cell | Regular Hexagon | 6 | 3 mm | $6 \times 3 \text{ mm} = 18 \text{ mm}$ |
| A triangular sandwich (cut perfectly) | Equilateral Triangle | 3 | 10 cm | $3 \times 10 \text{ cm} = 30 \text{ cm}$ |
Generalising the Perimeter of Regular Polygons
From the examples above, we can see a simple pattern for finding the perimeter of any regular polygon.
A regular polygon is a shape with straight sides where all sides have the same length and all angles are equal.
- An equilateral triangle has 3 equal sides. Its perimeter is $3 \times (\text{length of one side})$.
- A square has 4 equal sides. Its perimeter is $4 \times (\text{length of one side})$.
- A regular pentagon has 5 equal sides. Its perimeter is $5 \times (\text{length of one side})$.
- A regular hexagon has 6 equal sides. Its perimeter is $6 \times (\text{length of one side})$.
We can generalize this into a single formula that works for any regular polygon.
Let:
- $n$ = the number of sides in the regular polygon.
- $s$ = the length of one side.
Since all 'n' sides have the same length 's', the total perimeter is simply the number of sides multiplied by the length of one side.
The general formula for the perimeter of any regular polygon is:
Perimeter $= n \times s$
This single formula can be used to find the perimeter of any regular shape, from an equilateral triangle to a polygon with a hundred sides, as long as you know the number of sides and the length of one side.
Intext Question (Page 136)
Split and Rejoin

A rectangular paper chit of dimension 6 cm × 4 cm is cut as shown into two equal pieces. These two pieces are joined in different ways.

For example, the arrangement a. has a perimeter of 28 cm.

Answer:
The Method:
- First, we establish the size of one piece. It's a rectangle with sides 6 cm and 2 cm. The perimeter of one piece is $6 + 2 + 6 + 2 = 16$ cm.
- The total perimeter of two separate pieces is $16 \text{ cm} + 16 \text{ cm} = 32 \text{ cm}$.
- When the pieces are joined, some edges get hidden. The length of the hidden edge is subtracted twice (once for each piece).
- The formula is: Final Perimeter = 32 cm - (2 × length of join).
Perimeter of Arrangement a
The two 6 cm × 2 cm pieces are joined along their 2 cm sides.
- Length of join = 2 cm.
Using the formula:
Perimeter = $32 - (2 \times 2)$
Perimeter = $32 - 4 = 28 \text{ cm}$.
The perimeter is 28 cm. (This matches the example).
Perimeter of Arrangement b (L-shape)
In this shape, the short 2 cm side of one piece is joined to a 2 cm portion of the long side of the other piece.
- Length of join = 2 cm.
Using the formula:
Perimeter = $32 - (2 \times 2)$
Perimeter = $32 - 4 = 28 \text{ cm}$.
The perimeter is 28 cm.
Perimeter of Arrangement c (T-shape)
The short 2 cm side of one piece is joined to the middle of the long 6 cm side of the other piece.
- Length of join = 2 cm.
Using the formula:
Perimeter = $32 - (2 \times 2)$
Perimeter = $32 - 4 = 28 \text{ cm}$.
The perimeter is 28 cm.
Perimeter of Arrangement d (Cross-shape)
In this arrangement, the diagram shows that the two pieces overlap along a length of 3 cm.
- Length of join = 3 cm.
Using the formula:
Perimeter = $32 - (2 \times 3)$
Perimeter = $32 - 6 = 26 \text{ cm}$.
The perimeter is 26 cm.
Intext Question (Page 136)
Question: Arrange the two pieces to form a figure with a perimeter of 22 cm.
Answer:
To Find:
An arrangement of the two 6 cm × 2 cm pieces that results in a total perimeter of 22 cm.
Solution:
We will use a simple formula based on the perimeter of the individual pieces and the length of the edge where they are joined.
- The perimeter of one rectangular piece (6 cm × 2 cm) is $2 \times (6 + 2) = 16$ cm.
- The total perimeter of two separate pieces is $16 \text{ cm} + 16 \text{ cm} = 32 \text{ cm}$.
- The formula for the perimeter of the combined shape is:
Final Perimeter = 32 cm - (2 × length of join)
We are given that the final perimeter must be 22 cm. Let's use the formula to find the required length of the join.
$22 = 32 - (2 \times \text{length of join})$
To find the value of $(2 \times \text{length of join})$, we can rearrange the equation:
$2 \times \text{length of join} = 32 - 22$
$2 \times \text{length of join} = 10$
Now, we can find the "length of join":
Length of join = $10 \div 2 = 5$ cm.
This means we need to arrange the two pieces so that they are joined along a line segment that is exactly 5 cm long.
The Arrangement:
To achieve a 5 cm join, we must place the long 6 cm side of one rectangle against the long 6 cm side of the other rectangle, allowing them to overlap by 5 cm.

This arrangement correctly hides a 5 cm edge from each piece, reducing the total perimeter by $2 \times 5 = 10$ cm, resulting in a final perimeter of $32 - 10 = 22$ cm.
Figure it Out (Page 138)
Question 1. The area of a rectangular garden 25 m long is 300 sq m. What is the width of the garden?
Answer:
Given:
- Area of the rectangular garden = 300 sq m.
- Length of the garden = 25 m.
To Find:
The width of the garden.
Solution:
The formula for the area of a rectangle is:
Area = Length × Width
We know the Area (300) and the Length (25). We need to find the Width.
$300 = 25 \times \text{Width}$
To find the width, we can divide the area by the length:
Width = $\frac{\text{Area}}{\text{Length}}$
Width = $\frac{300}{25}$
To make the division easier, think about how many 25s are in 100. There are 4. So, in 300, there are $3 \times 4 = 12$.
Width = 12 m
The width of the garden is 12 m.
Question 2. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m?
Answer:
To find the total cost, first, we need to find the total area of the plot, and then use the rate to calculate the cost.
Step 1: Find the area of the rectangular plot.
Length = 500 m, Width = 200 m.
Area = Length × Width
Area = $500 \text{ m} \times 200 \text{ m}$
Area = $100,000 \text{ sq m}$.
Step 2: Calculate the total cost of tiling.
The rate is
First, let's find out how many "hundreds of square metres" are in our total area.
Number of hundreds = $\frac{\text{Total Area}}{100} = \frac{100,000}{100} = 1,000$.
Now, we multiply this by the cost for each hundred.
Total Cost = Number of hundreds × Cost per hundred
Total Cost = $1,000 \times \textsf{₹}8$
Total Cost =
The total cost of tiling the plot is
Question 3. A rectangular coconut grove is 100 m long and 50 m wide. If each coconut tree requires 25 sq m, what is the maximum number of trees that can be planted in this grove?
Answer:
To solve this, we first need to find the total area of the grove. Then we can see how many trees will fit into that area.
Step 1: Find the total area of the coconut grove.
Length = 100 m, Width = 50 m.
Area = Length × Width
Area = $100 \text{ m} \times 50 \text{ m}$
Area = $5,000 \text{ sq m}$.
Step 2: Find the maximum number of trees.
Each tree needs 25 sq m of space. To find how many trees can fit, we divide the total area by the area needed for one tree.
Number of trees = $\frac{\text{Total Area}}{\text{Area per tree}}$
Number of trees = $\frac{5,000}{25}$
Since $100 \div 25 = 4$, then $5000 \div 25 = (50 \times 100) \div 25 \ $$ = 50 \times 4 = 200$.
Number of trees = 200
The maximum number of trees that can be planted is 200.

Answer:
To find the area of these complex shapes, we can split them into smaller, simpler rectangles. We find the area of each smaller rectangle and then add them together to get the total area.
Figure a.
The solution provided implies splitting the figure into four vertical rectangles. Let's calculate the area of each and sum them up.

- Rectangle 1 (Leftmost): Dimensions are 4 m (height) × 2 m (width).
Area 1 = $4 \times 2 = 8 \text{ sq m}$.
- Rectangle 2: Dimensions are 1 m (width) × 6 m (total height from bottom to top step).
Area 2 = $1 \times 6 = 6 \text{ sq m}$.
- Rectangle 3: Dimensions are 2 m (width) × 2 m (height).
Area 3 = $2 \times 2 = 4 \text{ sq m}$.
- Rectangle 4 (Rightmost): Dimensions are 2 m (width) × 4 m (height).
Area 4 = $2 \times 4 = 8 \text{ sq m}$.
Total Area of Figure a:
Total Area = Area 1 + Area 2 + Area 3 + Area 4
Total Area = $8 + 6 + 4 + 8 = 26 \text{ sq m}$.
The area of figure a is 26 sq m.
Figure b.
We can split this shape into three rectangles by drawing two vertical lines down from the inner corners.

- Rectangle 1 (Left): The width is given as 1 m. The height is 3 m.
Area 1 = $3 \times 1 = 3 \text{ sq m}$.
- Rectangle 2 (Middle): This is the top connecting part. Its width is 3 m. Its height is the total height (3 m) minus the height of the inner gap (2 m), which is $3 - 2 = 1$ m.
Area 2 = $1 \times 3 = 3 \text{ sq m}$.
- Rectangle 3 (Right): The width is given as 1 m. The height is 3 m.
Area 3 = $3 \times 1 = 3 \text{ sq m}$.
Total Area of Figure b:
Total Area = Area 1 + Area 2 + Area 3
Total Area = $3 + 3 + 3 = 9 \text{ sq m}$.
The area of figure b is 9 sq m.
Figure it Out (Page 139)
Cut out the tangram pieces given at the end of your textbook.

Question 1. Explore and figure out how many pieces have the same area.
Answer:
Based on the tangram pieces, let's explore which ones have the same area. We can compare their sizes by seeing how many of the smallest pieces can fit into the larger ones.
The Pieces:
- A and B: Large Triangles
- F: Medium Triangle
- D: Square
- E and C: Small Triangles
- G: Parallelogram
Comparing the Areas:
Let's use the smallest pieces, the small triangles (E and C), as our basic unit of area.
- Pieces E and C (Small Triangles): These two triangles are identical in size and shape.
So, Area(E) = Area(C).
- Piece F (Medium Triangle): If you place the two small triangles (E and C) together along their longest side, they form a triangle that is identical in size and shape to the medium triangle, F.
So, Area(F) = Area(E) + Area(C). This means the area of F is twice the area of one small triangle.
- Piece D (Square): You can also form the shape of the square (D) by placing the two small triangles (E and C) together.
So, Area(D) = Area(E) + Area(C). This means the area of D is also twice the area of one small triangle.
- Piece G (Parallelogram): Similarly, the parallelogram (G) can also be formed by joining the two small triangles (E and C).
So, Area(G) = Area(E) + Area(C). This means the area of G is also twice the area of one small triangle.
- Pieces A and B (Large Triangles): These two triangles are identical in size and shape.
So, Area(A) = Area(B).
A large triangle (like A or B) can be formed by joining the medium triangle (F) and the two small triangles (E and C).
So, Area(A) = Area(F) + Area(E) + Area(C). Since Area(F) is equal to two small triangles, the area of a large triangle is equal to four small triangles.
Conclusion:
By comparing all the areas, we can group the pieces that are the same size:
- Group 1 (Largest): The two large triangles, A and B, have the same area.
- Group 2 (Medium): The medium triangle (F), the square (D), and the parallelogram (G) all have the same area.
- Group 3 (Smallest): The two small triangles, E and C, have the same area.
Question 2. How many times bigger is Shape D as compared to Shape C? What is the relationship between Shapes C, D and E?
Answer:
This question uses the original labels from the image, where:
- C is a small triangle.
- D is the square.
- E is also a small triangle.
How many times bigger is Shape D as compared to Shape C?
Shape C is one of the two smallest triangles. Let's say its area is 1 unit.
Shape D is the square. You can form the square (D) by placing the two small triangles (C and E) together.
So, the area of the square (D) is equal to the area of two small triangles.
Area(D) = Area(C) + Area(E)
Since Area(C) = Area(E), we can say:
Area(D) = 2 × Area(C)
Therefore, Shape D is twice as big as Shape C.
What is the relationship between Shapes C, D and E?
The relationship is based on their areas:
- Shapes C and E are the two small triangles, so they have the same area.
- Shape D is the square, and its area is equal to the sum of the areas of the two small triangles.
So, the relationship is: Area(C) = Area(E), and Area(D) = Area(C) + Area(E).
Question 3. Which shape has more area: Shape D or F? Give reasons for your answer.
Answer:
In this question, the shapes are:
- D is the square.
- F is the medium-sized triangle.
To compare their areas, we can see how many of the smallest triangles (like C or E) can fit into each shape.
Area of Shape D (the square):
As we found before, the square can be made by joining the two small triangles (C and E). So, its area is equal to 2 small triangles.
Area of Shape F (the medium triangle):
The medium triangle can also be made by joining the two small triangles (C and E). So, its area is also equal to 2 small triangles.
Conclusion:
Neither shape has more area. They have the same area.
Reason: Both Shape D (the square) and Shape F (the medium triangle) have an area that is equal to the area of two of the smallest tangram triangles combined. Since they are both equal to the same amount of area, their areas must be equal to each other.
Question 4. Which shape has more area: Shape F or G? Give reasons for your answer.
Answer:
In this question, the shapes are:
- F is the medium-sized triangle.
- G is the parallelogram.
We will compare their areas using the smallest triangles (C or E) as a reference.
Area of Shape F (the medium triangle):
The medium triangle can be formed by joining two small triangles (C and E). Its area is equal to 2 small triangles.
Area of Shape G (the parallelogram):
The parallelogram can also be formed by joining two small triangles (C and E). Its area is also equal to 2 small triangles.
Conclusion:
Neither shape has more area. They have the same area.
Reason: Both Shape F (the medium triangle) and Shape G (the parallelogram) have an area equal to two of the smallest tangram triangles. Therefore, their areas are equal.
Question 5.
What is the area of Shape A as compared to Shape G? Is it twice as big? Four times as big?
Hint: In the tangram pieces, by placing the shapes over each other, we can find out that Shapes A and B have the same area, Shapes C and E have the same area. You would have also figured out that Shape D can be exactly covered using Shapes C and E, which means Shape D has twice the area of Shape C or shape E, etc.
Answer:
To compare the areas, let's use the area of the smallest triangle (C or E) as our basic unit.
- Area of one small triangle (C or E) = 1 unit.
Area of Shape G (the parallelogram):
Shape G can be made from two small triangles. So, its area is 2 units.
Area of Shape A (the large triangle):
Shape A can be made from two medium triangles (like F), or from one medium triangle (F) and two small triangles (C and E). Since a medium triangle is worth 2 units, the large triangle is worth $2 + 2 = 4$ units.
So, the area of Shape A is 4 units.
Comparison:
To see how many times bigger Shape A is, we divide its area by the area of Shape G:
$\frac{\text{Area of Shape A}}{\text{Area of Shape G}} = \frac{4 \text{ units}}{2 \text{ units}} = 2$
This means the area of Shape A is 2 times the area of Shape G.
Shape A is twice as big as Shape G.
Question 6. Can you now figure out the area of the big square formed with all seven pieces in terms of the area of Shape C?
Answer:
Yes, we can find the total area by adding up the areas of all seven pieces. We will measure the area in "units," where 1 unit is the area of the small triangle, Shape C.
Let's list the area of each piece in terms of Shape C:
- A (Large Triangle): 4 units
- B (Large Triangle): 4 units
- C (Small Triangle): 1 unit
- D (Square): 2 units
- E (Small Triangle): 1 unit
- F (Medium Triangle): 2 units
- G (Parallelogram): 2 units
Now, let's add them all up:
Total Area = Area(A) + Area(B) + Area(C) + Area(D) + Area(E) + Area(F) + Area(G)
Total Area = $4 + 4 + 1 + 2 + 1 + 2 + 2$
Total Area = $16$ units.
Since 1 unit is the area of Shape C, the total area of the big square is 16 times the area of Shape C.
Question 7. Arrange these 7 pieces to form a rectangle. What will be the area of this rectangle in terms of the area of Shape C now? Give reasons for your answer.
Answer:
The area of the rectangle will be 16 times the area of Shape C.
Reason:
The area of a shape is the amount of space it covers. When we take the seven tangram pieces and arrange them into a new shape (like a rectangle), we are not adding or removing any pieces. We are simply changing their positions.
Since we are using the exact same seven pieces that formed the big square, the total area must remain the same.
In the previous question, we calculated that the total area of all seven pieces is 16 times the area of Shape C. Therefore, any shape you make using all seven pieces without any overlap will also have an area of 16 times the area of Shape C.
Question 8. Are the perimeters of the square and the rectangle formed from these 7 pieces different or the same? Give an explanation for your answer.
Answer:
The perimeters of the square and the rectangle will be different.
Explanation:
While the area of a shape made from the pieces always stays the same, the perimeter does not.
The perimeter is the distance around the outside edge of a shape. When we rearrange the seven pieces from a square into a rectangle, the way the pieces fit together changes. This changes which edges are on the outside and which are hidden on the inside.
For example, a long, thin rectangle will have a much larger perimeter than a compact square, even if they are made from the same pieces and have the same area.
Because the outer boundary is different for the square and the rectangle, their perimeters will also be different.
Intext Question (Page 140)

Answer:
To find the area of the figures, we will breakdown each shape into squares (S) and right triangles (R). We will calculate the total area based on these components.
We assume the following for our calculations:
- The area of one square (S) is 1 square unit.
- The area of one right triangle (R), which is half of a square, is 0.5 square units.
Area of the First Figure (Purple 'F' Shape)
The figure is described as being composed of 3 squares (3S) and 2 right triangles (2R).

- Area from squares: $3 \times 1 = 3$ square units.
- Area from triangles: $2 \times 0.5 = 1$ square unit.
Total Area:
Total Area = Area from squares + Area from triangles
Total Area = $3 + 1 = 4$ square units.
The area of the first figure is 4 square units.
Area of the Second Figure (Pink Heart Shape)
The figure is described as being composed of 6 squares (6S) and 6 right triangles (6R).

- Area from squares: $6 \times 1 = 6$ square units.
- Area from triangles: $6 \times 0.5 = 3$ square units.
Total Area:
Total Area = Area from squares + Area from triangles
Total Area = $6 + 3 = 9$ square units.
The area of the second figure is 9 square units.
Area of the Third Figure (Green 'U' Shape)
The figure is described as being composed of 7 squares (7S) and 6 right triangles (6R).

- Area from squares: $7 \times 1 = 7$ square units.
- Area from triangles: $6 \times 0.5 = 3$ square units.
Total Area:
Total Area = Area from squares + Area from triangles
Total Area = $7 + 3 = 10$ square units.
The area of the third figure is 10 square units.
Area of the Fourth Figure (Brown 'N' Shape)
The figure is described as being composed of 8 squares (8S) and 6 right triangles (6R).

- Area from squares: $8 \times 1 = 8$ square units.
- Area from triangles: $6 \times 0.5 = 3$ square units.
Total Area:
Total Area = Area from squares + Area from triangles
Total Area = $8 + 3 = 11$ square units.
The area of the fourth figure is 11 square units.
Intext Question (Page 141 - 142)
Question: On a squared grid paper (1 square = 1 square unit), make as many rectangles as you can whose lengths and widths are a whole number of units such that the area of the rectangle is 24 square units.
a. Which rectangle has the greatest perimeter?
b. Which rectangle has the least perimeter?
c. If you take a rectangle of area 32 sq cm, what will your answers be? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter as well as the least perimeter? Give examples and reasons for your answer.
Answer:
First, let's find all the possible rectangles with an area of 24 square units, where the length and width are whole numbers. To do this, we need to find all the pairs of factors for the number 24.
The factor pairs of 24 are:
- 1 and 24
- 2 and 12
- 3 and 8
- 4 and 6
Now, let's calculate the perimeter for each of these rectangles. The formula for the perimeter is $2 \times (\text{length} + \text{width})$.
| Length (units) | Width (units) | Area (sq units) | Perimeter (units) |
| 24 | 1 | 24 | $2 \times (24 + 1) = 50$ |
| 12 | 2 | 24 | $2 \times (12 + 2) = 28$ |
| 8 | 3 | 24 | $2 \times (8 + 3) = 22$ |
| 6 | 4 | 24 | $2 \times (6 + 4) = 20$ |
a. Which rectangle has the greatest perimeter?
Looking at the table, the greatest perimeter is 50 units. This corresponds to the rectangle with dimensions 24 units × 1 unit.
b. Which rectangle has the least perimeter?
Looking at the table, the least perimeter is 20 units. This corresponds to the rectangle with dimensions 6 units × 4 units.
c. If you take a rectangle of area 32 sq cm, what will your answers be? Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter as well as the least perimeter?
Let's repeat the process for an area of 32 sq cm.
The factor pairs of 32 are:
- 1 and 32
- 2 and 16
- 4 and 8
| Length (cm) | Width (cm) | Area (sq cm) | Perimeter (cm) |
| 32 | 1 | 32 | $2 \times (32 + 1) = 66$ |
| 16 | 2 | 32 | $2 \times (16 + 2) = 36$ |
| 8 | 4 | 32 | $2 \times (8 + 4) = 24$ |
For an area of 32 sq cm:
- The rectangle with the greatest perimeter is 32 cm × 1 cm, with a perimeter of 66 cm.
- The rectangle with the least perimeter is 8 cm × 4 cm, with a perimeter of 24 cm.
Prediction for any given area:
Yes, it is possible to predict the shape of the rectangles with the greatest and least perimeters for any given area.
Greatest Perimeter:
Prediction: For a fixed area, the rectangle with the greatest perimeter is always the one that is the longest and thinnest.
Reason: The perimeter is greatest when the difference between the length and width is largest. This always happens with the factor pair (1, Area). The shape is a long, thin strip.
Least Perimeter:
Prediction: For a fixed area, the rectangle with the least perimeter is always the one that is most "square-like."
Reason: The perimeter is smallest when the length and width are closest to each other in value. For example, for an area of 36, the factor pairs are (1,36), (2,18), (3,12), (4,9), and (6,6). The pair (6,6) gives a square, which has the least perimeter ($2 \times (6+6) = 24$). For an area of 24, the pair (4,6) is the closest, giving the least perimeter.
Intext Question (Page 142)
Question:
Draw a rectangle on a piece of paper and draw one of its diagonals.
Cut the rectangle along that diagonal and get two triangles.
Check! whether the two triangles overlap each other exactly. Do they have the same area?
Try this with more rectangles having different dimensions. You can check this for a square as well.
Answer:
Yes, the two triangles formed by cutting a rectangle along its diagonal will always overlap each other exactly. And yes, they will always have the same area.
Explanation
Let's imagine any rectangle. When you draw a diagonal line from one corner to the opposite corner and cut along it, you create two right-angled triangles.

1. Do they overlap exactly?
Yes. The two triangles are identical, or congruent. You can think of them as mirror images of each other. If you were to flip one of the triangles over and place it on top of the other, it would match perfectly. This is because:
- They share one side (the diagonal you cut along).
- The other two sides of each triangle are simply the original length and width of the rectangle.
Since all three sides of one triangle match the three sides of the other, they are identical in shape and size and will overlap exactly.
2. Do they have the same area?
Yes. Because the two triangles are identical in size, they must have the same area. The diagonal cut splits the rectangle into two equal halves. Therefore, the area of each triangle is exactly half the area of the original rectangle.
Area of each triangle = $\frac{1}{2} \times \text{Area of the rectangle}$
Trying with More Examples
This rule is always true for any rectangle, no matter its dimensions.
Example with a different rectangle (e.g., 8 cm × 3 cm):
- The area of the whole rectangle is $8 \times 3 = 24$ sq cm.
- If you cut it along the diagonal, you get two identical triangles.
- The area of each triangle will be $24 \div 2 = 12$ sq cm. They have the same area.

Example with a square (e.g., 5 cm × 5 cm):
A square is just a special type of rectangle where the length and width are equal. The same rule applies.
- The area of the square is $5 \times 5 = 25$ sq cm.
- If you cut it along the diagonal, you get two identical isosceles right-angled triangles.
- The area of each triangle will be $25 \div 2 = 12.5$ sq cm. They have the same area.

Conclusion
For any rectangle or square, a single cut along a diagonal will always produce two identical triangles that have the exact same area.
Intext Question (Page 142)
Question: Can you draw any inferences from this exercise? Please write it here.
Answer:
Yes, several important inferences can be drawn from this exercise.
Inference 1: A Diagonal Splits a Rectangle into Two Identical Triangles
The most direct observation is that a diagonal of any rectangle (or square) divides it into two right-angled triangles that are perfectly identical in size and shape. In geometry, these are called congruent triangles. Because they are congruent, they will always have the same area.
Inference 2: A Formula for the Area of a Right-Angled Triangle
This is the most powerful inference. Since the two triangles are equal and they perfectly make up the rectangle, the area of one of these triangles must be exactly half the area of the original rectangle.
We know the formula for the area of a rectangle is:
Area of Rectangle = length × width
The 'length' and 'width' of the rectangle become the two perpendicular sides of the right-angled triangle. We often call these the 'base' and 'height' of the triangle.
Therefore, we can create a formula for the area of a right-angled triangle:
Area of a Right-Angled Triangle = $\frac{1}{2} \times \text{base} \times \text{height}$
Inference 3: Generalization for All Triangles
This exercise provides the foundation for understanding the area of all triangles, not just right-angled ones. Any triangle can be seen as half of a parallelogram (and a rectangle is a special type of parallelogram). This means the formula we discovered, Area = $\frac{1}{2} \times \text{base} \times \text{height}$, is a universal formula for finding the area of any triangle.
Intext Question (Page 143)
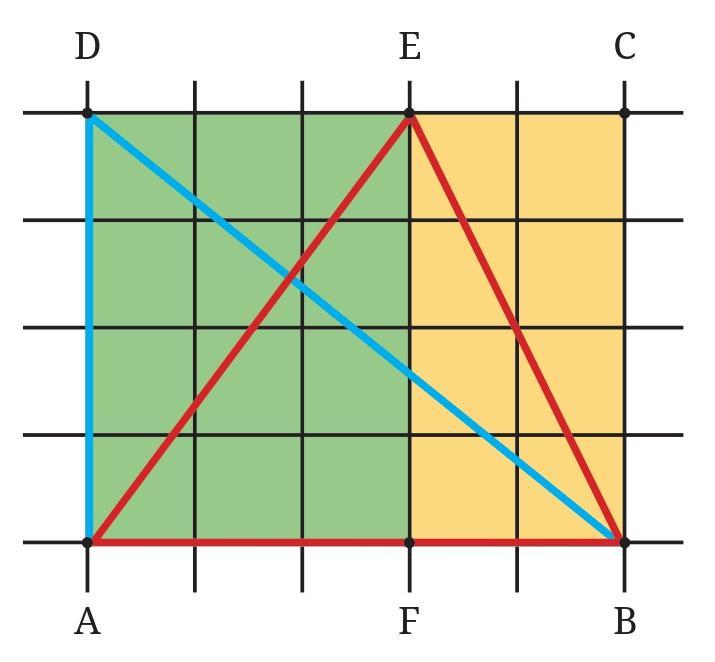
Question: Use your understanding from previous grades to calculate the area of any closed figure using grid paper and —
1. Find the area of blue triangle BAD. __________
2. Find the area of red triangle ABE. ___________
Area of rectangle ABCD = ________________
Answer:
To find the area of the shapes on the grid, we will count the number of squares. We will assume that each small square on the grid has an area of 1 square unit.
1. Find the area of blue triangle BAD.
Triangle BAD is a right-angled triangle. Its two perpendicular sides are AD (the height) and AB (the base).
- Base (AB): By counting the squares along the bottom, we see the length of the base AB is 5 units.
- Height (AD): By counting the squares along the left side, we see the length of the height AD is 4 units.
The area of a triangle is calculated using the formula:
Area = $\frac{1}{2} \times \text{base} \times \text{height}$
Substitute the values for triangle BAD:
Area of triangle BAD = $\frac{1}{2} \times 5 \times 4$
Area of triangle BAD = $\frac{1}{2} \times 20 = 10$ square units.
Alternatively, we can see that triangle BAD is exactly half of the rectangle ABCD.
Area of rectangle ABCD = $5 \times 4 = 20$ square units.
Area of triangle BAD = $\frac{1}{2} \times 20 = 10$ square units.
The area of the blue triangle BAD is 10 square units.
2. Find the area of red triangle ABE.
Triangle ABE has its base on the bottom line and its highest point at E.
- Base (AB): The length of the base AB is 5 units.
- Height: The height of the triangle is the perpendicular distance from the base AB to the highest point E. By counting the grid lines, we see the height is 4 units.
Using the area formula for a triangle:
Area = $\frac{1}{2} \times \text{base} \times \text{height}$
Substitute the values for triangle ABE:
Area of triangle ABE = $\frac{1}{2} \times 5 \times 4$
Area of triangle ABE = $\frac{1}{2} \times 20 = 10$ square units.
The area of the red triangle ABE is 10 square units.
Area of rectangle ABCD
The rectangle ABCD is formed by the grid lines.
- Length (AB): 5 units
- Width (AD): 4 units
The formula for the area of a rectangle is:
Area = length × width
Area of rectangle ABCD = $5 \times 4 = 20$ square units.
The area of rectangle ABCD is 20 square units.
Figure it Out (Page 144)
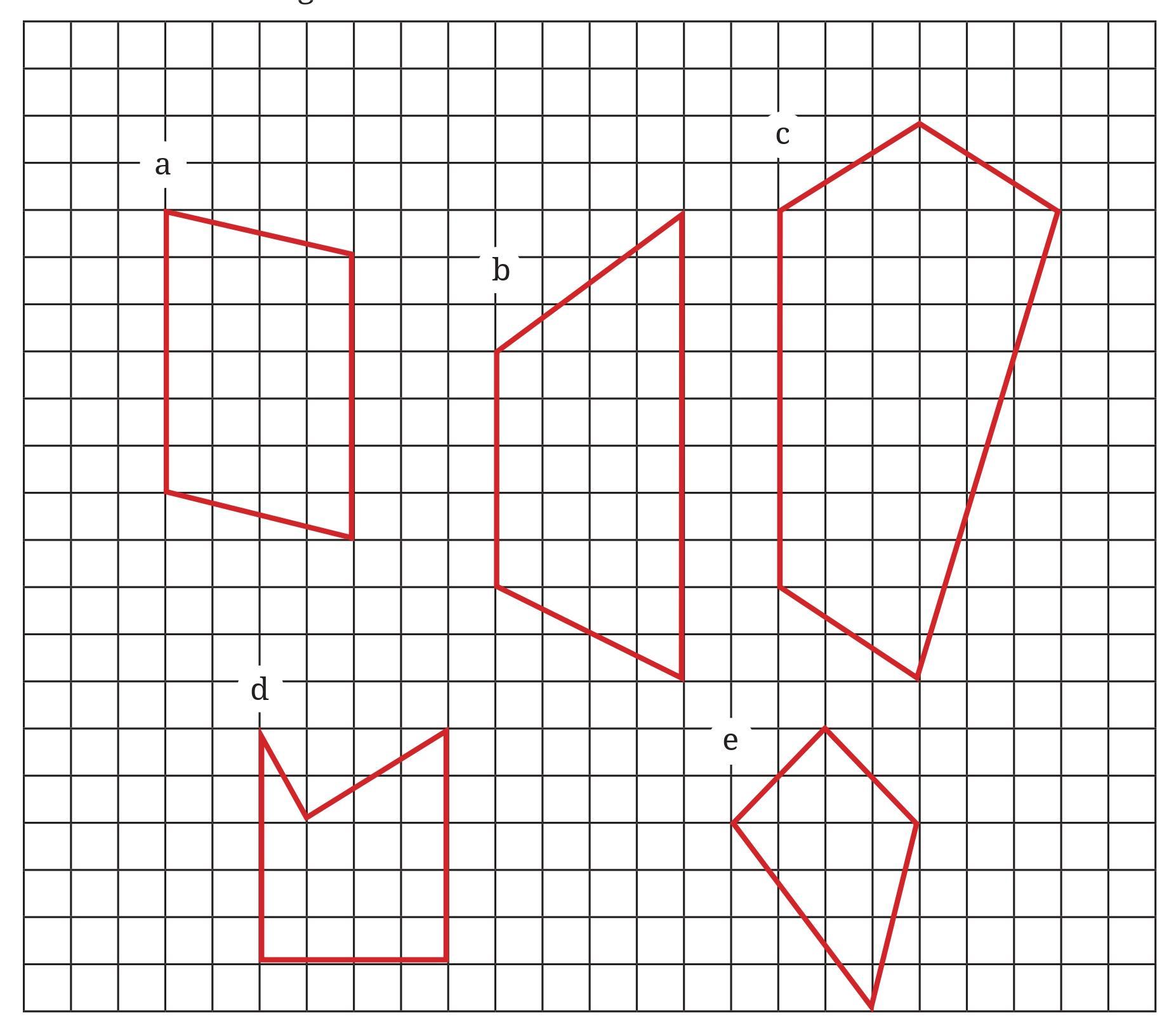
Answer:
Based on the decompositions and dimensions, we will calculate the area of each figure. The area of a rectangle is calculated using the formula $A = \text{length} \times \text{breadth}$, and the area of a triangle is calculated using the formula $A = \frac{1}{2} \times \text{base} \times \text{height}$.
Area of Figure (a)
The figure is divided into two triangles and one rectangle.

1. Area of the first triangle:
Given: base (b) = 1 unit, height (h) = 4 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 1 \times 4 = 2 $ sq. units.
2. Area of the second triangle:
Given: base (b) = 1 unit, height (h) = 4 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 1 \times 4 = 2 $ sq. units.
3. Area of the rectangle:
Given: length (l) = 5 units, breadth (b) = 4 units
$ \text{Area} = l \times b = 5 \times 4 = 20 $ sq. units.
Total Area of Figure (a) = Area of triangle 1 + Area of triangle 2 + Area of rectangle
$ = 2 + 2 + 20 = 24 $ sq. units.
Area of Figure (b)
The figure is divided into two triangles and one rectangle.

1. Area of the first triangle:
Given: base (b) = 3 units, height (h) = 4 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 3 \times 4 = 6 $ sq. units.
2. Area of the second triangle:
Given: base (b) = 2 units, height (h) = 4 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 2 \times 4 = 4 $ sq. units.
3. Area of the rectangle:
Given: length (l) = 5 units, breadth (b) = 4 units
$ \text{Area} = l \times b = 5 \times 4 = 20 $ sq. units.
Total Area of Figure (b) = Area of triangle 1 + Area of triangle 2 + Area of rectangle
$ = 6 + 4 + 20 = 30 $ sq. units.
Area of Figure (c)
The figure is divided into three triangles and one rectangle.

1. Area of the first triangle:
Given: base (b) = 12 units, height (h) = 3 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 12 \times 3 = 18 $ sq. units.
2. Area of the second triangle:
Given: base (b) = 2 units, height (h) = 3 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 2 \times 3 = 3 $ sq. units.
3. Area of the third triangle:
Given: base (b) = 2 units, height (h) = 3 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 2 \times 3 = 3 $ sq. units.
4. Area of the rectangle:
Given: length (l) = 8 units, breadth (b) = 3 units
$ \text{Area} = l \times b = 8 \times 3 = 24 $ sq. units.
Total Area of Figure (c) = Sum of areas of all parts
$ = 18 + 3 + 3 + 24 = 48 $ sq. units.
Area of Figure (d)
The figure is divided into two triangles and one rectangle.

1. Area of the first triangle:
Given: base (b) = 1 unit, height (h) = 2 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 1 \times 2 = 1 $ sq. unit.
2. Area of the second triangle:
Given: base (b) = 3 units, height (h) = 2 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 3 \times 2 = 3 $ sq. units.
3. Area of the rectangle:
Given: length (l) = 4 units, breadth (b) = 3 units
$ \text{Area} = l \times b = 4 \times 3 = 12 $ sq. units.
Total Area of Figure (d) = Area of triangle 1 + Area of triangle 2 + Area of rectangle
$ = 1 + 3 + 12 = 16 $ sq. units.
Area of Figure (e)
The figure is divided into two triangles.

1. Area of the first triangle:
Given: base (b) = 4 units, height (h) = 2 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 4 \times 2 = 4 $ sq. units.
2. Area of the second triangle:
Given: base (b) = 4 units, height (h) = 4 units
$ \text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 4 \times 4 = 8 $ sq. units.
Total Area of Figure (e) = Area of triangle 1 + Area of triangle 2
$ = 4 + 8 = 12 $ sq. units.
Intext Question (Page 145 - 148)
Question: Using 9 unit squares, solve the following.
1. What is the smallest perimeter possible?
2. What is the largest perimeter possible?
3. Make a figure with a perimeter of 18 units.
4. Can you make other shaped figures for each of the above three perimeters, or is there only one shape with that perimeter? What is your reasoning?
Answer:
This problem explores the relationship between the area and perimeter of shapes made from a fixed number of unit squares. Here, we are using 9 unit squares, so the area of every figure is fixed at 9 square units.
The perimeter of a figure is the total length of its boundary. For figures made of unit squares, the perimeter is the number of exposed sides of the squares. The total number of sides for 9 separate squares is $9 \times 4 = 36$. When two squares are placed adjacent to each other, they share an edge, and the total perimeter is reduced by 2. Therefore, the perimeter $P$ can be calculated as $P = 36 - 2S$, where $S$ is the number of shared edges between squares.
1. What is the smallest perimeter possible?
To achieve the smallest perimeter, we need to arrange the squares in the most compact way possible. This maximizes the number of shared edges between the squares.
The most compact arrangement of 9 squares is a 3x3 square.

Let's calculate its perimeter by counting the exposed sides:
Perimeter = (3 top sides) + (3 bottom sides) + (3 left sides) + (3 right sides) = $3+3+3+3 = 12$ units.
This arrangement has 12 shared internal edges, which is the maximum possible for 9 squares. Using the formula: $P = 36 - 2(12) = 36 - 24 = 12$ units.
So, the smallest possible perimeter is 12 units.
2. What is the largest perimeter possible?
To achieve the largest perimeter, we need to arrange the squares in the least compact way. This minimizes the number of shared edges while keeping all squares connected in a single figure.
To connect 9 squares, we need a minimum of $9-1=8$ shared edges. An arrangement that achieves this is a straight line, forming a 1x9 rectangle.

Let's calculate its perimeter:
Perimeter = $2 \times (\text{length} + \text{width}) = 2 \times (9 + 1) = 2 \times 10 = 20$ units.
This arrangement has 8 shared internal edges. Using the formula: $P = 36 - 2(8) = 36 - 16 = 20$ units.
So, the largest possible perimeter is 20 units.
3. Make a figure with a perimeter of 18 units.
To get a perimeter of 18 units, we need to find the required number of shared edges, $S$.
$18 = 36 - 2S$
$2S = 36 - 18$
$2S = 18$
$S = 9$
We need to arrange the 9 squares so that there are exactly 9 shared edges. Here is one possible shape:
This shape is a hollow 3x3 square with one extra square attached to an outer side.

Let's verify its perimeter by counting the outer and inner boundaries.
Outer boundary = $3$ (top) $+ 3$ (left) $+ 3$ (bottom) $+ 1$ (top right side) $+ 1$ (added square top) $+ 1$ (added square right) $+ 1$ (added square bottom) $+ 1$ (bottom right side) = $14$ units.
Inner boundary (hole) = $1+1+1+1 = 4$ units.
Total Perimeter = $14 + 4 = 18$ units.
4. Can you make other shaped figures for each of the above three perimeters, or is there only one shape with that perimeter? What is your reasoning?
Smallest Perimeter (12 units): There is only one shape (the 3x3 square), ignoring rotations and reflections. The reason is that the minimum perimeter is achieved by the most compact shape, which maximizes the number of internal shared edges. Any deviation from the 3x3 square arrangement involves moving a square, which will break more shared edges than it can form, thus increasing the perimeter.
Largest Perimeter (20 units): There are many possible shapes. The largest perimeter corresponds to the minimum number of shared edges (8) required to keep the figure connected. Any "snake-like" or "branching" arrangement where no loops are formed will have this perimeter. For example, a 1x9 line, an L-shape, or a zig-zag pattern all have 8 shared edges and a perimeter of 20.

Perimeter of 18 units: There are many possible shapes. Since this perimeter is intermediate, it corresponds to an intermediate number of shared edges (9). There is more than one way to arrange 9 squares to have 9 shared edges. Besides the one shown in part 3, here is another example (a "plus" sign shape):

This demonstrates that for perimeters between the minimum and maximum possible values, there are generally multiple configurations of the squares that can result in the same perimeter.
Let’s do something tricky now! We have a figure below having perimeter 24 units.
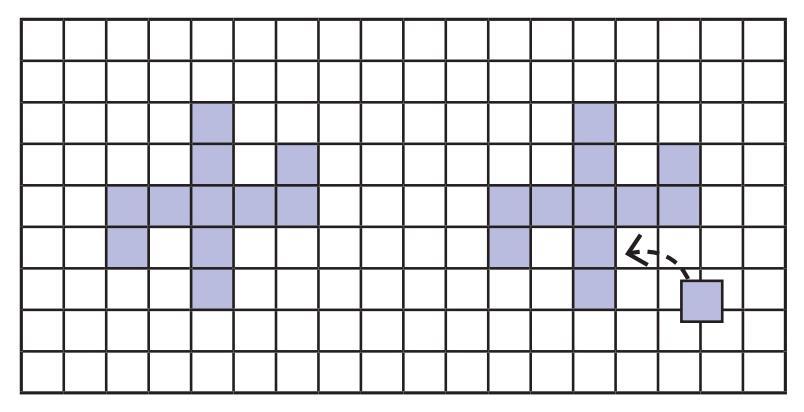
Experiment placing this new square at different places and think what the change in perimeter will be. Can you place the square so that the perimeter: a) increases; b) decreases; c) stays the same?
Answer:
The question is about the shape in the picture and what happens to its perimeter when we add one more square.
Step 1: Understand the Starting Shape
If you count the outside edges shape provided, you will find it has a perimeter of 24 units.
Step 2: Solve the Puzzle in the Picture
The picture shows us adding a new square to one corner of the right-hand shape. The question is, what does this do to the perimeter?
Let's think of it as a "trade":
- When we attach the new square, it covers up 2 side of the old shape. That side is now hidden and is not part of the perimeter anymore.
- But the new square itself adds 2 new sides to the outside boundary.
So, we lost 2 side but also gained 2 sides. The net change is: Gain 2 - Lose 2 = 0.
This means the perimeter stays the same.
The new perimeter will be $23 + 0 = 24$ units.
Step 3: Experimenting with Other Placements
Now, let's see if we can get different results by placing the square somewhere else.
Case 1: The Perimeter Gets BIGGER
This happens when you place the new square so it only touches the old shape by one side.

The Trade:
- You cover up 1 side of the old shape.
- The new square adds 3 new sides to the outside.
Result: You added 3 sides but took away 1. The total perimeter increases by 2. (3 - 1 = 2).
Case 2: The Perimeter Stays the SAME
This is the exact situation you described! It's a perfect trade. This happens when you fit the new square into an "inner corner" so it touches the old shape by two sides.

The Trade:
- You cover up 2 sides of the old shape.
- The new square adds 2 new sides to the outside.
Result: You added 2 sides and took away 2. It's an even trade! The perimeter stays exactly the same. (2 - 2 = 0).
Case 3: The Perimeter Gets SMALLER
This happens when you place the new square into a deeper space or a "hollow spot" where it can touch the old shape by three sides.

The Trade:
- You cover up 3 sides of the old shape.
- The new square can only add 1 new side to the outside.
Result: You added only 1 side but took away 3. The total perimeter decreases by 2. (1 - 3 = -2).
The Secret Trick
So, the logic is simple! To know what will happen to the perimeter, you just need to count how many sides the new square is touching on the old shape.
- If it touches 1 side, the perimeter goes UP by 2.
- If it touches 2 sides, the perimeter STAYS THE SAME.
- If it touches 3 sides, the perimeter goes DOWN by 2.
Below is the house plan of Charan. It is in a rectangular plot. Look at the plan. What do you notice?
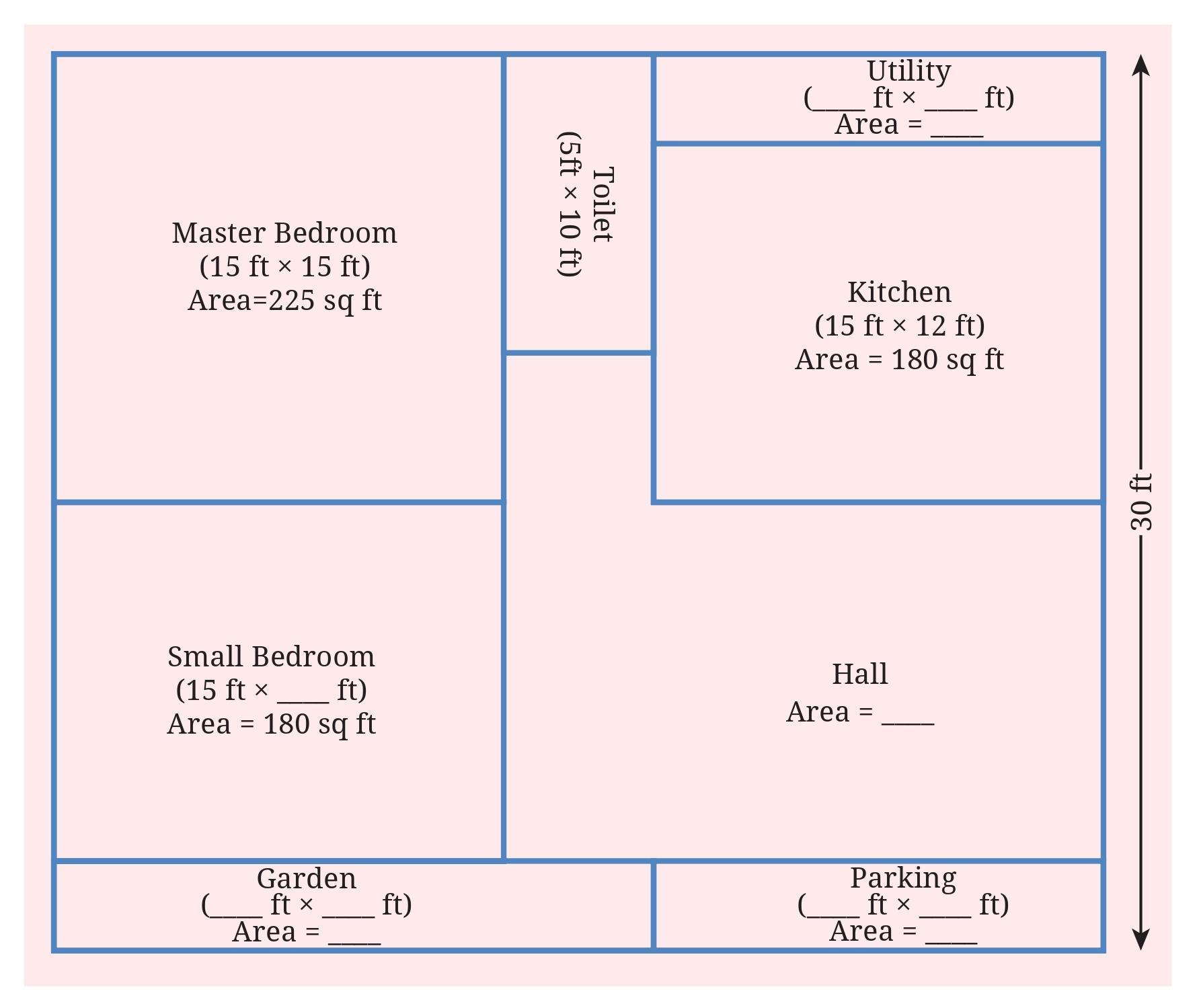
b. Find out the area of his house.
Answer:
To solve this problem, we carefully analyse the given house plan, use the provided dimensions to find the missing ones, and then calculate the areas. We treat the entire plan as a large rectangle and use the alignment of the rooms to deduce the unknown measurements. (All numeric work and formulae are given in Indian perspective.)
Given:
Master Bedroom: (15 ft × 15 ft), Area = 225 sq ft.
Small Bedroom: (15 ft × ___ ft), Area = 180 sq ft.
Toilet: (5 ft × 10 ft).
Kitchen: (15 ft × 12 ft), Area = 180 sq ft.
Plot height (vertical) = 30 ft.
Other regions labelled: Utility (top-right narrow strip), Garden (bottom-left strip), Parking (bottom-right strip), Hall (central/lower-right built-up portion).
To Find:
(1) Missing linear measurements (Small Bedroom width, Utility, Garden, Parking).
(2) Area of each such part (where missing).
(3) Total area of the house (built-up area) in sq ft.
Solution (step-by-step):
1. Small Bedroom (find missing side)
Area $= \text{Length} \times \text{Breadth}$. Given area $=180\text{ sq ft}$ and one side $=15\text{ ft}$. Thus
$180 = 15 \times \text{Missing Dimension}$
So, $\text{Missing Dimension} = \dfrac{180}{15} = 12\text{ ft}$.
Therefore Small Bedroom = (15 ft × 12 ft), Area = 180 sq ft.
2. Garden (find dimensions & area)
The vertical (height) of the Garden is the leftover of the column that contains Master Bedroom and Small Bedroom:
$ \text{Height of Garden} = 30\text{ ft (total)} - 15\text{ ft (Master)} - 12\text{ ft (Small)} \ $$ = 3\text{ ft}.$
The horizontal length of the Garden equals the width of Master Bedroom (15 ft) plus the width of the middle vertical strip that contains the Toilet (5 ft):
$ \text{Length of Garden} = 15\text{ ft} + 5\text{ ft} = 20\text{ ft}.$
Garden dimensions = (20 ft × 3 ft), Area = $20 \times 3 = 60\text{ sq ft}$.
3. Utility (find dimensions & area)
The rightmost vertical column (where Kitchen and Utility lie) has horizontal width $=15\text{ ft}$ (same as Master Bedroom width). The Kitchen height = 12 ft while the top row height that aligns with Master Bedroom is 15 ft, so
$ \text{Utility height} = 15 - 12 = 3\text{ ft}.$
Utility dimensions = (15 ft × 3 ft), Area = $15 \times 3 = 45\text{ sq ft}$.
4. Parking (find dimensions & area)
The Parking lies under the rightmost column; its horizontal length = 15 ft and its height equals the Garden's height = 3 ft.
Parking dimensions = (15 ft × 3 ft), Area = $15 \times 3 = 45\text{ sq ft}$.
5. Toilet and Kitchen (verification)
Toilet: (5 ft × 10 ft) ⇒ Area = $5 \times 10 = 50\text{ sq ft}$ (given by plan).
Kitchen: (15 ft × 12 ft) ⇒ Area = $15 \times 12 = 180\text{ sq ft}$ (given by plan).
6. Hall (find area)
We compute the total plot dimensions first.
Total plot width = width of Master column (15 ft) + middle strip/Toilet column (5 ft) + right column (15 ft) = $15 + 5 + 15 = 35\text{ ft}.$
Total plot height = $30\text{ ft}$ (given).
So total plot area $= 35 \times 30 = 1050\text{ sq ft}$. (This is the complete rectangle containing built-up area + open Garden & Parking.)
$ \text{Total plot area} = 35 \times 30 = 1050\text{ sq ft}$
... (i)
The open (outside) bottom strips: Garden area = 60 sq ft and Parking area = 45 sq ft. Sum = $60 + 45 = 105\text{ sq ft}$.
Therefore built-up (house) area = Total plot area − (Garden + Parking) = $1050 - 105 = 945\text{ sq ft}$. (This is the area covered by rooms/covered Hall, etc.)
Now compute the sum of known interior room areas (excluding Hall):
Master Bedroom = 225 sq ft
Small Bedroom = 180 sq ft
Toilet = 50 sq ft
Kitchen = 180 sq ft
Utility = 45 sq ft
Sum of known rooms = $225 + 180 + 50 + 180 + 45 = 680\text{ sq ft}.$
Hence Hall area = Built-up area − Sum(known rooms) = $945 - 680 = 265\text{ sq ft}.$
Total Area of Hall = 265 sq ft.
Summary of Missing Measurements and Areas:
| Part | Dimensions (ft) | Area (sq ft) |
| Master Bedroom | 15 × 15 | 225 |
| Small Bedroom | 15 × 12 | 180 |
| Toilet | 5 × 10 | 50 |
| Kitchen | 15 × 12 | 180 |
| Utility | 15 × 3 | 45 |
| Hall | — (irregular combined rectangles) | 265 |
| Garden | 20 × 3 | 60 |
| Parking | 15 × 3 | 45 |
| Total (Built-up area) | — | 945 |
Final Answer:
Small Bedroom: (15 ft × 12 ft), Area = 180 sq ft.
Utility: (15 ft × 3 ft), Area = 45 sq ft.
Garden: (20 ft × 3 ft), Area = 60 sq ft.
Parking: (15 ft × 3 ft), Area = 45 sq ft.
Hall Area: 265 sq ft.
Total (Built-up) Area of the House: 945 sq ft.
Now, find out the missing dimensions and area of Sharan’s home. Below is the plan:
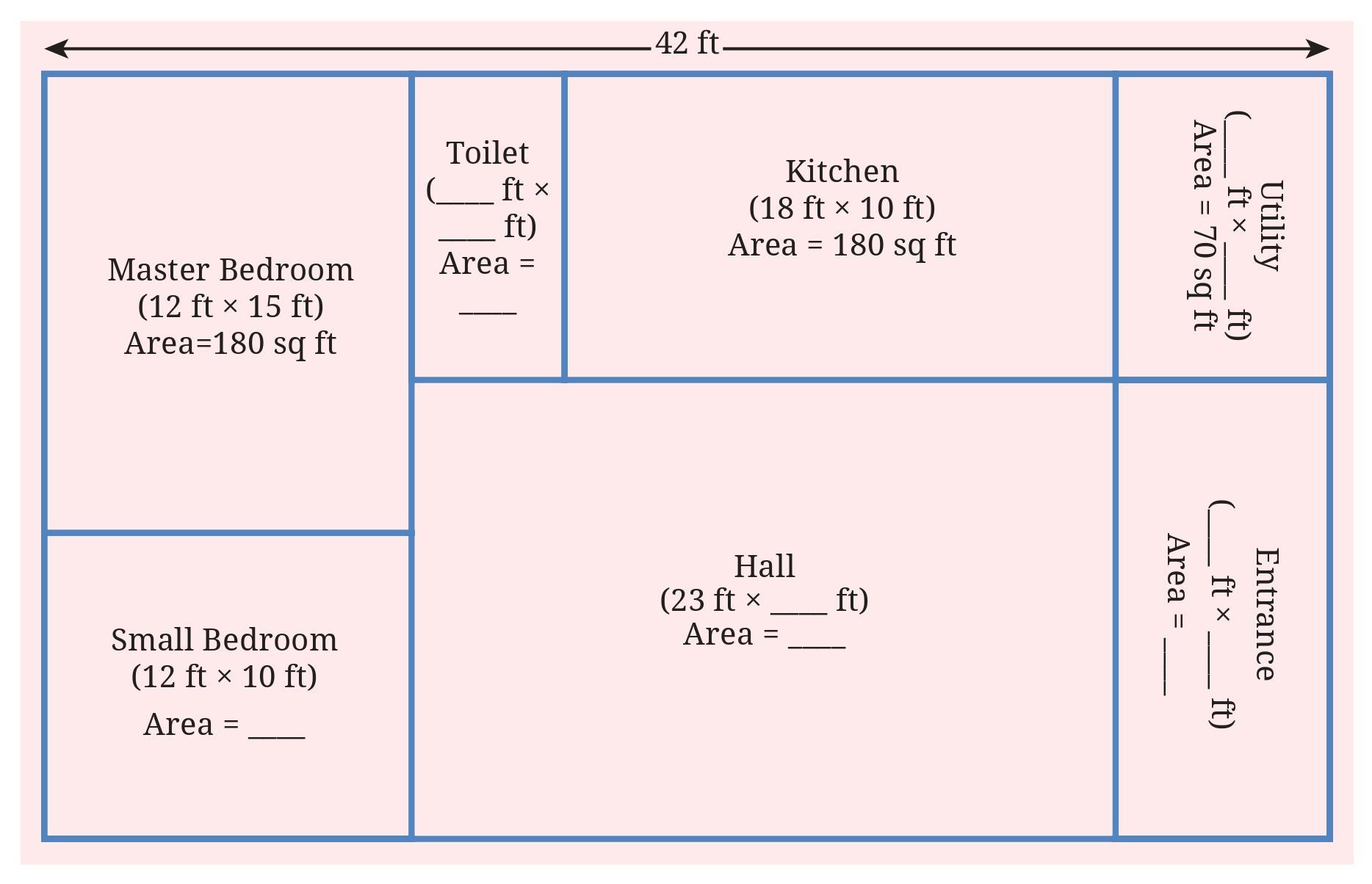
b. Find out the area of his house.
Answer:
To solve this problem, we carefully examine the given plan of Sharan’s home, use the provided measurements to find the missing ones, and then calculate the areas. All workings follow the Indian perspective and use $\,\text{Area}=\text{Length}\times\text{Breadth}\,$ where needed.
Given:
Master Bedroom: (12 ft × 15 ft), Area = 180 sq ft.
Small Bedroom: (12 ft × 10 ft), Area = ____ (to be found).
Toilet: (____ ft × ____ ft), Area = ____ (to be found).
Kitchen: (18 ft × 10 ft), Area = 180 sq ft.
Utility: (____ ft × ____ ft), Area = 70 sq ft. (given)
Hall: (23 ft × ____ ft), Area = ____ (to be found).
Total plot width (horizontal) = 42 ft.
To Find:
(1) Missing linear measurements: Toilet width/height, Utility dimensions (verify), Entrance dimensions.
(2) Area of Small Bedroom, Toilet, Hall, Entrance (where missing).
(3) Verify the total area balance of the plot.
Solution (step-by-step):
1. Find Small Bedroom area
Small Bedroom dimensions are given as (12 ft × 10 ft). So
$\text{Area of Small Bedroom} = 12 \times 10 = 120\text{ sq ft}.$
2. Find the width of the rightmost vertical strip (Utility + Entrance)
The Utility is a vertical rectangle at the top-right with area $70\text{ sq ft}$. From the plan the Utility's height matches the Kitchen height, i.e. $10\text{ ft}$. Thus
$\text{Utility width} = \dfrac{\text{Utility area}}{\text{Utility height}} = \dfrac{70}{10} = 7\text{ ft}.$
So the rightmost vertical strip width = 7 ft.
3. Find the width of the Toilet column
The plot is divided vertically into four columns (from left):
Left column (Master & Small) width = 12 ft,
Toilet column width = call it $w_T$,
Kitchen column width = 18 ft,
Rightmost strip (Utility/Entrance) width = 7 ft.
$12 + w_T + 18 + 7 = 42$
(Sum of column widths) ...(i)
From (i): $w_T = 42 - (12+18+7) = 42 - 37 = 5\text{ ft}.$
Toilet column width = 5 ft.
4. Find Toilet dimensions and area
Toilet occupies the top portion of the toilet column; its height equals the Kitchen height $=10\text{ ft}$ (from the plan). So
Toilet dimensions $= (5\text{ ft} \times 10\text{ ft})$.
Area of Toilet $= 5 \times 10 = 50\text{ sq ft}.$
5. Find total plot height and Entrance dimensions
Look at the left column: Master Bedroom height = 15 ft and Small Bedroom height = 10 ft. So total plot height
$\text{Total height} = 15 + 10 = 25\text{ ft}.$
The Entrance occupies the lower part of the rightmost vertical strip; its height = Total height − Utility height = $25 - 10 = 15\text{ ft}$.
Entrance width = rightmost strip width = 7 ft.
Entrance dimensions = (7 ft × 15 ft). Area = $7 \times 15 = 105\text{ sq ft}$.
6. Find Hall dimensions and area
The Hall width across equals the combined width of Toilet column and Kitchen column, i.e.
$\text{Hall width} = 5 + 18 = 23\text{ ft}$ (this matches the given label).
Hall height equals the remaining vertical length below the top row of Kitchen = Total height − Kitchen height = $25 - 10 = 15\text{ ft}.$
Therefore Hall dimensions $= (23\text{ ft} \times 15\text{ ft}).$
Hall area $= 23 \times 15 = 345\text{ sq ft}.$
Check by total area balance:
Total plot area $= 42 \times 25 = 1050\text{ sq ft}$
... (ii)
Sum of all rooms / parts:
Master Bedroom = $12 \times 15 = 180\text{ sq ft}$
Small Bedroom = $12 \times 10 = 120\text{ sq ft}$
Toilet = $5 \times 10 = 50\text{ sq ft}$
Kitchen = $18 \times 10 = 180\text{ sq ft}$
Utility = $7 \times 10 = 70\text{ sq ft}$ (given)
Entrance = $7 \times 15 = 105\text{ sq ft}$
Hall = $23 \times 15 = 345\text{ sq ft}$
Now add: $180 + 120 + 50 + 180 + 70 + 105 + 345 = 1050\text{ sq ft}$ which equals total plot area (ii). The calculations are consistent.
Summary of Missing Measurements and Areas:
| Part | Dimensions (ft) | Area (sq ft) |
| Master Bedroom | 12 × 15 | 180 |
| Small Bedroom | 12 × 10 | 120 |
| Toilet | 5 × 10 | 50 |
| Kitchen | 18 × 10 | 180 |
| Utility | 7 × 10 | 70 |
| Entrance | 7 × 15 | 105 |
| Hall | 23 × 15 | 345 |
| Total (Plot area) | 42 × 25 | 1050 |
Final Answers:
Small Bedroom: (12 ft × 10 ft), Area = 120 sq ft.
Toilet: (5 ft × 10 ft), Area = 50 sq ft.
Utility: (7 ft × 10 ft), Area = 70 sq ft (given).
Entrance: (7 ft × 15 ft), Area = 105 sq ft.
Hall: (23 ft × 15 ft), Area = 345 sq ft.
Total plot area: 1050 sq ft. (All parts sum up correctly.)
Question: In each figure, find the missing value of either the length of a side or the area of a region.
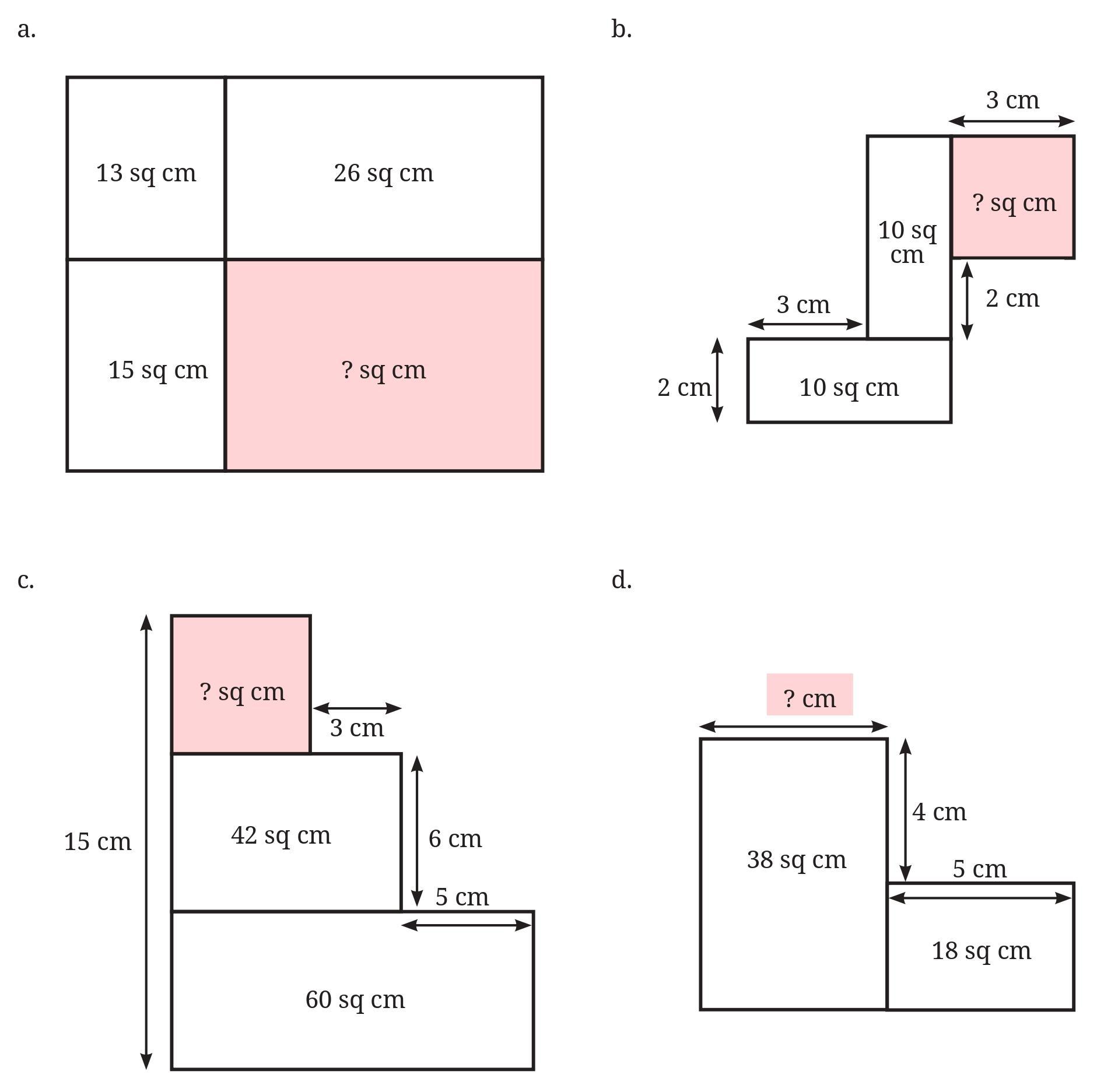
Answer:
To solve these problems, we use the fact that the area of a rectangle is $\,\text{Area}=\text{Length}\times\text{Breadth}\,$ and the given alignments in each figure. Each part (a), (b), (c) and (d) is solved separately below.
(a) Given / To find
Top-left area = $13\text{ sq cm}$, top-right area = $26\text{ sq cm}$, bottom-left area = $15\text{ sq cm}$. Find the bottom-right area.
Solution (a):
Let the top row height be $h$ and the bottom row height be $H$. Let the left column width be $w$ and the right column width be $W$.
From the top two areas: $13 = w\cdot h$ and $26 = W\cdot h$.
From the bottom-left area: $15 = w\cdot H$.
The bottom-right area is $W\cdot H$. Using $w=\dfrac{13}{h}$ and $W=\dfrac{26}{h}$ and $H=\dfrac{15}{w}$ we get
$W\cdot H = \dfrac{26}{h}\cdot \dfrac{15}{w} = \dfrac{26}{h}\cdot \dfrac{15}{13/h}$
...(i)
Simplifying (i): $W\cdot H = \dfrac{26\times15}{13} = 2\times15 = 30\text{ sq cm}$.
Answer (a): bottom-right area = $30\text{ sq cm}$.
(b) Given / To find
Bottom horizontal rectangle: area $=10\text{ sq cm}$ and its height (vertical) is $2\text{ cm}$. A vertical rectangle has area $=10\text{ sq cm}$ and its top is directly below the pink top-right square. The pink top-right square shows a horizontal arrow of $3\text{ cm}$ (its side). Find the area of the pink square.
Solution (b):
Bottom rectangle height $=2\text{ cm}$ and area $=10\text{ sq cm}$, so its length (width) is $ \dfrac{10}{2} = 5\text{ cm}$.
The pink top-right region is shown as a square with side length $3\text{ cm}$ (horizontal arrow). Hence its area is $3\times 3 = 9\text{ sq cm}$.
Answer (b): pink area = $9\text{ sq cm}$.
(c) Given / To find
Middle rectangle: area $=42\text{ sq cm}$ and a vertical arrow at its right indicates its height is $6\text{ cm}$. Bottom rectangle: area $=60\text{ sq cm}$; a horizontal arrow shows it extends $5\text{ cm}$ beyond the middle rectangle. Total left-column height = $15\text{ cm}$. Find the area of the pink top-left region.
Solution (c):
Middle rectangle height $=6\text{ cm}$, so its width $= \dfrac{42}{6} = 7\text{ cm}$.
Bottom rectangle width $= $ (middle width) $+5 = 7+5 = 12\text{ cm}$. Since bottom area $=60\text{ sq cm}$, bottom height $= \dfrac{60}{12} = 5\text{ cm}$.
Total height $=15\text{ cm}$, so the top pink height $= 15 - (\text{middle height}) - (\text{bottom height}) = 15 - 6 - 5 = 4\text{ cm}$.
The top pink region is a rectangle whose width equals the difference between the middle width and the horizontal gap (shown $3\text{ cm}$). Here middle width $=7\text{ cm}$ and gap $=3\text{ cm}$, so pink width $=7-3=4\text{ cm}$. Thus the pink region is $4\text{ cm}\times 4\text{ cm}$.
Area (c): top pink area $=4\times4 = 16\text{ sq cm}$.
(d) Given / To find
Large left rectangle: area $=38\text{ sq cm}$. A vertical arrow shows the difference between its top and the top of the right small rectangle is $4\text{ cm}$. Right small rectangle: area $=18\text{ sq cm}$ and a horizontal arrow shows its width $=5\text{ cm}$. Find the width of the small pink rectangle sitting above the left large rectangle (labelled “? cm”).
Solution (d):
Right small rectangle width $=5\text{ cm}$ and area $=18\text{ sq cm}$, so its height $= \dfrac{18}{5} = 3.6\text{ cm}$.
The large left rectangle's height is the small-right height plus the vertical difference $4\text{ cm}$, so large left height $= 3.6 + 4 = 7.6\text{ cm}$.
Since the large left rectangle area $=38\text{ sq cm}$, its width $= \dfrac{38}{7.6} = 5\text{ cm}$.
The small pink rectangle above the large left rectangle has the same width as the large left rectangle, so the required length is $5\text{ cm}$.
Answer (d): ? = $5\text{ cm}$.
Final summary of answers:
(a) bottom-right area = $\;30\text{ sq cm}$.
(b) pink square area = $\;9\text{ sq cm}$.
(c) top-left pink area = $\;16\text{ sq cm}$.
(d) required length = $\;5\text{ cm}$.
Figure it Out (Page 149)
Question 1. Give the dimensions of a rectangle whose area is the sum of the areas of these two rectangles having measurements: 5 m × 10 m and 2 m × 7 m.
Answer:
Given:
Dimensions of the first rectangle are $5 \text{ m} \times 10 \text{ m}$.
Dimensions of the second rectangle are $2 \text{ m} \times 7 \text{ m}$.
To Find:
The dimensions of a new rectangle whose area is the sum of the areas of the two given rectangles.
Solution:
First, we need to calculate the area of each of the two given rectangles. The formula for the area of a rectangle is Area = Length × Breadth.
Area of the first rectangle ($A_1$):
$A_1 = 5 \text{ m} \times 10 \text{ m} = 50 \text{ m}^2$
... (i)
Area of the second rectangle ($A_2$):
$A_2 = 2 \text{ m} \times 7 \text{ m} = 14 \text{ m}^2$
... (ii)
Next, we find the total area for our new rectangle ($A_{new}$) by adding the areas of the first two rectangles.
$A_{new} = A_1 + A_2$
$A_{new} = 50 \text{ m}^2 + 14 \text{ m}^2 = 64 \text{ m}^2$
... (iii)
Now, we need to find the dimensions (Length × Breadth) for a rectangle that has an area of $64 \text{ m}^2$. There are many possible pairs of numbers that multiply to give 64.
Some possible integer dimensions are:
- $1 \text{ m} \times 64 \text{ m}$
- $2 \text{ m} \times 32 \text{ m}$
- $4 \text{ m} \times 16 \text{ m}$
- $8 \text{ m} \times 8 \text{ m}$ (This is a square, which is a special kind of rectangle)
Answer:
The total area of the new rectangle is $64 \text{ m}^2$. Any pair of dimensions that multiply to 64 is a correct answer.
For example, the dimensions could be 16 m × 4 m or 8 m × 8 m.
Question 2. The area of a rectangular garden that is 50 m long is 1000 sq m. Find the width of the garden.
Answer:
Given:
Length of the rectangular garden (l) = $50 \text{ m}$.
Area of the rectangular garden (A) = $1000 \text{ m}^2$.
To Find:
The width of the garden (w).
Solution:
We know that the formula for the area of a rectangle is:
Area = Length $\times$ Width
Let's put the given values into this formula:
$1000 \text{ m}^2 = 50 \text{ m} \times \text{Width}$
... (i)
To find the width, we need to rearrange the formula. We can do this by dividing the area by the length.
Width = $\frac{\text{Area}}{\text{Length}}$
Width = $\frac{1000 \text{ m}^2}{50 \text{ m}}$
To simplify the fraction, we can cancel a zero from both the numerator and the denominator.
Width = $\frac{100}{5} \text{ m}$
Width = $20 \text{ m}$
Answer:
The width of the garden is 20 m.
Question 3. The floor of a room is 5 m long and 4 m wide. A square carpet whose sides are 3 m in length is laid on the floor. Find the area that is not carpeted.
Answer:
Given:
Dimensions of the rectangular floor: Length = $5 \text{ m}$, Width = $4 \text{ m}$.
Side length of the square carpet = $3 \text{ m}$.
To Find:
The area of the floor that is not covered by the carpet.
Solution:
To solve this, we will first find the total area of the room's floor. Then, we will find the area of the carpet. Finally, we will subtract the carpet's area from the floor's area.
Step 1: Calculate the area of the floor.
The floor is a rectangle, so we use the formula: Area = Length × Width.
Area$_{\text{floor}} = 5 \text{ m} \times 4 \text{ m} = 20 \text{ m}^2$
... (i)
Step 2: Calculate the area of the carpet.
The carpet is a square, so we use the formula: Area = Side × Side.
Area$_{\text{carpet}} = 3 \text{ m} \times 3 \text{ m} = 9 \text{ m}^2$
... (ii)
Step 3: Find the area of the floor not covered by the carpet.
We subtract the area of the carpet from the total area of the floor.
Uncarpeted Area = Area$_{\text{floor}}$ - Area$_{\text{carpet}}$
Uncarpeted Area = $20 \text{ m}^2 - 9 \text{ m}^2 = 11 \text{ m}^2$
Answer:
The area of the floor that is not carpeted is 11 m².
Question 4. Four flower beds having sides 2 m long and 1 m wide are dug at the four corners of a garden that is 15 m long and 12 m wide. How much area is now available for laying down a lawn?
Answer:
Given:
Dimensions of the rectangular garden: Length = $15 \text{ m}$, Width = $12 \text{ m}$.
Dimensions of each of the 4 flower beds: Length = $2 \text{ m}$, Width = $1 \text{ m}$.
To Find:
The area available for laying a lawn.
Solution:
To find the area for the lawn, we first need to calculate the total area of the garden. Then, we will calculate the total area taken up by the four flower beds and subtract it from the garden's area.

Step 1: Calculate the total area of the garden.
The garden is a rectangle, so we use the formula: Area = Length × Width.
Area$_{\text{garden}} = 15 \text{ m} \times 12 \text{ m} = 180 \text{ m}^2$
... (i)
Step 2: Calculate the total area of the four flower beds.
First, find the area of one flower bed:
Area$_{\text{one bed}} = 2 \text{ m} \times 1 \text{ m} = 2 \text{ m}^2$
Since there are four identical flower beds, we multiply this area by 4:
Area$_{\text{total beds}} = 4 \times 2 \text{ m}^2 = 8 \text{ m}^2$
... (ii)
Step 3: Find the area available for the lawn.
Subtract the area of the flower beds from the total area of the garden.
Area$_{\text{lawn}} = \text{Area}_{\text{garden}} - \text{Area}_{\text{total beds}}$
Area$_{\text{lawn}} = 180 \text{ m}^2 - 8 \text{ m}^2 = 172 \text{ m}^2$
Answer:
The area available for laying down a lawn is 172 m².
Question 5. Shape A has an area of 18 square units and Shape B has an area of 20 square units. Shape A has a longer perimeter than Shape B. Draw two such shapes satisfying the given conditions.
Answer:
Given:
Area of Shape A = $18$ square units.
Area of Shape B = $20$ square units.
The condition is: Perimeter of Shape A > Perimeter of Shape B.
To Do:
Find dimensions for two rectangles that satisfy these conditions and describe how to draw them.
Solution:
The key idea here is that for a fixed area, long and thin rectangles have a much larger perimeter than rectangles that are more square-like. We will try to find a long, thin rectangle for Shape A and a more compact, square-like rectangle for Shape B.
Let's list the possible integer dimensions and perimeters for each shape. (Perimeter = 2 × (Length + Width))
For Shape A (Area = 18 sq units):
| Dimensions | Perimeter Calculation | Perimeter |
| 1 unit × 18 units | 2 × (1 + 18) = 38 units | 38 units |
| 2 units × 9 units | 2 × (2 + 9) = 22 units | 22 units |
| 3 units × 6 units | 2 × (3 + 6) = 18 units | 18 units |
For Shape B (Area = 20 sq units):
| Dimensions | Perimeter Calculation | Perimeter |
| 1 unit × 20 units | 2 × (1 + 20) = 42 units | 42 units |
| 2 units × 10 units | 2 × (2 + 10) = 24 units | 24 units |
| 4 units × 5 units | 2 × (4 + 5) = 18 units | 18 units |
Now we need to pick one option from each table so that Perimeter(A) > Perimeter(B). Let's pick the long, thin Shape A and the compact Shape B that we highlighted.
- Shape A: Dimensions 1 unit × 18 units. Its perimeter is 38 units.
- Shape B: Dimensions 4 units × 5 units. Its perimeter is 18 units.
Let's check the conditions: Area(A) is 18, Area(B) is 20, and Perimeter(A) (38) is greater than Perimeter(B) (18). This works!
Answer:
One possible solution is:
Shape A: A rectangle with dimensions 1 unit × 18 units.

Shape B: A rectangle with dimensions 4 units × 5 units.

Question 6. On a page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides. What is the perimeter of the border?
Answer:
Given:
Margin from top edge = $1 \text{ cm}$.
Margin from bottom edge = $1 \text{ cm}$.
Margin from left edge = $1.5 \text{ cm}$.
Margin from right edge = $1.5 \text{ cm}$.
To Find:
The perimeter of the border.
Solution:
The perimeter of the border depends on the size of the book page, which is not given. To solve this, you need to first measure the length and width of your book page.
Let's assume we measure a page and find its dimensions. We can then calculate the border's dimensions.
Example Calculation:
Suppose your book page has a Length (L) of 25 cm and a Width (W) of 20 cm.
Step 1: Find the length of the border.
The border is 1 cm away from the top and 1 cm from the bottom. So, we subtract both margins from the total page length.
Length of border = Page Length - Top Margin - Bottom Margin
$= 25 \text{ cm} - 1 \text{ cm} - 1 \text{ cm} = 23 \text{ cm}$
Step 2: Find the width of the border.
The border is 1.5 cm away from the left and 1.5 cm from the right. So, we subtract both margins from the total page width.
Width of border = Page Width - Left Margin - Right Margin
$ = 20 \text{ cm} - 1.5 \text{ cm} - 1.5 \text{ cm} = 17 \text{ cm}$
Step 3: Calculate the perimeter of the border.
Now we use the perimeter formula: Perimeter = 2 × (length + width).
Perimeter of border = 2 × (23 cm + 17 cm)
$ = 2 \times (40 \text{ cm})$
$ = 80 \text{ cm}$
Answer:
The perimeter cannot be calculated without knowing the dimensions of the book page. You must first measure the length and width of your page and then follow the steps above.
For an example page of 25 cm × 20 cm, the perimeter of the border would be 80 cm.
Question 7. Draw a rectangle of size 12 units × 8 units. Draw another rectangle inside it, without touching the outer rectangle that occupies exactly half the area.
Answer:
Given:
Dimensions of the outer rectangle are 12 units × 8 units.
An inner rectangle must be drawn inside it without touching, and its area must be half the area of the outer rectangle.
To Do:
Find the dimensions of a suitable inner rectangle and describe how to draw it.
Solution:
We will solve this in a few simple steps.
Step 1: Calculate the area of the outer rectangle.
The formula for area is Area = Length × Width.
Area$_{\text{outer}} = 12 \text{ units} \times 8 \text{ units} = 96$ square units
... (i)
Step 2: Calculate the required area for the inner rectangle.
The problem states that the inner rectangle's area should be half of the outer one.
Area$_{\text{inner}} = \frac{\text{Area}_{\text{outer}}}{2} = \frac{96}{2} = 48$ square units
... (ii)
Step 3: Find suitable dimensions for the inner rectangle.
We need to find a length and width that multiply to 48. Also, to fit inside the 12 × 8 rectangle without touching, the length must be less than 12 and the width must be less than 8.
Let's try a few pairs that multiply to 48:
- 4 × 12: Cannot be used because 12 is not less than 12.
- 3 × 16: Cannot be used because 16 is not less than 12.
- 6 × 8: This is a great choice! Length = 8 units (which is < 12) and Width = 6 units (which is < 8).
So, we will use an inner rectangle with dimensions 8 units × 6 units.
Answer and Drawing Instructions:
1. First, draw the outer rectangle with a length of 12 units and a width of 8 units.
2. Inside it, draw the inner rectangle with a length of 8 units and a width of 6 units.
3. To make sure it doesn't touch, center it. Leave a gap of 2 units on the left and right sides ($12 - 8 = 4$, and $4 \div 2 = 2$). Leave a gap of 1 unit on the top and bottom ($8 - 6 = 2$, and $2 \div 2 = 1$).

Question 8. A square piece of paper is folded in half. The square is then cut into two rectangles along the fold. Regardless of the size of the square, one of the following statements is always true. Which statement is true here?
a. The area of each rectangle is larger than the area of the square.
b. The perimeter of the square is greater than the perimeters of both the rectangles added together.
c. The perimeters of both the rectangles added together is always $1\frac{1}{2}$ times the perimeter of the square.
d. The area of the square is always three times as large as the areas of both rectangles added together.
Answer:
Given:
A square is cut in half along a fold, creating two identical rectangles.
To Find:
The statement that is always true.
Solution:
Let's test this with a simple example first, and then we can prove it for any square.
Example: Using a 10 cm × 10 cm square

- Original Square:
Side = 10 cm
Area = $10 \times 10 = 100$ cm²
Perimeter = $4 \times 10 = 40$ cm
- Two New Rectangles:
When we cut the square, we get two rectangles, each with dimensions 10 cm × 5 cm.
Perimeter of one rectangle = $2 \times (10 + 5) = 2 \times 15 = 30$ cm.
Total perimeter of both rectangles added together = $30 + 30 = 60$ cm.
Now let's check the statements with our example numbers:
a. Is the area of one rectangle (50 cm²) larger than the square's area (100 cm²)? False.
b. Is the square's perimeter (40 cm) greater than the total perimeter of the rectangles (60 cm)? False.
c. Is the total perimeter of the rectangles (60 cm) equal to $1\frac{1}{2}$ times the square's perimeter?
$1\frac{1}{2} \times 40 \text{ cm} = 1.5 \times 40 \text{ cm} = 60 \text{ cm}$.
Yes, $60 = 60$. This statement is True.
d. Is the square's area (100 cm²) three times the total area of the rectangles (100 cm²)? False.
General Proof (for any square with side 's')
- Square Perimeter: $4s$
- Rectangle Dimensions: $s \times \frac{s}{2}$
- Perimeter of one rectangle: $2 \times (s + \frac{s}{2}) = 2 \times (\frac{3s}{2}) = 3s$
- Total perimeter of both rectangles: $3s + 3s = 6s$
Let's check statement (c):
Total perimeter of rectangles = $1\frac{1}{2} \times$ Perimeter of square
$6s = 1.5 \times (4s)$
$6s = 6s$
This is always true, no matter the size of the square.
Answer:
The statement that is always true is:
c. The perimeters of both the rectangles added together is always $1\frac{1}{2}$ times the perimeter of the square.

